Shock growth of ice crystal near equilibrium melting pressure under dynamic compression

Significance

Crystal growth and morphological transitions are crucial for fundamental science and wide applications. Nevertheless, their mechanisms under local nonequilibrium growth condition are unclear due to severe interference of thermal and mass transports on the interplay between thermodynamic driving force and interface kinetics. Here, we reveal the origin of the pressure-induced 2D shock growth of ice VI crystal by using dynamic compression, in which a dimensional transition from 3D to 2D is observed. Unlike generally expected, the 2D shock growth occurs from 3D crystal edges rather than from its corners upon fast compression, even near equilibrium growth condition. This is due to similar interface structure to the crystal edge plane facilitating the fast interface kinetics under local nonequilibrium growth.

Abstract

Crystal growth is governed by an interplay between macroscopic driving force and microscopic interface kinetics at the crystal–liquid interface. Unlike the local equilibrium growth condition, the interplay becomes blurred under local nonequilibrium, which raises many questions about the nature of diverse crystal growth and morphological transitions. Here, we systematically control the growth condition from local equilibrium to local nonequilibrium by using an advanced dynamic diamond anvil cell (dDAC) and generate anomalously fast growth of ice VI phase with a morphological transition from three- to two-dimension (3D to 2D), which is called a shock crystal growth. Unlike expected, the shock growth occurs from the edges of 3D crystal along the (112) crystal plane rather than its corners, which implies that the fast compression yields effectively large overpressure at the crystal–liquid interface, manifesting the local nonequilibrium condition. Molecular dynamics (MD) simulation reproduces the faster growth of the (112) plane than other planes upon applying large overpressure. Moreover, the MD study reveals that the 2D shock crystal growth originates from the similarity of the interface structure between water and the (112) crystal plane under the large overpressure. This study provides insight into crystal growth under dynamic compressions, which makes a bridge for the unknown behaviors of crystal growth between under static and dynamic pressure conditions.

In nature, one has observed tremendous fascinating crystal morphologies, like snowflakes (1, 2). Aside from its beauty, understanding the formation of crystal morphology and its transitions are essential for designing mechanical (e.g., deformation, yielding, strength, fracture, and toughness) and biological (e.g., pharmacological, reactivity, hydroactivity) properties in metallurgy (3, 4) and biology (5, 6), respectively.

In general, the crystal growth and morphology are mainly determined by an interplay between macroscopic thermodynamic driving forces and microscopic kinetic process taking place at a crystal–liquid interface. While the crystal growth is well understood near local-equilibrium growth condition in terms of the interplay (7–11), the formation and transition of diverse crystal morphologies remain poorly understood under local non- or far-from-equilibrium growth conditions, such as zigzag growth in 2D (12, 13), rapid or burst-like growth of helium crystal (14–16), ice crystals (17), and alloys (18). These anomalous growth behaviors imply that the local equilibrium condition at the crystal–liquid interface is disturbed by sudden application of a large driving force. While theoretical (19–21) and simulation (22, 23) studies have reported that both the interface kinetics and the thermodynamic driving forces indeed play a key role in morphological transitions and anomalously fast growth under nonequilibrium conditions, many experimental discoveries remain unexplained due to technical challenges of accessing the local nonequilibrium or far-from-equilibrium conditions on a consistent basis (9, 12–18). This is particularly true for applying the rate-dependent driving force, like cooling rate (13), yielding large driving force, since it evidently accompanies inherent thermal or concentration gradient due to the thermal and mass transport phenomena, causing time delay and spatial inhomogeneity of the physical events during experimental procedures. Thus, it ultimately affects interface kinetics.

The interference of a large driving force with interface kinetics may be resolved by adopting pressure as a driving parameter, since controlling pressure provides immediate and homogeneous change of an entire system under a hydrostatic condition. In addition, a huge driving force imparted by dynamic pressure (e.g., shock impact or meteor crash) can lead to rich crystallization behaviors under nonequilibrium conditions. Recently, intensive interest in pressure-induced crystal nucleation and growth has emerged in the fields of static- (14–16, 24–26) and dynamic compression (i.e., shock compression) (17, 27–32). Remarkably, the application of dynamic pressure could generate unexpected crystal growth behaviors, such as burst-like and oscillation growths in helium crystal with small overpressure even near equilibrium melting pressure (14–16). Moreover, a high compression rate changes ice crystal morphology from 3D to 2D with anomalously fast growth, and facet to dendritic growth (17). For over two decades, many experimental and theoretical studies (13, 18–21) have speculated that such anomalous growth kinetics and abrupt transitions in morphologies under rate-dependent driving forces are attributed to a dynamical mechanism. However, such phenomena and their exact nature remain still elusive.

Here, we manipulate the growth condition from (local) equilibrium to local nonequilibrium by using a dynamic diamond anvil cell (dDAC) technique (17, 27–29), and generate an anomalously fast crystal growth of the ice VI phase with a morphological transition from 3D to 2D, hereafter referred to as a shock crystal growth. The shock crystal growth is expected by a geometric model (33), showing discontinuous behavior of crystal growth when two or more facets meet at the same position at the same time (17, 24, 33). Moreover, we reveal the origin of the shock crystal growth using dDAC experiment and molecular dynamics (MD) simulation; surprisingly, the shock crystal growth originates from the 3D crystal edges rather than its corners under fast compression. In addition, the rapid growth of the 2D crystal formed even at small overpressure (i.e., near equilibrium melting pressure of ice VI phase) implies that the fast compression builds “effectively” large overpressure and affects fast interface kinetics in the vicinity of the 3D crystal edges. The MD simulation confirms that the interface structure of the edge plane is considerably similar to that of the bulk crystal compared with other planes under large overpressure, which causes fast interface kinetics. Ultimately, our findings provide a fundamental basis toward accessing the local nonequilibrium growth condition and a bridge for understanding various crystal growth phenomena between static (equilibrium) and dynamic (nonequilibrium) growth conditions.

Results

Anomalous Transitions in Growth Morphology and Speed.

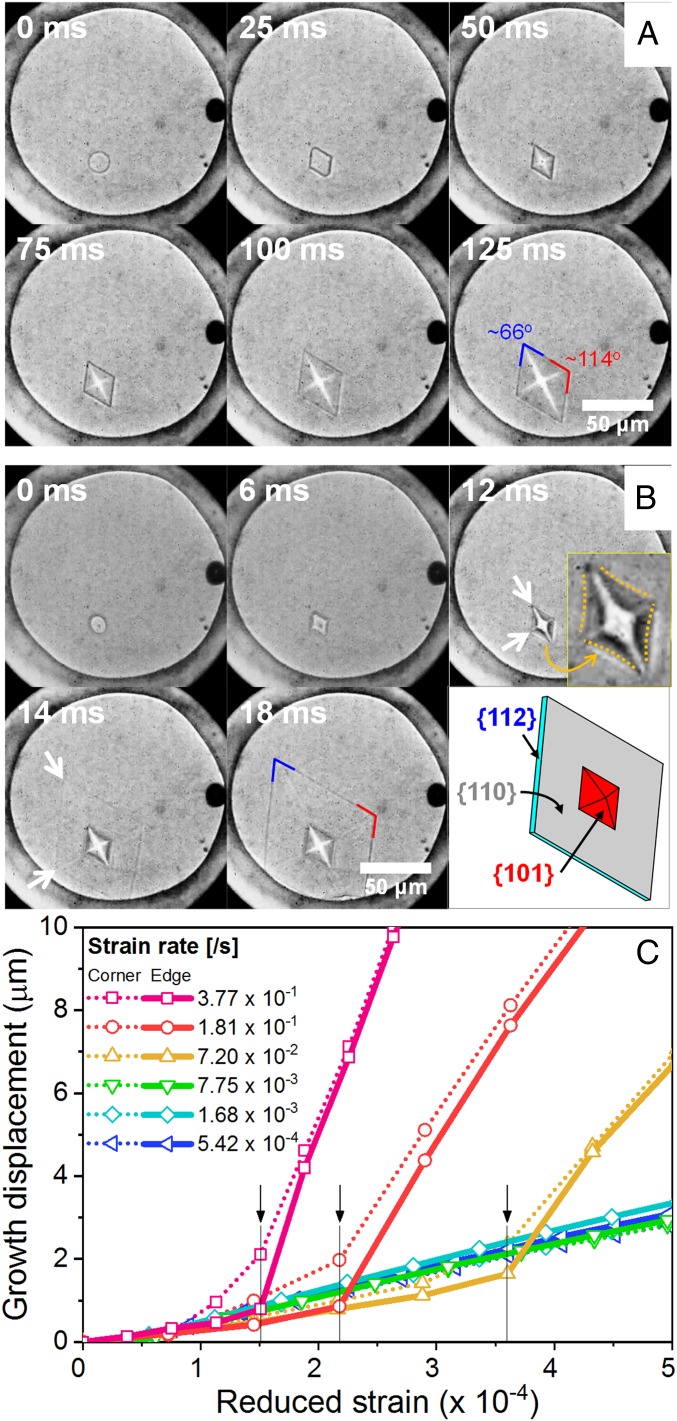
Fig. 1 shows the growth behavior of an ice VI crystal as a function of compression rate [i.e., strain rate ${\dot{\epsilon }}_v$, defined by Δl/l_o per time, where Δl and l_o are compressed displacement and initial thickness of the gasket cell, respectively (see SI Appendix for the details)]. A roughened ice VI crystal coexists with liquid water at an equilibrium melting pressure of 0.96 GPa within a gasket hole which is sealed by two diamond anvils. When the system is compressed slowly by the anvils at a rate less than ∼0.01/s, the ice grows slowly and the shape of the crystal shows a roughening to faceting transition (see the images from 0 to 50 ms in Fig. 1A). Then, the ice crystal continuously grows in the 3D faceted morphology, as expected (Fig. 1A). However, fast compression (≥ ∼0.1/s) yields a dramatic change in growth behavior (Fig. 1B); after faceting, the crystal corners protrude, and the crystal edges and faces form negative curvature signaling surface instability (Fig. 1B, Inset). Subsequently, the crystal plane (112) grows abruptly, like a thin film (see the images at 14 and 18 ms in Fig. 1B). A thickness of the 2D ice crystal is estimated to be ∼130 nm by simultaneously tracing the crystal growth dimension along two different growth modes of 3D and 2D and change of the gasket thickness (SI Appendix, Fig. S5). Interestingly, we observe that the faceting has not completed at all corners at the same time along in-plane and vertical directions; even under slow strain rate (or nearly hydrostatic pressure condition), the faceting along the in-plane direction is finished earlier than that along the vertical direction. This may underlie the 2D shock crystal growth along the in-plane direction only (see the detailed discussion in SI Appendix). In addition, the corner protrusion does not evolve into the dendrite, which implies that latent heat by crystal growth may not be a crucial factor of this 2D shock growth.

Fig. 1.

Evolution of crystal morphologies under (A) low compression strain rate less than ∼0.01/s and (B) high compression strain rate above ∼0.1/s. The corner angles of an ice VI crystal are ∼66° and ∼114°, indicating that the crystal is covered with {101} planes (SI Appendix, Fig. S3). A black particle at the right of the gasket hole is a ruby chip, used as a pressure marker. Surface instability is observed [Fig. 1B, Inset (12 ms)] and abruptly grown 2D crystal boundary is marked with arrows (14 ms). Schematic of the shock crystal growth is drawn with plane indices in Fig. 1B. (C) Crystal growth displacement along corner and edge directions as a function of strain. Growth displacement rapidly increases at the moment forming 2D shock growth from 3D facet growth (marked by arrows). The SD of the whole reduced strain is ±8.70 × 10⁻⁴.

Growth displacements of the 2D shock growth as a function of reduced strain (${\epsilon }_v={\dot{\epsilon }}_v\cdot t_{comp}$, where the compression time $t_{comp}$ is the elapsed time, taking from the start to the end of pressure change on compression) are different from those of the 3D crystal growth (Fig. 1C). As the strain rate increases, the deviation of the growth displacement from the 3D growth occurs early as marked by arrows in Fig. 1C. During the formation of the negative curvature, the corner grows faster than the edge, making it possible to expect that the corner will lead the crystal growth. However, upon the shock crystal growth, the growth displacement along the edge direction of the facet crystal shows an abrupt increase, of which the feature lacks along the corner direction. Contrary to general expectation, this observation implies that the shock crystal growth is initiated from the crystal edges.

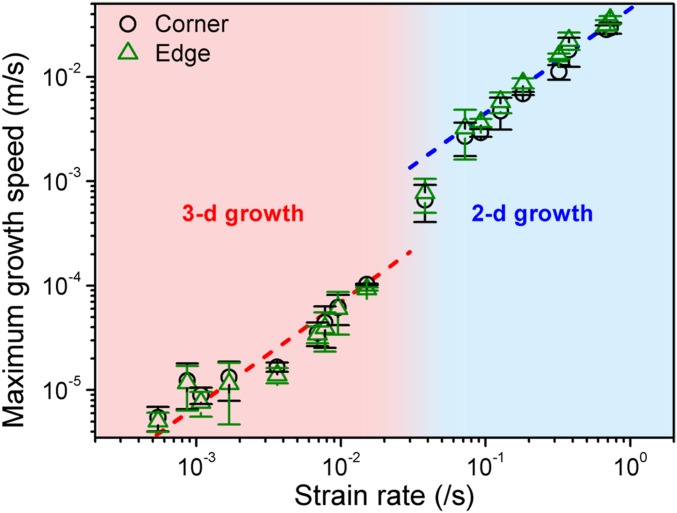
Fig. 2 shows the maximum growth speed as a function of strain rate. The growth speed increases for the strain rates less than ∼0.01/s, in which the 3D growth of the ice crystal is observed. Then, the growth speed increases by an order of magnitude under fast compression, accompanying the morphological transition. While a burst-like or rapid growth behavior has been reported for helium crystal (14–16), organic glasses (34), and colloidal crystals (22, 23), the dimensional transition from 3D to 2D crystal has never been observed as a function of compression rate. The dramatic changes in both morphology and growth speed imply that the local equilibrium growth condition at the crystal–liquid interface is severely disturbed by the fast compression, and thus large driving force (i.e., overpressure) may be applied.

Fig. 2.

Maximum crystal growth speed of 3D and 2D growth as a function of strain rate. The dotted lines are for an eye guide; crystal growth speed are lower than 1 × 10⁻⁴ m/s below 0.015/s and higher than 2.7 × 10⁻³ m/s above 0.072/s, respectively, for the 3D and 2D growths.

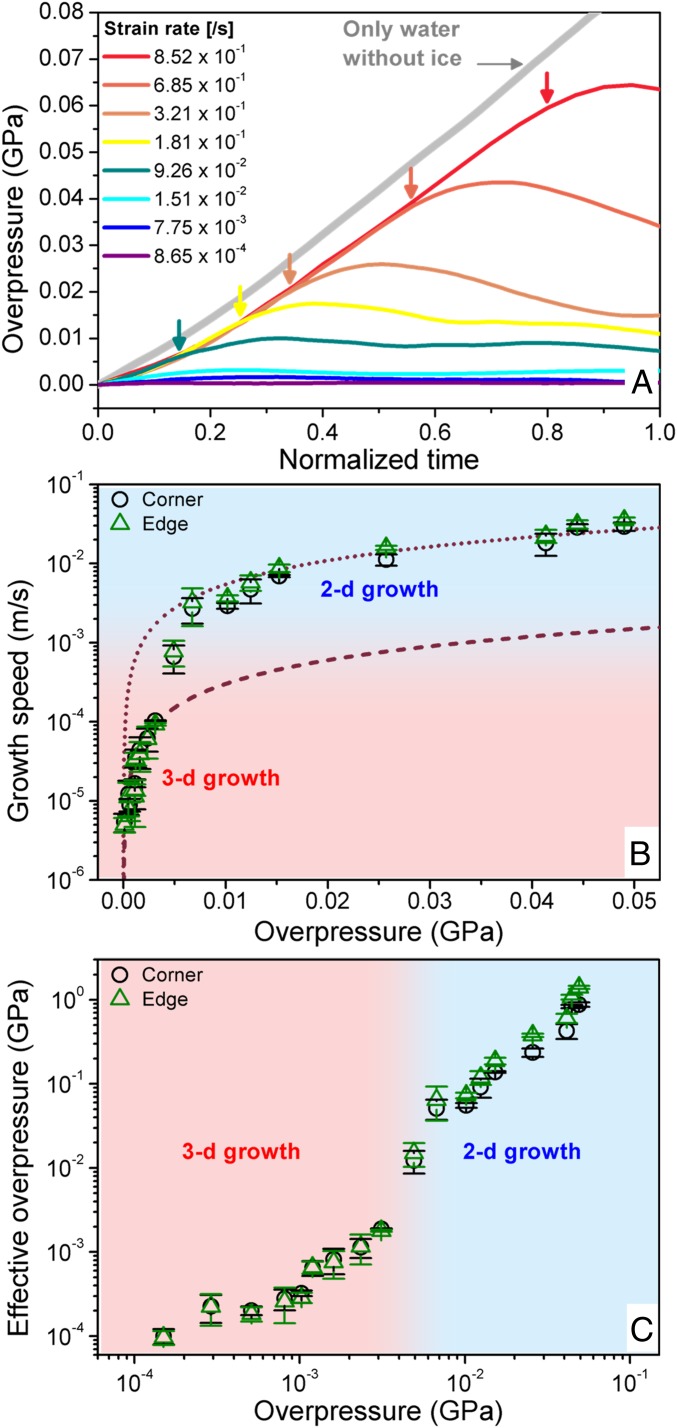
Accordingly, we carefully measured the pressure changes in the gasket cell during the dynamic compression (Fig. 3A). Slow compression produces small overpressurization (less than ∼0.005 GPa) which is kept nearly constant during compression. In other words, the local equilibrium growth condition is held during the 3D faceted crystal growth with slow compression. However, fast pressurization yields a transient increase of supercompression until the 2D shock growth occurs (marked by arrows), despite the presence of the ice crystal in liquid water. At the fastest compression rate of 0.852/s, the measured overpressure is ∼0.06 GPa. Surprisingly this overpressure introducing the shock growth is still small and close to the equilibrium melting pressure of ice VI.

Fig. 3.

(A) Measured overpressure of the entire system as a function of normalized time, which is compression time normalized by compression period (i.e., whole time period of compression step), with different strain rate. The overpressure increases with the strain rate until at the moment of the shock growth (marked as arrows). (B) Crystal growth speed as a function of overpressure for both 3D and 2D growths. Growth speeds of the crystal corners are fitted by Eq. 1 for estimating the kinetic prefactor. (C) Comparison of effective overpressure on the 3D crystal surface and the measured average overpressure. The effective overpressure can be estimated by finding the overpressure value corresponding to 3D growth speed equivalent to that of the 2D shock growth. Here the SD of pressure measurement is determined by ±2.8 MPa (see the details in SI Appendix).

The relation of the growth speed and the overpressure depicting the crystal growth is generally given by

$$v=v_{\text{o}}\left[1-\text{exp}\left(-\frac{\mathrm{\Delta }\text{G}}{k_{B}T}\right)\right],$$ [1]

where the driving Gibbs energy ΔG is ΔP·ΔV^l−s, ΔP is overpressure (= P − P_m, where P is externally applied pressure and P_m is melting pressure of ice VI), and ΔV^l−s is molar volume difference of liquid and crystal. ν_o is a kinetic prefactor, κ_B is the Boltzmann constant, and T is temperature. Fig. 3B shows the crystal growth speed with the overpressure which is measured in Figs. 2 and 3A. The whole growth speed data cannot be fitted with a single curve from Eq. 1. While the measured overpressure can reproduce the 3D growth speed with ν_o value of 0.0576 m/s, fitting the 2D growth speed requires a much larger value of ν_o (= 1.0436 m/s). Since the ν_o value is related to interface kinetics, the larger ν_o value indicates that the shock growth requires significantly enhanced interface kinetics.

Mechanism of the Shock Crystal Growth; Driving Force.

In general, fast growth speed can be explained with a large driving force, ΔG, as shown in Eq. 1. Since the 2D shock growth is initiated at the edges of the 3D crystal, the fast compression may induce effective overpressure near the 3D crystal surface, which is considerably greater than the measured overpressure in Fig. 3A. For instance, in Fig. 3B, the growth speed of ∼1.0 × 10⁻² m/s in the 2D crystal can be achieved in the 3D crystal growth, provided that a sufficiently large overpressure of 0.363 GPa is given. This pressure is significantly larger than the measured overpressure of ∼0.026 GPa for the entire system. We find that the growth speed of the 3D crystal can be equivalent to that of the 2D crystal if the overpressure is given by at least one order of magnitude higher than the average overpressure under fast compression (Fig. 3C). Ultimately, the fast compression may momentarily yield the effectively large overpressure at the crystal–liquid interface, if the compression time is faster than the time for rearrangement of water molecules near the crystal–liquid interface, causing the change in the interface kinetics, and thus enabling the anomalously fast 2D growth. In particular, we note that the 2D shock growth from the (112) plane of the 3D crystal shows a higher growth speed than other planes (Figs. 1 B and C and 2). This reflects that the local growth condition of the (112) plane may differ from those of other planes.

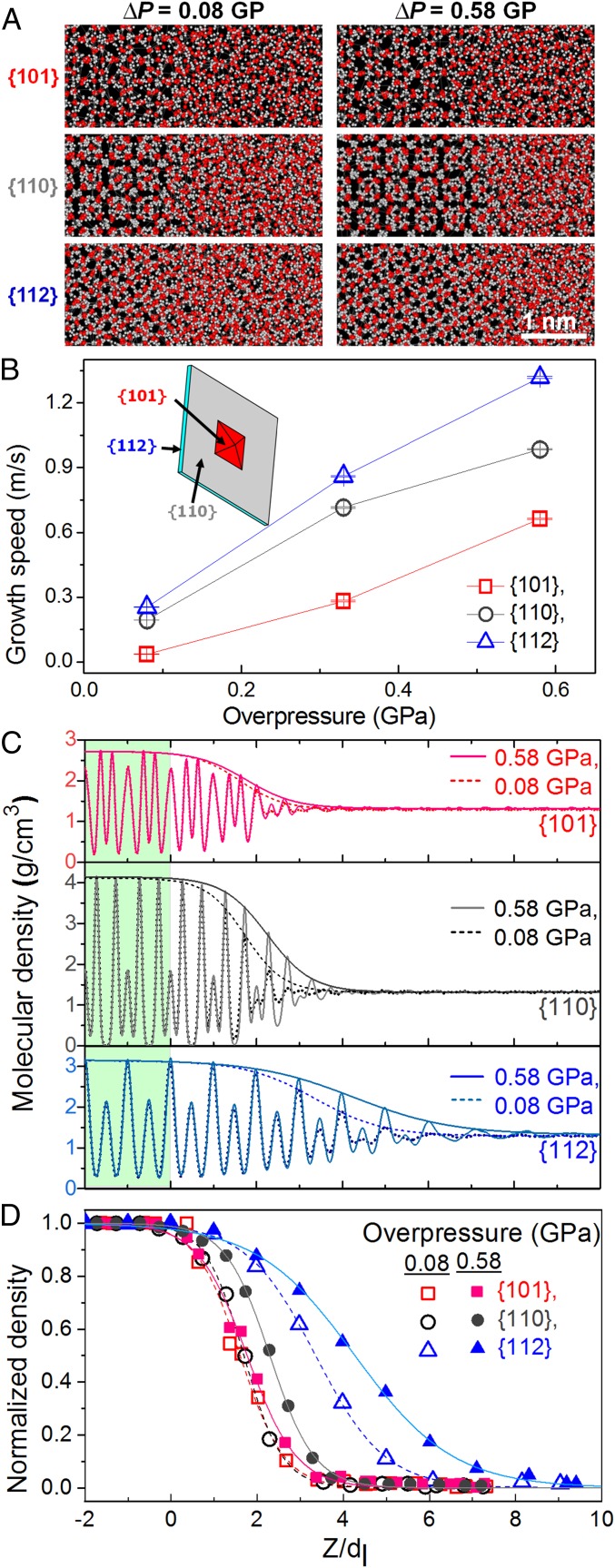
For more elaborate microscopic understanding of the physical situation at the crystal–liquid interface, MD simulation has been performed (see the details in SI Appendix). More specifically, why the (112) plane grows faster than other planes at a high strain rate, resulting in the 2D shock growth, should be addressed. We find an essential feature from the MD study that explains the origin of the unexpected fast growth mechanism of the ice, although it may not be directly compared with the experimental data due to the limitation in time- and size scales, and accuracy of the potential model.

Fig. 4 shows the crystal growth of ice VI on each crystal plane under different supercompression. The simulation is performed for low (0.08 GPa) and high (0.58 GPa) overpressures which mimic the effective overpressure conditions at the interface in the experiment. Using the transferable intermolecular potential 4-point/ice (35), the crystal growth speed is obtained along different crystal planes by taking the derivatives of potential energy change with time (25). As we expected, the growth speeds of three crystal planes are similar with small overpressure, 0.08 GPa, resulting in the growth of the 3D faceted crystal. However, the (112) plane shows much faster growth speed than other crystal planes under the large overpressure, 0.58 GPa (Fig. 4B). This result provides a plausible explanation for the 2D shock growth along the edge plane and is very consistent with our experimental findings shown in Figs. 1 and 3.

Fig. 4.

Simulation on crystal growth of each representative crystal plane in an ice VI crystal under overpressure of 0.08 and 0.58 GPa. (A) Snapshots at 0.5 ns of ice growing interface ahead of (101), (110), and (112) planes at both overpressures of 0.08 and 0.58 GPa. (B) Growth speed of each crystal plane as a function of overpressure. (Inset) Schematic of 3D and 2D crystal. (C) Density profiles of oxygen atoms from ice crystal to water in growing direction (see details in SI Appendix). An envelope plotting is overlapped on each density profile. (D) Normalized envelope is fitted with the scaled interface distance Z relative to the thickness of molecular layer, d_l of each crystal plane (25). Interface width of each crystal plane is quantitatively measured in terms of the so-called 10–90 interface width from the normalized density envelope, which is defined as the distance over which a normalized density parameter changes from 10 to 90% of the normalized crystal density of unity (36). While the interface width of the (110) plane increases from 1.97d_l(110) to 2.27d_l(110) with the increase of overpressure from 0.08 to 0.58 GPa, the (112)-plane interface shows a significant widening of interface from 3.54d_l(112) to 5.00d_l(112). Here the d_l values for (101), (110), and (112) planes are 0.424, 0.437, and 0.242 nm, respectively.

Mechanism of the Shock Crystal Growth: Interface Kinetics.

The MD simulation study showed that the growth along the (112) plane is indeed faster than along other planes when a large overpressure is applied to the crystal–liquid interface. This supports the effectively large overpressure in experiment, yielding the 2D shock growth behavior of the (112) plane on fast compression. However, the role of the interface kinetics on the 2D shock growth along the (112) plane still remains unclear. Here, we discuss the origin of the 2D shock crystal growth in the viewpoint of the interface kinetics.

Interface kinetics, an attaching or detaching movement of atoms or molecules on a crystal surface, is strongly affected by an interface structure between crystal and liquid. As well as crystal nucleation (27–32, 36–41), it has been reported that a similar interface structure to the crystal structure in its atomic periodicity and width can cause fast crystal growth (42). The interface structure may become a decisive factor for the fast kinetics for molecular crystal growth, if rearrangement speed of molecules arriving at the interface is compatible with the growth speed. Therefore, we here scrutinize the interface property to understand the fast interface kinetics.

Fig. 4C shows the interface structure of each representative plane which is normalized by its thickness of molecular layer for equivalent comparison (25). As well as more-broadened interface width of the (112) plane compared with those of other planes, the (112) plane under the large overpressure of 0.58 GPa shows significantly well-developed interface structure in molecular density, periodicity, and width, which is closer to its crystal structure (Fig. 4 C and D). The enhanced interface facilitates fast interface kinetics, leading to the 2D shock growth. Therefore, the fast compression yields effectively large overpressure ahead of the crystal edge plane until building the enhanced interface structure. This scenario may be applied to explain anomalous growth behaviors by cooling rate (12, 13) or abrupt pressure change (14–16) near equilibrium melting temperature or pressure, which have waited to be resolved.

Discussion

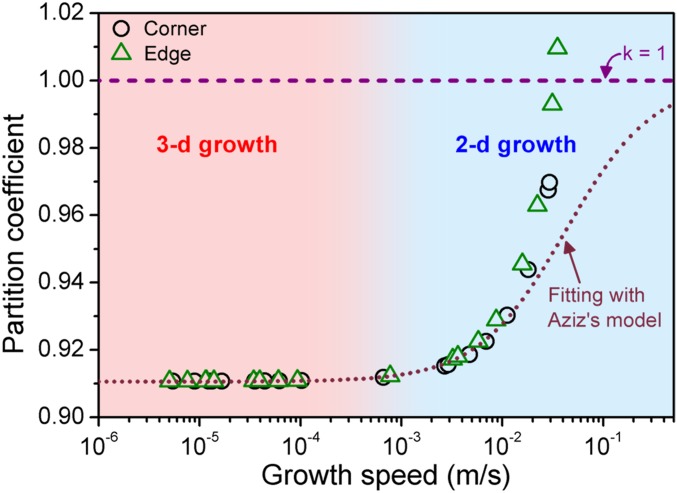
Under the local nonequilibrium growth condition, the abrupt change of the growth speed driven by a large driving force may cause different solute concentration ratio between liquid and crystal at the interface (19–21), which is described by the partition coefficient k. This implies the change of growth mechanism from diffusion to diffusionless process (7, 19–21). The Aziz model represents the relation of k and growth speed v, given by k = (k_eq + v/v_Di)/(1 + v/v_Di), where k_eq is the equilibrium partition coefficient of 0.91 at the equilibrium melting pressure of ice VI phase, v is the measured growth speed, and v_Di is the fitted characteristic speed for density trapping (∼0.04 m/s) (22, 23). For the case of pure substance and colloidal systems, the k definition is extended to characterize the density ratio between liquid and crystal at the interface, which can yield the density (or vacancy) trapping for the fast diffusionless growth (22, 23). Therefore, k is the density ratio of liquid water at effectively supercompressed state to ice VI at the equilibrium pressure [1.35 g/cm³ (43)]. In this study, we estimate the partition coefficient from the effective supercompression at the interface as shown in Fig. 3C. The effective overpressure is converted to the liquid density via the equation of state of water (44) and compared with density of the crystal (SI Appendix, Fig. S8B). Fig. 5 shows the partition coefficient as a function of the growth speed with a fitting curve based on the Aziz model (19). We find that the estimated partition coefficient deviates from the theoretical prediction for the growth speed higher than ∼10⁻² m/s. Contrary to the results from previous simulations (22, 23), the fast growth in this study starts just after the facet growth without a significant development of dendrite. As shown in Fig. 5, the density trapping (i.e., k = 1) occurs earlier than theoretically expected. The density-trapping effect by fast growth expects decreasing crystal density, increasing liquid density, and increasing crystal–liquid interface width in 2D colloidal growth (22, 23). However, the present study hardly shows the density change in crystal and liquid phase, except interface width. This discrepancy may be due to the anisotropic property of the crystal growth. A complete theoretical description for this phenomenon is still open to question.

Fig. 5.

Partition coefficient as a function of growth speed with fitting curves according to the Aziz model (19).

In the viewpoint of thermodynamic driving force and interface kinetics, we here studied the origin of the pressure-induced anomalous ice crystal growth, called shock growth, by using a dDAC technique. Such phenomenon is accompanied by a dimensional transition of morphology and anomalously fast growth speed as a function of compression rate. Under fast compression, the 2D shock growth is initiated from the edges of the 3D crystal rather than from its corners, although the measured overpressure of the entire system is still small. This implies the fast compression causes effectively large overpressure at the crystal edges. The MD simulation study shows that a large driving force leads to similar interface structure to the bulk crystal along the (112) plane, facilitating fast interface kinetics and thus resulting in 2D shock crystal growth. Our results open a way to investigate rate-dependent crystal growth and morphological transitions. In particular, the use of dynamic compression will stimulate theoretical development in crystal growths under local nonequilibrium conditions taking place at interior of the earth, planets, and meteorite impact, and also potential applications in pharmaceutical and biological fields.

Materials and Methods

Advanced dDAC Technique.

For studying ice crystal growth by controlling compression rate, we have developed an advanced dDAC technique which is combined with a Michelson interferometer for directly measuring a change in sample volume. The system is also equipped with a high-speed camera (Fastcam APX-RS, Photron Inc., a resolution of 512 × 512 pixels, and the frame speed of 60–10,000 frames per second) for observing crystal growth, and time-resolved micro-Raman spectrometers for recording system pressure and molecular bonding characteristics of sample simultaneously.

Sample Loading and Dynamic Compression for Crystal Growth.

Deionized water is loaded into a gasket hole with a diameter of ∼100–150 μm and a thickness of ∼30–50 μm sealed by two diamond anvils with a 300-μm culet. After forming an ice VI crystal by compressing the water, the dynamic crystal growth is studied by using piezoelectric actuators (PAHL 18/20; Piezosystem Jena Inc.) which are embedded in the dDAC body and push or pull the upper diamond anvil according to the waveform signal from a digital function generator. A trapezoidal shape function with a desired holding step is selected for dynamic pressure cycle to provide sufficient relaxation time between the dynamic ice growth and melting steps. The details appear in SI Appendix.

MD Simulation.

MD simulation with the TIP4P/ice potential model (35) is carried out to study ice VI crystal growth. Simulation works are performed for the (101), (110), and (112) crystal planes. Each simulation system consisted of a rectangular parallelepiped with 3D periodic boundary conditions. At the initial state, the ice–water interface is located at the one-third point of the rectangular–parallelepiped system to guarantee free advance of the interface into the wide water regime. For both (101) and (110) systems, bulk ice and water layers consist of 2,560 and 5,120 H₂O molecules, respectively. For the (112) system, bulk ice and water layers consist of 2,264 and 4,528 H₂O molecules, respectively. For further detail, refer to SI Appendix.