Facilitated Diffusion Mechanisms in DNA Base Excision Repair and Transcriptional Activation

Abstract

Preservation of the coding potential of the genome and highly regulated gene expression over the life span of a human are two fundamental requirements of life. These processes require the action of repair enzymes or transcription factors that efficiently recognize specific sites of DNA damage or transcriptional regulation within a restricted time frame of the cell cycle or metabolism. A failure of these systems to act results in accumulated mutations, metabolic dysfunction, and disease. Despite the multifactorial complexity of cellular DNA repair and transcriptional regulation, both processes share a fundamental physical requirement that the proteins must rapidly diffuse to their specific DNA-binding sites that are embedded within the context of a vastly greater number of nonspecific DNA-binding sites. Superimposed on the needle-in-the-haystack problem is the complex nature of the cellular environment, which contains such high concentrations of macromolecules that the time frame for diffusion is expected to be severely extended as compared to dilute solution. Here we critically review the mechanisms for how these proteins solve the needle-in-the-haystack problem and how the effects of cellular macromolecular crowding can enhance facilitated diffusion processes. We restrict the review to human proteins that use stochastic, thermally driven site-recognition mechanisms, and we specifically exclude systems involving energy cofactors or circular DNA clamps. Our scope includes ensemble and single-molecule studies of the past decade or so, with an emphasis on connecting experimental observations to biological function.

Graphical Abstract

1. INTRODUCTION

The most fundamental requirement of all biological processes is the collision of two or more particles to form a specific complex that gives rise to function. Higher-order requirements are that such complexes must form on a time scale that is compatible with life and at the right time and place inside a cell. Thus, every process in biology shares a diffusional step. Although Einstein derived the basic equations describing particle diffusion over 100 years ago,¹ the process is far more complex in the case of biological systems.

Complexity in the cellular environment can arise from several sources. Time-consuming nonspecific interactions between a protein and other macromolecules can increase the time frame for its initial collision with a specific partner. The time spent in nonspecifically bound states can be modulated by the high monovalent ion concentrations in the cell through electrostatic mechanisms.^2–6 In addition, the crowded environment of the cell—where as much as 40% of the volume is consumed by large molecules—impedes macroscopic diffusion over large distances and in principle reduces the frequency of collisions.^7–12 Although macromolecular crowding reduces macroscopic diffusion, it also has the general effect of shifting binding equilibria to favor low-volume complexes as compared to the free species (a favorable entropic effect) and creating low-viscosity cavities where rapid diffusion can occur.^13–15 Finally, in the case of DNA repair proteins and transcription factors that must locate their rare cognate sites in the context of billions of base pairs of noncognate DNA sites, nonspecific interactions with the DNA polymer can be used to localize the protein to its target macromolecule and reduce the target search from a three-dimensional (3D) to a one-dimensional (1D) problem. The role of the cellular environment and the utilization of nonspecific DNA interactions to reduce the search volume and facilitate the location of rare target sites in DNA (facilitated diffusion) are the focus of this review.

1.1. Scope of Review

There have been many excellent articles written in the last 15 years that review various experimental and theoretical aspects of facilitated diffusion on DNA chains (Table 1). Here we restrict our scope to the most quantitative experimental studies on mammalian DNA repair glycosylase enzymes and transcription factors that have appeared in roughly the past decade. We focus on these two protein classes not only because they have been well-studied but also because their properties are quite distinct and revealing of how the process of DNA translocation must be tuned to biological function. In this review, we specifically exclude theoretical studies and refer the reader to the theoretical reviews in Table 1 as a window into this literature. The experimental methods to interrogate facilitated diffusion can be broadly grouped into ensemble and single-molecule approaches. Although each approach provides a different vantage point on the process, it is nevertheless important that observations from both approaches point to a consistent mechanism. We also restrict the review to proteins that do not employ nucleotide energy factors and to structural interactions that do not involve fully encircling the DNA in a highly processive clamp mode of binding.^30–32 The exclusion of clamp proteins is justified by the fact that once the long-lived clamp is formed, only one-dimensional diffusion is possible and clamp proteins are usually associated with highly processive energy-coupled functions such as DNA replication and helicase-catalyzed duplex unwinding.^33,34 We hope that this review will be helpful by facilitating an understanding of the fundamental parameters that govern protein–DNA scanning as well as the most effective methods for quantitative characterization of these processes.

Table 1.

Reviews on Protein–DNA Translocation

year	scope	citation
2004	role of 1D diffusion in facilitating target-site search	Halford and Marko16
2009	how a protein searches for its site on DNA: the mechanism of facilitated diffusion	Mirny et al.17
2010	single-molecule studies of DNA repair factor target search	Gorman et al.18
2011	theoretical aspects of facilitated diffusion	Kolomeisky19
2012	speed and specificity in target search	Zabet and Adryan20
2012	theoretical perspective on target search speed	Sheinman et al.21
2012	role of disordered protein structures in target search	Vuzman and Levy22
2013	single-molecule methods to study facilitated diffusion	Monico et al.23
2013	single-molecule studies of target search in cells	Mueller et al.24
2017	single-molecule techniques to study transcription factor (p53) DNA translocation	Kamagata et al.25
2017	single-molecule techniques to study glycosylase DNA translocation	Lee and Wallace26
2018	NMR techniques to study protein–DNA translocation	Iwahara et al.27
2018	target search by single-strand DNA-binding protein	Antony and Lohman28
2018	visualizing transcription factor dynamics in living cells	Liu and Tjian29

1.2. General Principles of Facilitated Diffusion

1.2.1. Three-Dimensional Diffusion.

Facilitated diffusion of proteins on DNA (also known as DNA scanning or translocation) is reduced-dimension diffusion along a DNA chain that serves to decrease the search time of proteins for their target sites.^35–37 Facilitated diffusion starts after the initial encounter of a protein molecule with a DNA chain, which occurs by 3D diffusion through bulk solution. In a 3D search process without assistance from DNA chain translocation, the protein must roam the available volume (V) until its target site with radius r is encountered.^2,16 Intuitively, the target search time (t_search) under these conditions is proportional to the volume that must be searched and inversely related to the target size and diffusion constant (D₃, eq 1):¹⁶

$$t_{\text{search}}=V∕D_{3}r$$ (1)

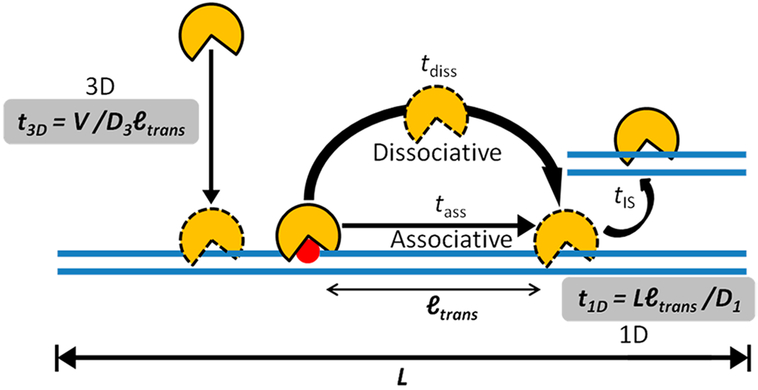
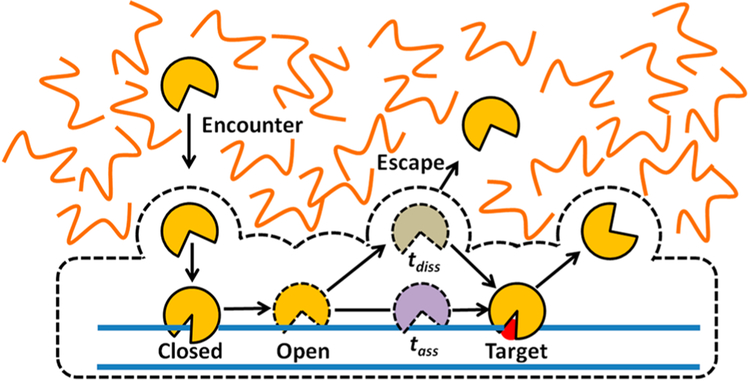
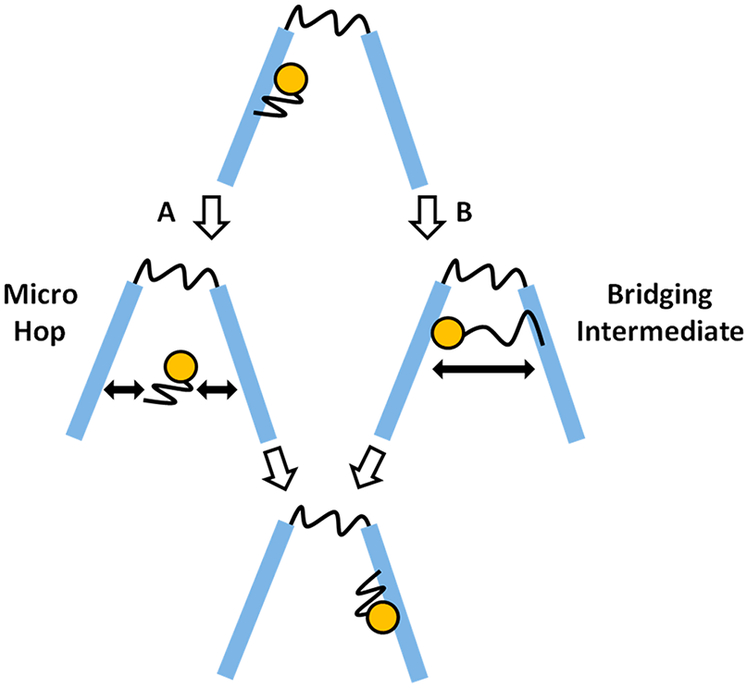
By this simple 3D search mechanism, an estimated search time of a few hours for a single-base-pair target site (r = 0.34 nm) may be calculated for a typical enzyme with a diameter of 5 nm in aqueous solution, with D₃ ≈ 100 μm²⋅s⁻¹ and a nuclear volume of ~100 μm³. The limitation of the 3D mechanism is that each encounter event only allows for a single DNA site to be probed and a large number of encounter events are required to search all base pairs in genomic DNA. Moreover, since nonspecific DNA sites are in much greater abundance than specific target sites, the vast majority of 3D encounter events involve landing on a nonspecific site. With no further mechanism for translocating along the DNA chain, t_search in the human nucleus would be prohibitively long due to weak binding and sequestration of proteins on nonspecific sites. To convert nonspecific binding into an asset for target-site location, proteins use three modes of facilitated diffusion on DNA (illustrated in Figure 1): associative chain transfers (which in some aspects resemble the process traditionally called DNA sliding) are described in section 1.2.2, dissociative chain transfers (which are synonymous with the traditional term DNA hopping) are covered in section 1.2.3, and intersegment transfers are discussed in section 1.2.4.

Figure 1.

Three- and one-dimensional processes involved in facilitated diffusion. Initial encounter with a DNA chain occurs by a 3D mechanism. Once a DNA chain is encountered two different 1D transfer mechanisms contribute to the overall translocation efficiency. These stochastic transfer mechanisms are called associative and dissociative (see text). For simplicity, the figure only depicts motion of the protein in one direction along the DNA chain. However, over a large number of transfer steps, the average direction of transfers is unbiased. Finally, when the density of DNA chains is very high (as in the cell nucleus), intersegmental (IS) transfers can frequently occur between DNA chains. The other terms in this figure are defined in the text and in eqs 1–4.

1.2.2. Associative Transfers on DNA (Sliding).

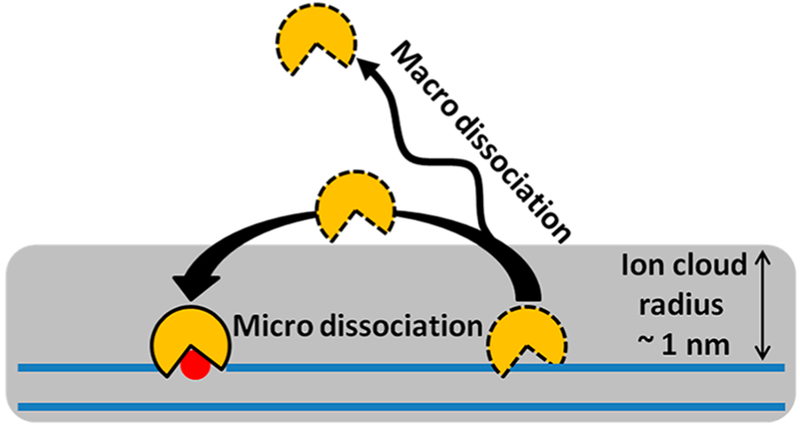
Associative transfers of a protein along a DNA chain keep the position of the protein and the DNA molecule correlated. Unlike free diffusion, associative transfer is kinetically a first-order process, where the protein stays associated with the DNA chain in a loose binding mode that allows movement (translocation) along the chain ^38,39 In the associative transfer state, the protein is still within the DNA ion cloud (~1 nm radius) but has lost the strong DNA interactions that are manifested in equilibrium binding measurements. The concept that associative transfers are not probed or reflected in equilibrium measurements is important. These transient excursions occur from the statically bound state that dominates equilibrium binding measurements and make up only a tiny fraction of the total bound population of the protein. Nevertheless, this transfer mode is advantageous in target-site location because it allows for near-continuous scanning of the DNA sequence. Associative transfers end when the protein takes a macro- or microdissociation step or finds its target site. A macrodissociation step leads to a sufficiently large distance separation between the protein and DNA that the protein is no longer spatially correlated with the DNA chain it just departed. In contrast, in a microdissociation step the protein remains spatially correlated with the DNA chain and frequently rebinds. The process of microdissociation and rebinding constitutes a dissociative transfer (hopping) event (Figure 1).

Several general mechanisms for sliding transfers along a DNA chain have been proposed, and each assumes the process is stochastic with no directional bias when averaged over many transfer steps (Figure 1). The simplest model is one of continuous protein tracking along a smooth electrostatic potential provided by the DNA phosphate backbone.⁴⁰ In this model, the protein is trapped by the low free energy of binding to a specific site when it is encountered. A more detailed model has been proposed that involves discrete states for associative transfers along the phosphate backbone.^3,41 In this model, translocation of a protein to adjacent sites at a step size of a single base pair is associated with breaking and reforming a hydrogen-bond network between the protein and DNA.⁴² Similar mechanisms have been proposed for tracking along the DNA major or minor grooves.^40,43,44 Much of the work on DNA glycosylases is not consistent with descriptions of sliding, because strict tracking along the DNA phosphate backbone or grooves for more than a few base pairs is not observed and the process has a two-dimensional (2D) component that may allow rolling on the surface of the DNA. Thus, the term associative transfer was coined to better account for the experimental observations. Experimental data that support these various mechanisms for translocation are described later in the context of individual DNA glycosylases and transcription factors.

Theoretical studies and most experimental measurements indicate that the optimal length of DNA for associative transfers is 10–100 bp, which is reasonable based on the facts that long stretches of protein-free genomic DNA are likely to be rare and that longer scanning lengths are associated with increased search times (see below).^{16, 19} Direct measurement of the microscopic 1D diffusion constants for associative and dissociative transfers on a DNA chain (D_ass and D_diss) have been challenging because these processes are difficult to spatially and temporally resolve.^39,45 Accordingly, a large range of apparent D₁ values have been reported (10⁴−10⁶ bp²⋅s⁻¹) that likely reflect the time-weighted averaging of associative and dissociative transfer events.^{3,25,44,46,47}

1.2.3. Dissociative Transfers on DNA (Hopping).

Like the associative pathway, dissociative transfers keep the protein and the DNA chain positionally correlated. Dissociative transfers involve microdissociation and rebinding events, and the protein leaves the electrostatic capture radius of the DNA (~1 nm), which we loosely define as the radial ion cloud around the DNA chain (Figure 2). Distinguishing dissociative from associative transfers is particularly challenging because the protein remains closely associated with the DNA in both transfer mechanisms. Thus, single-molecule imaging methods are not highly informative because the resolution is not sufficient to separate the two modes of transfer.⁴⁸ In ensemble experiments, dissociative transfers have been indirectly detected either by using small molecules that specifically trap the dissociated enzyme,³⁹ observing bypass of DNA-associated obstacles,^18,45,47 or detecting transfers when the target sites are placed on opposite strands of the DNA.^38,49 The biological advantage of dissociative transfers over the associative type is that bound proteins can be readily bypassed, and longer and faster diffusive steps can be taken by use of free diffusion near the DNA chain (~100 μm²⋅s⁻¹ for an average protein).

Figure 2.

Dissociative translocation involves microdissociation from the DNA chain. Many dissociation events of a protein from the DNA chain lead to rebinding before the protein moves outside the ion cloud surrounding the DNA. Such events are termed micro-dissociations and contribute to apparent 1D diffusion along the DNA chain (along with associative transfers). Dissociative transfers play an important role because the protein can diffuse freely in the vicinity of the DNA, whereas assocative transfers are slowed by weak intermolecular interactions with the DNA. Long-range (macro-) dissociative steps are also possible, which lead to escape of the protein from the vicinity of the DNA chain.

1.2.4. Intersegmental Transfers.

Intersegmental transfer (IS) between DNA chains occurs when a protein–DNA complex encounters another DNA chain.^50–53 This transfer mode is favored by the formation of a transient bridging intermediate, where the protein is bound to both DNAs simultaneously.^52,54–57 At that point, the protein may release the original DNA chain and transfer to the new DNA chain (Figure 1). Because binding of two DNA chains to a single protein is a favorable mode for intersegmental transfers, this mechanism is most efficient for proteins that have multiple DNA-binding subunits.^{3, 57–60} However, even monomeric proteins with only a single DNA-binding site can exhibit intersegment transfer, albeit less efficiently.^50,52 How a monomeric protein accomplishes such transfers with only a single DNA-binding site is unclear but it might be attributed to binding dynamics, where a partially dissociated protein is capable of loosely binding to two DNAs at the same time, or through microscopic hopping to the nearby second chain ⁵²

1.2.5. Efficient Target Search Requires One- and Three-Dimensional Steps.

As outlined above, neither 1D nor 3D diffusion in isolation serves as an effective target search mechanism. However, combining the two pathways provides a reasonable mechanism for an efficient and rapid search, which can be appreciated by considering eqs 2–4 (Figure 2):¹⁶

$$t_{\text{search}}=t_{3\mathrm{D}}+t_{1\mathrm{D}}+t_{\text{IS}}$$ (2)

$$t_{1\mathrm{D}}=t_{\text{ass}}+t_{\text{diss}}$$ (3)

$$t_{\text{search}}=V∕D_3{l}_{\text{trans}}+L{l}_{\text{trans}}∕D_1^{\text{app}}$$ (4)

(Equation 2 indicates that the overall search time (t_search) is the sum of the time the protein spends in the 1D, 3D, and intersegmental transfer search modes, and eq 3 states that the overall 1D search time is composed of the sum of associative and dissociative transfer times (t_ass and t_diss). For simplicity, the analysis below neglects the intersegmental transfer pathway because its contribution in cells depends on the local concentration of free DNA chains, which is unknown (i.e., the density of chains that are not bound by histones or other proteins). However, it is important to note that intersegment transfer is second-order with respect to DNA concentration, and it could become highly efficient in the human nucleus, where the concentration of DNA chains is high (~1 mM for 25 bp chain segments).³

The t_search time in eq 2 can be reduced in the presence of a 1D pathway because the target size is effectively increased to approximately the mean translocation distance (l_trans)¹⁶ rather than a single base pair (eq 4). Thus, if the enzyme lands within l_trans nanometers of its target site (Figure 1), it will find it by associative and dissociative chain translocation with high probability.As noted, l_trans consists of both associative and dissociative transfers and is estimated to fall in the range 10–100 bp (3.4–34 nm).^{3,16,54,61–63} The average length of the DNA that can be sampled in a translocation event (l_trans) will depend on the time that the protein spends in associative and dissociative transfer modes and on the respective diffusion constants for these modes (i.e., 〈l_trans〉 = √D_asst_ass + √D_disst_diss). It should be noted that because the protein is not bound to DNA during a dissociative transfer step, the diffusion constant (D_diss) is limited only by viscosity and thermal energy and is no different than diffusion through bulk solution (D₃ ≈ 100 μm²⋅s⁻¹). In contrast, D_ass has an increased frictional component arising from weak interactions of the protein with the DNA chain, and its contribution to D₁^app makes D₁^app < D₃ (eq 4). Accordingly, the second term in eq 4 defines the time it takes to translocate over an entire DNA chain of length L, using an apparent 1D search velocity of D₁^app/l_trans. Note that an optimal value for l_trans (~10–100 bp) is required in eq 4 because of its opposing effects on the first and second terms and D₁^app < D₃.^3,16,19 In many experimental measurements that will be described, D₁^app is about (1/1000) D₃.

1.3. Diffusion in Crowded Environments

The human intracellular environment is distinct from the solution conditions typically used to study proteins in the laboratory and is anticipated to have a profound effect on the diffusive properties of a macromolecule. Some relevant aspects of the cellular environment are high ion concentrations,⁶⁴ lower dielectric constant,⁶⁵ and higher macroscopic viscosity brought about by the high concentration of macromolecules that consume available volume (molecular crowding).^10,66,67 The concentration of macromolecules in human cells is estimated in the range 100–300 mg/mL,^68,69 which means that as much as 40% of the total cellular volume is consumed by large molecules. The volume occupied by macromolecules is often referred to as the excluded volume, because it is unavailable for free diffusion. It is expected that the increased macroscopic viscosity brought about by the crowded environment would slow the translational movement of macromolecules.⁷⁰ Due to entropic effects, crowding will also drive macromolecular association if the complex is more compact than the unbound species so that overall available volume is maximized^11,12

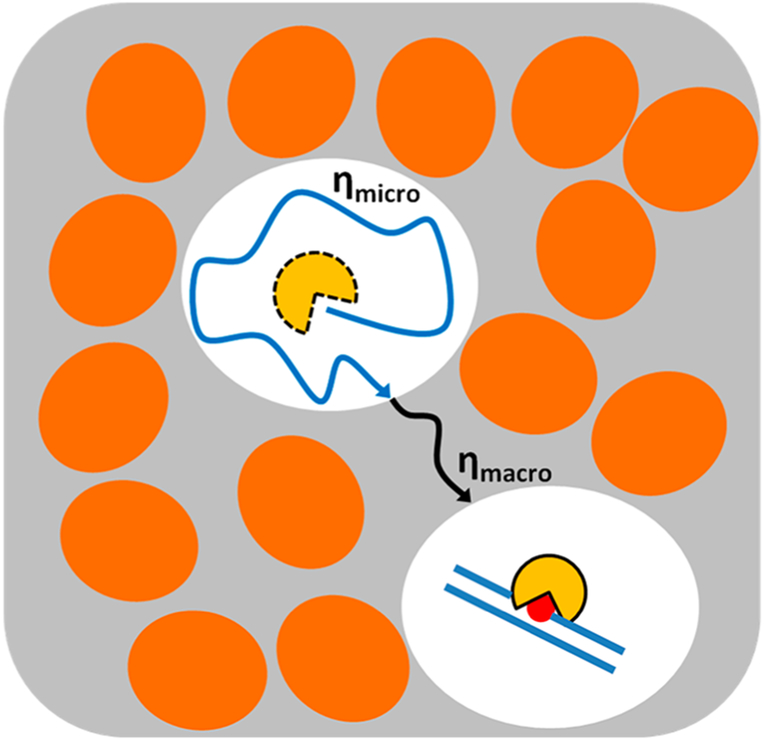
Surprisingly, despite the increase in macroscopic viscosity, crowding has been reported to have a small effect on diffusion-controlled association kinetics of macromolecules.^13,70 This result is not intuitive but can be understood by considering the difference between macroscopic and microscopic viscosities (Figure 3). Because the spaces between the large crowding molecules are filled with low-viscosity water and small solutes, the rotational and translational diffusion of a protein is not greatly affected over short nanometer distances inside these spaces (microscopic viscosity).^11,12,66 However, over greater distances, the effective viscosity increases due to hard-sphere repulsion between the protein and crowding molecules, which slows translational diffusion (macroscopic viscosity).^70–72 Counteracting the effects of viscosity is the low-viscosity cage created by the surrounding large crowding molecules. The cage serves to increase the probability of a productive encounter by confinement of the binding partners. Several in vitro and cell-based studies have shown that the caging effect nearly offsets the negative effects of high macroscopic viscosity on the overall association rate.^15,46 This model for the thermodynamic and kinetic effects of macromolecule crowding is sufficient to understand the effects of crowding on facilitated diffusion of proteins on DNA (see below).

Figure 3.

Effects of macromolecular crowding on diffusion and binding equilibria. Macromolecules (shown as ovals) consume volume (the excluded volume), thereby reducing the available volume for free diffusion of smaller proteins. Macromolecule crowding increases the macroscopic viscosity (η_macro) and is expected to reduce diffusion of proteins inside cells. However, the space between macromolecules has the microscopic viscosity of aqueous solution (η_micro), allowing rapid diffusion of smaller proteins within this available volume. Crowding also creates cages around proteins and target DNA that promotes efficient kinetic capture of binding partners.^46,54 Such favorable effects may completely compensate for the unfavorable effect of increased macroscopic viscosity. The equilibrium for binding is generally pushed toward the bound complex under crowded conditions, because the available volume is maximized if the complex is more compact than the two binding partners.

1.4. Biological Implications

Timely removal of mutagenic bases and fast activation of transcriptional cascades in response to external stimuli are fundamental requirements for proper cellular function that have different temporal and thermodynamic requirements. In both cases, sparse DNA target sites must be located by specialized proteins to give rise to downstream DNA repair or transcriptional activation outputs. As a result, the target search may be the rate-limiting step in these processes.^42,54,62 In the case of DNA repair glycosylases, which recognize specific damaged bases in DNA that are present at a density of only 1/100 000 000 normal bases (Table 2),⁷⁸ the relevant time frame for action is the cell cycle. If repair has not been completed by the time of DNA replication, permanent mutations can become fixed in the genome. For this reason, cells have evolved elaborate signaling mechanisms to rapidly detect damage or to delay progression through the cell cycle until repair is complete.^79,80 A unique aspect of the biological action of DNA repair glycosylases is that they must inspect all base pairs in genomic DNA to ensure the fidelity of DNA replication. This may explain their high copy number in cells (several hundred thousand copies per cell) and their relatively weak binding affinity for nonspecific DNA (~1–100 μM at physiological concentrations of monovalent ions): high copy number decreases the search time by reducing the amount of DNA that must be surveyed by a single enzyme molecule, and weak binding affinity allows these enzymes to rapidly inspect individual base pairs and then move on to new sites.

Table 2.

Structures, Enzymatic Activities, and DNA Binding Specificities of DNA Glycosylases and Transcription Factors Covered in This Review^a

Protein	Activity	Structure
Human uracil DNA glycosylase (hUNG catalytic domain; hUNG2 full length enzyme) PDB code: 20XM73	Uracil excision from ssDNA; U/A and U/G pairs in duplex DNA
Human 8-oxoguanine DNA glycosylase (hOGG1) PDB code: 3IH774	8-oxo-G excision from 8-oxoG/C pairs in duplex DNA
Human alkyladenine DNA glycosylase (AAG) PDB code: 3QI575	Excision of hypoxanthine and alkyladenine paired with T in duplex DNA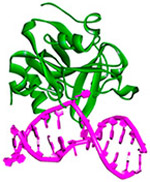
Human early growth response protein 1 (Egr1; Zif268 DNA binding domain) PDB code: 1AAY76	Binds to specific target sequence: 5' - GCG (T/G)GG GCG - 3'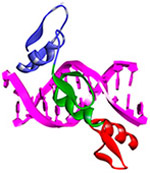
Human tumor repressor protein 53 (p53) PDB code: 5MF777	Binds to specific target sequence: 5'- AGA CAT GCC TAG ACA TGC CT - 3'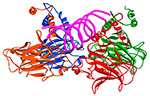

^ahUNG/hUNG2,⁷³ 2OXM; hOGG1,⁷⁴ 3IH7; AAG,⁷⁵ 3QI5; Egr-1,⁷⁶ 1AAY; p53,⁷⁷ 5MF7

In contrast, transcription factors (TFs) have no evolutionary requirement to inspect every base pair, and instead they must strike a balance between nonspecific DNA-binding affinity, which allows adequate one-dimensional diffusion, and specific binding affinity, which allows them to attain sufficient residence time at a specific site to affect the desired transcriptional output (Table 2). The recognition mechanisms of transcription factors can be further divided into constitutively expressed and inducible forms.^81,82 Constitutively expressed (housekeeping) TFs are present to maintain steady-state levels of housekeeping gene products. In such a setting, neither high affinity nor specificity is required to effectively execute function, because the specific site is occupied with high probability by simply overexpressing the TF. In contrast, inducible transcription factors and transcriptional activators/repressors have only several minutes to hours to find their specific sites on the DNA and initiate transcription in response to signal input. The short time frame and low TF copy number provides evolutionary pressure for these TFs to develop rapid search mechanisms with high site specificity.^3,42

2. DNA TRANSLOCATION BY DNA REPAIR GLYCOSYLASES

DNA glycosylases perform the initiating step of base excision repair, acting to sever the glycosidic bond between a variety of damaged bases and the DNA sugar–phosphate backbone (Table 2).^83–85 The human enzymes considered here act on uracil paired with guanine or adenine [human uracil DNA glycosylase catalytic domain (hUNG) and full-length nuclear enzyme (hUNG2)], oxidized guanine paired with cytosine [8-oxoguanine DNA glycosylase (hOGG1)], and hypoxanthine or alkylated purine bases [alkyladenine DNA glycosylase catalytic domain (AAG^cat) and full-length nuclear enzyme (AAG)]. The subsequent steps in the base excision repair pathway lead to incorporation of the correct deoxynucleoside triphosphate using the coding information on the opposite DNA strand.^86,87 These three enzymes share a damaged base recognition mechanism called base or nucleotide flipping, where the damaged base is rotated out of the DNA duplex into the enzyme active site (Table 2).^73,75,88 Several comprehensive reviews of the multistep reaction trajectory for the baseflipping process are available, and we will not cover this aspect of the damage search process here.^89,90 Nevertheless, it is essential for our purposes to realize that the time scale for damaged base flipping must match the residence time of the enzyme at individual DNA base pairs (the scanning rate) or else these enzymes will pass over damaged bases without initiating repair. Conceptually, the damage search process of DNA glycosylases can be broken down into three stages: (1) the search stage, which involves 3D diffusion to the DNA chain and translocation along the DNA chain; (2) the interrogation stage, in which base pairs are inspected for the presence of damage by the base-flipping method; and (3) the excision stage, where the chemical step of glycosidic bond cleavage occurs. In this review, we specifically focus on the search stage of DNA glycosylase action.

2.1. Human Uracil DNA Glycosylase

hUNG is responsible for the excision of uracil bases from both duplex and single-stranded DNA.⁸⁵ In humans the enzyme is found in both mitochondrial (hUNG1) and nuclear (hUNG2) forms that share catalytic domains but differ in the sequences of their ~90 amino acid unstructured N-termini.^91–93 hUNG2 is unique with respect to other glycosylases that act on uracil in that it efficiently excises uracil in the context of U/A and U/G base pairs, as well as uracils in single-stranded DNA.^94–96 hUNG2 contains proliferating cell nuclear antigen (PCNA) and replication protein A (RPA) interaction motifs in its N-terminal region that allow it to localize to DNA replication forks in S phase.^97–100 Presumably, this mode of enzyme action allows hUNG2 to efficiently excise uracils that are incorporated opposite adenine during DNA replication.^101,102 Extensive mechanistic studies have been performed on uracil DNA glycosylase over the last 20 years to unravel its chemical mechanism,^85,89,90 structure,^73,103,104 and base-flipping mechanism,^73,89,90,105 making it one of the most well-understood DNA repair enzymes. More recently, a series of studies on its mechanism of DNA translocation have generated one of the most comprehensive pictures of facilitated diffusion that spans both in vitro and cell-based measurements.

2.1.1. General Approach for Measuring DNA Chain Translocation.

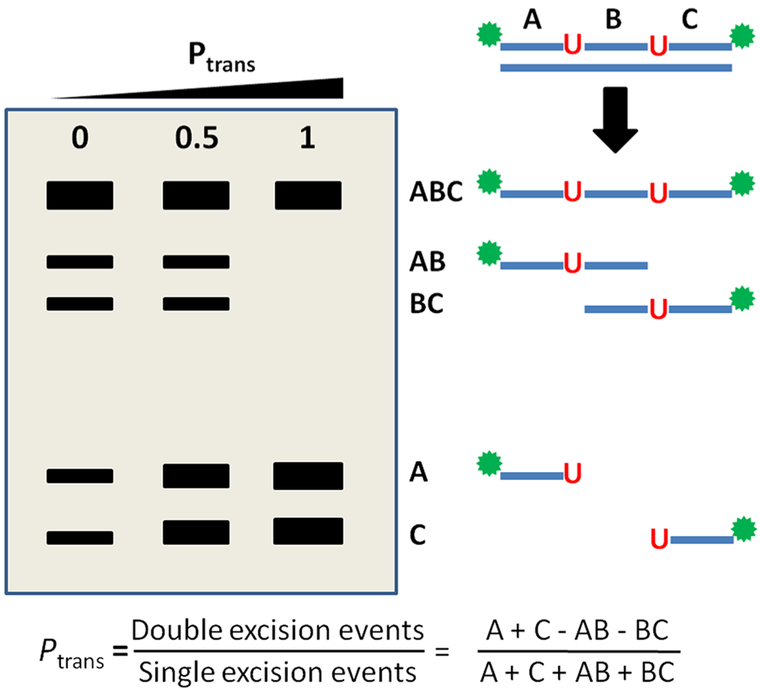
All of the DNA translocation studies with hUNG and hUNG2 have used ensemble-based measurements, building on the elegant approaches developed by Modrich and co-workers¹⁰⁶ and Halford and co-workers¹⁰⁷ for restriction enzymes. These measurements involve the construction of substrates containing two reactive sites in a single DNA chain and quantification of the frequency at which both sites are excised in a single enzyme encounter event (Figure 4).⁴⁹ Such measurements require incubation with low concentrations of enzyme under initial rate conditions such that the probability of two enzymes encountering a single substrate is extremely small. Upon initial encounter with a DNA chain, which most likely occurs at one of the more numerous canonical base pairs, hUNG2 then translocates to and excises one of the two uracils. Once the first uracil is excised, the instantaneous position of the enzyme relative to the second site is marked. When the enzyme departs the first excision site, one of two events then occurs: (i) escape of the enzyme from the DNA domain such that it encounters a new substrate or (ii) translocation and excision of the second uracil site in the same molecule. The goal of the experiment is to quantify the fraction of first-site excision events that are immediately followed by second-site excision in the same DNA chain, without dissociation of the enzyme to bulk solution. This probability (P) of successful transfer to the second site is termed P_trans and is calculated from the ratio of single- to double-site DNA excision products as described in references and Figure 4.^39,46,62,63

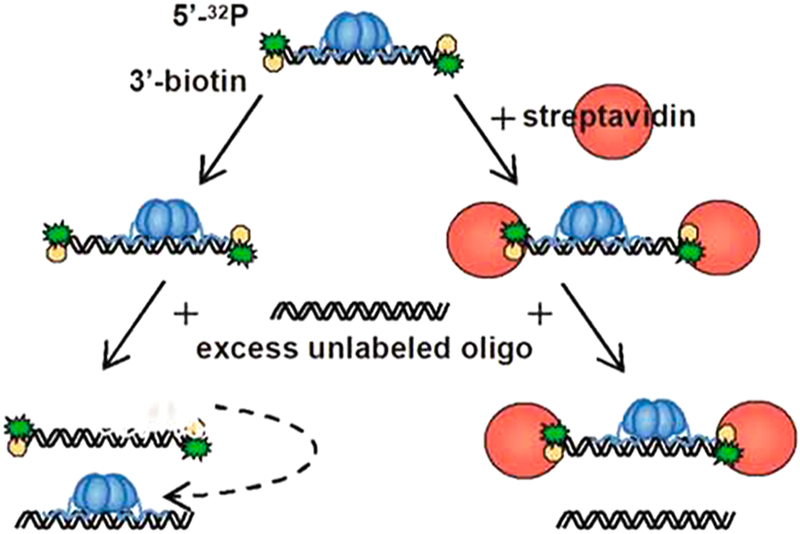
Figure 4.

Assay to measure the probability of successful site translocation (P_trans) in a single encounter event by uracil DNA glycosylase (UNG). Substrates containing two uracil sites are synthesized that contain radiolabels on both the 5′ and 3′ ends. Excision of uracil is performed under initial rate conditions with limiting amounts of enzyme to ensure single-hit conditions. Excision from either site produces a unique fragment designated AB or BC, while cleavage at both sites produces fragments A and C. As P_trans increases toward unity, two-site excision events occur in every encounter and only fragments A and C are observed. The probability for transfer (P_trans) is given by the ratio of fragment concentrations as indicated.¹⁰⁶

It is important to understand that P_trans alone does not distinguish whether the enzyme transferred to the second site by a dissociative or associative pathway. Instead, P_trans reflects the sum of the probabilities of transferring by both pathways (P_trans = P_diss + P_assoc). The microscopic pathway must be discerned either by the site distance dependence of P_trans^{3,16,42,47,54,63} or by trapping experiments that selectively capture enzyme molecules that follow the dissociative pathway (as will be described).^39,46,47

2.1.2. Timing Associative and Dissociative Site Transfers.

A new method was developed to clock the dissociative and associative translocation pathways for hUNG (Figure 5). The approach involved an active-site-directed inhibitor (uracil) that traps enzyme molecules in the process of a dissociative transfer but does not perturb enzyme molecules executing associative transfers because their active sites are shielded from the trap by DNA.^39,46,47 Uracil is an ideal active-site trap because it is a weak inhibitor, and high concentrations of uracil densely populate the solution volume surrounding the dissociated enzyme and facilitate rapid capture of the enzyme during the short lifetime of a dissociative transfer event. In other words, 1/k_trap[U] = τ_trap must be comparable to the lifetime of the dissociated hopping enzyme (τ_diss) (Figure 5a).

Figure 5.

Small-molecule trapping method to capture UNG molecules that transfer by a dissociative pathway. (a) When UNG departs its first uracil excision site, it begins to transfer to the second site by either the associative or dissociative pathway. If a small molecule (such as uracil) is present at a high concentration, it can bind and trap UNG molecules that are in the middle of a dissociative transfer. (b) The kinetic mechanism in panel a predicts that associative and dissociative transfer pathways will show very distinct dependencies on trap concentration.⁴⁷

The dependence of P_trans on the trap concentration is highly informative of mechanism, as shown in the simulations in Figure 5b. When associative transfers are the only pathway, the transfer is unaffected by the presence of trap. Conversely, when only the dissociative pathway is followed, all transfers are ablated at high trap concentration. Finally, when both pathways are present, a partial decrease in P_trans is observed as the trap concentration is increased, reflecting the presence of dissociative transfers (P_diss), but a residual amount of transfer persists at high trap concentration, reflecting the contribution from the associative pathway (P_assoc). All of these scenarios have been experimentally observed at various uracil site spacings with human UNG.⁴⁷

2.1.3. DNA Translocation by hUNG in Dilute Solution.

Using the described two-site ensemble approach in the absence of the uracil trap, P_trans for human UNG catalytic domain was observed to decrease from 0.75 to 0.27 as the uracil site spacing was increased from 5 to 55 bp in the presence of 22 mM NaCl.³⁹ When the same experiments were performed in the presence of the uracil trap to dissect the contributions from associative and dissociative transfers, transfers were completely ablated for site spacings greater than 10 bp but persisted at high uracil concentrations for site spacings less than 10 bp.³⁹ These observations indicated that all transfers by hUNG catalytic domain over spacings greater than 10 bp involved at least one enzyme dissociation event that allowed its capture by the uracil trap. Analysis of the associative transfers at site spacings less than 10 bp indicated that the mean associative transfer distance was only ~4 bp at 20 mM NaCl. Associative transfers were found to persist when the monovalent ion concentration was increased, but the dissociative transfers were strongly dependent on the salt concentration.^39,54 These observations indicated that short-range associative transfers occurred without the enzyme escaping the ~1 nm radius ion cloud surrounding the DNA^108,109 and that dissociative transfers involved diffusion of hUNG outside the ion cloud, where it experienced the bulk ion concentration.

The trapping data were used to estimate the average distance (r) traveled by hUNG during a dissociative transfer event of duration τ_diss by employing the Einstein diffusion equation, 〈r〉 = √6D₃τ_diss. In this analysis, calculated diffusion constants (D₃) for hUNG and uracil were used along with the relationship that half-maximal trapping by uracil occurs when τ_trap/[U] = τ_diss (Figure 5). This led to an estimate of an average dissociative transfer distance of 〈r〉 ≈ 7 nm, indicating that when UNG travels a greater distance from the DNA chain, its position is no longer correlated with the DNA it just departed and it frequently departs to bulk solution.

A very informative variation of the site-transfer experiment was performed where the two uracils were placed 5 bp apart on opposite strands of the DNA (S5_opp).³⁹ This experiment is informative because when two uracil sites are embedded on opposite strands of the DNA duplex, transfer must involve at least one dissociation event that allows the enzyme to reorient with respect to the DNA strand polarity.^38,39,110 We reasoned that, for such substrates, all transfers should follow the dissociative pathway and be trappable by uracil. These expectations were borne out because P_trans for S5_opp (0.54) fell to nearly zero as the uracil concentration was increased, whereas S5_same retained site transfers in the presence of the trap.³⁹ These findings establish that hUNG reaches uracil sites on the same strand by both dissociative and associative transfers and that the enzyme can efficiently reach a uracil site on the opposite strand primarily by the dissociative pathway.

In summary, these studies using hUNG catalytic domain at low monovalent ion concentration indicate that DNA translocation occurs by very short associative transfers (~4 bp), punctuated by frequent dissociative transfers where the enzyme moves outside the ion cloud yet reassociates with the same DNA molecule with high probability. The value of dissociative transfers is that the enzyme can diffuse rapidly and freely in bulk solution near the DNA chain, and the value of slower associative transfers is that this mode provides efficient and redundant surveying of DNA base pairs for damage on a time scale that is compatible with base-flipping kinetics.^39,90 Additionally, dissociative transfers allow the enzyme to move from one strand to the other, extending the coverage to both strands after a segment of DNA is encountered.

2.1.4. Role of DNA Phosphate Backbone and DNA Grooves.

The site-transfer efficiencies of hUNG in the presence and absence of the uracil trap revealed the individual contributions of associative and dissociative pathways but did not provide any information on the mechanism of translocation. Several molecular mechanisms for DNA translocation have been proposed that may be grouped into two general categories: phosphate backbone tracking^40,111 and groove tracking.^40,43,44

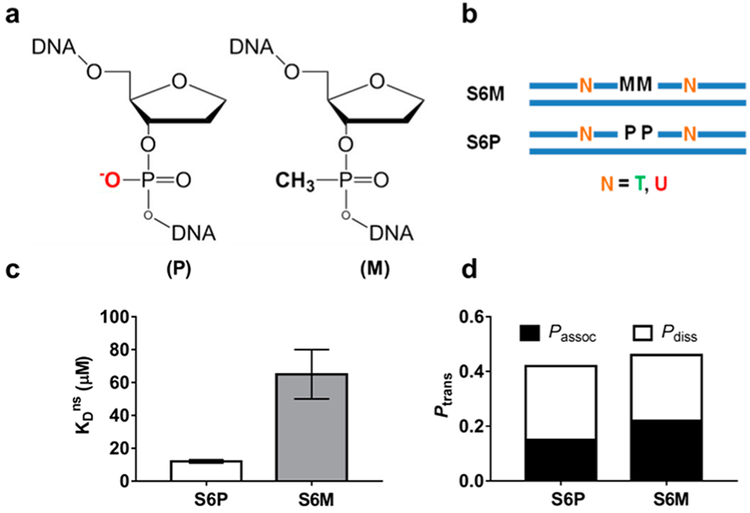
To understand if the anionic DNA phosphate backbone was essential for translocation by hUNG catalytic domain, an approach of substituting charge-neutral methylphosphonate (M) groups for the phosphate (P) esters of DNA was used (Figure 6a,b).^95,112 M substitution is an attractive approach because it effectively removes the phosphate charge and introduces only minor changes in the structural parameters of B-DNA.^113–115 The overall strategy was to measure the effect of M substitution on nonspecific DNA binding (K_D^ns) and site-transfer efficiencies (P_trans) and ascertain whether the equilibrium effects matched those for site transfer.

Figure 6.

Methylphosphonate substitution in the DNA phosphate backbone weakens nonspecific DNA binding but not site translocation by UNG. (a) Structure of phosphate (P) and methyl-phosphonate (M) diesters in the DNA backbone. (b) UNG substrates containing M or P linkages between two uracil sites. (c) M substitution weakens binding affinity by ~6-fold. (d) M substitution has no effect on P_trans, P_assoc, or P_diss. Adapted from ref 112. Copyright 2013 American Chemical Society.

The binding effect of making M substitutions at two phosphate esters located in the middle of a nonspecific DNA sequence was determined by fluorescence anisotropy measurements (Figure 6b,c).¹¹² Binding measurements clearly revealed that the two M substitutions reduced the binding affinity of hUNG by about 0.5 kcal/mol each and established that removal of phosphate charge had a significant damaging effect on nonspecific DNA binding.

Is a continuous negatively charged phosphate backbone also required for associative transfer between uracil sites in duplex DNA? To address this question, DNA substrates were synthesized that contained two M substitutions on the DNA strand connecting two uracils separated by 6 bp (S6M and S6P) (Figure 6b).¹¹² This short spacing was chosen because ~60% of site transfers occur by the associative pathway at this spacing with an all-phosphodiester substrate. In contrast to the M effects on nonspecific binding, the P_trans values for S6M and S6P were indistinguishable, with identical contributions from the associative and dissociative transfer pathways (Figure 6d). The absence of a functional requirement for a continuous negatively charged backbone in site translocation strongly suggested that the short-lived transition state for associative transfers on the DNA does not involve the same phosphate interactions that are present in the ground-state complex for nonspecific binding. These observations supported a two-state model for UNG translocation that is described in section 2.1.5.

To investigate whether the presence of DNA grooves was a requirement for DNA translocation, site-transfer studies were performed with ssDNA substrates.⁹⁵ Sequences (90-mer) were designed that contained uracil sites positioned 5 and 10 bp apart (S5_ss and S10_ss), with no potential for secondary structure formation. In the absence of the uracil trap, the P_trans values were indistinguishable from those of the duplex DNA forms S5 and S10. However, S5_ss and S10_ss showed residual transfers in the presence of increasing concentrations of uracil trap (P_assoc = 0.22 and 0.16, respectively), indicating that the mechanism for associative transfer in ssDNA differs from that in duplex DNA. It is possible that the additional flexibility of single-stranded DNA allows for hopping transfers or bridging intermediates that are not possible with rigid duplex DNA. The observation of associative transfers on these single-stranded DNA substrates establishes that the major and minor grooves of duplex DNA are not required for efficient site transfer on DNA.

2.1.5. Two-State Model for DNA Translocation.

The finding that the phosphate backbone forms electrostatic interactions in the ground state for nonspecific DNA binding, but does not play a role in associative site transfers, suggested that DNA translocation involved a different conformational state of hUNG where interactions with the phosphate backbone were not present (Figure 7). Given these results, a model was proposed where associative transfers proceed through an open state that interacts loosely with the DNA backbone and resembles the transition state for DNA dissociation.^112,116 During an associative transfer, hUNG closes on the DNA chain before diffusing outside the ion cloud and therefore successfully executes an associative transfer to another site. In contrast, dissociative transfers occur when the enzyme fails to close on the DNA chain and then diffuses outside the ion cloud. The description of short-range sliding as an aborted transition state for DNA dissociation differs considerably from other characterizations of protein sliding.^110,117 However, a two-state model does resemble that proposed by Mirny and co-workers^118,119 and others,¹²⁰ where proteins translocate on DNA by oscillating between static and mobile states.

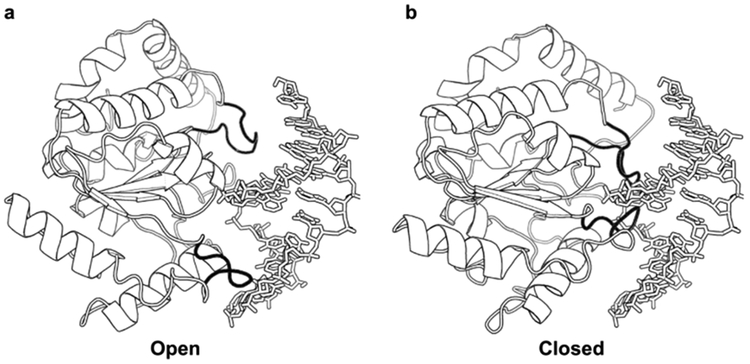
Figure 7.

UNG exhibits increased loop dynamics in the nonspecific DNA complex. NMR dynamic measurements detected increased conformation dynamics in two DNA- binding loops of UNG and in a hinge region away from the DNA-binding site. These dynamic measurements were interpreted in terms of an open-to-closed transition that was structurally suggested by a normal-mode analysis of the protein.⁸⁹

The proposal of a loose, transiently bound conformation that executes associative transfers is supported by NMR dynamics measurements of hUNG.^89,121 The NMR results indicated that free hUNG has little dynamic motion, but upon binding to nonspecific DNA it enters a free-energy landscape that allows it to oscillate between open and closed forms on the millisecond and microsecond time scale.⁸⁹ Mechanistically, the short-lived open form functions in stochastic movement along the DNA chain, and the closed form is the more highly populated ground- state configuration observed in crystal structures that allows hUNG to interrogate the integrity of base pairs. Recent structural evidence obtained with other DNA glycosylases also suggests the presence of more than one conformation involved in search and recognition by these enzymes.^73,122–125

2.1.6. Macromolecular Crowding Effects.

An in vitro system with inert macromolecule polymers was developed to approximate some aspects of the crowded environment of the cell nucleus and to explore how molecular crowding affected DNA translocation.⁴⁶ The findings were largely consistent with expectations based on the macroscopic and microscopic effects of large polymers on solution viscosity and excluded volume.^{46, 4}

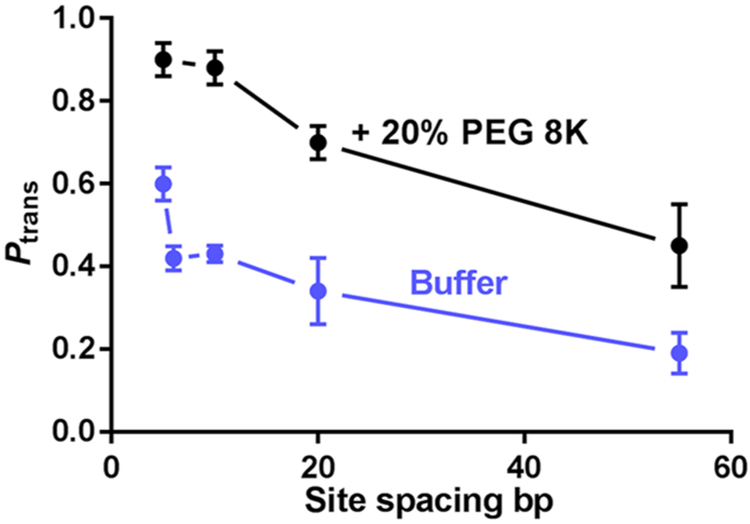
Solutions containing 0–30% (w/v) poly(ethylene glycol) (PEG)—PEG 600, 1500, 3350, or 8K—were employed to discern the effects of viscosity and crowding on associative and dissociative transfers of UNG catalytic domain in the presence of 22 mM NaCl. These experiments employed 90-mer duplex DNA substrates with two uracil sites spaced from 5 to 55 bp apart.⁴⁶ By varying both the polymer size and concentration, both viscosity and crowding effects could be probed. In this context, ethylene glycol is expected to exert a viscosity effect only, and the larger polymers are expected to show macromolecular crowding effects.^15,68 The site-transfer probabilities for all site spacings increased in the presence of the PEG polymers (Figure 8), but the small-molecule viscogen ethylene glycol showed no effect, establishing that increases in viscosity do not have a significant effect on the translocation efficiency. The largest increases were seen with PEG 8K, which were concentration-dependent and reached a plateau level at 20% (w/v) PEG 8K.⁴⁶ The high transfer probabilities persisted in the presence of the uracil trap out to site spacings as large as 55 bp, whereas in dilute buffer the associative pathway was nonexistent for site spacings ≥10 bp (see above). Thus, it was concluded that crowding increased both the likelihood and average distance of associative DNA translocation.

Figure 8.

Effects of PEG 8K on the DNA translocation efficiency of UNG. When the standard assay buffer is supplemented with 20% (m/v) PEG 8K, P_trans is significantly increased at uracil site spacings in the range from 5 to 55 bp.⁴⁶ Adapted with permission from ref 46. Copyright 2015 Oxford University Press.

A mechanism was proposed for the effects of macromolecular crowding (Figure 9). The first element of the mechanism is that crowding increases associative transfers by increasing the time that the enzyme remains confined within the ion cloud of the DNA (radius <1 nm). This confinement means that the enzyme can diffuse rapidly in the low-viscosity region (~10 nm) that exists between the DNA and the macromolecule cage.⁴⁶ The caging effect also serves to reflect the enzyme back to the DNA chain during dissociation attempts. The increased time spent in associative transfers allows for increased damage surveillance. However, the price for this additional inspection time is the reduced frequency of moving to new DNA chains, which slows the overall rate of uracil excision over a population of long DNA molecules.⁴⁶ Nevertheless, because glycosylases are abundant enzymes (>100 000 copies/nucleus),¹²⁶ and each enzyme only needs to scan less than 20 000 bp of DNA, a localized search mechanism with infrequent escape to bulk may be highly appropriate for the human cell nucleus. It is intriguing that the crowded nuclear environment might have as much of an impact on the damage search mechanism as the molecular properties of the enzyme.

Figure 9.

Mechanistic interpretation of how macromolecular crowding enhances DNA translocation by associative and dissociative pathways (see text). Most of the effects can be explained by a macromolecular cage that surrounds the protein–DNA complex.

2.1.7. Role of the N-Terminal Tail in DNA Translocation.

All the studies described above were performed at low monovalent salt concentration with the catalytic domain of hUNG that lacks its largely unstructured N-terminal domain.^127,128 In buffers that do not contain a crowding agent, there are only modest differences in the translocation and kinetic properties of the full-length enzyme (hUNG2) and the catalytic domain agent.⁶³ However, recent experiments have shown that the tail substantially contributes to DNA translocation when crowding agents are present.^62,63

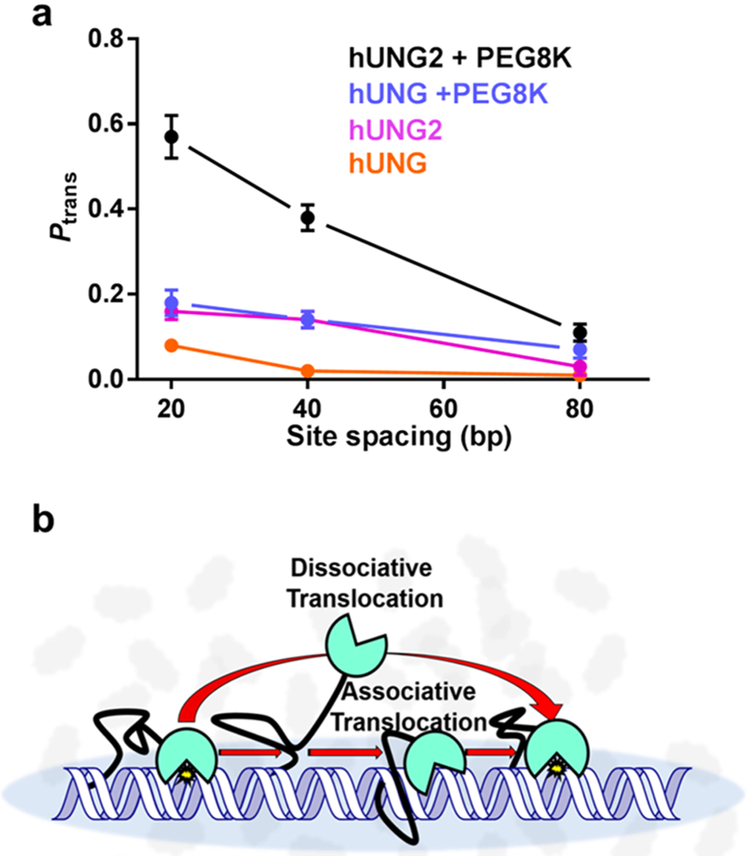
A comparison of the site-transfer efficiencies for hUNG catalytic domain and full-length hUNG2 was made by use of substrates with uracil site spacings of 20, 40, and 80 bp in the presence of 150 mM KAc, with and without supplementation with the inert crowding agent PEG 8K (Figure 10a). In the absence of PEG 8K, site transfer for both enzymes was small at all site spacings (P_trans < 0.15 at 150 mM KAc), but hUNG2 consistently showed at least a 3-fold larger value than hUNG.⁶³ Upon addition of 20% PEG 8K, site transfer for hUNG remained fairly low for all spacings at this high salt concentration (P_trans < 0.2), but transfers for hUNG2 were large at the 20-bp uracil spacing (P_trans ≈ 0.6) and persisted out to a site spacing of 80 bp (P_trans ≈ 0.1)(Figure 10a). In the presence of the uracil trap and 20% PEG 8K, hUNG2 retained 60% of its site transfers across a 20-bp spacing (P_assoc = 0.40), but at a spacings greater than 20 bp, associative transfers diminished to low or undetectable levels. These data suggested that crowded conditions in the human cell nucleus could promote the interaction of the N-terminus with duplex DNA during translocation, which is borne out in the cellular measurements described in section 2.1.8.

Figure 10.

The largely disordered N-terminal tail of full-length human UNG (hUNG2) increases the translocation efficiency of the enzyme, (a) The presence of the 90 amino acid tail enhances translocation in the absence and presence of PEG 8K and 150 mM KAc. (b) The N-terminal tail is proposed to facilitate translocation through a tethering interaction with the DNA that increases the probability of DNA binding after microscopic dissociation events. Adapted from ref 63. Copyright 2017 American Chemical Society.

2.1.8. DNA Translocation in Human Cells.

The culmination of the DNA translocation studies of hUNG2 involved moving the site-transfer assays into a cellular context. An approach was taken where human Hap1 cells were transfected with fluorophore-labeled DNA duplexes containing two uracils spaced 10, 40, or 80 bp apart (Figure 11).⁶² The labeled substrates were recovered from cell extracts at various times after transfection, and the fraction of DNA molecules where both uracil sites were cleaved by hUNG2 was determined as in the in vitro studies. Although this was a simple extension of the in vitro assay, many controls were required to validate the result.⁶² In cells, the two-site-transfer probabilities were 100% at 10-bp spacing and 54% at 40-bp spacing and dropped to 10% at 80-bp spacing. Thus, the mean transfer distance in cells was ~40 bp, which is within error of the value measured in vitro for full-length hUNG2 in the presence of 20% PEG 8K and a salt concentration that approximates the intracellular environment (Figure 11).⁶³ Intracellular uracil trapping experiments indicated that site transfers followed the dissociative pathway for site spacings greater than 40 bp.⁶² The observation of a dissociative transfer mode over this distance is similar to in vitro results under crowding conditions and indicates that purely associative transfers do not occur in human cells even over this short distance.

Figure 11.

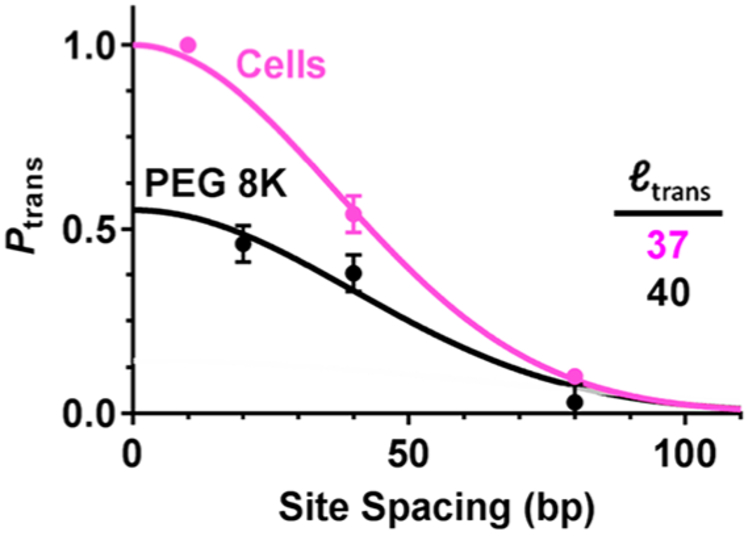
Comparison of the DNA translocation efficiency of hUNG2 as a function of site spacing in solutions containing PEG 8K and in the human Hap1 cell line (see text). The mean translocation distance (bp) for each condition is indicated. The curves are fits to a Gaussian function, P_trans = a exp(s²/2l_trans²), where l_trans is the mean transfer distance, 0 < a ≤ 1 is the amplitude of P_trans, and s is the site spacing. Adapted with permission from ref 62. Copyright 2017 Oxford University Press.

A striking aspect of the nuclear translocation results was that competitive binding of nuclear proteins to the probe DNA was not observed despite the high macromolecule concentration in the cell.^66,67 It seems highly likely that proteins would be bound to the intervening DNA as hUNG2 attempted to execute a transfer over the long 80-bp site spacing. Nevertheless, the efficiency of site transfer was slightly greater than in the in vitro measurements in the absence of protein competitors and presence of crowding. Efficient bypass of bound proteins and other obstacles by the dissociative transfer mode has precedence in vitro for both hOGG1 and AAG human DNA glycosylases,^47,52 and these intracellular findings suggest that bypass events occur efficiently in the nucleus.

The intracellular site-transfer measurements show how hUNG2 has evolved to search DNA in the most efficient manner possible, taking advantage of the crowded nuclear environment to overcome unfavorable salt effects on nonspecific DNA binding and enhance dissociative transfers that allow bypass of protein obstacles. The macromolecule cage surrounding the DNA chain also allows hUNG2 to take advantage of rapid diffusion in the low-viscosity microenvironment, which minimizes the 1D search time.⁶²

2.2. 8-Oxoguanine DNA Glycosylase (hOGG1)

Oxidative damage to guanine bases in humans is primarily repaired by 8-oxoguanine DNA glycosylase (hOGG1).⁸⁷ This glycosylase differs significantly from hUNG in structure, electrostatic features, and the conformational changes it induces in damaged and undamaged DNA upon binding.^124,129 Furthermore, it is a prototypical member of the helix–hairpin–helix Gly/Pro/Asp (HhH-GPD) superfamily and provides an excellent representative from this family for rigorous study.¹³⁰ These distinctions between hUNG and hOGG1 raise the possibility that different mechanisms might be used to solve the search problem. Unlike hUNG, the facilitated diffusion mechanism of hOGG1 has been studied extensively by both ensemble and single- molecule methods, allowing an evaluation of the mechanism from both perspectives.^{40,46,47,131,132} We review the results of these informative studies, and we compare and contrast the findings with the well-studied hUNG paradigm.

2.2.1. DNA Chain Translocation.

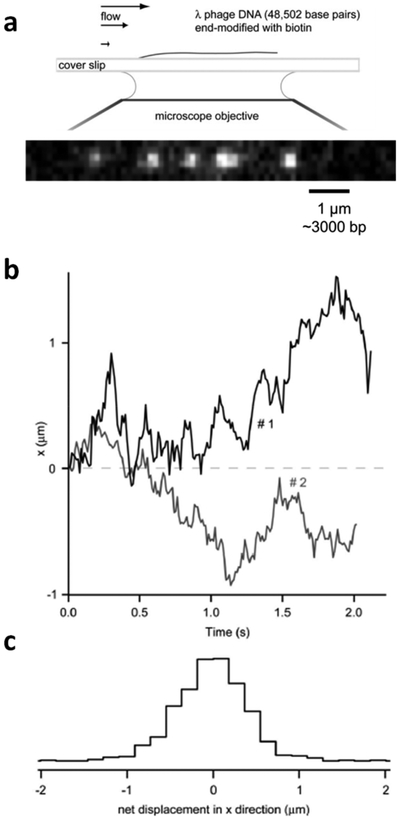
The first study of facilitated diffusion by hOGG1 used a groundbreaking single-molecule approach where a 50-kb length of DNA was attached to a bead on a slide and then stretched to its full extension under flow conditions (Figure 12).⁴⁰ Transient interactions of fluorophore-labeled hOGG1 with DNA were then followed by total internal reflectance fluorescence (TIRF) imaging after the enzyme was introduced into the buffer flow. Analysis of the data involved plotting the mean-squared displacements of hOGG1 trajectories (〈x²〉) against time (t), where the slope of such a plot is the apparent 1D diffusion constant (i.e., 〈x²〉 = 2Dt). The major findings from this work, much of which was performed at very low salt concentrations (10 mM NaCl) to maximize DNA-binding lifetimes, was that hOGG1 exhibited 1D transfers along the DNA with an apparent diffusion constant of D₁ = 5 × 10⁶ bp²⋅s⁻¹ and that the mean transfer distance was ~400 bp at a salt concentration approximating that of the cell nucleus. It was noted that D₁ is so large as to approach the theoretical upper limit for diffusion of a protein the size of hOGG1 in aqueous solution. Thus, these studies and the simple diffusion analysis indicated that translocation of hOGG1 on the DNA was nearly barrierless. This single-molecule description of the hOGG1 diffusion mechanism differs considerably from the behavior of hUNG, as well as ensemble studies of hOGG1 (see below), both of which indicate slow associative transfers and rapid diffusion through solution by dissociative transfers. A recent reanalysis of the original single-molecule data used a new approach (known as optimal estimator of diffusion coefficients) and suggested that hOGG1 switches between two diffusive modes that more closely resemble those observed in ensemble measurements of hUNG and hOGG1 (see below).^40,133

Figure 12.

Single-molecule measurements of DNA translocation by hOGG1 glycosylase. (a) The experimental setup involved attaching a ~50-kb linear DNA with a biotin end-label to a streptavidin bead on a glass slide. When flow is introduced, the DNA is extended to its full length. Introduction of fluorophore-labeled hOGG1 in the flow allows imaging of its movement along the DNA chain by the total internal reflectance fluorescence method. (b) Displacement of individual hOGG1 molecules as a function of time. (c) Histogram of the observed displacement frequencies. The mean sliding length (67% of the observations) is 0.3 μm or 1000 bp. Adapted with permission from ref 40. Copyright 2006 National Academy of Sciences.

Another single-molecule study, published in 2009 by the same group,⁴⁴ asked the question whether hOGG1 used simple one-dimensional diffusion or if it rotated with respect to the DNA axis to maintain a specific orientation while translocating. The theoretical basis for addressing this question revolved around the physical parameters of translational diffusion and the Stokes’ expression for viscous friction,⁴⁴ which indicates that the diffusion constant of a linearly translocating protein should vary as a function of 1/r, where r is the radius of the protein. Alternatively, if the protein tracks along a DNA groove or the phosphate backbone it will also rotate, and the increased protein rotational friction will lead to a 1/r³ dependence on protein size.⁴⁴ Thus, by increasing the radius of hOGG1 by making a fusion construct with streptavidin and then comparing the change in diffusion constant with the theoretical 1/r and 1/r³ dependences, it was concluded that hOGG1 followed rotation-coupled translocation. As with the first study, the average free-energy barrier for rotation-coupled translocation along the DNA was small. Although this study seems to indicate that translocation involves continuous contact with a groove or the phosphate chain, ensemble experiments reported below indicate that hOGG1 frequently dissociates from the DNA chain. One explanation for the different results is that the single-molecule measurements contain microscopic dissociative transfers that fall below the spatial and temporal resolution of the method.

The first ensemble translocation measurements of hOGG1 were performed in 2008 by Sidorenko and Zharkov,¹³² using low salt concentrations and employing a short 40-mer DNA duplex where two 8-oxo-guanine (8-oxoG) sites were separated by 21 bp. In the presence of 50 mM KCl, the measured transfer probability of hOGG1 was P_trans ≈ 0.4, which is modestly greater than that of hUNG under similar conditions but much less than the mean transfer distance of ~400 bp measured in single-molecule studies under similar salt conditions.^40,44 The lack of agreement between the ensemble and single-molecule measurements was perplexing, but the ensemble and single-molecule studies on hOGG1 described below have helped bridge the gap.

Further ensemble studies on DNA translocation by hOGG1 investigated its transfer between two 8-oxoG sites spaced from 5 to 156 bp apart in the presence and absence of a small-molecule trap (2-amino-6-chloropurine), following the same strategy as employed previously for hUNG.⁴⁷ In the absence of trap, P_trans decreased from 0.81 to 0 with increasing site spacing, indicating that the upper limit for translocation was <156 bp regardless of pathway. In the presence of high concentrations of the trap to block successful dissociative transfers, trap-resistant transfers were observed for site spacings less than or equal to 20 bp. From these data, it was concluded that dissociative and associative transfer pathways coexist at spacings less than 20 bp, but when hOGG1 transfers over ≥40 bp, it always makes at least one dissociative step. Thus, when compared to the studies with hUNG, hOGG1 appeared to execute associative transfers over about two turns of the DNA helix, whereas hUNG can only make associative transfers over a single turn of the helix.

2.2.2. Nature of Associative DNA Transfers.

Rowland et al.⁴⁷ used two complementary approaches to investigate the requirement for phosphate backbone tracking by hOGG1. The first was to generate substrates where the two 8-oxoG sites were located on the same and opposite strands of the DNA 10 bp apart (S10 and S10_opp) (Figure 13a,b). These substrates addressed the question of whether efficient site transfer can occur when hOGG1 must dissociate from the first strand and reassociate with the opposite strand without escaping to bulk solution. A second substrate was made that contained a single phosphorothioate group in the intervening strand segment between two sites located 15 bp apart on the same strand (S15_Ps) (Figure 13c). The phosphorothioate group provided a handle for covalent attachment of a bulky group (fluorescein iodoacetamide) to a single phosphate linkage. This construct addressed the question whether transfer between closely spaced sites on the same strand required continuous contact with the phosphate backbone as suggested by the singlemolecule measurements (i.e., rotation-coupled translocation).

Figure 13.

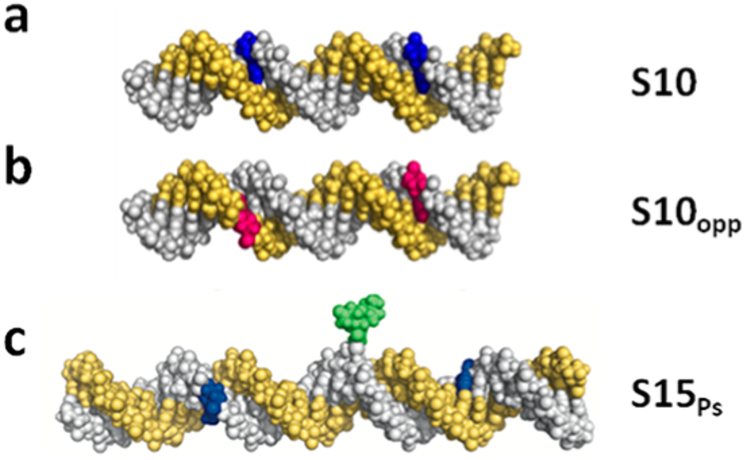
Methods for discerning whether damage site transfer involves continuous contact of hOGG1 with the DNA backbone. (a, b) Molecular models of a DNA duplex containing two 8-oxoG sites 10 bp apart, (a) on the same DNA strand (blue) or (b) on opposite strands (red).⁸⁷ (c) Molecular model of DNA duplex containing a site-specific fluorescein iodoacetamide covalent label (green) at a phosphorothioate linkage located between two 8-oxoG sites on the same DNA strand (blue). Adapted with permission from ref 47. Copyright 2014 Oxford University Press.

Both of the described experimental approaches indicated that continuous contact with the phosphate backbone was not a requirement for efficient DNA translocation by hOGG1.⁴⁷ Substrates S10 and S10_opp showed very similar transfer efficiencies [P_trans(S10) = 0.69 and P_trans(S10_opp) = 0.41],⁴⁷ which closely matched similar experiments with UNG. Thus, efficient site transfer can occur with S10_opp even though hOGG1 must dissociate from one DNA strand, rotationally reorient 180°, and then rebind to the other DNA strand during transfer, which is inconsistent with a rotation-coupled translocation mechanism. With the second substrate S15_Ps, there was no effect of the bulky group on total transfer efficiency as compared to the unmodified substrate S15 (P_trans ≈ 0.55 for both). Moreover, associative transfers in the presence of this substitution were only slightly decreased (P_assoc = 0.18, as compared to 0.28 for S15). Minimally, this finding indicates that hOGG1 does not maintain continuous contact with the phosphate backbone for distances longer than seven phosphate linkages, which was the position of the bulky roadblock in these experiments. These combined findings illustrate the different vantage points and degrees of spatial resolution provided by ensemble and single-molecule methods.

2.2.3. Salt Effects.

A key solution variable in studying DNA binding and translocation is the salt concentration and type of monovalent cation.^4–6,116 Through entropic and specific ion effects, higher salt concentrations can lower the binding lifetimes of proteins on DNA and reduce the opportunity for DNA translocation through well-known electrostatic effects.^2,3,54 Accordingly, many studies of DNA translocation have been performed at lower than physiological salt concentrations in order to facilitate the measurements (see above). Comprehensive studies of the effects of potassium acetate salt concentration on binding of hOGG1 and hUNG for nonspecific DNA showed that hOGG1 used primarily nonelectrostatic binding interactions, while hUNG used an electrostatic binding mode.⁵⁴ In their specific complexes with damaged bases in DNA, binding of both enzymes was primarily by a nonelectrostatic mechanism, which serves to increase specificity for damage sites at physiological ion concentrations. Although neither enzyme efficiently located its site when a physiological concentration of salt and a high concentration of bulk DNA chains was included to mimic conditions in the nucleus, the addition of an inert crowding agent largely restored their ability to track DNA chains and locate damaged sites.⁵⁴ These findings highlight the importance of exploring the effects of experimental conditions that approximate various aspects of the cellular environment.

2.2.4. Macromolecular Crowding Effects.

The enhancing effect of crowding agents on DNA translocation by hUNG suggested that similar crowding effects might extend to other DNA glycosylases. For hOGG1, the overall site-transfer probability also increased in the presence of 20% PEG 8K from P_trans = 0.34 to 0.50 (site spacing of 20 bp).⁴⁶ As found with hUNG, associative transfers of hOGG1 generally increased by ~3-fold in the presence of 20% PEG 8K, while the change in dissociative transfers was negligible. Since these two proteins arise from completely different fold families and bind to nonspecific DNA using different electrostatic contributions, the effect of crowding on DNA translocation appears to be quite general.

The crowding effect can be extended to protein crowders in the case of hOGG1.⁴⁶ In this case, hemoglobin was chosen because it is large enough to exclude significant volume and its low exposed charge minimized changes in ionic strength. Similar to 20% PEG 8K, translocation by hOGG1 increased in the presence of 50 mg/mL (5%) hemoglobin. Indeed, the increase in translocation with 5% hemoglobin was even greater than with 20% PEG 8K, supporting the contention that the effect is not due to viscosity because the hemoglobin solution was significantly less viscous.

2.2.5. Two-State Transfer Model.

Based on ensemble measurements of DNA translocation by the dissociative and associative pathways and binding lifetime measurements for hOGG1, a quantitative view of an average DNA search event of hOGG1 was obtained (Figure 14).⁴⁷ The mechanism begins with diffusional encounter of hOGG1 with the DNA and involves discrete states of the enzyme. The initial encounter leads to an associative transfer, or a conformational change in hOGG1 that results in stable nonspecific DNA interactions and an immobile stationary state. The stationary state is terminated by the reverse conformational change, which initiates an associative transfer. Such conformational changes between free and DNA-bound hOGG1 have been established in structural and rapid kinetic studies.^43,46,88,131 In this model, dissociative transfers occur from the mobile associative transfer state because the immobile closed conformation is incapable of movement on the DNA. As with hUNG, associative transfers appear to act as a transition state for dissociation from the DNA and connect the immobile state with free enzyme.

Figure 14.

Microscopic displacements during an average DNA search event of hOGG1 determined by Monte Carlo simulations constrained by experimental site-transfer data (see text).⁴⁷

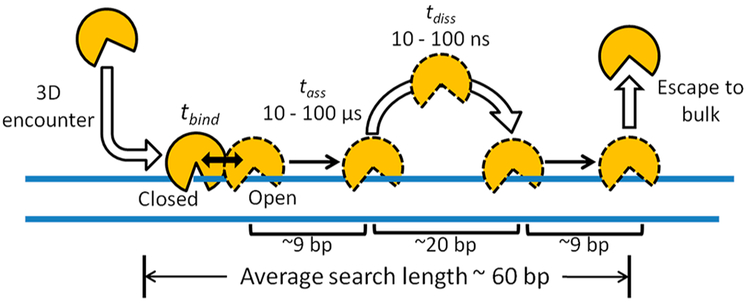
By use of this model, the microscopic aspects of an average DNA search event of hOGG1 were elucidated through the use Monte Carlo diffusion simulations and by fitting to the experimental site-transfer data (Figure 14).⁴⁷ This approach differed from molecular dynamics methods because no force constants were required. Instead, the simulations were constrained by the site-spacing dependence of P_diss and P_assoc, the average lifetime of the enzyme bound to nonspecific DNA (~3 ms), and the physical and stochastic properties of diffusion.⁴⁷ The microscopic features of the average search event revealed by this analysis included (i) the number of associative transfer events per binding event (four), (ii) the associative transfer time and transfer distance (tens to hundreds of microseconds and 9 bp), (iii) the dissociative hop time and distance (tens to hundreds of nanoseconds and 20 bp), and (iii) the damage search footprint arising from the use of associative and dissociative transfer pathways (~60 bp).

2.2.6. Connecting Ensemble and Single-Molecule Measurements.

In addition to generating a high-resolution view of the average search event for hOGG1, the numerical analysis method provided the opportunity to connect the bulk-averaged properties to the previous single-molecule studies of hOGG1.^40,47 In this approach, Monte Carlo simulations that best fit the ensemble site-transfer data were used to calculate the expected mean-squared displacements that would be observed in single-molecule trajectories. The simulated mean-squared trajectories were then plotted against time, and the slope closely reproduced the apparent barrierless 1D diffusion constant previously reported for hOGG1 (D₁^app = 4 × 10⁶ bp).^40,44 This method of connecting the ensemble and single-molecule measurements is important because it shows that an apparent macroscopic diffusion constant (D₁^app) can result from microscopic processes that involve both associative and dissociative transfer modes. It was proposed that the rapid microscopic pathways detected in the ensemble measurements were averaged in the single-molecule studies due to distance and time resolution limits of the method. Just recently, a reanalysis of the single-molecule hOGG1 trajectories, using a new optimal estimator of diffusion coefficients, revealed two-state transfer kinetics in which the protein stochastically switched between a highly mobile state and a less mobile state, as opposed to simple diffusion.¹³³ Although discrepancies still exist between the two measurement methods, the gap is narrowing in terms of mechanistic possibilities.

2.3. Alkyladenine DNA Glycosylase (AAG)

Human alkyladenine DNA glycosylase (AAG) is a monomeric enzyme with a flexible N-terminus that initiates repair of a diverse set of alkylated and deaminated purines by the same multistep base-flipping mechanism as hUNG and hOGG1.^125,134,135 The enzyme fold is distinct from that of hUNG and hOGG1, providing another opportunity to test whether similar facilitated diffusion mechanisms are shared across different protein folds. The experimental work on AAG has been ensemble-based, using similar correlated excision assays as described earlier for hUNG and hOGG1. However, several novel and informative variations were employed to investigate associative and dissociative transfer mechanisms, as well as the in vivo importance of DNA translocation.

2.3.1. DNA Chain Translocation.

The DNA translocation efficiency of AAG was first determined by correlated excision assays employing DNA substrates with two target bases separated by 25 and 50 bp.^45,136 For both site spacings, the translocation efficiency was remarkably high at 100 mM NaCl (P_trans ≈ 1) but dropped to zero at 300 mM salt. The strong dependence of the site-transfer efficiency on salt concentration is consistent with the positively charged DNA-binding surface of AAG, which gives a greater positive electrostatic potential than that of hUNG or hOGG1.^54,116,136 These initial experiments demonstrated that AAG could locate sites by DNA translocation and that electrostatic interactions were critical for efficient site transfers. Interestingly, with respect to the emerging role of the N-terminal domain of hUNG, the amino terminus of AAG was also found to contribute to efficient translocation.⁴⁵

2.3.2. Dissociative Transfers Dominate AAG DNA Translocation.

Several complementary approaches were used to evaluate the importance of associative and dissociative transfers with AAG. These included the use of substrates with two lesions on opposing strands,⁴⁵ comparing the ionic strength dependence of site transfers with theoretical models,⁴⁵ and testing whether site transfers could occur when the two sites were separated by a protein block, single-strand gap, bubble, or bent structure.^45,137

The use of AAG substrates with target sites positioned on opposing strands allowed for testing whether DNA translocation between sites was restricted to associative transfers.⁴⁵ At 100 mM NaCl concentration, AAG efficiently translocated to sites on opposing strands spaced 25 bp apart (P_trans ≈ 0.6), which was indistinguishable from translocation observed for the substrates with lesions on the same strand. Thus, like hUNG and hOGG1, AAG is able to hop between strands so that both target sites are excised before AAG escapes to another DNA molecule.

Hedglin and O’Brien⁴⁵ used both salt and site-spacing dependence of P_trans to determine the importance of associative and dissociative transfers with AAG. Experimental and theoretical work suggests that associative transfers occurring within the DNA ion cloud should be largely insensitive to changes in ionic strength and that dissociative transfers involving condensation of the ion cloud after dissociation of the protein should be strongly salt-dependent.^17,41,110 In addition, the site-spacing dependence of pure associative transfers should follow the relationship P_assoc = S^N, where S is the probability that the enzyme will fall off the DNA at each single-base-pair step and N is the number of steps that are taken before the second site is located.^138,139 These two approaches established that P_trans was strongly salt-dependent and invariant for site spacings of 25 and 50 bp. Both of these observations were inconsistent with pure associative transfers and suggested that AAG employed dissociative transfers under these conditions.

Further evidence for a dissociative transfer mode for AAG was obtained by placing obstacles between the two target sites (a protein, single-strand gaps, bubbles, and bent DNA structures).¹³⁷ The most striking result was obtained by inserting an EcoRI consensus binding site between two damage sites and measuring the ability of AAG to act at both sites in a single binding encounter while EcoRI was blocking the way. Remarkably, AAG bypassed this large roadblock in about 50% of the binding events (Figure 15).⁴⁵ This result suggested that AAG made ~5 nm excursions from the DNA to allow bypass of the protein obstacle and to allow transfer between target sites. This is a very similar distance calculated for hUNG and hOGG on the basis of the small-molecule trapping approach (see above). Similarly, single-strand gaps, bubbles, and bent structures did not impede translocation between target sites as compared to an intact duplex where the target sites were spaced 25 bp apart.¹³⁷ In many cases, these flexible or bent structures led to modestly increased translocation to the second site (P_trans increased from 0.6 to 0.8 at 200 mM NaCl). The ability of AAG to navigate these helix discontinuities is most readily explained by dissociative transfers.

Figure 15.

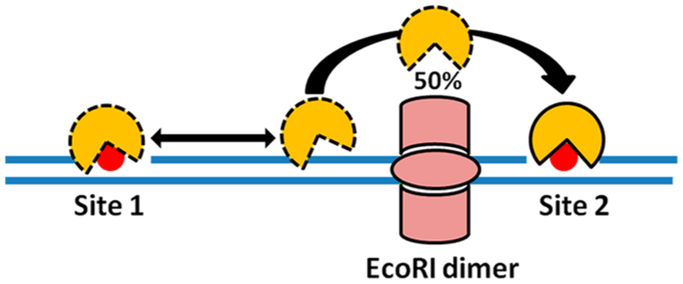
Experimental design for determining whether AAG can bypass protein obstacles positioned between two damage sites. About 50% of the AAG molecules that react at site 1 successfully transfer to site 2 in the presence of the block (see text).

2.3.3. Intersegmental Transfers.

A unique series of experiments was performed on AAG to evaluate its ability to execute intersegmental transfers that involved tethering two DNA substrates with single target sites by a PEG linker and measuring the frequency of correlated enzymatic excisions (Figure 16).⁵² The tether correlates the positions of the two substrates in three-dimensional space and makes their effective concentrations high enough that intersegmental transfer competes with transfer between separate DNA molecules. For a PEG substrate with 60 ethylene glycol units, the effective concentration is estimated to be about 3 mM,⁵² which is similar to DNA chain segment concentrations in the cell nucleus where intersegmental transfer might occur. In these experiments, the transfer efficiencies for the tethered substrates were compared with Those for a duplex in which the two target sites were spaced 25 bp apart. The investigators found that the translocation values for PEG tethers of 1, 4, and 10 units, as well as their salt dependence, were the same as for the intact duplex substrate, establishing that AAG was capable of intersegmental transfer. The absence of a length dependence for the tethers was attributed to the short persistence length of PEG polymers.⁵² Surprisingly, the flexible amino terminus was not required for intersegmental transfer, indicating that a bridging model for intersegmental transfer involving the N terminus was not operative. Thus, a dissociation–jump–rebind mechanism for site transfer was indicated.

Figure 16.

Experimental strategy to elucidate intersegmental transfers by AAG, using PEG glycol linkers to increase the effective concentration of two DNA duplexes containing target sites. Hypothetical hopping and bridging IS pathways are indicated.

2.3.4. DNA Translocation in the Eukaryotic Nucleus.

Ascertaining a connection between in vitro DNA translocation and intracellular DNA damage recognition is essential to establish that translocation truly contributes to biological function. Such a linkage was made with hUNG by use of model uracilated substrates that were transfected into cells. A different approach was taken with AAG that involved constructing a series of mutations in the DNA-binding cleft that affected processivity but not damaged base excision. This series of mutant proteins could then be used to correlate mutational effects on processivity with damage repair in cells.¹⁴⁰

AAG binds to DNA via its positively charged DNA-binding cleft, which contains conserved Arg and Lys residues.¹⁴⁰ Most of these residues are close enough to the phosphate backbone that direct or water-mediated contacts can be made. In vitro kinetic and site-transfer measurements, with serine or methionine substitutions for the conserved Arg and Lys residues, were performed to establish that none of these charged groups affected the kinetics for N-glycosidic bond hydrolysis but instead significantly diminished site transfers to varying extents. The cell-based part of this experiment was performed with a Mag1 glycosylase deletion mutant of bakers’ yeast that allowed for genetic complementation by human AAG. Thus, the deletion mutant was highly sensitive to DNA alkylating agents, which could be rescued to varying extents with the human AAG variants. Sensitive complementation assays were performed with each of the AAG charge variants, and the survival fractions after treatment with methylmetha-nesulfonate (MMS) ranged over 2 orders of magnitude as compared to wild-type AAG. When plots of log survival against log P_trans were made, a strong linear correlation was observed, indicating that DNA translocation ability promotes efficient repair (R² = 0.67). These are perhaps the strongest measurements yet made correlating translocation with DNA repair capacity.

3. DNA TRANSLOCATION BY TRANSCRIPTION FACTORS

Unlike DNA repair glycosylases that recognize isolated damaged bases, transcription factors (TFs) activate or repress transcriptional cascades by recognizing specific sites that span 6–12 bp of DNA (Table 2).^141–143 TFs may be divided into two classes, the housekeeping (constitutively expressed) and inducible categories. Housekeeping TFs are present in the cell at fairly high concentrations and serve to facilitate transcription of core genes. The high expression of housekeeping TFs lessens the requirement for fast DNA translocation, because lower search speeds can be compensated by the high protein copy number. High specific affinity for their target sites is beneficial for these TFs in order to maintain high occupancy and uninterrupted gene expression. On the other hand, inducible transcription factors (iTFs), are expressed at low copy number in response to specific stimuli and are short-lived (minutes to hours), providing a driving force for the selection of fast DNA scanning and high binding affinity. As a result, the apparent rate of target search for iTFs is orders of magnitude faster than for housekeeping transcription factors.^3,42,144,145 Since rapid movement on DNA is in conflict with tight binding, there is a fine balance under which the optimal search time and affinity can be achieved. As with DNA glycosylases, fine-tuning involves conformational switching between a search mode, where the TF can scan through DNA rapidly, and a high-affinity recognition mode.

3.1. General Ensemble Approaches

Ensemble studies of DNA translocation by TFs have used quite different methods than those described above for DNA glycosylases, partly because TFs have no enzymatic activity that would allow the use of the two-site translocation assays. Instead, a variety of spectroscopic and kinetic assays have been used. It is beyond the scope of this review to discuss these methods in detail, but we summarize their essential aspects in Figure 17 and briefly describe their basis below. The interested reader is referred to the literature for more information.^{3,27,42,144,145}

Figure 17.

General stopped-flow fluorescence approach for studying 1D, 3D, and IS pathways of target-site location by a transcription factor (TF).³ (a) Stopped-flow fluorescence measurements of the apparent rate of TF association with its target site (probe DNA) is done in the presence of a large excess of competitor DNA. After initial mixing, the TF is initially bound to the competitor DNA but then partitions to the target site following a mixture of the three available pathways, (b) The contribution of 1D translocation is determined by using probe DNAs of increasing length (L). As the probe length approaches the mean translocation distance of the TF (l_trans); the rate increases (eq 4). When the probe length exceeds l_trans, the enhancement declines because the TF falls off the probe before it finds the site. Eventually, the curve reaches an asymptote at very long probe lengths, as predicted by both theory and experiment.^3,146,147 (c) The contribution of the IS pathway is determined by increasing the competitor DNA concentration. If IS transfer is occurring, the apparent rate decreases more gradually than expected from a mechanism involving simple competitive inhibition (dashed line). Adapted with permission from ref 147. Copyright 2014 Elsevier.

One key method has been the stopped-flow fluorescence quenching technique, which has provided quantitative information on target search kinetics and the contributions of 1D, 3D, and intersegmental transfer search pathways.³ This method involves rapid mixing of the TF with probe DNA containing the target site in the presence of a large excess of unlabeled nonspecific competitor DNA under conditions where [probe] ≪ [protein] ≪ [decoy] (Figure 17a). Since the decoy DNA is in large excess, the TF is initially bound entirely to nonspecific DNA at the time of mixing, but since the target site has very high binding affinity, the TF is 100% bound to the target probe DNA when equilibrium is reached. Thus, the experiment measures the apparent rate constant (k_app) for transfer of the TF from the competitor DNA to its target site, which may occur by 3D, 1D, or intersegmental transfer mechanisms and is detected via fluorescence intensity quenching of the probe target DNA. It is important to realize that the competitor DNA plays an essential role in this approach because direct association of the TF with the target DNA is faster than the dead time of the stopped-flow instrument.

Since k_app is a complex parameter that contains information on all pathways that are used to locate the target site, several variations of the stopped-flow experiment must be performed to dissect out the individual 3D, 1D, and IS components. Information on the 1D mode is revealed by varying the probe DNA length (Figure 17b). When probe DNA length is increased to the range of the mean translocation distance of the TF, the association rate with the target increases because the target size is increased and nearly every encounter leads to location of the specific site by chain translocation (see eq 4). However, when the probe length becomes longer than the mean translocation distance, the association rate begins to plateau (Figure 17b). This effect is due to the TF binding distantly from the target site and frequently dissociating before finding it. The contribution of the IS pathway can be measured by increasing the concentration of competitor DNA to the point where every probe DNA is closely surrounded by competitor molecules, thereby increasing the probability of intersegmental transfer (Figure 17c). Finally, the contribution of the 3D mode can be calculated from the experimentally measured dissociation rate constants and equilibrium binding constants for the TF–nonspecific DNA interaction.

The described stopped-flow methodology provides little information on structural determinants that govern facilitated diffusion, and a variety of NMR dynamic methods have proved invaluable in this regard. These dynamic methods are powerful because they can cover an enormous range of time scales (~1–10⁻¹² s) and can yield residue-specific information on TF conformational changes that are involved in nonspecific and specific DNA complexes. In particular, NMR dynamic measurements using isotopically labeled TFs have allowed study of the elusive conformational switch that is implicated in DNA translocation by many proteins (see preceding and following text). The useful NMR methods that have been used are described in a recent review article.²⁷

Another ensemble approach for inferring the occurrence of DNA translocation was taken by McKinney et al.¹⁴⁸ Here the TF (p53) was bound to a 60 bp DNA containing biotin end-labels in the presence and absence of streptavidin. These researchers proposed that if p53 DNA translocation was important, it should slide off DNA containing the free ends but be blocked when the ends were occluded by streptavidin. Thus, by this reasoning, the presence of translocation would result in a greater rate of dissociation when the DNA ends were free. The experimental protocol involved mixing p53 with DNA (±strepavidin), challenging with an excess of competitor DNA, and assessing how much p53 was bound over time by an electrophoretic mobility shift assay (Figure 18). Although the authors detected more p53 bound when the ends were blocked, suggesting translocation, 50–60% of the initially bound complexes had dissociated at the first time point in the presence of strepavidin, which indicates the presence of an additional rapid pathway for escape that does not involve sliding off the DNA ends. This pathway would be consistent with dissociative transfers (hopping), as observed in similar studies with AAG (see section 2.3.2).

Figure 18.

DNA end-blocking method for detection of dissociation events involving sliding off the DNA ends. This approach was used in early studies of p53 and suggested the presence of linear diffusion (see text).¹⁴⁸ Adapted with permission from ref 148. Copyright 2004 Elsevier.

3.2. Early Growth Response Protein Egr-1

Egr-1 (Zif268) is an inducible transcription factor with crucial regulatory properties. In the brain it is responsible for synaptic signaling and long-term memory formation,¹⁴⁹ while at the same time it serves as a stress-induced TF in the cardiovascular system, initiating defenses against vascular injury.¹⁵⁰ Given the short lifetime of the protein in cells (~1 h), fast gene activation by Egr-1 in response to stimuli is central for its function. The very tight time constraints within which Egr-1 must locate its target site makes it a compelling system for study. Egr-1 has two primary structural elements, a zinc finger DNA-binding subunit that contains three Zn-finger domains and a protein recruitment subunit that is devoid of DNA-binding properties and acts as a scaffold for localizing other proteins needed for downstream transcriptional regulation.^151–153 Most studies have focused on the facilitated diffusion properties of the isolated DNA-binding domain of Egr-1. Recent work has provided extensive information on the role of thermodynamics and protein dynamics in DNA translocation by Egr-1. These studies were able to measure all three modes of facilitated diffusion during the target search by Egr-1.

3.2.1. Target Search Pathways of Egr-1.

The stopped-flow method (Figure 17a) was used to detect and quantify the contributions of the individual facilitated diffusion pathways of Egr-1. The DNA probe length dependence of the apparent association rate with the target sequence provided information on both 1D diffusion and the mean translocation length (l_trans).¹⁴⁷ In these studies, the apparent association rate first increased sharply when the probe length (L) was extended in the range 33–63 bp but ultimately reached a limiting value at a probe length of 88–112 bp (Figure 17b). The observed dependence on L is consistent with eq 4 and the model in Figure 1, because when L > l_trans, most initial encounter events with the probe DNA are far from the target site and most chain translocations do not lead to productive encounters with the target site. These data indicated that 1D translocation (associative or dissociative) was occurring with a mean transfer length of ~50 bp.^3,147 In separate experiments, the concentration of nonspecific competitor DNA was varied in order to measure the contribution of IS to the overall apparent target association rate (Figure 17c). In these experiments, as much as 100 μM DNA competitor was used to approximate the DNA nucleotide density found in the nucleus. Strikingly, the observed rates of association were weakly dependent on competitor DNA concentration ([C]), which deviated from the expectation of a simple kinetic competition model where the rate of target location rapidly approaches zero at high competitor DNA concentration (dashed line, Figure 17c). The observed competitor DNA concentration dependence is consistent with a model where at low competitor concentration k_app is large (because competition is weak), and then k_app decreases as the competitor concentration increases. Finally, when the competitor reaches a concentration that supports IS through a ternary complex involving TF, probe DNA, and competitor, the rate levels off (Figure 17c). It was concluded that, at high competitor DNA concentration, Egr-1 located its target site most frequently using the IS pathway (92% of all recognition events), suggesting that IS can contribute greatly when the concentration of DNA chains is high. The investigators used global minimization analysis of the kinetic traces to calculate an IS rate of about 10⁶ M⁻¹⋅s⁻¹. The investigators then used an analytical approach to calculate D₁ ≈ 10⁵ bp²⋅s⁻¹ by use of constraints derived from probe length dependence of association rates, protein residence time on the DNA, and IS rates.³

3.2.2. Salt Dependence.

The salt dependence of the target association rate of Egr-1 provided a convenient tool to investigate the interplay between the different pathways for locating the target site. Accordingly, the aforementioned probe length and competitor concentration dependence experiments were performed as a function of monovalent salt concentration (Figure 19). The IS rate (k_IS) showed a strong log–linear dependence on salt concentration (Figure 19a), which was interpreted in terms of salt-facilitated release of Egr-1 from the competitor DNA during IS. In contrast, the values for D₁ showed a biphasic response to increasing salt (Figure 19b). At low salt concentrations, D₁ was unaffected, but a strong log–linear increase in D₁ was observed as the salt concentration was increased. The biphasic response was interpreted in terms of a change in pathway from slower salt-resistant associative transfers at low salt to rapid salt-dependent dissociative transfers at higher salt. Presumably, associative transfers dominate at low salt because the closely associated protein and DNA exclude invasion of the binding interface by ions; as the salt concentration is increased, more of the associative transfers are interrupted, leading to the change to the dissociative transfer pathway. These studies indicated that Egr-1 showed maximum efficiency in its target search at about 145 mM K⁺, which optimally balanced the 1D, 3D, and IS pathways.

Figure 19.

Salt dependence of the apparent rate of target-site location by Egr-1 changes the relative contributions of the 1D, 3D, and IS pathways for target-site location, (a, left panel) The IS rate (k_IS) increases in a log–linear fashion with salt, which was attributed to salt-enhanced release of Egr-1 from competitor DNA. (b, right panel) The diffusion constant for 1D translocation increases in a biphasic fashion with respect to salt concentration.³ The salt-resistant region was attributed to associative DNA translocation, and the salt-enhanced region was attributed to salt-enhanced dissociative transfers. Adapted with permission from ref 3. Copyright 2014 Oxford University Press.

3.2.3. Dynamic Search Mode of Egr-1.

A two-state target search mode for Egr-1 was strongly indicated by NMR methods that focused on Zn-finger domain dynamics in the presence of nonspecific and specific DNA (Figure 20).⁴² In the search mode involving the nonspecific complex, the individual ZF1 and ZF2 domains exhibited large dynamic motions, resulting in transient dissociation of the individual domains (Figure 20a). This behavior was consistent with a highly populated open state (search mode, 99%), with the properties of low binding affinity and rapid DNA translocation, and a poorly populated closed state (recognition mode, ~1%), where the individual ZF1 and ZF3 domains were closely stacked on the DNA backbone, suppressing the domain motions observed in the search mode (Figure 20b). The recognition conformation has the properties of high binding affinity/specificity and poor DNA translocation.

Figure 20.

Two-state search and recognition by Egr-1 as determined by NMR dynamic measurements.⁴² (a) The search mode is suggested to involve only one Zn-finger domain interaction with the DNA, which gives rise to low specificity, weak binding, and rapid translocation. (b) The recognition mode involves interaction of two Zn-finger domains and is relatively immobile compared to the search mode conformation. The conformational equilibrium favors the search mode when nonspecific DNA sequences are being scanned.

Large structural differences between search and recognition states have not always been observed for TFs. For example, similar NMR experiments performed on the high-mobility group (HMG) proteins SOX, OCT, and HMBG1 detected a predominant population of the closed recognition state.^{55,145,154,155} A high population of the recognition state, with its suppressed domain dynamics and strong DNA binding, implied a lower target search rate for these proteins. This prediction was confirmed because HMG class proteins have slow IS rates of ~10⁴ M⁻¹⋅s⁻¹ and D₁ values <4 × 10⁴ bp²⋅s⁻¹, which may be compared with IS rates of ~10⁶ M⁻¹⋅s⁻¹ and D₁ ≈ 10⁵ bp²⋅s⁻¹ for Egr-1. These informative studies indicate how differences in protein dynamics can have a large impact on DNA translocation and intersegment transfer kinetics.

3.3. p53 Tumor Suppressor Protein

p53 is an inducible negative regulator of transcription that is activated in response to diverse stimuli ranging from DNA damage, hypoxia induced stress, and dNTP depletion and promotes cell cycle arrest or apoptosis.^156–158 The tumor suppressor activity of p53 is well-recognized and its loss is associated with a vast number of cancers.¹⁵⁹ Unlike other proteins in this review, p53 acts as a dimer of dimers, with each dimer recognizing half of a 20 bp target sequence (Table 2). p53 also contains two distinct DNA-binding domains: the core domain that binds DNA in a sequence-specific fashion and the C-terminal domain that interacts nonspecifically with DNA. This structural arrangement could give rise to complex diffusive behavior compared to the simpler systems discussed above. The Schaffer group was the first to detect linear diffusion of p53 on DNA by using solution time-lapse atomic force microscopy.¹⁶⁰ The presence of DNA translocation was further supported by ensemble studies in 2004 using the streptavidin end-blocking method (Figure 18).¹⁴⁸ In 2008, Tafvizi et al.¹⁶¹ were the first to use single-molecule imaging methods to directly visualize DNA translocation by p53 in vitro and make quantitative measurements of diffusive parameters. This initial work was followed by others in the past decade, providing extensive single-molecule information on the kinetics of DNA translocation by p53 in vitro and its diffusive behavior in living cells. Although outside the scope of this review due to our tight focus on mechanisms of DNA translocation, the elegant single-molecule work of Tjian and co-workers^162,163 and Hager and co-workers,¹⁶⁴ covering the dynamic behavior of transcription factors in living cells, overlaps conceptually and methodologically with topics covered here.

3.3.1. DNA Translocation by p53 in Vitro.

Tafvizi et al.¹⁶¹ studied translocation of fluorescently tagged p53 in flow stretched DNA using total internal reflection microscopy (TIRF), in analogous fashion to the previous single-molecule studies of hOGG1 (see section 2.2.1). By analysis of the singlemolecule displacement histograms as a function of time, the average translocation distance and 1D diffusion constants were calculated (Figure 21). For p53, the mean displacements were interpreted in terms of two overlapping distributions, which were attributed to distinct diffusive states on the DNA chain with diffusion constants of 10⁵ and 10⁶ bp²⋅s⁻¹. The faster diffusion mode approaches the magnitude of barrierless, as previously measured for hOGG1. As noted in section 2.2.6, a reanalysis of the original hOGG1 single-molecule trajectories also indicated a two-state process with similar D₁ values as p53, making the results from these divergent proteins quite similar.^133,144,161

Figure 21.

In vitro measurements of p53 diffusion. An in vitro two-state model of pseudo-WT p53 sliding on DNA was used, with a slow component of ~3 × 10⁵ bp²⋅s⁻¹ and a fast component of ~2 × 10⁶ bp²⋅s⁻¹. The solid line represents the best fit for a model with two diffusion components, and dashed lines represent the distribution of each of these modes. The mean sliding distance is ~300 bp and the mean diffusion coefficient is 10⁵ bp²⋅s⁻¹. The average residence time was reported as ~1 s. Adapted with permission from ref 165. Copyright 2015 Elsevier.

3.3.2. Structural Aspects.

The two-state target search model has been discussed for every system in this review, and it is not surprising that recent studies on p53 also favor this model.^{25,144,161,165} For p53, the bimodal distribution of the mean displacements (Figure 21) suggested that at least two unique conformations of p53 were involved with slow and fast diffusive properties, respectively. The slow population was interpreted as the recognition mode of p53, while the fast population was interpreted as the search mode. A structural interpretation for the two-state diffusive behavior of p53 was suggested from additional single-molecule studies using the isolated p53 core and C-terminal domains, both of which bind DNA (Figure 22).^144,165,166 From these combined results, it was proposed that p53 oscillates between a state where the C-terminal domain is bound and the core domain is dissociated (search mode) and a state where the core domain is associated and the C-terminus is dissociated (recognition mode).^144,165 Recent work from Kamagata and co-workers¹⁶⁶ indicates that the transition between the two modes is mediated by the linker domains connecting core and C-terminal domains (Figure 22).

Figure 22.

Structural model for two-state diffusive behavior of tetrameric p53, as suggested from in vitro single-molecule studies.^144,166 The model involves oscillation between a low-affinity search (fast) mode, where the C-terminal domains (CTD, shown in green) are engaged, and a slow recognition mode, where the core domains (CD, shown in blue) are engaged (see text). The transition is suggested to involve the linker regions connecting the domains (shown in red).¹⁶⁶ Adapted from ref 166. Copyright 2017 American Chemical Society.

3.3.3. p53 DNA Translocation in Mammalian Cells.

DNA translocation by p53 has also been extensively studied in living cells by single-molecule and ensemble fluorescence techniques (Figure 23).^167–170 A short summary of this work has recently been published,²⁵ but we take this opportunity to compare the in vitro and cell findings for p53 with the cellular translocation studies for DNA glycosylases.

Figure 23.

Fluorescence spectroscopic techniques to measure protein diffusion in living cells. (a) Fluorescence recovery after photobleaching (FRAP) method (see text). (b) Fluorescence correlation spectroscopy (FCS) method. A thin confocal plane containing 1–100 particles is irradiated over a given time period. Oscillations in fluorescence intensity due to particles moving in and out of the detection plane are detected. Intensity fluctuations as a function of time are deconvoluted through a correlation analysis. The resulting time-dependent decay of the autocorrelation function can be fit by models that report on the contributions of the diffusive components and the rates of diffusion; a diffusion system is depicted with three time scales with equal contributions from each component. (c) Single-molecule tracking (SMT) method. Individual particle trajectories are monitored in the cone of the excitation laser beam as a function of time. The individual trajectory displacements are plotted as a frequency histogram, allowing determination of the mean displacement distances and diffusion coefficients through Gaussian fitting (a hypothetical case for a one-component diffusion system is presented).

Three quantitative fluorescence techniques have been utilized to study the diffusive behavior of p53 in living cells: fluorescence recovery after photobleaching (FRAP),^167,169 fluorescence correlation spectroscopy (FCS),^167,171 and single-molecule tracking (SMT) (Figure 23).^167,168 The FRAP approach was used by Hinow et al.¹⁶⁹ to investigate translocation of green fluorescent protein (GFP)-tagged p53 in the H1299 cell line (Figure 23a). With this technique, a small volume within the cell is irradiated with laser light to photobleach all GFP–p53 molecules in the volume. The time-dependent recovery of fluorescence within the bleached volume is mediated through Brownian diffusion, providing information on the diffusive behavior of the protein and the mean residence times of any immobile bound states that are detected. These initial investigations suggested the presence of only a single diffusive state of p53 with a large diffusion constant of ~15 μm²⋅s⁻¹, which was attributed to free diffusion.¹⁶⁹ The magnitude of this constant is only 6-fold less than what would be expected in aqueous buffer, indicating that the crowded cellular environment does not dramatically impede diffusion. In addition, an immobile state was detected with a lifetime of about 3 s, which was interpreted as p53 bound to nonspecific DNA. However, this interpretation cannot be made conclusively from these experiments alone. To support this interpretation, further measurements employing p53 mutants¹⁶⁸ and other complementary single-molecule methods were required.^167,168

Methodological advances in single-molecule methods have emerged and have been applied to p53. FRAP in combination with FCS and SMT (Figure 23b,c) has been used to determine diffusion rates of GFP-tagged p53 in H1299 cells.¹⁶⁷ Two diffusion constants were detected by these measurements,¹⁶⁷ which were attributed to nonspecific and specifically bound states of p53 with a total bound lifetime of ~2 s and diffusion constants D_fast = 4 μm²⋅s⁻¹ and D_slow = 0.7 μm²⋅s⁻¹. These constants are quite similar to those measured in aqueous buffers, suggesting surprisingly that diffusion on chromatin is remarkably comparable to that on naked duplex DNA. SMT is an advantageous component in this approach because it permits direct tracking of individual molecules with a spatial resolution of ~80 bp, whereas the resolution of FCS and FRAP methods is ~900 and ~6000 bp, respectively.^48,167,168 Thus, SMT is the best technique for picking up diffusion modes that may be averaged in the other techniques due to lack of resolution. More recent SMT studies by Loffreda et al.¹⁶⁸ have also detected similar diffusive states of Halo-tagged p53 in the MCF-7 cell line.¹⁶⁸ In this work, the fractional contribution of the slowest diffusive state was increased after induction of DNA damage by ionizing radiation, suggesting that this state is a damage-specific p53–chromatin complex.

4. TARGET SEARCH REQUIREMENTS

The comprehensive measurements that have been performed on the systems described here provide the basis for making some unifying conclusions relating DNA target search mechanisms with the different biological functions of DNA glycosylases and sequence-specific transcription factors. We focus on two fundamental distinctions between DNA glycosylases and TFs: (1) the different size and accessibility of their respective target sites and (2) the requirement that DNA glycosylases must inspect all individual genomic base pairs in a timely manner, while TFs only need to find their specific sites with no genomewide surveillance requirement. These distinguishing aspects of function would be expected to drive evolution of distinct properties of the individual search mechanisms.

The small single-base targets of DNA glycosylases, which are buried within the DNA duplex, and the requirement for searching all genomic base pairs for damage imposes a strong selection pressure for short binding lifetimes at individual base pairs and rapid base-pair inspection by the base-flipping mechanism. It should be noted that the millisecond time-scale binding lifetimes of glycosylases to nonspecific DNA give an upper limit time frame for DNA translocation. These values are upper limits because a significant fraction of this time is spent in an immobile state. Biochemical, NMR, kinetic, and crystallographic studies have established how hUNG and hOGG1 use base flipping to rapidly determine the nature of DNA bases on a millisecond or less time scale, thereby minimizing the time spent at individual base pairs.^{43,46,73,124,125,172} The slower time scale for associative as compared to dissociative DNA translocation is critical because it provides a sufficient lifetime and redundancy at individual base pairs to allow inspection by the base-flipping mechanism (estimates for D_ass fall in the range 10⁴–10⁵ bp²⋅s⁻¹).^39,47 In contrast, rapid dissociative transfers serve the purpose of allowing the glycosylase to move frequently to the opposite strand of DNA, as well as to nearby DNA chain segments to increase coverage (IS pathway). The high copy number of DNA glycosylases in the cell nucleus is also important because no single glycosylase is responsible for surveying more than about 20 000 bp of DNA chain on average. For these enzymes, target specificity and binding affinity are only transiently realized after a large conformational change that results in extrusion of the damaged base into the enzyme active site.^89,90

In contrast to DNA glycosylases, TFs recognize a much larger target sequence and bind with high affinity and specificity. (The exception is p53, which shows a less than 10-fold difference between its specific and nonspecific binding to 30 bp DNA oligomers.¹⁷³ The basis for this difference is not clear, but it may reflect the complex cooperative DNA binding of p53 that involves the formation of high-affinity tetramers from dimers that predominate under low protein equilibrium binding conditions.¹⁷⁴) One ramification of high binding affinity for a specific sequence is that affinity for similar as well as random sequences in the genome will also be raised, which will slow movement along DNA chains.¹⁷⁵ Since high affinity is incompatible with rapid motion along the DNA, TFs have evolved conformational changes to kinetically partition between weak-binding search modes and tight-binding recognition modes to enhance speed and retain affinity. As with DNA glycosylases, the weakly bound search mode consists of associative and dissociative components that are important for achieving both recognition and speed.

5. RECONCILING ENSEMBLE AND SINGLE-MOLECULE MEASUREMENTS

Although ensemble and single-molecule measurements of protein diffusive parameters share some similarities, fundamental differences in mechanistic interpretation still exist between investigators that employ these different approaches. These distinctions go beyond mere semantic definitions of associative (sliding) and dissociative (hopping) mechanisms and have not been adequately addressed.

It is noteworthy that p53, hOGG1, and every other protein that has been probed by the single-molecule TIRF method shows identical barrierless 1D translocation constants.^{40,144,165,173,176} It is counterintuitive that proteins with different structures, functions, and widely different DNA-binding properties would share identical behavior in this regard because sliding (defined by remaining in contact with the DNA chain) should be impacted by the unique properties of the protein. However, from the single-molecule perspective there appear to be similar minimal drag forces induced by protein–DNA interactions. We suggest that barrierless diffusion is more easily explained by dissociative transfers that involve short-time-frame free diffusion in the vicinity of the DNA chain (D_diss ≈ 100 μm²⋅s⁻¹) . This type of movement has been established as the primary mode of transfer in all ensemble measurements. Thus, a dominant dissociative pathway for long-range translocation would appear to account for both the single-molecule and ensemble measurements.

However, it has been argued many times that the single-molecule process is exclusively sliding because the apparent 1D diffusion constants were independent of salt concentration (i.e., sliding inside the DNA ion cloud is not expected to be influenced by bulk ion concentration).^17,41 We interpret the salt dependence differently: there is no reason to expect that the diffusion constant for a dissociative process would be sensitive to salt, because salt does not alter free diffusion. In contrast, the mean translocation distance would be expected to decrease, because salt decreases the probability of productively rebinding to the DNA during a dissociative transfer. Indeed, for hOGG1, D₁ was insensitive to salt and the mean displacements were sharply decreased as the salt concentration was increased, consistent with a process that involved dissociative steps.⁵⁴ As discussed in section 2.2.6, Monte Carlo simulations based on ensemble translocation measurements of hOGG1 support this interpretation because the observed barrierless D₁ value could be reproduced by use of ensemble transfer parameters that included both associative and dissociative components.⁴⁷

The time resolution and data processing of single-molecule translocation data may also account for some of the differences with ensemble measurements. For instance, the analysis of single-molecule displacements typically involves filtering for long events that occur in the time window 250–500 ms,^144,165 which misses rapid events that can be detected in ensemble approaches. For p53, this filter window is over 10 times longer than its mean bound lifetime and suggests that short-range translocation events (if present) would not be well-characterized by the method. In contrast to barrierless sliding, estimates of the diffusion constants for associative transfers from ensemble experiments are generally much lower (10⁴–10⁵ bp²⋅s⁻¹),^39,47 indicating the presence of frictional forces (i.e., DNA–protein interactions) that impede free movement. The macroscopic friction arises from highly dynamic protein interactions with the DNA during associative transfers.^42,47 These associative transfers only occur during a tiny fraction of the total bound lifetime of the protein when it transiently accesses the open-conformation search mode (a time frame for associative transfers with hUNG has been estimated as 10–100 μs on the basis of NMR dynamic studies). Except for NMR dynamic measurements of hUNG and Egr-1, there are few if any measurements that provide estimates of the lifetime of the essential mobile associative search state.^42,121

6. PERSPECTIVE

After nearly 50 years of studies on various proteins that interact with DNA, the mechanisms and microscopic aspects of DNA translocation seem broadly similar. Most of what we have learned can be summarized by proximity effects: when two particles are close to one another, they will remain close and encounter many times until a stochastic translational step moves them far enough apart that their positions are no longer correlated. Nothing in this simple account deviates substantially from the expectations of simple local diffusion. Nevertheless, polymer and ion-cloud properties of DNA, electrostatic properties of the binding partners, caging effects of macromolecular crowding, and the action of disordered tails that interact with DNA all serve to promote DNA translocation. Thus, the efficiency of DNA translocation depends on the properties of protein, the solution environment, and the nature of the DNA polymer itself. The most significant and elegant role of the protein involves conformational changes that facilitate movement along DNA (dissociative or associative) and efficient site recognition.

Biography

Alexandre Esadze obtained a B.S. in theoretical and experimental physics from Tbilisi State University of Georgia in 2009. In 2014 he received a Ph.D. from the Department of Biochemistry and Molecular Biology (BMB) at University of Texas Medical Branch at Galveston, with growing interest in protein–DNA interactions. In 2015 he joined the Stivers laboratory, where he recently completed his long-term ambition of linking the in vitro and in vivo research on facilitated diffusion of proteins. Presently, he continues to work in the Stivers group, focusing on quantitative elucidation of HIV1 restriction through pharmacologic modulation of the DNA repair machinery and development of base-resolution uracil sequencing.

James T. Stivers obtained his Ph.D. in biochemistry from Johns Hopkins University in 1992, where he became interested in enzyme catalysis. He received postdoctoral training in heteronuclear NMR and enzymology in the laboratory of Albert Mildvan at Johns Hopkins Medical School, where he was an American Cancer Society postdoctoral fellow from 1993 to 1996. He then joined the faculty of the Institute for Bioscience and Biotechnology Research in Rockville, MD, as an assistant professor in 1996. In 2001, he moved his laboratory to the Department of Pharmacology and Molecular Sciences at Johns Hopkins Medical School, where he is now a professor and the interim director. His research focuses on understanding the nature of DNA repair and how DNA repair pathways impact viral infectivity.