Abstract
Gene transcription is a noisy process, and cell division cycle is an important source of gene transcription noise. In this work, we develop a mathematical approach by coupling transcription kinetics with cell division cycles to delineate how they are combined to regulate transcription output and noise. In view of gene dosage, a cell cycle is divided into an early stage and a late stage . The analytical forms for the mean and the noise of mRNA numbers are given in each stage. The analysis based on these formulas predicts precisely the fold change r* of mRNA numbers from to measured in a mouse embryonic stem cell line. When transcription follows similar kinetics in both stages, r* buffers against DNA dosage variation and r* ∈ (1, 2). Numerical simulations suggest that increasing cell cycle durations up-regulates transcription with less noise, whereas rapid stage transitions induce highly noisy transcription. A minimization of the transcription noise is observed when transcription homeostasis is attained by varying a single kinetic rate. When the transcription level scales with cellular volume, either by reducing the transcription burst frequency or by increasing the burst size in , the noise shows only a minor variation over a wide range of cell cycle stage durations. The reduction level in the burst frequency is nearly a constant, whereas the increase in the burst size is conceivably sensitive, when responding to a large random variation of the cell cycle durations and the gene duplication time.
Author summary
Gene transcription in single cells is inherently a stochastic process, resulting in a large variability in the number of transcripts and constituting the phenotypic heterogeneity in cell population. Cell division cycle has global effects on transcriptional outputs, and is thought to be an additional source of transcription noise. In this work, we develop a hybrid model to delineate the combined contribution of transcription activities and cell divisions in the variability of transcript counts. By working with the analytical forms of the mean and the noise of mRNA numbers, we show that if the transcription kinetic rates do not change considerably, then the average mRNA level is increased about 1 to 2 folds from earlier to later cell cycle stages. When transcription homeostasis is attained by varying a single kinetic rate between the two cell cycle stages, we find no significant changes in the transcription noise, and the homeostasis nearly minimizes the noise. In our continuous study on the transcript concentration homeostasis that the transcription level scales with the cellular volume, we find only minor variations of the noise if the homeostasis is maintained either by reducing the transcription burst frequency or by increasing the burst size in late cell cycle phase, in the face of a large cell cycle stage duration variation. The reduction in the burst frequency is relative robust, while the increase in the burst size is conceivably sensitive, to the large random variation of the cell cycle durations and the gene duplication time.
Introduction
Single cell studies over last decades have shown that gene transcription is inherently a stochastic process in a bursting fashion [1–5]. The transcriptional bursting, whereby a gene promoter transits randomly between short periods of mRNA production and long periods of no productions, has been widely studied and invoked to explain how the fluctuation of mRNA molecules arises among single cells of identical genes [6–8]. Early studies on the origin of variability in gene expression found that the noise is not solely due to the randomness in reactions intrinsic to gene expression [9].
Recent experiments have suggested that cell division cycle is an important source of gene expression noise [10–13]. In virtually all cells, from bacteria to mammalian cells, a conserved class of genes is involved in cell cycle stage-specific gene expression. For instance, SWI5 and CLB2 are responsible for mitotic progression, whose transcripts are stable during the interphase, but exhibit a 30-fold increase in degradation in the mitosis phase [12]. In budding yeast, acetylation of histone 3 suppresses transcription activity to buffer changes in DNA dose for expression homeostasis of other genes during DNA replication [13]. During cell division processes, genome duplication involves DNA dosage increase at discrete times in S phase, and introduces considerable variations in gene copies [13–15]. Moreover, the time spent between two successive cell-division events [11], the DNA replication catalyzed by DNA polymerases [16, 17], the variation in transcription kinetics between different cell cycle stages [9, 15, 18], and the partition of molecules between two daughter cells [19], are all observed to be stochastic and may contribute to cell-to-cell variability in transcript counts.
It remains largely unexplored how these random events govern mRNA outputs and their fluctuation among individual cells [1]. In this work, we initiate a mathematical approach by coupling the classical two-state model with cell division cycles to delineate the combined contribution of transcription activities and cell divisions in the variability of transcript counts [4, 6, 20]. In view of gene dosage, a cell cycle is divided into and stages. In each stage, the target gene transits randomly between active and inactive states with constant rates. As usual, we use the mean, the noise, and the noise strength to characterize stochastic gene transcription. For a given random variable N, we denote by E[N], E[N2], and Var[N] = E[N − E[N]]2 its mean, the second moment, and variance, respectively. Its noise and the noise strength are defined by
| (1) |
We will formulate the master equations for the model and derive the differential equations of the mean and the second moment. The analytical forms of the mean, the noise, and the noise strength at steady-state will be given.
We measure the fold change of mRNA copy numbers from to by , where and are the mean transcription levels at the two stages. Although r* may take any prescribed value in theory, we find that when the transcription kinetic rates are similar in the two stages, the fold change buffers against the DNA dosage variation and stays within (1, 2), as observed in yeast [12] and mammalian cells [15]. Furthermore, if stage transitions are considerably slower than transcription state transitions and mRNA turnover, then r* ≈ 2. The accuracy of our theoretical results is tested by numerical examples that generate nearly the same fold change measured in a mouse embryonic stem cell line [15]. Increasing either of the cell cycle durations up-regulates transcription with less noise, and rapid transitions between cell cycle stages are a major source of highly noisy transcription. Our numerical examples also demonstrate that transcription homeostasis does not bring significant changes in transcription noise. If transcription homeostasis is attained by varying a single kinetic rate in the two cell cycle stages, then the homeostasis nearly minimizes transcription noise. Motivated by increasing evidences that many cellular processes depend mainly on the concentration rather than the absolute number of enzymes [18, 21, 22], we continue to study the noise profile when the transcript concentration homeostasis is maintained. Our analysis reveals an interesting phenomenon that the transcription noise is relatively stable when the concentration homeostasis is maintained, either by reducing the transcription burst frequency or by increasing the burst size in late cell cycle phase, over a wide range of cell cycle stage durations. The reduction degree in the burst frequency is nearly a constant, while the increase in the burst size is conceivably sensitive, when responding to a large random variation of the cell cycle durations and the gene duplication time.
Models
Coupling transcription with cell division cycle
In past two decades, the two-state model has been a prevailing tool to characterize stochastic gene transcription in single cells, from bacteria, yeast, to mammalian cells [4–6, 8, 20, 23]. In the model, as depicted in the diagram
| (2) |
it is postulated that the gene promoter transits randomly between inactive (gene OFF) and active (gene ON) states with constant activation rate λ > 0 and inactivation rate γ > 0. The transcripts are produced only when the gene is active with a synthesis rate ν > 0, and are turned over with a degradation rate δ > 0. Apparently, as the four rates are all assumed to be constants, the transcription described by the model is independent of many important cellular processes such as cell growth and cell division.
Actively dividing eukaryote cells go through several stages known collectively as the cell division cycle, including Gap 1 phase (G1) for cell growth, the synthesis phase (S) for DNA replication, Gap 2 phase (G2) for DNA repairing, and the mitotic phase (M) for cell division; see Fig 1. During S phase, each gene is duplicated into two copies that are transcribed independently in the same cell [15]. During M phase, a cell is divided into two daughter cells and residual mRNA molecules are randomly partitioned. Cell division cycle has global effects on mRNA and protein synthesis, and is also an important source of gene expression noise [10–13]. In recent years, many real-time monitoring methods, such as single molecule fluorescent in situ hybridization (smFISH), have been developed to estimate mRNA copy numbers in different cell cycle stages. In mouse embryonic stem cells, nascent Oct4 and Nanog mRNAs were measured in different phases using smFISH method [15]. It was found that the ratio of the average number of mRNA copies in G2 phase to the average in G1 phase is 1.28 ± 0.09 for Oct4 mRNA, and 1.51 ± 0.15 for Nanog mRNA. In yeast cells, CLB2 mRNAs accumulate apace in late S phase and are degraded almost completely before cytokinesis [12]. From the measurements of [12], we estimated that the median of cytoplasmic CLB2 mRNA copy numbers is ∼10 in G2/M phase, and ∼5 in S phase. It remains an essential and widely open question to quantify how the transition of cell cycle phases, the variation of DNA content and transcription kinetics in different phases, and the random partition of mRNAs in daughter cells affect the dynamics and noise of gene transcription.
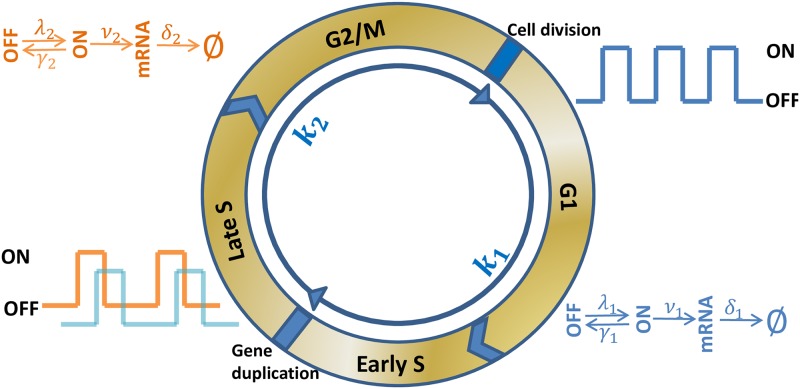
Fig 1. Coupling gene transcription with cell cycle.
Actively dividing eukaryote cells go through G1, S, G2 and M phases in one cell cycle. In our model, we divide one cycle into two stages: (from last division to gene duplication) and (from gene duplication to next division). Cells orderly rotate between and stages with constant rates κ1 and κ2. The promoter transits randomly between active and inactive states, and the transcription kinetics changes with the cell cycle stages. During stage, the kinetics is parameterized by activation rate λ1, inactivation rate γ1, synthesis rate ν1, and mRNA degradation rate δ1. After DNA replication, the gene is duplicated into two identical copies that are transcribed independently with constant rates λ2, γ2, ν2 and δ2 in the same cell during stage.
In this work, we initiate a quantitative approach to this important question by developing a model that couples gene transcription with cell cycles. During DNA replication in S phase, the two complementary strands in each double helix are separated and serve as templates for the production of their counterparts. After the completion of the whole DNA replication process, which takes hours in some cells [24], each gene copy is doubled with two copies. Normally, the duplication of a single gene takes much shorter time and is completed within seconds to minutes [17, 25]. For instance, the genome of Escherichia coli K12 has ∼ 4.64 million base pairs with ∼ 4375 genes [26], and is replicated at ∼470 ± 180 bp/s [17]. The average duplication time of each gene takes 1.63 ∼ 3.66 seconds. In our model, we treat the short duplication process of our target gene as instantaneous, and accordingly, divide a cell cycle into two stages:
stage, consisting of the whole G1 phase and the early S phase until the gene of our interest is duplicated.
stage, consisting of the late S phase after the gene is duplicated, and G2/M phases.
We make the following assumptions to complete the description of the model:
-
i
The durations T1 in stage and T2 in stage are independently and exponentially distributed with respective rates κ1 > 0 and κ2 > 0.
-
ii
At the beginning of each stage, the transcription activity is turned off and the gene remains in the OFF state.
-
iii
In stage, the transcription of the single gene copy is described by the two-state model with constant rates λ1, γ1, ν1 and δ1.
-
iv
In stage, the two identical copies of the gene are transcribed separately and independently, and the transcriptions are described by the two-state model with constant rates λ2, γ2, ν2 and δ2.
-
v
At the end of stage, each mRNA molecule has an equal probability to be distributed to the two daughter cells; see Fig 1.
We do not assume constant durations in and stages in (i), because the time spent in each cell cycle phase is often not fixed, and the timing for the duplication of the target gene is random. The cell cycle duration in mouse embryonic stem cells measured by flow cytometry varies in 11 ∼ 16 hours [27, 28], that are roughly distributed in G1 (26%), S (52%), and G2/M (22%) estimated by the percentage of cells in these phases [28]. The times spent in cell cycle phases were also measured by time-lapse microscopy and single cell tracking in T and B lymphocytes from reporter mice, and the total division time data were found to be well approximated by the sum of consecutive independent exponential and Gaussian distributions [11]. We assume that the transcription is turned off at the beginning of each stage, as DNA synthesis is catalyzed by DNA polymerase in nucleosomes, and during late stage, the chromatin shrinks into chromosome [29–31]. In either case, transcription factors and RNA polymerase II are usually prevented from reaching to gene promoters to initiate transcription [32]. Assumption (v) is equivalent to the binomial distribution of mRNA molecules in the two daughter cells, which has been assumed in most theoretical models, and supported by recent experiments. The partition in Escherichia coli measured by the MS2-GFP reporter strongly supports the assumption that each mRNA copy goes to one of the two daughter cells with equal probability [33].
The master equations
The transcription state of a gene of our interest in a single cell at a time t ≥ 0 can be characterized by the number of active gene copies, the cell cycle stage, and its mRNA copy number. Without loss of generality, we assume that the gene has exactly one copy in stage, and two copies in stage, in any single cell of an isogenic cell population. We let I(t) denote the number of active genes in a cell. In stage, I(t) = 0 if the gene is OFF, and I(t) = 1 if it is ON. In stage, I(t) = 0 if the two gene copies are OFF, I(t) = 2 if both are ON, and I(t) = 1 in the remaining cases. We let U(t) specify the cell cycle stage, with U(t) = 1 in stage, and U(t) = 2 in stage. Let M(t) denote the mRNA copy number for the gene in one cell. Then the transcription state can be fully quantified by the following joint probabilities
| (3) |
| (4) |
For clarity and simplicity in the following calculations, we assume that all cells in the isogenic population are synchronized at the beginning of stage, and count only newly produced mRNA molecules from time zero. Accordingly, we have the initial condition
| (5) |
By using the standard procedure in stochastic process, we calculate the time evolutions of these probabilities based on the basic assumptions (i)-(v) in our model and derive the master equations:
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
The last expression P2(n, t) in (6), defined by
gives the probability that the cell resides on stage with n transcripts, and P1(m, t) in (8), defined by P1(m, t) = P1(0, m, t) + P1(1, m, t), represents the probability that the cell resides on stage with m copies of mRNA molecules. The technical steps leading to (6)–(10) are given in S1 Text.
The determination of the moment functions
The transcription dynamics of a gene in a cell population is best characterized by the mean value m(t) = E[M(t)] of the random process M(t) that counts the number of its mRNA copies. The second moment μ(t) = E[M2(t)] is essential in the calculation of its noise that quantifies the fluctuation of mRNA copy numbers among individual cells. More importantly, as the cell division cycle is integrated into our model, we can extend m(t) and μ(t) to the two cell cycle stages and . The comparison of these quantities in the two stages can help us understand how the gene duplication contributes to the variation of transcription levels and noises. To start with, we give the formal definitions of these concepts and present the differential equations that provide a framework from which they can be solved analytically.
For this purpose, we need various probabilities by adding the joint probabilities Pj(i, m, t) introduced in (3)–(4) when i, j, or m runs through all possible values. We use a conventional simplification of notations: If any of i, j and m is removed from Pj(i, m, t), then the new probability is defined by summing Pj(i, m, t) over the range of the removed index. For instance,
| (11) |
are the respective probabilities that the cell resides on and stages with m copies of mRNA molecules, without specifying the promoter state. A further summation of the two probabilities in (11) defines
| (12) |
as the probability that there are m copies of mRNA molecules in the cell. Similarly, we can define P1(i, t) and P2(i, t). To avoid the confusion with these probabilities defined in (11), we change them to P1i(t) and P2i(t) with
| (13) |
By adding the probabilities in (13) we have
| (14) |
as the respective probabilities that the cell resides on and stages. By adding the master Eqs (6)–(10) in m, we obtain a closed system of P1i(t) and P2i(t),
| (15) |
The initial condition for this system can be derived by a summation of the initial data given in (5). This linear system of ordinary differential equations with constant coefficients can be solved analytically, and its solution subject to the corresponding initial condition determines uniquely P1i(t) and P2i(t).
Due to the technical complexity, we break down the process of determining m(t), μ(t), and their extensions in and in several steps, and move most involving calculations to S1 Text.
Step 1: The determination of the mean level m(t): With P1(m, t), P2(m, t), and P(m, t) defined in (11) and (12), we have
| (16) |
where
| (17) |
As we show in S1 Text, n1(t) and n2(t) satisfy the following system of inhomogeneous linear ordinary differential equations with constant coefficients:
| (18) |
As P11(t), P21(t), and P22(t) can be solved uniquely from (15), we can find n1(t) and n2(t) by solving (18) subject to the initial condition n1(0) = n2(0) = 0, and find m(t) by (16).
Step 2: The determination of the second moment μ(t): Similar to the definition of m(t) in (16), we have
| (19) |
where
| (20) |
As we show in S1 Text, the time evolutions of ω1(t) and ω2(t) are given by the system
| (21) |
where
| (22) |
and
Apparently, (21) is not a closed system, and finding ω1(t) and ω2(t) requires the following system of n1i(t) and n2i(t):
| (23) |
This system is obtained by multiplying (6)–(10) with m and then taking sums. As P11(t), P21(t), and P22(t) can be solved from (15), it is a closed system of n1i(t) and n2i(t). By substituting its unique solution subject to the zero initial condition into (21), we can determine ω1(t) and ω2(t), and therefore the second moment μ(t).
Step 3: The moment functions on and stages: To extend the definitions of m(t) and μ(t) to the two cell cycle stages and , we define the conditional probabilities
| (24) |
| (25) |
for the probabilities P1(t) and P2(t) defined in (14). Then
are the probabilities that there are m copies of mRNA molecules when the cell resides on or stage. The average transcription levels in and stages are defined by
| (26) |
and the second moments are defined by
| (27) |
By comparing (26) with the definition of n1(t) and n2(t) in (17), and (27) with the definition of ω1(t) and ω2(t) in (20), we find the simple relation
| (28) |
As a cell is either on or on stage, we have P1(t) + P2(t) ≡ 1. From the basic assumption (i), the two stages and transit each other by constant rates κ1 and κ2. It implies that P1(t) and P2(t) are simply related by
This simple equation can also be derived by adding equations in (15). By the assumption that all cells are synchronized on initially, we have P1(0) = 1. Hence
| (29) |
Our methods for finding n1(t) and n2(t) in Step 1, and ω1(t) and ω2(t) in Step 2, combined with (28) and (29), constitute a complete analytical approach for computing the mean values m1(t) and m2(t), and the second moments μ1(t) and μ2(t), in the two cell cycle stages.
Results
Analytic expressions of the first and the second moments
Our discussion in the previous section offers a clear analytical approach for finding the mean value m(t) and the second moment μ(t) of mRNA number M(t), along with their extensions to the two cell cycle stages and . However, neither of these functions has a simple analytical expression. For simplicity, we will only present their steady-state values in exact forms, and use their temporal forms in numerical simulations. Although the steady-state values are much simpler than the temporal forms, they are still rather complex and capture the delicate involvement of the system parameters as shown by the next two theorems. For a function f(t) that has a finite limit as t → ∞, we let f* denote its limit.
Theorem 1 If the transcription of a gene obeys the model described in Fig 1, then the mean transcription level of the gene in a population of isogenic cells at steady-state is
| (30) |
a linear combination of the mean levels in stage and in stage, and
| (31) |
| (32) |
Theorem 2 If the transcription of a gene obeys the model described in Fig 1, then the second moment of its mRNA copy number M(t) at steady-state is
| (33) |
where and are the second moments in and stages given by
| (34) |
| (35) |
with
| (36) |
| (37) |
and .
The proofs of Theorems 1 and 2 are given in S1 Text. By using definition (1), combined with the analytical expressions (31) and (32) of the stationary mean transcription levels, and (34) and (35) for the second moments, we derive the noise strengths of mRNA copy numbers in and as
| (38) |
| (39) |
The noises and are given by
| (40) |
| (41) |
The fold change of transcripts
The broad range of the fold change
We use , the ratio of the mean transcription levels in the two stages, as a measure to quantify the fold change of gene transcription from stage to stage [12, 15, 34]. Our formulas (31) and (32) imply
| (42) |
All ten system parameters are involved in this formula. If the transcripts are turned over extremely fast in stage such that δ1 dominates all other parameter values, then r* can be made arbitrarily large. On the contrary, if the transcripts are turned over extremely fast in stage, then r* can be made sufficiently small. Thus r* could take any arbitrary positive number as parameter values vary, and the range of the fold change predicted by (42) is the whole set (0, ∞) of positive numbers.
In many bacterial cells, it has been observed that the transcription kinetic rates of some genes remain the same in the whole cell cycle [35], that is,
| (43) |
If (43) holds, then (42) can be simplified to
| (44) |
What is the range of r* in this case? During S/G2/M phases, a cell contains twice as many copies of each gene as that in G1 phase. Intuitively, one may envisage that the number of mRNA copies in stage doubles the number in stage and so r* ≈ 2. Our next theorem shows that r* can deviate from 2 largely, and surprisingly, the constraint (43) does not reduce the range of r*.
Theorem 3 For any constant C > 0, there exist system parameters under the constraint (43) to make r* = C.
This counter-intuitive result predicts that, even when the transcription kinetic rates do not change in different cell cycle phases, the fold change of transcription levels from to can be made, in theory, arbitrarily large or small. A complete proof of this result is given in S1 Text. In the proof, we specify the stage transition rates κ1 and κ2 in terms of the kinetic rates to make r* = C for C ≤ 1, C ∈ (1, 3/2], C ∈ (3/2, 2), and C ≥ 2 separately. For instance, when C ≤ 1, we take
| (45) |
Substituting these parameters into (44) gives
We note that (45) requires κ1 = λ + γ and κ2 ≥ 4κ1 = 4(λ + γ), which corresponds to faster cell cycle stage transitions comparing to gene promoter transitions, and a much shorter stage than stage. These conditions may not hold regularly in real cells, and a fold change r* < 1 has been rarely observed under the constraint (43). However, there have been measurements reporting a slightly larger than 1-fold change. In 2016, Skinner et al. [15] quantified mature and nascent mRNA levels of Oct4 in individual mouse ES cells, and found that the increase from earlier cell cycle stage to later stage was only about 1.3-fold.
Cell cycle stage transitions are often slower than gene promoter state transitions, implying κ1 < λ + γ and κ2 < λ + γ. If we divide the numerator and denominator in (44) by δ(λ + γ), then we may change (44) to
It is evident that r* ≈ 2 if κ1, κ2 are considerably smaller than δ and λ + γ. It indicates that when the transcription kinetics are unchanged in the two cell cycle stages, and the stage transition is considerably slower than the transcription state transition and mRNA turnover, the mRNA number in stage doubles the number in stage at steady-state. This doubling property has been observed in several experimental measurements. In 2004, Vintersten et al. [34] reported a strong expression of a developed RFP variant, DsRed.T3, in mouse ES cells, and found that the nascent mRNA level exhibited a 2-fold increase from stage to stage. In 2011, Trcek et al. [12] measured the cytoplasmic mRNA level of CLB2 in yeast and also found an approximate 2-fold increase from late G2/M phases to S phase.
Next, we characterize the dependance of r* on the stage transition rates κ1 and κ2. To emphasize its dependance on these parameters, we write r* = r*(κ1, κ2).
Theorem 4 Let (43) hold. Then we have
-
aWhen κ1 increases from 0 to ∞, r* increases from r*(0, κ2) < 2 until it peaks uniquely and then decreases to approach 2 at ∞. In particular, r* > 2 if and only if
(46) -
bWhen κ2 increases from 0 to ∞, r* decreases from r*(κ1, 0) > 2 until it bottoms out uniquely and then increases to approach 1 at ∞. In particular, r* < 1 if and only if
(47) -
c
When κ1 ≤ κ2, r* has an upper bound strictly less than 2.
Theorem 4 gives a precise description on the nonlinear dependance of the fold change r* on the stage transition rates κ1 and κ2. Conditions (46) and (47) give the respective sufficient and necessary conditions for r* > 2 and r* < 1. The complete proof of this theorem is given in S1 Text.
Discussion
The fold change r* and its dependance on the stage durations
The accuracy of estimating the fold change
We use a set of experimental data to test how accurately our formula (42) may help estimate the fold change r* of mRNA copy numbers from the early cell cycle stage to the later stage . In mouse embryonic stem cells, it was observed that the mean OFF duration in the transcription of Oct4 increased from 108 min in stage to 173 min in stage, and the mean ON duration lasted about 56 min in the two stages [15], suggesting
| (48) |
In [15], Skinner found that the average duration of stage lasted about ∼560 min by using smFISH. Cartwright et al. [36] measured the cell division time in the same cell line under similar growth conditions, and estimated the average time for one cell cycle at ∼13 hr. These data suggest an average stage duration at ∼220 min. As the mean life of newly transcribed Oct4 mRNA before being converted to mature RNA was found to be close to 3.5 min, we estimate the other parameters as follows:
| (49) |
As the synthesis rate remains about the same in the two cell cycle stages, we can simplify (42) to
| (50) |
Substituting (48) and (49) into (50) gives r* = 1.2791, which matches precisely the experimental measurement r* = 1.28 ± 0.09 observed in [15].
The condensation of r* within [1, 2]
Although Theorem 1 predicts that r* could take any positive value even if the transcription kinetic rates remain the same in all cell cycle phases, we use numerical simulation to demonstrate that it is more likely to observe r* ∈ [1, 2] in some cells. As suggested by [15] in the transcription of Oct4 gene in mouse embryonic stem cells, we fix
| (51) |
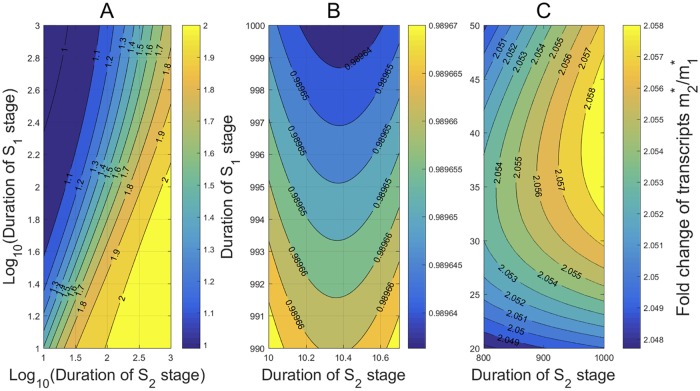
The mean OFF and ON durations are ∼108 min and ∼56 min, respectively, and the mean mRNA lifetime is ∼7.14 hr. To characterize the dependance of the ratio r* on the stage durations, we let the mean stage duration 1/κ1 and the stage duration 1/κ2 vary from 10 to 1, 000 min. The contours of r* on stage durations are shown in Fig 2, where the durations are rescaled in logarithm in Fig 2A. Very interestingly, the contours show that the ratio r* is within the narrow range [1, 2] over almost all the durations, in a good agreement with many experimental measurements [9, 13, 15, 34]. It is also seen that for fixed stage duration, r* decreases and tends to a stable value (≈ 1) when the stage duration increases. On the other hand, for fixed stage duration, r* increases and tends to a larger stable value (≈ 2) when the stage duration increases.
Fig 2. The condensation of r* within [1, 2] and its dependance on the stage durations.
All kinetic rates are estimated from [15] in the transcription of Oct4 gene in mouse embryonic stem cells. (A) For almost all the and stage durations ranging from 10 to 1, 000 min, r* is within a narrow range [1, 2]. When 1/κ1 ≫ 1/κ2 (or 1/κ1 ≪ 1/κ2), r* varies slowly over a narrow region around 1 (or 2). When the two durations are close, r* changes rapidly over (1.1, 2). (B) When the stage duration is far greater than the stage duration, r* < 1 and is very close to 1. (C) When the stage duration is far greater than the stage duration, r* > 2 and is very close to 2.
To see more clearly how r* changes in the limit cases, we enlarged the left upper corner of Fig 2A in Fig 2B, and the right lower corner of Fig 2A in Fig 2C. The contours in Fig 2B and 2C exhibit some minor deviations from our observation above for Fig 2A. In Fig 2B, where the stage duration is far greater than the stage duration, r* < 1 and is very close to 1. Also, for fixed large duration, r* displays a non-monotone growth as claimed by Theorem 4(b) when the duration increases from 10 min to 10.6 min. In Fig 2C, where the duration is far greater than the duration, r* > 2 and is very close to 2. For fixed large duration, r* displays a non-monotone growth as claimed by Theorem 4(c) when the duration increases from 20 min to 45 min.
The dependance of the fold change on the timing of gene duplication
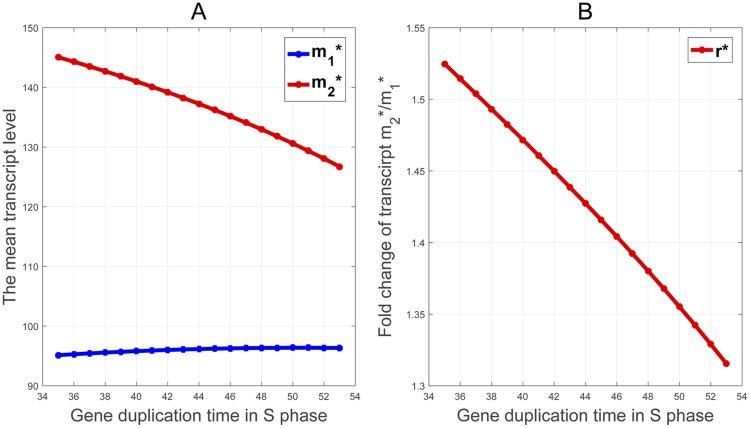
In the discussion above, the cell cycle duration changes synchronously when the durations of or change. In some cases, the cell division time may not change significantly, while the variation of and durations is mainly caused by the random timing of gene duplication that may occur in the early S phase or at the end of S phase. During S phase, DNA synthesis is catalyzed by DNA polymerases [17, 37], and the genome is replicated at a stable rate on leading and lagging strands [25]. In cell cycle-synchronized budding yeast, the total cell division time is ∼70 min, comprising by ∼35 min G1 phase, ∼18 min S phase and ∼17 min G2/M phase [13]. We examine how the mean levels , and the ratio r* change when the gene duplication time increases from the start of S phase at 35 min to the end of S phase at 53 min, and transcripts are produced and turned over with the rates:
We simplify our approach by taking λ1, λ2 → ∞ and obtain from (31) and (32)
It follows that
As shown in Fig 3A, although the mean transcription level in decreases in the gene duplication time as we expect, it is surprisingly to see that the mean level in remains almost a constant. Very interestingly, as shown in Fig 3B, the ratio r*, which changes moderately in a narrow range from 1.31 to 1.53, decreases almost linearly in the duplication time.
Fig 3. The dependance of the mean mRNA copy numbers , and the ratio r* on the timing of gene duplication during S phase.
(A) The mean level stays nearly at a constant level, while decreases linear as the gene duplication time increases from 35 min to 53 min in S phase. (B) The ratio r* decreases almost linearly from 1.53 to 1.31 as the gene duplication time increases.
The effect of cell cycles on transcription noise
Our gene transcription model coupling with cell division cycles offers six quantities to characterize the fluctuations of mRNA numbers in single cells: The noise η2* and the noise strength Φ* in cells without referring to cell cycle stages, along with and in stage, and and in stage. Theorems 1 and 2 provide the basic formulas by which these quantities can be computed from the system parameters.
The relations between these quantities are far more complicated than our intuition may envisage. We use simple example to demonstrate the delicacy of their relations: Assume (43) and fix the kinetic rates as in (51), and take the stage transition rates κ1 = κ2 = 1/1250 hr−1. Then applying Theorem 2, (38) and (39) gives and . Since and are nearly equal, one might expect by intuition that Φ* is about equal to each of and , which is in conflict with
obtained by using Theorems 1 and 2. Moreover Φ* = 89.3329 given here is significantly higher than Φ* ≈ 1 reported in various single cell measurements, including the classical studies by Taniguchi et al. [38] and Yu et al. [39]. In these studies, the genes were active most of time, so that m* and η2* exhibited a strict reciprocal relation, implying Φ* ≈ 1. The stochastic switching between gene promoter ON and OFF states, combined with transitions between cell cycle stages, may induce much noisier transcriptions.
Due to the wide range of the six noise measures and their complex relations, we will discuss their profiles in three special cases below:
The transcription kinetic rates remain constants in all cell cycle phases.
The transcription homeostasis is maintained that .
The concentration homeostasis is maintained that the mean transcription levels scale with the average volumes in the two stages.
The noise profile with constant kinetic rates
DNA replication during cell division cycles induces a doubling of gene copy numbers from to . In bacteria, the transcription kinetic rates of many genes do not change considerably in different cell cycle phases [13]. In this case, mRNA production follows gene dosage with a rapid increase after DNA replication. In a sharp contrast, the response of the transcription noises to the temporal variation of gene dosage is rather complicated and few results have been given to elucidate the complexity. Let the transcription kinetic rates remain constants in all cell cycle phases and fix the rate constants as in (51). We use numerical simulations based on our analytical formulas to depict the profiles of the transcription noise measures and their relations by varying the cell cycle durations over the large time interval (10 min, 104 min).
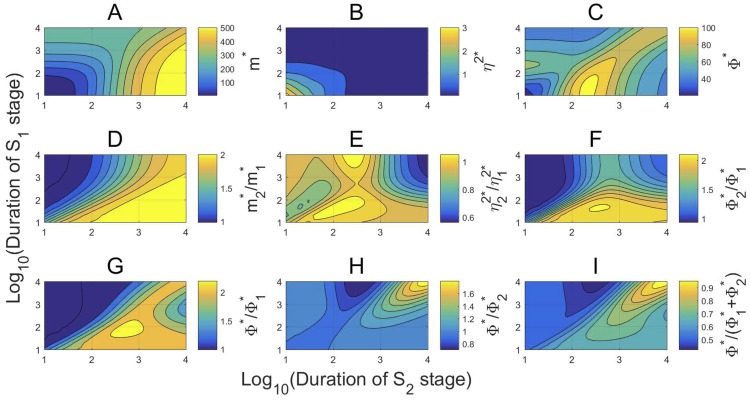
In Fig 4A, the contours of the mean transcription level m* in cells display a simple and monotonic variation over the stage durations. It increases in both stage durations and the increase is more sensitive on the second stage duration. Similarly, the contours of the noise η2* also display a simple and monotonic variation over the stage durations. However, it decreases in both stage durations and the dependance on the two durations are nearly symmetric. Such an inverse relation between m* and η2* has been observed in many living cell measurements and theoretical studies [23, 35], and a strict reciprocal relation between them has been observed in Taniguchi et al. [38] and Yu et al. [39] with Φ* ≈ 1. Nevertheless, as the transcription specified by (51) is frequently interrupted by long OFF periods, the contours of the noise strength Φ* in Fig 4C indicate that Φ* is significantly higher than 1 with Φ* ∈ [20, 100]. Moreover, Φ* displays a highly nonlinear, non-monotonic variation over the cell cycle stages. Intriguingly, among the durations shown in Fig 4C, Φ* peaks in a small region when stage lasts between 10 and 100 minutes on average, and stage lasts between 125 and 250 minutes.
Fig 4. The nonlinear behavior of the transcription noises.
The transcription kinetics are specified by (43) and (51), and the stage durations vary from 10 to 104 min. (A) The mean m* increases in the cell cycle durations. (B) The noise η2* is about equally sensitive to the variation of the stage durations and decreases from 3 to 0.5 as the stage durations increase. (C) The noise strength Φ* varies widely from 20 to 100 with a highly nonlinear dependance on the stage durations. (D)-(F) The ratios , , and over most durations. (G)-(I) Φ* is larger than both and but less than over most durations.
In Fig 4D–4F, the fold changes , , and from to all vary within a narrow range with , , and . The right upper corners in Fig 4D–4F seem to suggest that, as both stage durations become large,
| (52) |
Indeed, (52) can be supported by simple mathematical calculations. By taking limits in (31) and (32), we obtain
and verify the first part of (52). Taking limits in (34) and (35) gives
and
By the definition of the noise strength in (1), we find
| (53) |
and verify the third part in (52). Consequently, the second part in (52) is also verified since the noise equals the noise strength divided by the mean.
The approximate identities in (52) indicate that when the cell cycle stage transitions are sufficiently slow, the mean transcription levels are doubled and the noises are halved from to , while the noise strengths remain about the same. However, this simple statement is invalid in general as shown by the contours in Fig 4D–4F, where and display highly nonlinear and wild variations.
In Fig 4G–4I, we compare Φ* with , , and . In most of time,
However, these estimates do not hold universally. For instance, Fig 4H indicates that can be as low as 0.8 and so in some cases. Also, we have shown one example early that may hold. Overall, Φ* is rarely identical to either or , and stays between and most of time.
The noise profile in gene transcription homeostasis
It has been observed repeatedly that gene transcription in eukaryotic cells, ranging from yeast to mammals, has a limited dependency on DNA dosage [13]. Cells have a DNA dosage-compensating mechanism to precisely reduce mRNA production in late cell cycle stage, resulting in a gene transcription homeostasis that overall transcription remains constant across and stages [18]. Various compensating mechanisms for gene transcription homeostasis have been found [12, 13, 15, 18], including reducing transcription activation or mRNA synthesis rates, and increasing inactivation or mRNA degradation rates in stage. For all of the genes measured in foreskin fibroblast cells, Padovan-Merhar et al. [18] found that the number of active sites per gene copy in stage was approximately half of that in . In mouse embryonic stem cells, Skinner et al. [15] found that the activation rates of Oct4 and Nanog genes were reduced from 0.5556 hr−1 and 0.1124 hr−1 in stage to 0.3468 hr−1 and 0.08 hr−1 in stage, respectively. In cell cycle-synchronized budding yeast, Voichek et al. [13] found the reduction of mRNA synthesis rate during S phase. In yeasts, Trcek et al. [12] found a 30-fold increase in the mRNA degradation rates of SWI5 and CLB2 during prometaphase/metaphase.
Mathematically, we define the gene transcription homeostasis by that the mean transcription levels in and stages remain the same. If the homeostasis is brought by varying a single pair of corresponding kinetic rates, then substituting (31) and (52) into yields the relations of the two varied rates as follows:
| (54) |
| (55) |
| (56) |
| (57) |
In (54)–(57), the parameters with no subscripts are assumed to be independent of cell cycle stages. It is seen that ν2 and ν1 change proportionally, whereas δ2 and δ1, γ2 and γ1, and the two OFF durations depend linearly.
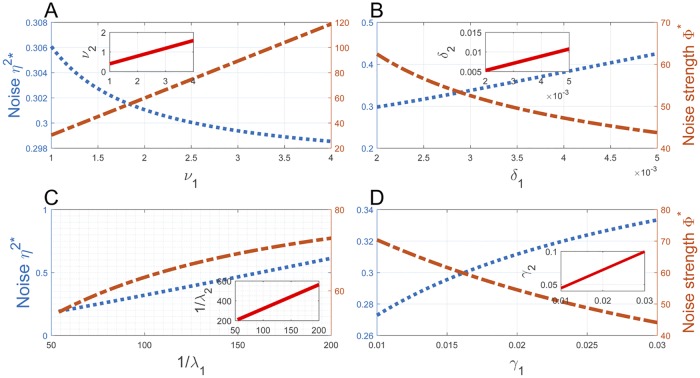
We test how the noise η2* and the noise strength Φ* respond when the parameter pair defined in each of (54)–(57) change linearly to maintain the homeostasis. We again fix the parameters with no subscripts in (54)–(57) as in (51), and let
| (58) |
that are approximately the average duration of and stages in a mouse embryonic stem cell line [15, 36]. In Fig 5A–5D, we vary ν1, δ1, λ1, and γ1 near the corresponding parameter values specified in (51), with ν1 ∈ [1, 4] in (A), δ1 ∈ [2 × 10−3, 5 × 10−3] in (B), λ1 ∈ [0.005, 0.02] in (C), and γ1 ∈ [0.01, 0.03] in (D), all sharing the same unit min−1. The linear relations of ν1 and ν2, δ1 and δ2, 1/λ1 and 1/λ2, and γ1 and γ2 defined by (54)–(57) are depicted in the inserts of these panels. It is easily seen that both η2* and Φ* vary monotonically on these intervals. Interestingly, η2* and Φ* change in opposite directions in Fig 5A, 5B and 5D, and they both decrease in the activation rate λ1 in Fig 5C. The noise η2* takes small values near 0.30 in all panels and shows only insignificant variations. The noise strength Φ* takes considerably larger values but the variation is also insignificant, except in Fig 5A where it increases from about 30 to 120 when ν1 increases from 1 to 4. Overall, these data suggest that if the transcription homeostasis is induced by varying a single pair of corresponding kinetic rates, then the variation of the rates does not bring significant changes in transcription noise.
Fig 5. The noise profile in gene transcription homeostasis.
The inserts in (A)-(D) depict the linear relations (54)–(57), where ν1, δ1, λ1, and γ1 have the same unit min−1 and vary near the corresponding values specified in (51). Both η2* and Φ* change monotonically on these intervals in opposite directions, except in (C) where they both decrease in λ1. The noise η2* takes small values near 0.30 in all panels and has only insignificant variations. The noise strength Φ* takes large values but also shows insignificant variations except in Fig 5A.
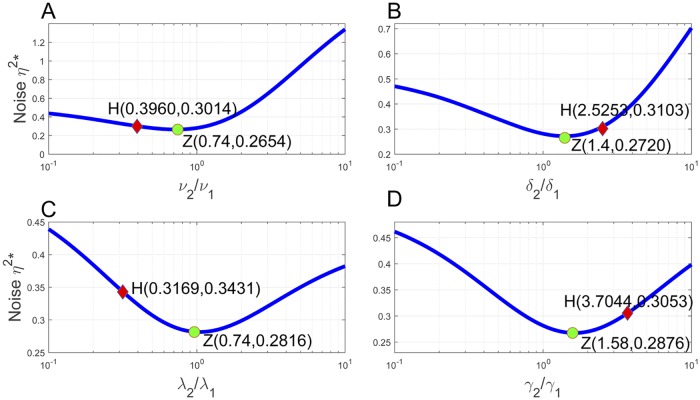
We examine the relation between the transcription noise η2* and transcription homeostasis further by varying ν2/ν1, δ2/δ1, λ2/λ1, and γ2/γ1 from 0.1 to 10 in Fig 6A–6D. All other parameters are kept as in (51) and (58). We label the points at which transcription homeostasis is reached as H, and the noise minimizing points as Z. In all panels from (A)-(D), it is seen that the two points stay very close. It suggests that if transcription homeostasis is attained by varying a single kinetic rate in the two cell cycle stages, then the homeostasis nearly minimizes transcription noise.
Fig 6. Transcription homeostasis nearly minimizes transcription noise.
The ratios ν2/ν1, δ2/δ1, λ2/λ1, and γ2/γ1 increase from 0.1 to 10 in (A)-(D), whereas other parameters are kept as in (51) and (58). In (A)-(D), the point H at which transcription homeostasis is reached and the noise minimizing point Z stay very close.
The noise profile in transcript concentration homeostasis
Cells reproduce by cell division. During cell mitosis, newly divided daughter cells are naturally smaller than their parent cells. Thus, a cell in stage is normally larger than itself in stage, although it has also been reported that cellular volumes are weakly related to cell cycle phases [18]. If the transcription homeostasis is maintained as we discussed above, then the transcript concentration in a cell decreases as it grows from to stage. However, in agree with the paradigm that biochemical reaction rates are determined mostly by the concentration of reactants and enzymes, increasing evidences have shown that many cellular processes depend on the concentration of gene expression products rather than their absolute numbers [18, 21, 22]. In cell populations with a large variability in cellular volumes, the numbers of most molecules need to scale with volumes to maintain a stable concentration for proper cellular functions [18, 21].
Let V1 and V2 denote the average volumes of individual cells on and stages, respectively, and let
denote the fold change of the volumes on the two stages. Recall that is the fold change of the mean transcription levels at steady-state. We define the transcript concentration homeostasis by
| (59) |
that is, the mean transcription levels scale with the volumes on both cell cycle stages.
We need to find an analytical formula of rv in terms of the cell cycle stage transition rates κ1 and κ2. By combining it with the expression of r* in (42) and the identity (59), we obtain an explicit relation of the system parameters for the transcript concentration homeostasis. The expression of rv depends on how cells grow and how the two cell cycle stage durations distribute. Various cell growth models have been proposed [22, 40–42], including the prevailing exponential growth model that cell volumes grow exponentially. Assume that a newly divided cell has a volume V0 = 1 at time t = 0. Then the cellular volume V(t) during the first cell cycle is given by
| (60) |
for a constant growth rate a > 0. Let (0, T1) be the duration of , and (T1, T1 + T2) be the duration of . We assume that the cell volume is doubled at the end of the cell cycle. Then V(T1 + T2) = 2. Recall that T1 and T2 are independently and exponentially distributed with rates κ1 and κ2. With these specifications, we have
| (61) |
We note that a increases in both κ1 and κ2, and rv ∈ (1, 2). When κ1 → 0, the cell stays sufficiently long in and has little growth in . In this case, (61) gives rv → 1 as we expect. On the other hand, rv → 2 as κ2 → 0.
To prove (61), we begin with the observation that
where E denotes expectation. We omit the detail of deriving this identity, which follows from the independent exponential distributions of T1 and T2, the renewal theory in stochastic processes, and Proposition 3.4.5 in [43]. From (60), we obtain
The distribution function of T1 + T2 is given by
when κ1 ≠ κ2 [5, 8]. By taking limits, it applies to the case κ1 = κ2 as well. Thus
Since it also holds that E[V(T1 + T2)] = 2, we derive
from which the expression of a in (61) is obtained. The second part in (61) can be verified by dividing the expressions of E[V(T1 + T2)] and E[V(T1)] directly.
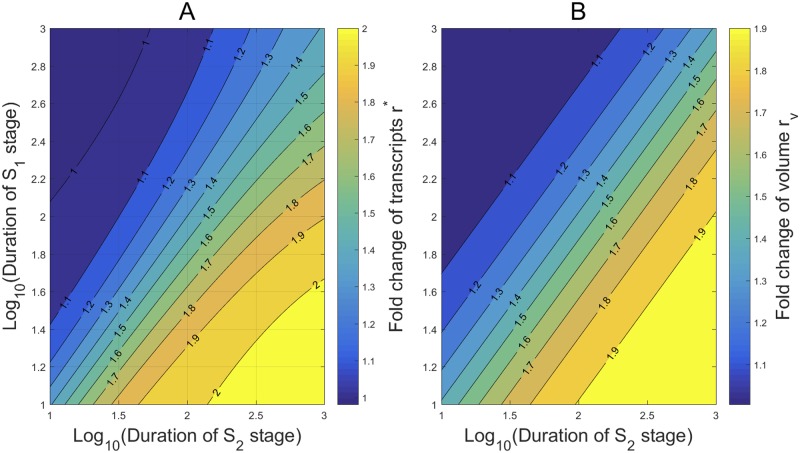
We apply our mathematical formulas (42) and (61) to examine how the transcript concentration homeostasis is attained by varying the transcription frequency λi, or the burst size νi/γi, i = 1, 2, in different cell cycle phases, and how the noise responds to the variation. In a recent interesting study elucidating the mechanism underlying the concentration homeostasis, Padovan-Merhar et al. [18] found a DNA-linked cis-acting factor in mammalian cells, that can lead to the reduction of transcription frequency of each gene copy in G2 phase, and therefore an overall balanced burst frequency in all cell cycle stages. Motivated by this observation, we reduce λ2 in (51) from 0.5556 to 0.3445, which is approximately a 38% reduction, and keep other kinetic rates as in (51). As the stage durations vary from 10 min to 1, 000 min, the contours of the fold change r* for the mean transcription levels and the fold change rv for the volumes are shown in Fig 7. Very interestingly, the contour of r* in Fig 7A and the contour of rv in Fig 7B are very similar over most area of the stage durations. This surprising similarity suggests that the concentration homeostasis could be reached by merely reducing the transcription burst frequency in G2 phase, in a uniform reduction degree that is robust against a large variation of cell stage durations and the randomness of gene duplication time.
Fig 7. The transcript concentration homeostasis by reducing the transcription burst frequency in G2 phase.
The burst frequency λ2 is reduced from 0.5556 in (51) to 0.3445, and other kinetic rates are taken from (51). (A) The contours of the fold change r* for the mean transcription levels from to . (B) The contours of the fold change rv for the volumes from to . The two sets of contours in (A) and (B) display a large similarity, indicating that the transcript concentration homeostasis is almost reached by reducing the frequency uniformly over most area of the stage durations.
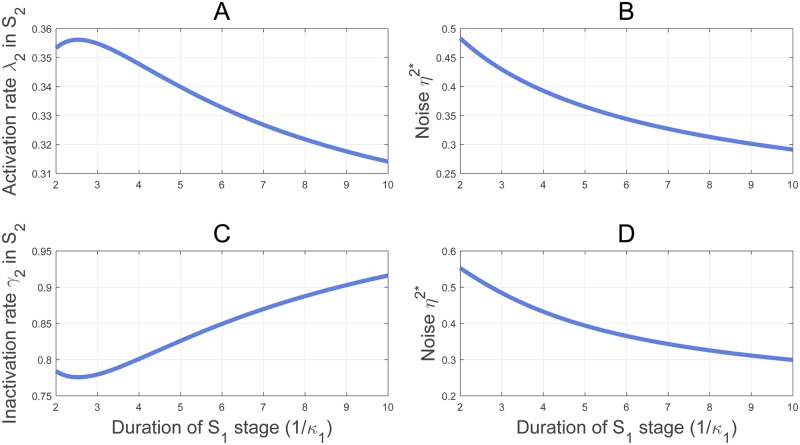
To test further the robustness in the reduction of the transcription burst frequency in against the variation of cell cycle stage durations, we fix the kinetic rates except λ2 as in (51), the duration of at as in (58), but let the duration of vary from 2 to 10 hours. By applying (42) and (61) to r* = rv, we determine a unique λ2 corresponding to each duration for the transcript concentration homeostasis. The curve of λ2 versus the duration 1/κ1 is shown in Fig 8A. It is interesting to see that λ2 exhibits only a minor variation within a narrow interval (0.315, 0.355) over a large span of the duration from 2 to 10 hours. As λ1 = 0.5556, this corresponds to a stable reduction, between 36% and 42%, of the transcription frequency from to . We note also that λ2 = 0.3445 fixed in Fig 7 is within (0.315, 0.355). More interestingly, the transcription noise sketched in Fig 8B, corresponding to the λ2 values of Fig 8A, also exhibits a minor variation within the narrow range (0.28, 0.48).
Fig 8. Minor variations of λ2, γ2 and η2* versus the large variation of the cell cycle durations in the concentration homeostasis.
(A) The transcription frequency for the concentration homeostasis stays within (0.315, 0.355) over a large span of the duration from 2 to 10 hours; , and other kinetic rates are taken from (58). (B) The noise corresponding to (A) remains within (0.28, 0.48). (C) The inactivation rate γ2 for the concentration homeostasis with the parameters in (A) except λ2 = λ1/2 to equalize the burst frequency in and . (D) The noise corresponding to (C) remains within (0.29, 0.56).
In Fig 8A and 8B, the transcription burst size νi/γi does not change in and stages. However, Caveney et al. [21] and Padovan-Merhar et al. [18] found that the transcription burst size increases in larger cells, while the burst frequency in shows no dramatic changes. These findings suggest that the increase in the burst size could be responsible for the concentration homeostasis. We are motivated to test how the burst size increase induces the concentration homeostasis by reducing the gene OFF rate γ2. We set λ1, γ1, and the mRNA synthesis and degradation rates as in (51), and define λ2 = λ1/2 to equalize the burst frequency on the two stages. As in Fig 8A and 8B, we fix , and let the average duration of vary from 2 to 10 hours. For each duration 1/κ1, there is a unique γ2 determined by the concentration homeostasis identity r* = rv as shown in Fig 8C. Again, γ2 displays only a minor variation within the narrow interval (0.78, 0.92) in Fig 8C where the duration increases from 2 to 10 hours. However, in contrast to the minor variation of γ2, the corresponding increase in the bust size is noticeable. As γ1 = 1.0714, the increase in the burst size in , given by (γ1 − γ2)/γ2 ranges from 16.45% to 37.35%. Very interestingly, the corresponding transcription noise sketched in Fig 8D does not show a noticeable variation but stays within the narrow range (0.29, 0.56).
The minor variation of η2* in Fig 8B and 8D suggests that the transcription noise is relatively stable when the transcript concentration homeostasis is maintained, either by reducing the transcription burst frequency or by increasing the burst size in late cell cycle phase, in the face of a large cell cycle stage duration variation. By comparing the profiles of η2* in Fig 8B and 8D it is also seen that the burst size variation creates a slightly larger noise than reducing the burst frequency, similar to the observation by Caveney et al. [21] in cell-free synthetic reaction chambers. Furthermore, our simulations in Figs 7 and 8A and 8C show that the reduction degree in the burst frequency for the transcript concentration homeostasis is relative robust, while the increase in the burst size is conceivably sensitive, to the random variation of the cell cycle durations.
Conclusion
Gene transcription involves inherently various probabilistic steps that create fluctuations in mRNA and protein counts [1–3]. The random transitions between the active and inactive promoter states have been widely invoked to explain the fluctuation of mRNA numbers among individual cells of identical genes [6, 7]. Recent experimental studies have revealed that the cell division cycle has global effects on transcriptional outputs, and is thought to be an additional source of transcription noise [10–13].
In this work, we integrated cell division cycles into an extended two-state model to delineate the combined contribution of transcription activities and cell divisions in the variability of transcript counts [4, 6]. In the model, a cell division cycle is divided into stage before the duplication of a target gene and the late stage , on which the durations are independently and exponentially distributed with rates κ1 and κ2. When a cell divides, each mRNA molecule has an even chance of being partitioned to one of the two daughter cells. We defined two joint probabilities to quantify the system state, and derived the master equations of their time evolutions. From the master equations we obtained the differential equations of the mean and the second moment of mRNA numbers in single cells. By solving these equations we presented in Theorem 1 the steady-state mean transcription level m* in cells, together with the means and on the two stages. The analytical forms of the second moments are presented in Theorem 2, which in turn help us determine six noise measures: the noise η2* and the noise strength Φ* without referring to cell cycle stages, along with and in , and and in . The fold change of mRNA counts from to is quantified by . As a cell contains twice as many copies of each gene in as that in , one may envisage by intuition that r* ≈ 2. However, our Theorem 3 shows that r* can take any prescribed value in theory, although we also found that r* ≈ 2 when the transcription kinetics are unchanged in the two stages, and stage transitions are considerably slower than mRNA turnover and transcription state transitions. The dependance of r* on κ1 and κ2 is examined deeply in Theorem 4, where the necessary and sufficient conditions for r* < 1 or r* > 2 are identified. In particular, it is proved that r* has an upper bound strictly less than 2 when κ1 ≤ κ2.
We tested the accuracy of our analytical results against various experimental data. For a gene in a mouse embryonic stem cell line, our result predicts r* = 1.2791, which offers a good match with r* = 1.28 ± 0.09 measured in [15]. The analysis also indicates that if the transcription kinetics do not change considerably in the two cell cycle stages, then the average mRNA counts increase about 1 to 2 folds from stage to stage as observed in mouse embryonic cells [15] and yeast [12]. The mean m* increases while the noise η2* decreases in each of the cell cycle durations. Rapid transitions between cell cycle stages were identified as a major source of highly noisy transcription. Eukaryotic cells have a DNA dosage-compensating mechanism to reduce mRNA production in late cell cycle stage, resulting in gene transcription homeostasis that overall transcription remains constant across and stages [13, 18]. Our analysis reveals that transcription homeostasis does not bring significant changes in transcription noise. If transcription homeostasis is attained by varying a single kinetic rate in the two cell cycle stages, then the homeostasis nearly minimizes transcription noise. As many cellular processes depend on the concentration of enzymes rather than their absolute numbers for proper cellular function [18, 21, 22], we also studied the noise profile when the transcript concentration homeostasis is maintained that the mean transcription level scales with the cellular volume in and . We found that the transcription noise is relatively stable when the transcript concentration homeostasis is maintained, either by reducing the transcription burst frequency or by increasing the burst size in late cell cycle phase, in the face of a large cell cycle stage duration variation. The reduction degree in the burst frequency is relative robust, while the increase in the burst size is conceivably sensitive, to the large random variation of the cell cycle durations and the gene duplication time.
This work provides one of the first theoretical explorations on how the coupling of stochastic promoter state transitions and cell cycle progressions regulates transcription abundance and noise. It presents a core model for further inclusion of more complex transcription kinetics and cell cycle progressions. The kinetic rates may display large variations in different cell cycle phases or within the same phase, or oscillate periodically in the cell cycle progression [44]. With the expansion of the model, motivated and tested by more upcoming experimental data, the approach initiated here is expected to be developed further to help understand the role played by the cell cycle dependent gene expression in cell functions and cell fate decision [45, 46].
Supporting information
The detailed derivation of master equations and differential equations is given in the former part. Theorems 1-4 are restated in the second part, and the detailed mathematical proofs are given behind these theorems.
(PDF)
Data Availability
All relevant data are within the manuscript and its Supporting Information files.
Funding Statement
This work was supported by National Natural Science Foundation of China grant (Nos. 11631005; 11871174), Program for Changjiang Scholars and Innovative Research Team in University (No. IRT-16R16), Science and Technology Program of Guangzhou (No. 201707010337). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Kaufmann BB, van Oudenaarden A. Stochastic gene expression: from single molecules to the proteome. Current Opinion in Genetics & Development. 2007; 17:107–112. 10.1016/j.gde.2007.02.007 [DOI] [PubMed] [Google Scholar]
- 2. Maheshri N, O’Shea EK. Living with noisy genes: how cells function reliably with inherent variability in gene expression. Annual Review of Biophysics and Biomolecular Structure. 2007; 36:413–434. 10.1146/annurev.biophys.36.040306.132705 [DOI] [PubMed] [Google Scholar]
- 3. Neuert G, Munsky B, Tan RZ, Teytelman L, Khammash M, van Oudenaarden A. Systematic identification of signal-activated stochastic gene regulation. Science. 2013; 339:584–587. 10.1126/science.1231456 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Raj A, Peskin CS, Tranchina D, Vargas DY, Tyagi S. Stochastic mRNA synthesis in mammalian cells. PLoS Biology. 2006; 4:1707–1719. 10.1371/journal.pbio.0040309 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Sun Q, Tang M, Yu J. Modulation of gene transcription noise by competing transcription factors. Journal of Mathematical Biology. 2012; 62:469–494. [DOI] [PubMed] [Google Scholar]
- 6. Dar RD, Razooky BS, Singh A, Trimeloni TV, McCollum JM, Cox CD, et al. Transcriptional burst frequency and burst size are equally modulated across the human genome. Proc Natl Acad Sci U S A. 2012; 109:17454–17459. 10.1073/pnas.1213530109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Munsky B, Neuert G, van Oudenaarden A. Using gene expression noise to understand gene regulation. Science. 2012; 336:183–187. 10.1126/science.1216379 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Sun Q, Tang M, Yu J. Temporal profile of gene transcription noise modulated by cross-talking signal transduction pathways. Bulletin of Mathematical Biology. 2012; 74:375–398. 10.1007/s11538-011-9683-z [DOI] [PubMed] [Google Scholar]
- 9. Zopf CJ, Quinn K, Zeidman J, Maheshri N. Cell-cycle dependence of transcription dominates noise in gene expression. PLoS Computational Biology. 2013; 9(7):e1003161 10.1371/journal.pcbi.1003161 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Bertoli C, Skotheim JM, de Bruin RAM. Control of cell cycle transcription during G1 and S phases. Nature Reviews Molecular Cell Biology. 2013; 14:518–528. 10.1038/nrm3629 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Dowling MR, Kan A, Heinzel S, Zhou JHS, Marchingo JM, Wellard CJ, et al. Stretched cell cycle model for proliferating lymphocytes. Proc Natl Acad Sci U S A. 2014; 111:6377–6382. 10.1073/pnas.1322420111 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Trcek T, Larson DR, Moldón A, Query CC, Singer RH. Single-molecule mRNA decay measurements reveal promoter-regulated mRNA stability in yeast. Cell. 2011; 147:1484–1497. 10.1016/j.cell.2011.11.051 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Voichek Y, Bar-Ziv R, Barkai N. Expression homeostasis during DNA replication. Science. 2016; 351:1087–1090. 10.1126/science.aad1162 [DOI] [PubMed] [Google Scholar]
- 14. Marguerat S, Bälher J. Coordinating genome expression with cell size. Trends in Genetics. 2012; 28:560–565. 10.1016/j.tig.2012.07.003 [DOI] [PubMed] [Google Scholar]
- 15. Skinner SO, Xu H, Nagarkar-Jaiswal S, Freire PR, Zwaka TP, Golding I. Single-cell analysis of transcription kinetics across the cell cycle. eLife. 2016; 5:e12175 10.7554/eLife.12175 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Fraser HB. Cell-cycle regulated transcription assocates with DNA replication timing in yeast and human. Genome Biology. 2013; 14:R111 10.1186/gb-2013-14-10-r111 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Graham JE, Marians KJ, Kowalczykowski SC. Independent and stochastic action of DNA polymerases in the replisome. Cell. 2017; 169:1201–1213. 10.1016/j.cell.2017.05.041 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Padovan-Merhar O, Nair GP, Biaesch AG, Mayer A, Scarfone S, Foley SW, et al. Single mammalian cells compensate for differences in cellular volume and DNA copy number through independent global transcriptional mechanisms. Molecular Cell. 2015; 58(2): 339–352. 10.1016/j.molcel.2015.03.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Huh D, Paulsson J. Random partitioning of molecules at cel division. Proc Natl Acad Sci U S A. 2011; 108:15004–15009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Yu J, Sun Q, Tang M. The nonlinear dynamics and fluctuations of mRNA levels in cross-talking pathway activated transcription. Journal of Theoretical Biology. 2014; 363:223–234. 10.1016/j.jtbi.2014.08.024 [DOI] [PubMed] [Google Scholar]
- 21. Caveney PM, Norred SE, Chin CW, Boreyko JB, Razooky BS, Retterer ST, et al. Resource sharing controls gene expression bursting. ACS Synthetic Biology. 2017; 6:334–343. 10.1021/acssynbio.6b00189 [DOI] [PubMed] [Google Scholar]
- 22. Kempe H, Schwabe A, Crémazy F, Verschure PJ, Bruggeman FJ. The volumes and transcript counts of single cells reveal concentration homeostasis and capture biological noise. Molecular Biology of the Cell. 2015; 26:797–804. 10.1091/mbc.E14-08-1296 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Kuang J, Tang M, Yu J. The mean and noise of protein numbers in stochastic gene expression. Journal of Mathematical Biology. 2013; 67:261–291. 10.1007/s00285-012-0551-8 [DOI] [PubMed] [Google Scholar]
- 24. Cameron IL, Greulich RC. Evidence for an essentially constant duration of DNA synthesis in renewing epithelia of the adult mouse. The Journal of Cell Biology. 1963; 18:31–40. 10.1083/jcb.18.1.31 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Pham TM, Tan KW, Sakumura Y, Okumura K, Maki H, Akiyama MT. A single-molecule approach to DNA replication in Escherichia coli cells demonstrated that DNA polymerase III is a major determinant of fork speed. Molecular Microbiology. 2013; 90:584–596. 10.1111/mmi.12386 [DOI] [PubMed] [Google Scholar]
- 26. Rogozin IB, Makarova KS, Natale DA, Spiridonov AN, Tatusov RL, Wolf YI, et al. Congruent evolution of different classes of non-coding DNA in prokaryotic genomes. Nucleic Acids Research. 2002; 30:4264–4271. 10.1093/nar/gkf549 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Jovic D, Sakaue-Sawano A, Abe T, Cho CS, Nagaoka M, Miyawaki A, et al. Direct observation of cell cycle progression in living mouse embryonic stem cells on an extracellular matrix of E-cadherin. SpringerPlus. 2013; 2:585 10.1186/2193-1801-2-585 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. White J, Dalton S. Cell cycle control of embryonic stem cells. Stem Cell Reviews. 2005; 1:131–138. 10.1385/SCR:1:2:131 [DOI] [PubMed] [Google Scholar]
- 29. Duderstadt KE, Geertsema HJ, Stratmann SA, Punter CM, Kulczyk AW, Richardson CC, et al. Simultaneous real-time imaging of leading and lagging strand synthesis reveals the coordination dynamics of single replisomes. Molecular Cell. 2016; 64:1035–1047. 10.1016/j.molcel.2016.10.028 [DOI] [PubMed] [Google Scholar]
- 30. Knezetic JA, Luse DS. The presence of nucleosomes on a DNA template prevents initiation by RNA polymerase II in vitro. Cell. 1986; 45:95–104. 10.1016/0092-8674(86)90541-6 [DOI] [PubMed] [Google Scholar]
- 31. Lorch Y, LaPointe JW, Korgberg RD. Nucleosomes inhibit the initiation of transcription but allow chain elongation with the displacement of histones. Cell. 1987; 49:203–210. 10.1016/0092-8674(87)90561-7 [DOI] [PubMed] [Google Scholar]
- 32. Shemoen AW, O’Farrell PH. Progression of the cell cycle through mitosis leads to abortion of nascent transcripts. Cell. 1991; 67(2):303–310. 10.1016/0092-8674(91)90182-X [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Golding I, Paulsson J, Zawilski SM, Cox EC. Real-time kinetics of gene activity in individual bacteria. Cell. 2005; 123:1025–1036. 10.1016/j.cell.2005.09.031 [DOI] [PubMed] [Google Scholar]
- 34. Vintersten K, Monetti C, Gertsenstein M, Zhang P, Laszlo L, Biechele S, et al. Mouse in red: red fluorescent protein expression in mouse ES cells, embryos, and adult animals. Genesis. 2004; 40:241–246. 10.1002/gene.20095 [DOI] [PubMed] [Google Scholar]
- 35. Bar-Even A, Paulsson J, Maheshri N, Carmi M, O’Shea E, Pilpel Y, et al. Noise in protein expression scales with natural protein abundance. Nature Genetics. 2006; 38:636–643. 10.1038/ng1807 [DOI] [PubMed] [Google Scholar]
- 36. Cartwright P, McLean C, Sheppard A, Rivett D, Jones K, Dalton S. LIF/STAT3 controls ES cell self-renewal and pluripotency by a Myc-dependent mechanism. Development. 2005; 132:885–896. 10.1242/dev.01670 [DOI] [PubMed] [Google Scholar]
- 37. Dohrmann PR, Correa R, Frisch RL, Rosenberg SM, McHenry CS. The DNA polymerase III holoenzyme contains γ and is not a trimeric polymerase. Nucleic Acids Research. 2016; 44:1285–1297. 10.1093/nar/gkv1510 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Taniguchi Y, Choi PJ, Li GW, Chen H, Babu M, Hearn J, et al. Quantifying E. coli proteome and transcriptome with single-molecule sensitivity in single cells. Science. 2010; 329:533–538. 10.1126/science.1188308 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Yu J, Xiao J, Ren X, Lao K, Xie XS. Probing gene expression in live cells, one protein molecule at a time. Science. 2006; 311:1600–1603. 10.1126/science.1119623 [DOI] [PubMed] [Google Scholar]
- 40. Campos M, Surovtsev IV, Kato S, Paintdakhi A, Beltran B, Ebmeier SE, Jacobs-Wagner C. A constant size extension drives bacterial cell size homeostasis. Cell. 2014; 159:1433–1446. 10.1016/j.cell.2014.11.022 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Schmoller KM. The phenomenology of cell size control. Current Opinion in Cell Biology. 2017; 49:53–58. 10.1016/j.ceb.2017.11.011 [DOI] [PubMed] [Google Scholar]
- 42. Si F, Li D, Cox SE, Sauls JT, Azizi O, Sou C, et al. Invariance of initiation mass and predictability of cell size in Escherichia coli. Current Biology. 2017; 27:1–10. 10.1016/j.cub.2017.03.022 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Ross SM. Stochastic Processes. 2nd ed John Wiley & Sons, Inc; 1996. [Google Scholar]
- 44. Müller GA, Stangner K, Schmitt T, Wintsche A, Engeland K. Timing of transcription during the cell cycle: Protein complexes binding to E2F, E2F/CLE, CDE/CHR, or CHR promoter elements define early and late cell cycle gene expression. Oncotarget. 2017; 8:97736–97748. 10.18632/oncotarget.10888 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Gonzales KAU, Liang H, Lim YS, Chan YS, Yeo JC, Tan CP, et al. Deterministic restriction on pluripotent state dissolution by cell-cycle pathways. Cell. 2015; 162:564–579. 10.1016/j.cell.2015.07.001 [DOI] [PubMed] [Google Scholar]
- 46. Pauklin S, Vallier L. The cell-cycle state of stem cells determines cell fate propensity. Cell. 2012; 155(1):135–147. 10.1016/j.cell.2013.08.031 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
The detailed derivation of master equations and differential equations is given in the former part. Theorems 1-4 are restated in the second part, and the detailed mathematical proofs are given behind these theorems.
(PDF)
Data Availability Statement
All relevant data are within the manuscript and its Supporting Information files.