Energy dissipation in mammalian collagen fibrils: Cyclic strain-induced damping, toughening, and strengthening

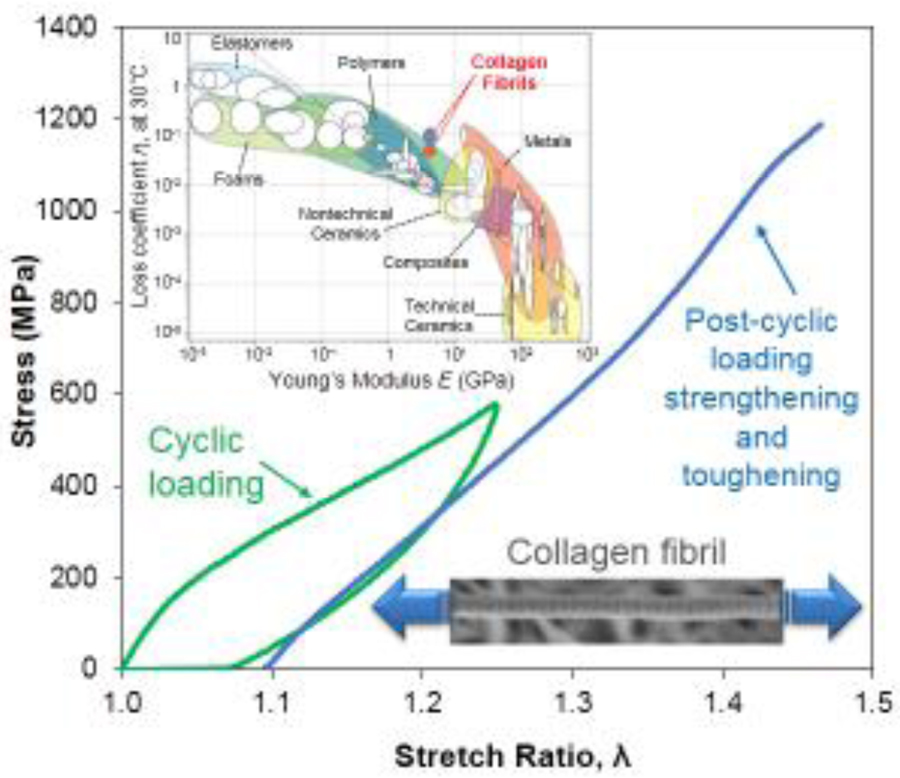
Abstract

As the fundamental structural protein in mammals, collagen transmits cyclic forces that are necessary for the mechanical function of tissues, such as bone and tendon. Although the tissue-level mechanical behavior of collagenous tissues is well understood, the response of collagen at the nanometer length scales to cyclical loading remains elusive. To address this major gap, we cyclically stretched individual reconstituted collagen fibrils, with average diameter of 145±42 nm, to small and large strains in the partially hydrated conditions of 60% relative humidity. It is shown that cyclical loading results in large steady-state hysteresis that is reached immediately after the first loading cycle, followed thereafter by limited accumulation of inelastic strain and constant initial elastic modulus. Cyclic loading above 20% strain resulted in 70% increase in tensile strength, from 638±98 MPa to 1091±110 MPa, and 70% increase in toughness, while maintaining the ultimate tensile strain of collagen fibrils not subjected to cyclic loading. Throughout cyclic stretching, the fibrils maintained a steady-state hysteresis, yielding loss coefficients that are 5–10 times larger than those of known homogeneous materials in their modulus range, thus establishing damping of nanoscale collagen fibrils as a major component of damping in tissues.

Graphical Abstract

1. Introduction

Collagen serves as the hierarchical building block of structural mammalian tissues [1]. This hierarchy begins with tropocollagen molecules (1.5 nm in diameter) that assemble into collagen fibrils (10s to 100s of nm in diameter) having a D-band structure with 67 nm repeated spacing [2–4]. The hierarchy continues across the length scales to fascicles (bundles of fibrils with micrometer diameter) and tissues (millimeters in diameter) [5–7]. Although the bulk mechanical properties of such tissues are well described, the hierarchical underpinnings continue to be the focus of research, especially at the nanoscale [8–13]. Although molecular dynamics predictions and experimental measurements of the low strain elastic behavior of hydrated collagen fibrils [14,15] are well established, their low and high strain response to cyclic loading remains unknown. Measurement of the dynamic response of collagen fibrils under cyclical forces, which is the focus of the current study, is important because tissues in our body experience mechanical cycling due, for instance, to cardiovascular outputs and routine movement.

The levels of strain transferred across the different hierarchies to the collagen fibrils are not definitively known, but are typically understood to span a broad distribution within a single tissue [16,17]. Mature collagen fibrils subjected to tension in fully hydrated environment have been shown to exhibit one, or more, of the following regimes of deformation: (a) An initial, nonlinear, toe regime followed by a nonlinear “heel” regime in which micrometer and nanometer level crimps straighten [7,13,15,18]; (b) an initial loading regime (often referred to as a “linear” regime) in which tropocollagen molecule uncoiling, assisted by a reduction in hydrogen bonds, takes place [19]; (c) an extended reduced stiffness regime in which molecular sliding occurs [10,13,20]; (d) a hardening regime in which stretching of the backbones of tropocollagen molecules, promoted by molecular cross-links, stiffens the fibril [21,22]; and finally, (e) a softening regime in which failure occurs. Having two or more cross-links per tropocollagen molecule substantially increases hardening [21] which becomes pronounced in the presence of mature, trivalent, cross-links. This hardening behavior leads to increased modulus in the aforementioned hardening regime, which is higher than the modulus of the initial loading regime (E₁) described above [10,22]. However, observations have varied significantly, with studies reporting rubber-like [10], linear/multi-linear [23], parabolic [24], or toe/heel/linear stress-strain curves [7,20], which do not include all five of the aforementioned regimes of the deformation response, depending on the type and density of cross-linking [10,18,21,22,25], and partially [26,27] or fully hydrated [10,18,28] conditions.

The key property that was investigated in this study is the ability of nanoscale collagen fibrils to absorb and dissipate energy in steady-state mode during cyclic loading, as quantified from mechanical loading-unloading hysteresis curves. Because energy dissipation is critical to the functions of collagenous tissues and their insertions [29], there is pressing need to understand the hierarchical origins and extent of the hysteretic behavior of collagenous tissues, especially in the context of engineering tissues and prosthetics. At the bulk level, hysteresis can arise in collagenous tissues due to fibril sliding [11], but the contribution of the dissipative material behavior of nanoscale fibrils has not yet been quantified. An important first step in this direction has been atomic force microscope (AFM) assisted testing of hydrated bovine collagen, which showed a stress-strain behavior that is characterized by hysteresis and plastic deformation for strains exceeding 6% [18]. These results suggested the possibility of nanoscale energy absorption in collagenous tissues, and, by comparison to the non-hysteretic behavior of dry collagen tested at the same strain levels [30], indicate that hydration affects the interactions between tropocollagen molecules, possibly by modulating hydrogen bonding [31]. To address this hypothesis, we undertook the first systematic cyclical loading study of reconstituted mammalian collagen fibrils in the absence of unbound water surrounding a collagen fibril in order to quantify the amount of energy dissipation per cycle and the associated changes in key mechanical properties, such as stiffness, strength and toughness. This study was conducted with partially hydrated collagen fibrils at 60% relative humidity (RH). The absence of external water molecules focuses this study in interfibrillar processes that affect energy dissipation inside individual collagen fibrils, rather than the exchange of water molecules between a collagen fibril and a buffer. The dissipated energy during mechanical cycling is normalized by an elastic term to yield the loss coefficient, a metric that enables a comparison amongst different materials [32], especially in the same modulus range as the collagen fibrils.

Furthermore, we quantified for the first time the effect of unloading on the recovery of the inelastic strain accrued during cyclic loading in different regimes of deformation, and the return to the mechanical behavior before mechanical cycling. The new insights presented in this work were made possible because of experiments at the low and the high strain regimes of the deformation of nanoscale collagen fibrils, which are controlled by some of the molecular mechanisms described above.

2. Materials and Methods

2.1. Synthesis and Characterization of Collagen Fibrils

The collagen used in this study was lyophilized collagen type I from calf skin (Elastin Products Co., No. C857 (1g) Lot 267), which was prepared according to Gallop and Seifter [33]. In this method, fresh calf skin is extracted with 0.5 M NaOAc to remove non-collagen proteins. The soluble collagen is then extracted with 0.075 M sodium citrate, pH 3.7, and precipitated as fibrils by dialysis against 0.02 M Na₂HPO₄. Reconstituted collagen was then synthesized at our lab according to [34,35]. Specifically, 500 μL of 2× triethylsaline (TES) buffer (30mM TES, 135 mM NaCl, 30 mM Na2HPO4 (Sigma-Aldrich Co., MO, USA), adjusted to a pH of 7.4–7.5 with drops of 10 N NaOH, were mixed with 400 μL dH₂O in a 1.5 mL centrifuge tube and placed on ice. Separately, 35 mg lyophilized collagen type I (Elastin Products Company, Inc., MO, USA) were dissolved in 10 mL 0.2 N acetic acid and mixed in a vortex mixer (Fisher Scientific Co. L.L.C., PA, USA). After solubilizing in acetic acid, 100 μL 3.5 mg/mL collagen solution were added on ice to the centrifuge tube containing 1× TES buffer. The solution was then mixed briefly in a vortex mixer before placed in a 28°C water bath for 5–6 hr. Two hours later the collagen solution was again briefly mixed in the vortex mixer and monitored for gel formation. The reconstituted collagen remained refrigerated at 4.0°C, until mechanical testing in ambient conditions. Single collagen fibrils were isolated under high optical magnification (50× objective) via a fine tungsten probe with tip diameter ~200 nm. The fibrils were handled from their free ends to prevent damage before testing.

Reconstituted collagen fibrils were imaged by transmission electron (TEM), scanning electron (SEM), and AFM, to confirm the consistency of 67-nm periodic banding as shown in Figure 1a. In their dry state, the fibrils tested in this work had diameters between 75 and 225 nm. The diameters of different fibrils in the buffer had a broad distribution of values, but each individual fibril demonstrated very limited diameter variation along the length, as this was determined with an SEM. The tested fibrils had average diameter 145±42 nm, as calculated from the values listed in Table I.

Figure 1.

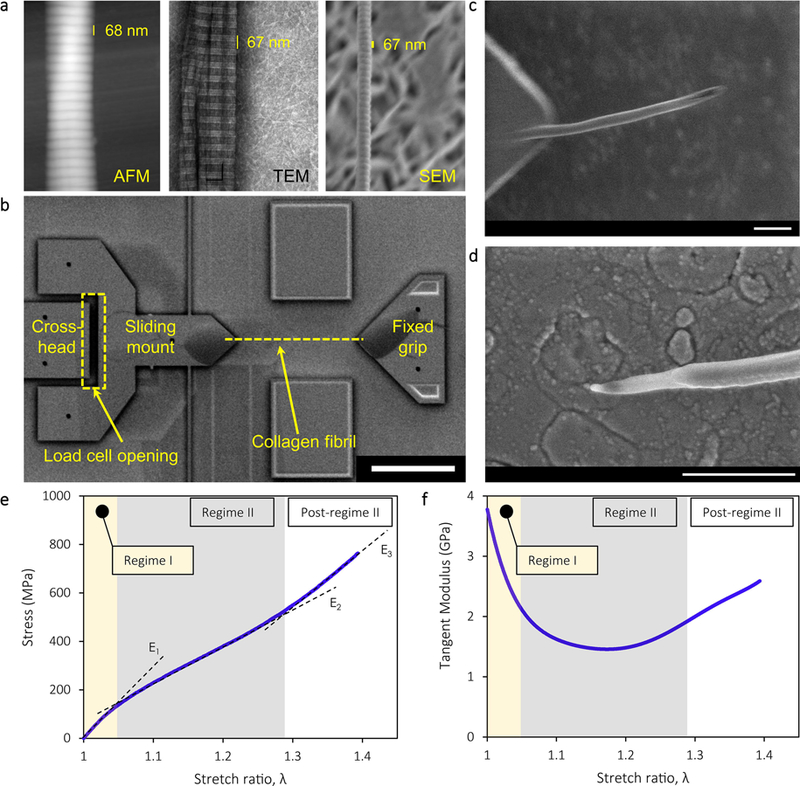
a. Reconstituted mammalian collagen fibrils with D-banding of ~67 nm as imaged by SEM, TEM, and AFM (in air). b. The collagen fibrils were tested under cyclic tension using a MEMS device. Each fibril was bonded between a sliding mount and a fixed grip as shown. The load cell opening, marked by the dashed rectangle, changes proportionally to the force applied to the fibril. MEMS device is shown after test is completed. The scale bar corresponds to 50 μm. c,d. Matching segments of a collagen fibril demonstrating shear failure. The scale bars correspond to 500 nm. e. Stress vs. stretch ratio curve, and f. local slope of stress vs. stretch ratio curve (tangent loading modulus) of a typical fibril, divided into: (I) an initial linear regime (regime I) with modulus E₁, (II) a softening regime (regime II) with modulus E₂, and (III) a final hardening regime (post-regime II) in which the modulus E₃ did not exceed E₁. For the curve shown, the fibril diameter was 90 nm.

TABLE I.

Summary of properties derived from monotonic and cyclic loading tests. The values shown are the mean ± standard deviation. The moduli values quoted in cyclic tests correspond to the steady-state values (i.e. cycles 2–9). The ultimate stretch ratio is reported for fibrils that reached post-regime II in their deformation.

Type (# Tests)	Monotonic Loading (6)	Cyclic, regime I (5)	Cyclic, regime II (8)	Cyclic, Post- regime II (5)
Fibril diameter (nm)	137± 62	140 ± 33	170 ± 23	117 ± 39
E1, series 1 (GPa)	4.3 ± 1.1	4.8 ± 0.4	4.3 ±0.9	4.5 ± 1.3
E1, series 2 (GPa)	-	4.6 ± 0.4	4.4 ± 0.9	4.8 ± 0.5
E2, series 1 (GPa)	1.8 ± 0.6	-	2.8 ± 0.5*	2.9 ± 0.7*
E2, series 2 (GPa)	-	1.7 ± 0.4	2.9 ± 0.3*	2.9 ± 0.6*
Tensile strength (MPa)	638 ± 98	667 ± 140	1059 ± 89*	1134 ± 140*
Toughness (MJ/m3)	119 ± 19	124 ± 25	204 ± 81	196 ± 78
Ultimate stretch ratio (final loading cycle)	1.33 ± 0.07	1.33 ± 0.04	1.36 ± 0.13	1.35 ± 0.09
Inelastic strain (%)		4 ± 2	11 ± 3	13 ± 4
Hysteresis (first cycle, series 1) (MJ/m3)	-	4.0 ± 3.0	35.7 ± 13.3	52.6 ± 18.9
Steady state hysteresis, series 1&2 (MJ/m3)	-	1.0 ± 0.8	7.4 ± 3.3	13.5 ± 4.1
Loss coefficient, first cycle, series 1	-	0.09 ± 0.01	0.10 ± 0.01	0.09 ± 0.01
Loss coefficient, steady- state, series 1&2	-	0.04 ± 0.01	0.04 ± 0.01	0.05 ± 0.01

^*Statistically different and significantly higher from the corresponding monotonic and regime I cyclic testing results (p-value < 0.05).

2.2. Tensile Testing of Individual Collagen Fibrils

The Microelectromechanical System (MEMS) based device used to test individual collagen fibrils under monotonic and cyclic loading was based on a method developed by this group to study the mechanical behavior of polymeric and biological nanofibers [36,37]. In this method, the MEMS devices are comprised of four components: a pedal for gripping, a folded beam load cell, a sliding mount and a fixed grip (Figure 1b). The entire MEMS device is less than 1 mm long. The pedal for adhesive gripping is used to actuate the folded beam load cell that ends to a grip for adhesive mounting of one end of the collagen fibril. The pedal, load cell and grip are freestanding. As shown in Figure 1b, the sliding mount is part of the load cell, while the right hand grip is fixed. A collagen fibril is attached to the tips of the two grips with an epoxy adhesive (Devcon 5 min epoxy) in the area marked with a dashed line in Figure 1b, and stretched when the crosshead is translated to the left. The distance between the grips can be varied; in the experiments presented here, the nominal distance was 30 μm, but the exact fibril gauge length was measured for each experiment.

The MEMS load cell behaves as a linear spring in series with a collagen fibril. Based on estimates for the fibril stiffness, the MEMS load cells were designed for a stiffness that maximized the force resolution while ensuring that it functioned as a linear spring [38]. Load cells with stiffnesses of 0.8 N/m, 3.5 N/m, and 7.0 N/m were used for fibrils with different diameter, and therefore stiffness, and were calibrated according to reference [39].

High magnification optical images (500×) of the field of view in Figure 1b were used to obtain the motion of the sliding mount and the crosshead with a resolution of ~20 nm [36] and, thus, measure nanometer-scale fibril extensions and nanonewton level applied forces. Such force and extension resolution are obtained without the use of an SEM which would damage a collagen fibril. The fibril cross-head extension and loadcell opening were calculated via Digital Image Correlation (DIC) by taking advantage of the natural speckle pattern on the surface of the MEMS devices due to the fine surface roughness (RMS ~10 nm) that was revealed by dark-field optical imaging. During fibril testing, the crosshead in Figure 1b was translated with the aid of a piezoelectric actuator at 125 nm/sec, resulting in a nominal strain rate of 4·10⁻³ s⁻¹. The relative motion of the crosshead and the sliding mount provided the opening of the pre-calibrated loadcell, as marked by the dashed rectangle in Figure 1b. The experimental measurements were used to construct the monotonic σ - λ curves, e.g. Figure 1e, with the stretch ratio, λ, defined as the ratio of the final to the initial fibril length and the engineering stress, σ, as the force divided by initial cross-sectional area. After testing, the initial fibril diameter was measured by an SEM in a segment of the fibril that was outside the test section. Post-mortem SEM images were also used to confirm that failure occurred in the gauge section, Figures 1c,d. The monotonic σ - λ curves revealed three distinct regimes of deformation: (a) an initial high stiffness regime (regime I), followed by (b) an extended regime of lower stiffness (regime II), and were terminated by (c) a final hardening regime. This last regime is termed “post-regime II” because E₃ < E₁, (Figures 1e,f), namely there is no clear transition to backbone stretching. This is due to the lack of mature, trivalent, crosslinks that would lead to a pronounced hardening “regime III” with E₃ > E₁. Based on the distinction of the three regimes of deformation shown in Figures 1e,f, cyclic tension experiments were carried out: a fibril was cyclically loaded to a maximum stretch ratio, λ_max, within one of the three regimes of deformation. A machine vision program developed in LabVIEW utilized a real-time edge detection algorithm to maintain the target λ_max by controlling the cross-head motion (Figure 1b) with displacement accuracy better than 50 nm. The cyclic experiments were conducted in two sets of 10 cycles that were interrupted by a 60-min relaxation interval with the fibril being fully unloaded. During this interval the fibrils were loose to ensure that strain recovery would not initiate early reloading. During each of the 10 cycles in series 1 and 2, a fibril was fully unloaded from λ_max to zero force, as determined in real time via edge detection from the load cell opening (Figure 1b), and immediately reloaded to λ_max. Since the nominal loading and unloading strain rates were constant in all experiments (4·10⁻³ s⁻¹), the cycling frequency depended on λ_max and the stiffness of the loadcell. This frequency varied from 0.012 Hz for fibrils cycled to λ_max = 1.05, to 0.006 Hz for fibrils cycled to λ_max = 1.25. In the results presented in this paper, the initial loading modulus, E₁, was calculated by linear fitting up to λ~1.02 and the loading modulus of regime II, E₂, was calculated from the linear segment of the curve in regime II.

The experiments were conducted at 60% RH, which corresponds to 26g H₂O/100g of dry collagen [40]. In comparison, 95% RH corresponds to 51g H2O/100g of dry collagen [41]. The authors in [42] reported that, at full occupancy, the water bound by hydrogen bonding to primary sites corresponds to a concentration of 51g H₂0/100g dry collagen while dehydrated collagen by air-drying has a concentration of merely 10g H₂0/100 g dry collagen. Therefore, the use of the term “partially hydrated” is appropriate for the present experiments. Notably, experiments conducted at 30% RH provided the same moduli, hysteresis and strength values as those at 60% RH. Therefore, the two data sets were merged together in the statistical analysis presented here.

2.3. Statistical analysis

Statistical comparisons between the means of different sample groups were made using a one-way analysis of variance (ANOVA), with p-values < 0.05 indicating a significant difference between the mean values. Post-hoc comparisons between any two sample groups in the pool were performed when the ANOVA test resulted in p-values < 0.05. Post-hoc analyses were done with Fisher’s least significant difference (LSD) test. Using the aforementioned method, comparisons were made among the mechanical parameters (E₁, E₂, tensile strength, toughness, ultimate stretch ratio, and loss coefficients) obtained via monotonic vs. cyclic loading. The experimentally derived properties that were found to be statistically different by using ANOVA are indicated with an asterisk in Table I.

Statistical comparisons between the means of two independent groups were evaluated using two-tailed Student t-tests, with p-values < 0.05 indicating a significant difference between the mean values. The assumption of homogeneity of variances was used and the validity of the assumption was tested using the Levene’s test with a p-value > 0.05. In the following Sections it is specifically noted when the t-test was used as a statistical measure.

3. Results

The reconstituted collagen fibrils tested herein assembled from acid-soluble collagen and had the characteristic native D-banding (Figure 1a). In general, reconstituted collagen approximates in vivo collagen better than fibers formed from enzyme digested collagen [43–45]. The σ - λ curves of 24 successfully tested fibrils under monotonic and cyclic loading, Table I, were comprised of three distinct regimes (Figures 1e,f): (I) an initial linear regime (regime I) with λ values up to 1.05–1.1 and E₁ = 4.5±0.9 GPa (average of all values from the 24 monotonic and cyclic tests listed in Table I); (II) a softening regime (regime II) with λ up to ~1.25 and average modulus E₂ = 1.8±0.6 GPa based on (6) fibrils subjected to monotonic loading (a statistically similar value, as determined via the two-tailed t-test, of E₂ = 1.7±0.4 GPa was obtained from a different set of 6 tests in which the fibrils were cycled in regime I only); and (III) a final hardening regime with gradually increasing modulus until failure (tensile strength 638±98 MPa and ultimate stretch ratio λ_f = 1.33±0.07 under monotonic loading).

3.1. Steady-state Hysteresis and Recovery of Collagen Fibrils

Figures 2a,b show an example of a fibril subjected to 20 cycles at λ_max=1.1. Because of the accumulation of inelastic strain, comprised of irrecoverable (“plastic”) strain and a viscoelastic component, the maximum applied stress decreased to a steady state value, following the same trend as the inelastic strain in Figure 2c. Fibrils loaded cyclically to strain levels approaching the end of regime I showed a repeatable hysteretic behavior that reached a steady-state after ~2 cycles (Figures 2d,e): the cyclic energy dissipation (area enclosed by a full loading-unloading curve) reached a plateau after the first loading-unloading cycle (Figure 2e). The inelastic strain also reached a steady-state value after the first three cycles (Figure 2c), while the elastic modulus, E₁, remained relatively constant throughout the entire mechanical cycling process (Figure 2d) providing strong evidence that the dissipative process taking place in the individual collagen fibrils is not accompanied by damage accumulation which, in turn, would have manifested as softening and a gradual reduction in the value of E₁.

Figure 2.

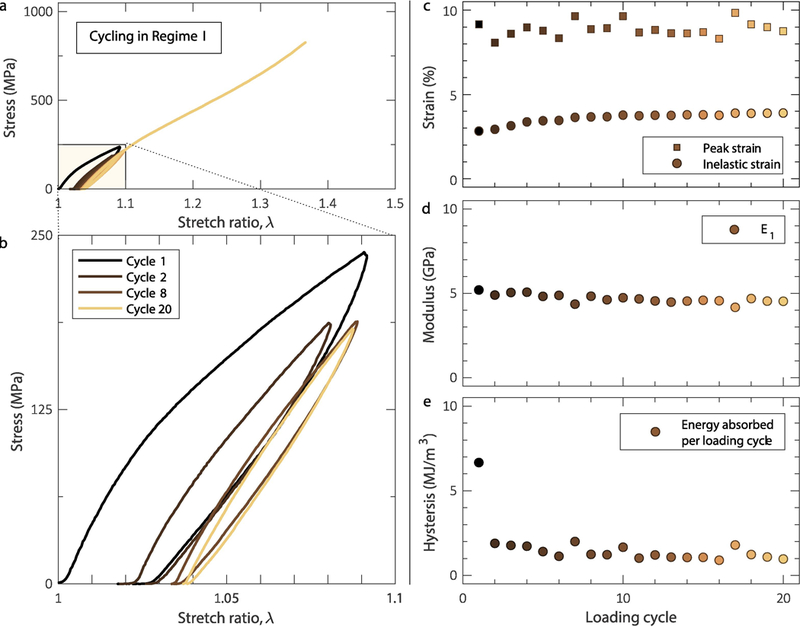
a,b. When cycled in regime I, collagen fibrils demonstrated repeatable hysteresis that reached steady-state after the very first cycle. c. Inelastic strain reaching a steady-state value after the first three cycles. Also shown is the peak stress during mechanical cycling. d. Elastic modulus insensitivity to mechanical cycling. e. Energy dissipation per loading cycle reaching steady-state after the first cycle. For the data shown, the fibril diameter was 197 nm.

Importantly, the same dissipative behavior was recorded for fibrils that were allowed to relax for 60 min after a series of ten loading cycles (shown as “series 1” in Figure 3), with partial recovery in the magnitude of the hysteresis of the very first cycle and a 50% recovery in the inelastic elongation, as evident by the first of the additional 10 cycles (shown as “series 2” in Figure 3) applied after the relaxation interval.

Figure 3.

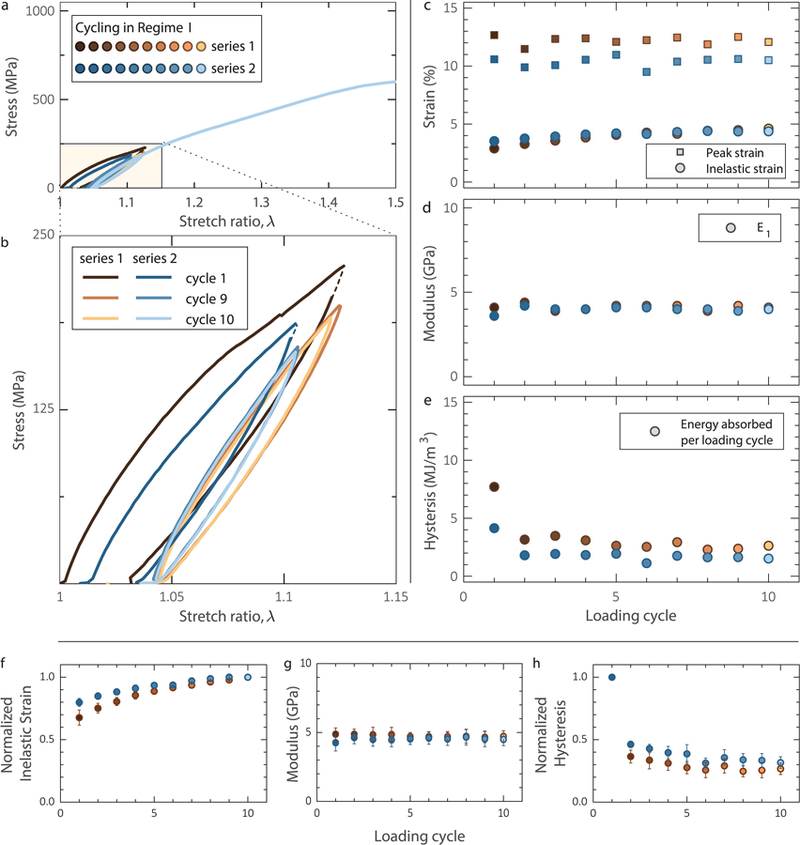
a,b. When cycled in regime I, collagen fibrils showed a hysteresis that reached steady-state within a few cycles both before (brown symbols) and after (blue symbols) 60-min relaxation. The dashed lines indicate a lapse in the data acquisition system. c. Inelastic strain before and after a 60 min relaxation interval, showing 50% strain recovery during the relaxation time. d. Elastic modulus insensitivity to cyclic loading before and after recovery. e. Energy dissipation reaching steady-state after only one cycle both before and after 60-min relaxation. For the data shown, the fibril diameter was 130 nm. Mean value of f. inelastic strain, g. elastic modulus E₁, and h. hysteresis vs. cycle before and after relaxation computed from (5) cyclic tests conducted in regime I. The inelastic strain was normalized with the steady-state value in the 10^th cycle, while the hysteresis was normalized with the value of the first cycle. Statistical data for inelastic strain and hysteresis are presented in normalized form because their absolute values depend on the applied λ_max (see later Figure 6a). The error bars correspond to one standard deviation.

The same steady-state dissipative behavior was recorded by cycling collagen fibrils in regime II (Figure 4) and post-regime II (Figure 5), with E₁ being invariant to mechanical cycling at low or high strains. However, mechanical cycling in regime II and post-regime II caused a contraction of the extent of regime I in the σ - λ curves and the transition region from regime I to II, as deduced from Figure 5b. In other words, the majority of tropocollagen molecule uncoiling in regime I may occur in the very first cycle.

Figure 4.

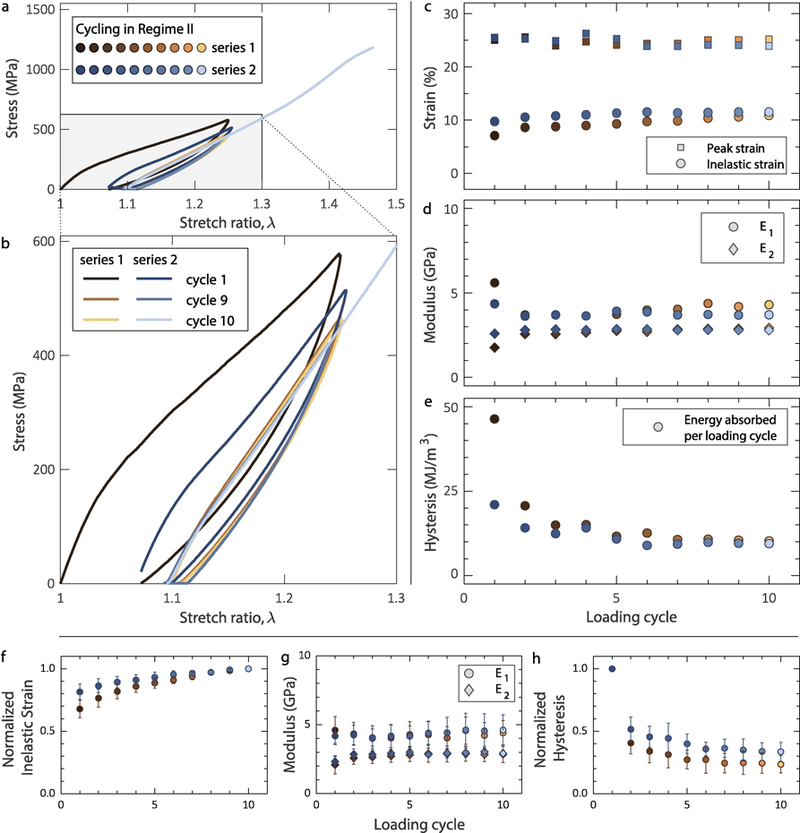
a,b. Collagen fibrils cycled within regime II demonstrated steady-state hysteresis. c. Inelastic strain showing a steady-state response after the first two cycles during cycling before (brown symbols) and after (blue symbols) a 60-min relaxation interval. d. Elastic modulus in regime I (E₁) and regime II (E₂) showing insensitivity to mechanical cycling. e. Energy dissipated per loading cycle showing a steady-state before and after 60 min relaxation. For the data shown, the fibril diameter was 157 nm. Mean value of f. inelastic strain, g. elastic moduli E₁ and E₂, and h. hysteresis vs. cycle before and after recovery for all (8) cyclic tests conducted in regime II. The inelastic strain was normalized with the steady-state value in the 10^th cycle, while the hysteresis was normalized with the value of the first cycle. Statistical data for inelastic strain and hysteresis are presented in normalized form because their absolute values depend on the applied λ_max (see later Figure 6a). The error bars correspond to one standard deviation.

Figure 5.

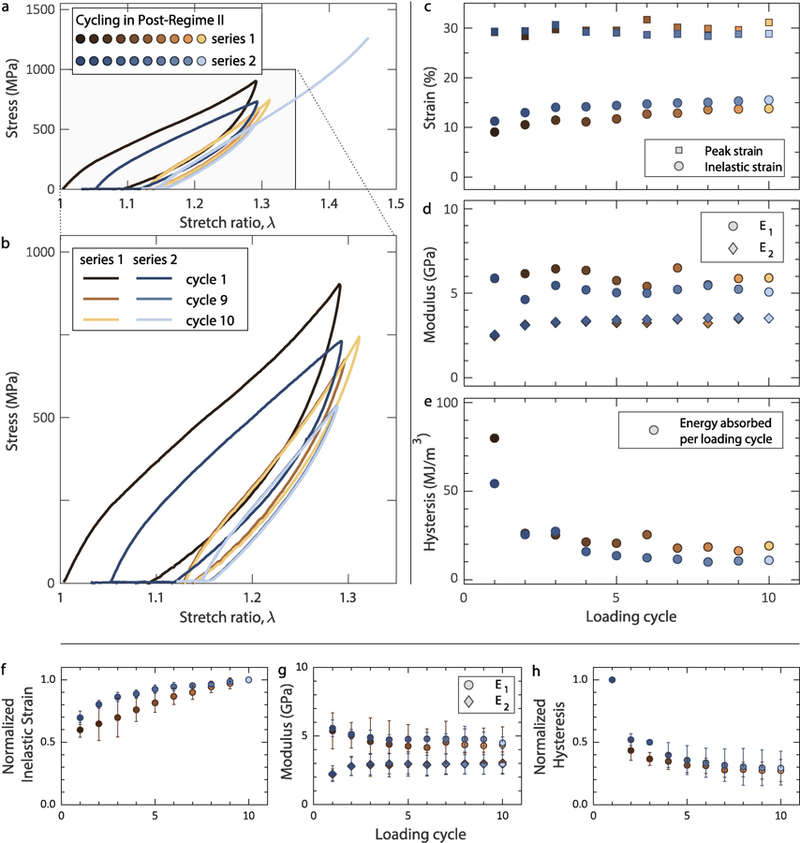
a,b. Collagen fibrils cycled in post-regime II, showing steady-state hysteresis both before (brown symbols) and after (blue symbols) a 60-min relaxation interval. c. Inelastic strain reaching steady-state after the first five cycles. d. Elastic modulus in regime I (E₁) and regime II (E₂). e. Energy dissipation per loading cycle reaching steady-state after the first five cycles before and after relaxation. For the data shown, the fibril diameter was 100 nm. Mean value of f. inelastic strain, g. elastic moduli E₁ and E₂, and h. hysteresis vs. cycle before and after relaxation for all (5) cyclic tests conducted in post-regime II. The inelastic strain was normalized with the steady-state value in the 10^th cycle, while the hysteresis was normalized with the value of the first cycle. Statistical data for inelastic strain and hysteresis are presented in normalized form because their absolute values depend on the applied λ_max (see later Figure 6a). The error bars correspond to one standard deviation.

Figures 3f, 4f, and 5f show the average normalized inelastic strain as a function of loading cycle before and after relaxation from 5, 8 and 5 experiments conducted in regimes I, II and post-regime II, respectively. The inelastic strain depends on the exact value of λ_max, hence the data are plotted in normalized form. The elastic modulus values E₁ and E₂ did not depend on λ_max, therefore, the average values and standard deviation are shown in Figures 3g, 4g, and 5g. Similarly, the average normalized hysteresis (energy per unit fibril volume) in regimes I, II and post-regime II, is shown in Figures 3h, 4h, and 5h, respectively. As in the case of inelastic strain, the hysteresis depends on the amplitude of λ_max, therefore, the average normalized values and the standard deviation in each cycle are shown. In terms of absolute values, Figure 6a shows a rapid increase of hysteresis with λ_max, which roughly follows a parabolic law. Table I summarizes the statistical values of all quantities derived from the experimental data.

Figure 6.

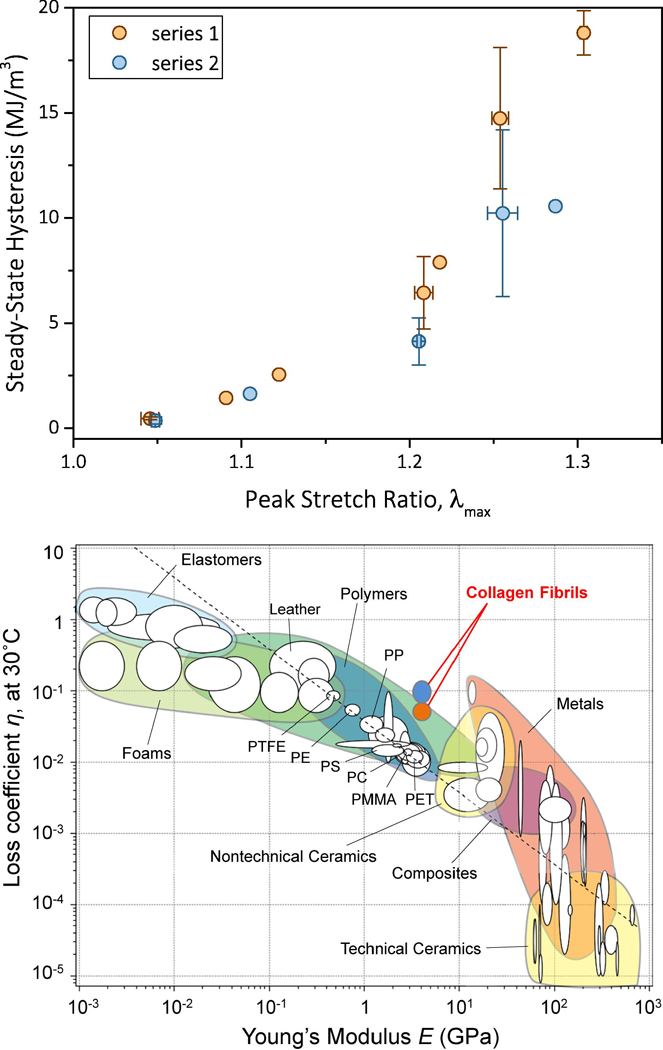
a. Steady-state hysteresis vs. λ_max in the entire range of applied λ_max before (series 1) and after (series 2) recovery. When available, the data points are the averages of two or more tests, while the error bars are equal to one standard deviation. b. Loss coefficient vs. elastic modulus for the entire range of homogeneous materials. Reconstituted mammalian collagen fibrils demonstrated a loss coefficient that was an order of magnitude higher than any material within their modulus range, thus expanding the envelope of material loss behavior. Orange bubble corresponds to the loss factor of steady-state response and cyan bubble corresponds to the loss factor of the first cycles of series 1 and 2. Chart adapted from [32] and modified to include the loss coefficients calculated based on the present results.

3.2. Loss Coefficient of Collagen Fibrils Compared to Bulk Solids

The capacity of individual collagen fibrils to dissipate energy by a steady-state hysteretic response was compared to the entire spectrum of engineering materials via the loss coefficient, η, defined as the ratio of hysteresis to the elastic energy supplied per cycle, πσ_maxΔε_max, (e.g. Figure 2e) where σ_max and ε_max are the peak engineering stress and the strain interval for which the specimen sustains a loading cycle, respectively [32]. The average initial (first) cycle and steady-state loss coefficients for collagen fibrils listed in Table I are plotted on an Ashby chart as a function of E₁ measured in each loading cycle (Figure 6b). The extended Ashby chart reveals that mammalian collagen fibrils have a loss coefficient that is 5–10 times higher than the materials within their modulus range.

3.3. Strengthening and Toughening due to Cyclic Loading

The final loading (until failure) σ - λ curves after cyclic loading revealed several adaptive effects of cyclic pre-stretching (Figure 7). Cyclic stretching in regime II increased the average strength of 638±98 MPa, as recorded in monotonic tests or from specimens cycled only in regime I (667±140 MPa), to 1059±89 MPa, with a maximum recorded tensile strength value of 1.26 GPa. Furthermore, cycling in regime II did not reduce the maximum stretch ratio attained at the final loading cycle to failure, which averaged 1.36±0.13. Thus, mechanical cycling at high strains increases both the tensile strength and the toughness of a collagen fibril, as given by the area under the σ - λ curves. Cyclical stretching in regime II (and post-regime II) also shortened the extent of regime I, thus resulting in quite linear curves during the entire final loading (Figures 7b,c). A relatively linear behavior over such a large strain range (~35%, Figure 7) is not commonly encountered in engineering materials, especially taking into account the relatively large values of the elastic moduli E₁ and E₂. Notably, mechanical cycling in post-regime II, although took place in the last segment of the σ - λ curve before failure, did not affect the mechanical strength or the maximum stretch ratio in the final loading cycle. Both quantities were comparable and statistically similar to those in regime II, namely 1059±89 MPa vs. 1134±140 MPa, and 1.36±0.13 vs. 1.35±0.09, for regime II and post-regime II, respectively. Additionally, the statistical analysis showed that the tensile strengths obtained after mechanical cycling in regime II and post-regime II were significantly higher than the strengths obtained in the monotonic and regime I cyclic tests. Further comparisons between the two regimes can be drawn from the data in Table I.

Figure 7.

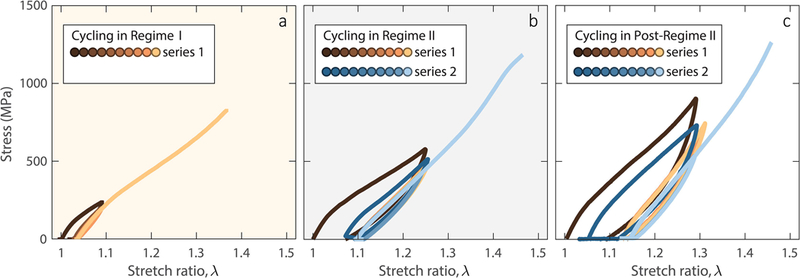
Cyclic stretching of three collagen fibrils followed by final loading to failure, demonstrating fibril strengthening upon cyclic loading at high strains. Final loading to failure after a. 20 loading cycles in regime I (fibril diameter: 197 nm), b. two series of 10 loading cycles in regime II (fibril diameter: 157 nm), and c. two series of 10 loading cycles in post-regime II (fibril diameter: 100 nm).

4. Discussion

The results presented herein suggest previously unforeseen ways in which nanoscale collagen may contribute to the mechanics of collagenous tissues, and that low frequency, high strain, “stretching” may improve their mechanics by resulting in a steady-state response at the lowest levels of the tissue hierarchy. As shown in Table I, stretching at strains 20% or higher (regime II and beyond) increased the tensile strength and the toughness by 70%, as compared to monotonic or small strain loading. From the perspectives of toughness and damping, the steady energy dissipation of individual fibrils, achieved after the first loading cycle, reveals that individual fibrils do contribute significantly to the energy dissipation in tissues, and that high strain cycling increases the resistance to failure by increasing the tensile strength and toughness. When compared to all engineering materials, these combined effects produce a loss coefficient that is 5 times higher than any other material in the modulus range of collagen. During the very first loading cycle, the loss coefficient at large strains (regime II and post-regime II) is the same as that of foams that are 100–1000 times more compliant than collagen fibrils, Figure 6b, and, therefore, under the same applied strain foams would dissipate a proportionally smaller amount of energy. The loss coefficient of collagen also results in 4.5 times larger loss modulus than the value predicted by the scaling law of Ashby [32]: whereas engineering polymers have loss moduli that scale as ηE = 0.04 GPa (corresponding to all materials crossed by the diagonal dashed line in Figure 6b), our data for collagen scale as ηE₁ = 0.18 GPa which also exceeds the loss modulus of leather, ηE = 0.04 GPa, a dry collagenous substance. Similarly, although elastomers have higher loss coefficients than the collagen fibrils, their vastly (three order or magnitude) smaller elastic moduli implies a proportionally smaller amount of dissipated energy, which places collagen in a unique place in the materials chart in Figure 6b. Moreover, the large elastic strain imposed during steady-state cycling distinguish the collagen fibrils as a highly dissipative biopolymer compared to all engineering polymers in the same modulus range: whereas engineering polymers typically sustain less than one percent strain during steady-state cyclic loading, the collagen fibrils sustained up to 20%, as evident from the difference between the applied peak strain and the steady-state inelastic strain in Figure 5c.

Following the aforementioned detailed measurements, the question naturally arises: How are these mechanical properties achieved in collagen fibrils? The first clues come from the observed plateaus in the inelastic deformation. The consistency and statistical similarity of the elastic modulus E₁ across all types of experiments, Table I, and the imparted strengthening and toughening after high strain cyclic loading, reveal that this inelastic deformation is not due to nanoscale damage accumulation. With the aid of mesoscale computational modeling, DePalle et al. [22] showed that intermolecular cohesive forces allow for uniform deformation inside fibrils, and attributed ~80% of the deformation in regime I to uncoiling of tropocollagen molecules and the remaining 20% to surface effects and molecular sliding. In agreement with these results, the plateaus of inelastic strain provide evidence that deformation in regime I does not impart major molecular rearrangements after the first cycle, and that the majority of unrecoverable molecular sliding takes place in the very first cycle of each loading series. At higher strains in regime II, MD simulations [22] have attributed the deformation to a combination of (a) molecular sliding because intermolecular forces have exceeded a threshold, and (b) relative sliding of collagen molecules associated with stretch of cross-links [15,22]. The large contribution of molecular sliding is consistent with our observations of a gradually increasing inelastic strain in regime II, which may localize in the gap regions of the banded collagen structure shown in Figure 1a, [15,22,46,52]. A steady-state relative sliding of collagen molecules due to breaking and reforming van der Waals bonds is supported by the long straight segment of the σ - λ curves in regime II, e.g. Figure 1e. Concomitantly, the increase in the value of E₂ during cyclic testing in regime II and post-regime II to an average of 2.9±0.5 GPa (for all the data in Table I), in conjunction with 70% increase in tensile strength and toughness, point to permanent molecular rearrangements taking place in regime II. The strengthening and toughening of fibrils in response to cycling at high strains is an intriguing result worthy of further study. Although the mechanisms underlying this behavior are not clear, we note that they are consistent with observations and an associated model for collagen fibrils reported in [47], in which periodic buckles that appear at the D-bands are reduced in number by stretches of sufficient magnitude and duration which also control the formation and annihilation of internal strain driven defects. This mechanism may provide an explanation for the higher steady-state value of E₂ due to cycling in regime II and post-regime II from 1.8±0.5 GPa (average of all values from monotonic loading and cyclic loading in regime I) to 2.9±0.5 GPa (average of all values from mechanical cycling in regime II and post-regime II).

The higher value of E₂ due to cycling in regime II and post-regime II is responsible for the increase in toughness, as calculated from the final σ - λ curve to failure immediately after cycling. First it should be noted that the toughness values of pristine collagen fibrils and those cycled only in regime I were 119±19 and 124±25 MJ/m³, respectively, namely mechanical cycling in regime I did not affect the large strain behavior of collagen fibrils. Following the periodic buckles model in [47], it is plausible that there is a strain threshold that is exceeded while cycling in regime II (λ_max ≈ 1.2) and post-regime II (λ_max ≥ 1.25), thus reducing the number density of such buckles and resulting in larger stiffness and toughness, 204±81 MJ/m³ and 196±78 MJ/m³ upon cycling in regime II and post-regime II, respectively.

On the other hand, the aforementioned molecular rearrangements and the recovery of inelastic strain after a 60 min relaxation interval are consistent with the role of backstresses, i.e. self-equilibrating internal stresses between tropocollagen molecules or collagen microfibrils, which build up during mechanical cycling. We expect the majority of the viscoelastic strain component of the total inelastic strain to be recovered during this 60-min relaxation interval: viscoelastic studies of collagen fibrils [48] and tissues [49] have shown that the time constant of the steady-state response is of the order of 100 s which would allow for the majority of the viscoelastic component of strain to be relaxed within the 60 min relaxation time. Since uncoiling reduces the hydrogen bonds [19], the partial recovery and return to the initial behavior during relaxation (compare cycle 1 data for series 1 and 2 in Figures 4b and 5b) implies that some of the severed hydrogen bonds are restored upon relaxation. Notably, in Table I E₂ was statistically equivalent for fibrils tested monotonically (1.8±0.6 GPa) and cyclically in regime I (1.7±0.4 GPa). However, mechanical cycling in regime II and post-regime II, where molecular sliding occurs [10,13,20], increased the average value of E₂ to 2.9±0.5 GPa which is significantly higher than the values obtained from monotonic and regime I cyclic tests. In the last segment of the σ - λ curves represented by post-regime II, the fibril stiffness did not exceed the initial fibril stiffness in regime I, Figure 1f. Reconstituted collagen lacks mature cross-links that would promote backbone stretching in this regime, contrary to collagen fibrils with mature cross-links that facilitate stretching of the backbones of tropocollagen molecules at high strains and, therefore, demonstrate significant fibril stiffening [10].

While at the tissue level [50,51] water molecules within fibrils [40] can rearrange during fibril deformation [48,52] and build backstresses that drive the recovery of inelastic strain during relaxation, the present collagen fibrils were only partially hydrated. As estimated by Grigera and Berendsen using statistical models [40], at 60% RH there is ~90% occupancy of specific sites by water. Therefore, while the structure of bound water is largely preserved at this humidity level, there is no exchange of water with the surrounding medium. In the presence of unbound water, deformation in regime I has been attributed to molecular uncoiling assisted by breakage of hydrogen bonds in tropocollagen molecules [19] and molecular sliding [10,13,20]. The same process of severing and reforming of sacrificial bonds could also explain the large hysteresis in regime II and post-regime II, as it has been shown that the loss of weakly bound water molecules in partially hydrated collagen and the associated significant reduction in fibril diameter compared to in vivo collagen, result in increased number and strength of hydrogen bonds [53] which, in turn, support large forces and deformation via a process of severing and reforming. The larger number and strength of hydrogen bonds in partially hydrated collagen contributes to the large values of the elastic modulus and ultimate tensile strength compared to in vitro studies.

As a final note, reconstituted collagen fibrils are acid soluble because they lack stable intermolecular cross-links, but contrary to enzyme digested collagen that lacks the telopeptide region where cross-links would form, the former can still form labile cross-links. In this regard, reconstituted collagen approximates the properties and structure of rat tail tendon collagen [45] which also lacks the mature, trivalent, crosslinks that are present in most collagenous tissues. Experiments with reconstituted collagen fibers and rat tail tendon fibers have shown comparable ultimate tensile strength and elastic moduli [45]. In comparison with the present data, E₁ of partially hydrated reconstituted collagen fibrils is twice as high as that reported for PBS-immersed collagen fibrils derived from rat tail tendon [10]. Interestingly, E₂ of monotonically loaded partially hydrated reconstituted collagen fibrils was statistically similar (using the two-tailed t-test) to that reported for collagen fibrils derived from rat tail tendon that were fully immersed in phosphate buffered saline (PBS) [10] (1.8±0.6 GPa vs. 1.4±0.7). The properties reported in [10] were also calculated using fibril cross-sections as measured in air by AFM; therefore, a direct comparison of these results can be made, as opposed to literature reports that utilized estimates for the diameter of hydrated collagen fibrils. Qualitatively, the σ - λ curves of partially hydrated reconstituted collagen fibrils demonstrated the onset of hardening, a feature absent in the case of PBS-rehydrated collagen fibrils derived from rat tail tendon [10] which soften before failure. Experiments with reconstituted collagen fibrils that were fully immersed in PBS (Supplementary File) showed the same qualitative behavior with pronounced softening before failure and no hardening (Figure S1), similar to PBS-immersed collagen fibrils derived from rat tail tendon.

5. Conclusions

It was shown that a single cycle of mechanical conditioning of reconstituted mammalian collagen fibrils tested under partially hydrated conditions can lead to steady-state hysteresis with large energy dissipation and inelastic deformation that reaches a plateau after the first few cycles of loading. The loss coefficient associated with this hysteresis was shown to be 5–10 times higher than the values reported for all homogeneous materials in the same elastic modulus range. Cyclic loading at 20% or higher strain, corresponding to the regime of fibril deformation that is characterized by molecular sliding, increased the tensile strength by 70%, reaching values as high as 1.26 GPa, and the fibril toughness by 70%, while also maintaining the ultimate tensile strain to ~35%. These results on the stability of the elastic properties and the steady-state values of inelastic strain and energy dissipation suggest that individual nanoscale fibrils at the lowest hierarchical level of collagenous tissues play a key role in the strength, toughness and energy dissipation of tissues at all levels of mechanical loading.

Statement of Significance:

It is shown that steady-state energy dissipation occurs in individual collagen fibrils that are the building blocks of hard and soft tissues. To date, it has been assumed that energy dissipation in tissues takes place mainly at the higher length scales of the tissue hierarchy due to interactions between collagen fibrils and fibers, and in limited extent inside collagen fibrils. It is shown that individual collagen fibrils need only a single loading cycle to assume a highly dissipative, steady-state, cyclic mechanical response. Mechanical cycling at large strains leads to 70% increase in mechanical strength and values exceeding those of engineering steels. The same cyclic loading conditions also lead to 70% increase in toughness and loss properties that are 5–10 times higher than those of engineering materials with comparable stiffness.