Methods for the Analysis of Missing Data in FMRI Studies

Functional neuroimaging has provided fundamental advances in our understanding of human brain function and is increasingly used clinically for defining atypical function and surgical planning. For example, functional imaging with blood oxygenation level dependent (BOLD) contrast as a response measure is used as a clinical tool for defining atypical development, pathology, surgical planning, and evaluating treatment outcomes. Despite years of statistical advances in the analysis of complete whole brain data, there has been a limited statistical advance to address the pronounced missingness in many functional imaging studies that use large discovery or small clinical case data. For example, functional magnetic resonance imaging (fMRI) analyses do not always include the entire brain due to image acquisition space limitations and susceptibility artifacts (a loss and spatial distortion of signal that results from a disruption in the magnetic field). The consequence is ‘no data’ or ‘bad data’, respectively. No data occurs when the image acquisition doesn’t cover the whole head which leads to no values. In addition to susceptibility artifacts, bad data can occur across the brain because of motion artifacts. Because statistic maps with applied effect size or significance thresholds do not typically include information about which voxels were omitted from analyses, missing data can result in Type II errors for regions that were not tested. Missing data in fMRI studies can therefore undermine the benefits provided by high quality imaging technology used to generate data testing predictions about brain function.

One approach to this problem is to use appropriate statistical techniques that account for the missing data. However, missing data are almost universally addressed by excluding voxels from analyses. For example, implicit masking in single subject analyses limits the analysis space across subjects when group analyses are performed with spatially varying masked single subject results. As a result, brain regions are excluded from the analysis that may be of theoretical or clinical interest, which directly increases risk for Type II errors. When voxels with incomplete observations are omitted from group-level analyses, the smaller number of tests and less conservative multiple comparison correction can also increase the Type I error rate. If the missing data are non-ignorable, analyzing the space with complete observations only may bias effect size estimates (Figure 1).

Figure 1:

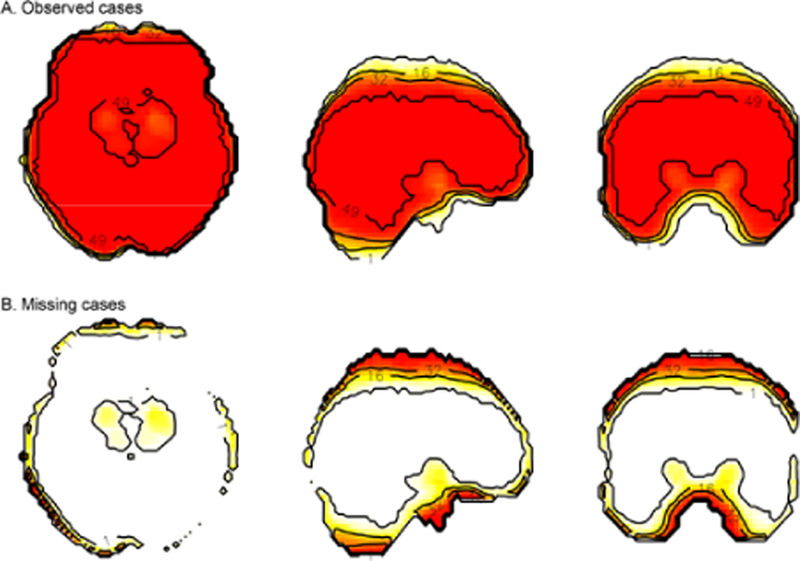
The fMRI missing ness problem. The standard approach in fMRI group statistics is to omit voxels from tests that do not contain observations from every subject. Omitting partial datasets from analysis is costly to spatial coverage, particularly along edges of the brain. In cross-sectional views (columns: axial, sagittal, and coronal planes), group-level statistics would be affected by missing data across subjects. A) Observed cases (top row) and B) missing cases (bottom row) show the number of individuals with data in each voxel after spatially normalizing an fMRI dataset. The colour scale and labelled contour lines indicate the number of (A) observed or (B) missing cases for each voxel, from a sample of 49 total study participants. Most missing data was due to susceptibility artefact and scanner operators who were inconsistent in their placement of an image acquisition bounding box that had limited brain coverage.

Missing fMRI data, resulting from incomplete voxel level information, can be missing completely at random (MCAR) because of variation in where images are acquired across the brains of different subjects or because of small variations in the quality of normalization at the edges of the brain across subjects. It can also be MAR because factors such as head size influence the coverage of a bounding box that determines the space of image acquisition. On the other hand, missing fMRI data can be MNAR, perhaps because the tissue is damaged. MCAR data can be addressed by removing voxels from group analyses, but this leads to biased inference if missingness is MAR or MNAR [1–3].

One solution for MAR is to impute missing data, which could significantly expand the coverage of the analysis, increase power, and enhance interpretations of fMRI results by leveraging the spatial and temporal features of the fMRI data. In particular, multiple imputation (MI) can be used to model spatial and temporal predictors of voxel intensity, as well as subject factors, such as head size and head motion, that exacerbate susceptibility artifact in the data [1,2]. However, MI is only valid when data are missing at random (MAR). An alternative method for MAR is incomplete Multi-Source Feature (iMSF) learning, where samples with at least one data source can be used to estimate missing values. But, this requires that data from different imaging modalities are available and may not be suitable for task-based fMRI experiments [3].

A more challenging missing data mechanism is when fMRI data are not missing at random (MNAR). For example, missingness due to the non-random exclusion of voxels that are associated with brain activity related to speech processing during a word recognition task can lead to MNAR. A systematic failure to measure the same anatomical space could also lead to MNAR if the reason for the missing data is related to the task under study. For example, a systematic failure to appropriately measure the BOLD signal due to a variety of factors, including neurovascular uncoupling in stroke and tumor patients, can produce bad data or no data when methods are used to appropriately exclude atypical BOLD responses [4,5]. There also may be differences for acquired brain regions in high resolution studies because of an interaction between head motion and slice selection across subjects. Excluded regions that are a focus of a study would then be MNAR. Little is known about how to deal with MNAR fMRI data. Thus, it is very important for statisticians in imaging to develop and validate methods to deal with missing fMRI data that leverage the spatial and temporal information in fMRI datasets.

Methods to address the missing data problem in fMRI datasets will have a broad impact. These methods should be able to substantially increase: 1) statistical power; 2) interpretability of theoretical models of brain function; and 3) use of fMRI biomarkers for treatment. Moreover, they should substantially improve clinical imaging where data is often lost (for example, because of patient motion artifact), thereby improving the clinical interpretation of functional imaging datasets and enhancing the sensitivity and specificity of results from neuroimaging studies. These will also help investigators meet funding agency requirements for handling missing data. Finally, these statistical methods for dealing with missing fMRI data should be capable of quantifying the extent to which these methods quantitatively (effect size), qualitatively (spatial coverage) increase the sensitivity and specificity of analyses of fMRI data compared to the standard approaches.

When missingness is MNAR, it is critical that sound methods are used to model both the missingness process and the BOLD measurement process. Valid inferences generally require either specifying the correct model for the missing data mechanism and/ or distributional assumptions for the BOLD response. The resulting estimators and tests are typically sensitive to these assumptions [6,7]. Pattern mixture and shared parameter models have been shown to lead to valid inference [6–10]. However, no single MNAR model is going to be reliable unless it is compared against other MNAR and MAR models. Thus, it is suggested that MNAR modeling be done in a sensitivity analysis framework [6,9,11–18]. Sensitivity analysis can be done in three different ways [12]. These include local sensitivity, global sensitivity and model-based sensitivity analysis. Despite the high significance of the problem, however, limited focus has been placed on development and adaptation of methods for missing fMRI data [11–17]. Thus, developing approaches for missing fMRI data in both frequentist and Bayesian frameworks is very important.

There are relatively few tools for analyzing MNAR data. Those available are in the form of tailored computer code and invariably target a specific model with restrictive assumptions. This is because, while analysis models are somewhat standard, the model for the probability of dropout has to be carefully chosen for the problem at hand. In particular, covariates that are predictive of dropouts have to be identified and included properly in the missing data model. There is limited development and implementations of Bayesian MNAR analysis [12]. Computing is commonly performed using OpenBUGS/ WinBUGS. Recent developments have allowed OpenBUGS/ WinBUGS to be directly called from high-level languages such as R via the R2OpenBUGS/R2WinBUGS package. The sensitivity analysis R package SAMON developed in can be used to implement both local SEN and global SEN analysis methods for MNAR in both group and subject level fMRI studies [18–20]. We have provided the neuroimaging community with code to perform multiple imputation (http://www. nitrc.org/projects/multimpute), but the relatively limited adoption of these types of missingness methods suggests that increased awareness of missingness pitfalls is critical.