Variation in sequence dynamics improves maintenance of stereotyped behavior in an example from bird song

Significance

In this work, we show a way by which the nervous system maintains precise, stereotyped behavior in the face of environmental and neural changes. Through a model of bird song learning, we show how instability in neural representation of stable behavior can allow a system to more readily adapt and maintain performance with minimal cost. In this perspective, behaviors are made more robust to environmental change by continually seeking subtly new ways of performing the same task. Thus, one should expect to find variability in neural systems executing stereotyped behaviors, and this variability can serve a constructive role in maintaining skilled behavior.

Abstract

Performing a stereotyped behavior successfully over time requires both maintaining performance quality and adapting efficiently to environmental or physical changes affecting performance. The bird song system is a paradigmatic example of learning a stereotyped behavior and therefore is a good place to study the interaction of these two goals. Through a model of bird song learning, we show how instability in neural representation of stable behavior confers advantages for adaptation and maintenance with minimal cost to performance quality. A precise, temporally sparse sequence from the premotor nucleus HVC is crucial to the performance of song in songbirds. We find that learning in the presence of sequence variations facilitates rapid relearning after shifts in the target song or muscle structure and results in decreased error with neuron loss. This robustness is due to the prevention of the buildup of correlations in the learned connectivity. In the absence of sequence variations, these correlations grow, due to the relatively low dimensionality of the exploratory variation in comparison with the number of plastic synapses. Our results suggest one would expect to see variability in neural systems executing stereotyped behaviors, and this variability is an advantageous feature rather than a challenge to overcome.

When we first learn to play the piano or ride a bicycle, the learning trajectory is similar: Initial attempts are clumsy and erratic, one quite different from the next. Over time, we can improve and eventually complete these tasks skillfully and reliably. Typically, we think of learning as complete when we execute desired tasks repeatedly and well. This trial-and-error learning process is common to many stereotyped tasks learned in development and performed in a seemingly automatic manner in adulthood. However, ongoing plasticity is needed to perform in a stereotyped manner despite changes over time, such as new environmental conditions or physiological growth or injury. Active maintenance must therefore be an important element of the neural pathways that carry out these repetitive tasks.

A well-characterized biological example of a learned, stereotyped behavior is the courtship song of songbirds, in which we might expect such maintenance to occur. Juvenile male songbirds learn to sing from a male tutor in a trial-and-error manner. Once the bird reaches adulthood, the song becomes stereotyped with millisecond precision. Despite the adult song stability, song plasticity continues in adulthood (1–6). Adult songbirds shift the pitch of individual syllables in response to white noise stimuli or shifted auditory feedback (1, 2). In deafened birds, song eventually degrades, implying ongoing plasticity (3, 4, 6).

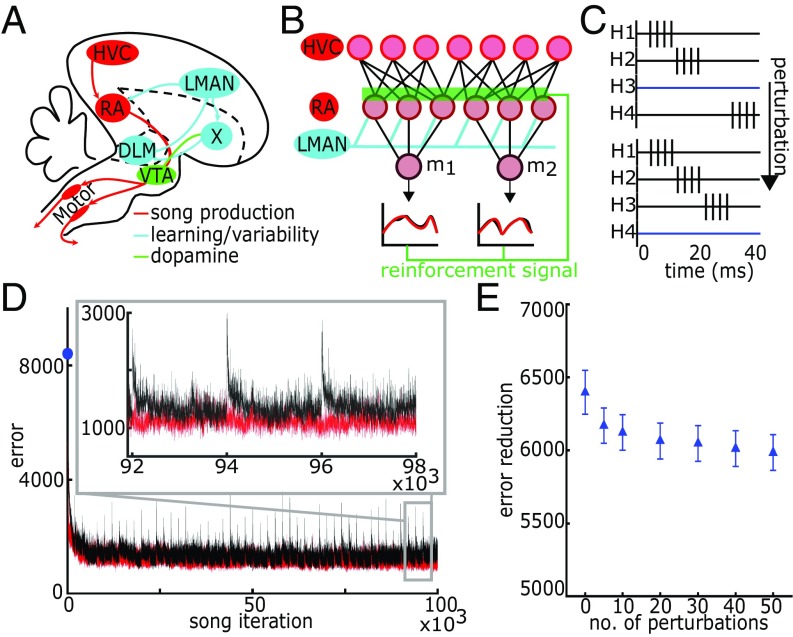
One hypothesis about how stereotyped motor output is generated is that it emerges from precisely controlled and sequenced neural activity. Is stable behavior therefore underpinned by long-term, stable representations at the population and single-neuron level? This question applies to the bird song system, where singing is governed by precisely timed and sequenced firing in the premotor nucleus HVC (proper name) (Fig. 1A). HVC neurons project to RA (the robust nucleus of the arcopallium) and, in the adult, fire in a rapid burst exactly once during the song (7). Temporally precise, although less sparse, firing patterns in RA drive downstream motor neurons, which then drive the vocal muscles during song (8–11). The HVC projection neurons’ burst-onset times collectively tile the duration of the song (7). In most mechanistic descriptions of the bird song system, the synaptic weights of the HVC projections onto RA are understood to encode the form of the song at each moment in time (12–14).

Fig. 1.

Model of bird song learning. (A) Schematic of the avian song system. (B) Schematic of learning model. Learning occurs on the synaptic weights from HVC (n = 500) to RA (n = 48). (C) Schematic of HVC firing patterns and perturbation events. (D) Learning trajectory. Error is defined as the absolute difference between the target m₁ and m₂ and the model output m₁ and m₂. Red trace shows unperturbed trajectory. Black trace shows trajectory with 50 HVC perturbation events. Blue dot on y axis indicates the error before learning. (Inset) Three perturbation events. (E) The difference between initial and final error in learning trajectory as a function the number of HVC perturbation events per 10⁵ iterations averaged over 50 trials. Error reduction is defined as difference between the first iteration and average of the last 500 iterations for each trial. HVC perturbations slightly decrease error reduction. Error bars represent standard error.

The long-term precision in song has been assumed to rely upon the scaffolding provided by long-term precision in HVC firing. Song maintenance has been thought to occur through retuning motor output relative to this precise timing. However, HVC neurons undergo cell death and replacement by neurogenesis, both continuously and in a seasonal manner (15). In addition, recent experimental results have revealed some degree of longer-term changes in single, premotor neuron activity patterns during singing (16, 17). These variations in the sequence dynamics raise intriguing questions. How can a static, stereotyped behavior survive variable premotor firing patterns? What advantage might be gained by instabilities in the neural representation of the song?

We investigate these questions through a computational model of the bird song learning system. Previous theoretical work has used a reinforcement learning (RL) framework to model song learning in the projection structure from HVC to RA (12–14). We adopt an RL model based on Fiete et al. (12) (Fig. 1B) and assume HVC’s sparse firing pattern has emerged earlier in development. The learning process trains RA to drive low-dimensional, motor outputs (here, the time-varying, scalar quantities m₁ and m₂, which represent the activity of pools of motor neurons) to reproduce the target song based on variable inputs from lateral magnocellular nucleus of the anterior nidopallium (LMAN) (Fig. 1B). Via gradient descent, RL changes the connection strengths from HVC to RA depending on the levels of coincident activation of an HVC-to-RA synapse and an LMAN-to-RA synapse, followed by a global reinforcement signal.

We explore three different approaches to perturbing premotor firing patterns in a subset of HVC cells: pausing activity while imposing synaptic decay, only pausing activity, and shifting firing timing. These approaches explore types of perturbation reported in HVC: cell death and replacement and variable cell participation. We then test the effects of these perturbations on network robustness in three different ways: performance error, robustness to RA cell loss, and speed of relearning an altered motor output. Next, we explore the underlying mechanisms for these effects. Finally, we make a quantitative comparison of the three different approaches. The three perturbation methods produce qualitatively similar results.

We find that varying HVC activity patterns balances two goals of the system: maintaining quality in song performance and adapting efficiently to environmental or physical changes that affect performance. Instability in HVC firing activity slightly degrades the performance quality. In exchange, however, the system is able to learn changes in muscle activity faster and is more robust to cell loss in the RA network. Our results also suggest a possible mechanism underlying this effect. Variability in neural representation of stereotyped tasks may thus confer robustness and facilitate active maintenance of motor performance.

Results

Basic Learning Framework.

Fig. 1D shows the learning trajectory, defined as the total error between the m₁ and m₂ templates and the produced versions. Although learning converges, error continues to fluctuate and does not go to zero, in part because gradient descent converges to a local, not a global, minimum and in part because of the fixed learning rate in our model. Continued error fluctuations are due to the ongoing variable inputs from LMAN to RA, which drive both trial-to-trial variability in the RA firing patterns and changes in the HVC-to-RA connection strengths. After the initial convergence, the average error is stable over the ∼10⁵ subsequent iterations of the simulation (Fig. 1D, red trace) and is consistent with the stable form of adult birdsong (18).

Introducing Changes in HVC Activity.

We next examine how random changes in HVC firing activity affect circuit activity and plasticity once the song has been learned. We assume the basic temporal structure of HVC inputs and the song dynamics have been learned previously during development, but synaptic plasticity and learning continue in adulthood (1–6). In our first perturbation scheme, “paused with synaptic weakening,” we halt activity in 6% of active HVC projection cells while simultaneously activating the same number of previously paused cells in discrete offline episodes that occur periodically throughout the 10⁵ song trials (see Methods) (Fig. 1D, black trace). The timing of the activity patterns of the paused and activated cells is independent and random. The synaptic projections of paused cells undergo synaptic weakening. Figs. 2 and 3 report effects of this perturbation scheme.

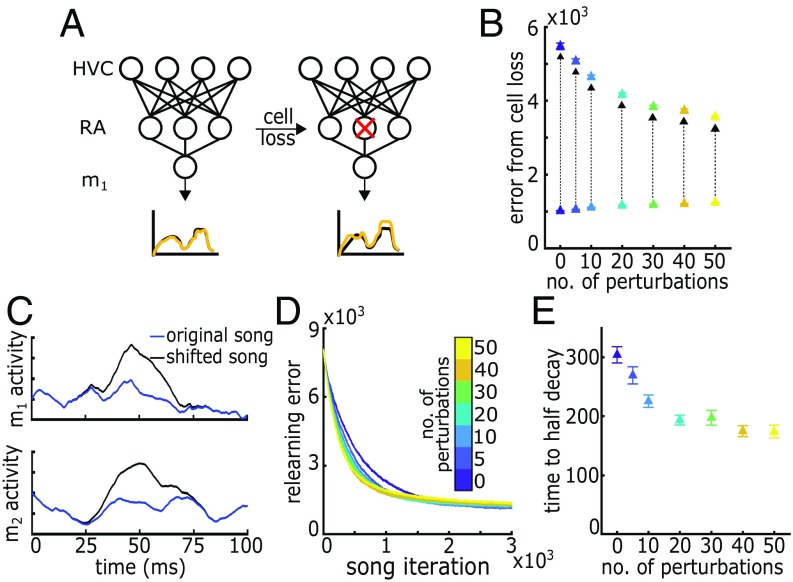
Fig. 2.

Tests of robustness. (A) Schematic RA cell loss. After a subset of RA is removed, the song is performed, and the new error is computed. (B) Error in song as a function of number of HVC perturbations per 10⁵ iterations for the full RA network and for subpopulations of RA. Arrows indicate error from full RA network to error from RA network after cell loss. Error is averaged over randomly drawn subsets of RA and over trials. HVC perturbations increase the ability of a subpopulation of the RA network to represent song. (C) Target song shift. After 10⁵ iterations, the target song is altered, and relearning proceeds for 3,000 iterations. (D) Relearning trajectory after target song changes. (E) Number of iterations to half-decay of learning trajectory. HVC perturbations speed up the adaptation process with minor penalty in final error. Error bars represent standard error.

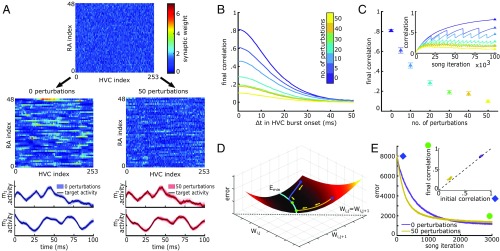
Fig. 3.

Mechanisms underlying robustness. (A) Example initial and final W matrices after 10⁵ iterations of learning with HVC index ordered by when the HVC cell bursts. (Top) Initial W for 0 and 50 HVC perturbations; (Middle) final W for 0 (Left) and 50 (Right) HVC perturbation events; (Bottom) learned motor trajectories for 0 (Left) and 50 (Right) HVC perturbations. Black line is the target. Light colored lines are learned trials after 10⁵ iterations. (B) Average pairwise correlations after 10⁵ iterations of learning between HVC cells’ synaptic projections to RA (columns of W) as a function of the time difference in firing onset. Averages are taken over HVC cells and learning trials. Correlations decrease with more HVC perturbation events. (C) Maximum pairwise correlations between HVC neurons’ synaptic projections to RA as a function of the number of HVC perturbation events. (Inset) Trajectory of maximum correlations over learning iterations. Drops in correlation occur at HVC perturbation events. (D) Schematic of the progression of W over the course of learning. Error first proceeds quickly to a minimum. Correlations in the LMAN inputs then slowly push the solution toward higher correlations if learning continues without perturbations. Solid white line shows region of approximately equal error. Purple trajectory shows W matrix undergoing learning from an initial position of low pairwise correlation. Gold trajectory shows W matrix undergoing learning from an initial position of high pairwise correlation. Blue and green dots show initial and final positions. The region near and at W_ij = W_i,j+1 where error increases again is not shown in this schematic. (E) Average relearning trajectory (over 50 trials) for altered song target. (Inset) Maximum HVC pairwise correlation in W at the beginning and end of 3,000 song iterations for representative trials from E. The correlations of the initial weight matrix before learning strongly influences the correlations of the final weights after learning. Error bars represent standard error.

As expected, changing a subset of HVC firing activity increases song error (Fig. 1 D and E). However, asymptotic error is only slightly increased by increasing the frequency of HVC disruption events (Fig. 1 D and E). This error trajectory is consistent with the behavioral observation that song is more variable in the morning than in the evening (Fig. 1D) (19).

Impacts of HVC Perturbations on Network Robustness.

Although introducing pauses in a subset of HVC firing increases the overall error in song performance, advantages are gained. A likely change during aging is cell loss. After completing the 10⁵ song iterations, we first ask how robust the song system is to partial loss of the RA network, a test which replicates experimental ablations or cell death. We also consider changes in the muscle transformation of the RA output to song or in the target song itself, both of which require a relearning of the upstream HVC-to-RA connection structure. Although adult zebra finch song is highly stereotyped, there are several reasons an adult bird might alter the network structure generating song. Injury or simply aging in the vocal muscles leads to the same neuronal drive generating a different song output; to keep the song stable, the bird must learn to control the altered muscles in a new manner. These two tests of robustness are conducted independently of one another and after the HVC perturbations and 10⁵ song iterations are complete.

Adaptations to Partial Loss of Network.

After 10⁵ iterations of song, we randomly remove a subset (8%) of RA cells and measure the resulting increase in error when the song is performed using the partial RA network without any additional relearning (Fig. 2A). Removing a subset of RA cells increases error; however, the magnitude of the induced error decreases with the introduction of HVC perturbation episodes (Fig. 2B). Perturbing HVC firing activity allows subsets of the RA network to continue to represent the song more accurately.

Adaptation to Environmental and Physical Changes.

We model environmental and physical changes in song context as shifts in the motor target trajectory that the network is trying to produce: m₁→m₁’ and m₂ →m₂’ (Fig. 2C). We then ask how quickly and successfully the shifted song target is learned by the network as a function of the number of HVC perturbation episodes occurring in the initial 10⁵ iteration maintenance protocol. Speed of relearning increases with the frequency of HVC perturbation episodes (Fig. 2 D and E). However, a penalty is paid for the increased adaptation speed, with an increase in final error after 3,000 iterations of relearning (Fig. 2D and SI Appendix, Fig. S1).

Origins of Increased Robustness.

What changes in the network structure due to perturbations in HVC activity that could increase robustness? The learned components of our model are the synaptic strengths of projections, W. Each entry, W_ij, represents the connection strength from HVC cell “j” to RA cell “i.” The distributions of synaptic weights after 10⁵ song iterations change little due to HVC perturbations (SI Appendix, Fig. S2). However, when we order the HVC cells according to the time in the song when the cell fires, a clear change in W emerges due to HVC perturbations, although motor trajectories are very similar (Fig. 3A). Without variations in HVC activity, projection patterns from HVC cells that fire at similar times become highly correlated (Fig. 3 B and C). HVC perturbations decorrelate nearby HVC projections as a monotonic function of the frequency of HVC perturbations. This is quantified by the average pairwise correlation values of individual HVC cells’ projections to RA as a function of the time difference of the HVC cells’ burst onset (Fig. 3 B and C).

These correlations grow much more slowly than the learning trajectory (Fig. 3C, Inset). In the absence of any HVC activity changes, error decreases to within 5% of its final value within 2,000 iterations, whereas correlations in the weight matrix reach 95% of their final values only at 75,000 iterations (Fig. 3C, Inset). This suggests the continued plasticity causes drift in the weight matrix structure along a valley of solutions with approximately equal error but increasing correlation strength (Fig. 3D).

What causes this drift? HVC synapses made onto a single RA cell share variability from LMAN. Because of the extended synaptic time course of inputs from LMAN [∼70 ms to 75 ms (20)], a single LMAN firing event affects plasticity at synapses from multiple HVC cells that fire at similar times. We expect that correlated variability from LMAN biases the reachable search space toward solutions that themselves are correlated. We confirm that LMAN’s synaptic timescales drive the buildup of correlations in a simplified linear version of our system (SI Appendix) as well as in additional simulations where we vary the synaptic time course of the inputs from LMAN. We observe a monotonic dependency of the correlations in W on the time course of individual LMAN inputs (SI Appendix, Fig. S3).

Disrupting the activity of HVC cells slows this growth in correlation. Temporarily silencing HVC cells while weakening synapses introduces a random change into the local projection structure from HVC to RA at that moment in song. This lowers the total exposure sequentially firing HVC cells have to correlated noise inputs and therefore allows the cells’ synaptic strengths to remain more independent.

Because HVC and RA have many more degrees of freedom than the downstream motor pools, multiple firing patterns in RA will produce the same m₁ and m₂ output. Within these firing patterns with identical motor pool output, the correlation structure of W can vary substantially. These redundancies give rise to a manifold of equivalent local minima on the error function (21).

Randomly varying HVC activity pushes the synaptic weight structure into a region in W space with higher error but lower pairwise correlation. Learning that begins in a less correlated state first approaches the asymptotic error value in a less correlated solution state, even though the value of the local error minimum is essentially the same (Fig. 3E) (22). This daily repositioning of the projection structure on the error landscape leads to a slower accumulation of passive correlations due to the correlated LMAN variability. The flexibility and generality of this repositioning is possible because of the multiplicity of solutions with comparable error.

To test the hypothesis that correlations across cells’ synapses slow relearning, we compare learning trajectories from sets of initial random weight matrices wherein each HVC cell’s initial projection weights are drawn from identical Gaussian distributions but the correlations between HVC cells’ synapses vary by set (SI Appendix, Extended Methods and Fig. S4 A–C). This isolates correlation level in W while holding the overall distribution of weight values constant. Increasing correlations in the initial W structure also slows learning (SI Appendix, Fig. S4 D and E), further suggesting this network feature leads to variable relearning speeds. When we similarly compare learning trajectories across sets of initial projection weights with identical correlation levels but different weight distributions, there is no significant change in learning speed (SI Appendix). This suggests that the observed change in synaptic strengths (SI Appendix, Fig. S2B) does not significantly impact relearning speed. We have not tested this same explicit correspondence to robustness to cell loss.

The network structure due to HVC perturbations additionally leads to a more efficient representation of song in RA: Fewer RA cells fire at any one time in song, and the overall firing rate is lower (SI Appendix, Fig. S5). RA sparsity increases robustness to cell loss: Removing a cell from the RA population, on average, impacts the song less (SI Appendix, Origins of Robustness). Sparser RA activity is likely due to two changes in the HVC to RA projection structure: The low correlations in projections from HVC cells hinder the integration of voltage to threshold in RA cells, and weaker weights from HVC to RA decrease the overall excitatory drive to RA. Weaker weights affect only our first HVC perturbation scheme (paused with synaptic weakening); in the two other schemes, the weight distributions are unchanged (SI Appendix, Fig. S2).

Other Forms of HVC Plasticity.

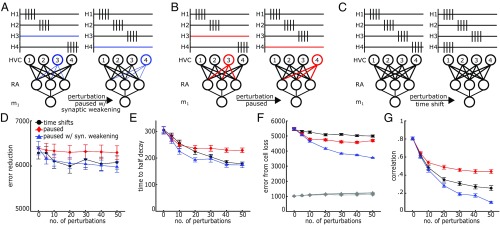
Lastly, we compare our initial form of HVC plasticity with two other perturbation schemes (Fig. 4 A–C). The second scheme (“paused”) is the same as the original scheme but with no synaptic decay in paused cells (Fig. 4B). In our third scheme (“time shift”), instead of silencing subsets of HVC cells, we shift the timing of 6% of HVC projection cells such that they fire at new, random times in the song (Fig. 4C). This third scheme represents an extreme version of HVC plasticity in our hypothesized role decorrelating synaptic structure.

Fig. 4.

Model comparisons of perturbing HVC activity. (A) HVC perturbation scheme wherein a subset of HVC cells are silenced and reactivated at each perturbation event. Synapses weaken in silent cells. (B) The same scheme as in A, but without synaptic weakening. (C) HVC perturbation scheme wherein a subset of HVC cells’ firing times randomly shift at each perturbation event. (D–G) Comparison of performance and robustness metrics across perturbation schemes and frequency. (D) Error improvement over 10⁵ iterations. Minor cost is incurred for increased perturbation frequency. (Same as in Fig. 1E.) (E) Number of iterations to half decay of relearning trajectory. (Same as in Fig. 2E.) (F) Increase in error due to RA cell loss. Gray indicates performance error with full RA network. Other colors indicate performance error with partial RA network. (Same as in Fig. 2B.) (G) Maximum pairwise correlations between HVC neurons’ synaptic projections to RA. Error bars represent standard error.

All of the tested perturbations lead to qualitatively similar increases in network robustness (Fig. 4 D–F). The perturbation scheme we show in detail (paused with synaptic weakening) performs best under cell loss and motor relearning. However, this form of perturbation is the only scheme that leads to slightly higher error in motor relearning (Fig. 2D and SI Appendix, Fig. S1A). From these comparisons, we predict that this robustness advantage is a general property of varying upstream HVC firing activity and does not rely on the form of variations we chose.

Discussion

The main finding of this work is that perturbations in the activity of HVC cells, while slightly elevating overall song error, increase robustness to physical, environmental, and neural changes. Broadly, this work identifies a way in which ongoing plasticity can lead to deleterious correlations when a portion of the system is static and to a mechanism for preventing these correlations from building. Here, keeping the firing activity of HVC cells fixed while allowing plasticity at the HVC to RA synapses leads to a buildup of correlations and weakens the system’s response to stressors that the continued plasticity presumably exists to address. In contrast, when HVC activity patterns vary, synaptic weights remain decorrelated, allowing greater robustness. This work suggests that repetitive behaviors should be performed in a dynamic manner that pushes the system to retain access to many degrees of freedom. These behaviors are made more robust to environmental change by continually seeking new ways of performing the same task.

The extent to which stable behavior is underpinned by stable representation at the population and single-neuron level varies across systems and contexts and is a question of active debate. A common assumption is that, once mastered, stereotyped tasks are represented by stable neural activity, and plasticity occurs due to learning. However, when monkeys perform a familiar reaching task, the tuning curves of neurons in the supplementary motor area undergo slow, random drift (21). Ref. 21 attributed this drift to noisy synaptic plasticity and found that behavior remains stable despite this noise, presumably due to the high redundancy of the active neural networks. This type of random drift is exactly what one would expect from the ongoing plasticity we consider in this work, and we predict that similar shifts in RA firing properties should be observable over long timescales. We theorize that this random drift, although still allowing stable representation of an otherwise static system, will pose a challenge to the long-term maintenance of the task unless accompanied by other types of variation in the network dynamics.

The presence of correlations in exploratory inputs across plastic synapses is critical to our findings and is based on neuroanatomical observations in the song system. While using a single Poisson varying LMAN input for each RA cell is a modeling simplification, we expect that the true connectivity structure still gives rise to high correlations. There are ∼50 synaptic connections from LMAN onto a single RA cell, possibly from a small number of colocalized LMAN cells (23–25). There are as many as 1,000 HVC synaptic projections onto one RA cell from as many as 200 HVC cells (26). Therefore, if all HVC synapses are affected by some portion of LMAN activity, correlations in LMAN activity across HVC inputs must exist.

Furthermore, correlations in an exploratory drive are likely for any system where synaptic strengths are learned individually: If the most relevant unit of independent variation in a network is a single cell, then the number of independent exploratory processes will be approximately the number of independent cells, whereas the number of synaptic connections to be learned will be the number of synapses per cell times the total number of cells. The finite dimensional space of the exploratory inputs will limit the independent variation the learning synapses can undergo.

How much variation is enough for adaptation advantages to be relevant? Fully answering this question depends on the rate of ongoing plasticity as well as the degree to which adaptation is needed and is likely to depend critically on the specific system. However, we saw a significant robustness advantage even at our lowest frequency of perturbation (once per 20,000 song iterations). Note that the two experimental, zebra finch results differ in the amount of variability reported in the HVC nucleus: Liberti et al. (16) report that, in undirected song, ∼40% of HVC projection cells change activity patterns over a period of 5 d, whereas Katlowitz et al. (17) report that, in directed song, 3.6% of projection cells change activity patterns over timescales ranging from 3 d to 56 d, as well as ongoing, random jitter in the burst-onset timing. In other songbird species, HVC cell death and neurogenesis are seasonally regulated, with an almost doubling of HVC projection cells to RA during breeding season (27). Our model considers a range of variation frequencies and approximately spans the frequency regimes of these experimental results. We predict that our results would be qualitatively the same were perturbations to happen continuously, and would perhaps result in even better performance, since punctate changes to network structure would not exist.

In addition to HVC perturbations, other methods could potentially accomplish the same decorrelation of HVC projections. Recent experimental work has identified synaptic plasticity in the LMAN to RA synapses, but it is not known whether this form of plasticity redistributes LMAN−HVC coincident activity onto individual RA neurons (28). In addition, recurrent connections among RA neurons show synaptic plasticity (29); their functional role in a learning model has not yet been explored, but they could contribute to the type of decorrelation needed for robust learning. In other systems, a variety of decorrelation mechanisms could achieve the same effect that we observed with HVC perturbations. Furthermore, the notion of robustness is broad, and other studies have approached network robustness in different ways (30, 31). Our perturbations span the space of possible perturbations by adding in features at arbitrary times. This method could, in theory, create spectral or temporal changes. However, spectral changes are separable from temporal changes and require LMAN, whereas temporal changes do not necessarily require inputs from LMAN (32). This suggests that temporal changes may come from changes in HVC dynamics. We have not explored this issue.

This biological learning strategy can be seen in the context of machine-learning techniques that introduce a stochastic element in the forward pass of the network, such as “dropout.” Methods using dropout are similar to the bird song strategy presented here, wherein a subset of neurons and the connections to and from the subset are probabilistically removed during portions of training to avoid overfitting (33). In the context of artificial neural networks, overfitting is generally taken to mean that a network has been too closely tuned to the training set of inputs and outputs. The result is that, when a new input is introduced from the same statistical class, the network has learned the vagaries of the training set rather than the statistical properties of the full set of possible inputs. Again, there is an interesting parallel to the bird song strategy: Maintenance of song through the trials of normal life may require adapting to an altered version of the target song or muscle program. Varying HVC inputs prevents the system from overfitting to a single target. The addition of synaptic weakening during the equivalent dropout periods in our model presents a potentially beneficial feature in artificial learning systems as well. Another biophysical mechanism for dropout that we have not explored is synaptic failure, which could provide similar benefits. However, there are important ways in which this finding is uniquely biological. The issue of maintenance plasticity is currently specific to biological systems; it is not a feature of most machine learning algorithms, because it is not needed. Once an artificial RL system reaches an asymptotic final error, changes to the weight structure of the system are halted. However, ongoing plasticity is an inherent feature of biological systems. It is in the context of this ongoing plasticity that correlations grow around static components of the system.

In this work, we find perturbing HVC firing activity balances two goals of the system: maintaining quality in song performance and adapting efficiently to environmental or physical changes that affect performance. This result is, to an extent, antioptimal: In our model, the bird is not learning a single stereotyped behavior to the greatest possible precision but retains the ability to adapt to environmental and physical changes. In this contingent picture, optimality must be broadly interpreted as maximizing performance quality across competing goals. It is notable that this contingent strategy is possibly present even in the zebra finch song system, which has traditionally been thought of as an extreme example of learning a single, highly stereotyped behavior. For biological systems, learning always takes place in a fluctuating environment that may, at any moment, change the conditions of performance. This requires a contingent relationship to optimal behaviors and to the notion of optimality itself.

Methods

Base Model.

The base model comprises three feed-forward layers, HVC (n = 500), RA (n = 48), and Motor Pools (n = 2), with an independent, Poisson firing process synapsing onto each RA cell from LMAN and was modified from Fiete et al. (12). HVC and RA layers are modeled as conductance-based leaky integrate-and-fire neurons. We model song production as nonspiking motor pool output units that receive input from RA. The learning goal is for the motor pools to a reproduce a target motor trajectory.

Learning Parameters.

Only HVC projections to RA are plastic and are determined by $d{W}_{ij}/dt=\eta R\left(t\right)e_{ij}\left(t\right)$, where $W_{ij}$ is the synaptic strength from the jth HVC cell to the ith RA cell, R(t) is the reinforcement signal, $\eta$ is the learning rate, and $e_{ij}\left(t\right)$ is the eligibility trace over which weight changes occur, defined as $e_{ij}\left(t\right)={\displaystyle \underset{0}{\overset{t}{\int }}dt\text{'}\text{G}\left(t-t\text{'}\right)\left(s_i^{LMAN}\left(t\text{'}\right)-\langle s_i^{LMA\text{N}}\rangle \right)s_{ij}^{HVC}\left(t\text{'}\right)}\hspace{0.17em},$where $G\left(t\right)=t^n{e}^{t/{\tau }_e}$, $s_i^{LMA\text{N}}\left(t\right)$ is the LMAN input to the ith RA cell, and $s_{ij}^{HVC}\left(t\right)$ is the synaptic input from the jth HVC cell to the ith RA cell. The reinforcement signal, R(t), is defined as $R\left(t\right)=2^{*}\mathrm{\Theta }\left[D\left(t\right)-\overline{D}\left(t\right)\right]-1$, where D(t) is the mean-squared error of the current motor output and $\overline{D}\left(t\right)$ is the average mean-squared error of the previous five trials.

Perturbations to HVC.

HVC perturbation events occur offline at regular intervals. We vary the number of perturbation events from 0 to 50 over 10⁵ song iterations. We model three perturbation schemes: (i) In the paused with synaptic weakening scheme, 500 cells are active and 200 cells are silent. At each perturbation event, 30 active cells go silent and 30 silent cells activate. Synaptic decay occurs while cells are silent. (ii) The paused scheme is the same as i except synapses of silent cells are frozen. (iii) In the time-shift scheme, 500 cells are active. At each perturbation event, 5% of cells randomly shift burst-onset times within the song. We simulate each perturbation frequency and scheme 50 times.

Tests of Network Robustness.

Shift in motor targets.

We add a Gaussian deformation to the target motor output and measure the time to half-decay of error and the final error after 3,000 iterations of relearning.

Cell loss in RA.

We silence 1/12 of the RA network, and measure performance. We average the resulting error over 500 randomly drawn subpopulations.

Pairwise Correlation of HVC Synaptic Structure.

We calculate the pairwise correlation between HVC cells’ projections as a function of the difference in timing between the HVC cells’ burst onsets. We denote the outgoing weights for HVC cell p at time t as ${W^t}_p\equiv {W^t}_{\left(:,p\right)}$. For all pairs of HVC projection vectors ${W^t}_p$ and ${W^{t\text{'}}}_q$ for which the HVC cells’ burst onset times t and t’ are within $\tau \pm \mathrm{\Delta }\tau$ ($\mathrm{\Delta }\tau$= 0.5 ms), we compute the average pairwise correlation at time separation, $\tau ,$ as

$$C_{\tau }\left({W^t}_p,{W^{t\text{'}}}_q\right)=\langle \frac{\left({W^t}_p-\overline{{W^t}_p}\right)\left({W^{t\text{'}}}_q-\overline{{W^{t\text{'}}}_q}\right)}{\sqrt{{\left({W^t}_p-{\overline{W^t}}_p\right)}^2{\left({W^{t\text{'}}}_q-{\overline{W^{t\text{'}}}}_q\right)}^2}}\langle all\hspace{0.17em}p,q:\left(t-t\text{'}\right)\subseteq \tau \pm \mathrm{\Delta }\tau .$$