The dynamics of adaptive genetic diversity during the early stages of clonal evolution

Abstract

The dynamics of genetic diversity in large clonally evolving cell populations are poorly understood, despite having implications for the treatment of cancer and microbial infections. Here, we combine barcode lineage tracking, sequencing of adaptive clones and mathematical modelling of mutational dynamics to understand adaptive diversity changes during experimental evolution of Saccharomyces cerevisiae under nitrogen and carbon limitation. We find that, despite differences in beneficial mutational mechanisms and fitness effects, early adaptive genetic diversity increases predictably, driven by the expansion of many single-mutant lineages. However, a crash in adaptive diversity follows, caused by highly fit double-mutant ‘jackpot’ clones that are fed from exponentially growing single mutants, a process closely related to the classic Luria-Delbrück experiment. The diversity crash is likely to be a general feature of asexual evolution with clonal interference; however, both its timing and magnitude are stochastic and depend on the population size, the distribution of beneficial fitness effects and patterns of epistasis.

Reporting Summary.

Further information on research design is available in the Nature Research Reporting Summary linked to this article.

In large clonally evolving populations, lineages harbouring beneficial ‘driver’ mutations expand, compete with one another and acquire further beneficial mutations, shaping genetic diversity^1–3. Recent studies employing deep genomic sequencing have shown that large laboratory^4–6 and clinical^7–13 cell populations harbour high levels of genetic diversity that change through time. In disease-relevant scenarios, such as cancer^7–11 and within-host microbial dynamics¹³, the timescale over which diversity builds up is often short, such that dominant clones only accumulate a handful of driver mutations. When the supply of driver mutations is low, evolution is characterized by successive selective sweeps, wherein a single adaptive lineage periodically purges genetic diversity^14,15. However, when the supply of driver mutations is high, evolution is characterized by clonal interference, with multiple adaptive lineages expanding and competing through time^5,16–19. In the clonal-interference regime, mutations often rise and fall together in cohorts^5,11,20,21. However, due to a limited ability to detect low-frequency mutations via genomic sequencing, it remains unclear what controls diversity changes through time in this regime, whether large purges of diversity might also occur as happens with a selective sweep and whether these diversity crashes are predictable across replicates and environments²².

Results

To address these questions, we introduced ~500,000 unique DNA barcodes into S. cerevisiae²³ and evolved populations of ~5 × 10⁸ cells in triplicate under two well-mixed environments: carbon limitation (C-lim) and nitrogen limitation (N-lim). Lineages were tracked by barcode sequencing approximately every 8–24 generations and those harbouring adaptive mutations were identified by deviation from a neutral expectation²³. Tracking all adaptive lineages reveals the changing levels of adaptive lineage diversity (Fig. 1). Initially, adaptive diversity expands, driven by thousands of independent mutations. This expansion is quantitatively different between environments; in N-lim, the expansion is slower and fewer lineages reach high frequencies. Later, however, similarities between environments emerge: a handful of lineages dominate the population, causing a crash in adaptive lineage diversity.

Fig. 1|. Muller plots of adaptive lineages.

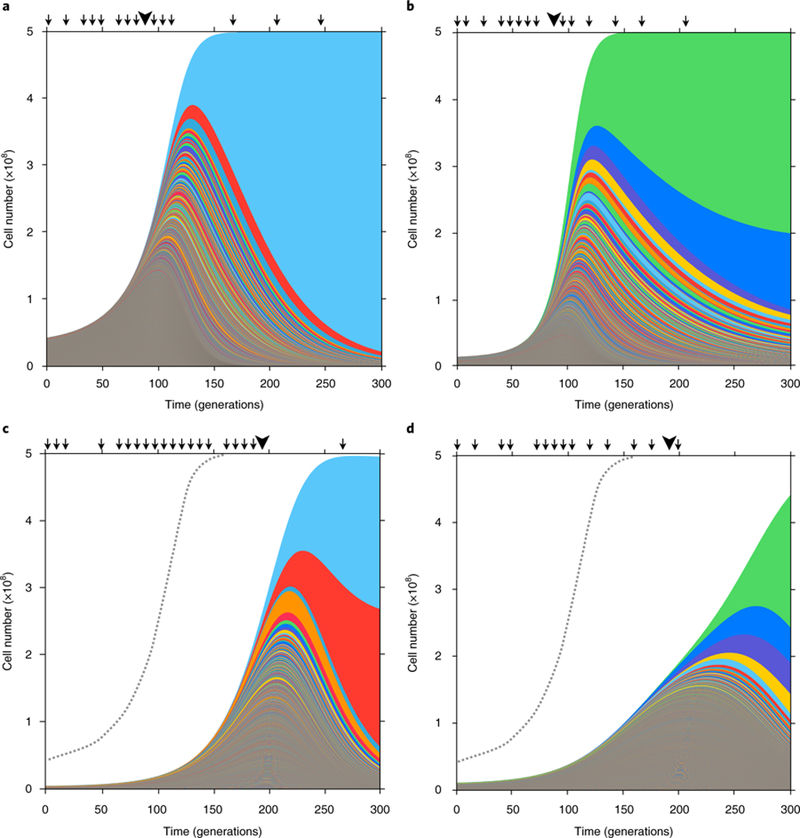
a-d, The cell numbers of all adaptive lineages (colours) inferred from barcode sequencing (arrows) and whole-genome sequencing of picked clones (large arrowheads) of replicate evolutions in C-lim (a and b) and N-lim media (c and d). Colours are for visualization purposes only and do not represent lineages harbouring specific mutations.

The distribution of fitness effects shapes early adaptive genetic diversity in a predictable way.

We suspected that differences in lineage diversity dynamics between environments could be attributed, in part, to differences in the mutational distribution of fitnesses effects (mDFE), defined as the distribution of mutation rates over fitness effects for single beneficial mutations arising on the ancestor. We have shown that high-resolution lineage tracking over short times can be used to infer the mDFE²³. In C-lim, the mDFE results in approximately 10⁴ beneficial mutations with fitness effects, s, greater than 3% entering over the first approximately 100 generations. This initially produces a quasi-deterministic expansion in diversity because the low fitness-effect beneficial mutations that dominate early occur at high rates. Later, the diversity expansion becomes more stochastic because the high fitness-effect beneficial mutations that dominate occur at lower rates. To test whether these features generalize to other environments, we inferred the mDFE for N-lim (Supplementary Information: Section 1). We find that the shape of the mDFE in N-lim is qualitatively different from C-lim (Fig. 2): the rates of mutation to higher fitness effects (s > 5%) are approximately three-fold lower in N-lim and fall off rapidly, with no detectable fitness effects above 8%. With time, the lineage dynamics become exponentially more sensitive to these differences at the higher fitness effects (expanded region Fig. 2 and Supplementary Information: Section 2). In C-lim, these mutations establish (escaping stochastic loss), expand and compete over shorter timescales (Fig. 1a versus c). In N-lim, the lower mutation rate to higher fitness effects results in more stochastic dynamics: high-fitness mutations occur in smaller numbers, causing larger variations between replicates (Fig. 1c versus d and Supplementary Information: Section 2).

Fig. 2|. Barcode-directed whole-genome sequencing of adaptive clones to find the mutational targets underlying the distribution of beneficial fitness effects (mDFE).

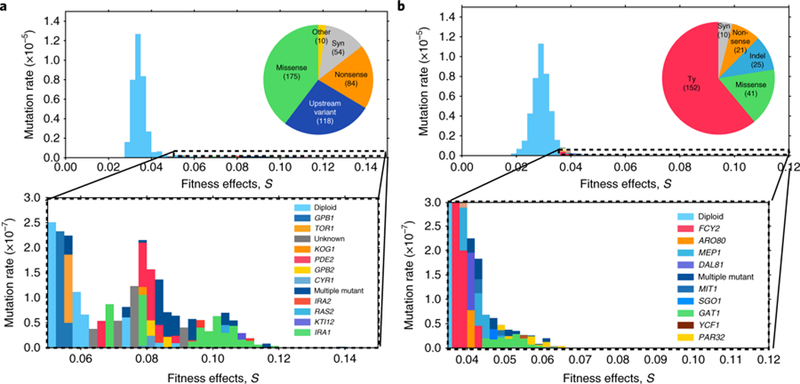
a, C-lim. b, N-lim. Most adaptive events are diploidizations (top, light blue), but high fitness effects are caused by mutations in or near genes (bottom, colour key). Each fitness bin is coloured according to the estimated rate of mutation of verified single mutants to each gene in that bin (S3). The colour key is roughly ordered from lowest to highest fitness effect of a mutational event. Pie charts indicate the mutational mechanisms of adaptive mutations.

To verify that single beneficial mutations determine the early adaptive diversity dynamics, we whole-genome sequenced hundreds of unique adaptive mutations spanning a wide range of fitness effects. In C-lim, we previously found a near-comprehensive spectrum of adaptation-driving single mutations by sequencing 418 clones²⁴. Here, we repeated this for N-lim, sequencing 310 adaptive clones and re-measuring their fitness (Supplementary Information: Section 3). In both environments, the majority of clones contain a single adaptive mutation (>75%), consistent with single mutants determining the early adaptive diversity dynamics. Lineages containing two adaptive mutations are crucial to the later time-diversity dynamics, as discussed below. Focusing on single-mutant clones, we find major differences in mutational mechanisms and mutational targets (Fig. 2). Surprisingly, Ty transposition events play a major role in driving adaptation in N-lim but not C-lim. In both environments, adaptation is first driven by cells undergoing a frequent diploidization (Dip) event, and later, by cells that acquire mutations in a small set of nutrient sensing pathway genes (Fig. 2 and ref. ²⁴). The majority of recurrently mutated genes are putative loss-of-function (LoF) mutations, with a minority being putative gain-of-function (GoF) mutations (Supplementary Information: Section 3).

A crash in adaptive lineage diversity is observed in all evolutions.

Estimation of the mDFE required approximately 100 generations of lineage tracking in C-lim²³ and ~192 generations in N-lim. To study the clonal dynamics beyond the initial expansion of single-mutant clones, we tracked lineages for approximately 300 generations in C-lim and N-lim. In both environments, we find that lineage diversity crashes, with a handful of lineages dominating (Fig. 1). One possible explanation for this is that multiple adaptive clones within each lineage contribute to its dominance. Alternatively, a single large clone within each lineage may be responsible; however, it is unclear how such large clones would arise. Also unclear is whether crashes are specific to our experiments or are a general feature of clonal-interference dynamics. To investigate these questions, we first appeal to the simplest model of this evolutionary process, the fitness-staircase model¹⁷. Next, we perform simulations using mDFEs measured experimentally. Finally, we validate predictions of our model using whole-genome sequencing and tracking the frequency of diploids.

A fitness-staircase model predicts a stochastic diversity crash and subsequent recovery.

In the fitness-staircase model, all beneficial mutations confer fitness advantage s, such that a clone with m mutations grows at rate ms relative to the wild type (Fig. 3a). Beneficial mutations occur at rate, U, in a constant population, of size N and establish with probability proportional to their ‘lead’, Q, over the mean fitness (Methods¹⁷). Mirroring our experiment, we focus on the multiple-mutation regime in which NU » 1 (Supplementary Information: Section 4). Clone-size dynamics in this model (coloured lines, Fig. 3b) are controlled by two parameters: the initial feeding rate of mutations from one fitness class to the next, R, and the ratio of fitnesses, α = g/(g + s), between fitness class growing at rate g, and the newly established fitness class growing at rate g + s. For wild-type cells (g = 0) feeding single mutants (g + s = s), the initial feeding rate R = NU » 1 and the ratio of fitnesses α = 0 (Supplementary Information: Section 4). Since R is high, new mutations occur frequently and many mutant clones (~R) expand together with roughly equal size. This produces deterministic dynamics (Fig. 3b,c, light-green data). For single mutants (g = s) feeding double mutants (g + s = 2 s), the initial feeding rate R = NU²/s « 1 and the ratio of fitnesses α = ½. Since R is low, new mutations occur rarely and the first few mutant clones to occur are typically much larger than the rest. This produces large ‘jackpot’ events in which a handful of early clones dominate the population (Fig. 3b,c, dark green). The size of jackpots is controlled by α. If α « 1, the first established clone will become large before the sub-sequent clones establish and the cumulative size of all subsequent clones will be small relative to the first. Thus, the population will be dominated by the first mutant clone to occur. In contrast, if the new mutant population grows at the same rate as the one feeding it (α = 1), which is the case for the classic Luria–Delbrück experiment²⁵, a large number of clones that occur late collectively contribute just as much to the expanding mutant population as the early clones do.

Fig. 3|. The dynamics of adaptive genetic diversity in the fitness-staircase model.

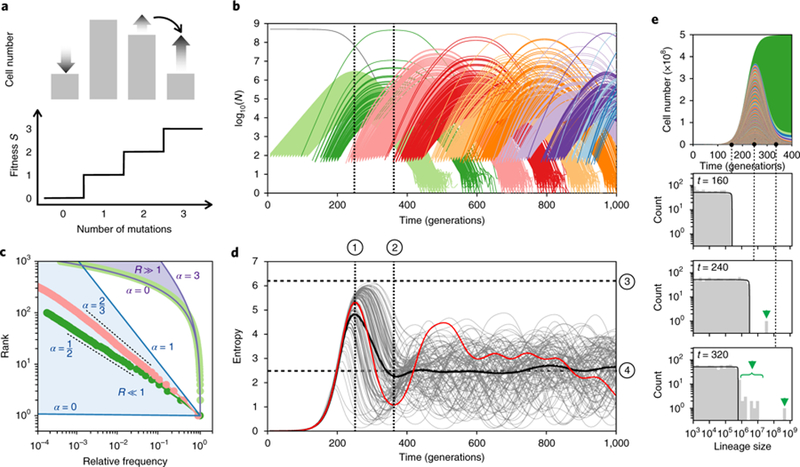
a, The fitness-staircase model in the multiple-mutation regime. Clones with different numbers of mutations expand in the population concurrently. The distribution of cells containing different numbers of mutations changes through time, with the distribution at t ≈ 250 (from simulation in b) shown. Clones expand or contract in relation to their advantage over the mean population fitness. b, The trajectories of all unique adaptive clones (lines, coloured by fitness class) from a typical simulation with population size N= 5×10⁸, beneficial mutation rate U = 10⁻⁶ and additive fitness effects of size s = 0.05. c, The rank-frequency plot for single-(light green), double-(dark green) and triple-(pink) mutant clones averaged over 100 simulations, one instance of which is shown in b. Frequencies shown are relative to the first mutant to establish. Single mutants establish deterministically with a clone-size distribution that is approximately exponential (purple lines). Double and triple mutants establish stochastically with power-law clone-size distributions (dashed lines). Solid blue and purple lines indicate the limiting behaviours: no fitness difference between mutant classes (α ≈ 1, blue line), the Luria-Delbrück limit, and constant feeding (α ≈ 0). d, The entropy of all adaptive clones in the population over time for 100 simulations (grey lines). The particular simulation from b is highlighted in red and the mean of all 100 simulations is shown in black. Diversity approaches its steady state non-monotonically, reproducibly crashing below the long-term average and subsequently recovering to above long-term average levels. The parameter combinations that determine the positions of the various features labelled (1)-(4) are outlined in the text. e, The barcode trajectories from b and, beneath, their size distributions at three time points. At intermediate times, the largest barcode lineages are inconsistent with the single-mutant size distribution (black line) and, instead, are driven by anomalously large double mutants expanding within (and dominating) these lineages (green arrows). These are detectable before double mutants dominate the total population.

By considering when the feeding population will give rise to a new mutation (Supplementary Information: Section 4 and refs. ^15,17), we find that the median size of the kth mutant clone to occur will have a frequency relative to the first (k = 1) clone of

$$f_k\propto {\left(1+\frac{k\alpha }{R}\right)}^{-1/\alpha }$$

For single mutants (R » 1 and α = 0), the expected rank–frequency relationship is k ≈ Rln(f_k) (Fig. 3c, purple line), which agrees closely with simulated data (Fig. 3c, light-green points). Large numbers of single mutants (~NUs) establish and expand together; however, only those that enter within the first ~1/s generations contribute substantially to the class. Therefore, approximate NU clones (~NUs × 1/s) drive the single-mutant expansion. We characterized adaptive diversity using the Shannon entropy, $S=-{\Sigma }_k{\text{f}}_k\ln \left(f_k\right)$²⁶ of adaptive clones. Because approximately NU single mutants each reach a maximum frequency of approximately 1/NU, the entropy peaks at S ≈ ln(NU), around when single mutants peak in abundance, t ≈ (1/s)ln(s/U) (dashed lines, marked (3) and (1), respectively, in Fig. 3d). Because many mutations contribute to the single-mutant expansion, stochasticity in establishment times is averaged out, resulting in highly predictable entropy dynamics (Fig. 3d).

For double mutants (R « 1 and$(R«1\text{ and }\alpha =\mathrm{½})$, the expected rank–frequency relationship is $k\approx f_k^{-1/2}$ (Fig. 3c, dashed line), which agrees closely with simulated data (Fig. 3c, dark-green points). Because the rank–frequency curves of second mutants follow a power law, the first double mutants to establish dominate: on average the top one and five clones comprise >55% and >87% of the total double-mutant class, respectively (Fig. 3b,c). Because a few clones are so consequential, variation in their establishment times result in large fluctuations in the rank–frequency distribution: sometimes the first clone nearly sweeps the population (for example, Fig. 3b). As double mutants outcompete single mutants (after t ≈ (1/s)ln((s/U)³/Ns), the earliest double-mutant clones cause the diversity to crash below the long-term average (dashed lines (2) and (4) in Fig. 3d). A precedent of this crash is observable: after t ≈ (2/s)ln(s/NU²), approximately 180 generations in Fig. 3, lineages harbouring double mutants become larger than the predicted size of any single mutant (Fig. 3e, dark-green arrows). These double-mutant lineages drive the diversity crash.

Triple mutants cause the diversity to recover (Fig. 3d). This is because α is higher for triple mutants than double mutants. In general, α is controlled by the lead, Q, the difference between the fittest mutant class and the mean fitness (Supplementary Fig. 6). Because single and double mutants establish when the mean fitness is close to ancestral, Q is s and 2s, respectively, and double mutant$\alpha =\mathrm{½}$. For triple mutants and subsequent mutant classes, the lead is determined by (Q/s) ≈ 2ln(Ns)/ln(s/U) ≈ 3.1 (ref.¹⁷; Supplementary Fig. 6). Thus, for triple mutants α = 2s/3s = 2/3 and the expected rank–frequency relationship is $k\approx f_k^{-2/3}$ (Fig. 3c, dashed line), in close agreement with simulated data (Fig. 3c, pink points). This distribution results in smaller jackpots than double mutants: on average, the top one and five triple-mutant clones comprise only approximately 43% and 72% of the triple-mutant class, respectively (Fig. 3b,c). As a consequence, when the triple mutants outcompete double mutants, the diversity recovers (Fig. 3d).

Simulations using the experimentally inferred mDFE also predict a diversity crash.

To investigate whether differences in the rank–frequency relationship could also cause the crashes in our experiments, we simulated the lineage dynamics using the experimentally determined mDFE inferred in each environment, removing any lineages that contain a double mutant (Supplementary Information: Section 5). Plotting the Shannon entropy of both adaptive lineages and clones shows that two measures of the adaptive genetic diversity track one another closely until triple mutants first appear. Simulations accounting only for the stochastic occurrence of, and competition between, single mutants (single-mutant model, with no further mutations occuring) predict that diversity should crash slowly, at odds with observations (Fig. 4a). However, additive model simulations, which allow for multiple mutants drawn from the single-mutant mDFE, produce diversity crashes that are qualitatively consistent with the observed lineage diversity crash (Fig. 4b). In qualitative agreement with what is observed in the staircase model, typically fewer than five lineages comprise >90% of the population at times beyond 150 generations. This demonstrates that, even with a more complicated mDFE, the same general behaviour emerges: early jackpot double mutants cause a diversity crash of both lineages and clones.

Fig. 4|. Exponential feeding of double mutants causes a diversity crash.

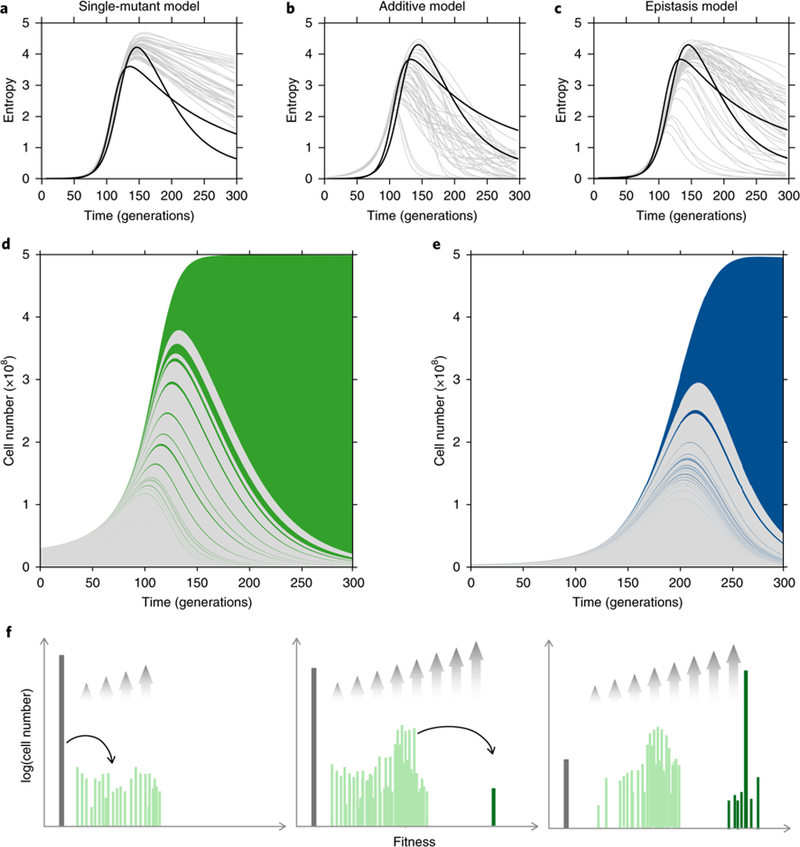
a-c, Shannon entropy of adaptive lineages from replicate experiments in C-lim (black lines) and stochastic simulations (grey lines) using a single-mutant model (a), additive model (b) or epistasis model (c). The entropy of adaptive clones closely tracks the entropy of adaptive lineages (Supplementary Figs. 9–14). d,e, Muller plots from Fig. 1 recoloured to depict single-mutant (grey) and early double-mutant (green and blue) adaptive lineages in C-lim (d) and N-lim (e). f, Schematic showing the statistical behaviour of the ancestor (grey), single-(light green) and double-(dark green) mutants. Grey arrows show the relative growth rates due to selection.

Experimental validation of double-mutant jackpot events driving an adaptive diversity crash.

We next sought to experimentally validate that early double mutants drive the adaptive diversity crash by examining whole-genome sequencing data of single-cell derived colonies. While >75% of sequenced clones were verified single mutants, we reasoned that the remaining <25% might include early double mutants that have yet to become abundant. Because these double mutants are expected to be highly fit, they should quickly expand in frequency. As predicted, these early double mutants do indeed dominate the population, driving a diversity crash in both C-lim and N-lim (Fig. 4d,e). To our surprise, however, clonal sequencing revealed that the dominant double mutants were not composed of two high fitness-effect mutations (for example, LoF + LoF) as would be predicted by our additive model simulations. Instead, sequenced dominant clones were Dip + GoF double mutants (Dip + ras2 in C1; Dip + mep1 in N1), despite neither GoF mutation occurring at a high rate. We reasoned that this inconsistency with the additive model could be due to epistasis: some classes of beneficial mutations combine sub-additively and these interactions might determine which first mutants eventually dominate. To test this, we modified our additive model simulations (above) to ban second mutations that are implausible or unobserved (Dip + Dip, Dip + LoF, LoF + LoF or LoF + GoF, see Supplementary Fig. 5). Simulations using this ‘epistasis model’ produce diversity crashes and lineage trajectories that are in qualitative agreement with observations (Fig. 4c). Crucially, the epistasis model (not the additive model) predicts that clones driving the diversity crash will usually be Dip + GoF if the crash is deep and LoF + Dip if the crash is shallow. The reason for this difference relates to α, discussed above. Both Dip + GoF and LoF + Dip double mutants have similar fitnesses (~0.14, see Fig. 2). In the case of Dip + GoF, the single-mutant fitness (~0.035) results in α ≈ 0.25, a very broad distribution and a deep crash. However, in the case of LoF + Dip, the single-mutant fitness (~0.10) results in α ≈ 0.7, a narrower distribution and a shallow crash.

Evidence for broad ‘categorical’ epistasis between mutations.

Lineage trajectories alone have limited power to quantitatively distinguish between the additive and epistasis models (Fig. 4b,c). To further interrogate our models, we therefore asked if the dynamics of mutations, rather than lineages, are consistent with predictions of either model. We measured the abundance of diploids in the population every 8–24 generations using a colony-growth assay (Supplementary Information: Section 6 and ref. ²⁴), not only for the four evolutions described above, but for two additional evolutions (one in C-lim, one in N-lim) that were not characterized by lineage tracking (Fig. 5b–e). Consistent with our observations, both models predict that replicate diploid trajectories will track each other closely—first, as large numbers of ancestral cells diploidize and expand, and second, as diploids begin to be out-competed by haploids that have acquired fitter LoF and GoF mutations. At later times, however, the models deviate. In C-lim, the additive model predicts that LoF + LoF or LoF + GoF double mutants drive the continuing decline of diploids (Fig. 5b). In N-lim, the additive model predicts that Dip + LoF mutations should expand fast enough that diploid trajectories never dip (Fig. 5d). However, consistent with observations, the epistasis model predicts that the diploid trajectory will dip and subsequently recover, driven by LoF and GoF haploids that diploidize and by diploids that acquire GoF mutations (Fig. 5c,e). Since this diploid recovery is driven by rare double mutants, its timing and depth are predicted to be highly stochastic, resulting in large variations between replicates, in agreement with our data.

Fig. 5|. Simulations of diploid dynamics using the additive and ‘categorical’ epistasis models.

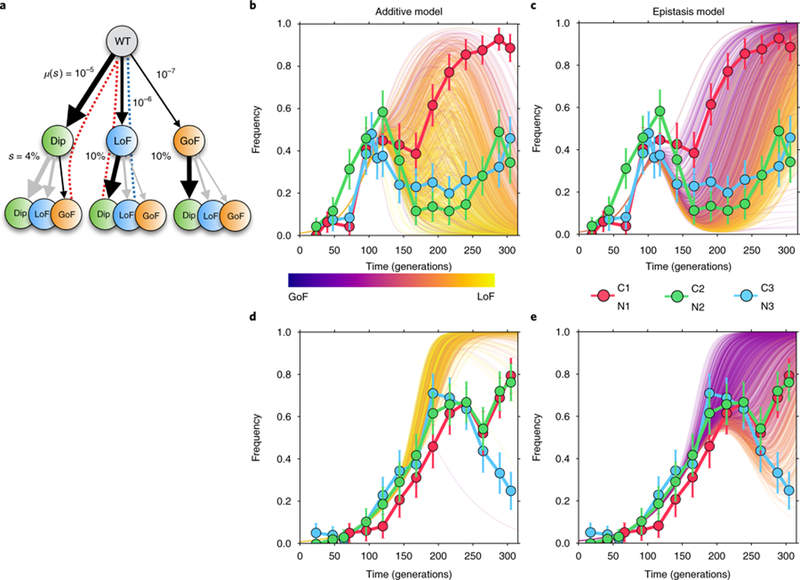
a, The simplified fitness landscape used for simulations in C-lim, where μ(s) indicates the mutation rates and s indicates the fitness effects, of Dip, LoF and GoF mutations. Greyed arrows are paths disallowed by the epistasis model. Dashed lines indicate the paths taken by the dominant clones in the additive (blue) and epistasis (red) models. b-e, The diploid trajectories in C-lim and N-lim predicted by the additive model (b and d, respectively) and the epistasis model (c and e, respectively) compared to the measured diploid trajectories (data points) from the three replicate populations in each condition. Colour scale indicates the extent to which the diploid rescue is driven by Dip + GoF (purple) versus LoF + Dip or Dip + LoF (yellow) mutants, with early rescue being more likely to be driven by Dip + GoF mutations. Error bars are one standard deviation.

To further test which model is more consistent with the observed data, we calculated the likelihood of the data under a binomial error model for the categorical epistasis and the additive models (Supplementary Information: Section 7). We found a higher likelihood when double mutants are restricted to occur through the Dip + GoF route alone (categorical epistasis model, log-like-lihood L ≈ 360) than when all mutations are available (additive model, L ≈ 730). In addition, the maximum-likelihood parameters obtained for the additive model are inconsistent with measured values; for example, the best-fit mutation rate to fit mutations (LoF and GoF) is three orders of magnitude smaller than the measured value (2 × 10^–10 versus 3 × 10^–7).

Discussion

In our experiments, the adaptive genetic diversity first increases quasi-deterministically, caused by a large number of single mutants, and later crashes stochastically, caused by a handful of jackpot events: highly fit double mutants occuring anomalously early. These diversity dynamics are a consequence of the clone-size distributions for single-, double-and subsequent multiple-mutant clones. The distribution of clone sizes is controlled by the initial feeding rate (R) and the ratio of the fitnesses (α) between a clone and its parent. When the dynamics are dominated by rare beneficial mutations (R « 1) that grow exponentially faster than their parent (α < 1), clone sizes are power-law distributed, with the largest clones dominating the population. This effect is closely related to the Luria–Delbrück experiment in which one observes jackpots of neutral mutations (α = 1). However, a key difference is that when adaptive mutations are accumulating (α < 1), mutants grow faster and the population is dominated by small numbers of large clones instead of large numbers of small clones. Jackpots drive a predictable crash in diversity followed by a subsequent recovery. These diversity expansions and crashes are likely to be general features of clonal interference; however, the expansion rate, timing and the depth of the crash are influenced by population size, mDFE and patterns of epistasis between adaptive mutations.

In environments where the mDFE of first mutations lacks extremely high fitness effects, mutations that cause the diversity expansion are fed from a large, effectively constant-sized (ancestral) population, while mutations that cause the crash are fed from a small, exponentially growing (single-mutant) population. When extremely high fitness-effect mutations are possible, such as in the presence of a growth-inhibiting drug²⁷, a crash is sometimes driven by the expansion of very rare highly fit single mutants (Supplementary Information: Section 8). Thus, a diversity crash is likely to occur, whether driven by a traditional selective sweep of a single mutant^14,15 or by a multiple mutant that occurs anomalously early. While we have focused on well-mixed yeast populations, expansion of spatially structured populations exhibit qualitatively similar dynamics²⁸. Furthermore, ‘clonal dominance’ is a common feature to many cancers^11,29,30 with one recent example explicitly showing that the stochastic emergence of a highly fit double mutant underlies a diversity crash³¹. High levels of tumour diversity are associated with poorer survival^29,32. Thus our work raises the possibility of exploiting fluctuations in diversity to optimize treatment schedules. More generally, our work highlights that while genetic diversity evolves stochastically and depends on rare events, the diversity dynamics are statistically predictable in an analogous way to a weather forecast²².

While in our experiments the deterministic to stochastic transition occurs between first and second mutations, in small populations (NU < 1), first adaptive mutations are stochastic and diversity crashes (of neutral mutations) will occur at nearly every adaptive event. In even larger populations ((s/U)² < Ns < (s/U)³), double mutants will occur deterministically, but triple mutants stochastically, and therefore the diversity crash will be caused by a handful of triple mutants. More generally, for mDFEs that lack a supply of high fitness-effect mutations, the dynamics are driven by ‘predominant’ mutations of similar fitness¹⁷ and the diversity crash will be caused by clones harbouring q beneficial mutations, where q is the smallest integer for which (s/U)^q > Ns, where U is the mutation rate to the ‘predominant’ fitness mutations¹⁷. Previous work has found that beneficial cohorts—multiple beneficial mutations co-occurring in clones that are at frequencies below the detection limit of genomic sequencing—commonly drive laboratory^5,20 and clinical¹¹ evolution. Our results suggest that, at least during the early stages of evolution, these cohorts are expected, with cohort size being determined by q (Supplementary Information: Section 4).

Theoretical work presented here and elsewhere^21,33 predicts that beneficial cohorts and fluctuations in genetic diversity should occur throughout evolution, driven by the stochastic occurrence of anomalously early and/or fit multiple mutants. Our results indicate that the precise nature of these fluctuations will depend on patterns of epistasis. For example, we find that Dip + GoF mutations (α ≈ 0.25) are the dominant route for acquiring a fit double mutant in our experiments, making the dynamics particularly stochastic. Due to limitations of our barcoding platform, we were unable to validate that triple mutations resulted in a recovery of the adaptive diversity, as is predicted by our simulations. However, the development of new double-barcoding technologies³⁴ or barcodes that continuously generate diversity through time^35–37 offer a promising path forward to address these questions.

Methods

Experimental evolutions.

The barcoded yeast library from ref. ²³, containing approximately 500,000 barcodes, was evolved by serial batch culture under carbon or nitrogen limitation in 100 ml of ×5 Delft media²³. Nitrogen limited media contained 0.04% ammonium sulfate and 4% dextrose. Carbon limited contained 4% ammonium sulfate and 1.5% dextrose. Cells were grown in 500 ml Delong flasks (Bellco) at 30 and 223 r.p.m. for 48 h between each bottleneck. Bottlenecks were performed by adding 400 μl of the evolution to fresh media. Cell counts were performed using a Coulter Counter at each bottleneck to estimate the generation time. Contamination checks for bacteria or other non-yeast microbes were performed regularly (every 2–4 bottlenecks).

Barcode sequencing.

The barcode sequencing follows the same protocol as in ref. ²³. Briefly, genomic DNA was prepared by spooling. A two-step directed PCR was used to amplify the lineage tags for sequencing. We amplified ~14 μg of template per sample, which corresponds to ~10⁹ genomes or ~2,000 copies per barcode initially. First, a three-cycle PCR with OneTaq polymerase (New England Biolabs) was performed in 24 reaction tubes, with ~600 ng of template and 50 μl total volume per tube. Primers for this reaction were

ACACTCTTTCCCTACACGACGCTCTTCCGATCTNNNNNNNNXXXXXTTAATATGGACTAAAGGAGGCTTTT and CTCGGCATTCCTGCTGAACCGCTCTTCCGATCTNNNNNNNNXXXTCGAATTCAAGCTTAGATCTGATA

where Ns are degenerate bases used for the Unique Molecular Identifiers and Xs correspond to a one of several multiplexing tags. The PCR product was pooled into four 50 μl aliquots using four PCR Cleanup columns (Qiagen) at six PCR reactions per column. A second 24-cycle PCR was performed with high-fidelity PimestarMAX polymerase (Takara) in 12 reaction tubes, with 15 μl of cleaned product from the first PCR as template and 50 μl total volume per tube. Primers for this reaction were

AATGATACGGCGACCACCGAGATCTACACTCTTTCCCTA-CACGACGCTCTTCCGATCT and CAAGCAGAAGACGGCATACGAGATCGGTCTCGGCATTCCTGCTGAACCGCTCTTCCGATCT

PCR product from all reaction tubes was pooled into 50 μl using a PCR Cleanup column (Qiagen). The appropriate PCR band was isolated by E-Gel agarose gel electrophoresis (Life Technologies) and quantitated by Bioanalyzer (Agilent) and Qubit fluorometry (Life Technologies).

Identifying adaptive lineages.

Adaptive lineages were identified using the same methods as in ref. ²³. Briefly, for a given lineage trajectory (read number measurements over time) we evaluated two hypotheses: (1) no adaptive mutation established in the lineage and (2) an adaptive mutation with fitness effect, s, occurred in the lineage and established to grow exponentially with an establishment time, τ. We used a uniform prior over a broad range of τ (– 150 < τ < 100) and an exponential prior over s, with decay length 0.1. To calculate the probability of each hypothesis given the data we developed a noise model²³ that accounted for the variance introduced into barcode frequency estimates from three sources: (1) finite depth of coverage during sequencing, (2) noise introduced during DNA extraction and PCR amplification of the barcodes and (3) biological noise introduced during the growth cycle. Each of these were quantified by performing replicate measurements (1) on the same sequencing library, (2) on the sample sample and (3) on samples from adjacent time points, respectively (see supplemental information of ref. ²³). We then evaluated each (s, τ) hypothesis in intervals of (Δs = 0.005, Δτ = 1) and determined whether any of these were more probable than the neutral hypothesis. If so, we took the (s, τ) hypothesis with the largest posterior as our best estimate.

Isolating and sequencing of adaptive clones.

We isolated clones from generation 192 of N1, and re-measured the fitness of the 310 clones within that pool, whose trajectories indicated they were adaptive. We whole-genome sequenced all clones from this pool to a mean coverage of 30×. Variants were called using the same pipeline as outlined in ref. ²⁴. Details of the top 100 clones ranked by re-measured fitness are shown in Supplementary Fig. 5.

From the whole-genome sequencing data, we identified single nucleotide polymorphisms, small indels, larger deletions and insertions, Ty transposition events and copy number variations, including aneuploidy and segmental aneuploidy, and annotated the genes within which those mutations fell. To determine whether mutations were adaptive, or simply neutral passenger mutations, we used the following criteria. First, if a gene was mutated multiple times in clones with distinct barcodes, mutations in that gene were designated as adaptive. Because of the low mutational burden of clones, the number of times this is expected for two neutral mutations is small (<0.005). Second, if a mutation in a gene was only observed once, but that clone was clearly non-neutral (mean re-measured fitness >0.01) and no other mutations were identified in the clone, then that gene was labelled as adaptive. A clone was labelled as a multiple mutant if it contained two or more mutations that were identified as adaptive via the above criteria.

Simulated lineage and clone dynamics.

To simulate lineage and clone trajectories in python, we initiate a dictionary object ‘barcodes’ whose keys are tuples that are the barcode IDs entered in the form (BC1_id, BC2_id…), which can be adapted for simulating a re-barcoding process. For single-barcodes the keys are (1,), (2,), (3,) and so on. The value for each key is a list of all genotypes belonging to that barcode, for example, ‘barcodes[(1,0)]’ might return [([(0,’WT’, 0.0)],10**8), ([(0,’WT’, 0.0),(0,’DIPLOID’, 0.04)],10**4)]. Each entry of the list is a ‘(genotype, abundance)’ tuple. The abundance is how many cells share that genotype. The genotype itself is list of ‘(unique_mutation_integer, NAME, selective effect)’; that is [(0,’WT’, 0.0), (12,’DIPLOID’, 0.04), (21,’IRAT’, 0.10)] would mean that the sequence of mutations in this clones was wild-type, then a ‘DIPLOID’ mutation (which was the 12th mutation to occur in the simulation and confers a 4% advantage) and an ‘IRA1’ mutation that was the 21st mutation to occur and confers an additional 10% advantage. The genotype would grow at 14% relative to wild type. Mutations are generated from another dictionary ‘dfe_dict’, which is a dictionary whose keys are floats of possible fitness effects: for example, 0.02. The value for each key is a dictionary of ‘{NAME: mutation rate}’ key–value pairs. Mutations occur stochastically each generation determined by the mutation rate, U. New mutant clones are born from their parents by calling a random Poisson variate with mean given by the product of the parent clone size, n, and the mutation rate, U. Establishment of new clones is determined by calling a random variate from a uniform distribution on the interval [0,1]. If this random variate is less than the fitness advantage of the new clone relative to the mean fitness the clone establishes with a starting establishment size 1 per fitness advantage, capped at 200 for weakly beneficial clones. The dynamics of each established clone is then deterministic: obtained by the exponential growth rate of its fitness advantage over the mean fitness. Low-frequency and low-fitness clones are removed from the population when their fitness advantage is negative and when their size drops below n = 10.