SUMMARY.
In environmental and nutritional epidemiology and in many other fields, there is increasing interest in estimating the effect of simultaneous exposure to several agents (e.g., multiple nutrients, pesticides, or air pollutants) on a health outcome. We consider estimating the effect of a multivariate exposure that includes several continuous agents and their interactions—on an outcome, when the true confounding variables are an unknown subset of a potentially large (relative to sample size) set of measured covariates. Our approach is rooted in the ideas of Bayesian model averaging: the exposure effect is estimated as a weighted average of the estimated exposure effects obtained under several linear regression models that include different sets of the potential confounders. We introduce a data-driven prior that assigns to the likely confounders a higher probability of being included into the regression model. We show that our approach can also be formulated as a penalized likelihood formulation with an interpretable tuning parameter. Through a simulation study, we demonstrate that the proposed approach identifies parsimonious models that are fully adjusted for observed confounding and estimates the multivariate exposure effect with smaller mean squared error compared to several alternatives. We apply the method to an Environmental Wide Association Study using National Heath and Nutrition Examination Survey to estimate the effect of mixtures of nutrients and pesticides on lipid levels.
Keywords: Bayesian model averaging, Confounding, Exposome, Model uncertainty, Multiple exposures, Multivariate exposure effects
1. Introduction
With the rapidly increasing availability of environmental exposure data, there is growing interest in studying the multitude of exposures, often referred to as the exposome, that may influence complex diseases (Wild, 2005; Louis and Sundaram, agents for associations with health outcomes and biological endpoints (Patel et al., 2013; Patel and Ioannidis, 2014). Increasingly, research is focused on estimating the health risks associated with simultaneous exposure to a mixture of multiple agents, rather than single-agent analyses (Zanobetti et al., 2014; Bobb et al., 2015).
Due to the predominant reliance on observational data, confounding remains a common consideration when estimating the effects of multiple agents. Methods for confounding adjustment in this context are met with the challenge that the proliferation of data on multiple agents is typically accompanied by a similar proliferation in measurement of possible confounding factors. As a consequence, researchers are confronted with the need to develop data-driven approaches to prioritize which of a high-dimensional set of possible confounders to include in a statistical model for adjustment (Hirano and Imbens, 2001; Vansteelandt et al., 2012; Wang et al., 2012, 2015; Wilson and Reich, 2014; Ghosh et al., 2015).
We consider data-driven confounder selection in the context of estimating the effect of a change in exposure to several continuous agents, X = (X1, …, Xm)T, on a health outcome Y. Specifically, in the situation where the number of agents is large and the effect of a change in X on Y includes interactions between agents. Three distinguishing features characterize this work: 1) estimating the health effect of exposure to a large number of continuous agents and their interactions; 2) confronting the need to choose from a high-dimensional set of possible confounders, and 3) accounting for the uncertainty in the selection of confounders.
The problem of confounding adjustment for estimating effects of multiple agents has been considered in causal inference literature rooted to the potential-outcomes framework (Rubin, 1978). Taubman et al. (2009) use g-estimation (Robins, 1986) to estimate the effects of joint treatment that may vary over time. Hernán et al. (2001) consider the related problem of multiple, time-varying treatments using marginal structural models. Imbens (2000) proposed the generalized propensity score for multivalued treatments. Imai and van Dyk (2004) develop a propensity function approach for multiple continuous agents that relies on matching or subclassification by the multivariate propensity function. Importantly, all of this and related work operates under the assumption that the confounders required for effect estimation are known and specified a priori.
To accommodate settings where the confounders required for effect estimation are not known a priori, there has been recent interest in methods to select or prioritize confounders from a possibly high-dimensional set of covariates. Brookhart et al. (2006) provided simulation evidence to motivate the importance of model selection for causal inference. Hirano and Imbens (2001) proposed a method based on univariate tests with both the propensity score and mean outcome model. Several recent approaches are based on evaluating the change in estimates produced with different confounding sets including methods based on cross-validation (Brookhart and Van Der Laan, 2006), on the mean square error of effect estimates (Vansteelandt et al., 2012), or change-in-deviance coupled with change-in-estimate (Crainiceanu et al., 2008). Targeted maximum likelihood estimation uses an outcome model, an exposure model, and a “targeting” step to optimize the bias-variance trade-off of the parameter of interest while the super learner adds ensemble learning to select confounders for a single binary treatment, multiple binary treatments, or a single continuous agent (van der Laan and Rose, 2011; Kreif et al., 2015). For estimating effects with a regression model, Wang et al. (2012) proposed Bayesian adjustment for confounding (BAC), which uses the ideas of Bayesian model averaging (BMA, Raftery et al., 1997) to prioritize confounders based jointly on a regression model for the exposure and a regression model for the outcome, with extensions of this approach in Wang et al. (2015) and Lefebvre et al. (2014). Ghosh et al. (2015) and Wilson and Reich (2014) propose lasso-style estimators, the former based on the predictive distribution between full and reduced models and the latter embedded in a Bayesian decision theoretic approach. Hahn et al. (2016) take a regularization approach to regression adjustment with shrinkage priors. Importantly, existing work for confounder selection and prioritization is primarily grounded in settings where interest lies in the effect of a single agent. Wilson and Reich (2014) extend their approach to selecting confounders when estimating the additive effect of multiple agents. None of these approaches consider confounder selection in the context of multiple continuous agents including interactions between agents.
In this article, we adopt an approach with conceptual ties to BAC in its focus on estimating effects with a linear regression model, which is well suited to the setting where interest lies in exposure to multiple continuous agents and their interactions. The goal is to provide a data-driven approach to prioritize confounders while respecting the full nature of confounding in settings of multiple agents and their interactions. Using the principles of BMA, the method accounts for the model uncertainty inherent to the choice of confounding variables.
2. Effects of Simultaneous Exposure to Multiple Agents: Notation, Estimand, and Confounding
We begin by formulating notation, defining the estimand of interest, and clarifying notions of confounding. Each of the quantities defined in this section are assumed available for a sample of i = 1, …, n individuals, but quantities are defined for a single individual for ease of exposition. Let X = (X1, X2, … , Xm) denote the levels of m agents, for example, measures of m persistent pesticides measured in a person’s blood. Let Y denote the measured health outcome of interest. In addition, we observe a large vector of covariates, C = (C1, …, Ck), all assumed to be unaffected by X and Y.
Let δ be an m-dimensional vector that denotes a change in each of the m agents that could arise from a (possibly hypothetical) intervention on X. Formally, interest lies in the change in Y that would result from a change in simultaneous exposure to the m agents, that is, a shift from x to x + δ. When m > 1, there is a key distinction between the agents and what we term the multivariate exposure because simple shifts in each of the m agents may produce complicated changes to the multivariate exposure comprised of the individual agents and any functions of the agents (e.g., interactions). Let , where is a pre-specified deterministic function, denote the r-dimensional multivariate exposure comprised of the m individual agents and functions of the agents. We focus on Z containing all agents and pairwise multiplicative interactions between agents (thus r > m).
In order to be explicit about the estimand of interest and the threat of confounding, we use the potential outcomes notation (Rubin, 1978). Let denoting the potential outcome that would be observed under multivariate exposure z induced by the agents x. We define the average causal effect of a shift in Z from to as:
| (1) |
The estimand in (1) can be estimated from observed data under the assumption of strongly ignorable multivariate exposure assignment:
| (2) |
for all possible values of x and . Note that the deterministic relationship between X and Z induces some implicit redundancy in the notation employed above, as potential outcomes could be equivalently indexed by X or . In order to be explicit about notions of confounding in the multivariate exposure context, we continue to index potential outcomes by . For example, empirical manifestation of confounding with respect to levels of z (X) occurs as covariate imbalance across levels of the multivariate exposure and may include imbalance across levels of the interactions, even if there is balance across levels of the individual agents. Web Appendix A outlines a simple illustration.
Under the conditional independence from (2), ∆ is identifiable from the observed data as
| (3) |
analogous to the g-formula (Robins, 1986), using parametric or non-parametric methods (Lunceford and Davidian, 2004).
We consider a minimal set of covariates sufficient to satisfy (2) as the confounders (VanderWeele and Shpitser, 2013), denoted by . When C is high-dimensional, it is often necessary to choose which of the available C belong to C*. We introduce a data-driven method to estimate which covariates are members of C* while accounting for uncertainty.
3. Model
3.1. Approach
The above discussion of confounding is not tied to any specific statistical model. However, in this article, we develop an estimation approach under a linear regression model. We assume
| (4) |
In (4), is an unknown parameter that indicates whether a covariate Cj is included into the model. Conditionally on , we can estimate the posterior distribution of the observed data contrast in (3), , using standard methods. To account for uncertainty about the choice of αl, we define the model averaged posterior distribution of ∆ as
| (5) |
where , Pr (αl) is the prior on al, and l € A indexes the 2k possible values of αl and, therefore, all the possible combinations of observed covariates (Raftery et al., 1997). Note that the approximation in (5) derives from the fact that not all ∆αl are interpretable as the causal effect ∆. Specifically, let be the class of regression models that always contain the minimal set of confounders C* and potentially others covariates. Following Wang et al. (2012), we can re-write (5) as
| (6) |
where only the models in the first summation over l € A* are unbiased for ∆ because those models contain C*. For models in , the second summation, the posterior mean of ∆αl will be a biased estimator of ∆ because such models omit some of the key confounders. The key idea of this article is to specify a prior distribution on αl, for l € A, such that most of the posterior mass on the model space will be assigned to A*, whereas A\A* will have a posterior probability close to zero. The extent of the proposed method’s ability to apportion posterior mass to A* and away from A\A* will dictate the extent of approximation, with (5) nearing equality as nearly all posterior mass concentrates on A*.
For settings where prior scientific knowledge cannot inform which Cj are required to satisfy (2), we develop a prior specification for α that prioritizes covariates for inclusion into the regression model based on their association with Z.
3.2. Construction of Prior to Adjust for Confounding
Our goal is to leverage the information on (Z, C) to construct a prior distribution on the model space A that results in most of the posterior mass on models in A*. For each covariate Cj, we specify Pr(αj = 1) which indicates the prior probability for including Cj into the regression model in (4). Our rationale is: under the assumption that the full model provides an unbiased estimate of ∆ (i.e., no unmeasured confounding and correct model specification), we assume a priori that if Cj is highly associated with Z then omitting Cj from the model is likely to lead to confounding bias. Therefore, it is likely that . For these covariates, we then assume a priori that Pr(αj = 1) is very large. Our ideas on constructing this prior leverage previous work by our own team (Wang et al., 2012; Zigler and Dominici, 2014; Wang et al., 2015; Cefalu et al., 2017) and by others who developed a data-dependent prior for variable selection in the context of sparse prediction (e.g.,Yuan and Lin, 2005).
To construct the prior on α, we start by calculating the confounding bias for ∆ that would occur if model (4) were fit without any adjustment, for example, α = 0. This is the difference between the posterior mean of ∆α under a model that includes all observed covariates and that of ∆α under a model that includes no covariates. With flat priors on and and inverse-gamma prior on , the confounding bias of under these two models is
| (7) |
where and . The bias in (7) is zero when or and, therefore, is zero when C is linearly independent of either Z or Y.
Under the assumption that the shift in exposure being studied is in the column space of the observed multivariate exposures, for some vector a, (7) is equal to 0 if:
| (8) |
where is the spectral decomposition.
We construct our informative prior for α by: 1) isolating the part of (8) that is a function only of Z and C, so as not to have the prior depend on the outcome Y; and 2) assigning higher prior inclusion probabilities to the covariates that are linearly dependent with Z and therefore contribute most to the confounding bias in (8). Specifically, the prior on αj is Bernoulli with mean , where is a k-vector taken from (8), ωj(Z, C) is the jth element of ω (Z, C), and λ ≥ 0 is a tuning parameter. Hence, λωj (Z, C) is the prior log-odds of including Cj into the model in (4).
This prior specification has the following desirable properties. If Cj is linearly independent of Z then ωj (Z, C) = 0 and the prior probability of including Cj is . When λ > 0, if Cj is linearly dependent with Z then ωj (Z, C) > 0, and is governed by the strength of this association. The stronger the association between Cj and Z, the larger the potential confounding bias that could result from omitting Cj, and the higher prior odds (larger ωj, (Z, C)) that Cj is included in the regression model.
This prior for α allows for covariates that are associated only with Z and independent from Y to be excluded from the model. These variables are known to reduce precision. We address this with the tuning parameter λ. When any covariate that is linearly associated with Z (even weakly) is forced into the model regardless of whether it is associated with Y. In this situation (large λ), we prioritize confounding adjustment over model parsimony. In contrast, when λ = 0 the prior on α is flat,, and we prioritize model parsimony over confounding adjustment. Hence, the structure of the prior comes from ωj,(Z, C) and the strength of the prior comes from the choice of the tuning parameter λ.
We complete the Bayesian specification for the model following that of Raftery et al. (1997) and provide details in Web Appendix B. We compare the proposed prior with alternatives and show details of the calculations used in this section in Web Appendix B.
3.3. Relation to a Penalized Likelihood Approach and Selecting λ
The proposed approach can be formulated as a penalized likelihood problem where the prior translates to a penalty that reflects the goal of minimizing confounding bias while maximizing model parsimony. This will guide the selection of the tuning parameter λ.
We approximate the posterior model probability of using the Bayesian information criterion (BIC; Schwarz, 1978) as
| (9) |
The three terms on the right hand side of (9) are, from left to right: 1) the negative profile log-likelihood of the normal linear regression model which is minimized when covariates predictive of Y are included into the regression model; 2) the negative prior log-odds of covariate inclusion defined in Section 3.2; and 3) the BIC sparsity penalty.
The second and third terms of (9) can be combined and viewed as a single penalty where λ controls the balance between confounder adjustment (large λ) and model parsimony (small λ). The penalty for including covariate j is . This penalty can be either positive, acting as a penalty, or negative, acting as an incentive for covariate inclusion.
This provides a theoretical basis to select a value of λ that balances parsimony and confounder adjustment. We balance these competing interests by choosing λ so that the penalty is on average zero:. The balancing penalty is
| (10) |
In practice, λ = λ* can be seen as a benchmark choice. By taking λ > λ*, we include more covariates and take a more conservative approach to confounder adjustment at the expense of less parsimony. Alternatively λ < λ* prioritizes sparsity over confounder adjustment.
4. Simulation
4.1. Simulation Scenario 1
The first simulation scenario includes a multivariate exposure containing two agents and their interaction, Z = (X1, X2, X1X2_T and 100 covariates C. We generate data so that: C1,…,C15 are associated with Y and X1 and/or X2; C16,…,C20 are associated with Y and X1X2; C21,…, C30 are associated with Y but not with Z (predictors of Y); C31,…,C35 are associated with Z but not Y (instrumental variables) and should not be included in the model; and C36, …, C100 are independent of both Y and Z (noise). The true model contains only covariates C1, …,C30. The minimal set of confounders is {C1,…, C20}. Specifically, for observation, we simulate 1000 data sets with for j = 1, …, 100. The two agents are generated and . The outcome is generated as . For X1i and X2i the regression coefficients 11−½ and 21−½ are chosen so that both agents have variance one. Finally, and , are simulated as independent Uniform(0.2, 0.5).
We compare the proposed method, henceforth ACPME (adjustment for confounding in the presence of multivariate exposures), to five alternatives: 1) BMA (equivalent to ACPME with λ = 0, that is ; 2) BayesPen (Wilson and Reich, 2014) using one exposure model for each agent but not for the interactions; 3) the full Bayesian regression model that includes all 100 covariates; 4) the true Bayesian regression model that includes only covariates 1 to 30; and 5) the unadjusted Bayesian regression model that regresses the outcome on Z with no covariate adjustment. For ACPME, we use λ = λ* as described in Section 3.3. We estimate the effect of a simultaneous change in both agents from 0 to 1.
Figure 1 shows the prior (panel 1a and b) and posterior (panel 1c and d) inclusion probabilities for each Cj with ACPME. The posterior inclusion probabilities for the (j = 1, …, 20) with ACPME are all near one. Covariates associated with Z and not Y (j = 31,…, 35) have high prior inclusion probabilities but posterior inclusion probabilities less than 0.5. Hence, setting λ = λ* balances the goals of parsimony and confounder adjustment and does not force covariates associated with Z and not Y into the model.
Figure 1.
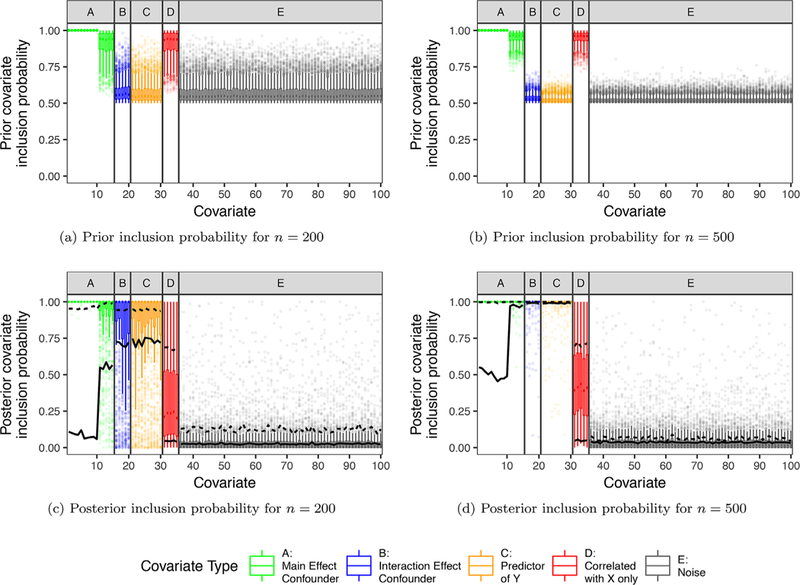
Prior (top) and posterior (bottom) inclusion probabilities for each covariate in simulation scenario 1 for our proposed method. The box plots show the distribution of prior and posterior probabilities across 1000 simulated data sets. For comparison, the lines in panel 1c and d show the average posterior inclusion probability for BMA (solid line) and the proportion of times each covariate was selected into the model with BayesPen (dashed line). The variable types, denoted by the letters on the top of each panel and by color, are: (A) correlated with Y and X (covariates 1–15); (B) correlated with Y and a exposure interaction (16–20); (C) predictor of Y independent of Z (21–30); (D) correlated with X only (31–35); and (E) noise variables (36–100). This figure appears in color in the electronic version of this article.
For comparison, Figure 1c and d show the mean posterior inclusion probability with BMA and the covariate selection rate with BayesPen. BMA has lower posterior inclusion probabilities than ACPME for the confounders. BayesPen selects true confounders at a high rate but includes covariates independent of the outcome at a higher rate than ACPME.
Table 1 shows results for estimating ∆. At both sample sizes, ACPME has lower root mean square error (RMSE) compared to all the alternatives except for the true model. In addition, ACPME has credible interval coverage near or at the nominal level. Estimates of ∆ from BMA are biased and have larger RMSE because the approach does not include all confounders. BayesPen had lower RMSE than the full model but higher than ACPME. We repeated this scenario with β= 0, a weaker association between C and Y, but the same association between C and Z. The proposed approach forces Z into the model regardless of whether there is a true exposure effect or not. Including Z in the model when null and strongly confounded resulted in decreased selection of true confounders and decreased interval coverage (0.90 for n = 200 and 0.93 for n = 500) (Web Appendix Table S1).
Table 1.
Simulation results for simulation scenario 1. The first four columns show the mean bias, mean RMSE, mean posterior SD or SE, and 95% interval coverage rate. The right most columns show statistics for covariate inclusion–the true inclusion rate defined as the mean probability that the true confounders and predictors of the outcome (covariates 1 to 30) are included into the regression model and the false selection rate defined as the mean probability that covariates independent of the outcome are included in the model (covariates 31 to 100). Covariates are considered included if they have posterior inclusion probability exceeding 0.5.
| Method | Bias | RMSE | Mean SD / SE |
95% Int. coverage |
True Inc. rate |
False Sel. rate |
|---|---|---|---|---|---|---|
| n = 200 | ||||||
| ACPME | 0.07 | 0.34 | 0.34 | 0.94 | 0.89 | 0.06 |
| BayesPen | 0.11 | 0.42 | 0.28 | 0.78 | 0.96 | 0.17 |
| BMA | 1.23 | 1.25 | 0.17 | 0.00 | 0.48 | 0.03 |
| Unadjusted | 1.65 | 1.66 | 0.21 | 0.00 | 0.00 | 0.00 |
| Full | 0.00 | 0.43 | 0.44 | 0.95 | 1.00 | 1.00 |
| True | 0.00 | 0.28 | 0.29 | 0.96 | 1.00 | 0.00 |
| n = 500 | ||||||
| ACPME | 0.02 | 0.18 | 0.19 | 0.96 | 1.00 | 0.07 |
| BayesPen | 0.03 | 0.21 | 0.18 | 0.91 | 1.00 | 0.11 |
| BMA | 0.66 | 0.78 | 0.15 | 0.24 | 0.84 | 0.04 |
| Unadjusted | 1.64 | 1.65 | 0.13 | 0.00 | 0.00 | 0.00 |
| Full | 0.02 | 0.21 | 0.21 | 0.96 | 1.00 | 1.00 |
| True | 0.01 | 0.17 | 0.17 | 0.95 | 1.00 | 0.00 |
4.2. Simulation with Large Number of Agents
The second scenario evaluates model performance in the context of a high-dimensional multivariate exposure for n = 200 and n = 500. For n = 200, the number of agents is allowed to vary from m = 2 to m = 13 and includes all pairwise interactions so that Z has m + m(m – 1)/2 columns (ranging from 3 to 91 including main effects and interactions). For n = 500, the number of agents is allowed to vary from m = 2 to m = 25 so that the columns of Z ranges from 3 to 325. For both sample sizes there are 100 covariates.
We simulate the covariates so that: C1 …, C15 are associated with at least one of the agents X1,…,Xm and Y; C16,…,C25 are associated with Y and at least one of the interactions between agents; C26, …, C30 are predictors of Y that are independent of Z; and C31, …, C100 are independent of both Y and Z. The true model includes C1 …, C30 and the minimal set of confounders is C1 …, C25. Web Appendix C contains the exact data generating mechanism.
Figure 2 shows the RMSE for estimating the change in Y due to a one unit increase in all agents. These results are presented in table format in Web Appendix C along with additional measures: bias, SD, interval coverage, and true and false selection rates. At n = 200, ACPME and BayesPen both have lower RMSE than the full model. ACPME has slightly lower RMSE than BayesPen, except for when the total model size approaches n and the full model, which is used to construct the ACPME prior, is challenging to estimate. When n ≈ p, ACPME maintains lower RMSE than the full model but has inflated type I error rate.
Figure 2.
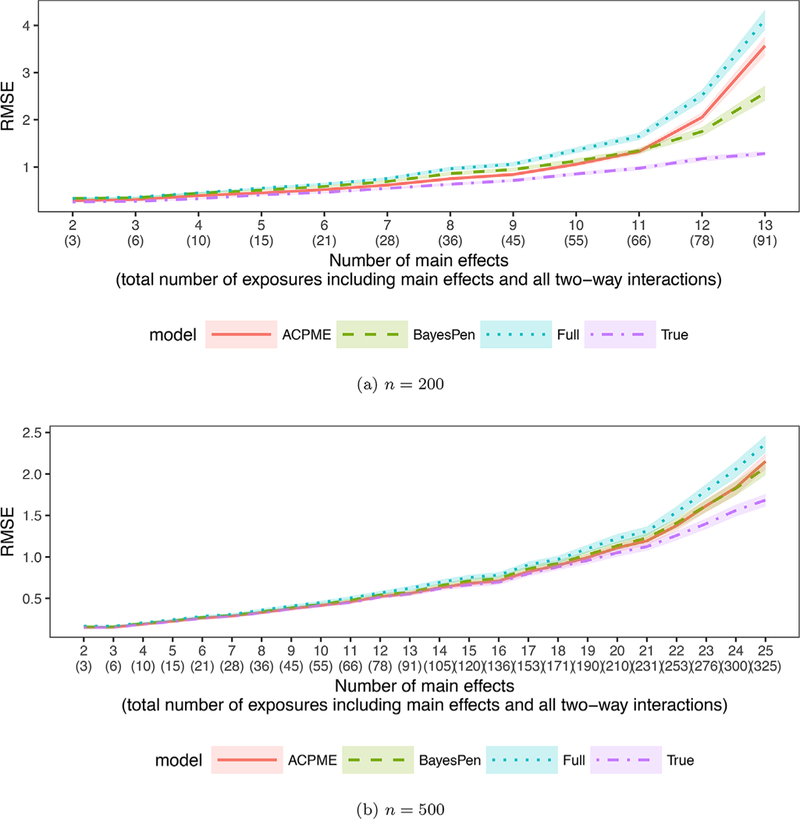
RMSE of the estimated exposure effect for simulation scenario 2 for n = 200 (panel 2a) and n = 500 (panel 2b). The x-axis shows the number of agents and in parentheses the dimension of the multivariate exposure including all main effects and two-way interactions. In all cases, there are 100 additional covariates in the model of which 30 are true confounders or and predictors of the outcome that should be included in the model. The true model only includes the 30 important covariates, the multivariate exposure, and an intercept. These data are also presented in Web Appendix Tables S2 and S3. This figure appears in color in the electronic version of this article.
5. Analysis of the NHANES Data
5.1. Overview of the Data and Analysis
We apply ACPME to the National Health and Nutrition Examination Survey (NHANES) data previously described by Patel et al. (2012). The data include blood serum and urine biomarker measurements of 132 nutrients and persistent pesticides (agents). We consider three lipid levels as outcomes: 1) low-density lipoprotein-cholesterol (LDL), 2) high-density lipoprotein-cholesterol (HDL), and 3) triglyceride. In an EWAS analysis, Patel et al. (2012) screened these agents independently for their marginal associations with each of the three outcomes, controlling for a small set of pre-specified covariates but not other co-exposures. We perform a reanalysis of these data that extends to group-level analyses, pairwise interaction between agents, and adjustment for confounding by exposure to other agents.
We group the 132 agents into 24 mutually exclusive exposure groups of related agents, defined by Patel et al. (2012), that may affect the same biological pathways. We are interested in estimating the effect of a simultaneous 1 standard deviation increase in exposure to all agents on each of the three outcomes. We conduct separate analyses to estimate the exposure effect of each of the 24 groups on the three outcomes (72 models total). The multivariate exposure includes all agents within each of the 24 groups and their pairwise interactions. The potential confounders include: agents in the other groups that are measured in the same subsample; nine body measurements; and 13 demographic and socioeconomic status variables. Details on data processing and a list of potential confounders are included in Web Appendix D.
Table 2 shows the 24 exposure groups, the sample size (n ranging from 158 to 1370), number of agents in each group (m ranging from 1 to 22), and the number of potential confounders (k ranging from 22 to 92). The ratio p/n ranges from 0.03 to 0.77.
Table 2.
Summary of the NHANES data by exposure group. The table shows the total number of subjects with complete observations (n); the number of agents (m); the dimension of the multivariate exposure including the main effect of each agent and each two-way interaction (r); the total number of potential confounders including the main effect of agents in other groups (k); the total number of independent variables including the multivariate exposure, potential confounders, and an intercept (p = r + k + 1); and the p/n ratio.
| Exposure group | Sample size (n) |
# Agents (m) |
Dim(Z) (r) |
# Potential confounders (k) |
# Indep. variables (p) |
p to n
ratio (p/n) |
|---|---|---|---|---|---|---|
| Volatile compounds | 179 | 10 | 55 | 82 | 138 | 0.77 |
| pcbs | 558 | 22 | 253 | 59 | 313 | 0.56 |
| Phenols | 179 | 3 | 6 | 92 | 99 | 0.55 |
| Dioxins | 201 | 5 | 15 | 83 | 99 | 0.49 |
| Furans—dibenzofuran | 201 | 5 | 15 | 83 | 99 | 0.49 |
| pest.—pyrethyroid | 201 | 1 | 1 | 87 | 89 | 0.44 |
| Diakyl | 225 | 6 | 21 | 76 | 98 | 0.44 |
| pest.—phenols | 225 | 4 | 9 | 78 | 88 | 0.39 |
| pest.—chloroacetanilide | 225 | 1 | 1 | 81 | 83 | 0.37 |
| pest.—organophosphate | 225 | 1 | 1 | 81 | 83 | 0.37 |
| Heavy metals | 444 | 13 | 91 | 48 | 140 | 0.32 |
| Phthalates | 387 | 11 | 66 | 51 | 118 | 0.30 |
| pest.—organochlorine | 288 | 7 | 28 | 53 | 82 | 0.28 |
| Nutrients—minerals | 158 | 2 | 3 | 37 | 41 | 0.26 |
| Polyflourochemicals | 444 | 10 | 55 | 51 | 107 | 0.24 |
| Hydrocarbons | 292 | 9 | 45 | 22 | 68 | 0.23 |
| Phytoestrogens | 432 | 6 | 21 | 49 | 71 | 0.16 |
| Nutrients—vitamin C | 444 | 1 | 1 | 60 | 62 | 0.14 |
| Nutrients—carotenoid | 1370 | 5 | 15 | 33 | 49 | 0.04 |
| Nutrients—vitamin A | 1370 | 3 | 6 | 35 | 42 | 0.03 |
| Nutrients—vitamin B | 1370 | 3 | 6 | 35 | 42 | 0.03 |
| Nutrients—vitamin E | 1370 | 2 | 3 | 36 | 40 | 0.03 |
| Cotinine | 1370 | 1 | 1 | 37 | 39 | 0.03 |
| Nutrients—vitamin D | 1370 | 1 | 1 | 37 | 39 | 0.03 |
5.2. Estimate of the Multivariate Exposure Effect
We estimate the multivariate exposure effect with ACPME, the full model including all potential confounders, the unadjusted model that controls for no potential confounders, BMA, and BayesPen. Figure 3 presents the point estimates and 95% posterior intervals.
Figure 3.
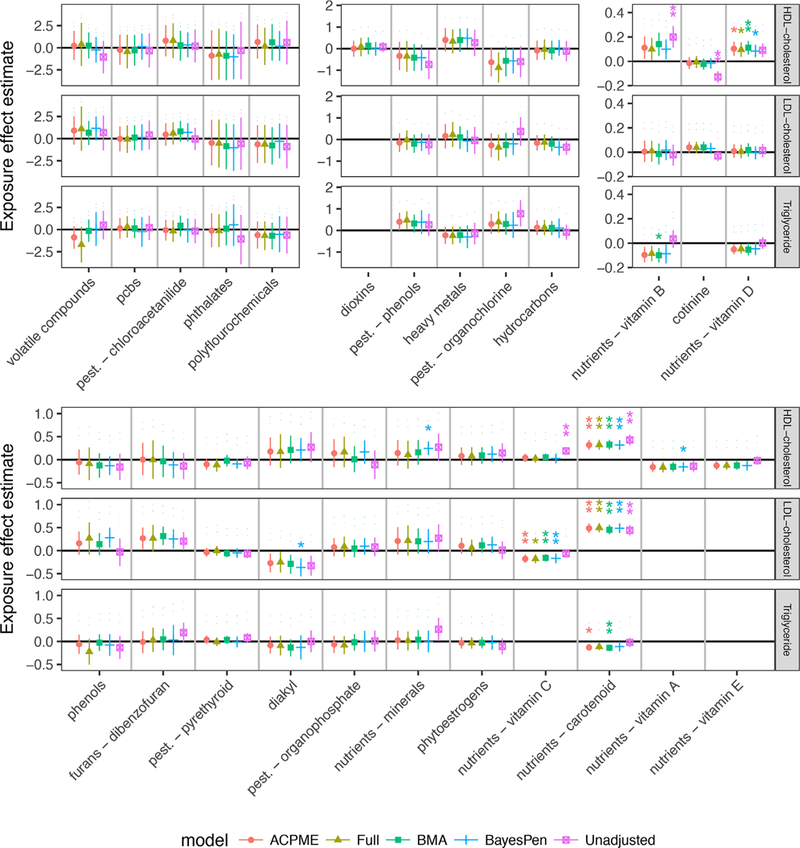
Point estimates and 95% credible intervals of the association between the multivariate exposure Z and each of the three outcome adjusted by the exposure to the other 23 groups and baseline covariates. Results are reported under the ACPME model, the full model (α = 1), the unadjusted model (α = 1), BMA, and BayesPen. Omitted estimates were flagged for potentially selection bias. The black asterisks indicate 0.05 (*) and 0.01 (**) significance levels after Bonferroni adjustment for multiple comparisons. Omitted estimates were flagged for potentially selection bias (see Web Appendix D for details). The four panels have different y-axis scales. This figure appears in color in the electronic version of this article.
To highlight the advantage of ACPME, we focus on the volatile compounds group. In this group, there are n = 179 individuals, k = 82 potential confounders, m = 10 agents and all 45 pairwise interactions (dim(Z) = 55), and the p to n ratio is 0.77 (138/177). The effect of volatile compounds on HDL and triglyceride both change sign with confounder adjustment using ACPME and with the full model relative to the unadjusted model. In addition, using ACPME resulted in approximately a 30% decrease in posterior standard deviation of ∆ compared to the full model for all three outcomes as shown in Figure 4.
Figure 4.
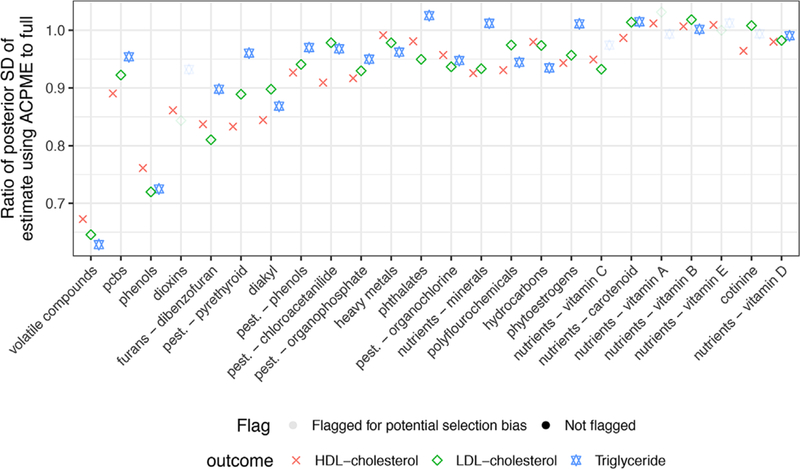
Ratio of the posterior standard deviation of exposure effect estimate under the ACPME model compared to the full model. Results are showed ranked by groups with the largest (left) to the smallest (right) p/n. In general, the estimates from ACPME have lower SD because of the reduced model size. Faded estimates were flagged for potentially selection bias (see Web Appendix D for details). This figure appears in color in the electronic version of this article.
Across all groups the ACPME point estimates are generally similar to the full model. This suggests that all important confounders are included using ACPME. In contrast, the unadjusted estimates are notably different in several cases. Relative to the full model, estimates with ACPME had smaller variance on average due to decreased model size (Figure 4).
Figure 3 also shows significance at the 0.05 and 0.01 posterior probability level after Bonferroni adjustment. Using the unadjusted model, four groups (carotenoid, vitamin B, vitamin C, and cottoning) had a statistically significant effect on HDL levels and one group (carotenoid) has a significant effect on LDL levels. Only the effects of carotenoid on HDL and LDL are significant after adjustment with ACPME and the fully adjusted model.
There are two cases where the posterior probability of a positive exposure effect substantially increased with ACPME compared to the full model. Vitamin C was significant for LDL at the 0.01 level using ACPME but only at the 0.05 level with the full model and not at all with the unadjusted model nor in the original analysis by Patel et al. (2012). Finally, the effect of vitamin D on HLD is significant at the 0.05 level only with ACPME.
5.3. Model Diagnostics
When using regression adjustment, it is imperative that the model is correctly specified as lack of balance can exacerbate sensitivity to model misspecification. We have assumed homoskedastic normal errors and a linear relationship between covariates and outcome. To assess whether these model assumptions are reasonable, we have plotted the standardized residuals verse the observed covariates (Cj’s), the standardized residuals verse the fitted values , and qq-plots (see Web Appendix D figures and further discussion). There were no signs of misspecification.
6. Discussion
We address the challenge of estimating the health effect of a multivariate exposure when there is uncertainty about which of the many measured covariates are confounders. When the number of observed covariates is large, it is imperative to identify a parsimonious model that is fully adjusted for confounding. We consider the special case of a multivariate exposure that includes several continuous agents and all their pairwise interactions. Using the BMA framework, we develop an informative prior on covariate inclusion to adjust for confounding. As shown by our simulation study, the proposed method identifies a parsimonious model that includes important confounders.
The proposed approach relies on specification of a parametric linear regression model, which is appealing in this situationbecause it naturally allows for estimation of the effect of a large multivariate exposure comprised of many agents and their interactions. Other approaches such as stratification based on the propensity function for each agent (e.g., Imai and van Dyk, 2004) require an unfeasible number of subclasses as the number of agents increases. The parametric regression model approach also permits the use of model-averaging computations and provides a framework for constructing the proposed prior distribution.
The proposed approach has limitations. There is an implicit assumption that the model is fully adjusted for confounding when all the observed covariates are included into the model as linear terms. This may not always be the case and the results could be prone other biases such as M-bias (Greenland, 2003). As such, the method can only be considered a causal estimator under fairly strict conditions. These include that the linear model is correctly specified and no unmeasured confounding.
The proposed approach is designed for a multivariate exposure with a large number of potential confounders that could be correlated with each other and also with the multivariate exposure. Our approach is challenged in the following situations. The first situation is when the potential confounders are very highly correlated with each other (e.g., a large number of pairwise correlations ≥0.8). In this situation, our proposed approach will lead to posterior inclusion probabilities that are spread across the group of correlated covariates and not concentrated on models that include the true confounders. This is a situation where BMA and many other variable selection approaches are also challenged. In this context, we could orthogonalize C which has been showed to improve BMA performance for prediction (Clyde et al., 1996). The second situation is when the true effect of Z on the outcome is null and the confounders are strongly associated with Z and weakly with Y. In this context, the model forces Z into the regression model despite being null and can under-adjust for confounding. Our simulations indicated that in this situation our approach has an increased type I error rate and some bias, but lower RMSE than the full model. To overcome this issue, we could choose a larger value of the tuning parameter to be conservative with confounder adjustment. The third situation is when and dimension of Z is large and always forced into the model. In this situation, the model also had increased type I error rate, but lower RMSE than the full model. Finally, when the sample size is very large relative to the total number of parameters no dimension reduction is needed and the full model can be used.
We applied the method to the previous analysis of Patel et al. (2012) which featured separate analyses of many agents grouped into multiple exposure groups (each group consisting of multiple related agents). To most closely parallel Patel et al. (2012), our reanalysis used the same groups but added group-level analyses, pairwise interactions between agents in each group, and adjusting for agents in other exposure groups. This presents an inconsistency with the required assumption that confounders be measured pre-exposure: volatile compounds cannot simultaneously be regarded “pre-exposure” in the analysis of phenols when a separate analysis regards phenols as “pre-exposure” in the analysis of volatile compounds. This should be regarded as a limitation of the data illustration designed to compare with the existing analysis of Patel et al. (2012), not as a general feature of the proposed method.
With increased availability of high-dimensional exposure data there is growing interest in understanding the effect of the exposome on complex diseases (Wild, 2005; Louis and Sundaram, 2012). However, there is often uncertainty as to which covariates to include in the model to estimate the multivariate exposure effect. The proposed method fills a methodological gap to adjust for confounding when estimating multivariate exposure effects.
Supplementary Material
Acknowledgements
Supported in part by NIH grants 1P50MD010428–01, K99ES023504, P01CA134294, R21ES025052, R21ES020152, R21ES024012, R21ES022585–01, R01ES019560, R01GM1 11339, R01ES024332, R01ES026217, R35CA197449, T32ES 007142, U54HG007963, and by HEI4909, HEI4953-RFA14–3/16–4, AHRQ HS021991, and PhRMA Foundation. This publication was made possible by USEPA grant RD-83587201–0. Its contents are solely the responsibility of the grantee and do not necessarily represent the official views of the USEPA. Further, USEPA does not endorse the purchase of any commercial products or services mentioned in the publication.
Footnotes
Supplemental Material
Web Appendices, Tables, and Figures referenced in Sections 2,3, 4, and 5 are available with this article at the Biometrics website on Wiley Online Library.
Software for ACPME is in the R package regimes available at anderwilson.github.io/regimes.
References
- Bobb JF, Valeri L, Claus Henn B, Christiani DC, Wright RO, Mazumdar M, et al. (2015). Bayesian kernel machine regression for estimating the health effects of multi-pollutant mixtures. Biostatistics 16, 493–508. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brookhart MA, Schneeweiss S, Rothman KJ, Glynn RJ, Avorn J, and Stürmer T (2006). Variable selection for propensity score models. American Journal of Epidemiology 163, 1149–56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brookhart MA and Van Der Laan MJ (2006). A semi-parametric model selection criterion with applications to the marginal structural model. Computational Statistics and Data Analysis 50, 475–498. [Google Scholar]
- Cefalu M, Dominici F, Arvold N, and Parmigiani G (2017). Model averaged double robust estimation. Biometrics 73, 410–421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clyde M, Desimone H, and Parmigiani G (1996). Prediction Via Orthogonalized Model Mixing. Journal of the American Statistical Association 91, 1197. [Google Scholar]
- Crainiceanu CM, Dominici F, and Parmigiani G (2008). Adjustment uncertainty in effect estimation. Biometrika 95, 635–651. [Google Scholar]
- Ghosh D, Zhu Y, and Coffman DL (2015). Penalized regression procedures for variable selection in the potential outcomes framework. Statistics in Medicine 34, 1645–1658. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greenland S (2003). Quantifying biases in causal models: Classical confounding vs collider-stratification bias. Epidemiology (Cambridge, Mass.) 14, 300–306. [PubMed] [Google Scholar]
- Hahn PR, Carvalho CM, Puelz D, and He J (2016). Regularization and confounding in linear regression for treatment effect estimation. Bayesian Analysis 13, 1–20. [Google Scholar]
- Hernán MA, Brumback B, and Robins JM (2001). Marginal structural models to estimate the joint causal effect of non randomized treatments. Journal of the American Statistical Association 96, 440–448. [Google Scholar]
- Hirano K and Imbens GW (2001). Estimation of causal effects using propensity score weighting: An application to data on right heart catheterization. Health Services & Outcomes Research Methodology 2, 259–278. [Google Scholar]
- Imai K and van Dyk DA (2004). Causal inference with general treatment regimes. Journal of the American Statistical Association 99, 854–866. [Google Scholar]
- Imbens GW (2000). The role of the propensity score in estimating dose-response functions. Biometrika 87, 706–710. [Google Scholar]
- Kreif N, Grieve R, Díaz I, and Harrison D (2015). Evaluation of the effect of a continuous treatment: A machine learning approach with an application to treatment for traumatic brain injury. Health Economics 24, 1213–1228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lefebvre G, Atherton J, and Talbot D (2014). The effect of the prior distribution in the Bayesian adjustment for confounding algorithm. Computational Statistics and Data Analysis 70, 227–240. [Google Scholar]
- Louis GMB and Sundaram R (2012). Exposome: Time for transformative research. Statistics in Medicine 31, 2569–2575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lunceford JK and Davidian M (2004). Stratification and weighting via the propensity score in estimation of causal treatment effects: A comparative study. Statistics in Medicine 23, 2937–2960. [DOI] [PubMed] [Google Scholar]
- Patel CJ, Cullen MR, Ioannidis JP, and Butte AJ (2012). Systematic evaluation of environmental factors: Persistent pollutants and nutrients correlated with serum lipid levels. International Journal of Epidemiology 41, 828–843. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patel CJ and Ioannidis JPA (2014). Studying the elusive environment in large scale. Journal of the American Medical Association 311, 2173–2174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patel CJ, Rehkopf DH, Leppert JT, Bortz WM, Cullen MR, Chertow GM, et al. (2013). Systematic evaluation of environmental and behavioural factors associated with all-cause mortality in the united states national health and nutrition examination survey. International Journal of Epidemiology 42, 1795–1810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raftery AE, Madigan D, and Hoeting JA (1997). Bayesian model averaging for linear regression models. Journal of the American Statistical Association 92, 179. [Google Scholar]
- Robins J (1986). A new approach to causal inference in mortality studies with a sustained exposure periodapplication to control of the healthy worker survivor effect. Mathematical Modelling 7, 1393–1512. [Google Scholar]
- Rubin DB (1978). Bayesian inference for causal effects: The role of randomization. The Annals of Statistics 6, 34–58. [Google Scholar]
- Schwarz G (1978). Estimating the dimension of a model. The Annals of Statistics 6, 461–464. [Google Scholar]
- Taubman SL, Robins JM, Mittleman MA, and Hernán MA (2009). Intervening on risk factors for coronary heart disease : An application of the parametric g-formula. International Journal of Epidemiology 38, 1599–1611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van der Laan MJ and Rose S (2011). Targeted Learning: Causal Inference for Observational and Experimental Data. New York, NY: Springer-Verlag. [Google Scholar]
- VanderWeele TJ and Shpitser I (2013). On the definition of a confounder. The Annals of Statistics 41, 196–220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vansteelandt S, Bekaert M, and Claeskens G (2012). On model selection and model misspecification in causal inference. Statistical Methods in Medical Research 21, 7–30. [DOI] [PubMed] [Google Scholar]
- Wang C, Dominici F, Parmigiani G, and Zigler CM (2015). Accounting for uncertainty in confounder and effect modifier selection when estimating average causal effects in generalized linear models. Biometrics 71, 654–665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang C, Parmigiani G, and Dominici F (2012). Bayesian effect estimation accounting for adjustment uncertainty. Biometrics 68, 661–71. [DOI] [PubMed] [Google Scholar]
- Wild CP (2005). Complementing the genome with an “expo-some”: The outstanding challenge of environmental exposure measurement in molecular epidemiology. Cancer Epidemiology Biomarkers and Prevention 14, 1847–1850. [DOI] [PubMed] [Google Scholar]
- Wilson A and Reich BJ (2014). Confounder selection via penalized credible regions. Biometrics 70, 852–861. [DOI] [PubMed] [Google Scholar]
- Yuan M and Lin Y (2005). Efficient empirical Bayes variable selection and estimation in linear models. Journal of the American Statistical Association 100, 1215–1225. [Google Scholar]
- Zanobetti A, Austin E, Coull BA, Schwartz J, and Koutrakis P (2014). Health effects of multi-pollutant profiles. Environment International 71, 13–19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zigler CM and Dominici F (2014). Uncertainty in propensity score estimation: Bayesian methods for variable selection and model-averaged causal effects. Journal of the American Statistical Association 109, 95–107. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


