Genomic SEM Provides Insights into the Multivariate Genetic Architecture of Complex Traits

Abstract

Genetic correlations estimated from GWAS reveal pervasive pleiotropy across a wide variety of phenotypes. We introduce genomic structural equation modeling (Genomic SEM), a multivariate method for analyzing the joint genetic architecture of complex traits. Genomic SEM synthesizes genetic correlations and SNP-heritabilities inferred from GWAS summary statistics of individual traits from samples with varying and unknown degrees of overlap. Genomic SEM can be used to model multivariate genetic associations among phenotypes, identify variants with effects on general dimensions of cross-trait liability, calculate more predictive polygenic scores, and identify loci that cause divergence between traits. We demonstrate several applications of Genomic SEM, including a joint analysis of summary statistics from five psychiatric traits. We identify 27 independent SNPs not previously identified in the contributing univariate GWASs. Polygenic scores from Genomic SEM consistently outperform those from univariate GWAS. Genomic SEM is flexible, open ended, and allows for continuous innovation in multivariate genetic analysis.

Genomic Structural Equation Modeling

Genome-wide association studies (GWASs) are rapidly identifying loci affecting multiple social, behavioral, and psychiatric phenotypes.^1,2 Moreover, using cross-trait versions of methods such as genomic-relatedness-based restricted maximum-likelihood (GREML)³ and LD-score regression (LDSC)⁴ researchers have identified genetic correlations between diverse traits, e.g., age of first birth and risk of smoking,⁵ insomnia and psychiatric traits (e.g., schizophrenia),⁶ major depressive disorder and number of children,⁷ and educational attainment and cognitive performance.⁸ Widespread statistical pleiotropy appears to be the rule rather than the exception across complex traits. Although these findings are currently suggestive of constellations of phenotypes affected by shared sources of genetic liability, existing methods do not permit the causes of the observed genetic correlations to be investigated systematically. Here we introduce Genomic Structural Equation Modeling (Genomic SEM), a new method for modeling the multivariate genetic architecture of constellations of traits and incorporating genetic covariance structure into multivariate GWAS discovery. Genomic SEM is a flexible framework for formally modeling the genetic covariance structure of complex traits using GWAS summary statistics from samples of varying and potentially unknown degrees of overlap, in contrast to existing methods that model phenotypic covariance structure,⁹ with specific applications,¹⁰ using raw data. Moreover, Genomic SEM allows for the specification and comparison of a range of proposed multivariate genetic architectures, which improves upon existing approaches for combining information across genetically correlated traits to aid in discovery.¹¹

One powerful feature of Genomic SEM is the capability to model shared genetic architecture across phenotypes with factors representing broad genetic liabilities, and compare the fit of different factor structures to the empirical data. When an appropriate model has been identified at the level of the genome-wide covariance structure, the researcher may incorporate individual SNPs into the model in order to identify variants with effects on general dimensions of cross-trait liability, boost power for discovery, and calculate more valid and predictive polygenic scores. Genomic SEM can also evaluate whether the multivariate genetic architecture implied by a specific model is applicable at the level of individual variants using developed estimates of heterogeneity. When certain SNPs only influence a subset of genetically correlated traits, a key assumption of other multivariate approaches is violated.¹¹ SNPs with high heterogeneity estimates can be flagged as likely to confer disproportionate liability toward individual traits, be removed when constructing polygenic risk scores, or be studied specifically to understand the nature of heterogeneity.

We validate key properties of Genomic SEM with a series of simulations and illustrate the flexibility and utility of Genomic SEM with analyses of real data. These include a joint analysis of GWAS summary statistics from five genetically correlated psychiatric case-control traits: schizophrenia, bipolar disorder, major depressive disorder (MDD), post-traumatic stress disorder (PTSD), and anxiety. We model their joint genetic architecture using a general factor of psychopathology (p), for which we identify 27 independent SNPs not previously identified in the univariate GWASs, 5 of which can be validated based on separate GWASs. Polygenic scores derived using this p-factor consistently outperform polygenic scores derived from GWASs of the individual traits in out-of-sample prediction of psychiatric symptoms. Other demonstrations include a multivariate GWAS of neuroticism items, an exploratory factor analysis of anthropometric traits, and a simultaneous analysis of the unique genetic associations between schizophrenia, bipolar disorder, and educational attainment.

Results

Genomic SEM is a Two-Stage Structural Equation Modeling approach.^12–14 In Stage 1, the empirical genetic covariance matrix and its associated sampling covariance matrix are estimated. The diagonal elements of the sampling covariance matrix are squared standard errors (SEs). The off-diagonal elements index the extent to which sampling errors of the estimates are associated, as may be the case when there is sample overlap across GWASs. In Stage 2, a SEM is specified and parameters are estimated by minimizing the discrepancy between the model-implied genetic covariance matrix and the empirical covariance matrix obtained in the previous stage. We evaluate fit with the standardized root mean square residual (SRMR), model χ², Akaike Information Criteria (AIC), and Comparative Fit Index (CFI; Method).^13,15 In a set of simulations we verify key properties of Genomic SEM (Method). We find that Genomic SEM produces unbiased parameter estimates when the correct structural model is specified, and that model fit indices consistently favor the correct model over alternative models. In a second set of simulations, we demonstrate that the inclusion of data from overlapping samples does not bias Genomic SEM parameter estimates or their standard errors.

Genomic SEM can be employed as a tool for multivariate GWAS based on univariate summary statistics. First, the genetic covariance matrix and its associated sampling covariance matrix are expanded to include SNP effects. A Genomic SEM is then specified in which SNP effects occur at the level of a latent genetic factor defined by several phenotypes, at the level of the genetic components of each of several (potentially genetically correlated) phenotypes, or some combination of the two. The Genomic SEM is then run once per SNP (or each set of SNPs, should the user incorporate multiple SNPs into a model) to obtain its effects within the multivariate system.

We provide an index that quantifies the extent to which an observed vector of univariate regression effects of a given SNP on each of the phenotypes can be explained by a common pathway model that assumes that the effects are entirely mediated by the common genetic factor(s). In other words, the index enables the identification of loci that do and do not plausibly operate on the individual phenotypes exclusively by way of their associations with the common factor(s). Because of its intuitive and mathematical similarity to the meta-analytic Q-statistic used in standard meta-analyses to index heterogeneity of effect sizes¹⁶ we label this heterogeneity statistic, Q_SNP. Q_SNP is a χ²-distributed test statistic with larger values indexing a violation of the null hypothesis that the SNP acts entirely through the common factor(s).

Confirmatory Factor Analysis of Genetic Covariance Matrices

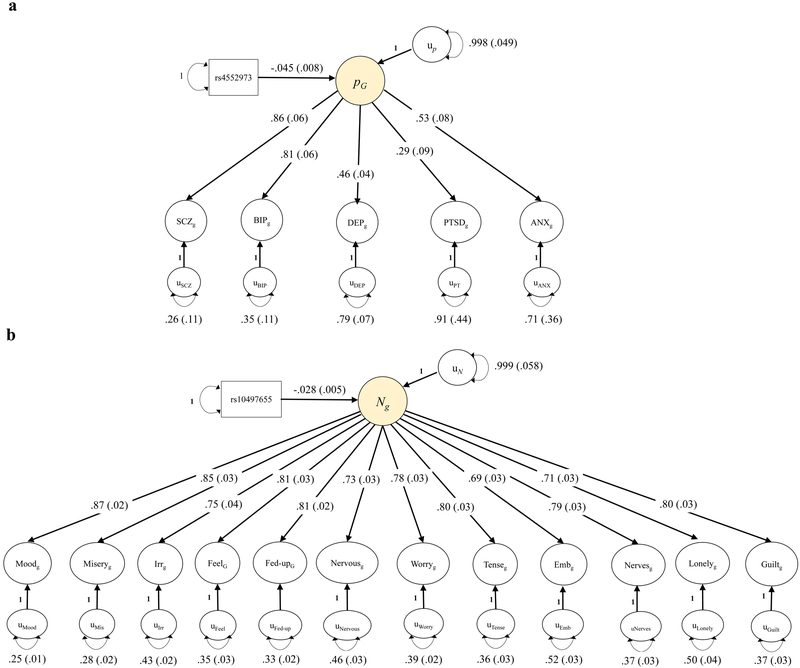
We provide two examples of confirmatory factor analysis (CFA) using Genomic SEM. In our first example, we fit a genetic factor model to psychiatric case-control traits. Recent findings indicate that the comorbidity across psychiatric disorders is captured by a general psychopathology factor (i.e., the p-factor) and is widely supported based on previous results.^17–21 We tested for the presence of a single common genetic p-factor using Genomic SEM with European-only summary statistics for schizophrenia, bipolar disorder, major depressive disorder (MDD), post-traumatic stress disorder (PTSD), and anxiety (Table S1 for phenotypes and sample sizes). Model fit was adequate (χ²[5] = 89.55, AIC = 109.50, CFI = .848, SRMR = .212). Results indicated that schizophrenia and bipolar disorder loaded the strongest onto the genetic p-factor (Supplementary Figure 1), a pattern of findings that closely replicates prior findings from twin/family studies.¹⁹

In a second example, we tested for the presence of a single common genetic factor of neuroticism using summary statistics from 12 item-level indicators from UK Biobank (UKB; Supplementary Table 1) as estimated using the Hail software.²² Model fit was good (χ²[54] = 4884.10, AIC =4932.11, CFI = .893, SRMR = .109). Results indicated strong positive loadings for all indicators (Supplementary Figure 2). We used this single common factor model for both neuroticism and the p-factor when estimating SNP effects for discovery under the section SNP Effects, below.

Exploratory Factor Analysis of a Genetic Covariance Matrix

We provide two examples of how one might use exploratory methods to guide the specification of more nuanced factor models. In the first example, we submitted the LDSC-derived genetic correlation matrix of the 12 neuroticism items in UKB to exploratory factor analysis (EFA; see Supplementary Results). Based on these initial EFA results, follow-up CFAs (Supplementary Figure 3) were specified using Genomic SEM (standardized loadings > .4 were retained; Supplementary Table 2). The two-factor solution (χ²[53] = 2758.18, AIC = 2808.18, CFI = .940, SRMR = .077) and three-factor solution (χ²[51] = 1879.31, AIC = 1933.31, CFI = .959, SRMR = .057) both provided excellent fit to the data and exceeded the fit of the single, common factor model. Consistent with the superior model fit indices for the two- and three-factor solutions, only 28 and 20 of the 69 Q_SNP hits from the single common factor model (described in further detail, under the SNP Effects section, below) continued to surpass genome-wide significance for the two- and three-factor models, respectively (Supplementary Figure 4; Supplementary Table 3). In addition, a GWAS of all HapMap3 SNPs for the two- and three-factor models revealed the average size of Q_SNP across all SNPs was largest for the common factor (χ²[1] = 1.68), followed by the two-factor (χ²[1] = 1.64), and three-factor model (χ²[1] = 1.51). Thus, heterogeneity indices of individual SNP effects in the GWAS data agree with model fit indices, with both favoring the three-factor model of neuroticism.

In the second example, EFA was applied to the LDSC-derived genetic correlation matrix for nine anthropometric traits from the EGG and GIANT consortia (Supplementary Table 4). EFA results indicated that two factors explained 61% of the total genetic variance. Moreover, a heatmap of the genetic correlation matrix suggests two primary factors that index overweight and early life-growth phenotypes (Supplementary Figure 5). A follow-up CFA (Supplementary Figure 6) within Genomic SEM was specified based on the EFA parameter estimates (standardized loadings > .25 were retained). The CFA showed good fit to the data (χ²[25] = 12994.71, AIC = 13034.71, CFI = .962, SRMR = .092). Results indicated highly significant loadings, and a small correlation between the two factors (r_g = .10, SE = .03, p < .001). This indicates that early life physical growth is modestly associated with later life obesity traits via genetic pathways.

Genetic Multivariable Regression (Replicating GWIS)

Nieuwboer et al. (2016)²³ use summary statistics for educational achievement (EA)²⁴ and both schizophrenia and bipolar disorder²⁵ to determine if genetic correlations with EA are driven by variation specific to either disorder. EA is genetically correlated with schizophrenia (r_g = .148, SE = .050, p = .003) and bipolar disorder (r_g = .273, SE = .067, p < .001). Using a method called genome-wide inferred statistics (GWIS), they find that the correlation of EA with schizophrenia unique of bipolar is small (r_g = .040, SE = .082, p = .627), whereas the genetic correlation between bipolar unique of schizophrenia and EA is far less attenuated (r_g = .218, SE = .102, p = .032). We use Genomic SEM with the aim of replicating these results using a conceptually similar, but statistically distinct, framework. We present this example to demonstrate that Genomic SEM is not limited to factor analytic models, but can be used to construct and test an array of hypotheses using a general SEM approach.

Using the same univariate GWAS summary statistics employed in the original application of GWIS, we used Genomic SEM to fit a structural multivariable regression model in which the genetic component of EA was simultaneously regressed onto the genetic components of schizophrenia and bipolar disorder. Results confirmed the findings by Nieuwboer et al. (2016);²³ the conditional standardized association between schizophrenia and EA was small (b_g = −.016, SE = .096, p = .867), whereas there was a strong conditional standardized association between bipolar disorder and EA (b_g = .283, SE = .113, p = .012; Supplementary Figure 7).

SNP Effects

Common Factor Models.

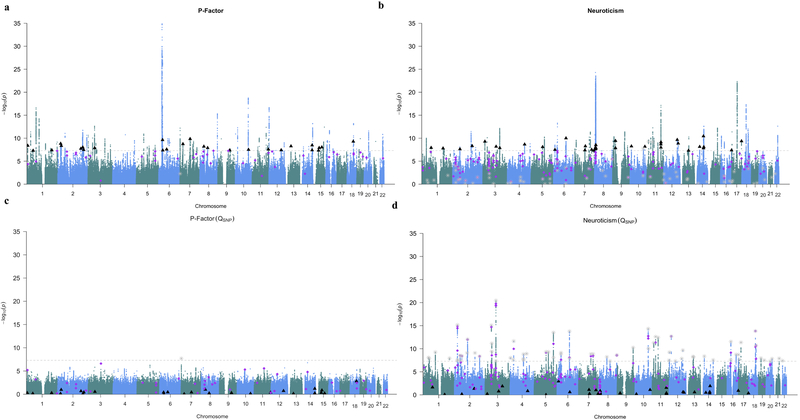
A powerful application of Genomic SEM is to include individual SNP effects in both the genetic covariance matrix and the sampling covariance matrix, in order to estimate the effect of a given SNP on the latent genetic factor(s). If the summary statistics are composed of M different SNPs, then M models are estimated to obtain genome-wide summary statistics for the latent factor. As an example of Genomic SEM used for multivariate GWAS, we incorporated SNP effects into the p-factor and neuroticism models presented above. LD-independent hits are defined below as r² < .1 in a 500Kb window, with the exception of a 1Mb window for chromosomes 6 and 8. 128 independent loci were genome-wide significant for the p-factor (p < 5 × 10⁻⁸; Supplementary Figures 8–10; Figure 1a, Figure 2a). Of the 128 loci, 27 independent loci were not previously identified in any of the contributing univariate GWASs (Table 1, Supplementary Table 5). Of these 27 loci, five loci were identified as either genome-wide significant or suggestive of significance (p < 1 × 10⁻⁵) in a separate, previously published GWAS of one of the five traits. 118 loci were genome-wide significant for neuroticism, with 38 loci not identified in the univariate item-level GWASs (Supplementary Table 6; Figure 1b, Figure 2b). Plots of item-level effects for individual SNPs revealed high consistency in magnitude and direction for SNPs identified as genome-wide significant for the common factors (Supplementary Figure 11). Although there is early lift-off in the QQ-plots for both common factors, LDSC analyses of the summary statistics produced by Genomic SEM indicated that results were not due to uncontrolled inflation for either the p-factor (intercept = .987, SE = .014) or neuroticism (intercept = .997, SE = .001).

Figure 1. Genomic SEM solutions for p-factor and neuroticism factor models with SNP effect.

Standardized results from using Genomic SEM (with WLS estimation) to construct a genetically defined p-factor of psychopathology (panel a) and a genetic neuroticism factor (panel b) with a lead independent SNP predicting the factors. SEs are shown in parentheses. For a model that was standardized with respect to the outcomes only, the effect of the SNP was −.093 (SE = .017; SNP variance = .252) for the p-factor, and for neuroticism the SNP effect was −.042 (SE = .007, SNP variance = .432); this can be interpreted as the expected standard deviation unit difference in the latent factor per effect allele. SCZ = schizophrenia; BIP = bipolar disorder; DEP = major depressive disorder; PTSD = post-traumatic stress disorder; ANX = anxiety. Irr = irritability; Feel = sensitivity/hurt feelings; fed-up = fed-up feelings; emb = worry too long after embarrassment.

Figure 2. Manhattan plots of unique, independent hits from Genomic SEM.

Genomic SEM (with WLS estimation) was used to conduct multivariate GWASs of the p-factor (panels a and c) and neuroticism (panels b and d). Manhattan plots are shown for SNP effects (top panels) and for Q_SNP (bottom panels). The gray dashed line marks the threshold for genome-wide significance (p < 5 × 10⁻⁸). In all four panels, black triangles denote independent hits for SNP effects from the GWAS of the general factor that were not in LD with independent hits for the univariate GWAS or hits for Q_SNP. In all four panels, purple diamonds denote independent hits for the SNP effects from univariate GWASs that were not in LD with independent hits from the GWAS of the general factor. Grey stars denote independent hits for Q_SNP.

Table 1.

Summary of multivariate (Genomic SEM) and univariate GWAS results.

	Lead SNPs (p < 5 × 10−8)	QSNP hits	Unique Hits	No. of gene sets	No. prioritized genes	No. tissues and cells	Mean χ2
P-Factor
Genomic SEM (WLS)	128	1 (1)	27	71	37	24	1.88
Schizophrenia	127	-	34 (0)	2	25	21	1.82
Bipolar	4	-	4 (0)	0	0	0	1.15
MDD	5	-	5 (0)	0	0	0	1.31
PTSD	0	-	0 (0)	0	0	0	1.01
Anxiety	1	-	1 (0)	0	0	0	1.03
Neuroticism
Genomic SEM (WLS)	118	69 (5)	38	1	19	20	1.64
Mood	43	-	19 (5)	0	0	15	1.37
Misery	31	-	6 (4)	0	0	0	1.32
Irritability	36	-	17 (4)	0	0	0	1.37
Hurt Feelings	24	-	11 (0)	0	0	0	1.33
Fed-up	38	-	21 (6)	0	0	0	1.36
Nervous	41	-	25 (12)	0	0	0	1.36
Worry	56	-	26 (6)	0	13	0	1.46
Tense	19	-	10 (3)	0	0	0	1.32
Embarrass	17	-	6 (2)	0	0	0	1.33
Nerves	12	-	7 (3)	0	0	0	1.26
Lonely	6	-	4 (3)	0	0	0	1.19
Guilt	21	-	8 (1)	0	0	0	1.28

Note. In parentheses for Q_SNP reports how many Q_SNP hits were in LD with hits identified as significant for the common factor. Unique hits for the common factor refers to lead SNPs that were not in LD with hits for the individual indicators. Unique hits for the individual indicators refers to hits for the respective indicator that were not in LD with hits for the common factor. Unique hits for the common factor excluded hits in LD with Q_SNP hits. For unique hits for indicators, values in parentheses indicate whether any of these hits were identified as significant for Q_SNP. For unique hits for the common factor, hits were excluded that were in LD with previously reported indicator hits that were removed due to missing values across the other phenotypes. The single Q_SNP hit for WLS estimation of the p-factor was significant for both the common factor and schizophrenia. For the common factor and the indicators, independent hits were defined using a pruning window of 500Kb and r² > 0.1. For chromosomes 6 and 8, an additional pruning filter was used of 1Mb and r² > 0.1 to account for long-range LD due to the MHC region and pericentric inversion, respectively. For univariate statistics, we used only the SNPs present across all indicators in order to facilitate a direct comparison to Genomic SEM results.

General Trends.

Mean χ² statistics were higher for the Genomic SEM-derived summary statistics of common factors relative to univariate indicators (Table 1). It is important to note here that, whereas Genomic SEM may boost power in many cases, this is not the primary purpose of the method. Rather, it is to identify the relationship between SNPs and observed phenotypes as meditated through a user-specified model and to concurrently evaluate the construct validity of said model. Inspecting the distribution of univariate p-values for the newly identified SNPs for the general factors indicated that these SNPs were generally characterized by relatively low p-values, albeit not low enough to cross the genome-wide significance threshold for any individual phenotype (Supplementary Figures 12–13).

Q_SNP Results.

Results revealed 1 and 69 independent Q_SNP loci for the p-factor and neuroticism, respectively (Figure 2c and Figure 2d; Supplementary Figure 14). For neuroticism, significant Q_SNP estimates were obtained for SNPs that were highly significant for some traits but not others (Supplementary Table 7; Supplementary Figure 15). The association between p-values for SNP effects and Q_SNP estimates were minimal (Supplementary Figure 16). Comparing the Q_SNP estimates for SNPs identified as significant for only the p-factor or neuroticism relative to SNPs identified as significant for one of the indicators, but not the common factor, indicated that the latter group of SNPs were characterized, as would be expected, by larger Q_SNP estimates (i.e., greater heterogeneity in individual effects; Supplementary Figure 17). Intercepts from LDSC analyses of the Q_SNP statistics also indicated that results for the heterogeneity index were not attributable to inflation (p-factor: intercept = .978, SE = .009; neuroticism: intercept = .963, SE = .009). Slopes from the same LDSC analyses further indicated genetic signal in heterogeneity (p-factor: Z = 13.65, p-value = 6.68E-42; neuroticism: Z = 30.23, p-value = 9.98E-201).

Comparison to MTAG.

Existing multivariate methods use summary statistics of genetically correlated phenotypes to boost power for discovery and prediction for a particular trait.^11,26,27 Boosting power is only one application of Genomic SEM. That said, a Genomic SEM common factor GWAS approach has already been shown by an independent research group to perform comparably to existing multivariate approaches for out-of-sample prediction.²⁸ Moreover, as a flexible modeling framework, Genomic SEM may encompass other multivariate approaches. For example, we show mathematically that Genomic SEM can be specified to satisfy the same moment conditions as multi-trait analysis of GWAS (MTAG¹¹; see Supplementary Methods). Simulation results also revealed near perfect correspondence from a linear regression in which Z statistics from MTAG were used to predict those from a Genomic SEM specified to satisfy the MTAG moment conditions (Supplementary Figure 18; unstandardized slope = .999, intercept = 2.65E-4).

Performance in Empirical Data under Controlled Missingness.

We contrast estimates obtained from the common factor model of neuroticism described above with estimates for a GWAS with an imposed missing structure. We first transformed the binary scale neuroticism items into a smaller number of quantitative scores. To do so, we created three parcels of neuroticism items consisting of 4 items each with scores ranging from 0 to 4, at which point it is appropriate to treat the parcel as continuous.²⁹ Parcels were constructed based on the same EFA results described above and mirrored the composition of the three-factor model, with the exception that the irritability item was included with parcel 2 so as to have an equal distribution of 4 items per parcel. Of the 300,000 participants, 100,000 non-overlapping participants were removed from two of the three parcels for missing data models. The best powered results (indexed by mean χ² values) were for Genomic SEM of the individual neuroticism items presented above, indicating that construction of composite indices via averaging, though convenient, removes multivariate information that can otherwise be retained with Genomic SEM (Supplementary Table 8). Genomic SEM analyses that incorporated supplemental information from parcels containing imposed missing data consistently outperformed GWAS of individual parcels with complete data, and performed nearly as well as analyses of complete data across all three parcels. Thus, inclusion of summary data from genetically correlated, phenotypes in Genomic SEM may boost power relative GWAS of the individual phenotypes, even when there is high sample overlap and sample sizes are uneven across phenotypes.

Parcel Comparison of Q_SNP.

Using the three constructed parcels without any missing data, the distribution of p-values was compared across SNPs with high (p < 5e-8) and low (p > 5e-3) Q_SNP estimates from the item-level Genomic SEM analysis of neuroticism for SNPs that were genome-wide significant in at least one of the parcels. These results indicated that, for SNPs with a higher Q_SNP for the common factor, there was more discordance of effect sizes among three lower-order factors relative to SNPs that produced lower heterogeneity estimates (Supplementary Figure 19). The average difference between the highest and lowest –log10 p-values was 10.56 and 4.96 for high and low Q_SNP, respectively. This suggests that Q_SNP is appropriately indexing discordance in SNP level effects across genetically correlated indicators.

Polygenic Prediction.

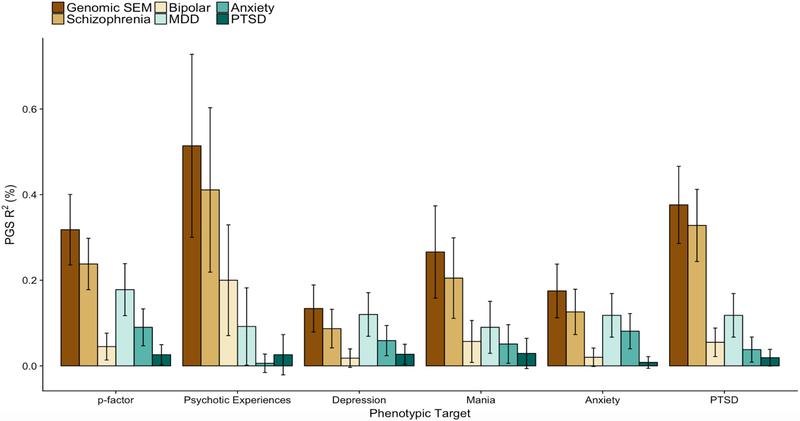
We re-estimated the p-factor model using the summary statistics from the SCZ and MDD GWASs that did not overlap with the UKB dataset, in order to predict psychiatric symptoms in UKB (Supplementary Figure 20 for phenotypic model). In order to produce a reliable set of targets for polygenic prediction, and to focus our analyses on construct validation, latent factors of psychiatric symptoms were specified as the out-of-sample targets. We compared the magnitude of out-of-sample-prediction for the p-factor PGSs predicting the phenotypic p-factor and factors of individual psychiatric domains relative to the prediction using PGSs derived from univariate summary statistics (Figure 3, Supplementary Table 9). The PGSs for the genetic p-factor predicted more variance in symptoms of depression, psychotic experiences, mania, anxiety, PTSD and a phenotypic p-factor than any univariate PGS.

Figure 3. Out-of-sample prediction using Genomic SEM based and univariate based polygenic scores for psychiatric traits.

Polygenic scores (PGSs) were constructed using the same set of SNPs for all predictors. R² (%) on the y-axis indicates the percentage of variance (possible range: 0-100) explained in the outcome unique of covariates. The summary statistics for Genomic SEM were estimated using WLS. The Genomic SEM-based PGS was derived from a model estimating SNP effects on a common “p”-factor, constructed from SCZ, BIP, MDD, PTSD, and ANX (as in Fig. 1a.). In order to prevent bias, the Genomic SEM summary statistics were produced using SCZ and MDD GWAS summary statistics that did not include UKB participants. Error bars indicate 95% confidence intervals estimated using the delta method. Phenotypes were constructed for European participants in the UKB for five symptom domains and for a general p factor spanning all five symptom domains.

For neuroticism, univariate PGSs were constructed in data from the Generation Scotland study using summary statistics for the 12 neuroticism items, the Genomic SEM factor of items, the three neuroticism parcels, the Genomic SEM factor of parcels, and the neuroticism sum score. We used PGSs to predict a sum score composed of the same neuroticism items administered in UKB. We also calculated mean χ² values for each of these summary statistics, which we used to infer their relative power. Of all the summary statistics considered, summary statistics derived from a Genomic SEM analysis of a common factor of the neuroticism items produced both the largest mean χ² in the summary statistics and predicted the greatest variance in the out-of-sample phenotype (Supplementary Figure 21). In both cases, the superior performance of Genomic SEM analysis of the common factor of items relative to the sum score of the items is likely, in part, a reflection of the fact that the sum score in UKB was created using listwise deletion, resulting in a reduced sample size of 274,008. Conversely, Genomic SEM uses all available information from neuroticism items, with sample sizes of ~325,000 each. In more severe cases of sample non-overlap, we would expect even larger power benefits of Genomic SEM-derived summary statistics relative to individual items or sum scores. Indeed, in instances of minimal sample overlap, it is not possible to compute sum scores, but Genomic SEM can still be used to integrate data across phenotypes.

Biological Annotation.

The biological function of the SNPs related to the p-factor and neuroticism was examined using DEPICT.³⁰ Table 1 presents the number of enriched gene sets, prioritized genes, and enriched tissues and cell types across the univariate statistics and common factors (Supplementary Tables 10–18 for detailed output). Common factors produced more informative results than the individual indicators. As expected, all of the tissue enrichment for the common factors was identified in the nervous system (Supplementary Figure 22). Neuroticism prioritized genes indicated a central role of synaptic activity (e.g., STX1B, NR4A2, PCLO), including glutamatergic neurotransmission (GRM3). The p-factor gene sets were largely characterized by communication between neurons (e.g., “dendrite development”, “dendritic spine”, “abnormal excitatory postsynaptic potential”). Biological annotation of Q_SNP statistics for neuroticism indicated that genes within the 69 loci related to neuroticism, but not through a single factor, include: GRIA1, a glutamate receptor subunit (i.e. involved in signaling is excitatory neurons) which has previously been related to schizophrenia,³¹ chronotype,³² and autism;³³ and PCDH17, a gene involved in cellular connections in the brain that has been related to intelligence.³⁴

General Guidelines

When implementing Genomic SEM, users should be aware of the limitations and assumptions of the method. First, because Genomic SEM is a method for modeling genetic covariance matrices, it relies on the same assumptions as the method used to estimate genetic covariances, and best practices for implementing such method should be followed. For example, when LDSC is used to construct the genetic covariance matrix, SNPs should not first be pruned for linkage disequilibrium, and summary statistics for different phenotypes should be obtained from ethnically homogeneous samples of similar ancestral backgrounds.⁴ With respect to selecting between competing models, users should take into account a variety of both absolute fit (e.g. SRMR and model χ²) and relative fit indices (e.g. AIC and χ² difference). We provide general standards for absolute model fit in the Method section. Finally, a formal power analysis should take into account specific characteristics of the summary data, the genetic architecture of the phenotypes, and the model to be specified. This can typically be achieved with simulation. Generally speaking, we would expect power to detect SNP effects on a common genetic factor to be high when the phenotypes composing the factor have high heritabilities, and high genetic correlations, sample sizes are larger and sample overlap is lower. That said, we still expect some power benefits relative to univariate GWAS when the constituent phenotypes are only moderately heritable and/or moderately genetically correlated and/or sample overlap is high. The choice of included summary statistics, phenotypes, and model(s) will of course depend on the researcher’s objectives and the model(s) to be specified.

Discussion

Applications of genome-wide methods to data from large scale population-based samples have uncovered clear evidence of pervasive statistical pleiotropy. Genomic SEM is a method for modeling the multivariate genetic architecture of constellations of genetically correlated traits and incorporating genetic covariance structure into multivariate GWAS discovery. In contrast to methods⁹ that model phenotypic, rather than genetic covariance structure, and rely on raw data, Genomic SEM employs summary GWAS data to model genetic covariance structure. Genomic SEM is computationally efficient, accounts for potentially unknown degrees of sample overlap, and allows for flexible specification of covariance structure, such that several broad classes of structured covariance models can be applied. The Genomic SEM approach shares benefits of some existing approaches¹¹ for boosting power by combining information across genetically correlated phenotypes. However, Genomic SEM uniquely allows one to compare different hypothesized genetic covariance architectures and to incorporate such architectures into multivariate discovery. Importantly, shared genetic liabilities across phenotypes can be explicitly modeled as factors that may be treated as broad genetic risk factors with equally broad downstream consequences. Multivariate genetic methods have existed for decades in the twin literature, with Martin and Eaves (1977)³⁵ providing a framework for fitting structural equation models of genetic and environmental variance components to multivariate twin data. Using GWAS summary data from unrelated individuals, Genomic SEM can be used to estimate multivariate genetic models similar to those from the existing twin literature. Moreover, Genomic SEM offers new promise as a method that allows for modeling genetic covariance even among phenotypes for which phenotypic covariance cannot be estimated.

Genomic SEM is not the first method for multivariate GWAS. Other methods, such as MTAG,¹¹ SHom/SHet,³⁶ metaUSTAT,³⁷ min-P,³⁸ and TATES²⁷ allow researchers to perform multivariate meta-analyses based solely on summary data. The methods can generally be divided into 2 distinct classes: methods that aggregate test statistics or effect sizes based on a model (Genomic SEM, SHom and MTAG) and those that select from the univariate p-values while taking care not to inflate Type-I error (min-P, TATES, and SHet). As we show with respect to MTAG, models on which existing methods are based may can be fit within the Genomic SEM framework. We also anticipate that the approaches for selecting the p-values from a set of analyses while maintaining proper Type-I error control could be integrated into the Genomic SEM framework. For instance, whereas TATES is currently applied to select p-values from a series of univariate analyses of correlated traits, the same analysis could be used to select p-values from a series of Genomic SEM models. The multivariate methods available need not be mutually exclusive. With respect to other multivariate analyses of genome-wide data that go beyond multivariate GWAS discovery, the major alternatives to Genomic SEM that we are aware of are GWIS²³ and GW-SEM.⁹ When considering linear relationships between traits, Genomic SEM is more flexible and user friendly than GWIS, and GW-SEM requires access to phenotypic data, which is a substantial limitation for many applications.

Unlike approaches that assume homogeneity of effects across SNPs,¹¹ Genomic SEM includes diagnostic indices for its key assumptions, including a test for heterogeneity, Q_SNP, that can be applied at the level of the individual SNPs. This offers the unique ability to identify SNPs that confer specific risk to individual phenotypes. This question may be of particular interest as the large degrees of genetic overlap identified across phenotypes (e.g., bipolar disorder and schizophrenia) beg the question: what are the genetic causes of phenotypic divergence? Whereas previous GWASs have combined items tapping genetically-related phenotypes into a single score, or even combined cases with different diagnoses to obtain a shared genetic effect, Genomic SEM allows researchers to interrogate shared genetic effects between diagnoses or indicators, while concurrently testing for causes of divergence (i.e., loci that are related only to a specific phenotype, or subset of phenotypes, but not the more general liability). In the context of neuroticism, for example, we identified 69 loci that were significantly involved in one manifestation of neuroticism but whose effects were not shared through a common factor, offering novel evidence of biological heterogeneity in the etiology of a construct long thought to be unidimensional. Because Genomic SEM relies only on GWAS summary data, it can be applied to a broad spectrum of traits, including social, economic, cognitive, and psychiatric outcomes.

Method

Overview of Genomic SEM

Genomic SEM is a Two-Stage Structural Equation Modeling approach.^12–14 In the first stage, the empirical genetic covariance matrix and it sampling covariance matrix are estimated. In principle, these matrices may be obtained using a variety of methods for estimating SNP heritabilities, genetic covariances, and their joint estimation errors. Here we use a novel version of LDSC that accounts for potentially unknown degrees of sample overlap by populating the off-diagonal elements of the sampling covariance matrix. The same strengths, as well as assumptions and limitations, that are known to apply to LDSC^39,40 apply to its extension used here and to Genomic SEM. In Stage 2, the user specifies a multivariate system of regression and covariance associations involving the genetic components of phenotypes with one another and/or more general latent factors. These associations are represented by parameters that may be fixed or freely estimated, so long as the model is statistically identified (e.g., the number of freely estimated parameters does not exceed the number of nonredundant elements in the genetic covariance matrix being modeled). A set of parameters (θ) is estimated such that the fit function indexing the discrepancy between the model-implied covariance matrix, ∑(θ), and the empirical covariance matrix, S, estimated in Stage 1 is minimized. Model fit is considered good when ∑(θ) closely approximates S. In the main text of the article, we highlight results from weighted least squares (WLS) estimation that weights the discrepancy function using the inverse of the diagonal elements of the sampling covariance matrix, and produces model SEs using the full sampling covariance matrix. In the Supplementary Results, we additionally report results from an alternative normal theory maximum likelihood (ML) estimation method.

Form of Structured Covariance Models

Genomic SEM provides substantial user flexibility with respect to the particular SEM that is specified to produce the model-implied covariance matrix ∑(θ) that approximates the empirical covariance matrix, S. SEMs can be partitioned into two sets of equations, one describing the measurement model, and the other describing the structural model. In the measurement model, the genetic components of k “indicator” phenotypes are described as linear functions of a smaller set of m (continuous) latent variables, y=Λη+ε. In this equation, y is a k×1 vector of indicators, ε is a k×1 vector of residuals, η is an m×1 vector of latent variables, and Λ is a k×m matrix of factor loadings, i.e. regressions relating the latent variables to the set of indicators. In a typical application of Genomic SEM, each indicator is a function of exactly one of the latent variables (though this so-called “simple structure” restriction may be relaxed). In a confirmatory factor analysis (CFA) model, only the measurement model is specified, and the set of latent variables are allowed to freely covary. Thus, the model-implied covariance matrix of a CFA is Σ(θ) = ΛΨΛ′+Θ, where Ψ is an m × m latent variable covariance matrix and Θ is a k × k matrix of covariances among the residuals, ε. Typically, Θ is diagonal, which implies that indicators are mutually independent conditional on the set of latent variables. That constraint may be relaxed such that select pairs of indicators are allowed to covary over and above their associations via the latent variable structure (i.e., residual covariances are allowed). CFA models are typically used to assess the strength of relations between sets of indicators and their respective underlying latent variables, as well as to assess the fit of a measurement model to data. A well-fitting CFA model implies that the latent variable structure is able to account for the observed covariances among a set of indicator variables.

When a theory aims to explain associations among latent variables, a structural model can be added to the measurement model to produce a full SEM. The structural model of a SEM relates latent variables to each other via directed regression coefficients. It can be written in matrix notation as η=Bη+ζ, where B is an m × m matrix of regression coefficients that relate latent variables to each other and ζ is an m × 1 vector of latent variable residuals. The model implied covariance matrix of observed variables is Σ(θ)=Λ(I-B)⁻¹ Ψ(I-B′)⁻¹ Λ′+Θ, where I is an k × k identity matrix.⁴¹ Thus, in a full SEM, the empirical matrix is represented by a set of parameters that relate observed variables to latent variables, and relate latent variables to each other in a series of linear equations.

Path Diagrams

SEMs can be represented graphically as path diagrams representing regression and covariance relations among variables.⁴² In path diagrams, observed variables are represented as squares and unobserved (i.e., latent) variables are represented as circles. Regressions relationships between variables are represented as one-headed arrows pointing from the independent variable to the dependent variable. Covariance relationships between variables are represented as two-headed arrows linking the two variables. The variance of a variable (i.e., the covariance between a variable and itself), is represented as a two-headed arrow connecting the variable to itself. In Genomic SEM, we represent the genetic component of each phenotype with a circle, as the genetic component is a latent variable that is not directly measured, but is inferred from LDSC (it is the phenotype itself that is observed in the raw data that is used to produce the summary statistics). SNPs are directly measured, and are therefore represented as squares. When all elements in a SEM are represented in a path diagram, the diagram contains the full system of algebraic equations needed to estimate the full set of SEM parameters, θ, and produce the model-implied covariance matrix, ∑(θ).

Stage 1 Estimation

In Stage 1, the empirical genetic covariance matrix (S_LDSC) and its associated sampling covariance matrix (V_SLDSC) are estimated using our multivariable extension of LDSC. S_LDSC is a k × k symmetric matrix with SNP heritabilities on the diagonal and genetic covariances (σ_gi,gj) between phenotypes i and j off the diagonal. The genetic covariance between phenotypes i and j can be computed as the genetic correlation scaled relative to the total genetic variance of each of the two contributing phenotypes (themselves scaled to unit variances), ${\sigma }_{\mathit{gi},\mathit{gj}}=r_{\mathit{gi},\mathit{gj}}\cdot \sqrt{h_i^2\cdot h_j^2}$. Thus, the genetic covariance matrix of order k has k* = k(k+1)/2 nonredundant elements. It can be written as:

$$S_{\mathit{LDSC}}=\left[\begin{array}{cccc}\hfill h_1^2\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill {\sigma }_{g1,g2}\hfill & \hfill h_2^2\hfill & \hfill \hfill & \hfill \hfill \\ \hfill ⋮\hfill & \hfill \hfill & \hfill \ddots \hfill & \hfill \hfill \\ \hfill {\sigma }_{g1,gk}\hfill & \hfill {\sigma }_{g2,gk}\hfill & \hfill \cdots \hfill & \hfill h_k^2\hfill \end{array}\right]$$

To produce unbiased SE estimates and test statistics, we require the sampling covariance matrix, V_SLDSC, of the LDSC estimates that is composed of all nonredundant elements in the S_LDSC matrix. Thus, it is a symmetric matrix of order k*, with k*(k* +1)/2 nonredundant elements. The diagonal elements of V_SLDSC are sampling variances, that is, squared SEs of the elements in S_LDSC. The off-diagonal elements of V_SLDSC are sampling covariances that indicate the extent to which the sampling distributions of the variance and covariance estimates in S_LDSC covary with one another, as would be expected when there is overlap among the samples from which the terms are estimated. This V_SLDSC matrix can be written as:

$$V_{{{}_S}_{{}_{{}_{\mathit{LDSC}}}}}=\left[\begin{array}{ccccccccc}\hfill SE(h_1^2{)}^2\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \mathrm{cov}(h_1^2,{\sigma }_{g1,g2})\hfill & \hfill SE({\sigma }_{g1,g2}{)}^2\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \mathrm{cov}(h_1^2,{\sigma }_{g1,gk})\hfill & \hfill \mathrm{cov}({\sigma }_{g1,g2},{\sigma }_{g1,gk})\hfill & \hfill \hfill & \hfill SE({\sigma }_{g1,gk}{)}^2\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \ddots \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \mathrm{cov}(h_1^2,h_j^2)\hfill & \hfill \mathrm{cov}({\sigma }_{g1,g2},h_j^2)\hfill & \hfill \hfill & \hfill \mathrm{cov}({\sigma }_{g1,gk},h_j^2)\hfill & \hfill \hfill & \hfill SE(h_j^2{)}^2\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \ddots \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \mathrm{cov}(h_1^2,{\sigma }_{gj,gk})\hfill & \hfill \mathrm{cov}({\sigma }_{g1,g2},{\sigma }_{gj,gk})\hfill & \hfill \hfill & \hfill \mathrm{cov}({\sigma }_{g1,gk},{\sigma }_{gj,gk})\hfill & \hfill \hfill & \hfill \mathrm{cov}(h_j^2,{\sigma }_{gj,gk})\hfill & \hfill \hfill & \hfill SE({\sigma }_{gj,gk}{)}^2\hfill & \hfill \hfill \\ \hfill \mathrm{cov}(h_1^2,h_k^2)\hfill & \hfill \mathrm{cov}({\sigma }_{g1,g2},h_k^2)\hfill & \hfill \hfill & \hfill \mathrm{cov}({\sigma }_{g1,gk},h_k^2)\hfill & \hfill \hfill & \hfill \mathrm{cov}(h_j^2,h_k^2)\hfill & \hfill \hfill & \hfill \mathrm{cov}({\sigma }_{gj,gk},h_k^2)\hfill & \hfill SE(h_k^2{)}^2\hfill \end{array}\right]$$

The diagonal elements of V_SLDSC can be estimated using the jackknife resampling procedure in the bivariate version of LDSC that is currently available by its original developers.^4,43 The LDSC function introduced in the GenomicSEM software package expands the jackknife procedure to the multivariable context in order to additionally produce sampling covariances (which index dependencies among estimation errors) among the elements of S_LDSC, needed to populate the off-diagonal elements of V_SLDSC.

Incorporating Individual SNP Effects

Several steps are needed to incorporate individual SNP effects into Genomic SEM. The first step requires that the inputted genetic covariance matrix be expanded to include covariances between the SNP and each of the phenotypes, g₁ through g_k, by appending a vector of SNP-phenotype covariances (S_SNP) to S_LDSC:

$$S_{{}_{\mathit{Full}}}=\left[\begin{array}{cccccc}\hfill {\sigma }_{{}_{\mathit{SNP}}}^2\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill {\sigma }_{{}_{\mathit{SNP},g1}}\hfill & \hfill h_1^2\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill {\sigma }_{{}_{\mathit{SNP},g2}}\hfill & \hfill {\sigma }_{{}_{g1,g2}}\hfill & \hfill h_2^2\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill {\sigma }_{{}_{\mathit{SNP},g3}}\hfill & \hfill {\sigma }_{{}_{g1,g3}}\hfill & \hfill {\sigma }_{{}_{g2,g3}}\hfill & \hfill h_3^2\hfill & \hfill \hfill & \hfill \hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \hfill & \hfill \hfill & \hfill \ddots \hfill & \hfill \hfill \\ \hfill {\sigma }_{{}_{\mathit{SNP},gk}}\hfill & \hfill {\sigma }_{{}_{g1,gk}}\hfill & \hfill {\sigma }_{{}_{g2,gk}}\hfill & \hfill {\sigma }_{{}_{g3,gk}}\hfill & \hfill \cdots \hfill & \hfill h_k^2\hfill \end{array}\right]$$

The sampling covariance matrix, V_SFull, associated with this expanded S_Full covariance matrix includes a number of components. One block of this V_SFull matrix, V_SLDSC, contains the sampling variances and sampling covariances of the latent genetic variances (SNP heritabilities) and genetic covariances, which are obtained from the multivariable LDSC approach introduced above. A second block of the V_SFull matrix, V_SSNP, is composed of the sampling covariance matrix of the SNP effects on the phenotypes. The SNP variance (derived from reference panel data) is treated as fixed, and its sampling variance and sampling covariance with all other terms are fixed to 0 (or to a very small value to facilitate computational tractability). The sampling covariances of the SNP-genotype covariances with one another are obtained using cross-trait LDSC intercepts (which represent sampling correlations weighted by sample overlap) after being rescaled relative to the sampling variances of the respective SNP-genotype covariances.^11,44 A final block of the V_SFull matrix represents the sampling covariance of the SNP-genotype covariances with the genetic variances and genetic covariances. These are fixed to 0, as sampling variation of the SNP-genotype covariance is expected to be independent of the test statistics of all LD blocks except the one it occupies. Because the sampling variance of the heritabilities and genetic correlations derive from sampling variability in the test statistics within all of the LD blocks, their sampling covariances with a single SNP effect is expected to approach 0. In sum, the V_SFull matrix can be written in compact form as:

$$V_{{{}_S}_{{}_{{}_{Full}}}}=\left[\begin{array}{cc}\hfill V_{{{}_S}_{{}_{{}_{SNP}}}}\hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill V_{{{}_S}_{{}_{{}_{\mathit{LDSC}}}}}\hfill \end{array}\right]$$

Stage 2 Estimation

In Stage 2, the genetic covariance matrix obtained in the previous stage, S, is used to estimate the parameters in a SEM. In this stage, we allow for both weighted least squares (WLS) and normal theory maximum likelihood (ML) estimators. WLS does not strictly require positive definite S and V_S matrices, but may still benefit from positive definiteness during optimization. ML estimation requires both S and V_S to be positive definite. The GenomicSEM software package therefore smooths S and V_S to the nearest positive definite matrices prior to Stage 2 estimation using the R function nearPD.⁴⁵

The fit function minimized in the diagonally weighted version of WLS estimation that is standard in the GenomicSEM software package is the following:

$$F_{{}_{WLS}}(\theta )={\left(s-\sigma (\theta )\right)}^{\prime }{D}_s^{-1}\left(s-\sigma (\theta )\right),$$

where S and Σ(θ) have been half-vectorized to produce s and σ(θ) respectively, and D_S is V_S with its off-diagonal elements set to 0. We choose the diagonally weighted version of WLS because it is more tractable to implement for large (highly multivariate) matrices and is more stable than fully weighted WLS in finite samples.^46,47

ML estimation proceeds by minimizing the following fit function:

$$F_{{}_{ML}}(\theta )=\log \mid \Sigma (\theta )\mid -\log \mid S\mid +tr\left\{S{\Sigma }^{-1}(\theta )\right\}-k$$

where Σ(θ) is the covariance matrix implied by the set of parameter estimates. Note that, while the formulation of the ML fit function does not explicitly include a weight matrix, it is asymptotically equivalent to a more general formulation that is identical to the WLS fit function, with $.5D_k^{\prime }\left({\Sigma }^{-1}\left(\tilde{\theta }\right)\otimes {\Sigma }^{-1}\left(\tilde{\theta }\right)\right)D_k$, where D_k is the duplication matrix of order k, in place of D_S . Thus, the difference between ML and WLS estimation can be construed as a difference in weight matrices only. A comparison between ML and WLS results can be found in the Supplementary Results (see also Supplementary Figures 23–27, Supplementary Table 19).

WLS estimation more heavily prioritizes reducing misfit in those cells in the S matrix that are estimated with greater precision. This has the desirable property of potentially decreasing sampling variance of the Genomic SEM parameter estimates, which may boost power for SNP discovery and increase polygenic prediction. However, because the precision of cells in the S matrix is contingent upon the sample sizes for the contributing univariate GWASs, WLS may produce a solution that is dominated by the patterns of association involving the most well powered GWASs, and contain substantial local misfit in cells of S that are informed by lower powered GWASs. In other words, WLS relative to ML may more heavily prioritize minimizing sampling variance of the parameter estimates in the so-called variance bias tradeoff.⁴⁸ We expect that this will only occur when the model is overidentified (i.e., df > 0), such that exact fit cannot be obtained, and that divergence in WLS and ML estimates will be most pronounced when there is lower sample overlap and the contributing univariate GWASs differ substantially in power. ML estimation may be preferred when the goal is to most evenly weight the contribution of the univariate sample statistics.

Both WLS and ML fit functions will produce consistent estimates of the model parameters when the model is true.⁴⁷ However, the “naïve” SEs and fit statistic produced in Stage 2 estimation will be incorrect, because neither estimator uses the full V_S matrix in estimation. Thus, robust corrections must be applied to produce consistent estimates of SEs and test statistics. The correct sampling covariance matrix of the Stage Two, Genomic SEM parameter estimates (i.e., V_θ) can be obtained using a sandwich correction:^13,47

$$V_{{}_{\theta }}={\left(\widehat{\Delta }{}^{\prime }{\Gamma }^{-1}\widehat{\Delta }\right)}^{-1}\widehat{\Delta }{}^{\prime }{\Gamma }^{-1}{V}_{{}_s}{\Gamma }^{-1}\widehat{\Delta }{\left(\widehat{\Delta }{}^{\prime }{\Gamma }^{-1}\widehat{\Delta }\right)}^{-1}$$

where $\tilde{\Delta }={\phantom{\mid }\frac{\partial \widehat{\mathit{LD}}(\theta )}{\partial {\theta }^{\prime }}\mid }_{\theta =\tilde{\theta }}$ is the matrix of model derivatives evaluated at the parameter estimates , Γ is the naïve Stage 2 weight matrix that takes its form depending on the estimation method used (WLS or ML), and V_S is the sampling covariance matrix of S obtained using multivariable LDSC.

It may not always be possible to obtain the full sampling covariance matrix, V_S. For example, for highly sensitive data only the matrix S and the SEs of its elements may be available (i.e., the diagonal of V_S). However, we note that when there is low sample overlap across the GWASs for each phenotype, off-diagonal elements of the sampling covariance matrix are small and pragmatically ignorable. Moreover, in other contexts with complete sample overlap, SE inflation of the SEM parameters estimated using diagonally-weighted versions of WLS has been estimated to be less than 8%⁹ without robustness corrections, and nil with robustness corrections.⁴⁷

Standardization and Scaling of Summary Statistics for Multivariate GWAS

Typically, GWAS summary statistics for quantitative phenotypes are not reported in terms of covariances, but are reported as ordinary least squared (OLS) unstandardized regression coefficients, with the phenotypes standardized prior to analyses (i.e., the coefficients are standardized with respect to the outcome, but not the predictor). In order to transform these partially standardized regression coefficient (b_SNP,P) of a SNP effect on phenotype P to a covariance, we multiply by the variance of scores on the SNP. The variance (${\sigma }_{\mathit{SNP}}^2$) of scores (0, 1, 2) of a biallelic autosomal SNP is estimated as 2pq, assuming Hardy-Weinberg-Equilibrium, where p = the minor allele frequency (MAF) and q = 1-MAF, with the MAF typically obtained from a reference sample. As the latent genetic factors estimated in LDSC are scaled relative to unit-variance scaled phenotypes (by virtue of the SNP heritability estimates being placed on the diagonal of S), no further scaling is needed to transform this SNP-phenotype covariance into a SNP-genotype covariance.

When OLS regression coefficients and standard errors are provided from an analysis in which the phenotype has not been standardized prior to analyses, or only Z statistics or p-values (for which Z statistics can be readily obtained) are provided, the partially standardized regression coefficients and their standard errors can be obtained as $Z=\frac{b_{\mathit{SNP},P}^{\ast }}{{\mathit{SE}}_{b_{\mathit{SNP},P}^{\ast }}}$, $b_{\mathit{SNP},P}=\frac{Z}{\sqrt{N{\sigma }_{\mathit{SNP}}^2}}$, and ${\mathit{SE}}_{b_{\mathit{SNP},P}}=\frac{b_{\mathit{SNP},P}}{Z}$, where $b_{\mathit{SNP},P}^{\ast }$ is equal to the regression coefficient for the OLS GWAS of the unstandardized phenotype. These derived partially standardized coefficients are then transformed into covariances by multiplying by the variance of scores on the SNP, as per above.

When the GWAS summary statistics are reported for logistic regressions of liabilities for categorical outcomes (e.g. case/control status) on the SNP, the logistic regression coefficients can be transformed into covariances as above, by multiplying by the SNP variances. However, it is appropriate to further transform the coefficients and their SEs such that they are scaled relative to unit-variance scaled liability. This can be achieved by dividing by $\sqrt{{\sigma }_{\mathit{SNP}}^2\times b{\text{logit}}_{\mathit{SNP},P}^2+\frac{{\pi }^2}{3}}$, as a logistic regression model implies a residual variance of $\frac{{\pi }^2}{3}$. If GWAS summary statistics are reported for odds ratios (ORs), they can be transformed to logistic regression coefficients by taking their natural logarithm. Standard errors for the logistic regression coefficient are obtained as SE_OR/OR. The derived logistic coefficients and their SEs should further be transformed such that they are scaled relative to unit-variance scaled phenotypes, as per above. Note that when the outcomes are categorical, the liability scale heritabilities and genetic covariances from multivariable LDSC (and not what are referred to as the “observed scale” heritabilities and genetic covariances) should be used to populate the S matrix. This has the desirable property of both modeling the continuous scale of risk in the population and providing estimates that are independent of the observed prevalence of the categorical outcomes.

On occasion, summary statistics will be provided from OLS GWASs of categorical outcomes (e.g., case/control status). Such an analysis is sometimes referred to as a linear probability model, as it (incorrectly) assumes that the association between the predictor and the probability of being in the comparison (e.g. case) group relative to the reference (e.g. control) group is linear. Parameters from the linear probability model are dependent not only on the strength of the association between the SNP and the continuous underlying liability, but also on the MAF and the proportion of comparison group members (cases) in the sample. Thus, parameters from the linear probability model cannot be used directly in Genomic SEM. However, particularly in the case of complex traits, for which the effect sizes for individual SNPs are small, results from the linear probability model can be used to very closely approximate logistic regression coefficients and SEs that are amenable for use in Genomic SEM.⁴⁹ This approximation can be obtained as $Z=\frac{b_{\mathit{SNP},P}^{\ast \ast }}{{\mathit{SE}}_{b_{\mathit{SNP},P}^{\ast \ast }}}$, $b{\text{logit}}_{\mathit{SNP},P}^{\ast }=\frac{Z}{\sqrt{\nu (1-\nu )N{\sigma }_{\mathit{SNP}}^2}}$, and ${\mathit{SE}}_{b_{\mathit{SNP},P}}=\frac{b{\text{logit}}_{\mathit{SNP},P}^{\ast }}{Z}$, where $b_{\mathit{SNP},P}^{\ast \ast }$ is equal to the regression coefficient from the linear probability model, $b{\text{logit}}_{\mathit{SNP},P}^{\ast }$ is the expected logistic regression coefficient that is derived from the linear probability model results, v is equal to the proportion of cases in the sample, and ${\sigma }_{\mathit{SNP}}^2$ is the variance of the SNP, computed from its MAF obtained from a reference sample, as per above. To scale the derived logistic coefficient such that it is scaled relative to unit-variance scaled liability, the coefficient should be divided by $\sqrt{{\sigma }_{\mathit{SNP}}^2\times {(b{\text{logit}}_{\mathit{SNP},P}^{\ast })}^2+\frac{{\pi }^2}{3}}$. Lloyd-Jones et al. (2018)⁴⁹ report that in a real data analysis of UKB data, the exponentiated regression coefficient (i.e., the odds ratio) obtained directly from a logistic regression-based GWAS and that derived from the linear probability model-based GWAS was nearly perfect (R² > 98%, slope ≈ 1). We have verified this nearly perfect correspondence in our own simulations (Supplemental Figure 28).

Even within samples of the same ethnicity, there is likely to be discrepancies between the MAFs of a reference sample and the sample that GWAS summary statistics were generated from. However, some summary statistics may not include allele frequencies, and using the same reference panel for standardization across phenotypes has the desirable property of maintaining consistency across summary statistics. To examine the effect of this decision, the betas for 30,000 randomly selected SNPs for the mood phenotype from UKB were standardized using either sample or reference panel MAF. The correlation between the betas was .982, and a linear regression of betas standardized using reference panel MAF predicting standardization using sample MAF revealed near perfect correspondence (slope = 1.044, intercept = −6.54e-6; Supplemental Figure 29).

Model Fit Statistics

Model χ² is an index of exact fit of a SEM. It indexes whether the model-implied genetic covariance matrix, Σ(θ), differs from the empirical genetic covariance matrix, S. Model χ² can also be used as a relative fit index for comparing nested models. Conventional SEM approaches to indexing model χ² are based on formulas that directly incorporate N. Because there is not an N that directly corresponds to the genetic covariance matrix that is modelled by Genomic SEM in the same way that N typically corresponds to an observed covariance matrix, we derived a formula for estimating model χ² that does not require N, but instead incorporates the sampling covariance matrix of the model residuals. This is done in two steps. In Step 1, the proposed model (e.g., a common factor model) is estimated. In Step 2, all of the Step 1 estimates are fixed, and the residual covariances and residual variances of the indicators are freely estimated. Residual variances are estimated in Step 2 by estimating the variances of k residual factors defined by the indicators. This provides an estimate of the discrepancy between the model implied and observed covariance matrices, R = S – Σ(θ), along with the sampling covariance matrix (V_R) of R. While the discrepancy between model implied and observed covariance matrices can be computed simply by deriving covariance expectations from the Step 1 model and subtracting the observed covariance matrix, such an approach would not provide the corresponding V_R matrix necessary for the calculations below. The V_R matrix is expected to be positive semidefinite and, consequently, have no negative eigenvalues. Therefore, the V_R matrix has the following eigendecomposition:

$$V_{{}_R}=({\mathrm{P}}_1{\mathrm{P}}_0)\left(\begin{array}{cc}\hfill \mathrm{E}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right)\left(\begin{array}{c}\hfill P_1^{\prime }\hfill \\ \hfill P_o^{\prime }\hfill \end{array}\right)$$

where P₁ is a matrix of principal components (eigenvectors) of V_R, and E is a corresponding diagonal matrix consisting of non-zero eigenvalues. P₀ reflects the null space of V_R. Projecting R_i—a vector of residual covariances estimated from the Step 2 Model—onto P₁ and adjusting for corresponding eigenvalues, we have that:

$$E^{\frac{-1}{2}}{P}_1{}^{\prime }{R}_{i}N(0,I_r)$$

Therefore,

$$R_i{}^{\prime }{P}_1{E}^{-1}{P}_1{}^{\prime }{R}_i\sim {\chi }^2(r)$$

This equation produces a test statistic that is χ² distributed with degrees of freedom (r) equal to the difference between the number of nonredundant elements (k*) in the empirical covariance matrix (S) and the number of freely estimated parameters in the proposed model.

The Comparative Fit Index (CFI) is a test of approximate model fit. CFI indexes the extent to which the proposed model fits better than a model that allows all phenotypes to be heritable, but assumes that they are genetically uncorrelated. The χ² statistic can be used to calculate CFI by calculating a second χ² statistic for a so-called independence model, i.e. a model that estimates genetic variances of all phenotypes but assumes all genetic covariances to be zero, such that ∑(θ) is diagonal. CFI is calculated using the formula below,⁵⁰ with f = χ² – degrees of freedom:

$$\frac{f(\text{Independence Model})-f(\text{Proposed Model})}{f(\text{Independence Model})}$$

For the χ² of the independence model, a model is estimated in Step 1 that includes only the variance of the indicators and no common factor. In Step 2, these variances are fixed and the covariances among the indicators and variances of k residual factors defined by the indicators are estimated and used to populate the same equation above used to calculate the proposed model χ². CFI values theoretically range from 0 to 1, with higher values indicating good fit. CFI values of .90 and above are typically considered acceptable fit, and values of .95 and above are typically considered good model fit.⁵¹ When the empirical covariance matrix contains a large number of cells that are very close to 0, CFI values may be low, even when such cells are approximated well by the model.

Akaike Information Criterion (AIC) is a relative fit index that balances fit with parsimony, and can be used to compare models regardless of whether they are nested. AIC is calculated as:

$$\text{AIC}={\chi }^2+2\times \text{fp},$$

where fp is the number of free parameters in the model.⁵² Lower AIC values are considered superior.

Standardized Room Mean Square Residual (SRMR) is an index of approximate model fit that is calculated as the standardized root mean squared difference between the model-implied and observed correlations in Σ(θ) and S, respectively.⁵³ Higher SRMR values indicate a larger discrepancy between Σ(θ) and S. It is positively-biased, with larger bias resulting when the contributing univariate GWAS samples are lower powered. SRMR values below .10 indicate acceptable fit, values less than .05 indicate good fit, and a value of 0 indicates perfect fit.⁵⁴

We recommend that model fit indices be considered concurrently, as individual indices each have their own strengths and limitations. Model χ² is an index of exact fit, with lower values indicating better fit. Model χ² may oftentimes be statistically significant, indicating that the model-implied genetic covariance matrix significantly differs from the empirical (unrestricted) genetic covariance matrix, even when the model-implied covariance matrix very closely approximates the empirical genetic covariance matrix. Oftentimes, models that closely, albeit imperfectly approximate the empirical genetic covariance matrix may be scientifically and inferentially useful. We thus recommend considering CFI and SRMR indices of absolute fit, even when model χ² is significant. We also recommend using indices of relative fit to compare competing models of the same data (i.e. different models fit to genetic covariance matrices derived from the exact same summary data for the exact same phenotypes). When models are nested, their respective χ² values can be subtracted from one another to calculate a χ² difference test, with df equal to the difference in df between the two models. This χ² difference test, indexes the extent to which the less complex model (i.e. the model with more df) approximates the empirical genetic covariance matrix significantly worse than the more complex model (i.e. the model with fewer df). If the χ² difference test is significant, the more complex model should be chosen. If the χ² difference test is not significant, the less complex model should be chosen, as it is more parsimonious and approximates the empirical genetic covariance matrix no worse than the more complex model. Two models are nested when the set of possible model implied covariance matrices from one model is a subset of the set of possible model implied covariance matrices of the second model.⁵⁵ Nesting can typically be confirmed if the less restrictive model can be derived from the more restrictive model by dropping or fixing parameters. Regardless of whether models are nested, they can be compared on CFI, SRMR, and AIC, so long as the same data are being modeled.

Q_SNP Test of Heterogeneity

As with the computation of model χ² outlined above, Q_SNP is calculated using a two-step procedure. In Step 1, a common pathway model is fit in which both factor loadings, the SNP effect on the common factor(s), and the residual variances of the common and unique factors are freely estimated (with one factor loading fixed to unity for factor identification and scaling). No paths representing direct effects of the SNP on the genetic components of the individual phenotypes are estimated. In Step 2, a common plus independent pathways model is specified, in which the factor loadings and the SNP effect on the common factor are fixed to the values estimated in Step 1, and direct effects of the SNP on individual indicators and the residual variances of each indicator are freely estimated. Supplementary Figure 30 depicts this model, as applied to a single common factor model, with parameters that are fixed in Step 2 depicted in red and those that are freely estimated in Step 2 depicted in black.

Genomic SEM Simulations

Validation of Summary-Based Model Fit Statistics via Simulation.

A generating population with a common factor model defined by four, five, or six indicators was used to examine the null distribution of the newly derived χ² test statistic using a set of 1,000 simulations per model. These simulations did not include individual genotypes, and were simulated solely based on a generating factor structure. For the six indicator models the standardized factor loadings in the generating population were .42, .64, .22, .59, .19, and .64. The four and five indicator models specified the same factor loadings, excluding the last, or last two loadings, respectively. Results indicated that the two-step procedure described above produced a test statistic equivalent to the χ² statistic calculated by lavaan from the raw data (Supplementary Figure 31 and Supplementary Table 20). For a χ² distributed test-statistic, the mean of the null sampling distribution should match the df of the test. As expected, the distribution of the test-statistic conformed to a χ² distribution with an average approaching the df (Supplementary Figure 32). Calculated CFI values were also highly consistent with those observed using the CFI statistic provided by lavaan when using raw data (Supplementary Figure 33, Supplementary Table 20). Calculated AIC values were not contrasted with those obtained using the lavaan package in R in the simulations below as the software uses a formula that includes a log-likelihood estimate contingent on the provided sample size.

Null Distribution of Q_SNP.

To verify that the null distribution for Q_SNP is χ² distributed, a set of simulations specified a generating population in which the direct effects of the SNP on the indicators were entirely mediated through the common factor. Each simulation included 1,000 datasets, with N = 100,000 completely overlapping participants per dataset. All simulated datasets were analyzed using both WLS and ML. We examined three models with F = 1 factor, and k = 4, 5, or 6 phenotypes. Supplementary Table 21 presents descriptive statistics for Q_SNP. Using a genome-wide significance threshold, in all cases the false discovery rate for Q_SNP was 0, and the power to detect a SNP effect on the common factor was 1. Both WLS and ML estimation produced mean estimates of Q_SNP that were approximately equal to the df of the corresponding model. Supplementary Figure 34 depicts the null sampling distributions of Q_SNP estimated using WLS or ML. Supplementary Figure 35 plots Q_SNP from these two estimation methods against χ² distributions and against one another. These results indicate that both estimation methods produce results that are approximately χ² distributed.

Simulation of Factor Structure.

In order to evaluate the ability of Genomic SEM to capture the genetic factor structure in the generating population, the GCTA package³ was used to generate 100 sets of 6 independent, 100% heritable phenotypes (“orthogonal genotypes”) to pair with genotypic data for 39,909 randomly selected, unrelated individuals of European descent from UKB data for the 1,209,498 SNPs present in HapMap3. The generating list of causal SNPs was set to 10,000 for all 600 genotypes, with the specific list of causal variants sampled with replacement from the 1,209,498 SNPs. One of the six orthogonal genotypes per set was designated an index of the general genetic factor and the remaining five were designated indices of domain-specific genetic factors. All of these orthogonal genotypes were scaled to M=0, SD=1. Five new correlated genotypes were then constructed, each as the weighted linear combination of the general genetic factor and one domain-specific genetic factor. Weights for contribution of the general genetic factor were λ_Fg,k =.70, .60, .50, .40, and .30, for correlated genotypes 1–5, respectively. Weights for the domain-specific factors were $\sqrt{(1-{\mathrm{\lambda }}_{\mathit{Fg},k}^2)}$. Phenotypes were then each constructed as the weighted linear combination of one of the correlated genotypes and domain-specific environmental factors (randomly sampled from a normal distribution with M=0, SD=1). Heritabilities for phenotypes 1-5 were set to $h_k^2$=35%, 40%, 50%, 60%, and 70%, respectively, such that the weights for the genotypes were $\sqrt{h_k^2}$ and the weights for the environmental factors were $\sqrt{(1-h_k^2)}$. We chose these figures to stabilize the properties of the distributions across simulations at 100 replications with N~39K each. We expect that with lower SNP h²’s, the same patterns would hold, albeit at larger sample sizes. Each of the 500 phenotypes (100 sets of 5 phenotypes) was then analyzed as a univariate GWAS in PLINK⁵⁶ to produce univariate GWAS summary statistics. Our multivariable LDSC function was then used to construct 100 sets of 5×5 genetic covariance matrices (S) and associated sampling covariance matrices (V_S), and Genomic SEM was used to fit a one factor model to each set.

Using this procedure, we performed 100 runs of Genomic SEM on raw individual-level genotype data for which we simulated multivariate phenotypic data to conform to a single genetic factor model (a latent trait that partially causes 5 observed outcomes). Across the 100 simulations, Genomic SEM estimates closely matched the parameters specified in the generating population (Supplementary Figure 36). Model SEs also closely matched the standard deviations of parameter estimates. We also compared fit statistics (CFI, AIC, and model χ²) for the correctly specified common factor model and two deliberately misspecified models: (i) a model in which all indicators were constrained to have the same factor loading, and (ii) a model for which the loading of the third indicator was set to 0. As expected, results indicated that the common factor model matching the generating population was favored ≥ 99% of the time across model fit indices (Supplementary Figure 37).

Simulation of Partial Sample Overlap.

In order to examine the effect of sample overlap on estimates obtained from Genomic SEM, the GCTA package package³ was used to generate a 50% heritable, quantitative phenotype with 30,000 causal SNPs. The phenotype was paired with genetic data from 100,000 randomly selected, unrelated individuals of European descent from UKB data for 1,209,498 HapMap3 SNPs. Three sets of 60,000 participants each were created using this same phenotype, with 40,000 participants overlapping across all three identical phenotypes and 20,000 participants unique to each phenotype (i.e., 100,000 total participants). These three subsamples were individually analyzed in PLINK⁵⁶ to produce univariate GWAS summary statistics. The multivariable LDSC function was then used to construct the genetic covariance and sampling covariance matrix using the three sets of summary statistics, and Genomic SEM was used to fit a one factor model with the SNP predicting the common factor. Two key results were verified at this stage. First, we confirmed that the standardized factor loadings on the common factor were 1 for the identical phenotypes. Second, we verified that the bivariate ld-score intercepts that are used to account for sample overlap in the sampling covariance matrix were as expected. The equation for the ld-score bivariate intercept is:⁴ N_sρ/√(N₁N₂), where N_s = sample overlap, ρ = the phenotypic correlation, N₁ = sample size of trait 1, and N₂ = sample size of trait 2. In this simulation, we observed bivariate intercepts of .67, which is as expected given sample overlap of 40,000, a phenotypic correlation of 1, and sample sizes of 60,000 (i.e., 40,000*1/√(60,000*60,000) = .67). Finally, estimates from this multivariate GWAS were compared to estimates from the univariate GWAS in PLINK for the full set of 100,000 participants. If sample overlap is not appropriately accounted for in this example, such that data are incorrectly treated as deriving from 180,000 participants (as opposed to 100,000 total participants), we would expect the Z statistics for the SNP effects from Genomic SEM to be upwardly biased relative to those from a univariate GWAS applied directly to the single phenotype in the 100,000 participants. We observed no such bias. A linear regression of Z statistics from Genomic SEM (from the three overlapping samples of 60,000 participants each) predicting univariate GWAS Z statistics in the complete sample (of 100,000 participants) revealed near perfect correspondence (unstandardized slope = 1.003, intercept = −.003).

MTAG Simulation.

In order to evaluate the relationship between estimates from MTAG and those from a Genomic SEM formulation of the MTAG model, we specified a bivariate system of heritable phenotypes, A and u. Phenotype A was constructed using the GCTA package³, and specified to be 60% heritable, and affected by a random selection 30,000 HapMap3 SNPs. Phenotype u was constructed separately using the GCTA package, and also specified to be 60% heritable, and affected by a different random selection of 30,000 HapMap3 SNPs. Both A and u were standardized (M=0, SD=1). Phenotype B was constructed from phenotypes A and u according to the equation B = .7A + .7u. This procedure resulted in 60% heritabilities for both traits A and B, with a genetic correlation of .7 between them. Sample sizes for phenotypes A and B were 25,000 each, with 10,000 participants contributing data for both phenotypes A and B (i.e. 40% sample overlap), such that the analytic dataset was composed of 40,000 unique individuals in total. Both MTAG¹¹ and a Genomic SEM model specified to satisfy the same moment conditions as MTAG (see Supplementary Methods) were then each run with Trait A as the supporting phenotype used to boost power for target Trait B and estimates from MTAG and from Genomic SEM specified to satisfy the MTAG moment conditions were compared. Results indicated near perfect correspondence from a linear regression in which Z statistics from MTAG were used to predict those from a Genomic SEM specified to satisfy the MTAG moment conditions (Supplementary Fig. 20; unstandardized slope = .999, intercept = 2.65E-4).

Quality Control Procedures

LD-Score Regression.

For the p-factor, neuroticism, and anthropometric traits, quality control (QC) procedures for producing the S and V_S matrix followed the defaults in LDSC. We recommend using these defaults for multivariable LDSC, including removing SNPs with an MAF < 1%, information scores < .9, SNPs from the MHC region, and filtering SNPs to HapMap3. Quality control procedures for the multivariable regression example mirrored those used by Nieuwboer et al. (2016)²³ for comparative purposes. More specifically, SNPs were excluded with MAFs < .05 as determined by the HapMap Consortium,⁵⁷ and with information values less than 0.9 or greater than 1.1. SNPs were also filtered to HapMap3. The LD scores used for the analyses presented were estimated from 1000 Genomes Phase 3, but restricted to HapMap3 SNPs.

Multivariate GWAS.

Summary statistics are only restricted to HapMap3 SNPs for the estimation of the genetic covariance and sampling covariance matrix in LD-Score regression, whereas all SNPs passing QC filters are included for multivariate GWAS. To obtain summary statistics for multivariate GWAS, we recommend using QC procedures of removing SNPs with an MAF < .01 in the reference panel, and those SNPs with an INFO score < 0.6. MAFs were obtained for the current analyses using the 1000 Genomes Phase 3 reference panel. Using these QC steps, 1,979,881 SNPs were present across schizophrenia, bipolar disorder, MDD, PTSD, and anxiety. For neuroticism, there were 7,265,104 SNPs that were present across all phenotypes. These QC procedures are the defaults for the processing function within the GenomicSEM package. The regression effects for the univariate indicators of the p-factor were standardized using the procedure for logistic coefficients outlined above. Regression effects for neuroticism indicators were converted from linear probability to logistic coefficients and then standardized with respect to the variance in the outcome.

Out-of-Sample Prediction

p-factor.

Genomic SEM analyses that were used to produce the summary statistics for construction of polygenic scores for out-of-sample prediction omit the PGHC MDD 2018 GWAS and SCZ 2018 GWAS and replace them with the PGC MDD 2013⁵⁸ and PGC SCZ 2014⁵⁹ GWAS to prevent overlap between discovery and target samples. This resulted in a Genomic SEM-based multivariate GWAS using 930,581 SNPs. Analyses used to construct a phenotypic p-factor for polygenic prediction in the UKB dataset were restricted to data on up to N=332,050 European participants. The Genomic SEM of the p-factor employed case-control GWAS statistics to construct summary statistics for a general factor of liability for clinically-severe levels of psychopathology as the discovery phenotype. For out-of-sample prediction, we selected a set of psychiatric symptoms (rather than diagnoses) to construct liability for general and domain-specific factors of psychiatric symptomology across the subclinical-to-clinical ranges as the target phenotypes. From the UKB dataset, we chose symptoms falling within the following domains: psychosis, mania, depression, post-traumatic stress, and anxiety. We fit a confirmatory factor model (diagram shown in Supplementary Fig. 29) to the phenotypic symptom endorsements, treating them as ordered categorical variables. Analyses were run in Mplus,⁶⁰ with the target phenotypes—the p-factor and each of the individual domains—specified as latent variables. PGS variables were specified to directly predict the latent phenotypes within the model (i.e., factor score estimates were not used). To construct PGSs, we removed from both the p-factor and univariate summary statistics the 5 SNPs that were identified as having genome-wide significant Q_SNP estimates for ML, along with SNPs that were in LD with these SNPs using an r² threshold of 0.1 and 500-kb window. PGSs were constructed using PRSice,⁶¹ with LD clumping set to r² > 0.25 over 250kb sliding windows. PGSs for the p-factor were based on the WLS summary statistics produced using Genomic SEM. We ran PGS analyses using a p-value threshold of 1.0 (i.e., we used all available SNPs apart from those removed due to Q_SNP analyses). In order to maintain comparability, PGSs for the univariate summary statistics were constructed based on the same SNPs with which the PGSs for the p-factor were constructed. In the confirmatory factor models, we included controls for age, sex, genotyping array, and 40 principal components of ancestry in conjunction with the PGS predictor.

Neuroticism.

The raw total on the 12-item neuroticism subtest of the Eysenck Personality Questionnaire-Revised⁶² (maximum score = 12) was used as the target phenotype for out-of-sample prediction. Both genetic and neuroticism target data was available on 19,876 European participants in the Generation Scotland cohort⁶³. Neuroticism scores were residualized for age, sex, and 20 principal components of ancestry prior to examining out-of-sample prediction. PGSs were constructed using PRSice,⁶¹ with LD clumping set to r² > 0.25 over 250kb sliding windows and using a p-value threshold of 1.0. PGSs for neuroticism were based on the WLS summary statistics produced using Genomic SEM. Regression analyses were run using the lmekin function within the coxme package in R with a random intercept to account for nesting of individuals within families.

Clumping and Biological Annotation

Lead SNPs for univariate indicators and the common factors were identified using the clumping algorithm in PLINK.⁵⁶ We defined LD-independent SNPs using an r² threshold of 0.1 and a 500-kb window using the same 1000 Genomes Phase 3 reference panel used for obtaining MAF. For chromosomes 6 and 8 an additional pruning filter was used of 1Mb and r² > 0.1 to account for long-range LD due to the MHC region and pericentric inversion, respectively. Increasing the pruning window further to 4Mb did not influence our findings on chromosome 6 or 8. The lead SNPs identified using PLINK were entered into DEPICT. Prioritized genes, enriched gene sets, and enriched tissues were identified using the standard false discovery rate of 5%.

Description of GenomicSEM Software

The Genomic SEM software package, GenomicSEM, is written as an R package and is available through GitHub at https://github.com/MichelNivard/GenomicSEM. GenomicSEM contains several functions, including procedures for QCing and standardizing summary statistics, a function for producing genetic covariance matrices (S_LDSC) and their associated sampling covariance matrices (V_SLDSC) using a multivariable extension of LD Score regression, functions for fitting Genomic Structural Equation Models to S_LDSC and V_SLDSC, and functions for adding SNP level data to the S_LDSC and V_SLDSC matrices (referred to as S_Full and V_SFull) that are used for implementing Genomic SEM for multivariate GWAS discovery. Functions include both pre-specified models (e.g., a single common factor model) and user-specified models. Output includes both unstandardized and standardized solutions, along with the fit indices described above. WLS estimation is the default in the GenomicSEM package. GenomicSEM uses the lavaan Structural Equation Modeling package⁶⁴ as the primary workhorse for model specification and numerical optimization. We also provide limited support for OpenMx.⁶⁵ To run the multivariable LDSC function on five phenotypes takes ~15 minutes, a step in the analyses that only needs to be performed once. For models of multivariate genetic architecture that do not incorporate individual SNP effects, the typical run time observed for 3–15 traits is <1 second on a standard personal computer. Using parallel processing implemented in the GenomicSEM package on a 4-core/8-thread laptop, a multivariate Genomic SEM GWAS with five indicators and ~1 million SNPs took ~8 hours. With the time needed to run the models will increase with increasing model complexity, and with increasing numbers of variables or SNPs. In these cases, computing time can be greatly reduced by using a computing cluster to distribute SNP models across nodes/cores.