Growth model interpretation of planet size distribution

Significance

The discovery of numerous exoplanet systems containing diverse populations of planets orbiting very close to their host stars challenges the planet formation theories based on the solar system. Here, we focus on the planets with radii of 2–4 R_⊕, whose compositions are debated. They are thought to be either gas dwarfs consisting of rocky cores embedded in H₂-rich gas envelopes or water worlds containing significant amounts of H₂O-dominated fluid/ice in addition to rock and gas. We argue that these planets are water worlds.

Abstract

The radii and orbital periods of 4,000+ confirmed/candidate exoplanets have been precisely measured by the Kepler mission. The radii show a bimodal distribution, with two peaks corresponding to smaller planets (likely rocky) and larger intermediate-size planets, respectively. While only the masses of the planets orbiting the brightest stars can be determined by ground-based spectroscopic observations, these observations allow calculation of their average densities placing constraints on the bulk compositions and internal structures. However, an important question about the composition of planets ranging from 2 to 4 Earth radii (R_⊕) still remains. They may either have a rocky core enveloped in a H₂–He gaseous envelope (gas dwarfs) or contain a significant amount of multicomponent, H₂O-dominated ices/fluids (water worlds). Planets in the mass range of 10–15 M_⊕, if half-ice and half-rock by mass, have radii of 2.5 R_⊕, which exactly match the second peak of the exoplanet radius bimodal distribution. Any planet in the 2- to 4-R_⊕ range requires a gas envelope of at most a few mass percentage points, regardless of the core composition. To resolve the ambiguity of internal compositions, we use a growth model and conduct Monte Carlo simulations to demonstrate that many intermediate-size planets are “water worlds.”

Thousands of exoplanets discovered during the last two decades cover a wide range of masses and sizes. In the 1- to 20-M_⊕ and 1- to 4-R_⊕ ranges, several types of planets have been identified. The planets with high densities are considered rocky, while the ones with low densities have been modeled either as gas dwarfs or water worlds. The gas dwarfs are thought to have a rocky core enveloped in a H₂–He gaseous envelope, while the water worlds contain a significant amount of multicomponent, H₂O-dominated ices/fluids in addition to rock and gas.

Here, we focus on such small planets, namely, the super-Earths (1–2 R_⊕) and the sub-Neptunes (2–4 R_⊕). Mass–radius curves (Figs. 1 and 2) show that they contain a few percent of gas by mass at most; that is, their masses are dominated by the cores that must have formed by the accretion of solids in the disk.

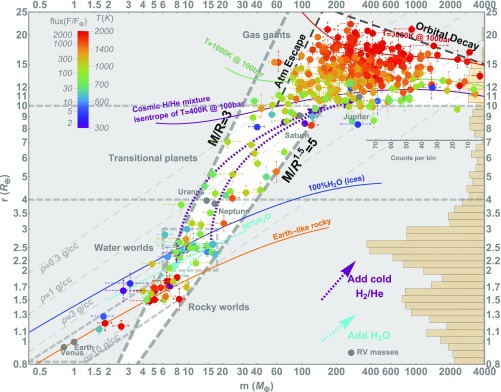
Fig. 1.

The mass–radius variations among selected exoplanets with masses determined by the radial-velocity (RV) method and densities constrained to better than ±50% (1-σ). The plotted data are listed in SI Appendix, Table S1. The color of the data points denotes stellar insolation (see legend in the upper left corner) in the Earth units (expressed as either the amount of stellar bolometric radiation reaching a given area at their orbital distances, assuming negligible orbital eccentricities, normalized to the Earth’s value or surface equilibrium temperatures assuming Earth-like albedo). The vertical histogram on the right y axis shows the log-binned radius distribution of 1,156 Kepler confirmed/candidate planets with radius errors less than ±10% (1-σ, the average error is about ±7%), orbiting only the main-sequence host stars within the effective temperatures in the 5,000–6,500 K range [Gaia Data Release 2 (7)]. The dotted cyan and purple arrows show the growth trajectories of planets formed by continuous addition of either H₂O ices or H₂-plus-He gas to a planetary core of a given mass (SI Appendix). The area outlined by the gray dashed rectangle is shown in Fig. 2.

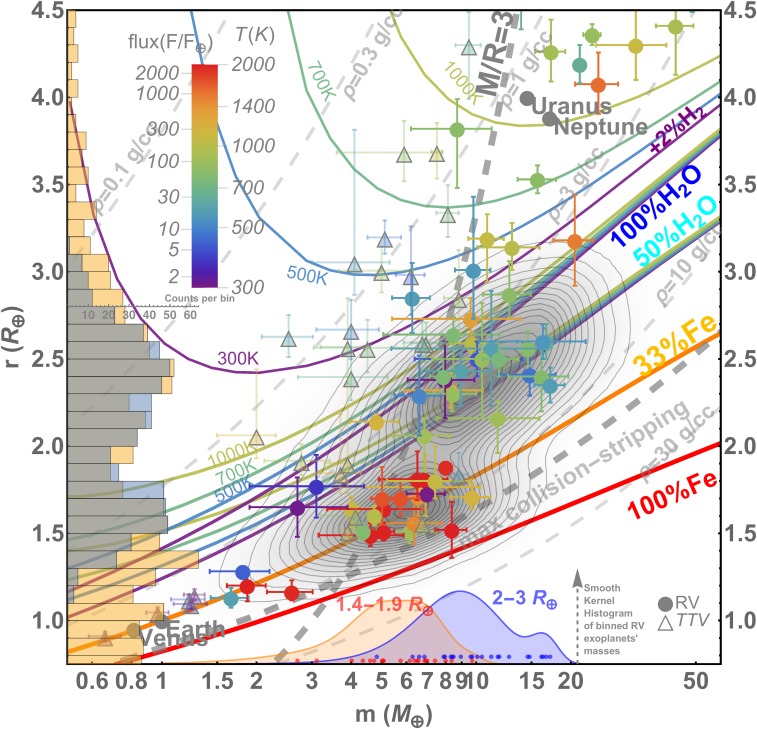
Fig. 2.

Blowup of Fig. 1. Radius gap at 2 R_⊕ separates two distinctive groups of RV planets (1.4–1.9 and 2–3 R_⊕). Their smooth kernel mass distributions on the bottom x axis show a significant offset, with truncation of the super-Earths (yellow) and sub-Neptunes (purple) at ∼10 and ∼20 M_⊕, respectively. The histogram on the left y axis compares the results of Monte-Carlo simulation (light blue) with the observations (yellow). Two sets of H₂O M–R curves (blue, 100 mass% H₂O; cyan, 50 mass% H₂O; cores consist of rock and H₂O ice in 1:1 proportion by mass) are calculated for an isothermal fluid/steam envelope at 300, 500, 700, and 1,000 K, sitting on top of ice VII-layer at the appropriate melting pressure. A set of mass–radius curves (upper portion of the diagram) is calculated for the same temperatures assuming the addition of an isothermal 2 mass% H₂-envelope to the top of the 50 mass% H₂O-rich cores.

The measurements of planetary radii and orbital periods of more than 4,000 confirmed or candidate exoplanets by the National Aeronautics and Space Administration Kepler mission (1–6) revealed a bimodal distribution of planet sizes in the 1- to 4-R_⊕ range. This discovery was interpreted as the evidence for the presence of two populations of planets—smaller rocky worlds and the intermediate-size planets, which, because of their proximity to the host star, were interpreted as gas dwarfs rather than water worlds.

Further refinement of the host stellar parameters by the Gaia astrometry mission (7–11) yields a better resolved bimodal distribution of planetary radii with two peaks and a local minimum or gap at 1.8–2 R_⊕ (Figs. 1 and 2). The gap separates two subpopulations of planets on the mass–radius diagram (Figs. 1 and 2): super-Earths (1–2 R_⊕) and sub-Neptunes (2–4 R_⊕). Whether this gap is a direct result of planet formation or a secondary feature formed by photoevaporation of gas envelopes is debated. The distances to the host stars in both subpopulations appear to be distributed log-uniform, that is, flat in semimajor axis a or orbital period P, beyond ∼10 d (figure 7 of ref. 12). Such orbit distributions of both populations challenge the photoevaporation scenario as the cause of the gap because it strongly depends on the orbital distance. If the gap is caused by photoevaporation, then an anticorrelation in their orbital distributions is expected (13). We interpret the flatness in distributions as additional evidence for both populations arising from their intrinsic properties (14).

The distinction between gas dwarfs and water worlds cannot be made based on the mass–radius relationship alone or the presence or lack of a H₂–He gas layer (15). Therefore, we invoke a mass–radius distribution among small planets and their growth models to argue that at least some intermediate-size planets are water worlds.

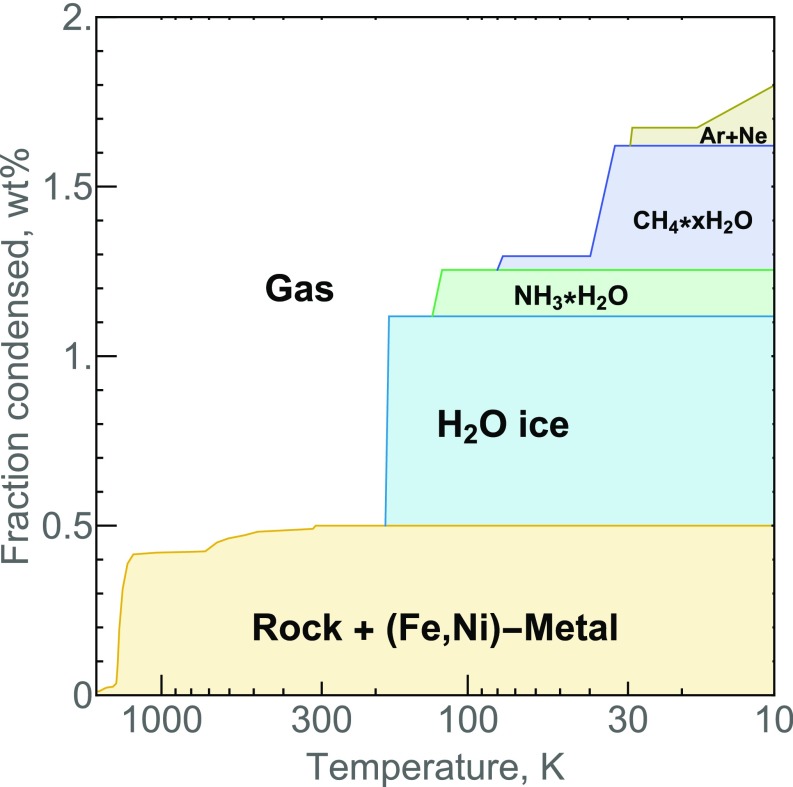
Protoplanetary disks of solar-like composition contain three principal planet-building components—nebular gas, H₂O-rich ices, and rocky [silicates-plus-(Fe,Ni)-metal] materials—whose compositions are a function of element volatility (characterized by the equilibrium condensation temperatures; Fig. 3) and, therefore, change radially and temporally with changing temperature. In the case of cooling, a gradual decrease in temperature results in progressive condensation of Fe–Mg–Ca–Al silicates and (Fe,Ni)-metal making up 0.5% of the total disk mass at ∼1,000 K, until C,N,O,H-bearing ices (1.0% total mass) start to sequentially condense below ∼200 K. The condensation of ices is a sharp feature in the protoplanetary disk. Once the temperature drops a bit (a few kelvins) below its condensation temperature, a very large amount of ice would form. In the case of heating, for example, due to inward dust drift, the sequence of phase changes reverses. The disk never gets cold enough for condensation of He and H₂, so ∼98 wt% of the disk always remains gaseous.

Fig. 3.

The stability fields of planet-building materials in a protoplanetary disk of solar composition at 10⁻⁴ bar. The fraction of condensed rocky matter (>200 K) is calculated with the GRAINS code (58), while condensation temperatures and abundances of ices are taken from ref. 59. The composition of gas is temperature dependent and always complementary to the composition of the condensed phase assemblage.

Because the condensation temperatures of silicate and ice phases are quite different, it is their condensation fronts in the midplane of protoplanetary disks that set the rough boundaries of planetesimals with different compositions (16). The most important among them—the snowline—marks the stability field of the H₂O ice. The presence of ices would significantly enhance the local mass surface density of solids in the disk. H₂O snowlines are prominent features in protoplanetary disks, which have been predicted theoretically (17–19), then inferred around TW Hya (20) and HL Tau (21), and now observed by ALMA around young star V883 Ori undergoing FU Ori outburst, which pushes the water snowline to 40 a.u. to make it observable (22, 23).

If a planet forms in the presence of ices, the phase diagram predicts a similar amount of multicomponent, H₂O-dominated ices to be added to the rocky material. The rock/ice ratio does not strongly depend on the host star metallicity ([Fe/H] or [M/H]) because the metallicity mostly reflects the ratio of the total condensable solid materials (metal-plus-rock-plus-ices) to the H₂-plus-He gas.

Planet formation in the solar system is thought to have started in an accretion disk that fed the initial mixture of interstellar H₂-plus-He gas, C,N,O-rich ices, and Mg,Si,Fe-rich silicates to the growing Sun. At some point, the disk became thermally zoned, with the inner regions being hot enough for complete evaporation of all ices and some silicates and the colder outer zone where only a portion of ices could evaporate. Within each zone, the dust grains first coagulated into kilometer-sized planetesimals, and then, within ∼10⁵ y, Moon- to Mars-sized planetary embryos accreted. The initial differences in radial proportions of silicates and ices in the protoplanetary disk, along with other factors, resulted in the formation of three types of planets in our solar system—the small terrestrial rocky planets, the large gas giants Jupiter and Saturn, and the intermediate ice giants Uranus and Neptune. Whether the formation of our solar-system planets is typical or not is still an open question.

Pebble accretion has been proposed to explain the fast growth of planets to a few Earth masses (ref. 24, figure 7). Growth by pebble accretion is only effective for icy pebbles where H₂O occurs as layers of ice coating silicate dust (25). When drifting across the snowline, ices may (partially) sublimate (SI Appendix, Fig. S1). The inward drift of icy pebbles may effectively push the snowline closer to the star (26), making the snowline a dynamic feature with location changing as the disk evolves (27–29). If a planet growth involves pebble accretion, then, regardless of the detailed growth mechanisms, both ice and rock should participate in the growth process, with the ice amount being comparable to the silicates. In the case of gas dwarfs, this means that at least some of their cores should contain ices in addition to rock.

Icy planets can migrate inward through planet–disk interactions (30) or planet–planet scattering (31) and continue growing, as illustrated by the growth tracks in the planet mass–semi-major axis diagrams of ref. 32. We propose such a mechanism to form the two subpopulations of exoplanets with radii between 1 and 4 R_⊕. This point is reinforced by the bimodality of densities, and thus compositions, of the satellites of Jupiter, Saturn, Uranus, and Neptune (SI Appendix, Fig. S2).

To interpret the observed mass–radius distributions, we modeled the growth curves of planets by adding either ice or gas to a rocky core (Materials and Methods and SI Appendix).

The mass distributions of small planets are compared with each other (Fig. 2, histograms on the x axis) and the calculated growth tracks (Fig. 1). Planets of 1.4–1.9 R_⊕ and 2–3 R_⊕ are compared, where each bin contains about 20 planets (SI Appendix, Table S1). The mass distributions of sub-Neptunes range from 3 to 20 M_⊕, while super-Earths truncate at 10 M_⊕. The first population has masses of 5.3 ± 1.5 M_⊕. The second population has masses of 8.3 ± 3 M_⊕. The offset of 3 M_⊕ suggests that the cores of the second population are significantly more massive, which coincides with adding ice to rock (Fig. 1, cyan arrows, growth curves of ices).

Bimodal mass distribution of the radial-velocity (RV) sub-Neptune population (2–4 R_⊕) is identified, and the higher peak of this, with the mass of ∼16 M_⊕, may result from the merging of primary icy cores. This can explain why Uranus (33), Neptune, and similar planets did not accrete significant amount of H₂-plus-He gas, although their final mass appears to be greater than the critical core mass (34) for a runaway gas accretion. This means that the Uranus, Neptune, and many other icy cores like them are mergers of many smaller, less massive, primordial icy cores. Each primordial core is less massive than the critical core mass. The collision and merging of two primordial cores can partially remove their H₂/He envelopes (35), if such existed, while retaining most of their core masses. The colliding icy cores are more likely to stick and merge, yielding a core of doubled mass. In contrast, a collision of two rocky cores, each bigger than ∼10 M_⊕, tends to catastrophically disrupt them rather than to merge (36).

Transit–timing–variation (TTV) planets (Fig. 2, triangles) of 2–4 R_⊕, on the other hand, show systematically smaller masses. They are preferably found around metal-poor host stars ([Fe/H] less than −0.3) (37), as opposed to RV sub-Neptunes, which are found across a wide range of metallicity (12), suggesting somewhat different formation environments.

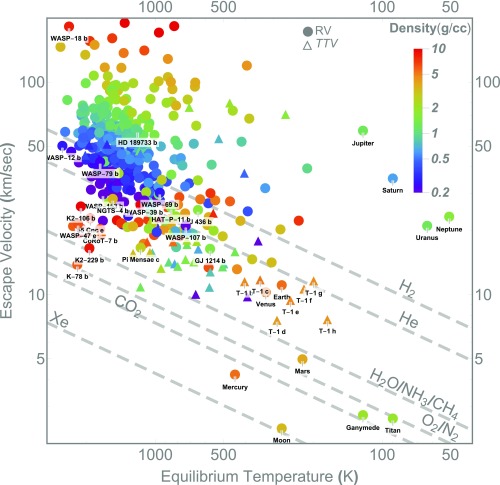
Atmospheric escape has a correlation between the escape velocities and atmospheric compositions of objects in our solar system (Fig. 4). Applying the same physics to exoplanets, one can calculate, for a given surface temperature, what gaseous species a planetary atmosphere can hold. Super-Earths and sub-Neptunes have escape velocities on the order of ∼20 km/s, marked by the contour of M_p/R_p = 3 in the Earth units (Figs. 1 and 2). A value of 20 km/s roughly corresponds to the thermal escape threshold of atomic hydrogen at 150 K, or molecular hydrogen (H₂) at 300 K, or helium at 600 K. Therefore, bodies with M_p/R_p < 3 are susceptible to the escape of H₂ and He. The H₂ in their atmospheres/envelopes cannot last over billion-year timescale unless being continuously replenished by an underlying reservoir. It is possible that methane CH₄, ammonia NH₃ (38–40), and even H₂ (41) outgas gradually from an initial H₂O reservoir to replenish a primary envelope, or to form a secondary one. During this process, He and heavier species are preferentially retained (42). There is a huge density contrast among planets residing around the He escape threshold (gray dashed line labeled “Helium” in Fig. 4). Some of such planets, for example, WASP-107 b (43, 44), WASP-69 b (45), HD 189733 b (46), and HAT-P-11 b (47, 48), are observed to be surrounded by He-rich extended atmospheres suggestive of He escape from them. Because of similar temperatures and escape velocities (depth of surface gravity potential well), all planets residing there would be losing He (and H₂) at this moment, if they have any. We infer that the He escape threshold is the boundary separating the populations of puffy hot-Saturns and small (<4 R_⊕) exoplanets. The latter likely possess higher mean molecular weight atmospheres with H₂O in their deeper interior (above a few gigapascals) partitioned among condensed phases including fluids, insulating solids, and superionic ices (49).

Fig. 4.

Atmospheric escape velocities versus surface equilibrium temperature. Data from ref. 60. Color coding is the bulk density of planet. Many super-Earths and sub-Neptunes are not expected to retain a H₂-He–dominated envelope over a billion-year timescale.

Water worlds have other observational evidence including the following: (i) spectroscopy of metal-polluted white dwarfs showing that some planetary debris accreted by white dwarfs are ice-rich (50, 51); (ii) transmission spectroscopy of an inflated Saturn-mass exoplanet WASP-39b that shows strong water absorption features corresponding to the estimated H₂O/H ratio of 151×solar in the planet’s atmosphere (52).

Monte Carlo simulation was used to show that the bimodal radius distribution (yellow histograms on the y axis in Figs. 1 and 2) could arise from the dichotomy of rocky and icy cores. It is performed with the following assumptions. The protoplanetary disk is assumed to have solar-like major element ratios (Fe:Mg:Si:O:C:N), inferred from the tight distribution of C/O and Mg/Si ratios around solar values in the main-sequence stars in the solar neighborhood (53). Besides the H₂–He gas, the disk contains roughly one part of Mg–silicate–rock-plus-(Fe,Ni)-metal, one part of H₂O ice, and one part of other ices (methane clathrates and ammonia hydrates, which are still dominated by the H₂O in their compositions) by mass. Due to the disk temperature gradient and condensation temperature gap between the rock-plus-metal and ice, the disk is thermally zoned into an inner zone with solid rock-plus-metal dominating, and an outer zone with both rock-plus-metal and ices (mostly H₂O) suspended in H₂-plus-He gas.

The simulation reproduces the bimodal radius distribution (Fig. 2, blue vertical histogram). It also reproduces the mass–radius distribution of RV planets with their gap, groupings (Fig. 2, gray contours in the background), and mass offset. Planets >3 R_⊕ generally require the presence of a gaseous envelope.

Conclusions

We divide exoplanets around sun-like stars into four main categories according to the cumulative planet radius distribution (14) and mass–radius diagram (Figs. 1 and 2):

• i)Rocky worlds (<2 R_⊕) consist primarily of Mg–silicate–rock and (Fe,Ni)-metal; they broadly follow the extrapolation of mass–radius relation of Earth and Venus.
• ii)Water worlds (2–4 R_⊕) contain significant amounts (>1/4, and possibly more than 1/2, by mass) of H₂O-dominated ices in addition to rock. TTV planets in this radius range are consistent with a less massive core possessing a gaseous envelope; they tend to be found around metal-poor stars (37).
• iii)Transitional planets (4–10 R_⊕) are likely to be ice-rich with substantial gaseous envelopes (≳5–10% by mass). They are typically a few tens of M_⊕ forming a bridge between small exoplanets and gas giants on the mass–radius diagram. The microlensing surveys (54, 55) find some of them at a few astronomical-units distance.
• iv)Gas giants (>10 R_⊕) are dominated by H₂–He in the bulk composition and have masses and radii comparable to Jupiter.

Our own solar system planets fit into this classification. However, two puzzles remain unsolved: the compactness of many Kepler planetary systems compared with our own solar system and the lack of planets intermediate in size between Earth and Neptune in our own solar system. These two puzzles may be interrelated. Solving them is the key to understanding the unique initial conditions that form our own solar system. The abundance of these intermediate-size planets (water worlds) in our galaxy challenges us to understand their formation, migration, interior structure, atmosphere, and habitability.

Materials and Methods

The planet radii are calculated as: R = M^1/3.7 for rocky cores (56), and R = f $\times$ M^1/3.7 for icy cores (which also contain rock-plus-metal), where f is an increasing function of ice mass fraction “x.” For instance, if x = 0 (no ice), then f = 1; if x = 1 (100% ice), f = 1.41. Interpolation gives f = (1 + 0.55 x −0.14 x^2) (57). From disk element abundance, “x” of icy cores typically range from 1/2 to 2/3, depending on the incorporation of more volatile clathrate and hydrate ices. Then, “x” is assumed to follow a uniform distribution in-between 1/2 (solar rock/H₂O-ice ratio) and 2/3 (solar rock/total-ices ratio) for icy cores. The masses of rocky and icy cores are assumed to follow their observed mass distributions, respectively (histograms on the x axis in Fig. 2). Considering the mass balance between the rock-plus-metal and ices, the number ratio of rocky to icy cores is ∼1:2, matching the occurrence rate of super-Earths (1–2 R_⊕) versus sub-Neptunes (2–4 R_⊕) (12). With geometric transit probability, their observed number by Kepler is about equal. Additional ±7% 1-σ Gaussian errors in R_p and ±30% 1-σ Gaussian errors in M_p are included in the simulation to account for the observational uncertainties. See more details in SI Appendix.