Abstract
The QM/MM method has become a useful tool to investigate various properties of complex systems. We previously introduced the Layered Interacting Chemical Models (LICHEM) package to enable QM/MM simulations with advanced potentials by combining various (unmodified) QM and MM codes (JCC, 27, 1019). LICHEM provides several capabilities such as the ability to use polarizable force fields, such as AMOEBA, for the MM environment. Here, we describe an updated version of LICHEM (v1.1), which includes several new functionalities including a new method to account for long–range electrostatic effects in QM/mm (QM/MM–LREC), a new implementation for QM/MM with the Gaussian Electrostatic Model (GEM), and new capabilities for path optimizations using the quadratic string model (QSM) coupled with restrained MM environment optimization.
Graphical TOC Entry
Introduction
The Layered Interacting CHEmical Models (LICHEM) program,1 enables the use of unmodified quantum mechanics (QM) and molecular mechanics (MM) packages for QM/MM simulations. LICHEM provides a platform to perform QM/MM calculations with polarizable force fields such as AMOEBA,2–4 as well as several different simulation modes including single-point energies, frequencies, geometry optimizations, reaction path optimizations, and Monte Carlo simulations. The calculations are performed by interfacing different software packages including Gaussian,5 PSI4,6 NWChem,7 TINKER,8 and TINKER–HP.9 Here, we present recent improvements to our code, as well as new capabilities, to address several issues that may arise in QM/MM calculations.
Most QM/MM simulations are performed by neglecting the effect of long–range electrostatics (LRE) or are carried out using approximations such as spherical or stochastic boundary conditions. Several methods have been developed to take these long–range effects into account including the local reaction field method for empirical valence bond/molecular mechanics (EVB/MM),10,11 generalized solvent boundary potential (GSBP),12,13 the solvated macromolecule boundary potential (SMBP),14,15 the spherical solvent boundary potential (SSBP),16 QM/MM–Ewald,17,18 QM/MM–PME,19 Ladd lattice summation,20 shifting–switching function,21–24 among others. We have recently introduced the QM/MM long range electrostatic correction (QM/MM–LREC),25,26 which uses a smoothing function coupled with the minimum image convention approach to smoothly decrease the electrostatic interactions and forces to zero at the cutoff radius.
The use of polarizable/multipolar potentials such as AMOEBA2–4 in QM/MM simulations provides an improvement on the description of the MM environment. However, some issues still remain, including (but not limited to) possible over–polarization of the QM wave-function27 and loss of anisotropy and errors related to charge penetration effects.28,29 We have recently reported a proof–of–principle implementation in LICHEM for QM/MM simulations using our Gaussian Electrostatic Model (GEM).30–35 GEM is a density–based polarizable force fields that uses Hermite Gaussians to reproduce the molecular electronic density of individual fragments, and includes separate terms for Coulomb, exchange–repulsion, polarization, charge–transfer, and dispersion. We have recently developed an initial implementation of QM/GEM in LICHEM that provides the ability to employ GEM for the MM environment.36
One of the main applications of QM/MM simulations is to investigate the kinetics of chemical processes. To this end, it is useful to determine the minimum energy paths (MEPs) and transition states (TSs) associated with the desired processes. A popular group of methods to determine MEPs on a potential energy surface (PES) is the so–called chain–of–replica family. These methods rely on the knowledge of two minima on the PES (e.g. reactant and product). Based on these points, it possible to create a series of images (replicas) connecting the two end–points and use the relation between the gradient of the energy and the tangent to the path to optimize the MEP.
One widely used method to determine MEPs is the nudged elastic band (NEB) method.37 NEB is a first order method that uses a ”spring” between adjacent images (replicas of the system), to maintain them equidistant along the path and the path is minimized in the direction perpendicular to the spring force. Burger and Yang introduced the quadratic string method (QSM), where each point on the MEP is minimized in a downhill direction perpendicular to the path using a quadratic surface, which is approximated by a damped BFGS updated Hessian and the integration is done by an adaptive step-size method (N-order Runge-Kutta).38 This method has the advantage that it is independent of the integration step-size and the spring constant, and it can be used in reactions with multiple barriers.
One more issue that can arise in path optimization calculations involves the initial guess for the structures along the path (i.e. the chain–of– replicas). This initial guess is generally obtained by performing a simple linear interpolation between the two local minima (e.g. reactant and intermediate/product). When this approach is performed in a QM/MM system, the interpolation is usually done only for the QM region, whereas the environment atoms in the MM region is generally approximated by the environment from one of the two local minima, and is replicated for all the images. This approximation of the MM environment may result in path discontinuities in early iterations, especially if overlapping atoms exist within the intermediate structures or if multiple MEPs exist between the endpoints.39–41
In the restrained environment optimization approach, the initial path is iteratively minimized, first optimizing the QM atoms with QSM followed by the restrained optimization of the environment using a truncated Newton method.40,42 In the MM optimization, the environmental atoms are under restrain constants, which are gradually removed in each internal cycle, until all restraints are removed.39
In this new update, LICHEM v1.1, we include four major capabilities: the long–range electrostatic corrections (QM/MM–LREC) approach,25,26 the QM/GEM implementation,36 the Quadratic string method (QSM)38,43 for determining minimum-energy path, and the Restrained environment optimization. 39,40,42 In addition, we have included other minor improvements to LICHEM such as the capability to freeze QM atoms in QM/MM optimizations, the ability to specify particular QM atoms involved in the QSM or NEB calculations (to better describe the degrees of freedom involved in the elementary reaction step39), additional flexibility for QM/MM optimizations by enabling the use of specific energy and force tolerances for both QM and MM regions, and a debug option to save all output files from the QM and MM software.
The paper is organized as follows, in the next section (Methodology), we introduce a description for the new algorithms and approaches implemented in LICHEM. Given that the implementation details for LREC can be found elsewhere,25,26,36 and the QM/GEM implementation36 is in the initial stages (the full implementation with pmemd.gem will be we reported in a forthcoming report), we will only provide a brief overview, and concentrate on the new implementation of the quadratic string method and the restrained environment optimization, and how they were incorporated into LICHEM QM/MM scheme. Subsequently, results and discussion are presented on two model systems: a double proton transfer between two aspartic acids, and the path optimization for the reaction mechanism of N-tert-butyloxycarbonylation of aniline in [EMIm][BF4], followed by concluding remarks.
Methodology
QM/MM Long–range electrostatic correction
Our recently developed algorithm to include long–range electrostatic (LRE) effects, QMMM–LREC, relies on the use of a smoothing function to scale the electrostatic potential (coupled with the minimum image convention where needed) based on the distance between the atoms.25,26 This approach smooths the electrostatic potential and forces until they are set to zero at the cutoff radius and has been designed to produce energies and forces in good agreement with PME.
The smoothed Coulomb potential resulting from the LREC method, Vij,lrec, is given by
| (1) |
where
| (2) |
and
| (3) |
The function f in Eq. 2 is the LREC smoothing function and s is an adjustable integer exponent. The LREC exponent and cutoff can be adjusted to control the convergence, cost, and accuracy of the method. In general, QMMM–LREC shows energies and forces in good agreement with PME with a cutoff ≥ 20 Å.25,26 In addition, the LREC smoothing function can be combined with other LRE methods such as PME, as well as used for multipolar potentials. 26
QM/MM simulations with GEM
The combination of QM and MM descriptions can lead to issues of over-polarization at the QM/MM boundary. One possibility to ameliorate this issue is to employ a continuous description of the charge density on the MM environment. The Gaussian Electrostatic Model (GEM) is a force field based on frozen molecular densities that can be used to represent the MM environment, as we have recently reported.36 In our first proof–of–principle implementation, the total energy of the system in QM/GEM calculations is expressed by:
| (4) |
where the last term in the left hand side of Eq. 4 denotes the QM/MM inter–molecular interactions. This last term can be separated as follows:
| (5) |
where , and correspond to the Coulomb, exchange–repulsion, polarization and dispersion interactions between the two subsystems respectively. In our recent implementation, the first two terms (Coulomb and exchange–repulsion) are explicitly included in the effective Hamiltonian.36 As mentioned above, this initial implementation is only at the experimental stages and thus is not included in the release version of LICHEM. The QM/GEM implementation including the use of pmemd.gem34,44 will be reported in a forthcoming contribution.
Quadratic string method
The new version of LICHEM also includes an implementation of QSM for reaction path optimizations in order to address convergence and efficiency issues. The method eliminates the need for an artificial spring constant, and does not require a predetermined step size. Instead, the surface and the trust radius of the approximate Hessians are updated at the end of each iteration.
The details of the QSM algorithm can be found in the work of Burger and Yang.38 Briefly, in the QSM implementation available in LICHEM, the QSM algorithm starts with the calculation of energies and gradients of all beads that are provided by the user. The approximate Hessians (Hk) that were constructed with the gradients in the initial step are then updated with the damped Broyden-Fletcher-Goldfarb-Shanno (DBFGS) algorithm;
| (6) |
where i represents the iteration number. The δi and ri in Eqn. 6 are defined as;
| (7) |
| (8) |
with γi and θi as;
| (9) |
| (10) |
The update of Hk is followed by the update of the trust radii using the energy as a merit function;
| (11) |
where k represents the respective bead and ρ is used to compute how close the merit function is to the expected value. After the computation of the new trust radii, the path is integrated by using Runge–Kutta explicit 4/5 integration scheme with Cash–Karp parameters. The integration is performed until a bead reaches its trust radius, or the calculation is converged. The beads are redistributed if necessary by using a polynomial interpolation scheme.38 In our QSM implementation, the projection of the gradients, and the redistribution of the beads are performed by taking only the coordinates of the “active” atoms into consideration (see below). If no “active” atoms are specified, all atoms in the QM subsystem are considered as active.
A flowchart of the QSM algorithm implemented in LICHEM is depicted in Figure 1. Briefly, after the calculation of initial energies and gradients, a QM optimization is performed where the reaction path is updated in every QM step (minor iteration). QM iterations are finalized when convergence is achieved or the maximum number of QM steps is reached. If the desired calculation type is QM/MM, an MM optimization is performed. Calculations are carried out until convergence is achieved or the maximum number of optimization steps is reached (major iteration). In our implementation, calculations are performed with frozen ends, meaning that the optimization is performed only for the beads between the reactant and the product. Thus, the choice of the reactant and the product beads will have a great impact on the computed MEP.
Figure 1:
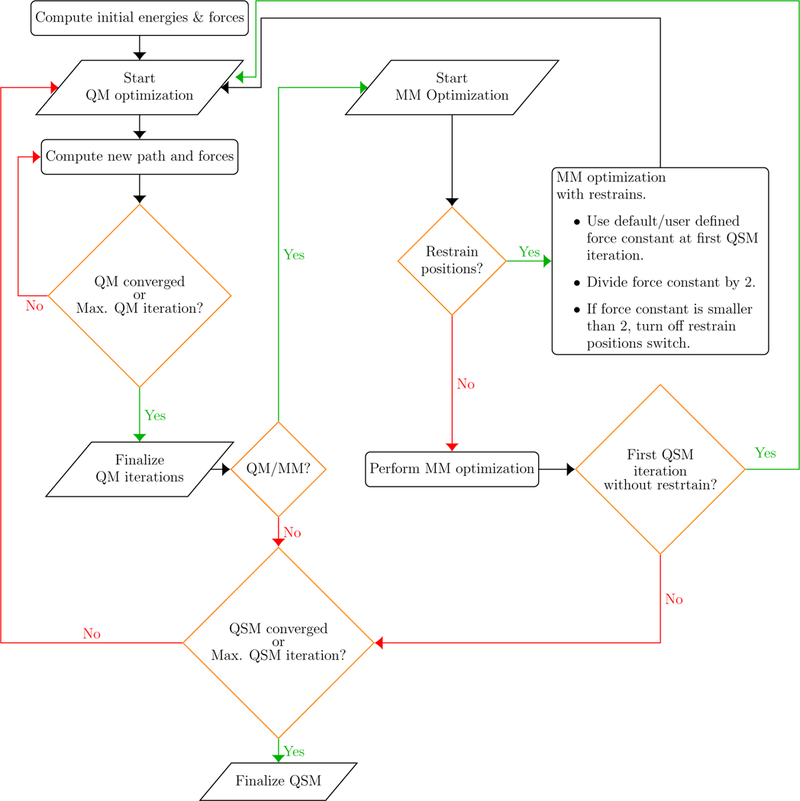
Flowchart of QSM algorithm implemented within LICHEM.
Restrained MM path optimizations
If the initial guess for the reaction path optimization is generated using the LICHEM path utility, beads are generated by performing a linear interpolation only for the atoms in the QM region. Atoms located in the MM region are assigned the same coordinates as the MM subsystem of the reactant structure for all beads except for the product bead. However, this approximation may not be an appropriate choice if the MM environment between the reactant and product are significantly different, which can lead to path discontinuities during the QM/MM path optimization.39,40 This obstacle can be overcome by performing a restrained MM optimization in the initial stages of the path optimization. At each subsequent iteration, the restraints are reduced until no restraints are left.39,40
We have included a version of this restrained MM path optimization approach for QSM path optimizations. In this implementation, the number of restrained MM iterations is defined by the initial force constant in kcal mol−1 Å−2 for the harmonic restraint potential. After every MM optimization with restrains, the force constant is reduced by half. The updated force constant is used in the following QSM iteration. The positions of the MM atoms are restrained in every QSM iteration until the force constant is < 2 kcal mol−1 Å−2. When the new force constant is < 2kcal mol−1 Å−2, the restrain position switch is turned off to perform MM optimizations without restrains in the following QSM steps (macro iterations). For instance, if the initial force constant, k, is defined as 100 kcal mol−1 Å−2, the number of restrained MM iterations will be 6 (k=100, 50, 25, 12, 6.25, and 3.125 kcal mol−1 Å−2). After the restrained MM iterations are finished (force constant is < 2), the MM optimizations are performed without restrains for at least two QSM iterations.
The QSM version in LICHEM has been also developed using a hybrid–parallel paradigm. Given that the codes used for the QM and MM calculations for each bead can be performed in parallel using the native parallelization of the specific code (OpenMP, MPI, cuda, etc), it is possible to add a hybrid parallelization scheme where the QSM optimization algorithm is further parallelized such that each bead may distributed to a separate compute resource as assigned by the user.
The hybrid–parallel QSM algorithm in LICHEM is implemented with the use of the MPI library. Here, the reactant bead is always owned by the first processor/node, while the product bead is always owned by the last processor/node. The remaining beads are then distributed in a cyclic manner. Calculations for reactant and product beads are performed only in the first optimization step since the QSM algorithm requires frozen ends.
Therefore, the best load balance in QSM calculations (with odd number of beads) is achieved when
| (12) |
where Nprocs is the total number of MPI cores (processor/node), and Nbeads is the total number of beads. During QSM calculations, each processor/node performs QM and MM calculations for the beads that they own (force calculations). After the forces are computed, the information is collected to the first processor which then computes the new path. Before every macro and micro iteration, first processor that owns all of the information distributes the new information (path, forces, switches etc.) to the remaining processors/nodes.
In addition to the inclusion of the new algorithms, several minor improvements have been introduced for performance and/or accuracy. These include added flexibility for convergence parameters in QM/MM optimization procedures by enabling user–defined maximum number of iterations, convergence parameters for deviation of the atomic coordinates, root mean square (RMS) force, and maximum force. Additional improvements involve an option to save all of the outputs from QM and MM software packages, the capability to freeze QM atoms in QM/MM optimizations, and an option to specify specific QM atoms involved in the reaction path optimization algorithms.
Computational Details
This subsection presents selected cases to test the new utilities in LICHEM, in particular the new path optimization options. As explained above, the LREC and QM/GEM implementations have been described in detail previously,25,26,36 and thus specific examples will not be provided here. All calculations were performed on a cluster based on individual nodes containing 20 core Intel SkyLake (E5–2660@2.6GHz) with 128 GM of memory and InfiniBand 56 mbps fully non-blocking interconnect (for the parallel calculations).
In order to compare NEB and QSM capabilities in LICHEM, we have conducted calculations for two reactions. The first reaction involves a double proton transfer between the side chains of two aspartic acids (di–Asp). This reaction is chosen in order to test the effect of different convergence criteria, to compare computed MEPs, and the required times for computation by NEB and QSM algorithms (this model system had been previously employed).26 The second test case involves the calculations of the rate limiting-step for the reaction mechanism of the N-tert-butyloxycarbonylation of aniline in [EMIm][BF4] using QM/AMOEBA, which as been previously reported.45
Double proton transfer in a model di–Asp system
The di–Asp test case has been carried out using the Gaussian 09 program package5 for energy and gradient calculations for the QM region, and TINKER8 for MM optimizations. The QM calculations are performed using ωB97}D level of theory using 6–311G(d,p) basis for atoms in the QM region, and pseudobonds for the boundary atoms. 46 The total number of beads for the path is set to 9 and the initial guess for the path was generated using the path utility in LICHEM. The optimization conditions for NEB and QSM calculations are set to be same. Optimizations are performed only for the beads between reactant and product. The maximum number of NEB/QSM iterations (macro iterations) was set to 10, while the maximum number of QM steps (micro iterations) was set to 25. The tolerance for the deviation of the atomic positions for the QM atoms was set to 0.001 Å. Three different combination of tolerance values for the maximum force and the RMS force were tested. The combination of these criteria are depicted in Table 1. For the NEB calculations the RMS force tolerance for the MM optimization was set to 0.1 kcal/Å, The spring constant was set to 1 eV/Å2, and the maximum step size and step scale factor were set to 0.1Å and 0.5 respectively. All calculations involved 14 QM atoms (with 6 active atoms involved in the reaction), 2 pseudobonds, 10 boundary atoms, and 24 MM atoms as depicted in Figure 2.
Table 1:
Convergence criteria for the QM steps (micro iterations). RMS and MAX force tolerances are given in Hartree/Bohr while the deviation of the atomic positions are in Å.
| Tolerance | Atomic Positions | RMS Force | MAX Force |
|---|---|---|---|
| Tight | 0.001 | 0.0025 | 0.015 |
| Moderate | 0.001 | 0.0250 | 0.015 |
| Loose | 0.001 | 0.0250 | 0.150 |
Figure 2:
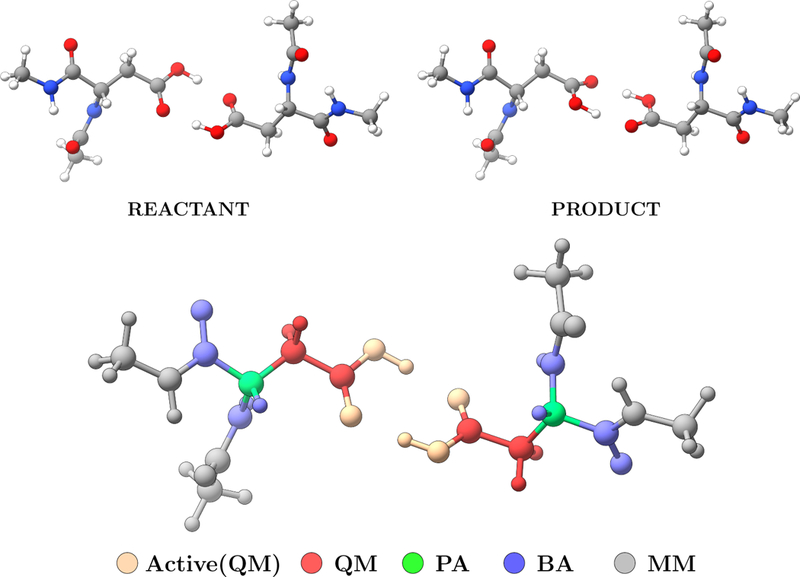
The QM (red), MM (gray), boundary (blue), pseudo (green), and active (light orange) atoms during NEB and QSM path optimizations for di–Asp test case.
The parallel implementation of QSM was tested with the same di–Asp model system solvated in a box containing 31981 water molecules using the polarizable AMOEBA force field.2–4 Calculations were performed with frozen ends using 7 nodes in order to obtain an optimal load balance. The distribution of the beads are depicted in Figure 3. Each node was set up to own one bead except the reactant and the product beads which were owned by the first and the last node respectively.
Figure 3:
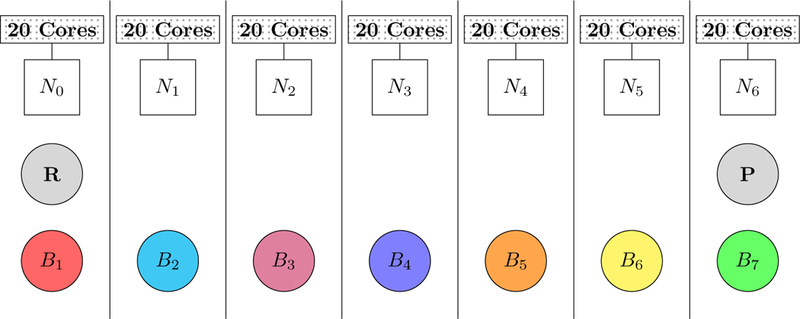
Distribution of 9 beads among 7 nodes in parallel QSM calculations. Each bead is depicted alphanumerically (Bbead_number) and is represented with different colors of circles except the frozen ends. The reactant (R) and the product (P) beads are depicted with gray circles. Each node, consisting 20 CPU cores, is depicted alphanumerically (Nnode_number) and represented with squares.
The same QM and MM subsystem definitions were employed for the solute as in gas phase calculations (see Figure 2), and all the solvent molecules were described by the MM environment. The QM region was calculated using the Gaussian 16 program package,47 at the HF/6–311G(d) level. The convergence criteria for the QM calculations were defined as 0.025 Hartree/bohr, 0.05 Hartree/bohr and 0.0lÅ for RMS force, maximum force, and the deviation of atomic positions respectively. The RMS force tolerance for the MM optimization was set to 0.1 kcal/Å. The LRE effects were taken into account using LREC with a cutoff radius of 25Å. Two different scenarios were taken into account for the calculations using QSM; calculations without restrains on MM atoms, and calculations with positional restrains on MM atoms for a certain number of macro iterations (see Figure 1). The initial force constant for calculations using restrains on positions was defined as 100 kcal mol−1 Å−2 leading to a total number of 6 pre-iterations. The same system is also investigated with the serial NEB algorithm using the same spring constant, maximum step size, and step scale factor as in gas phase calculations.
Rate-limiting step in the N-tert-butyloxycarbonylation of aniline in [EMIm][BF4]
Some of us have previously studied the N-tert-butoxycarbonylation of aniline in a water/IL mixture.45 Here, we present one of the proposed reaction mechanisms (configuration 1, nearby IL ion pair). This reaction mechanism corresponds to the nucleophilic attack by the aniline to the carbonyl of one of the Boc groups, without the simultaneous formation of CO2.
Details of the parameter determination and system setup for the simulations have been described previously.45 All the QM/MM calculations were performed using LICHEM.1 The QM region (149 atoms) was calculated at the ω97XD/6–31G(d) level. The MM region (26,688 atoms) was modeled using the AMOEBA force field.2–4 LRE effects were taken into account using LREC,26 with an LREC exponent of 2 and a cutoff radius of 20 Å ( see Ref.45 for details). The initial guess for the MEP was obtained by a linear interpolation between the reactant and product structure using 7 beads (Figure 4) using the path utility in LICHEM.
Figure 4:
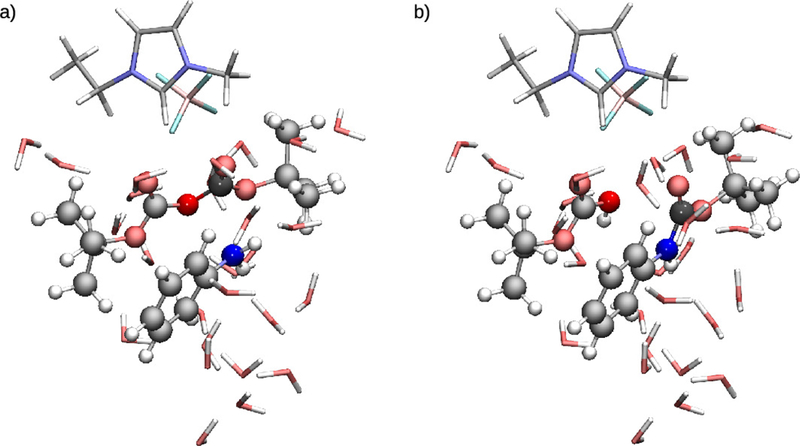
Optimized reactant (a) and product (b) QM regions for the N-tert-butyloxycarbonylation of aniline. Atoms are colored by: C-gray, O-red, N-blue, H-white, B-pink, F-cyan.
The QSM–parallel implementation was used to minimize the path and approximate the TS structure. The maximum number of QSM iterations (macro iterations) was set to 15, and the maximum QM iterations was set to 50 (micro iterations). The tolerances for the simulation were set to: QM RMS deviation: 0.001 Å, QM RMS force: 0.005 EH/Bohr, QM max force: 0.025 EH/Bohr, MM RMS deviation: 0.2 Å, MM RMS force: 0.2 kcal mol−1 Å−2. The path was optimized using the restrained MM optimization method described above, starting with an initial restraint on the MM atoms of 100 kcal mol−1 Å−2. Additionally, the same initial MEP was optimized without the contribution of the polarization term from the AMOEBA force field,2–4 using the same optimization criteria previously described, to qualitatively investigate the effect of the contribution of the polarization term from the MM environment for this system.
Results and Discussion
Double proton transfer in a model di–Asp system
Reaction path optimizations were performed using both the NEB and QSM algorithms in serial in order to asses the new path optimization utilities implemented in LICHEM. Inclusion of new convergence criteria enabled us to perform calculations with different tolerance values. The effect of the convergence criteria on the final path, and on the total wall time wass studied by performing calculations with tight, moderate, and loose tolerance values.
The double proton transfer reaction of di-Asp case was studied using seven intermediate structures, which were optimized throughout the calculations. The results obtained with NEB and QSM algorithms are depicted in Figure 5.
Figure 5:
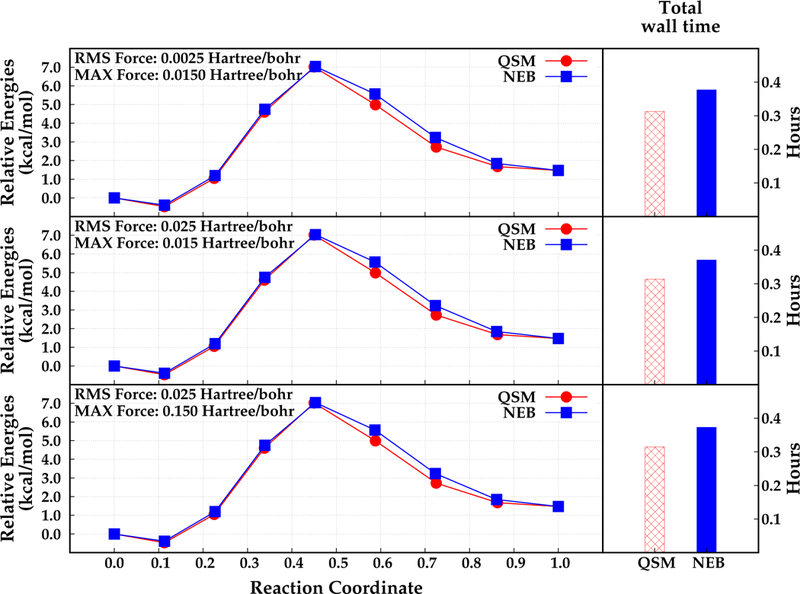
Relative energies that are obtained by NEB (blue, square) and QSM (red, circle) along the reaction coordinate (left), and total wall time required for the optimization in hours (right). Different convergence criteria are depicted in different rows. Reactant, product and the optimized structures (beads) are represented with filled dots.
The computed relative energies of every bead along the reaction coordinate for the di–Asp system are similar regardless of the chosen path optimization algorithm. In addition, the relative energies of any corresponding bead differ from each other at most 0.001 kcal mol−1 using different convergence criteria. These results suggest that the optimization of this double proton transfer reaction path is not significantly affected by the convergence criteria. However, it should be noted that a very tight or a very loose convergence criterion may alter the final reaction path, especially for larger systems. Thus, a moderate convergence criteria would be sufficient for small systems such as the di-Asp model system. In case of larger systems that involves hundreds of atoms, using a slightly tight convergence criteria with high number of QM iterations and/or high number of path optimization steps will provide more reliable results (see below).
The locations of the optimized beads along the reaction coordinate are almost the same with the NEB and QSM algorithms. However, the computed relative energies of the beads are slightly different from each other regardless of the convergence criteria. It is observed that the NEB algorithm results in slightly higher relative energies than QSM. The largest difference is approximately 0.58 kcal mol−1 for bead 6 which is located after the transition state structure, bead 5 (see Figure 5). Both algorithms found a slightly more stable reactant structure (bead 2) that has a relative energy of −0.47 kcal mol−1 and −0.38 kcal mol−1 with QSM and NEB respectively. Furthermore, the activation energy barrier for the double proton transfer in di-Asp case found almost same with QSM and NEB algorithms, 7.02 kcal mol−1 and 7.03 kcal mol−1 respectively.
Total wall times for QSM and NEB using the three convergence criteria are computed and are depicted in Figure 5. It is observed that NEB requires more time relative to QSM algorithm for all convergence criteria. The reaction path optimization with NEB is found to require 10 micro iterations and 2 macro iterations. Conversely, for QSM the MEP is converged in 7 micro iterations and 2 macro iterations The total wall time for QSM is approximately 0.31 hours regardless of the convergence criteria. Conversely, NEB required approximately 0.06 hours (3.6 min) more than QSM. Wall time for MM optimization was about 0.03 hours (1.8 min) regardless of the convergence criteria for both algorithms. As expected, the most time consuming part of the reaction path optimization is the QM subsystem optimization. It is observed that even with a small number of QM atoms, QSM is approximately 18% faster relative to NEB.
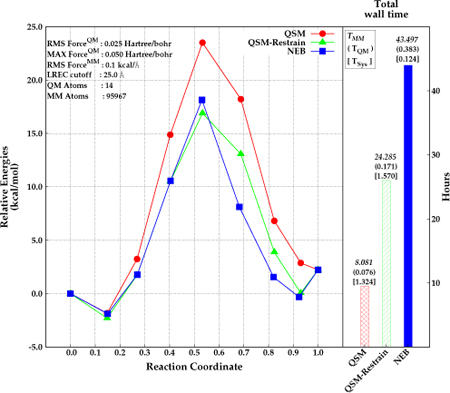
The parallel implementation of QSM was investigated for the same test system including explicit solvent. Specifically, the di–Asp system was embedded in a 90 Å3 box of AMOEBA2–4 water. The QSM calculations were performed both with and without restraints on the MM atoms. The reaction path for the solvated system was also calculated with NEB for comparison. The results are depicted in Figure 6. The energy barrier for the di–Asp system was found to be 25.4 kcal mol−1, 20.0 kcal mol−1, and 19.2 kcal mol−1 using the QSM algorithm without restrained MM optimization, NEB (climbing image in serial), and QSM with restrained MM optimization (parallel) respectively. The paths obtained with QSM with restrained MM, and NEB give similar relative energies for the first half of the reaction (beads before the TS). However, the path is slightly steeper after the transition state with NEB than with QSM. The use of restraints on the MM region in the initial stages of the path optimization result in an optimized MEP with a corresponding activation energy that is about about 6.2 kcal −1 lower compared with the QSM calculations without the restrained MM optimization.
Figure 6:
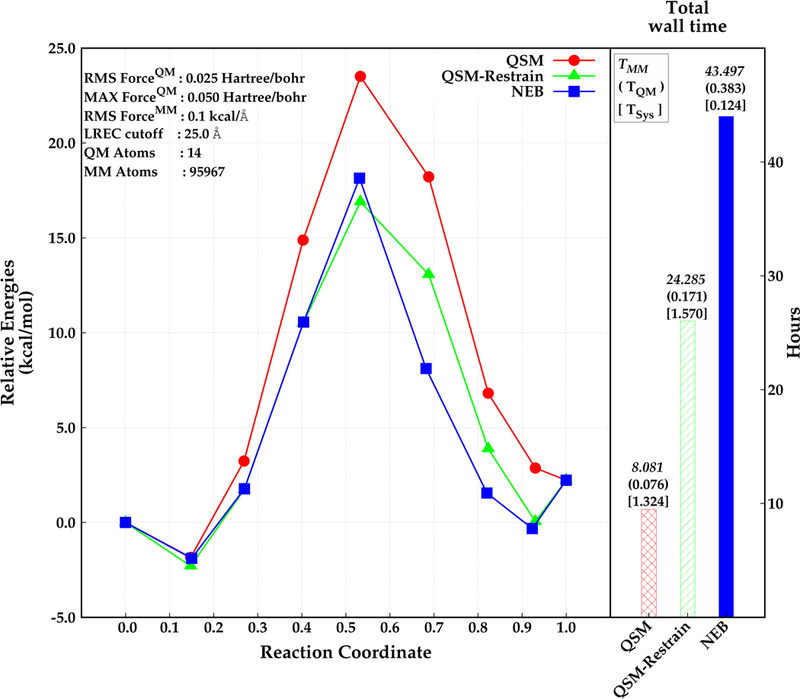
Relative energies obtained by NEB (blue, square) and QSM (red, circle), and QSM using the restrained–MM method (green, triangle) along the reaction coordinate (left), and total wall time required for the optimization in hours (right). Reactant, product and the optimized structures (beads) are represented with filled circles. The wall time for MM calculations, QM calculations, and for system calls are depicted above the wall time bars (right).
The lower barrier for the QSM path with restrained MM is most likely due to a better convergence of every image to the MEP. The initial guess for every image along the path in all cases is obtained by a linear interpolation of the QM degrees of freedom (DOF), while the MM DOF for every image are approximated by the MM coordinates of one of the end–points. Thus, the MM environment for the images that are further away from the end point used to approximate the MM environment will not have an MM environment that is close to the minimum. The use of restraints in the initial stages allows for a smoother convergence of the MM DOF especially for the images that are far from the minimum.
The restrained MM optimization approach is useful in cases where the MM environment for the images along the path is not optimal. In our experience, this is observed for elementary steps. In cases where the MEP is comprised of several elementary steps, as in the case of the reaction catalyzed by TET2,48 although it is theoretically possible to optimize the full path from the reactant to the final product, the MM environment is significantly different between the two end points. In these cases, even the use of the restrained MM might be useful only to an extent and path discontinuities can arise. A possible alternative is to separate every elementary step of the path, optimize the critical points and perform separate MEP optimizations.
The wall time for QSM was about 8 hours without the restrained MM optimization. Applying restrains on the MM region for 6 iterations (reducing them at each iteration) in QSM increased the total wall time for the calculation by about 16 hours. The wall time for NEB was found to require almost twice as much time to obtain a converged path relative to QSM with restrained–MM. Most of the time was spent for the calculations involving MM region. The time required for the system calls is around 1 hour longer in QSM than in NEB. This is due to the calls by the MPI library for the communications between 7 nodes. The increase of the total number of macro and micro iterations when restrains are applied to the MM region (8 macro and 27 micro iterations) did not increase the wall time for the system calls relative to the QSM calculations without restrained MM (2 macro and 7 micro iterations). Taken together, these results suggest that the use of the hybrid-parallel scheme in QSM coupled with the restrained MM optimization during the initial stages of the calculation provides an efficient strategy for path optimization.
Rate-limiting step in the N-tert-butyloxycarbonylation of aniline in [EMIm][BF4]
The second test system used to investigate the performance of the new QSM investigation is the rate limiting step for one selected configuration (configuration 1) of the N-tert-butyloxycarbonylation of aniline in a mixture of [EMIm][BF4]/water.45 This step involves a concerted nucleophilic attack by the aniline coupled with release of carbon dioxide. For the aniline nucleophilic attack, the calculated energy barriers with explicit polarization using NEB, QSM without restrained MM and QSM with restrained MM were 24.08 kcal mol−1, 21.08 kcal mol−1 and 18.35 kcal mol−1 (Figure 7), respectively. On the other hand, the energy barriers without explicit polarization using NEB, QSM without restrains and QSM with restrains were 35.97 kcal/mol, 30.43 kcal/mol and 29.89 kcal/mol (Figure 8), respectively.
Figure 7:
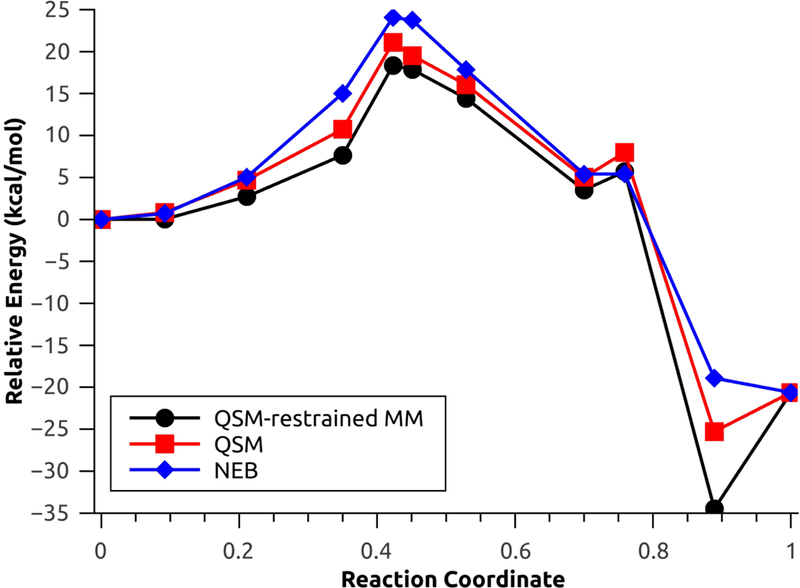
Minimum energy path for the aniline nucleophilic attack, with explicit polarization.
Figure 8:
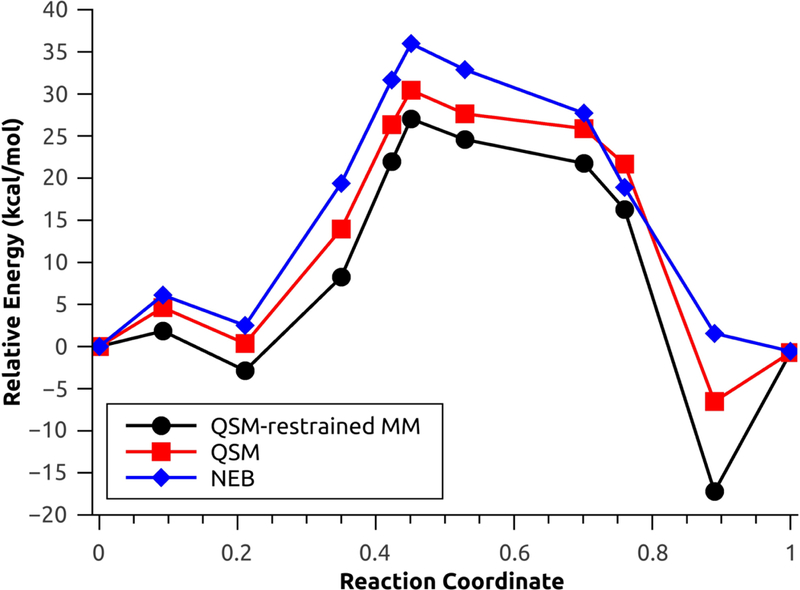
Minimum energy path for the aniline nucleophilic attack, without explicit polarization.
The large energetic differences (approx. 10 kcal/mol in all cases) are due to the lack of the polarization component, which results in the rearrangement of solvent molecules in the MM environment,1,45 which is comprised by highly polarizable monomers49 (water and [EMIm][BF4]). The MM optimizations with restrains result in a decreased of the energy barriers for both cases: 2.72 kcal/mol with polarization and 0.54 kcal/mol without polarization (Figures S2 and S3). Additionally, the MEP found using QSM with and without restrains result in product (and reactant without polarization, Figure 8) structures with lower relative energy; these behaviour is characteristic of QM/MM simulations without the inclusion of thermal and entropic effects.
A comparison for the total wall time employing NEB, QSM without restrains and QSM with restrains for both cases is depicted in figures S4 and S5 (see supporting information). In general, the NEB and QSM calculations with restrains for both cases required a similar total wall time; in contrast, the QSM optimization without restrained MM took between 36–38% of the total wall time of the QSM calculations with restrained MM.
Conclusions
The new version of LICHEM provides several new algorithms and improvements including methods to address long–range electrostatic effects via the QM/MM–LREC approach, and new path optimization methods including QSM. The ability to perform restrained MM environment optimizations during the initial cycles of the QM/MM path optimization procedure provides a more robust procedure for path optimization of high–dimensional systems. Additional improvements for path convergence and selection of specific degrees of freedom related to the reaction process provide increased performance and accuracy. Two test cases have been presented to test the new path optimization capabilities with an observed reduction of 15–20% in computational time. LICHEM is available free of charge at https://github.com/CisnerosResearch/LICHEM.
Supplementary Material
Acknowledgements
This work was supported by grant R01GM108583 to GAC. We thank the UNT Chemistry Department for computer time on CRUNTCh3 and NSF Grant No. CHE–1531468. E.A.V.-M. thanks CONACyT for funding.
Footnotes
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website. Flowchart describing the capabilities of LICHEM 1.1 Additional plots for rate-limiting step in the N-tert-butyloxycarbonylation of aniline in [EMIm][BF4]. Sample LICHEM input for QSM calculations
References
- (1).Kratz EG; Walker AR; Lagardère L; Lipparini F; Piquemal J; Cisneros GA LICHEM: A QM/MM program for simulations with multipolar and polarizable force fields. Journal of Computational Chemistry 2016, 37, 1019–1029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (2).Ponder JW; Wu C; Ren P; Pande VS; Chodera JD; Schnieders MJ; Haque I; Mobley DL; Lambrecht DS; DiStasio RA; Head-Gordon M; Clark GNI; Johnson ME; Head-Gordon T Current Status of the AMOEBA Polarizable Force Field. The Journal of Physical Chemistry B 2010, 114, 2549–2564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (3).Ren P; Ponder JW Consistent treatment of inter- and intramolecular polarization in molecular mechanics calculations. Journal of Computational Chemistry 2002, 23, 1497–1506. [DOI] [PubMed] [Google Scholar]
- (4).Ren P; Wu C; Ponder JW Polarizable Atomic Multipole-Based Molecular Mechanics for Organic Molecules. Journal of Chemical Theory and Computation 2011, 7, 3143–3161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (5).Frisch MJ; Trucks GW; Schlegel HB; Scuseria GE; Robb MA; Cheeseman JR; Scalmani G; Barone V; Mennucci B; Petersson GA; Nakatsuji H; Caricato M; Li X; Hratchian HP; Izmaylov AF; Bloino J; Zheng G; Sonnenberg JL; Hada M; Ehara M; Toyota K; Fukuda R; Hasegawa J; Ishida M; Nakajima T; Honda Y; Kitao O; Nakai H; Vreven T; Montgomery JA Jr.; Peralta JE; Ogliaro F; Bearpark M; Heyd JJ; Brothers E; Kudin KN; Staroverov VN; Kobayashi R; Normand J; Raghavachari K; Rendell A; Burant JC; Iyengar SS; Tomasi J; Cossi M; Rega N; Millam JM; Klene M; Knox JE; Cross JB; Bakken V; Adamo C; Jaramillo J; Gomperts R; Stratmann RE; Yazyev O; Austin AJ; Cammi R; Pomelli C; Ochterski JW; Martin RL; Morokuma K; Zakrzewski VG; Voth GA; Salvador P; Dannenberg JJ; Dapprich S; Daniels AD; Farkas Ã; Foresman JB; Ortiz JV; Cioslowski J; Fox DJ GaussianâĹij09 Revision D.01. Gaussian Inc; Wallingford CT: 2009. [Google Scholar]
- (6).Parrish RM; Burns LA; Smith DGA; Simmonett AC; DePrince AE; Hohenstein EG; Bozkaya U; Sokolov AY; Di Remigio R; Richard RM; Gonthier JF; James AM; McAlexander HR; Kumar A; Saitow M; Wang X; Pritchard BP; Verma P; Schaefer HF; Patkowski K; King RA; Valeev EF; Evangelista FA; Turney JM; Crawford TD; Sherrill CD Psi4 1.1: An Open-Source Electronic Structure Program Emphasizing Automation, Advanced Libraries, and Interoperability. Journal of Chemical Theory and Computation 2017, 13, 3185–3197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (7).NWChem: A comprehensive and scalable open-source solution for large scale molecular simulations. Computer Physics Communications 2010, 181, 1477 – 1489. [Google Scholar]
- (8).Rackers JA; Wang Z; Lu C; Laury ML; Lagardère L; Schnieders MJ; Piquemal J-P; Ren P; Ponder JW Tinker 8: Software Tools for Molecular Design. Journal of Chemical Theory and Computation 2018, 14, 5273–5289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (9).Lagardère L; Jolly L-H; Lipparini F; Aviat F; Stamm B; Jing ZF; Harger M; Torabifard H; Cisneros GA; Schnieders MJ; Gresh N; Maday Y; Ren PY; Ponder JW; Piquemal J-P Tinker-HP: a massively parallel molecular dynamics package for multiscale simulations of large complex systems with advanced point dipole polarizable force fields. Chem. Sci. 2018, 9, 956–972. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (10).Alden RG; Parson WW; Chu ZT; Warshel A Calculations of Electrostatic Energies in Photosynthetic Reaction Centers. Journal of the American Chemical Society 1995, 117, 12284–12298. [Google Scholar]
- (11).Electrostatic effects in macromolecules: fundamental concepts and practical modeling. Current Opinion in Structural Biology 1998, 8, 211 – 217. [DOI] [PubMed] [Google Scholar]
- (12).Schaefer P; Riccardi D; Cui Q Reliable treatment of electrostatics in combined QM/MM simulation of macromolecules. The Journal of Chemical Physics 2005, 123, 014905. [DOI] [PubMed] [Google Scholar]
- (13).Im W; BernÃĺche S; Roux B Generalized solvent boundary potential for computer simulations. The Journal of Chemical Physics 2001, 114, 2924–2937. [Google Scholar]
- (14).Benighaus T; Thiel W A General Boundary Potential for Hybrid QM/MM Simulations of Solvated Biomolecular Systems. Journal of Chemical Theory and Computation 2009, 5, 3114–3128. [DOI] [PubMed] [Google Scholar]
- (15).Benighaus T; Thiel W Long-Range Electrostatic Effects in QM/MM Studies of Enzymatic Reactions: Application of the Solvated Macromolecule Boundary Potential. Journal of Chemical Theory and Computation 2011, 7, 238–249. [DOI] [PubMed] [Google Scholar]
- (16).Aleksandrov A; Field M Efficient solvent boundary potential for hybrid potential simulations. Phys. Chem. Chem. Phys. 2011, 13, 10503–10509. [DOI] [PubMed] [Google Scholar]
- (17).Nam K; Gao J; York DM An Efficient Linear-Scaling Ewald Method for Long-Range Electrostatic Interactions in Combined QM/MM Calculations. Journal of Chemical Theory and Computation 2005, 1, 2–13. [DOI] [PubMed] [Google Scholar]
- (18).Giese TJ; York DM Ambient-Potential Composite Ewald Method for ab Initio Quantum Mechanical/Molecular Mechanical Molecular Dynamics Simulation. Journal of Chemical Theory and Computation 2016, 12, 2611–2632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (19).Walker RC; Crowley MF; Case DA The implementation of a fast and accurate QM/MM potential method in Amber. Journal of Computational Chemistry 29, 1019–1031. [DOI] [PubMed] [Google Scholar]
- (20).Dehez F; Martins-Costa MTC; Rinaldi D; Millot C Long-range electrostatic interactions in hybrid quantum and molecular mechanical dynamics using a lattice summation approach. The Journal of Chemical Physics 2005, 122, 234503. [DOI] [PubMed] [Google Scholar]
- (21).Fennell CJ; Gezelter JD Is the Ewald summation still necessary? Pairwise alternatives to the accepted standard for long-range electrostatics. The Journal of Chemical Physics 2006, 124, 234104. [DOI] [PubMed] [Google Scholar]
- (22).McCann BW; Acevedo O Pairwise Alternatives to Ewald Summation for Calculating Long-Range Electrostatics in Ionic Liquids. Journal of Chemical Theory and Computation 2013, 9, 944–950. [DOI] [PubMed] [Google Scholar]
- (23).Acevedo O Simulating Chemical Reactions in Ionic Liquids Using QM/MM Methodology. The Journal of Physical Chemistry A 2014, 118, 11653–11666. [DOI] [PubMed] [Google Scholar]
- (24).Acevedo O; Jorgensen WL Quantum and molecular mechanical Monte Carlo techniques for modeling condensed-phase reactions. Wiley Interdisciplinary Reviews: Computational Molecular Science 2014, 4, 422–435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (25).Fang D; Duke RE; Cisneros GA A new smoothing function to introduce long-range electrostatic effects in QM/MM calculations. The Journal of Chemical Physics 2015, 143, 044103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (26).Kratz EG; Duke RE; Cisneros GA Long-range electrostatic corrections in multipolar/polarizable QM/MM simulations. Theoretical Chemistry Accounts 2016, 135, 166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (27).KÃúnig PH; Hoffmann M; Frauenheim T; Cui Q A Critical Evaluation of Different QM/MM Frontier Treatments with SCC-DFTB as the QM Method. The Journal of Physical Chemistry B 2005, 109, 9082–9095. [DOI] [PubMed] [Google Scholar]
- (28).Freitag MA; Gordon MS; Jensen JH; Stevens WJ Evaluation of charge penetration between distributed multipolar expansions. The Journal of Chemical Physics 2000, 112, 7300–7306. [Google Scholar]
- (29).Gresh N; Cisneros GA; Darden TA; Piquemal J-P Anisotropic, Polarizable Molecular Mechanics Studies of Inter- and Intramolecular Interactions and LigandâĹŠ-Macromolecule Complexes. A Bottom-Up Strategy. Journal of Chemical Theory and Computation 2007, 3, 1960–1986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (30).Cisneros GA; Piquemal J-P; Darden TA Intermolecular electrostatic energies using density fitting. The Journal of Chemical Physics 2005, 123, 044109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (31).Cisneros GA; Piquemal J-P; Darden TA Generalization of the Gaussian electrostatic model: Extension to arbitrary angular momentum, distributed multipoles, and speedup with reciprocal space methods. The Journal of Chemical Physics 2006, 125, 184101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (32).Cisneros GA; Elking D; Piquemal J-P; Darden TA Numerical Fitting of Molecular Properties to Hermite Gaussians. The Journal of Physical Chemistry A 2007, 111, 12049–12056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (33).Piquemal J-P; Cisneros GA In Many-body effects and electrostatics; Qiang Cui PR, Meuwly M, Eds.; multi-scale computations of Biomolecules 28; Pan Standford Publishing, 2016; pp 269–299. [Google Scholar]
- (34).Duke RE; Starovoytov ON; Piquemal J-P; Cisneros GA GEM*: A Molecular Electronic Density-Based Force Field for Molecular Dynamics Simulations. Journal of Chemical Theory and Computation 2014, 10, 1361–1365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (35).Piquemal J-P; Cisneros GA; Reinhardt P; Gresh N; Darden TA Towards a force field based on density fitting. The Journal of Chemical Physics 2006, 124, 104101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (36).Gökcan H; Kratz E; Darden TA; Piquemal J-P; Cisneros GA QM/MM Simulations with the Gaussian Electrostatic Model: A Density-based Polarizable Potential. The Journal of Physical Chemistry Letters 2018, 9, 3062–3067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (37).Henkelman, G.; Uberuaga, B. P.; Jónsson, H.
- (38).Burger SK; Yang W Quadratic string method for determining the minimum-energy path based on multiobjective optimization. The Journal of Chemical Physics 2006, 124, 054109. [DOI] [PubMed] [Google Scholar]
- (39).Xie L; Liu H; Yang W Adapting the nudged elastic band method for determining minimum-energy paths of chemical reactions in enzymes. The Journal of Chemical Physics 2004, 120, 8039–8052. [DOI] [PubMed] [Google Scholar]
- (40).Cisneros GA; Liu H; Lu Z; Yang W Reaction path determination for quantum mechanical/molecular mechanical modeling of enzyme reactions by combining first order and second order âĂIJchain-of-replicasâĂi methods. The Journal of Chemical Physics 2005, 122, 114502. [DOI] [PubMed] [Google Scholar]
- (41).Tao P; Larkin JD; Brooks BR In Some Applications of Quantum Mechanics; Pahlavani MR, Ed.; IntechOpen: Rijeka, 2012; Chapter 2. [Google Scholar]
- (42).Cisneros GA; Yang W In Multi-scale Quantum Models for Biocatalysis: Modern Techniques and Applications; York DM, Lee T-S, Eds.; Springer; Netherlands: Dordrecht, 2009; pp 57–78. [Google Scholar]
- (43).Sheppard D; Terrell R; Henkelman G Optimization methods for finding minimum energy paths. The Journal of Chemical Physics 2008, 128, 134106. [DOI] [PubMed] [Google Scholar]
- (44).Case D; Ben-Shalom I; Brozell S; Cerutti DS, T. C. I.;Cruzeiro V; Darden T; Duke R; Ghoreishi D; Gilson M; Gohlke H; Goetz A; Greene D; Harris R; Homeyer N; Izadi S; Kovalenko A; Kurtzman T; Lee T; LeGrand S; Li P; Lin C; Liu J; Luchko T; Luo R; Mermelstein D; Merz K; Miao Y; Monard G; Nguyen C; Nguyen H; Omelyan I; Onufriev A; Pan F; Qi R; Roe D; Roitberg A; Sagui C; Schott-Verdugo S; Shen J; Simmerling C; Smith J; Salomon-Ferrer R; Swails J; Walker R; Wang J; Wei H; Wolf R; Wu X; Xiao L; York D; Kollman P AMBER 2018, University of California, San Francisco: 2018. [Google Scholar]
- (45).Vázquez-Montelongo EA; Vázquez-Cervantes JE; Cisneros GA Polarizable ab initio QM/MM Study of the Reaction Mechanism of N-tert-Butyloxycarbonylation of Aniline in [EMIm][BF4]. Molecules 2018, 23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (46).Parks JM; Hu H; Cohen AJ; Yang W A pseudobond parametrization for improved electrostatics in quantum mechanical/molecular mechanical simulations of enzymes. 2008, 129, 154106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (47).Frisch MJ; Trucks GW; Schlegel HB; Scuseria GE; Robb MA; Cheeseman JR; Scalmani G; Barone V; Petersson GA; Nakatsuji H; Li X; Caricato M; Marenich AV; Bloino J; Janesko BG; Gomperts R; Mennucci B; Hratchian HP; Ortiz JV; Izmaylov AF; Sonnenberg JL; Williams-Young D; Ding F; Lipparini F; Egidi F; Goings J; Peng B; Petrone A; Henderson T; Ranasinghe D; Zakrzewski VG; Gao J; Rega N; Zheng G; Liang W; Hada M; Ehara M; Toyota K; Fukuda R; Hasegawa J; Ishida M; Nakajima T; Honda Y; Kitao O; Nakai H; Vreven T; Throssell K; Montgomery JA Jr.; Peralta JE; Ogliaro F; Bearpark MJ; Heyd JJ; Brothers EN; Kudin KN; Staroverov VN; Keith TA; Kobayashi R; Normand J; Raghavachari K; Rendell AP; Burant JC; Iyengar SS; Tomasi J; Cossi M; Millam JM; Klene M; Adamo C; Cammi R; Ochterski JW; Martin RL; Morokuma K; Farkas O; Foresman JB; Fox DJ GaussianËIJ16 Revision A.03. 2016; Gaussian Inc; Wallingford CT. [Google Scholar]
- (48).Torabifard H; Cisneros GA Insight into wild-type and T1372E TET2-mediated 5hmC oxidation using ab initio QM/MM calculations. Chem. Sci. 2018, 9, 8433–8445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (49).Torabifard H; Cisneros GA Computational investigation of O2 diffusion through an intra-molecular tunnel in AlkB; influence of polarization on O2 transport. Chem. Sci. 2017, 8, 6230–6238. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


