Metal-organic framework based on hinged cube tessellation as transformable mechanical metamaterial

A metal-organic framework based on porphyrin boxes exhibits metamaterial behavior.

Abstract

Mechanical metamaterials exhibit unusual properties, such as negative Poisson’s ratio, which are difficult to achieve in conventional materials. Rational design of mechanical metamaterials at the microscale is becoming popular partly because of the advance in three-dimensional printing technologies. However, incorporating movable building blocks inside solids, thereby enabling us to manipulate mechanical movement at the molecular scale, has been a difficult task. Here, we report a metal-organic framework, self-assembled from a porphyrin linker and a new type of Zn-based secondary building unit, serving as a joint in a hinged cube tessellation. Detailed structural analysis and theoretical calculation show that this material is a mechanical metamaterial exhibiting auxetic behavior. This work demonstrates that the topology of the framework and flexible hinges inside the structure are intimately related to the mechanical properties of the material, providing a guideline for the rational design of mechanically responsive metal-organic frameworks.

INTRODUCTION

Mechanical metamaterials are an interesting class of materials where their unconventional mechanical properties, such as negative Poisson’s ratio (NPR) (see Fig. 1) (1–10), are closely related to their topological arrangement of structural building blocks. For example, hinged tessellations can be served as blueprints for designable NPR materials (11–16). Highly deformable geometries (17, 18) are desirable structural features of NPR materials, as exemplified by α-cristobalite (17), natrolite, thomsonite (18), pyrite (19), black phosphorus (20), metal nanoplates (21), graphene (22), protein (23), and a variety of microarchitectures (24–28).

Fig. 1. Schematic representation of Poisson’s ratio.

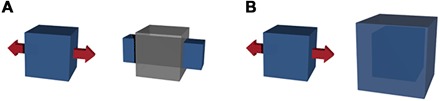
(A) Conformation of conventional material (Poisson’s ratio, >0). (B) Conformation of NPR material (Poisson’s ratio, <0). The gray-colored cubes represent the original geometry of the materials.

Metal-organic frameworks (MOFs), a rising class of metal-organic hybrid materials, can be an ideal platform for mechanical metamaterials because their structural building units, e.g., organic linkers and metal-based secondary building units (SBUs), are highly tunable, and therefore, rational design strategies using MOFs are now feasible (29–31). Such a combinatorial synthetic protocol generated more than 70,000 MOF structures with several hundred net topologies accumulated (32, 33). Among those MOFs reported, MOFs crystallized in deformable net topologies (34–36) demonstrate anomalous mechanical properties (37), such as negative thermal expansion (38, 39), negative linear compressibility (40, 41), and NPR (42–44). Despite such a unique advantage of MOFs, the flexibility of metal-based SBUs has been rarely explored in MOFs as pivoting points in mechanical metamaterials.

Here, we report a UPF-1 [UPF stands for Ulsan National Institute of Science and Technology (UNIST) porphyrin framework] as a mechanical NPR metamaterial, self-assembled from a porphyrin linker and a Zn-based SBU. The Zn-based SBU serves as a hinged point, responsible for the resulting NPR property. Synchrotron x-ray diffraction, structural model study, and theoretical calculation indicate that the origin of these peculiar mechanical properties stems from (i) the synergistic hinged movement of SBUs and (ii) the rotation of nanosized porphyrin boxes. This work demonstrates that the topology of UPF-1 is intimately related to its mechanical properties, suggesting that various metamaterial design strategies are possible for MOFs. We expect new streams of NPR MOFs in the near future.

RESULTS

UPF-1

Crystals of UPF-1 were synthesized with Zn(NO₃)₂·6H₂O and two types of organic linkers, meso-tetra(3-carboxyphenyl) porphyrin (3-TCPP; shown in scheme S1) and 4,4′-bipyridine (BPY), via a solvothermal reaction. Single-crystal x-ray structure analysis of UPF-1 revealed a peculiar structural feature, which is the presence of unprecedented SBUs of [(Zn(COO)₃(μ₂−O)Zn(COO)₃], composed of two “three-blade” Zn paddlewheel clusters [Zn₂(COO)₃]⁺ bridged by oxygen (Fig. 2A). A single SBU coordinates six porphyrin ligands, ultimately forming a cubic porphyrin box (Fig. 2B), where porphyrin linkers and SBUs are located on the faces and corners of the box, respectively. Each porphyrin box is surrounded by eight other boxes, and the overall arrangement of the cubes becomes a slightly distorted body-centered tetragonal structure (Fig. 2C and fig. S3). BPY linkers are used as pillars, connecting two SBUs and two cofacial porphyrins. Depending on the existence of BPY pillars, the Zn²⁺ ions reside in from four tetrahedral (Td) to six octahedral (Oh) environments (see figs. S1 and S2).

Fig. 2. Description of UPF-1 structure.

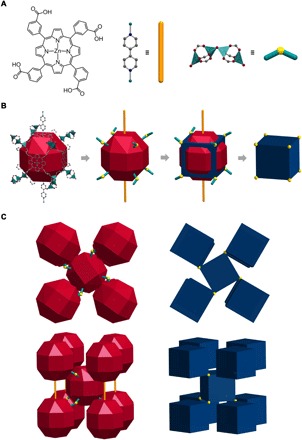
(A) Three building blocks of UPF-1: 3-TCPP, BPY, and [Zn₂(COO)₃]₂O. Zn, green; C, gray; N, blue; O, red; all hydrogen and solvents are omitted for clarity. (B) A nanocage of UPF-1 consists of three constituents and is represented by rhombicuboctahedron. The nanocage has 10 linkages, BPY as its pillars and oxo ligands. The oxygen of oxo ligands and BPY are represented by balls (yellow) and rods (orange), respectively. The rhombicuboctahedron and 10 linkages of the structure are simplified to a cuboid form. The vertex of the cuboid is the oxygen of the oxo ligands. (C) Packing system of rhombicuboctahedra and cuboids in UPF-1. The oxo ligands were bent to a clockwise direction. The rods connect between cages in the picture showing the sides of the structure. The connection by rods is omitted because packing of the cuboid emphasizes the connectivity of oxo ligands.

We also noted that the porphyrin boxes are interconnected by Zn─O─Zn oxo bridges, potential pivoting joints, which are notably similar to those T─O─T joints (or Si─O─Si) found in zeolites such as cristobalite (10) and natrolite (11). For example, the T─O─T joints in cristobalite are known to connect two TO₄ tetrahedra, inducing highly flexible behavior relative to pressure changes. Inspired by this, we hypothesized that UPF-1, constructed from porphyrin boxes connected by new SBUs with oxo bridges, might also show flexible movement with changes in the temperature. To test the hypothesis, we performed temperature-dependent synchrotron single-crystal x-ray diffraction (SCXRD) and powder x-ray diffraction (PXRD) analyses at Pohang Accelerator Laboratory (PAL), South Korea. UPF-1 was characterized using thermogravimetric analysis, N₂ adsorption, and ¹H nuclear magnetic resonance (NMR) experiments. UPF-1 decomposed around 380°C (fig. S4). Using Materials Studio, the theoretical surface area of UPF-1 was calculated to be 2801 m²/g. To confirm the porosity of UPF-1 experimentally, we conducted an N₂ adsorption experiment. However, after activating the UPF-1 sample (at 90°C for 10 hours), the framework collapsed, becoming nonporous, as shown in the N₂ adsorption data. Such a phenomenon is common for Zn-containing MOFs. The solvent content of as-synthesized UPF-1 was confirmed by the ¹H NMR experiment. In the framework, N,N′-dimethylformamide (DMF) and ethanol (EtOH) were included at a ratio of 6:1 (fig. S5).

Thermal response

Both temperature-dependent synchrotron SCXRD and PXRD analyses were conducted. The results showed that the framework of the UPF-1 was well maintained (fig. S6). Unexpectedly, UPF-1 expanded anisotropically as the temperature was increased, as shown in Fig. 3A and fig. S7. The (220) reflection changed noticeably, while the (002) reflection remained essentially the same. Figure 3B shows the normalized changes in the cell parameters obtained from the SCXRD and PXRD data (tables S1 and S2). The cell parameters a and b changed drastically within the range of 173 to 193 K. This phenomenon is analogous with guest-induced thermal expansion reported in an MOF (45). Confined solvent molecules in the pores give rise to changes in the structure with nonlinear expansion depending on the temperature. The thermal expansion coefficients (α) were calculated from the a and c parameters and the cell volume (fig. S8 and tables S3 and S4). In the PXRD data, the highest value of α_a was found to be 338 × 10⁻⁶ K⁻¹ at 173 K. Such a coefficient is one of the highest values among those reported for MOF materials, even comparable to colossal expansion cases found in other material types (table S5).

Fig. 3. Thermal response of UPF-1.

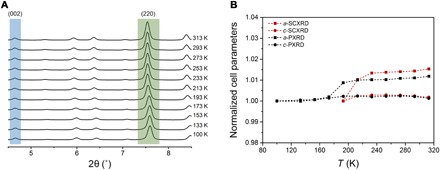
(A) PXRD pattern depending on temperature. Immovable peak of the (002) plane represents that the value of the c parameter is not changed with temperature. Shifted peak of the (220) plane signifies that connected parts are changed by temperature. (B) The relative change of the normalized a and c parameters from SCXRD (193 to 313 K; red dashed lines) and PXRD data (100 to 313 K; black dashed lines).

Geometrical model of colossal thermal expansion

To locate the origin of the drastic cell parameter change obtained from the x-ray diffraction analysis, we carefully analyzed the cell volume changes in UPF-1. First, we divided a unit cell of UPF-1 into three parts: porphyrinic cubic box (blue), cubic void (gray), and hexahedron (yellow) (Fig. 4, A and B). Figure 4C shows a cubic tessellation pattern along the [001] direction for UPF-1. Second, we monitored volume changes in each of these parts from temperature-dependent SCXRD measurements. The volume of both cubic boxes (blue and gray) changed slightly (less than 0.2 %) with temperature (fig. S9 and table S6), whereas the hexahedra showed a substantial change up to 9%. This shows that the total volume change found in UPF-1 is mainly due to the change in the volume of the hexahedra in the unit cell. We speculate that the angle of the rhombus, θ, defined as an acute angle in the rhombus face of a hexahedron formed by the rotating cubes (Fig. 4D), might be a critical structural parameter responsible for the colossal thermal expansion observed in UPF-1.

Fig. 4. Definition of space-filling in UPF-1.

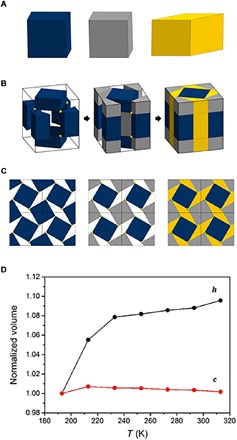
(A) Three main classes, divided from simplified cuboid form. Cuboid, blue; another cuboid, gray; hexahedron with rhombus face, yellow. (B) Filled UPF-1 using four cuboids and a hexahedron in a unit cell. (C) Space-filled UPF-1 in 2 by 2 unit cells from the c axis. (D) Comparison with normalized volume of cuboid (red) and hexahedron (black). The volume of the cuboid is rarely changed, while the hexahedron is largely changed depending on temperature.

Rotating cubes in the solid state

To confirm the actual movement of UPF-1, special attention was paid to the angle θ, which can be related to the Cartesian coordinates obtained from the square face of the rotating cubes (Fig. 5A). In this model, the change in θ is directly affected by the rotation of these cubes and is derived from the SCXRD data, which showed a change of ~3° from 193 to 313 K. This result is in excellent agreement with the simulated value based on our simple geometrical model (Fig. 5B and fig. S10). The angle θ (derived from the cell parameters and the vertex of the cuboid) was calculated as a² = 2l²(1 + sin θ), where l is the size of the box. Then, the equation was applied to calculate θ from the PXRD data (fig. S11). From these calculations, we could predict that the angle θ determined from the PXRD data would show a change of ~2.5° from 100 to 313 K. The variation in θ is analogous to the value from the SCXRD data.

Fig. 5. Transition of two factors following corotating mechanism.

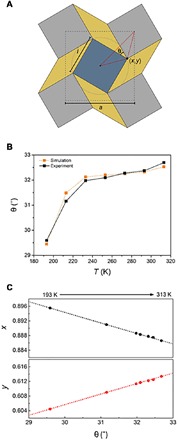
(A) Schematic representation of the relation between θ and (x, y) coordinates showing rotating squares in geometry model. (B) Comparison with θ transition of calculation and SCXRD data depending on temperature. (C) Movement of the coordinates in accordance with the change of θ. The points, x coordinate (red) and y coordinate (black), are experimental data and matched well with the calculated dotted lines.

To confirm the real movement of the oxygen bridge in the SBU, the Cartesian coordinates of the shifts in the oxygen position were derived using Eq. 1 from our geometrical model (figs. S12 and S13)

$$\mathit{x}=\frac{1}{4}(3+\frac{\text{cos} \mathrm{\theta }}{1+\text{sin} \mathrm{\theta }}),\mathit{y}=\frac{1}{4}(3-\frac{\text{cos} \mathrm{\theta }}{1+\text{sin} \mathrm{\theta }})$$ (1)

As shown in Fig. 5C, the Cartesian coordinates (x, y) of the temperature-dependent SCXRD results matched well with the simulated ones. Therefore, the temperate-dependent movement of the oxygen bridge could be the confirmation of the cube-rotating mechanism with UPF-1.

New NPR MOF: UPF-1

The fact that the rotating cube model matched well with the structural change through the temperature-dependent experiment led us to further investigate the NPR property of UPF-1. The rotating mechanism from hinged squares is known to cause NPR behavior in materials such as zeolites (18) and a protein (23). The model of the three-dimensional (3D) framework shows how the rotation of the square matrix results in a drastic isotropic increase (Fig. 6A and movie S1). On the basis of this model, we performed semiempirical calculations to establish the NPR behavior of UPF-1.

Fig. 6. Poisson’s ratio of UPF-1.

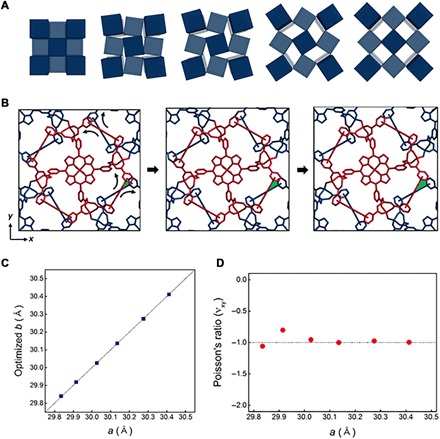
(A) Schematic representation of rotating mechanisms based on square tessellation. (B) Simulated UPF-1, which has an applied uniaxial strain along the x (or y) direction. The red skeleton (A) rotates counterclockwise, and the blue part (B) rotates clockwise based on the hinged point (Zn─O─Zn). The skeletons rotate, and the colored area (green) becomes wider as strain is increased. The cell parameters increased as well, from 29.835 to 30.026 Å and then 30.412 Å. (C) Optimized b for different a value. The value b is optimized, while a and c are fixed. The dotted line shows the line a = b. The optimized crystal structure remains in tetragonal symmetry. (D) The calculated Poisson’s ratio is close to −1 with respect to various unit cell parameters.

As a definition of Poisson’s ratio, we apply a uniaxial strain along the x direction and calculate the optimized lattice parameter. For this calculation, we assume that the c parameter, showing a cell change of only 0.24%, is constant as in the experimental results. As shown in Fig. 6B and movie S2, the optimized crystal structure is a body-centered tetragonal structure with two moieties (A and B), where A and B both exhibit a simple tetragonal crystal structure and relate to the Zn─O─Zn bonding, which is potentially a crucial component of the NPR behavior. The crystal structures are changed when we apply a uniaxial strain along the x direction. As the lattice parameters a and b increase, the angle of Zn─O─Zn increases, whereas the relative atomic positions in moieties A and B do not change substantially. The optimized lattice constants b with respect to a are reported in table S7. Here, the calculated bond angle of Zn─O─Zn, projected on the xy plane, increases gradually as we apply the strain. According to Fig. 6C and table S7, a and optimized b can be fitted with the dotted line in a = b perfectly, which presents Poisson’s ratio (ν_xy) as determined by the numerical differentiation. As a result, the Poisson’s ratio (ν_xy) of UPF-1 is close to −1 (Fig. 6D).

Furthermore, other elastic properties such as Young’s modulus (E), shear modulus (G), bulk modulus (B), and Poisson’s ratio (ν) are calculated to verify that the methodology is correct (table S8 and fig. S14). Young’s modulus (E), showing stiffness of the material, is 1.156 and 17.123 GPa along the x(y) direction and the z direction, respectively. The shear modulus (G) is also used to confirm the rigidity of the material. UPF-1 has shear moduli of 1.943 and 2.823 GPa along the x(y) direction and the z direction, respectively. In comparison with conventional materials, such as ceramics, metals, glasses, foams, and polymers and MOFs based on the two elastic properties, UPF-1 exhibits structural softness similar to that of relatively foam-like zeolitic imidazolate framework (ZIF-8) along the x(y) direction (44). The bulk modulus of UPF-1 is 1.268 GPa. Last, we confirmed that Poisson’s ratio (ν_xy = ν₁₂), which was calculated from the elastic constants, is −0.920 (table S9). This NPR value is almost equal to the value obtained by the semiempirical calculations.

Isotropic 3D materials exhibit Poisson’s ratios within the range of −1 ≤ ν ≤ 0.5. Isotropic 2D materials have Poisson’s ratios within −1 ≤ ν ≤ 1 (46). The rotating cube model of UPF-1 is analogous to that of isotropic 2D materials showing NPR behavior. Although there are several MOFs with NPR properties predicted, including ZIFs, Hong Kong University of Science and Technology (HKUST-1), and the Matérial Institut Lavoisier (MIL) series (42–44), UPF-1 has an NPR closer to the theoretical value of −1 such as isotropic materials and exhibits NPR behavior (table S10).

DISCUSSION

In summary, we successfully reported a highly flexible MOF, UPF-1, with colossal thermal expansion and the NPR property. The origin of the peculiar mechanical properties is the oxo bridge in a novel SBU. Such a slight movement of oxygen causes a significant volume change in the unit cell, which matches well with the geometrical structure and calculation. Following the trace of oxygen, we demonstrated a 2D deformation that originated from a rotating mechanism. It is interesting to know that such a rotating mechanism shown here is scale independent. An atomic-level movement can generate highly predictable NPR behavior in a MOF. Furthermore, to the best of our knowledge, such a combination of colossal thermal expansion and the NPR behavior in MOFs has not been observed so far. We expect that the systematic analysis of geometric models can unveil many MOFs with the NPR property. Design of mechanical “meta-MOF” is now possible using similar hinged tessellations as blueprints. We expect that pressure-induced experiments might expand the study of mechanical meta-MOFs.

MATERIALS AND METHODS

Temperature-dependent synchrotron SCXRD

A single crystal was loaded and sealed into a capillary with a diameter of 0.3 mm (wall thickness, 0.01 mm), and the container was filled with a small amount of mother liquid. SCXRD data of UPF-1 were collected at 2D SMC with a silicon (111) double-crystal monochromator using synchrotron radiation (λ = 0.70000 Å) on an Area Detector Systems Corporation (ADSC) Quantum-210 detector at PAL, Korea. Temperature was increased in 20-K increments from 193 to 313 K and stabilized for 15 to 20 min. SCXRD data were not collected at lower temperatures than 193 K due to generating ice around the capillary. A total diffraction data of 7 points were collected from the PAL BL2D-SMDC program (47), and data processing, such as cell refinement, reduction, and absorption correction, was performed using HKL-3000 (48). The crystal structure of UPF-1 was solved by the direct method and refined with the SHELX program (49). The least-squares refinement of the structural model was performed under displacement parameter restraints such as DANG, DFIX, DELU, ISOR, and SIMU. The final refinement was performed with the modification of the structure factors for the electron densities of the disordered solvents using the SQUEEZE option of PLATON (50).

Temperature-dependent synchrotron PXRD

The well-ground crystals were packed and sealed into a capillary with a diameter of 0.3 mm (wall thickness, 0.01 mm) to maintain a constant status. PXRD data were collected at 2D SMC with a silicon (111) double-crystal monochromator, PAL. An ADSC Quantum-210 detector was used at a distance of 120-mm using synchrotron radiation (λ = 1.39995 Å). A total of 11 points of temperature scans were collected from 100 to 313 K. Temperature was increased in 20-K increments, except 100 K, and stabilized for 15 to 20 min in each step. The PAL BL2D-SMDC program (47) was used for data collection, and the FIT2D program (51) was used for data conversion from a 2D diffraction image to a 1D diffraction pattern. The cell parameters were determined by the Pawley refinement in DASH 3.3.4 of the Cambridge Crystallographic Data Centre (52).

¹H nuclear magnetic resonance

¹H NMR data were obtained using an Agilent Fourier transform NMR spectrometer (400 MHz) at UNIST Central Research Facilities.

Thermogravimetric analyzer

Thermogravimetric analysis was performed on a TA Instruments SDT Q600, heated from 25°C to 1000°C under N₂ atmosphere at a scan rate of 10°C min⁻¹.

Thermal expansion coefficient (α)

The coefficients of thermal expansion (α) of UPF-1 were calculated from SCXRD and PXRD data. Each cell parameter and cell volume of SCXRD from 193 to 313 K were fitted, and the best polynomial fit was taken by five derivatives. The coefficients of PXRD data were calculated relative to next temperature using Eq. S1. ΔL is a rate of change of parameter, and ΔT is a rate of change of temperature. L₀ is the initial value of the cell parameter. The volumetric expansion coefficient (α_V) was calculated by substituting ΔV for ΔL and V₀ for L₀ in the following equation

$$\mathrm{\alpha }=-\frac{\mathrm{\Delta }\mathit{L}}{{\mathit{L}}_0\mathrm{\Delta }\mathit{T}}$$ (S1)

Synthesis of UPF-1

C₄₈H₃₀O₈N₄·(C₁₀H₄N₂)_1.7 (7.9 mg, 0.008 mmol), Zn(NO₃)·6H₂O (10.8 mg, 0.037 mmol), BPY (3.3 mg, 0.020 mmol), and 1.0 M HNO₃ in EtOH (30 μl, 0.03 mmol) were added to a solution of DMF and EtOH (v/v = 3:1, 2 ml) in a 16-ml vial. The mixture was sonicated for homogeneity, heated to 100°C for 48 hours, followed by cooling over 9 hours. The purple crystals were obtained in the vial after reaction.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/5/eaav4119/DC1

Scheme S1. Synthetic procedure of 3-TCPP.

Fig. S1. Characterization of BPY as a pillar in UPF-1.

Fig. S2. Coordination environment of Zn²⁺ ion of new SBU, [(Zn(COO)₃(μ₂−O)Zn(COO)₃].

Fig. S3. Packing of rhombicuboctahedron and cuboid of UPF-1.

Fig. S4. Thermogravimetric analysis data for UPF-1.

Fig. S5. ¹H NMR data for trace of solvent content in the UPF-1.

Fig. S6. Simulated and experimental PXRD patterns of UPF-1 from 100 to 313 K.

Fig. S7. Perspective view of the (002) and (220) planes in UPF-1.

Fig. S8. Thermal expansion coefficients of UPF-1.

Fig. S9. Transformation of a cuboid in UPF-1.

Fig. S10. Schematic representation in a corotating model.

Fig. S11. Calculated θ values from temperature-dependent PXRD data of UPF-1.

Fig. S12. Schematic illustration of the corotating model.

Fig. S13. Calculated (x, y) coordinates from 0° to 90°, derived from equation.

Fig. S14. Energy as a function of deformations D_i’s.

Table S1. Temperature-dependent cell parameters (Å) and unit cell volume (ų) data from synchrotron PXRD.

Table S2. Temperature-dependent SCXRD of UPF-1.

Table S3. Thermal expansion coefficients from the a and c parameters and cell volume of SCXRD.

Table S4. Thermal expansion coefficients from the a and c parameters and cell volume of PXRD.

Table S5. Thermal expansion coefficient of reported solid-state structures.

Table S6. The values of d₁, d₂ and volume of cuboid depending on temperature.

Table S7. Optimized lattice parameters L_y (${\mathit{L}}_{\mathit{y}}^{*}$) and bond angles Zn─O─Zn projected on the xy plane with respect to strained L_x’s.

Table S8. Stiffness tensor components (C_ij’s) of UPF-1 in GPa.

Table S9. Elastic constants of UPF-1.

Table S10. Poisson’s ratio of a variety of materials.

Data file S1. Crystallographic data for UPF-1_193K.

Data file S2. Crystallographic data for UPF-1_213K.

Data file S3. Crystallographic data for UPF-1_233K.

Data file S4. Crystallographic data for UPF-1_253K.

Data file S5. Crystallographic data for UPF-1_273K.

Data file S6. Crystallographic data for UPF-1_293K.

Data file S7. Crystallographic data for UPF-1_313K.

Data file S8. checkCIF for crystal structures of UPF-1_193K.

Data file S9. checkCIF for crystal structures of UPF-1_213K.

Data file S10. checkCIF for crystal structures of UPF-1_233K.

Data file S11. checkCIF for crystal structures of UPF-1_253K.

Data file S12. checkCIF for crystal structures of UPF-1_273K.

Data file S13. checkCIF for crystal structures of UPF-1_293K.

Data file S14. checkCIF for crystal structures of UPF-1_313K.

Movie S1. Animation of hinged cube tessellation.

Movie S2. Rotating movement of UPF-1 structure depending on temperature.

Reference (53–76)