Simultaneous cosegmentation of tumors in PET‐CT images using deep fully convolutional networks

Abstract

Purpose

To investigate the use and efficiency of 3‐D deep learning, fully convolutional networks (DFCN) for simultaneous tumor cosegmentation on dual‐modality nonsmall cell lung cancer (NSCLC) and positron emission tomography (PET)‐computed tomography (CT) images.

Methods

We used DFCN cosegmentation for NSCLC tumors in PET‐CT images, considering both the CT and PET information. The proposed DFCN‐based cosegmentation method consists of two coupled three‐dimensional (3D)‐UNets with an encoder‐decoder architecture, which can communicate with the other in order to share complementary information between PET and CT. The weighted average sensitivity and positive predictive values denoted as Scores, dice similarity coefficients (DSCs), and the average symmetric surface distances were used to assess the performance of the proposed approach on 60 pairs of PET/CTs. A Simultaneous Truth and Performance Level Estimation Algorithm (STAPLE) of 3 expert physicians’ delineations were used as a reference. The proposed DFCN framework was compared to 3 graph‐based cosegmentation methods.

Results

Strong agreement was observed when using the STAPLE references for the proposed DFCN cosegmentation on the PET‐CT images. The average DSCs on CT and PET are 0.861 ± 0.037 and 0.828 ± 0.087, respectively, using DFCN, compared to 0.638 ± 0.165 and 0.643 ± 0.141, respectively, when using the graph‐based cosegmentation method. The proposed DFCN cosegmentation using both PET and CT also outperforms the deep learning method using either PET or CT alone.

Conclusions

The proposed DFCN cosegmentation is able to outperform existing graph‐based segmentation methods. The proposed DFCN cosegmentation shows promise for further integration with quantitative multimodality imaging tools in clinical trials.

1. Introduction

Positron emission tomography and computed tomography (PET‐CT) have revolutionized modern cancer therapy. Several studies have demonstrated that the estimate of tumor extent and distribution is most accurate when functional and morphological image data are combined using PET‐CT.^{1, 2, 3} Outcomes are reported to improve with PET‐CT guided radiotherapy.^{4, 5, 6, 7} To make full use of both PET and CT image modalities, accurate tumor delineation on PET‐CT images is vital for tumor staging, response prediction, treatment planning, and prognostic assessment. The current standard of care for radiation therapy target determination relies on manually contouring the CT portion of combined PET‐CT image dataset often combined with a threshold method for volume definition on the PET images. The manual contouring on CT is performed visually on a slice‐by‐slice basis by the radiation oncologist for tumor delineation. They have very limited support from automated segmentation tools and threshold determined volumes on PET often require significant manual editing. The development of standardized and highly reproducible PET‐CT segmentation techniques would be immensely valuable for clinical care and for research.⁸

Although PET‐CT images are routinely used in clinic, many clinically available PET‐CT segmentation algorithms only work for a single modality or work for the fused PET‐CT images. A major challenge in CT segmentation is that the pathological and physiological contrast uptake cannot be distinguished; meanwhile, the pathological and physiological changes are often more differentiable using molecularly based PET radiotracers. The American Association of Physics in Medicine (AAPM) Task Group (TG) 211⁹ and the MICCAI challenge¹⁰ have published recommendations for PET image segmentations. To take advantage of the dual modality nature of PET‐CT imaging, cosegmentation aims to simultaneously compute the tumor volume defined on the CT image as well as that defined on the PET image by combining physiological information from the PET image with the anatomical information from CT image.^{11, 12} Substantial progress has been made in automating the tumor definition extracted from PET‐CT scans.^{11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28} Although these methods showed promise, there are still limitations when adapting them for clinical use. Most previous methods depend on user‐defined foreground seeds belonging to the tumor.^{11, 12} Secondly, features modeling components in graph‐based cosegmentation algorithms were designed to complement human experience or more complicated clinical priors.^{12, 23, 24, 25} Therefore, finding optimal parameters and features is difficult especially with the presence of lesions. These challenges have restricted clinical application. Efforts to automate PET‐CT tumor segmentation are consequently needed in modern radiotherapy.

Due to inherent differences in PET and CT imaging modalities, the tumor boundary defined in PET does not always match that in CT. Therefore, simultaneously segmenting tumors in both PET and CT while admitting the (subtle) difference of the boundaries defined in the two modalities is a more reasonable approach than using fused PET‐CT images where identical tumor boundaries are assumed. Figure 1 shows the tumor boundary differences between CT and PET images in a lung tumor.

Figure 1.

Tumor contours are different in computed tomography (CT) (left), positron emission tomography (PET) (middle), and the fused PET and CT images (right). Due to the inherent differences between molecular imaging (PET) and morphological images (CT), the tumor boundary as defined between PET and CT images may differ. [Color figure can be viewed at wileyonlinelibrary.com]

In this work, we attempt to address these challenges and seek data‐driven deep learning solutions for automatically delineating features directly from PET‐CT scans to develop a computer‐aided automatic processing tool for tumor segmentation. Deep learning is able to outperform most conventional approaches²⁹ and is able to manage many medical tasks.^{30, 31, 32, 33, 34, 35, 36, 37, 38} Several publications detail the potential power of this approach.^{39, 40} In this paper, we focus on investigating 3D‐UNet, deep‐fully convolutional networks (DFCN) for tumor delineation in PET‐CT scans. The 3D‐UNet for semantic segmentation^{31, 38, 41} performs voxel‐wise classification and was adopted to label each voxel as lesion or background. To achieve PET‐CT tumor cosegmentation, we propose a novel DFCN network which integrates two coupled 3D‐UNets within an encoder‐decoder architecture. One 3D‐UNet performs the PET tumor segmentation and the other is used for performing CT tumor segmentation. The two U‐Nets communicate with each other to allow the complementary features from both modalities to “flow” between the two U‐Net networks to produce more consistent tumor contours. To demonstrate the applicability and performance of our method, we evaluate the proposed segmentation approach on PET‐CT scans of nonsmall cell lung cancer (NSCLC) patients and compare its results to manual segmentation, which is the standard of care for NSCLC segmentation in PET‐CT volumes.

2. Methods and materials

2.A. Image data

A total of 60 NSCLC patients who received stereotactic body radiation therapy (SBRT) were analyzed in this study following institutional review board (IRB) approval. All patients had PET‐CT images for simulation and received follow‐up CT images between 2 and 4 months after radiotherapy treatment. Fluorine 18‐fluorodeoxyglucose (18F‐FDG) PET and CT images were obtained using a dual PET/CT scanner (Siemens Biograph 40, Siemens Medical Solutions, Erlangen, Germany). All patients were injected with 370 BMq ± 10% of 18F‐FDG with an uptake time of 90 min ± 10%. In all cases, subjects fasted for more than 4 h and had a blood glucose of less than 200 mg/dl. The gross tumor volume (GTV) for each of the PET and CT image datasets was separately delineated by three radiation oncologists on both CT and 18F‐FDG PET images, with the guidance of the corresponding images in the other modality. All contouring was completed using VelocityAI (Varian Medical System, Inc., Palo Alto, CA). In this study, while physicians referred to the other modality to define the tumor contours on either PET or CT, they did not visualize the corresponding PET and CT scans at the same time using the software's fusion feature. The reference standard for each scan was then generated by applying the STAPLE algorithm⁴² to the three manual delineations.

2.B. Methods

2.B.1. Data preprocessing

In our experiments, we first resampled each pair of the registered PET‐CT scans with an isotropic spacing in all 3D, and then cropped a fixed size of each 3D volume (that is, 96 × 96 × 48 voxels) centered at each lesion. In order to remove unrelated image details, we took a similar intensity thresholding strategy as that used by Zhong et al.²⁸ For the CT images, we truncated the intensity values of all scans to the range of [−500, 200], and for the PET images, we truncated the SUV of all scans to the range of [0.01, 20.0].

2.B.2. DFCN‐based cosegmentation

The proposed DFCN‐based cosegmentation framework (briefly called DFCN‐CoSeg) consists of two coupled 3D‐UNets with an encoder‐decoder architecture, as illustrated in Fig. 2.

Figure 2.

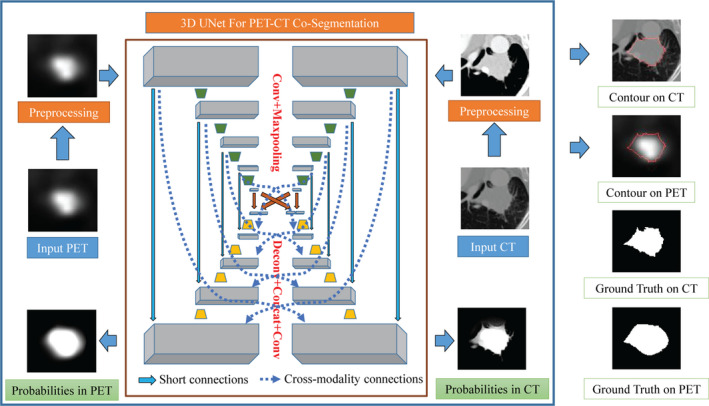
A schematic illustration of our proposed deep learning, fully convolutional networks (DFCN)‐CoSeg network with feature fusion for positron emission tomography (PET)‐computed tomography (CT) cosegmentation. Two parallel 3D‐UNets are built for CT and PET respectively. In DFCN‐CoSeg, all feature maps produced by all the encoders of either the CT or PET branch are concatenated in the corresponding decoders, as depicted by the dotted arrow lines. [Color figure can be viewed at wileyonlinelibrary.com]

Each 3D‐UNet is used to handle the tumor segmentation in PET or in CT, and both are communicating with each other to share the complementary features from the other modality.

In this work, we mainly employ the 3D version of the original two‐dimensional (2D) U‐Net with encoder‐decoder architecture,³⁸ for single‐modality segmentation, (CT‐only or PET‐only). This consists of a number of down‐sampling (encoder) and up‐sampling (decoder) modules,³⁸ as depicted in Fig. 2 and Table 1. Given an input image cube with a size of 96 × 96 × 48, the first convolutional layer which produces 32 features maps is mainly adopted to extract the low level features. Based on these feature maps, a U‐type network architecture is formed, in which the encoder module contains four convolutional and max‐pooling (for down‐sampling) layers with 64, 128, 256, and 512 feature maps, respectively; and the decoder module contains four de‐convolutional (for up‐sampling) and convolutional layers with 256, 128, 64, 32 feature maps respectively. For each convolutional layer, the size of all convolutional kernels is 3 × 3 × 3; while for all max‐pooling layers, the pooling size is 2 × 2 × 2 with a stride of 2. In all deconvolutional layers, we up‐sample the input features maps by a factor of 2. Using a technique similar to that described by Cicek et al.³¹, the feature maps are concatenated after deconvolution with those corresponding features in the prior encoder module. More specifically, using the CT data as the input, the first convolutional layer produces 32 feature maps (denoted by F1), the encoder 1 produces 64 feature maps (denoted as F2), and so on and so forth. Then, in the corresponding decoder module, we concatenate them to ensure maximizing information flow between layers, which helps improve the gradient flow computation and the network training. After the decoder, a softmax classifier implemented by the fully convolutional operation is used to generate voxel‐level probability maps and the final predictions. After that, the probabilities and predictions were given as inputs to the loss functions. In this work, two kinds of well‐known loss functions were studied:

1. The cross‐entropy loss function (denoted as CELoss), which is defined as:

   $$L_{\mathit{CE}}=-\frac{1}{N}\sum _{i=1}^N\sum _{c=1}^2{y}_i^{c}log{p}_i^c,$$

   where $p_i^c$ denotes the probability of each voxel i belongs to class c (i.e., nontumor or tumor), $y_i^c$ indicates the ground truth label for voxel i.

Table 1.

Architecture of a basic three‐dimensional (3D)‐UNet

	Feature size	3DUNet
Input	1 × 96 × 96 × 48
Conv 1(F1)	32 × 96 × 96 × 48	Conv, 3 × 3 × 3, 32, stride 1
Encoder 1(F2)	64 × 48 × 48 × 24	Conv, 3 × 3 × 3, 64, maxpool, stride 2
Encoder 2(F3)	128 × 24 × 24 × 12	Conv, 3 × 3 × 3, 128, maxpool, stride 2
Encoder 3(F4)	256 × 12 × 12 × 6	Conv, 3 × 3 × 3, 256, maxpool, stride 2
Encoder 4(F5)	512 × 6 × 6 × 3	Conv, 3 × 3 × 3, 512, maxpool, stride 2
Decoder 4	256 × 12 × 12 × 6	Deconv, concat(F4), 3 × 3 × 3, 256, conv
Decoder 3	128 × 24 × 24 × 12	Deconv, concat(F3), 3 × 3 × 3, 128, conv
Decoder 2	64 × 48 × 48 × 24	Deconv, concat(F2), 3 × 3 × 3, 64, conv
Decoder 1	32 × 96 × 96 × 48	Deconv, concat(F1), 3 × 3 × 3, 32, conv
Output	2 × 96 × 96 × 48	Conv, 1 × 1 × 1, 2, conv, stride 1

1. The dice coefficient loss function (denoted as DICELoss), which is defined as:

   $$L_{\mathit{DICE}}=\frac{1}{N}\sum _{i=1}^N\left(1-2\frac{|A\cap B|}{|A|+|B|}\right),$$

   where A is the reference standard volume (ground truth), and B is the predicted volume.

To facilitate the complementary feature flow between the two 3D‐UNets to achieve PET/CT tumor co segmentation, we propose a feature‐level fusion scheme, which takes advantage of skipping connections between layers. Figure 2 shows the organization of the proposed feature fusion scheme. The network has two parallel 3D‐UNets, one for CT and the other for PET, which share the same network architecture as previously described. For feature fusion, we concatenate the feature maps from the corresponding encoders from both CT and PET branches using either the CT or the PET decoder in each branch. In this way, the decoder module can incorporate the complementary features each modality extracted in their respective encoder modules, which maximizes the information flow between either short or long range connections while preserving the various low‐mid‐high semantic scales of the levels of the layers. In contrast with the single 3D‐UNet, the DFCN‐CoSeg network simultaneously generates two tumor label predictions: one for CT and the other for PET. During the process of network training, the DFCN‐CoSeg loss function is the sum of the two separate losses for CT and PET.

The 3D‐UNets were implemented using the open source TensorFlow‐GPU⁴³ package. All networks ran on NVIDIA GeForce GTX 1080 Ti GPU with 11GB of memory. The 3D‐UNets were trained by the Adam optimization method with a mini‐batch size of 4 and for 21 epochs. For the proposed DFCN‐CoSeg network, the mini‐batch size is set to two due to the GPU memory limit. The learning rate was initialized as 10⁻⁴ and half‐decreased according to a piecewise linear scheme. With regard to weight initialization, we adopted the truncated normal distribution with zero mean and a standard deviation of 0.01. To avoid overfitting, the weight decay was adopted to obtain the best performance on the test set.

2.B.3. DFCN‐CoSeg network training

Of the total 60 pairs of PET‐CT scans, 38 pairs were used as the training set, and the remaining 22 pairs were used as the test set. The selection procedure began by sorting all scan pairs according to the size of the tumor volume. Then three scan pairs out of every five pairs in that order were selected to be in the training set. The test set consisted of the remaining 22 scans. This stratified strategy ensured that the training set is representative of the whole dataset in terms of tumor volume. All parameters were tuned on the training set. All reported results were obtained on the test set. Among the 22 cases of the test set, 10 cases were selected as the validation set to observe the learning curves for single‐ modality 3D‐UNets and DFCN‐CoSeg. Based on the learning curves, their best models on the validation set were determined and used to evaluate their performance on the whole test set (22 cases). None of the 22 cases in the test set were employed for training the networks.

Due to the extremely limited annotated data, several data augmentation methods were adopted to enhance the training set. For each pair of coregistered PET‐CT scans in the training set, a number of rigid translation, rotation and flip operations were performed to obtain additional training datasets. To perform rigid translation, the corresponding region‐of‐interest (ROI) bounding boxes were cropped by shifting the gravity mass center in a fixed voxel range in (5, 10, 15, 20). This shift occurred along the eight combinations of the three axis directions. For each original ROI this resulted in 32 translated ROIs. The rotation and flip operations were extended to those ROIs to further enlarge the training set. For the rigid rotation operation, each ROI image was rotated 90°, 180°, and 270° counter‐clockwise around the z axis (slice‐axis) to generate new ROI images. In addition, each ROI image was flipped horizontally and vertically to generate new ones. In this augmentation process, the duplicated ROIs were removed.

See Fig. 3 for detailed some examples of these data augmentations.

Figure 3.

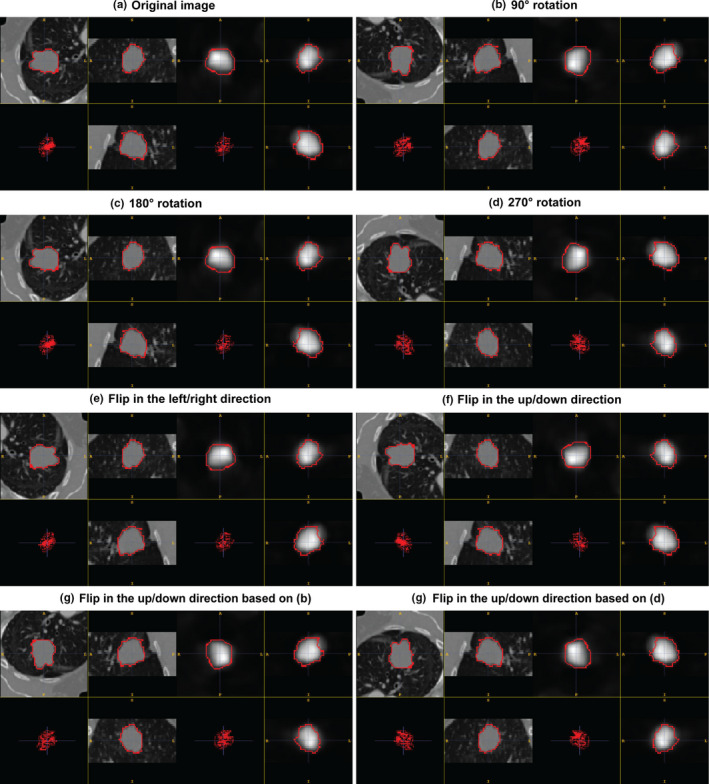
Illustration of some examples using data augmentation. And these augmentation operations were conducted in the X–Y plane. [Color figure can be viewed at wileyonlinelibrary.com]

2.C. Compared methods

We conducted quantitative comparisons for three semiautomatic graph‐based cosegmentation approaches: (a) the graph‐based PET‐CT cosegmentation method,¹² (b) the random‐walker‐based cosegmentation method²³ and (c) the matting‐based cosegmentation method.²⁸ For these semiautomatic methods, a few manual seeds should be defined on the tumor. In our experiment, the same initialization procedure was employed as described by Song et al.¹² The user needs to specify two concentric spheres with different radii to serve as object and background seeds. All voxels inside the smaller sphere were used as the object seeds. All voxels outside the larger sphere were used as background seeds. For the hyper‐parameters, a grid search strategy based on a training set was used.

The proposed DFCN‐CoSeg method was compared to the deep learning‐based method, where 3D‐UNet was directly applied to segment the tumor boundaries using either PET or CT.

According to AAPM TG2116 recommendations,⁴⁴ the segmentation performance was evaluated using three criteria:

1. Accuracy score (Score), which is defined as the weighted average sensitivity (SE) and positive predictive value (PPV). Following the characterization of Hatt et al.²⁰, we computed the accuracy Score as Score = 0.5 × SE + 0.5 × PPV.

2. Dice similarity coefficient (DSC), which measures the volume overlap of two segmentations, A and B. It is defined as 2|A ∩ B|/(|A| + |B|), with a range of [0,1]. The higher the DSC is, the better volume overlap the two segmentations have.

3. Average symmetric surface distance (ASSD), which is defined as:

   $$ASSD=\frac{{\sum }_{a\in A}{min}_{b\in B}d(a,b)+{\sum }_{b\in B}{min}_{a\in A}d(a,b)}{|A|+|B|}$$

   where A denotes the boundary surface of the reference standard and B denotes the computed surface; a and b are mesh points on the reference surface and the computed surface respectively. d(a, b) Represents the distance between a and b. |A| and |B| are the number of points on A and B respectively. The lower the ASSD is, the better volume overlap the two segmentations have.

Statistical significance of the observed differences was determined using a 2‐tailed paired t‐test for which a P value of 0.05 was considered significant.

3. Results

Table 2 shows the mean values and standard deviations for the three performance metrics (Score, DSC and ASSD) for the evaluated methods on the test scans (22 cases). In addition to the cosegmentation results, we include three reference methods (Song et al.¹², Ju et al.²³, and Zhong et al.²⁸) using either CT or PET. Compared to the three reference methods, the proposed DFCN‐CoSeg approach (with the best Scores of 0.865 ± 0.034 on CT and 0.853 ± 0.063 on PET) achieves significantly better results using either the DSCs or ASSDs as metrics. This demonstrates that the trained deep learning network can learn to be more descriptive and better discriminate between features than the traditional manual methods. When incorporating dual image modality information (PET‐CT) into the segmentation process, segmentation accuracy using either deep learning based or other graph‐cut based methods can consistently improve the results of both CT and PET scans than a single modality is able to achieve alone. This suggests that the dual image modality information (PET‐CT) facilitates simultaneous cosegmentation. Considering the different loss functions for the deep learning based methods (3D‐UNets or DFCN‐CoSeg), the models trained with dice coefficient loss performed better than those using cross‐entropy based models. For example, the deep learning based 3D‐UNet method with the dice coefficient loss, achieved much higher DSCs on both CT and PET (0.811 ± 0.151 over 0.638 ± 0.165, and 0.794 ± 0.111 over 0.643 ± 0.141, respectively), compared to either method used by Song et al.¹², Ju et al.²³, or Zhong et al.²⁸ The first MICCAI challenge for PET tumor segmentation (Hatt et al.¹⁰) reported 0.642 to 0.810 DSC values from 15 different segmentation methods (see Table 1, Hatt et al.¹⁰). The DSC values of the DFCN‐CoSeg approach with results of over 80% are comparable to and even competitive with the results of the MICCAI challenge. The DFCN‐CoSeg method achieved the best overall Score on both CT and PET (0.865 ± 0.034 and 0.853 ± 0.063, respectively) and revealed much smaller standard deviations than any other of the compared methods. Although the average Scores, DSCs or ASSDs from the DFCN‐CoSeg are higher than those obtained when using the single‐modality 3D‐UNets, the statistical comparison did not show a significant improvement on either CT or PET. However, the DFCN‐CoSeg standard deviation is much smaller than those from the single‐modality 3D‐UNets (0.037 over 0.151 on CT, 0.087 over 0.111 on PET). This suggests that while the 3D‐UNets can effectively learn to discriminate features to recognize tumor voxels, the simple multimodality feature fusion can only provide limited improvement given the high segmentation accuracy on the PET image. We surmise that although the features learned by the network from PET images are able to localize the overall tumor position, they may not provide more useful information on the true tumor boundary. This provides an advantage over the previous single modality graph‐cut based semiautomatic methods that promise to diminish physician work load and consequently facilitate the widespread use of PET‐CT images.

Table 2.

Statistics of the compared methods on the test set (22 cases) based on the contours generated by Simultaneous Truth and Performance Level Estimation Algorithm (STAPLE). Average values and their standard deviations were reported

Methods	Modalities	Score		DSC		ASSD
		Single	Dual	Single	Dual	Single	Dual
Song et al.	CT	0.712 ± 0.140	0.734 ± 0.089	0.597 ± 0.257	0.638 ± 0.165	2.574 ± 2.447	1.938 ± 1.132
	PET	0.735 ± 0.084	0.740 ± 0.074	0.629 ± 0.158	0.643 ± 0.141	2.901 ± 2.607	2.656 ± 2.131
Ju et al.	CT	0.778 ± 0.082	0.765 ± 0.098	0.765 ± 0.093	0.759 ± 0.100	1.484 ± 0.745	1.650 ± 0.823
	PET	0.817 ± 0.064	0.820 ± 0.061	0.776 ± 0.106	0.782 ± 0.099	1.526 ± 1.068	1.473 ± 0.970
Zhong et al.	CT	0.798 ± 0.058	0.809 ± 0.058	0.766 ± 0.095	0.783 ± 0.095	1.186 ± 0.828	1.080 ± 0.714
	PET	0.774 ± 0.065	0.816 ± 0.054	0.711 ± 0.123	0.778 ± 0.086	2.102 ± 2.002	1.502 ± 1.083
3D‐UNet (CELoss)	CT	0.812 ± 0.115	—	0.780 ± 0.185	—	1.667 ± 1.863	—
	PET	0.846 ± 0.084	—	0.811 ± 0.133	—	1.127 ± 0.718	—
DFCN‐CoSeg (CELoss)	CT	—	0.850 ± 0.061	—	0.836 ± 0.095	—	0.895 ± 0.661
	PET	—	0.848 ± 0.064	—	0.823 ± 0.086	—	1.066 ± 0.660
3D‐UNet (DICELoss)	CT	0.839 ± 0.085	—	0.811 ± 0.151	—	1.291 ± 1.313	—
	PET	0.832 ± 0.075	—	0.794 ± 0.111	—	1.229 ± 0.587	—
DFCN‐CoSeg (DICELoss)	CT	—	0.865 ± 0.034	—	0.861 ± 0.037	—	0.806 ± 0.605
	PET	—	0.853 ± 0.063	—	0.828 ± 0.087	—	1.079 ± 0.761

The bold values indicates the best results achieved among all the methods compared using the dual PET‐CT images.

Figure 4 illustrates the segmentation results of the compared methods on four PET‐CT scan pairs. The proposed DFCN‐CoSeg method can obtain more consistent results against the STAPLE‐generated ground truth. The example results demonstrate that the proposed DFCN‐CoSeg method is able to locate tumor boundaries on PET images more accurately than the other compared methods.

Figure 4.

Segmentation results of compared methods on four positron emission tomography‐computed tomography scan pairs. Red: ground truth generated by Simultaneous Truth and Performance Level Estimation Algorithm, Blue: Song et al's.¹² method, Green: the 3D‐UNet method (first two columns), Green: Proposed deep learning, fully convolutional networks‐CoSeg method (last two columns). [Color figure can be viewed at wileyonlinelibrary.com]

The intermodality consistency between the STAPLE based ground truth on each image modality and the manual contours of three physicians were tested and summarized in Table 3. The DCS value of all manual contours on CT images over their ground truth of STAPLE was 0.867, while that on PET images was 0.875. No significant interimage modality variations were found between the STAPLE ground truth and all corresponding manual contours (P = 0.423). In Table 3, the three physicians are denoted as P1, P2, and P3. Their respective manual contours on CT (PET) are denoted as P1_CT, P2_CT, and P3_CT (P1_PET, P2_PET, and P3_PET). The STAPLE_CT (STAPLE_PET) is obtained from the STAPLE algorithm with P1_CT (P1_PET), P2_CT (P2_PET) and P3_CT (P3_PET) as inputs.

Table 3.

Dice similarity coefficients (DSC) values of each physician expert

Dice similarity coefficients (DSC)
STAPLE_CT
P1_CT	P2_CT	P3_CT
0.846	0.819	0.934
STAPLE_PET
P1_PET	P2_PET	P3_PET
0.901	0.901	0.825

4. Discussion

4.A. Performance

Accurate tumor delineation in image‐guided radiotherapy, is critically important yet efforts to automate the process for radiotherapy treatment planning or delivery remain elusive.¹⁹ In this work, our DFCN‐CoSeg approach for PET‐CT offers improved automation, requires no direct interaction and enables efficient computer‐aided segmentation which may facilitate eventual clinical use. Our framework takes advantage of the assumption that the combination of information derived from dual image modality (PET‐CT) would vastly improve the capability of an automated, learning‐based segmentation approach. Our goal is to automate the manual delineation done by radiation oncologists to define tumor by contouring PET‐CT images so that the radiation oncologists can review and modify the automated tumor efficiently. Owing to the successful adoption of deep fully convolutional neural network architecture, the automated feature extraction is conducted on both dual‐modality PET‐CT images and able to discriminate between tumors or nontumors. The proposed DFCN‐CoSeg was evaluated on 60 NSCLC cases and the promising experimental results have demonstrated the efficiency over previous graph‐based PET‐CT cosegmentation methods.

Feature fusion between medical images acquired using distinct modalities is a challenging problem due to the interimage variability inherent in each type. These include: different noise, various image resolutions, different contrast, or misregistration of the images to mention a few.^{45, 46} Traditional methods include morphology‐based fusion,⁴⁷ wavelet‐based fusion,⁴⁸ component analysis based fusion,⁴⁹ and hybrid fusion.⁵⁰ Different feature fusion approaches using deep neural networks are discussed:

1. The first and most basic method is to combine the input images/features and process them jointly in a single UNET. This describes most methods in the literature for handling multi‐image modality datasets such as the fusion of multiparametric brain MR images of T1‐ and T2‐ weighted MRI for brain tumor segmentation.^{34, 37}

2. The second approach is to conduct feature fusion on images of different resolutions³⁴ through two steps of extracting different sizes of input patches in the input images and giving them as inputs of different networks to obtain the different feature levels to conduct the feature fusion.

3. The last method is to conduct feature fusion based on deep convolutional and recurrent neural networks (RNN), where the RNNs are responsible for exploiting the intraslice and interslice contexts respectively.⁵¹

The novelty of our approach lies in the investigation of the encoder‐decoder based 3D‐UNet for the cosegmentation in dual‐modality PET‐CT images. Our contribution is to consider the difference between each segmentation on either the PET or the CT image and to design a coupled feature fusion network based on the 3D‐UNet architecture. This allows us to simultaneously produce high quality, voxel‐wise segmentation for tumors in PET‐CT images and specifically to cosegment tumors in PET‐CT images. A novel DFCN network was proposed where two coupled 3D‐UNets with an encoder‐decoder architecture were integrated. One 3D‐UNet is used to perform the PET image tumor segmentation and the other to perform the CT image segmentation. The two UNets communicate with each other to allow the complementary features from both modalities to “flow” between the two 3D‐UNet networks to produce consistent tumor contours.

Figure 5 shows the DSC training curves on single‐modality 3D‐UNets trained on either CT‐ or PET‐ only data, and the training curves of DFCN‐CoSeg on both PET and CT. From the learning behaviors in those figures we can observe that the training set accuracy is much higher than that on the validation set on the single‐modality 3D‐UNet, for either CT or PET. The curves show a relatively large fluctuation compared to those from DFCN‐CoSeg.

Figure 5.

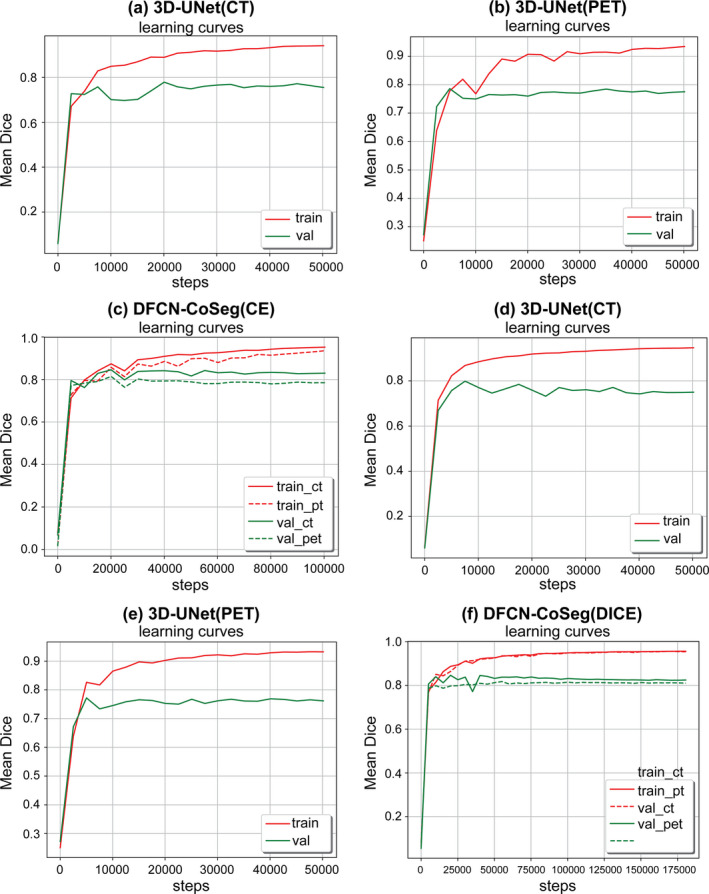
Mean dice similarity coefficient (DSC)s on training and validation sets during the network training with CELoss (a,b,c) and DICELoss (d,e,f). 3D‐UNet computed tomography (CT)/positron emission tomography (PET) means 3D‐UNet trained on CT or PET only data. Deep learning fully convolutional networks (DFCN)‐CoSeg means the feature fusion DFCN‐CoSeg network architecture for PET‐CT cosegmentation. [Color figure can be viewed at wileyonlinelibrary.com]

This may be due to the lack of complementary information from the other modality and the large variation in the tumor volume sizes. By contrast, the learning curves are much smoother than that of the single‐modality 3D‐UNet for the dual‐modality DFCN‐CoSeg network. This indicates that the complementary information exchanged between CT and PET images can help learn to better discriminate features, which in turn helps locate the local optimum for network training. Second, considering the loss functions, the DICELoss has achieved smoother learning curves compared to the CELoss, which indicates that the dice loss function is more robust on data variability in the training set compared to the simple cross‐entropy loss. Third, as shown in these figures, we can see the mean DSCs on the training set are consistently increasing and become steady after about 15 epochs, while the mean DSCs on the validation set did not increase. We determined the best models for these networks based on their respective mean DSCs on the validation set, then evaluated them on the 22 cases that did not participate in the real network training.

4.B. Data augmentation improves general performance

In this subsection we study if data augmentation can improve general performance in PET‐CT segmentation. We again ran the same experiments described above, but without the data augmentation on the training set, that is, the training set only includes the original 38 cases. All models were trained in the same way as described above. Table 4 shows the segmentation performances based on Score, DSC and ASSD on our test set (22 cases) for these models trained either with or without data augmentation. Figure 6 illustrates the accuracy curves trained without data augmentation. As we can see in the table and figures, those network models trained with data augmentation can achieve significantly better performance than those without data augmentation. Compared to Fig. 5, the learning curves in Fig. 6 also get steady more quickly (about 10 000 steps), which indicates that these models were quickly fitted on the training set without data augmentation.

Table 4.

Statistics of the compared methods on the test set (22 cases) based on the contours generated by Simultaneous Truth and Performance Level Estimation Algorithm. Those networks trained with data augmentation can achieve significantly better performance than those without data augmentation

Methods	Modalities	With data‐augmentation			Without data‐augmentation
		Score	DSC	ASSD	Score	DSC	ASSD
3D‐UNet (CELoss)	CT	0.812 ± 0.115	0.780 ± 0.185	1.667 ± 1.863	0.752 ± 0.157	0.719 ± 0.207	3.154 ± 4.336
	PET	0.846 ± 0.084	0.811 ± 0.133	1.127 ± 0.718	0.819 ± 0.078	0.779 ± 0.127	2.491 ± 2.809
DFCN‐CoSeg (CELoss)	CT	0.850 ± 0.061	0.836 ± 0.095	0.895 ± 0.661	0.818 ± 0.084	0.806 ± 0.108	1.226 ± 0.987
	PET	0.848 ± 0.064	0.823 ± 0.086	1.066 ± 0.660	0.793 ± 0.101	0.771 ± 0.116	1.993 ± 2.346
3D‐UNet (DICELoss)	CT	0.839 ± 0.085	0.811 ± 0.151	1.291 ± 1.313	0.759 ± 0.156	0.728 ± 0.204	3.431 ± 5.176
	PET	0.832 ± 0.075	0.794 ± 0.111	1.229 ± 0.587	0.832 ± 0.076	0.808 ± 0.105	1.308 ± 0.750
DFCN‐CoSeg (DICELoss)	CT	0.865 ± 0.034	0.861 ± 0.037	0.806 ± 0.605	0.811 ± 0.098	0.785 ± 0.152	2.632 ± 4.657
	PET	0.853 ± 0.063	0.828 ± 0.087	1.079 ± 0.761	0.803 ± 0.087	0.778 ± 0.107	1.856 ± 1.976

Figure 6.

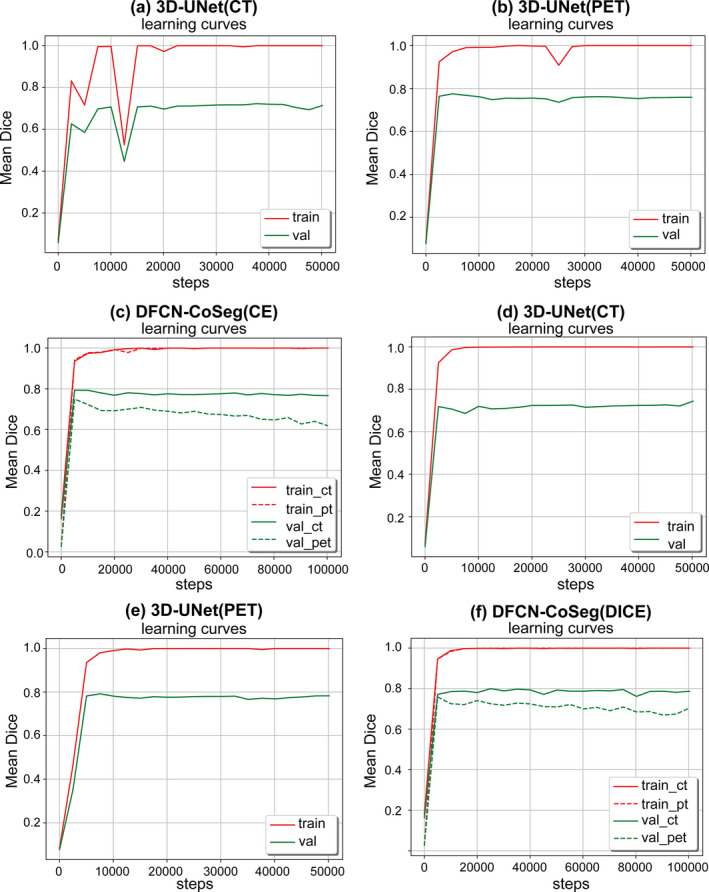
Mean dice similarity coefficients (DSC)s on training and validation sets during the network training with CELoss(a,b,c) and DICELoss(d,e,f). These networks were trained with only the original 38 cases as the training set, i.e., without data augmentation. [Color figure can be viewed at wileyonlinelibrary.com]

Table 5.

Statistics of SEs, PPVs on the whole‐body PET/CT images of the test set. The “Voxels” means the number of tumor voxels in the resampled data with volume spacing of 1 × 1 × 1 mm

Name	Voxels‐ct	Voxels‐pt	3D‐Unets(CT)		3D‐Unets(PET)		DFCN‐CoSeg(CT)		DFCN‐CoSeg(PET)
			SE	PPV	SE	PPV	SE	PPV	SE	PPV
A‐IA002126	3430	6496	0.903	0.105	0.645	0.093	0.871	0.171	0.590	0.135
A‐IA002122	16806	31164	0.678	0.402	0.964	0.278	0.864	0.421	0.903	0.407
A‐IA0002096	12424	22990	0.502	0.143	0.166	0.430	0.655	0.748	0.074	1.000
A‐IA002119‐M	10522	7888	0.854	0.168	0.567	0.485	0.861	0.821	0.721	0.758
A‐IA0002111	2034	2476	0.755	0.015	0.999	0.141	0.873	0.249	0.924	0.323
A‐IA0002114	37628	23224	0.044	0.026	0.745	0.020	0.370	0.062	0.440	0.027
A‐IA0002097	2786	7036	0.293	0.025	0.891	0.114	0.857	0.087	0.867	0.260
A‐IA000991‐M	3116	12318	0.587	0.090	0.821	0.035	0.934	0.014	0.930	0.042
A‐IA0001254	65604	104091	0.365	0.023	0.599	0.610	0.564	0.540	0.558	0.793
A‐IA002135‐M	4494	5240	0.852	0.081	0.927	0.090	0.900	0.089	0.961	0.140
A‐IA002133	6910	9458	0.837	0.071	0.739	0.480	0.916	0.516	0.558	0.671
A‐IA0002094	1026	2040	0.175	0.006	0.647	0.032	0.666	0.030	0.578	0.025
A‐IA002130	5018	6156	0.886	0.254	0.633	0.946	0.938	0.817	0.927	0.852
A‐IA002134	21210	41666	0.425	0.083	0.870	0.208	0.869	0.234	0.896	0.257
A‐IA002131	11156	6510	0.767	0.258	0.012	0.000	0.768	0.029	0.736	0.010
A‐IA0002108	7832	2258	0.797	0.111	0.752	0.024	0.789	0.427	0.882	0.070
A‐IA001491	2068	1206	0.517	0.016	0.912	0.021	0.613	0.046	0.949	0.034
A‐IA0001345	39432	44552	0.844	0.590	0.949	0.787	0.869	0.839	0.885	0.883
A‐IA0002109	2908	6730	0.863	0.055	0.995	0.037	0.879	0.024	0.989	0.044
A‐IA0002117	12292	17586	0.699	0.108	0.787	0.671	0.870	0.906	0.838	0.983
Mean			0.632	0.132	0.731	0.275	0.796	0.354	0.760	0.386

4.C. Testing on whole‐body PET‐CT images

The inputs for the proposed DFCN‐CoSeg network are two fixed‐size bounding boxes (i.e., cropped from the original whole‐body PET/CT images respectively). In our experiments we first crop the bounding boxes containing lesions according to the ground truth segmentation as the input of the networks. However, it is very important in clinical practice to directly segment the whole‐body PET‐CT scans simultaneously. To this end, we conducted additional experiments to test the segmentation performance of the proposed method on resampled whole‐body PET‐CT scans (i.e., with voxel spacing of 1 × 1 × 1 mm). Specifically, we first resampled the whole‐body PET/CT scans to isotropic voxel spacing (1 × 1 × 1 mm), then based on the sliding window technique, cropped the paired PET/CT sub‐volume, gave them as inputs of the 3D‐UNets or DFCN‐CoSeg, and generated the final results on whole‐body predictions.

Table 4 shows the statistics of the segmentation results on the respective whole‐body PET/CT images of the test set. As shown in this table, for most cases, the SEs and PPVs of the proposed DFCN‐CoSeg are overall higher than those of the 3D‐UNets. The high sensitivities indicate the proposed DFCN‐CoSeg can correctly detect and segment the tumors in the whole‐body images. However, in some cases (e.g., A‐IA002114), the specificities of the proposed DFCN‐CoSeg are lower than 50%.

The main reason for the relatively poor results for the tumor segmentation is that it is located in the boundary between two adjacent sliding windows. The tumor region located in the boundary presented relatively poor predictive results when compared to the tumor located in the center region. From the viewpoint of fully convolutional networks, as our DFCN‐CoSeg models were trained based on tumor‐centralized PET/CT bounding boxes, they may be biased in the centralized inputs.

The automatic object localization techniques could help improve this. It is worth noting that much research has been devoted to automatically obtaining these bounding boxes with a high degree of confidence that they will contain lesions within them (e.g., lung nodule object detection⁵²), and results from these modules can be used as the inputs for the proposed DFCN‐CoSeg method. It is also worth observing that recent advances in computer vision have demonstrated the efficiency of simultaneously conducting object detection and segmentation in a single deep network framework (e.g., Mask‐RCNN).⁵³

4.D. Limitations

Although the proposed DFCN‐CoSeg method has achieved some improvement over the traditional graph‐based method, the absolute assessment based on DSCs is still about 82% on PET and 86% on CT. There is still much improvement needed in terms of performance, robustness, and stability. For the single‐modality 3D‐UNets, we observed that the DSCs on two test datasets were below 70%. It seems the tumor patterns in the two datasets were not adequately represented in the training set. We thus plan to enlarge the training set in the future.

In terms of the network architecture design, our DFCN‐CoSeg network was inspired by the encoder‐decoder based 3D fully convolutional networks (3D‐FCN)^{32, 37}and the 3D‐UNets.^{30, 31, 34} As a natural extension of the well‐known 2D FCN proposed by Long et al.⁴¹, 3D‐FCNs have been successfully applied to semantic segmentation tasks in medical imaging, such as liver segmentation,³² brain tumor segmentation,³⁴ and pancreas segmentation.⁵⁴ As demonstrated in these studies, the skip connections designed in 3D‐FCNs or 3D‐UNets were very important to help recover the full spatial resolution at the network outputs, which is suitable for voxel‐wise segmentation tasks. Various typical extensions include the extended U‐Net based on the DenseNet,⁵⁵ or the short skip connection.⁵⁶ In this work, we utilized a coupled skip connection between the two 3D‐UNets for CT or PET, taking advantage of both modalities to produce two separate segmentations. Although our proposed method achieved good results, designing a more efficient feature fusion architecture would be very beneficial.

The proposed DFCN‐CoSeg method utilizes a pixel‐wise cross‐entropy loss or dice coefficient loss in the last layer of its network, which is insufficient to learn both local and global contextual relations between pixels. Although the use of UNet architecture may alleviate this problem, enabling it to implicitly learn some local dependencies between pixels; it is still limited by their pixel‐wise loss function. This is because it lacks the ability to enforce the learning of multi‐scale spatial constraints directly in the end‐to‐end training process. We propose the future integration of Conditional Random Fields (CRFs) into our DFCN‐CoSeg framework with an end‐to‐end training process to enforce the pixel‐wise labeling consistency to improve the segmentation accuracy.

AAPM Task Group 211⁶ recommends the use of different types of ground truth datasets including phantom and clinical contouring. The proposed DFCN‐CoSeg method has been thoughtfully validated on clinical contouring. It is natural to also validate our method on simulated PET‐CT images and those obtained from phantoms. However, the performance of a model with supervised learning frequently deteriorates on data from a new deployment domain, which is known as a domain shift problem.⁵⁷ The domain shift from simulated images to real data can be particularly challenging.^{58, 59} Our DFCN‐CoSeg model, as a supervised learning method trained on physician's manual contours, may not well work on the simulated and phantom data.

In this study, all PET and CT datasets were obtained from a single PET‐CT scanner (Siemens Medical Solutions, Inc.). Different PET‐CT scanners have unique acquisition and reconstruction properties, for PET datasets especially: spatial reconstruction, noise properties, and voxel size. The sensitivity study of the proposed DFCN‐CoSeg method for each specific PET‐CT scanner needs to be investigated. In fact, this is another domain shift problem in transfer learning, which has been widely recognized in machine learning or computer vision. Pretrained convolutional neural networks have been designed and trained on the ImageNet dataset such as AlexNet,⁶⁰ Google InceptionNet,⁶¹ and ResNet‐50.⁶² These pretrained models or weights have been widely adopted and transferred into other tasks such as RGBD segmentation⁶³ or remote sensing image analysis⁶⁴ to initialize the target networks.

4.E. Impact

For one unique tumor, one segmentation represents pathologically and morphologically true tumor boundaries. However, the tumor boundaries are defined according to whether they are macroscopically or microscopically identified. If two image modalities are the same type of morphological or anatomical image such as CT and MRI, then the macroscopic tumor boundaries can be similar depending on tumor sites. For instance, lung cancer tumor boundaries that presented considerable image intensity changes on both MRI and CT are similar due to the significant electron density difference between the tumor and the adjacent lung tissue. The segmentations based upon their image intensities are similar even though the physics underlying the image generation for these images is different. In the case of cervical cancer, CT and MRI tumor boundaries vary considerably due to the poor soft‐tissue contrast on CT. MRI is critical for tumors requiring high soft‐tissue contrast such as gynecologic cancer, breast cancer, or prostate cancer. Even though each tumor is unique its boundary identification is different due to the physics underlying the generation of each medical image. This is especially true between molecular images such as PET or functional MRI (e.g., DCE (dynamic contrast enhanced) or DWI (diffusion weighted image) MRI) and anatomical images such as CT. PET images visualize the uptake region of radiotracer such as F18‐FDG (Fludeoxyglucose) as a marker for the tissue uptake of glucose, indicating a close correlation with tumor metabolism.⁶⁵ The high glucose uptake in tumor cells is used as a surrogate to identify an active tumor region using PET images, thus the highly active regions identified by F18‐FDG PET images do not necessarily represent every single tumor cell or anatomically defined tumor. When tumor cells are not active or highly hypoxic, they are not included in the F18‐FDG PET positive regions. In addition, when other radiotracers for PET images such as F18‐FMISO (fluoromisonidazole) or F18‐FLT are used, then specific subtumor regions are identified based on molecularly defined criteria. F18‐FMISO PET images present hypoxic tumor regions⁶⁶ while F18‐FLT PET images efficiently identify proliferating tumor regions.⁶⁷ In general, the identified tumor regions using molecular imaging are considerably different from anatomical CT imaging which identifies high electron density regions.

Besides the fundamental technical differences required to generate functional or anatomical images, PET images take a longer time (typically 10–20 min for acquisition vs less than 2 min in CT acquisition) to acquire. For a tumor site affected by respiratory motion like lung cancer, the acquisition time will include the full range of motion for PET images, while the tumor region in a CT scan (often fully acquired in a breath hold) is less affected by breathing motion. As a result, the tumor boundary varies between PET and CT images. In addition, PET images have a relatively poor spatial resolution (∼3–5 mm), while the spatial resolution of CT images can be submillimeter (e.g., 0.6 mm). These inherent imaging features all cause challenges in identifying tumor boundaries between PET and CT images.

Simultaneously segmenting tumors from both PET and CT while admitting the difference of the boundaries defined in the imaging modalities is a more reasonable method than those previously applied to fused PET‐CT images, where identical tumor boundaries were assumed.

Advances in radiomics and machine learning in PET‐CT images involve the accurate, robust, and reproducible segmentation of the tumor volume in each imaging modality to extract numerous unique features from each imaging modality. These radiomics features include 3D shape descriptors, intensity‐ and histogram‐based metrics and 2nd or higher order textural features (Hatt et al.¹⁰). By obtaining different radiomics features from each imaging modality, including different segmentations from each image modality, we expect that the use of radiomics and CNN would improve the efficiency of diagnosis, prognosis determination and clinical decision‐making critical for therapeutic interventions such as surgery, chemotherapy, or radiotherapy.

In our study, we presented two PET‐CT cosegmentation approaches; Segmentation of PET images while interacting with CT images and vice versa. Two different cosegmentations could be variously adapted in current clinical applications. The PET‐based cosegmentations can be further investigated to improve current PET‐based prognostic assay studies in nuclear medicine in which the metrics of PET images, such as standardized uptake value (SUV) and metabolic tumor volume (MTV) have been extensively studied.⁶⁸ In addition, the CT‐based cosegmentation potentially improves contouring accuracies and robustness for radiation therapy, especially for determining high dose regions used in approaches such as SBRT in which the target (tumor) contouring accuracy is critical. To our knowledge, the proposed DFCN‐CoSeg network is the first CNN‐based, simultaneous segmentation approach for both PET and CT.

Our proposed deep learning DFCN‐CoSeg cosegmentation framework can be successfully applied to the simultaneous cosegmentation of GTVs in the PET‐CT image dataset. The cosegmented GTV is expected to improve the efficacy of radiotherapy. The proposed DFCN‐CoSeg approach will not fully replace input and review by physicians. However, we expect this supplementary segmentation tool would act as an aid and would improve the robustness and consistency of contouring. Beichel at al.⁶⁹ compared a semiautomated segmentation vs experts contouring method, and presented the intra‐ and interoperator standard deviations that were significantly lower for the semi‐automated segmentation. Also, contouring capability is expected to improve the efficiency of molecular image guided radiotherapy when used in concert with a PET‐CT Linac system⁷⁰ in which fast, accurate contouring is critical for adaptive replanning on each fraction. The developed deep fully convolutional network based segmentation can also be applied to current kV‐cone‐beam, CT based, adaptive replanning approaches. The improved accuracy of using deep learning based cosegmentation is expected to improve its prognostic power for the therapy selection for lung cancer patients and improve clinical outcomes. In addition, the current state‐of‐the‐art in tumor diagnosis and characterization does not perform 3D contouring due to its extended acquisition time but instead performs three, 1D tumor measurements (length, width, and height) from which tumor size and stage is determined. Before and after chemotherapy, 3D contouring (segmentation) is not clinically performed for response assessment. No contouring is performed following radiation therapy in order to assess response to therapy. DFCN‐CoSeg could provide a metric following treatment if correctly applied. The prognostic power, of DFCN‐CoSeg applied to GTV is being studied and its results will be assessed. Given that integrated PET‐CT scanners are widely available, the developed deep learning based cosegmentation technique in this work is readily available as a tool to be utilized in nonsmall cell lung carcinoma clinical trials. In addition, the proposed computer‐aided, automated tumor volume identification method using deep learning is expected to advance the accuracy of target delineation for radiation therapy planning. This will be especially important for SBRT in which high‐precision tumor identification is crucial in the process of defining the spatial extent of the therapeutic radiation dose distribution. It is expected that the improved accuracy and robustness of using deep learning based cosegmentation on both PET and CT images would improve outcomes and reduce the toxicity of radiation therapy for nonsmall cell lung cancer.

5. Conclusions

In this work, we investigated the deep 3D fully convolutional neural networks for tumor cosegmentation on dual‐modality PET‐CT images. Experimental results demonstrated the effectiveness of our proposed method and improved accuracy compared to several common existing methods. Our method would benefit clinics as it does not require unique knowledge to implement effectively. Our dual 3D UNet cosegmentation framework could be further applied to other multi‐modality data, for example, PET/MR. Validation of the PET/CT segmentation on other datasets including multi‐institutional trials and more different neural network architectures will also be investigated in the future.

Conflict of interest

The authors have no relevant conflicts of interest to disclose.