Abstract
We analyse the effect of intrinsic fluctuations on the properties of bistable stochastic systems with time scale separation operating under quasi-steady state conditions. We first formulate a stochastic generalisation of the quasi-steady state approximation based on the semi-classical approximation of the partial differential equation for the generating function associated with the chemical master equation. Such approximation proceeds by optimising an action functional whose associated set of Euler-Lagrange (Hamilton) equations provides the most likely fluctuation path. We show that, under appropriate conditions granting time scale separation, the Hamiltonian can be re-scaled so that the set of Hamilton equations splits up into slow and fast variables, whereby the quasi-steady state approximation can be applied. We analyse two particular examples of systems whose mean-field limit has been shown to exhibit bi-stability: an enzyme-catalysed system of two mutually inhibitory proteins and a gene regulatory circuit with self-activation. Our theory establishes that the number of molecules of the conserved species is order parameters whose variation regulates bistable behaviour in the associated systems beyond the predictions of the mean-field theory. This prediction is fully confirmed by direct numerical simulations using the stochastic simulation algorithm. This result allows us to propose strategies whereby, by varying the number of molecules of the three conserved chemical species, cell properties associated to bistable behaviour (phenotype, cell-cycle status, etc.) can be controlled.
I. Introduction
The networks of interacting genes and proteins that are responsible for regulation, signalling and response, and which, ultimately, orchestrate cell function, are under the effect of noise.1–5 This randomness materialises in the form of fluctuations of the number of molecules of the species involved, subsequently leading to fluctuations in their activity. Besides external perturbations, biochemical reactions can be intrinsically noisy, especially when the number of molecules is very low.
Far from necessarily being a mere disturbance, fluctuations are an essential component of the dynamics of cellular regulatory systems which, in many instances, are exploited to improve cell function.6,7 For example, randomness has been shown to enhance the ability of cells to adapt and increase their fitness in random or variable environments.8–10 Random noise also serves the purpose of assisting cell populations to sustain phenotypic variation by enabling cells to explore the phase space.3–5,7,11,12
One of the mechanisms that allows noise-induced phenotypic variability relays on multi-stability.13,14 The basis of this mechanism was first proposed by Kauffman,15 who associated phenotypes or differentiated states to the stable attractors of the dynamical systems associated to gene and protein interaction networks. In the presence of noise, the corresponding phase space generates an epigenetic landscape, where cells exposed to the same environment and signalling cues coexist in different cellular phenotypes.16
Multi-stability is also an essential element in the control of cell response and function via signalling pathways.17 In particular, bi-stability as a means to generate reliable switching behaviour is widely utilised in numerous pathways such as the apoptosis,18 cell survival,19 differentiation,20 and cell-cycle progression21,22 pathways. For example, bi-stability is used to regulate such critical cell functions such as the transition from quiescence to proliferation through bistable behaviour associated with the Rb-E2F switch within the regulatory machinery of the mammalian cell-cycle.23–28
A common theme which appears when trying to model cell regulatory systems is separation of time scales, i.e., the presence of multiple processes evolving on widely diverse time scales. When noise is ignored and systems are treated in terms of deterministic mean-field descriptions, such separation of time scales and the associated slow-fast dynamics are often exploited for several forms of model reduction, of which one of the most common is the so-called quasi-steady state approximation (QSSA).29 This approximation is ubiquitously used whenever regulatory processes involve enzyme catalysis, which is a central regulation mechanism in cell function.17 In this paper, we investigate the effects of intrinsic noise on the bi-stability of two particular systems, namely, an enzyme-catalysed system of mutual inhibition and a gene regulatory circuit with self-activation. The mean-field limit of both these systems has been shown to exhibit bi-stability.22,30 The aim of this paper is to analyse how noise alters the mean-field behaviour associated to these systems when they operate under quasi-steady state conditions.
We note that this work does not concern the subject of noise-induced bifurcations.31 Such phenomenon has been studied in many situations, including biological systems. An example which is closely related to the systems we analyse here is the so-called enzymatic futile cycles. Samoilov et al.32 have shown that noise associated to the number of enzymes induces bistability. In the absence of this source of noise, i.e., in the mean-field limit, the system does not exhibit bistable behaviour. The treatment of these phenomena would require to go to higher orders in the Wentzel–Kramers–Brillouin (WKB) expansion,57 which we do not explore here.
The issue of separation of time scales in stochastic models of enzyme catalysis has been addressed using a number of different approaches. Several such analyses have been carried out in which the QSSA is directly applied to the master equation by setting the fast reactions in partial equilibrium (i.e., the probability distribution corresponding to the fast variables remains unchanged), and letting the rest of the system to evolve according to a reduced stochastic dynamic.33,34 Other approaches have been proposed such as the QSSA to the exact Fokker-Planck equation that can be derived from the Poisson representation of the chemical master equation (CME).35 Approaches based on enumeration techniques have also been formulated.36 Furthermore, Thomas et al.37 have recently formulated a rigorous method to eliminate fast stochastic variables in monostable systems using projector operators within the linear noise approximation.37 Methods for model reduction based on perturbation analysis have been developed in Refs. 38 and 39. Additionally, driven by the need of more efficient numerical methods, there has been much activity regarding the development of numerical methods for stochastic systems with multiple time scales.40–42 Several of these methods are variations of the stochastic simulation algorithm33,43–47 or the τ-leap method48 where the existence of fast and slow variables is exploited to enhance their performance with respect to the standard algorithms. Another family of such numerical methods is that of the so-called hybrid methods, where classical deterministic rate equations or stochastic Langevin equations for the fast variables are combined with the classical stochastic simulation algorithm for the slow variables.49,50 Other related methods were studied in Refs. 51–53.
Here, we advance the formalism developed in Ref. 38, in which a method based on the semi-classical approximation of the chemical master equation allows to evaluate the effects of intrinsic random noise under quasi-steady conditions. In our analysis of the Michaelis-Menten model of enzyme catalysis in Ref. 38, we showed that the semi-classical quasi-steady state approximation (SCQSSA) reveals that the velocity of the enzymatic reaction is modified with respect to the mean-field estimate by a quantity which is proportional to the total number of molecules of the (conserved) enzyme. In this paper, we extend this formalism to show that, associated to each conserved molecular species, the associated (constant) number of molecules is a bifurcation parameter which can drive the system into bi-stability beyond the predictions of the mean-field theory. We then proceed to test our theoretical results by means of direct numerical simulation of the chemical master equation using the stochastic simulation algorithm.54 We should note that the Hamiltonian formalism derived from the semi-classical approximation is formulated on a continuum of particles, which requires the number of particles to be large enough. This must hold true for all the species in our model, both fast and slow. Since this separation between fast and slow species is based on their relative abundance, one must be careful that the scaling assumptions are consistent, particularly in the case of the model of self-activating gene regulatory circuit where the number of binding sites is typically small. This assumption, however, has been used in previous studies.55 Also we show that our simulation results of the full stochastic processes agree with our analysis and, therefore, our re-scaled equations are able to predict the behaviour of the system. We note that the mean-field limit, which is conventionally obtained by ignoring noise in the limit of large particle numbers, is obtained by setting the momenta in our phase-space formalism to 1.
The approximation we develop in this paper falls within the general framework of the optimal fluctuation path theory.56 This framework is a particular case of the large deviation theory which allows us to study rare events (i.e., events whose frequency is exponentially small with system size). Within these frameworks, we will show that, upon carrying out the QSSA, the only source of noise in the system is associated to the random initial conditions of the species whose numbers are conserved. We therefore predict that a population of cells, each having a random number of conserved molecules, will have a bimodal distribution.
This paper is organised as follows. Section II is devoted to a detailed exposition of the semi-classical quasi-steady state approximation for stochastic systems. In Sections III and IV, we apply this formalism to analyse the behaviour of a bistable enzyme-catalysed system and a gene regulatory circuit of auto-activation, respectively. We will show that our semi-classical quasi-steady state theory allows us to study the effect of intrinsic noise on the behaviour of these systems beyond the predictions of their mean-field descriptions. We also verify our theoretical predictions by means of direct stochastic simulations. Finally, in Section V, we summarise our results and discuss their relevance.
II. Semi-Classical Quasi-Steady State Approximation
Our aim in this paper is to formulate a stochastic generalisation of the quasi-steady state approximation for enzyme-catalysed reactions and simple circuits of gene regulation and use such approximation to determine if the presence of noise has effects on the behaviour of the system beyond the predictions of the corresponding mean-field models. Specifically, we analyse stochastic systems for which the mean-field models predict bi-stability and investigate how such behaviour is affected by stochastic effects. Our analysis is carried out in the context of Markovian models of the corresponding reaction mechanisms formulated in terms of the so-called CME.57 Two examples of such stochastic systems, a bistable enzyme-catalysed system and a gene regulatory circuit of auto-activation, are formulated and analysed in detail in Sections III and IV, respectively. Following Ref. 38, we formulate the QSS approximation for the asymptotic solution of the CME obtained by means of large deviations/WKB approximations.58–60 The CME is given as
| (1) |
where Wi(X) is the transition rate corresponding to reaction channel i and ri is a vector whose entries denote the change in the number of molecules of each molecular species when reaction channel i fires up, i.e., P(X (t + Δt) = X(t) + ri|X(t)) = Wi(X)Δt.
An alternative way to analyse the dynamics of continuous-time Markov processes on a discrete space of states is to derive an equation for the generating function, G(p1,…, pn, t), of the corresponding probabilistic density,
| (2) |
where P(X1,…, Xn, t) is the solution of master equation (1). G(p1,…, pn, t) satisfies a partial differential equation (PDE) which can be derived from the master equation. This PDE is the basic element of the so-called momentum representation of the master equation.51,53,61–63
Although closed, analytic solutions are rarely available, the PDE for the generating function admits a perturbative solution, which is commonly obtained by means of the WKB method.63 More specifically, the (linear) PDE that governs the evolution of the generating function can be written as
| (3) |
where the operator Hk is determined by the reaction rates of master equation (1). Furthermore, the solution to this equation must satisfy the normalisation condition G(p1 = 1, … , pn = 1, t) = 1 for all t. This PDE, or, equivalently, the operator H, is obtained by multiplying both sides of master equation (1) by and summing up over all the possible values (X1, … , Xn).
From the mathematical point of view, Eq. (3) is a Schrödinger-like equation and, therefore, there is a plethora of methods at our disposal in order to analyse it. In particular, when the fluctuations are (assumed to be) small, it is common to resort to WKB methods.58,59,64 This approach is based on the WKB-like Ansatz that G(p1,…, pn, t) = e−S(p1,…, pn, t). By substituting this Ansatz in Eq. (3), we obtain the following Hamilton-Jacobi equation for the function S(p1, … , pn, t):
| (4) |
Instead of directly tackling the explicit solution of Eq. (4), we will use the so-called semi-classical approximation. We use the Feynman path-integral representation which yields a solution to Eq. (3) of the type58,62,65–68
| (5) |
where 𝒟Q(s)𝒟p(s) indicates integration over the space of all possible trajectories and S(p1, … , pn, Q1,…, Qn) is given by58
| (6) |
where the position operators in the momentum representation have been defined as Qi ≡ ∂pi with the commutation relation [Qi, pj] = S0, iδi, j. S0, i(pi, Qi) corresponds to the action associated with the generating function of the probability distribution function of the initial value of each variable, Xi(t = 0), which is assumed to be independent random variables.
The so-called semi-classical approximation consists of approximating the path integral in Eq. (5) by
| (7) |
where p1(t), … , pn(t) are now the solutions of the Hamilton equations, i.e., the orbits which maximise the action S,
| (8) |
| (9) |
where the pair (Qi, pi) is the generalised coordinates corresponding to chemical species i = 1, … , n. These equations are (formally) solved with boundary conditions67 Qi(0) = xi(0), pi(t) = pi, where xi(0) is the initial number of molecules of species i.
Eqs. (8) and (9) are the starting point for the formulation of the SCQSSA.38 In order to proceed further, we assume, as per the Briggs-Haldane treatment of the Michaelis-Menten model for enzyme kinetics,26,69 that the species involved in the system under scrutiny are divided into two groups according to their characteristic scales. More specifically, we have a subset of chemical species whose numbers, Xi, scale as
| (10) |
where xi = O(1), whilst the remaining species are such that their numbers, Xj, scale as
| (11) |
where xj = O(1). Key to our approach is the fact that S and E must be such that
| (12) |
We further assume that the generalised coordinates, Qi, scale in the same fashion as the corresponding variable Xi, i.e.,
| (13) |
where qi = O(1). We refer to the variables belonging to this subset as slow variables. Similarly,
| (14) |
where qj = O(1), which are referred to as fast variables. Moreover, we assume that the moment coordinates, pi, are all independent of S and E and therefore remain invariant under rescaling.
Under this scaling for the generalised coordinates, we define the following scale transformation for the Hamiltonian in Eq. (6):
| (15) |
where J identifies the reaction with the largest order among all the reactions that compose the dynamics and kJ is the corresponding rate constant. For example, in the case of the bistable enzyme-catalysed system whose reactions or elementary events and the corresponding transition rates are given in Table I, J = 1, as this reaction is order 3 whereas all the others are order 0, 1, or 2. In the case of the self-activating gene regulatory circuit, Table IV, J = 3, since this reaction is order 3 whereas the remaining ones are order 1 at most. The exponents k and l correspond to the number of slow and fast variables involved in the transition rate WJ, respectively.
Table I.
Random variables and transition rates of the stochastic model associated to the enzymatic reaction shown in Fig. 1.
| Variable | Description | |
|---|---|---|
| X1, X2 | Number of active and inactive (respectively) Cdh1 molecules | |
| X3, X4 | Number of Cdh1-inactivating and Cdh1-activating (respectively) enzyme molecules | |
| X5, X6 | Number of enzyme-active Cdh1 and enzyme-inactive Cdh1 (respectively) complexes | |
| X7 | Number of active cyclin molecules | |
| Transition rate | r | Event |
| W1(x) = k1X7X1X3 | r1 = (−1, 0,−1, 0,+1, 0, 0) | Enzyme and active Cdh1 form complex |
| W2(x) = k2X7X5 | r2 = (+1, 0,+1, 0,−1, 0, 0) | Enzyme-active Cdh1 complex splits |
| W3(x) = k3X7X5 | r3 = (0,+1,+1, 0,−1, 0, 0) | Inactivation of Cdh1 and enzyme release |
| W4(x) = k4X2X4 | r4 = (0,−1, 0,−1, 0,+1, 0) | Enzyme and inactive Cdh1 form complex |
| W5(x) = k5X6 | r5 = (0,+1, 0,+1, 0,−1, 0) | Enzyme-inactive Cdh1 complex splits |
| W6(x) = k6X6 | r6 = (+1, 0, 0,+1, 0,−1, 0) | Activation of Cdh1 and enzyme release |
| W7(x) = k7 | r7 = (0, 0, 0, 0, 0, 0,+1) | CycB synthesis |
| W8(x) = k8(1 + aX1)X7 | r8 = (0, 0, 0, 0, 0, 0,−1) | CycB degradation |
Table IV.
Random variables and transition rates associated to the stochastic dynamics of an auto-activation gene regulatory circuit.30,74 X2 corresponds to the number of transcription-factor dimer/promoter binding site trimers. See Fig. 6 for a schematic representation.
| Variable | Description | |
|---|---|---|
| X1 | Number of transcription factor molecules | |
| X2 | Number of bound promoter sites in the gene promoter region | |
| X3 | Number of unoccupied (unbound) binding sites in the gene promoter region | |
| Transition rate | r | Event |
| W1(x) = +k1X2 | r1 = (1, 0, 0) | Synthesis of the transcription factor |
| W2(x) = k2X1 | r2 = (−1, 0, 0) | Degradation of the transcription factor |
| W3(x) = k3X1(X1−1)X3 | r3 = (−2,+1,−1) | Dimer binding to the gene promoter region |
| W4(x) = k4X2 | r4 = (+2,−1,+1) | Unbinding from the gene promoter region |
The last step is to rescale the time variable so that a dimensionless variable, τ, is defined such that
| (16) |
It is now a trivial exercise to check that, upon rescaling, Eqs. (8) and (9) read
| (17) |
| (18) |
for the slow variables. By contrast, rescaling of the Hamilton equations corresponding to the subset of fast variables leads to
| (19) |
| (20) |
where ϵ is defined in Eq. (12). The QSS approximation consists on assuming that in Eqs. (19) and (20),
| (21) |
| (22) |
resulting in a differential-algebraic system of equations which provides us with the SCQSSA.
III. Bistable Enzyme-Catalysed Systems
As a prototype of a bistable enzyme-catalysed system, we analyse a stochastic system proposed in Refs. 38 and 70, whose mean-field limit has been shown to correspond to a bistable system which is a part of a model for the G1/S transition of the eukaryote cell cycle proposed in Ref. 22. Tyson and Novak22 have formulated a (deterministic) model of the cell cycle such that the core of the system regulating the G1/S transition is a system of two mutually repressing proteins (Cdh1 and CycB). This system of mutual repression gives rise to a bistable system where one of the stable steady states is identified with the G1 phase whereas the other corresponds to a state where the cell is ready to go through the other three phases of the cell-cycle, known as S, G2, and M. This central module, which is the one we focus on, is acted upon by a complex regulatory network which monitors if conditions are met for the cell to undergo this transition and accounts for its accurate timing. Presently, we ignore this network and focus on the central bistable system. It is shown in Ref. 22 that the mean field version of the model exhibits bistable behaviour as a function of a bifurcation parameter m, i.e., the mass of the cell. For very small values of m, the system is locked into a high (low) Cdh1(CycB)-level stable fixed point (i.e., into the G1 phase). For very large values m, the system has only one stable steady state corresponding to a low (high) Cdh1(CycB)-level fixed point. For intermediate values of m, the system exhibits bistability, i.e., both of these stable fixed points coexist with an unstable saddle point. In this section, we focus on how noise alters the behaviour of the mean-field dynamics.
The transition rates corresponding to the different reactions involved in the stochastic model associated to the enzyme-regulated kinetics shown in Fig. 1 are given in Table I. This kinetics corresponds to the enzyme regulated activation and inhibition of Cdh1 (an inhibitor of cell-cycle progression). Cdh1 inactivation is further (up)regulated by the presence of CycB, an activator of cell-cycle progression. CycB is synthesised and degraded at basal rates and is further degraded in the presence of active Cdh1 (see Fig. 1). Therefore, the resulting dynamics leads to a system with mutual inhibition which produces bistable behaviour. It is important to note that the associated reaction kinetics exhibits three conservation laws (see Table I): X3 + X5 = e0, X4 + X6 = e0, and X1 + X2 + X5 + X6 = s0. The first two of these conservation laws are associated to the conservation of the number of Cdh1-inhibiting and Cdh1-activating enzymes, respectively, whilst the latter expresses the conservation of the total number of Cdh1 molecules. The quantities e0 and s0 are the (conserved) number of enzymes and Cdh1, respectively. Note that, as per the methodology developed in Section II, we assume that s0 = O(S) and e0 = O(E).
Fig. 1.
Reactions for the bistable enzyme-catalysed system proposed by Tyson and Novak.22 X1 represents active Cdh/Apc, X2 inactive Cdh/Apc, X3 inactivating enzymes, X4 activating enzymes, X5 active Cdh/Apc-inactivating-enzyme complexes, X6 inactive Cdh/Apc-activating-enzyme complexes, and X7 the number of CycB-CDK complexes. The first two reactions correspond to enzyme-catalysed inactivation and activation of Cdh/APC. The third reaction corresponds to the dynamics of CycB activity: synthesis at a constant rate, k7, and degradation by natural decay and active Cdh/Apc-induced inactivation.
The corresponding stochastic Hamiltonian, Hk, which is derived by applying the methodology of Section II to the master equation associated to the chemical kinetics described in Table I, can be split into three parts,
| (23) |
where HI is the Hamiltonian corresponding to the CycB-regulated enzymatic inactivation of Cdh1 (reactions 1 to 3 in Table I),
| (24) |
HA corresponds to enzymatic activation of Cdh1 (reactions 4 to 6 in Table I),
| (25) |
and, finally, HB, which corresponds to synthesis and degradation of CycB, is given by (reactions 7 and 8 in Table I),
| (26) |
We now proceed to apply the procedure explained in Section II in order to obtain the SCQSSA for the system determined by the transition rates given in Table I. We first need to determine which of the variables are slow variables and which ones are fast variables. As shown in Table II, the pairs (p1, Q1), (p2, Q2), and (p7, Q7), corresponding to the active and inactive forms of Cdh1 and to CycB, respectively, are the slow generalised coordinates, as the generalised positions scale with s0. The remaining generalised coordinates scale as e0 and, therefore, are fast variables. Furthermore, the rescaled Hamiltonian is given by
| (27) |
where
| (28) |
with
| (29) |
The rescaled parameters κi are given in Table II. Last, by rescaling time and defining the dimensionless time variable as τ = k1ESt (Table II), SCQSSA equations (17), (18), (21), and (22) lead to (see Ref. 38 for a detailed derivation),
| (30) |
| (31) |
| (32) |
| (33) |
| (34) |
| (35) |
where p1 = p2, p3, and p4 are constants to be determined and J1 = κ2 + κ3 and and pe3 = e3/E and pe4 = e4/E. Note that for q1(τ) + q2(τ) = pc, with pc = s0/S, to hold p7 = 1 must be satisfied. In this case, we have
| (36) |
| (37) |
| (38) |
| (39) |
Table II.
Dimensionless variables used in Eq. (29). S and E are the average concentration of Cdh1 (active plus inactive) and the average concentration of both Cdh1-activating and Cdh1-inactivating enzymes, respectively. We further assume that the stationary concentration of active CycB also scales with S.
| Rescaled variables | Dimensionless parameters |
|---|---|
| τ = k1ESt | 𝝐 = E/S, α = aS |
| q1 = Q1/S | κ2 = k2/(k1S) |
| q2 = Q2/S | κ3 = k3/(k1S) |
| q3 = Q3/E | κ4 = k4/(k1S) |
| q4 = Q4/E | κ5 = k5/(k1S2) |
| q5 = Q5/E | κ6 = k6/(k1S2) |
| q6 = Q6/E | κ7 = k7/(k1ES2) |
| q7 = Q7/S | κ8 = k8/(k1ES) |
As shown in Ref. 38, the parameter values are determined by comparing the corresponding mean-field approximation, which is obtained by taking pi = 167 and pc = pe3 = pe4 = 1, i.e., the total number of molecules of Cdh1 and its activating and inhibiting enzymes be exactly equal to its average, i.e., s0 = S and e3 = e4 = E, to the system originally proposed by Tyson and Novak.22 In Eq. (36), we have redefined κ3 → κ3m in order to make explicit the dependence on the bifurcation parameter, m, as used by Tyson and Novak.22 The parameter values are shown in Table III.
Table III.
Parameter values used in simulations of the stochastic bistable enzyme-catalysed system.
Upon rescaling of the variables (Table II) and the Hamiltonian (Eq. (15)), the action functional reads
| (40) |
It is straightforward to check that in SCQSSA conditions Hκ(p,q) = 0. Furthermore, since p1 = p2 = const. and p7 = 1, and for the fast generalised coordinates, the SCQSS approximation of the action Eq. (40), SQSS, reduces to
| (41) |
where, as per the SCQSSA, p5 and p6 are determined by Eqs. (38) and (39), respectively, p7 = 1, which implies S0,7(p7) = 0 and p1 = p2, p3, and p4 are constants that remain to be determined. In order to do so, we resort to the method developed in Ref. 38. The quasi-steady state characteristic function, GQSS(p, τ), is given by
| (42) |
where G0,i(pi) = e−S0,i(pi) is the generating function of the probability distribution for the initial condition of species Xii = 1, … , 6. In Ref. 38, we have shown that, applying a Laplace-type asymptotic method71,72 to the integrals,
| (43) |
where p1 = p2, p3, and p4 can be given as functions of s0 and ei, i = 3, 4, i.e., the initial numbers of Cdh1 molecules and Cdh1-inactivating and Cdh1-activating enzymes, respectively,
| (44) |
P(X1(τ = 0) = s0), P(X3(τ = 0) = e3), and P(X4(τ = 0) = e4) are the probabilities that X1 initially takes the value X1(τ = 0) = s0 and that X3 and X4 have initial values X3(τ = 0) = e3 and X4(τ = 0) = e4. These probabilities can be interpreted to correspond to variability in the abundance of these enzymes within a population of cells. A particularly simple case results from assuming that P(X1(τ = 0) = s0), P(X3(τ = 0) = e3), and P(X4(τ = 0) = e0) are Poisson distributions with parameters S and E, respectively. In this case,38
| (45) |
Note that, in the particular case in which the total numbers of Cdh1 and enzyme molecules are random Poisson variables, we have that p1 = pc, p3 = pe3, and p4 = pe4.
A. Bifurcation analysis
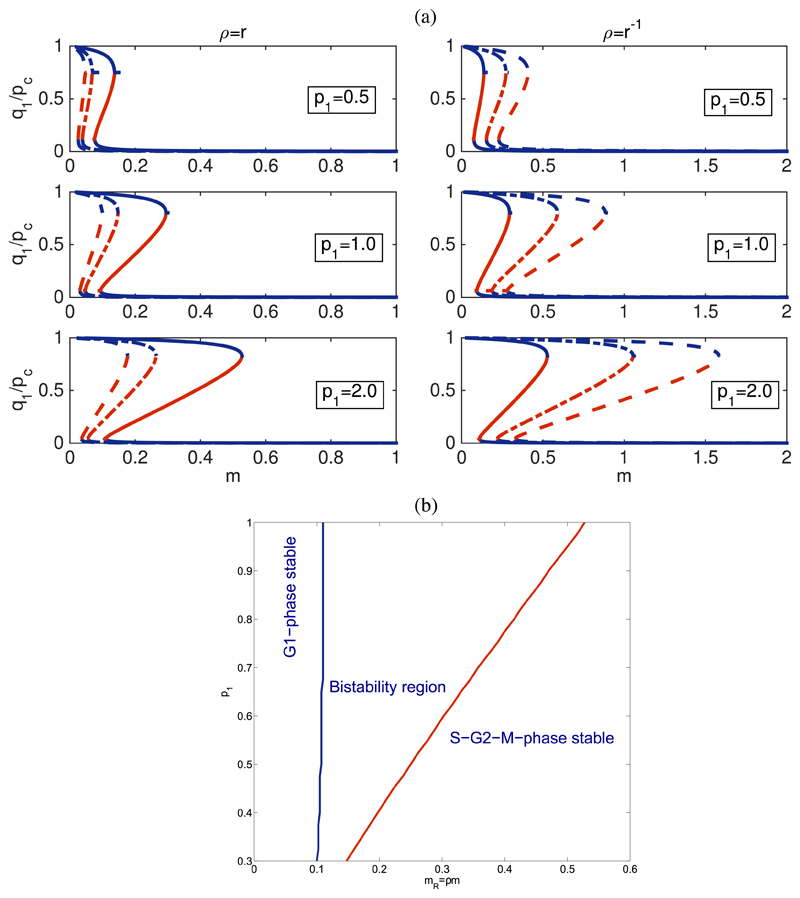
Fig. 2 shows results regarding the bifurcation behaviour of the SCQSS approximation of the stochastic bistable enzyme-catalysed system Eqs. (36)-(39). In particular, we are interested in a comparison between the bistable behaviour of the mean-field model, corresponding to taking pi = 1 for all i, and that of the SCQSS approximation with p1, p3, and p4 given by Eq. (44), i.e., they are determined as functions of s0 and e0.
Fig. 2.
(a) Bifurcation analysis for the SCQSS approximation of the stochastic bistable enzyme-catalysed system Eqs. (36)-(39). The panels on the top plot (a) show the bifurcation diagrams for different values of the parameters p1, pc = p1, and If e0 and s0 are random Poisson variables with parameter S and E, respectively, then (see Eq. (45)). In these panels, solid lines correspond to r = 1, dotted-dashed lines to r = 2, and dashed lines to r = 3. The bottom plot (b) shows the bi-stability boundaries in p1–mR parameter space. The region between the boundaries corresponds to the bistable region of the stochastic Tyson and Novak system according to the SCQSS approximation.
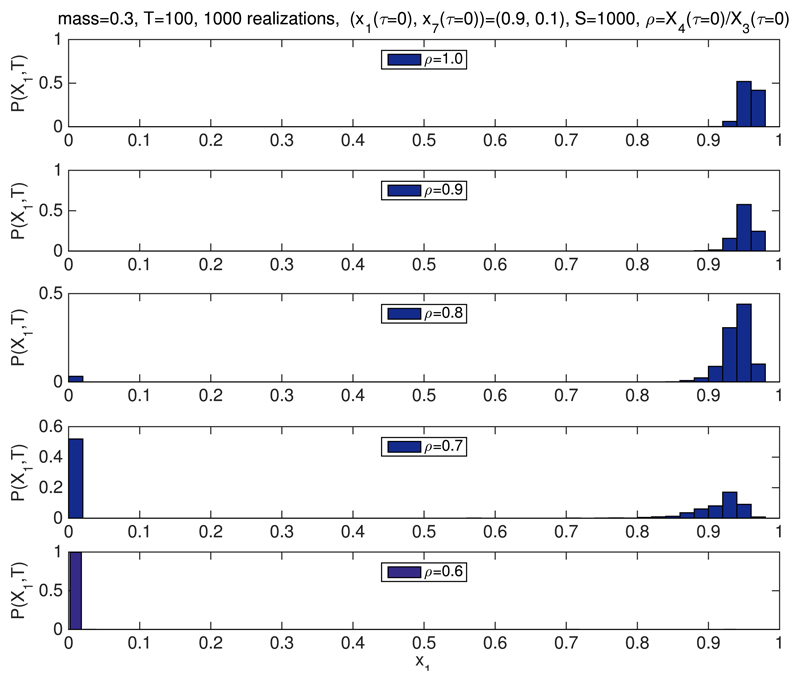
We have shown that both the ratios of p3 and p4, and p1 alter the bistable behaviour of the system beyond the predictions of the mean-field model. In particular, we observe that decreasing the value of ρ extends the region of stability of the G1-fixed point, i.e., the fixed point corresponding to the steady-state value of q1, such that q1 ~ 1. By contrast, when ρ is increased, the stability region of the G1-fixed point shrinks. Intuitively, given the relation between p3 and p4 and the number of Cdh1-inactivating and Cdh1-activating enzyme, this result is straightforward to interpret: decreasing the number of Cdh1-inactivating enzyme demands a larger value of m in order to de-stabilise the G1-fixed point. This is fully confirmed by direct simulation using Gillespie stochastic simulation algorithm.54 Fig. 3 shows simulation results in which we compute the probability P(x1,T) = Prob(x1(τ = T)) for different values of ρ ≤ 1. T has been chosen so that the system has reached steady state conditions. We observe, that for ρ = 1 and m = 0.3, the system evolves towards the q1 ≪ 1-fixed point (i.e., the S-G2-M fixed point). As ρ decreases, i.e., there is more Cdh1-inactivating enzyme than Cdh1-activating enzyme, the system enters the bistable regime. If ρ reaches low-enough values (depending upon the initial condition), we may even observe an exchange of stability, i.e., the system evolves towards the q1 ~ 1-fixed point.
Fig. 3.
Simulation results for the stochastic bistable enzyme-catalysed system Table I. We have plotted the probability P(x1, T) = Prob(x1(τ = T)), where x1 = X1/S and T = 100 for different values of ρ. The initial number of Cdh1-inactivating and Cdh1-activating enzymes is fixed according to and X4(t = 0) = e0, respectively, m = 0.3. We aim to check our predictions regarding the effect of the ratio on the stability properties of the system. According to our results shown in Fig. 2, decreasing the ratio between the number of Cdh1-inactivating (e4) and Cdh1-activating (e3) enzymes, the system should be driven away from bistability and into the stable G1-phase regime (see Fig. 2(b)). The remaining parameter values are inferred from those given by Tyson and Novak22 as shown in Tables II and III. We see that when varying ρ, the system switches from a state of high x1 (ρ ≥ 0.9) to a state of low x1 (ρ ≤ 0.6), whereas at the intermediate levels (e.g., ρ = 0.7 and ρ = 0.8), the system is in a bistable state. We take p1 = pc = 1 in all the simulations shown in this figure. Average is performed over 1000 realisations.
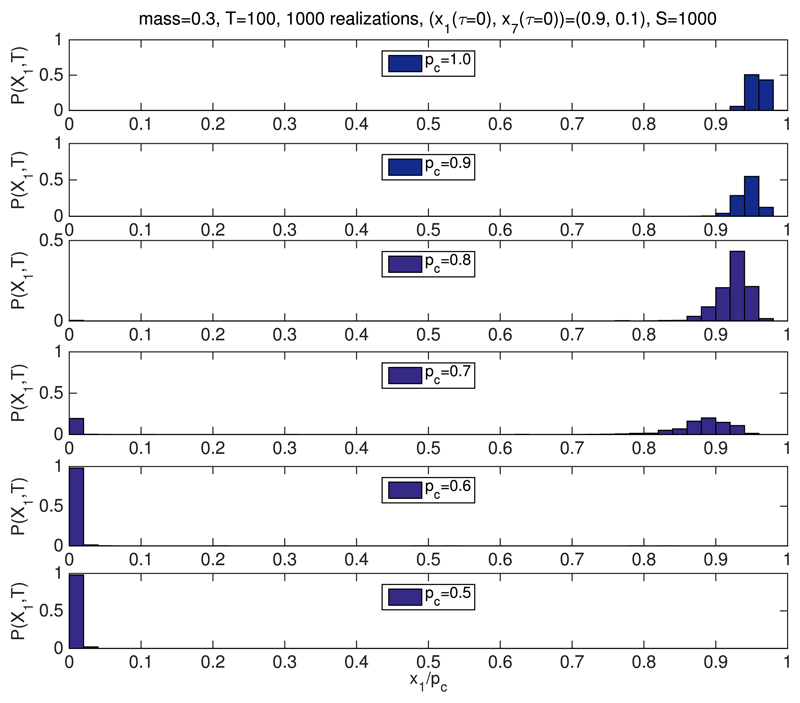
Regarding the dependence on p1, we have checked the predictions of the SCQSS approximation by means of simulations with different values of s0. Figure 2 shows the bi-stability region of system Eqs. (36)-(39) in p1–mR-space, where mR = ρm. For a fixed value of mR, there is a threshold value for p1 below which the system stops being bistable to become entrapped into the S-G2-M fixed point (i.e., q1 ≪ 1). In order to validate this prediction, we have conducted stochastic simulations for different values of s0. Figure 4 shows simulation results for P(x1,T) = Prob(x1(τ = T)). We observe that for small values of s0, the system is locked into the S-G2-M fixed point, as predicted by the SCQSS approximation. As s0 increases, the system enters a fluctuation-dominated bistable regime where, as the system goes through the bifurcation point, the system undergoes bistable behaviour. This behaviour is typical in a system undergoing a phase transition, where fluctuations unboundedly increase.73 Finally, as s0 continues to increase, the system becomes trapped into G1-fixed point (see Figure 4). These results fully reproduce the behaviour predicted by our SCQSSA stability analysis.
Fig. 4.
Simulation results for the stochastic bistable enzyme-catalysed system Table I. We have plotted the probability P(x1, T) = Prob(x1(τ = T)), where x1 = x1/S and T = 100 with different initial conditions and different values of pc. Average is performed over 1000 realisations. m = 0.3 and X3(t = 0) = e0 and X4(t = 0) = e0. The remaining parameter values are inferred from those given by Tyson and Novak22 as shown in Tables II and III. We see that when varying pc, the system switches from a state of high x1 (pc ≥ 0.8) to a state of low x1 (pc ≤ 0.6), whereas at the intermediate levels of pc = 0.7, the system is in a bistable state.
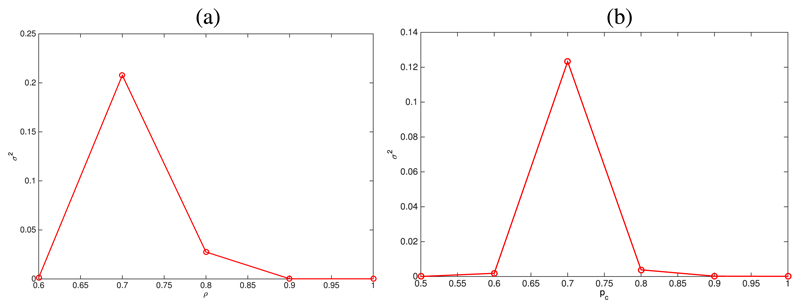
The aforementioned behaviour regarding unbounded increase of fluctuations close to a bifurcation73 is used to locate the critical value of the associated control parameter, i.e., ρ and pc for the simulations shown in Figs. 3 and 4, respectively. This property allows us to do a quantitative comparison between the simulations and asymptotic analysis. To this end, we plot how the variance, σ2 = 〈(x1 − 〈x1〉)2〉, where x1 = X1(τ = T)/S, changes as the corresponding control parameter varies. Regarding the results shown in Fig. 5(a) (associated to the simulations shown in Fig. 3), we observe that the critical value of the control parameter ρ, ρB, is approximately ρB ≃ 0.7, which, taking into account that m = 0.3, implies that the critical value of the renormalized mass, mR = ρm, mB = ρBm ≃ 0.21. Our asymptotic analysis predicts that mB = 0.11 (see Fig. 2(b) with pc = 1). The results shown in Fig. 5(b) (corresponding to the simulations shown in Fig. 4), the critical value of pc, pB, is approximately pB ≃ 0.7. The prediction of our asymptotic analysis (see Fig. 2(b) with ρ = 1) is pB = 0.6.
Fig. 5.
Plots showing the variance σ2 = 〈(x1 – 〈x1〉)2〉, where x1 = X1(τ = T)/S associated to the simulation results shown in Fig. 3 (panel (a)) and in Fig. 4 (panel (b)). These plots show how σ2 changes as the control parameter (ρ, for the simulations associated to plot (a), and pc for the simulations shown in plot (b)). The maximum of σ2 as a function of the control parameter helps us to quantitatively determine the corresponding critical value.73
IV. Auto-Activation Gene Regulatory Circuit
We now proceed to analyse the effects of intrinsic noise in a model of a bistable self-activation gene regulatory circuit30,55,74 in the context of the quasi-steady regime. Many instances of genetic switches, i.e., bistable gene regulatory circuits, have been identified.25,26,75–77 Most of them are characterised by the presence of a positive feedback in which one of the molecular species involved in the system upregulates its own production. All of these systems exhibit bi-stability and hysteresis, i.e., a form of memory associated to bistable systems, and some of them are thought to exist in regimes where stochastic switching is frequent.77,78 Noise effects on this kind of system have been extensively analysed and found to have both constructive and deleterious effects. For example, Frigola et al.30 have found that noise stabilises the inactive (OFF) steady-state of a model of a bistable self-activation gene regulatory circuit by extending its stability region. In this section, we analyse the effects of noise specifically associated to the quasi-steady state regime in the large-deviations (large number of molecules) limit.
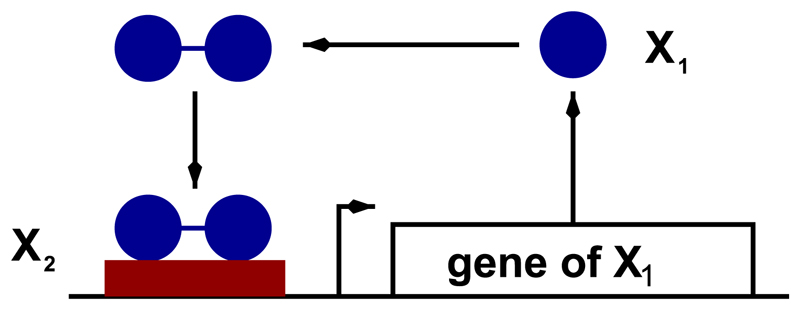
We study the stochastic system of the simple self-activating gene regulatory circuit schematically represented in Fig. 6. In this circuit, the gene product binds to form dimers which then act as its own transcription factor by binding to the promoter region of the gene. The rate-limiting factor is therefore the number of available binding sites within the promoter of the gene. For simplicity, our stochastic model associated to the rates shown in Table IV does not explicitly account for dimer formation. We will assume that this process is very fast so it can be subsumed under the formation of transcription-factor dimer/promoter binding site trimers (reaction 3, Table IV). Furthermore, it is important to note that our stochastic dynamics exhibits a conservation law: X2 + X3 = e0 at all time. This conservation law expresses the fact that the total number of binding sites, e0, is constant.
Fig. 6.
Schematic representation of the self-activating gene regulatory circuit. The gene product X1 is its own transcription factor which, upon dimerisation, binds the promoter region of the gene thus triggering gene transcription. The transition rates corresponding to this gene regulatory circuit are given in Table IV. For simplicity, we use an effective model in which the formation of the dimer and binding to the promoter region are taken into account in a single reaction, and the resulting number of promoter sites bound by two transcription factors is denoted as X2.
In order to proceed with our analysis of the stochastic model of self-activated gene regulation (see Table IV and Fig. 6), we apply the general methodology associated to our SCQSS approximation. Following the general procedure explained in Secs. I–III, we start by deriving the stochastic Hamiltonian associated to the process defined by the transition rates shown in Table IV (see Section II),
| (46) |
which, according to our theory (see Section II), gives rise to the re-scaled Hamiltonian, Hκ(p, q), defined by
| (47) |
where H(p, Q) = k3ES2Hκ(p, q) and the re-scaled variables, qi, and re-scaled rate constants, κj, are defined in Table V. The re-scaled Hamilton equations are thus given by
| (48) |
| (49) |
| (50) |
| (51) |
| (52) |
| (53) |
From these equations, we observe that for q2(τ) + q3(τ) = p, where p = e0/E, to hold we must have that p1(τ) = 1 for all τ. Imposing this condition on Eq. (51) implies that p2(τ) = p3(τ), which, in turn, together with Eqs. (52) and (53), imply that p2 = p3 = const. Finally, applying the QSS approximation to remaining equations, Eqs. (48)-(50), we obtain
| (54) |
| (55) |
As for the bistable enzyme-catalysed system, the parameter values are determined by matching the mean-field limit of our stochastic model, which is obtained by setting pi = 1 for all i67 and p = 1 (i.e., the number of binding sites exactly equal to its average), to the mean-field system proposed by Frigola et al.30 The mapping of our parameters to those of Ref. 30 and their associated values is given in Table VI.
Table V.
Dimensionless variables used in Eq. (29). s0 is a characteristic scale associated to the average number of molecules of transcription factor, X1, and E is the average number of binding sites in the promoter of the self-activating gene. We further assume that S ≫ E.
| Rescaled variables | Dimensionless parameters |
|---|---|
| τ = k3ESt | ϵ = E/S, R = /(k3ES2) |
| q1 = Q1/S | κ1 = k1/(k3S2) |
| q2 = Q2/E | κ2 = k2/(k3ES) |
| q3 = Q3/E | κ4 = k4/(k3S2) |
Table VI.
Parameter values used in simulations of the stochastic self-activation gene regulatory circuit.
Finally, according to the theory developed in Section II, p2 is determined in terms of the total number of binding sites within the gene promoter, e0,
| (56) |
where S0(p) = ln(G0(p)) and G0(p) is the generating function associated to the probability distribution of e0, P(e0). This probability distribution can be interpreted as corresponding to the distribution over a cell population of the number of binding sites in the promoter of gene x1. For example, if P(e0) is a Poisson distribution, the Eq. (56) reads38
| (57) |
where E ≡ 〈e0〉, i.e., the average of e0 over a population of cells. Therefore, according to this analysis, we have that p = p2, provided that P(e0) is a Poisson distribution with parameter E.
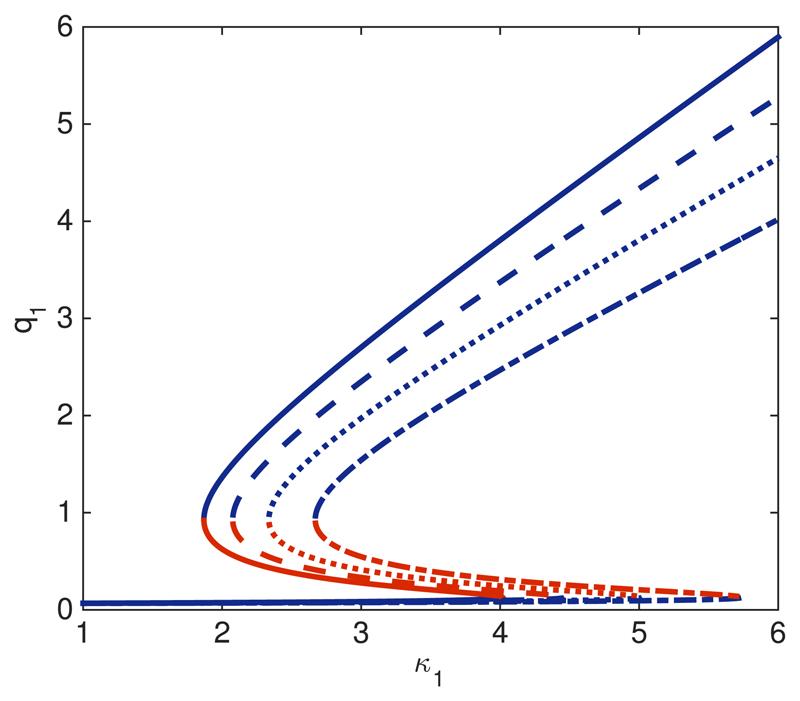
A. Bifurcation analysis
Fig. 7 shows results regarding how the bifurcation diagram varies as we change which, we recall, is determined by the (probability distribution of the) total number of binding sites within the gene promoter. Inspection of Eq. (54) shows that p2 has the effect of renormalising the self-activation rate κ1. If then the rate of gene self-activation is effectively reduced, and consequently, the stability region of the inactive steady-state, q1 ~ 0, is extended. That is, we need to go to larger values of κ4 to enter the region where the active steady-state, q1 > 1, becomes stable (see Fig. 7). On the contrary, has the effect of extending the stability region of the active steady-state, q1 > 1.
Fig. 7.
Bifurcation analysis for the SCQSS approximation of the stochastic auto-activation gene regulatory circuit Eqs. (54) and (55). This figure shows the bifurcation diagram for different values of the parameters of p2. In these, solid lines correspond to = 1, dashed lines to = 0.9, dotted to = 0.8, and dashed-dotted lines to = 0.7 (recall that p2 = p). Parameter values as given in Table VI.
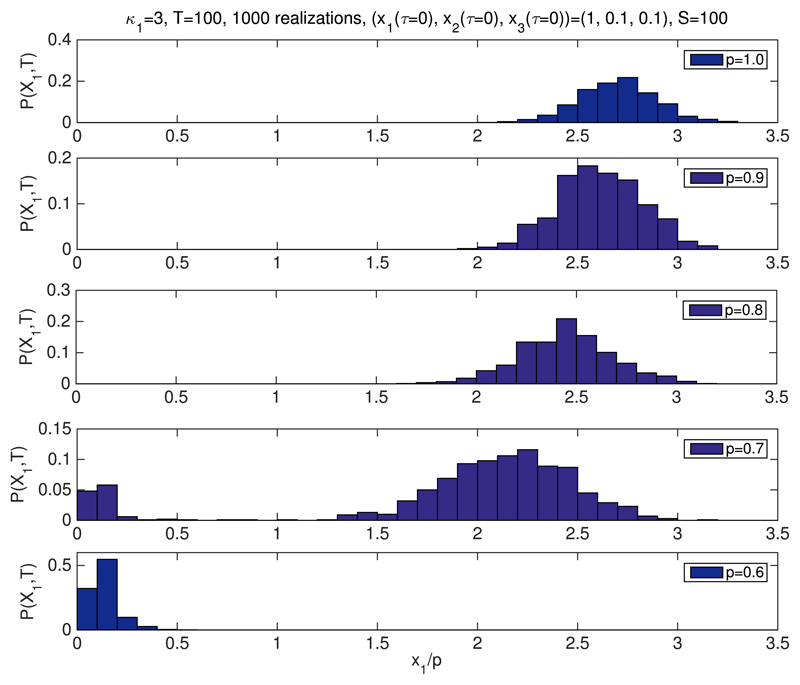
In order to verify the predictions of our bifurcation analysis (Fig. 7), we consider Eqs. (56) and (57), which relate the momentum variable p2 to the number of binding sites within the gene promoter. If we assume that the latter is distributed according to a Poisson distribution, then Eq. (57) holds and p2 = p = e0/E. Under these conditions, our bifurcation analysis predicts that the probability distribution of X1, i.e., the random variable associated to the generalised coordinate q1, should change, as e0 decreases, from being uni-modal with a single maximum about the ON value of X1 (or, when scaled with s0, q1) to exhibiting bi-modality, as the system approaches the saddle-node bifurcation which annihilates the ON state as it collides with the saddle point, with two peaks about the ON and OFF states. If e0 is further reduced, the system will be driven passed this saddle-node bifurcation, the probability distribution becomes uni-modal but, unlike its large e0 counterpart, its peak is about the OFF q1-steady-state. We have verified this prediction by running simulations using the SSA. The results, which agree with our prediction, are shown in Fig. 8.
Fig. 8.
Simulation results for the stochastic gene regulatory circuit of self-activation (Table IV). We have plotted the probability P(x1, T) = Prob(x1(τ = T)), where x1 = X1/S and T = 100 as the number of binding sites in the gene promoter, given by X3(t = 0) = p E. Average is performed over 1000 realisations. Parameter values are inferred from those given by Frigola et al.30 as shown in Tables V and VI. We see the emergence of bistability at p = 0.7, whereas for smaller(larger) values of p, the system will be in the stable steady state corresponding to low(high) number of transcription factor molecules.
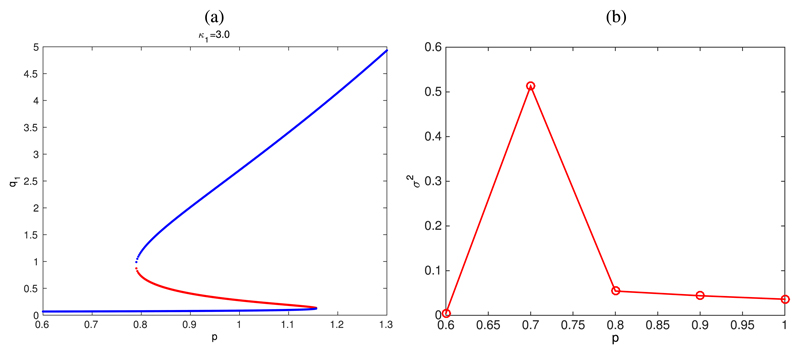
Quantitative comparison between our asymptotic analysis and the simulation results follows the same procedure as in Section III, i.e., we look at how the variance aforementioned behaviour regarding unbounded increase of fluctuations close to a bifurcation73 is used to locate the critical the variance σ2 = 〈(x1 − 〈x1〉)2〉, with x1 = X1(τ = T)/S changes as the control parameter varies: the maximum of σ2 as a function of the control parameter corresponds to the critical value. According to Fig. 9(b), the critical value of p, pB, is approximately given by pB ≃ 0.7. Our asymptotic analysis (see Fig. 9(b)) predicts that pB = 0.78.
Fig. 9.
Plot (a): bifurcation analysis for the SCQSS approximation of the stochastic auto-activation gene regulatory circuit Eqs. (54) and (55), with κ1 = 3.0. Parameter values as given in Table VI. Plot (b): simulation results for the variance σ2 = 〈(x1–〈x1〉)2〉, with x1 = X1(τ =T)/S, associated to the simulation results shown in Fig. 8. This plot shows how σ2 changes as the control parameter, p. The maximum of σ2 as a function of the control parameter helps us to quantitatively determine the corresponding critical value.73
V. Conclusions and Discussion
By means of the semi-classical quasi-steady state approximation, Section II, we have analysed stochastic effects affecting the onset of bi-stability in cell regulatory systems. Our theory shows that there exists a conserved momentum coordinate associated to each conserved chemical species. In the case of the enzyme-catalysed bistable system, Section III, there are three such conserved momenta, associated to each of the conserved chemical species, i.e., Cdh1 and its activating and inhibiting enzymes. For the self-activation gene regulatory network, we have one conserved momentum, corresponding to conservation of the number of binding sites of the gene’s promoter region.
According to the SCQSSA analysis of Ref. 38, the maximum rate achieved by an enzymatic reaction, Vmax, predicted by the mean-field theory29 is renormalised by a factor which equals the value of the (constant) momentum coordinate pi associated to the conserved enzyme: where is the maximum rate predicted by the SCQSSA. Similarly, we have shown that the mean-field maximum activation rate associated to the auto-activation gene regulatory model, Amax, is renormalised in the presence of noise by a factor equal to the conserved momentum coordinate corresponding to the number of binding sites in the gene promoter, p2, i.e., with being the SCQSSA maximum activation rate. As a consequence of this parameter renormalisation, we have shown that variation in the value of the conserved momenta can trigger bifurcations leading to the onset of bistable behaviour beyond the predictions of the mean-field limit, i.e., for values of parameters where the mean-field limit predicts the system to be mono-stable, the SCQSSA predicts bi-stability, and vice versa (see Figs. 2 and 7).
Furthermore, we have established that the value of the constant momenta is actually determined by the probability distribution of the associated conserved chemical species, and, ultimately, by the number of molecules of these species (see Eqs. (44), (56), and (57)). Therefore, our theory establishes that the numbers of molecules of the conserved species are order parameters whose variation should trigger (or cancel) bistable behaviour in the associated systems. This prediction is fully confirmed by direct numerical simulation using the stochastic simulation algorithm (see Figs. 3, 4, and 8). Quantitative comparison between the predictions of our asymptotic analysis and the simulation results (see Figs. 5 and 9) shows that our theoretical approach slightly underestimates the critical value for the bistable enzyme-regulated system. The theoretical prediction for the self-activating gene regulatory network appears to slightly overestimate the critical value.
Our results allow us to propose a means of controlling cell function. For example, regarding the enzyme-catalysed bistable model analysed in Section III, varying the number of molecules of the three conserved chemical species (Cdh1 and the associated activating and inhibiting enzymes) enables us to lock the system into either of the G1 or the S-G2-M stable fixed points or to drive the system into its bistable regime where random fluctuations will trigger switching between these two states. This could be accomplished by ectopically increasing the synthesis of the corresponding molecule or by targeting the enzymes with enzyme-targeted drugs.79,80 Similarly, the dynamics of the self-activating gene regulatory system could be driven into or out of its bistable regime by supplying an inhibitor that irreversibly binds to the promoter region, thus decreasing the effective number of binding sites.
This result allows us to explore strategies, for example, in the field of combination therapies in cancer treatment. Cellular quiescence is a major factor in resistance to unspecific therapies, such as chemo- and radio-therapy, which target proliferating cells. Bi-stability is central to control cell-cycle progression and to regulate the exit from quiescence, with enzyme catalysis (usually accounted for by (mean-field) Michaelis-Menten, quasi-steady state dynamics) being ubiquitously involved.25,26,28,77 Our findings will allow us to formulate combination strategies in which chemo- or radio-therapy is combined with a strategy aimed at driving cancer cells into proliferation or quiescence depending on the phase of the treatment cycle. Evaluation of the viability and efficiency of such combination require the formulation of multi-scale models70,81 whose analysis is beyond this scope of this paper, and it is therefore postponed for future work.
Our approach differs from previous work, such as Dykman et al.82 in a significant aspect, namely, whilst their aim is to estimate the rate of noise-induced transition between metastable states in systems exhibiting multi-stability, the purpose of our analysis is to ascertain whether noise can alter the multi-stability status of the system. Dykman et al.82 do not address such issue.
Eqs. (36)-(39), (54), and (55) are derived from a semi-classical approximation of the master equation (or its equivalent description in terms or the generating function PDE). This approximation yields a set Hamilton equations (Eqs. (8) and (9)) whose solutions are the optimal fluctuation paths and, as such, they describe fluctuation-induced phenomena which cannot be accounted for by the mean-field approximation. One of the best known examples of this is exit problems from metastable states in noisy systems (e.g., extinctions), where the semi-classical approximation provides the optimal escape path from which information such as mean-first passage time or waiting time for extinction can be obtained (see, for example, Refs. 63, 67, and 83). Furthermore, Eqs. (36)-(39), (54), and (55) are derived from the general Hamilton equations, Eqs. (8) and (9), by means of an approximation based on separation of time scales, not on any mean-field assumption.
A closely related subject to that analysed in this paper is that of noise-induced bifurcations.31 Such phenomenon has been studied in biological systems where the mean-field limit does not predict bistability, such as the so-called enzymatic futile cycles32 where noise associated to the number of enzymes induces bistability. In the absence of this source of noise, the system does not exhibit bistable behaviour. We have not dealt with such noise-induced phenomena in the present paper, in the sense that all the systems analysed in this paper are such that their mean-field limit exhibits bistability. We leave the interesting issue of whether our SCQSSA framework can be used to analyse noise-induced bifurcation phenomena for future research.
Acknowledgments
R.C. and T.A. acknowledge the Spanish Ministry for Science and Innovation (MICINN) for funding (No. MTM2011-29342) and Generalitat de Catalunya for funding under Grant No. 2014SGR1307. R.C. acknowledges AGAUR-Generalitat de Catalunya for funding under its doctoral scholarship programme. P.G. thanks the Wellcome Trust for financial support under Grant No. 098325.
References
- 1.Kepler TB, Elston TC. Biophys J. 2001;81:3116. doi: 10.1016/S0006-3495(01)75949-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Kaern M, Elston TC, Blake WJ, Collins JJ. Nat Rev Genet. 2005;6:451. doi: 10.1038/nrg1615. [DOI] [PubMed] [Google Scholar]
- 3.Maheshri N, O’Shea EK. Annu Rev Biophys Biomol Struct. 2007;36:413. doi: 10.1146/annurev.biophys.36.040306.132705. [DOI] [PubMed] [Google Scholar]
- 4.Losick R, Desplan C. Science. 2008;320:65. doi: 10.1126/science.1147888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Raj A, van Oudenaarden A. Cell. 2008;135:216. doi: 10.1016/j.cell.2008.09.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Cai L, Dalal CK, Elowitz MB. Nature. 2008;455:485. doi: 10.1038/nature07292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Eldar A, Elowitz MB. Nature. 2010;467:167. doi: 10.1038/nature09326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Kussell E, Leibler S. Science. 2005;309:2075. doi: 10.1126/science.1114383. [DOI] [PubMed] [Google Scholar]
- 9.Acar M, Mettetal JT, van Oudenaarden A. Nat Genet. 2008;40:471. doi: 10.1038/ng.110. [DOI] [PubMed] [Google Scholar]
- 10.Guerrero P, Byrne HM, Maini PK, Alarcon T. From invasion to latency: intracellular noise and cell motility as key controls of the competition between resource-limited cellular populations. J Math Biol. doi: 10.1007/s00285-015-0883-2. published online. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.MacArthur BD, Please CP, Oreffo ROC. PLoS One. 2008;3:e3086. doi: 10.1371/journal.pone.0003086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Balazsi G, van Oudenaarden A, Collins JJ. Cell. 2011;144:910. doi: 10.1016/j.cell.2011.01.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Cinquin O, Demongeot J. J Theor Biol. 2005;233:391. doi: 10.1016/j.jtbi.2004.10.027. [DOI] [PubMed] [Google Scholar]
- 14.Jaeger J, Monk N. J Physiol. 2014;592:2267. doi: 10.1113/jphysiol.2014.272385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Kauffman SA. The Origins of Order. Oxford University Press; New York, USA: 1993. [Google Scholar]
- 16.Huang S. BioEssays. 2012;34:149. doi: 10.1002/bies.201100031. [DOI] [PubMed] [Google Scholar]
- 17.Tyson JJ, Chen KC, Novak B. Curr Opin Cell Biol. 2003;15:221. doi: 10.1016/s0955-0674(03)00017-6. [DOI] [PubMed] [Google Scholar]
- 18.Legewie S, Bluthgen N, Herzel H. PLoS Comput Biol. 2006;2:e120. doi: 10.1371/journal.pcbi.0020120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Legewie S, Bluthgen N, Herzel H. Biophys J. 2007;93:2279. doi: 10.1529/biophysj.107.109132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kalmar T, Lim C, Hayward P, Munoz-Descalzo S, Nichols J, Garcia-Ojalvo J, Martinez-Arias A. PLoS Biol. 2009;7:e1000149. doi: 10.1371/journal.pbio.1000149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ferrel JE, Xiong W. Chaos. 2001;11:227. doi: 10.1063/1.1349894. [DOI] [PubMed] [Google Scholar]
- 22.Tyson JJ, Novak B. J Theor Biol. 2001;210:249. doi: 10.1006/jtbi.2001.2293. [DOI] [PubMed] [Google Scholar]
- 23.Gerard C, Goldbeter A. Proc Natl Acad Sci U S A. 2009;106:21643. doi: 10.1073/pnas.0903827106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Gerard C, Goldbeter A. Front Physiol. 2012;3:413. doi: 10.3389/fphys.2012.00413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Yao G, Lee TJ, Mori S, Nevins JR, You L. Nat Cell Biol. 2012;7:476. doi: 10.1038/ncb1711. [DOI] [PubMed] [Google Scholar]
- 26.Yao G. Interface Focus. 2014;4:20130074. doi: 10.1098/rsfs.2013.0074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Gerard C, Goldbeter A. Interface Focus. 2014;4:20130075. doi: 10.1098/rsfs.2013.0075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Bedessem B, Stephanou A. Math Biosci. 2014;248:31. doi: 10.1016/j.mbs.2013.11.007. [DOI] [PubMed] [Google Scholar]
- 29.Keener J, Sneyd J. Mathematical Physiology. Springer-Verlag; New York, NY, USA: 1998. [Google Scholar]
- 30.Frigola D, Casanellas L, Sancho JM, Ibañes M. PLoS One. 2012;7:e31407. doi: 10.1371/journal.pone.0031407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.García-Ojalvo J, Sancho JM. Noise in Spatially-Extended Systems. Springer-Verlag; 1999. [DOI] [PubMed] [Google Scholar]
- 32.Samoilov M, Plyasunov S, Arkin AP. Proc Natl Acad Sci U S A. 2005;102:2310. doi: 10.1073/pnas.0406841102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Rao CV, Arkin AP. J Chem Phys. 2003;118:4999. [Google Scholar]
- 34.Turner TE, Schnell S, Burrage K. Comput Biol Chem. 2004;28:165. doi: 10.1016/j.compbiolchem.2004.05.001. [DOI] [PubMed] [Google Scholar]
- 35.Thomas P, Straube AV, Grima R. J Chem Phys. 2010;133:195101. doi: 10.1063/1.3505552. [DOI] [PubMed] [Google Scholar]
- 36.Dóka É, Lente G. J Chem Phys. 2012;136:054111. doi: 10.1063/1.3681942. [DOI] [PubMed] [Google Scholar]
- 37.Thomas P, Grima R, Straube AV. Phys Rev E. 2012;86:041110. doi: 10.1103/PhysRevE.86.041110. [DOI] [PubMed] [Google Scholar]
- 38.Alarcón T. J Phys Chem. 2014;140:184109. doi: 10.1063/1.4874653. [DOI] [PubMed] [Google Scholar]
- 39.Bruna M, Chapman SJ, Smith MJ. J Chem Phys. 2014;140:174107. doi: 10.1063/1.4871694. [DOI] [PubMed] [Google Scholar]
- 40.Burrage K, Tian T, Burrage P. Prog Biophys Mol Biol. 2004;85:217. doi: 10.1016/j.pbiomolbio.2004.01.014. [DOI] [PubMed] [Google Scholar]
- 41.Vlachos DG. Adv Chem Phys. 2005;30:1. [Google Scholar]
- 42.MacNamara S, Burrage K, Sidje RB. Multiscale Model Simul. 2008;6:1146. [Google Scholar]
- 43.Cao Y, Gillespie DT, Petzold LR. J Comput Phys. 2005;206:395. [Google Scholar]
- 44.Cao Y, Gillespie DT, Petzold LR. J Chem Phys. 2005;122:014116. doi: 10.1063/1.1824902. [DOI] [PubMed] [Google Scholar]
- 45.Samant A, Vlachos DG. J Chem Phys. 2005;123:144114. doi: 10.1063/1.2046628. [DOI] [PubMed] [Google Scholar]
- 46.Liu WED, Vanden-Eijnden E. J Comput Phys. 2007;221:158. [Google Scholar]
- 47.Sanft KR, Gillespie DT, Petzold LR. IET Syst Biol. 2011;5:58. doi: 10.1049/iet-syb.2009.0057. [DOI] [PubMed] [Google Scholar]
- 48.Rathinam M, Petzold LR, Cao Y, Gillespie DT. J Chem Phys. 2006;10:12784. [Google Scholar]
- 49.Haseltine EL, Rawlings JB. J Chem Phys. 2002;117:6959. [Google Scholar]
- 50.Salis H, Kaznessis Y. J Chem Phys. 2005;122:054103. doi: 10.1063/1.1835951. [DOI] [PubMed] [Google Scholar]
- 51.Assaf M, Meerson B. Phys Rev E. 2006;74:041115. doi: 10.1103/PhysRevE.74.041115. [DOI] [PubMed] [Google Scholar]
- 52.Newby J, Chapman J. Math Biol. 2013;69:941. doi: 10.1007/s00285-013-0723-1. [DOI] [PubMed] [Google Scholar]
- 53.Kang H-W, Kurtz TG. Ann Appl Probab. 2013;23:529. [Google Scholar]
- 54.Gillespie DT. J Comput Phys. 1976;22:403. [Google Scholar]
- 55.Assaf M, Roberts E, Luthey-Schulten Z. Phys Rev Lett. 2011;106:248102. doi: 10.1103/PhysRevLett.106.248102. [DOI] [PubMed] [Google Scholar]
- 56.Bressloff PC. Stochastic Processes in Cell Biology. Springer-Verlag; Berlin, Germany: 2014. [Google Scholar]
- 57.Kampen NGV. Stochastic Processes in Physics and Chemistry. Elsevier; The Netherlands: 2007. [Google Scholar]
- 58.Kubo R, Matsuo K, Kitahara K. J Stat Phys. 1973;9:51. [Google Scholar]
- 59.Alarcón T, Page KM. J R Soc Interface. 2007;4:283. doi: 10.1098/rsif.2006.0170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Touchette H. Phys Rep. 2009;479:1. [Google Scholar]
- 61.Doi M. J Phys A: Math Gen. 1976;9:1479. [Google Scholar]
- 62.Peliti L. J Phys France. 1985;46:1469. [Google Scholar]
- 63.Assaf M, Meerson B, Sasorov PV. J Stat Mech. 2010 P07018. [Google Scholar]
- 64.Gonze D, Halloy J, Gaspard P. J Chem Phys. 2002;116:10997. [Google Scholar]
- 65.Feynman RP, Hibbs AR. Quantum Mechanics and Path Integrals. Dover Publications; Mineola, NY, USA: 2010. [Google Scholar]
- 66.Dickman R, Vidigal R. Braz J Phys. 2003;33:73. [Google Scholar]
- 67.Elgart V, Kamenev A. Phys Rev E. 2004;70:041106. doi: 10.1103/PhysRevE.70.041106. [DOI] [PubMed] [Google Scholar]
- 68.Täuber UC, Howard M, Vollmayr-Lee BP. J Phys A: Math Gen. 2005;38:R79. [Google Scholar]
- 69.Briggs GE, Haldane JBS. Biochem J. 1925;19:338. doi: 10.1042/bj0190338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Guerrero P, Alarcón T. Math Modell Nat Phenom. 2015;10:64. [Google Scholar]
- 71.Murray JD. Asymptotic Analysis. Springer-Verlag; New York, NY, USA: 1984. [Google Scholar]
- 72.Ablowitz MJ, Fokas AS. Complex Variables. Introduction and Applications. Cambridge University Press; Cambridge, UK: 2003. [Google Scholar]
- 73.Goldenfeld N. Lectures on Phase Transitions and the Renormalisation Group. Perseus Books Publishing; Reading, MA, USA: 1992. [Google Scholar]
- 74.Weber M, Buceta J. PLoS One. 2013;8:e73487. doi: 10.1371/journal.pone.0073487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Gardner TS, Cantor CR, Collins JJ. Nature. 1999;403:339. doi: 10.1038/35002131. [DOI] [PubMed] [Google Scholar]
- 76.Ozbudak EM, Thattai M, Lim HN, Shraiman BI, van Oudenaarden A. Nature. 2004;427:737. doi: 10.1038/nature02298. [DOI] [PubMed] [Google Scholar]
- 77.Lee TJ, Yao G, Bennett DC, Nevins JR, You L. PLoS Biol. 2010;8:e1000488. doi: 10.1371/journal.pbio.1000488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Acar M, Becksei A, van Oudenaarden A. Nature. 2005;435:228. doi: 10.1038/nature03524. [DOI] [PubMed] [Google Scholar]
- 79.Robertson JG. Biochem. 2005;44:5561. doi: 10.1021/bi050247e. [DOI] [PubMed] [Google Scholar]
- 80.Singh J, Petter RC, Baillie TA, Whitty A. Nat Rev Drug Discovery. 2012;10:307. doi: 10.1038/nrd3410. [DOI] [PubMed] [Google Scholar]
- 81.Alarcón T, Byrne HM, Maini PK. Multiscale Model Simul. 2005;3:440. [Google Scholar]
- 82.Dykman MI, Mori E, Ross J, Hunt PM. J Chem Phys. 1994;100:5735. [Google Scholar]
- 83.Khasin M, Dykman MI. Phys Rev Lett. 2009;103:068101. doi: 10.1103/PhysRevLett.103.068101. [DOI] [PubMed] [Google Scholar]