AR(1) Latent Class Models for Longitudinal Count Data

Abstract

In a variety of applications involving longitudinal or repeated-measurements data, it is desired to uncover natural groupings or clusters which exist among study subjects. Motivated by the need to recover clusters of longitudinal trajectories of conduct problems in the field of developmental psychopathology, we propose a method to address this goal when the response data in question are counts. We assume the subject-specific observations are generated from a first-order autoregressive process which is appropriate for count data. A key advantage of our approach is that the class-specific likelihood function arising from each subject’s data can be expressed in closed form, circumventing common computational issues associated with random effects models. To further improve computational efficiency, we propose an approximate EM procedure for estimating the model parameters where, within each EM iteration, the maximization step is approximated by solving an appropriately chosen set of estimating equations. We explore the effectiveness of our procedures through simulations based on a four-class model, placing a special emphasis on recovery of the latent trajectories. Finally, we analyze data and recover trajectories of conduct problems in an important nationally representative sample. The methods discussed here are implemented in the R package inarmix, which is available from the Comprehensive R Archive Network (http://cran.r-project.org).

1 |. INTRODUCTION

Many longitudinal studies have the aim of tracking the change in some outcome or response over time. This is an important and common goal in the field of developmental psychopathology, which aims to study the natural history of common childhood psychiatric diseases such as conduct disorder and delinquency. Often, there exists substantial variability in the observed response trajectories across subjects, and grouping subjects with similar trajectories may reveal certain sub-populations that exhibit interesting developmental patterns. In conduct disorder research, for example, such distinct “developmental sub-types” of trajectories are of great interest because the classification carries important information about level of impairment, future life outcomes, and possible etiologic origin.^1,2 Furthermore, it is of interest to robustly estimate such trajectory sub-types using large and representative samples, to do so in a computationally efficient way, and to use those estimates to recover class membership at the subject level. The problem of identifying a finite number of sub-populations is frequently formulated as a latent class or finite mixture model³ where the distribution governing the observations on a given subject is determined by an unobserved class label.

In an alternative approach to the analysis of longitudinal data, random effects are introduced to account for the heterogeneity across subjects and the correlation among observations on the same subject. If the conditional distribution of the response given the values of the random effects is not Gaussian, however, the marginal distribution of the response will typically not have a closed form. In these cases, evaluation of the likelihood requires numerical integration over the distribution of the random effects. Direct maximization of the likelihood then involves numerical integration for every evaluation of the likelihood. A number of other estimation approaches for models of this type, commonly referred to as generalized linear mixed models (GLMMs), have been proposed, including approximate methods such as penalized quasi-likelihood,^4,5 Monte Carlo methods,⁶ and marginalized random effects models.⁷

More recently, some authors have combined the latent class and random effects approaches. They have observed that with longitudinal data, a small number of latent classes is not sufficient to account for the association among repeated observations within subjects. They have therefore developed models with latent random effects in addition to the latent discrete variables indicating class membership.^8,9 Although this approach has gained traction in the applied literature, it poses two potential methodological drawbacks in the context of count data. First, the addition of class-specific random effects to the latent class model may complicate computation considerably. For example, if using an EM algorithm for estimation, not only does one confront, within each iteration, the difficulties associated with GLMMs, but one must also use numerical integration to update the class-membership probabilities within each iteration. A class-specific closed-form likelihood would be much more computationally tractable.

The second problem involves the distinction between what we refer to as global and local correlation among observations on the same subject. To articulate this concern, we first posit that one key role of the latent class structure is to account for the global correlation, i.e., the correlation that exists between all observations on a subject, whether they are separated by a short or by a long time lag. In a classic latent class analysis, given class membership, all observations on a given subject are independent, and this assumption drives the identification of the model. This assumption is, however, somewhat restrictive, and there are concerns that it could lead to models with too many classes that are too small if there remains residual correlation (conditional on class membership) among the repeated observations within the same subject. An obvious solution is to allow—and model—in a restricted way some correlation among some observations. The introduction of random effects into growth mixture models attempts to address this need. A concern, however, is that random effects also account for a more global type of correlation, potentially confounding the role of the latent classes and that of the class-specific correlation structure in model identifiability, fitting, and testing, especially when classes are not crisply separated.

To elaborate on this point, we note that classic latent class, or finite mixture, models can be thought of as being identified through two mechanisms. First, in multivariate data, the responses on a given unit (in this case a person) are posited as being independent given class membership, so that the latent class structure accounts for the realized association between univariate components on a given person. Second, the marginal distributional form of a univariate component of a multivariate response is specified as a mixture of class-specific forms. We view the first mechanism as being the more informative of the two. The concern is that random effects models also account for association between univariate components on a given person, as do the latent classes, thereby weakening model identifiability for the latent class structure. In contrast to random effects models, auto-regressive processes represent an alternative and more local source of within-subject correlation, allowing observations close together in time to be more strongly correlated than those further apart. Local correlation is not at all accounted for by the latent class structure. With a class-specific local correlation model, the observations far apart in time will be nearly independent, strengthening model identifiability.

To address these issues, we propose a longitudinal latent class model for count data which yields a closed-form class-specific likelihood, accounts for local correlation among the repeated measures on a given subject, and allows for global association to be accounted for by the latent class structure. With our approach, correlations between observations far apart in time will be especially informative about class membership because the subject-specific correlation between these two observations will be negligible due to the assumed AR(1) correlation structure. The closed-form class-specific likelihood offers gains in computational efficiency, and the implementation of our method provides an additional resource to existing software¹⁰ for estimating latent class models with longitudinal, non-Gaussian outcomes.

Our contributions in this paper are as follows. In the next section, we provide a technical description of our discrete data AR(1) process latent class trajectory model, followed in Section 3 with our approach to estimating and making inferences on model parameters. There, we rely on a variation of the EM algorithm that exploits a general estimating function rather than the true likelihood score function. In Section 4, we briefly introduce a measure of the inherent ability of latent class data to discriminate among classes for subjects in the population. To our knowledge, this is a previously unexplored, but important construct in a latent class analysis, especially when such analysis is used to assign subjects to their classes based on their manifest data. Because it is based on the true data generating mechanism, our measure represents an upper bound on the ability for any fitted statistical model to perform class assignment, which makes it a useful index for quantifying the underlying separation of the latent classes. Section 5 presents a simulation study with the aims of quantifying the statistical operating characteristics of our proposed model in terms of parameter estimation, bias, and confidence interval coverage. Additionally, we examine the ability of our approach to recover the mean trajectories when the data generating mechanism is different from the one specified by our model. Finally, in Section 6, we examine a longitudinal study of conduct problems and illustrate the use of our model for class definition and assignment in that study. The methods discussed here are implemented in the R package inarmix, which is available from the Comprehensive R Archive Network (http://cran.r-project.org).

2 |. MODEL DESCRIPTION

2.1 |. Data Structure and Trajectory Model

Let ${\mathbf{y}}_i=(y_{i1},\hspace{0.17em}\dots \hspace{0.17em},y_{i{n}_i})$ be observed longitudinal counts associated with the i ^th subject. In total, we have measurements on m subjects Y = (y₁, … , y_m). We have observations on subject i at each of the time points $(t_{i1},\hspace{0.17em}\dots \hspace{0.17em},t_{i{n}_i})$, and we let y_ij denote the observation on subject i at time t_ij. For each subject and each observed time point, we observe a p × 1 covariate vector x_ij, with ${\mathbf{X}}_i={({\mathbf{x}}_{i1},\hspace{0.17em}\dots \hspace{0.17em},{\mathbf{x}}_{i{n}_i})}^T$ denoting the n_i ×p design matrix for subject i ; X_i will typically include and encode the time points t_{i j}. In addition, each subject has an unobserved “latent class” Z_i with Z_i ∈ {1, … , C } indicating membership in one of C latent classes.

The distribution of (y_i |X_i, Z_i = c) is governed by a vector of class-specific parameters θ_c with p(y_i |X_i, Z_i = c) = p_i (y_i ; θ_c ) denoting the distribution of y_i given covariates X_i and class label c. Observations made on different subjects are assumed to be independent, and the class labels (Z₁, … , Z_n ) are assumed to be i.i.d. random variables with the vector π = (π₁, … , π_C ) denoting the class-membership proportions (i.e., P (Z_i = c) = π_c ) in the population.

Conditional on a subject’s class, the mean-response curve or latent trajectory is

$$E({\mathbf{y}}_i|Z_i=c,{\mathbf{X}}_i)=E_{{\mathit{\theta }}_c}({\mathbf{y}}_i)={\mu }_i^c=({\mu }_{i1}^c,\hspace{0.17em}\dots \hspace{0.17em},{\mu }_{i{n}_i}^c),$$

where $E_{{\mathit{\theta }}_c}(\cdot )$ denotes taking expectation conditional on subject i belonging to class c and design matrix X_i.

We relate the mean curve ${\mu }_i^c$ to the covariates through $\log ({\mu }_{ij}^c)={\mathbf{x}}_{ij}^T{\mathit{\beta }}_c$, where ${\mathit{\beta }}_c=({\mathit{\beta }}_1^c,\hspace{0.17em}\dots \hspace{0.17em},{\mathit{\beta }}_p^c)$ are the class-c regression coefficients. To allow for overdispersion, the variance function is assumed to have the form ${\text{Var}}_{{\mathit{\theta }}_c}(y_{ij})={\varphi }_c{\mu }_{ij}^c$, with scale parameter ϕ_c allowed to vary across classes. Due to our data-generating model (Section 2.2), we must have ϕ_c > 1. For this reason, we often write the scale parameter as ϕ_c = 1 + γ_c, where γ_c > 0.

2.2 |. The INAR-(1) Negative Binomial Process

Conditional on class-membership, the observations from subject i comprise a multivariate outcome with distribution p_i (y_i ; θ_c ), governed by the (p + 2) × 1 class-specific parameter vector ${\mathit{\theta }}_c={({\mathit{\beta }}_c^T,{\alpha }_c,{\varphi }_c)}^T$ where β c and ϕ_c play the roles described in Section 2.1 and α_c is a parameter controlling the correlation between observations on the same subject. The distribution of ${\mathbf{y}}_i=(y_{i1},\hspace{0.17em}\dots \hspace{0.17em},y_{i{n}_i})$ is modeled by assuming that the components y_{i j} of y_i arise from a first-order Markov process governed by θ_c. The joint distribution of y_i is built up directly through the transition function, p(y_{i j} |y_{i,j −1}, X_i ; θ_c ), associated with the underlying process $p_i({\mathbf{y}}_i;{\mathit{\theta }}_c)=p(y_{i1}|{\mathbf{X}}_i;{\mathit{\theta }}_c){\prod }_{j=2}^{n_i}p(y_{ij}|y_{i,j-1},{\mathbf{X}}_i;{\mathit{\theta }}_c)$, and the correlation structure of y_i then arises from the various dependencies introduced by this Markov process.

A stochastic process tailored specifically for count data is the integer-valued autoregressive (INAR(1)-NB) process with negative binomial (NB) marginals described both by McKenzie¹¹ and by Bockenholt.¹² For a subject in class c, observations from the INAR(1)-NB process arise as follows: the first observation y_{i 1} follows a negative binomial distribution with $E_{{\mathit{\theta }}_c}(y_{i1})={\mu }_{i1}^c$ and ${\text{Var}}_{{\theta }_c}(y_{i1})={\mu }_{i1}^c(1+{\gamma }_c)$. We denote this by $y_{i1}~NB\left\{{\mu }_{i1}^c,{\mu }_{i1}^c(1+{\gamma }_c)\right\}$ meaning that y_{i 1} has probability mass function

$$P(y_{i1}=k)=\left(\begin{array}{c}k+{\mu }_{i1}^c/{\gamma }_c-1\\ k\end{array}\right){\left(\frac{1}{1+{\gamma }_c}\right)}^{{\mu }_{i1}^c/{\gamma }_c}{\left(\frac{{\gamma }_c}{1+{\gamma }_c}\right)}^k;k\ge 0.$$

The subsequent observations $(y_{i2},\hspace{0.17em}\dots \hspace{0.17em},y_{i{n}_i})$ are determined through

$$y_{ij}=H_{ij}+I_{ij},\hspace{1em}j=2,\hspace{0.17em}\dots \hspace{0.17em},n_i.$$ (1)

In (1), the term H_{i j} is a random variable whose distribution depends on the previous value of the outcome y_i,_,j−1. Specifically, conditional on the value of y_{i,j −1} and a latent success probability q_{i j}, H_{i j} ∼ Binomial $(y_{i,j-1},q_{ij})$ with the understanding that H_{i j} = 0 whenever y_{i,j −1} = 0. The latent success probabilities $(q_{i2},\hspace{0.17em}\dots \hspace{0.17em},q_{i{n}_i})$ are themselves independent random variables with $q_{ij}~\text{Beta}\{{\alpha }_c\sqrt{{\mu }_{i,j-1}^c{\mu }_{ij}^c}/{\gamma }_c,{\mu }_{i,j-1}^c(1-{\alpha }_c{\lambda }_{ij}^c)/{\gamma }_c\}$, where ${\lambda }_{ij}^c=\sqrt{{\mu }_{ij}^c/{\mu }_{i,j-1}^c}$ and where Beta(α, β ) represents a Beta distribution with shape parameters α and β. Because this implies that $E[H_{ij}|y_{i,j-1}]={\alpha }_c{\lambda }_{ij}^c{y}_{i,j-1}$ marginally over q_{i j}, we must have $0\le {\alpha }_c\sqrt{{\mu }_{ij}^c/{\mu }_{i,j-1}^c}\le 1$ for each class; see below. One may also note that given y_{i ;j} −1 ≥ 1 and class membership c, marginally over q_{i j} ; H_{i j} follows a beta-binomial distribution with parameters $(y_{i,i-1},{\alpha }_c\sqrt{{\mu }_{i,j-1}^c{\mu }_{ij}^c}/{\gamma }_c,{\mu }_{i,j-1}^c(1-{\alpha }_c{\lambda }_{ij}^c)/{\gamma }_c)$. The innovation component I_{i j} is assumed to follow a $\text{NB}\{{\mu }_{ij}^c(1-{\alpha }_c/{\lambda }_{ij}^c),{\mu }_{ij}^c(1-{\alpha }_c/{\lambda }_{ij}^c)(1+{\gamma }_c)\}$ distribution where $(I_{i2},\dots ,I_{i{n}_i})$ are mutually independent and where each I_{i j} is independent of the history (y_{i 1}, … , y_{i,j −1}).

Although the transition function p(y_{i j} |y_{i,j −1}, X_i, θ_c ) associated with the INAR(1)-NB process does not have a simple closed form (see part A of the supporting material), it may be directly computed using the fact that it is the convolution of a beta-binomial distribution and a negative binomial distribution. In addition, under the INAR(1)-NB process, the marginal distribution (conditional on class membership) of y_{i j} is negative binomial with $E_{{\theta }_c}(Y_{ij})={\mu }_{ij}^c$ and ${\text{Var}}_{{\theta }_c}(y_{ij})={\mu }_{ij}^c(1+{\gamma }_c)$, and the class-specific correlation structure of y_i is first-order autoregressive. That is, for two observations y_{i k} and y_{i j} on the same subject, the class-specific correlation is ${\text{corr}}_{{\mathit{\theta }}_c}(y_{ik},y_{ij})={\alpha }_c^{|k-j|}$. The conditional expectation of y_{i j} given y_{i,j −1} is a linear function of y_{i,j −1},

$$E_{{\theta }_c}(y_{ij}|y_{i,j-1})={\mu }_{ij}^c\left(1-{\alpha }_c/{\lambda }_{ij}^c\right)+{\alpha }_c{\lambda }_{ij}^c{y}_{i,j-1},$$

and the conditional variance of y_{i j} given y_{i,j −1} is given by

$${\text{Var}}_{{\theta }_c}(y_{ij}|y_{i,j-1})={\mu }_{ij}^c\left(1-{\alpha }_c/{\lambda }_{ij}^c\right){\varphi }_c+{\alpha }_c{\lambda }_{ij}^c{y}_{i,j-1}\left(1-{\alpha }_c{\lambda }_{ij}^c\right)\frac{{\mu }_{i,j-1}^c/{\gamma }_c+y_{i,j-1}}{1+{\mu }_{i,j-1}^c/{\gamma }_c}.$$

It is also worth mentioning that our specification of the INAR(1)-NB process implies the additional restriction on the relation between the autocorrelation parameters and the latent trajectories: ${\alpha }_c^2<{\min }_{i,j}\{{\mu }_{i,j-1}^c/{\mu }_{ij}^c,{\mu }_{ij}^c/{\mu }_{i,j-1}^c\}$ for each c. Nevertheless, when all of the latent trajectories are reasonably smooth, this constraint is not especially restrictive as the values of $\{{\mu }_{i,j-1}^c/{\mu }_{ij}^c\}$ will be close to one.

3 |. ESTIMATION

Because a finite mixture model with a pre-specified number of components can easily be formulated as a “missing-data” problem, the EM algorithm provides an attractive estimation approach. In our model, if the individual class-membership labels Z = (Z₁, … , Z_n ) were observed, the “complete-data” log-likelihood would be

$$\log L(\mathbf{\Theta },\mathit{\pi };\mathbf{Y},\mathbf{Z})=\sum _{i=1}^m\sum _{c=1}^{C}1\{Z_i=c\}\left(\log ({\pi }_c)+\log \{p_i({\mathbf{y}}_i;{\text{θ}}_c)\}\right).$$

Above, Θ = (θ₁, … , θ_C ) where ${\text{θ}}_c={({\text{β}}_c^T,{\alpha }_c,{\gamma }_c)}^T$ are the parameters associated with class c, and π = (π₁, … , π_C ) is the vector of mixture proportions.

Given current, iteration-k, estimates of parameters (Θ^{(k )}, π^{(k )}), each EM iteration obtains new parameter estimates by maximizing the current exp1ectation of the complete-data log-likelihood, with the expectation being taken over the unobserved class labels, viz.

$$\begin{gathered} ({\mathbf{\Theta }}^{(k+1)},{\mathit{\pi }}^{(k+1)})=\underset{\Theta ,\pi }{\text{argmax}}E\{\log L(\mathbf{\Theta },\mathit{\pi };\mathbf{Y},\mathbf{Z})|\mathbf{Y},{\mathbf{\Theta }}^{(k)},{\mathit{\pi }}^{(k)}\} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=\underset{\Theta ,\pi }{\text{argmax}}\sum _{c=1}^C\sum _{i=1}^m{W}_{ic}({\mathbf{\Theta }}^{(k)},{\mathit{\pi }}^{(k)})\left(\log ({\pi }_c)+\log \{p_i({\mathbf{y}}_i;{\text{θ}}_c\}\right). \end{gathered}$$

Here, W_{i c} (Θ^{(k )}, π^{(k )}) is the current estimated posterior probability that subject i belongs to class c, namely

$$W_{ic}({\mathbf{\Theta }}^{(k)},{\mathit{\pi }}^{(k)})=P(Z_i=c|{\mathbf{y}}_i,{\mathbf{\Theta }}^{(k)},{\mathit{\pi }}^{(k)})=\frac{{\pi }_c^{(k)}{p}_i({\mathbf{y}}_i;{\text{θ}}_c^{(k)})}{{\Sigma }_s{\pi }_s^{(k)}{p}_i({\mathbf{y}}_i;{\text{θ}}_s^{(k)})}.$$

3.1 |. Estimating Equation Approach for Computation

In each step of the EM algorithm, updating the class probabilities is straightforward because the “M” update is simply the average of the current posterior probabilities,${\pi }_c^{(k+1)}=\frac{1}{m}{\sum }_{i=1}^m{W}_{ic}({\mathbf{\Theta }}^{(k)},{\mathit{\pi }}^{(k)})$. However, to update the remaining parameters, we must maximize C separate weighted log-likelihood functions

$${\text{θ}}_c^{(k+1)}=\underset{{\mathit{\theta }}_c}{\text{argmax}}\sum _{i=1}^m{W}_{ic}({\mathbf{\Theta }}^{(k)},{\mathit{\pi }}^{(k)})\log \{p_i({\mathbf{y}}_i;{\text{θ}}_c)\},\hspace{1em}\hspace{1em}c=1,\dots ,C.$$ (2)

Because each such log-likelihood function is a sum over many complicated transition probabilities, implementing the maximization in (2) may be challenging.

Instead of updating the parameters by maximizing each of the weighted log-likelihood functions directly, we found that replacing the score function with a more manageable estimating function provides a less cumbersome approach. That is, rather than solving

$$\sum _{i=1}^m{W}_{ic}({\mathbf{\Theta }}^{(k)},{\mathit{\pi }}^{(k)})\frac{\partial \log p_i({\mathbf{y}}_i;{\text{θ}}_c)}{\partial {\text{θ}}_c}=0$$

for each class, we instead solve

$$\sum _{i=1}^m{W}_{ic}({\mathbf{\Theta }}^{(k)},{\mathit{\pi }}^{(k)})U_i({\text{θ}}_c)=0,\hspace{1em}\hspace{1em}\text{for}\hspace{0.17em}\hspace{0.17em}c=1,\dots ,C,$$ (3)

where U_i (θ_c ) forms an unbiased estimating function (i.e.,$E_{{\theta }_c}[U_i({\text{θ}}_c)]=0$) for each class. Such an approach, where within each EM iteration the maximization step is approximated by solving an estimating equation, is similar to the estimation strategy detailed by Elashoff and Ryan.¹³ Replacing the score function with an alternative estimating function has also been found to be useful in a variety of other domains, for example, in fitting robust mixture regression models.¹⁴

Our choice of U_i (θ_c ) relies on the extended quasilikelihood function procedure for constructing estimating equations proposed by Hall and Severini.¹⁵ These estimating functions considerably simplify computation (i.e., by solving (3)) when compared to using score functions. Tailoring the estimating functions of Hall and Severini to the case of a log-link function and an AR(1) correlation structure yields the (p + 2) × 1 estimating function

$$U_i({\text{θ}}_c)=\left[\begin{array}{c}{U}_i^{[1]}({\mathit{\theta }}_c)\\ U_i^{[2]}({\mathit{\theta }}_c)\\ U_i^{[3]}({\mathit{\theta }}_c)\end{array}\right]=\frac{1}{{\varphi }_c}\left[\begin{array}{c}{\mathbf{X}}_i^T{\mathbf{A}}_i^{1/2}({\mathit{\mu }}_i^c){\mathbf{R}}_i^{-1}({\alpha }_c){\mathbf{A}}_i^{-1/2}({\mathit{\mu }}_i^c)({\mathbf{y}}_i-{\mathit{\mu }}_i^c)\\ \frac{2{\varphi }_c{\alpha }_c(n_i-1)}{1-{\alpha }_c^2}-{({\mathbf{y}}_i-{\mathit{\mu }}_i^c)}^T\frac{d{\mathbf{R}}_i^{-1}({\alpha }_c)}{d{\alpha }_c}({\mathbf{y}}_i-{\mathit{\mu }}_i^c)\\ \frac{1}{{\varphi }_c}{({\mathbf{y}}_i-{\mathit{\mu }}_i^c)}^T{\mathbf{A}}_i^{-1/2}({\mathit{\mu }}_i^c){\mathbf{R}}_i^{-1}({\alpha }_c){\mathbf{A}}_i^{-1/2}({\mathit{\mu }}_i^c)({\mathbf{y}}_i-{\mathit{\mu }}_i^c)-n_i\end{array}\right].$$ (4)

In (4), ${\mathbf{A}}_i({\text{μ}}_i^c)$ is the n_i × n_i matrix defined by $A_i({\mathit{\mu }}_i^c)=\text{diag}\{{\mu }_{i1},\dots ,{\mu }_{i{n}_i}\}$ and R_i (α_c ) is the n_i × n_i correlation matrix whose (k, j ) entry is $R_i({\alpha }_c)[k,j]={\alpha }_c^{|k-j|}$.

The equation determined by setting the p-component vector ${\sum }_{i=1}^m{U}_i^{[1]}({\text{θ}}_c)$ to zero

$$\frac{1}{{\varphi }_c}\sum _{i=1}^m{\mathbf{X}}_i^T{\mathbf{A}}_i^{1/2}({\mathit{\mu }}_i^c){\mathbf{R}}_i^{-1}({\alpha }_c){\mathbf{A}}_i^{-1/2}({\mathit{\mu }}_i^c)({\mathbf{y}}_{\mathbf{i}}-{\mathit{\mu }}_i^c)=0,$$ (5)

corresponds to the generalized estimating equation (GEE) described by Zeger and Liang.¹⁶ In GEE, the autocorrelation parameter α_c is first estimated separately and then plugged into (5) in order to solve for regression coefficients β c. Picking up on that theme, to solve (3) for a fixed c, we first update β c by solving ${\sum }_{i=1}^m{W}_{i,c}({\mathbf{\Theta }}^{(k)},{\mathit{\pi }}^{(k)})U_i^{[1]}({\text{θ}}_c)=0$, using initial values for (α_c, ϕ_c ). Using this value of β c and the initial overdispersion ϕ_c, α_c is updated by solving ${\sum }_{i=1}^m{W}_{i,c}({\mathbf{\Theta }}^{(k)},{\mathit{\pi }}^{(k)})U_i^{[2]}({\text{θ}}_c)=0$. The value of ϕ_c can then be updated non-iteratively because, given values of (β c, α_c ), the solution to ${\sum }_{i=1}^m{W}_{i,c}({\mathbf{\Theta }}^{(k)},{\mathit{\pi }}^{(k)})U_i^{[3]}({\text{θ}}_c)=0$ for ϕ_c has a closed form. This procedure is repeated until convergence.

3.2 |. Approximate EM Procedure and Standard Errors

Our approximate EM algorithm, where the score function is replaced with another, more manageable estimating function, may be summarized as follows:

1. Find initial estimates Θ⁽⁰⁾, π⁽⁰⁾. (Our initialization procedure is described in part C of the supporting material).

2. Compute current estimated posterior probabilities W_{i c} (Θ^{(k )}, π^{(k )}) for each class c and subject i.

3. Update mixture proportions through ${\pi }_c^{(k+1)}=\frac{1}{m}{\sum }_{i=1}^m{W}_{ic}({\mathbf{\Theta }}^{(k)},{\mathit{\pi }}^{(k)})$. Update other parameters (θ₁, … , θ_C ) by solving ${\sum }_{i=1}^m{W}_{i,c}({\mathbf{\Theta }}^{(k)},{\mathit{\pi }}^{(k)})U_i({\text{θ}}_c)=0$

4. Repeat steps (2) and (3) until convergence.

Parameter estimates $(\widehat{\mathbf{\Theta }},\widehat{\mathit{\pi }})$ produced from the above iterative procedure may be viewed as a solution to the estimating equation $G(\mathbf{\Theta },\mathit{\pi })={\sum }_{i=1}^m{G}_i(\mathbf{\Theta },\mathit{\pi })=0$ where G_i (Θ, π) is the (p + 3)C – 1 × 1 victor defined as $G_i(\mathbf{\Theta },\mathit{\pi })={[\text{vec}{({\mathbf{V}}_i)}^T,{\mathbf{b}}_i^T]}^T$ and where V_i is the (p + 2) × C matrix ${\mathbf{V}}_i=[W_{i1}(\mathbf{\Theta },\mathit{\pi })U_i({\text{θ}}_1),\dots \dots ,W_{iC}(\mathbf{\Theta },\mathit{\pi })U_i({\text{θ}}_C)]$ and b_i is the (C − 1) × 1 vector ${\mathbf{b}}_i={[W_{i1}(\mathbf{\Theta },\mathit{\pi })-{\pi }_1,\dots \dots ,W_{iC-1}(\mathbf{\Theta },\mathit{\pi })-{\pi }_{C-1}]}^T$. The notation vec(Vi ) means that vec(Vi ) is the (p + 2)C × 1 vector formed by stacking the columns of V_i on top of one another.

It can be shown that G (Θ, π) is an unbiased estimating function (see part B of the supporting material), and conditions under which consistent solutions of unbiased estimating equations are asymptotically normal are discussed in a number of sources.^17,18 When it is further assumed that the number of classes C is correctly specified and that $(\widehat{\mathbf{\Theta }},\widehat{\mathit{\pi }})$ are consistent estimates of the true model parameters, we have that ${\widehat{\mathbf{\Sigma }}}^{-1/2}\{{(\widehat{\mathbf{\Theta }},\widehat{\mathit{\pi }})}^T-{(\mathbf{\Theta },\mathit{\pi })}^T\}{\to }_{d}N(0,\mathbf{I})$, as m−→ ∞. The estimated covariance matrix $\widehat{\mathbf{\Sigma }}$ is given by

$$\widehat{\mathbf{\Sigma }}={\left(\frac{1}{m}\sum _{i=1}^{m}E\{\mathbf{D}{\mathbf{G}}_i(\widehat{\mathbf{\Theta }},\widehat{\mathit{\pi }})\}\right)}^{-1}\left(\frac{1}{m}\sum _{i=1}^m{\mathbf{G}}_i(\widehat{\mathbf{\Theta }},\widehat{\mathit{\pi }}){\mathbf{G}}_i{(\widehat{\mathbf{\Theta }},\widehat{\mathit{\pi }})}^T\right){\left(\frac{1}{m}\sum _{i=1}^{m}E\{\mathbf{D}{\mathbf{G}}_i(\widehat{\mathbf{\Theta }},\widehat{\mathit{\pi }})\}\right)}^{-1^T}.$$ (6)

In (6), DG_i (Θ, π) is the ((p + 3) C − 1) ((p + 3) C − 1) matrix of partial derivatives $\mathbf{D}{\mathbf{G}}_i(\text{θ},\mathit{\pi })=\partial {\mathbf{G}}_i(\mathbf{\Theta },\mathit{\pi })/\partial (\mathbf{\Theta },\mathit{\pi })$. Standard errors are computed from the diagonal elements of $\widehat{\mathbf{\Sigma }}$.

4 |. CLASS ASSIGNMENT AND MEASURES OF DISCRIMINATION

After estimating latent trajectories for each class, one often wishes to go back and assign or classify subjects based on their empirical resemblance to one of the estimated trajectories. Even though all model parameters may be estimated accurately, however, the associated classification procedure may not have a high rate of correct assignment, and this poor class-discrimination may be due to little underlying class-separation between the latent trajectories ${\text{μ}}_i^c$ or to high levels of noise ϕ_c in the response. In these cases, the ability to correctly classify subjects is limited by the class separation inherent in the underlying true data generating model rather than any deficiencies in the model specification or estimation procedure.

To separate the roles that underlying class separation and estimation error play in the accuracy of estimating latent class trajectories, we, in our simulations (see Section 5), employ a measure of class separation which can be thought of as a rough upper bound on one’s ability to correctly assign subjects to classes based on our or any other latent class model or estimation procedure. Specifically, we define the class separation index (CSI) as the expected discrimination that would be obtained by an oracle using knowledge of both the true generative model and the true parameter values of that model to compute posterior probabilities of class membership for each subject and to utilize these posterior probabilities for class assignment. In other words, the CSI represents the class discrimination that could be obtained if one knew the true data generating model and hence, represents an intuitive measure of underlying separation between the latent classes. In our simulation studies, we use the all-pairwise c-statistic¹⁶ as the measure of multi-class discrimination through which to compute the class separation index. The all-pairwise c-statistic lies between 0 and 1 with larger values indicating better discriminatory performance, and as with the more well-known two-class c-statistic, a value of the all-pairwise c-statistic near 0.5 indicates that the model performs no better than predicting class labels at random. Other multi-class measures of discrimination such as the polytomous discrimination index¹⁹ could be used, but we found the relation between the CSI and estimation performance to be quite similar for either choice of discrimination index. The CSI is defined more formally in Appendix A, and the definitions of both the all-pairwise c-statistic and polytomous discrimination index are also reviewed in more detail in Appendix A.

5 |. SIMULATIONS

5.1 |. Autoregressive Models with Four Latent Classes

Simulation Design

To evaluate the performance of our estimation procedure and to test our implementation, we performed a simulation study using two central scenarios (Scenarios I and II) as our point of reference. Each of Scenarios I and II involves a model with four latent classes where the class-specific model is the autoregressive negative binomial model described in Sections 2.1 and 2.2. In Scenario I, each subject is observed over 8 equally spaced time points, and in Scenario II, subjects are observed over 5 equally spaced time points. The latent trajectories for both of these scenarios are qualitatively similar: one trajectory is persistently low, one trajectory is persistently high, and the other two trajectories move from high (low) to low (high) values over time. The four mixture proportions are set to 0.5, 0.1, 0.25, and 0.15 in each of the simulation scenarios. Plots of the latent trajectories used in Scenarios I and II are shown in Figure 1. The choice of four classes for the simulation scenarios is meant to reflect the wide use of four-class models when identifying subtypes in the childhood development of conduct disorders.^1,2 The goals of this simulation study include examining the empirical bias of latent trajectory estimates, quantifying the degree to which the standard errors provide approximately desired coverage levels, and assessing how each of these operational characteristics vary as a function of sample size and of degree of model identifiability, as quantified by the class separation index. In this simulation study, we focus on the setting where the only covariate is time and where the main goal is recovering the class-specific trajectories, but simulations which include subject-specific covariates would be useful for further studying the estimation and classification performance of our method.

FIGURE 1.

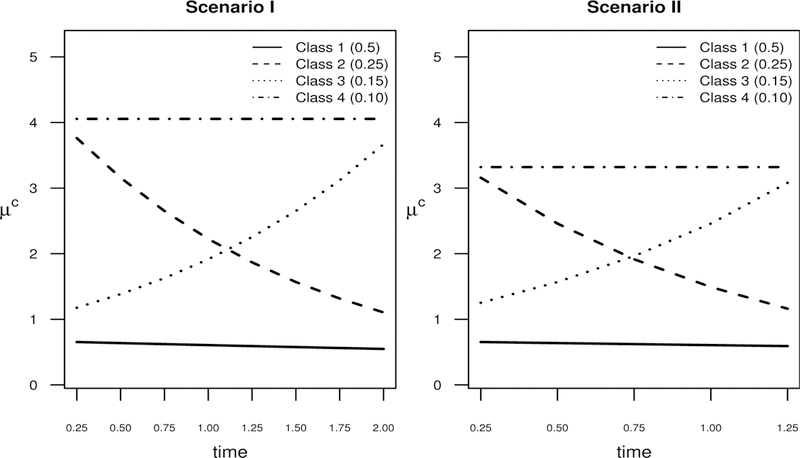
Mean latent trajectories µ^c (t ) for the two central simulation scenarios. In Scenario I, observations for each subject are made at each of the eight time points t_{i j} = j /4, j = 1, … , 8, and in Scenario II, observations for each subject are made at each of the five time points t_{i j} = j /4, j = 1, … , 5. For both scenarios, the class-membership proportions are as follows: Class 1: 50%, Class 2: 25%, Class 3: 15%, and Class 4: 10%.

The values of the class separation index for variants of Scenarios I and II may be found in Table S1 of the supporting material. For each of Scenarios I and II, we varied the autocorrelation parameter across two levels, α ∈ {0.1, 0.4}, and the scale parameter across two levels, ϕ ∈ {1.25, 3}. Higher values of the scale parameter and higher levels of autocorrelation reduce the class separation and thereby the inherent ability to make correct inference on model parameters. Also, for each parameter configuration (i.e., a particular scenario and choice of (α, ϕ)), we ran our estimation procedure for each of the sample sizes m = 2, 000, m = 500, and m = 200. For each parameter configuration and sample size, we computed estimates on each of 200 replicated data sets. To determine convergence with a given tolerance level ε, we used the criterion ${\max }_k|m^{-1}{G}^k(\widehat{\mathit{\Theta }},\widehat{\mathit{\pi }})|\hspace{1em}\le \hspace{1em}\epsilon$, where G (Θ, π) is as defined in Section 3.2, and G^k (Θ, π) denotes the k ^th element of G (Θ, π). In all of the simulation studies, we used ε = 0.0001, and in the data analysis (see Section 6), we set ε = 0.001 due to slow convergence when using this dataset. Though not explored in the simulation studies or data analysis, we have examined using the norm of G (Θ, π) to determine convergence (i.e., stopping whenever ||G (Θ, π)|| ≤ ε). This is a somewhat less strict convergence criterion that did not appear to make a substantial difference in the simulation studies, but a more detailed comparison of these stopping criteria may be worthwhile. Another possible stopping rule is to base convergence on the norm of the parameter residuals (i.e. stopping when ${\Vert {\mathit{\theta }}^{(k+1)}-{\mathit{\theta }}^{(k)}\Vert }^2+{\Vert {\mathit{\pi }}^{(k+1)}-{\mathit{\pi }}^{(k)}\Vert }^2\le \epsilon$).

Because the class labels are not identifiable, for each model fitted, we permuted the class labels of the estimated parameters to minimize the L₂ distance between the estimated and true mean curves. That is, for a set of estimates $\tilde{\mathbf{\Theta }}=({\widetilde{\text{θ}}}_1,\dots ,{\widetilde{\text{θ}}}_4)$ and $\tilde{\mathit{\pi }}=({\tilde{\pi }}_1,\dots ,{\tilde{\pi }}_4)$ obtained through our approximate EM procedure, we computed the optimal permutation according to

$$s^{*}=\underset{\mathcal{S}\in \mathcal{P}}{\text{argmin}}\sum _{c=1}^4{({\mathit{\mu }}^c-{\widehat{\mathit{\mu }}}^{\mathcal{S}(c)})}^T({\mathit{\mu }}^c-{\widehat{\mathit{\mu }}}^{\mathcal{S}(c)}),$$

where $\mathcal{P}$ simply denotes the set of permutations of class labels (1, 2, 3, 4). We then computed the final estimates of the parameters through $\widehat{\mathbf{\Theta }}=({\widetilde{\text{θ}}}_{{\mathcal{S}}^{*}(1)},\dots ,{\widetilde{\text{θ}}}_{{\mathcal{S}}^{*}(4)})$ and $\widehat{\mathit{\pi }}=({\tilde{\pi }}_{{\mathcal{S}}^{*}(1)},\dots ,{\tilde{\pi }}_{{\mathcal{S}}^{*}(4)})$. Note that ${\text{μ}}^c=\exp ({\mathbf{X}}_i{\mathit{\beta }}_c)$ and ${\widehat{\text{μ}}}^c=\exp ({\mathbf{X}}_i{\widehat{\beta }}_c)$ do not depend on i because all subjects share the same design matrix in our simulation scenarios, though this need not be the case in real applications.

Results

Figure 2 displays the average absolute empirical bias for all latent trajectories in each of the eight simulation settings. The empirical bias for a particular latent class was found by taking the mean absolute difference between the average of the estimated trajectory values and the associated true values of the underlying trajectories. In Figure 2, empirical bias is plotted versus the values of the class separation index illustrating how the underlying separation among the classes tends to influence this property of estimation. Figure 2 shows good overall performance for simulation settings with highly distinct classes and large sample sizes; the average absolute empirical bias is less than 0.051 for all simulations with a CSI greater than 0.90 and m = 2, 000. For high values of the CSI, the empirical biases are packed closely to zero but spread out considerably as the CSI declines. Comparisons between the empirical discrimination obtained from the fitted INAR(1)-NB models and the CSI are shown for each of the simulation settings in Figure S1 of the supporting material.

FIGURE 2.

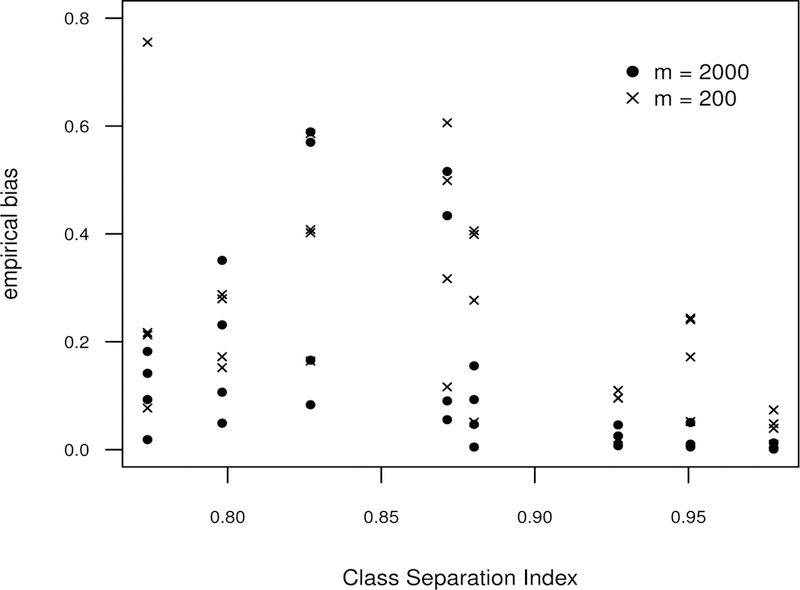
Average absolute empirical bias for the latent trajectories using data simulated under the eight simulation settings of the INAR(1)-NB model. For each simulation setting and number of subjects, empirical bias is calculated for each of the four latent classes. For each latent class, bias is calculated as $T^{-1}{\sum }_{j=1}^T|{\tilde{\mu }}^c(t_j)-{\mu }^c(t_j)|$, where ${\tilde{\mu }}^c(t_j)$ is the average estimate of µ^c (t _j ) (average over simulation replications) and µ^c (t _j ) is the true value of the mean curve at time t _j. Absolute empirical bias values are plotted versus the class separation index (CSI) of the associated simulation settings. The values of the empirical bias were obtained using 200 replications for each of the eight scenarios and each choice of the number of subjects (either m = 200 or m = 2, 000).

Empirical coverage proportions for the regression coefficients and mixture proportions are shown in Figure 3. As shown in this figure, the computed confidence intervals generally give the desired 95% coverage for large sample sizes (m = 2, 000) in highly separated settings. Specifically, when m = 2, 000 and the CSI is greater than 0.85, coverage levels are centered around 0.95 for most parameters. However, the results from this figure suggest that confidence intervals should be interpreted with caution for relatively small sample sizes. For most simulation settings, coverage appears to be consistently less than 0.95 for smaller sample sizes (i.e., m = 200), and for both sample sizes, the level of coverage and variability in coverage tends to deteriorate as the class separation decreases.

FIGURE 3.

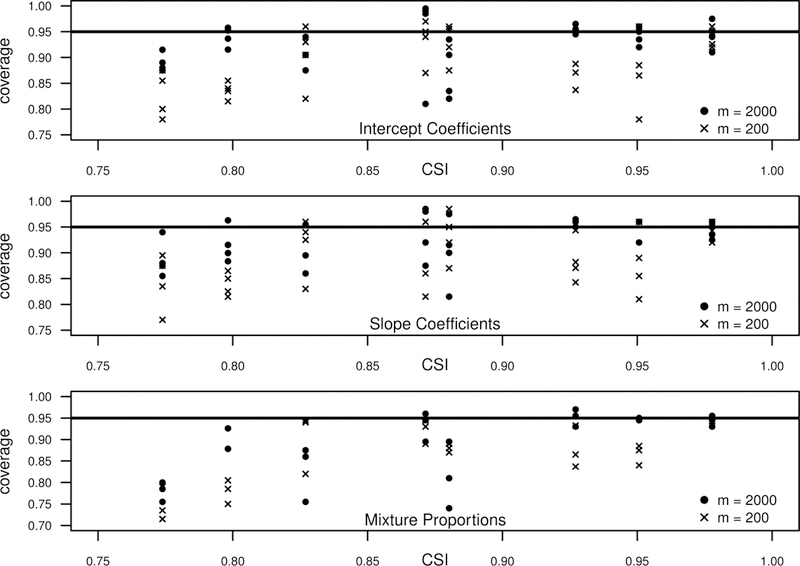
Coverage proportions (using 95% confidence intervals) for the regression parameters (both the intercept and slope) and mixture proportions using data simulated under the eight simulation settings of the INAR(1)-NB model. Empirical coverage proportions are plotted versus the associated class separation index (CSI) of the associated simulation settings. Coverage proportions are shown for simulations with m = 200 subjects and m = 2, 000 subjects.

5.2 |. Poisson Outcomes with Normal Random Effects

Design

To evaluate the performance of our proposed fitting procedure under model misspecification, we performed several simulations involving latent class models where, within each class, data are generated from a generalized linear mixed model with Poisson responses and Normal random effects. The motivation for this simulation exercise is to assess how well our method recovers latent trajectories when this alternative model holds rather than our count-valued AR(1) model.

In these simulations, conditional on a subject-specific random slope, intercept, and class label, the response of each subject was generated according to a Poisson distribution. In particular, for subject i in class c, the j ^th response was generated as $Y_{ij}|a_{i0},a_{i1},Z_i=c~\text{Poisson}({\mu }_{ij}^c)$ where $\log ({\mu }_{ij}^c)={\mathit{\beta }}_0^c+{\mathit{\beta }}_1^c{t}_{ij}+a_{i0}+a_{i1}{t}_{ij},j=1,\dots ,T$, and where (a_{i 0}, a_{i 1}) are jointly distributed Normal random variables with $a_{i0}~N(0,{\sigma }_{c0}^2+\frac{{(T-1)}^2{\sigma }_{c1}^2}{4})$, $a_{i1}~N(0,{\sigma }_{c1}^2)$, and $\text{Cov}(a_{i0},a_{i1})=-[(T-1){\sigma }_{c1}^2]/2$. Consequently, marginally over (a_{i 0}, a_{i 1}), the mean trajectories are quadratic on the log scale, viz,

$$\log \{E(Y_{ij}|Z_i=c)\}={\mathit{\beta }}_0^c+\frac{{\sigma }_{c0}^2}{2}+\frac{{(T-1)}^2{\sigma }_{c1}^2}{8}+[{\mathit{\beta }}_1^c+\frac{(T-1){\sigma }_{c1}^2}{2}]t_{ij}+\frac{{\sigma }_{c1}^2}{2}{t}_{ij}^2.$$ (7)

As in the simulations of Section 5.1, we used four latent classes c = 1, … , 4 for each simulation setting. In total, we considered four simulation settings of the Poisson-Normal model: one with eight time points and the other three having five time points. In each of these, the parameters were chosen so that the mean trajectories were similar to those of Scenario I and Scenario II. The parameter values used for each of these four simulations settings are provided in Table S4 of the supporting material. For each setting of the Poisson-Normal model and each simulation replication, we fit a four-class INAR(1)-NB model, assuming that, within each class, the mean trajectory µ^c is quadratic on the log scale. As in the INAR(1)-NB simulations of Section 5.1, we used 200 replications for each simulation setting.

Results

For the Poisson-Normal simulations, we computed the average absolute empirical bias for each of the latent trajectories as was done for the INAR(1)-NB simulations. Empirical bias values obtained from fitting the INAR(1)-NB model to data generated from the four simulation settings of the Poisson-Normal model are shown in Figure 4. Results are shown for sample sizes m = 500 and m = 2, 000. Because the latent trajectories in these simulations were chosen to closely match those of the INAR(1)-NB simulations, the empirical biases from these simulation may, to some degree, be compared to those from Figure 2. The empirical bias shown in Figure 4 suggest that our procedure is fairly robust to this form of misspecification for highly distinct classes. However, the results for the two simulation settings with a lower CSI suggest a lack of robustness to model misspecification of this type when the underlying class separation is not especially high.

FIGURE 4.

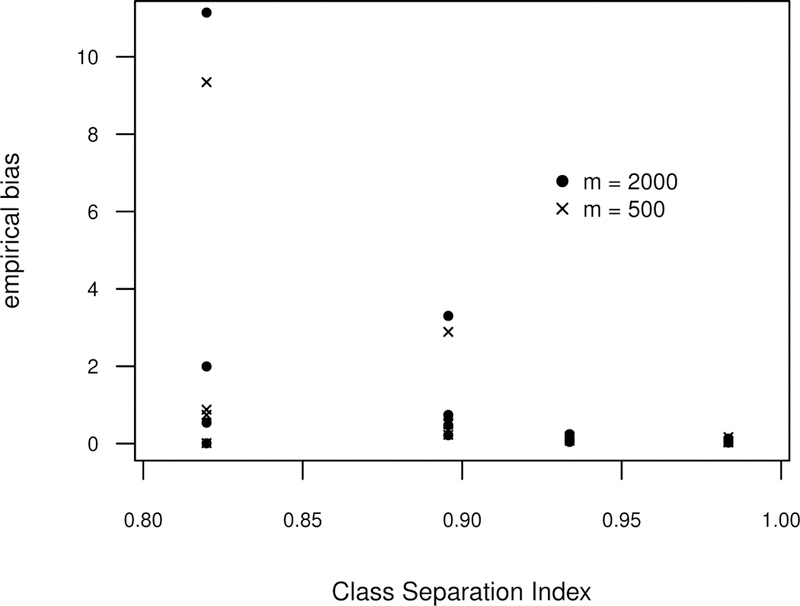
Average absolute empirical bias for the latent trajectories when fitting an INAR(1)-NB model to data simulated under the four settings of the Poisson-Normal model. For each simulation setting and number of subjects, empirical bias is calculated for each of the four latent classes. Empirical bias for each latent trajectory was computed as described in Figure 2.

6 |. APPLICATION TO CNLSY DATA

6.1 |. Description and Model Fitting

In this section, we consider data collected on Children of the National Longitudinal Study of Youth (CNLSY). The National Longitudinal Study of Youth (NLSY79) is a longitudinal study initiated in 1979 on a nationally representative sample of young adults. In 1986, the NLSY launched a survey of children of female subjects from the original NLSY79 cohort. Assessments of the children of the NLSY were performed biennially, and in each assessment, mothers were asked to respond to a series of questions regarding each of their children’s behavior and environment.

Though the mothers were asked to respond on a wide variety of measures, our focus lies in the severity of behavioral problems as measured by the “Behavior Problems Index” (BPI) in early childhood and by the number of delinquent acts committed during the adolescent years. The BPI is recorded for children ages 4 − 13 and is constructed by asking the mother to rate her child on a scale of 0 to 2 on each item from a list of seven common behavioral problems. Consequently, this yields a BPI value which is an integer between 0 and 14. Starting at the age of 10, the children were also asked to report the number of delinquent acts they committed during the past year. From age 14 onward, the mothers no longer responded to the BPI, leaving only the self-reported delinquency counts as a measure of behavioral conduct for children older than 13. In total, these data contain 9, 626 subjects each of whom was surveyed biennially over the ages 4 to 16 (or 5 to 17). Because of this, we grouped the data so that, in the absence of missing values, each individual had 7 observations with the first observation occurring when a subject was age 4–5, the second observation at age 6–7, and the last observation occurring when a subject was age 16–17.

To model the evolution of behavioral problems throughout childhood and adolescence, we combined the BPI and delinquency counts into a single response variable. For children with ages less than 10, we used the BPI as the only response, and for children aged 10–13, we summed the delinquency counts and the BPI. For children aged 14–17, the response is simply the delinquency counts. To account for this methodological feature of the measurement process, we added a dummy variable for the time points corresponding to the age range 10–13 and a dummy variable for the time points corresponding to the age range 14 − 17. Summary statistics regarding the BPI from the CNLSY are shown in Table S2 of the supporting material.

We modeled the class-specific trajectories ${\mathit{\mu }}_i^c=({\mu }_{i1}^c,\dots ,{\mu }_{i{n}_i}^c)$, with ${\mu }_{ij}^c$ denoting the mean response of subject i at time t_{i j} conditional on belonging to class c, as

$$\log ({\mu }_{ij}^c)={\mathit{\beta }}_0^c+\sum _{k=1}^3{\mathit{\beta }}_k^c{B}_k(t_{ij})+{\mathit{\beta }}_4^c(1\{t_{ij}=4\}+\{t_{ij}=5\})+{\mathit{\beta }}_5^{c}1\{t_{ij}\ge 6\}.$$ (8)

In (8), ${\{B_k(\cdot )\}}_{k=1}^3$ are the B-spline basis functions of degree 3 with no interior knots and boundary knots placed at 1 and 7. We coded the time variable as follows: t_{i j} = 1 for children ages 4–5, t_{i j} = 2 for children ages 6–7 with the remaining five time points coded similarly.

Due to missing responses, the number of observations varied somewhat across subjects, and the observations for some subjects were spaced irregularly.

To handle this, we made the working assumption that the correlation only depended on the order of the observed responses. For instance, if subject i was observed at times 1, 2, and 4 with a missing value at time point 3, then we would have ${\text{corr}}_{{\theta }_c}(y_{i4},y_{i2})={\alpha }_c$ and ${\text{corr}}_{{\theta }_c}(y_{i4},y_{i2})={\alpha }_c^2$. If one did not want to use this modified assumption about the correlation structure, an inverse probability weighting approach such as that described by Robins²⁰ could be implemented under a missing at random (MAR) assumption. In this case, one would need to use a weighted version of U_i (θ_c ) when updating the parameters θ₁, … , θ_C in the EM algorithm. Due to the MAR assumption, the posterior probabilities of class membership would only depend on the observed data and thus W_{i c} (Θ, π) and the updates of the mixture proportions would only depend on the distribution of the observed responses.

The CNLSY provides sampling weights which are estimates of how many individuals in the population are represented by a particular subject in the data. The sampling weights reflect the inverse probability that a subject was included in the sample. Because the sampling weights arise from a known survey sampling plan, we treat them as fixed in this analysis. To account for this aspect of the sampling process, we fitted latent class models where, within each iteration of the algorithm, we solved a weighted version of (3) and evaluated convergence with a weighted version of the estimating function G (Θ, π) defined in Section 3.2. This modified version of the fitting procedure that accounts for sampling weights is described in more detail in part D of the supporting material.

Because the number of latent classes is unknown, we applied our procedure to the CNLSY data varying the number of classes from 3 to 6 where, in each case, we modeled the mean trajectories with (8). As is advisable in latent class modeling applications, for each choice of the number of classes, we repeated the estimation procedure with 20 different starting values; in each case, the (weighted) log-likelihood converged to the same maximum value for at least two runs. When comparing the best runs of these four different models (i.e., the 3 to 6 class models), the four-class model possessed the lowest weighted BIC though the four and five-class models had nearly identical values of the weighted BIC. In particular, the best values of the weighted BIC for the 3 to 6 class models were 161751.3, 161651.2, 161651.4, and 161681.0 respectively. It is worth noting that these computed BIC values may be regarded as a type of approximate BIC since our estimation method is not purely likelihood based and instead uses estimates obtained from the estimating equation method described in Section 3 rather than the maximum likelihood estimates. For methods such as ours which are not purely likelihood based, one interesting alternative to traditional BIC is the modified BIC measure described by Lumley and Scott.²¹ Designed for pseudo-likelihood methods in the context of complex survey data, their suggested BIC criteria uses the Wald-type test statistic $({\widehat{\mathbf{\Theta }}}^T,{\widehat{\mathit{\pi }}}^T){\widehat{\mathbf{\Sigma }}}^{-1}{({\widehat{\mathbf{\Theta }}}^T,{\widehat{\mathit{\pi }}}^T)}^T$ as a measure of fit and adds a modified penalty term.

The fitted trajectories and estimated class-membership proportions from the four-class solution are displayed in Figure 5, and here we labeled the four classes to roughly reflect increasing levels of conduct disorder severity with Class 1 (4) denoting the least (most) severe class. The right-hand panel of Figure 5 displays the estimated mean curves $({\widehat{\mu }}_{i1},\dots ,{\widehat{\mu }}_{i7}^c)$ including all the predictors from (8). The left-hand panel displays the mean curves obtained by excluding the time point indicators 1{t_{i j} = 4 or t_{i j} = 5} and 1{t_{i j} ≥ 6}, and is intended to reflect population trajectories in terms of the BPI only. The values of ${\widehat{\mu }}_{ij}^c,{\widehat{\pi }}_c$ and their accompanying standard errors are displayed in Table 1. Note that ${\widehat{\mu }}_{ij}^c$ does not depend on i since we did not include any subject-specific covariates in our analysis.

FIGURE 5.

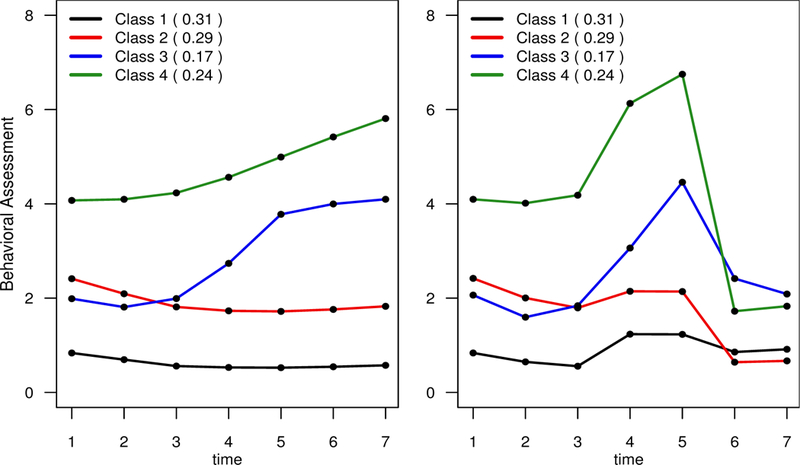
Estimated trajectories for the CNLSY data assuming four latent classes. The terms in parentheses represent estimated class-membership proportions. The left panel displays the estimated trajectories adjusted for the different measurement scales used at different time points; these can be thought of as the fitted latent trajectories on the mother-reported BPI measurement scale. More specifically, the fitted curves in the left panel do not include the time indicators present in equation (8) while the right-hand panel displays the fitted trajectories associated with the full model in equation (8).

TABLE 1.

Values of estimates ${\widehat{\mu }}_{ij}^c$ and associated standard errors for each time point t_{i j} = 1, … , 7 and class c = 1, … , 4. Standard errors are shown in parentheses. Note that the fitted values ${\widehat{\mu }}_{ij}^c$ shown here correspond to the right-hand panel of Figure 5. Values of estimates ${\widehat{\pi }}_c$ and associated standard errors are also shown for each class.

Parameter	Class 1	Class 2	Class 3	Class 4
${\mu }_{i1}^c$	0.84 (0.43)	2.42 (0.56)	4.10 (0.22)	2.06 (0.16)
${\mu }_{i2}^c$	0.65 (0.48)	2.00 (0.52)	4.01 (0.21)	1.60 (0.23)
${\mu }_{i3}^c$	0.56 (0.36)	1.79 (0.37)	4.18 (0.22)	1.84 (0.13)
${\mu }_{i4}^c$	1.24 (1.11)	2.14 (0.58)	6.13 (0.29)	3.06 (0.71)
${\mu }_{i5}^c$	1.23 (0.65)	2.14 (0.30)	6.75 (0.30)	4.46 (0.61)
${\mu }_{i6}^c$	0.86 (0.48)	0.64 (0.06)	1.72 (0.17)	2.41 (0.19)
${\mu }_{i7}^c$	0.91 (0.29)	0.67 (0.07)	1.83 (0.12)	2.09 (0.15)
${\pi }_c$	0.31 (0.06)	0.29 (0.05)	0.24 (0.03)	0.17 (0.10)

Under models from developmental psychopathology for conduct problems and antisocial behavior², “normative”, “adolescent onset”, and “life course persistent” groups have been posited and empirically verified in various studies. These correspond to our fitted Classes 1, 3, and 4. It has, however, always been recognized that there is a “fourth group” not fitting into those categories. In this analysis, that fourth group is Class 2, which has persistent, but mild and not-impairing levels of behavioral problems. Some have posited a “child limited” category (similar to Class 2 in Figure 1), and we did not find such a group here.

6.2 |. Model Validation and Diagnostics

Additional variables in the CNLSY such as gender and criminal history allow us to examine associations between these variables and the latent classes identified by the four-class solution. Because this is an analysis relevant to the domain area of developmental psychopathology, these associations are critical for substantive validation of the four extracted classes. To investigate these associations, we randomly assigned each subject to one of the four identified classes using the estimated posterior probabilities of class membership, and cross-tabulated these assignments with other variables in the CNLSY. Table 2 displays a weighted contingency table of the random class assignment and maternal age at birth (< 20 years old, or ≥ 20 years old) only for male subjects; the resulting frequencies seem to support the validity of the four identified classes as the proportion of subjects in Classes 1 or 2 with maternal age ≥ 20 is considerably higher than the proportion of subjects in Classes 1 or 2 with maternal age < 20. Table 2 also shows a weighted cross tabulation of class assignment and of ever being convicted of a crime between ages 14 − 18, and, as demonstrated by this contingency table, the prevalence of criminal outcomes in Classes 3 and 4 is substantially higher than in Classes 1 and 2. Moreover, the frequency of criminal outcomes in those assigned to Class 4 is considerably greater than that of the other three classes.

TABLE 2.

Weighted cross-tabulation of random class assignment and maternal age at the birth of the child using only male subjects, and weighted cross-tabulation of class assignment and of ever being convicted of a crime during ages 14 − 18 using only male subjects. The class assignments were obtained by using the estimated posterior probabilities to randomly assign each subject to one of the four latent classes. The random assignment procedure was repeated 1, 000 times, and the results were averaged. In the top table, we display in parentheses class proportions conditional on maternal age while in the bottom table we show conviction proportions conditional on class.

	Class 1	Class 2	Class 3	Class 4
maternal age < 20	34.2 (0.178)	44.8 (0.233)	40.2 (0.209)	73.1 (0.380)
maternal age ≥ 20	968.7 (0.284)	941.7 (0.276)	581.7 (0.171)	917.6 (0.269)
	Class 1	Class 2	Class 3	Class 4
ever convicted-yes	18.7 (0.031)	16.5 (0.025)	42.6 (0.105)	102.9 (0.144)
ever convicted-no	588.0 (0.969)	646.8 (0.975)	363.1 (0.895)	609.4 (0.856)

While there is a variety of aspects of the model we could assess, our main interest here lies in using diagnostics to check whether our specification of the class-specific distribution is reasonable. In particular, we are especially interested in examining whether the assumed class-specific correlation structure $\text{corr}(y_{ik},y_{ij}|Z_i=c)={\alpha }_c^{|k-j|}$ appears to hold in the CNLSY data. If the class labels were known, we could check the class-specific correlation structure by directly stratifying subjects into their respective classes and computing the desired correlations. We mimic this process by using each subject’s estimated posterior probabilities to randomly assign each subject to one of the latent classes. Such a diagnostic approach, where class-specific quantities are checked by sampling from the estimated posterior probabilities, is justified by the diagnostic procedure described by Bandeen-Roche et al.²² As shown in that paper, this procedure is valid for detecting departures from the model if the assumed latent class model is indeed false.

Estimated autocorrelation functions obtained from the random stratification procedure described above are displayed in Figure 6 with the same class labels as used in Figure 5. For each random stratification, we used the subject-specific sampling weights to compute weighted estimates of the autocorrelation and then averaged the results from 1, 000 replications of this random stratification process. The autocorrelation plots in Figure 5 show that the AR(1) structure seems plausible for the CNLSY data in that the class-specific correlations decay substantially over time. However, for most classes, the correlations do not seem to decay quite as quickly as would occur under an AR(1) assumption. A similar diagnostic plot for the scale parameters ϕ_c shown in the supporting material suggests that the assumption of constant class-specific overdispersion over time is quite reasonable.

FIGURE 6.

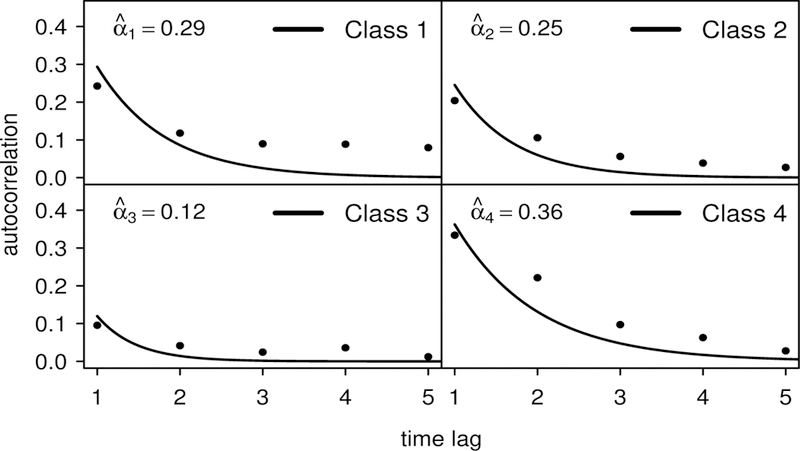
ECNLSY data: estimated class-specific autocorrelation functions and sample autocorrelation values (weighted) obtained by using the estimated posterior probabilities of class membership to randomly assign each subject to one of the four latent classes. The random assignment procedure was repeated 1, 000 times; the displayed autocorrelation values (i.e., the points in the figure) represent the average autocorrelation values from these replications. The solid lines represent the estimated class-specific estimated AR(1) autocorrelation functions from the four-class model.

7 |. DISCUSSION

We have presented a method for performing a latent class analysis on longitudinal count data. The motivation behind this work has been to express many of the core features of latent class models or growth mixture models in a straightforward, computationally tractable framework that will improve computational performance and model identifiability and that will perform well even if the true data generating mechanism is the popular growth mixture model. The autoregressive structure used in our model serves both as a natural way to model dependence over time and to achieve clearer separation of correlation due to the repeated-measurements structure and correlation due to the latent class structure.

In terms of computation, one of the chief advantages of this approach is the availability of the subject-specific likelihood in closed form; this simplifies computation considerably at least when compared with procedures that employ random effects and which require the use of numerical integration procedures within each class. In addition, because computational efficiency has been a primary motivation, we outlined an approximate EM approach which we found to be especially useful in this setting. Because our approximate EM algorithm relies on solving a series of weighted generalized estimating equations, our approach could be directly extended to handle other correlation structures. In any such extension, one would still need to specify a class-specific likelihood function in order to compute the weights used in the estimating equations defined in (3). For example, as an alternative to the INAR(1)-NB model, one could use one of the INAR(p) processes described by Pedeli et al.²³ to compute posterior probabilities of class membership and, within each EM iteration, solve weighted GEEs that have an assumed AR(p) correlation structure.

We also have utilized novel notions of class separation inherent in the data and of a given modeling procedure to recover that level of discrimination. Based on model classification indices such as those used in classification regression models, the oracle-based CSI quantifies the degree to which the information in the data can correctly classify subjects given the correct model and parameters. In this paper, we have used the CSI as a way of judging the difficulty of recovering class-specific trajectories. Though not fully explored here, this index of class separation could be further used to evaluate classification performance across a wider range of latent class models. Because the CSI may be computed for any number of alternative latent class models, comparing the CSI of an alternative latent class model with the empirical discrimination obtained from an assumed INAR(1)-NB model may serve as an effective check of the robustness of class assignment from the INAR(1)-NB model.

Supplementary Material

Supplement

Figure S1. Empirical discrimination (EED) vs. Class Separation Indices (CSI) for Scenarios I and II of the INAR(1)-NB model

Figure S2. Diagnostics for the overdispersion parameters

Table S1. Empirical discrimination (EED) vs. Class Separation Indices (CSI) for Scenarios I and II of the INAR(1)-NB model

Table S2. Diagnostics for the overdispersion parameters

Table S3. Values of regression coefficients in the main simulation scenarios

Table S4. Parameter values used for the Poisson-Normal simulations

A |. THE CLASS SEPARATION INDEX AND MEASURES OF DISCRIMINATION FOR MULTIPLE CLASSES

A.1 |. Class Separation Index

Let Y = (y₁, … , y_m ) denote all observed data and let A_C (Y) = [a₁(Y), … , a_m (Y)]^T be a procedure which maps data Y into an m × C matrix of nonnegative entries whose rows sum to one; the (i, c) entry of this matrix can be thought of as a reported probability that subject i belongs to class c. For instance, we could have A_C (Y) = W^C (Θ, π; Y), where W^C (Θ, π; Y) = [w^C (Θ, π; y₁), … , w^C (Θ, π; y_m )]^T denotes the m × C matrix whose i ^th row, w^C (Θ, π; y_i )^T, contains the posterior probabilities for subject i computed with the parameters (Θ, π). Alternatively, we could have A_C (Y) = V (η, Y), where V (η, Y) denotes a matrix of class membership probabilities computed under an incorrect working model with specified parameter η.

To measure how well a procedure A_C (Y) predicts class membership, we use a discrimination index D, which, given class labels Z = (Z₁, … ,Z_m), returns a score in [0, 1] such that D(Z, A_C(Y)) = 1 if A_C (Y) has a . in the correct cell for all observations (rows), and is less than or equal to one otherwise, and for any D (·, ·) considered, values closer to one imply better classification performance. The class separation index (CSI) is defined as

$$CSI=\underset{m\to \infty }{\lim }E\{D(\mathbf{Z},{\mathbf{W}}^C({\mathbf{\Theta }}_0,{\mathit{\pi }}_0;\mathbf{Y}))\},$$ (9)

provided that the above limit exists. where (Θ₀, π₀) denote the true parameter values and where the expectation is taken over Z_i and Y_i using the true parameter values.

Turning to finite samples, the realized or empirical discrimination resulting from using procedure A_C (Y) is D Z, A_C (Y) , and the expectation of this quantity is what we define to be the expected empirical discrimination (EED), namely

$$EED=E\{D(\mathbf{Z},A_C(\mathbf{Y}))\},$$ (10)

where the expectation in (10) is taken over (Z, Y) for a given sample size m, under the true data generating model.

A.2 |. Measures of Discrimination for Multiple Classes

Consider a two-category outcome. If we let Z_i ∈ {1, 2} denote the class labels and let ${\widehat{p}}_i(c)$ denote the reported probability that Z_i = c, c = 1, 2, the c-statistic C₁₂ is defined as

$$C_{12}(\mathbf{Z},\widehat{\mathbf{p}}(1),\widehat{\mathbf{p}}(2))=\frac{1}{N_1{N}_2}\left\{\sum _{i\in A_1}\sum _{j\in A_2}\left(1\{{\widehat{p}}_i(1)>{\widehat{p}}_j(1)\}+\frac{1}{2}1\{{\widehat{p}}_i(1)={\widehat{p}}_j(1)\}\right)\right\},$$ (11)

where A_c = {i : Z_i = c } is the set of subjects with class label c and $N_c={\sum }_{i=1}^{m}1\{Z_i=c\}$.

For a C -category outcome (C > 2), the all-pairwise c-statistic (APC_C ) is defined as

$${\text{APC}}_c={\left(\begin{array}{c}C\\ 2\end{array}\right)}^{-1}\sum _{k<j}{C}_{kj}(\mathbf{Z},\widehat{\mathbf{p}}(k),\widehat{\mathbf{p}}(j)),$$

where C_{k j} (·) is defined as in (11) and is computed using only subjects from classes k and j.

An alternative multi-class discrimination index is the polytomous discrimination index¹⁶ (PDI). To define the PDI, we first let ${\widehat{p}}_i=({\widehat{p}}_i(1),\dots ,{\widehat{p}}_i(C))$ denote the i ^th subject’s vector of predicted probabilities with ${\widehat{p}}_i(c)$ representing the predicted probability that subject i belongs to class c. Then, for a C -class model, the PDI is defined to be

$${\text{PDI}}_C=\frac{1}{C{N}_1\cdots N_C}\sum _{i_1\in A_1}\cdots \sum _{i_C\in A_C}\sum _{c=1}^C{g}_c({\widehat{\mathbf{p}}}_{i_1},\dots ,{\widehat{\mathbf{p}}}_{i_C}),$$ (12)

where A_c = {i : Z_i = c } is the set of subjects in class c and where $g_c({\widehat{\mathbf{p}}}_{i_1},\dots ,{\widehat{\mathbf{p}}}_{i_C})$ equals one if ${\widehat{p}}_{i_c}(c)>{\widehat{p}}_{i_j}(c)$ for all j ≠ c, and equals zero if there is a j* ≠ c such that ${\widehat{p}}_{i_c}(c)>{\widehat{p}}_{i_{j*}}(c)$. If $({\widehat{p}}_{i_C}(c),\dots ,{\widehat{p}}_{i_C}(c))$ does not contain a unique maximizer and ${\widehat{p}}_{i_c}(c)$ is one of those tied for the maximum value, then one sets $g_c({\widehat{\mathbf{p}}}_{i_1},\dots ,{\widehat{\mathbf{p}}}_{i_C})=1/t$, where t is the number of cases tied with ${\widehat{p}}_{i_c}(c)$. Unlike the all-pairwise c-statistic, a method producing predictions at random will generate a PDI value near 1/C (where C is the number of classes) rather than 0.5.