Detection of Shared Balancing Selection in the Absence of Trans-Species Polymorphism

Abstract

Trans-species polymorphism has been widely used as a key sign of long-term balancing selection across multiple species. However, such sites are often rare in the genome and could result from mutational processes or technical artifacts. Few methods are yet available to specifically detect footprints of trans-species balancing selection without using trans-species polymorphic sites. In this study, we develop summary- and model-based approaches that are each specifically tailored to uncover regions of long-term balancing selection shared by a set of species by using genomic patterns of intraspecific polymorphism and interspecific fixed differences. We demonstrate that our trans-species statistics have substantially higher power than single-species approaches to detect footprints of trans-species balancing selection, and are robust to those that do not affect all tested species. We further apply our model-based methods to human and chimpanzee whole-genome sequencing data. In addition to the previously established major histocompatibility complex and malaria resistance-associated FREM3/GYPE regions, we also find outstanding genomic regions involved in barrier integrity and innate immunity, such as the GRIK1/CLDN17 intergenic region, and the SLC35F1 and ABCA13 genes. Our findings not only echo the significance of pathogen defense but also reveal novel candidates in maintaining balanced polymorphisms across human and chimpanzee lineages. Finally, we show that these trans-species statistics can be applied to and work well for an arbitrary number of species, and integrate them into open-source software packages for ease of use by the scientific community.

Introduction

Balancing selection is an evolutionary mechanism for maintaining diversity within populations (Charlesworth 2006). A number of different modes of balancing selection exist, such as heterozygote advantage (Charlesworth 2006), pleiotropy (Johnston et al. 2013), negative frequency-dependent selection (Mitchell-Olds et al. 2007), environmental fluctuations (Bergland et al. 2014), and segregation distortion balanced by negative selection (Ubeda and Haig 2004; Charlesworth B and Charlesworth D 2010). Though these different modes vary in how they maintain polymorphism over long periods of time, they all leave behind similar genomic signatures of increased density of polymorphic sites nearby a balanced polymorphism, and often an enrichment of middle-frequency alleles in a narrow window surrounding the selected locus (Charlesworth 2006). These characteristic footprints have been utilized by a number of statistical approaches for detecting long-term balancing selection (e.g., Hudson et al. 1987; Tajima 1989; Andrés et al. 2009; Leffler et al. 2013; DeGiorgio et al. 2014; Gao et al. 2015; Hunter-Zinck and Clark 2015; Sheehan and Song 2016; Siewert and Voight 2017; Bitarello et al. 2018).

However, until recently, the availability of methods for detecting long-term balancing selection has been limited, and the most commonly used approaches were the Hudson–Kreitman–Aguadé (HKA; Hudson et al. 1987) and Tajima’s D (Tajima 1989) statistics. While the HKA statistic captures increases in polymorphism density, it does not consider allele frequency information, and therefore cannot sense the enrichment of intermediate-frequency alleles. On the other hand, Tajima’s D measures the distortion of the allele frequency spectrum from the expectation under a constant size neutrally evolving population, and has the ability to identify the footprint of an increased number of middle-frequency alleles in a genomic region. However, as it does not require an outgroup to call substitutions, Tajima’s D ignores information on changes in the density of polymorphism nearby a selected site. Despite the frequent application of these two statistics, neither is specifically designed for long-term balancing selection, and both have been shown to have limited power under such scenarios (DeGiorgio et al. 2014; Siewert and Voight 2017; Bitarello et al. 2018).

There has been a recent surge in the development of methods for specifically identifying signatures of long-term balancing selection (DeGiorgio et al. 2014; Gao et al. 2015; Siewert and Voight 2017; Bitarello et al. 2018). Based on the Kaplan–Darden–Hudson model (Hudson and Kaplan 1988;Kaplan et al. 1988), DeGiorgio et al. (2014) presented a mechanism to compute probabilities of polymorphism and substitution under long-term balancing selection, and developed the likelihood ratio test statistics T₁ and T₂. The latter statistic uses both polymorphism density and allele frequency information, and exhibits higher power than a number of methods (DeGiorgio et al. 2014; Siewert and Voight 2017). Complementary to model-based methods, whose high power partly relies on sophisticated data, novel summary statistics have also recently been developed for detecting long-term balancing selection. Notably, two new summary statistics, β (Siewert and Voight 2017) and noncentral deviation (NCD; Bitarello et al. 2018), have been proposed to capture departures of allele frequencies in a genomic window from a certain equilibrium frequency, and both have been demonstrated to outperform the HKA and Tajima’s D statistics. Moreover, β, which adopts a formulation similar to Tajima’s D, regards the equilibrium frequency as that of the polymorphic site that a window is centered on, whereas NCD takes a user-assigned value. Further, while β does not benefit much from incorporating sites of substitution (Siewert and Voight 2017), Bitarello et al. (2018) have shown that NCD exhibits substantially higher power and outperforms β when substitutions are provided in addition to polymorphisms.

However, while several key examples (Klein et al. 1998; Ségurel et al. 2012; Leffler et al. 2013; Teixeira et al. 2015) have illustrated that it is possible and potentially common for long-term balancing selection to be established prior to speciation events, few extant approaches address the issue of identifying loci under balancing selection shared by multiple species via genome-wide scans. Traditionally, polymorphisms shared across species have been used in many studies as a tell-tale sign of shared long-term balancing selection (e.g., Takahata et al. 1992; Klein et al. 1998; Cho et al. 2006; Ségurel et al. 2012; Leffler et al. 2013), as they are highly suggestive of its footprints (Wiuf et al. 2004). However, such coincident (i.e., trans-species) polymorphisms can also result from high mutation rates or technical artifacts introduced in sequencing and mapping. Gao et al. (2015) addressed this issue by deriving, under the Kaplan–Darden–Hudson model, the length of the balanced ancestral segment, the expected number of trans-species polymorphisms, as well as the extent of linkage disequilibrium between such polymorphisms. Although powerful, this framework is difficult to extend to an arbitrary number of species, and also requires that such trans-species polymorphisms are not missing from the data set due to sampling or filtering. To circumvent some of these hurdles, it would be useful to be able to uncover footprints of ancient trans-species balancing selection by only using between-species substitutions and within-species polymorphisms, rather than trans-species polymorphisms.

In this study, we present a number of summary- and model-based approaches for detecting ancient trans-species balancing selection that do not rely on trans-species polymorphisms. In particular, we adapted the framework of DeGiorgio et al. (2014) to construct likelihood ratio test statistics, $T_{1,\text{trans}}$ and $T_{2,\text{trans}}$, to detect trans-species balancing selection (see Theory and supplementary note 5, Supplementary Material online). Moreover, we modified the HKA test so as to better accommodate genomic data of multiple species (denoted as HKA_trans; see supplementary note 1, Supplementary Material online), and extended the NCD statistic to NCD_trans (see supplementary note 2, Supplementary Material online) for application on multispecies data. Note that although the β statistic has been demonstrated to perform well in detecting ancient balancing selection in single species, it does not benefit from the inclusion of substitutions (as shown by Siewert and Voight 2017), which can be highly informative when analyzing population-scale genomic data of multiple species. We therefore chose to only consider single- and trans-species variants of T₁, T₂, HKA (summary statistic analog to T₁), and NCD (summary statistic analog to T₂). We performed extensive simulations to evaluate the performances of these methods and addressed a variety of confounding factors, such as recent population size changes, inaccurate recombination maps, elevated mutation rates, convergent balancing selection, and window size used to compute each statistic. Next, we applied the model-based $T_{2,\text{trans}}$ statistic to whole-genome human and chimpanzee data to gain insights on ancient balancing selection affecting these lineages. Further, so that these multispecies statistics can be readily applied by the scientific community, we implemented the model-based and summary statistic approaches into new software packages MULLET (MULti-species LikElihood Tests) and MuteBaSS (MUlTi-spEcies BAlancing Selection Summaries), respectively.

Theory

Given a sample of n lineages, the equilibrium frequency x of a balanced polymorphism, and population-scaled recombination rate $\rho =2Nr$ between a focal neutral site and a putative selected site, DeGiorgio et al. (2014) demonstrated how the expected tree height $H(n,x,\rho )$ and expected tree length $L(n,x,\rho )$ of a neutral genealogy linked to a site under strong balancing selection can be efficiently calculated. These quantities can be utilized to identify genomic segments undergoing ancient balancing selection by using polymorphism and divergence data in a pair of species.

Detecting Trans-Species Balancing Selection on Two Species

Consider polymorphism data from a pair of species, 1 and 2, in which we have obtained sites that are polymorphic only in species 1, polymorphic only in species 2, and substitutions (fixed differences) between the species. Suppose that at a site in the genome, the number of lineages sampled from species 1 is n₁ and the number from species 2 is n₂. Denote the collection of sample sizes for the two species at a locus by $\mathbf{n}=[n_1,n_2]$. Further, suppose that by using genome-wide data, the estimated coalescence time between the two species is $\widehat{C}$. Assuming a site is ρ recombination units from a site with alleles maintained at frequencies x and $1-x$ through strong balancing selection, analogous to the computations of DeGiorgio et al. (2014), the probability (fig. 1) of observing a polymorphic site only in species k, k = 1 or 2, is

$$p_k(\mathbf{n},\rho ,x)=\frac{L(n_k,x,\rho )}{2\widehat{C}-H(n_1,x,\rho )-H(n_2,x,\rho )+L(n_1,x,\rho )+L(n_2,x,\rho )}$$

and the probability of observing a substitution between the species is

$$s(\mathbf{n},\rho ,x)=\frac{2\widehat{C}-H(n_1,x,\rho )-H(n_2,x,\rho )}{2\widehat{C}-H(n_1,x,\rho )-H(n_2,x,\rho )+L(n_1,x,\rho )+L(n_2,x,\rho )}.$$

Note that $s(\mathbf{n},\rho ,x)=1-p_1(\mathbf{n},\rho ,x)-p_2(\mathbf{n},\rho ,x)$, and that our model assumes that species 1 and 2 are reciprocally monophyletic.

Fig. 1.

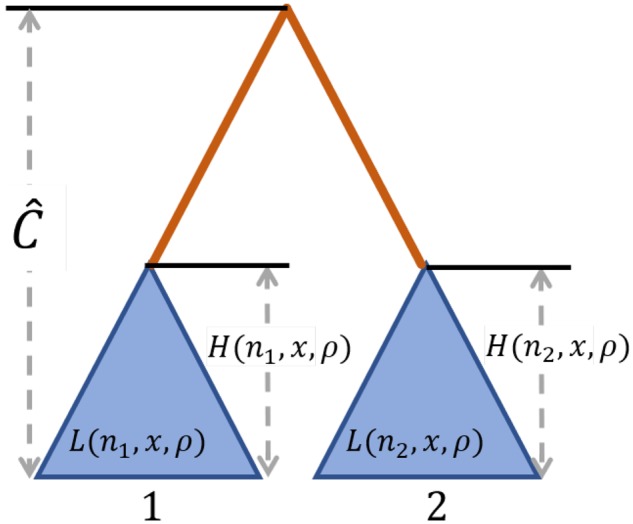
Schematic of the procedure for computing probabilities of polymorphism and substitution for a pair of species, under a model of long-term balancing selection. Blue triangles represent the subtrees of the neutral genealogy comprised all sampled lineages for each species, where within-species polymorphic sites are generated. The orange line, which has length $2\widehat{C}-H(n_1,x,\rho )-H(n_2,x,\rho )$, represents the length of the branch separating the two species, where substitutions are generated. $\widehat{C}$ denotes the estimated expected coalescence time between species 1 and 2. $H(n,x,\rho )$ is the expected height of the subtree for a site with n alleles observed that is ρ population-scaled recombination units from a site undergoing long-term balancing selection and maintaining alleles at frequencies x and $1-x$. $L(n,x,\rho )$ is the expected length of this subtree.

A Composite Likelihood Ratio Test

We can use these probabilities of polymorphism and substitution to create a likelihood ratio test for detecting trans-species balancing selection. Consider a genomic window containing I informative sites, where an informative site is a polymorphism only in species 1, a polymorphism only in species 2, or a substitution. Let the sample sizes in species 1 and 2 at site i, $i=1,2,\dots ,I$, be $n_{i1}$ and $n_{i2}$, respectively. Further, suppose the derived allele counts in species 1 and 2 at site i are $a_{i1}$ and $a_{i2}$, respectively. Moreover, assume site i is ρ_i recombination units from a site that we believe to be undergoing strong balancing selection, maintaining a pair of alleles at frequencies x and $1-x$ in the population. We call this site under selection our test site. Assuming that ${\mathbf{n}}_i=[n_{i1},n_{i2}]$ and ${\mathbf{a}}_i=[a_{i1},a_{i2}]$, we define the vectors $\mathbf{N}=[{\mathbf{n}}_1,{\mathbf{n}}_2,\dots ,{\mathbf{n}}_I],\hspace{0.17em}\mathbf{A}=[{\mathbf{a}}_1,{\mathbf{a}}_2,\dots ,{\mathbf{a}}_I]$, and $\mathit{\rho }=[{\rho }_1,{\rho }_2,\dots ,{\rho }_I]$ for convenience. Under the alternative hypothesis of balancing selection, the composite likelihood that the test site is undergoing strong long-term balancing selection is

$${\mathcal{L}}_1(\mathbf{N},\mathit{\rho },x;\mathbf{A})=\prod _{i=1}^I[s({\mathbf{n}}_i,{\rho }_i,x)1_{\{{\mathbf{a}}_i=n_{i1}{\mathbf{e}}_1\vee {\mathbf{a}}_i=n_{i2}{\mathbf{e}}_2\}}+\sum _{k=1}^2{p}_k({\mathbf{n}}_i,{\rho }_i,x)\sum _{j=1}^{n_{ik}-1}{1}_{\{{\mathbf{a}}_i=j{\mathbf{e}}_k\}}],$$

where ${\mathbf{e}}_k$ is the 2D standard basis vector in which all elements are 0 except for the kth element, which is 1. This likelihood function is maximized at $\widehat{x}=\underset{x\in (0,1)}{\text{arg max}}{\mathcal{L}}_1(\mathbf{N},\mathit{\rho },x;\mathbf{A})$.

If we condition only on informative sites, then denote the proportion of such sites across the genome that are polymorphic only in species k with derived allele count a, $0<a<n_k$, by ${\widehat{p}}_k(\mathbf{n},a)$, and the proportion of such sites that are substitutions between the species by $\widehat{s}(\mathbf{n})$. From these definitions, it follows that the proportion of informative sites that are polymorphic only in species k is ${\widehat{p}}_k(\mathbf{n})={\sum }_{a=1}^{n_k-1}{\widehat{p}}_k(\mathbf{n},a)$. Under the null hypothesis of neutrality, the composite likelihood that the test site is evolving neutrally is

$${\mathcal{L}}_0(\mathbf{N};\mathbf{A})=\prod _{i=1}^I[\widehat{s}({\mathbf{n}}_i)1_{\{{\mathbf{a}}_i=n_{i1}{\mathbf{e}}_1\vee {\mathbf{a}}_i=n_{i2}{\mathbf{e}}_2\}}+\sum _{k=1}^2{\widehat{p}}_k({\mathbf{n}}_i)\sum _{j=1}^{n_{ik}-1}{1}_{\{{\mathbf{a}}_i=j{\mathbf{e}}_k\}}].$$

Based on the likelihoods under the null hypothesis of neutrality and the alternative hypothesis of trans-species balancing selection, we can compute a log composite likelihood ratio test statistic that the test site is undergoing strong long-term trans-species balancing selection as

$$T_{1,\text{trans}}=2\{\ln {\mathcal{L}}_1(\mathbf{N},\mathit{\rho },\widehat{x};\mathbf{A})-\ln {\mathcal{L}}_0(\mathbf{N};\mathbf{A})\}.$$

A Composite Likelihood Ratio Test Using the Allele Frequency Distribution

DeGiorgio et al. (2014) demonstrated that such composite likelihood approaches can exhibit greater power if information on the frequency spectrum is used in addition to information on the proportions of polymorphisms and substitutions in a genomic region. For a sample of n alleles, conditioning on a mutation leading to a polymorphic site and assuming a locus undergoing strong balancing selection maintaining a pair of alleles at frequencies x and $1-x$, the probability under the Kaplan–Darden–Hudson model (Hudson and Kaplan 1988; Kaplan et al. 1988) of observing a derived allele with count a, $0<a<n$, at a neutral locus ρ recombination units away from the selected site is $f(n,a,\rho ,x)$. Calculating $f(n,a,\rho ,x)$ analytically is nontrivial, and we instead utilize a set of frequency spectra simulated under the Kaplan–Darden–Hudson model as in DeGiorgio et al. (2014). Using the knowledge of this distribution of allele frequencies, we can modify the likelihood under the alternative hypothesis of trans-species balancing selection by including information on the frequency spectrum as

$${\mathcal{L}}_1(\mathbf{N},\mathit{\rho },x;\mathbf{A})=\prod _{i=1}^I[s({\mathbf{n}}_i,{\rho }_i,x)1_{\{{\mathbf{a}}_i=n_{i1}{\mathbf{e}}_1\vee {\mathbf{a}}_i=n_{i2}{\mathbf{e}}_2\}}+\sum _{k=1}^2{p}_k({\mathbf{n}}_i,{\rho }_i,x)\sum _{j=1}^{n_{ik}-1}f(n_{ik},j,{\rho }_i,x)1_{\{{\mathbf{a}}_i=j{\mathbf{e}}_k\}}],$$

which is maximized at $\widehat{x}=\underset{x\in (0,1)}{\text{arg max}}{\mathcal{L}}_1(\mathbf{N},\mathit{\rho },x;\mathbf{A})$.

Analogous to the case without the distribution of allele frequencies, under the null hypothesis of neutrality, the composite likelihood that the test site is evolving neutrally is

$${\mathcal{L}}_0(\mathbf{N};\mathbf{A})=\prod _{i=1}^I[\widehat{s}({\mathbf{n}}_i)1_{\{{\mathbf{a}}_i=n_{i1}{\mathbf{e}}_1\vee {\mathbf{a}}_i=n_{i2}{\mathbf{e}}_2\}}+\sum _{k=1}^2\sum _{j=1}^{n_{ik}-1}{\widehat{p}}_k({\mathbf{n}}_i,j)1_{\{{\mathbf{a}}_i=j{\mathbf{e}}_k\}}].$$

Based on the likelihoods under the null hypothesis of neutrality and the alternative hypothesis of trans-species balancing selection, we can compute a log composite likelihood ratio test statistic that the test site is undergoing strong long-term trans-species balancing selection as

$$T_{2,\text{trans}}=2\{\ln {\mathcal{L}}_1(\mathbf{N},\mathit{\rho },\widehat{x};\mathbf{A})-\ln {\mathcal{L}}_0(\mathbf{N};\mathbf{A})\}.$$

Results

To evaluate the performances of both extant and novel methods for detecting long-term balancing selection, we chose to consider statistics that operate on the same set of informative sites, which are comprised of within-species polymorphisms and cross-species substitutions. Specifically, we considered single- and trans-species variants of T₁ and its summary statistic analog HKA (see supplementary note 1, Supplementary Material online), as well as T₂ and its summary statistic analog NCD (see supplementary note 2, Supplementary Material online). Considering there are eight different statistics to compare, hereafter we will refer to those designed for two or more species as “trans-species methods,” and the original variants as “single-species methods.” For empirical application, we applied the trans-species variant of the T₂ statistic ($T_{2,\text{trans}}$) to whole-genome data from humans (1000 Genomes Project Consortium 2015) and chimpanzees (Auton et al. 2012) to examine ancient balancing selection affecting both great ape species.

Evaluating Method Performance on Simulated Data

We employed the forward-time simulator SLiM (Messer 2013) to generate sequences of length 50 kilobases (kb) evolving along a three-species phylogeny (fig. 2; see Materials and Methods), under diverse selection scenarios with varying selection strength (s), dominance parameter (h), and selected allele age, as well as confounding factors such as population size changes, skewed recombination rates, and elevated mutation rates. Because footprints of ancient balancing selection are typically narrow (Hudson and Kaplan 1988; Charlesworth 2006; Leffler et al. 2013; Siewert and Voight 2017), and considering that summary statistics for detecting such footprints often reach optimal performances when utilizing data from neighboring regions of similar length, we adopted a window size of 1 kb for single- and trans-species variants of HKA and NCD when applying them on simulated data to optimize their performances (see supplementary fig. S1, Supplementary Material online, for their performances using window sizes of 0.5, 1, 1.5, 2, 2.5, and 3 kb). In particular, the footprints of long-term balancing is in theory $1/(4N_{\mathrm{e}}r)$, which equals 2.5 kb when assuming a recombination rate of $r={10}^{-8}$ per site per generation and an effective population size of $N_{\mathrm{e}}={10}^4$. To ensure 1 kb is indeed a better choice of window size than 2.5 kb, we tested and compared their power for detecting balance selection of varying age under three distinct demographic models (fig. 2 and supplementary fig. S2, Supplementary Material online, for methods using 1- and 2.5-kb windows, respectively). To match the amount of data available at each step (e.g., DeGiorgio et al. 2014; Siewert and Voight 2017), we performed scans with the T₁ and T₂ variants with ten informative sites on either side of the test site (see supplementary note 3, Supplementary Material online).

Fig. 2.

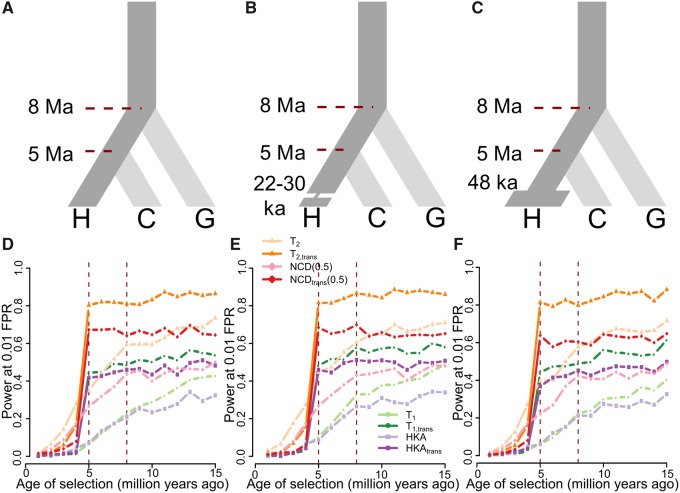
Performances of single- and trans-species variants of HKA, NCD(0.5), T₁, and T₂. (A–C) Schematic of demographic models relating three species, representing human (species H), chimpanzee (species C), and gorilla (species G), adopted in simulations. (A) All three species maintain constant population size of $N={10}^4$ diploid individuals, with species H diverging from species C 5 million years ago (Ma), and the common ancestor of species H and C diverging from species G 8 Ma. (B) Species H went through a 400-generation population bottleneck with size N_b = 550 diploids 22–30 thousand years ago (ka). (C) Species H doubled its population size to $N_{\mathrm{e}}=2\times {10}^4$ diploids 48 ka. Simulations assumed a generation time of 20 years across the entire phylogeny. (D–F) Powers at a 1% FPR of single- and trans-species variants of HKA, NCD(0.5), T₁, and T₂ to detect balancing selection (s = 0.01 with h = 100) of varying age under (D) constant population size, (E) recent strong population bottleneck, and (F) recent population expansion scenarios. Red vertical dashed lines represent the times at which species H and C split, and at which species G split, respectively.

High Power of Trans-Species Methods for Detecting Shared Balancing Selection

To assess the performance of each method in detecting balancing selection of varying age, we first modeled heterozygote advantage with selective coefficient s = 0.01 and dominance coefficient h = 100 at a genomic position, with the selected allele introduced at varying time points along the branch ancestral to species H under a demographic history of constant population size (fig. 2A). We then evaluated the powers at a 1% false positive rate (FPR) for each method. All single-species methods gain power with increasing age at which the selected allele was introduced (fig. 2D). For example, the power of T₂ for detecting balancing selection has increased from almost zero to over 0.7 when the age of selection increased from 1 to 15 million years (My). Meanwhile, all trans-species methods have minimal power to detect selection established after species H and C diverge, and exhibit a surge of power for balancing selection predating the species split (fig. 2D). This jump in power is both expected and sensible because trans-species methods take polymorphism data from both species into consideration, and the adaptive changes in only one of the two should not be conspicuous enough for trans-species methods. Additionally, when balancing selection was established prior to species divergence, all trans-species methods show higher power than methods designed for single species, likely due to the greater amount of information used in their inferences.

For methods designed to operate on the same number of species, their relative performances follow similar orders. Both only utilizing polymorphism density data, the HKA and T₁ variants show comparable powers (fig. 2D). Integrating allele frequency information in addition to polymorphism density data, both T₂ and NCD variants outperform the T₁ and HKA variants. Moreover, the T₂ variants exhibit substantially higher power than the NCD variants, which is sensible given that T statistics are based on an explicit model and take distances between informative sites and the test site into consideration. The superior performance of T₂ variants over other approaches remains consistent across varying selection strengths s and dominance coefficients h (supplementary fig. S3A, D, and G, Supplementary Material online), and both display decreased power as selective advantage of heterozygotes (i.e., composite parameter hs) decreases. T₁ and HKA still have similar powers, and both perform better when hs decreases. Meanwhile, the close margin between the HKA and T₁ variants is probably because HKA and HKA_trans were given optimal window sizes, whereas T₁ and $T_{1,\text{trans}}$ may be able to effectively use information outside of the window size it was given. When the window size increases (supplementary fig. S4, Supplementary Material online), T₁ variants exhibit higher power than HKA variants.

Recent collapses or expansions in population size can also affect the allele frequency spectrum, as well as polymorphism density, and therefore potentially confound inferences of balancing selection. To test the robustness of each method to recent population size changes, we simulated models with a recent bottleneck (fig. 2B) or expansion (fig. 2C), using parameters inferred by Lohmueller et al. (2009) (see Materials and Methods). We first tested the robustness of each statistic to falsely attributing effects of population bottlenecks or expansions as footprints of balancing selection (supplementary fig. S5, Supplementary Material online). These results illustrate that all methods are robust to neutral regions that are affected by strong recent bottlenecks (supplementary fig. S5A, Supplementary Material online) and by recent expansions (supplementary fig. S5B, Supplementary Material online). When species H underwent a recent bottleneck (fig. 2E) or expansion (fig. 2F), we observed that all trans-species methods still maintain high power to detect balancing selection whose onset predated the species divergence, outperforming their single-species counterparts. Moreover, their specificity for trans-species balancing selection also remained unaltered, and these properties also persist across different selection parameters (supplementary fig. S3, Supplementary Material online).

Distinguishing Ancestral and Convergent Balancing Selection

The trans-species statistics we developed for shared balancing selection evaluate whether there exists an increased density of polymorphic sites, an enrichment of middle-frequency alleles at polymorphic sites, or both, and whether this pattern is shared across the species examined. Because they do not directly address whether balancing selection on a candidate site predates speciation as would that of Gao et al. (2015), the statistics may be sensitive to shared, nonancestral (i.e., convergent) balancing selection.

To test whether our trans-species methods can distinguish ancestral from convergent balancing selection, we simulated three scenarios in which a mutation under selection (s = 0.01 with h = 100) was introduced in one species (supplementary fig. S6A and D, Supplementary Material online), two selected mutations were introduced independently in both sister species at the same site (supplementary fig. S6B and E, Supplementary Material online), and two selected mutations were introduced independently in both sister species but at different sites that are 10 kb apart (supplementary fig. S6C and F, Supplementary Material online). Unsurprisingly, all trans-species statistics exhibit substantially higher power than single-species statistics when the balanced alleles independently arose in both species at the same site (supplementary fig. S6B and E, Supplementary Material online), compared with when only one species was affected (supplementary fig. S6A and D, Supplementary Material online). This result suggests that convergent balancing selection can indeed leave similar footprints as ancestral balancing selection, provided it is old enough (4 My, or $2\times {10}^5$ generations in our simulations), and acts on the same site in both species.

Nonetheless, when balancing selection in two species occurred instead at two nearby sites, the trans-species statistics (supplementary fig. S6C and F, Supplementary Material online) show only moderate increases in power to falsely identify this convergent process as ancestral, and perform no better than the single-species variants. This robustness is sensible because long-term balancing selection leaves a small footprint in the genome (Hudson et al. 1987; Charlesworth 2006; Siewert and Voight 2017; Bitarello et al. 2018), such that the footprints around sites that are relatively close in the genome would still be unlikely to overlap and confound our trans-species methods. These results suggest that balancing selection acting on distinct sites has limited misleading effects for trans-species methods, provided the distance between these sites is larger than the expected long-term balancing selection footprint. Further, in situations where the distance between selected sites is smaller than the selection footprint, the biological mechanisms leading to their maintenance of polymorphisms are likely similar.

Effect of Error in Recombination Rate Estimation

In addition to the improved power of trans-species methods to detect ancient balancing selection, we have demonstrated the superior specificity and robustness of the model-based T₂ statistics, especially $T_{2,\text{trans}}$. Nonetheless, other nonadaptive events, such as skewed recombination rates or inaccurate recombination maps, may potentially interfere with the detection of long-term balancing selection, and perhaps have a more deleterious impact on the model-based T statistics that rely on estimates of recombination rates. To examine method robustness to skewed recombination rates, we generated 50-kb-long sequences under models of unevenly distributed recombination rates fluctuating every 1 kb along the sequence, and we considered fluctuations of two different orders of magnitude. Specifically, assuming a recombination rate of $r={10}^{-8}$ per site per generation under our earlier scenarios of a uniform recombination map, we set recombination rate to alternate along the sequence from 10r to $r/10$ (10²-fold change between adjacent regions; supplementary fig. S7A and C, Supplementary Material online) or from 100r to $r/100$ (10⁴-fold change between adjacent regions; supplementary fig. S7B and D, Supplementary Material online). With the correctly informed coalescence time, polymorphism-to-substitution ratio, and derived allele frequency spectra, we applied all methods on the simulated sequences, and let T statistics assume a uniform and constant recombination rate of $\rho =2N_{e}r$, as they do in all other simulation scenarios. Providing T statistics with such an erroneous recombination map permits us to evaluate the robustness of these statistics when the recombination rates are grossly misspecified.

All methods are robust to falsely identifying neutrally evolving regions with massive fluctuations in recombination rate as balancing selection (supplementary fig. S7A and B, Supplementary Material online). Furthermore, for sequences with recombination rate fluctuating by 10⁴-fold (supplementary fig. S7B, Supplementary Material online), the proportion of false signals for each method further decreases, most outstandingly for T₂ and $T_{2,\text{trans}}$. On the other hand, when an allele under balancing selection (s = 0.01 with h = 100) was introduced in the ancestral population 15 Ma, all methods show increased power when recombination rate fluctuates by 10²-fold (supplementary fig. S7C and E, Supplementary Material online). When the rate fluctuates by 10⁴-fold (supplementary fig. S7D, Supplementary Material online), all single-species methods show compromised power compared with those under 10²-fold change (supplementary fig. S7D and E, Supplementary Material online). However, single- and trans-species variants of both polymorphism density-based methods, T₁ and HKA, exhibit improved power under skewed recombination maps compared with those under a uniform map, whereas variants of methods that incorporate information on allele frequencies, T₂ and NCD, do not always gain power (supplementary fig. S7E, Supplementary Material online). Despite that $T_{2,\text{trans}}$ and NCD_trans both have marginally higher power under skewed recombination maps, the increase in power exhibited by $T_{1,\text{trans}}$ and HKA_trans was considerably greater. This discrepancy may be due to irregular recombination shifting the spatial distribution of polymorphic sites around a selected site, while exerting little influence on allele frequencies at these polymorphic sites.

Robustness to High Mutation Rate

Another nonadaptive phenomenon that may confound inferences of ancient balancing selection is the increase in mutation rate at a genomic region. To test the robustness of each method against elevated mutation rate, we simulated sequences neutrally evolving along the demographic history in figure 2A, and mutating at rates that are 5-, 10-, or 20-fold higher than the original rate of $\mu =2.5\times {10}^{-8}$ per site per generation. In addition to mutational hotspots shared across all species, we also considered the scenarios in which the hotspots are species-specific. To examine the robustness of each method to species-specific elevation of mutation rates, we simulated a set of scenarios in which sequences in species H (as labeled in fig. 2A) started to mutate at rate $5\mu ,\hspace{0.17em}10\mu$, or $20\mu$ after splitting from species C (see Materials and Methods). We then applied both single- and trans-species methods on these sequences with the same window sizes used in previous power analyses so as to mimic the effect of unexpected mutation hotspots. Note that for T statistics, we provided estimates of coalescence time, proportions of polymorphisms and substitutions, and site frequency spectra based on neutral data generated under the original mutation rate μ. Similarly, we provided the HKA statistics with proportions of polymorphisms and substitutions expected from neutral data simulated with the original mutation rate μ.

When mutation rates were elevated across all sequences along the phylogeny, most statistics exhibited elevated proportions of false signals (supplementary fig. S8, Supplementary Material online), with higher mutation rates leading to greater numbers of false signals. One exception is NCD, whose proportion of false signals at a 1% FPR remains substantially smaller than 0.01 for all scenarios with elevated mutation rates (supplementary fig. S8, Supplementary Material online). This robustness of NCD results from the increased number of informative sites incorporated in each window, which leads to smaller variance of NCD scores. Among the statistics that exhibited increased misidentification rates, T statistics (especially $T_{\text{trans}}$) reported lower proportions of false signals than others. Meanwhile, both single- and trans-species HKA statistics exhibit considerable proportions of false signals at a 1% FPR (supplementary fig. S8D–F, Supplementary Material online), even reaching 0.7 when the mutation rate elevated 20-fold (supplementary fig. S8F, Supplementary Material online), which is almost twice the misidentification rates of T₁ and T₂. Nonetheless, this inflation is sensible for HKA because its chi-square formulation (supplementary note 1, Supplementary Material online) accounts for the number of informative sites within the window (i.e., number of observations), and would yield larger values when more sites are considered. Further, because HKA was not specifically designed for detecting balancing selection, but rather to identify departures from expected numbers of polymorphisms and substitutions, it is natural that it should uncover regions with higher mutation rates.

When instead the mutation rate increased only in species H, we found that all single-species methods misidentified substantial proportions of such sequences as evolving under long-term balancing selection (supplementary fig. S9, Supplementary Material online). In particular, they showed considerably inflated misidentification rates compared with scenarios of mutation rates elevated uniformly across all species (supplementary fig. S8, Supplementary Material online), among which single-species variants of T₁ and HKA even reported over 90% false signals at a 1% FPR across all three elevated mutation rates considered. Meanwhile, although trans-species methods (except for ${\text{NCD}}_{\text{trans}}$) displayed considerable increases in proportions of false signals under species-specific accelerated mutation (supplementary fig. S9, Supplementary Material online) compared with those under uniformly elevated mutation rates (supplementary fig. S8, Supplementary Material online), this inflation in false signals was substantially less dramatic than for variants of single-species statistics. This higher robustness of trans-species relative to single-species methods is consistent with their behaviors under uniform mutation rate increases (supplementary fig. S8, Supplementary Material online).

Despite the large performance margin for each statistic between scenarios of shared and species-specific mutational hotspots, it is sensible that the latter would be more misleading, especially for T₁ and HKA. When the mutational process is only partially accelerated along the phylogenic tree relating multiple species, the accumulation of mutations along certain lineages can lead to elevated polymorphism-to-substitution ratios. Such distortions can be observed in our simulated sequences in species H (supplementary fig. S10, Supplementary Material online), which explains the drastic inflation of the false signals identified by T₁ and HKA (supplementary fig. S9, Supplementary Material online). Meanwhile, as expected, the allele frequency spectra are unaffected (supplementary fig. S10, Supplementary Material online), thereby providing advantage to methods, such as T₂ and NCD, that also employ information on allele frequencies. When data from both species are considered, however, the distortion in polymorphism density was ameliorated (supplementary fig. S11, Supplementary Material online), but the proportion of polymorphisms segregating in species H drastically increased as the species-specific mutation rate increased. Considering that the overall proportions of substitutions (supplementary fig. S11, Supplementary Material online) as well as allele frequency spectra remain relatively constant, this distortion in proportions of sites being polymorphic in species H makes it reasonable that trans-species methods identify more false signals than they would under uniformly high mutation rate, but are still much less affected by the species-specific mutational hotspot than were the single-species statistics. We further explore the reasons for the inflation of T statistic misidentification rates under scenarios of increased mutation rate in the Discussion section.

Effect of Window Size

For all extant methods to detect signatures of long-term balancing selection, the length of the genomic region considered (hereafter referred to as “window size”) when computing their scores could substantially impact their powers. In our study, we applied all summary statistics on windows with a fixed number of nucleotides, and T statistics with a fixed number of informative sites surrounding each test site. To best match the amount of data provided to T statistics, we set the number of informative sites flanking the test site on either side as I, such that $2I+1$ is closest to the expected number of sites included in a 1-kb region under neutrality given the simulation parameters (see supplementary note 3, Supplementary Material online). Because long-term balancing selection typically leaves behind narrow genomic footprints, that is, of length ∼$1/(4N_{e}r)$, where r is the per-site per-generation recombination rate (Hudson and Kaplan 1988), extant methods often reach optimal power when the window size is of the same magnitude of this size, which in humans is ∼2.5 kb, given an effective size of $N={10}^4$ and $r={10}^{-8}$. To choose the optimal window size for our analyses on simulated data, we examined the relative performances of summary statistics under 0.5-, 1-, 1.5-, 2-, 2.5-, and 3-kb windows (supplementary fig. S1, Supplementary Material online), and accordingly adopted the size of 1 kb for other simulated data. However, although their powers can be optimized by adopting window sizes close to the narrow footprint generated by long-term balancing selection, with data derived from such a limited genomic region, estimation of these statistics can be noisy and potentially misleading. In empirical applications, it may therefore be preferable to incorporate information from a wider genomic region for the estimation of these statistics to reduce stochasticity. Hence, it is important to examine how window size affects method performance.

To this end, we applied all single- and trans-species methods considered in this study to simulated data, and varied window sizes under which the statistics were calculated (see Materials and Methods), and compared their powers. To ensure that all methods operated on the same data, we applied the summary statistics with windows containing a fixed number of informative sites, which is how the T statistics are computed. We tested windows with I = 5, 10, 30, 50, 100, 150, 200, 250, 300, and 350 informative sites on each side of the test site (i.e., the site on which windows are centered). Because we are interested in ancient trans-species balancing selection, we chose to examine the scenario in which the selected allele (s = 0.01 with h = 100) arose 15 My (assuming a generation time of 20 years) prior to sampling.

As predicted, powers of all methods drastically decrease as window size increases (supplementary fig. S12A, Supplementary Material online). While powers of all other methods eventually decrease toward zero for large windows, T₂ and $T_{2,\text{trans}}$ still maintain considerably higher power than other methods, with powers reaching ∼0.2 when the number of informative sites considered is larger than 200 sites on either side of the test site (i.e., 401 informative sites covered by each window). This contrast can be better illustrated in supplementary figure S12B, Supplementary Material online, where T₂ and $T_{2,\text{trans}}$ are the only two statistics that, as the window size increases, experience decay in power substantially slower than all other statistics, and stabilize at nonzero values. The relative robustness of T₂ and $T_{2,\text{trans}}$ is sensible because they incorporate distances from the test site of each informative site, reducing the influence of sites too far from the tested site. However, although both T₁ and T₂ account for the spatial distribution of informative sites, the powers of T₁ and $T_{1,\text{trans}}$ decrease more drastically than of T₂ and $T_{2,\text{trans}}$, albeit not as quickly as its summary-statistic counterpart HKA (supplementary fig. S12B, Supplementary Material online). Additionally, the powers of HKA variants decay much faster than those of NCD variants as window size increases. In general, statistics based only on polymorphism density, such as single- and trans-species variants of T₁ and HKA, are more vulnerable to large window sizes when compared with those accounting for allele frequency, such as single- and trans-species variants of T₂ and NCD. This gap in robustness between these two classes of statistics is likely due to the large emphasis that allele frequency-based statistics place on the presence of moderate-frequency alleles, thereby requiring a larger number of additional neutral informative sites for the evidence of the signal established from these intermediate-frequency alleles to attenuate.

Applying $T_{2,\text{trans}}$ on Great Ape Genomic Data

To examine long-term balancing selection affecting both human and chimpanzee lineages, we applied $T_{2,\text{trans}}$ on genomic data merged from human (108 Yoruban [YRI] individuals; 1000 Genomes Project Consortium 2015) and chimpanzee (ten western chimpanzees [Pan troglodytes verus]; Auton et al. 2012). Variant calls from both species were mapped to human reference genome hg19 and polarized with the matching sequence from gorilla reference genome gorGor3 (Kent et al. 2002). We retained biallelic sites that were polymorphic within a single species or that were substitutions between the two species, and adopted stringent filters (see Materials and Methods) to reduce the potential influence of technical artifacts. We then performed a whole-genome scan with $T_{2,\text{trans}}$ based on an inferred human recombination map (International HapMap Consortium 2007), and considered 100 informative sites directly upstream and directly downstream of the test site (i.e., 201 informative sites in total).

To infer statistical significance of each test site, we employed the coalescent simulator ms (Hudson 2002) to generate $5\times {10}^7$ independent replicates of 25-kb-long sequences, evolving neutrally along the inferred demographic histories of the YRI, chimpanzee, and gorilla lineages (Auton et al. 2012; Prado-Martinez et al. 2013; Terhorst et al. 2017, see Materials and Methods), with sample sizes matching the empirical data. We applied $T_{2,\text{trans}}$ on the first 201 informative sites of each sequence, using the 101st site as the test site, providing a single $T_{2,\text{trans}}$ score for each replicate (see Materials and Methods). We assigned p-values to each test site in the empirical scan based on the distribution of $T_{2,\text{trans}}$ scores from the neutral replicates (supplementary fig. S13, Supplementary Material online). To correct for multiple testing, a test site reaches genome-wide significance if its p-value is smaller than $0.05/{10}^6=5\times {10}^{-8}$, which uses the common assumption that there are ∼10⁶ independent sites in the human genome (Altshuler et al. 2008). Thus, based on the distribution shown in supplementary figure S13, Supplementary Material online, sites with a $T_{2,\text{trans}}$ score >223.709 were considered statistically significant outliers.

Significant Evidence of Shared Balancing Selection on the Major Histocompatibility Complex Region, FREM3/GYPE Locus, and GRIK1/CLDN17 Intergenic Region

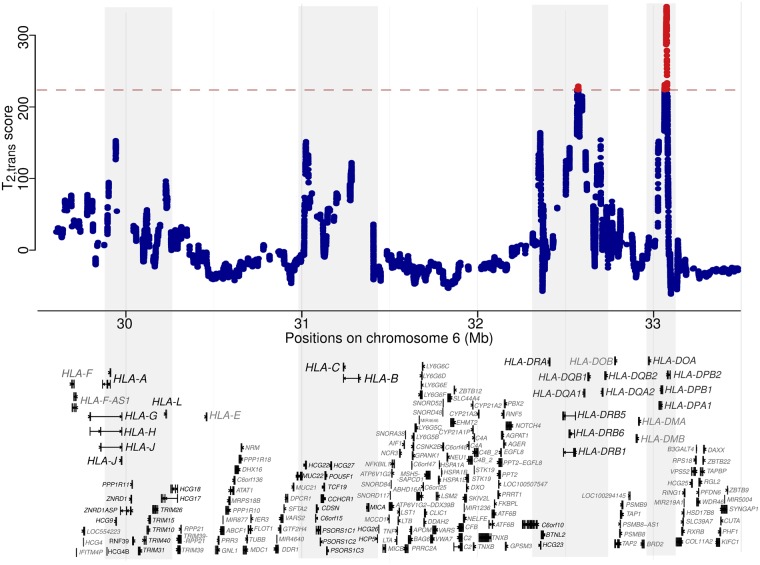
The major histocompatibility complex (MHC) has been repeatedly demonstrated to maintain high polymorphism levels across multiple species (Takahata et al. 1992; Leffler et al. 2013). Consistent with previous evidence, the $T_{2,\text{trans}}$ statistic exhibits significantly outstanding scores in the MHC region (fig. 3). A closer examination reveals that all peaks identified in the MHC region (fig. 3) locate on the genes previously identified to exhibit signatures of long-term balancing selection (Hedrick et al. 1991; Takahata et al. 1992; Andrés et al. 2009; Sanchez-Mazas 2007; DeGiorgio et al. 2014; Siewert and Voight 2017; Bitarello et al. 2018). Specifically, across the region (fig. 3) approximately four clusters of genes exhibit prominent scores, with large peaks over HLA-A, over HLA-B and HLA-C, over HLA-DRB genes, and over HLA-DPB genes. This pattern is consistent with the one reported by DeGiorgio et al. (2014), where these regions were extreme outliers in the scan for long-term balancing selection in human populations. Noteworthily, we observed that the most outstanding signal within this region falls on the gene HLA-DPB1 and its pseudogene HLA-DPB2 (supplementary fig. S14, Supplementary Material online), with the former making up the beta chain of the MHC II molecules. The beta chain of MHC II is responsible for presenting extracellular immunogens, and contains polymorphisms that diversify peptide-binding specificity (Díaz et al. 2003). These results agree with the observations that polymorphisms in the MHC region are often shared among species (Takahata 1993), and have been maintained since before the split of multiple great ape species (Takahata et al. 1992; Meyer et al. 2017).

Fig. 3.

$T_{2,\text{trans}}$ scores within the MHC region on chromosome 6. Gene tracks are displayed below, with only the longest transcript of each gene shown. If a gene does not have a longest transcript to cover all exons, then the minimum number of transcripts are displayed. Regions enriched with high-scoring peaks are shaded in gray, and genes falling in these areas are labeled with black fonts. The red dashed line represents the cutoff value for statistical significance, and the test sites with significant scores are shown in red.

In addition to the MHC region, we observed similarly extraordinary signals on chromosome 4, between the genes FREM3 and GYPE (supplementary fig. S15, Supplementary Material online). This locus was previously reported by Leffler et al. (2013) to harbor trans-species polymorphisms shared by humans and chimpanzees, and is functionally associated with malaria defense (Malaria Genomic Epidemiology Network 2015; Leffler et al. 2017). More specifically, the polymorphisms on this locus exist in accordance with the copy number variation of GYPB and GPYA, which can result in polymorphism of a blood-group antigen that effectively defends malaria infection (Leffler et al. 2017). Interestingly, while both the MHC and FREM3/GYPE regions exhibit an enrichment of polymorphic sites (supplementary figs. S14D and S15D, Supplementary Material online), we only observed a specific enrichment of minor allele frequency on the FREM3/GYPE locus, where a 400-kb-long region surrounding the peak still exhibits a distinguishable enriched frequency of ∼0.3 (supplementary fig. S15B and C, Supplementary Material online). In the MHC region, however, even after narrowing the range considered down to 200 kb around its largest peak, multiple modes can still be observed (supplementary fig. S14B and C, Supplementary Material online), suggestive of complex balancing selection processes operating on this region and matching the footprints of multiple balanced loci with different equilibrium frequencies (Meyer et al. 2017).

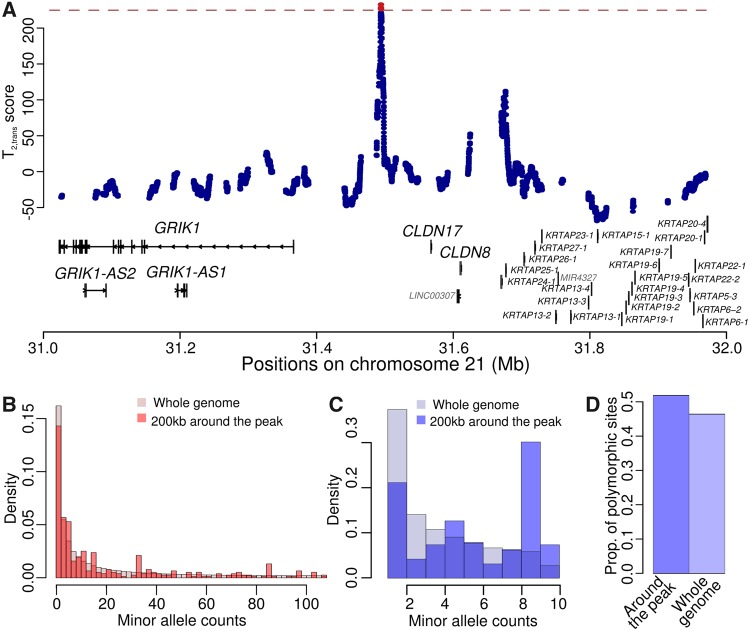
Another significant candidate region falls on chromosome 21, between the genes GRIK1 and CLDN17 (fig. 4). A number of transcription factor binding sites locate on the peak region, binding the factors CTCF, RAD21, and FOS (data from Ziller et al. 2013, as the ENCODE transcription factor ChIP-seq track shown on the UCSC genome browser). Although the regulatory activity of this intergenic region still remains elusive, the genes surrounding the region have potentially intriguing functional implications. Upstream of the peak locates a kainate-selective glutamate receptor gene GRIK1, which has been associated with epilepsy (Sander et al. 1997) and schizophrenia (Shibata et al. 2001). Mice knocked-out of GRIK1 would exhibit decreased pain perception (Gardiner and Costa 2006), implying that the fine-tuning of its expression may be important for an appropriate level of perceptional acuity. On the other side of the peak, the CLDN17 gene encodes claudin-17, which forms anion-selective channels on tight-junction barriers. It is highly expressed in kidneys and is hypothesized to be involved in chloride reuptake (Krug et al. 2012). It is also expressed in intestine and the brain (Lonsdale et al. 2013), potentially contributing to the integrity of important barriers such as intestine and blood–brain barriers. Similarly, claudin-8, encoded by the nearby CLDN8 gene, is also involved in chloride resorption in kidneys (Hou et al. 2010). It is an integral part of the intestine barrier (Groschwitz and Hogan 2009), and studies have associated the gene with inflammatory bowel diseases (Zeissig et al. 2007). Moreover, claudin-8 has also been reported to be susceptible to gut bacteria endotoxin (Shrestha and McClane 2013). To make the case more intriguing, there seems to be another high-scoring region upstream of the two claudin genes (fig. 4A), which is in the vicinity of a cluster of genes encoding hair keratin-associated proteins (Shibuya et al. 2004). As if corresponding to the two peaks, the site frequency spectra of both human and chimpanzees (fig. 4B and C) show enrichment of two different frequencies, suggesting that two distinct equilibrium frequencies may have been maintained if balancing selection were acting on this region.

Fig. 4.

Patterns consistent with long-term balancing selection within the GRIK1/CLDN17 intergenic region. (A) $T_{2,\text{trans}}$ scores within the 1-Mb genomic region on chromosome 21 encompassing the GRIK1/CLDN17 intergenic region. Gene tracks are shown on the corresponding location, with key genes labeled with larger fonts. The red dashed line represents the cutoff value for statistical significance, and the test sites with significant scores are shown in red. (B–D) Minor allele frequency spectra at polymorphic sites for human (B) and chimpanzee (C), and proportion of informative sites that are polymorphisms (D) within a 200-kb region encompassing the GRIK1/CLDN17 intergenic region, compared with those of the whole genome.

Multiple Genes with Outstanding Evidence of Trans-Species Balancing Selection

Because we took a conservative approach to obtain p-values of test sites (see Discussion), few outstanding peaks are identified as significant genome-wide. However, some of them do show top scores that are close to the genome-wide significance cutoff, and locate on genes with potentially important functional implications, including SLC35F1 (supplementary fig. S16, Supplementary Material online) and ABCA13 (supplementary fig. S17, Supplementary Material online). Among the regions that did not meet the genome-wide significance threshold, the highest-scoring candidate is SLC35F1, which is located on chromosome 6 and encodes a putative ion channel. Although no functional study has been reported on this gene, multiple studies have associated it with resting heart rate levels (Pfeufer et al. 2009; Den Hoed et al. 2013), risk of atrial fibrillation (Christophersen et al. 2017), and heart attack risks (van der Ende et al. 2018). However, despite its associations with cardiac health, SLC35F1 is mainly expressed in brain tissues, especially the cerebral cortex (Uhlén et al. 2015). Additionally, while the single nucleotide polymorphisms previously associated with cardiac functions mostly enrich under the minor peak around position 118.6 Mb of chromosome 6 (supplementary fig. S16A, Supplementary Material online; expression quantitative trait locus (eQTL) data from Lonsdale et al. 2013; Ziller et al. 2013), the major peak on this gene locates around position 118.3 Mb on chromosome 6 within a cluster of DNAaseI sensitive loci (Ziller et al. 2013) in the first intron on SLC35F1. These results suggest a possible role of selection on regulatory function and potential pleiotropy. Another candidate gene ABCA13, the longest in its gene family, harbors a region with outstanding $T_{2,\text{trans}}$ scores (supplementary fig. S17, Supplementary Material online). This ATP-binding cassette (ABC) transporter gene is highly expressed in multipotent adult progenitor cells (MAPC; Tang et al. 2010), a rare type of multipotent stem cells that can differentiate into not only mesodermal but also endodermal and ectodermal cells (Hof et al. 2007), and are important for wound-healing and tissue repair (Reyes and Verfaillie 2001). In addition to bone marrow (Uhlén et al. 2015), where most blood stem cells are found, expression of ABCA13 can also be detected in tracheae, thymus, testes, and ovaries (Prades et al. 2002; Barros et al. 2003). Moreover, the peak within this gene sits immediately upstream of the transmembrane ABC2 domain (supplementary fig. S17, Supplementary Material online), suggesting a potential selective force to diversify either the splicing or the functionality of this domain, which may be sensible given the wide variety of cell lineages that MAPC can differentiate into. Although functional studies of ABCA13 are lacking, both its expression pattern and the location of the peak present an intriguing case for a potential target of long-term balancing selection.

Extending Extant Frameworks to K > 2 Species

So far, we have demonstrated that the two-species versions of the T₁, T₂, HKA, and NCD statistics are specifically tailored to detect trans-species balancing selection, display substantially higher power than single-species statistics, and can recover well-characterized cases of balancing selection shared between the human and chimpanzee lineages. Furthermore, as described in supplementary notes 1, 2, and 5, Supplementary Material online, all extant frameworks can be extended to an arbitrary number of species K.

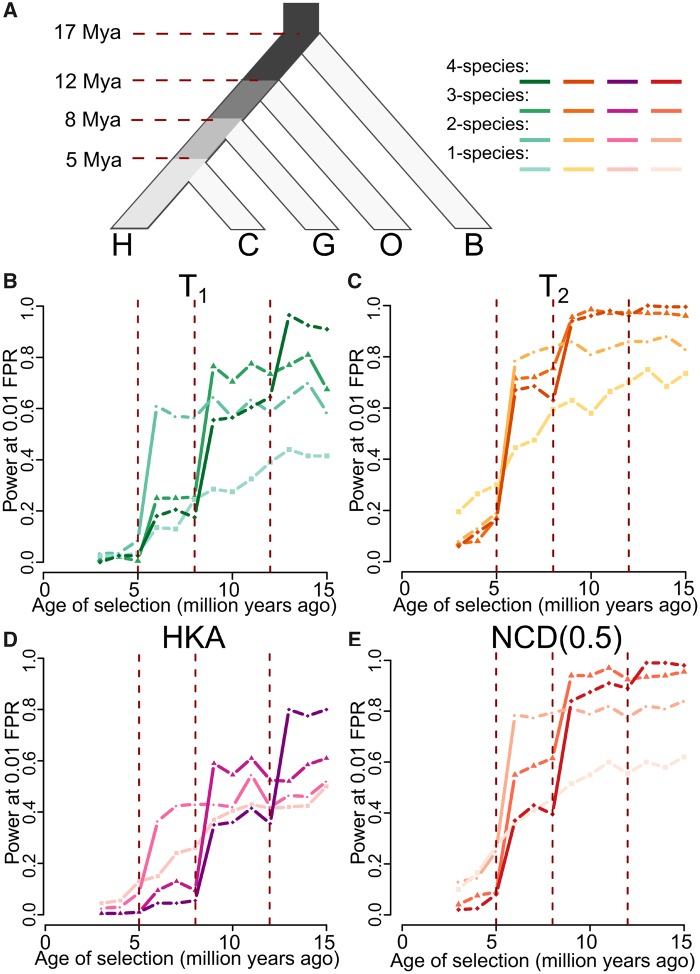
To test the performances of these K-species extensions, we simulated 50-kb-long sequences over a five-taxon tree (fig. 5A), which in addition to the three-species (species H, C, and G) examined in earlier simulations, features a fourth and fifth species diverging from the others 12 and 17 Ma, respectively, analogous to that of orangutans (denoted by species O) (Scally et al. 2012) and gibbons (denoted by species B) (Carbone et al. 2014). All other parameters remained the same as for the three-species tree with constant population sizes (see Materials and Methods). We introduced a selected mutation with strength s = 0.01 and dominance h = 100 in the lineage ancestral to species H at varying time points, and evaluated the performances of each method. For each statistic, we tested their extensions for application on two, three, and four species, and traced their powers as a function of time at which the selected allele arose, in addition to their single-species variant (fig. 5).

Fig. 5.

Performances of K-species variants of HKA, NCD(0.5), T₁, and T₂, with K = 1, 2, 3, or 4. (A) Schematic of the simulated five-species tree, relating species H, C, G, O, and B. Branches ancestral to species H are shaded based on the number of species that descend from that branch, with darker shades corresponding to larger numbers of species. (B–E) Powers at a 1% FPR of one-, two-, three-, or four-species variants for (B) T₁, (C) T₂, (D) HKA, and (E) NCD(0.5) to detect balancing selection (s = 0.01 with h = 100) of varying age. K-species variants of HKA, NCD(0.5), T₁, and T₂ with darker shaded lines are those that consider a greater number of species K.

Consistent with earlier results for two-species statistics (fig. 2), all two-species statistics show substantially higher power than their single-species counterparts in uncovering balancing selection introduced prior to the split of species H and C. Similarly, all three-species statistics exhibit a surge in power once the age of balancing selection surpasses that of the divergence of species G, and all four-species statistics show an analogous increase for selection predating the divergence of species O. This relation among each K-species (K = 1, 2, 3, or 4) variant remains consistent for T₁, T₂, HKA, and NCD (fig. 5B–E, respectively). Moreover, for every statistic and for each branch of interest (colored using incrementally darker shades in fig. 5) where balancing selection was introduced, the highest power can always be observed in the variant of a method that is specifically tailored for the corresponding number of species sharing the selection event. That is, for a specific method, the variant with the highest power is the one that operates on the entire set (and only this set) of species descending from a specific ancestral branch in which the selected allele arose. These results illustrate the applicability of K-species extensions of extant methods for detecting long-term balancing selection, and also for broadly constraining the time at which selected alleles arose at sites undergoing balancing selection.

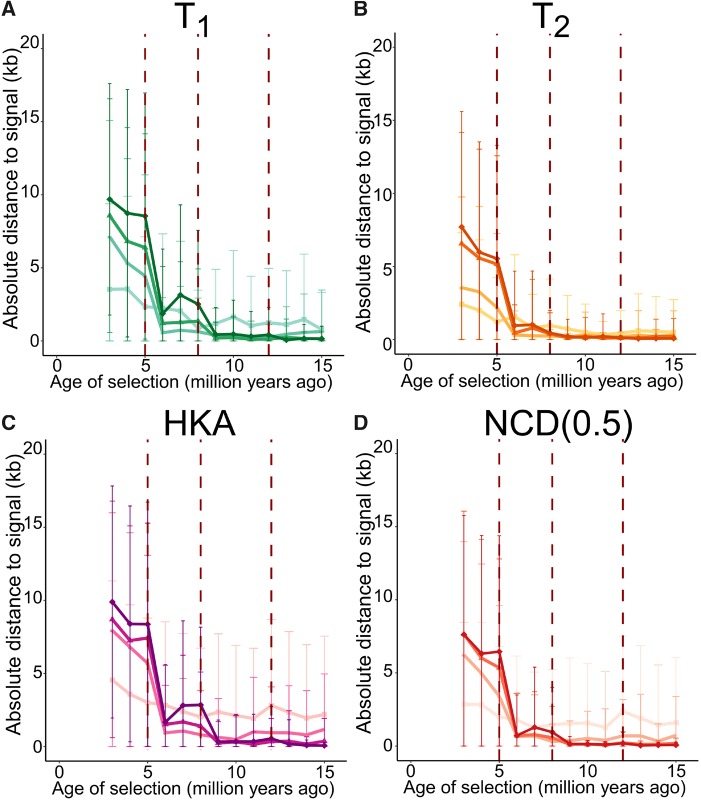
In addition to their powers, we also examined the abilities of each method to localize the site under balancing selection (fig. 6). For each statistic, the absolute distance from their highest score to the true location decreases as the age of the balanced allele increases, consistent with the fact that older balancing selection would leave characteristically narrower genomic footprints. Within each method, each trans-species variant exhibits a steep drop in mean distance to the true site of selection once the age of selection predates the divergence of all species it examines. This improvement in accuracy accords with the sharp increase in power. As the power of each method surpasses 0.8 (fig. 5), the mean distance to the true site of selection decreases to <1 kb (fig. 6). This result demonstrates that under scenarios in which methods exhibit high power to detect ancient balancing selection, their ability to isolate the true location of the selected site is considerable.

Fig. 6.

Mean absolute distances from location of signal peak to true site under balancing selection (s = 0.01 with h = 100) of varying age for K-species variants of (A) T₁, (B) T₂, (C) HKA, and (D) NCD(0.5). Error bars represent the standard deviation of all 200 replicates of the corresponding simulated scenario. Statistics are color-coded as in figure 5.

Discussion

In this study, we developed multispecies variants of summary-statistic and model-based approaches that employ polymorphism and substitution data from an arbitrary number of sampled species to localize sites undergoing shared balancing selection, and have comprehensively evaluated their performances through simulations. We applied the model-based $T_{2,\text{trans}}$ statistic to genomic data from humans and chimpanzees, and recovered the previously reported MHC and FREM3/GYPE regions as the most outstanding candidates. We have also characterized novel candidate regions on the cardiac health-associated SLC35F1 and the ABC gene ABCA13, presenting intriguing cases of long-term balancing selection shared by human and chimpanzee lineages that potentially diversifies these genes’ functionality.

Performance of Trans-Species Methods on Simulated Data

In our simulation study, we demonstrated that all trans-species statistics exhibit specificity in detecting long-term balancing selection shared by multiple species. They have low power relative to their single-species variants when only a single species is undergoing balancing selection, and display high power when selection initiated prior to the divergence of all input species (fig. 2). Moreover, we tested the performances of each method under different demographic parameters (fig. 2), varying selection parameters (supplementary fig. S3, Supplementary Material online), skewed recombination maps (supplementary fig. S7, Supplementary Material online), and elevated mutation rates (supplementary figs. S8–S10, Supplementary Material online). Our results have shown that the specificity of trans-species methods for shared balancing selection remains robust across diverse scenarios. Overall, as expected, methods using more information for the same genomic region generally attained higher power. Specifically, T₂ and NCD, which consider information on allele frequencies in addition to polymorphism density, outperform T₁ and HKA, which do not consider allele frequencies. Similarly, the model-based T statistics also outperform their corresponding summary statistic analogs (i.e., HKA to T₁, and NCD to T₂), as the model accounts for the spatial distribution of informative sites, in addition to regional polymorphism density and allele frequency distribution. We are also aware that Bitarello et al. (2018) reported a superior performance of NCD over T₂, and that both β (Siewert and Voight 2017) and NCD outperform T₁. However, in the Bitarello et al. (2018) experiments, both T statistics were assigned a window size of 100 informative sites on either side of the test site (i.e., covering 201 informative sites, which matches a physical window of ∼10 kb), whereas NCD was assigned a window size of 3 kb. We have shown in the Results that after matching the window size used by each method, both the single- and trans-species variants of T₁ and T₂ outperform the respective single- and trans-species HKA and NCD variants, respectively. An exception is under settings with elevated mutation rates, which we further explore in the subsequent subsection The Effect of Multiple Tests under Elevated Mutation Rates. Additionally, we noticed that the powers of NCD statistics tended to be close to those of T₂ when the equilibrium frequency is close to the target frequency assigned to NCD. Integrating an optimization processes into the NCD framework, however, did not improve the robustness to varying equilibrium frequencies, but instead lowered the power of the specific optimization approach that we employed (see supplementary note 6, Supplementary Material online). In contrast, the performances of variants of the T₂ statistics were not hindered by optimization (see supplementary note 6, Supplementary Material online). Taken together, these results indicate that the model-based $T_{\text{trans}}$ statistics have superior performance relative to complementary approaches for robustly identifying loci evolving under ancient trans-species balancing selection.

The Effect of Multiple Tests under Elevated Mutation Rates

We observed that, regardless of whether high mutation rate was uniform across the phylogeny or was species-specific, the model-based T statistics reported notable increases in their proportions of false signals (supplementary figs. S8 and S9, Supplementary Material online). However, because these statistics are computed at every informative site in a genomic region, regions with a higher density of informative sites due to elevated mutation rates will by chance harbor larger test scores. To examine whether this multiple testing issue can explain the inflated proportions of false signals in T statistics, we downsampled the number of test sites so that the number of T scores computed along sequences with elevated mutation rates matched that of the original mutation rate. We considered two downsampling approaches, which we refer to as “dense” and “sparse.” In the dense scenario, we sampled a specified number of test sites contiguously along the sequence, such that each pair of neighboring test sites had the same number of informative sites in common used in their computation as do those under the original mutation rate. In the sparse scenario, we evenly sampled the test sites along the simulated genomic region, such that informative sites distributed across the whole simulated region could be considered, but the neighboring test sites would share fewer informative sites in their computation compared with the sequences with the original mutation rate.

Indeed, either by densely (supplementary fig. S18A–C, Supplementary Material online) or sparsely (supplementary fig. S18D–F, Supplementary Material online) downsampling, all T statistics showed substantially improved performances for sequences under uniformly elevated mutation rates (compared with supplementary fig. S8, Supplementary Material online), highlighting the effect of multiple testing on inflating the proportions of false signals. For sequences with species-specific increase of mutation rates, T statistics also respond to downsampling (supplementary fig. S19, Supplementary Material online) in a similar fashion. Moreover, we observed that the sparse downsampling scheme (supplementary figs. S18D–F and S19D–F, Supplementary Material online) did not rescue the proportions of false signals as much as the dense scheme (supplementary figs. S18A–C and S19A–C, Supplementary Material online). This performance margin echoes the fact that test sites that were sampled in the sparse scheme are less correlated. That is, because two neighboring test sites have fewer informative sites in common used for their calculation, even after downsampling to match the number of sites on sequences under the original mutation rate, the set of test sites from the sparse scheme still has a larger effective number of tests. Therefore, multiple testing contributed to the substantially inflated misidentification rates of T statistics, and when the number of tests is properly controlled, the T statistics (especially $T_{2,\text{trans}}$) should be robust to genomic regions with high mutation rate.

Further, it is worth pointing out that this multiple-testing issue does not result from inherent statistical properties of T statistics, but rather the way in which windows were chosen to compute the statistics. We set the T statistics to perform a test on every informative site that could be centered on, and computed the likelihood ratios based on a test window with a fixed number of informative sites. As a consequence, the number of computed tests for T statistics will be close to the number of available informative sites, and similarly, if other statistics were computed using windows identical to T statistics, then their numbers of computed tests would also match the number of informative sites. When we computed single- and trans-species variants of NCD and HKA with a window size of 21 informative sites and step size of one informative site (i.e., making the identical number of computations on identical data as do T statistics) both summary statistics mimicked the behaviors of their respective model-based analogs (i.e., HKA to T₁, and NCD to T₂; supplementary fig. S20, Supplementary Material online) under scenarios of high mutation rate, both when all species have high mutation rate (supplementary fig. S20A–C, Supplementary Material online) and when it is specific to only species H (supplementary fig. S20D–F, Supplementary Material online). These results highlight that the performance of a statistic is highly dependent on the type and number of windows it is applied with, and that the poor performance of HKA and the excellent performance of NCD under elevated mutation rate were simply due to the manner in which we computed the statistics, with physical-length windows and a fixed number of windows per simulated genomic region.

Detecting Long-Term Balancing Selection with and without Trans-Species Polymorphisms

Because our aim has been to circumvent potential issues surrounding trans-species polymorphisms, we only considered within-species polymorphisms and cross-species fixed differences as input data for multispecies variants of T₁ and T₂. Nonetheless, when conditions allow, it is possible for multispecies variants of T₁ and T₂ to include trans-species polymorphisms in the model (hereafter referred to as $T_{1,\text{TSP}}$ and $T_{2,\text{TSP}}$, respectively; see supplementary note 4, Supplementary Material online), and be applied to input data with all three types of informative sites. To assess the ability of these new statistics to detect trans-species balancing selection, we examined the powers of $T_{1,\text{TSP}}$ and $T_{2,\text{TSP}}$ under settings in which trans-species polymorphisms are removed and in which they are included in the data set.

When applied to the same set of simulated sequences as in previous analyses while also permitting information on trans-species polymorphisms, $T_{1,\text{TSP}}$ and $T_{2,\text{TSP}}$ show substantial increases in power relative to $T_{1,\text{trans}}$ and $T_{2,\text{trans}}$ (supplementary fig. S21, Supplementary Material online), while remaining largely unaffected by balancing selection occurring after the split of the pair of species. Both statistics reached a power higher than 0.8 when selection was older than 13 My, and $T_{2,\text{TSP}}$ almost reached a power of 1.0 when the selected allele was introduced 15 Ma. This power increase is expected due to the high probability that trans-species balancing selection would lead to trans-species polymorphisms, particularly compared with the relatively low probability expected from neutrality (e.g., Takahata 1993; Leffler et al. 2013; Gao et al. 2015). Moreover, in contrast to $T_{1,\text{trans}}$ and $T_{2,\text{trans}}$, we observed that $T_{1,\text{TSP}}$ and $T_{2,\text{TSP}}$ display a gradual increase in power with increasing age of trans-species balancing selection. This pattern resembles that of single-species T₁ and T₂ statistics, and can partially explain why $T_{1,\text{trans}}$ and $T_{2,\text{trans}}$, which do not utilize information on polymorphisms established prior to species splits, maintain their powers around a constant level instead of gaining power with selection age. Moreover, when trans-species polymorphisms are absent from the data, the powers of $T_{1,\text{TSP}}$ and $T_{2,\text{TSP}}$, albeit, respectively, slightly lower than $T_{1,\text{trans}}$ and $T_{2,\text{trans}}$, remain similar to the $T_{1,\text{trans}}$ and $T_{2,\text{trans}}$ variants that do not account for trans-species polymorphisms, suggesting that the trans-species polymorphism-inclusive model can be robustly applied to data with or without trans-species polymorphisms present.

Despite this improvement in performance, however, incorporating trans-species polymorphisms in our analysis can increase the vulnerability of T statistics to nonadaptive processes such as mapping errors at paralogs across species and high mutation rate, both of which can lead to trans-species polymorphisms. To test the robustness of $T_{\text{TSP}}$ statistics to elevated mutation rates, we applied them on sequences neutrally evolving with mutation rate 5- or 20-fold higher than the original rate of $\mu =2.5\times {10}^{-8}$ (supplementary fig. S22A and D, Supplementary Material online, respectively). In both scenarios, when trans-species polymorphisms are included in the input, $T_{\text{TSP}}$ statistics falsely identified considerably more sequences as undergoing trans-species balancing selection than when such information was not provided. Moreover, higher mutation rates lead to a greater number of false signals identified by $T_{\text{TSP}}$ statistics when trans-species polymorphisms are included (supplementary fig. S22, Supplementary Material online). In contrast, without using trans-species polymorphisms, $T_{\text{TSP}}$ statistics perform only slightly worse than $T_{\text{trans}}$ statistics in misclassifying highly mutable regions as undergoing balancing selection. On the other hand, when we applied $T_{\text{TSP}}$ statistics on sequences with mutation rate 20-fold higher in species H, $T_{\text{TSP}}$ statistics no longer report a greater number of false signals than do $T_{\text{trans}}$ statistics (supplementary fig. S22G, Supplementary Material online). This is because when the elevation in mutation rate occurred only in species H, the resulting trans-species polymorphisms would not increase as much as they did when both species H and C have high mutation rate.

To examine the effect of multiple testing on the proportion of false signals identified by $T_{\text{TSP}}$ statistics, we performed downsampling following the same procedures as described in subsection The Effect of Multiple Tests under Elevated Mutation Rates, such that regardless of whether trans-species polymorphisms are considered, the same number of test sites were sampled to infer proportions of false signals for all T statistics. We found that although accounting for the number of tests rescued the misidentification rates of all $T_{\text{trans}}$ and $T_{\text{TSP}}$ statistics (supplementary fig. S22B, C, E, F, H, and I, Supplementary Material online), the relative differences in the rates of identifying false signals between $T_{\text{TSP}}$ and $T_{\text{trans}}$ still persist. These results are likely due to the emphasis that $T_{\text{TSP}}$ statistics place on trans-species polymorphisms, and highlight the sensitivity of $T_{\text{TSP}}$ to the presence of such polymorphisms regardless of the processes that generated them. Therefore, because such trans-species polymorphisms can be generated by technical artifacts in addition to nonadaptive evolutionary processes, we recommend excluding trans-species polymorphisms while applying T statistics, and when such data are included, candidate regions obtained by $T_{\text{TSP}}$ statistics that also harbor trans-species polymorphisms should be further validated using the framework of Gao et al. (2015), which only considers trans-species polymorphisms and is complementary to our T statistics.

Applicability of Trans-Species Methods on Empirical Data

In this study, we introduced a number of trans-species methods, including summary- and model-based approaches. In addition to their nuanced performances on simulated data, their applicability on empirical data also varies. In particular, two major considerations are the evolutionary relationship of the set of study species as well as the availability of sophisticated data. With respect to evolutionary relationships, divergence times between pairs of species are crucial—particularly for the model-based $T_{\text{trans}}$ statistics, as their underlying models assume reciprocal monophyly. Specifically, under the Kaplan–Darden–Hudson model (Hudson and Kaplan 1988; Kaplan et al. 1988), the tallest coalescent tree manifests at the site under long-term balancing selection, where the symmetric population-scaled mutation rate ${\theta }_{\text{sel}}$ between the balanced alleles further controls the expected tree height. The greater the value of ${\theta }_{\text{sel}}$, the shorter time to the most recent common ancestor for the set of alleles sampled within a species (Hudson and Kaplan 1988). To ensure monophyly at neutral sites close to the selected site, we set ${\theta }_{\text{sel}}=0.05$, as did DeGiorgio et al. (2014), such that the mean coalescence time within a species is ∼12 coalescent units at the site under selection. Therefore, sister species such as humans and chimpanzees, which have a split time of ∼12.5 coalescent units (Prado-Martinez et al. 2013), would be suitable for our current implementation of $T_{\text{trans}}$ statistics. Meanwhile, for more recently diverged species such as chimpanzees and bonobos, whose interspecies divergence is approximately three coalescent units (Prüfer et al. 2012; Prado-Martinez et al. 2013), the value of ${\theta }_{\text{sel}}$ needs to be increased for $T_{\text{trans}}$ to be applied. However, lowering the maximum expected tree height to such a small level would reduce the distinction between the model of balancing selection and neutrality, and likely lead to a dramatic decrease in the power of the $T_{\text{trans}}$ statistics. On the other hand, the complementary summary-based HKA_trans and NCD_trans statistics can be applied regardless of the species split times.

Differences in data requirements between the summary- and model-based approaches will also influence the breadth of their application. For all methods we introduced, it is important that polymorphism data are available for at least two species, and that the reference genomes of these species can be aligned. Further, because the footprint of long-term balancing selection is small (Hudson and Kaplan 1988), all the methods discussed here are applicable on species with draft genomes that may have relatively short scaffolds, although larger scaffolds may be important for biological interpretations. Moreover, all these methods must be applied to chromosomes that recombine, as their application hinges on the premise that only neutral variation nearby a selected site is influenced by balancing selection.

In addition to these requirements, the model-based approaches also require a recombination map, which may limit their applicability on nonmodel organisms. Nonetheless, we argue that adopting a uniform recombination rate should be reasonable as well, considering that recombination maps may not necessarily match across the set of study species (Smukowski and Noor 2011). Moreover, our simulations (supplementary fig. S7, Supplementary Material online) have demonstrated that dramatic changes in recombination rate and grossly misspecified recombination maps have limited effect on the performance of $T_{\text{trans}}$ statistics. Another limitation to the application of the $T_{2,\text{trans}}$ statistic is that it uses derived allele frequency spectra, and therefore requires a reference genome from an outgroup species to polarize alleles as ancestral or derived. In contrast, the $T_{1,\text{trans}}$ statistic (as well as HKA_trans) is not subject to this constraint, as it does not require information on allele frequency. As a consequence, both ${\text{HKA}}_{\text{trans}}$ and $T_{1,\text{trans}}$ can be applied to data sets in which allele frequencies cannot be estimated well, but in which polymorphic sites may be inferred with confidence (Van Tassell et al. 2008; Cutler and Jensen 2010; Schlötterer et al. 2014).

Examining Ancient Balancing-Selection Shared by Humans and Chimpanzees

In our empirical study, we applied $T_{2,\text{trans}}$ on human and chimpanzee genomic data to reexamine long-term balancing selection shared by these sister species. Without employing information from trans-species polymorphisms, we recovered well-established cases, such as the MHC and FREM3/GYPE regions, both of which were previously well-characterized with ample evidence of shared polymorphisms. We additionally reported a number of novel and relevant candidate regions with outstanding scores, such as the GRIK1/CLDN17 intergenic region, the cardio health-related SLC35F1 gene, and the ABC transporter gene ABCA13. Despite SLC35F1’s frequent association with cardiac health (Den Hoed et al. 2013; Christophersen et al. 2017; van der Ende et al. 2018), it is, in contrast, mainly expressed in brain (Uhlén et al. 2015). Meanwhile, the gene ABCA13 encodes a lipid transporter (Prades et al. 2002), and is mainly expressed in MAPCs (Tang et al. 2010), one of the bone marrow stem cells that have high differentiation potency, and are heavily involved in wound-healing and tissue repair (Hof et al. 2007). Though both novel candidates lack empirical functional studies, they are both involved in multiple intriguing tasks, and further functional investigations could potentially substantiate their selection mechanisms.

Despite the array of trans-species statistics we presented, we chose to perform the empirical scan with $T_{2,\text{trans}}$ due to the high power and robustness it shows in our simulation study, including its ability to integrate more information within a larger genomic region than summary-based approaches, thereby minimizing the noise accompanied with smaller window sizes (see Robustness to Large Window Sizes). Specifically, because we observed that $T_{2,\text{trans}}$ had substantially higher power than other approaches with a large window size of 100 informative sites upstream and downstream of the test site (supplementary fig. S12, Supplementary Material online), we chose this window size so that T₂ can make use of as much data as possible, while still maintaining reasonable power.

To infer statistical significance of each test site, we performed rigorous and extensive simulations to generate a neutral distribution for p-value inference. We performed $T_{2,\text{trans}}$ with the exact same set of parameters used in the empirical scan, such that scores from neutral simulations were based on the empirical interspecies coalescence time, polymorphism density, and site frequency spectra as well as the same window size of 100 informative sites. Although the significant candidate regions are less than a handful, we believe the significance cutoff based on our simulations was conservative, as we did not include ubiquitous processes such as background selection that lead to overall reductions in diversity (McVicker et al. 2009; Comeron 2014), and because the simulated data sets tended to have a higher density of informative sites due to the stringent filters applied to the empirical data set. With these factors considered, it is sensible that the distribution of $T_{2,\text{trans}}$ scores for neutral replicates is right-shifted, compared with that for the empirical data (supplementary fig. S13, Supplementary Material online), further highlighting the outstanding footprints of balancing selection on our significant candidate regions—the MHC, FREM3/GYPE, and GRIK1/CLDN7 loci.

Curating and Validating Candidate Regions

The detection of long-term balancing selection has long been hindered by numerous confounding factors, such as high mutation rate, the effects of which we have evaluated extensively (see Results and Discussion), as well as technical artifacts during sequencing and mapping, which were not accounted for in our genetic simulations. We applied stringent filters (see Materials and Methods) on our empirical data to remove as many regions as possible that were repetitive and that exhibited mapping issues based on available tracts. Despite that more than half of all mappable sites were removed from analyses using these filters, we still observed outstanding signals likely resulting from artifacts (e.g., the largest peak on chromosome 13, shown in supplementary fig. S23, Supplementary Material online). To further distinguish artifacts and true signals, for high-scoring candidate regions we obtained the sequencing coverage separately averaged across human and chimpanzee samples (see Materials and Methods), and also performed single-species T₂ scans on each of the two sister species.

For a reliably mapped genomic region, a majority of sampled individuals should harbor reasonable numbers of sequencing reads at the region, and the mean sequencing depth should not be an outlier with respect to the neighboring genomic regions or to the entire genome. Therefore, in addition to using tracts from data sets of known problematic regions (e.g., RepeatMasker and CRG100 alignability and mappability tracts), another approach to ensure data quality is to flag abnormalities in the numbers of sequencing reads across sampled individuals. Additionally, for regions with high data quality, it would be reassuring if footprints of long-term balancing selection also manifested separately in each species if selection occurred ancestrally and affected all species. However, this should not be a requirement, as the power to detect true signals using single-species statistics is considerably lower than with trans-species approaches.

In our results, we found that both the MHC (supplementary fig. S24, Supplementary Material online) and the FREM3/GYPE (supplementary fig. S25, Supplementary Material online) regions exhibited these positive features. Specifically, the peaks at these regions in single-species scans with T₂ aligned well with those of the trans-species scan with $T_{2,\text{trans}}$ (supplementary figs. S24A and S25A, Supplementary Material online). Moreover, within either humans or chimpanzees, most of the samples reported sequencing reads, and the mean numbers of reads (i.e., sequencing depths) across all samples within each species at these peaks did not deviate substantially from neighboring genomic regions. Note that although the sequencing depths did fluctuate at a small region around gene GYPB on chromosome 4, and around HLA-DQA and HLA-DQB genes on chromosome 6, these abnormal patches either were already removed by filters prior to the scan, or did not produce high scores. Similarly, within the 1-Mb genomic regions covering GRIK1/CLDN17 (supplementary fig. S26, Supplementary Material online), SLC35F1 (supplementary fig. S27, Supplementary Material online), or ABCA13 (supplementary fig. S28, Supplementary Material online), the sequencing depths across all samples in both species are evenly distributed across the genomic regions. Meanwhile, the T₂ scores of both species across these regions do not align as well as in the peaks at HLA-DPB2 or FREM3/GYPE, and $T_{2,\text{trans}}$ seems to match closer with the T₂ score for chimpanzees.

In contrast, we observed potential signs of artifacts when curating other candidate regions, such as at the gene THSD7B, the PGLYRP3/PGLYRP4 cluster, and the gene SNTG2. For one, although THSD7B (Thrombospondin Type I Domain Containing 7B) harbors an outstanding peak surrounding one of its variants (rs1469621) associated with atopic dermatitis and asthma (supplementary fig. S29, Supplementary Material online; Weidinger et al. 2013), this peak region also features abnormally high numbers of reads in chimpanzee genomes (supplementary fig. S30, Supplementary Material online), which often occurs at regions with problematic mapping, such as duplicated and repetitive regions. Similarly, in the case of the PGLYRP3/PGLYRP4 gene cluster (supplementary fig. S31, Supplementary Material online), these two genes not only encode the bactericidal peptoglycan recognition proteins (Kashyap et al. 2011, 2014) but also locate within the psoriasis-sensitive PSORS4 locus (Sun et al. 2006) with associations to several autoimmune disorders (Dziarski and Gupta 2010; Zulfiqar et al. 2013). However, despite that innate immunity has been speculated to be a major target of balancing selection (Prugnolle et al. 2005; Ferrer-Admetlla et al. 2008; Fumagalli et al. 2009), sequencing depths around the PGLYRP3/PGLYRP4 cluster in the chimpanzee genomes are also abnormally high (supplementary fig. S32, Supplementary Material online), raising concerns for potential mapping issues in this region. In addition to abnormal increases of sequencing depths, an abrupt decrease in the numbers of reads may also be indicative of a region that is problematic to map, as in the case for the SNTG2 (Syntrophin Gamma 2; supplementary figs. S33 and S34, Supplementary Material online) gene on chromosome 2. As a cytoplasmic adaptor protein, γ-2 syntrophin is heavily expressed in neuronal cells (Piluso et al. 2000), and interacts with the autism-related neuroligin 3 and 4X (Yamakawa et al. 2007). However, although there are several eQTLs for its expression in testes in the peak region (supplementary fig. S33A, Supplementary Material online; eQTL data from Lonsdale et al. 2013), the genomic segment immediately upstream of the peak is almost devoid of sequencing reads across the YRI samples (supplementary fig. S34B, Supplementary Material online). Such regions of low coverage are suggestive of a deletion, where erroneous mapping is prone to occur, and therefore we believe that caution should be warranted before making functional interpretations at this candidate gene.

Likewise, the peak located on chromosome 13 (supplementary figs. S23 and S35A, Supplementary Material online) is highly suspicious. Although this peak is a statistically significant outlier and has some transcription factor-binding sites enriched nearby (ChIP-seq data from Ziller et al. 2013), we could not identify any coding genes within the 1-Mb region surrounding this peak. A closer look at the sequencing depths of this region (supplementary fig. S36, Supplementary Material online) reveals an elevated plateau in depth under the peak followed by a sudden drop across the human samples (supplementary fig. S36B, Supplementary Material online), suggesting that this region could harbor incorrectly mapped reads, potentially from an unfiltered duplicated region. Further, although sequencing depths in chimpanzees are evenly distributed under the peak, due to the lack of a segmental duplication filter for chimpanzee genomes, it is possible that the erroneous mapping resulted from a duplicated segment elsewhere in the genome confounded the variant calls. This suspicion is echoed when we examined the spatial distribution of allele frequencies on this region (supplementary figs. S23B, S23C, and S37, Supplementary Material online). We observed long tracks of alleles with identical moderate frequencies in the chimpanzee samples, some extending as long as almost 500 kb. Such extended tracks of identical allele frequencies are unlikely to be produced by natural processes, and further cast doubt on the validity and reliability of the signal at this region.

Lastly, it is worth noting that although these dubious signals arise on regions not included in filters such as RepeatMasker and CRG100 alignability and mappability, applying more filters does not necessarily guarantee their removal, and may discard true signals in the process. For example, when we removed all regions with copy number variation in the human genome (data obtained from Firth et al. 2009), the dubious peak on chromosome 13 was indeed successfully removed (supplementary fig. S35B, Supplementary Material online). However, this additional filter halved the usable data in the process, and removed the functionally relevant and established (Prugnolle et al. 2005; Leffler et al. 2017; Meyer et al. 2017) signals at the MHC and FREM3/GYPE regions as well. We therefore recommend that comprehensive curation of candidate regions be considered when searching for genomic regions evolving under long-term balancing selection, which, in addition to extensive filters, should take both sequencing quality and potential biological mechanisms into account.

Concluding Remarks

In this study, we presented a set of methods, including both model-based and summary statistic approaches, for detecting multispecies balancing selection without dependence on the knowledge of trans-species polymorphism, and have comprehensively evaluated their performances. We have shown that all multispecies methods have specificity in detecting shared balancing selection, and have addressed how their powers could be influenced by recent demographic changes, uneven recombination rates, selection strengths and equilibrium frequencies at loci undergoing balancing selection, as well as large window sizes. We also demonstrated that our model-based approaches can be augmented to accommodate data on trans-species polymorphism to increase detection ability, but caution the use of such alterations as they can lead to false signals due to nonadaptive processes, whereas avoidance of such issues was a major impetus of this study. Application of the model-based method $T_{2,\text{trans}}$ on human and chimpanzee genomic data not only recovered well-established candidates but also revealed a number of novel putative targets that contribute to the hypothesis that pathogen defense, both in terms of adaptive immunity and of innate immunity, has been one of the prime driving forces maintaining polymorphisms across humans and chimpanzees. Lastly, we developed the software packages MULLET (http://www.personal.psu.edu/mxd60/mullet.html) and MuteBaSS (http://www.personal.psu.edu/mxd60/mutebass.html) for the respective implementation of the multispecies model-based and summary statistic approaches presented here, and we provide values for the $T_{2,\text{trans}}$ test statistic and associated p-values from our empirical scans at http://www.personal.psu.edu/mxd60/mullet.html.

Materials and Methods

Simulating Genetic Data

We employed SLiM (Messer 2013) to generate simulated sequence data. As recommended, we initiated each replicate simulation with a burn-in of $10N={10}^5$ generations, where $N={10}^4$ is the diploid effective population size. Our simulations assumed a per-base per-generation mutation rate of $\mu =2.5\times {10}^{-8}$ (Nachman and Crowell 2000), and a per-base per-generation recombination rate of $r={10}^{-8}$ (Payseur and Nachman 2000). To speed up simulations, we applied the common method of scaling parameters by a factor λ. Under this scaling, we multiplied the per-generation mutation rate, per-generation recombination rate, and per-generation selection coefficient by λ, and we divide all times in generations by λ and the diploid effective size also by λ. This scaling generates the same levels of variation expected under a simulation without scaling, except simulations run approximately ${\lambda }^2$ faster, permitting an interrogation of a wider parameter space. For scenarios based on a model of constant population size or on a model of recent population expansion, we used λ  =  100. For scenarios based on a model of a recent population bottleneck, we used λ  =  50.

Examining Performances of Two-Species Statistics

We simulated a demographic history analogous to that of the great apes, assuming a uniform generation time of 20 years, as did numerous prior studies (Caswell et al. 2008; Becquet and Przeworski 2007; Langergraber et al. 2012). To comprehensively examine performances of two-species statistics, we simulated a three-species demographic history (fig. 2A) in which two sister species, analogous to humans and chimpanzees (Kumar et al. 2005), diverging ${\tau }_1=5\times {10}^6$ years ago, split with the reference species ${\tau }_2=8\times {10}^6$ years ago, analogous to gorillas (Scally et al. 2012). At the end of each simulated replicate, we sampled 50 haploid lineages from each of the sister species, and one haploid lineage from the outgroup species (species G in fig. 2A) to polarize alleles as derived or ancestral.

To examine common demographic histories that are consistent with human evolution, we simulated models with a recent population bottleneck and a recent population expansion based on parameters inferred by Lohmueller et al. (2009). Under a scenario of a recent population bottleneck, we modeled forward in time a reduction in population size from $N={10}^4$ diploid individuals to N_b = 550 diploid individuals ${\tau }_b=3.0\times {10}^4$ years ago, followed by an increase in population size to $N={10}^4$ diploid individuals ${\tau }_e=2.2\times {10}^4$ years ago. Under a scenario of a recent population expansion, we modeled forward in time an increase in population size from $N={10}^4$ diploid individuals to $N_g=2\times {10}^4$ diploid individuals ${\tau }_g=4.8\times {10}^4$ years ago.

We generated 10³ replicates evolving neutrally along the three-species demographic history with constant population sizes (fig. 2A), and 400 replicates evolving neutrally under those of a recent population bottleneck (fig. 2B) or expansion (fig. 2C). For every scenario in which balancing selection was introduced, we generated 500 replicates for scenarios with selection coefficient s = 0.01 and dominance parameter h = 100, and 200 replicates for all other scenarios. For a given demographic model, we used the polymorphism and substitution data across all neutral replicate simulations to estimate the mean interspecies coalescence time $\widehat{C}$, the proportions of polymorphism and substitution observed in each species, and the derived allele frequency spectra for each species (DeGiorgio et al. 2014). These quantities were provided as background genomic data for single- and trans-species variants of HKA, T₁, and T₂, as they require information about patterns of variation expected across the genome. For single-species variants of HKA, NCD, T₁, and T₂, substitutions were called as fixed differences between one ingroup species and the outgroup species. However, for two-species variants HKA_trans, NCD_trans,$T_{1,\text{trans}}$, and $T_{2,\text{trans}}$, substitutions were called as fixed differences between the two sister species. In addition, for application of HKA_trans, NCD_trans,$T_{1,\text{trans}}$, and $T_{2,\text{trans}}$, we filtered out any site that was polymorphic in both sister species.

To simulate species-specific elevations in mutation rates, we employed SLiM2 (Haller and Messer 2017, version 2.6), which allows the mutation rate to be reset, albeit globally, at a given generation. We adopted all the parameters of the three-species demographic model with constant population size (fig. 2A), and used a scaling factor of λ = 100. For each replicate, we set up two simulations, denoted as mut and null, to run in parallel using the same seed and initial model parameters. Immediately after species H and C split, all sequences in the mut simulation experienced a change in mutation rate, whereas the mutation parameter did not change in the null simulation. When simulations completed, 50 haploid lineages of species H were sampled from the mut simulation, whereas 50 lineages of species C and one lineage of species G were sampled from the null simulation. Data from these samples were then merged for downstream analyses. In this pipeline, because mut and null simulations start with the same seed and initial parameters, we can consider the evolutionary process in the two as identical until species H and C split, and that the elevation in mutation rate only occurs in species H, as we only sample lineages from species H in the mut simulation.

We considered three scenarios in which the mutation rate was increased to $5\mu ,\hspace{0.17em}10\mu$, or $20\mu$, with μ being the initial mutation rate of $2.5\times {10}^{-8}$ per site per generation, which was used throughout the null simulations. We also simulated one additional scenario where neither the mut nor the null simulation reset their mutation rate and instead remained constant at rate μ. We applied the same sampling and parsing procedures to this set of simulations, and used these simulation replicates to generate a null distribution to obtain FPRs. We simulated 400 replicates for each of these four scenarios, and performed the same analysis procedures as in other simulation settings. We supplied single- and trans-species variants of HKA and T₁ with proportions of polymorphisms and substitutions inferred from the concatenated sequences from the constant mutation rate scenario, from which we also derived the interspecies coalescence time and allele frequency spectra for the application of T₂ variants. All summary statistics were applied with windows of size 1 kb, and model-based T statistics with ten informative sites flanking each side of the test site.

Assessing Power of K-Species Statistics

To assess the ability of K-species ($K=2,$ 3, or 4) variants of NCD, HKA, T₁, and T₂ to detect and localize sites undergoing ancient balancing selection, we included two additional species onto the three-species demographic history in figure 2A, with the fourth and fifth species diverging ${\tau }_3=12\times {10}^6$ and ${\tau }_4=17\times {10}^6$ years ago, respectively, analogous to that of orangutans (Auton et al. 2012) and gibbons (Carbone et al. 2014) (respectively denoted by species O and B in fig. 5A). We simulated 50-kb-long sequences evolving along the tree, with a uniform recombination rate of $r={10}^{-8}$ per site per generation, and a mutation rate of $\mu =2.5\times {10}^{-8}$ per site per generation across all species, consistent with our previous simulations. We also assumed a constant population size of $N={10}^4$ diploids across the entire phylogeny. Fifty haploid lineages were sampled each from species H, C, G, and O in the present, and one lineage was sampled from species B. Derived alleles were called based on a single sampled lineage from the nearest outgroup species to the set of K species examined. That is, we used one sampled lineage from species C to polarize alleles in species H for one-species experiments, species G to polarize alleles in species H and C for two-species experiments, species O to polarize alleles in species H, C, and G for three-species experiments, and species B to polarize alleles in species H, C, G, and O for four-species experiments.

We generated 400 neutral replicates under the five-species demographic history, and 200 replicates for each scenario featuring alleles under balancing selection. We parsed each replicate such that the informative sites include only intraspecies polymorphisms and interspecies substitutions that agree with the phylogeny. We provided K-species HKA variants with the proportion of each type of informative site computed across the entire set of neutral replicates. We provided K-species T₁ and T₂ variants with polymorphism and substitution configurations and site frequency spectra computed across the entire set of neutral replicates, in addition to the interspecies coalescence times calculated from known simulation parameters. We applied all K-species variants of HKA and NCD with sliding windows of length 1 kb with a step size of 500 nucleotides to advance the window. To match the approximate quantity of data utilized by each summary statistic, we provided K-species variants of T₁ and T₂ with 10 informative sites on either side of the test site.

Empirical Data Analyses

We used allele frequency data of all ten unrelated western chimpanzee individuals from the PanMap Project (Auton et al. 2012), as well as 108 African human individuals of the YRI population from the 1000 Genomes Project (1000 Genomes Project Consortium 2015). The data for the two species were originally mapped to the chimpanzee panTro2 (March 2006, Washington University Build 2 Version 1) and the human hg19 (February 2009, GRCh37 Genome Reference Consortium Human Reference 37) reference genomes, respectively. We mapped the chimpanzee variant call data to hg19, and used the sequence information from the gorilla gorGor3 reference genome (Kent et al. 2002, downloaded from UCSC Table Browser) to polarize alleles as ancestral or derived. Aligned sites that are not included in the variant call data sets were assumed to be monomorphic for the reference allele, and only biallelic single-nucleotide sites segregating across lineages from all three species were considered. Moreover, we only considered genomic regions mappable among all three species, and regions of human reference genome hg19 that did not uniquely map to chimpanzee reference genome panTro2 were also removed.

To circumvent potential mapping issues from paralogs, we performed one-tailed tests on both chimpanzee and human data for Hardy–Weinberg equilibrium as described by Wigginton et al. (2005), and discarded sites with excessive heterozygosity in each data set as determined by p-values <${10}^{-4}$. For the one-tailed Hardy–Weinberg test in humans, we used human genotype data from all individuals in the 1000 Genomes Project, as mapping issues would manifest across all populations, and the larger sample would increase power to reject Hardy–Weinberg equilibrium. Moreover, this pooling of individuals is not affected by the Wahlund effect (Wahlund 2010), as we specifically performed a one-tailed test to uncover sites with excess heterozygotes rather than also testing for excess homozygotes. Further, we discarded genomic regions with 100-mer mappabilities (i.e., CRG scores computed by Derrien et al. 2012) <1.0. We also removed all variants that intersected segmental duplications annotated in hg19 or simple repeats annotated in panTro2, as well as all repetitive regions in both hg19 and panTro2 suggested by repeatMasker (all obtained from UCSC Table Browser; Kent et al. 2002). Matching the filtered data, we adopted the inferred recombination map of human hg19 reference genome (International HapMap Consortium 2007), and removed the chromosomal regions not covered by the map. We then examined the proportions of polymorphism and substitution, derived allele frequency spectra, and estimated human–chimpanzee interspecies coalescence time (Prado-Martinez et al. 2013) for consistency with our expectations.

To assign p-values to test sites in our empirical scan, we employed the coalescent simulator ms (Hudson 2002) and generated $5\times {10}^7$ independent replicates of 25-kb-long sequences. We simulated a three-species demographic history, with parameters for the YRI human population adopted from Terhorst et al. (2017), and from Prado-Martinez et al. (2013) for chimpanzees and gorillas. Specifically, for temporal changes in great ape population sizes, we used the parameters estimated by PSMC in Prado-Martinez et al. (2013). For humans, we adopted the SMC++ estimates of Terhorst et al. (2017). For the split times between humans and chimpanzees, and between humans and gorillas, we adopted the ILS CoalHMM estimates reported by Prado-Martinez et al. (2013). For all simulated sequences, we assumed a generation time of 20 years, a uniform mutation rate of $1.25\times {10}^{-8}$ per site per generation and a uniform recombination rate of ${10}^{-8}$ per site per generation (as used by Terhorst et al. 2017). For each sequence, we applied $T_{2,\text{trans}}$ on the first 201 informative sites to compute a single score at the 101st informative for each simulated replicate, with the same parameters adopted in the empirical scan, including interspecies coalescence time, genome-wide proportions of polymorphisms and substitutions, as well as genome-wide estimates of the site frequency spectra of both species.

To further interrogate the footprints uncovered in candidate regions, we reexamined the sequencing quality in both humans and chimpanzees at these regions. We obtained the BAM files of mapped sequencing reads for each human and chimpanzee individual included in this study, and generated whole-genome maps of sequencing depth across individuals. For each genomic region, we computed the mean sequencing depth across individuals from the same species, and flagged regions with more than half of the sampled individuals devoid of sequencing reads. Furthermore, to investigate whether copy number variation could have contributed to false signals due to technical artifacts, we took advantage of the human copy number variation map provided by the DECIPHER project (Firth et al. 2009), and performed another scan with $T_{2,\text{trans}}$ applied to data with regions containing copy number variation further filtered. Moreover, we also separately applied the single-species T₂ statistic (DeGiorgio et al. 2014) on human and chimpanzee data to examine whether there was concordance with shared signals identified from our $T_{2,\text{trans}}$ scan. Specifically, to ensure the data used in the scans within each species were comparable, we only considered sites that were mappable across hg19, panTro2, and gorGor3 reference genomes, and that have passed all the aforementioned filters. For application to human (chimpanzee) data, we applied T₂ on sites that were either polymorphic within human (chimpanzee) or substitutions with respect to gorGor3.

Supplementary Material

Supplementary data are available at Molecular Biology and Evolution online.