Boolean Network Modeling in Systems Pharmacology

Abstract

Quantitative systems pharmacology (QSP) is an emerging discipline that aims to discover how drugs modulate the dynamics of biological components in molecular and cellular networks and the impact of those perturbations on human pathophysiology. The integration of systems-based experimental and computational approaches is required to facilitate the advancement of this field. QSP models typically consist of a series of ordinary differential equations (ODE). However, this mathematical framework requires extensive knowledge of parameters pertaining to biological processes, which is often unavailable. An alternative framework that does not require knowledge of system-specific parameters, such as Boolean network modeling, could serve as an initial foundation prior to the development of an ODE-based model. Boolean network models have been shown to efficiently describe, in a qualitative manner, the complex behavior of signal transduction and gene/protein regulatory processes. In addition to providing a starting point prior to quantitative modeling, Boolean network models can also be utilized to discover novel therapeutic targets and combinatorial treatment strategies. Identifying drug targets using a network-based approach could supplement current drug discovery methodologies and help to fill the innovation gap across the pharmaceutical industry. In this review, we discuss the process of developing Boolean network models and the various analyses that can be performed to identify novel drug targets and combinatorial approaches. An example for each of these analyses is provided using a previously developed Boolean network of signaling pathways in multiple myeloma. Selected examples of Boolean network models of human (patho-)physiological systems are also reviewed in brief.

Introduction

At the turn of the 21^st century, there has been a paradigm shift, from a reductionist viewpoint of biology, in which the characteristics of individual components are studied in isolation, back towards one that is holistic and aims to understand how the complex interactions amongst components give rise to emergent properties of biological systems [1]. In order to understand such complexities, the integration of experimental and computational methods is sine qua non in systems science [2]. Advances in experimental methods, such as genomics, proteomics, and metabolomics, have enabled the comprehensive assessment of drug-induced alterations in signaling pathways. Systems pharmacology is an emerging discipline that integrates principles from systems biology and pharmacology to study the effects of drugs on biological systems. To gain a quantitative understanding of how a biological system responds to drug exposure, pharmacokinetic/pharmacodynamic (PK/PD) and systems biology models can be combined to form quantitative systems pharmacology (QSP) models [3,4]. Although QSP is still in its infancy, this field has great potential to impact drug discovery, development, and utilization. QSP models require vast amounts of data in order to characterize the complex dynamics of system components, which are multi-scale (i.e., temporospatial differences from molecular to physiological scales) and often unavailable or highly variable. Therefore, a mathematical framework that does not require knowledge about kinetic parameters, such as Boolean network modeling, could provide an initial foundation for the development of QSP models.

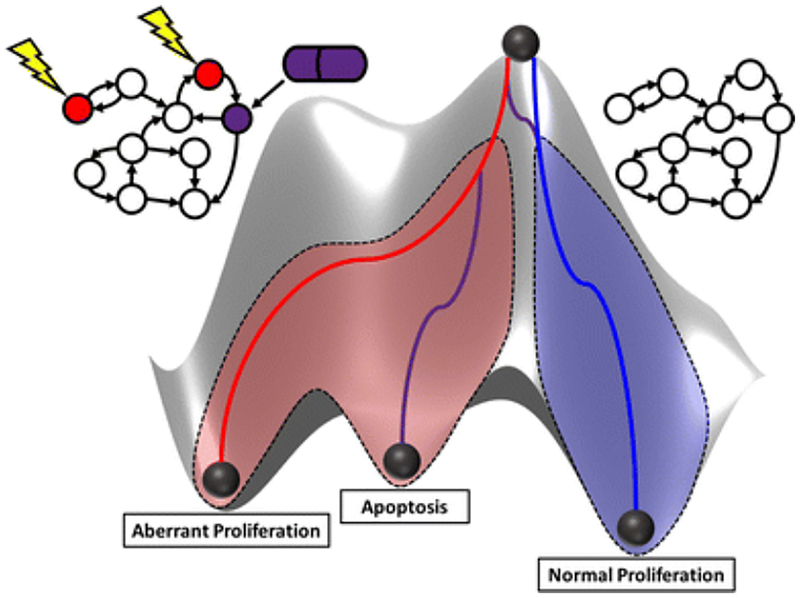
The major challenge in biological network modeling is to map how system components interact amongst each other to give rise to physiological functions, disease processes, and variable responses to therapy. There are several types of biological networks, such as gene regulatory, protein-protein interaction, metabolic, and signal transduction networks, which differ based upon how nodes (vertices) and edges are defined. Nodes often represent genes, proteins, or other biological components, and edges between nodes reflect regulatory relationships (stimulatory/inhibitory). The principles of graph theory can be used to model the interactions of intracellular components as a network [5], and topological analyses, such as centrality measures and clustering techniques, can identify important components and functional modules [6]. Network-based analyses serve to evaluate disease and drug effects on the entire system, rather than individual components, which can lead to the identification of novel drug targets, improvement of therapeutic efficacy, and minimization of toxicity [7]. Conceptual biological networks can be converted to dynamical models through the incorporation of a mathematical formalism that allows the concentration or activity of components to change over time. Time is defined as discrete, represented as finite time steps/intervals, or continuous, and the state of components can be qualitative or quantitative. Although quantitative and continuous mechanistic models are preferred [8], most interaction networks have not been studied in such detail, and qualitative logic-based models may provide key insights into systems in the absence of rich quantitative measurements [9]. Boolean networks, originally described by Kauffman in 1969, are the simplest type of discrete dynamic models [10]. Nodes occupy a state of either 1 or 0, which indicates whether the concentration/activity is above or below an activation threshold. The state of each node is governed by the previous states of its regulating nodes through a set of logical functions. Boolean networks have been applied to model signal transduction, gene regulation, and cellular differentiation for several types of physiological and pathophysiological systems, such as the immune system and related diseases [11–23], breast cancer [24–29], gastrointestinal cancers [30–32], hepatic cancer [33,34], lung cancer [35], and several others [36–40]. In oncology, Boolean network modeling can provide a framework for studying system trajectories under pathophysiological conditions and in response to drug treatment. A network state space contains all possible combinations of states for which nodes of the network can reside, and an attractor is a stable set of states that other states evolve towards, manifesting as cellular phenotypes and fates [41,42]. Waddington, inspired by dynamical systems theory, proposed the concept of an “epigenetic landscape” and described a metaphor of a ball traversing a landscape of cellular differentiation processes [43]. Considering network state space, the ball would correspond to an initial set of states, and valleys would correspond to basins of attraction that lead to attractors. Figure 1 is an adaptation of Waddington’s epigenetic landscape showing a normal cell trajectory (blue) and an abnormal trajectory (red), in which a cell becomes cancerous through the accumulation of mutations. In this diagram, a pharmacological intervention (purple) could shift the abnormal trajectory towards one that is favorable, whether it falls back to the normal trajectory or into an apoptotic attractor. Quantifying the frequency at which initial states reach an attractor identifies the relative importance of each attractor and its associated biological phenotype, underscoring the utility of performing attractor analyses on Boolean networks.

Fig. 1.

Waddington’s epigenetic landscape from a systems pharmacology perspective. Lines represent the trajectories of the ball towards valleys. Valleys are represented as attractors of normal proliferation, aberrant proliferation, or apoptosis. The unperturbed network (right) is representative of a trajectory towards a healthy normal attractor (blue), whereas a network that has gained mutations in specific nodes (left) is representative of a trajectory towards a neoplastic attractor (red). Yellow bolts indicate nodes that have been mutated. A pharmacological intervention (purple) may shift the trajectory towards one that is favorable, whether it is back towards normal proliferation or apoptosis. Adapted from [43].

In this review, we highlight the applications of Boolean network modeling in systems pharmacology as well as provide examples of various analyses using a previously published Boolean network of signaling pathways in multiple myeloma [23]. The process of Boolean network development is described, which includes construction of an interaction network, conversion of an interaction network into a Boolean framework, determination of initial conditions, network validation, and reduction. Types of Boolean network analyses useful in drug discovery and development are covered, such as dynamic simulations, attractor analysis, and minimal intervention analysis. Finally, a brief overview is provided of previously developed Boolean networks of human intracellular physiology/pathophysiology and their various applications.

Network Development

In this section, steps involved in the development of Boolean network models are covered, which consists of constructing an interaction network, adding Boolean logic, determining initial conditions, and network validation. In addition, network reduction techniques are reviewed for deriving smaller networks for certain applications.

Constructing and Analyzing an Interaction Network

Network construction begins with compiling a list of nodes relevant to the biological outcome of interest. The type of network is determined according to how vertices (nodes) and edges are defined. Nodes typically represent different biological components, such as DNA, RNA, proteins, and metabolites. The regulatory interactions between these components, either stimulatory or inhibitory, are modeled through the incorporation of edges. The network may contain several different types of regulatory relationships, such as protein-protein interactions observed in signal transduction and DNA-protein interactions in transcriptional and translational processes. Network components are often derived from the literature and supplemented with experimental data. If a pre-existing model is available (also referred to as a prior knowledge network), then the network could be expanded for a specific purpose, such as to include the mechanism of action of a drug or a pathway of interest. There are two main approaches for identifying nodes and pathways to include in the development of interaction networks. First is a bottom-up knowledge-driven approach that consists of an extensive literature evaluation and the use of biological pathway databases (e.g., KEGG and Reactome) and text mining software (e.g., Chilibot) [44–46]. Second is a top-down data-driven approach, which identifies differentially expressed components (i.e., genes, proteins, and/or metabolites), from omics-based analyses and bioinformatics resources (e.g., DAVID and IPA), to perform functional annotation and biological pathway mapping [47]. A knowledge-driven approach is time intensive, whereas a data-driven approach is more resource intensive. Nodes and pathways that are important to the biological system may be missed with each of these approaches. Developing a network based primarily on information in the literature may overlook an important feature of the system or require selecting between conflicting results. For the data-driven approach, an important system component may not appear to be differentially expressed depending upon the nature of the experimental design, statistical methods, the time of measurement, and the magnitude of biological variability. Ideally, a hybrid knowledge/data-driven approach should be used to identify important components for the construction of an interaction network. Components of the physiological system of interest could be compiled using a knowledge-based approach and integrated with differentially expressed measurements from a data-driven method. Lastly, the addition of endpoint nodes, representing a biological phenomenon of interest, should be incorporated. For example, networks of cancer typically contain nodes that represent cell proliferation and apoptosis; other endpoint nodes of interest could be DNA damage, epithelial-mesenchymal transition, and metastasis.

Once network components have been complied and edges between them have been defined as either having an activating or inhibiting relationship, a topological analysis could be performed to obtain information about the system. Although this review is focused on dynamical analyses, a brief overview of the graph-theoretical analyses that can reveal nodes of high importance in biological networks is provided, which include measures of closeness, betweenness, degree, and bridging centrality. Closeness centrality of a given node is calculated as the inverse sum of minimal distances between that node and all other nodes [48]. In essence, a central node is one that is, on average, close to other nodes. Betweenness centrality, on the other hand, is the sum of proportions of times that a node is present in the shortest paths between any pair of nodes [49]. Therefore, betweenness indicates the flux of information that is being relayed through a specific point in an active network and reveals the degree to which a node can influence the flow of information in a system [50]. In other words, betweenness centrality allows assessment of functional importance of a node in a wide context of the entire network. If a vertex with high betweenness centrality falls inoperative due to a mutation, the communication between near and distant sites of a network may become less likely or cease completely. Degree centrality is based on the notion that central nodes are ones with the most connections. Node degree refers to the number of edges that a node shares with other nodes, which can be divided into the number of edges that lead to the node (in-degree) and edges that originate from the node (out-degree). These measures are not necessarily correlated. Joy et al. examined a yeast protein interaction network and discovered a wide occurrence of proteins with high betweenness but low connectivity [49]. These proteins may act as essential bridges between various modules within a network, and their presence could be explained by adaptive evolutionary mechanisms or inherent system constraints. Assessments of bridging centrality can pinpoint elements of the system that might cause network failure if disrupted, and this property may be particularly useful for identifying targets in drug discovery [6]. Aside from centrality measures, clustering analysis can determine the tendency of vertices to create tightly packed regions with dense links, and this tendency is referred to as a clustering coefficient. Global clustering coefficients give an overall indication of the clustering within a network based upon three connected nodes [51]. In contrast, a local clustering coefficient reflects the local density of single nodes [52]. Compared to random networks of equivalent size and degree distributions, nearly all known real networks exhibit high clustering, which gives rise to functional modules [5]. Although topological analyses allow for the identification of important network nodes, an interaction network needs to be converted into a dynamical form in order study how components respond to perturbations and evolve over time.

Converting an Interaction Network to a Boolean network

After an interaction network has been constructed, the next step is to use Boolean logic to describe regulatory interactions amongst species of the network. A Boolean network G(V, F) contains a set of nodes, V = {x₁, …, x_N} and a list of Boolean functions, F = (f₁, …, f_n). A Boolean function is assigned to each node $f_i\left(x_{i_1},\dots ,x_{i_k}\right)$, where k is the in-degree of a node. The spatiotemporal dynamics of Boolean networks are discrete, and the state of each node is binary, x_i ∈ {0,1}, i = (1, …, N). Nodes of the network are updated based upon the states of its regulators at the previous time-step:

$$x_i(t+1)=f_i\left(x_{i_1}(t),x_{i_2}(t),\dots ,x_{i_k}(t)\right)$$ (1)

The state of a node can be either zero (OFF) or one (ON) by solving the Boolean function assigned to that node. Updating nodes for multiple time steps, in a synchronous manner (all nodes are updated at the same time), generates an arbitrary time-course for the dynamics of each node. Other updating methods include asynchronous, probabilistic, and continuous approaches, which are described in detail later. Boolean functions represent the relationships between a node and its regulators through the incorporation of Boolean operators, such as AND (∩), OR (∪), and NOT (~). The NOT operator is used to describe an inhibitory edge. For example, if B inhibits A, then the Boolean function assigned to node A would be A = ~(B). The AND and OR operators are used when a node is regulated by at least two nodes. For example, if A is activated only when both B and C are present, then the Boolean function assigned to node A would be A = (B ∩ C). If either B or C activates A, then the expression is A = (B ∪ C). The combination of Boolean logic operators to describe complex interactions between biological components provides a simplistic yet robust framework to model the qualitative dynamics of biological systems.

The Boolean operator that best represents the complex interactions between a node and its multiple regulators can be determined through experimental studies. Gene knockout or pharmacological inhibition studies are useful for determining which Boolean operator to assign. For cases in which there are multiple regulators and insufficient experimental data to justify an AND relationship, one approach is to assume an OR relationship for stimulatory edges and AND NOT relationships for inhibitory edges. Flobak et al. describes the application of this approach in the development of a Boolean network for cell fate decisions in gastric cancer [30]. A signaling component is active if any of its regulatory activators are active, while at the same time none of its regulatory inhibitors are active. For example, if node A is affected by activators (B, C, and D) and inhibitors (E, F, and G), then expression of A would be:

$$A=(B\cup C\cup D)\cap ~(E\cup F\cup G)$$ (2)

Multiple Boolean networks could also be generated in order to select the best network that describes experimental findings. CellNOptR (CellNetOptimizerR) is an R package developed for logic-based model selection that utilizes a prior knowledge/interaction network, to identify logic functions to describe an experimental data set [53]. For each node with multiple regulators, CellNOptR generates all possible logic gates and evaluates each against high throughput experimental data in order to determine the most appropriate Boolean network. Saez-Rodriguez et al. (2011) applied this approach to generate approximately 10³⁸ Boolean networks of immediate-early signal transduction pathways in order to compare signaling networks between primary hepatocytes and four hepatocellular carcinoma (HCC) cell lines [33]. Boolean networks that best characterized normal and transformed hepatocytes were determined by minimizing an objective function (θ) based on the sum of the mean squared error between experimental data and model predictions and a penalty for increasing model size:

$$\theta =\frac{1}{n_E}{\sum }_{k=1}^s{\sum }_{l=1}^m{\sum }_{t=1}^n{\left(B_{k,l,t}^M-B_{k,l,t}^E\right)}^2+\alpha \frac{1}{v^S{}_e}{\sum }_{e=1}^r{v}_e{P}_e$$ (3)

with $B_{k,l,t}^M\in \{0,1\}$ and $B_{k,l,t}^E\in \{0,1\}$ as model predictions and discretized observed data. The function is summed across endpoints (m), time points (n) and experimental conditions (s) and is weighted by the total number of data points (n_E). The penalty for model size is calculated by weighting each solution (P_e) by the number of regulating nodes (v_e) for each hyperedge (r), where hyperedges are defined as edges that allow multiple inputs and have one output. This accounts for the fact that AND gates have multiple inputs and should carry a greater penalty. Hence, an AND gate with two inputs will carry the same penalty as two regulating nodes with an OR operator. The size penalty is also normalized to the total number of tail nodes in the network $\left(v_e^S={\sum }_{e=1}^r{v}_e\right)$ and is multiplied by a tunable parameter (α), which was fixed to 0.0001. This optimization algorithm resulted in several models that differed slightly in structure but had nearly the same value of the objective function. Models that best fit the data and differed by 1% in goodness of fit were grouped together and retained as a family of models representing either primary hepatocytes or HCC cells. On comparison, several pathway differences in signaling networks were identified amongst primary hepatocytes and HCC cells. The existence of a new interaction between Jak-Stat and NFκB signaling was inferred, which was found to arise from the polypharmacology of an IκB kinase inhibitor rather than a new protein-protein interaction. This application illustrates an automated approach to converting an interaction network to a Boolean model. To address identifiability concerns the incorporation of several high throughput data sets with multiple perturbations as well as novel model-selection criteria could aid in the identification of a unique model.

Extensions of classic Boolean networks have been implemented in order to address certain limitations. Shmulevich et al. developed probabilistic Boolean networks (PBNs) for gene networks to overcome the deterministic rigidity of classic Boolean models [54]. PBNs are defined as a collection of Boolean networks in which a constituent network governs the states of nodes for a random period of time until another randomly chosen constituent network takes over. In PBNs nodes, V = (x₁,…, x_n), are assigned a set of possible Boolean predictor functions, $F_i=\left\{f_1^{(i)},f_2^{(i)},\dots ,f_{l(i)}^{(i)}\right\},$ where $f_j^{(i)}\left(1\le j\le l\left(i\right)\right)$ is a possible function determining the value of node x_i and l(i) is the number of possible Boolean predictor functions assigned x_i. Thus, if l(i) = 1 for all i = 1, n, then the PBN reduces to a standard Boolean network. For each time step the probability of choosing $f_j^{(i)}$ as the predictor function is $c_j^{(i)},$ where $0\le c_j^{(i)}\le 1$ and ${\sum }_{j=1}^{l(i)}{c}_j^{(i)}=1$. A realization of the PBN at a given instant of time is determined by randomly selecting a vector of Boolean predictor functions, where the ith element of the selected vector contains the predictor function for node x_i. A PBN consisting of N possible realizations, constituent networks, contains N vectors of Boolean predictor functions, f₁, f₂, f_N of the form, for $f_k=\left(f_{k_1}^{(1)},f_{k_2}^{(2)},\dots ,f_{k_n}^{(n)}\right),$ for k = 1, 2, …, N, 1 ≤ k_i ≤ l(i) and where $f_{k_i}^{(i)}\in F_i(i=1,\dots ,n)$. The vector function $f_k:{\{0,1\}}^n\to {\{0,1\}}^n$ acts as a transition function that represents a possible realization of the PBN. Each of the possible N realizations can be viewed as a standard Boolean network responsible for transitioning the network through its state space prior to randomly switching to another network to drive the updates. In other words, at every state x(t) ∈ {0,1}ⁿ, one of the N Boolean networks is chosen and used to transition to the next state x(t + 1) ∈ {0,1}ⁿ. Assuming the selection of Boolean functions for each gene are independent of each other, the number of possible realizations is $N={\prod }_{i=1}^{n}l(i)$ and the probability of selecting the kth Boolean network is defined as $P{r}_k={\prod }_{i=1}^n{c}_{k_i}^{(i)}$. At each update, a decision is made to switch the constituent network based upon a binary random variable (λ). If λ = 0, then the current network is retained, whereas with λ = 1, a constituent network is randomly selected from amongst all constituent networks according to its probability distribution ${\left\{c_k\right\}}_{k=1}^N,{\sum }_{k=1}^N{c}_k=1$. The switching probability q = Pr(λ = 1) is a system parameter. When q = 1, a switch of constituent networks is made, and the PBN is said to be instantaneously random. Whereas if q < 1, the current constituent network is used for transitions until a switch is called for (λ = 1), a case termed as context sensitive. The dynamics of PBNs can be framed within the theory of Markov chains, with or without perturbations. Probabilistic Boolean models can be developed and analyzed using the Matlab-based toolbox BN/PBN (https://code.google.com/archive/p/pbn-matlab-toolbox/) or the R-package BoolNet [55]. A Matlab-based toolbox (optPBN) has been developed for the generation and optimization of probabilistic Boolean networks [56]. Overall, this framework introduces stochasticity to overcome the deterministic rigidity of original Boolean networks and enables a different analysis of the systems attractors since state transitions are random. Determining the steady-state probability distribution for nodes in a network provides quantitative insights into the long-term regulation of gene expression [57]. Methods have been developed to solve and approximate the steady-state probability distribution of PBNs [58,59]. The application of PBNs for describing and analyzing complex biological systems has been reviewed [60]. PBN modeling has been used as a mathematical framework to describe cancer-specific intracellular signaling of deregulated platelet-derived growth factor in gastrointestinal stromal tumors and the differential regulation of L-plastin phosphorylation by genes of the ERK/MAPK pathway across four breast cancer cell lines [31,61].

To address the spatial limitations of Boolean network modeling, multi-state models can be developed. In a three-state model, nodes may take on three different values, such as x ∈ {0,1,2} or x ∈ {−1,0,1}. These states represent underactive (downregulated), normal activity, and overactive (upregulated). For example, Flobak et al. constructed a logical network of gastric cancer and allowed two output nodes (i.e., Prosurvival and Antisurvival) to take on four values (0, 1, 2, or 3), and their immediate upstream nodes could take on three values (0, 1, or 2) [30]. The software packages GINsim and CellNetAnalyzer both support the construction and analysis of multi-state logical models [62,63].

For temporal limitations of Boolean networks, the discrete time scale can be converted into a continuous one. Odefy is a matlab-compatible toolbox that has been developed to convert Boolean networks into a system of ODEs [64]. For example, Chudasama et al. converted a Boolean network of signaling pathways in multiple myeloma to a system of ODEs to simulate the dynamics of species for select inhibitors as well as to ensure the dynamics are consistent between the full and reduced networks [23]. Another method known as the standardized qualitative dynamical systems method (SQUAD) can convert a Boolean network into a continuous dynamical system [65]. This method was used to convert a B cell regulatory network into a continuous dynamical model, which enabled the identification of additional fixed point attractors that could be viewed as intermediate unstable transition states in the differentiation process [14]. The benefit of this approach is that it enables the construction and analysis of species dynamics, in a continuous manner, despite the lack of kinetic information. The conversion of a Boolean network into a series of ODEs could provide an initial framework for the development of quantitative systems pharmacology models [23].

Determining Initial Conditions

Once an interaction network has been converted to a Boolean network, the next step is to determine the initial condition of the network, which will be further denoted as the control attractor. The control attractor represents the initial states of nodes in the network when the biological system is at rest, which can be difficult to determine since there is not a formalized method to identify this initial resting state. Quantitative information for each node regarding the basal level of expression and a threshold concentration or activation required to activate/inhibit a downstream component would be ideal. If the concentration or activity of a species at resting conditions, prior to perturbations, is below a threshold of activation, then the initial state of the node would be 0. In contrast, if concentrations are above an activation threshold, then the initial state would be 1 [66]. Thus, the definition of the initial states should not be confused with the absence or presence of a component. Since quantitative information for all of the processes within a complex system is often unknown, a combination of known a priori information about the baseline activity of biological components along with sampling the network state space can be used to determine the control attractor. Determining the initial conditions of network components has been reviewed before [66]. Here we have provided a stepwise process that can be used as a guideline for obtaining initial conditions.

1. Obtain information about the resting concentration/activity and threshold of activation for network components.

2. Convert available a priori quantitative data of concentrations/activity of network components into binary qualitative states.

3. Use converted binary values to perform a logical steady state analysis in order to obtain a set of nodes that have fixed states.

4. Utilize the set of nodes with fixed states to perform an attractor analysis in order to identify attractors in which the system resides.

5. Analyze the identified attractors in the network and select the attractor that best represents a known biological resting condition.

Initial states for input nodes, such as ligands and drugs, are often known. Initial states of the input nodes along with additional a priori information about a biological relevant resting state, can be used to determine the fixed states of downstream nodes via its logical steady state. If there are nodes that remain undefined, an exhaustive exploration of all remaining initial states can be performed to identify attractors. To select an attractor that represents a control attractor, amongst all possible attractors of the system, the attractor with the highest frequency of being reached or the attractor that best corresponds to a relevant biological phenotype can be selected. If discrepancies exist between initial states of the nodes in the control attractor and known information about a biological resting state, this would indicate a model misspecification in the networks structure or Boolean logic functions.

Network Validation

Once a Boolean network has been developed, the network should be validated by comparing model predictions with experimentally obtained data. Network validation is a crucial step in the development process in order to gain confidence in model predictions. Experimental data sets should include several molecular perturbations and cover a broad range of signaling pathways included in the model in order to avoid fine-tuning towards a specific scenario and enhance model predictions under new conditions. Several experimental methods can be used to validate components of the network. Small molecule drugs, biologics, and gene editing can alter the expression of specific biological components, and downstream elements can be measured using various immunoassays, such as Western-blots and enzyme linked immunosorbent assays (ELISA). For validation, the qualitative change in expression of proteins or genes downstream of the perturbed target can be compared to network predictions. A time-course for the change in expression is desirable in order to confirm that the model recapitulates intermediate states as well as long-term behavior. Given the size and complexity of biological networks, obtaining experimental data for the behavior of every node under multiple perturbations is not practical with classical methods. However, advanced analytical approaches, such as large-scale transcriptomic and proteomic analyses, can provide insights in to how the entire biological system responds to individual or a combination of perturbations. For example, the Gene Expression Omnibus (GEO) is a public data repository that contains microarray, next-generation sequencing, and other high-throughput functional genomic data that could be used for gene network validation [67].

Prior to comparing network simulations with an experimental data set for validation, the initial states of the network should align with a known biological resting state. For anticancer chemotherapy, cancer system nodes pertaining to cell growth, proliferation, and survival should be ON, and nodes representing senescence or apoptosis should be OFF. Opposite outcomes in the control attractor would, indicate that the network structure is incomplete or there is an error in the Boolean logic functions. Once the control attractor is in agreement with the known resting condition, network simulations can be performed and compared against the trends of differentially expressed genes, proteins, or metabolites for a perturbation of interest. Here we discuss network validation using a synchronous updating scheme due to ease of interpretation. Simulations should be performed until an attractor is reached. The states of nodes in the control attractor, compared to a new attractor, indicate that a node is increasing (0/1 → 1) or decreasing (0/1 → 0) in expression. Since the states of nodes are binary, a node expressing a state of one (or zero) in both the control and new attractors can be viewed as either increasing (or decreasing) or remaining the same. An oscillatory state, as in the case of cyclic attractors, could be viewed as having a state between zero and one. A metric for network validity can be obtained by calculating the number of node states that correspond with differentially expressed components relative to the total number of comparisons. For semi-quantitative validation, an asynchronous updating scheme with random sampling or the conversion to ODEs can project a trajectory for the fractional activation of nodes, which can be compared with experimental measurements.

Network Reduction

Due to the complex nature of gene regulatory and signal transduction networks, network size can lead to problems that are computationally infeasible to solve. Therefore, in order to reduce complexity but maintain important system properties, a network reduction algorithm can be implemented to reduce the size of the network. The state space of a Boolean network is a finite and discrete number equal to 2^N, where N is the number of nodes in the network. Since the network state space increases exponentially as a function of the number of nodes, network size can limit the ability to perform certain types of analyses. The time that an algorithm takes to identify attractors of the system increases exponentially with the number of nodes: O(2^N) [68,69]. Therefore, the identification of attractors in large networks by searching entire state spaces can become unfeasible. To address this challenge, Boolean network reduction algorithms have been proposed to reduce the number of nodes and the network state space. Network reduction algorithms can be applied to obtain a final reduced network or as an immediate step prior to further analysis. In either case, the overall goal is to reduce the network to a reasonable size while conserving inherent complex dynamics, topological features, and attractors.

Nodes that exhibit the same state throughout all attractors, initially termed stable variables/elements, are commonly referred to as frozen nodes. Bastolla and Parisi showed that in order for a node to be relevant and have an effect on the dynamics of other nodes, it must be unstable (not frozen) and regulate another unstable node [70]. Therefore, methods have been developed to identify and remove frozen nodes [71,72]. Sampling only a subset of possible initial conditions could potentially miss attractors with a small basin size and possibly result in incorrectly identified frozen nodes [72]. To overcome this limitation, novel algorithms have been developed to find all attractors in Boolean networks [73]. Frozen nodes might also emerge through the introduction of constraints on the system. For example, fixing the values of source nodes and performing a logical steady-state analysis will identify nodes whose state does not change [71,74,75]. However, this simplifying assumption must be biologically justifiable. Similarly, Zañudo and Albert developed a network reduction approach that identifies motifs stabilized in a fixed state and nodes that become frozen due to their regulation by these stable motifs [76]. Additional topological approaches are proposed and non-functional nodes and edges can be removed using Boolean algebra. A common method is to remove mediator nodes, which are defined as nodes that have both an in-degree and out-degree equal to one [77,75]. These nodes are seen as non-functional as they serve only as an intermediate between the information flow of two other nodes. Leaf nodes, also known as terminal nodes, have an out degree of zero and can be removed if they are not important for network analyses [72]. Another method iteratively removes nodes while maintaining self-regulatory nodes, which likely results in an oversimplification of complex network dynamics [78].

A simplistic stepwise reduction method is to:

1. Remove irrelevant source (in-degree = 0) and leaf nodes (out-degree = 0)

2. Remove mediator nodes (in-degree and out-degree = 1)

3. Remove quasi-mediator nodes (in-degree or out-degree = 1)

4. Remove frozen nodes (fixed to 0 or 1 in all attractors), if frozen nodes are upstream of network perturbations of interest and there are no feedback loops.

Nodes with either an in-degree or out-degree of one, or quasi-mediator nodes, can also be removed. However, the conservation of attractors upon the removal of quasi-mediator nodes has not been mathematically proven. In addition, the order in which quasi-mediator nodes are removed may have an impact on the final reduced network structure. Lastly, frozen nodes can be identified and removed, either through identifying all attractors in the network or by fixing source nodes followed by a logical steady-state analysis. However, since network perturbations can transform attractors and potentially “unfreeze” nodes, frozen nodes should be removed with caution. One suggestion is to only remove frozen nodes that are not in the path of network perturbations of interest.

Boolean Network Analyses

In this section, a variety of network simulation and analysis techniques are introduced that can be used to evaluate how drugs affect the qualitative dynamics of species in the network. We describe and compare network simulations using synchronous, asynchronous, and HillCube updating methods. In addition, techniques that are useful for identifying and evaluating drug targets and combination therapies are described, specifically minimal intervention and attractor analyses.

Network Simulations

There are a wide range of perturbations that can be tested, both internal and external, such as small molecule drugs, biologics, and gene modifications. Boolean network simulations are commonly performed to determine the qualitative effects of therapeutic perturbations. For cancer, the dynamics of intracellular components are simulated to reveal their state in newly reached attractors, which are related to biological phenotypes [42], such as apoptosis, quiescence, differentiation, and proliferation [79]. A comparison of attractors in which the system resides, before and after a perturbation, may provide insight into the probability of therapeutic interventions. The shift from a proliferative attractor towards an apoptotic attractor would indicate a favorable response. In certain cancer networks, other attractors may exist that represent additional complex phenotypes such as the epithelial-mesenchymal transition, which has been described in a Boolean network model of TGFβ signaling in hepatocellular carcinoma [34]. In order to simulate the effect of a drug perturbation, the mechanism of action of the drug must be within the scope of the network, and a node for the drug is introduced and stimulatory/inhibitory edges are drawn from this node to all of the drug targets. Drugs often have multiple direct and indirect targets, and thus it is critical to incorporate all possible mechanisms in order to add confidence in model predictions. An incomplete understanding of mechanisms of drug action can create a major challenge to implementing Boolean networks for systems pharmacology applications. Networks for drugs that are promiscuous or interact with yet unknown targets are difficult to define. An option under such conditions is to identify drug targets through the integration of direct biochemical, genetic interaction, and computational inference methods [80]. Coupling gene expression signatures following drug exposure and computational inference methods to identify drug-target interactions has shown promise. For example, the Connectivity Map has been used to generate hypotheses about mechanisms of action of uncharacterized small molecule drugs by comparing their gene expression profile against gene expression profiles of reference compounds with known targets [81]. This comparative analysis approach was used to identify the mechanism of action of gedunin, an HSP90 inhibitor. Network-based approaches have been used to identify drug-target interactions by using gene expression profiles to infer the mechanisms of drug action based upon the perturbation of gene regulatory and protein-protein interaction networks. Detecting Mechanism of Action by Network Dysregulation (DeMAND) and Protein Target Inference by Network Analysis (ProTINA) are two network-based methods that infer drug-target interactions from gene expression profiles [82,83]. These two methods were compared, and ProTINA exhibited superiority over DeMAND for predicting known targets of drugs across three datasets: NCI-DREAM drug synergy challenge [84], a genotoxicity study [85], and a chromosome drug targeting study [86].

In addition to external perturbations, internal perturbations of species that already exist in the network are useful for emulating the effects of mutations and over/under expressed components. For a gain of function mutation (knock-in) or gene/protein overexpression, the state of a particular species would be fixed to one. Regardless of the states of its regulating nodes, the state of the mutated node will always be one. For a loss of function mutation (knockout) or gene/protein repression, the state would be fixed to zero. Alternatively, the transient modification of a node can be incorporated to model a pharmacological intervention and a permanent modification of a node to model a gene knock in/out. For a transient effect, the state of a node could be modulated for a defined number of time-steps. Simulations of multiple perturbations can be performed, which enables the assessment of combinatorial drug regimens, drug effects in the presence of specific gene mutations, and variability in therapeutic response due to individual genetic differences.

Synchronous updating is the original and simplest method used to simulate the dynamics of Boolean networks [10]. In Equation 1, the states of nodes are updated in a time-discretized fashion, in which the future state of a node (t+1) is a function of the current states (t) of its regulators. The states of all nodes are updated at the same time, based upon their previous states. A limitation of the synchronous updating scheme is that it makes the assumption that all biological processes in the network occur at the same rate. This assumption is unrealistic as most biological networks include a temporal distribution of cellular processes, such as receptor binding, signal transduction, and gene transcription. Synchronous models are deterministic, and the trajectory in a network state space towards an attractor will always be the same given the same initial conditions.

In contrast, one node is updated at any one time interval in asynchronous updating to account for the fact that biological processes occur at different rates [87,88]. Asynchronous updating schemes include stochastic algorithms, such as random order asynchronous and general asynchronous, as well as deterministic asynchronous algorithms. For random order asynchronous models, all nodes are updated sequentially at each time step based upon a randomly generated order [88,89]. The state of node x_i will be updated according to the most recently updated states of its regulator nodes:

$$x_i(t+1)=f_i\left(x_{i_1}\left({\tau }_{i1}\right),x_{i_2}\left({\tau }_{i2}\right),\dots ,x_{i_k}\left({\tau }_{iN}\right)\right)\in \{0,1\},i=1,\dots ,N$$ (4)

with τ_ij ∈ {t, t + 1} and j =1, 2, …, N. If node x_j is updated before node x_i, then τ_ij = t + 1, otherwise, τ_ij = t. In random order asynchronous models each node is updated only once during a full round of updating. In general asynchronous models, a single node is randomly selected to be updated at each time step and the same node can be updated multiple times in a row [88]. In addition, time is normalized to the number of nodes in the network. Each time step is 1/N^th of the time step in a random order asynchronous model. Deterministic asynchronous updating schemes may include fixed individual time scales and delays. Chaves et al. incorporated fixed individual time scales into a deterministic asynchronous model where each node is assigned an intrinsic time unit and is updated at intervals of this time unit [90]. Deterministic asynchronous models are particularly useful when information about the kinetics of biological processes is known. When prior kinetic information is not available, time scales/delays can be randomly sampled from a time interval that is within biological limitations. This allows nodes associated with fast processes, such as receptor binding and protein phosphorylation, to be updated more frequently in comparison to slower processes, such as gene transcription.

Asynchronous simulations have been performed more frequently than synchronous simulations, as the former often offers a better representation of real biological dynamics. Synchronous simulations are able to transition to only one other point in a networks state space at each time step. Hence, the dynamics are deterministically rigid. Asynchronous updating allows for the transition to more than one point in network state space, and simulation results may be different given the same initial conditions. Therefore, multiple asynchronous simulations must be performed and the average state of a node, after a fixed time step or upon reaching an attractor, can be used to represent the node dynamics. In other words, performing X simulations using an asynchronous updating scheme for Y time-steps and calculating the fraction at which the state of a node is ON relative to the total number of simulations indicates how the activation of a species evolves over time. The dynamics of a node fractional activation can be compared with the shape of experimental time-courses. This is particularly useful if the goal is to compare how different perturbations affect outcomes of interest.

Boolean networks can be converted into a system of ODEs to transform discrete time steps into continuous time [64]. Odefy contains three transformation methods, BoolCube, HillCube, and normalized HillCube, which are all based on multivariate polynomial interpolation. The advantage of these techniques is that they bridge a gap between the qualitative dynamics of Boolean network models and quantitative modeling. Discrete dynamics (Eq. 1) are converted into a continuous form:

$$\frac{d{\overline{x}}_i}{dt}=\frac{1}{{\tau }_i}\left({\overline{B}}_i\left({\overline{x}}_{i1},{\overline{x}}_{i2},\dots ,{\overline{x}}_{i{N}_i}\right)-{\overline{x}}_i\right)$$ (5)

Which allows nodes to take on any value between 0 and 1, $x_i\in \{0,1\}\to {\overline{x}}_i\in [0,1]$. The function ${\overline{B}}_i$ describes the production of species ${\overline{x}}_i$, and τ_i is a parameter that represents the species lifetime. For HillCubes, each species is modeled as a Hill function $\left({\overline{x}}_i\right)=\frac{{\overline{x}}_i^n}{{\overline{x}}_i^n+k^n}$, where k corresponds to the activation threshold, and the Hill coefficient n is a measure of cooperativity. In normalized HillCubes, the Hill function is normalized to the unit interval. These logic-based mathematical formalisms have been applied in several models, such as the β-adrenergic signaling pathway and cell growth regulation [91,92].

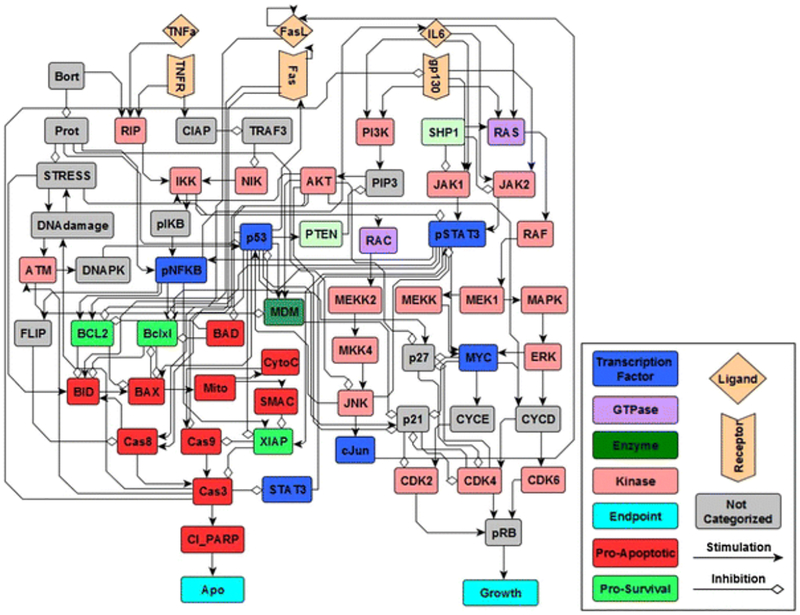
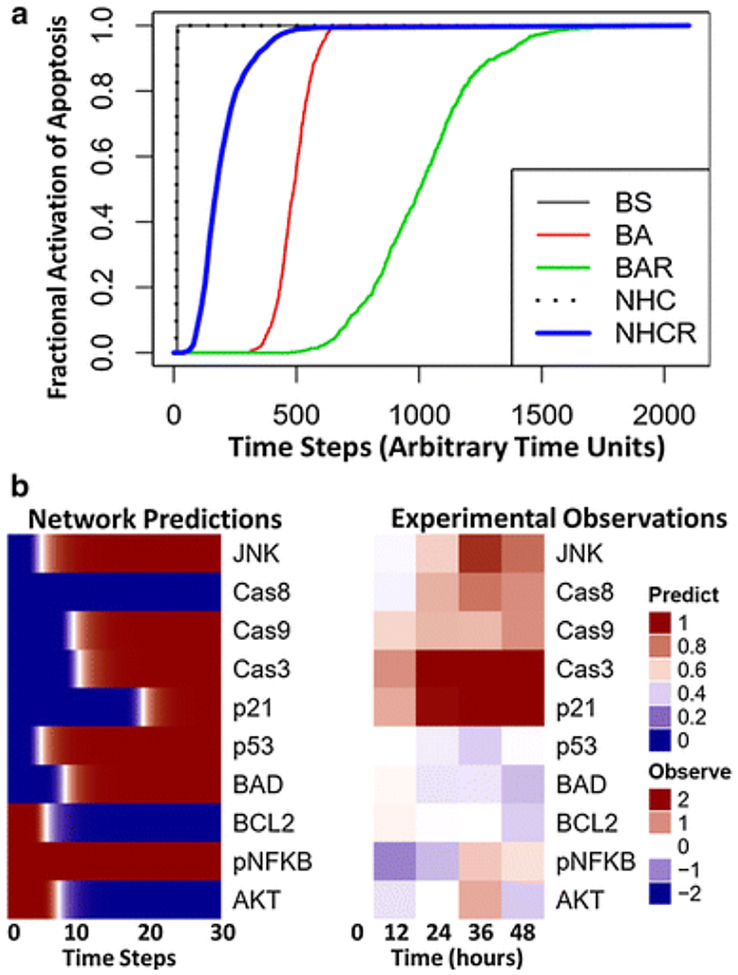
To provide an example of these different simulation methods, we performed simulations using a previously developed Boolean network of intracellular signaling in multiple myeloma (Fig. 2) [23]. We simulated the inhibition of the proteasome by bortezomib, a proteasome inhibitor used for the treatment of multiple myeloma, to obtain a profile for the dynamics of a node that represents apoptosis. We performed and compared five different simulation methods: synchronous (BS), general asynchronous (BA), random-order asynchronous (BAR), normalized HillCube with default parameters (NHC), and normalized HillCube with randomly sampled parameter values (NHCR) (Fig. 3a). For synchronous updating, one simulation was performed, whereas 1000 simulations were performed for the remaining methods, and the average activation of each node was calculated for every discrete time step. We observed that random order asynchronous (green) and normalized HillCube with randomly sampled parameters (blue) display a delayed and slower increase in apoptosis, whereas synchronous (black) and normalized HillCube (dotted black) simulations exhibit an abrupt increase (Fig. 3a). The comparable abrupt increase in apoptosis, between synchronous and normal HillCube methods, can be attributed to the large time scale used in the network simulations. Simulation results for all individual nodes using each method are displayed as heat maps in supplementary materials (Supplementary Fig. S1). Network simulations were compared with a published dataset of select intracellular proteins in U266 multiple myeloma cells exposed to bortezomib (Fig. 3b) [93]. Overall, network simulations capture the general trends of the observed data. However, there are a few discrepancies between network predictions and experimental observations (e.g., Cas8, p53, and BAD), which indicates that the network could be missing some important mechanisms related to bortezomib action or cellular regulation. The Boolean network used in this case study was an early attempt to characterize the complex intracellular signaling dynamics in U266 multiple myeloma cells, and this model has been refined and extended to account for cellular heterogeneity [94].

Fig. 2.

Boolean network model of cellular signal transduction in U266 multiple myeloma cells. Legend shown to the right of the network. Figure adapted from Chudasama et al. (2016) [23].

Fig. 3.

(a) Comparison of five Boolean network simulation methods. Simulations were performed for the effect of bortezomib (proteasome = OFF) on the Boolean network of signaling pathways in multiple myeloma [23]. The fractional activation of apoptosis is determined by dividing the frequency that apoptosis is activated by the total number of simulations (n=1000) across each time step: Synchronous (BS; black line), general asynchronous (BA; red line), random-order asynchronous (BAR; green line), normalized HillCube with default parameters (NHC; dotted line), and normalized HillCube with randomly sampled parameter values (NHCR; blue line). Default parameters values used for NHC simulations were: τ = 1, k = 0.5, and n = 3. Parameter values used for NHCR simulations were randomly generated from a Log-normal distribution with a mean (and standard deviation) of: τ = 1 (1), k = 0.5 (1), and n = 3 (1). (b) Boolean network normalized HillCube simulations compared with intracellular protein dynamics of U266 cells cultured with 3 nM bortezomib for 0, 12, 24, 36, and 48 hours. Data were obtained using a multiplex immunoassay (Luminex® MAGPIX®) and have been described in detail elsewhere [93].

Attractor Analysis

An attractor is a stable set of states that other states evolve toward. Attractors represent stable states of the system and, with respect to cellular signaling networks, can be associated with a biological phenotype or cell fate. Hence, an attractor analysis, which aims to identify all attractors of the network and their relative importance, provides key information about the behavior of the biological system. The basin of attraction, or basin size, of an attractor is the number of initial states that converge towards the attractor. The state space of a network contains a landscape of attractors, where each attractor has its own respective basin of attraction. The network state space can be depicted as a separate network, or state transition graph, where nodes represent sets of states for nodes in the Boolean network and edges indicate the transition of these sets of states towards an attractor. Nodes in Boolean models can take on a value of either one or zero, and a network with N nodes will contain 2^N sets of states in the network state space. The total number of possible initial conditions is finite (2^N) and will eventually be repeated, indicating the existence of an attractor. Fixed points and limit cycles are two types of attractors in Boolean networks, which can be reached by a synchronous updating scheme. A fixed-point attractor is a finite point in the networks state space that does not change with time, meaning that the set of final states repeats indefinitely. A fixed-point attractor is depicted as a node with a self-loop in the state transition network. A limit cycle attractor is a set of points in the network state space through which transitions repeat. In a state transition network, n-limit cycle attractors are depicted as simple loops with n transitions. Fixed point attractors typically correspond with static phenotypes/processes, such as differentiated cell types or activation of apoptosis, whereas limit cycles correspond to oscillatory behaviors, such as calcium signaling, cell cycle, and circadian rhythms. In synchronous Boolean networks, a set of states is able to transition to only one other set of states due to the nature of this updating scheme. In asynchronous Boolean networks, a set of states is able to transition to more than one other set of states. Therefore, different attractors may arise due to differences in the updating scheme between synchronous and asynchronous Boolean networks. In addition to fixed points and limit cycles, asynchronous Boolean networks may also exhibit complex attractors. Complex attractors are sets of states that oscillate irregularly amongst each other.

Analyzing the state space of a network in order to identify attractors is referred to as an attractor analysis. In essence, an attractor analysis consists of multiple dynamic simulations with different initial conditions in order to observe the frequency of reaching each attractor and to determine its basin size. To perform an attractor analysis a networks state space must first be sampled by selecting initial sets of states. An exhaustive search, where all possible initial conditions (2^N) are sampled, is often desired. However, due to computational limitations, simulating all possible initial conditions is unfeasible for large networks. Approaches have been developed to bypass this limitation that are capable of identifying all attractors in a network via model checking, but they are unable to provide any knowledge about the basin size of each attractor [73]. If the basin size of attractors cannot be identified owing to network size limitations, the fraction at which node x is activate across all attractors (S_x) can be calculated:

$$\begin{array}{lll}{S}_x=\frac{{\sum }_{i=1}^{n_{A_{Total}}}{x}_i}{n_{A_{\text{Total}}}}\hfill & x_i\in \{0,1\}\hfill & i=1,\dots ,n_{A_{Total}}\hfill \end{array}$$ (6)

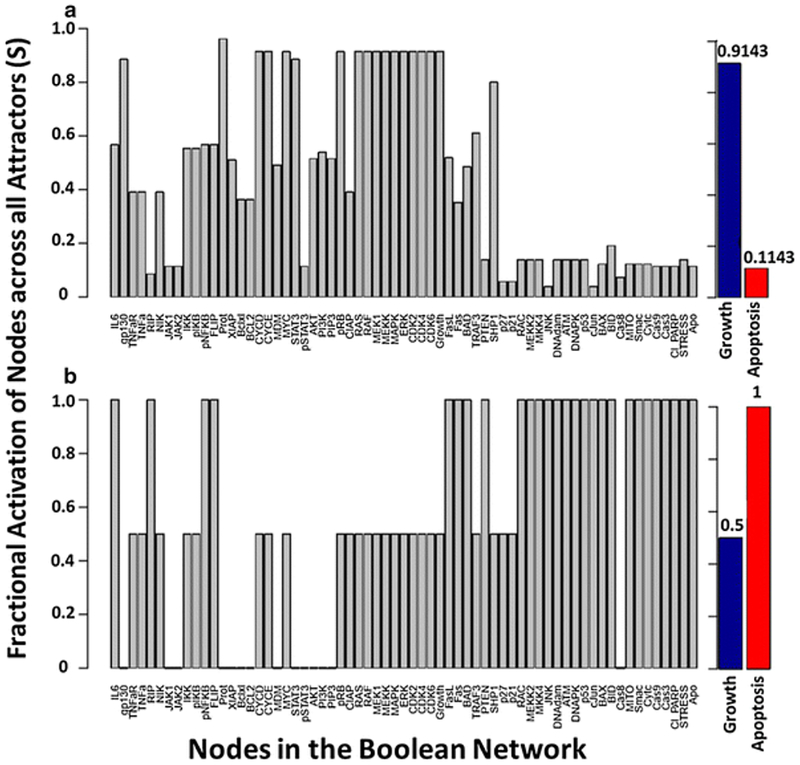
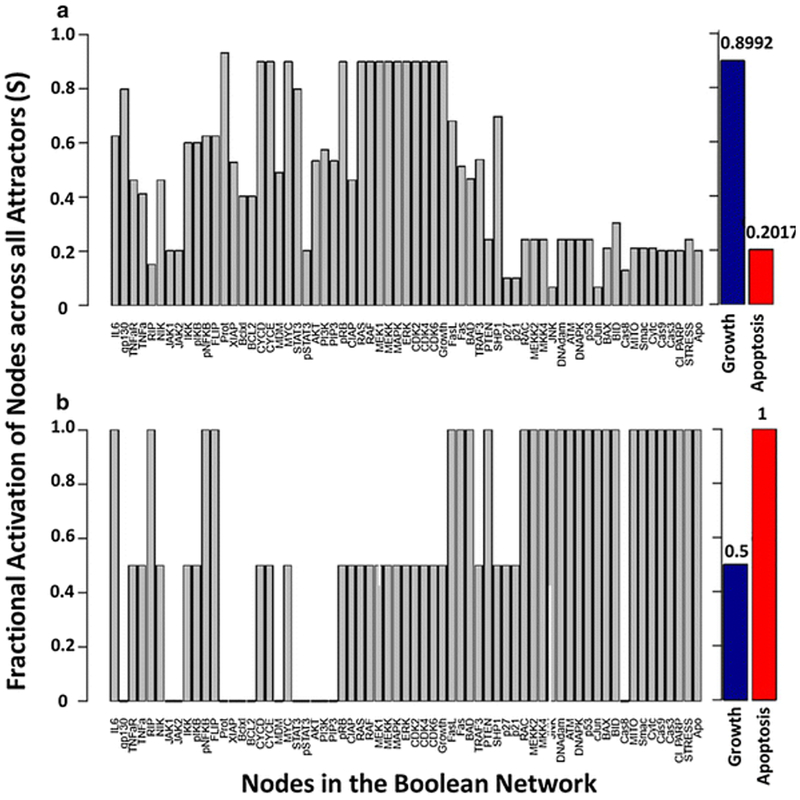
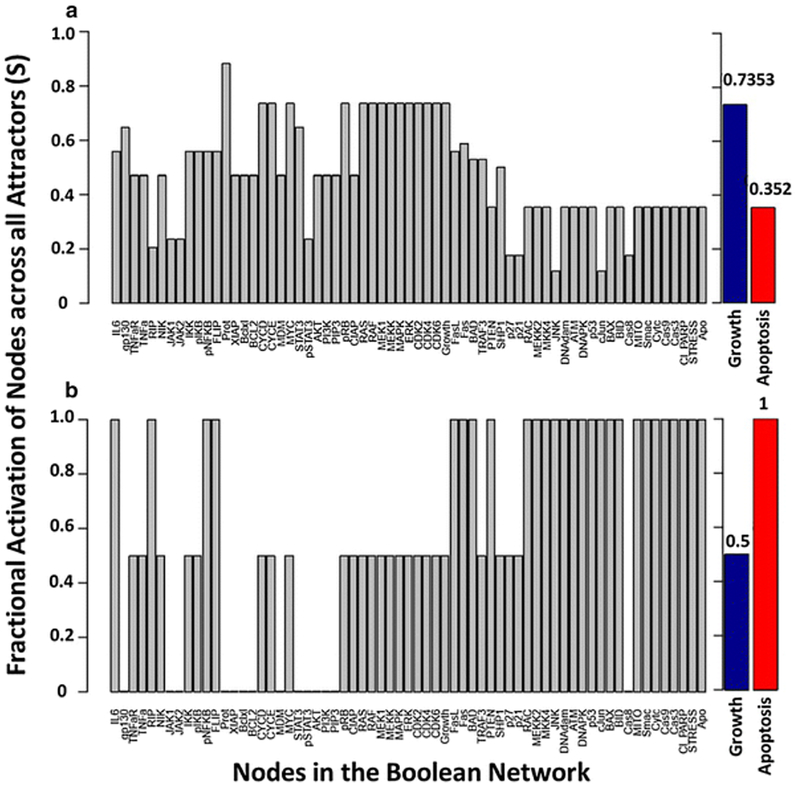
with S_x as the relative fractional activation of node x across all attractors and $n_{A_{Total}}$ is the total number of attractors in the network. In the case where an attractor is cyclical, the state of a node throughout each transition can be averaged. We performed an exhaustive state space search for the multiple myeloma Boolean network to identify all attractors in the network, in the absence of external perturbations and in the presence of bortezomib. This particular algorithm is limited to synchronous updating [73]. In the absence of external perturbations, a total of 210 attractors were identified, which consisted of 68 fixed points and 142 limit cycles. In the presence of bortezomib, the 210 attractors of the network reduced to eight fixed-point attractors. In addition to identifying attractors, we calculated the fractional activation of each node in the absence and presence of bortezomib (Fig. 4). The fractional activation of the apoptosis node, across all attractors, shifted from 0.114 to 1 in the presence of bortezomib, indicating that proteasome inhibition results in the activation of apoptosis throughout all eight attractors. In addition, the fractional activation of growth across all attractors decreased from 0.914 to 0.5 in the presence of bortezomib. We also determined the fractional activation of each node across attractors when a random number of initial conditions were selected (n = 10⁵) for both synchronous (Fig. 5) and general asynchronous (Fig. 6) updating schemes. Similar to the synchronous updating algorithm, there was an increase in the fractional activation of apoptosis across attractors when bortezomib was present. In the normal condition (absence of proteasome inhibition), the asynchronous updating scheme results in a greater activation of apoptosis than the synchronous updating scheme (0.352 vs. 0.202). This is likely due to the merging of attractors by the asynchronous updating scheme and the introduction of attractors as an artifact of the synchronous updating scheme [95]. In support of this hypothesis, the asynchronous updating scheme only identified the same 68 fixed-points that where identified by the synchronous updating scheme. Indicating that all 142 limit cycle attractors have merged into fixed-point attractors or formed complex attractors. In the presence of bortezomib, both updating schemes resulted in the same 8 apoptotic fixed-point attractors. The exhaustive state space search (Fig. 4) exhibits similar results to the random state space search (Fig. 5), despite the vast difference in the sample sizes between these two analyses (2⁶⁵ (approximately 10¹⁸) compared to 10⁵). The synchronous random state space search, in the absence of external perturbations, identified 119 of the 210 attractors in the Boolean network. The fractional activation of apoptosis is smaller in the exhaustive vs. random state space search (Fig. 4a vs. 5a; 0.1143 vs. 0.2017), which indicates that the missed attractors likely have a small basin size and apoptosis in the OFF state. As the number of starting initial states increase, the number of identified attractors will approach 210 and the fractional activation of apoptosis will approach 0.1143. Overall, incorporating the effects of bortezomib on the network has shifted the attractors towards those that are representative of apoptosis. Biologically this can be interpreted as proteasome inhibition drives multiple myeloma cells towards an apoptotic fate.

Fig. 4.

Attractor analysis with an exhaustive search and synchronous updating for the multiple myeloma Boolean network [23] for the (a) absence and (b) presence of bortezomib. The y-axis represents the fractional activation of a node across all network attractors, and the x-axis represents all nodes in the network. The fractional activation of growth and apoptosis are represented as blue and red bars.

Fig. 5.

Attractor analysis with a set of random initial states (10⁵) and synchronous updating for the multiple myeloma Boolean network [23] for the (a) absence and (b) presence of bortezomib. The y-axis represents the fractional activation of a node across all network attractors, and the x-axis represents all nodes in the network. The fractional activation of growth and apoptosis are represented as blue and red bars.

Fig. 6.

Attractor analysis with a set of random initial states (10⁵) and general asynchronous updating for the multiple myeloma Boolean network [23] for the (a) absence and (b) presence of bortezomib. The y-axis represents the fractional activation of a node across all network attractors, and the x-axis represents all nodes in the Boolean network. The fractional activation of growth and apoptosis are represented as blue and red bars.

A basin of attraction reflects the importance and robustness of a particular cellular state associated with an attractor. Attractors that have large basin sizes tend to be more robust to perturbations and represent the predominate phenotype of the system. There are two possible ways to gain information about the basins of attraction in large networks: (1) apply a network reduction technique that decreases network size to make simulations computationally feasible, or (2) sample a random finite set of initial conditions to use for simulations. When the network is sufficiently small, an exhaustive state space search can be performed to simulate all 2^N initial conditions, identify every attractor, and determine the basin size for each attractor. If the network is too large for an exhaustive search, one can sample a finite number of random initial conditions to obtain the basins of attraction for each attractor. When the basins of attraction are known, the relative frequency of attractors and relative activation frequency of nodes can be determined. The relative frequency (v_A) at which an attractor (A) is reached can be calculated:

$$\begin{array}{lll}{v}_{A_i}=\frac{B{S}_i}{{\sum }_{i=1}^{n_A}B{S}_i}\hfill & i=1,\dots ,n_A\hfill & {\sum }_{i=1}^{n_A}{v}_{A_i}=1\hfill \end{array}$$ (7)

with $v_{A_i}$ and BS_i as the relative frequency and apparent basin size of attractor A_i. If initial states are randomly selected, BS_i is an apparent basin size, not the exact basin size of attractor A_i, since the entire state space is not sampled and the same initial state can be sampled more than once. Note that n_A represents the total number of attractors identified via the state space search, which can be less than the total number of attractors in the network, $n_A\le n_{A_{Total}}$ For an exhaustive state space search, where all possible initial conditions are sampled ${\sum }_{i=1}^{n_{A_{Total}}}B{S}_i=2^N,$ BS_i will equal the basin size of attractor A_i, and the relative frequency of an attractor will equal its probability: $Pr\left(A_i\right)=v_{A_i}$. When the limit of the number of randomly selected initial states approaches infinity, the relative frequency of an attractor will be equal to its probability: $Pr\left(A_i\right)={\text{lim}}_{{\Sigma }_{i=1}^{n_A}B{S}_i\to \infty }{v}_{A_i}$.

The relative frequency of an attractor may shed light on the importance of a certain phenotype to the biological system, since attractors can be associated with biological phenotypes [96]. When multiple attractors exist, they can be binned into groups that relate to a specific phenotype. To give a theoretical example, consider a Boolean network of cell signaling pathways for a type of cancer. This network contains 1 attractor when no drug is present and 10 attractors when an anticancer agent is present. For the control condition, let us denote the only attractor when no drug is present as proliferation. Hence, 100% of the cancer cells are in a proliferative state in the absence of drug. When drug is introduced, the system divides into 10 attractors. Of the 10 attractors, five, three, and two attractors are associated with apoptosis, proliferation, and cell cycle arrest, respectively. The relative frequencies of the attractors, in each group, can be summed and directly related with the overall frequency of that particular cellular fate. For simplicity, let us also assume that the basin size of each attractor is the same, which results in a relative frequency of 0.10 for each attractor. Therefore, the overall frequency for apoptosis is 0.50, proliferation is 0.30, and cell cycle arrest is 0.20. In a biological context, 50% of the cancer cells would undergo apoptosis, 30% would continue to proliferate, and 20% would enter a state of cell cycle arrest. Quantifying the relative frequency of attractors in biological networks has been applied to identify potential therapeutic targets in T-cell large granular lymphocyte leukemia and breast cancer, evaluate outcomes of molecularly targeted cancer therapies, and describe B-cell differentiation [17,29,97,14].

Frequently, cell fates or other phenotypes of interest, are modeled as nodes in the network. The relative activation frequency of individual nodes can be calculated as:

$$\begin{array}{lll}{v}_x={\sum }_{i=1}^{n_A}\left(v_{A_i}\times x_i\right)\hfill & x_i\in \{0,1\}\hfill & i=1,\dots ,n_A\hfill \end{array}$$ (8)

with v_x as the relative activation frequency of node x. Lu et al. calculated the activation frequencies of nodes in a Boolean network of colitis-associated colon cancer for a non-inflammatory and a pro-tumor inflammatory microenvironment [32]. To simulate the non-inflammatory condition, states of the nodes in the pro-inflammatory microenvironment were set to OFF, and the dynamics were simulated using general asynchronous updating for 5000 initial sets of states. The fractional activation of the proliferation node was plotted over time and eventually reached zero, indicating that the premalignant cells were unable to proliferate in a non-inflammatory microenvironment. The network was then simulated under a pro-tumor inflammatory condition, which resulted in an increase in proliferation and apoptosis reached zero. A node perturbation analysis was then performed to observe how various interventions modified proliferation and apoptosis, which led to the identification of potential therapeutic targets and provided insight into combinatorial cancer therapies. A node perturbation analysis is a sensitivity analysis in which a perturbation is introduced (by fixing certain nodes to 0 or 1), and the change in relative activation frequency of other nodes is calculated. The sensitivity at which a node changes due to a perturbation can be quantified as a ratio of a nodes activation frequency in the presence and absence of a perturbation, known as a perturbation index (PI):

$$PI=\frac{v_x(perturbation)}{v_x(normal)}$$ (9)

Ruiz-Cerda et al. constructed a Boolean network of systemic lupus erythematosus and performed a perturbation analysis coupled with a clustering algorithm to identify potential drug targets, select optimal combination therapies, and identify subpopulations that may have a differential response to drug treatment [21]. SPIDDOR (Systems Pharmacology for efficient Drug Discovery On R) is an R package that can be used to perform such simulations, attractor analyses, and perturbation analyses with clustering of Boolean network models [98].

When the state space of a network is too large to characterize all attractors and basins of attraction, a random finite number of initial conditions can be generated and used for simulations. Since the number of randomly generated initial conditions can be infinitesimal in comparison to the entire state space of large networks, attractors with small basins of attraction are often missed. This raises the concern about whether this sampling approach is an adequate representation of the whole system. However, this approach seems adequate based upon the assumption that attractors with smaller basins are less important than attractors with large basins. In support of this conjecture, the probability of reaching an attractor with a small basin size is very low and will have a negligible effect on the activation frequencies of nodes. A concern with these sampling methodologies, both exhaustive and random, is that some initial conditions may be irrelevant and cannot exist because they are outside of natural biological constraints.

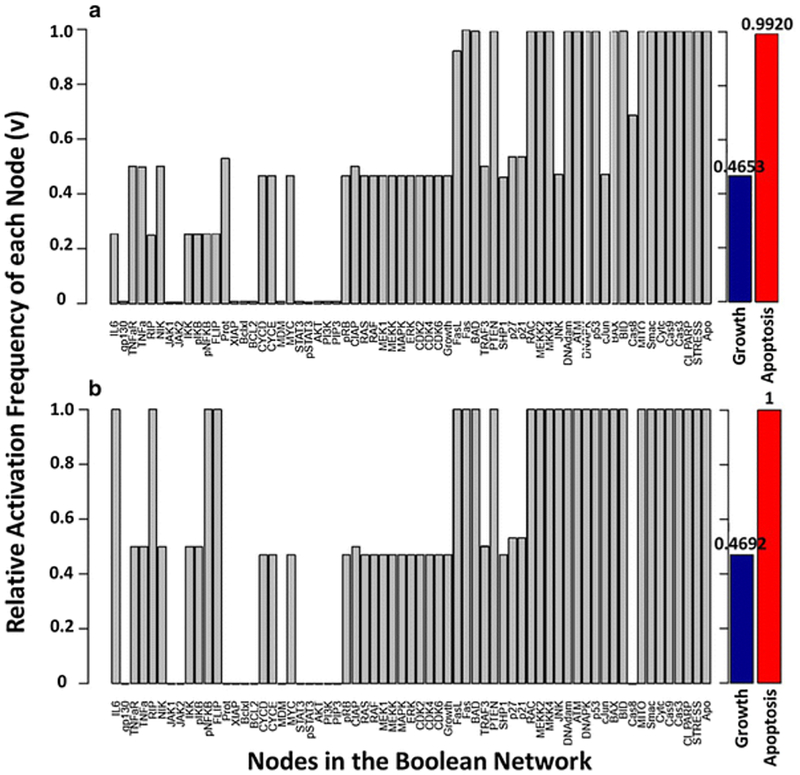
In our multiple myeloma case, 10⁵ initial conditions were sampled and used to determine the relative activation frequency of each node in the presence/absence of bortezomib (Fig. 7). Although we observed differences in the relative activation frequencies of certain species in the network, there were only slight differences in the relative activation frequencies of growth and apoptosis between these two conditions. This could be attributed to a variety of factors. First, the network was not constrained by fixing components that are known to be constitutively active or mutated in U266 multiple myeloma cells. There may be certain constitutively active species, such as growth factors, that prevent the system from evolving towards an apoptotic attractor. For example, apoptosis turns off when certain nodes in the PI3k-Akt signaling pathway are fixed (such as PIP3). This pathway is altered across several types of cancers and is associated with survival and growth [99]. Second, there are positive feedback loops in the network that can cause species to become and remain active as a result of randomly sampling initial conditions. Biological systems are known to be robust to transient perturbations, and pathways may dampen and diminish overexpression instead of remaining active. This phenomenon could be due to unrealistic initial conditions, missing regulatory components, or an artifact of the updating scheme [95]. Lastly, the model contains only a small portion of the entire biological regulatory network. Since the network has been constructed to contain pathways that lead to apoptosis in multiple myeloma cells, it is not surprising that sampling random initial conditions results in a high activation frequency of apoptosis.

Fig. 7.

Attractor analysis with a set of random initial states (10⁵) and synchronous updating for the multiple myeloma Boolean network [23] for the (a) absence and (b) presence of bortezomib. The y-axis represents the relative activation frequency of each node, and the x-axis represents all nodes in the network. The relative activation frequency of growth and apoptosis are represented as blue and red bars.

Minimal Intervention Analysis

Minimal intervention analyses can be conducted to identify targets, either single or multiple, for therapeutic intervention. Klamt and Gilles introduced the concept of minimal cut sets for biochemical networks [100]. A minimal cut set was originally defined as a minimal set of reactions whose removal blocks the operation of a chosen objective and has been extended to include structural interventions (removal of nodes) [101]. Minimal intervention analysis identifies the least number of interventions, referred to as minimal interventions sets, required to satisfy a user-defined goal. For cancer, a user-defined goal could be the activation of apoptosis. In this case, the node for apoptosis would be defined as 1 (ON), and the minimal intervention algorithm searches for all possible combinations of node perturbations that result in the activation of apoptosis. A node intervention can represent a permanent activation (1) or deactivation (0), and results are based upon whether the logical steady state satisfies the intervention goal. Thus, interventions will only be identified when no other regulators are influencing the state of the node. In other words, the analysis identifies combinations of node perturbations that results in the node of interest becoming frozen to the defined value. Single or multi-node perturbations can be identified. However, for large networks, identifying combinations greater than three or four nodes starts to become computationally unfeasible. In addition, multiple intervention goals can be defined, and perturbations that satisfy a subset or all of these goals can be identified. CellNetAnalyzer is a Matlab-based toolbox that has been commonly used to perform minimal intervention analyses of cellular networks [62].

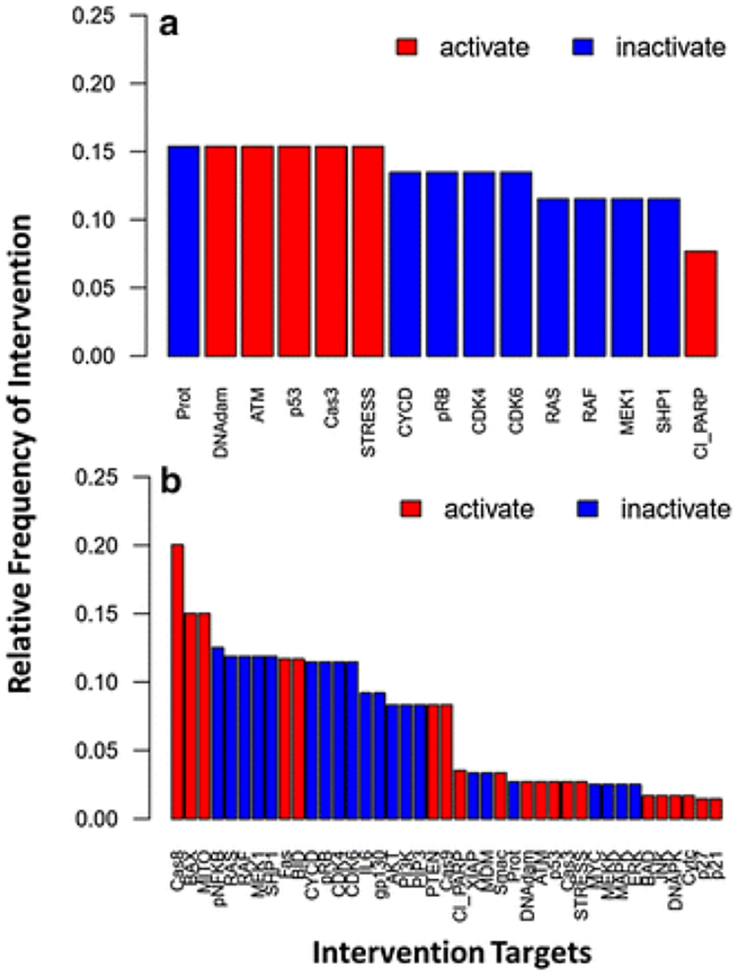
Two minimal intervention analyses were conducted on the Boolean network of intracellular signaling in multiple myeloma. In the first analysis, up to two node combinations were identified that result in apoptosis turning ON and growth turning OFF. The analysis identified 52 combinations of two node perturbations that result in apoptosis and growth equaling 1 and 0 (Fig. 8a; Supplementary Table S1). Thus, 52 potential drug target combinations may be further investigated to determine their efficacy for the treatment of multiple myeloma. The proteasome was the most frequently inactivated target, which was not surprising since proteasome inhibition is a crucial component of the current standard-of-care treatment for multiple myeloma. For the second analysis, we identified up to three node combinations that result in apoptosis turning ON and growth turning OFF. Here, in addition to the 52 previously identified two node combinations, we found 427 three-node perturbations that result in apoptosis and growth equaling 1 and 0 (Fig. 8b; Supplementary Table S2). Caspase-8 (Cas8) was the most frequently activated node, present in approximately 20% (96/479) of all perturbations. This result was intriguing since activation of the caspase-8-mediated apoptosis pathway is the primary mechanism of action for the cytotoxic effects of lenalidomide, which is another chemotherapeutic agent used in combination with proteasome inhibitors for the treatment of multiple myeloma [102,103]. Overall, this approach has led to the identification of several two-drug combinations and a vast number of three-drug combinations, which may be useful for the treatment of multiple myeloma. Although minimal intervention analysis is a useful tool to narrow down and identify potential drug combinations, information regarding prioritization and differences in efficacy amongst these combinatorial treatments remains unknown. Therefore, performing minimal intervention analyses to identify combination therapies can be seen as a high throughput method, which would subsequently warrant further investigations through in silico quantitative analyses, such as the development of a QSP models, and experimental qualifications [9].

Fig. 8.

A minimal intervention analysis of the Boolean network of signaling pathways in multiple myeloma [23]. Network perturbations that result in apoptosis turning ON and growth turning OFF were identified for up to (a) two-node and (b) three-node interventions. The number of times a node was perturbed relative to the total number of intervention sets (52 and 427 intervention sets for two-node and three-node perturbations) is shown on the y-axis, and the x-axis depicts the intervention targets. Red bars indicate the activation of a node (ON), and blue bars indicate the inactivation of a node (OFF).

In addition to minimal intervention analysis, other network-control methodologies have been used to identify points of intervention. A stable motif is a set of nodes that achieves a single cellular state irrespective of input by the rest of the network. Such a motif, can be used to identify stable motif control sets, which are sets of nodes whose states are able to drive the dynamics of the network towards a specific attractor [104]. In essence, the states of nodes in a control set are able to provide insights into the behavior of the system, and perturbing specific nodes of a control set can guide the behavior toward one that is favorable. This stable motif-control methodology has been applied to identify control sets in an epithelial-mesenchymal transition (EMT) network model that drives the system towards an epithelial steady state [105]. Steinway and colleagues identified seven individual targets (all related to E-cadherin transcription), and three targets in combination with SMAD complex inhibition, that were able to suppress EMT. Select targets were then verified to suppress EMT using an in vitro cell migration assay. As a comparison, minimal intervention analysis identifies targets that lead to a specific predefined outcome of select nodes (a steady-state); whereas, network motifs enable the identification of targets that drive the system towards a desired attractor and considers network dynamics as opposed to steady states.

An Overview of Boolean Network Applications

Table S3 lists a sample of previously developed Boolean networks that pertain to human physiology and disease. The majority of these networks focused on signaling pathways in cancer, and these networks are grouped based upon the type of cancer, including: the immune system, breast, gastrointestinal, hepatic, and lung cancers. Nodes in these networks are primarily gene products, with the exception of endpoint nodes. Edges represent several types of regulatory interactions within signaling pathways, such as protein-protein, protein-DNA, and metabolic interactions. These networks have been constructed primarily through the utilization of pathway databases and extensive evaluation of the literature, and are listed as knowledge-derived networks (Table S3). Networks that have been constructed based on large datasets, such as genomic, proteomic, and metabolomic studies, are referred to as a data-derived networks. In addition, a few studies have extended pre-existing networks to investigate specific interests. The main goals for developing Boolean networks have been to identify potential therapeutic strategies [106,17,18,107,25,26,28–32,34], characterize cellular differentiation [14,11,13,36], understand differential responses to cancer therapies due to mutational differences [27], understand the impact of patient heterogeneity on the response to drug treatments [21,35], and as an initial framework prior to the development of quantitative models [23]. The networks provided in this table could be potentially extended or repurposed for investigating additional features of interest, as opposed to starting from the ground up. A useful resource is the Cell Collective, which is a web-based platform that contains several published biological networks for users to build upon and perform simulations [108]. Previously developed Boolean networks can also be accessed from BioModels, GINsim’s model repository, and PyBoolNet’s model repository [109,63,110]. Additionally, there is a Consortium for Logical Models and Tools (CoLoMoTo) that provides useful information for logic-based modeling, such as commonly used methods and software tools [111]. Lastly, a tutorial on logic modeling in quantitative systems pharmacology has been published [112], and serves as another great resource to help guide the development of network-based systems pharmacology models.

Conclusions

Encoding complex biological processes into mathematical models enables the prediction of responses to various perturbations, which has the potential to uncover emergent properties, discover new therapeutics, and individualize therapy to maximize therapeutic benefits while minimizing adverse drug reactions. These goals can be pursued through a combination of quantitative experiments and mathematical analyses of biological networks. Despite the simplifications and limitations of Boolean network models, they have proven to be effective for qualitatively describing the dynamics of biological systems. Boolean network models of intracellular signal transduction could act as a bridge to connect drug exposure with physiological responses to form a hybrid multiscale model of drug action. Kirouac et al. developed a multiscale model of the ErbB signaling pathway with the objective of designing drug combination regimens for ErbB2-positive breast cancer patients [26]. The model contains biological processes occurring at four different time scales: Receptor-ligand binding (minutes), signal transduction (minutes to hours), transcription (hours), and phenotypic effects (days to weeks). Quantitative logic, an extension of Boolean logic, was incorporated in the model to describe intracellular signal transduction events and link the time-course of drug exposure to tumor growth dynamics. The rational for selecting a quantitative logic-based modeling formalism was the rapid time scale of signal transduction events relative to clinical phenotypes and the nature of available biochemical data. A combination regimen that targets both ErbB3 and ErbB2 was identified as a potential treatment strategy to improve therapeutic efficacy. The breadth of utility offered by a mathematical model that can accurately predict complex biological responses to pharmacological perturbations, especially for drug development, has fueled the rise of interest in quantitative systems pharmacology [113]. Quantitative systems pharmacology/toxicology models could improve drug efficacy while minimizing toxicity, reduce late-stage drug attrition, and aid in the movement toward precision medicine [114].

In this review, we have covered an important application of Boolean network modeling in drug discovery, namely the identification of drug targets and combination therapies. The innovation gap across the pharmaceutical industry, in which drug development costs are increasing exponentially while the number of new molecular entities remains relatively constant, is well appreciated [115]. A novel systems-level approach to drug discovery is needed, which focuses on a comprehensive understanding of drug effects rather than the modulation of a single target. Network-based systems pharmacology approaches, such as Boolean network modeling, may help to fill the innovation gap through the identification of novel drug targets and combination therapies. A quantitative systems-level understanding of cellular physiological responses to pharmacons is key, and novel mathematical modeling approaches and strategies are needed that enable better representation and analysis of biological systems.

Supplementary Material

4

Table. S3 Summary of selected Boolean network models for various human physiological and pathophysiological systems. A brief description of network construction, reduction/refinement, validation, analyses, and findings are presented. Networks are highlighted based upon the physiological system that they represent: immune system (blue), breast (pink), gastrointestinal (brown), liver (green), lung (red), and uncategorized (gray).