Invasion reproductive numbers for periodic epidemic models

Abstract

There are many cases within epidemiology where infections compete to persist within a population. In studying models for such cases, one of the goals is to determine which infections can invade a population and persist when other infections are already resident within the population. Invasion reproductive numbers (IRN), which are tied to the stability of boundary endemic equilibria, can address this question. By reinterpreting resident infections epidemiologically, this study extends methods for finding IRNs to periodic systems, and presents some examples which illustrate the often complex computations required. Results identify conditions under which a simple time-average can be used to derive IRNs, and apply the methods to examine how seasonal fluctuations in influenza incidence facilitate the year-round persistence of bacterial respiratory infections.

1. Introduction

Many infections persist endemically in affected populations. When they do, it is important to understand when, if ever, other infections can invade this system. These invasions could have multiple effects on the population. When coinfection is not possible, competitive exclusion may result, since these pathogens are competing for the same resource: susceptible individuals; it could be that one pathogen holds an advantage and will thus win the competition over the other pathogen. This outcome has been observed in studies of several infections where primary infections generate cross-immunity against closely related secondary infections, such as competing strains of the parasite Trypanosoma cruzi (Kribs-Zaleta & Mubayi, 2012). However, there is also the case both pathogens could co-persist at endemic levels within the population. One example is human papillomavirus (HPV), of which over one hundred strains are known; infection with a primary strain creates lesions which facilitate secondary infections (coinfections) by other strains, so that the persistence of one strain can in some cases enable other strains to remain endemic as well (Crawford & Kribs-Zaleta, 2009). Another well-studied coinfection example is the “cursed duet” of HIV and tuberculosis, which share an almost commensal relationship in which HIV weakens the body's immune system to the point where it is susceptible to tuberculosis (as well as many other opportunistic infections).

In order to study these scenarios, invasion reproductive numbers (IRNs) are used. These are similar to basic reproductive numbers (BRNs), the key epidemiological threshold quantity. The basic reproductive number (also called the basic reproduction ratio) in different types of epidemiological models has most often been found by tying the local stability criterion for the disease-free equilibrium to the epidemic threshold $R_0<1$. A canonical process for deriving $R_0$ was developed by Diekmann et al. and later van den Driessche and Watmough using next-generation methods (Diekmann, Heesterbeek, & Metz, 1990; van den Driessche & Watmough, 2002). Diekmann et al. defined $R_0$ as the expected number of secondary cases produced by a typical infected individual during its entire period of infectiousness in a completely susceptible population (Diekmann et al., 1990). The IRN of one pathogen with respect to another or the others is defined as the average number of secondary infections caused by introducing one person infected with that pathogen into an environment where the given combination of other pathogen(s) is already at an endemic state (Zhang, Sandland, Feng, Xu, & Minchella, 2007). IRNs, often denoted ${\tilde{R}}_i$ where i is the invading infection, measure the ability of a pathogen to invade while other pathogens are already at equilibrium and are often used in studies where competitive exclusion exists (Kribs-Zaleta & Mubayi, 2012; Porco & Blower, 1998; Zhang et al., 2007). Using this notation, the set of resident infections is made implicit. However, one can also define a different, overall IRN, ${\tilde{R}}_0$, where all possible invading strains are joined into one category and not distinguished from each other. Then ${\tilde{R}}_0$ is the expected number of secondary cases one infected individual with some infection not resident in the population produces in a population where all (and only) infections assumed to be resident are present. It measures the ability of a set of pathogens to invade a state where other pathogens are already at equilibrium without distinguishing which pathogen is actually able to invade.

Other types of reproduction numbers have also been defined, such as target and type reproduction numbers (van den Driessche, 2017). Knipl recently generalized the definition of next-generation matrices to define BRNs in a larger class of systems (Knipl, 2016).

Most studies that calculate IRNs only do so for two infections (Crawford & Kribs-Zaleta, 2009; Gao, Porco, & Ruan, 2016; Porco & Blower, 1998; Zhang et al., 2007), that is, for a system with one resident and one invading pathogen, so that by identifying the invader, the resident infection may be left implicit. It is possible, however, to consider multiple infections, though the models will be very complex. In systems with more than two infections, the resident infections must be made explicit. IRNs are associated with the same kind of threshold behavior as BRNs: if a given IRN is greater than 1 then the invading pathogen can persist in a population where the established pathogen(s) is resident. This gives information about the stability of an endemic equilibrium in a similar way that the BRN gives information about the stability of a disease-free equilibrium. Competition makes the IRN less than the BRN in value (e.g. cross-immunity examples like T. cruzi) while predisposition to secondary infections makes the IRN greater than the BRN (as in the case of HPV or HIV). The methods for finding invasion reproductive numbers are similar to those for basic reproductive numbers, only the system is assumed to be at an endemic equilibrium for at least one of the infections.

Previous studies of IRNs have been limited in scope and focused on individual applications of autonomous dynamical systems as well as on scenarios with only two infections. In the case of autonomous models, many follow next-generation methods for the basic reproductive number (Diekmann et al., 1990; van den Driessche & Watmough, 2002), extending them to models involving more than one infection. Recent developments, however, have extended next-generation definitions for the BRN to cover periodic systems (Bacaër & Ait Dads, 2012; Bacäer & Guernaoui, 2006; Mitchell & Kribs, 2017; Wang & Zhao, 2008), since many infectious diseases exhibit seasonal patterns. The goal of this study is to give a clear definition of IRNs including systems with more than two cocirculating pathogens, and to extend methods for deriving them to cover periodic epidemiological systems for the first time.

Section 2 explores and defines several types of invasion reproductive numbers in a general context with several cocirculating pathogens. It reviews the extension of next-generation methods to derive IRNs for autonomous systems before discussing the similar extension of methods for periodic systems. Multiple approaches have been used to derive the BRN for continuous-time periodic systems. The main methods, each of which has its advantages and limitations (Mitchell & Kribs, 2017), involve time-averages (Gao, Liu, Nieto, & Andrade, 2011; Grassly & Fraser, 2006; Greenhalgh & Moneim, 2003; Keeling, Rohani, & Grenfell, 2001; Ma & Ma, 2006; Wesley & Allen, 2009) and linear operators (Bacäer, 2007; Bacaër & Ait Dads, 2012; Bacäer & Guernaoui, 2006; Wang & Zhao, 2008). For each type of system, the extension of methods for deriving BRNs to IRNs turns on key epidemiological reinterpretations of what constitutes an infection, exploiting the distinction between resident and invading pathogens. Although the epidemiological context of an IRN involves analyzing an endemic equilibrium rather than the trivial (disease-free) equilibrium, we establish conditions that allow an IRN to be derived using the simpler time-average approach. Section 3 presents examples: one autonomous, one periodic using the time-average approach, and one periodic using the more general linear operator approach. Section 4 presents a case study on the effects of influenza's seasonal incidence on the persistence and prevalence of bacterial respiratory infections.

2. Invasion reproductive numbers

2.1. Definitions

In a previously uninfected population exposed to one or more pathogens, the basic reproductive number $R_0$ measures the ability of at least one of the pathogens to invade the susceptible population. If there are multiple pathogens, each may have its own BRN, say $R_i$ for $i=\mathrm{1,2},\dots ,k$, and the overall BRN of the system is most often given as the maximum of the $R_i$, so that $R_0<1$ implies that none of the pathogens individually is able to invade the population. The same distinction holds for IRNs in a context where a set A of the pathogens is already resident in the population in an endemic state. In this case, the system has an overall IRN which measures the ability of any of the remaining (nonresident) pathogens to invade the A-endemic system; if there is more than one invading pathogen, there are also pathogen-specific IRNs for the A-endemic system. Since for a large number of pathogens there are many possible subsets A, a single system may therefore have many distinct IRNs (in fact, a total of $k\cdot 2^{k-1}$ single-pathogen reproductive numbers if there are k pathogens), so it is worth defining them carefully.

We begin with notation. Previous studies involving IRNs have been limited to two pathogens, in which case the notation remains relatively simple: single-pathogen BRNs $R_1$ and $R_2$, the overall BRN typically has $R_0=\text{max}\left(R_1,R_2\right)$, and two IRNs ${\tilde{R}}_1$, measuring the ability of pathogen 1 to invade a population where pathogen 2 is resident, and ${\tilde{R}}_2$, measuring the reverse invasion. For each of the IRNs, the set A of resident pathogens may be left implicit, since it must include only the non-invading pathogen, and the overall IRN in each case is by default already a single-pathogen IRN, since there is only one invading pathogen. For systems with more than two cocirculating pathogens, the situation is more complicated—for instance, with three pathogens, the abilities of pathogen 1 to invade pathogen 2 alone, to invade pathogen 3 alone, or to invade a population where both pathogens 2 and 3 are resident, may be quite different—so the set of resident pathogens must be made explicit.

Let k be the number of different infections, either multiple strains of the same pathogen or infections of different types, and let $A\subseteq \left\{1,\dots ,k\right\}$ be a subset of these infections considered resident within the population. Any infections not in A (call this set $A_c$, the complement of A) which appear are then considered invading infections. We then define the system's overall A-endemic IRN ${}_A{\tilde{R}}_0$ to be the average number of secondary $A_c$-infections produced by a single $A_c$-infective introduced into a population where the infections in A are resident. (By $A_c$-infection we mean infection with any, but not necessarily all, of the pathogens in $A_c$.) Here the set of resident pathogens is given as a left subscript. The system's overall IRN with respect to the given set A of resident infections corresponds most closely to the concept underlying the BRN, as it measures the collective ability of any or all of the infections in $A_c$ to invade the system, at a state in which the infections in A are resident. If there is more than one pathogen in $A_c$, then the system also has multiple single-pathogen IRNs for this context, denoted ${}_A{\tilde{R}}_i$ for each $i\in A_c$. ${}_A{\tilde{R}}_i$ gives the average number of infections of type i produced by a single infective of type i in an A-endemic population. In such a case, typically ${}_A{\tilde{R}}_0={\text{max}}_{i\in A_c}\left({}_A{\tilde{R}}_i\right)$. As an example, the three pathogen-1 IRNs mentioned in the preceding paragraph can now be distinguished and denoted ${}_2{\tilde{R}}_1$, ${}_3{\tilde{R}}_1$, and ${}_{23}{\tilde{R}}_1$.

It is also important to note that defining an A-endemic IRN assumes implicitly that an A-endemic equilibrium exists. In the case of simple threshold dynamics—that is, without phenomena such as backward bifurcations which allow equilibria to exist at subthreshold levels—this requires appropriate reproductive numbers to exceed 1. For instance, with two pathogens, ${\tilde{R}}_2$ (pathogen 2 invading 1) is only defined when $R_1>1$, so that a 1-endemic equilibrium exists, and likewise ${\tilde{R}}_1$ is only defined when $R_2>1$. For a dual-endemic equilibrium (pathogens 1 and 2) to exist typically requires ${\tilde{R}}_1>1$ and ${\tilde{R}}_2>1$: each pathogen must be able to invade the other. IRNs with a larger set A of endemic pathogens thus require a larger set of threshold conditions for their definitions.

2.2. Derivations

Methods for deriving IRNs for a given system are adaptations of methods originally developed for deriving BRNs. The principal conceptual difference driving these adaptations is a shift in epidemiological perspective. All methods for deriving BRNs begin by classifying the compartments in a model as infected or uninfected. This first step is purely epidemiological: the classification of compartments as infected or uninfected comes from context rather than from mathematical structure. To derive an IRN with respect to a set A of resident infections, one begins by reclassifying all resident infections as non-infected. Only those classes involving infections in $A_c$, including singly infected and coinfected classes, are considered to be infected. (This includes coinfected classes with at least one infection from $A_c$ and at least one from A.) Now the method can be applied to calculate the [overall] invasion reproductive number ${}_A{\tilde{R}}_0$ of all the infections not in A with respect to all the infections in A, that is, the IRN of $A_c$.

As noted earlier, in cases where $A_c$ contains multiple pathogens, the form of the overall A-endemic IRN typically takes the form ${}_A{\tilde{R}}_0={\text{max}}_{i\in A_c}\left({}_A{\tilde{R}}_i\right)$, where the ${}_A{\tilde{R}}_i$ give the single-pathogen A-endemic IRNs for each pathogen in $A_c$. These single-pathogen IRNs can also be derived directly by removing the other pathogens in $A_c$ (and their associated compartments) from the system.

2.2.1. Autonomous systems

Next-generation methods for deriving the BRN of an autonomous dynamical systems model (Diekmann et al., 1990; van den Driessche & Watmough, 2002) are well known. For a model with the population divided into n compartments (typically $n\gg k$, and if all coinfection combinations are possible, $n\ge 2^k$), these methods typically reduce the dimension of the calculation to only the infected classes. To calculate an IRN, these methods reduce the dimension even further, to only those $m\left(<n\right)$ classes involving invading pathogens. Consistent with (van den Driessche & Watmough, 2002; Wang & Zhao, 2008), let $x={\left(x_1,\dots ,x_n\right)}^T$, with each $x_i\ge 0$, denote the number of individuals in each compartment of the system, and let the infection dynamics of the system be described by $\dot{x}=f\left(x\right)$, where f is a vector such that ${\dot{x}}_i=f_i\left(x\right)$. Next-generation methods then impose a set of hypotheses, denoted (A1)–(A5) in (van den Driessche & Watmough, 2002), on the vector f, to ensure that a disease-free equilibrium exists and is stable in the disease-free subspace, and that no infections arise other than from infectives present in the system.

To adapt these methods to derive an IRN, these hypotheses must be reinterpreted in terms of invading infections only (see our supplementary document). Most significantly, the existence, and stability in the $A_c$-free subspace, of an A-endemic equilibrium require that each pathogen $j\in A$ be able to invade a population where all other pathogens in A are resident. If A consists of a single pathogen j, that pathogen's individual BRN must exceed 1, $R_j>1$. If A consists of multiple pathogens, then for each $j\in A$, the condition is on an IRN instead: ${}_{A\setminus \left\{j\right\}}{\tilde{R}}_j>1$. Each of those conditions, in turn, may imply further hypotheses. In the absence of backward bifurcations, the general requirement is that all BRNs and IRNs in the A-only subspace exceed 1. This requires a hierarchical approach to deriving IRNs for a system, beginning with those which assume only a single pathogen resident and building from there.

2.2.2. Nonautonomous systems

The basic reproductive number for an epidemiological model is defined epidemiologically as the average number of secondary infections produced by a single infected individual in a pool of susceptibles. The term average is usually interpreted, for autonomous systems, as an average over a potentially heterogeneous population of infectives as well as a heterogeneous population of susceptibles. (For stochastic systems the average usually aligns with mean-field interpretations of expected value.) For periodic systems, however, the average must also take into account the point within the periodic cycle when the infective individual begins to spread the pathogen. The mathematical method used to derive a reproductive number articulates (implicitly or explicitly) the ways in which all these types of heterogeneity are averaged to obtain a single value that measures infection's ability to spread in the given population.

There are two methods used to find the basic reproductive number for nonautonomous periodic systems. In (Mitchell & Kribs, 2017), Mitchell and Kribs review these methods in detail. The simpler method replaces each periodic parameter with its long-term average, reducing the system to an autonomous one so that the methods from the previous section can be applied. This method often yields a closed-form expression but is not always applicable. The other method uses linear operators and Floquet theory to solve a related periodic linear system that gives the value for $R_0$. This linear operator method describes accurate threshold behavior for a larger class of systems than the time-average method, but its results can typically only be computed numerically. Mitchell and Kribs give conditions on when the two methods agree.

For the time-average method, it is simple to interpret the way in which the number of secondary infections produced is averaged over the periodic cycle of the epidemiological landscape. Studies detailing the linear operator approach have defined the BRN in mathematical terms and generally interpreted the linear operator epidemiologically rather than the resulting reproductive number. Bacaër and Guernaoui (2006) and Wang and Zhao (2008) each define $R_0$ as the spectral radius of a next infection operator, a linear operator defined on a Banach space of ω-periodic functions. Wang and Zhou interpret the kernel of their linear operator as the distribution of individuals infected a time units ago who remain infected now, and the kernel of Bacaër and Guernaoui's linear operator as the distribution of individuals newly infected now by infectives introduced a time units ago. Both linear operators have the same spectral radius (Wang & Zhao, 2008). Since the linear operators are defined on ω-periodic functions, this spectral radius, the BRN, can be interpreted as the maximum growth factor (caused by the infection process described in the periodic system) among the infected compartments from one ω-periodic function to another. Although in general the infection process does not simply magnify the [ω-periodic] size of an infected class by a constant, for some linear combination of infected classes (the eigenvector to the eigenvalue representing the spectral radius) it does so, and it is in this context that the BRN gives the maximal average growth factor caused by introducing a single infective into the periodic epidemiological environment. In the context of discrete generations of infectives, Bacaër and Ait Dads interpret $R_0$ as “the asymptotic ratio of total infections in two successive generations of the infection tree” (Bacaër & Ait Dads, 2012).

Both methods can be extended to IRNs of periodic systems analogously to how next-generation operator methods were extended for BRNs of autonomous systems. When applicable, the time-average method has the potential to offer an analytical expression for the invasion reproductive number of a periodic epidemiological model. The system can be transformed to an autonomous system by simply using the long-time averages for any parameters that are varying with time (Martcheva, 2009) in place of the original parameters. The next-generation method for autonomous systems can now be used to find an expression for the IRN as $\rho \left(F{V}^{-1}\right)$. Unfortunately, as when used to find the BRN, this method only applies to a limited set of periodic systems; otherwise it may overestimate or underestimate the capability of the invading infections. The rest of this section focuses on extending the more broadly applicable linear operator method to calculate IRNs for nonautonomous systems. To distinguish the two methods, ${}_A{\tilde{R}}_T$ will denote the result of the time-average method whereas ${}_A{\tilde{R}}_0$ will denote the [linear operator] IRN. We begin, as before, by considering a system's overall IRN with respect to a given set of resident infections. This gives the average number of secondary $A_c$-infections produced by a single $A_c$-infective introduced to a population where infections in A are resident, in a periodic environment where the average is taken among growth factors of ω-periodic solutions to the system (as in (Bacaër & Ait Dads, 2012), this growth factor can be interpreted as the asymptotic ratio of two periodic distributions of infections, initial and resultant).

Like next-generation methods for autonomous systems, the linear operator method for periodic systems ${\dot{x}}_i=f_i\left(t,x\right)$ imposes hypotheses on the vector f in order to decompose the corresponding linearized system by how each term affects infection status (Bacäer & Guernaoui, 2006; Mitchell & Kribs, 2017; Wang & Zhao, 2008). These hypotheses ensure that new infections arise only from infectives within the system, and that a disease-free periodic state is stable within the disease-free subspace. Assumptions on the periodic nature of the system's coefficients increase the number of hypotheses from five (for autonomous systems) to seven, denominated (A1)–(A7). The last two of these are significantly more complex to verify for periodic systems than for autonomous systems, as they involve monodromy matrices. All of these hypotheses must be adjusted for IRNs, as before, to consider only invading pathogens as infections. Also as before, the condition that an A-endemic periodic state exist and be stable in the $A_c$-free subspace requires that the underlying reproductive numbers exceed 1, necessitating a hierarchical approach to any IRNs for which the endemic set A includes several pathogens.

Details of the derivation of IRNs via the linear operator method, including how conditions (A1)–(A7) are adapted for IRNs and why the procedure yields a quantity linked to the stability of periodic states, are given in the appendix.

In explicating the method's original application to an ω-periodic system's BRN, Wang and Zhou showed that, for purposes of computing $R_0$ as well as verifying its traditional role as threshold quantity, one can use the evolution operator W of the linear ω-periodic system

$$\frac{dw}{dt}=\left[-V\left(t\right)+\frac{F\left(t\right)}{\lambda }\right]w,t\in \mathrm{ℝ}$$ (1)

with parameter $\lambda \ge 0$, where the periodic matrices $F\left(t\right)$ and $V\left(t\right)$ are defined in the appendix. In particular, for the evolution operator $W\left(t,s,\lambda \right),t\ge s,s\in \mathrm{ℝ}$ of (1) on ${\mathrm{ℝ}}^m$, $R_0$ is given by the unique root λ of $\rho \left(W\left(\omega ,0,\lambda \right)\right)=1$. Their result also holds for the A-endemic system ${\dot{x}}_i=f_i\left(t,x\right)$, and, with conditions (A1)–(A7) already verified (including existence of the A-endemic periodic state), Theorems (2.1) and (2.2) from (Wang & Zhao, 2008) can then be translated to apply to IRNs:

Theorem (2.1)

• i.If $\rho \left(W\left(\omega ,0,\lambda \right)\right)=1$ has a positive solution ${\lambda }_0$, then ${\lambda }_0$ is an eigenvalue of L (as defined in (25)), and hence ${}_A{\tilde{R}}_0>0$.
• ii.If ${}_A{\tilde{R}}_0>0$, then $\lambda {=}_A{\tilde{R}}_0$ is the unique solution of $\rho \left(W\left(\omega ,0,\lambda \right)\right)=1$.
• iii.${}_A{\tilde{R}}_0>0$ if and only if $\rho \left(W\left(\omega ,0,\lambda \right)\right)<1$ $\forall \lambda >0$.

Theorem (2.2)

• i.${}_A{\tilde{R}}_0=1$ if and only if $\rho \left({\text{Φ}}_{F-V}\right)=1$.
• ii.${}_A{\tilde{R}}_0>1$ if and only if $\rho \left({\text{Φ}}_{F-V}\right)>1$.
• iii.${}_A{\tilde{R}}_0<1$ if and only if $\rho \left({\text{Φ}}_{F-V}\right)<1$.

Thus the $A_c$-free solution, $x_0\left(t\right)$, is asymptotically stable if ${}_A{\tilde{R}}_0<1$ and unstable if ${}_A{\tilde{R}}_0>1$.

These results show that to find the invasion reproductive number, one needs to find the monodromy matrix of the system (1) for the given value of λ, ${\text{Φ}}_{F-V}\left(\lambda \right)$. Then find the spectral radius of ${\text{Φ}}_{F-V}\left(\lambda \right)$ and solve the equation $\rho \left({\text{Φ}}_{F-V}\left(\lambda \right)\right)=1$ for λ. This value of λ is the overall invasion reproductive number ${}_A{\tilde{R}}_0$ . The threshold behavior for the $A_c$-free solution can then be studied. In many cases, it is not possible to find the monodromy matrix analytically. In these cases numerical work, described in section 2.2.3, will have to be done to find the IRN.

It is natural to ask when the time-average and linear-operator methods agree, since the simpler method leads to an interpretable closed-form expression for the IRN. Similar to the case for the BRN, the methods and Theorem from (Mitchell & Kribs, 2017) can be extended here for the IRN.

Theorem 1

Consider an n-dimensional ω-periodic system (19) with m invading infected classes. If the $m\times m$ matrices $F\left(t\right)$ and $V\left(t\right)$ are triangular of the same form, that is they are both upper or lower triangular, then the time-average method for calculating the invasion reproductive number gives the same expression as the linear operator method. That is, ${}_A{\tilde{R}}_T={}_A{\tilde{R}}_0$.

The condition that F and V be triangular of the same form implies a kind of hierarchy among the invading infections. If they are lower triangular, then each invading infection j is influenced only by lower-numbered infections $i\le j$ but can influence higher-numbered infections $i\ge j$. (For upper triangular matrices, the hierarchy is reversed.) For such hierarchical sets of invading infections $A_c$, the system's IRN can be derived using the simpler time-average method.

An especially important special case that falls under this Theorem is when there is only a single invading infected class. In this case the matrices are trivially triangular, so the methods agree. However, this is not the same as a single invading pathogen if it occurs in coinfection with resident infections. If there are invading/resident coinfection classes, then the matrices $F\left(t\right)$ and $V\left(t\right)$ will be $m\times m$ matrices and thus must be triangular of the same form in order for both methods to produce the same expression for ${}_A{\tilde{R}}_0$. An example given in section 3.3 shows that indeed not every model allows for both methods to produce the same result, just as with the BRN.

It is also worth noting that although the analogue of Theorem 1 for BRNs in (Mitchell & Kribs, 2017) offers similar conditions on the equivalence of the two methods for deriving the BRN of a periodic system, the conditions here for the IRN are actually less strict, as they only require the hierarchical structure for classes of invading infections, not all infections. A simple example would be a two-pathogen system with two-way superinfection rather than coinfection, so that infections of each type can be replaced with infections of the other type. The two infective classes together lack a hierarchical structure, but either invasion reproductive number considers only a single invading infective class, which is trivially hierarchical.

2.2.3. Numerical methods

For most periodic dynamical systems, in practice one cannot derive closed-form expressions for even the periodic solutions (such as the A-endemic solutions at which IRNs are defined). In some cases, even when a system's fundamental matrix can be found analytically, deriving the resulting monodromy matrix's eigenvalues proves intractable, often involving a transcendental equation (an example is given in (Mitchell & Kribs, 2017)). Therefore very few studies have derived explicit expressions for ${}_A{\tilde{R}}_0$. This is the same issue that arises in the calculation of the basic reproductive number for nonautonomous systems. For these systems, numerical analysis must be done.

Most studies which develop IRNs report only numerical values for particular models without detailing more general implementation procedures. Safi et al. (Sufi, Imran, & Gumel, 2012) sketch an outline for calculating the BRN for a nonautonomous system ((Posny & Wang, 2014) provides another), but the procedure can be adapted for IRNs as well since the methods produce similar systems to solve. An example will be worked in the next section which illustrates this method.

In applying the linear operator method, hypotheses (A1)–(A5) can normally be verified by inspection. However, (A6) and (A7) involving monodromy matrices often require numerical work. To verify them one must first solve the systems (20) and (21) (see appendix). The difficulty in doing so is that these systems come from linearization about the A-endemic solution, which is typically periodic. In order to use numerical methods to find the fundamental matrix, this periodic solution must first be approximated numerically. For a given set of parameters, the system is solved numerically using initial conditions where only the resident infections are present, i.e. setting all invading infection initial conditions to 0. Once the periodic solution is approximated, it can be used to find the fundamental matrix as outlined in (Mitchell & Kribs, 2017): namely, one uses each of the standard basis vectors, in turn, as initial conditions and then augments the resulting solution vectors together to form a matrix. This approach guarantees a principal fundamental matrix—that is, its initial value is the identity matrix.

For the system (1) used to derive the IRN, more work must be done. First let $W\left(t,\lambda \right)$ be the standard fundamental matrix. For a given set of parameters, since the IRN is being calculated and not the BRN, this system is linearized about the endemic solution. Again this solution must be approximated in some way to program it into the calculations. Once that is done, an initial guess for λ must be given. Using this value of λ, the matrix $W\left(\omega ,\lambda \right)$ is numerically computed using some standard integrator to generate the necessary linearly independent solutions to (1) using standard basis vectors as respective initial condition vectors. Then the spectral radius $\rho \left(W\left(\omega ,\lambda \right)\right)$ is calculated. Last use a root-finding method to find the zero of $\left(\lambda \right)=\rho \left(W\left(\omega ,\lambda \right)\right)-1$ for a given value of λ. Adjust this value of λ in a particular way until the root of is found.

3. Examples

3.1. Autonomous system

Consider the following model in which two infections spread through a population. Susceptibles become infected when coming into contact with an individual with infection one or two at a rate ${\beta }_1,{\beta }_2$ respectively. These infections are cleared at a rate of ${\gamma }_1,{\gamma }_2$ respectively as well. There is a mortality rate of μ for all classes. In this example it is also assumed that coinfection can occur. In this case, an infected individual with infection 1 can come in contact with someone infected with infection 2 and will move into the coinfection class. $k_1$ and $k_2$ are multipliers that represent the influence of a primary infection on the rate of (or susceptibility to) coinfection. This leads to the following system:

$$\begin{array}{l}\frac{d{I}_1}{dt}={\beta }_{1}S\left(\frac{I_1}{N}+\frac{I_{12}}{N}\right)-k_1{\beta }_2{I}_1\left(\frac{I_2}{N}+\frac{I_{12}}{N}\right)-\left(\mu +{\gamma }_1\right)I_1+{\gamma }_2{I}_{12},\\ \frac{d{I}_2}{dt}={\beta }_{2}S\left(\frac{I_2}{N}+\frac{I_{12}}{N}\right)-k_2{\beta }_1{I}_2\left(\frac{I_1}{N}+\frac{I_{12}}{N}\right)-\left(\mu +{\gamma }_2\right)I_2+{\gamma }_1{I}_{12},\\ \frac{d{I}_{12}}{dt}=k_1{\beta }_2{I}_1\left(\frac{I_2}{N}+\frac{I_{12}}{N}\right)+k_2{\beta }_1{I}_2\left(\frac{I_1}{N}+\frac{I_{12}}{N}\right)-\left(\mu +{\gamma }_1+{\gamma }_2\right)I_{12},\\ \frac{dS}{dt}=\mu N+{\gamma }_1{I}_1+{\gamma }_2{I}_2-\left({\beta }_{1}S\left(\frac{I_1}{N}+\frac{I_{12}}{N}\right)+{\beta }_{2}S\left(\frac{I_2}{N}+\frac{I_{12}}{N}\right)\right)-\mu S.\end{array}$$ (2)

This system is similar to that of Gao et al. (2016) but, importantly, involves altered susceptibilities for infected individuals (the $k_i$), rather than altered infectivities for coinfected individuals as in (Gao et al., 2016), in order to consider the possibility of cross-immunity ($k_i=0$).

To find ${}_2{\tilde{R}}_0$, infection 2 is assumed resident within the population. Then the equations are reordered to place only the invading infection classes at the beginning. In this example, that means placing $I_1$ and $I_{12}$ first, making the system:

$$\begin{array}{l}\frac{d{I}_1}{dt}={\beta }_{1}S\left(\frac{I_1}{N}+\frac{I_{12}}{N}\right)-k_1{\beta }_2{I}_1\left(\frac{I_2}{N}+\frac{I_{12}}{N}\right)-\left(\mu +{\gamma }_1\right)I_1+{\gamma }_2{I}_{12},\\ \frac{d{I}_{12}}{dt}=k_1{\beta }_2{I}_1\left(\frac{I_2}{N}+\frac{I_{12}}{N}\right)+k_2{\beta }_1{I}_2\left(\frac{I_1}{N}+\frac{I_{12}}{N}\right)-\left(\mu +{\gamma }_1+{\gamma }_2\right)I_{12},\\ \frac{d{I}_2}{dt}={\beta }_{2}S\left(\frac{I_2}{N}+\frac{I_{12}}{N}\right)-k_2{\beta }_1{I}_2\left(\frac{I_1}{N}+\frac{I_{12}}{N}\right)-\left(\mu +{\gamma }_2\right)I_2+{\gamma }_1{I}_{12},\\ \frac{dS}{dt}=\mu N+{\gamma }_1{I}_1+{\gamma }_2{I}_2-\left({\beta }_{1}S\left(\frac{I_1}{N}+\frac{I_{12}}{N}\right)+{\beta }_{2}S\left(\frac{I_2}{N}+\frac{I_{12}}{N}\right)\right)-\mu S.\end{array}$$ (3)

Then we write $f=\mathcal{F}-\mathcal{V}$, with:

$$\begin{array}{l}\mathcal{F}=\left[\begin{array}{c}{\beta }_{1}S\left(\frac{I_1}{N}+\frac{I_{12}}{N}\right)\\ k_2{\beta }_1{I}_2\left(\frac{I_1}{N}+\frac{I_{12}}{N}\right)\\ 0\\ 0\end{array}\right],\end{array}\mathcal{V}={\mathcal{V}}^{-}-{\mathcal{V}}^{+}=\left[\begin{array}{c}{k}_1{\beta }_2{I}_1\left(\frac{I_2}{N}+\frac{I_{12}}{N}\right)+\left(\mu +{\gamma }_1\right)I_1-{\gamma }_2{I}_{12}\\ \left(\mu +{\gamma }_1+{\gamma }_2\right)I_{12}-k_1{\beta }_2{I}_1\left(\frac{I_2}{N}+\frac{I_{12}}{N}\right)\\ k_2{\beta }_1{I}_2\left(\frac{I_1}{N}+\frac{I_{12}}{N}\right)+\left(\mu +{\gamma }_2\right)I_2-{\beta }_{2}S\left(\frac{I_2}{N}+\frac{I_{12}}{N}\right)-{\gamma }_1{I}_{12}\\ {\beta }_{1}S\left(\frac{I_1}{N}+\frac{I_{12}}{N}\right)+{\beta }_{2}S\left(\frac{I_2}{N}+\frac{I_{12}}{N}\right)+\mu S-\mu N-{\gamma }_1{I}_1-{\gamma }_2{I}_2\end{array}\right].$$

Verification of hypotheses (A1)–(A5) is simple from observation of the matrices. Since infection 2 is assumed resident within the population, there exists an endemic equilibrium, $\left(\mathrm{0,0},I_2^{\text{*}},S^{\text{*}}\right)=\left(\mathrm{0,0,1}-\frac{1}{R_2},\frac{1}{R_2}\right)N$, when $R_2={\beta }_2/\left(\mu +{\gamma }_2\right)>1$. The system is assumed to be at this equilibrium.

Define the derivatives $F\left(t\right)$ and $V\left(t\right)$ of $\mathcal{F}$ and $\mathcal{V}$ as follows:

$$F=\left[\begin{array}{cc}{\beta }_1\frac{S^{\text{*}}}{N}& {\beta }_1\frac{S^{\text{*}}}{N}\\ k_2{\beta }_1\frac{I_2^{\text{*}}}{N}& k_2{\beta }_1\frac{I_2^{\text{*}}}{N}\end{array}\right],V=\left[\begin{array}{cc}{k}_1{\beta }_2\frac{I_2^{\text{*}}}{N}+\mu +{\gamma }_1& -{\gamma }_2\\ -k_1{\beta }_2\frac{I_2^{\text{*}}}{N}& \mu +{\gamma }_1+{\gamma }_2\end{array}\right].$$

The eigenvalues of the matrix $F{V}^{-1}$ are:

$$\left\{0,\frac{{\beta }_1\left(N+I_2^{\text{*}}\left(k_2-1\right)\right)}{\left(\mu +{\gamma }_1\right)N}\right\}$$ (4)

and ${}_A{\tilde{R}}_0=\rho \left(F{V}^{-1}\right)$, which yields an IRN of:

$${}_A{\tilde{R}}_0=\frac{{\beta }_1}{\mu +{\gamma }_1}\frac{S^{\text{*}}+I_2^{\text{*}}{k}_2}{N}.$$ (5)

This can be interpreted as a weighted average among the susceptibles and the already infected. In this example, ${}_A\tilde{R}_0$ is really just ${}_2{\tilde{R}}_1$ or ${\tilde{R}}_1$, since infection 2 is the only resident infection. Furthermore, ${\tilde{R}}_1<R_1$ iff $k_2<1$. It should be noted that ${}_1{\tilde{R}}_2$ can be calculated in an analogous way by assuming that infection 1 is resident. The only differences in the final expression will be that 1 and 2 will be switched in each subscript.

3.2. Triangular periodic system

For purposes of illustration, the next example considers a simple two-pathogen periodic system with only one invading infected class, so that the time-average and linear operator methods agree in their expression for ${}_A{\tilde{R}}_0$. In this model susceptibles become infected with infection 1 or 2 by coming in contact with infected individuals from those populations at rates of ${\beta }_1\left(t\right),{\beta }_2\left(t\right)$ respectively, which are assumed to be ω-periodic. The infections are cleared at respective rates ${\gamma }_1,{\gamma }_2$. Cross-immunity is assumed between the infections.

As in section 3.1, it is assumed that infection 2 is resident in the population ($A=\left\{2\right\}$). This leads to the following system:

$$\begin{array}{l}\frac{d{I}_1}{dt}={\beta }_1\left(t\right)\frac{S{I}_1}{N}-\left(\mu +{\gamma }_1\right)I_1\\ \frac{d{I}_2}{dt}={\beta }_2\left(t\right)\frac{S{I}_2}{N}-\left(\mu +{\gamma }_2\right)I_2\\ \frac{dS}{dt}=\mu N+{\gamma }_1{I}_1+{\gamma }_2{I}_2-\left({\beta }_1\left(t\right)\frac{S{I}_1}{N}+{\beta }_2\left(t\right)\frac{S{I}_2}{N}\right)-\mu S\end{array}$$ (6)

Then $f=\mathcal{F}-\mathcal{V}$, with:

$$\begin{array}{l}\mathcal{F}\left(t\right)=\left[\begin{array}{c}{\beta }_1\left(t\right)\frac{S{I}_1}{N}\\ 0\\ 0\end{array}\right],\mathcal{V}\left(t\right)={\mathcal{V}}^{-}-{\mathcal{V}}^{+}=\left[\begin{array}{c}\left(\mu +{\gamma }_1\right)I_1\\ \left(\mu +{\gamma }_2\right)I_2-{\beta }_2\left(t\right)\frac{S{I}_2}{N}\\ {\beta }_1\left(t\right)\frac{S{I}_1}{N}+{\beta }_2\left(t\right)\frac{S{I}_2}{N}+\mu S-\mu N-{\gamma }_1{I}_1-{\gamma }_2{I}_2\end{array}\right].\end{array}$$

Verification of (A1)–(A5) is simple from observation of the matrices.

Since infection 2 is assumed resident within the population, (A6) requires that when $R_2>1$ (the BRN of infection 2 alone) there exist a unique endemic periodic solution, $\left(0,I_2^{\text{*}}\left(t\right),S^{\text{*}}\left(t\right)\right)$ which is asymptotically stable in the infection-1-free subspace

$$\frac{d{I}_2}{dt}={\beta }_2\left(t\right)S{I}_2/N-\left(\mu +{\gamma }_2\right)I_2,S\left(t\right)=N-I_1\left(t\right).$$

In general one cannot solve such equations analytically, so that the existence and stability of such solutions must be shown numerically for a given set of parameter values and (for ${\beta }_2\left(t\right)$) functions. However, this particular reduced system is a special case of the so-called periodic Bernoulli equation, and has been studied before in (Martcheva, 2009; Zu & Wang, 2015). In fact, Martcheva showed (Martcheva, 2009) the existence and global stability of such a 2-endemic solution under hypotheses covering those needed here, for a general ω-periodic function ${\beta }_2\left(t\right)$, so (A6) is verified. The system is henceforth assumed to begin near this periodic solution.

Now define $F\left(t\right)$ and $V\left(t\right)$ as follows:

$$\begin{array}{l}F\left(t\right)={\beta }_1\left(t\right),\\ V\left(t\right)=\mu +{\gamma }_1.\end{array}$$

For verification of (A7) consider the system $\frac{dy}{dt}=-Vy=-\left(\mu +{\gamma }_1\right)y.$ This system gives the principal fundamental solution $y=e^{-\left(\mu +\gamma \right)t}$ and thus the monodromy matrix ${\text{Φ}}_{-V}=e^{-\left(\mu +\gamma \right)\omega }$, from which (A7) clearly holds.

As discussed in section 2.2.2, there are two methods to calculate the IRN. First consider the autonomous system given by replacing the infection rates with their time averages, which in this case are $\langle {\beta }_1\left(t\right)\rangle ,\langle {\beta }_2\left(t\right)\rangle$. All periodic parameters must be substituted for their time-averages as the system will not be autonomous if only $\langle {\beta }_1\left(t\right)\rangle$ is used. Since the system is now autonomous, one can use the method described for autonomous systems in section 2 and need only calculate $F{V}^{-1}$ which is:

$$F{V}^{-1}=\frac{\frac{1}{\omega }{{\int }^{}}_0^{\omega }{\beta }_1\left(t\right)dt}{\mu +{\gamma }_1}=\frac{\langle {\beta }_1\rangle }{\mu +{\gamma }_1}.$$ (7)

The spectral radius of this is just the scalar itself and so:

$${}_2{\tilde{R}}_T=\frac{\langle {\beta }_1\rangle }{\mu +{\gamma }_1}.$$ (8)

To characterize ${}_2{\tilde{R}}_0={}_2{\tilde{R}}_1$ using the linear operator method, consider the following ω-periodic equation:

$$\frac{dw}{dt}=\left[-\left(\mu +{\gamma }_1\right)+\frac{{\beta }_1\left(t\right)}{\lambda }\right]w,t\in \mathrm{ℝ}$$ (9)

which has fundamental solution:

$$w\left(t\right)=\text{exp}\left(\frac{1}{\lambda }{{\int }^{}}_0^t{\beta }_1\left(s\right)ds-\left(\mu +{\gamma }_1\right)t\right).$$ (10)

Then the monodromy matrix is defined as before, and the goal is to find ${\lambda }_0$ such that $\rho \left({\text{Φ}}_{F-V}\left({\lambda }_0\right)\right)=1$, which happens exactly when the exponent in $w\left(t\right)$ equals 0. This yields:

$${}_2{\tilde{R}}_1={\lambda }_0=\frac{\frac{1}{\omega }{{\int }^{}}_0^{\omega }{\beta }_1\left(t\right)dt}{\mu +{\gamma }_1}=\frac{\langle {\beta }_1\rangle }{\mu +{\gamma }_1}.$$ (11)

So in this case the time-average IRN, ${\tilde{R}}_T$, has the same expression as the linear operator IRN, ${\tilde{R}}_0$. In reference to Theorem 1, the matrices $F\left(t\right)$ and $V\left(t\right)$ are trivially triangular since they each consist of a single element. Thus the methods should agree in their expression. It should be stated again that this is not always the case, as illustrated in the following example.

3.3. Nontriangular periodic system

The previous example illustrated analytically how the methods for periodic systems' IRNs work and can be applied. However, for most periodic dynamical systems, the linear operator method must be implemented numerically. We now consider such a case.

Consider the example given in calculating the IRN for autonomous systems in which two infections spread through a population. In order to make this a nonautonomous system, let the infection rates ${\beta }_1\left(t\right),{\beta }_2\left(t\right)$ be periodic functions. These infections are cleared at rates ${\gamma }_1,{\gamma }_2$ respectively. Let there be a mortality rate of μ for all classes. It is also assumed that coinfection can occur. $k_1$ and $k_2$ represent multipliers of the influence of a primary infection on the coinfection. The system is then:

$$\begin{array}{l}\frac{d{I}_1}{dt}={\beta }_1\left(t\right)S\left(\frac{I_1}{N}+\frac{I_{12}}{N}\right)-k_1{\beta }_2\left(t\right)I_1\left(\frac{I_2}{N}+\frac{I_{12}}{N}\right)-\left(\mu +{\gamma }_1\right)I_1+{\gamma }_2{I}_{12},\\ \frac{d{I}_2}{dt}={\beta }_2\left(t\right)S\left(\frac{I_2}{N}+\frac{I_{12}}{N}\right)-k_2{\beta }_1\left(t\right)I_2\left(\frac{I_1}{N}+\frac{I_{12}}{N}\right)-\left(\mu +{\gamma }_2\right)I_2+{\gamma }_1{I}_{12},\\ \frac{d{I}_{12}}{dt}=k_1{\beta }_2\left(t\right)I_1\left(\frac{I_2}{N}+\frac{I_{12}}{N}\right)+k_2{\beta }_1\left(t\right)I_2\left(\frac{I_1}{N}+\frac{I_{12}}{N}\right)-\left(\mu +{\gamma }_1+{\gamma }_2\right)I_{12},\\ \frac{dS}{dt}=\mu N+{\gamma }_1{I}_1+{\gamma }_2{I}_2-\left({\beta }_1\left(t\right)S\left(\frac{I_1}{N}+\frac{I_{12}}{N}\right)+{\beta }_2\left(t\right)S\left(\frac{I_2}{N}+\frac{I_{12}}{N}\right)\right)-\mu S.\end{array}$$ (12)

To find ${}_2{\tilde{R}}_1$, infection 2 is assumed resident within the population. Then to measure infection 1's ability to invade, the equations are reordered so that only those classes considered to be infected (with an invading infection) are at the beginning. In this example that means classes $I_1$ and $I_{12}$. The resulting system is:

$$\begin{array}{l}\frac{d{I}_1}{dt}={\beta }_1\left(t\right)S\left(\frac{I_1}{N}+\frac{I_{12}}{N}\right)-k_1{\beta }_2\left(t\right)I_1\left(\frac{I_2}{N}+\frac{I_{12}}{N}\right)-\left(\mu +{\gamma }_1\right)I_1+{\gamma }_2{I}_{12},\\ \frac{d{I}_{12}}{dt}=k_1{\beta }_2\left(t\right)I_1\left(\frac{I_2}{N}+\frac{I_{12}}{N}\right)+k_2{\beta }_1\left(t\right)I_2\left(\frac{I_1}{N}+\frac{I_{12}}{N}\right)-\left(\mu +{\gamma }_1+{\gamma }_2\right)I_{12},\\ \frac{d{I}_2}{dt}={\beta }_2\left(t\right)S\left(\frac{I_2}{N}+\frac{I_{12}}{N}\right)-k_2{\beta }_1\left(t\right)I_2\left(\frac{I_1}{N}+\frac{I_{12}}{N}\right)-\left(\mu +{\gamma }_2\right)I_2+{\gamma }_1{I}_{12},\\ \frac{dS}{dt}=\mu N+{\gamma }_1{I}_1+{\gamma }_2{I}_2-\left({\beta }_1\left(t\right)S\left(\frac{I_1}{N}+\frac{I_{12}}{N}\right)+{\beta }_2\left(t\right)S\left(\frac{I_2}{N}+\frac{I_{12}}{N}\right)\right)-\mu S.\end{array}$$ (13)

Then $\mathcal{F}$ and $\mathcal{V}$ are:

$$\begin{array}{l}\mathcal{F}=\left[\begin{array}{c}{\beta }_1\left(t\right)S\left(\frac{I_1}{N}+\frac{I_{12}}{N}\right)\\ k_2{\beta }_1\left(t\right)I_2\left(\frac{I_1}{N}+\frac{I_{12}}{N}\right)\\ 0\\ 0\end{array}\right],\mathcal{V}={\mathcal{V}}^{-}-{\mathcal{V}}^{+}=\left[\begin{array}{c}{k}_1{\beta }_2\left(t\right)I_1\left(\frac{I_2}{N}+\frac{I_{12}}{N}\right)+\left(\mu +{\gamma }_1\right)I_1-{\gamma }_2{I}_{12}\\ \left(\mu +{\gamma }_1+{\gamma }_2\right)I_{12}-k_1{\beta }_2\left(t\right)I_1\left(\frac{I_2}{N}+\frac{I_{12}}{N}\right)\\ k_2{\beta }_1\left(t\right)I_2\left(\frac{I_1}{N}+\frac{I_{12}}{N}\right)+\left(\mu +{\gamma }_2\right)I_2-{\beta }_2\left(t\right)S\left(\frac{I_2}{N}+\frac{I_{12}}{N}\right)-{\gamma }_1{I}_{12}\\ {\beta }_1\left(t\right)S\left(\frac{I_1}{N}+\frac{I_{12}}{N}\right)+{\beta }_2\left(t\right)S\left(\frac{I_2}{N}+\frac{I_{12}}{N}\right)+\mu S-\mu N-{\gamma }_1{I}_1-{\gamma }_2{I}_2\end{array}\right].\end{array}$$

Verification of (A1)–(A5) is simple from observation of the matrices. Hypothesis (A6) requires that when $R_2>1$ a unique 2-endemic periodic solution $\left(\mathrm{0,0},I_2^{\text{*}}\left(t\right),S^{\text{*}}\left(t\right)\right)$ be globally stable in the infection-1-free subspace

$$\frac{d{I}_2}{dt}={\beta }_2\left(t\right)S{I}_2/N-\left(\mu +{\gamma }_2\right)I_2,S\left(t\right)=N-I_1\left(t\right).$$

However, this is identical to (A6) in the previous example of Section 3.3, and has thus already been verified.

Verification of the final hypothesis (A7) is more complex, however, than in the preceding example. One defines the $2\times 2$ matrices $F\left(t\right)$ and $V\left(t\right)$ as follows:

$$F=\left[\begin{array}{cc}{\beta }_1\left(t\right)\frac{S^{\text{*}}\left(t\right)}{N}& {\beta }_1\left(t\right)\frac{S^{\text{*}}\left(t\right)}{N}\\ k_2{\beta }_1\left(t\right)\frac{I_2^{\text{*}}\left(t\right)}{N}& k_2{\beta }_1\left(t\right)\frac{I_2^{\text{*}}\left(t\right)}{N}\end{array}\right],V=\left[\begin{array}{cc}{k}_1{\beta }_2\left(t\right)\frac{I_2^{\text{*}}\left(t\right)}{N}+\mu +{\gamma }_1& -{\gamma }_2\\ -k_1{\beta }_2\left(t\right)\frac{I_2^{\text{*}}\left(t\right)}{N}& \mu +{\gamma }_1+{\gamma }_2\end{array}\right].$$

(A7) requires that for the linearized system $\frac{dy}{dt}=-V\left(t\right)y$, the corresponding monodromy matrix ${\text{Φ}}_{-V}$ have $\rho \left({\text{Φ}}_{-V}\right)<1$. Since this system cannot be solved outright, we consider the simplest possible nonautonomous special case, which allows as much analytical work as possible, and define the β functions as the following square waves:

$${\beta }_1\left(t\right)=\{\begin{array}{cc}{a}_1& :0<t<\tau ,\\ b_1& :\tau <t<\omega ;\end{array}$$ (14)

$${\beta }_2\left(t\right)=\{\begin{array}{cc}{a}_2& :0<t<\tau ,\\ b_2& :\tau <t<\omega .\end{array}$$ (15)

This produces a system where the fundamental matrix can be found for each interval, on which the system is then autonomous. However, finding ${}_2{\tilde{R}}_1$ must be done numerically. It should be noted that this can also be done for ${}_1{\tilde{R}}_2$ and the procedure is analogous, with only the subscripts changed in each case.

(A7) must be verified for each value of τ since changing τ changes the periodic solution. If $\tau =0$ or $\tau =\omega$ then the system is autonomous and the verification is done. However, if $\tau \in \left(0,\omega \right)$ then the periodic endemic solution must be found for each value of τ. For the purposes of illustration in the numerical work that follows, (A7) is verified here for the particular case $\tau =\omega /2$. For the parameter values given in Table 1, $\tau =0.5$, and equations (14), (15), the fundamental matrix for the system $\frac{dy}{dt}=-V\left(t\right)y$ is numerically approximated using two linearly independent initial conditions, so that the resulting fundamental matrix has linearly independent solutions. Evaluating this matrix at ω yields the monodromy matrix ${\text{Φ}}_{-V}$, for which the maximum eigenvalue is found to be $\rho \left({\text{Φ}}_{-V}\right)=0.288$ which is less than 1, verifying (A7). This process can be automated to check for as many values of τ as desired in the interval $\left(0,\omega \right)$.

Table 1.

Parameter values for (12), Fig. 1, Fig. 2, Fig. 3.

Parameter	Value	Units
$a_1$	2	1/time
$b_1$	1	1/time
$a_2$	1	1/time
$b_2$	2	1/time
μ	1	1/time
${\gamma }_1$	0.35	1/time
${\gamma }_2$	0.35	1/time
$k_1$	2	–
$k_2$	2	–
ω	1	time

Before proceeding to the IRN for system (12), a special case of the model is worth observing. If $k_1=k_2=1$, then the model can be reduced in some sense. An interesting thing happens in this case in that even though the $F\left(t\right)$ and $V\left(t\right)$ matrices are not triangular, both the time-average method and the linear operator method end up producing the same result. To see how, one must make a simplification in the model. If the two infected invading classes and what are considered the two susceptible classes are added together, then the model will be the following:

$$\begin{array}{l}\frac{d\left(I_1+I_{12}\right)}{dt}=\frac{{\beta }_1\left(t\right)}{N}\left(I_2+S\right)\left(I_1+I_{12}\right)-\left(\mu +{\gamma }_1\right)\left(I_1+I_{12}\right)\\ \frac{d\left(I_2+S\right)}{dt}=\mu N+{\gamma }_1\left(I_1+I_{12}\right)-\frac{{\beta }_1\left(t\right)}{N}\left(I_2+S\right)\left(I_1+I_{12}\right)-\mu \left(I_2+S\right)\end{array}$$ (16)

This produces a trivially triangular system that represents the original system and so Theorem 1 can be applied so that the methods agree in their expression for the IRN.

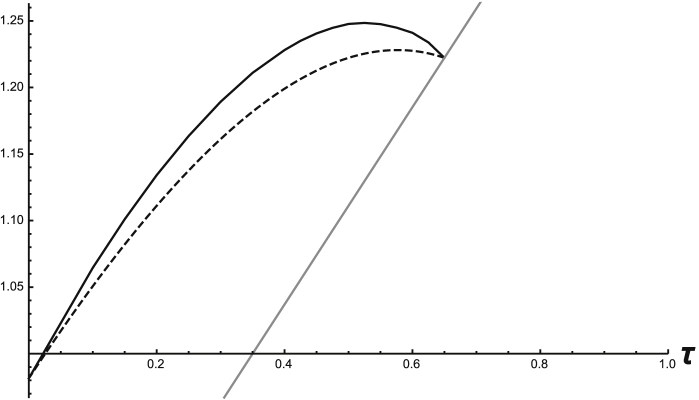
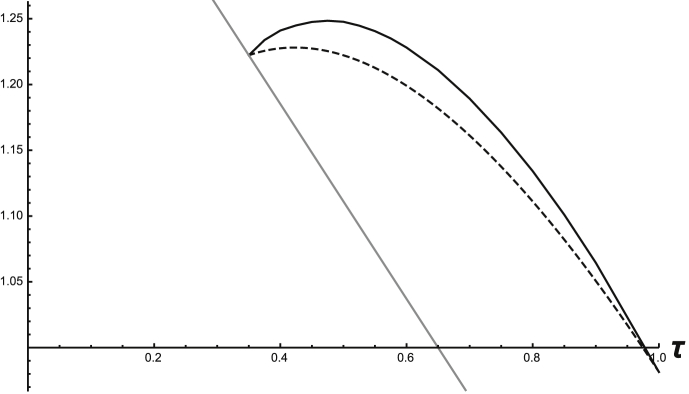
To find ${}_2{\tilde{R}}_1$ for system (12) with (14) and (15), having verified (A1)–(A7) for a given τ, one must then approximate the A-endemic state (here, $S^{\text{*}}\left(t\right)$ and $I_2^{\text{*}}\left(t\right)$) for that same value of τ, in order to find the evolution operator of (1). In practice this requires solving system (12) numerically for initial conditions where the resident infection does not exist, i.e. $I_1=0$ and $I_{12}=0$. One lets the system run long enough to exhaust transient behavior (to within a given tolerance) and then uses the result to approximate the A-endemic solution. In the case of the example above with square-wave infection rates and the given parameter values, the A-endemic periodic solution can be approximated as piecewise linear. For each value of τ a new periodic solution must be found to compute the corresponding value of the IRN. This was done for a range of values of τ and other parameters as in Table 1; the results are shown in Fig. 1, with the time-average values ${\tilde{R}}_{1T}$ shown (dashed curve) for comparison. The same can be done for ${\tilde{R}}_2$. The results are shown in Fig. 2, again using parameter values from Table 1.

Fig. 1.

Graphs of system (12) that show ${\tilde{R}}_{1T}$ (dashed) and ${\tilde{R}}_1$ (solid) for varying values of τ. At the cutoff point, ${\tilde{R}}_{1T}=R_{1T}=R_1={\tilde{R}}_1$. The solid gray line is $R_1[=R_{1T}]$.

Fig. 2.

Graphs of system (12) that show ${\tilde{R}}_{2T}$ (dashed) and ${\tilde{R}}_2$ (solid) for varying values of τ. At the cutoff point, ${\tilde{R}}_{2T}=R_{2T}=R_2={\tilde{R}}_2$. The solid gray line is $R_2[=R_{2T}]$.

In Fig. 1, the graph of ${\tilde{R}}_1$ only extends to $\tau =0.65$ because $R_2=1$ at this value. At $\tau =0.65$, the endemic prevalence of pathogen 2 is zero, making ${\tilde{R}}_1=R_1$. For $\tau >0.65$, $R_2<1$, violating (A5), and hence ${\tilde{R}}_1$ is undefined. Pathogen 1's ability to invade when $\tau >0.65$ is held constant at $R_1$ independent of τ, since there is no pathogen 2 endemic equilibrium to invade in those cases, only the DFE. The reverse holds in Fig. 2, where (by the symmetry in the parameter values used) for $\tau <0.35$, $R_1<1$, so ${\tilde{R}}_2$ is undefined, and pathogen 2's ability to invade is measured instead by $R_2$, since the only equilibrium it can invade is the DFE. Since $k_1,k_2>1$ in these examples, the primary infections facilitate secondary ones and the pathogens can invade more easily. To make matters simpler, the time-average and the linear operator methods for calculating the BRN in this example agree and give the same expression. This allows one to know exactly when the individual BRNs are equal to 1, which occurs at the points in Fig. 1 where the curves meet and in Fig. 2 where the curves begin. This can be seen in the graphs where the gray lines represent the respective BRNs.

At any value of τ for which each IRN is greater than one, the two infections should co-persist. In Fig. 3 one can clearly see this is the case for $\tau =0.5$ and other parameter values as given in Table 1. If the parameters were changed to make only one pathogen's IRN greater than 1, then a numerical solution of the system would show that only the corresponding infection is able to invade and persist within the population.

Fig. 3.

Simulation of system (12) for a set of parameters in which ${\tilde{R}}_1,{\tilde{R}}_2>1$ ($\tau =0.5$ and see Table 1).

Having shown illustrative values of the IRNs as functions of τ (with the other parameters fixed), we next vary instead the mean infection rates to generate a graph that shows regions of parameter space where each infection wins and where there can be co-persistence. To do this, a new parameter must be incorporated into the system in order to separate the mean amplitude (long-term average) from the periodic variability. Fixing $a_1$ and $a_2$ in the range of $\left(0,\frac{\omega }{\tau }\right)$, define now the following for $b_i$:

$$b_i=\frac{\omega -a_i\tau }{\omega -\tau },i=\mathrm{1,2}.$$ (17)

Now attach to the original transmission rates a new parameter, ${\tilde{\beta }}_j,j=\mathrm{1,2}$. Then the transmission rates become:

$${\beta }_j\left(t\right)={\tilde{\beta }}_j\{\begin{array}{cc}{a}_j,& 0<t<\tau ;\\ b_j,& \tau <t<\omega .\end{array}$$ (18)

These ${\tilde{\beta }}_j$ parameters, which now give the mean values for the ${\beta }_j\left(t\right)$, will be used as proxies for the BRNs to generate a graph illustrating the different infection outcomes in terms of the BRNs.

To produce the graphs, one must seek ${\tilde{\beta }}_1,{\tilde{\beta }}_2$ that make their corresponding IRN equal to 1. Take for example ${\tilde{R}}_1$. For all ${\tilde{\beta }}_2$ that make $R_2>1$, find the periodic solution $E_2\left({\tilde{\beta }}_2\right)=\{(S\left(t\right),I_2\left(t\right)),0\le t<\omega \}$. Use this to find the value of ${\tilde{\beta }}_1$ for which ${\tilde{R}}_1\left({\tilde{\beta }}_1,{\tilde{\beta }}_2,E_2\left({\tilde{\beta }}_2\right)\right)=1$. When ${\tilde{\beta }}_1$ and ${\tilde{\beta }}_2$ have been found, graph $\left(R_1\left({\tilde{\beta }}_1\right),R_2\left({\tilde{\beta }}_2\right)\right)$ using a list plot command and connect. The other example is analogous with only subscripts changing. In the resulting graph, shown in Fig. 4, the time-average curves were included for comparison (note the BRNs are identical in this model for the time-average and linear operator methods). The parameter values used to generate the graph are given in Table 2.

Fig. 4.

Graph showing 4 regions in $\left(R_1,R_2\right)$ parameter space representing different behaviors of system (12). $E_0$ is disease-free, $E_1$ is only infection 1 prevalent, $E_2$ is only when infection 2 is prevalent, and $E_3$ is coinfection. The dashed curves indicate where an IRN (derived via the linear operator method) equals 1, while the solid curves represent thresholds generated by the time-average method.

Table 2.

Parameter values for (12) and Fig. 4.

Parameter	Value	Units
$a_1$	1.5	1/time
$b_1$	0.5	1/time
$a_2$	0.5	1/time
$b_2$	1.5	1/time
μ	1	1/time
${\gamma }_1$	0.35	1/time
${\gamma }_2$	0.35	1/time
$k_1$	2	–
$k_2$	2	–
ω	1	time

As seen in Fig. 4, the time-average will always overestimate the coinfection risk for this system. So, it appears, periodicity makes coinfection less likely here. The linear operator method still correctly identifies the infection risk for the model. If ${\tilde{\beta }}_1=1.07$ and ${\tilde{\beta }}_2=1.85$, for instance, the time-average method would predict co-existence with IRN values of ${\tilde{R}}_{1T}=1.00681$ and ${\tilde{R}}_{2T}=1.01177$, while the linear operator method has values of ${\tilde{R}}_1=0.861499$ and ${\tilde{R}}_2=1.40866$. The BRNs at these values are $R_1=0.792593$ and $R_2=1.37037$. If the system is run for those parameters, infection 2 will persist while infection 1 dies out.

The next section offers an application of this model which illustrates the impact of cocirculating seasonal infections with different peak times.

4. An application to influenza and bacterial pneumonia

Influenza, one of the most common seasonal diseases, is commonly associated with bacterial respiratory infections. Most influenza-related deaths occur in conjunction (coinfection) with bacterial pneumonia (Pasman, 2012). Similarly, although an estimated 90% of some populations are colonized (Austin, Kakehash, & Anderson, 1997), infections develop into pneumonia primarily in conjunction with other ailments, notably influenza. Most secondary bacterial infections in influenza patients are caused by Staphylococcus aureus or Streptococcus pneumoniae, while Haemophilus influenzae is associated with complications of pandemic influenza (Pasman, 2012). Influenza infection has been shown to increase the adherence of all three bacteria to host pharyngeal cells (Fainstein, Musher, & Cate, 1980). On the other hand, S. aureus may increase the infectivity of influenza at the cellular and molecular level via proteases that it produces (Morris, Cleary, & Clarke, 2017). In this section we apply the notion of invasion reproductive numbers for seasonal infections to annual influenza and bacterial respiratory infection.

Influenza is well known for its seasonality, e.g., (Centers for Disease Control and Prevention), typically peaking in winter. Perhaps less well known are seasonal variations in bacterial infectivity. A review of 41 studies on seasonality of S. aureus infection found that 76% indicated some kind of seasonal trends, typically associated with summer or high temperatures (Leekha, Diekema, & Perencevich, 2012). Invasive pneumococcal disease often peaks in winter, but is frequently associated with S. pneumoniae in the presence of influenza coinfections. Another review of its incidence in the USA found no seasonality in group B (beta-hemolytic) streptococcal infection but “a mild spring peak” in that of group A (alpha-hemolytic), which includes S. pneumoniae (Dowell, Whitney, Wright, Rose, & Schuchat, 2003). Although reports of S. pneumoniae causing disease are highest in the winter and spring, the bacteria colonize many people without incident year-round, so it is difficult to disentangle the association of more severe symptoms for patients who also have influenza, from other seasonal factors affecting S. pneumoniae's ability to colonize in the absence of influenza.

We apply this coinfection scenario directly to the model of system (12), but use sinusoidal rather than square-wave seasonality in the infection rates. Influenza data from the CDC covering the period 2010–2018 (Centers for Disease Control and Prevention) fit (least-squares regression) to a linear+cosine form yield an amplitude of variation that is 0.1444 times the mean, with a maximum in the 7th week (1/8 of the way through the year) and a minimum 26 weeks later. We apply this sinusoidal variation to the mean infectivity given in (Chowell, Miller, & Viboud, 2008) to describe influenza's infection rate. Based on the observed milder spring peak in (Dowell et al., 2003) for bacteria like S. pneumoniae, we similarly incorporate a 10% sinusoidal fluctuation in the bacterial infection rate, peaking 3/8 of the way through the year (in mid-spring).

For influenza, parameter values taken from (Chowell et al., 2008) give a mean value for ${\beta }_1\left(t\right)$ of 0.3177/day and a mean duration of infection of $1/{\gamma }_1=4.1$ days, leading to a BRN of 1.3. For bacterial respiratory infection (Austin et al., 1997), report a mean duration of $1/{\gamma }_2=2$ months (say 60 days) and a basic reproductive number of 10 (based on 90% colonization). Based on a context of either early childhood or nursing homes—the two high-risk populations at the ends of the age spectrum—both studies use an average residence time in the system ($1/\mu$) of 6 years, which implies a mean infectivity (for ${\beta }_2\left(t\right)$) of 0.1713/day. In (Fainstein et al., 1980), an increase in bacterial infectivity of $k_1=2.5$ was seen for influenza patients. We found no studies identifying a precise increase in influenza infectivity for bacteria-colonized patients and use here a more moderate $k_1=1.5$.

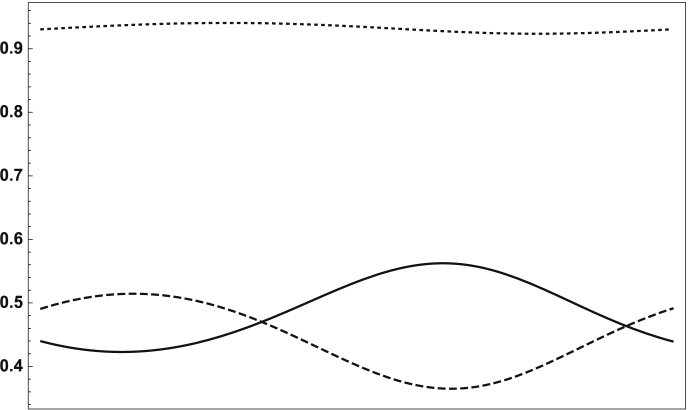
Using the methods described for IRNs yields the values ${\tilde{R}}_1=1.884$, ${\tilde{R}}_{1T}=1.885$, ${\tilde{R}}_2=13.322$, ${\tilde{R}}_{2T}=13.305$. Thus coinfection increases each pathogen's ability to persist, increasing its reproductive number by 45% and 33% respectively. Although the pathogens' relatively mild and nearly synchronized seasonality means that the true IRNs differ little from the time-averaged IRNs, we see that here the time-average method overestimates influenza's coinfection “boost” but underestimates the bacteria's. The effect of influenza's seasonality on the incidence of bacterial pneumonia is illustrated in Fig. 5, which shows one period (year) of $I_2$ (bacterial infection only) and $I_{12}$ (coinfection) over time. While their sum, the total proportion of the population colonized with the bacteria, remains more or less constant throughout the year, the proportion coinfected and thus likely to develop potentially fatal pneumonia varies significantly, reaching a majority of the at-risk population during late winter and early spring, in between the two infectivity peaks. If, instead, ${\beta }_2\left(t\right)$ is assumed to peak in summer, as with S. aureus (but keeping all other parameters the same), ${\tilde{R}}_2$ drops to 13.228, a relatively small change but indicating that bacterial infection being out of phase with influenza reduces the coinfection “boost” (${\tilde{R}}_1$ remains effectively unchanged, as do of course the two time-average numbers). In this case the time-average method overestimates both IRNs because the out-of-phase seasonality works against the synergy of coinfection.

Fig. 5.

$I_2\left(t\right)$ (bacterial infection, solid curve), $I_{12}\left(t\right)$ (influenza/bacterial coinfection, dashed curve), and their sum (dotted curve) vs. time, over a period of one year.

In summary, the calculations above illustrate how the mutualism between influenza and bacterial respiratory infections is affected by seasonality: In particular, influenza gives a stronger advantage to bacteria like S. pneumoniae whose seasonal cycles are more closely synchronized with influenza's than to bacteria like S. aureus whose infective peaks are more out of phase with influenza's.

5. Conclusion

The methods for calculating basic reproductive numbers in both autonomous and nonautonomous epidemic models have been extended in a natural way to calculate invasion reproductive numbers. These IRNs give a way to study stability of endemic states by determining whether certain cocirculating infections can invade populations which already have other infections resident.

For autonomous systems, the framework of van den Driessche and Watmough detailing next-generation methods first proposed by Diekmann et al. was adapted by exploiting the fact that the first steps for the method are epidemiological rather than mathematical, and reinterpreting the definition of infection to distinguish invading from resident pathogens. This shift in epidemiological context (from BRN to IRN) also shifts computational complexity by reducing the dimension of the next-generation matrix while centering it around an endemic equilibrium rather than the trivial (disease-free) one. In the same way the methods of Wang and Zhao detailing the linear operator approach first proposed by Bacäer and colleagues were extended for nonautonomous systems. In periodic systems, generally one cannot derive an explicit formula for the IRN, so one must approximate it numerically; since the resulting computations are often involved, we outline and illustrate them in some detail.

In addition, analysis identified an important subclass of periodic epidemic models for which IRNs can be derived using a much simpler method involving time-averages, which often allows one to write closed-form expressions for them. This subclass involves systems with a hierarchy to the invading infections—that is, where the invading infections (including coinfections, if any) can be ordered in such a way that infections at the top of the hierarchy influence the growth of infections below them, but not vice versa. The simplest and most common such case is that with only one invading infected class (the invading pathogen must then not be able to coinfect hosts with resident infections). Worthy of note is that this result holds independently of the number and structure of resident infections. In cases with multiple, non-hierarchical invading infections, our numerical examples illustrate how IRNs can be used to study co-persistence and competition in the presence of seasonality.

In particular, we examine the effects of influenza's seasonal incidence on the year-round persistence and prevalence of bacterial pneumonia. Although the total colonization prevalence remains nearly constant throughout the year, the mutualism which promotes coinfection offers greater benefits to bacteria like S. pneumoniae whose seasonal infective peaks align closely to influenza's, than to bacteria like S. aureus whose peaks are out of phase.

The results of this study lead naturally to future work examining the impact of seasonality on cocirculating infections. Invasion reproductive numbers in periodic systems can help identify whether seasonal changes exacerbate or mitigate interactions between pathogens in the same host populations. One such infection is Chagas disease, where competing strains of the parasite Trypanosoma cruzi have been observed to co-persist in some transmission cycles, despite an autonomous model for the cycle predicting competitive exclusion. Further work (in preparation) has been done using periodic models to explore whether seasonality can account for this co-persistence.

Handling Editor: J. Wu

Appendix A. Derivation of IRN for periodic systems

To adapt the linear operator method to invasion reproductive numbers, consider a setup similar to that in (Wang & Zhao, 2008) (and in next-generation methods for autonomous systems) where a heterogeneous population is grouped into n homogeneous compartments. Seasonality is assumed to make some parameters of the system ω-periodic, so this is a nonautonomous system. Assume that there are k different infections, and let $A\subseteq \left\{1,\dots ,k\right\}$ be a subset of these infections assumed resident within the population. As with autonomous systems, this allows one to exploit the fact that the first step in next-generation operator methods is epidemiological. In measuring invading pathogens' ability to persist, one considers all classes with only resident pathogens to be uninfected. Now one can calculate the invasion reproductive number of all infections not in A, that is $\forall j\in A_c$ where $A_c$ denotes the complement of A. The IRN is calculated for infections in $A_c$, so only those classes with invading infections, including singly and co-infected classes, are considered to be infected. (This includes coinfected classes mixing infections from both A and $A_c$.) Suppose there are m such invading ($A_c$) classes.

The compartments are then arranged so that the first m compartments correspond to infected individuals with infections from $A_c$. Let the set ${\mathbf{E}}_A$ contain all $A_c$-free states; note ${\mathbf{E}}_A$ includes periodic solutions and not just equilibria. Let ${\mathcal{F}}_i\left(t,x\right)$ be the input rate of newly infected individuals in the ith compartment, ${\mathcal{V}}_i^{+}\left(t,x\right)$ be the input rate of individuals by other means and ${\mathcal{V}}_i^{-}\left(t,x\right)$ be the rate of transfer out of compartment i. The model is then given by:

$$\frac{d{x}_i}{dt}={\mathcal{F}}_i\left(t,x\right)-{\mathcal{V}}_i\left(t,x\right)=f_i\left(t,x\right),i=1,\dots ,n$$ (19)

where ${\mathcal{V}}_i={\mathcal{V}}_i^{-}-{\mathcal{V}}_i^{+}$. Similar to autonomous models, the following conditions must be imposed, to ensure the model is well posed and makes biological sense. Assumptions (A1), (A3), (A4), and (A5) correspond to assumptions (A1)–(A4) of the autonomous case. The only new one here is (A2) which states that there are periodic coefficients in the system.

• •(A1) For each $1\le i\le n$, the functions ${\mathcal{F}}_i\left(t,x\right),{\mathcal{V}}_i^{+}\left(t,x\right),$ and ${\mathcal{V}}_i^{-}\left(t,x\right)$ are nonnegative and continuous on $\mathrm{ℝ}\times {\mathrm{ℝ}}_{+}^n$ and continuously differentiable with respect to x.
• •(A2) There is a real number $\omega >0$ such that for each $1\le i\le n$, the functions ${\mathcal{F}}_i\left(t,x\right),{\mathcal{V}}_i^{+}\left(t,x\right),$ and ${\mathcal{V}}_i^{-}\left(t,x\right)$ are ω-periodic in t.
• •(A3) If $x_i=0$ then ${\mathcal{V}}_i^{-}\left(t,x\right)=0$. If $x\in {\mathbf{E}}_A$, then ${\mathcal{V}}_i^{-}\left(t,x\right)=0$ for $i=1,\dots m$.
• •(A4) ${\mathcal{F}}_i\left(t,x\right)=0$ if $i>m$.
• •(A5) If $x\in {\mathbf{E}}_A$ then ${\mathcal{F}}_i\left(t,x\right)=0$ and ${\mathcal{V}}_i^{+}\left(t,x\right)=0$ for $i=1,\dots m$.

In addition to these assumptions, two more must be verified. These are separated from those above because the systems that need to be solved for them are nonautonomous and thus require new conditions based on monodromy matrices. The first assumption, (A6), is analogous to (A5) in the autonomous case, holding that an [ω-periodic] A-endemic state is stable in the reduced space without the invading ($A_c$) pathogens. As discussed in the main text, the existence of an A-endemic state requires the further hypothesis that the underlying reproductive numbers exceed 1. Assume the model has an $A_c$-infection-free periodic solution, $x_0\left(t\right)$. Define an $\left(n-m\right)\times \left(n-m\right)$ matrix

$$M\left(t\right):={\left(\frac{\partial f_i\left(t,x_0\left(t\right)\right)}{\partial x_j}\right)}_{m+1\le i,j\le n}.$$ (20)

Let ${\text{Φ}}_M$ be the monodromy matrix of the linear ω-periodic system $\frac{dz}{dt}=M\left(t\right)z$; that is, a principal fundamental matrix for the system, evaluated at $t=\omega$ (Hale, 1969) (see section 2.2.3 for computational details). To verify that $x_0\left(t\right)$ is linearly asymptotically stable in the $A_c$-infection free subspace, ${\mathbf{E}}_A$, one must show that the spectral radius of the monodromy matrix is less than one, or (A6) $\rho \left({\text{Φ}}_M\right)<1$.

Finally, following the notation from (van den Driessche & Watmough, 2002; Wang & Zhao, 2008), define two $m\times m$ matrices by

$$F\left(t\right)={\left[\frac{\partial {\mathcal{F}}_i\left(t,x_0\left(t\right)\right)}{\partial x_j}\right]}_{1\le i,j\le m},V\left(t\right)={\left[\frac{\partial {\mathcal{V}}_i\left(t,x_0\left(t\right)\right)}{\partial x_j}\left(x_0\right)\right]}_{1\le i,j\le m}.$$

Let $Y\left(t,s\right),t\ge s$ be the evolution operator of the linear ω-periodic system $\frac{dy}{dt}=-V\left(t\right)y$. That is, for each $s\in \mathrm{ℝ}$ the $m\times m$ matrix $Y\left(t,s\right)$ satisfies

$$\frac{d}{dt}Y\left(t,s\right)=-V\left(t\right)Y\left(t,s\right),\forall t\ge s,Y\left(s,s\right)=I$$ (21)

where I is the $m\times m$ identity matrix. The monodromy matrix ${\text{Φ}}_{-V}$ of the system then equals $Y\left(\omega ,0\right)$. The last assumption that must be verified in order to apply the method is that the populations of individuals with invading pathogens eventually die out in the absence of new infections. For this $A_c$ subsystem to be dissipative, we assume that (A7) $\rho \left({\text{Φ}}_{-V}\right)<1$.

The theory for nonlinear autonomous systems has been well established for studying stability of equilibria. In 1960, the Hartman-Grobman Theorem was proved showing that the local behavior of an autonomous system around a hyperbolic equilibrium point can be studied using the linearized system around the same point (Aulbach & Wanner, 2000). In 1975 this theorem was extended by Kenneth Palmer to nonautonomous systems (Palmer, 1975). This allows the use of the linearized system in (A6) to be used to study the stability of the $A_c$-infection-free solution $x_0\left(t\right)$ in the full system.

Assumptions (A1)–(A7) therefore make it possible to develop invasion reproductive numbers by considering a perturbation (ϕ) to the $A_c$-infection-free periodic state $x_0\left(t\right)$. Following (Wang & Zhao, 2008), standard theory of linear periodic systems (Hale, 1969) implies that there exist a $K>0$ and $\alpha >0$ such that

$$\Vert Y\left(t,s\right)\Vert \le K{e}^{-\alpha \left(t-s\right)},\forall t\ge s,s\in \mathrm{ℝ}.$$ (22)

In this way, we can bound the product $Y\left(t,s\right)F\left(s\right)$ which gives the next infection kernel:

$$\parallel Y(t,t-a)F(t-a)\parallel \le K\parallel F(t-a)\parallel e^{-\alpha a},\forall t\in ℝ,a\in [0,\infty )$$ (23)

If we now apply this kernel to the perturbation $\varphi \left(s\right)$, the initial ω-periodic distribution of $A_c$-infected individuals, then (still following (Wang & Zhao, 2008)) $F\left(s\right)\varphi \left(s\right)$ gives the distribution of those infected at time s by newly introduced infectious individuals. Next, for $t\ge s$, $Y\left(t,s\right)F\left(s\right)\varphi \left(s\right)$ counts those such infected individuals newly infected at time s who remain infected at time t. Finally, to count all such $A_c$-infected individuals remaining at time t, we sum over all prior times s:

$${{\int }^{}}_{-\infty }^{t}Y\left(t,s\right)F\left(s\right)\varphi \left(s\right)ds={{\int }^{}}_0^{\infty }Y\left(t,t-a\right)F\left(t-a\right)\varphi \left(t-a\right)da.$$ (24)

This accounting of all infections resulting from the initial introduction of new $A_c$-infectives forms the basis for the system's overall IRN.

Following the motivation of next-generation approaches (Diekmann et al., 1990; van den Driessche & Watmough, 2002), both Bacaër and Guernaoui (Bacäer & Guernaoui, 2006) and Wang and Zhou (Wang & Zhao, 2008) formalized this accounting by defining it as a linear operator L, termed the next-infection operator, and then defining the BRN $R_0$ as the spectral radius (maximum growth factor across all dimensions of infection) of L. From (Wang & Zhao, 2008):

Let $C_{\omega }$ be the ordered Banach space of all ω-periodic functions from $\mathrm{ℝ}$ to ${\mathrm{ℝ}}^m$, which is equipped with the maximum norm $\left|\right|\cdot \left|\right|$ and the positive cone $C_{\omega }^{+}:=\left\{\varphi \in C_{\omega }:\varphi \left(t\right)\ge 0,\forall t\in \mathrm{ℝ}\right\}$. Then we can define a linear operator $L:C_{\omega }\to C_{\omega }$ by

$$\left(L\varphi \right)\left(t\right)={{\int }^{}}_0^{\infty }Y\left(t,t-a\right)F\left(t-a\right)\varphi \left(t-a\right)da,\forall t\in \mathrm{ℝ},\varphi \in C_{\omega }.$$ (25)

Once the infections in A are reclassified so as not to be considered infectious states, the IRN can be defined in an analogous way using this approach.

Wang and Zhou went on to show that, for purposes of computing $R_0$ as well as verifying its traditional role as threshold quantity, one can use instead the evolution operator W of the simpler linear ω-periodic system

$$\frac{dw}{dt}=\left[-V\left(t\right)+\frac{F\left(t\right)}{\lambda }\right]w,t\in \mathrm{ℝ}$$ (26)

with parameter $\lambda \ge 0$. In particular, for the evolution operator $W\left(t,s,\lambda \right),t\ge s,s\in \mathrm{ℝ}$ of (26) on ${\mathrm{ℝ}}^m$, $R_0$ is also given by the unique root λ of $\rho \left(W\left(\omega ,0,\lambda \right)\right)=1$. Their result also holds for the A-endemic system (19), and Theorems (2.1) and (2.2) from (Wang & Zhao, 2008) can then be translated to apply to IRNs, as described in the main text.

Appendix B. Supplementary data

The following is the supplementary data to this article: