Quantifying Dynamic Regulation in Metabolic Pathways with Nonparametric Flux Inference

Abstract

One of the central tasks in systems biology is to understand how cells regulate their metabolism. Hierarchical regulation analysis is a powerful tool to study this regulation at the metabolic, gene-expression, and signaling levels. It has been widely applied to study steady-state regulation, but analysis of the metabolic dynamics remains challenging because it is difficult to measure time-dependent metabolic flux. Here, we develop a nonparametric method that uses Gaussian processes to accurately infer the dynamics of a metabolic pathway based only on metabolite measurements; from this, we then go on to obtain a dynamical view of the hierarchical regulation processes invoked over time to control the activity in a pathway. Our approach allows us to use hierarchical regulation analysis in a dynamic setting but without the need for explicitly time-dependent flux measurements.

Introduction

It is important to understand how microbes regulate their metabolism in response to changes in environmental conditions. A key aspect of regulation of metabolism (or metabolic fluxes) is to modulate enzyme abundance, either through transcriptional regulation or through signaling and post-translational modification. Experimental studies of central metabolism, e.g., in three species of parasitic protists (1) and in Bacillus subtilis (2), show that flux regulation is rarely achieved exclusively at the transcriptional level. It is thus important to take a more comprehensive assessment of metabolic regulation, including substrate and product changes, allosteric regulation, and post-translational enzyme modifications.

Hierarchical regulation analysis (1, 3) (HRA) is a powerful tool to study regulatory processes across different levels. For each reaction step, HRA quantifies the contributions stemming from different regulatory levels, including gene expression and signaling, to the regulation of overall flux. This approach has been successfully used to analyze the regulatory properties of many important metabolic pathways (2, 4, 5, 6, 7); for all instances, it was found that regulation is typically distributed across levels.

We consider an example in which the rate v_i of an enzyme-catalyzed reaction i depends linearly on two functions, which we denote by h and g. The former is related to hierarchical effects due to changes in enzyme concentration or covalent modification. The latter is related to metabolic effects, in which changes in rate are caused by changes in the concentrations of substrates, products, and metabolic effectors. Identifying the rate v_i at steady state with the flux through the enzyme J, we obtain

$$J=v_i=h\left(e_i\right)\times g_i\left(X\right).$$ (1)

e_i represents the concentration of the enzyme catalyzing the process v_i; X denotes a vector of concentrations of metabolites that are involved in reaction i. For covalent modifications, the first term can be expanded as h(e_i) = e_i × φ_a,i, with φ_a,i denoting the fraction of the enzyme that is in the active covalent modification state (Fig. 1 b). Then, the change in the logarithm of the steady-state flux J can be expressed as

$$\mathit{\Delta }\ln J=\mathit{\Delta }\ln h\left(e_i\right)+\mathit{\Delta }\ln g_i\left(X\right);$$ (2)

rearranging this expression, we have

$$1=\frac{\mathit{\Delta }\ln h\left(e_i\right)}{\mathit{\Delta }\ln J}+\frac{\mathit{\Delta }\ln g_i\left(X\right)}{\mathit{\Delta }\ln J}={\mathit{\rho }}_h^i+{\mathit{\rho }}_m^i,$$ (3)

where Δ denotes the difference between two steady states. The hierarchical regulation coefficient ${\mathit{\rho }}_h^i$ quantifies the contribution of changes in enzyme concentration (or enzyme capacity, i.e., $h\left(e_i\right)=V_{max}^i$) to the regulation of the flux. The relative contribution of the changes in the enzyme activity through its interaction with the rest of the metabolism is quantified by the metabolic regulation coefficient ${\mathit{\rho }}_m^i$ (see Fig. 1 for illustration of hierarchical and metabolic regulation). The hierarchical regulation coefficient can be further expressed as a sum of the gene-expression and signal-transduction regulation coefficients (i.e., ${\mathit{\rho }}_h^i=d\ln h\left(e_i\right)/d\ln J=d\ln e_i/d\ln J+d\ln {\mathit{\phi }}_{a,i}/d\ln J={\mathit{\rho }}_g^i+{\mathit{\rho }}_s^i$). Experimentally, it is relatively easy to measure the hierarchal regulation coefficient because only enzyme concentration measurements, e_i (or $V_{max}^i$), and the flux are required; this is normally done under two experimental conditions. More recently, Chubukov et al. (2) generalized this to multiple conditions—which increases computational accuracy—by using linear regression to relate ln(e_i) and ΔlnJ. The metabolic regulation coefficient can then be calculated from ${\mathit{\rho }}_m^i=1-{\mathit{\rho }}_h^i$.

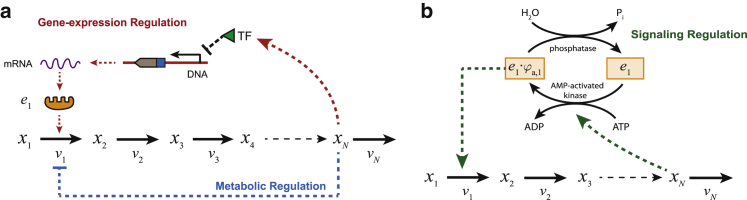
Figure 1.

Illustration of hierarchical and metabolic regulation in an unbranched metabolic pathway. (a) The enzyme e₁ that catalyzes the first reaction is regulated through both transcriptional repression (gene-expression regulation) and allosteric inhibition (metabolic regulation) by the end product. (b) A fraction of the enzyme that is in a covalent modification state (e_i × φ_a,i) actively catalyzes the first reaction. Hierarchical regulation comprises gene-expression and signaling regulation. To see this figure in color, go online.

Most existing HRA studies investigate steady-state regulation; however, it is typically important to know how cells adapt to environmental changes. Time-dependent regulation analysis aims to quantify the regulation coefficients as a function of time (8, 9). The integrative version of time-dependent regulation analysis integrates all the regulation between time t₀ (the start of the perturbation) and t. For instance, the time-dependent hierarchical regulation coefficients can be calculated as

$${\mathit{\rho }}_h^i\left(t\right)=\frac{\ln h\left(e_i\left(t\right)\right)-\ln h\left(e_i\left(t_0\right)\right)}{\ln v_i\left(t\right)-\ln v_i\left(t_0\right)}\approx \frac{\left(h\left(e_i\left(t\right)\right)-h\left(e_i\left(t_0\right)\right)\right)/h\left(e_i\left(t_0\right)\right)}{\left(v_i\left(t\right)-v_i\left(t_0\right)\right)/v_i\left(t_0\right)}.$$ (4)

Here, the reaction rate, v, is employed in the denominator rather than the flux, J, because we are studying the transient effect rather than the steady states. The latter expression only provides a good approximation when h(e_i(t))/h(e_i(t₀)) ≈ 1 and v_i(t)/v_i(t₀) ≈ 1. When there is no post-translational modification, h(e_i(t)) can be simplified as e_i(t) or V_max(t) (9). The time-dependent metabolic regulation coefficients are simply ${\mathit{\rho }}_m^i\left(t\right)=1-{\mathit{\rho }}_h^i\left(t\right)$. We can also develop an instantaneous version of time-dependent regulation analysis (8, 10) that quantifies the contribution of hierarchical and metabolic regulation to the change in the reaction rate at time point, which will not be discussed here.

Dynamic flux measurement or estimation is a key limitation for generalizing HRA from steady-state to dynamic regulatory analysis: it is hard to directly measure fluxes, whereas intracellular fluxes can be estimated by tracking isotope-labeled (e.g., ¹³C and ¹⁵N) metabolites (11, 12), but this is only suitable for steady-state analysis. The only time-dependent regulation analysis (9) for nitrogen starvation in yeast that has been presented is based on fluxes estimated at a limited number of time points, but the results cannot capture the complete temporal behavior, and it requires several independent experiments to generate the confidence limits on the HRA results; experimentally, this is both expensive and time-consuming.

Here, we develop a new, to our knowledge, nonparametric Bayesian modeling framework for dynamic (or time-dependent) HRA. High-resolution time-dependent metabolite profiles can be first estimated from discrete metabolite concentration measurements using nonparametric Gaussian process regression (GPR). Dynamic reaction rates or fluxes can then be inferred from the derivatives of the corresponding metabolite profiles and the network stoichiometry. Finally, the time-dependent hierarchical regulation coefficients are calculated from the time-dependent reaction rates and enzyme profiles. A key advantage of our approach lies in its reliance on only experimental protein and metabolite data without the need of time-dependent flux measurements. With this, we obtain complete temporal hierarchical regulation profiles for each reaction together with statistical confidence.

Materials and Methods

Dynamic reaction rate estimation from metabolite measurements: motivation examples

We first consider the simple linear metabolic pathway example (Fig. 1 a). We assume that x₁ is an external substrate with constant concentration, and the last reaction rate v_N depends only on the concentration of the last metabolite x_N with known degradation kinetics g_N(x_N); e_N is a constant because gene-expression regulation is not considered in this last step. The ordinary differential equations (ODEs) of this linear pathway are

$$\begin{array}{lll}{\dot{x}}_2=e_1\times g_1\left(x_1,x_n\right)-e_2\times g_2\left(x_2,x_3\right)=v_1-v_2\hfill & \hfill & v_1={\dot{x}}_2+v_2\hfill \\ {\dot{x}}_3=e_2\times g_2\left(x_2,x_3\right)-e_3\times g_3\left(x_3,x_4\right)=v_2-v_3\hfill & \hfill & v_2={\dot{x}}_3+v_3\hfill \\ ⋮\hfill & \Rightarrow \hfill & ⋮\hfill \\ \begin{array}{l}{\dot{x}}_{N-1}=e_{N-1}\times g_{N-1}\left(x_{N-1},x_N\right)-g_N\left(x_N\right)=v_{N-1}-g_N\left(x_N\right)\\ {\dot{e}}_1=g_e\left(x_N\right)-k_d\times e_1.\end{array}\hfill & \hfill & v_{N-1}={\dot{x}}_N+g_N\left(x_N\right)\hfill \end{array}$$ (5)

The changes of metabolite concentration can also be expressed by the differences between incoming and outgoing reaction rates. After the derivatives of metabolite concentrations are approximated from the Gaussian process (GP) derivatives, the reaction rate of each reaction can be calculated. The generic expression of the i^th reaction rate is

$$v_i={\dot{x}}_{i+1}+\dots +{\dot{x}}_N+g_N\left(x_N\right).$$ (6)

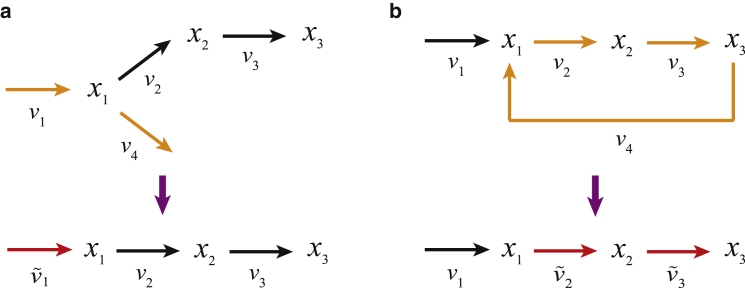
This example illustrates that dynamic reaction rates in a linear metabolic pathway can be expressed in terms of the derivatives of time-dependent metabolite concentrations. For branched pathways or pathways with feedback/feedforward reactions, in general, there can be more reactions than metabolites. Therefore, not all the reaction rates can be expressed explicitly in terms of metabolite concentrations. In such cases, either some reaction rates need to be measured experimentally to reduce the total number of unknown reactions or some reactions may need to be combined or merged together so that the number of unknown reactions is equal to the number of metabolites. For instance, the reaction rates, v₁ and v₄, as shown in the branched pathway in Fig. 2 a, cannot be uniquely determined and shall be combined into an overall net-reaction rate ${\tilde{v}}_1$ as

$$\begin{array}{ccc}{\dot{x}}_1=v_1-v_2-v_4& & {\tilde{v}}_1=v_1-v_4={\dot{x}}_1+v_2\\ {\dot{x}}_2=v_2+v_3& \Rightarrow & v_2={\dot{x}}_2+v_3\\ {\dot{x}}_3=v_3& & v_3={\dot{x}}_3\end{array}.$$ (7)

Figure 2.

Illustration of (a) a branched metabolic pathway and (b) a pathway with a feedback reaction. The lower diagram shows the equivalent unbranched pathway, with reactions from the original pathway (orange) merged to form “net” reactions (red). To see this figure in color, go online.

Similarly, for a pathway with a feedback reaction as given in Fig. 2 b, there are four reactions but only three metabolites. To estimate reaction rates from metabolites, the feedback reaction rate (−v₄) can be expressed via the forward reaction rates v₂ and v₃ (i.e., ${\tilde{v}}_2=v_2-v_4$, ${\tilde{v}}_3=v_3-v_4$). In such a way, the original pathway can be approximated as a linear pathway and the net-reaction rates between metabolites can be estimated:

$$\begin{array}{ccc}{\dot{x}}_1=v_1-{\tilde{v}}_2& & v_1={\dot{x}}_1+{\tilde{v}}_2\\ {\dot{x}}_2={\tilde{v}}_2-{\tilde{v}}_3& \Rightarrow & {\tilde{v}}_2={\dot{x}}_2+{\tilde{v}}_3\\ {\dot{x}}_3={\tilde{v}}_3& & {\tilde{v}}_3={\dot{x}}_3\end{array}.$$ (8)

For a pathway with branches or feedback/feedforward loops, we will not be able to compute the regulation coefficients with respect to each reaction unless practically one can measure the flux go through some of the branches. However, a hierarchical regulation coefficient of a specific enzyme with respect to a joint net-reaction rate can still be defined and calculated, but its summation with the corresponding metabolic regulation coefficient will no longer be conserved (i.e., always equal to one). For instance, the relative change of the ${\tilde{v}}_2$ in the feedback pathway example is

$$\begin{array}{l}\mathit{\Delta }\ln {\tilde{v}}_2=\mathit{\Delta }\ln \left(v_2-v_4\right)=\mathit{\Delta }\ln \left(e_2\times g_2\left(x_1,x_2\right)-e_4\times g_4\left(x_1,x_3\right)\right)\\ =\mathit{\Delta }\ln \left(e_2\times g_2\left(x_1,x_2\right)\left(1+e_4\times g_4\left(x_1,x_3\right)/e_2\times g_2\left(x_1,x_2\right)\right)\right)\\ =\mathit{\Delta }\ln e_2+\mathit{\Delta }\ln g_2\left(x_1,x_2\right)+\mathit{\Delta }\ln \left(1+e_4\times g_4\left(x_1,x_3\right)/e_2\times g_2\left(x_1,x_2\right)\right).\end{array}$$

Dividing both sides of the equation by $\Delta \ln {\tilde{v}}_2$, the first term $\mathit{\Delta }\ln e_2/\mathit{\Delta }\ln {\tilde{v}}_2$ is a hierarchical regulation coefficient that quantifies the contribution of relative change of enzyme e₂ to the relative change of net-reaction rate ${\tilde{v}}_2$. The second term is the corresponding metabolic regulation coefficient. However, the last term depends not only on the enzymes but also on metabolite interactions with respect to both reactions 2 and 4. Hence, the conservation law is not applicable for branched or feedback/feedforward pathways, and we will not be able to directly calculate the metabolic regulation coefficient even if the hierarchical coefficient is available. For a pathway with multiple branches or feedback/feedforward loops, several branches will be combined to form the net flux, which does not require multiple transformations, although the definition of “net” flux may not be unique (because one can have multiple ways to combine different branches).

Time-dependent metabolites estimation using GPR

The examples given in the previous subsection indicate that to estimate dynamic fluxes, we first need to estimate time-dependent metabolite concentrations. In general, metabolic pathways can be modeled by a set of ODEs,

$$\dot{\mathbf{x}}\left(t\right)=\mathbf{f}\left(\mathbf{x}\left(t\right),t;\mathit{\theta }\right),$$ (9)

where x(t) = [x₁(t), x₁(t),..., x_N(t)] is the vector of metabolite concentrations at time t and θ is the vector of model kinetic parameters. The rate of change of the i^th metabolite is ${\dot{x}}_i\left(t\right)=f_i\left(\mathbf{x}\left(t\right),t;\mathit{\theta }\right)$. We assume that the i^th metabolite can be measured with some additive normally distributed noise (with constant variance):

$$y_i\left(t\right)=x_i\left(t\right)+\mathit{\xi },\mathit{\xi }\sim \mathcal{N}\left(0,{\mathit{\sigma }}_{\xi }^2\right).$$ (10)

Identifying the underlying time-dependent metabolic processes from limited noisy observations is challenging, especially when the “true” kinetics and parameters are unknown. GPR (13), a nonparametric Bayesian inference approach, can then be employed to recover the underlying dynamic process without having to estimate reaction kinetics.

Single-output GPR

The most straightforward approach is to use standard single-output GPR to model the concentration of each metabolite as a function of time x_i(t) from the noisy observations y_i(t). GPR assumes that outputs (x_i) evaluated at a finite number of inputs (i.e., time points t = {t₁, t₂,..., t_S}) have a multivariate Gaussian distribution. A prior can be put directly on a function rather than the parameters of a parametric function. A GP prior over the observed outputs (a function over time) for the i^th metabolite is

$$y_i\left(\mathbf{t}\right)\sim \mathcal{GP}\left(m\left(\mathbf{t}\right),k\left(\mathbf{t},{\mathbf{t}}^{\prime }\right)+{\mathit{\sigma }}_{\xi }^2\mathit{\delta }\left(\mathbf{t},{\mathbf{t}}^{\prime }\right)\right),$$ (11)

where m(t) is a mean function of the metabolite concentrations taken at times t, δ(t, t′) is the Kronecker δ function, and k(t, t′) is a covariance function. Normally, a squared covariance function is selected, $k\left(t_p,t_q\right)={\mathit{\sigma }}_f^2\text{exp}\left(-{\left(t_p-t_q\right)}^2/2l_d^2\right)$, where the hyperparameters, (σ_f, l_d, σ_ξ), can be determined by maximizing the likelihood function (14). Given the GP prior, it is possible to compute the posterior because the joint (prior) probability distribution of the training outputs, y_i, and the test outputs is again multivariate Gaussian,

$$\left[\begin{array}{c}{\mathbf{y}}_i\\ {\mathbf{x}}_i^{\ast }\end{array}\right]\sim \mathcal{N}\left(\left[\begin{array}{c}{\mathbf{m}}_o\\ {\mathbf{m}}_{\ast }\end{array}\right],\left[\begin{array}{cc}{K}_o+{\mathit{\sigma }}_{\xi }^2\text{I}& K_{o\ast }\\ K_{\ast o}& K_{\ast \ast }\end{array}\right],\right),$$ (12)

where y_i = [y_i(t₁),..., y_i(t_S)]^T is a set of output observations; ${\mathbf{x}}_i^{\ast }={\left[x_i\left(t_1^{\ast }\right),\dots ,x_i\left(t_R^{\ast }\right)\right]}^T$ is the test outputs to be estimated at any finite set of time points, (K_o)_pq = k(t_p, t_q), ${\left(K_{o\ast }\right)}_{pq}=k\left(t_p,t_q^{\ast }\right)$, ${\left(K_{\ast o}\right)}_{pq}=k\left(t_p^{\ast },t_q\right)$, and ${\left(K_{\ast \ast }\right)}_{pq}=k\left(t_p^{\ast },t_q^{\ast }\right)$.

The posterior distribution for the i^th time-dependent metabolite concentrations x_i(t) can be obtained by updating the GP prior using the observed data set y_i(t) (from conditioning the joint Gaussian prior distribution),

$$\left[x_i\left(t_1^{\ast }\right),\dots ,x_i\left(t_R^{\ast }\right)\right]|{\mathbf{y}}_i\sim \mathcal{N}\left({\mathbf{m}}_{post}^i,K_{post}^i\right),$$ (13)

where ${\mathbf{m}}_{post}^i={\mathbf{m}}_{\ast }+K_{\ast o}{\left(K_o+{\mathit{\sigma }}_{\xi }^2\text{I}\right)}^{-1}\left({\mathbf{y}}_i-{\mathbf{m}}_o\right)$ and $K_{post}^i=K_{\ast \ast }-K_{\ast o}{\left(K_o+{\mathit{\sigma }}_{\xi }^2\text{I}\right)}^{-1}{K}_{o\ast }$. From the GP posterior, we can obtain dense metabolite concentration time series from limited experimental samples.

Multi-output GPR

Different metabolites in a metabolic pathway often interact with one another, e.g., via substrate/product effects or allosteric regulation or if they are affected by the same noise process (e.g., enzyme gene expression). Single-output GPR is computationally efficient at modeling individual metabolite trajectories, where such (often unknown or neglected) interactions between metabolites can be ignored. Multi-output GPs can account for such unknown relationships and are implemented either by specifying positive definite covariance functions between different outputs through so-called co-kriging (or coregionalization) (15, 16) or through parameterizing impulse responses function via linear systems theory (17, 18, 19). In this work, the latter approach is employed. Considering a stationary linear system with M independent white noise processes, u₁(t),..., u_M(t), as inputs, it produces N outputs y₁(t),..., y_N(t) with n^th defined as

$$y_n\left(t\right)=z_n\left(t\right)+w_n\left(t\right),$$ (14)

where w_n(t) is stationary Gaussian white noise with variance ${\mathit{\sigma }}_n^2$, and the multi-input multi-output filter is defined as

$$z_n\left(t\right)=\sum _{m=1}^M{h}_{mn}\left(t\right)\otimes u_m\left(t\right)=\sum _{m=1}^M{\int }_{-\infty }^{\infty }{h}_{mn}\left(\mathit{\tau }\right)u_m\left(t-\mathit{\tau }\right)d\mathit{\tau ,}$$ (15)

where h_mn is the Gaussian kernel connecting input m to output n; hence, a multi-input multi-output filter can capture the dependencies among output variables y_n(t). By evaluating the convolution integral, the covariance between y_i(t_p) and y_j(t_q) is

$$C_{ij}\left(d\right)=\sum _{m=1}^M{\int }_{-\infty }^{\infty }{h}_{mi}\left(\mathit{\tau }\right)h_{mj}\left(\mathit{\tau }+d\right)d\mathit{\tau }=\sum _{m=1}^M\frac{{\left(2\mathit{\pi }\right)}^{\frac{p}{2}}{v}_{mi}{v}_{mj}}{\sqrt{A_{mi}+A_{mj}}}\text{exp}\left\{-\frac{1}{2}{\left(d-\left[{\mathit{\mu }}_{mi}-{\mathit{\mu }}_{mj}\right]\right)}^{2}S\right\},$$ (16)

where d = t_p − t_q is the distance between two input points, S = A_mi(A_mi + A_mj)⁻¹A_mj, and μ_mi is the offset parameter. The (positive definite) covariance matrix between N output variables becomes

$$C=\left[\begin{array}{ccc}{C}_{11}+{\mathit{\sigma }}_1^2\text{I}& \cdots & C_{1N}\\ ⋮& \ddots & ⋮\\ C_{N1}& \cdots & C_{NN}+{\mathit{\sigma }}_N^2\text{I}\end{array}\right].$$ (17)

C is a R × R matrix with $R={\sum }_{i=1}^N{R}_i$ and R_i observations of output i. The hyperparameters θ = {ν_mn, μ_mn, A_mn, σ_n} can be estimated by maximizing the log-likelihood, $\mathcal{L}\left(\mathit{\theta }\right)=-\left(1/2\right)\text{log}\left|C\left(\mathit{\theta }\right)\right|-\left(1/2\right){\mathbf{y}}^{T}C{\left(\mathit{\theta }\right)}^{-1}\mathbf{y}-\left(R/2\right)\text{log}2\mathit{\pi }$, using a multistart or constrained Nelder-Mead algorithm implemented in MATLAB’s (The MathWorks, Natick, MA) nonlinear optimization toolbox, where ${\mathbf{y}}^T=\left[\left(y_{\mathrm{1,1}}\cdots y_{1,R_1}\right)\cdots \left(y_{i,1}\cdots y_{i,R_i}\right)\cdots \left(y_{N,1}\cdots y_{N,R_N}\right)\right]$. The distribution of predictions over $R^t={\sum }_{i=1}^N{R}_i^t$ ($R_i^t$ are the testing time points, i.e., $t_1^{\ast },t_2^{\ast },\dots ,t_{R_i^t}^{\ast }$, for output i) for all the output variables (e.g., metabolites in a pathway) has mean and variance

$$\left[z_1\left(t_{\mathrm{1,1}}^{\ast }\right),\dots ,z_1\left(t_{1,R_1^t}^{\ast }\right),\cdots ,z_N\left(t_{N,1}^{\ast }\right),\dots ,z_N\left(t_{N,R_N^t}^{\ast }\right)\right]|\mathbf{y}\sim \mathcal{N}\left(K_{\ast o}^M{C}^{-1}\mathbf{y},K_{\ast \ast }^M-K_{\ast o}^M{C}^{-1}{K}_{o\ast }^M\right),$$ (18)

where $K_{\ast o}^M$, $K_{o\ast }^M$ and $K_{\ast \ast }^M$ are defined in the Supporting Materials and Methods. For notational simplicity, the conditional probability distribution in Eq. 18 will below be written as [z₁,..., z_N]|[y₁,..., y_N].

Derivative processes and reaction rate estimation

As shown above, reaction rates depend on the derivatives of metabolite concentrations in a pathway. Because differentiation is a linear operator, the derivative of a GP is another GP. We thus obtain for the GP posterior distribution for the derivatives of metabolite concentrations

$$\left[\dot{x_i}\left(t_1^{\ast }\right),\dots ,\dot{x_i}\left(t_R^{\ast }\right)\right]|{\mathbf{z}}_i\sim \mathcal{N}\left({\mathbf{m}}_{post}^i,K_{post}^i\right),$$ (19)

where the training set z_i are the time-dependent estimates of the i^th metabolite obtained from the multi-output GPR and the expressions for ${\mathbf{m}}_{post}^i$ and $K_{post}^i$ are the same as in Eq. 13; $K_{\ast o}$, $K_{o\ast }$, and $K_{\ast \ast }$ are defined differently here (14, 20):

$$K_{\ast o}=\left(\begin{array}{c}{K}_o\\ L_{D}F\end{array}\right),K_{o\ast }=\left(\begin{array}{cc}{K}_o& L_{D}F\end{array}\right),\text{and}{K}_{\ast \ast }=\left(\begin{array}{cc}{K}_o& L_{D}F\\ L_{D}F& M\end{array}\right),$$

with ${\left(L_{DF}\right)}_{pq}=cov\left(\dot{x}\left(t_p\right),x\left(t_q\right)\right)=d/d{t}_{p}k\left(t_p,t_q\right)$, ${\left(L_{FD}\right)}_{pq}=cov\left(x\left(t_p\right),\dot{x}\left(t_q\right)\right)=d/d{t}_{q}k\left(t_p,t_q\right)$, and ${\left(M\right)}_{pq}=cov\left(\dot{x}\left(t_p\right),\dot{x}\left(t_q\right)\right)=d^2/d{t}_{p}d{t}_{q}k\left(t_p,t_q\right)$. Because the sum of GPs is another GP, according to Eq. 6, the distribution of the reaction rate of the i^th reaction (over the same finite time points) can be expressed in terms of the derivatives of corresponding metabolite concentrations,

$$\left[v_i\left(t_1^{\ast }\right),\dots ,v_i\left(t_R^{\ast }\right)\right]|{\mathbf{z}}_i\sim \mathcal{N}\left({\mathbf{m}}_v^i,K_v^i\right),$$ (20)

where ${\mathbf{m}}_v^i={\mathbf{m}}_{post}^{i+1}+\dots +{\mathbf{m}}_{post}^N+g_N\left({\mathbf{m}}_{post}^N\right)$, $K_v^i=K_{post}^{i+1}+\dots +K_{post}^N$. This expression is generic for estimating reaction rates in a linear metabolic pathway or the net-reaction rates in a branched or feedback/feedforward pathways.

Practically, when estimating reaction rates of a large metabolic pathway with many metabolites, there can be a large number of parameters associated with the multi-output GP (as in Eq. 16), and if only limited data are available, the optimization can become an ill-posed problem. In such cases, single-output GPs may be used as an alternative by replacing the z_i in Eq. 18 with x_i in Eq. 13; correlations between metabolites will then no longer be modeled explicitly.

Time-dependent regulation coefficients estimation

The time-dependent hierarchical regulation coefficient expression Eq. 4 for the i^th reaction at time t is defined as a ratio of the relative changes of enzyme concentration to the relative change of the reaction rate. Because of the dependency between reaction rate and enzyme concentration, the relative changes between these two variables (over finite time points $t_1^{\ast },t_2^{\ast },\dots ,t_R^{\ast }$) are therefore calculated as joint posterior predictions of a multi-output GP,

$$\left[{\mathbf{z}}_e,{\mathbf{z}}_v\right]|\left[{\mathbf{y}}_e,{\mathbf{y}}_v\right]\sim \mathcal{N}\left({\mathbf{m}}_{\mathit{\rho }},K_{\mathit{\rho }}\right),$$ (21)

where ${\mathbf{m}}_{\rho }=K_{\ast o}^M{C}^{-1}\mathbf{y}$, $K_{\mathit{\rho }}=K_{\ast \ast }^M-K_{\ast o}^M{C}^{-1}{K}_{o\ast }^M$. The training data y_e are the relative changes of enzyme concentrations; y_v is the relative change of the estimated reaction rate from Eq. 20. By assuming the previous steady-state (or the one before perturbation) enzyme concentrations e_i(t₀) and reaction rates v_i(t₀) are known, the distribution of time-dependent hierarchical regulation coefficients $\left[{\mathit{\rho }}_h^i\left(t_1^{\ast }\right),\dots ,{\mathit{\rho }}_h^i\left(t_R^{\ast }\right)\right]$ can be evaluated according to

$$\frac{\left[\ln e_i\left(t_1^{\ast }\right),\dots ,\ln e_i\left(t_R^{\ast }\right)\right]-\ln e_i\left(t_0\right)}{\left[\ln v_i\left(t_1^{\ast }\right),\dots ,\ln v_i\left(t_R^{\ast }\right)\right]-\ln v_i\left(t_0\right)}=\frac{{\mathbf{z}}_e}{{\mathbf{z}}_v}.$$ (22)

For each time t, this is the ratio of two GPs, and the probability density of the hierarchical regulation coefficient $p\left({\mathit{\rho }}_h^i\left(t\right)\right)$ can be evaluated as a ratio between two Gaussian variables,

$$p\left({\mathit{\rho }}_h^i\left(t\right)\right)=p\left(\frac{\ln e_i\left(t\right)-\ln e_i\left(t_0\right)}{\ln v_i\left(t\right)-\ln v_i\left(t_0\right)}\right)=p\left(\frac{z_e\sim \mathcal{N}\left({\mathit{\mu }}_{z_e},{\mathit{\sigma }}_{z_e}^2\right)}{z_v\sim \mathcal{N}\left({\mathit{\mu }}_{z_v},{\mathit{\sigma }}_{z_v}^2\right)}\right).$$ (23)

Because the reaction rate v_i is a function of enzyme concentration, e_i, the probability density of the ratio (i.e., z = z_e/z_v, $z_e\sim \mathcal{N}\left({\mathit{\mu }}_{z_e},{\mathit{\sigma }}_{z_e}^2\right)$ and $z_v\sim \mathcal{N}\left({\mathit{\mu }}_{z_v},{\mathit{\sigma }}_{z_v}^2\right)$) can be calculated from the means, SDs and correlation coefficient of the two Gaussian variables (i.e., $p_z\left(z;{\mathit{\mu }}_{z_e},{\mathit{\mu }}_{z_v};{\mathit{\sigma }}_{z_e},{\mathit{\sigma }}_{z_v};r\right)$); see Supporting Materials and Methods and (21). Here, the correlation coefficients between two GPs over all test sampling times (i.e., $\text{corr}\left({\mathbf{z}}_e,{\mathbf{z}}_v\right)=\left[r\left(t_1^{\ast }\right),\dots ,r\left(t_R^{\ast }\right)\right]$) is calculated from the covariance matrix C employed in the multi-output GP (Eq. 16),

$$\text{corr}\left({\mathbf{z}}_e,{\mathbf{z}}_v\right)=\frac{\text{cov}\left({\mathbf{z}}_e,{\mathbf{z}}_v\right)}{{\mathit{\sigma }}_{{\mathbf{z}}_e}·{\mathit{\sigma }}_{{\mathbf{z}}_v}}=\frac{\text{diag}\left(C_{12}\right)}{\sqrt{\text{diag}\left(C_{11}+{\mathit{\sigma }}_1^2\text{I}\right)}·\sqrt{\text{diag}\left(C_{22}+{\mathit{\sigma }}_2^2\text{I}\right)}}.$$ (24)

After obtaining the probability density $p\left({\mathit{\rho }}_h^i\left(t\right)\right)$, we can also compute the mean and the confidence intervals at each time t. The most recently updated source code for the implementation is available to download from https://github.com/FeiHeIC/DynamicRegAnalysis/.

Results

An unbranched pathway with negative feedback transcriptional regulation

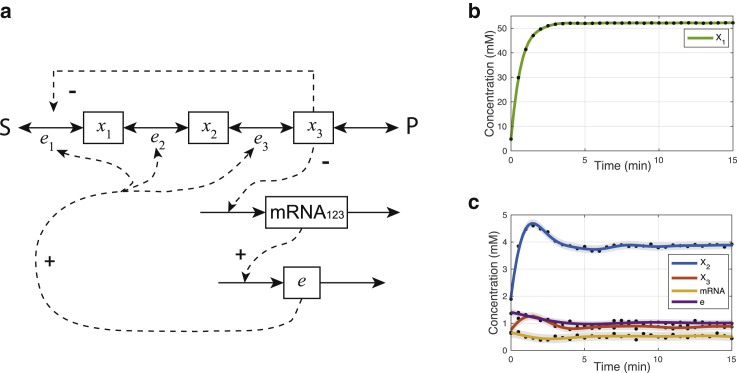
Fig. 3 a shows an unbranched metabolic pathway with three metabolites, where for all the three enzymes, gene expression is regulated by the last metabolite. We describe this as (with all the kinetic equations and parameters provided in Eq. 8)

$$\begin{array}{l}{\dot{x}}_1=v_1\left(S,x_1,e\right)-v_2\left(x_1,x_2,e\right)\\ \begin{array}{cc}{\dot{x}}_2=v_2\left(x_1,x_2,e\right)-v_3\left(x_2,x_3,e\right)& v_1={\dot{x}}_1+v_2\\ {\dot{x}}_3=v_3\left(x_2,x_3,e\right)-g_3\left(x_3,P\right)& \Rightarrow v_2={\dot{x}}_2+v_3\\ \begin{array}{l}\dot{mRNA}=v_{trscsyn}-v_{trscdeg}\\ \dot{e}=v_{trnlsyn}-v_{trnldeg}\end{array}& v_3={\dot{x}}_3+g_3\left(x_3,P\right)\end{array}.\end{array}$$ (25)

Figure 3.

A three-metabolite unbranched metabolic pathway and estimation results. (a) The pathway model diagram is given. The metabolites are denoted by x_i and enzymes by e. S and P are the external metabolites. The first enzyme e₁ is regulated through both transcriptional repression and allosteric inhibition by the third metabolite. Enzymes 1, 2, and 3 are encoded on the same operon. (b and c) GPR to simulated metabolite observations x₁, x₂, x₃, mRNA, and enzymes e after the change in S from 0.1 to 1 at t = 0 is shown. The noisy metabolite observations are shown in dot, and the confidence intervals in gray represent the ± 2× SDs of the GP posterior distribution. To see this figure in color, go online.

We add additive Gaussian random noise (σ² = 0.05) to the simulated metabolite, messenger RNA (mRNA), and enzyme concentrations. The system is perturbed from a reference steady state with S = 0.1 to S = 1 at t = 0. We fit a GP to each of the metabolite time courses (Fig. 3, b and c) and calculate their derivatives. The time-dependent reaction rate (v_i) for each reaction i can then be calculated from the GP derivative processes (Fig. 4, a–c). Finally, we calculate the time-dependent hierarchical and metabolic regulation coefficients for each reaction and the corresponding confidence intervals (Fig. 4, d–f).

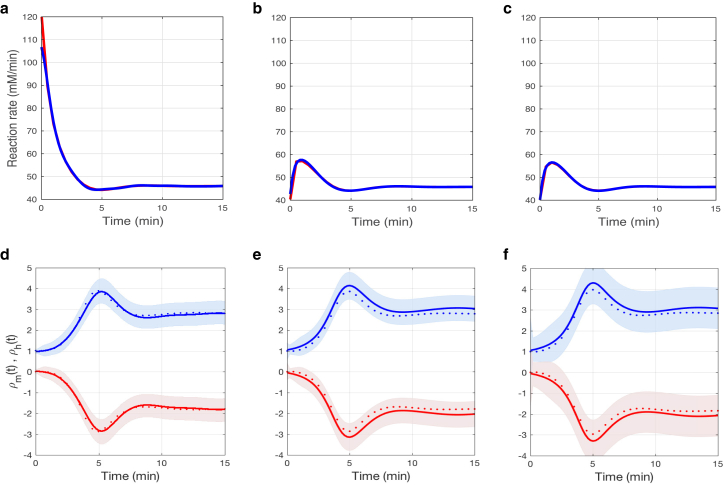
Figure 4.

Time-dependent reaction rates (a–c) and regulation coefficients (d–f) with respect to the three reactions in the metabolic pathway. In (a)–(c), the time-dependent reaction rates estimated from GP regression are shown in blue; for comparison, the results based on ODE model simulations are shown in red. In (d)–(f), metabolic regulation coefficients, ${\mathit{\rho }}_m^i\left(t\right)$, are shown in blue, and hierarchical regulation coefficients ${\mathit{\rho }}_h^i\left(t\right)$ are in red. Results based on ODE model simulations are shown as dotted lines; results based on nonparametric GP regression are shown as a solid line, with confidence intervals indicated by the bands. To see this figure in color, go online.

After perturbing external metabolite S, only the first reaction rate v₁ increases instantaneously (from 40 to 120 from time t = 0₋ to 0₊, not shown) because it is directly affected by the changes in S; all other metabolite concentrations and reaction rates have not yet had time to respond. At the new steady state, all metabolite concentrations are increased—i.e., x₁ from 4.8 to 52.2, x₂ from 1.9 to 3.8, and x₃ from 0.7 to 0.9—and all the reaction rates increase from 40 to 46, whereas enzyme concentrations decrease from 1.3 to 1. This explains the negative hierarchical regulation coefficients shown in Fig. 4, d–f. The estimated regulation coefficients in Fig. 4, d–f show that metabolic regulation is initially responsible for the decrease in the reaction rate v₁ and increase in the reaction rates v₂ and v₃ because the hierarchical regulation coefficient is close to zero. It takes some time for the negative hierarchical regulation to come into effect because gene expression is a relatively slow process. Although the first reaction is under a negative allosteric regulation, the overall metabolic regulation shows a positive effect because it also includes substrate and product effects. The regulation coefficients for all three reactions are very similar. This is because the relative changes in the enzyme concentration are very small in magnitude compared to the reaction rates, although the latter vary differently after perturbation.

Leucine biosynthetic pathway with positive feedforward transcriptional regulation

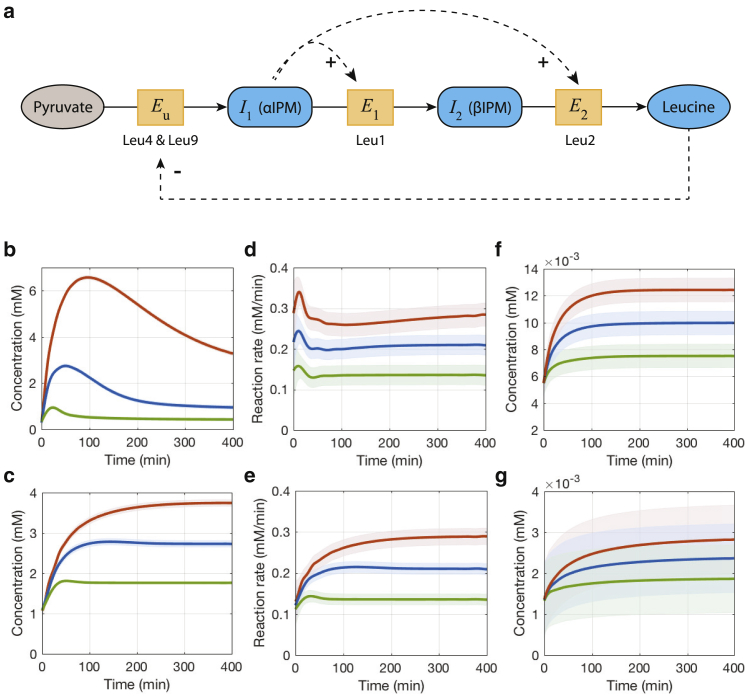
The previous example shows a metabolic intermediate inhibits upstream enzymes through transcriptional regulation. Here, we investigate a different regulatory structure: a metabolite activating downstream enzymes through transcriptional regulation. A simplified mathematical model describing the leucine biosynthetic pathway in Saccharomyces cerevisiae (22) is used to demonstrate such positive feedforward regulation (Fig. 5 a). This pathway converts pyruvate into leucine with two major regulatory mechanisms: metabolic/allosteric feedback inhibition of Leu4 and Leu9 (E_u) by leucine and transcriptional regulation of downstream enzymes Leu1 (E₁) and Leu2 (E₂) by αIPM (I₁). It has been demonstrated that positive feedforward regulation has similar effects in maintaining pathway flux as negative feedback regulation from a control engineering perspective (23). The kinetic model describing the dynamics of αIPM (I₁), βIPM (I₂), leucine (P), Leu1 (E₁), and Leu2 (E₂) together with parameters estimated from experimental data are provided in (22). The dynamics can be described as

$$\begin{array}{l}{\dot{I}}_1=v_1-v_2\\ \begin{array}{ccc}\begin{array}{l}{\dot{I}}_2=v_2-v_3\\ \dot{P}=v_3+F_{ext}-d_{5}P\end{array}& \Rightarrow & \begin{array}{l}{v}_2={\dot{I}}_2+v_3\\ v_3=\dot{P}-F_{ext}+d_{5}P\end{array}\end{array}.\end{array}$$ (26)

Figure 5.

A simplified leucine biosynthetic pathway and estimation results. (a) The pathway model diagram is given. Multi-output GPR estimates of (b) I₂ (βIPM) and (c) P (leucine) concentrations under different levels of perturbation (adding exogenous αIPM flux ϕ_ext = 0.1 mM/min as shown in green, ϕ_ext = 0.2 mM/min in blue, and ϕ_ext = 0.3 mM/min in red) are shown. The time-dependent reaction rates v₂ and v₃ can then be estimated as shown in (d) and (e). The GPR fits to the proteins E₁ (Leu1) and E₂ (Leu2) are given in (f) and (g). To see this figure in color, go online.

F_ext is the external leucine flux. Because the enzyme E_u is treated as a constant in the model, we will only investigate the hierarchical regulation with respect to the reactions catalyzed by E₁ and E₂. To investigate flux regulation, the pathway is perturbed by adding an external flux of αIPM after the system reaches a quasi-steady state. This is achieved by adding a constant external flux term ϕ_ext in the first equation of Eq. 26. To evaluate the system’s responses and regulation strength under different perturbations, three levels of perturbations are considered by adding ϕ_ext = 0.1, 0.2, and 0.3 mM/min at t = 0 min, respectively. The system is simulated for 400 min with a sampling time of 20 min. The multi-output GPR estimates of I₂ (βIPM) and P (leucine) are shown in Fig. 5, b and c, with reaction rate estimates given in Fig. 5, d and e. Before perturbation, the steady-state concentration of βIPM is 0.27 mM, leucine is 1.1 mM, enzymes Leu1 and Leu2 are 0.0055 and 0.0014 mM, and the quasi-steady-state flux is 0.08 mM/min. It is clear that after perturbation, βIPM, leucine, enzymes, and reaction rates all increase.

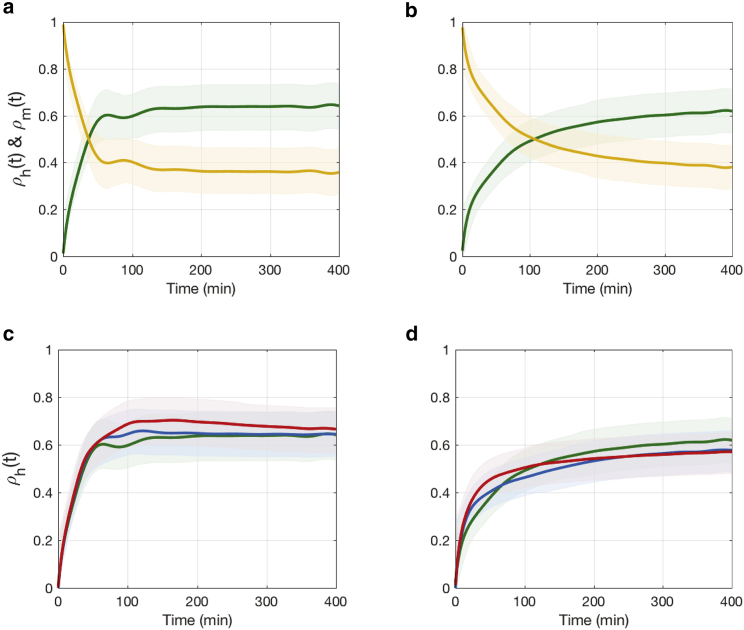
The time-dependent regulation coefficients for the last two reactions under relatively small perturbation (ϕ_ext = 0.1) are first calculated (Fig. 6, a and b). Because both enzymes are regulated by positive feedforward transcriptional regulation from αIPM, the hierarchical regulation coefficients of both steps are positive, in contrast to the previous example. Initially, the increases in the pathway’s reaction rates mainly stem from metabolic regulation because the metabolic regulation coefficient is close to 1; the hierarchical regulation gradually comes into effect and eventually becomes a more important contributor to the increase of reaction rates. Such a switch takes less than 40 min for the reaction catalyzed by Leu1 to happen, whereas it takes around 100 min for the reaction catalyzed by Leu2, indicating the transcriptional regulatory strength for the former reaction is stronger.

Figure 6.

Time-dependent hierarchical regulation coefficient ${\mathit{\rho }}_h^i\left(t\right)$ (in green) and metabolic regulation coefficient ${\mathit{\rho }}_m^i\left(t\right)$ (in yellow) for reactions catalyzed by (a) E₁ and (b) E₂ under a constant flux perturbation (ϕ_ext = 0.1 mM/min) to αIPM. Time-dependent hierarchical regulation coefficients for reactions catalyzed by (c) E₁ and (d) E₂ under different levels of flux perturbations to αIPM are shown (i.e., ϕ_ext = 0.1 mM/min in green, ϕ_ext = 0.2 mM/min in blue, and ϕ_ext = 0.3 mM/min in red). To see this figure in color, go online.

It is also interesting to investigate how regulation changes with the strength of the perturbation; see Fig. 6, c and d. For the reaction catalyzed by E₁, hierarchical regulation increases at the same rate despite changes in perturbation strength; the regulation will only last for longer periods if the perturbation increases. For the reaction catalyzed by E₂, hierarchical regulation increases more quickly as the perturbation increases, whereas it stops sooner by settling at a lower steady-state value. This is probably due to E₂ reaching its maximal catalytic capacity more quickly than E₁ (i.e., with a smaller Michaelis constant).

Nitrogen assimilation pathway in Escherichia coli

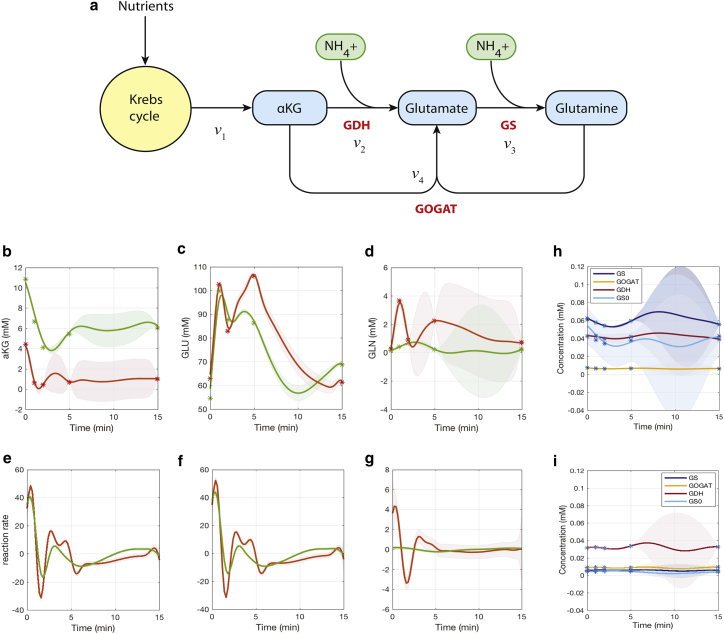
Finally, we apply our approach to experimental data from E. coli and study the regulation in the nitrogen assimilation. Ammonium is a preferred nitrogen source for E. coli growth, and there are two ammonium assimilation pathways (24): glutamate dehydrogenase (GDH) and glutamine synthetase (GS)-glutamate synthase (GOGAT) (Fig. 7 a). After a period of nitrogen starvation, the ammonium level in the bacterial cultures is instantaneously increased. Fig. 7, b–d present experimental measurements for α-ketoglutarade (αKG), glutamate (GLU), and glutamine (GLN) concentrations over time (i.e., at 0, 1, 2, 5, and 15 min) after an ammonium spike. Red stars are the wild-type metabolite measurements; green stars indicate the isogenic glnG deletion measurements. The relationships between pathway metabolites and reaction rates can be described as below.

$$\begin{array}{ccc}\dot{\alpha KG}=v_1-\left(v_2+v_{4.1}\right)=v_1-{\tilde{v}}_2& & v_1=\dot{\alpha KG}+\dot{GLU}+\dot{GLN}\\ \dot{GLU}=v_2+v_{4.1}-\left(v_3-v_{4.2}\right)={\tilde{v}}_2-{\tilde{v}}_3& \Rightarrow & {\tilde{v}}_2=\dot{GLU}+\dot{GLN}\\ \dot{GLN}=v_3-v_{4.2}={\tilde{v}}_3& & {\tilde{v}}_3=\dot{GLN}\end{array}$$ (27)

Figure 7.

The nitrogen assimilation pathway in E. coli and estimation of metabolite, protein concentrations, and reaction rates. (a) The pathway model diagram is given. (b–d) Multi-output GP predictions of metabolite αKG, GLU, and GLN concentrations under wild-type (red) and isogenic glnG deletion (green) conditions are shown. Experimental measurements are shown by star symbols. (e–g) Time-dependent reaction rate estimations of v₁, ${\tilde{v}}_2$, and ${\tilde{v}}_3$ from derivate GP processes are shown. Time-dependent estimates of enzymes GS (and its active form GS0), GOGAT, and GDH under (h) wild-type and (i) glnG deletion conditions are shown. To see this figure in color, go online.

Because we can only infer three reaction rates from three metabolites, reaction rate v₄ (as shown in Fig. 7 a) can be split into two parts, i.e., v_4.1 and v_4.2, which can be summarized with reaction rates v₂ and v₃ to form the “net” reaction rates ${\tilde{v}}_2$ and ${\tilde{v}}_3$. Multi-output GP models are first used to fit the metabolite measurements under both wild-type and glnG deletion conditions, as given in Fig. 7, b–d. Time-dependent reaction rates for all the three reactions (i.e., v₁, ${\tilde{v}}_2$, and ${\tilde{v}}_3$) can then be estimated according to Eq. 27 and are shown in Fig. 7, e–g. It can be clearly noted that most of the flux is through the GDH reaction in such an ammonium-rich condition, which confirms previous studies (24). When comparing the results of wild-type and glnG deletion conditions, the rate ${\tilde{v}}_3$ under glnG deletion is significantly reduced to a very low level (Fig. 7 g), whereas the glutamine decreases and αKG increases (Fig. 7, b and d). This can be explained by glnG encoding the transcription factor Ntrc that controls GS enzyme expression, which catalyzes GLN synthesis in its active form. The experimental measurements of protein concentrations (i.e., GS and its active form GS0, GOGAT, and GDH) and GP model predictions are provided in Fig. 7, h and i. Clearly, we can see that the GS protein (and its active form) concentrations under glnG deletion are significantly lower compared to the corresponding wild-type condition, whereas other proteins remain at similar levels in both conditions.

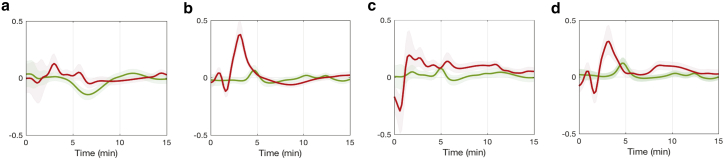
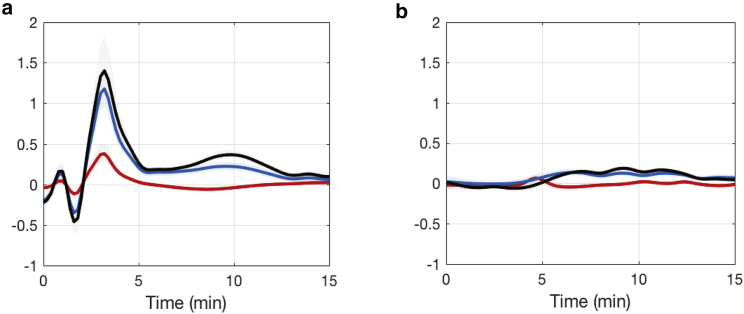
Next, we quantify the contributions from hierarchical regulation effects, i.e., those involving gene expression and post-translational modifications, to the regulation of reaction rates after ammonium spike. Because we have the time-dependent estimates of protein GS, GOGAT, and GDH profiles and the reaction rates, ${\tilde{v}}_2$ and ${\tilde{v}}_3$, we can compute the gene-expression regulation coefficients, i.e., $\mathit{\Delta }\ln \text{GDH}/\mathit{\Delta }\ln {\tilde{v}}_2$, $\mathit{\Delta }\ln \text{GS}/\mathit{\Delta }\ln {\tilde{v}}_3$, $\mathit{\Delta }\ln \text{GOGAT}/\mathit{\Delta }\ln {\tilde{v}}_2$, and $\mathit{\Delta }\ln \text{GOGAT}/\mathit{\Delta }\ln {\tilde{v}}_3$, with respect to both reactions as given in Fig. 8. The results indicate that gene-expression regulation has a relatively minor effect on modulating reaction rates ${\tilde{v}}_2$ after ammonium fluctuations under both conditions. This observation indicates metabolic regulation would play a major role in regulating ${\tilde{v}}_2$. For the reaction rate ${\tilde{v}}_3$, gene-expression regulation of GS and GOGAT increases after an ammonium spike under the wild-type condition, whereas it remains at low levels in the glnG deletion condition.

Figure 8.

Time-dependent gene-expression regulation coefficients (wild-type: red, glnG deletion: green). (a) $\mathit{\Delta }\ln \text{GDH}/\mathit{\Delta }\text{Δ}\ln {\tilde{v}}_2$, (b) $\mathit{\Delta }\ln \text{GS}/\mathit{\Delta }\ln {\tilde{v}}_3$, (c) $\mathit{\Delta }\ln \text{GOGAT}/\mathit{\Delta }\ln {\tilde{v}}_2$, and (d) $\mathit{\Delta }\ln \text{GOGAT}/\mathit{\Delta }\ln {\tilde{v}}_3$ are shown. To see this figure in color, go online.

It is well known that signal transduction and post-translational modification (here adenylyltransferase) play crucial roles in regulating GS activity. Because the time-dependent measurements (and GP estimates) of total GS protein and its active form GS0 are available (Fig. 7, h and i) and GS0 = GS × φ_a, with φ_a denoting the fraction of the enzyme that is in active form because of post-translational modification, we can further calculate the time-dependent signal-transduction regulation coefficient, ${\mathit{\rho }}_s=\mathit{\Delta }\ln {\mathit{\phi }}_a/\mathit{\Delta }\ln {\tilde{v}}_3$, and total hierarchical regulation coefficient, ${\mathit{\rho }}_h=\mathit{\Delta }\ln \text{GS}0/\mathit{\Delta }\ln {\tilde{v}}_3$, with respect to net-reaction rate, ${\tilde{v}}_3$. The results for both conditions are shown in Fig. 9. It is interesting to see that signal-transduction regulation is much higher after an ammonium spike compared to the gene-expression regulation and that the former contributes a major part to the overall hierarchical regulation under the wild-type condition, indicating the importance of post-translational modification in regulating pathway flux. Under the glnG deletion condition, all three regulation coefficients are small over time, whereas signal-transduction regulation still contributes more to the overall hierarchical regulation for the majority of the time.

Figure 9.

Time-dependent estimates of hierarchical, gene-expression, and signal-transduction regulation coefficients (i.e., ρ_h in black, ρ_g in red, and ρ_s in blue) of protein GS with respect to net rate ${\tilde{v}}_3$, under (a) wild-type and (b) glnG deletion conditions. To see this figure in color, go online.

Discussion

To conclude, we have developed a nonparametric method that uses Gaussian processes to accurately infer temporal profiles (and associated uncertainties) of reaction rates in metabolic pathways and to characterize the time-dependent hierarchical regulation in a metabolic pathway.

A key contribution of the proposed approach is to generalize the widely used steady-state regulation analysis to the dynamic scenario without the need for time-dependent flux measurements. Simulation studies demonstrate that the proposed approach can accurately capture the true regulation profile, even in the presence of experimental noise. It can therefore be used to quantify subtle changes in regulation even away from steady state. This can be particular useful for the analysis of real pathway perturbations or synthetic biosensor design. When both time-dependent measurements of enzyme concentration and the fraction that is in the active post-translational modification state are measurable, we can further quantify the time-dependent contributions from gene expression and signal transduction to the regulation of metabolic activity.

For a branched pathway or a pathway with feedback or feedforward structures, we can still evaluate the hierarchical regulation of an enzyme with respect to the “net” reaction rate, although the summation law between the hierarchical and metabolic regulation no longer holds. For a large-scale reaction network with complex structure, a practical strategy is to partition the large network into several smaller subnetworks because one can assume metabolites that are far away from each other would have weaker interactions (this may not always be true, e.g., long-range allosteric regulation, so one needs to carefully partition the network according to the specific pathway structure). In such a way, within each subnetwork with a relatively small number of metabolites, multi-output GPR and the proposed time-dependent regulation analysis can still be applied.

There are other parametric or nonparametric modeling methods that can be used to interpolate the data and then estimate time derivatives, such as local polynomial regression or smoothing splines. The advantage of using GP over these approaches are 1) GP can be easily used to fit a wide range of functions or data without assuming the data are characterized by a specific function; and 2) the estimation errors (for both time-course data and derivatives) can be automatically obtained from a GP posterior, whereas other interpolation methods (e.g., nonlinear regression or splines) often only provide a maximal a posteriori point estimate and can be very difficult for determining the estimation errors. This is important for this work because we are interested in knowing the estimation errors of the regulation coefficients.

The use of GPR in this work requires the additive Gaussian noise assumption, and the noise in a metabolic pathway can be introduced from intrinsic or extrinsic stochasticity of molecular interactions (e.g., enzyme gene expression) or from the measurement process. Simulation studies (25, 26) have demonstrated that linear noise approximation (with Gaussian stochastic distribution) would be a good approximation to the exact stochastic simulation in metabolic reactions if the enzyme kinetic parameters satisfy certain conditions. In a more general case, if we have to consider non-Gaussian stochasticity or noise effects in the data, using warped GP (27) would be a promising alternative to the standard GP; it would be relatively straightforward to compute the mean values, but it would be difficult to compute the confidence intervals or the distribution of the regulation coefficients because a ratio between non-Gaussian distributions will need to be evaluated at each sampling time point.

The computational or optimization cost is an important limitation of generalizing multi-output GPR to high-dimensional cases; apart from partitioning a large network into several smaller ones as discussed above, practically, one can possibly reduce the optimization cost by using one of the following tricks: 1) sometimes, we can assume some of the hyperparameters are the same across different variables (e.g., set the noise SDs of different outputs to be one parameter if we know the noise levels of different variables are similar) 2); constraining the hyperparameters into a reduced parameter space by setting appropriate lower and upper bounds, especially for the parameters that control the kernel length-scale and noise SD, which often leads to a more efficient optimization if we have some ideas of the smoothness of the time series data and the noise levels; 3) replacing the multi-output GP with a number of single-output GPs if we have a sufficient number of samples.

For cases in which discrete flux measurements are available at limited time points (e.g., as in the study by (9)), the proposed method can be easily adapted to estimate time-dependent reaction rate profiles directly by applying multi-output GPR to the discrete flux data (rather than indirectly inferring these from the derivative processes using metabolite measurements).

Author Contributions

F.H. and M.P.H.S. designed the research. F.H. carried out all simulations and analyzed the data. F.H. and M.P.H.S. wrote the article.

Editor: Kevin Janes.