Machine Learning of Coarse-Grained Molecular Dynamics Force Fields

Abstract

Atomistic or ab initio molecular dynamics simulations are widely used to predict thermodynamics and kinetics and relate them to molecular structure. A common approach to go beyond the time- and length-scales accessible with such computationally expensive simulations is the definition of coarse-grained molecular models. Existing coarse-graining approaches define an effective interaction potential to match defined properties of high-resolution models or experimental data. In this paper, we reformulate coarse-graining as a supervised machine learning problem. We use statistical learning theory to decompose the coarse-graining error and cross-validation to select and compare the performance of different models. We introduce CGnets, a deep learning approach, that learns coarse-grained free energy functions and can be trained by a force-matching scheme. CGnets maintain all physically relevant invariances and allow one to incorporate prior physics knowledge to avoid sampling of unphysical structures. We show that CGnets can capture all-atom explicit-solvent free energy surfaces with models using only a few coarse-grained beads and no solvent, while classical coarse-graining methods fail to capture crucial features of the free energy surface. Thus, CGnets are able to capture multibody terms that emerge from the dimensionality reduction.

Short abstract

We develop CGnets, a deep learning framework for coarse-grained molecular dynamics. CGnets automatically learn the multibody terms required for accurate coarse-grained force fields.

Introduction

Recent technological and methodological advances have made possible to simulate macromolecular systems on biologically relevant time-scales.¹⁻³ For instance, one can simulate binding, folding, and conformation changes of small to intermediate proteins on time-scales of milliseconds, seconds, or beyond.⁴⁻⁸ However, the extensive sampling of large macromolecular complexes on biological time-scales at atomistic resolution is still out of reach. For this reason, the design of simplified, yet predictive, models is of great interest,⁹⁻¹¹ in particular, to interpret the experimental data that are becoming increasingly accessible in high throughput and resolution. Experimental data provide a partial view of certain aspects of a macromolecular system but do not directly give a full dynamical representation, and simulation can help obtain a more comprehensive understanding.¹²⁻¹⁴ As it is clear that not every single atom is important in determining the relevant collective features of biomolecular dynamics and function, simplified models could provide more insights into the general physicochemical principles regulating biophysical systems at the molecular level. Here we use recent advances in machine learning to design optimal reduced models to reproduce the equilibrium thermodynamics of a macromolecule.

Significant effort has been devoted in the past few years to apply machine learning (e.g., deep neural network or kernel methods) to learn effective models from detailed simulations¹⁵⁻¹⁹ and specifically to learn potential energy surfaces from quantum-mechanical calculations on small molecules.²⁰⁻³⁶ In principle a similar philosophy could be used to define models at lower resolutions, that is, to learn the effective potential energy of coarse-grained (CG) models from fine-grained (e.g., atomistic) molecular dynamics (MD) simulation data.³⁷⁻⁴¹

There are however important differences. In the definition of potential energy surfaces from quantum calculations, the relevant quantity to reproduce is the energy, and it is relatively straightforward to design a loss function for a neural network to minimize the difference between the quantum-mechanical and classical energy (and forces^25,33) over a sample of configurations. In contrast, in the definition of a CG model, the potential energy can not be matched because of the reduction in dimension, and it is important to define what are the properties of the system that need to be preserved by the coarse-graining. The approximation of free energy surfaces, e.g., from enhanced sampling simulations, is therefore a related problem.⁴²⁻⁴⁴

Several approaches have been proposed to design effective CG energy functions for large molecular systems that either reproduce structural features of atomistic models (bottom-up)⁴⁵⁻⁵⁰ or reproduce macroscopic properties for one or a range of systems.^{12−14,51−54} Popular bottom-up approaches choose that the CG model reproduce the canonical configuration distribution determined by the atomistic model. For instance, one may want to be able to represent the different metastable states populated by a protein undergoing large conformational changes. One of the difficulties in the practical application of these methods has been that, in general, a CG potential optimally reproducing selected properties of a macromolecular system includes many-body terms that are not easily modeled in the energy functions.

Here, we formulate the well-known force-matching procedure for coarse-graining as a supervised machine learning problem. Previously, coarse-graining has been mostly discussed as a fitting procedure, but the aim of machine learning is to find a model that has minimal prediction error on data not used for the training. We use classical statistical learning theory to show that the force-matching error can be decomposed into Bias, Variance, and Noise terms and explain their physical meaning. We also show that the different CG models can be ranked using their cross-validation score.

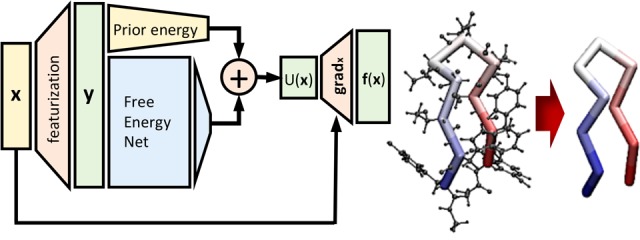
Second, we discuss a class of neural networks, which we refer to as CGnets, for coarse-graining molecular force systems. CGnets have a lot of similarities with neural networks used to learn potential energy surfaces from quantum data, such as enforcing the relevant invariances (e.g., rotational and translational invariance of the predicted energy, equivariance of the predicted force). In contrast to potential energy networks, CGnets predict a free energy (potential of mean force) and then use the gradient of this free energy with respect to the input coordinates to compute a mean force on the CG coordinates. As the CG free energy is not known initially, only the force information can be used to train the network.

Third, CGnets are extended to regularized CGnets. Using a generic function approximator such as a neural network to fit the CG force field from training data only may lead to force predictions that are “catastrophically wrong” for configurations not captured by the training data, i.e., predictions of forces in the direction of increasingly unphysical states that lead to diverging and unrealistic simulation results. We address this problem by adding a prior energy to the free energy network that does not compromise the model accuracy within the training data region, but ensures that the free energy approaches infinity for unphysical states, resulting in a restoring force toward physically meaningful states.

Finally, we demonstrate that CGnets succeed in learning the CG mean force and the CG free energy for a 2D toy model, as well as for the coarse-graining of all-atom explicit-solvent simulations of (i) alanine dipeptide to a CG model with 5 particles and no solvent and (ii) the folding/unfolding of the polypeptide Chignolin to a CG model consisting only of the protein C_α atoms and no solvent. We show explicitly that CGnets achieve a systematically better performance than classical CG approaches which construct the CG free energy as a sum of few-body terms. In the case of the Chignolin protein, the classical few-body model can not reproduce the folding/unfolding dynamics. On the contrary, the inherently multibody CGnet energy function approximates the all-atom folding/unfolding landscape well and captures all free energy minima. This study highlights the importance of machine learning and generic function approximators in the CG problem.

Theory and Methods

Here we introduce the main theoretical concepts and define the machine learning problems involved in coarse-graining using the force-matching principle and introduce CGnets and regularized CGnets. The more practically inclined reader may skip to the CGnets: Learning CG Force Fields with Neural Networks section.

Coarse-Graining with Thermodynamic Consistency

We first define what we mean by coarse-graining and which physical properties shall be preserved in the coarse-grained model.

The starting point in the design of a molecular model with resolution coarser than atomistic is the definition of the variables. The choice of the coarse coordinates is usually made by replacing a group of atoms by one effective particle. Because of the modularity of a protein backbone or a DNA molecule, popular models coarse-grain a macromolecule to a few interaction sites per residue or nucleotide, e.g., the C_α and C_β atoms for a protein.^51,54−56 Alternative schemes have also been proposed for the partitioning of the atoms into coarse-grained coordinates.^57,58 In general, given a high-dimensional atomistic representation of the system r ∈ 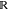^3N, a CG representation is given by a coordinate transformation to a lower-dimensional space:

1

with n < N. Here we assume that ξ is linear; i.e., there is some coarse-graining matrix Ξ ∈ 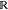^3n×3N that clusters atoms to coarse-grained beads: x = Ξr.

The aim is to learn a coarse-grained energy function U(x; θ) that will be used in conjunction with a dynamical model, e.g., Langevin dynamics, to simulate the CG molecule. θ is the parameters of the coarse-grained model—in classical CG approaches these are parameters of the potential energy function, such as force constants and partial charges, while here they denote the weights of the neural network.

A common objective in coarse-graining methods is to preserve the equilibrium distribution; i.e., the equilibrium distribution of the coarse-grained model shall be as close as possible to the equilibrium distribution of the atomistic model when mapped to the CG coordinates. We will be using a simulation algorithm for the dynamics such that the system’s equilibrium distribution is identical to the Boltzmann distribution of the employed potential U; therefore this objective can be achieved by enforcing the thermodynamic consistency:

2

where k_BT is the thermal energy with Boltzmann constant k_B and temperature T, the probability distribution p^CG(x) is the equilibrium distribution of the atomistic model, mapped to the CG coordinates

3

and μ(r) = exp(−V(r)/k_BT) is the Boltzmann weight associated with the atomistic energy model V(r). Note that the additive constant in eq 2 can be chosen arbitrarily. Therefore, this constant will be omitted in the expressions below, which means that it will absorb normalization constants that are not affecting the CG procedure, such as the logarithm of the partition function.

Several methods have been proposed for defining a coarse-grained potential U(x) that variationally approximates the consistency relation 3 at a particular thermodynamic state (temperature, pressure etc.) Two popular approaches are the multiscale coarse-graining (force-matching)^48,59 and the relative entropy method⁵⁰ (the two approaches are connected⁶⁰).

CG Parameter Estimation as a Machine Learning Problem

Here, we follow the force-matching scheme. It has been shown that thermodynamic consistency (eq 2) is achieved when the CG model predicts the instantaneous CG forces with minimal mean square error.^48,59 We call the instantaneous atomistic forces F(r) and the instantaneous force projected on the CG coordinates ξ(F(r)). At the same time, the CG model predicts a force −∇U(x; θ) for a CG configuration x. The force-matching error is defined as

4

The average ⟨·⟩_r is over the equilibrium distribution of the atomistic model, i.e., r ∼ μ(r).

We reiterate a result shown in ref (59) that has important consequences for using eq 4 in machine learning. For this, we introduce the mean force:

5

where r|x indicates the equilibrium distribution of r constrained to the CG coordinates x, i.e., the ensemble of all atomistic configurations that map to the same CG configuration. Then we can decompose expression 4 as follows (see the SI for derivation):

6

with the terms

7

This loss function differs from the force-matching loss function used in the learning of force fields from quantum data by the Noise term. The Noise term is purely a function of the CG map ξ (and when training with finite simulation data also of the data set), and it cannot be changed by varying the parameters θ. As a result, the total force-matching error cannot be made zero, but it is bounded from below by χ²(θ) ≥ Noise.⁵⁹ On the contrary, when matching force fields from quantum data, the error χ² approaches zero for a sufficiently powerful model. Physically, the Noise term arises from the fact that instantaneous forces on the CG coordinates vary in the different atomistic configurations associated with the same CG configuration. Here, we call this term Noise as it corresponds to the noise term known in statistical estimator theory for regression problems.⁶¹

The learning problem is now to find a CG model and its parameters θ that minimizes the potential of mean force (PMF) error term. To obtain a physical interpretation, we apply eq 1 and write the average purely in CG coordinates:

This error term is the matching error between the mean force at the CG coordinates, f(x), and the CG forces predicted by the CG potential

8

Hence, the machine learning task is to find the free energy U whose negative derivatives best approximate the mean forces in eq 5, and U is thus called a potential of mean force (PMF). Equation 8 implies that the mean force field f̂ is conservative, as it is generated by the free energy U(x).

Machine learning the CG model is complicated by two aspects: (i) As the PMF error cannot be computed directly, its minimization in practice is accomplished by minimizing the variational bound eq 6. Thus, to learn f(x) accurately, we need to collect enough data “close” to every CG configuration x such that the learning problem is dominated by the variations in the PMF error term and not by the variations in the Noise term. As a result, machine learning CG models typically require more data points than force-matching for potential energy surfaces. (ii) The free energy U(x) is not known a priori but must be learned. In contrast to fitting potential energy surfaces we can therefore not directly use energies as inputs.

For a finite data set R = (r₁, ..., r_M) with M samples, we define the force-matching loss function by the direct estimator:

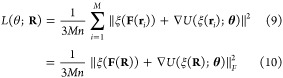where ξ(R) = [ξ(r₁), ..., ξ(r_M)]^Τ ∈ ^M×3n and ξ(F(R)) = [ξ(F(r₁)), ..., ξ(F(r_M))]^Τ ∈ 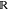^M×3n are data matrices of coarse-grained coordinates and coarse-grained instantaneous forces that serve as an input to the learning method, and F denotes the Frobenius norm.

CG Hyperparameter Estimation as a Machine Learning Problem

While eq 9 defines the training method, machine learning is not simply about fitting parameters for a given data set but rather about minimizing the expected prediction error (also called “risk”) for data not used for training. This concept is important to be able to select an optimal model, i.e., to choose the hyperparameters of the model, such as the type and number of neurons and layers in a neural network, or even to distinguish between different learning models such as a neural network and a spline model.

Statistical estimator theory is the field that studies optimal prediction errors.⁶¹ To compute the prediction error, we perform the following thought experiment: We consider a fixed set of CG configurations X = [x₁, ..., x_M]^Τ at which we want to fit the mean forces. We assume that these configurations have been generated by MD or MCMC such that the full atomistic configurations, R = (r₁, ..., r_M), are Boltzmann distributions conditioned on the CG configurations, i.e., r_i ∼ r|x_i. Now we ask if we repeat this experiment, i.e., in every iteration we produce a new set of all-atom configurations r_i ∼ r|x_i, and thereby a new set of instantaneous forces on the CG configurations, what is the expected prediction error, or risk of the force-matching error, 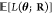? More formally, the following is performed:

• 1.given CG coordinates X, generate training set R^train ∼ R|X and find θ̂ = arg min_θL(θ; R^train);
• 2.generate test set R^test ∼ R|X and compute L(θ̂; R^test)

where R^train and R^test are two independent realizations. Although we cannot execute this thought experiment in practice, we can approximate it by cross-validation, and we can obtain insightful expressions for the form of the expected prediction error. As the loss function in force-matching is a least-squares regression problem, the form of the expected prediction error is well-known (see the SI for a short derivation) and can be written as

11

with the Noise term as given in eq 7 and the bias and variance terms given by

12

13

where

is the mean estimator, i.e., the average force field learnt when the training is repeated many times for different data realizations. The terms in eqs 12 and 13 have the following meaning: Equation 12 is the expected error between the mean forces and the average predicted force field. It is therefore the systematic bias of the machine learning model. The variance (eq 13) is the fluctuation of the individual estimates from single training procedures around the mean estimator and thus represents the estimator’s fluctuation due to finite-sample effects.

As the optimal model minimizes the PMF error, it must balance bias and variance. These contributions are typically counteracting: A too simple model (e.g., too small neural network) typically leads to low variance but high bias, and it corresponds to “underfitting” the data. A too complex model (e.g., too large neural network) leads to low bias but large variance, and it corresponds to “overfitting” the data. The behavior of bias, variance, and estimator error for a fixed data set size is illustrated in Figure 1.

Figure 1.

Typical bias–variance trade-off for fixed data set size, indicating the balance between underfitting and overfitting. The noise level is defined by the CG scheme (i.e., which particles are kept and which are discarded) and is the lower bound for the mean prediction error.

The optimum at which bias and variance balance depends on the amount of data used, and in the limit of an infinitely large data set, the variance is zero, and the optimal model can be made very complex to also make the bias zero. For small data sets, it is often favorable to reduce the model complexity and accept significant bias, to avoid large variance.

To implement model selection, we approximate the “ideal” iteration above by the commonly used cross-validation method^62,63 and then choose the model or hyperparameter set that has the minimal cross-validation score. In cross-validation, the estimator error (eq 11) is estimated as the validation error, averaged over different segmentations of all available data into training and validation data.

CGnets: Learning CG Force Fields with Neural Networks

It is well-known that the CG potential U(x; θ) defined by thermodynamic consistency may be a complex multibody potential even if the underlying atomistic potential has only few-body interactions.⁵⁹ To address this problem, we use artificial neural networks (ANNs) to represent U(x; θ) as ANNs can approximate any smooth function on a bounded set of inputs, including multibody functions.⁶⁴

Therefore, we use ANNs to model U(x), train them by minimizing the loss (eq 9), and select optimal models by minimizing the cross-validation error. For the purpose of training CG molecular models, we would like to have the following physical constraints and invariances, which determine parts of the architecture of the neural network.

• Differentiable free energy function: To train U(x; θ) and simulate the associated dynamics by means of Langevin simulations, it must be continuously differentiable. As the present networks do not need to be very deep, vanishing gradients are not an issue, and we select tanh activation functions here. After D nonlinear layers we always add one linear layer to map to one output neuron representing the free energy.

• Invariances of the free energy: The energy of molecules that are not subject to an external field only depends on internal interactions and is invariant with respect to translation or rotation of the entire molecule. The CG free energy may also be invariant with respect to permutation of certain groups of CG particles, e.g., exchange of identical molecules, or certain symmetric groups within molecules. Compared to quantum-mechanical potential energies, permutation invariance is less abundant in CG. For example, permutation invariance does not apply to the α-carbons in a protein backbone (not even for identical amino acids), as they are ordered by the MD bonding topology. CGnets include a transformation

  

  from CG Cartesian coordinates x to a set of features that contain all desired invariances, and use the features y as an input to the network that computes the free energy, U(g(x); θ). This transformation can be chosen in many different ways, e.g., by using local coordinate systems,³⁴ two- or three-body correlation functions,²⁰ permutation-invariant distance metrics,⁶⁵⁻⁶⁷ or by a learned representation.²⁹ In this work, only translation and rotation invariances are needed, and we hence choose the following features: distances between all pairs of CG atoms, the angles between three consecutive CG atoms, and the cos and sin of torsion angles defined by the CG atoms.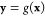

• Conservative PMF: The PMF is a conservative force field generated by the free energy (eq 8). As in quantum potential energy learning,^25,29 we enforce this requirement by computing the free energy U with a neural network and then adding a gradient layer to compute the derivatives with respect to the input coordinates:

Figure 2a shows the neural network architecture resulting from these choices. The free energy network is D layers deep, and each layer is W neurons wide. Additionally, we use L2 Lipschitz regularization⁶⁸ in the network, with a tunable parameter λ that regulates the strength of the regularization. Thus, (D, W, λ) are the remaining hyperparameters to be selected (as discussed in the Results section).

Figure 2.

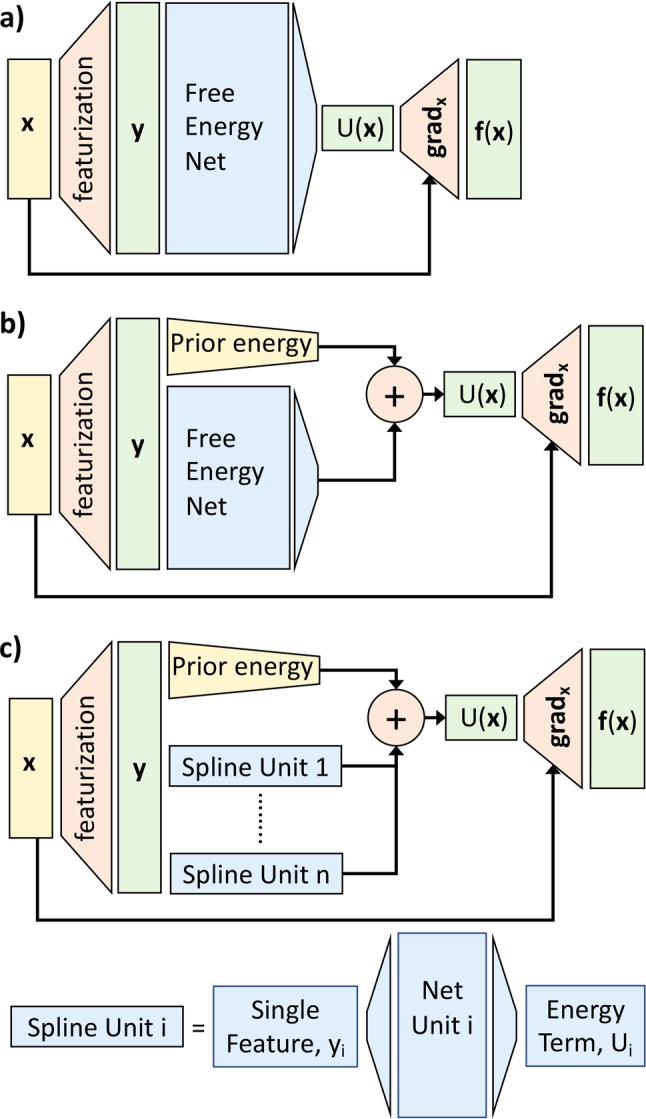
Neural network schemes. (a) CGnet. (b) Regularized CGnet with prior energy. (c) Spline model representing a standard CG approach, for comparison. Each energy term is a function of only one feature, and the features are defined as all the bonds, angles, dihedrals, and nonbonded pairs of atoms.

Simulating the CGnet Model

Once the neural network has been trained to produce a free energy U(x), it can be used to simulate dynamical trajectories of the CG model. Here we use overdamped Langevin dynamics to advance the coordinates of the CG model from x_t at time t to x_t+τ after a time-step τ:

14

where x_t is the CG configuration at time t (e.g., the x coordinate in the toy model, a 15-dimensional vector in the alanine dipeptide, and a 30-dimensional vector in the Chignolin applications presented below), ξ is Gaussian random noise with zero mean and identity as covariance matrix, τ is the integration time-step, and D is the diffusion constant of the system. In the following, we use reduced energy units; i.e., all energies are in multiples of k_BT.

Since the implementation of CGnet is vectorized, it is more efficient to compute free energies and mean forces for an entire batch of configurations rather than a single configuration at a time. Therefore, we run simulations in parallel for the examples shown below. This is done by sampling 100 starting points randomly from atomistic simulations, coarse-graining them, and then integrating eq 14 stepwise.

Regularizing the Free Energy with a Baseline Energy Model

Training the free energy with a network as shown in Figure 2a and subsequently using it to simulate the dynamics with eq 14 produces trajectories of new CG coordinates x_t. When parts of the coordinate space are reached that are very different from any point in the training set, it is possible that the network makes unphysical predictions.

In particular, the atomistic force field used to produce the training data has terms that ensure the energy will go toward infinity when departing from physical states, e.g., when stretching bonds or when moving atoms too close to each other. These regions will not be sampled in the underlying MD simulations, and therefore result in “empty” parts of configuration space that contain no training data. Simulating a network trained only on physically valid training data via eq 14 may still produce points x_t that enter this “forbidden regime” where bonds are overstretched or atoms start to overlap. At this point the simulation can become unstable if there is no regularizing effect ensuring that the predicted free energy U(x; θ) will increase toward infinity when going deeper into the forbidden regime.

Methods to modify a learning problem to reduce prediction errors are collectively known as “regularization” methods.⁶⁹ To avoid the catastrophically wrong prediction problem described above, we introduce regularized CGnets (Figure 2b). In a regularized CGnet, we define the energy function as

15

where U_net(x; θ) is a neural network free energy as before, and U₀(x) is a baseline energy that contains constraint terms that ensure basic physical behavior. Such baseline energies to regularize a more complex multibody energy function have also been used in the machine learning of QM potential energy functions.⁷⁰⁻⁷² Note that eq 15 can still be used to represent any smooth free energy because U_net(x; θ) is a universal approximator. The role of U₀(x) is to enforce U → ∞ for unphysical states x that are outside the training data.

As for many other regularizers, the baseline energy U₀(x) in eq 15 takes the role of a prior distribution in a probabilistic interpretation: The equilibrium distribution generated by eq 15 becomes

Here, U₀(x) is simply a sum of harmonic and excluded volume terms. For the 2D toy model, a harmonic term in the form 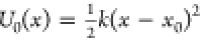is used, and the parameters k and x₀ are determined by the force-matching scheme restricted to the scarcely populated regions defined by the 100 sampled points with highest and the 100 with lowest x-value (see Figure 3).

Figure 3.

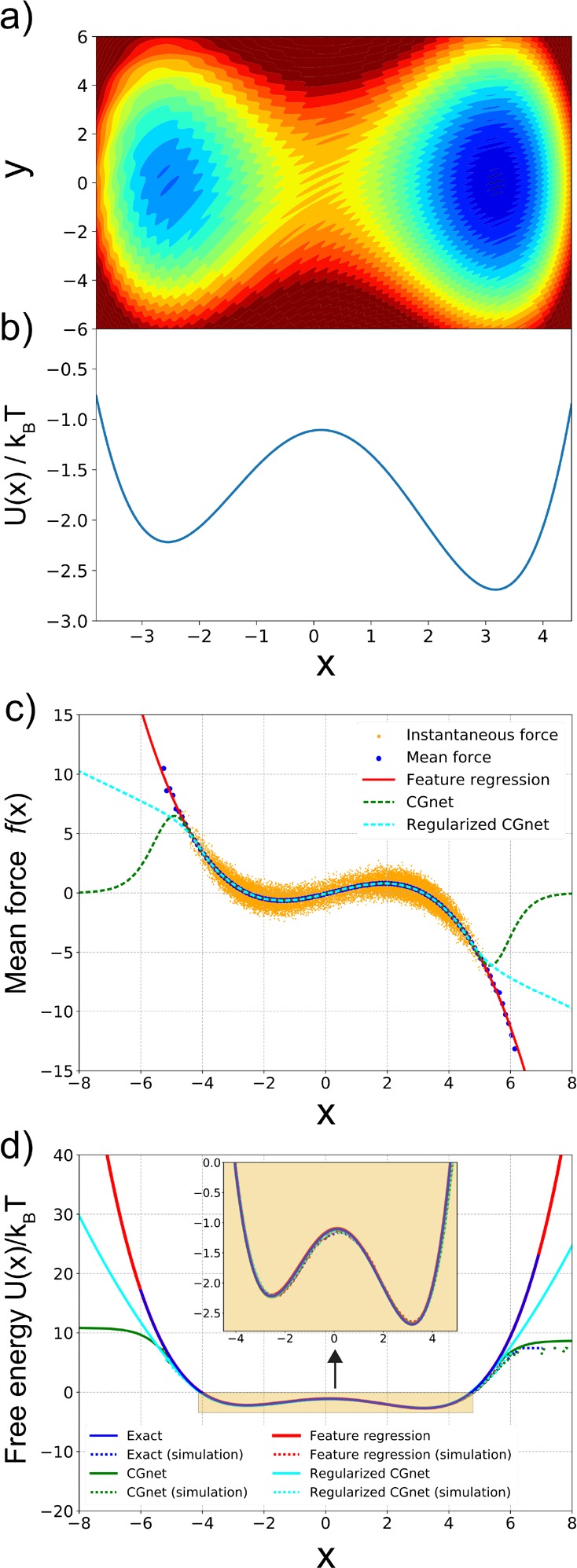
Machine-learned coarse-graining of dynamics in a rugged 2D potential. (a) Two-dimensional potential used as a toy system. (b) Exact free energy along x. (c) Instantaneous forces and the learned mean forces using feature regression and CGnet models (regularized and unregularized) compared to the exact forces. The unit of the force is k_BT, with the unit of length equal to 1. (d) Free energy (PMF) along x predicted using feature regression, and CGnet models compared to the exact free energy. Free energies are also computed from histogramming simulation data directly, using the underlying 2D trajectory, or simulations run with the feature regression and CGnet models (dashed lines).

For alanine dipeptide, we use harmonic terms for the distance between atoms that are adjacent (connected by covalent bonds) and for angles between three consecutive atoms. For each bond i, we use 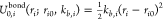, where r_i is the instantaneous distance between the two consecutive atoms defining the bond, r_i0 is the equilibrium bond length, and k_b,i is a constant. Analogously, for each angle j, we use 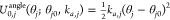, where θ_j is the instantaneous value of the angle, θ_j0 is the equilibrium value for the angle, and k_a,j is a constant. When statistically independent, each such term would give rise to a Gaussian equilibrium distribution:

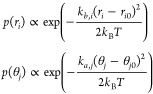with mean μ = r_i0 (or μ = θ_j0), and variance σ² = k_BT/k_b,i (or σ² = k_BT/k_a,j). The prior energy is obtained by assuming independence between these energy terms and estimating these means and variances from the atomistic simulations.

For the application of CGnet to the protein Chignolin, an additional term is added to the baseline energy to enforce excluded volume and penalize clashes between nonbonded CG particles. In particular, we add a term U_rep(r) for each pairwise distances between CG particles that are more distant than two covalent bonds, in the form

16

where the exponent c and effective excluded volume radius σ are two additional hyperparameters that are optimized by cross-validation.

We note that in general one could use classical CG approaches with predefined energy functions to first define the prior CG energy U₀ and then use an ANN to correct it with multibody terms.

Results

Two-Dimensional Toy Model

As a simple illustration, we first present the results on the coarse-graining of a two-dimensional toy model. The potential energy is shown in Figure 3 and given by the expression

17

The potential corresponds to a double well along the x-axis and a harmonic confinement along the y-axis. The last term in eq 17 adds small-scale fluctuations, appearing as small ripples in Figure 3a.

The coarse-graining mapping is given by the projection of the 2-dimensional model onto the x-axis. In this simple toy model, the coarse-grained free energy (potential of mean force) can be computed exactly (Figure 3b):

We generate a long (one million time-steps) simulation trajectory of the 2-dimensional model and use the x component of the forces computed along the trajectories in the loss function (eq 9). We report below the resulting CG potential obtained by (1) using a feature regression, i.e., least-squares regression with a set of feature functions defined in the SI, Section B, and (2) a CGnet (regularized and unregularized).

Cross-validation is used to select the best hyperparameters for the least-squares regression and the CGnet architectures. For the feature regression, the same cross-validation procedure as introduced in ref (73) was used and returned a linear combination of four basis functions among the selected set (see Figure S1a and the Supporting Information for details). For the regularized CGnet, a two-stage cross-validation is conducted, first choosing the depth D with a fixed width of W = 50, and then choosing the width W (Figure S1b,c). The minimal prediction error is obtained with D = 1 (one hidden layer) and W = 50. For the unregularized CGnet, a similar procedure is performed, and the best hyperparameters are selected as D = 1, W = 120. Note that the prediction error cannot become zero, but is bounded from below by the chosen CG scheme (Figure 1, eq 11)—in this case by neglecting the y variable.

Figure 3c,d shows the results of the predicted mean forces and free energies (potentials of mean force) in the x-direction. The instantaneous force fluctuates around the mean but serves to accurately fit the exact mean force in the x range where sampling is abundant using both feature regression and CGnet (Figure 3c). At the boundary where few samples are in the training data, the predictors start to diverge from the exact mean force and free energy (Figure 3c,d). This effect is more dramatic for the unregularized CGnet; in particular, at large x values, the CGnet makes an arbitrary prediction: here the force tends to zero. In the present example, reaching these states is highly improbable. However, a CGnet simulation reaching this region can fail dramatically, as the simulation may continue to diffuse away from the low energy regime. As discussed above, this behavior can be avoided by adding a suitable prior energy that ensures that the free energy keeps increasing outside the training data, while not affecting the accuracy of the learned free energy within the training data (Figure 3c,d). Note that the quantitative mismatch in the low-probability regimes is not important for equilibrium simulations.

The matching mean forces translate into matching free energies (potentials of mean force, Figure 3d). Finally, we conduct simulations with the learned models and generate trajectories {x_t} using eq 14. From these trajectories, free energies can be computed by

18

where p̃_X(x) is a histogram estimate of the probability density of x in the simulation trajectories. As shown in Figure 3d, free energies agree well in the x range that has significant equilibrium probability.

Coarse-Graining of Alanine Dipeptide in Water

We now demonstrate CGnets on the coarse-graining of an all-atom MD simulation of alanine dipeptide in explicit solvent at T = 300 K to a simple model with 5 CG particles located at the five central backbone atoms of the molecule (Figure 4). One trajectory of length 1 μs was generated using the simulation setup described in ref (74); coordinates and forces were saved every picosecond, giving rise to one million data points. The CG model has no solvent; therefore, the CG procedure must learn the solvation free energy for all CG configurations.

Figure 4.

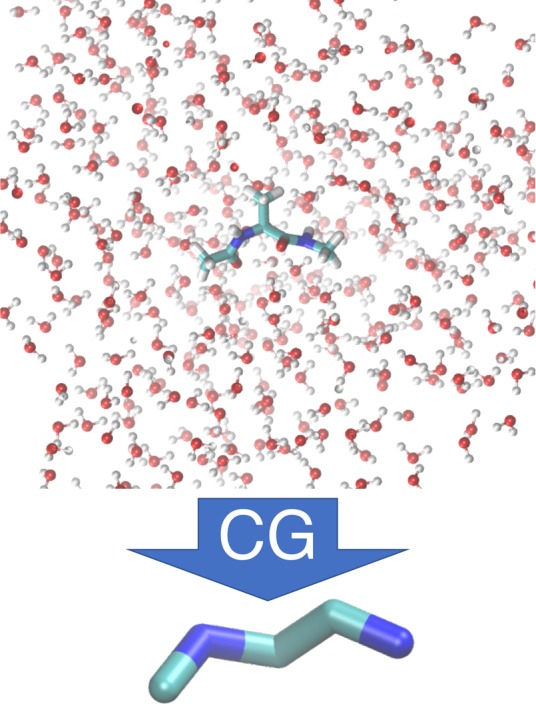
Mapping of alanine dipeptide from an all-atom solvated model (top) to a CG model consisting of the five central backbone atoms (bottom).

We compare two different CG models. The first model, called “spline model”, uses the state-of the art approach established in MD coarse-graining:^11,49,59 to express the CG potential as a sum of few-body interaction terms, similar as in classical MD force fields. The most flexible among these approaches is to fit one-dimensional splines for each of the pairwise distance, angle, and dihedral terms to parametrize two-, three-, and four-body interactions.⁷⁵ To ensure a consistent comparison, we represent 1D splines with neural networks that map from a single input feature (pairwise distance, angle, or dihedral) to a single free energy term, resulting in the spline model network shown in Figure 2c. We use the same regularization and baseline energy for spline model networks and CGnets.

The second model uses a regularized multibody CGnet, i.e., a fully connected neural network shown in Figure 2b, to approximate the CG free energy. The comparison of the results from the two models allows us to evaluate the importance of multibody interactions that are captured by the CGnet but are generally absent in CG models that use interaction terms involving a few atoms only.

The hyperparameters for both models consist of the number of layers (depth, D), the number of neurons per layer (width, W) of the network, and the Lipschitz regularization strength (λ)⁶⁸ and are optimized by a three-stage cross-validation. In the first stage, we find the optimal D at fixed W = 30 and λ = ∞ (no Lipschitz regularization); subsequently, we choose W at the optimal D, and λ at the optimal W, D. This results in D = 5, W = 160, and λ = 4.0 for CGnet and D = 4, W = 30 (for each feature), and λ = 10.0 for the spline model (Figure 5). The cross-validation error of CGnet is significantly lower than the cross-validation error of the spline model (Figure 5a–c). We point out that the cross-validation error cannot become zero but is bounded from below by the chosen CG scheme (Figure 1, eq 11)—in this case by coarse-graining all solvent molecules and all solute atoms except the five central backbone atoms away. Hence, the absolute values of the cross-validation error in Figure 5a–c are not meaningful and only differences matter.

Figure 5.

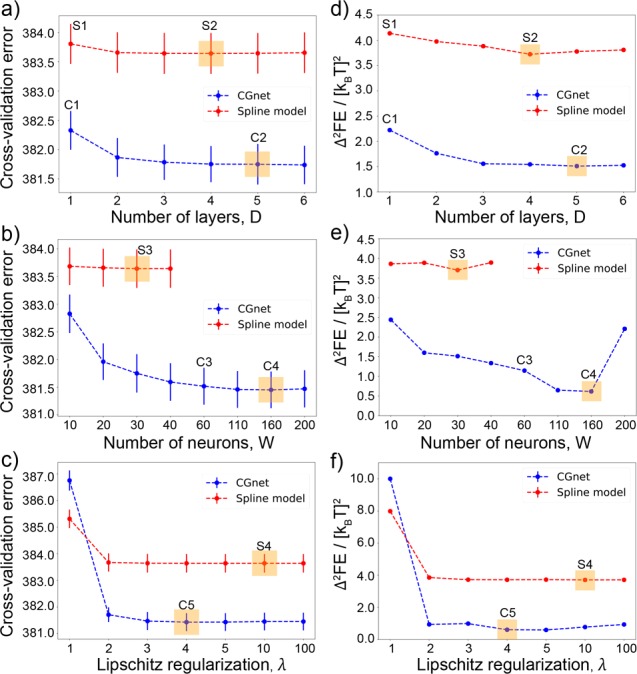
(a–c) Cross-validated force-matching error in [kcal/(mol A)]² for the selection of the optimum structure of the network. (d–f) Difference between the two-dimensional free energy surfaces obtained from the CG models and from the reference all-atom simulations (see Figure 6) for the regularized CGnet and the spline model of alanine dipeptide. (a) Selection of the number of layers, D. (b) Selection of the number of neurons per layer, W. (c) Selection of the Lipschitz regularization strength, λ. The selected hyperparameters, corresponding to the smallest cross-validation error, are highlighted by orange boxes. Blue dashed lines represent the regularized CGnet, red dashed lines the spline model, and vertical bars the standard error of the mean. (d–f) Difference between the reference all-atom free energy surface and the free energy surfaces corresponding to the choices of hyperparameters indicated in panels a–c as (C1, C2, C3, C4, C5) for CGnet and as (S1, S2, S3, S4) for the spline model.

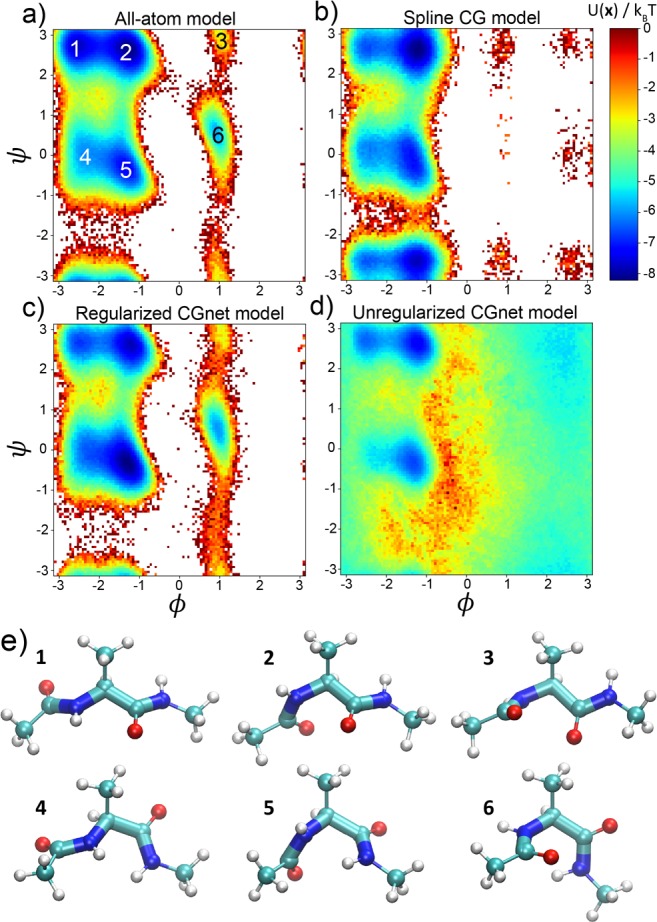
CG MD simulations are generated for the selected models by iterating eq 14. For each model, one hundred independent simulations starting from structures sampled randomly from the atomistic simulation are performed for 1 million steps each, and the aggregated data are used to produce the free energy as a function of the dihedral coordinates. Figure 6 compares the free energy computed via eq 18 from the underlying atomistic MD simulations and the free energy resulting from the selected CG models. Only the regularized CGnet model can correctly reproduce the position of the all main free energy minima (Figure 6a,c). On the contrary, the spline model is not able to capture the shallow minima corresponding to positive values of the dihedral angle ϕ, and introduces several spurious minima (Figure 6b). This comparison confirms that selecting CG models by minimal mean force prediction error achieves models that are better from a physical viewpoint.

Figure 6.

Free energy profiles and simulated structures of alanine dipeptide using all-atom and machine-learned coarse-grained models. (a) Reference free energy as a function of the dihedral angles, as obtained from direct histogram estimation from all-atom simulation. (b) Standard coarse-grained model using a sum of splines of individual internal coordinates. (c) Regularized CGnet as proposed here. (d) Unregularized CGnet. (e) Representative structures in the six free energy minima, from atomistic simulation (ball-and-stick representation) and regularized CGnet simulation (licorice representation).

As an a posteriori analysis of the results, we have performed MD simulation for the CG models corresponding to different choices of hyperparameters, both for the spline model and CGnet. For each choice of hyperparameters, we have computed the difference between the free energy as a function of the dihedral angles resulting from the CG simulations and the one from the all-atom models. Differences in free energy were estimated by discretizing the space spanned by the two dihedral angles and computing the mean square difference on all bins. The difference between a given model and CGnet was computed by shifting the free energy of CGnet by a constant value that minimizes the overall mean square difference. The free energy difference for the spline models is always significantly larger than for the CGnet models (Figure 5d–f). Interestingly, the minima in the difference in free energy correspond to the minima in the cross-validation curves reported in Figure 5a–c, and the optimal values of hyperparameters selected by cross-validation yield the absolute minimum in the free energy difference (indicated in Figure 5f as C5 for CGnet and S4 for the spline model). This point is illustrated more explicitly in the SI (Section E, Figures S4 and S5), and demonstrates that the cross-validation error of different models is correlated with errors in approximating the two-dimensional free energy surface of alanine dipeptide.

For the CGnet, regularization is extremely important: without regularization, the free energy only matches near the most pronounced minima, and unphysical structures are sampled outside (Figure 6d and the SI, Section D). With regularization, these unphysical regimes are avoided; all sampled structures appear chemically valid (Figure 6e), and the distributions of bonds and angles follow those in the atomistic simulations (SI, Section D and Figure S3).

Coarse-Graining of Chignolin Folding/Unfolding in Water

Finally, we test the CGnet on a much more challenging problem: the folding/unfolding dynamics of the polypeptide Chignolin in water. Chignolin consists of 10 amino acids plus termini and exhibits a clear folding/unfolding transition. The all-atom model contains 1881 water molecules, salt ions, and the Chignolin molecule, resulting in nearly 6000 atoms. To focus on the folding/unfolding transition, data were generated at the melting temperature 350 K, mimicking the setup used for the Anton supercomputer simulation in ref (76). To obtain a well-converged ground truth, we generated 3742 short MD simulations with an aggregate length of 187.2 μs on GPUgrid⁷⁷ using the ACEMD program.⁷⁸ The free energy landscape is computed on the two collective variables describing the slowest processes, computed by the TICA method.⁷⁹ Since the individual MD simulations are too short to reach equilibrium, the equilibrium distribution was recovered by reweighting all data using a Markov state model.⁸⁰ See the SI for details on the MD simulation and Markov model analysis.

Figure 7a shows the free energy as a function of the first two TICA coordinates. Three minima are clearly identifiable on this free energy landscape: states a (folded), b (unfolded), and c (partially misfolded), ordered alphabetically from most to least populated. Representative configurations in these minima are as shown in Figure 7e. As a result, the first TICA mode is a folding/unfolding coordinate, while the second is a misfolding coordinate.

Figure 7.

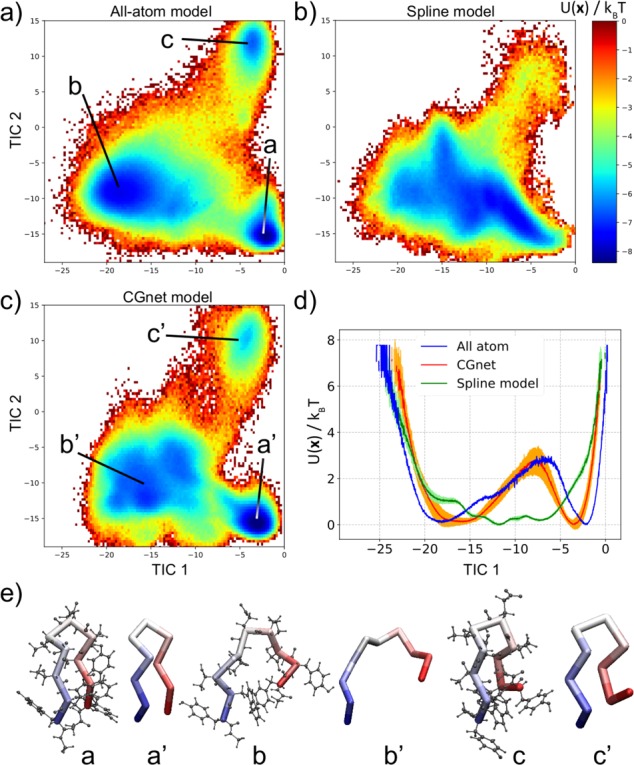
Free energy landscape of Chignolin for the different models. (a) Free energy as obtained from all-atom simulation, as a function of the first two TICA coordinates. (b) Free energy as obtained from the spline model, as a function of the same two coordinates used in the all-atom model. (c) Free energy as obtained from CGnet, as a function of the same two coordinates. (d) Comparison of the one-dimensional free energy as a function of the first TICA coordinate (corresponding to the folding/unfolding transition) for the three models: all-atom (blue), spline (green), and CGnet (red). (e) Representative Chignolin configurations in the three minima from (a–c) all-atom simulation and (a′–c′) CGnet.

Using a regularized CGnet, we coarse-grain the 6000-atom system to 10 CG beads representing the α-carbons of Chignolin. Thus, not only is the polypeptide coarse-grained, but also the solvation free energy is implicitly included in the CG model. Similar to what was done for alanine dipeptide, roto-translational invariance of the energy was implemented by using a CGnet featurization layer that maps the C_α Cartesian coordinates to all pairwise distances between CG beads, all angles defined by three adjacent CG beads, and the cos and sin of all the dihedral angles defined by four CG adjacent beads. The regularizing baseline energy includes a harmonic term for each bond and angle and an excluded volume term for each pairwise distance between CG particles that are separated by more than two bonds.

Similar to the case of alanine dipeptide, a classical few-body spline model was defined for comparison whose CG potential is a sum of bonded and nonbonded terms, where each term is a nonlinear function of a single feature (pairwise distances, angles, dihedrals).

Both the CGnet and spline model are optimized through a five-stage cross-validation search for the hyperparameters in the following order: depth D, width W, exponent of the excluded volume term c, radius of the excluded volume term σ, and Lipschitz regularization strength λ. The results of the cross-validation are shown in Figure S8. This optimization resulted in the hyperparameter values D = 5, W = 250, c = 6, σ = 5.5, and λ = 4.0. For the spline model, the optimal values of the hyperparameters are D = 3, W = 12 (for each feature), c = 10, σ = 4.0, and λ = 5.0 (Figure S8). The potential resulting from CGnet and the spline model is then used to run long simulations with eq 14. One hundred simulations of 1 million steps each were generated using randomly sampled configurations from the training data as starting points. For comparison, the aggregated data are projected onto the TICA coordinates obtained from all-atom simulations, and free energy landscapes are computed directly using eq 18 (Figure 7b,c). For a more quantitative comparison, the free energies are also reported along the first TICA coordinate that indicates folding/unfolding (Figure 7d).

These figures clearly show that the spline model cannot reproduce the folding/unfolding dynamics of Chignolin, as the folded and unfolded states are not well-defined (Figure 7b,d). On the contrary, CGnet not only can consistently fold and unfold the protein but also correctly identifies three well-defined minima: the folded (a′), unfolded (b′), and partially misfolded (c′) ensembles corresponding to the minima a, b, and c in the all-atom fully solvated model (Figure 7c,d). Representative structures in the three minima are shown in Figure 7e: the structures obtained from the CGnet simulations are remarkably similar to the ones obtained in the all-atom simulations. These results reinforce what has been already observed for alanine dipeptide above: the multibody interactions captured by CGnet are essential for correct reproduction of the free energy landscape for the protein Chignolin. The absence of such interactions in the spline model dramatically alters the corresponding free energy landscape to the point that the model can not reproduce the folding/unfolding behavior of the protein.

Conclusions

Here we have formulated coarse-graining based on the force-matching principle as a machine learning method. An important consequence of this formulation is that coarse-graining is a supervised learning problem whose loss function can be decomposed into the standard terms of statistical estimator theory: Bias, Variance, and Noise. These terms have well-defined physical meanings and can be used in conjunction with cross-validation to select model hyperparameters and rank the quality of different coarse-graining models.

We have also introduced CGnets, a class of neural networks that can be trained with the force-matching principle and can encode all physically relevant invariances and constraints: (1) invariance of the free energy and mean force with respect to translation of the molecule, (2) invariance of the free energy and equivariance of the mean force with respect to rotation of the molecule, (3) the mean force being a conservative force field generated by the free energy, and (4) a prior energy able to be applied to prevent the simulations with CGnets to diverge into unphysical state space regions outside the training data, such as states with overstretched bonds or clashing atoms. Future CGnets may include additional invariances, such as permutational invariance of identical CG particles, e.g., permutation of identical particles in symmetric rings.

The results presented above show that CGnet can be used to define effective energies for CG models that optimally reproduce the equilibrium distribution of a target atomistic model. CGnet provides a better approximation than functional forms commonly used for CG models as it automatically includes multibody effects and nonlinearities. The work presented here provides a proof of principle for this approach on relatively small solutes, but already demonstrates that the complex solvation free energy involved in the folding/unfolding of a polypeptide such as Chignolin can be encoded in a CGnet consisting of only the C_α atoms. The extension to larger and more complex molecules presents additional challenges and may require to include additional terms to enforce physical constraints.

Additionally, the CG model considered here is designed ad hoc for a specific molecule and is not transferable to the study of different systems. Transferability remains an outstanding issue in the design of coarse-grained models,¹¹ and its requirement may decrease the ability to reproduce faithfully properties of specific systems.^49,81−84 In principle, transferable potentials can be obtained by designing input features for CGnet imposing a dependence of the energy function on the CG particle types and their environment,⁸² similarly to what is done in the learning of potential energy functions from quantum mechanics data (see, e.g., refs (20, 24, 27, 33, and 66)). This approach may be able to define transferable functions if enough data are used in the training.^27,33 We leave the investigation on the trade-off between transferability and accuracy for future studies.

It is also important to note that the formulation used here to define an optimal CG potential aims at reproducing structural properties of the system, but it does not determine the equations for its dynamical evolution. If one is interested in designing CG models that can reproduce molecular dynamical mechanisms, e.g., to reproduce the slow dynamical processes of the fine-grained model, alternative approaches need to be investigated.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acscentsci.8b00913.

• Derivation of eq 6, cross-validation for all the models presented in the manuscript, additional details on the training of the models, distribution of bonds and angles for the different models of alanine dipeptide, changes in the free energy of alanine dipeptide with different hyperparameters, energy decomposition for the CGnet model of alanine dipeptide, details on Chignolin setup and simulation, and Markov state model analysis of Chignolin all-atom simulations (PDF)

The authors declare no competing financial interest.