Interaction Driven Quantum Hall Wedding cake-like Structures in Graphene Quantum Dots

Abstract

Quantum-relativistic matter is ubiquitous in nature; however it is notoriously difficult to probe. The ease with which external electric and magnetic fields can be introduced in graphene opens a door to creating a table-top prototype of strongly confined relativistic matter. Here, through a detailed spectroscopic mapping, we provide a spatial visualization of the interplay between spatial and magnetic confinement in a circular graphene resonator. We directly observe the development of a multi-tiered “wedding cake”-like structure of concentric regions of compressible/incompressible quantum Hall states, a signature of electron interactions in the system. Solid-state experiments can therefore yield insights into the behaviour of quantum-relativistic matter under extreme conditions.

Energy quantization due to quantum confinement takes place when the particle’s de Broglie wavelength becomes comparable to the system’s length scale. Confinement can arise through spatial constraints imposed by electric fields or through cyclotron motion induced by magnetic fields. Combined together, confinement and quantization strengthen the effects of electron-electron interactions, providing a setting to probe a range of exotic phenomena in strongly correlated quantum systems. In the solid-state setting different types of confined strongly correlated states and transitions between them have been studied in quantum dots (QD) in the presence of external magnetic fields (1). Evolution from atomic-like shell structure to magnetic quantization in QDs was first probed using Coulomb blockade spectroscopy (2–4). For QDs at large magnetic fields, i.e. in the quantum Hall regime, it is expected that Coulomb interactions and the redistribution of carriers between Landau levels (LLs) will lead to a characteristic wedding cake-like shape in the density of electronic states (Fig. 1E) (4–8). Although similar structures have been observed in ultracold atoms undergoing transition from the superfluid to Mott insulator (9, 10), they have not been mapped spatially in a solid-state system.

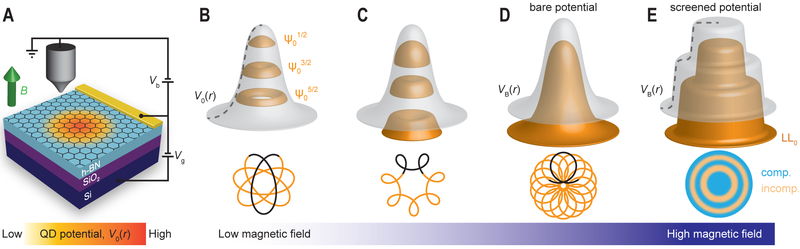
Fig. 1. Schematic evolution of states with magnetic field in a graphene quantum dot.

(A) The device geometry for the graphene quantum dot resonator with a p-doped center inside a n-doped background used in the current experiment. (B-E), (top) Schematic of the potential profile (grey surface), and corresponding wavefunction density (orange surfaces), and (bottom) semi-classical orbits, as a function of applied magnetic field. Confined states start out as quasi-bound QD states and condense into LLs with increasing field. The corresponding screened potential develops a wedding cake-like appearance through electron interactions. Semi-classical orbits start out as expected for a central force potential and then develop into cyclotron motion drifting along equipotential lines forming compressible (blue) and incompressible (yellow) density rings, as shown in (E).

Graphene offers an ideal platform for this enquiry as it hosts a fully exposed two-dimensional electron gas amenable to local probes (11–17). Graphene circular p-n junction resonators (18–22) with built-in local potentials (Fig. 1A) are particularly well suited to the present study; they circumvent the problems of edge roughness and edge impurities encountered in lithographically fabricated graphene QDs. Further, they enable fine control of the confining potential as well as QD doping by means of local gate potentials, offering an opportunity to directly visualize the transition of electron states from spatial to magnetic confinement (Fig. 1, B to E).

In the absence of a magnetic field, confinement of graphene carriers in a p-n junction resonator gives rise to a series of quasi-bound single particle states. These states result from oblique Klein scattering at the p-n interface (18–22). At the same time, Klein tunneling, although present, is very weak for oblique scattering angles and thus has little impact on confinement (23). Analogous to atomic physics, the many-electron shell-like states are characterized by radial and azimuthal quantum numbers (n, m), forming a ladder of states within the spatially confined potential (Fig. 1B) (20, 22). In weak magnetic fields, there is a giant splitting of energy levels corresponding to time-reversed ±m states induced by the π Berry phase in graphene (22, 24). At higher fields, the system enters the quantum Hall regime, with confined states transitioning to highly degenerate LLs (Fig. 1, C and D). A signature of the transition is formation in the electron density of wedding cake-like structures comprised of a series of compressible and incompressible electron liquid rings (Fig. 1E) (4–8). Extending the single-particle description to include Coulomb interactions is essential in this regime.

Our experiment involves spectroscopic mapping of a graphene QD by tunneling measurements. The QD is formed by ionized impurities in the hexagonal boron nitride (hBN) insulating layer acting as a fixed built-in confining potential (see Fig. 1A and Refs. (22) and (25) for device fabrication). The transition from spatial to magnetic confinement occurs when the magnetic length becomes smaller than the confining potential width. By following the bright envelope in the spectral map in Fig. 2A at zero field, we can estimate the effective confining potential as $V_{B=0}(r)\approx U_0\text{exp}\left(-\frac{{\mathit{r}}^2}{R_0^2}\right)+U_{\infty }$, with U₀ ≈ 210 meV, R₀ ≈ 104 nm and U_∞ = −55 meV. This defines a characteristic length scale for the confining potential $l_V={\left(\frac{{R_0}^2\hslash v_{\mathrm{F}}}{U_0}\right)}^{1∕3}\approx 32\text{nm}$. Here ℏ is Plank’s constant, e is the elementary charge, and ν_F ≈ 10⁶ m/s is the graphene Fermi velocity. Such a potential gives rise to quasi-bound states with energy splitting $\Delta E\approx (\hslash v_{\mathrm{F}})∕l_{\mathrm{V}}\approx 20\text{meV}$. Application of a magnetic field tends to confine electrons in a region of size $l_B={\left(\frac{\hslash }{\mathit{eB}}\right)}^{1∕2}$ and leads to the characteristic Landau quantization in graphene, ${\epsilon }_N=\text{sgn}(N)\hslash v_F\sqrt{2\mid N\mid }∕l_B$, with N = ±0, ±1, ±2,…. Each LL is highly degenerate and can host $n_{\text{LL}}=g∕2\pi l_B^2$ carriers per unit area, where g = 4 is the valley/spin degeneracy. Therefore, we expect a transition from atomic-like QD states to LL states occurring at l_B ≅ l_v, which gives a transitional magnetic field of B ≈ 0.6 T.

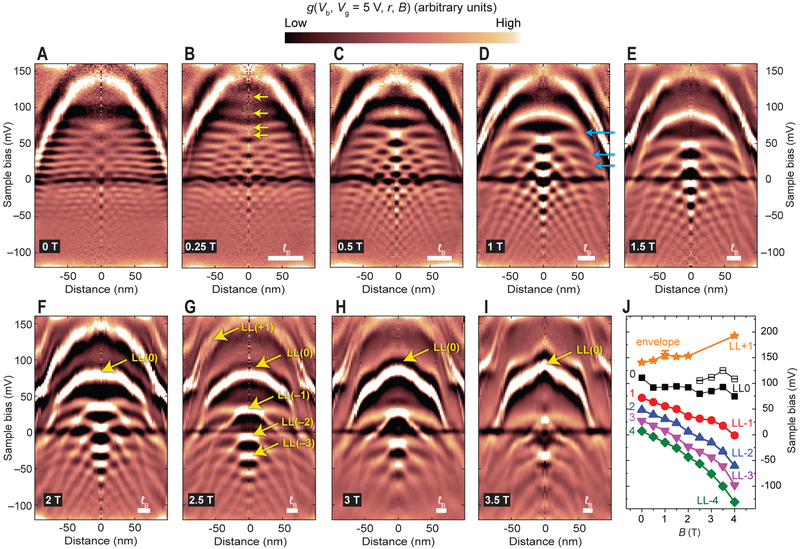
Fig. 2. Visualization of the condensation of states from spatial to magnetic quantization.

(A-I) Experimental differential conductance (T = 4.3 K), g(V_b, V_g, r, B), maps the local density of states as a function of applied magnetic field, showing manifolds of spatially confined QD states condensing into LLs at higher fields. The magnetic field and corresponding magnetic length l_B is indicated in the bottom of each map. The 2D maps are radially averaged from a 2D grid of spectra. A smooth background was subtracted to remove the graphene dispersive background (25). The yellow arrows in (B) indicate the splitting of the m = ±1/2 degeneracy at r = 0 due to the turn on of a π Berry phase. The blue arrows in (D) indicate the shell-like states merging into the N=0 Landau level edge mode. (J) Energy positions of the (n, m = 1/2) states (symbols) obtained from the maps in (A-I) at r = 0 are observed to evolve into separate LLs with increasing applied magnetic field. LL(0) splits into two peaks above 2.5 T, indicated by the open and solid square symbols. The experimental uncertainty, determined from fitting the peak positions in the spectra, represents one standard deviation and is smaller than the symbol size.

The transition and intricate evolution of QD states from spatial to magnetic confinement with increasing magnetic field is displayed in Fig. 2. The measured differential conductance signal, proportional to the local density of states (LDOS), shows the evolution of the QD states in the energy vs radial plane that cuts through the diameter of the QD. The zero-field shell-like QD states are well-resolved in Fig. 2A under the bright concave band, which follows the confining potential. States with ($m=\pm \frac{1}{2}$) have the largest weight in the center at r = 0, whereas states with a common radial quantum number n, have a large weight in the form of arcs following the concave potential outline. The first critical field is reached by 0.25 T, where the ±m degeneracy is lifted owing to the turn on of a π Berry phase (22, 24), as seen by the doubling of the anti-nodes at r = 0 (arrows in Fig. 2B). The onset of the transition into the quantum Hall regime can be observed at B = 0.5 T (Fig. 2C) in agreement with the estimate above. Here states in the center of the resonator start to flatten out, have increased intensity, and shift lower in energy. Beginning at B = 1 T various interior resonator states (arrows in Fig. 2D) merge into the N = 0 Landau level (LL(0)). With progressively higher fields, the number of QD resonances decreases as they condense into the flattened central states forming a series of highly degenerate LLs (Fig. 2, F to I). Beginning at about 2 T (Fig. 2F), LL(0) develops kinks near the QD boundary and an additional concave cusp near the center. Below we argue that these are related to electron interaction effects. Additionally, LL(0) develops a splitting, which increases with field, whereas LL(−1) continually moves down in energy. In this field range, a decrease in conductance over a small energy range is also observed at the Fermi level, which we attribute to a Coulomb pseudogap (26, 27).

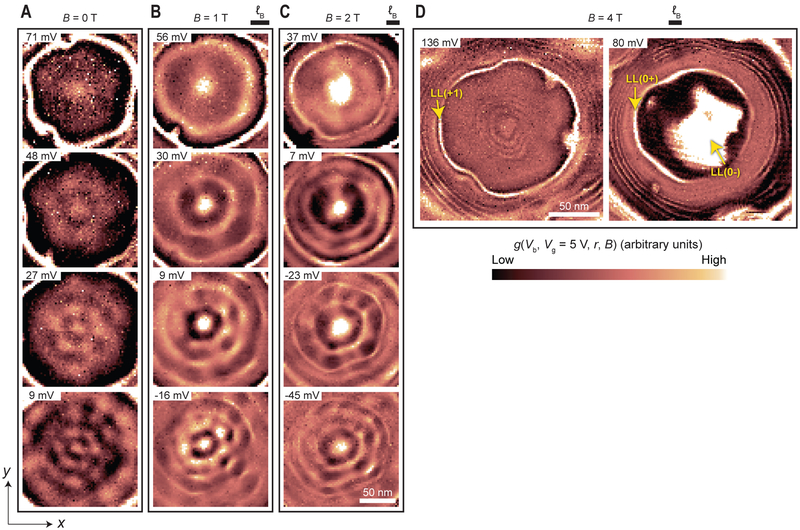
We now discuss the spatial pattern associated with the eigenstate evolution observed in Fig. 2. Experimental spatial maps of the differential conductance, corresponding to resonator LDOS wavefunction probability amplitudes, are obtained by taking a two-dimensional slice in the x-y plane of the data set in Fig. 2 at a specific energy (Fig. 3). Only a subset of the data is shown in Fig. 3 corresponding to specific energies of the prominent central states at r = 0 in Fig. 2, with increasing magnetic field for each column of maps [a complete view of the data set can be seen in the movie file S1]. The spatial extent of the m=±1/2 states at the selected energies is observed at zero field in the first column of the maps in Fig. 3. As we increase field and progress from the left to the right of the figure, we observe the formation of rings with diameters that narrow both in diameter and width with increasing field. For higher n states (progressing down in a column), more rings are seen. Some of these rings originate from the quasibound resonances that have not yet developed into Landau levels and some reflect the presence of magnetic confinement. The former can have a relatively narrow spatial profile if they are dispersing up or down in energy. At a still higher field (Fig. 3D) LLs plateaus are formed as seen in Fig. 2 and show up as bright rings in the spatial maps as indicated by the arrows pointing to LL(+1) and the valley-split (28) LL(0+), LL(0−) state in Fig. 3D. When LL states cross, or are pinned at the Fermi level, they form compressible (metallic) rings and disks, which start to show Coulomb charging effects (13), as indicated by the fine quartet of rings in the center and outside edge of Fig. 3D (see also vertically dispersing lines in Fig. 4E and rings in Fig 4G).

Fig. 3. Differential conductance spatial maps of QD states vs magnetic field.

Each column in the figure corresponds to differential conductance maps (T = 4.3 K) in the x-y plane, g(V_b, V_g, r, B), at a specific energy and at fixed magnetic fields from 0 T to 4 T, (A-D), respectively, indicated in the top of each column along with the magnetic length bar. The maps in each column are at energies corresponding to prominent QD states observed in Fig. 2, at the sample bias voltages indicated on top. With increased magnetic field, various circular rings appear to get narrower, reflecting the drift states schematically indicated in Fig. 1, B to E. Charging of compressible rings develops at the larger field in (D) evidenced by the quartets of fine rings in the center and outside edge (see Fig. 4E for the corresponding radial map). A smooth background was subtracted from each dI/dV vs V_b spectra in the 2D grid to remove the graphene dispersive background (25).

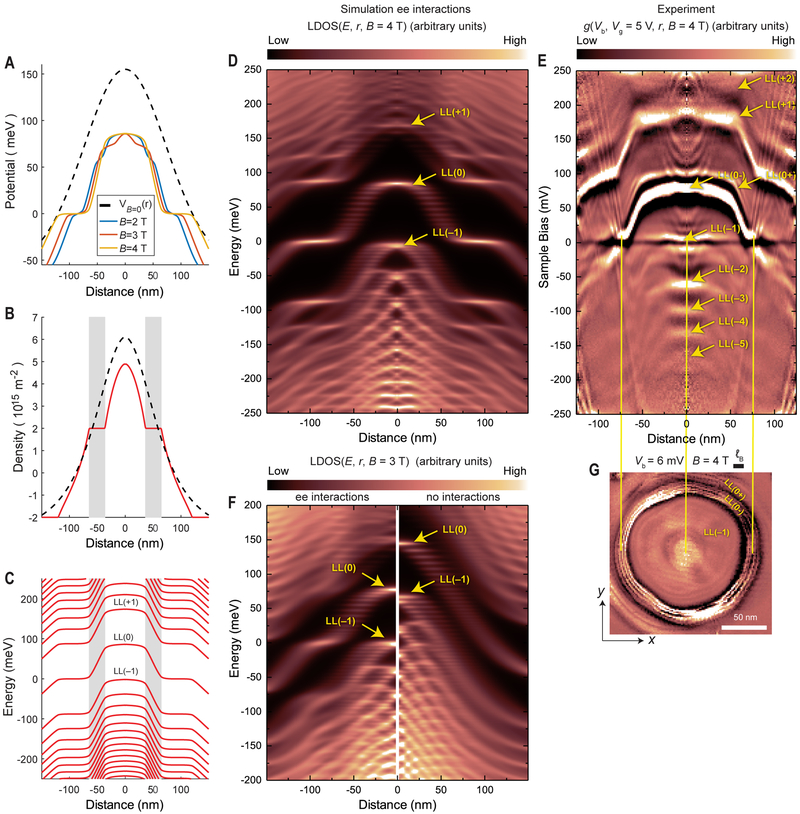
Fig. 4. Electron Interactions and the Wedding Cake-like Structure.

(A) Effective potential for several magnetic field values (solid lines) and the V_B=0(r) fit based on Fig. 2A (dashed line). (B-C) Carrier density and Landau levels at B=4 T as predicted by the model from Eq. 1. Screening produces compressible regions, where LLs are flat and pinned at the Fermi level, separated by incompressible regions (marked in grey). The size of incompressible regions is estimated in Eq. 4. The dashed line in (B) describes charge density in the compressible limit obtained by excluding the kinetic term K[n(r)] from the functional in Eq. 1. (D) LDOS map calculated using the screened potential from (A). A Fermi velocity of 1.2 × 10⁶ m/s was used in the calculations to match the LL positions between theory and experiment at B = 4 T. (E) Experimental differential conductance map (T = 4.3 K), g(V_b, V_g, r, B), as a function of V_b and r at B = 4 T showing the wedding cake structure in the LLs in the QD. (F) LDOS simulated using the potential at B=3 T and V_B=0(r) from (A) (see text for discussion). (G) An x-y slice of the g(V_b, V_g, r, B) map in (F) at V_b=6 mV (near the Fermi level) showing the inner compressible disk from LL(−1) and the outer compressible ring from LL(0), as schematically indicated in Fig. 1E. The solid yellow lines show where LL(0) and LL(−1) cut through the Fermi level, creating the compressible rings.

A striking and unexpected feature observed in Fig. 3 is the appearance of circular nodal patterns in the spatial maps of differential conductance, which are present even at zero field. The origin of these nodal patterns is not clear at present, but they can either be attributed to interactions as they resemble the shell-like structure predicted for Wigner crystals (7, 29–31) or to deviations from a rotationally symmetric confining potential. Deviations from perfect symmetry will partially lift the m-state degeneracy and give rise to nodal patterns. Moiré superlattice effects can be ruled out as an origin of the potential asymmetry because of the large angular mismatch (≈29 °) between the graphene and hBN insulator for this device, which gives a superlattice period of ≈0.5 nm, much smaller than the nodal separation length scales (22). A non-symmetric potential can result from the shape of the probe tip, which gets imprinted in the QD potential shape from the electric field generated during the tip voltage pulse.

As a simple theoretical model, we use the edge state picture of the quantum Hall effect. In a circular geometry, it yields a system of compressible and incompressible rings formed in the electron liquid (Fig. 1D) owing to the interplay between Landau levels and electron interactions (4). In our measurement, interaction effects are observed already at low fields, signaled by the shifting and flattening of the LL states in Fig. 2. A minimal model incorporating interactions at low fields is the energy functional (4)

$$E[n]=\int {\mathrm{d}}^{2}r\left(K[n(r)]+V_{\text{ext}}(r)n(r)+\frac{1}{2}\int {\mathrm{d}}^2{r}^{\prime }{V}_{\text{ee}}(\mid \mathit{r}-{\mathit{r}}^{\prime }\mid )n(r)n(r^{\prime })\right),$$ (1)

where n(r) is charge density at position r. This functional describes the competition between carriers’ kinetic energy K[n(r)] and the effective potential V_B(r). We approximate these quantities as:

$$\frac{\delta K}{\delta n(r)}={\epsilon }_N,\left(N-\frac{1}{2}\right)n_{\text{LL}}<n(r)<\left(N+\frac{1}{2}\right)n_{\text{LL}},$$ (2)

$$V_B(r)=V_{\text{ext}}(r)+\int d^2{r}^{\prime }{V}_{\text{ee}}(\mid \mathit{r}-{\mathit{r}}^{\prime }\mid )n(r^{\prime }).$$ (3)

These relations are valid in the limit l_B ≪ l_v. Here N = 0, ±1, ±2 … is the LL number, V_ext is the electrostatic potential defining the dot, $V_{\mathit{ee}}(r)=\frac{{\tilde{e}}^2}{r}$ is the Coulomb interaction and $\tilde{e}$ is the screened electron charge (see (25) for details).

The calculated effective potential V_B(r) is shown in Fig. 4A for a few magnetic field values. The joint effect of the magnetic field and interactions is to create a series of plateaus forming a multi-tiered wedding cake-like pattern of concentric rings within the dot. At the same time the potential is reduced compared to V_B=0(r) due to screening. Notably, the reduced potential causes LL(0) to move toward the Fermi level in agreement with the energy dependence of LL(0) in Fig. 2. The extra concave features in the potential in the central region match those in the experimental maps of LL(0) in Fig. 2, F to I. The effect of interactions on the LLs is shown by comparing the LDOS with and without interactions in the left and right panels of Fig. 4F. Before interactions are turned on (right panel), the LLs seen through the LDOS essentially track the potential V_B=0(r). After including interactions (left panel), the evolution of the LDOS mimics that of potential V_B(r): LLs shift to lower energy and flatten in the central region, in agreement with the evolution seen in the measurements (Fig. 2).

The incompressible and compressible rings become considerably clearer in higher magnetic field. The experimental spectral map in Fig. 4E shows the LLs becoming flat in the central region of the QD even though the bare external electrostatic potential is concave (see QD outline Fig. 2A), and then they progress sharply to a new energy level as new LLs become occupied, forming a wedding cake-like structure. Here LL(N), N = −5 to 2 can be observed as plateaus in the center of the QD (Fig. 4E). Both LL(0) and LL(−1) cross the Fermi level at zero bias as indicated by the yellow lines, forming a LL(−1) compressible disk in the center and an outer LL(0) compressible ring separated by an incompressible ring, as shown in the Fermi-level spatial map in the x-y plane (Fig. 4G). We observe Coulomb charging of these LLs as charging lines intersecting the LLs at the Fermi level and progressing upward at sharp angles in Fig. 4E. These lines correspond to a quartet of rings in Fig. 4G and Fig. 3D. The charging of the compressible regions occurs in groups of four, reflecting the four-fold (spin and valley) graphene degeneracy (13).

To understand these observations, we use a two-stage approach. We first use the mean field functional Eq. 1 to find LL occupancies and determine the screened potential V_B(r) (25). We then use this potential to calculate the density of microscopic states, which can be directly compared to the measurements. The features seen in the measured LDOS can be understood by comparing them to a simple calculation of the LLs (25), shown in Fig. 4C. The highest LL that is partially filled can be obtained by counting the number of LLs that need to be populated to accommodate the carrier density equal to that in the fully compressible regime (dashed line in Fig. 4B). In the simulated LDOS map in Fig. 4D, we can identify the LL states, which track the screened potential V_B(r) pictured in Fig. 4A, and exhibit plateaus as expected from theory (4, 5). This behavior is in good agreement with the experimental results shown in Fig. 4E.

The width of the observed incompressible ring can be estimated from the functional in Eq. 1 following the approach of Ref. (5) and yields the strip width (25),

$$l={\left(\frac{4\Delta {\epsilon }_{\text{LL}}}{{\pi }^2{\tilde{e}}^2\frac{\mathit{dn}}{\mathit{dr}}}\right)}^{\frac{1}{2}}\approx 34\text{nm}.$$ (4)

The estimate in Eq. 4 is slightly greater than the width inferred from our measurement results shown in Fig. 4E. The small discrepancy can partly be attributed to the result of Ref. (5), derived for LL spacing Δε_LL much smaller than the external potential, being used in the regime when Δε_LL is not small on the V_B (r) scale.

Fingerprints of electron-electron interactions that are as clear and striking as the observed electronic wedding cake-like patterns are relatively rare in solid-state experiments. The measurements reported here suggest, as hinted by the charging lines and nodal patterns in the differential conductance maps, that even more exotic signatures of electronic interactions may be within experimental grasp in future scanned probe measurements at lower temperatures.