Calibrating a predictive model of tumor growth and angiogenesis with quantitative MRI

Abstract

The spatiotemporal variations in tumor vasculature inevitably alters cell proliferation and treatment efficacy. Thus, rigorous characterization of tumor dynamics must include a description of this phenomenon. We have developed a family of biophysical models of tumor growth and angiogenesis that are calibrated with diffusion-weighted magnetic resonance imaging (DW-MRI) and dynamic contrast-enhanced (DCE-) MRI data to provide individualized tumor growth forecasts. Tumor and blood volume fractions were evolved using two, coupled partial differential equations consisting of proliferation, diffusion, and death terms. To evaluate these models, rats (n=8) with C6 gliomas were imaged seven times. The tumor volume fraction was estimated using DW-MRI, while DCE-MRI provided estimates of the blood volume fraction. The first three time points were used to calibrate model parameters, which were then used to predict growth at the remaining four time points and compared directly to the measurements. The best performing model predicted tumor growth with less than 10.3% error in tumor volume and with less than 9.4% error at the voxel-level at all prediction time points. The best performing model resulted in less than 9.3% error in blood volume at the voxel-level. This pre-clinical study demonstrates the potential for image-based, mechanistic modeling of tumor growth and angiogenesis.

1. Introduction

Angiogenesis is a critical component of tumor growth and invasion that is required to provide the delivery of nutrients and removal of waste to support growth past 2-3 mm³ in size. The recruited vasculature, however, is often disorganized (i.e., non-hierarchical), inefficient, and leaky, resulting in heterogeneous tumor perfusion^10,17. This spatially and temporally varying tumor perfusion yields heterogeneous delivery of nutrients (e.g., oxygen and glucose) and systemic therapies as well as heterogeneous response to radiation therapy¹⁰. Accurate characterization of the recruitment of new vessels and the death (or collapse) of existing vessels, may provide a valuable tool for predicting response or optimizing therapeutic regimens for an individual subject. Specifically, knowledge of the temporal and spatial change of tumor vasculature could be used to determine optimal dosing schedules for anti-angiogenic and chemotherapy agents or predicting reoxygenation or reperfusion of tissue following radiation therapy. Mathematical modeling of tumor-induced angiogenesis is well developed with several discrete and continuum approaches characterizing the recruitment of vasculature to avascular tumors. One barrier for translating these modeling approaches from the in silico setting to the in vivo setting is the personalization of model parameters or initial conditions to characterize an individual’s unique tumor and vasculature state. To this end, we have developed a modeling approach that integrates non-invasive medical imaging measures to characterize an individual’s tumor and vasculature with a mechanistic model of tumor growth and angiogenesis.

Medical imaging has evolved well-beyond morphological characterization and can provide 3D, non-invasive, quantification of the critical properties of the tumor microenvironment³⁰. In particular, magnetic resonance imaging (MRI) techniques have been developed to characterize tissue oxygenation, cellularity, blood volume, and perfusion, which may be sensitive or predictive of response. We and others have suggested using these quantitative imaging measurements to initialize, calibrate, and inform predictive mathematical models of tumor growth^12,18,19,23 to predict response and potentially be used to adapt ongoing treatment. In this effort, we utilize diffusion-weighted MRI (DW-MRI) to provide estimates of tumor cellularity. DW-MRI is an imaging technique that is sensitive to the diffusion of water molecules²¹. DW-MRI methods have been developed to map the apparent diffusion coefficient (ADC), which, in-well controlled situations, has been shown to correlate inversely with tissue cellularity over a range of tumor types^3,27.

To provide estimates of tumor vascularity we use dynamic contrast-enhanced (DCE-MRI). In DCE-MRI, several T₁-weighted images are collected before, during, and after the injection of a contrast agent so that each voxel in each image set yields a time course that can be analyzed with a pharmacokinetic model³¹. As the contrast agent moves through tissue, it decreases the local T₁ resulting in an increase in the measured signal. In areas of the brain with an intact blood-brain barrier, the contrast agent remains largely within the vasculature. However, in areas with permeable vasculature or disrupted blood-brain barrier, some of the contrast agent leaks out resulting in signal from both the vasculature and tissue space. Blood volume can be estimated using a pharmacokinetic model (such as the Kety-Tofts model³¹) or by calculating the ratio of area under the curve for the concentration of the contrast agent in tissue to the concentration of the contrast agent in the blood vessel²⁵. Recently, DCE-MRI data was used by Roque et al²³ to estimate fractions of proliferative and necrotic cells within the tumor, as well as estimate blood flow. However, it was not employed to inform a mathematical model on the development of tumor vasculature. Here, we use DCE-MRI data to estimate the spatial-temporal variation of tumor vasculature which we hypothesize will have a significant effect on the proliferation and death of tumor cells as estimated from DW-MRI.

Both DW-MRI and DCE-MRI have been well-studied and applied in the pre-clinical and clinical settings to assess and predict response^4,20 to therapy. By utilizing non-invasive imaging techniques such as DW-MRI and DCE-MRI, we are able to acquire a snapshot of tumor development without disrupting or altering the tumor, which can be used to initialize and calibrate model parameters for an individual subject. These calibrated parameters are then used to provide a “forecast” of future tumor development that can then be directly compared to future imaging data³². In this contribution, we employ serial DW-MRI and DCE-MRI data acquired in a murine glioma model to initialize and calibrate coupled, mechanistic models of tumor growth and angiogenesis. We develop a family of coupled biophysical models of tumor growth and angiogenesis and evaluate the accuracy of the predictions of future changes in cellularity and blood volume on a subject-specific basis. All modeling predictions are then directly compared to MRI measurements. To the best of our knowledge, we are the first to develop and apply a biophysical model that is capable of being initialized and calibrated with individualized DCE-MRI and DW-MRI data to make individualized tumor growth and blood volume forecasts.

2. Material and Methods

2.1. Biophysical models of tumor growth

2.1.1. Mechanically coupled reaction diffusion model of tumor growth

The reaction-diffusion model shown in Eq. (1), provides the foundation upon which the proposed models are built. Eq. (1) describes the spatial and temporal change in the tumor cell volume fraction due to the random movement of tumor cells and proliferation:

$$\frac{\partial N_T(\overline{x},t)}{\partial t}=\stackrel{\text{Diffusion}}{\overbrace{\nabla \cdot \left(D_T(\overline{x},t)\nabla \left(\frac{N_T(\overline{x},t)}{{\theta }_T}\right)\right)}}+\stackrel{\text{Proliferation}}{\overbrace{k_{p,T}{N}_T(\overline{x},t)\left(1-\frac{N_T(\overline{x},t)}{{\theta }_T}\right)}},$$ (1)

where $N_T(\stackrel{‒}{x},t)$ is the tumor cell fraction at three-dimensional position $\stackrel{‒}{x}$ and time t, θ_T is the tumor cell carrying capacity (i.e., the maximum packing fraction that a voxel can functionally support), and k_p,T is the tumor cell proliferation rate. $D_T(\stackrel{‒}{x},t)$ changes spatially and temporally as a function of the local tissue stress^8,14,15 In vitro experiments have demonstrated that tumor expansion is restricted as local mechanical stresses increase¹¹. Thus, it is natural to relate $D_T(\stackrel{‒}{x},t)$ to stress as shown in Eq. (2):

$$D_T(\overline{x},t)=D_{T,0}\exp (-{\lambda }_1\cdot {\sigma }_{\mathit{vm}}(\overline{x},t)),$$ (2)

where D_T,0 represents tumor cell diffusion in the absence of mechanical restrictions, λ₁, is the stress-tumor cell diffusion coupling constant, and ${\sigma }_{\mathit{vm}}(\stackrel{‒}{x},t)$ is the von Mises stress which reflects the total stress experienced for a given section of tissue. ${\sigma }_{\mathit{vm}}(\stackrel{‒}{x},t)$ is determined by solving for tissue displacement, $\overrightarrow{u}$, using the linear elastic, isotropic equilibrium equation (Eq. (3)):

$$\nabla \cdot G\nabla \overrightarrow{\text{u}}\text{ + }\nabla \frac{G}{1-2\text{v}}(\nabla \cdot \overrightarrow{\text{u}})-{\lambda }_2\nabla N_T(\overline{x},t)=0,$$ (3)

where G is the shear modulus, ν is the Poisson’s Ratio, and λ₂ is second coupling constant. Literature values are used to assign G and v for different tissue regions within the brain (described in detail in¹⁵) as we assume that these tissue properties will not change dramatically from animal to animal (we return to this important point in the Discussions section). Eqs. (2)–(3), tumor cell diffusion decreases as local stress increases. In our previous effort¹⁴, θ_T and k_p,T were estimated estimated within the tumor region of interest, resulting in a locally varying, but temporally static parameter map. For this work, we expand upon our previous model¹⁴ described by Eqs. (1) – (3) to propose a means to effectively temporally update the θ_T or k_p,T by coupling to the spatial temporal evolution of tumor blood volume.

2.1.2. Coupling cell death to vascularity

Eq. (1) is expanded to incorporate the effect of the local blood volume fraction, $N_V(\stackrel{‒}{x},t)$, on tumor cell diffusion and cell death:

$$\frac{\partial N_T(\overline{x},t)}{\partial t}=\stackrel{\text{Diffusion}}{\overbrace{\nabla \cdot \left(D_T(\overline{x},t)\cdot \left(\left(1-\frac{N_V(\overline{x},t)}{{\theta }_{T,V}}\right)\nabla \frac{N_T(\overline{x},t)}{{\theta }_{T,V}}\right)+\left(\frac{N_T(\overline{x},t)}{{\theta }_{T,V}}\nabla \frac{N_V(\overline{x},t)}{{\theta }_{T,V}}\right)\right)}}+\stackrel{\text{Logistic Growth}}{\overbrace{k_{p,T}{N}_T(\overline{x},t)(1-N_T(\overline{x},t)/{\theta }_T)}}-\stackrel{\text{Cell Death}}{\overbrace{k_{d,T}{N}_T(\overline{x},t)\exp (-{\alpha }_1{N}_V(\overline{x},t))}},$$ (4)

where θ_T,V is the summation of tumor and the blood volume fraction carrying capacities, k_d,T is a cell death rate, and α₁ is a constant which weights the rate of exponential tumor cell death per local N_V. To account for the interaction of $N_T(\stackrel{‒}{x},t)$ and $N_V(\stackrel{‒}{x},t)$, we alter the diffusion term in Eq. (1) as in Burger et al.⁵. This diffusion term is a non-linear cross-diffusion term that accounts for the interactions of multiple species. In the absence of a second species, this simplifies to the diffusion term in Eq. (1). There are two primary effects accounted for in this multi-species diffusion term. First, the volume occupied by the vasculature (i.e., $\left(1-N_V\left(\stackrel{‒}{x},t\right)∕{\theta }_{T,V}\right)$) decreases tumor cell diffusion in those directions. Second, local gradients of the vasculature induces an additional flux (or directed movement) on the tumor cells. Combining these terms, in Eq. (4) results in altered mobility (compared to Eq. (1)) that is dependent on the space occupied by $N_V(\stackrel{‒}{x},t)$. Cell death is spatially and temporally varied by $N_V(\stackrel{‒}{x},t)$. Similarly, the spatial-temporal evolution of $N_V(\stackrel{‒}{x},t)$ is described with a reaction-diffusion type model consisting of the diffusion of vasculature, angiogenesis, and death as shown in Eq. (5):

$$\frac{\partial N_V(\overline{x},t)}{\partial t}=\stackrel{\text{Diffusion}}{\overbrace{\nabla \cdot \left(D_V(\overline{x},t)\cdot \left(\left(1-\frac{N_T(\overline{x},t)}{{\theta }_{T,V}}\right)\nabla \frac{N_V(\overline{x},t)}{{\theta }_{T,V}}\right)+\left(\frac{N_V(\overline{x},t)}{{\theta }_{T,V}}\nabla \frac{N_T(\overline{x},t)}{{\theta }_{T,V}}\right)\right)}}+\stackrel{\text{Logistic Growth}/\text{Angiogenesis}}{\overbrace{k_{p,V}{N}_V(\overline{x},t)(1-N_V(\overline{x},t)/{\theta }_V)d}}-\stackrel{\text{Death}}{\overbrace{k_{d,V}{N}_V(\overline{x},t)(1-d)}},$$ (5)

where $D_V(\stackrel{‒}{x},t)$ is the vascular diffusion coefficient, θ_V is the blood volume fraction carrying capacity, k_p,V is the vascular growth rate, d is a normalized parameter describing the distance to the periphery of the tumor, and k_d,V is the vascular death rate. θ_V is assigned to the maximum blood volume fraction observed in the tumor. We assume $D_V(\stackrel{‒}{x},t)$ is also coupled to local tissue stress as in Eq. (2), where D_V,0 represents vascular diffusion in the absence of mechanical restrictions. (From a biological perspective, directed movement via chemotaxis may more accurately describe vasculature movement. However, at the tissue scale, individual vasculature paths are lost and we therefore simplify this phenomenon with a bulk diffusion term.) d ranges from 1 (i.e., a voxel at the periphery of the tumor) to 0 (i.e., a voxel at the furthest distance from the periphery). θ_V and θ_T represent the maximum fraction of vascular and tumor cells, respectively, that the voxel can support. That is, we assume that once $N_T(\stackrel{‒}{x},t)$ or $N_V(\stackrel{‒}{x},t)$ reaches their respected carrying capacity, proliferation ceases as there are not enough resources to support further proliferation. We also assume that tumor cell and vascular diffusion will be affected by the overall space for movement (related to θ_T,V).

2.1.3. Coupling the carrying capacity to vascularity

For a first approximation of the relationship between $N_V(\stackrel{‒}{x},t)$ and the number of cells that can be supported for a given voxel, ${\theta }_T(\stackrel{‒}{x},t)$, we assume a simple linear relationship. To spatially and temporally vary θ_T, we utilize the local blood volume fraction, $N_V(\stackrel{‒}{x},t)$:

$${\theta }_T(\overline{x},t)=\{\begin{array}{cc}{\theta }_{\max }& N_V(\overline{x},t)\ge N_{V,thresh}\\ {\theta }_{\min }+N_V(\overline{x},t)\left(\frac{{\theta }_{\max }-{\theta }_{\min }}{N_{V,thresh}}\right)& N_V(\overline{x},t)<N_{V,thresh}\end{array},$$ (6)

where θ_min to θ_max represents the range of expected carrying capacity values, and N_V,thresh represents a critical value for $N_V(\stackrel{‒}{x},t)$ that would begin to change the number of cells a voxel can support. θ_min is assigned as the lowest volume fraction within the tumor. The death term in Eq. (4) is now removed, and a spatially-varying ${\theta }_T(\stackrel{‒}{x},t)$ is added to the logistic growth term, as shown in Eq. (7):

$$\frac{\partial N_T(\overline{x},t)}{\partial t}=\stackrel{\text{Diffusion}}{\overbrace{\nabla \cdot \left(D_T(\overline{x},t)\cdot \left(\left(1-\frac{N_V(\overline{x},t)}{{\theta }_{T,V}(\overline{x},t)}\right)\nabla \frac{N_T(\overline{x},t)}{{\theta }_{T,V}(\overline{x},t)}\right)+\left(\frac{N_T(\overline{x},t)}{{\theta }_{T,V}(\overline{x},t)}\nabla \frac{N_V(\overline{x},t)}{{\theta }_{T,V}(\overline{x},t)}\right)\right)}}+\stackrel{\text{Logistic Growth}}{\overbrace{k_{p,T}{N}_T(\overline{x},t)(1-N_T(\overline{x},t)/{\theta }_T(\overline{x},t))}}.$$ (7)

By spatially and temporally varying ${\theta }_T(\stackrel{‒}{x},t)$ we are able to induce cell death when $N_T(\stackrel{‒}{x},t)>{\theta }_T(\stackrel{‒}{x},t)$, or increase cell proliferation when $N_T(\stackrel{‒}{x},t)<{\theta }_T(\stackrel{‒}{x},t)$. Table 1 summarizes all of the model parameters and their sources. The forward problem for Eqs. (1) through (7) is solved in 3D using a fully explicit in time finite difference simulation (numerical details are presented in the supplemental material).

Table 1.

Model parameters and their source

Parameter	Interpretation	Source
kp,T	Tumor cell proliferation rate	Calibrated
θT	Tumor cell carrying capacity	Calibrated (M1-M4) Calculated (M5-M8)
DT,0	NT diffusion coefficient in absence of mechanically coupling	Calibrated
G	Shear modulus	Literature 15
v	Poisson’s Ratio	Literature 15
λ1	Coupling Constants	Calibrated
λ2	Coupling Constants	Assigned to 1
kd,T	Tumor cell death rate	Calibrated
α1	Weight of exponential decrease in cell death per local NV	Calibrated
DV,0	NV diffusion coefficient in absence of mechanically coupling	Calibrated
kp,V	Vasculature proliferation rate	Calibrated
kd,V	Vasculature death rate	Calibrated
d	Distance top the periphery of the tumor	Calculated
θV	Maximum blood volume	Assigned from DCE-MRI
θmax	Max carrying capacity	Calibrated
θmin	Minimum value for carrying capacity	Assigned from DW-MRI
NV,thresh	Threshold on NV for carrying capacity to decrease	Calibrated

M1-M4 refers to model 1 to model 4, see Table 2.

2.2. Experimental methods

All experimental procedures were approved by our Institutional Animal Care and Use Committee. Eight female Wistar rats (252 ± 8 g, mean ± 95% confidence interval) were anesthetized and inoculated intracranially with 10⁵ C6 glioma cells (Sigma-Aldrich, St. Louis, Mo, USA) at via stereotaxic injection on day 0. On day 8, permanent jugular catheters were placed in each rat for injection of an MRI contrast agent. The first imaging time point occurred 10 days after injection of the C6 glioma cells. Rats were imaged on days 10, 12, 14, 15, 16, 18 and 20. Not all rats were imaged on days 18 (n = 7) and 20 (n = 4) as some were euthanized due to 20% weight loss or other health concerns. MRI data was acquired using a 9.4T horizontal-bore magnet (Agilent, Santa Clara, CA) with a 38 mm diameter Litz quadrature coil (Doty Scientific, Columbia, SC, USA). We present the salient imaging details here, while the complete details of the imaging experiments can be found in the supplemental material.

DW-MRI was used to provide voxel-wise estimates of ADC using a standard mono-exponential decay model. ADC was then used to estimate $N_T(\stackrel{‒}{x},t)$ ^14,18,29 using Eq. (8):

$$N_T(\overline{x},t)=\left(\frac{AD{C}_w-ADC(\overline{x},t)}{AD{C}_w-AD{C}_{\min }}\right),$$ (8)

where ADC_W is the ADC of free water at 37° C, $\mathit{ADC}(\stackrel{‒}{x},t)$ is the ADC value at position $\stackrel{‒}{x}$ and time t, and ADC_min is the minimum ADC observed within the tumor regions-of-interest (ROIs) across all animals. Figure 1A shows an example of the transformation from $\mathit{ADC}(\stackrel{‒}{x},t)$ to $N_T(\stackrel{‒}{x},t)$.

Figure 1. Schematic of experimental and computational methods.

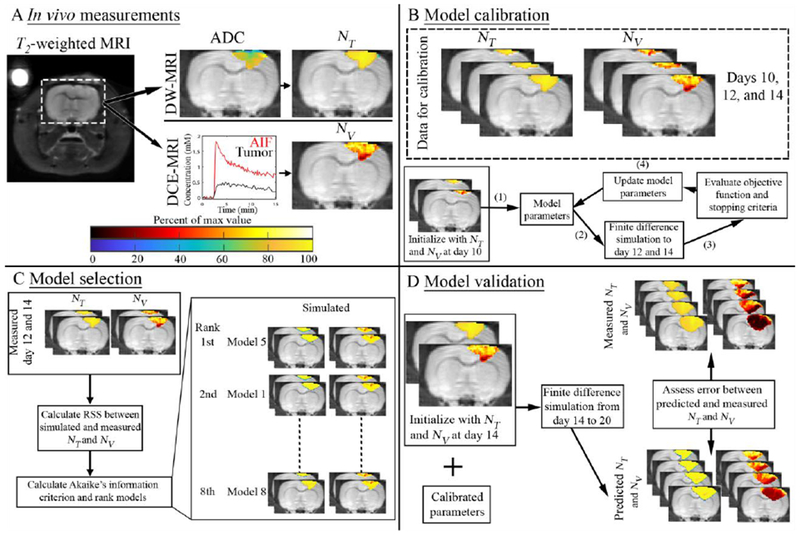
Panel A depicts a T₂-weighted MRI through the central slice of a representative rat in addition to examples of the transformations of ADC to N_T and DCE-MRI time courses to N_V. Panel B illustrates the salient features of the model calibration approach. Briefly, data on days 10, 12, and 14 are used to calibrate model parameters. Model calibrations are initialized with data on day 10 and an initial guess of model parameters. Tumor growth is then simulated to days 12 and 14 using a finite difference scheme. The objective function and stopping criteria are evaluated to determine how to update the current guess of model parameter values. This process repeats until stopping criteria are met. Panel C describes our model selection approach where Akaike’s information criteria (AIC) is used to select the most appropriate model. Panel D summarizes the model validation approach. The model system is initialized with data on day 14 as well as the calibrated model parameters and then simulated forward to the final imaging time point. Error is then assessed between the predicted and observed tumor growth at the imaging time points not used for model calibration.

DCE-MRI was data collected before and after the injection of a 200 μL bolus (0.05 mmol kg⁻¹) of Gd-DTPA^™ (BioPhysics Assay Lab, Worcester, MA). Relative blood volume fraction, $N_V(\stackrel{‒}{x},t)$ was calculated by evaluating the ratio of the area under the concentration of the contrast agent in tissue time course to the arterial input function over the first 60 seconds. A rat population arterial input function was used in lieu of an individual input function¹³ for DCE-MRI analysis. Tumor ROIs were identified using the difference in signal intensity in the pre- and post-contrast agent images from DCE-MRI. Figure 1A shows an example of the transformation from DCE-MRI data to $N_V(\stackrel{‒}{x},t)$.

2.3. Numerical methods

2.3.1. Model parameter calibration

A sensitivity analysis using Sobol’s method²⁴ (details presented in supplemental material) was used to identify model parameters that could benefit from being estimated locally rather (i.e., at each voxel location) than globally (i.e., a uniform value for all voxels). We focused primarily on the total effect indices that identify the importance of a given parameter on a model output including secondary effects from parameter interactions. The Total effect indicies (supplemental Figure 1) indicated that k_p,T was a highly sensitive parameter for $N_T(\stackrel{‒}{x},t)$ and $N_V(\stackrel{‒}{x},t)$ while k_p,V was a highly sensitive parameter for $N_V(\stackrel{‒}{x},t)$. Thus, we generated a family of eight models consisting of two sub-families where blood volume is coupled to cell death (models 1 - 4), and where blood volume is coupled to the carrying capacity (models 5 - 8). Within each sub-family we evaluate whether k_p,T and/or k_p,V should be assigned globally or locally. The model differences are summarized in Table 2.

Table 2:

Summary of model variations

	Model Name	kp,T	kp,V	Calibrated Parameters
Reaction Diffusion	NT,m0	global	NA	3
Coupled via cell death	NT,m1 and NV,m1	global	global	10
	NT,m2 and NV,m2	local	global	9 + m
	NT,m3 and NV,m3	global	local	9 + m
	NT,m4 and NV,m4	local	local	8 + 2 × m
Coupled via carrying capacity	NT,m5 and NV,m5	global	global	9
	NT,m6 and NV,m6	local	global	8 + m
	NT,m7 and NV,m7	global	local	8 + m
	NT,m8 and NV,m8	local	local	7 + 2 × m

m is equal to the number of calibrated local parameters within the tumor. m ranged from 202 to 461, depending on the animal.

Figure 1B–D summarizes the model calibration, selection, and validation approach. We present the salient details of the model calibration approach here, while a more complete description is found in the supplemental material. First, model parameters are initialized with $N_T(\stackrel{‒}{x},10)$ and $N_V(\stackrel{‒}{x},10)$ (calculated from the imaging data as described in section 2.2) and initial guesses of model parameters. Second, these parameters are then used in a finite difference simulation of the model system to return estimates of $N_T(\stackrel{‒}{x},t=12,14)$ and $N_V(\stackrel{‒}{x},t=12,14)$. Third, the objective function (i.e., the normalized, sum of squares error between the model and measurement) and stopping criteria are evaluated. Fourth, if the stopping criteria are not met, the model’s parameters are updated based on the Levenberg-Marquardt algorithm, and the process returns to the first step. We used a hybrid, simulated-annealing Levenberg-Marquardt algorithm, which works identically to a standard Levenberg-Marquardt approach¹⁵, with the exception of a stochastic component to determine if the change in model parameters (and thus change in objective function) is acceptable. All of the model parameters were calibrated for a global value (spatially uniform) unless otherwise indicated in Table 2, in which case a locally varying parameter was estimated. We assess the robustness of this inversion to measurement noise in the supplemental material.

2.3.2. Model selection

To select the model that balances model complexity and model-data agreement we utilized the Akaike Information criterion (AIC¹) defined as:

$$AIC=2k+n\ln \left(\frac{RSS}{n}\right)+2k\left(\frac{k+1}{n-k-1}\right),$$ (9)

where k is equal to the number of parameters calibrated for a given model, n is the number of data points used to calibrate the model, and RSS is the residual sum squares between the measured and model $N_T(\stackrel{‒}{x},t)$ and $N_V(\stackrel{‒}{x},t)$. We considered two different model selection scenarios. First, we investigated which model was selected during the calibration phase (i.e., how well the model describes the data used for calibration). Then, we study how the models performed at predicting tumor growth from days 15 to 20 (as described in the following section) in the prediction phase. Models were selected by recording (for each model) its rank (1-8) for each animal in each of the selection scenarios. We then selected the top three ranking models for further comparison. Figure 1c, shows an example of the model selection approach.

2.3.3. Model validation

The model validation stage is summarized in Figure 1d. The calibrated model parameters were used in a forward finite difference simulation to predict the tumor and blood volume distribution at the remaining imaging time points for each rat. Model predictions of $N_T(\stackrel{‒}{x},t)$ and $N_V(\stackrel{‒}{x},t)$ were compared to $N_{T,\mathit{meas}}(\stackrel{‒}{x},t)$ and $N_{V,\mathit{meas}}(\stackrel{‒}{x},t)$ at the global and local levels. At the global level, error was assessed by calculating the percent error in tumor volume between the predicted and measured tumor ROIs on days 15 through 20. At the local level, error was assessed by calculating the average percent error in N_T and N_V and the concordance correlation coefficient (CCC) at voxels within the measured tumor ROI. All results are presented as the mean and 95% confidence interval when appropriate. Additionally, to provide a standard to which our model errors could be compared, we implemented a 3-parameter, reaction-diffusion model (Eq. (1), model 0) and a “no growth” model. For the no growth model, we simply assume the predicted $N_T(\stackrel{‒}{x},t)$ at days 15 – 20 is simply equal to $N_{T,\mathit{meas}}(\stackrel{‒}{x},14)$. The no growth model was add to provide an estimate of how much the tumor changes compared to $N_{T,\mathit{meas}}(\stackrel{‒}{x},14)$.

3. Results

The results of model selection are shown in Table 3. In both the calibration and prediction scenarios models 1,5, and 6 had the lowest cumulative score based on their AIC value, and were selected for further consideration and evaluation. Figures 2–4 present the results for models 1, 5, and 6, while the results for all models can be found in supplemental material. Figure 2 shows the $N_T(\stackrel{‒}{x},t)$ and $N_V(\stackrel{‒}{x},t)$ fields used for calibration (row A), validation (row B), and the predicted $N_T(\stackrel{‒}{x},t)$ and $N_V(\stackrel{‒}{x},t)$ (rows C-E), for a representative rat. For comparison, row F shows the 3-parameter, reaction diffusion model (model 0). For N_T predictions (left column in Figure 2), all three models have less than 9.5% error in the volume predictions at all time points, and have an average of 12.5% error at the voxel level. All three models predict areas of low cell density (approximately 0.8 × θ_T) relative to the high-density regions at the periphery (greater than 0.9 × θ_T). However, model 5 has a stronger level of agreement at the voxel level (panel D) resulting in a higher average CCC value (0.74) from day 15 to 20 compared to models 1 and 6 (0.71 and 0.62, respectively). Model 0 systematically overestimated tumor size, especially at later time points, and resulted in an average CCC of 0.50. For N_V predictions (right column in Figure 2), all three models predict a well vascularized periphery (approximately 0.4 × θ_V) and a poorly vascularized core (less than 0.1 × θ_V). However, the models underestimate the extent of low vascularized regions compared to N_V,true. For example, at day 20, 15.4% of voxels in N_V,true has a value less than 0.1 × θ_V, whereas all three models predict less than 5.0% of the voxels have a value less than 0.1 × θ_V. High percent errors (greater than 60%) are observed in the low vascularized regions where N_V,true approaches 0; however, the absolute difference between the predicted and measured N_V is negligible.

Table 3:

Model Selection

Model	Calibration	Prediction
NT,m1 & Nv,m1	23* (3)	29* (3)
NT,m2 & Nv,m2	26 (4)	40 (5)
NT,m3 & Nv,m3	48 (6)	43 (6)
NT,m4 & Nv,m4	61 (8)	63 (8)
NT,m5 & Nv,m5	18* (1)	14* (2)
NT,m6 & Nv,m6	18* (1)	10* (1)
NT,m7 & Nv,m7	38 (5)	32 (4)
NT,m8 & Nv,m8	56 (7)	57 (7)

Cumulative score for all animals (rank)

^*indicates top three

Figure 2: Predicted N_T and N_V for a representative animal.

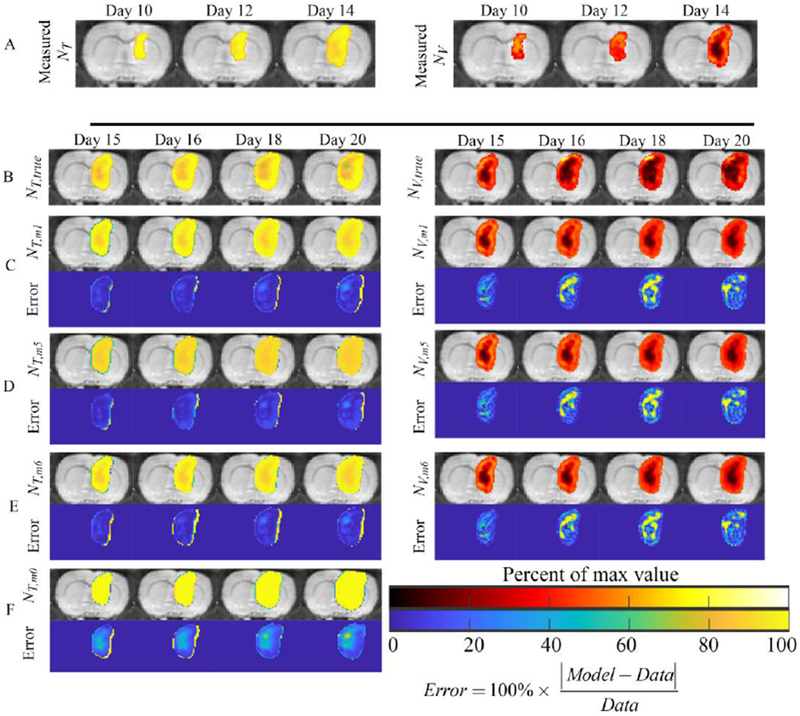
Results from a representative rat are shown for the models coupling N_V to N_T via cell death (model 1) or carrying capacity (models 5 and 6). F-test results comparing the more complex models to model 5, resulted in selection of models 1 and 6 as the best model candidates for model prediction. Panel A shows the measured N_T (left column) and N_V (right column) at days 10, 12, and 14 used to calibrate the model, while panel B shows the measured N_T and N_V at days 15, 16, 18, and 20 used to validate the model. Panels C-E show the predicted N_T and N_V using models 1, 5, and 6, respectively, as well as the error between the model and measurement. For comparison, panel F shows the model 0, the 3 parameter reaction-diffusion model. For this particular rat, N_T is strongly coupled to N_V (i.e., areas of low N_T are often low N_V) demonstrating that incorporating voxel-specific parameters for k_p,T (model 6) does not significantly improve predictions o f N_T compared to model 1 or 5. Generally, all models match the overall tumor shape, while high error is typically observed in N_V (right column) predictions in areas where the model overestimates the measured N_V. For this rat, model 1 had the lowest sum squared error for models 5 and 6, respectively. For comparison, panel F shows model 0, the 3 parameter reaction-diffusion model. Model 0 overestimates tumor area (especially at day 20) and does not predict the development of areas of low cell density .(Supplemental Figures 2 and 3 show the results for models 1-8).

Figure 4: Summary of results for the cohort of animals.

Panels A-C summarize the errors for model predictions of N_T, while panels D-E show the results for model predictions of N_V for the cohort of rats for models 1, 5, and 6. For comparison, we also included model 0 in panels A – C and a model of “no growth” in panel A. In panel A, percent error in tumor volume ranged from 0.4 to 10.3% at all prediction time points for models 1, 5, and 6. Model 0 had greater than 27.98 % at all time points. The “no growth” bars demonstrate that the tumor is rapidly growing over time. In panel B, voxel level error generally increased overtime with values ranging from 3.7 to 9.4%, with model 0 having greater than 12.7% at all time points Conversely, in panel C, the CCC decreased overtime with values ranging from 0.55 to 0.77 for models 1, 5, and 6. Model predictions of N_V also resulted in voxel level error, panel D, with error ranging from 6.0 to 9.3%. The level of agreement as assessed by CCC values, generally decreased over time, panel E, with values ranging from 0.35 to 0.70. No significant differences were observed between models. All values are reported as the mean and 95% confidence interval. (Supplemental Figures 4 and 5 show the results for models 1-8).

Figure 3 compares the predicted versus measured data for model 6 for all rats at their final imaging time point. The measured $N_T(\stackrel{‒}{x},t)$ and are shown in rows A and D, the predicted $N_{T,m6}(\stackrel{‒}{x},t)$ and $N_{V,m6}(\stackrel{‒}{x},t)$ are shown in rows B and E, while rows C and F show the percent error. The RSS for N_T ranged from 138 (rat 6) to 791 (rat 4), while the RSS for N_V ranged from 29 (rat 6) to 3 (rat 5). Areas of lower cell density are observed in for rats 1-5. Notably, in rat 4, model 6 underestimates both the tumor size and total cell number by predicting large areas of low cell density (less than 60% × θ_T). The vasculature model, N_V,m6 predicted areas of increased blood volume fraction particularly at the periphery relative to the tumor center. Notably in rats 3, 7, and 8, the N_V,m6 model predicted high blood volume fractions greater than 60% × θ_V at the periphery whereas the measured data $N_V(\stackrel{‒}{x},t)$ indicated volume fractions less than 30% × θ_V.

Figure 3: Results for the cohort of animals.

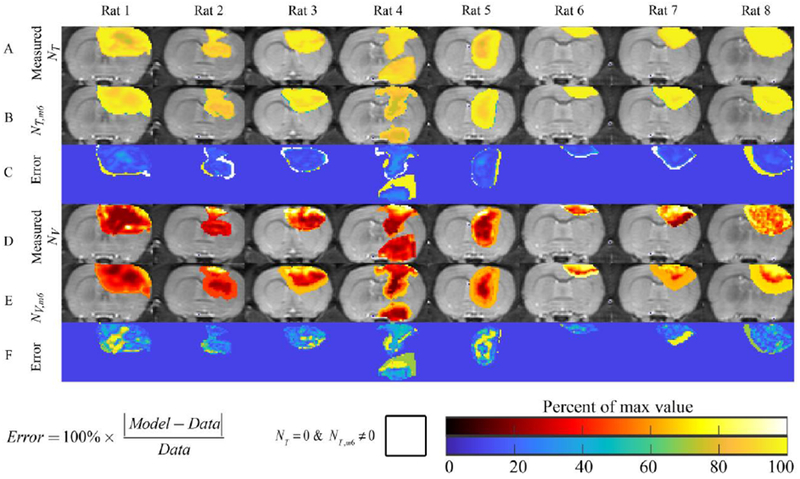
Results for the final time point, and central tumor slice, are shown for all eight rats. Row A shows the measured N_T, while Rows B and C show N_T,m6 and the error between the measurement and model, respectively. Rats 1-5 show varying degrees of intra-tumor heterogeneity in cell density, while rats 6-8 appear to have a relatively homogenous density of tumor cells. The N_T,m6 model predicted the development of low-cell density regions (potentially necrosis) in all rats except rat 6. For rat 4, the N_T,m6 model resulted in an under estimation of the amount of cells (~60% of carrying capacity, versus 90%) compared to the measured N_T. Similarly, row D shows the measured N_V, while Rows E and F show N_V,m6 and the error between the measurement and model, respectively. In general, N_V,m6 predicts increased blood volume fraction at the periphery of the tumor relative to the interior. For the vasculature model, high error (greater than 60%) is often observed in areas with low measured N_V.

Figure 4A–C shows the summary statistics for tumor cell predictions, and blood volume predictions (panels D-E). For tumor cell predictions, all models had less than 10.3% error in tumor volume with model 1 having less than 6% error in tumor volume at all time points (panel A). Similarly, less than 9.4% error was observed at the voxel level (panel B). A high level of agreement was observed for all three models with CCCs ranging from 0.55 to 0.77 (panel C). For comparisons, the 3-parameter, reaction diffusion model (model 0) was included in panels A – C. We observed greater than 28.0% error in tumor volume, greater than 12.7% error at the voxel-level, and CCC’s ranging from 0.44 to 0.56. Model 0 had statistically significant (p < 0.05) differences between models 1, 5, and 6 in percent error in tumor volume and percent error in voxel cell number. Model 0 also had significantly lower CCCs (p < 0.05) between models 1, 5, and 6 at day 15 and only model 6 at day 16. We also included a model of no growth in panel A. Error in tumor volume predictions for the no growth model ranged from 21.7% to 64.7%. The no growth model had statistically significant differences (p < 0.05) between it and models 1, 5, and 6. For blood volume predictions, less than 9.3% error was observed at the voxel level (panel D). The level of agreement declined overtime with CCCs ranging from 0.70 at day 15 to less than 0.35 at day 20 (panel E). No significant differences were observed between models 1, 5, and 6 and the summary statistics; however, model 6 had the lowest AIC rank in the prediction phase (supplemental table 2) based on its AIC value.

4. Discussion

DW-MRI and DCE-MRI data were used to initialize and calibrate a reaction-diffusion model for tumor growth and angiogenesis on an animal specific basis. By employing non-invasive imaging measures, we are able to calibrate model parameters on an individual basis to provide animal-specific tumor growth forecasts. To evaluate the predictive strength of this model system, we evaluated the accuracy of model predictions on an animal specific basis using our family of biophysical models. From the eight models, we selected the top three (models 1, 5 and 6) that had the lowest AIC during the calibration stage. We also implemented the 3-parameter reaction-diffusion model which has been extensively studied and a “no growth” model to reflect how much the tumor grows. When models 1, 5, and 6 were used to predict future tumor growth, they resulted in low global level errors (less than 10.3%) and low local level errors (less than 9.4%). Similarly, blood volume predictions resulted in low voxel level error (less than 9.3%) at all prediction time points. In addition to these three modeling scenarios, we investigated the predictive strength of local (i.e., voxel-specific) versus global parameters. We observed that while incorporating local parameters reduced residual error in the calibration stage, it did not significantly improve tumor growth predictions (Figure 4). These results demonstrate the potential strength of using subject-specific measures from DW-MRI and DCE-MRI to initialize and calibrate predictive biophysical models of tumor and vascular growth.

The recruitment of new vasculature via angiogenesis is vital to sustain tumor growth, and the spatial-temporal evolution of the vasculature volume directly effects the spatial heterogeneity of growth patterns of the tumor. Developing mathematical models that can predict this process for individual subjects could facilitate the development of optimized treatment regimens. Angiogenesis has been well studied and described with mathematical models, most notably in the early stages, or transition, from avascular to vascular tumors^2,9,26. Discretized models of angiogenesis⁹ often at the resolution of single vessels or single cells, can characterize the development of regions of well vascularized (and rapidly proliferating) and poorly vascularized (and necrotic) regions. One major limiting factor of personalizing (i.e., calibrating models to individual patients) existing modeling efforts is that they rely on parameters or model species that cannot be initialized or measured using non-invasive means. In this effort we focused on modeling angiogenesis at the tissue level. While failing to resolve individual vessel segments, modeling dynamics at the tissue level allows quantification of vascular volume fractions through non-invasive imaging techniques. Currently, there is a paucity of models that attempt to characterize vasculature at the tissue scale, where individual small vessels are indistinguishable from each other. One such model that describes the phenomena of angiogenesis at the tissue scale is the multi-species proliferation-invasion-hypoxia-necrosis-angiogenesis (or PIHNA) tissue-scale model by Swanson et al²⁸. Literature or estimated parameters are used to assign a majority of model parameters while patient-specific data are used estimate proliferation and diffusion parameters. Using these parameters, the PIHNA model is then simulated to provide insight into predictable patterns of disease progression (e.g., extent of hypoxia or necrosis) based off tumor growth kinetics (i.e., proliferation and diffusion coefficients).

In this effort, instead of explicitly modeling hypoxic, necrotic, and angiogenic factors, we have developed a coupling between tumor and vascular tissues that implicitly includes the dynamics of the development of tumor necrosis and the production of angiogenic factors. The motivation behind this approach is the development of a predictive mechanistic model where model parameters and model species can be initialized or calibrated via subject-specific, non-invasive measures. In particular, we investigated two different couplings of N_V to N_T. First, we assumed the local N_V would affect local tumor cell death rates. That is, in areas with high N_V, tumor cells have enough resources to continue proliferating, whereas in areas with low N_V there is increased cell death due to insufficient resources. This approach recapitulates in vivo observations of highly proliferative, highly vascularized regions and necrotic (or quiescent), poorly vascularized regions ²². While the necrotic fraction is not explicitly characterized mathematically, we hypothesize that areas of low tumor cell density and low blood volume fraction would correlate with areas of necrosis as assessed from histology. Second, we assumed that local N_V would affect the local carrying capacity with the assumption that cells share an inherent proliferation rate, k_p,T. k_p,T can be interpreted as a function of the local microenvironment’s ability to support tumor growth (i.e., nutrient rich versus nutrient poor voxels), as a function of a given cell population’s cell division rate, or a mixture of these two effects. When we spatially and temporally evolve the carrying capacity, we assume the k_p,T is a property of the cell line under investigation, while physiological variations are reflected by decreased or increased carrying capacities. We¹⁴ and others⁷ have investigated modulating the carrying capacity to reflect the changes in the number of cells that the local tissue can support implicitly, or explicitly (as in our case), as a function of local blood volume. Evolving θ_T performs a dual role of dynamically increasing or decreasing the net proliferation. While no significant differences were observed in prediction metrics (i.e., total volume or average voxel level error), we observed that models where N_V was coupled to N_T via the carrying capacity (models 5-8) were selected more frequently in the calibration and prediction phase (Supplemental Table 2). We hypothesize that while incorporating local parameters reduced model-measurement discrepancy in the calibration stage, it may have not have dramatically improved model predictions. That is, for models with local parameters, the model relies less on the coupling between N_V and N_T to temporally effect tumor or vasculature proliferation. However, for models with global parameters, there may be a stronger reliance on the coupling between species to spatially and temporally effect proliferation or death. The stronger coupling could potentially be more desirable as it will result in a spatially and temporally varying net growth rates for N_T and N_V.

In the vascular model, Eq. (5), N_T altered both the proliferation rate and death rate due to the hypothesized relationship between necrosis, pseudopalisading cells, and angiogenesis²². In this hypothesis, vascular occlusion results in the development of hypoxic and then necrotic regions. The development of hypoxia creates a wave (or pseudopalisade) of cells migrating away from these regions, secreting angiogenic factors. The secretion of angiogenic factors by the pseudpalisading cells then results in angiogenesis in at the periphery of these hypoxic regions. In our model, we assume vessel regression is likely to occur near the center of the tumor due to high cell density occluding the vessels. The vessel death results in the development of hypoxia, then necrosis, then pseudopalisading cells (which release angiogenic factors). Thus, we assume angiogenesis is more likely to occur the further the cell is from the center of the tumor. These assumptions are a simplification of a complex, multi-scale process; however, this approximation may accurately describe tissue scale dynamics for tumors that form a central necrosis. Ongoing efforts are investigating ways to improve predictions of vascular evolution for tumors with non-centralized necrosis.

There are several limitations to the current study. First, the measured values of N_T and N_V are calculated from ADC and DCE-MRI, which provide estimates at the tissue level of the cellular and vascular components of that tissue, respectively. While ADC has strong correlation to histology estimates of tumor cellularity^3,27 there are other factors such as changes in cell membrane permeability, cell size, and edema at the sub-tissue level that can affect the measured ADC; indicating that the ADC may only be a first-order approximation of cellularity. There are some studies that have identified a positive correlation between DCE-MRI estimates of blood volume fraction and histology estimates of microvessel density⁶; however, providing an accurate quantification of the blood volume fraction can be challenging due to low blood volume in tumors (and thus low signal from this component)²⁰. Additionally, DCE-MRI measures may reflect the highly perfused volume versus the true vascular volume. In this scenario, our model would be characterizing the evolution of tissue perfusion, providing a more direct connection between the blood vessel function and the number of cells it can support.

A second limitation of the current study is that the C6 glioma line may not recapitulate all aspects of human glioblastoma or angiogenesis; thus, future efforts should investigate using (for example) patient derived xenografts or non-immunogenic models to provide a more accurate representation of human glioblastoma.

Third, we acknowledge that our approach may not be tenable in a data limited setting such as current standard-of-care studies. However, the selected imaging techniques (DW-MRI and DCE-MRI) are readily used in clinical cancer trials to assess response to therapies, and our approach may be reasonable in such a studies which do require repeat imaging²⁹.

Fourth, we acknowledge that tissue properties may change in the proximity of the tumor; however, that is beyond the scope of this current contribution and is indeed an important area of investigation. In particular, imaging approaches, such as elastograpghy¹⁶ could be used to provide serial estimates of tissue properties (shear modulus, stiffness) in future studies.

Fifth, we acknowledge that the relationship between tumor associated vasculature and carrying capacity may not be linear as indicated by Eq. (6). There are potential prediction scenariors where this linear assumption will fail and result in the over- or underestimation of the true effect of vasculature on tumor cell carrying capacity. Additionally, other factors my effect the tumor cell carrying capacity (e.g., occupation by healthy cells or immune cells, cells ability to survive in low nutrient environments); however, we designed this relationship based on the correlation observed in imaging (i.e., cellularity generally trends with vascularity, see supplemental Figure 7). Other coupling options should be considered in future work, such as exponential or time delayed effects. However, without additional biological information we opted for the simplest relation.

In summary, we have developed a novel, coupled model of tumor growth and angiogenesis that can be personalized via non-invasive imaging techniques. Notably, we developed a novel means to incorporate vasculature and cellular information, which can be acquired non-invasively on an individual basis, into biophysical models of tumor and blood volume growth. We then validated this model in a murine model of glioma growth, demonstrating low global and local level errors in tumor growth predictions as well as low local level errors in the prediction of blood volume. Through this coupling, local tumor growth rates and local carrying capacities can be altered spatially and temporally resulting in the prediction of heterogenous distributions of tumor cells and blood volume. By incorporating tumor blood volume, this modeling approach may facilitate the development of predictive, personalized, models of drug delivery or the response to radiation therapy due to dynamics of tissue oxygenation. Indeed, future work will seek to include the effects of systemic (e.g., anticancer or anti-angiogenesis therapies) and radiation therapy on tumor cells and vasculature.