Emergence of three-dimensional order and structure in growing biofilms

Abstract

Surface-attached bacterial biofilms are self-replicating active liquid crystals and the dominant form of bacterial life on earth (1–4). In conventional liquid crystals and solid-state materials, the interaction potentials between the molecules that comprise the system determine the material properties. However, for growth-active biofilms it is unclear whether potential-based descriptions can account for the experimentally observed morphologies, and which potentials would be relevant. Here, we overcame previous limitations of single-cell imaging techniques (5,6) to reconstruct and track all individual cells inside growing three-dimensional (3D) biofilms with up to 10,000 individuals. Based on these data, we identify, constrain, and provide a microscopic basis for an effective cell-cell interaction potential, which captures and predicts the growth dynamics, emergent architecture, and local liquid crystalline order of Vibrio cholerae biofilms. Furthermore, we show how external fluid flows control the microscopic structure and 3D morphology of biofilms. Our analysis implies that local cellular order and global biofilm architecture in these active bacterial communities can arise from mechanical cell-cell interactions, which cells can modulate by regulating the production of particular matrix components. These results establish an experimentally validated foundation for improved continuum theories of active matter and thereby contribute to solving the important problem of controlling biofilm growth.

V. cholerae cells can swim through liquids as isolated individuals, but are more commonly attached to surfaces where they grow into clonal colonies termed biofilms, with reproducible spatial organization, global morphology, and cellular arrangements (7,8). Biofilm architectures often display striking local nematic order analogous to molecular ordering in abiotic liquid crystals, yet biofilms differ fundamentally in that they are active systems, driven by cell growth and metabolism (1–4). As these active nematic systems operate far from thermodynamic equilibrium (9), there are no relevant fundamental conservation laws known that could be used to characterize the biofilm developmental dynamics. To achieve a detailed qualitative and quantitative understanding of such biologically-ubiquitous yet physically-exotic bacterial communities, we developed new experimental imaging and image analysis techniques for obtaining high spatiotemporal-resolution data of the biofilm developmental process up to 10⁴ cells, representing mid-sized biofilm microcolonies that have already established the architectural state of macroscopic V. cholerae biofilms5. By using automated confocal microscopy, with an adaptive live-feedback between image acquisition, feature recognition, and microscope control, followed by a ground-truth-calibrated, novel 3D-image-segmentation technique (see Methods, Supplementary Information) we were able to observe complete 3D biofilm development at cellular resolution with minimal phototoxicity (Fig. 1a,b), and minimal segmentation error (Supplementary Information). The high temporal resolution (Δt = 5–10 min) allows for cell lineage reconstruction, measurements of local growth rates, and the identification of all cells in a field of view which are not related to the original biofilm founder cell (Fig. 1b,d, Supplementary Movie 1).

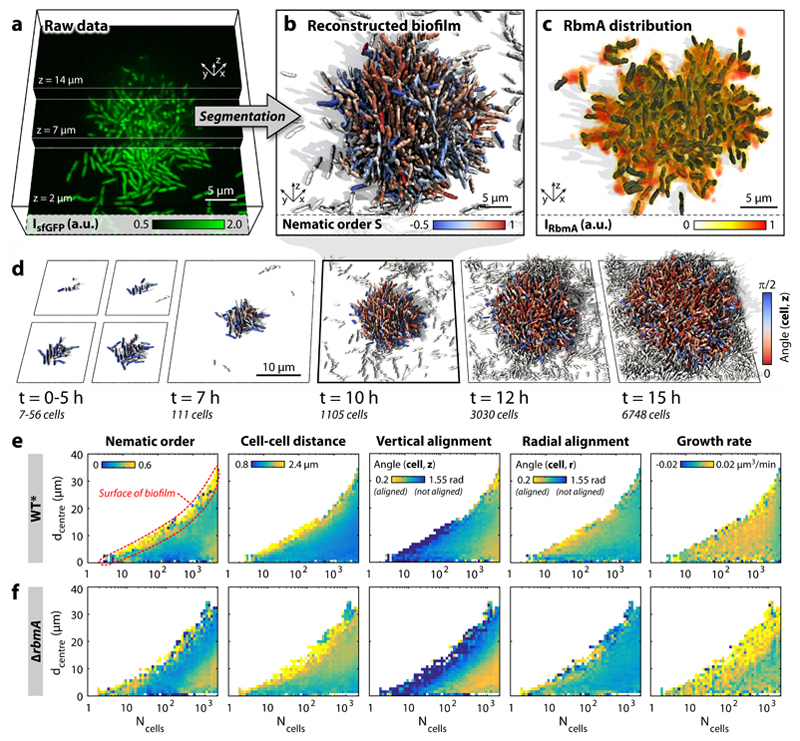
Figure 1. Dynamics of V. cholerae biofilm formation.

a, Cells constitutively expressing a green fluorescent protein (sfGFP) were imaged with spinning disc confocal microscopy. Images at three different z-planes are highlighted. b, 3D reconstruction of the biofilm shown in panel a, where each cell is coloured according to the nematic order parameter $\mathit{\text{S}}=<\mathbf{3}/\mathbf{2}{({\widehat{\mathit{\text{n}}}}_{\mathit{\text{i}}}·{\widehat{\mathit{\text{n}}}}_{\mathit{\text{j}}})}^{\mathbf{2}}-\mathbf{1}/\mathbf{2}>$ in its vicinity. High time resolution (Δt = 5–10 min) imaging allowed us to track cell lineages and discriminate cells (white) which are not direct descendants of the biofilm founder cell. c, The extracellular matrix protein RbmA mediates cell-cell adhesion and is distributed throughout the biofilm, as visualized by immunofluorescence. d, Time-resolved WT* biofilm growth series. Each cell is coloured according to the cellular alignment with the z-axis (for the ΔrbmA mutant see Supplementary Fig. 6). e-f, Heatmaps showing spatially resolved single-cell measurements of different biofilm structural properties inside WT* (e) and ΔrbmA (f) biofilms, which are used to characterize biofilm formation (n > 3 biofilms, standard deviations are shown in Supplementary Figs. 5 and 7 and the differences among both strains are highlighted in Supplementary Fig. 8), as a function of the distance to the biofilm centre (d_centre) and the number of cells inside the biofilm (N_cells).

When investigating whether the non-equilibrium dynamics of biofilm development and the emergence of local order can be captured quantitatively through effective cell-cell interaction potentials, it is important to account for the essential biophysical processes: cell growth, cell division, cell-surface interactions, and cell-cell interactions (4,10–17). Whereas growth and division are driven by nutrient availability and metabolism, cell-surface and cell-cell attraction are typically mediated by secreted or membrane-associated polysaccharides and proteins (10,18). For V. cholerae biofilms, the molecular basis for cell-cell interactions has been intensively investigated: cells are embedded in a self-secreted extracellular matrix, comprised of the Vibrio polysaccharide (VPS), extracellular DNA, and proteins (19–21). The osmotic pressure resulting from a high concentration of matrix components in the intercellular space, as well as steric cell-cell interactions, are both expected to contribute to cell-cell repulsion. Cell-cell attraction is primarily mediated by the protein RbmA, which localizes throughout the biofilm (Fig. 1c) (20,21), links cells to each other (21–23), and whose expression levels are inversely related to cell-cell spacing (Fig. 2a). VPS also weakly binds cells together, yet elevated levels of VPS production do not cause stronger cell-cell attraction or a decreased cell-cell spacing (Supplementary Figure 11). Based on these cell-cell interaction processes, we hypothesized that biofilm architectures are primarily determined by the relative strength of effective mechanical cell-cell attraction and repulsion forces.

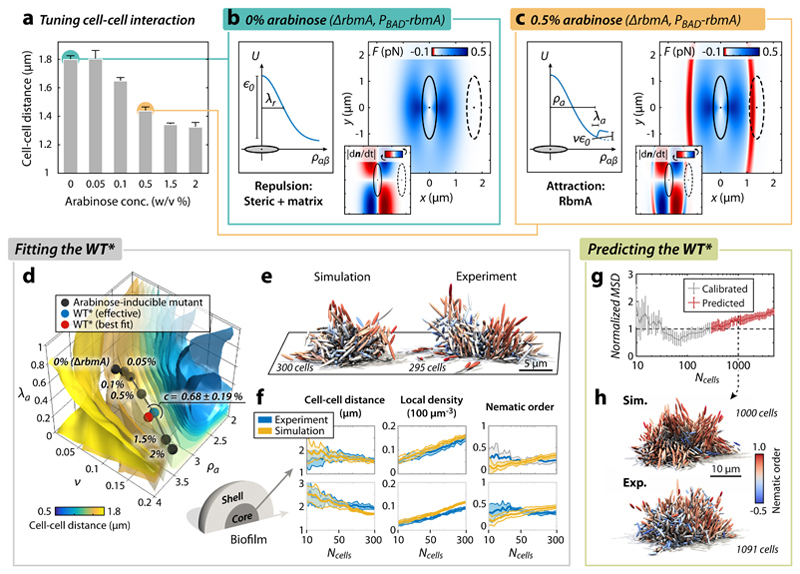
Figure 2. Biofilm architecture development is captured by an effective mechanical cell-cell interaction potential.

a, Increased RbmA production (achieved by increasing arabinose concentration, see Methods) decreases the average cell-cell distance in biofilms. Without arabinose, no RbmA is produced and the biofilm architecture is identical to the ΔrbmA mutant (n > 3 biofilms). b, Cell-cell interaction inside ΔrbmA mutant biofilms lacking cell-cell adhesion, modelled by the repulsive interaction potential (left) and the resulting cell-cell interaction forces (right) for the best-fit potential and the most prominent cellular orientation (red: attractive, blue: repulsive). Inset: rotational interaction dynamics (red: clockwise rotation, blue: counter-clockwise rotation). For more details and additional orientations see Supplementary Figs. 18 and 19. The dashed cell is plotted at the average cell-cell distance obtained from the corresponding experiment in panel a. c, The cell-cell interaction potential (left) and force (right) resulting from the best-fit potential for biofilms with a particular level of cell-cell adhesion (0.5% arabinose). RbmA-mediated cell-cell adhesion gives rise to an attractive part (red), acting within the range of the experimentally determined average cell-cell distance (dashed cell). d, Best-fit simulation parameters for varying RbmA and arabinose concentrations (black dots) follow a line in (v, λ_a, λ_a, ρ_a)-parameter space and cross isosurfaces of average cell-cell distance (see colour bar, and compare with panel a; for more details about the fitting see Supplementary Fig. 23). The RbmA level of the WT* biofilms is inferred in terms of an effective arabinose concentration by locating the WT* along the line of different arabinose concentrations (blue point), which is very close to the best fit of the WT* (red point). e, Simulated (best fit) vs. experimental WT* biofilm. f, Comparison of biofilm architectural properties for the WT* experiment (blue) and the WT* simulation prediction (yellow). The architectural properties are spatially resolved for the core (left) and shell (right) of the biofilm (experiment: n = 7; simulation: n = 10). g,h, Simulation predictions of large (N_cells = 1000) WT* biofilms (based on the WT*-interaction potential calibrated with N_cells < 300) show quantitative (g) and qualitative (h) agreement with experiments (experiment: n = 4; simulation: n = 10). All error bars correspond to standard errors.

To determine the impact of cell-cell attraction, we quantitatively compared the 3D biofilm architecture dynamics of a rugose wild type strain with straight cell shape (WT*) with that of a mutant strain (ΔrbmA) with significantly weakened intercellular adhesion (see Methods). Biofilms grown in a low-shear environment approximately display hemispherical symmetry (Fig. 1d), which allows us to characterize the biofilm architectures (Fig. 1e) as a function of the distance to the biofilm centre in the basal plane, d_centre, using the cell number in the biofilm, N_cells, as a quantification of the developmental state. Our measurements reveal strong structural differences between the outer biofilm layer and its central part as well as several distinct architectural phases of the biofilm during growth (Fig. 1e,f). Interestingly, the cellular growth rate remains homogeneous in space during WT* biofilm development in our conditions and for our biofilm sizes (Fig. 1e, Supplementary Fig. 5), contrary to theories assuming steep nutrient gradients inside biofilms (8,10). The nematic order, cell-cell spacing, and cellular orientations with respect to the vertical (z) and radial (r) directions differ significantly between WT* and ΔrbmA mutants (Fig. 1e–f, see Supplementary Fig. 5–8), revealing the strong effect of cell-cell adhesion on biofilm architecture dynamics.

Based on the high-resolution spatiotemporal data of biofilm development of different bacterial strains, we investigated the hypothesis that the biofilm internal structure and external shape originate from mechanical interactions between cells. Focusing on a minimal model, we describe the effective mechanical interactions in terms of an effective potential that depends on the distance r_αβ between neighbouring cells α and β, and their orientations ${\widehat{\mathit{\text{n}}}}_{\alpha }$ and ${\widehat{\mathit{\text{n}}}}_{\beta }.$ We made the simplifying assumption that the potential is independent of the biofilm developmental state or nutrient levels. As shown below, this simplification suffices to capture the main features of the small to medium-sized biofilms studied here but is expected to become inaccurate at the later stages of biofilm development, when spatio-temporal heterogeneities become relevant. Given the molecular components of the cell-cell interaction and their qualitative effects on attraction and repulsion outlined above, we assume the potential

$$U={ϵ}_0{ϵ}_1\left(e^{-\frac{{\rho }^2}{{\lambda }_r^2}}+\frac{v}{1+e^{\left(\frac{{\rho }_a-\rho }{{\lambda }_a}\right)}}\right),$$ (1)

where ρ = r_αβ/σ is the shape-normalized cell-cell distance. The range parameter $\sigma ({\widehat{\mathit{\text{r}}}}_{\alpha \beta },{\widehat{\mathit{\text{n}}}}_{\alpha },{\widehat{\mathit{\text{n}}}}_{\beta })$ depends on the instantaneous cell lengths, the orientation of the cells relative to each other, and the individual cell orientations, and it maps the potential onto non-identical ellipsoidal cells (see Supplementary Information, Eq. 20). The amplitude is set by the repulsion strength ϵ₀ and instantaneous cell lengths and cell orientations through the strength parameter ${ϵ}_1({\widehat{\mathit{\text{n}}}}_{\alpha }·{\widehat{\mathit{\text{n}}}}_{\beta })$ (Supplementary Information, Eq. 19). The first term of the interaction potential describes the combined effects of hard steric and osmotic repulsion with range λ_r (Fig. 2b). The second term corresponds to cell-cell attraction and adds an attractive well of relative depth v, width λ_a, and position ρ_a (Fig. 2c). Each contribution and parameter in the potential U thus has a well-defined physical meaning (see schematic diagram in Supplementary Figure 15, Supplementary Table 3). We assume here that the interaction parameters are taken to be constant for a given bacterial strain, a simplification that could be relaxed in future models. With these simplifying assumptions, initial estimates of the potential parameters prior to systematic scans can be obtained from basic physical considerations (see Methods).

This potential was then implemented in a particle-based model of biofilm development, in which individual cells were modelled as growing and dividing ellipsoids without self-propulsion (see Supplementary Information) whose interactions are described by U. Bypassing previous limitations of individual-based biofilm models(24,25), all parameters of our model (cell aspect ratio, division time distribution; Supplementary Table 3) were determined from single-cell properties of experimental biofilms, and the dynamics were solved with a massively parallel computation approach using graphics processing units for evaluating all pair-wise interactions (Supplementary Information). To obtain the key potential parameters ϵ₀, λ_r, v, λ_a and ρ_a for V. cholerae biofilms, we assumed that the attractive term in U can be attributed primarily to RbmA levels, with the VPS acting as a Woods-Saxon background potential (Methods) akin to the mean-field potential in nucleon models. This assumption is motivated by the experimental findings that increased VPS levels do not increase the cell-cell attraction (Supplementary Figure 11), yet biofilms that lack RbmA display a small residual mechanical cohesion (Fig. 3e), indicating that VPS does contribute weakly to cell-cell binding. To first obtain the parameters ϵ₀ and λ_r, we fitted the repulsive part of the potential U by comparing experimental ΔrbmA biofilms, which lack the attractive potential term (v = 0), with simulated biofilms, using the mean squared difference (MSD) of a feature vector as a metric. The feature vector contains 14 different architectural properties and their temporal variation up to 300 cells (see Supplementary Fig. 14), allowing a comprehensive comparison of biofilm architecture and development between simulations and experiment at the same time. Note that even at small sizes, the V. cholerae biofilms used in this study produce RbmA and VPS (Supplementary Fig. 10). For ΔrbmA biofilms we found a broad minimum in the (ϵ₀,λ_r)-space as shown in the MSD heatmap (Supplementary Fig. 16), resulting in best-fit simulations that show high similarity to experiments (Supplementary Fig. 17). The effective translational and rotational interaction forces acting on two neighbouring ΔrbmA cells for the best fit potential are illustrated in Fig. 2b for different cellular orientations. The interaction range for two aligned cells is very close to the experimentally observed average cell-cell spacing of the ΔrbmA mutant (dashed cell).

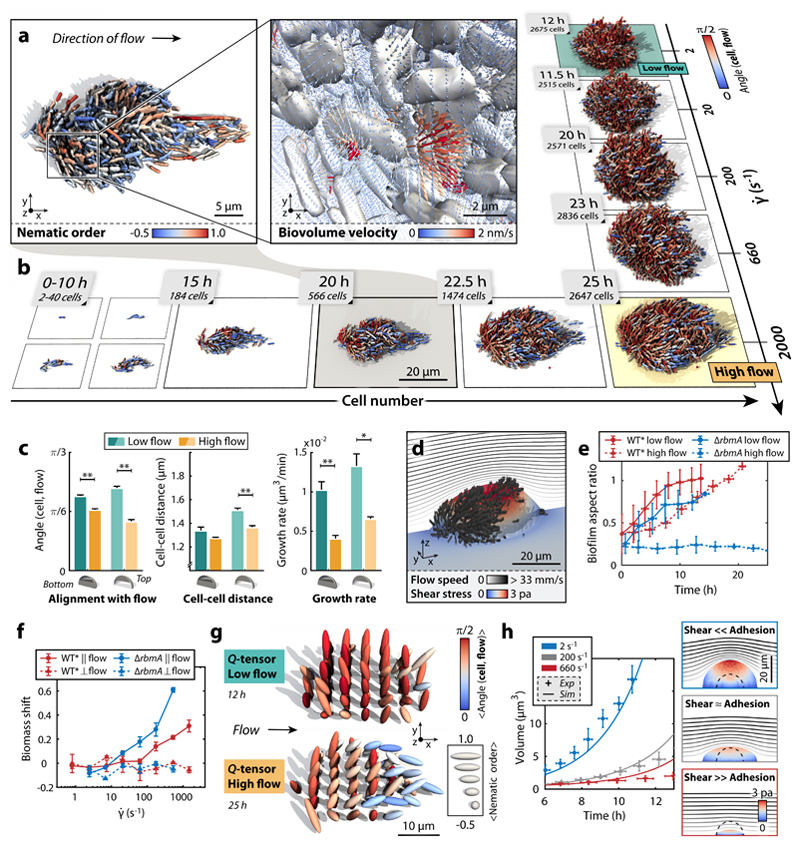
Figure 3. Biofilm architecture is shaped by external shear flow.

a, WT* biofilms grown under strong shear $(\dot{\gamma }=2000{\text{s}}^{\text{-}1})$ display droplet-like shapes. Inset: Biovolume flux field inside the biofilm (see Supplementary Information). b, WT* biofilms in high shear $(\dot{\gamma }=2000{\text{s}}^{\text{-}1})$ display strong alignment with flow throughout growth, yet biofilms grown in flow with low shear $(\dot{\gamma }=2-200{\text{s}}^{\text{-}1})$ do not show strong architectural modifications. c, Quantification of the effect of shear on biofilm architecture: measurements of cellular alignment with flow, cell-cell distance, and cell growth rate at the bottom and top of biofilms with sizes of N_cells ~800 cells show that WT* biofilms in high shear are smaller, more compact, and display stronger flow-alignment. Statistical significance: * is p < 0.05 and ** is p < 0.01 (t-test); error bars are standard error (n = 4 biofilms, error bars: standard errors). d, Simulated shear stress distribution for a WT* biofilm, demonstrating that the region of highest shear is at the top of the biofilm. The streamlines indicate the profile of the external flow. e, Biofilm aspect ratio (height/width) increases in time for WT* (red) biofilms, but decreases for ΔrbmA mutant biofilms (blue) in high flow owing to shear-induced erosion (n = 4, error bars: standard deviations). f, Biomass shift is defined as the fraction of the average total biomass flux through planes parallel (‖) or perpendicular (⊥) to flow (see Supplementary Fig. 2 for details). Positive biomass shift along the flow direction at higher shear rates indicates anisotropic biofilm expansion towards the downstream direction of the external flow. Zero biomass shift perpendicular to the flow indicates no directional bias (n ≥ 3, error bars: standard errors). g, The tensorial nematic order parameter (Q-tensor, see Supplementary Information) and cellular alignment with the flow direction were measured at equally spaced points inside biofilms at low and high shear rates, indicating the regions in which cells are predominantly aligned with the flow and each other. h, Biofilm volumetric growth for ΔrbmA mutant biofilms is captured by a continuum model (see Supplementary Information) with varying ratios of shear-induced erosion and cell-cell adhesion (experiment: n = 4, error bars: standard deviations).

Because the attraction parameters (v, λ_a, ρ_a) in the potential U depend on the concentration of RbmA, we genetically modified V. cholerae such that we can tune the production of RbmA (and therefore tune the strength of the attraction), by adding different concentrations of a compound that induces the rbmA-expression construct homogeneously inside the biofilm: arabinose (see Methods, Supplementary Fig. 13). Experimentally, we observed that increasing arabinose concentrations resulted in a decreased cell-cell spacing (Fig. 2a), consistent with the assumption that RbmA mediates cell-cell attraction. By fixing the repulsive component (ϵ₀,λ_r) based on the ΔrbmA biofilms, we then fitted the attractive potential component (v, λ_a, ρ_a) for a range of different arabinose concentrations (Fig. 2c,d). The MSD isosurfaces in (v, λ_a, ρ_a)-space and corresponding 3D renderings for simulated and experimental biofilms grown at 0.5% (w/v) of arabinose reveal tight fits (Supplementary Fig. 21-23), and the resulting best-fit interaction force displays an attractive region (red) at the average experimental cell-cell distance (Fig. 2c).

With the calibrated simulation, we then inferred an effective arabinose concentration for the WT* of c = 0.68 ± 0.19% (w/v), by locating the WT* biofilm architecture in the (v, λ_a, ρ_a)-space along the curve of different arabinose concentrations (Fig. 2d). Extracting an effective arabinose concentration and RbmA level for the WT* is based on the simplifying assumption that all cells in the biofilm express the same levels of the key matrix components, which represents a minimal model that is in quantitative agreement with the experimental data, as the best-fit (v, λ_a, ρ_a)-values for the WT* are close to the effective (v, λ_a, ρ_a)-values for WT* on the curve of different arabinose concentrations (Fig. 2d). The simulations based on the WT* parameters for biofilms up to 300 cells show good quantitative agreement with experiments (Fig. 2f). Remarkably, these simulations also show architectural properties that were not included in the feature vector used for MSD-minimization, such as local density variations and the occurrence of patches of highly aligned cells inside the biofilm (red cells in Fig. 2e, characterized by high local ordering), which are characteristic for biofilms with high concentrations of RbmA. Predictions of the architectural development for larger biofilms (N_cells > 300) show high quantitative and qualitative agreement with experimental data, for both the WT* (Fig. 2g,h, Supplementary Movie 5) and ΔrbmA (Supplementary Fig. 24b, Supplementary Movie 5) biofilms up to 10³ cells. To achieve accurate simulation results for very large biofilms (>10³ cells), spatiotemporal heterogeneity in gene expression, matrix composition, and growth rates likely have to be included in future simulations. Our combined experimental and theoretical analysis therefore suggests that mechanical interactions between cells suffice to account for the internal cellular order and architecture up to mid-sized V. cholerae biofilms.

To determine how external fields can affect orientational order and morphology of 3D biofilms, we perturbed biofilm growth by applying external flow fields of varying strength, corresponding to shear rates of $\dot{\gamma }=2-2000{\text{s}}^{\text{-}1},$ typically encountered by bacteria in natural and man-made environments (26). At high shear rates (> 600 s^-1, corresponding to average flow speeds >10 mm/s through the growth chamber), the WT* cells formed smaller, more compact biofilm colonies with droplet-like shapes, compared with low shear environments (Fig. 3a,b, Supplementary Movie 1, 3). To understand the mechanisms underlying these architectural changes, we investigated both local and global effects of increased shear on biofilms, and changes in matrix production. Exposure to higher shear resulted in a significantly decreased cell-cell spacing and lower growth rate in WT* biofilms (Fig. 3c), but the height-to-width aspect ratio was unaffected when comparing biofilms with similar N_cells (Fig. 3e) despite the increased levels of shear stress applied to the top (Fig. 3d). We therefore hypothesized that cells in WT* biofilms at higher shear secrete increased levels of RbmA, allowing increased cell-cell attraction forces to balance shear forces, but leading to a strong reduction in overall growth rate owing to the metabolic cost of increased RbmA production. Using a fluorescent transcriptional reporter for rbmA expression, we confirmed that high shear increases RbmA levels (Supplementary Fig. 12), indicating that cells actively modulate the mechanical cell-cell interactions via gene expression.

To explain the observed droplet-like shapes of biofilms grown at high shear rate, we investigated cellular alignment with flow and analysed biovolume flux inside the biofilm using the optical flow method (Fig. 3a,f, see Supplementary Information). We determined that cell alignment with flow increases with increasing shear rate (Fig. 3c,g) and an anisotropic “biomass shift” downstream occurs at $\dot{\gamma }=60{\text{s}}^{\text{-}1}$ (Fig. 3f), indicating that the observed biofilm shapes were caused by anisotropic expansion of cells aligned with the flow as a result of growth and viscoelastic deformation. Our above measurements regarding increased RbmA levels in WT* biofilms at high shear predict that if RbmA levels are in fact primarily responsible for cell-cell attraction, then most effects of shear on ΔrbmA-mutant biofilms should be explained by shear-induced cell erosion. Indeed, these biofilms showed a reduction in upward growth with higher flow (Fig. 3e), indicating that shear forces are larger than cell-cell attraction forces. This was confirmed by simulations of shear-dependent erosion using a continuum model (see Supplementary Information), which captured the decreased volumetric growth of ΔrbmA-mutant biofilms owing to cell erosion (Fig. 3h, Supplementary Movie 4). Fluid flow therefore strongly affects biofilm architectural development through the effect of shear on growth rate, matrix composition, alignment with flow, biomass shift, and shear-induced erosion (27). These results demonstrate that mechanical interactions at the cellular scale remain important in sculpting biofilm architecture when an external field is applied.

In conclusion, our combined experimental and theoretical analysis shows that the emergence of local nematic order in growing V. cholerae biofilms can be captured by an experimentally constrained minimal effective cell-cell interaction potential that translates molecular mechanisms into force parameters. Given the immense complexity of molecular interactions, metabolism, and signalling that occurs between the cells, the availability of an experimentally validated potential-based description of biofilm development presents a significant conceptual advance that can provide a microscopic basis for constructing predictive macroscopic continuum theories, by building on coarse-graining techniques recently developed for other classes of active matter (9,28). At the same time, a refined model will be needed to account for spatial heterogeneities and time-dependencies that likely become relevant at the later stages of biofilm development. Such progress is essential for identifying new strategies towards understanding, controlling and inhibiting biofilm growth under realistic physiological conditions, which remains one of the foremost challenges in biomedical (18,29,30) and biophysical research (5,10,31).

Methods

Media and cloning approaches

All strains were grown in LB medium supplemented with appropriate antibiotics at 37°C for normal growth and during cloning. Biofilm experiments with V. cholerae were performed in M9 minimal medium, supplemented with 2 mM MgSO₄, 100 mM CaCl₂, MEM vitamins, 0.5% glucose, and 15 mM triethanolamine (pH 7.1). Standard molecular biology techniques were applied to construct plasmids and strains (32). Restriction enzymes and DNA polymerase enzymes were purchased from New England Biolabs. Oligonucleotides were commercially synthesized by Eurofins. All V. cholerae strains used in this study are derivatives of the rugose variant of the wild type V. cholerae O1 biovar El Tor strain N16961 (termed strain KDV148). V. cholerae deletion mutations were engineered using the pKAS32 suicide vector harbored in E. coli S17-1 λpir (33). Complementation constructs were inserted at the lacZ site with the help of the suicide plasmid pKAS32. The plasmid pNUT542, containing the gene coding for the super-folder green fluorescent protein (sfgfp) expressed under the control of the P_tac promoter, was conjugated into all V. cholerae strains except for the complementation strain KDV1082 (29). Plasmid clones were first constructed in the E. coli strain Top10 and then mated into V. cholerae with the help of an additional E. coli strain harbouring the conjugation plasmid pRK600. Arabinose was used as inducer to control the expression of rbmA from the arabinose-regulated promoter P_BAD. Details of the strains, plasmids, and oligonucleotides are listed in the Supplementary Information.

Strain Construction

The rugose variant of the V. cholerae N16961 (strain KDV148) displays strong surface attachment and biofilm formation as a consequence of high c-di-GMP production (34). V. cholerae cells are usually characterized by a slightly curved cell shape. To allow V. cholerae cells to be modelled by ellipsoids in theory and simulations, we generated a mutant with a straight cell shape (i.e. the common bacterial rod shape), by deleting the gene ΔcrvA according to the method of Bartlett et al. (35). In detail, the 1 kb flanking regions of gene crvA (VCA1075) were amplified with the oligonucleotides kdo1182/kdo1183 and kdo1183/kdo1184, and the fused polymerase chain reaction (PCR) product was amplified using kdo1182/kdo1185. The final PCR product was ligated into plasmid pNUT144 (a derivative of pKAS32). The resulting plasmid pNUT961 was conjugated into strain KDV148, to generate the ΔcrvA deletion mutant, following the selection protocol described earlier by Skorupski et al. (33). Finally, cells containing the correct mutation were screened by PCR. Plasmid pNUT542 was conjugated into KDV611 strain to construct strain KDV613 containing the ΔcrvA deletion (referred to as WT*). The ΔrbmA deletion strain (KDV698) was constructed by conjugating plasmid pNUT336 into strain KDV611. The mutant screening was performed by PCR (36).

Tuning cell-cell interaction by inducing rbmA expression

To control the timing and rate of RbmA production, an inducible strain (KDV1082) was generated by conjugating plasmid pNUT1519 into the ΔrbmA strain KDV698. Plasmid pNUT1519 was created by cloning a P_tac-sfgfp construct into plasmid pNUT1268. Plasmid pNUT1268 is a derivative of plasmid pNUT542 in which P_tac-sfgfp was replaced with a construct of P_BAD-rbmA. P_BAD, an arabinose inducible promoter, and the rbmA gene were joined by PCR amplification with oligonucleotides kdo1435/kdo1436.

Visualization of secreted RbmA

To visualize RbmA during biofilm growth, the wild type copy of rbmA was exchanged by a FLAG-tagged rbmA (16) (with the octapeptide DYKDDDDK) by mating the plasmid pNUT462 into the strain KDV148, resulting in V. cholerae strain KDV829. Successful FLAG-tagging of RbmA was confirmed by PCR and sequencing. The final strain KDV835 was generated by conjugating the fluorescence protein expression plasmid pNUT542 into strain KDV829. For RbmA visualization in flow chambers, biofilms were grown in M9 medium containing 1 μg/mL of FLAG tag monoclonal antibody (L5) conjugated to AlexaFluor 555 (Thermo Scientific) and 1 mg/mL of filter-sterilized bovine serum albumin (BSA).

Measuring rbmA expression

To measure RbmA production during biofilm growth, the gene mRuby3 was transcriptionally fused to rbmA on the chromosome, by introducing plasmid pNUT1401 into the strain KDV611. The transcriptional fusion of rbmA-mRuby3 in the resulting strain (KDV1026) was confirmed by PCR and sequencing. The final strain KDV1027 was generated by mating the plasmid pNUT542 into strain KDV1026.

Flow chamber biofilm experiments

V. cholerae biofilms were grown in microfluidic flow chambers as described by Drescher et al.(5) (chamber dimensions: [width, height, length] = [500, 100, 7000] μm). Flow chambers were constructed from poly(dimethylsiloxane) (PDMS) bonded to glass coverslips using an oxygen plasma. The microfluidic design contained four independent channels on each coverslip. The manufacturing process of these microfluidic channels guarantees highly reproducible channel dimensions and surface properties. Each channel was inoculated with a culture of a particular V. cholerae strain. Cultures were grown overnight at 28° C in liquid LB medium under shaking conditions, back-diluted 1:200 in LB medium in the morning, and grown to OD₆₀₀ = 0.5 prior to channel inoculation. After inoculation of the channels, the cells were given 1 h to attach to the glass surface of the channel, before a flow of 100 μL/min M9 medium was initiated for 45 s to wash away non-adherent cells and to remove LB growth medium from the channels. The flow rate was then set to a value between 0.1 and 100 μL/min, corresponding to an average flow speed <v> between 0.03 and 33 mm/s and a shear rate $\dot{\gamma }$ between 2 and 2000 s^-1 (as indicated) until the end of the experiments. Flow rates were controlled using a high-precision syringe pump (Pico Plus, Harvard Apparatus).

Image acquisition

Single cells were reconstructed from confocal fluorescence image stacks acquired with a Yokogawa CSU confocal spinning disk unit mounted on a Nikon Ti-E inverted microscope, using an Olympus 100× silicone oil (refractive index = 1.406) objective with NA 1.35, a 488 nm and 552 nm laser (Coherent Sapphire), and an Andor iXon EMCCD camera. By using this specific objective, heavy distortions at axial positions >10 μm into the biofilm (owing to refractive index mismatch of biofilms and standard immersion oil) are reduced. The physical resolution was 63.2 nm/pixel in the xy-plane and was set to 400 nm along axial direction. Images were acquired every 10 min at very low excitation light intensities with 90 ms exposure time, using the “EM-gain” of the Andor iXon EMCCD camera. A Nikon hardware autofocus was used to correct for focus drift. The hardware was controlled using μManager (37). During acquisition a live feedback between image acquisition, image analysis, and microscope control was used to automatically detect the biofilm height to avoid imaging of empty space below and on top of the biofilm, to eliminate tracking of XY coordinates of non-biofilm forming cells, and to control temporal resolution (to reduce photobleaching and phototoxicity).

Image processing

Detailed descriptions of image processing, segmentation, segmentation validation, cell tracking, biomass shift, optical flow, 3D visualization, quantitative biofilm features that are measured, and the calculation of space-time heatmaps are provided in the Supplementary Information.

Individual cell particle-based model

Model description and implementation

The cells are modelled as interacting ellipsoids of half-length ℓ and half-width r, described by their centre position x and orientation $\widehat{\mathit{\text{n}}}.$ As cells operate at low Reynolds number (Re ≈ 10⁻⁴), we approximate the dynamics as over-damped, ignoring inertial effects. Cells can interact with the wall boundary and other cells through interaction potential functions, U_bdy and U (Eq. 1). Denoting the identity matrix by I, the over-damped translational and orientational dynamics of a single cell are described by

$$\frac{d\mathit{\text{x}}}{dt}={\mathit{\Gamma }}^{-1}\left[-\frac{\partial U_{bdy}}{\partial \mathit{\text{x}}}-\frac{\partial V}{\partial \mathit{\text{x}}}\right]$$ (2)

$$\frac{d\widehat{\mathit{\text{n}}}}{dt}=(\mathit{\text{I}}-\widehat{\mathit{\text{n}}}{\widehat{\mathit{\text{n}}}}^T)\left[{\mathit{\Omega }}^{-1}\left(-\frac{\partial U_{bdy}}{\partial \widehat{\mathit{\text{n}}}}-\frac{\partial V}{\partial \widehat{\mathit{\text{n}}}}\right)\right]$$ (3)

where Γ and Ω are friction tensors and is the total interaction potential with all other cells as described in the Supplementary Information. The steric interaction between a cell and the wall boundary is modelled with a repulsive interaction potential that is proportional to the overlap between a cell and the wall boundary. The instantaneous cell-length growth rate for a single cell is defined as

$$\frac{d\ell }{dt}=\frac{\ell }{{\tau }_g}\text{ln}(2)$$ (4)

where ℓ is the half-length of the cell at time t and τ_g is the growth time constant. The cell width is constant throughout the simulation. For further details of the particle-based model, see the Supplementary Information.

Simulation implementation

A custom highly parallelized individual cell-based code employing graphics processing units (GPUs) was developed to perform the simulations. At each time step, we calculate cell-cell interactions using the all-pairs approach (38) such that all pair-wise interactions are evaluated. We use a standard explicit Euler scheme to numerically integrate the translational and orientational dynamics, Eq. (2) and (3), as described in the Supplementary Information.

Parameter estimation

Initial order-of-magnitude estimates for systematic scans of the parameters in the potential U were obtained from basic physical considerations (see also Supplementary Information), before systematic scans of the parameters were computed. The energy scale ϵ₀ ~ 0.05 - 5 pN·μm of the cell-cell interactions was assumed to be within a few orders of magnitude of the energy scale of cell-flow interactions, which were calculated via Stokes drag on a typical cell near the edge of the biofilm at low flow rate (0.1 μL/min). The repulsive length scale λ_r ~ 1 (corresponding to approximately 1 μm for typically aligned cells) was estimated via the average cell-cell distance in the core of biofilms, where cell-cell repulsion dominates. The attraction shift ρ_a ~ 1 was estimated via the average cell-cell distance at the edge of biofilms, where attraction dominates. The attraction width λ_a ~ 0.1 was determined by considering the standard deviation of experimental cell-cell distances at the edge of biofilms.

Background potential

Cell-cell adhesion mediated by the VPS matrix component was modeled by a mean-field background Woods-Saxon potential (39), and was assumed to provide the weak cell-cell binding that prevents the disintegration of biofilms owing to fluid shear acting on ΔrbmA mutant biofilms (which lack the major cell-cell attraction, mediated by RbmA). The mean-field VPS-mediated binding strength was estimated to be approximately equal to the Stokes drag felt by a cell at the edge of the biofilm at low flow rate (0.1 μL/min), because significant numbers of cells in the ΔrbmA background were sheared off at higher flow rate (100 μL/min). However, WT* biofilms were found to be robust to this increased fluid shear, suggesting that the increased expression of rbmA at higher flow rate (Supplementary Information) increases the RbmA-mediated cell-cell attraction strength by approximately two orders of magnitude above the value predicted at low flow rate. In simulations performed at zero shear, the VPS contribution to cell-cell attraction can neglected as the Woods-Saxon potential is approximately constant in the bulk.

Comparing simulations with experimental data

The dynamic biofilm architecture was summarized in a feature vector representing key phenotypic and structural properties temporally. The similarity between a vector characterizing a simulation and a real biofilm was assessed in terms of the mean square distance (MSD) between them. For details, see the Supplementary Information.

Continuum model

The mathematical continuum model of growing biofilms in shear flow is described in the Supplementary Information.

Supplementary Material

Supplementary information is available in the online version of the paper. Raw imaging and analysed data is available at our online data repository: http://drescherlab.org/data/biofilm_architecture.