Abstract
A long-standing goal in neuroscience has been to bring together neuronal recordings and neural network modeling to understand brain function. Neuronal recordings can inform the development of network models, and network models can in turn provide predictions for subsequent experiments. Traditionally, neuronal recordings and network models have been related using single-neuron and pairwise spike train statistics. We review here recent studies that have begun to relate neuronal recordings and network models based on the multi-dimensional structure of neuronal population activity, as identified using dimensionality reduction. This approach has been used to study working memory, decision making, motor control, and more. Dimensionality reduction has provided common ground for incisive comparisons and tight interplay between neuronal recordings and network models.
Introduction
For decades, the fields of experimental neuroscience and neural network modeling proceeded largely in parallel. Whereas experimental neuroscience focused on understanding how the activities of individual neurons relate to sensory stimuli and behavior, the modeling community sought to understand theoretically how neural networks can give rise to brain function. In recent years, developments in neuronal recording technology have enabled the simultaneous recording of hundreds of neurons or more [1]. Concurrently, increases in computational power have enabled the simulation of large neural networks [2]. Together, these developments should enable experimental data to more stringently constrain network model design and network models to better predict neuronal activity for subsequent experiments [3,4].
A key question is how to relate large-scale neuronal recordings with large-scale network models. Network models typically do not attempt to replicate the precise anatomical connectivity of the biological network from which the neurons are recorded, since the underlying anatomical connectivity is usually unknown (although technological developments are making this possible [5]). In such settings, there is not a one-to-one correspondence of each recorded neuron with a model neuron. To date, comparisons between recordings and models have primarily relied on aggregate spike train statistics based on single neurons (e.g., distribution of firing rates [6], distribution of tuning preferences [7], Fano factor [8]) and pairs of neurons (e.g., spike time [9] and spike count correlations [10,11]), as well as single-neuron activity time courses [12,13]. To go beyond single-neuron and pairwise statistics, recent studies have examined the multi-dimensional structure of neuronal population activity to uncover important insights into mechanisms underlying neuronal computation (e.g., [14–24]). This has motivated the inquiry of whether network models reproduce such population activity structure, in addition to single-neuron and pairwise statistics, raising the bar on what constitutes an agreement between a network model and neuronal recordings [3].
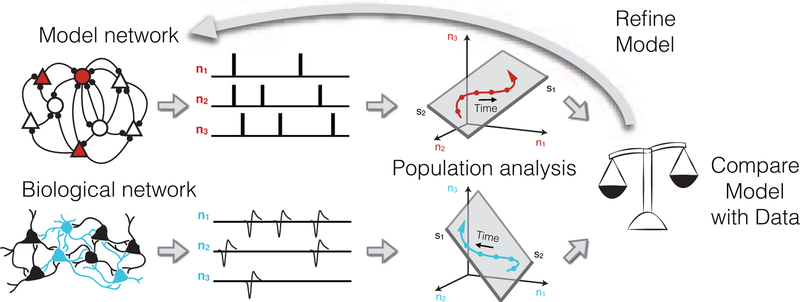
Population activity structure can be characterized using dimensionality reduction [25–27], which provides a concise summary (i.e., a low-dimensional representation) of how a population of neurons covaries and how their activities unfold over time. Several dimensionality reduction methods have been applied to neuronal population activity, including principal component analysis (e.g., [14,15,20,28,29]), demixed principal component analysis [30], factor analysis [16,19,31], Gaussian-process factor analysis [32], latent factor analysis via dynamical systems [33], tensor component analysis [34], and more (see [25] for a review). The low-dimensional representation describes a neuronal process being carried out by the larger circuit from which the neurons were recorded [32,35]. The same dimensionality reduction method can be applied to the recorded activity and to the network model activity, resulting in population activity structures that can be directly compared (Fig. 1). This benefit is also true of related methods for comparing neuronal recordings and network models involving neuronal decoding, population response similarity, and predicting the activity of one neuron from a population of other neurons [3].
Fig 1. Relating biological and model networks using population analyses:
Because a model network typically does not attempt to replicate the precise anatomical connectivity of a biological network, there is not a one-to-one correspondence of each biological neuron with a model neuron. Dimensionality reduction can be used to obtain a concise summary of the population activity from each network. This provides common ground for incisive comparisons between biological and model networks. Discrepancies in the population activity structure between biological and model networks can then help to refine model networks.
Dimensionality reduction has been adopted by recent studies to relate neuronal recordings and network models to study working memory, decision making, motor control, and more. Although many studies have separately employed large-scale neuronal recordings, large-scale network models, and dimensionality reduction, this review focuses on studies that incorporate all three components. Below we describe these studies, organized by the aspect of population activity structure used to relate neuronal recordings and network models: population activity time courses, functionally-defined neuronal subspaces, and population-wide neuronal variability. These were chosen first because they represent the key ways in which dimensionality reduction has been used in the literature to relate population recordings and network models. More importantly, these three categories represent fundamental aspects of population activity structure – how it unfolds over time, how different types of information can be encoded in different subspaces, and how it varies from trial to trial.
Population activity time courses
Dynamical structures, such as point attractors, line attractors, and limit cycles, arising from network models have long been hypothesized to underlie the computational ability of biological networks of neurons [36–38]. Such dynamical structures have been implicated in decision making [39,40], memory [41–43], oculomotor integration [44,45], motor control [46], olfaction [47], and more. A fundamental question in systems neuroscience is whether these dynamical structures are actually used by the brain. Although single-neuron and pairwise metrics can be informative [42,45], analyzing the activity of a population of neurons together has enabled deeper connections. In particular, the time course of the activity of a population of neurons can be summarized by low-dimensional neuronal trajectories [25], as identified by dimensionality reduction. These neuronal trajectories can provide a signature of a particular dynamical structure. For example, a point attractor shows convergent trajectories. The neuronal trajectories extracted from the recorded activity can then be compared with those extracted from the network model activity. Such a comparison does not require a one-to-one correspondence between each recorded neuron and a model neuron, but instead relies on a summary of the population activity time courses.
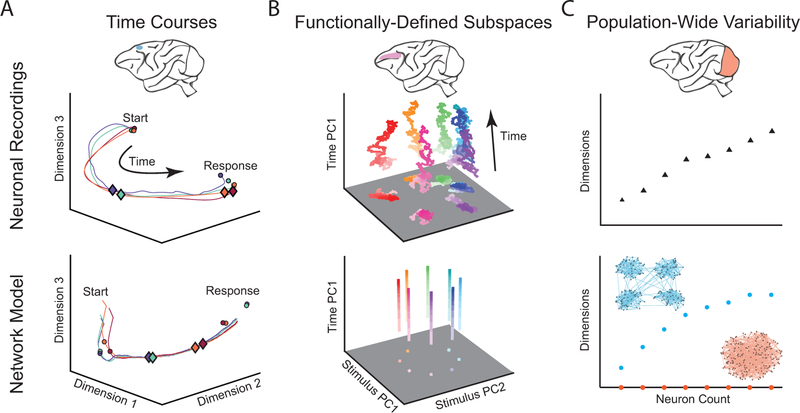
This approach was recently used to study how the brain flexibly controls the timing of behavior [48,49]. By applying dimensionality reduction to neuronal activity recorded from medial frontal cortex, Wang et al. found that population activity time courses for different time intervals followed a stereotypical path, but traversed that path at different speeds (Fig. 2A, top). To understand how a network of neurons can accomplish this, the authors trained a recurrent network model with 200 neurons to produce only the appropriate stimulus-behavior relationships. Wang et al. then applied dimensionality reduction to the activity from the network model. They surprisingly observed that the neuronal trajectories of the network model also followed a stereotypical path, even though the network model was not trained to reproduce the recorded activity (Fig. 2A, bottom). This population-level correspondence enabled by dimensionality reduction laid the foundation for them to then dissect the network model to understand the core neuronal mechanisms [50]. They found that the input to the network drove the network activity from one fixed point to another, where the transition speed was determined by the depth of the energy basin created by the input (Fig. 2A, bottom).
Fig 2. Examples of comparing neuronal recordings and network models using dimensionality reduction.
A. (Top) Population activity time courses from medial frontal cortex during a time production task. Each trajectory represents a time course of neuronal activity during a different produced time interval. Circles represent the start and end of the time production interval and diamonds represent a fixed time interval after the start circle. Diamonds appear closer to the start of the trajectory on long-interval trials (blue) than short-interval trials (red), indicating that neuronal activity traverses the path at different speeds during the two intervals. (Bottom) Circles represent fixed points in the model network’s dynamics and diamonds represent a fixed time interval after the start of the time production task. A similar difference in traversal speed is observed in the model network as was observed in the neural recordings. Adapted with permission from [48]. B. (Top) Delay period activity from prefrontal cortex during a delayed saccade task. Each trajectory represents a different stimulus condition. The trajectories for different stimuli remain well-separated in a stimulus subspace throughout the delay period. (Bottom) Network model activity demonstrating similar subspace stability. Adapted with permission from [20]. C. (Top) Dimensionality of population-wide neuronal variability in primary visual cortex increases with the number of neurons recorded. (Bottom) A similar dimensionality trend is observed for a spiking network model with clustered excitatory connections (blue), but not for a model with unstructured connectivity (red). Adapted with permission from [31].
Other studies have also used this approach to understand how the time course of neuronal activity relates to computations underlying motor control [12,51–53] decision making [17,54–56], and working memory [13,57]. In each of these studies, a network model was constructed without referencing the recorded activity. Dimensionality reduction was applied to extract neuronal trajectories to obtain a correspondence between the neuronal recordings and network models. To study the neuronal mechanisms underlying the observed time courses, the network models were then dissected to reveal dynamical structures, such as fixed points or point attractors [17,54,55], line attractors [17], and oscillatory modes [12,51–53]. Whether or not these dynamical structures are indeed at play in real neuronal networks is still an open question. Nevertheless, these studies are beginning to demonstrate that it is at least fruitful to interpret neuronal activity in terms of these dynamical structures, a process facilitated by dimensionality reduction.
Functionally-defined neuronal subspaces
Recent studies have investigated how distinct types of information encoded by the same neuronal population can be parsed by downstream brain circuits [58–60]. An enticing proposal is that different types of information are encoded in different subspaces within the population activity space, where the subspaces are identified using dimensionality reduction. For example, Kaufman et al. [18] asked how it is possible for neurons in the motor cortex to be active during motor preparation, yet not generate an arm movement. They found that motor cortical activity during motor preparation resided outside of the activity subspace most related to muscle contractions. This allows the motor cortex to prepare arm movements without driving downstream circuits, a characteristic which can be implemented by a linear readout mechanism. This concept of functionally-defined neuronal subspaces has also been used in other studies of motor control [23,61–63], decision making [30,64], short-term memory [30,65], learning [19], and visual processing [24].
To understand how a neuronal circuit can implement and exploit such functionally-defined neuronal subspaces, one can construct a network model to see whether it reproduces the empirical observations. If so, one can then dissect the network to study the underlying mechanisms. Mante et al. [17] applied dimensionality reduction to recordings in prefrontal cortex to find that motion and color of the visual stimulus were encoded in distinct subspaces. They then trained a recurrent network model with 100 neurons to produce only the appropriate stimulus-behavior relationships. When they applied the same dimensionality reduction method to the network model activity, they surprisingly found that the motion and color of the visual stimulus were also encoded in distinct subspaces, even though the network model was not trained to reproduce the recorded activity. This population-level correspondence between the network model and recordings was enabled by dimensionality reduction and went beyond comparisons based on individual neurons or pairs of neurons. Mante et al. then dissected the network model to uncover how the two types of information encoded in distinct subspaces can be selectively used to form a decision.
Dimensionality reduction has also revealed that, in some cases, standard network models do not reproduce the functionally-defined subspaces identified from neuronal recordings. For example, Murray et al. [20] applied dimensionality reduction to recordings in prefrontal cortex during a working memory task to find that, even though firing rates of individual neurons changed over time, there was a subspace in which the activity stably encoded the memorized target location (Fig. 2B, top). They then applied the same analyses to activity from several prominent network models and found that none of them reproduced both the time-varying activity of individual neurons and the subspace in which the memory was stably encoded. This provided the impetus to develop a new network model that did reproduce these features of the recorded activity (Fig. 2B, bottom) (see also [66]). As another example, Elsayed et al. [67] found that standard network models do not reproduce the empirical observation described above that neuronal activity during movement preparation and movement execution lie in orthogonal subspaces. Such insights obtained using dimensionality reduction can guide the development of more sophisticated network models.
Population-wide neuronal variability
The previous sections focus largely on neuronal activity that is averaged across trials and on firing rate-based network models. This naturally obscures the trial-to-trial variability that is a fundamental feature of neuronal responses across the cortex [68], both at the level of single neuron responses [69] as well as variability shared by the population [11,70]. Theoretical and experimental studies have focused on how the structure of that variability places limits on information coding [71–74], and in turn influences our behavior. At the same time, a growing body of work has demonstrated that variability can be thought of not only as noise to be removed, but also a signature of ongoing decision processes and cognitive variables (e.g., [75–77]). To move beyond single-neuron and pairwise measurements of neuronal variability, recent studies have begun to consider population-wide measures of neuronal variability [78–82], as enabled by dimensionality reduction. Such measures allow one to i) assess whether the large number of single-neuron and pairwise variability measurements can be succinctly summarized by a small number of variables (e.g., the entire population increasing and decreasing its activity together can be described by a single scalar variable), and ii) relate the population activity on individual experimental trials to behavior [22,32–34,83–85].
In parallel with the growing interest in neuronal variability, there have been attempts to create network models that exhibit variability matching recorded neurons. In particular, a class of models has used the balance between excitation and inhibition as a way to generate variability as an emergent property of network structure, rather than via an external variable source [71,86,87]. In these models, the particular structure of the network has a large impact on the population-wide variability that emerges. Using the lens of factor analysis, Williamson et al. [31] found that the dimensionality of spontaneous activity fluctuations in V1 neurons increases with the number of recorded neurons (Fig. 2C, top). This was more consistent with activity generated by networks with clustered excitatory connections [8] than networks with unstructured connectivity [86] (Fig. 2C, bottom). The combination of population-wide measures of variability (in this case, dimensionality) and the ability to manipulate model network structures facilitated an understanding of how features of variability observed in biological networks relate to network structure.
The approach of using dimensionality reduction to compare the population-wide variability of neuronal recordings and network models has also been applied to study spontaneous versus evoked activity [88,89], the activity of different classes of neurons [90], and the activity during different behavioral conditions, such as attention [81,82]. Dimensionality reduction has also been used to analyze population activity from balanced network models to help identify the crucial network architecture and synaptic timescales required to produce the low-dimensional shared variability that is widely reported in neuronal recordings [82,87]. Together these studies demonstrate the power of combining dimensionality reduction and network models to understand the mechanisms and effects of neuronal variability.
Conclusion
Dimensionality reduction has enabled incisive comparisons between biological and model networks in terms of population activity time courses, functionally-defined neuronal subspaces, and population-wide neuronal variability. Such comparisons result in either i) a correspondence between the neuronal recordings and the network model, in which case the model can be dissected to understand underlying network mechanisms, or ii) discrepancies between the neuronal recordings and standard network models, leading to the development of improved models. This approach (cf. Fig. 1) has already provided insight into the neuronal mechanisms underlying brain functions such as working memory, decision making, and motor control, and is likely to become even more important as the scale of neuronal recordings and network models grows.
A key consideration in network modeling is what aspects of neuronal recordings the model should reproduce. We posit that the population activity structure (including population activity time courses, functionally-defined neuronal subspaces, and population-wide neuronal variability) will provide key signatures of how neurons work together to give rise to brain function. Thus, if a network model is to provide a systems-level account of brain function, we should require it to reproduce the population activity structure of neuronal recordings, in addition to existing population metrics [3] and standard spike train statistics based on individual and pairs of neurons.
Most studies described here have used neuronal recordings to inform network models via dimensionality reduction. An important future direction is to use network models and dimensionality reduction to design new experiments and form predictions. For example, if one day we can experimentally perturb neuronal activity in specified directions in the population activity space [91], we can test whether driving the population activity in particular directions leads to particular decisions or movements predicted by the network model. The hope is to establish a virtuous cycle, where neuronal recordings and network models closely inform each other through the common ground provided by dimensionality reduction.
Highlights.
The interplay of neuronal recordings and network models is becoming ever stronger.
Population activity structure provides common ground for incisive comparisons.
Dimensionality reduction can be used to identify population activity structure.
This approach is used to study working memory, decision making, motor control, etc.
Acknowledgements
This work was supported by a Richard King Mellon Foundation Presidential Fellowship in the Life Sciences (RCW), NIH R01 EB026953 (BD, MAS, BMY), Hillman Foundation (BD, MAS), NSF NCS BCS 1734901 and 1734916 (MAS, BY), NIH CRCNS R01 MH118929 (MAS, BY), NIH CRCNS R01 DC015139 (BD), ONR N00014–18-1–2002 (BD), Simons Foundation 325293 and 542967 (BD), NIH R01 EY022928 (MAS), NIH P30 EY008098 (MAS), Research to Prevent Blindness (MAS), Eye and Ear Foundation of Pittsburgh (MAS), NSF NCS BCS 1533672 (BMY), NIH R01 HD071686 (BMY), NIH CRCNS R01 NS105318 (BMY), and Simons Foundation 364994 and 543065 (BMY).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Stevenson IH and Kording KP (2011). How advances in neural recording affect data analysis. Nature Neuroscience 14, 139–142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Brette R, Rudolph M, Carnevale T, Hines M, Beeman D, Bower JM, Diesmann M, Morrison A, Goodman PH, Harris FC, et al. (2007). Simulation of networks of spiking neurons: a review of tools and strategies. Journal of Computational Neuroscience 23, 349–398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Yamins DLK and DiCarlo JJ (2016). Using goal-driven deep learning models to understand sensory cortex. Nature Neuroscience 19, 356–365. [DOI] [PubMed] [Google Scholar]
- 4.Barak O (2017). Recurrent neural networks as versatile tools of neuroscience research. Current Opinion in Neurobiology 46, 1–6. [DOI] [PubMed] [Google Scholar]
- 5.Lee WCA, Bonin V, Reed M, Graham BJ, Hood G, Glattfelder K, and Reid RC (2016). Anatomy and function of an excitatory network in the visual cortex. Nature 532, 370–374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Roxin A, Brunel N, Hansel D, Mongillo G, and van Vreeswijk C (2011). On the distribution of firing rates in networks of cortical neurons. Journal of Neuroscience 31, 16217–16226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Chariker L, Shapley R, and Young LS (2016). Orientation selectivity from very sparse LGN inputs in a comprehensive model of macaque V1 cortex. Journal of Neuroscience 36, 12368–12384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Litwin-Kumar A and Doiron B (2012). Slow dynamics and high variability in balanced cortical networks with clustered connections. Nature Neuroscience 15, 1498–1505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Trousdale J, Hu Y, Shea-Brown E, and Josić K (2012). Impact of network structure and cellular response on spike time correlations. PLoS computational biology 8, e1002408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Stringer C, Pachitariu M, Steinmetz NA, Okun M, Bartho P, Harris KD, Sahani M, and Lesica NA (2016). Inhibitory control of correlated intrinsic variability in cortical networks. eLife 5, e19695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Doiron B, Litwin-Kumar A, Rosenbaum R, Ocker GK, and Josić K (2016). The mechanics of state-dependent neural correlations. Nature neuroscience 19, 383–393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Sussillo D, Churchland MM, Kaufman MT, and Shenoy KV (2015). A neural network that finds a naturalistic solution for the production of muscle activity. Nature Neuroscience 18, 1025–1033.*: The authors trained a recurrent network model to produce muscle activity patterns observed in an arm reaching task. The model activity surprisingly showed rotational dynamics that mimicked those observed empirically in M1 population recordings.
- 13.Rajan K, Harvey CD, and Tank DW (2016). Recurrent Network Models of Sequence Generation and Memory. Neuron 90, 128–142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Mazor O and Laurent G (2005). Transient Dynamics versus Fixed Points in Odor Representations by Locust Antennal Lobe Projection Neurons. Neuron 48, 661–673. [DOI] [PubMed] [Google Scholar]
- 15.Churchland MM, Cunningham JP, Kaufman MT, Foster JD, Nuyujukian P, Ryu SI, and Shenoy KV (2012). Neural population dynamics during reaching. Nature 487, 51–56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Harvey CD, Coen P, and Tank DW (2012). Choice-specific sequences in parietal cortex during a virtual-navigation decision task. Nature 484, 62–68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Mante V, Sussillo D, Shenoy KV, and Newsome WT (2013). Context-dependent computation by recurrent dynamics in prefrontal cortex. Nature 503, 78–84.*: In a context-dependent decision-making task, the authors found that color and motion information were encoded in distinct subspaces of PFC population activity. A recurrent network model trained to perform the same task revealed a network-level mechanism of how the two types of information can be selectively used to form a decision.
- 18.Kaufman MT, Churchland MM, Ryu SI, and Shenoy KV (2014). Cortical activity in the null space: permitting preparation without movement. Nature Neuroscience 17, 440–448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Sadtler PT, Quick KM, Golub MD, Chase SM, Ryu SI, Tyler-Kabara EC,Yu BM, and Batista AP (2014). Neural constraints on learning. Nature 512, 423–426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Murray JD, Bernacchia A, Roy NA, Constantinidis C, Romo R, and Wang XJ(2017). Stable population coding for working memory coexists with heterogeneous neural dynamics in prefrontal cortex. Proceedings of the National Academy of Sciences 114, 394–399.**: The authors analyzed population activity recorded in prefrontal cortex and identified a low-dimensional subspace in which stimulus information was reliably encoded, despite the fact that individual neurons showed substantial time-varying activity. They then found that standard models did not reproduce this empirical observation, and proceeded to develop a “stable subspace” model that did reproduce this observation.
- 21.Remington ED, Egger SW, Narain D, Wang J, and Jazayeri M (2018). A Dynamical Systems Perspective on Flexible Motor Timing. Trends in Cognitive Sciences 22, 938–952. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Ruff DA, Ni AM, and Cohen MR (2018). Cognition as a Window into Neuronal Population Space. Annual Review of Neuroscience 41, 77–97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Perich MG, Gallego JA, and Miller LE (2018). A Neural Population Mechanism for Rapid Learning. Neuron 100, 964–976.e7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Semedo JD, Zandvakili A, Machens CK, Yu BM, and Kohn A (2018). Cortical areas interact through a communication subspace. Neuron , in press. [DOI] [PMC free article] [PubMed]
- 25.Cunningham JP and Yu BM (2014). Dimensionality reduction for large-scale neural recordings. Nature Neuroscience 17, 1500–1509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Gao P and Ganguli S (2015). On simplicity and complexity in the brave new world of large-scale neuroscience. Current Opinion in Neurobiology 32, 148–155. [DOI] [PubMed] [Google Scholar]
- 27.Gallego JA, Perich MG, Miller LE, and Solla SA (2017). Neural Manifolds for the Control of Movement. Neuron 94, 978 – 984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Cowley BR, Smith MA, Kohn A, and Yu BM (2016). Stimulus-Driven Population Activity Patterns in Macaque Primary Visual Cortex. PLoS Computational Biology 12, e1005185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Gallego JA, Perich MG, Naufel SN, Ethier C, Solla SA, and Miller LE(2018). Cortical population activity within a preserved neural manifold underlies multiple motor behaviors. Nature Communications 9, 4233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Kobak D, Brendel W, Constantinidis C, Feierstein CE, Kepecs A, Mainen ZF,Qi XL, Romo R, Uchida N, and Machens CK (2016). Demixed principal component analysis of neural population data. eLife 5, e10989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Williamson RC, Cowley BR, Litwin-Kumar A, Doiron B, Kohn A, Smith MA, and Yu BM (2016). Scaling Properties of Dimensionality Reduction for Neural Populations and Network Models. PLoS Computational Biology 12, e1005141.**: This study compared the population activity structure of V1 recordings and spiking network models while varying the number of neurons and trials analyzed. The scaling trends of the V1 recordings better resembled a model with clustered excitatory connections than one with unstructured connectivity.
- 32.Yu BM, Cunningham JP, Santhanam G, Ryu SI, Shenoy KV, and Sahani M(2009). Gaussian-Process Factor Analysis for Low-Dimensional Single-Trial Analysis of Neural Population Activity. Journal of Neurophysiology 102, 614–635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Pandarinath C, O’Shea DJ, Collins J, Jozefowicz R, Stavisky SD, Kao JC, Trautmann EM, Kaufman MT, Ryu SI, Hochberg LR, et al. (2018). Inferring single-trial neural population dynamics using sequential auto-encoders. Nature Methods 15, 805–815. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Williams AH, Kim TH, Wang F, Vyas S, Ryu SI, Shenoy KV, Schnitzer M, Kolda TG, and Ganguli S (2018). Unsupervised Discovery of Demixed, Low-Dimensional Neural Dynamics across Multiple Timescales through Tensor Component Analysis. Neuron 98, 1099–1115.e8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Buonomano DV and Maass W (2009). State-dependent computations: spatiotemporal processing in cortical networks. Nature Reviews Neuroscience 10, 113–125. [DOI] [PubMed] [Google Scholar]
- 36.Wilson HR and Cowan JD (1973). A mathematical theory of the functional dynamics of cortical and thalamic nervous tissue. Kybernetik 13, 55–80. [DOI] [PubMed] [Google Scholar]
- 37.Hopfield JJ (1982). Neural networks and physical systems with emergent collective computational abilities. Proceedings of the National Academy of Sciences 79, 2554–2558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Brody CD, Romo R, and Kepecs A (2003). Basic mechanisms for graded persistent activity: discrete attractors, continuous attractors, and dynamic representations. Current Opinion in Neurobiology 13, 204–211. [DOI] [PubMed] [Google Scholar]
- 39.Machens CK, Romo R, and Brody CD (2005). Flexible Control of Mutual Inhibition: A Neural Model of Two-Interval Discrimination. Science 307, 1121–1124. [DOI] [PubMed] [Google Scholar]
- 40.Wang XJ (2008). Decision Making in Recurrent Neuronal Circuits. Neuron 60, 215–234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Wang XJ (2001). Synaptic reverberation underlying mnemonic persistent activity. Trends in Neurosciences 24, 455–463. [DOI] [PubMed] [Google Scholar]
- 42.Wimmer K, Nykamp DQ, Constantinidis C, and Compte A (2014). Bump attractor dynamics in prefrontal cortex explains behavioral precision in spatial working memory. Nature Neuroscience 17, 431–439. [DOI] [PubMed] [Google Scholar]
- 43.Chaudhuri R and Fiete I (2016). Computational principles of memory. Nature Neuroscience 19, 394–403. [DOI] [PubMed] [Google Scholar]
- 44.Seung HS (1996). How the brain keeps the eyes still. Proceedings of the National Academy of Sciences 93, 13339–13344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Miri A, Daie K, Arrenberg AB, Baier H, Aksay E, and Tank DW (2011). Spatial gradients and multidimensional dynamics in a neural integrator circuit. Nature Neuroscience 14, 1150–1159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Shenoy KV, Sahani M, and Churchland MM (2013). Cortical Control of Arm Movements: A Dynamical Systems Perspective. Annual Review of Neuroscience 36, 337–359. [DOI] [PubMed] [Google Scholar]
- 47.Rabinovich M, Huerta R, and Laurent G (2008). Transient Dynamics for Neural Processing. Science 321, 48–50. [DOI] [PubMed] [Google Scholar]
- 48.Wang J, Narain D, Hosseini EA, and Jazayeri M (2018). Flexible timing by temporal scaling of cortical responses. Nature Neuroscience 21, 102–110.**: Recording from medial frontal cortex during a timing task, the authors found that population activity time courses followed a stereotypical path, but traversed the path at different speeds based on the duration of the timing interval. They found similar trends in a recurrent network model trained to perform the task and showed that speed of traversal was determined by the network inputs.
- 49.Remington ED, Narain D, Hosseini EA, and Jazayeri M (2018). Flexible Sensorimotor Computations through Rapid Reconfiguration of Cortical Dynamics. Neuron 98, 1005–1019.e5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Sussillo D and Barak O (2013). Opening the Black Box: Low-Dimensional Dynamics in High-Dimensional Recurrent Neural Networks. Neural Computation 25, 626–649. [DOI] [PubMed] [Google Scholar]
- 51.Hennequin G, Vogels TP, and Gerstner W (2014). Optimal Control of Transient Dynamics in Balanced Networks Supports Generation of Complex Movements. Neuron 82, 1394 – 1406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Michaels JA, Dann B, and Scherberger H (2016). Neural Population Dynamics during Reaching Are Better Explained by a Dynamical System than Representational Tuning. PLoS Computational Biology 12, e1005175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Russo AA, Bittner SR, Perkins SM, Seely JS, London BM, Lara AH, Miri A, Marshall NJ, Kohn A, Jessell TM, et al. (2018). Motor Cortex Embeds Muscle-like Commands in an Untangled Population Response. Neuron 97, 953–966.e8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Carnevale F, de Lafuente V, Romo R, Barak O, and Parga N (2015). Dynamic Control of Response Criterion in Premotor Cortex during Perceptual Detection under Temporal Uncertainty. Neuron 86, 1067–1077. [DOI] [PubMed] [Google Scholar]
- 55.Chaisangmongkon W, Swaminathan SK, Freedman DJ, and Wang XJ (2017). Computing by Robust Transience: How the Fronto-Parietal Network Performs Sequential, Category-Based Decisions. Neuron 93, 1504–1517.e4.*: The authors found that PFC and LIP neurons show mixed selectivity during a delayed match-to-category task, and that the neuronal trajectories extracted using dimensionality reduction are interpretable during each epoch of the task. They then constructed a recurrent network model to understand the network principles that govern the activity time courses during this task.
- 56.Mastrogiuseppe F and Ostojic S (2018). Linking Connectivity, Dynamics, and Computations in Low-Rank Recurrent Neural Networks. Neuron 99, 609–623.e29. [DOI] [PubMed] [Google Scholar]
- 57.Barak O, Sussillo D, Romo R, Tsodyks M, and Abbott LF (2013). From fixed points to chaos: Three models of delayed discrimination. Progress in Neurobiology 103, 214–222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Park IM, Meister MLR, Huk AC, and Pillow JW (2014). Encoding and decoding in parietal cortex during sensorimotor decision-making. Nature Neuroscience 17, 1395–1403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Pagan M and Rust NC (2014). Quantifying the signals contained in heterogeneous neural responses and determining their relationships with task performance. Journal of Neurophysiology 112, 1584–1598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Fusi S, Miller EK, and Rigotti M (2016). Why neurons mix: high dimensionality for higher cognition. Current Opinion in Neurobiology 37, 66–74. [DOI] [PubMed] [Google Scholar]
- 61.Li N, Daie K, Svoboda K, and Druckmann S (2016). Robust neuronal dynamics in premotor cortex during motor planning. Nature 532, 459–464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Miri A, Warriner CL, Seely JS, Elsayed GF, Cunningham JP, Churchland MM, and Jessell TM (2017). Behaviorally Selective Engagement of Short-Latency Effector Pathways by Motor Cortex. Neuron 95, 683 – 696.e11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Hennig JA, Golub MD, Lund PJ, Sadtler PT, Oby ER, Quick KM, Ryu SI,Tyler-Kabara EC, Batista AP, Yu BM, et al. (2018). Constraints on neural redundancy. eLife 7, e36774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Raposo D, Kaufman MT, and Churchland AK (2014). A category-free neural population supports evolving demands during decision-making. Nature Neuroscience 17, 1784–1792. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Daie K, Goldman M, and Aksay EF (2015). Spatial Patterns of Persistent Neural Activity Vary with the Behavioral Context of Short-Term Memory. Neuron 85, 847–860. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Druckmann S and Chklovskii DB (2012). Neuronal Circuits Underlying Persistent Representations Despite Time Varying Activity. Current Biology 22, 2095–2103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Elsayed GF, Lara AH, Kaufman MT, Churchland MM, and Cunningham JP(2016). Reorganization between preparatory and movement population responses in motor cortex. Nature Communications 7, 13239.*: This study found that M1 population activity during movement preparation and movement execution resides in orthogonal subspaces. Standard network models did not reproduce this empirical observation.
- 68.Renart A and Machens CK (2014). Variability in neural activity and behavior. Current Opinion in Neurobiology 25, 211–220. [DOI] [PubMed] [Google Scholar]
- 69.Faisal AA, Selen LP, and Wolpert DM (2008). Noise in the nervous system. Nature Reviews Neuroscience 9, 292–303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Cohen MR and Kohn A (2011). Measuring and interpreting neuronal correlations. Nature Neuroscience 14, 811–819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Shadlen MN and Newsome WT (1998). The Variable Discharge of Cortical Neurons: Implications for Connectivity, Computation, and Information Coding. Journal of Neuroscience 18, 3870–3896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Abbott LF and Dayan P (1999). The Effect of Correlated Variability on the Accuracy of a Population Code. Neural Computation 11, 91–101. [DOI] [PubMed] [Google Scholar]
- 73.Averbeck BB, Latham PE, and Pouget A (2006). Neural correlations, population coding and computation. Nature Reviews Neuroscience 7, 358–366. [DOI] [PubMed] [Google Scholar]
- 74.Moreno-Bote R, Beck J, Kanitscheider I, Pitkow X, Latham P, and Pouget A(2014). Information-limiting correlations. Nature Neuroscience 17, 1410–1417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Cohen MR and Maunsell JHR (2009). Attention improves performance primarily by reducing inter neuronal correlations. Nature Neuroscience 12, 1594–1600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Mitchell JF, Sundberg KA, and Reynolds JH (2009). Spatial Attention Decorrelates Intrinsic Activity Fluctuations in Macaque Area V4. Neuron 63, 879–888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Nienborg H, Cohen MR, and Cumming BG (2012). Decision-related activity in sensory neurons: correlations among neurons and with behavior. Annual Review of Neuroscience 35, 463–483. [DOI] [PubMed] [Google Scholar]
- 78.Ecker A, Berens P, Cotton RJ, Subramaniyan M, Denfield G, Cadwell C, Smirnakis S, Bethge M, and Tolias A (2014). State Dependence of Noise Correlations in Macaque Primary Visual Cortex. Neuron 82, 235–248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Rabinowitz NC, Goris RL, Cohen M, and Simoncelli EP (2015). Attention stabilizes the shared gain of V4 populations. eLife 4, e08998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Lin IC, Okun M, Carandini M, and Harris KD (2015). The Nature of Shared Cortical Variability. Neuron 87, 644–656. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Kanashiro T, Ocker GK, Cohen MR, and Doiron B (2017). Attentional modulation of neuronal variability in circuit models of cortex. eLife 6, e23978. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Huang C, Ruff D, Pyle R, Rosenbaum R, Cohen M, and Doiron BD (2018). Circuit models of low dimensional shared variability in cortical networks. bioRxiv , in press. [DOI] [PMC free article] [PubMed]
- 83.Cohen MR and Maunsell JH (2010). A neuronal population measure of attention predicts behavioral performance on individual trials. Journal of Neuroscience 30, 15241–15253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Kiani R, Cueva CJ, Reppas JB, and Newsome WT (2014). Dynamics of Neural Population Responses in Prefrontal Cortex Indicate Changes of Mind on Single Trials. Current Biology 24, 1542–1547. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Kaufman MT, Churchland MM, Ryu SI, and Shenoy KV (2015). Vacillation, indecision and hesitation in moment-by-moment decoding of monkey motor cortex. eLife 4, e04677. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Van Vreeswijk C and Sompolinsky H (1996). Chaos in neuronal networks with balanced excitatory and inhibitory activity. Science 274, 1724–1726. [DOI] [PubMed] [Google Scholar]
- 87.Rosenbaum R, Smith MA, Kohn A, Rubin JE, and Doiron B (2017). The spatial structure of correlated neuronal variability. Nature Neuroscience 20, 107–114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Mazzucato L, Fontanini A, and La Camera G (2016). Stimuli Reduce the Dimensionality of Cortical Activity. Frontiers in Systems Neuroscience 10.*: Comparing gustatory cortex recordings and spiking network models, the authors examined how the dimensionality of population activity grows with population size during spontaneous and evoked activity. They then developed a theoretical upper bound on dimensionality based on the level of pairwise correlations.
- 89.Hennequin G, Ahmadian Y, Rubin DB, Lengyel M, and Miller KD (2018). The Dynamical Regime of Sensory Cortex: Stable Dynamics around a Single Stimulus-Tuned Attractor Account for Patterns of Noise Variability. Neuron 98, 846–860.e5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Bittner SR, Williamson RC, Snyder AC, Litwin-Kumar A, Doiron B, Chase SM, Smith MA, and Yu BM (2017). Population activity structure of excitatory and inhibitory neurons. PLoS One 12, e0181773. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Jazayeri M and Afraz A (2017). Navigating the Neural Space in Search of the Neural Code. Neuron 93, 1003–1014. [DOI] [PubMed] [Google Scholar]