A new dynamical systems perspective on atmospheric predictability: Eastern Mediterranean weather regimes as a case study

Dynamical systems metrics provide an informative qualitative estimate of eastern Mediterranean weather regimes predictability.

Abstract

The atmosphere is a chaotic system displaying recurrent large-scale configurations. Recent developments in dynamical systems theory allow us to describe these configurations in terms of the local dimension—a proxy for the active number of degrees of freedom—and persistence in phase space, which can be interpreted as persistence in time. These properties provide information on the intrinsic predictability of an atmospheric state. Here, this technique is applied to atmospheric configurations in the eastern Mediterranean, grouped into synoptic classifications (SCs). It is shown that local dimension and persistence, derived from reanalysis and CMIP5 models’ daily sea-level pressure fields, can serve as an extremely informative qualitative method for evaluating the predictability of the different SCs. These metrics, combined with the SC transitional probability approach, may be a valuable complement to operational weather forecasts and effective tools for climate model evaluation. This new perspective can be extended to other geographical regions.

INTRODUCTION

In most of the mid-latitudes, synoptic-scale patterns exert a strong control on regional weather. Since the pioneering work of Lamb (1, 2), the classification of synoptic systems has therefore elicited a broad interest in meteorology and climatology, especially in the context of weather forecasting. Lamb proposed a catalog of daily weather types over the British Isles during 1898–1947, related to synoptic-scale circulation categories. Other approaches have later been implemented in different regions, including, for example, Greece (3) and the United States (4). Synoptic classifications (SCs) have been primarily based on manual, correlation, eigenvector, compositing, and machine learning schemes (5).

These methodologies are not, however, immediately applicable to all regions. For example, in the eastern Mediterranean (EM) region, very different synoptic configurations are associated with similarly warm and dry weather conditions. Weather in this region is largely governed by small-scale synoptic systems originating from both mid-latitude and tropical regions that are modified over the complex terrain of the eastern Mediterranean (6). This has motivated the development of a semi-objective SC method, targeted specifically at the southeastern part of the EM region (7). This classification successfully describes the local weather conditions and has found numerous applications. For example, the method has been linked to local temperature and rainfall regimes (8, 9), used for defining eastern Mediterranean seasons and projecting season length changes during the 21st century (10, 11), and to diagnose changes in the local atmospheric dynamics during the 20th and 21st centuries (7, 12). Crucially, the synoptic classification method is widely used by the regions’ weather forecasters.

Recently, the traditional description of synoptic systems—and more generally atmospheric configurations—has been complemented by a novel approach issued from dynamical systems theory. This is grounded in the seminal work of Lorenz (13, 14) and is based on metrics describing the instantaneous state of atmospheric fields (15). Contrary to this, previous dynamical systems approaches focused on the mean properties of the atmosphere, with limited applications in the context of atmospheric variability (16). Faranda et al. (15) have shown that key instantaneous properties of an atmospheric field can be summarized by two metrics: the local dimension (d) and the persistence of the state being considered (θ⁻¹). The value of d for a given atmospheric state ξ is a proxy for the number of active degrees of freedom and provides information on the state’s intrinsic predictability (15). θ⁻¹ is instead a measure of average persistence time of the atmosphere around that state. For discrete time data, the value of θ will depend on the dataset’s time step. If an atmospheric state ξ is a fixed point of the dynamics, θ(ξ) = 0. For a trajectory that leaves the neighborhood of state ξ immediately, θ(ξ) = 1. Accordingly, low d and high θ⁻¹ (or low θ) imply a high predictability state and vice versa. Full details of how d and θ are computed are provided in the Methods.

The aim of this study is to integrate the SC approach with the above dynamical systems metrics. This provides a new perspective on regional atmospheric configurations with direct implications for weather forecasting. Furthermore, the combination of these two approaches presents a powerful tool for evaluating the ability of climate models to capture the fundamental dynamical features of regional synoptic systems.

RESULTS

Predictability measures of synoptic systems in the NCEP/NCAR reanalysis

We assign each day of the NCEP/NCAR (National Centers for Environmental Prediction/National Center for Atmospheric Research) reanalysis (17, 18) database (1948–2017) to a specific synoptic class, or system, over the southeastern part of the EM region (fig. S1) based on the semi-objective classification of Alpert et al. (7). The five systems are Red Sea Troughs (RSTs), Persian Troughs (PTs), Highs, Cyprus Lows (CLs), and Sharav Lows (SLs). The θ and d metrics are calculated for the daily sea-level pressure (SLP) of the same dataset over the same region. This allows us to define cumulative distribution functions (CDFs) of θ (Fig. 1A) and d (Fig. 1B) for the different synoptic systems. All the synoptic systems display significantly different CDFs according to both the Mann-Whitney rank sum (RS) (19) and the Kolmogorov-Smirnov (KS) (20, 21) tests. The only exception is the CL/SL pair. This exception may result from the very rare occurrence of SLs (less than 1% of the days), which makes the comparison of distributions difficult.

Fig. 1. CDFs of inverse persistence (θ) and local dimension (d) for EM synoptic systems.

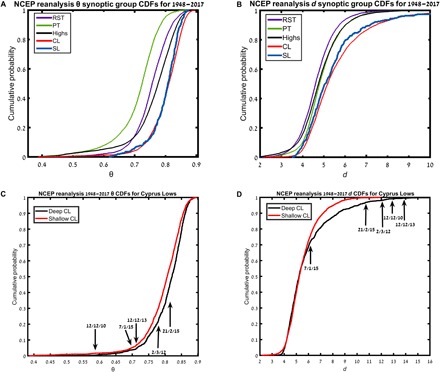
The NCEP/NCAR reanalysis 1948–2017 θ (A) and d (B) CDFs for the different synoptic systems: Red Sea Troughs (RSTs), Persian Troughs (PTs), Highs (H), Cyprus Lows (CLs), and Sharav Lows (SLs). CDFs for θ (C) and d (D) of deep and shallow CLs as defined by Alpert et al. (7). Arrows indicate the snow events in Jerusalem for the available TIGGE data (27, 28). The 12 December 2013 storm named Alexa with values of d = 13.71 and θ = 0.71 is also shown.

In addition to successfully distinguishing between the different synoptic systems the dynamical systems indicators also underscore their salient physical characteristics. The PTs and RSTs are quasi-stationary systems (22), which typically display high persistence. On the contrary, the CL and SL systems are moving disturbances (23) and would hence be expected to have lower persistence. The θ CDFs show the distinction between the two (Fig. 1A). The high persistence of the PT and RST systems is accompanied by low values of d (Fig. 1B), while the opposite is seen for the CL and SL cases.

These results are supported by the SC transition probability matrix (Fig. 2A). The matrix describes the probability of occurrence of a synoptic system at time t + 1 as a function of the synoptic system occurring at time t. This is a simple complement to the dynamical systems approach, providing additional information on the evolution and predictability of the synoptic systems that govern eastern Mediterranean weather. Although beyond the scope of the present discussion, we note that more rigorous transition analysis tools, which consider the evolution over an arbitrary number of time steps, have been developed (24). The low-dimensional, high-persistence RST and PT systems have the highest fraction of self-transitions, namely, cases where the RST/PT systems are followed by another day with the same configuration. The CL and SL cases display lower values (Fig. 2A). Figures 1 (A and B) and 2A therefore reveal that the CL and SL systems have a lower intrinsic predictability than the PT and RST systems, which instead emerge as high-predictability states.

Fig. 2. Transition probability matrices for EM synoptic systems.

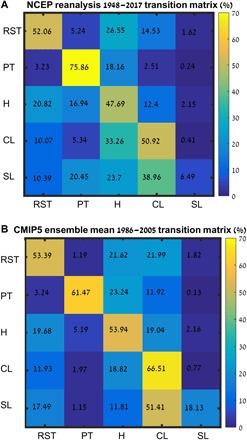
(A) NCEP/NCAR reanalysis synoptic systems probability transition matrix for 1948–2017. (B) CMIP5 ensemble mean probability transition matrix for 1986–2005. Rows sum up to 100%. The synoptic systems are RSTs, PTs, Highs (H), CLs, and SLs.

As a further test, we plot the CDFs for deep and shallow CLs, as defined by Alpert et al. (7) (Fig. 1, C and D; see also Methods). The instantaneous dynamical systems properties capture the difference between these two types of CLs and indicate that the deeper lows are less predictable than the shallow ones. Figure 1 (C and D) also displays the d and θ values for the 11 to 14 December 2013 storm named “Alexa.” The storm, associated with a deep CL, led to widespread snowfall and caused mayhem to millions of people across the region, especially refugees from the Syrian conflict. In Israel, four people were killed, 35,000 homes were disconnected from electricity for about a week, 9000 flights were canceled, and roads, including those leading to Jerusalem, were blocked for more than 48 hours. The damage was estimated at about $100 million, which is the cost liest natural disaster ever recorded in Israel. This storm is considered an exceptional and rare event; the weather forecasters in the region struggled to predict its extent, especially concerning snow cover and depth at such an early stage of winter (www.ims.gov.il/IMS/CLIMATE/ClimateSummary/2013/dec10-14+event.htm; in Hebrew).

Beginning 11 December, there was a big anticyclone over Europe, whose eastern edge drew cold air southward from the Arctic. This polar air outbreak then spread over the EM, pushing ahead of it moist air associated with a cold front and causing heavy snowfall over higher grounds and heavy precipitation and flooding over warmer locations, peaking on 13 December. The calculation of d and θ for 12 December shows that the large-scale atmospheric pattern associated with Alexa was relatively persistent with a very high local dimension (d = 13.71; θ = 0.71). This is an unusual combination, as co-occurring high d and low θ extremes are rarely seen for atmospheric fields (25). The d and θ values therefore highlight the uniqueness of the situation and the potentially large uncertainty in the forecasts. As an example, the European Centre for Medium-Range Weather Forecasts (ECMWF) ensemble forecast for Jerusalem initialized at 00:00 UTC on 11 December (31.9°N 35.2°E; fig. S2) displayed a large uncertainty for the short-range total precipitation and wind speed forecasts on 11 December and the morning of 12 December. While the ECMWF forecast predicted a median total precipitation for the entire storm of ~50 mm, snow cover of ~10 cm, and wind speeds of ~7 m/s, the observed values in Jerusalem were 227 mm, 50 cm, and 14 to 17 m/s, respectively, with wind gusts over 25 m/s (www.ims.gov.il/IMS/CLIMATE/ClimateSummary/2013/dec10-14+event.htm; in Hebrew).

Snow events in Jerusalem are extremely rare events, which the weather forecasters in the region have long considered challenging (26). Thus, we have tested the dynamical systems indicators on four additional Jerusalem snow events, which occurred during the period covered by The Interactive Grand Global Ensemble (TIGGE) dataset (27, 28). Four of the five events (including Alexa) are found in the upper five percentile of the d distribution, and three of the five events are found in the lower five percentile of the θ distribution (Fig. 1, C and D). The other one to two events are still in the high/low percentiles of d and θ, respectively. All events display a large ensemble spread with large differences between observed and predicted precipitation and snow depth (table S1). For the small five-event sample considered here, the d ranking from high to low exactly follows the ranking of the difference between predicted and observed snow depth, i.e., forecast snow-depth error. That is, low predictability events according to the dynamical systems indicator have large errors in the predicted snow depth (table S1 and Fig. 1D).

A critical appraisal of the information provided by both the dynamical systems indicators and the ensemble forecast for “Alexa” may have allowed more appropriate warnings to be issued and more effective measures to be taken. We also highlight that the dynamical systems indicators, which are inexpensive to compute, could have been available to forecasters several hours before the ensemble forecast was issued. This points to the relevance of investigating further the use of dynamical systems indicators in operational weather forecasting. While the five-event sample considered above is insufficient to fully demonstrate the operational relevance of d and θ, it may be seen as an encouraging plausibility test.

Last, we verify whether the synoptic systems can be recovered purely based on the information provided by the two dynamical systems metrics considered here. We select the top and bottom five percentiles of the (d, θ) distributions and compare the SLP composites of these four groups of days to those of the four most frequently occurring synoptic systems: RSTs, CLs, PTs, and Highs, which account for ~99% of the days in the dataset (Fig. 3; fig. S3 shows the corresponding synoptic systems’ mean composites, including SLs). A visual inspection highlights that the high d and θ values resemble CLs, the low d’s liken RSTs (although they also display some features of the Highs and PTs), and the low θ’s match PTs. Euclidean distances between the maps largely confirm these inferences. A number of key features of the semi-objective classification used here are therefore mirrored by the dynamical systems metrics. The fact that the Highs are not recovered from the (d, θ) extremes is not surprising, as they are characterized by intermediate (d, θ) values (e.g., Fig. 1, A and B) and therefore should not emerge as dynamical extremes. As a caveat of our analysis, we note that the synoptic systems are defined using multiple variables, while d and θ only use SLP. A full analysis of the bidirectional link between the synoptic systems and dynamical systems indicators would require more advanced pattern recognition techniques and the computation of multivariate d and θ values.

Fig. 3. SLP mean composites for eastern Mediterranean synoptic systems.

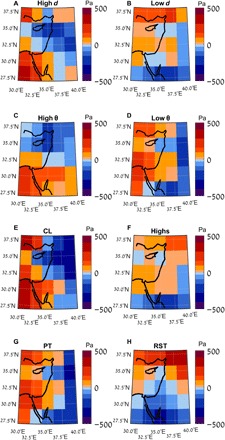
SLP composites for the top and bottom five percentiles of the d and θ distributions (A to D) and the CL, High, PT, and RST synoptic systems (E to H). The values are provided as deviations in Pa from the mean SLP value of each composite. The corresponding absolute SLP patterns for the synoptic systems are shown in fig. S3.

Evaluation of CMIP5 models: Predictability measures of the synoptic systems

Figures 4 and 5 show the CDFs of θ and d, respectively, for SLP fields from models participating in the fifth phase of the Coupled Model Intercomparison Project (CMIP5) (29) over the period 1986–2005 (table S2; see the “Data” section for the choice of years). Each panel corresponds to a single model. The results for the NCEP/NCAR reanalysis over the same period are shown for reference. As in Fig. 1 (A and B), each line in the plots is related to the CDF of a specific synoptic system (RSTs, PTs, Highs, CLs, and SLs). It can be seen that all models capture the main (d, θ) differences between the synoptic systems. Specifically, the models adequately represent the significant differences in the persistence (θ⁻¹) between PTs and CLs, as well as the lower predictability of the CL system with respect to the other synoptic systems (high θ and d, i.e., low predictability). The SL synoptic system displays noisier results due to their low frequency of occurrence in the CMIP5 models, again matching the results from the NCEP/NCAR reanalysis. A rank score (30) for each model with respect to NCEP/NCAR is presented in table S3 (see table caption for details of the score’s calculation). The German Max Planck Institute (MPI), Canadian Center for Climate Modeling and Analysis (CANESM), Meteorological Research Institute of Japan (MRI) and National Center for Atmospheric Research (CCSM) models, capture the median dynamical properties of the synoptic groups comparatively well. Nonetheless, both these and the other models struggle to capture the finer details of the CDFs, with only a few of the model-synoptic class combinations actually matching the NCEP/NCAR distributions according to the RS and KS tests at the 5% significance level.

Fig. 4. CDFs of inverse persistence (θ) for CMIP5 models and NCEP/NCAR reanalysis.

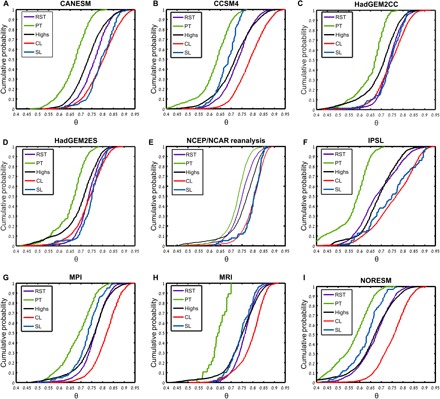
Inverse persistence (θ) CDFs for the synoptic systems in eight CMIP5 models (table S2) and the NCEP/NCAR reanalysis over 1986–2005: (A) CANESM, (B) CCSM4, (C) HadGEM2CC, (D) HadGEM2ES, (E) NCEP/NCAR reanalysis, (F) IPSL, (G) MPI, (H) MRI, and (I) NORESM.

Fig. 5. CDFs of local dimension (d) for CMIP5 models and NCEP/NCAR reanalysis.

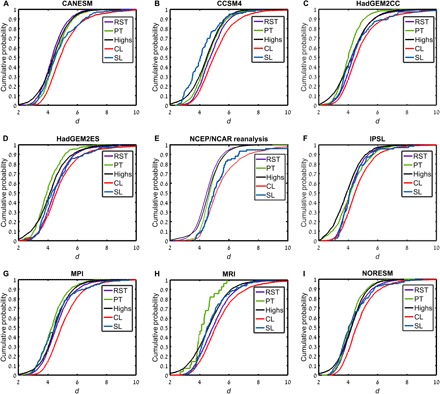
Local dimension (d) CDFs for the synoptic systems in eight CMIP5 models (table S2) and the NCEP/NCAR reanalysis over 1986–2005: (A) CANESM, (B) CCSM4, (C) HadGEM2CC, (D) HadGEM2ES, (E) NCEP/NCAR reanalysis, (F) IPSL, (G) MPI, (H) MRI, and (I) NORESM.

Figure 6 (see also table S4) shows the transition probability matrices of the synoptic systems based on the CMIP5 and NCEP/NCAR data. Again, these refer to transitions between successive days. The CMIP5 models show a reasonable agreement for CL and RST transitions, in both absolute and relative terms, as compared with the NCEP/NCAR reanalysis. The self-transitions of CLs are, however, systematically overestimated. The transition probabilities for PTs show good agreement except for an underestimation of self-transitions and an overestimation of transitions between PTs and CLs in most models. The CCSM, Norwegian Climate Center (NORESM), and CANESM models reproduce very closely the NCEP/NCAR rates for all PT transitions. Most models show good agreement for the Highs’ transitions except for an underestimation of those between Highs and PTs. The bias is particularly severe in the MRI model, which essentially excludes the possibility of such a transition. All models struggle to capture the SL transition probabilities. There is no single model that performs best for all transition probabilities between synoptic systems. The mean transition probability rates from all the CMIP5 models considered here (Fig. 2B) compare relatively well with the NCEP/NCAR reanalysis (Fig. 6E), although many of the biases discussed above emerge in the multimodel mean values. Table S5 shows the mean absolute and weighted differences for each model with respect to the NCEP/NCAR reanalysis. The ranking of the models does not always correspond to that of the CDF medians (see table S3), highlighting the complementary information provided by these two diagnostics. No obvious link between the horizontal spatial resolution of the models and the dynamical properties was found (see table S2). However, a number of other factors may be responsible for the spread in model performances. There are several processes that are known to exert a strong control over the eastern Mediterranean weather and climate. These include large-scale teleconnections, such as the North Atlantic Oscillation or the Indian monsoon (6), as well as local processes, such as EM sea surface fluxes (31). Both sets of features may not be well simulated by some of the models (31–33), leading to the abovementioned biases in eastern Mediterranean synoptic system diagnostics.

Fig. 6. Transition probability matrices for CMIP5 models and the NCEP/NCAR reanalysis.

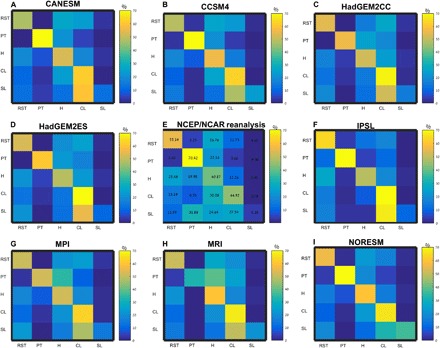
Rows sum up to a 100%. The synoptic systems are RSTs, PTs, Highs (H), CLs, and SLs. The numerical values of the matrices are shown in table S4. (A) CANESM, (B) CCSM4, (C) HadGEM2CC, (D) HadGEM2ES, (E) NCEP/NCAR reanalysis, (F) IPSL, (G) MPI, (H) MRI, and (I) NORESM.

To conclude, the models capture some of the salient dynamical features of the synoptic systems but fail on a number of other aspects. The evaluation of the dynamics of weather patterns in climate models is a key component for assessing the credibility of model projections, and d and θ provide a key tool in this respect.

Conclusions

We combined a very recent dynamical systems theory approach with a daily classification of synoptic systems over the eastern Mediterranean to investigate atmospheric predictability. It was found that the instantaneous measures of local dimension (d) and persistence (θ⁻¹), derived from daily SLP data, can serve as an extremely informative qualitative method to evaluate the intrinsic predictability of synoptic systems. Moreover, the two dynamical systems indicators discriminate between synoptic classes such that Cyprus Lows, Red Sea Troughs, and Persian Troughs emerge as extreme values of d and θ. This complements the results of Faranda et al. (15), who found that d and θ could be used to recover the four canonical North Atlantic weather regimes.

Because the synoptic classification approach has been widely used by weather forecasters, the information provided by d and θ may have implications for operational forecasts. Here, we have made a plausibility argument in support of this idea, which we plan to pursue in future research. Extreme d and θ values often correspond to cyclonic atmospheric systems, which, in turn, commonly match extreme weather conditions in the EM region. Furthermore, it was shown that these new measures, combined with the synoptic classification method, can be used as an evaluation tool for the dynamics of climate models [see also (30)]. The evaluation of CMIP5 models presented here suggests that the models capture a number of the salient qualitative features found in reanalysis data, thus providing the basis for an investigation of the changes in the predictability of synoptic systems under future climate scenarios. At the same time, they fail to reproduce a number of the reanalysis’ quantitative features. The novel perspective presented here, which leverages a dynamical systems approach to investigate the predictability of weather patterns, outlines an important avenue for future research, and we envisage that it may be fruitfully applied to other regions of the globe.

Data

Data were acquired from the NCEP/NCAR reanalysis archive (17, 18). We used daily values over 1948–2017 on a 2.5° × 2.5° horizontal grid. This work is also based on TIGGE data. TIGGE is an initiative of the World Weather Research Program available from July 2008 to present (27, 28).

Model data were retrieved from the World Data Centre for Climate (WDCC-DKRZ; www.ipcc-data.org/sim/gcm_monthly/AR5/Reference-Archive.html) portal for eight models participating in the CMIP5 (29). This selection follows that previously used by Hochman et al. (11, 12). We use daily data for the period 1986–2005. The choice of this period follows the recommendation of the 5th Assessment Report (AR5) of the Intergovernmental Panel on Climate Change (IPCC) (34). The horizontal spatial resolution varies from 0.94° × 1.25° to 1.9° × 3.75°, depending on the model (table S2).

METHODS

The semi-objective synoptic classification

The semi-objective SC algorithm (7) was applied to both the NCEP/NCAR reanalysis and the CMIP5 models using SLP, air temperature, and horizontal wind components U and V at 850 hPa at 25 grid points (27.5°N-37.5°N, 30°E-40°E; fig. S1) over the southeastern part of the EM, as recently presented by Hochman et al. (11, 12). Five main synoptic systems were defined as follows: the PT characterizing the summer; the RST peaking in the autumn; the SL, which is noticeable during spring, albeit with a low frequency of occurrence relative to the other systems; the High pressure system, which appears throughout the year, with the lowest occurrence in summer; and the CL, which is dominant during the winter (10). CLs are mid-latitude disturbances that tend to develop in the Levantine Basin when upper troughs or cutoff lows penetrate the EM (35). CLs transport cool air, originating from eastern Europe, over the warmer Mediterranean, where it becomes moist and unstable (36, 37). These lows contribute ~90% of the annual precipitation in Israel (26). The rainfall yield and its spatial distribution over Israel are highly sensitive to the depth and location of CLs (9). The deep and shallow CLs in the semi-objective SC were defined subjectively by five expert weather forecasters of the region (7).

Instantaneous dynamical properties of atmospheric fields

In this study, we exploited a recently developed approach, which combines extreme value theory with Poincaré recurrences to compute the local properties of a dynamical system. We applied this approach to daily SLP latitude-longitude fields over the EM. We interpreted the succession of daily fields as a long trajectory in the phase space of the atmosphere. Each field therefore corresponds to a single point in phase space, for which local properties can be computed. Locality in phase space therefore translates to instantaneity in time. We focused our analysis on two metrics, namely, the local dimension d and the persistence θ⁻¹.

To compute these metrics for an atmospheric state ξ(t₁), corresponding to a point on the phase-space trajectory, we considered recurrences of the system around the said point. We defined the distance between the point of interest ξ(t₁) and all other observations ξ(t) along the trajectory as

$$g(\mathrm{\xi }(t))=-\text{log}(\text{dist}(\mathrm{\xi }(t),\mathrm{\xi }(t_1)))$$

where dist is a distance function (in our case, the Euclidean distance between the SLP maps). The logarithm was applied to increase the discrimination of close recurrences. Following the Freitas-Freitas-Todd theorem (38), modified by Lucarini et al. (39), the probability of a recurrence within a hypersphere of radius η centered on ξ(t₁) converges to a generalized Pareto distribution

$$P(g(\mathrm{\xi }(t))>q,\mathrm{\xi }(t_1))\simeq e^{(\mathrm{\vartheta }(\mathrm{\xi }(t_1))\frac{g(\mathrm{\xi }(t))-\mathrm{\mu }(\mathrm{\xi }(t_1))}{\mathrm{\sigma }(\mathrm{\xi }(t_1))})}$$

where the radius can be related to a high threshold q by

$$\mathrm{\eta }=e^{-q}$$

Imposing that g(ξ(t)) > q is therefore equivalent to the condition that the trajectory returns within a radius η of ξ(t₁). Here, we set q as the 98th percentile of g(ξ(t)).

The parameters μ and σ depend on the chosen ξ(t₁). The instantaneous (local) dimension is then given by

$$d(\mathrm{\xi }(t_1))=\frac{1}{\mathrm{\sigma }(\mathrm{\xi }(t_1))}$$

We can further compute a measure of the residence time of ξ(t) in the neighborhood of ξ(t₁) by estimating the extremal index ϑ. Its inverse is a measure of consecutive exceedances of a threshold (40). We computed ϑ using the Süveges estimator (41), which has been shown to provide robust estimates for climatic data series (15). Then, θ(ξ(t₁)) = ϑ(ξ(t₁))/Δt, where Δt is the time step of our data.

The above procedure results in a value of d and θ for every time step in our dataset. The first is a proxy for the number of active degrees of freedom of the system. The second represents the mean residence time of the trajectory in the neighborhood of a given point ξ. Both therefore have a direct link to the ease with which the evolution of the trajectory to/from this state can be predicted, which we have termed here the state’s intrinsic predictability. This is a somewhat different type of information from that gleaned from the spread of an ensemble numerical weather forecast initialized from ξ because it is independent of the characteristics of the forecast model and because of its local nature.

This approach is relatively general and has been successfully applied to a variety of climate fields (15, 25, 30, 42). For the limits of applicability to nonstationary systems, we refer the reader to the study of Freitas et al. (43). As a caveat, we note that θ is dependent on the temporal resolution of the data used, because θ⁻¹ is in units of the time step. For a very long time step, all instantaneous states will tend to θ = 1. However, as long as the time resolution of the dataset being used is smaller than the typical time scale of the process being studied (in our case, the typical persistence of a synoptic system in the EM), θ values should be informative. For further details on the abovementioned metrics, the reader is referred to the studies of Lucarini et al. (44), Faranda et al. (15), and Messori et al. (42).

Instantaneous dynamical systems properties complement the SC

Here, the daily semi-objective SC for the EM and two dynamical systems metrics (d and θ) were combined to evaluate the intrinsic predictability of EM synoptic systems in the NCEP/NCAR reanalysis and CMIP5 models. The daily dynamical systems properties were calculated from the time series of SLP over the EM region (fig. S1). Each day was also classified as one of five synoptic systems: RST, PT, High, CL, and SL. Accordingly, the CDFs of d and θ for each synoptic type could be calculated. The difference between the CDFs was tested with the Mann-Whitney RS (19) and KS (20, 21) tests at the 5% significance level. Last, the transition probability matrices (also known as Markov probability matrices) for the five synoptic systems were portrayed for both the NCEP/NCAR reanalysis and the CMIP5 models.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/6/eaau0936/DC1

Table S1. Snow events in Jerusalem from the available TIGGE database (27, 28).

Table S2. The eight CMIP5 models used in the present study with the following information: Modeling center (or group), institute ID, model name, and horizontal resolution (°) following Taylor et al. (29).

Table S3. Model rank scores for each synoptic group with respect to the NCEP/NCAR reanalysis.

Table S4. CMIP5 models and NCEP/NCAR reanalysis transition probabilities for the different synoptic groups.

Table S5. Model mean absolute differences for the transition probabilities of each synoptic group with respect to the NCEP/NCAR reanalysis (%).

Fig. S1. The study region following Alpert et al. (7).

Fig. S2. Meteogram from ECMWF’s EPS (Ensemble Prediction System) forecast system initialized on Wednesday, 11 December 2013, 00:00 UTC at the location of Jerusalem (31.9°N 35.2°E; 815 m).

Fig. S3. Mean SLP composite maps from NCEP/NCAR reanalysis as classified by the Alpert et al. (7) synoptic classification algorithm for 1986–2005.