Abstract
Identifying patient-specific prognostic biomarkers is of critical importance in developing personalized treatment for clinically and molecularly heterogeneous diseases such as cancer. In this article, we propose a novel regression framework, Bayesian hierarchical varying-sparsity regression (BEHAVIOR) models to select clinically relevant disease markers by integrating proteogenomic (proteomic+genomic) and clinical data. Our methods allow flexible modeling of protein-gene relationships as well as induces sparsity in both protein-gene and protein-survival relationships, to select ge-nomically driven prognostic protein markers at the patient-level. Simulation studies demonstrate the superior performance of BEHAVIOR against competing method in terms of both protein marker selection and survival prediction. We apply BEHAV-IOR to The Cancer Genome Atlas (TCGA) proteogenomic pan-cancer data and find several interesting prognostic proteins and pathways that are shared across multiple cancers and some that exclusively pertain to specific cancers.
Keywords: Prognostic biomarker, tumor heterogeneity, precision medicine, p-splines, threshold
1. Introduction
1.1. Scientific background and data description
Clinical proteogenomics in cancer.
Cancer is a molecular disease caused by a series of accumulating genomic alterations that trigger abnormal cell growth and division, causing damage to surrounding tissues and eventual formation of metastases. Global genomic profiling and especially mRNA-based gene expression changes have greatly improved the characterization of cancer development and progression (McLendon et al., 2008; TCGA, 2012). Proteins, however, represent the downstream summation of changes that happen at the DNA and RNA levels in each tumor and are more directly related to the phenotypical changes in cancer cells. Several studies have shown poor concordance between mRNA and protein abundance due to many factors such as degradation and post-translational modifications; therefore, clinical utilization of genomic data alone is limited (Gygi et al., 1999; Akbani et al., 2014). Direct studies of protein levels and function have improved our understanding of the molecular basis of cancer, and treatments that target mutated protein kinases have shown promising clinical benefits in many cancers (Davies et al., 2006).
However, proteomics has its limitations as well. For example, mass spectrometry assays are expensive to run, require plenty of sample material, and relatively little publicly available data sets exist for them (Paweletz et al., 2001; Tibes et al., 2006). Reverse phase protein arrays (RPPAs) are much cheaper proteomics assays that require less material, but they are limited to a relatively small number of known proteins for which antibodies are available; yet proteins that are unknown or for which antibodies are unavailable may also be of critical clinical relevance. Since these unobservable proteins are completely missing due to technological limitation of RPPAs, imputing their abundance seems to be a challenging and unreliable task, which we do not pursue in this paper. This drawback can be mitigated by integrating proteomic information with genomic data (hence the term, proteogenomics) because many genes code for multiple proteins through alternative post-transcriptional or post-translational modifications, and gene-level information (e.g. transcript expressions of known isoforms) complements the unobserved protein activation status. Proteogenomics is a relatively new research area at the interface of proteomics and genomics that was initially proposed for refining genome annotation and characterizing the protein-coding potential (Church, 2004; Nesvizhskii, 2014). Recent proteogenomic studies have enabled a better understanding of the basic biology of cancers and provided novel insights into pathophysiology and tumorigenesis and the development of novel diagnostic and therapeutic options (Jacob et al., 2009; Alfaro et al., 2014; Locard-Paulet et al., 2016).
Tumor heterogeneity and precision medicine.
Over the past few decades, cancer researchers have reached a consensus that tumors are inherently heterogeneous (Heppner and Miller, 1983; Longo, 2012). Even within the same type of cancer, different patients exhibit distinct genomic aberrations that subsequently result in varied response to treatments, due to inter-patient tumor heterogeneity. The widespread awareness of tumor heterogeneity has opened an era of personalized molecular-based treatments, formally termed precision medicine, which has shown great clinical benefit to cancer patients who otherwise have poor response to traditional therapies such as chemotherapy (De Bono and Ashworth, 2010). One of the key steps in the discovery and implementation of the precision medicine paradigm is the construction of prognostic proteomic markers that can be used as potential targets for subsequent drug development. To this end, we aim to exploit the proteomic-genomic regulatory axes to build clinically relevant prognostic models by linking clinical outcomes with proteogenomics. The core conceptual idea of the scientific question motivating our models is illustrated with a sparse tripartite graph (Figure 1) in which vertices are divided into 3 disjoint sets, clinical outcomes Y = {Y1,…, Yn} for n patients, proteins P = {P1,…, Pp} and genes G = {G1,…, Gg} (where n,p,g indicate the number of patients, proteins, and genes, respectively), such that every edge connects a vertex in G to one in P and/or a vertex in P to one in Y. The genomic information is incorporated through modifying the downstream effects of a selective subset of proteins on clinical outcomes. The significance of these effects is identified by a novel subject-specific variable selection technique, which allows for the detection of protein markers on the patient level. For example, in our case study (Section 6.2), a protein BCL2 is found to be prognostic only for a subgroup of patients with concordant homogeneous genomic features, which may guide certain targeted BCL2-antagonists (Lessene et al., 2008). In general, such “genomically homogeneous” patients may have favorable (or unfavorable) responses to a certain treatment which is, perhaps, not as effective or dominant for other heterogeneous subgroups. Our aim is to build models that help to improve our understanding of the biological underpinnings of prognostic pro-teogenomic biomarkers on the patient level; and perhaps provide a new insight into tumor heterogeneity that potentially leads to the development of novel personalized treatments.
Figure 1:
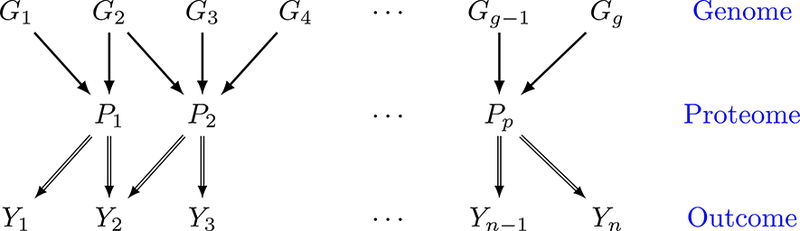
Illustration of the model. Y1,…, Yn denote patient-specific clinical outcomes for n patients, P1,…, Pp denote proteins and G1,…, Gg denote genes. Double-lined arrows represent the patient-level relationship between clinical outcome and proteins, and single-lined arrows connect genes to their protein products on the population level.
Data description.
The Cancer Genome Atlas (TCGA) is a project that was launched in 2005 to explore, evaluate and characterize the genomic and proteomic landscape of over 30 human cancers, both common and rare forms. For gene expression, TCGA uses RNA sequencing (RNA-Seq), a next-generation sequencing technology, to generate genomic data at a fine molecular resolution. RNA-Seq has very low background noise and is very accurate in measuring gene expression levels compared to traditional technologies such as microarrays (Wang et al., 2009; Nagalakshmi et al., 2010). Since May 2012, the pipeline RNASeqV2 has been adopted by TCGA to generate the Level 3 expression data: they use MapSplice (Wang et al., 2010) to align the sequence data and RSEM (Li and Dewey, 2011) to quantify transcript abundances, which we use for our analyses. The proteomic data on the same tumor samples have been generated at UT MD Anderson Cancer Center using RPPAs, a high-throughput antibody-based technique (see tcpaportal.org and Li et al. 2013). RPPA technology has been developed for large-scale functional proteomic studies that evaluate protein/phosphoprotein activities in signaling networks and is more reliable and less expensive than traditional high-throughput proteomic technologies such as enzyme-linked immunosorbent assay and mass spectroscopy (Paweletz et al., 2001; Tibes et al., 2006). In addition to gene expression and proteomic data, TCGA collects clinical information, e.g., cancer stage, histologic subtype, and survival times, with some cancers (e.g., kidney and ovarian cancers) having more mature survival data with a sufficient number of events and follow-up times to allow us to build prognostic models for those cancers.
Although there are many underlying scientific questions posed by these data, we focus on integrating genomic, proteomic and clinical information to select relevant prognostic markers. Our main interest is the following biologically and clinically meaningful tasks across multiple cancers: 1) Detect patient-level prognostic protein markers, and 2) Investigate the mechanism of genomically driven protein markers. In Section 6, we analyze data from multiple cancers and identify both cancer-specific and pan-cancer prognostic proteins.
1.2. Overview of our model
To address these tasks, we propose a novel statistical model to construct clinically relevant protein biomarkers by integrating the genomic, proteomic and clinical information, which may assist in developing proteogenomically driven precision medicine (Pinto et al., 2014). One naive way would be to regress clinical outcomes on the genomic and proteomic data and apply a variable selection technique to select protein markers. However, this simple approach does not consider interactions between genes and proteins, which is inappropriate because some proteins form complexes with other proteins or RNA molecules and function very differently in the presence of these other molecules (Hartwell et al., 1999). One remedy would be to add interaction terms into the model, but since the biochemistry of the interaction is often quite complex (Kitano, 2002), in practice, it is hard to pre-specify the type or form of such interactions a priori. To allow for flexible interactions, one can incorporate varying coefficients (Hastie and Tibshirani, 1993) into the regression model. However, that cannot account for tumor heterogeneity because the selected biomarkers are presumably the same for all patients. In this paper, we propose a novel Bayesian hierarchical framework, Bayesian hierarchical varying-sparsity regression (BEHAVIOR) models, to achieve our scientific goal and overcome the aforementioned drawbacks. Our framework has three major innovations:
Sparsity in both protein-outcome and protein-gene relationships. Sparsity is a critical assumption in a high-dimensional setting where the number of parameters is much larger than the sample size. Here, we impose two levels of sparsity: (i) sparsity in the protein-outcome relationship and (ii) sparsity in the protein-gene relationship, which allows us to simultaneously identify clinically relevant, genomically driven protein biomarkers. This two-level sparsity is induced through a combination of a thresholding function/parameter and spike-and-slab priors.
Accounting for genomic heterogeneity. Our approach selects genomically driven protein markers by “borrowing strength” among patients with similar genomic profiles. We take tumor heterogeneity into account by integrating patient-specific genomic information and allowing protein makers and their effects on clinical outcomes to vary across patients. For each patient, our approach can identify a set of protein markers that can be potentially targeted by personalized clinical treatments.
Functional nonlinearity in protein-gene relationships. We allow for flexible nonlinear relationships between the proteins and genes, using spline-based semiparametric formulations and relaxing the usual and often biologically unrealistic linearity constraint on the interaction between proteins and genes. This allows the model to distinguish the functional form of the relationships (linear or nonlinear) through suitable orthogonal basis decompositions.
We remark that the well-known varying-coefficient model (VCM, Hastie and Tibshirani (1993)) is a special case of our model. VCM is a class of flexible statistical models which, if applied to our setting, allows the effect of proteins to vary with gene expressions. Several papers, for example, Wang et al. (2008a) and Fan et al. (2014), have been proposed to obtain sparse estimators for VCMs by using variable selection techniques. However, none of these methods allows the sparsity of the protein-outcome relationship to vary simultaneously with gene expression, which is a novel feature of our approach. Empirically, we illustrate our approach through simulation studies in which we compare our approach to VCM.
The rest of this paper is organized as follows. We present BEHAVIOR in Section 2 and discuss the prior distributions in Section 3. We summarize the posterior inference and prediction in Section 4. We present detailed simulation studies in Section 5 and a real data application in Section 6. Section 7 describes our visualization web application and online supplementary materials. Section 8 provides our closing discussion.
2. Bayesian hierarchical varying-sparsity regression model
The two main components that define our proposed model are described in the following sections: we introduce the concept of varying-sparsity mechanism in Section 2.1 and define specific varying sparsity model constructions in Section 2.2. In Section 2.3, we introduce a regression model for time-to-event outcomes that will be used to analyze our motivating TCGA-based cancer proteogenomics data.
2.1. Varying-sparsity regression model
Let Yi denote a patient’s outcome of interest, such as survival time, and let Pi = (Pi1, …, Pip) denote a p-dimensional vector of protein expressions for patient i = 1,…, n. A regression model can be used to study the relationship between response Yi and protein expressions Pi. For generality, we do not specify the regression type in this section (which can be, for example, generic linear regression, survival regression, quantile regression, generalized linear models), but only assume that the regression function is linear in Pi, i.e., .
In our study, for each protein Pij, j = 1, …, p, we also observe its matched gene expressions Gij = (Gij1, …, Gijqj), which can be a qj-dimensional vector to reflect the fact that multiple genes can translate to the same protein. Notice that it is possible for Gijk = Gij’k’ for all i = 1, …., n because one gene may code for multiple proteins due to, for example, alternative splicing (Chen and Manley, 2009). In addition, we expect that some of the proteins Pij’s may not be relevant to every patient’s outcome Yi and that the effect βj of each protein may also vary across patients, both of which we assume are determined by patients’ gene expressions Gij. To incorporate this, we propose a varying-sparsity model that allows βj to vary with Gij in terms of both strength and sparsity,
| (1) |
where βj(Gij) is an unknown function of Gij, termed the varying-sparsity coefficient. The modeling details of βj(Gij) are given in the next section.
2.2. Modeling varying-sparsity coefficient and protein selection
In this section, we discuss the construction of the varying-sparsity coefficient βj(Gij). We first model βj(Gij) as a smooth function of Gij· and then threshold it to induce (varying) sparsity and allow for protein selection.
Modeling βj(Gij) as a smooth function has two motivations. First, it reflects the assumption that patients with similar genomic characteristics should have similar protein markers. The smoothness ensures that the sparsity of βj changes smoothly with the genes Gij. Second, it can also be understood as a way of continuously “borrowing strength” by pooling genomic information from “neighboring” patients. Otherwise, we would not have sufficient power for estimation since our goal is to allow each patient to have his/her own set of protein markers. Specifically, we construct βj (·) as the sum of the spline functions (although in general, any other nonlinear functional representation can also be adopted):
| (2) |
with fjk(Gijk) = where represents the spline bases for Gijk and αjk is the corresponding spline coefficient. Discussion on the choices of spline bases is provided in Supplementary Material A.
Since βj(·) is modeled by a set of smooth spline functions, no coefficient would be exactly zero, even if the corresponding protein has little effect on the survival time. This is an undesirable feature because in our application we do not expect all proteins to be prognostic for a patient’s survival time; therefore, it is hard to interpret those non-zero and insignificant coefficients. Hence, we would like to encourage the sparsity in the varying-sparsity coefficients by shrinking small effects to exact zeros. A common Bayesian approach to induce sparsity is through spike-and-slab priors, where a binary latent variable is assigned to each coefficient to indicate its significance. However, this approach is not suitable in our case because the coefficients in our model are subject-specific and we will heavily overfit the data if we assign a latent variable for each coefficient and each patient. As the number of parameters would substantially increase, we take a different variable selection approach via introducing a Bayesian hard-thresholding function to truncate small effects to zeros and select prognostic proteins. To this end, let h(x,t) = xI(|x| > t) denote a hard-thresholding operator on variable x with a random threshold t. We modify (2) to
where the first argument of h(·, ·) is the spline components in (2). The thresholding parameter λj can be interpreted as a minimum effect size of the varying-sparsity coefficient βj (·). Moreover, we do not fix the thresholding parameter but let the data dictate the choice of minimum effect size by assigning a prior distribution, which will be discussed in Section 3. We illustrate the difference between Bayesian and classic hard-thresholding mechanisms in Supplementary Material A.
We note that VCM can be viewed as a special case of BEHAVIOR by fixing λj = 0. In VCM, the regression coefficients vary smoothly with the covariates (i.e., genes in our case study), but the sparsity/structure of the model remains constant across subjects. We compare the variable selection and predictive performance of BEHAVIOR with those of VCM in simulation studies (Section 5).
2.3. Hierarchical varying-sparsity accelerated failure time model
In this paper, we focus on a prognostic model where the response is the patient’s survival time, denoted by Ti. The main reason is that the information of survival times is mature (and well-calibrated) for many cancers across TCGA and this allows for pan-cancer comparisons of prognostic markers (both gene and protein). The accelerated failure time (AFT) model is commonly used to model the direct relationship between survival Ti and covariates Pi. While, in principle any time-to-event regression model could be adopted here e.g., Cox and Weibull; we choose AFT to make inferences on the varying-sparsity coefficients comparable across cancers. Here, we propose to embed AFT in our BEHAVIOR framework to accommodate gene expressions Gij, which take the form in (1) with an identity link g(·) and Yi = log(Ti). When Yi is normally distributed (i.e., Ti is log-normally distributed), our model can be equivalently expressed as
| (3) |
with ϵi ~ N(0,1). However, in general, ϵi can be any distribution such as an extreme value distribution. Survival times are often observed subject to censoring. In what follows, let Ci be the independent censoring time. Instead of directly observing the survival time Ti, we observe and Δi = I(Ti < Ci). Let and then the likelihood of model (3) is given by
where f (·) and S(·) are the respective density and survival functions of ϵi.
3. Priors and gene selection
In this section, we discuss the prior specifications of the three sets of parameters defined in the previous sections: (i) spline coefficients αjk; (ii) thresholding parameter λj; and (iii) variance parameter σ2.
Spline coefficients.
We penalize the curvature of spline functions fjk(·) (Ruppert et al., 2003) to obtain a flexible fit with appropriate smoothness. We choose a large enough number of knots to capture the local features and regularize the spline coefficients by imposing an improper Gaussian random walk prior αjk ~ N(0,sK−) where the singular penalty matrix K is constructed from the second order differences of the adjacent spline coefficients. There are two caveats. First, equation (2) is not identifiable since adding a constant to any term in the summation of (2) and subtracting it from any other term does not change the value of the summation. Second, the singularity of K implies that there is no penalty on the constant and linear trend of fjk(·). To address these two issues, we follow the treatment in Scheipl et al. (2012) and transform the bases of the splines into orthonormal bases. Let and take the spectral decomposition of the covariance of where Ujk is an orthonormal matrix of eigenvectors associated with the positive eigenvalues in the diagonal matrix Djk. With orthogonal bases and an independent proper prior parameterizes the nonlinear part of fjk(·) and has a proper distribution that is proportional to that of the improper prior of . Therefore, the full reparameterization of fjk(·) is , where is the ith row of and the intercept is merged into a global constant term αj,
| (4) |
This parameterization allows us to assign separate shrinkage/selection priors and hence to separately shrink/select relevant constant effect αj, linear effect and nonlinear effect (details are given in Section 3). For efficient computation in practice, we usually only retain the first several eigenvectors and eigenvalues that explain 99.5% of the variability. For example, in our case study, we choose 20 bases, but the dimension of is around 10.
The smooth function in (4) defines a constant effect αj, a linear effect and a nonlinear effect . In our model, we assume that the relationship between the gene and the protein is sparse, that is, only a small number of genes are expected to have influence on the prognostic effect of proteins. To this end, we impose a parameter-expanded normal- mixture-of-inverse-gamma (peNMIG) prior on each of αj, and . peNMIG gives rise to a more efficient Markov chain Monte Carlo (MCMC) algorithm than conventional spike-and-slab priors due to the multivariate nature of the spline coefficients; details are provided in Supplementary Material A. Here, for notational ease, we use as an example to describe the construction of the peNMIG prior; the same prior is used for αj and . We multiplicatively expand , where ηjk is a scalar parameter indicating the relevance of and ξjk is a vector of the same size as .
Prior for gene selection.
We assign a spike-and-slab prior on ηjk’s as:
where γjk ~ Bernoulli(p), where v0 is a fixed very small number. The binary variable γjk indicates the significance of j and hence i.e. γjk = 1(0), the effect of protein j on the clinical outcome is (not) modified nonlinearly by its coding gene k. Conjugate hyper-priors are assumed for Tjk ~ IG(αT, αT) and ρ ~ Beta(αp,αp) to complete the prior formulation. The beta-Bernoulli prior automatically correct for multiplicity since the posterior distribution of ρ will become more concentrated at small values near 0 as the total number of genes increases (Scott et al., 2010).
For each element of vector , we impose a normal mixture prior which avoids assigning too much mass around zero and hence discourages small effects. Similarly, we assume peNMIG priors for αj and .
Prior for protein selection.
As discussed in Section 2.2, the thresholding parameter λ j encourages sparsity of the protein-survival relationship and determines the minimum size of the protein effect on the patient’s survival time. When αj, , all equal 0, λ j can take any positive value since ßj(·) is always zero. We resolve this identifiability issue by setting λj = λ, ∀j. As long as at least one of βj(·)’s is non-zero, λ is well defined as the minimum effect size. Since we have no prior knowledge of the true minimum effect size, we put a non-informative prior on λ ~ Unif(0, bλ). The upper bound bλshould be greater than the smallest protein effect size that one is still willing to consider as significant. A practical guidance of choosing bλ and a sensitivity analysis of bλ are given in Supplementary Materials A and C, respectively.
Finally, we assume a conjugate prior for the variance parameter0 σ2 ~ IG(aσ,bσ). A schematic representation of the complete hierarchical model is provided as a directed tree graph in Supplementary Material A.
4. Posterior inference and prediction
Since the posterior is not analytically available, we sample parameters from the posterior distributions using an MCMC algorithm. At each iteration, each parameter is updated by Gibbs sampler. When the full conditional distribution is not available in closed form, we update it through a Metropolis step. Protein and gene selection are based on marginal posterior inclusion probabilities. We use median probability model motivated by its predictive optimality in linear models (Barbieri et al., 2004). However, different probability cutoffs can be considered as well. For example, to adjust for multiplicity, one can choose a cutoff such that the posterior expected false discovery rate (FDR) is controlled under a desired level. The detailed MCMC algorithm and expected FDR calculation are provided in Supplementary Material B. Here, we discuss the process of using posterior samples for predictions.
Suppose we have a new patient with protein and gene expressions (Pn+1, Gn+1)and we want to predict his/her survival time. We need to transform back to since there is no straightforward calculation for the new design matrix due to the spectral decomposition. This can however be done by solving the linear equations , where the superscript (l) indicates the 1th MCMC sample. Then the log(Tn+1) can be predicted by
where L is the total number of MCMC samples and .
5. Simulations
In this section, we empirically evaluate the variable selection and predictive performance of BEHAVIOR through simulation studies. To the best of our knowledge, we are not aware of any other methods that carry out the same type of inference as our model; therefore, we compare BEHAVIOR to its special case, VCM, which is given by setting A = 0. The setup of our simulation mimics the kidney renal clear cell carcinoma (KIRC) data we analyze in Section 6.2. We generate p = 9 proteins (for a given pathway) as Pij ~ N(0,1) and for each protein j, we generate qj genes Gij = (Giji,…, Gijqj ) ~ N(0,Iqj), where q1 = q2 = 2, q3 = q4 = 3 and q5 = · · · = q9 = 1. We use the first three proteins to generate the survival times
| (5) |
with σ = 1, n = 400 and βj(Gij) = h ßj(Gij),λ} where θ1(Gi1) = —2Gi11, and θ3(Gi3) = 2sin(πGi31/2). The error term ϵi is simulated from a standard extreme value distribution ϵi ~ f (ϵi) = exp(ϵi)exp{— exp(ϵi)}. An independent set of censoring times is sampled from log(Ci) ~ N(c, 1) where the constant c is chosen such that the censoring rate is close to that of the KIRC data (~ 65%) in our later application. We also generate an independent test dataset in the same manner for evaluating the predictive power. We consider four scenarios with different true thresholds, λ ϵ {0,0.1,0.3, 0.5}, to reflect different true minimum effect sizes.
We use cubic B-splines with 16 interior knots (i.e., 20 bases). The hyperparameters are specified as (ατ,bT) = (5,100), v0 = 2.5 × 10−4,bλ = 1, (ασ,6σ) = (10−4,10−4), (ap,bp) = (0.5, 0.5) to be non-informative (sensitivity analyses are provided in Supplementary Material C). For both methods, we run 200,000 MCMC iterations with a burn-in of 100,000 iterations and a thinning of 5. For each scenario, we report the results based on 50 repetitions.
To assess the two-level variable selection performance, we calculate the true positive rate (TPR), FDR, Matthews correlation coefficient (MCC) and area under the receiver operating characteristic curve (AUC) for both gene and protein selections where
with TP, TN, FP and FN denoting the true positives, true negatives, false positives and false negatives, respectively. The operating characteristics are summarized in Table 1, with prefixes g and p denoting gene and protein, respectively. Clearly, BEHAVIOR is able to select important (linear or nonlinear) protein-gene relationships (gAUC~1 for all scenarios) with a spike-and-slab prior and spline construction. BEHAVIOR also accurately identifies patient-specific prognostic proteins (pAUC>0.99 across scenarios) because we allow patient-level genomic information to be shared across patients.
Table 1:
Varying-sparsity accelerated failure time model versus generalized additive coefficient model in four scenarios. The numbers are calculated on the basis of 50 repetitions; standard errors are within parentheses.
| λ | BEHAVIOR | VCM | λ | BEHAVIOR | VCM | ||
|---|---|---|---|---|---|---|---|
| 0 | 0.3 | ||||||
| gTPR | 1.000 (0.000) | 1.000 (0.000) | gTPR | 1.000 (0.000) | 1.000 (0.000) | ||
| gFDR | 0.035 (0.088) | 0.020 (0.069) | gFDR | 0.035 (0.088) | 0.030 (0.082) | ||
| gMCC | 0.976 (0.060) | 0.986 (0.047) | gMCC | 0.976 (0.060) | 0.979 (0.056) | ||
| gAUC | 1.000 (0.000) | 1.000 (0.000) | gAUC | 1.000 (0.000) | 1.000 (0.000) | ||
| pTPR | 0.929 (0.037) | 1.000 (0.000) | pTPR | 0.976 (0.029) | 1.000 (0.000) | ||
| pFDR | 0.018 (0.041) | 0.077 (0.117) | pFDR | 0.056 (0.063) | 0.180 (0.130) | ||
| pMCC | 0.927 (0.046) | 0.926 (0.119) | pMCC | 0.936 (0.058) | 0.832 (0.165) | ||
| pAUC | 0.996 (0.010) | 0.965 (0.061) | pAUC | 0.998 (0.004) | 0.926 (0.084) | ||
| MSPE | 0.061 (0.034) | 0.062 (0.039) | MSPE | 0.065 (0.034) | 0.070 (0.040) | ||
| 0.1 | 0.5 | ||||||
| gTPR | 1.000 (0.000) | 1.000 (0.000) | gTPR | 1.000 (0.000) | 1.000 (0.000) | ||
| gFDR | 0.025 (0.076) | 0.025 (0.076) | gFDR | 0.033 (0.092) | 0.035 (0.088) | ||
| gMCC | 0.983 (0.052) | 0.983 (0.051) | gMCC | 0.977 (0.065) | 0.976 (0.060) | ||
| gAUC | 1.000 (0.000) | 1.000 (0.000) | gAUC | 1.000 (0.000) | 1.000 (0.000) | ||
| pTPR | 0.954 (0.034) | 1.000 (0.000) | pTPR | 0.973 (0.023) | 1.000 (0.000) | ||
| pFDR | 0.036 (0.056) | 0.141 (0.132) | pFDR | 0.060 (0.070) | 0.243 (0.122) | ||
| pMCC | 0.933 (0.054) | 0.867 (0.144) | pMCC | 0.932 (0.061) | 0.784 (0.138) | ||
| pAUC | 0.997 (0.007) | 0.938 (0.077) | pAUC | 0.998 (0.003) | 0.907 (0.076) | ||
| MSPE | 0.066 (0.030) | 0.066 (0.038) | MSPE | 0.068 (0.033) | 0.088 (0.043) |
In comparison, our method BEHAVIOR outperforms VCM in all scenarios in terms of protein selection. This can be easily seen from Figure 2. As expected, the performance of VCM is closer to that of our method when the true threshold decreases and the pMCC’s are almost identical for the two approaches when the true λ = 0 (i.e., the true model is VCM). For gene selection, our method slightly outperforms VCM, but the difference is not substantial.
Figure 2:
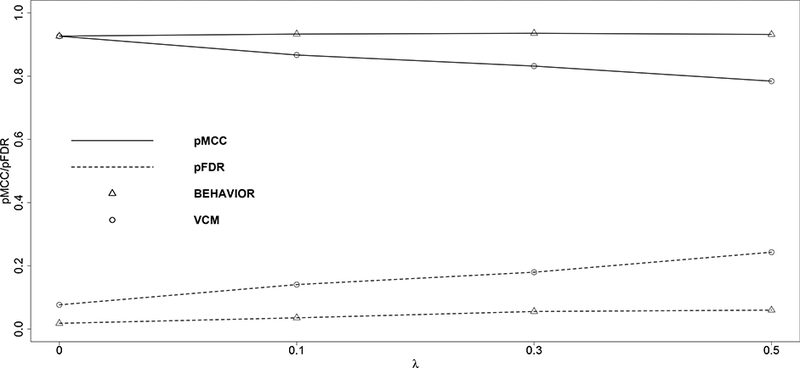
Matthews correlation coefficient (solid lines) and false discovery rate (dashed lines) are plotted against the true values of the thresholds. Triangular markers indicate BEHAVIOR; circular markers indicate VCM.
For predictive performance, we compute the mean squared prediction error (MSPE) on the independent test dataset. Again, our method BEHAVIOR is slightly better than VCM, especially when the true λ is larger. For example, when λ = 0.5, the MSPE’s are 0.068 and 0.088 for BEHAVIOR and VCM, respectively. We construe that the additional prediction efficiency gained with BEHAVIOR over VCM is likely due to the extra parsimony and better signal detection that BEHAVIOR introduces to the protein-survival relationship by the thresholded prior.
We perform additional simulations to assess the performance of BEHAVIOR under different sample sizes n, numbers of proteins p and numbers of genes qj per protein. We set true λ = 0.3, σ = 1 and qj = q for j = i.e.,…, p, i.e. q genes per protein. We consider p + 1 ϵ {20, 50,100}, n G {100, 200, 300} and q ϵ {5,10}. The data are generated from (5) with the true number of protein makers and gene-protein interactions and censoring rate kept approximately the same as previous simulation studies. The results are reported in Table 2. We found that the overall performance of BEHAVIOR does not deteriorate quickly as sample size decreases and the number of proteins and the number of genes per protein increase. And we observe that reducing the number q of genes per protein does not seem to affect the protein selection and prediction.
Table 2:
BEHAVIOR models under different combinations of the sample size n and the number of proteins p. The number of gene per protein is set to qj = q for j = 1,…, p. The summary is based on 50 repetitions; standard errors are within parentheses.
|
n = 400, q = 1 |
p + 1 = 10, q = 1 |
n = 400, p + 1 = 10 |
||||||
|---|---|---|---|---|---|---|---|---|
|
p + 1 |
n |
q |
||||||
| 20 | 50 | 100 | 100 | 200 | 300 | 5 | 10 | |
| gTPR | 1.000 (0.000) | 1.000 (0.000) | 1.000 (0.000) | 0.927 (0.139) | 1.000 (0.000) | 1.000 (0.000) | 1.000 (0.000) | 1.000 (0.000) |
| gFDR | 0.005 (0.035) | 0.078 (0.122) | 0.143 (0.183) | 0.060 (0.145) | 0.081 (0.150) | 0.102 (0.197) | 0.034 (0.142) | 0.058 (0.123) |
| gMCC | 0.997 (0.023) | 0.955 (0.071) | 0.917 (0.112) | 0.885 (0.185) | 0.926 (0.151) | 0.884 (0.259) | 0.973 (0.133) | 0.967 (0.071) |
| gAUC | 1.000 (0.000) | 0.999 (0.003) | 0.998 (0.005) | 0.998 (0.011) | 1.000 (0.000) | 1.000 (0.000) | 1.000 (0.002) | 1.000 (0.002) |
| pTPR | 0.984 (0.019) | 0.969 (0.032) | 0.971 (0.024) | 0.945 (0.061) | 0.939 (0.041) | 0.947 (0.037) | 0.985 (0.025) | 0.965 (0.073) |
| pFDR | 0.089 (0.088) | 0.148 (0.147) | 0.220 (0.194) | 0.236 (0.136) | 0.113 (0.109) | 0.062 (0.068) | 0.089 (0.097) | 0.088 (0.119) |
| pMCC | 0.933 (0.056) | 0.896 (0.089) | 0.854 (0.125) | 0.744 (0.138) | 0.854 (0.092) | 0.908 (0.052) | 0.911 (0.094) | 0.894 (0.116) |
| pAUC | 0.999 (0.001) | 0.999 (0.002) | 0.999 (0.001) | 0.972 (0.024) | 0.988 (0.007) | 0.994 (0.005) | 0.997 (0.003) | 0.993 (0.028) |
| MSPE | 0.074 (0.043) | 0.097 (0.062) | 0.146 (0.124) | 0.459 (0.215) | 0.183 (0.071) | 0.109 (0.057) | 0.084 (0.046) | 0.098 (0.148) |
6. Pan-Cancer Proteogenomic Analyses
TCGA launched a Pan-Cancer initiative in 2012 to study differences as well as similarities in molecular alterations across cancer types (www.nature.com/tcga). It currently has aggregated comprehensive genomic, proteomic and survival data across 33 cancer types.
In Section 6.1, we represent a pan-cancer analyses, across tumor-types that have the most mature survival data, and investigate commonalities as well as disparities across these cancers. In Section 6.2, we present a more granular analysis for kidney cancer that exhibited the strongest prognostic proteogenomic signals.
6.1. Pan-cancer analysis
Several pan-cancer studies (Weinstein et ah, 2013; Omberg et ah, 2013) have shown that disparate cancers share many common molecular characteristics. Studying such commonalities across cancer types and organs of origin improves our understanding of cancer biology, and shared molecular patterns can potentially allow us to extend therapeutic discoveries in one cancer to other cancers with similar genomic prohles. Our goal of this analysis is to correlate patient outcome with pathways/proteins and differentiate cancer-specihc pathways/proteins with those related to multiple cancer types.
Through a literature review, we focus on 12 core signaling pathways that have known/estab-lished role in cancer progression and development: apoptosis, breast reactive, cell cycle, core reactive, DNA damage response, EMT, hormone receptor, hormone signaling, PI3K/AKT, RAS/MAPK, RTK, and TSC/mTOR. Pathway members (proteins and their coding genes) are given in Supplementary Material D; details of selecting these pathways and their members can be found in Akbani et al. (2014). We retrieve and match genomic, proteomic and clinical data using software TCGA-Assembler (Zhu et al., 2014) and map them to the 12 pathways. The data generating and preprocessing procedures are described in Supplementary Material D. We consider four cancers for which TCGA has the most mature survival data (i.e., the greatest number of deaths/events): kidney renal clear cell carcinoma (KIRC), ovarian serous cystadenocarcinoma (OVCA), skin cutaneous melanoma (SKCM) and head and neck squamous cell carcinoma (HNSC). KIRC and OVCA have similar numbers of events, 142 and 135, respectively; SKCM and HNSC have smaller and similar numbers of events, 105 and 103, respectively. The characteristics of each cancer is summarized in Supplementary Material D. We apply BEHAVIOR separately to each type of cancer and pathway combination (4× 12 = 48 analyses). We run four parallel MCMC chains, each with 500,000 iterations, a burn-in of 250,000 iterations and a thinning of 5. The Markov chains appear to be convergent by MCMC diagnostics (details provided in Supplementary Material D). The average (standard deviation) computation time across cancers and pathways is 0.67 (0.19) hours on a 3.5 GHz Intel Core i7 processor. The average posterior expected FDR is 8.6% across 4 cancers and 12 pathways. The average numbers of selected protein markers per patient per pathway across cancers are provided in Table 3 of Supplementary Material D.
Protein-based analysis.
We find that some protein markers are shared by multiple cancers while others are exclusively relevant to one cancer. For example, protein PTEN is found to be prognostic for both HNSC and KIRC, which is consistent with the findings from the biological literature (Cantley and Neel, 1999; Squarize et al., 2013; Wang et al., 2015). The effect of PTEN on patients’ survival times changes with the expression of its coding gene and is quite different between HNSC and KIRC, which is depicted in Figure 3 (first two plots). The effect of protein PTEN for KIRC is almost always negative, whereas it varies between negative and positive values for HNSC. There is an interesting parabolalike relationship between the effect of protein PTEN and its coding gene PTEN in KIRC, possibly due to a feedback mechanism and interaction with proteins that are also coded by gene PTEN. In fact, a previous study (Wang et al., 2015) discovered that gene PTEN codes for multiple proteins, some of which (e.g., PTEN and PTEN-Long) are of therapeutic significance in KIRC.
Figure 3:
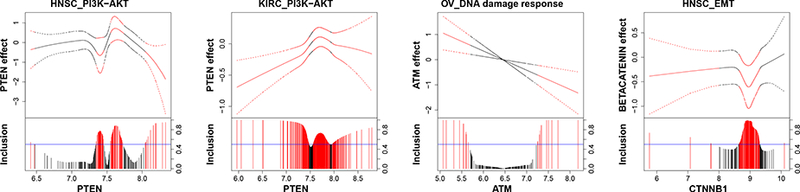
Protein markers. For each graph, the fitted curve of protein effects (solid line) with 95% credible bands (dashed line) are shown in the top portion, and marginal posterior inclusion probabilities are shown in the bottom portion. The gene expression that modifies the protein effect is given on the x-axis. Blue horizontal line is the 0.5 probability cutoff. Red lines and curves indicate significant coefficients.
There are also protein markers that are only prognostic for a particular cancer type. For instance, we found constant effects (independent of their coding genes) of pro-apoptotic proteins BIM and BAX that are prognostic in SKCM, which has been shown to be crucial for melanoma tumor cell survival (Anvekar et al., 2011). We also found some varying effects, for example, a linearly varying effect of protein ATM in OVCA and a nonlinearly varying effect of beta-catenin in HNSC are delineated in Figure 3 (right two plots), both of which are supported by the oncological literature (Thorstenson et al., 2003; Yang et al., 2006).
To visualize the genomic-heterogeneity (or homogeneity) patterns between patients, we cluster the estimated prognostic protein effects βj(Gij). In Figure 4, we present a heatmap of estimated effects for HNSC, with blue (red) indicating negative (positive) effects. The rows (patients) and columns (proteins) are grouped by a hierarchical clustering algorithm with complete linkage. We observe that patients with similar prognostic protein effects naturally form subpopulations. For example, patients are divided into at least three subgroups by the effect of PTEN: positive, negative and neutral. Therefore, a treatment that targets PTEN is not likely to be successful for patients from all subgroups. Another promising finding is androgen receptor (AR) which also exhibits clear heterogeneity across patients (a similar heatmap with PTEN removed for better visualization of other protein effects is provided in Supplementary Material D). Although PTEN-targeted therapy is limited for HNSC, androgen deprivation therapy (ADT) has been proved effective for certain patient subpopulations (Rades et al., 2013; Soper et al., 2014; Chintakuntlawar et al., 2016; Dalin et al., 2017). Our analysis generates a hypothesis that patients with negative AR effects on survival may have better response to ADT. We also observe that the effect of beta-catenin is less variable across patients and is mostly negative for HNSC patients. In fact, a potent differentiation therapeutic agent, all-trans-retinoic acid, is found to inhibit growth of HNSC stem cells by suppressing beta-catenin and its signaling pathway (Lim et al., 2012).
Figure 4:
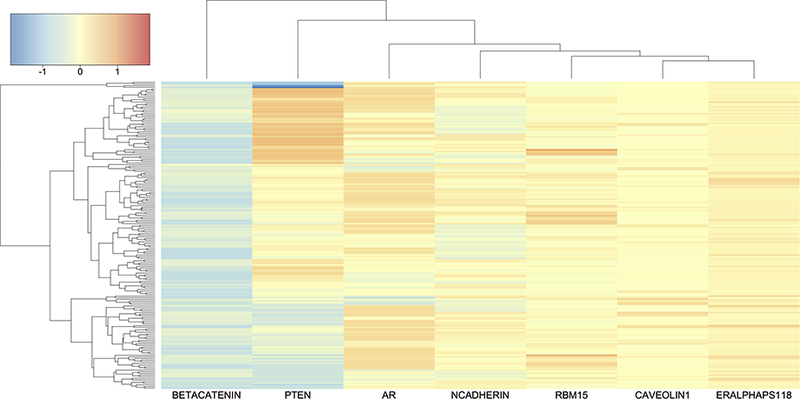
Heatmap of prognostic protein effects βj (Gij) for HNSC. The rows (patients) and columns (proteins) are grouped by hierarchical clustering with complete linkage. Color scale is given in the top left corner.
Pathway-based analysis.
To further evaluate the prognostic abilities of proteomic path-ways, we score each pathway/cancer combination by a concordance index (c-index) of within-sample survival time prediction. C-index is a measure of how well the survival model predicts the data and is defined as the ratio of the number of concordant predicted survival times against the number of all possible pairs that can be ordered,
where O = {(i, j)|Δi = 1, Yi < Yj}. C-index reaches 1 when the prediction is perfect (in terms of ranking) and equals 0 when the ranking of the prediction is completely reversed. C-index is usually above 0.5, the value for which the model has no power in predicting survival. We show c-indices across cancers and pathways using a radial plot in Figure 5, which is also reported as a table in Supplementary Material D. In the radial plot, the distance between a dot and the center represents the c-index for different cancers (indicated by color) and pathways (indicated by radius).
Figure 5:
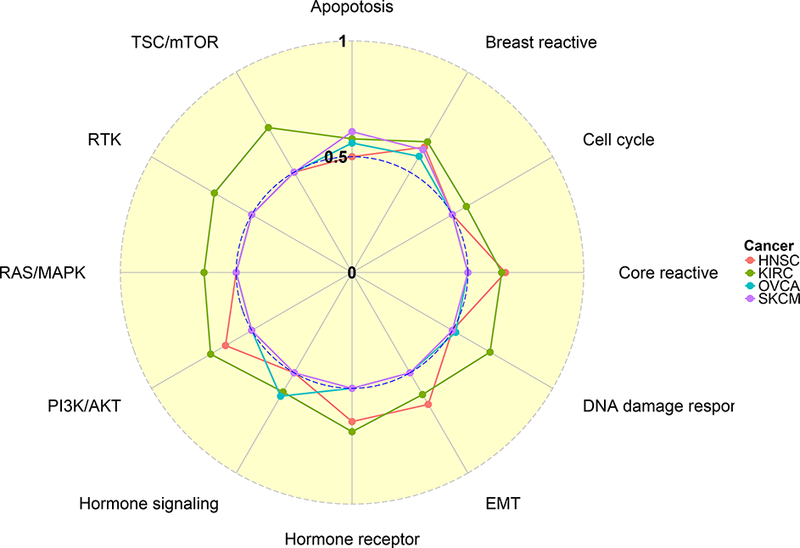
Radial plot of c-index. C-indices of survival time prediction are computed across 4 cancers and 12 pathways. Pathways are shown at the outer ring and cancer types are represented by different colors, for which the legend key is given on the right. Each dot lies on one of the 12 radii and represents a c-index for a specific pathway/cancer combination. The c-index takes values of 0, 0.5 and 1 at the center, inner ring and outer ring, respectively.
Interestingly, some pathways are unique to certain cancers while others are shared by several cancers. For example, the hormone receptor pathway is only prognostic for F1NSC and KIRC. The former is confirmed by the biological literature (Akbani et ah, 2014) and the latter is a potential target for novel molecular drugs. In contrast, the breast reactive pathway appears to be prognostic for all four cancers and the apoptosis pathway is prognostic for KIRC, OVCA and SKCM. An effective therapy that targets a particular pathway for one cancer can be potentially used to treat other cancers for which the same pathway shows similar prognostic relevance. Since the analysis for KIRC shows the strongest signal among the four cancers (Figure 5), which is also observed from a pan-cancer proteomic analysis on virtually the same TCGA dataset by Akbani et al. (2014), we present a more comprehensive analysis for KIRC in Section 6.2.
6.2. Detailed analysis for kidney renal clear cell carcinoma
Kidney renal clear cell carcinoma (KIRC) is a chemotherapy-resistant cancer that is in great need of personalized molecular therapy (TCGA, 2013). We have data available from 428 patients, 286 of whom are censored (67% censoring rate). The median survival time is 2256 days from Kaplan-Meier estimates.
Our BEHAVIOUR analyses identify a total of 44 protein markers across 12 pathways, some of which have well understood biological and clinical significance in KIRC. For example, DNA repair protein RAD50, a member of the DNA damage response pathway, shows a linearly varying effect on patients’ survival times (Figure 6). Individuals with mutations in RAD50 and the DNA damage response pathway are at higher risk of developing KIRC (Margulis et al., 2008). Interestingly, the sign for the effect of RAD50 changes around 7, and the implication is that if a drug targeting RAD50 is assigned to two groups of patients with distinct genomic profiles (e.g., one group with gene expression of RAD50 > 7 and another with RAD50 < 7), they may experience very different responses to the drug.
Figure 6:
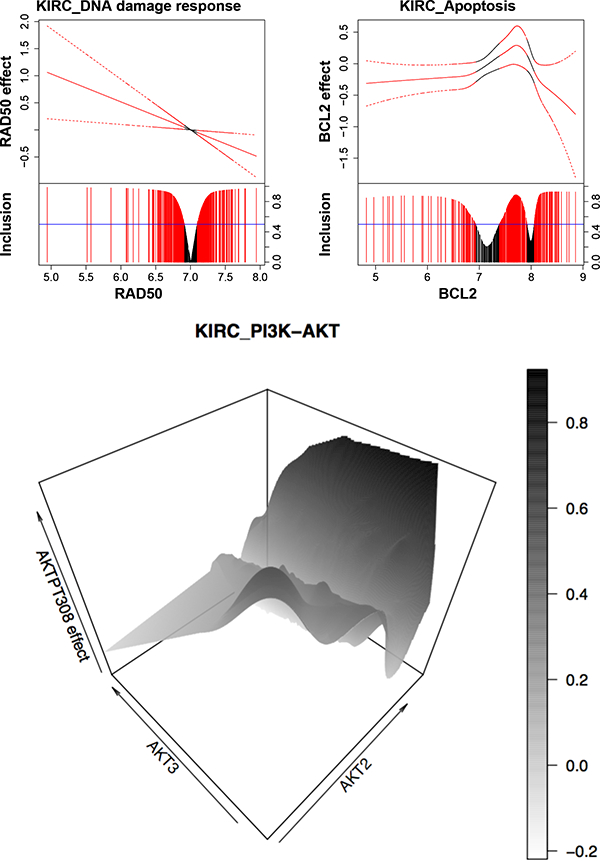
Protein markers for KIRC. For the first two graphs, the fitted curve (solid line) with 95% credible bands (dashed line) are shown in the top portion, and marginal posterior inclusion probabilities are shown in the bottom portion. Blue horizontal line is the 0.5 probability cutoff. Red lines and curves indicate significant coefficients. The last graph is a 3-D plot with gene expressions of AKT2 and AKT3 on X- and Y-axes, and the effect of protein AKTPT308 on Z-axis.
We also find protein BCL2 to be prognostic for KIRC, which is supported by the findings from prior studies (Lee et al., 2003) that oncoproteins of the BCL2 family are important regulators of apoptosis (programmed cell death). This is consistent with our finding that the effect of BCL2 is mostly negative on patients’ survival times (Figure 6). The exception is when the expression of oncogene BCL2 is between around 7 and 8. Treatments that aim to downregulate BCL2 may show little effect for patients with BCL2 expression within that range.
Another interesting finding is that the effect of protein AKTPT308 (also known as phosphoAKT-PT308) varies with two coding genes, AKT2 (nonlinearly) and AKT3 (linearly), which is presented as a 3-D plot in Figure 6. Protein AKT is a hub for key oncogenic processes, including cell proliferation, survival and angiogenesis for multiple cancers such as KIRC (Banumathy and Cairns, 2010). In KIRC in particular, AKT is constitutively activated compared to its status in normal renal tissue (Lin et al., 2006). Our study suggests there may be a complex interaction or feedback loop within the AKT family, that is, interaction between AKTPT308 and proteins that are also coded from AKT2 and AKT3, which further implies that therapy that simultaneously blocks multiple members of the AKT family would be more likely to be effective than treatment that targets phosphoAKT-PT308 alone. We also assess the prognostic effect aggregated across patients of each protein for all pathways in KIRC in Supplementary Material D.
For comparison, we include the tumor stage as a predictor in our analysis. Expectedly, c-index is increased across 12 pathways (by 0.09 on average). However, the number of selected protein markers was significantly reduced by 65.5% (0.81 vs 2.36 proteins per patient per pathway) because the tumor stage is so informative to the prognostics that it overwhelms the contribution of proteomic and genomic data in predicting the survival. We also apply a sparse AFT model with elastic net penalty (Wang et al., 2008b) to protein data only. We find BEHAVIOR has a greater predictive power (higher c-index) in 8 out of 12 pathways.
7. Web application for visualization and supplementary materials
In order to allow for broad dissemination of our results and software, we have created, using the R package shiny (Chang et al., 2015), an interactive web application (available at https://sites.google.com/site/yangniresearchsite/behavior) to interactively display the varying effects of prognostic proteins of different critical pathways in response to the user’s choice of the desired expressions of their respective encoding genes. This allows our results easily accessible to the broader scientific and research community. We provide two screenshots of the application in Figure 7.
Figure 7:
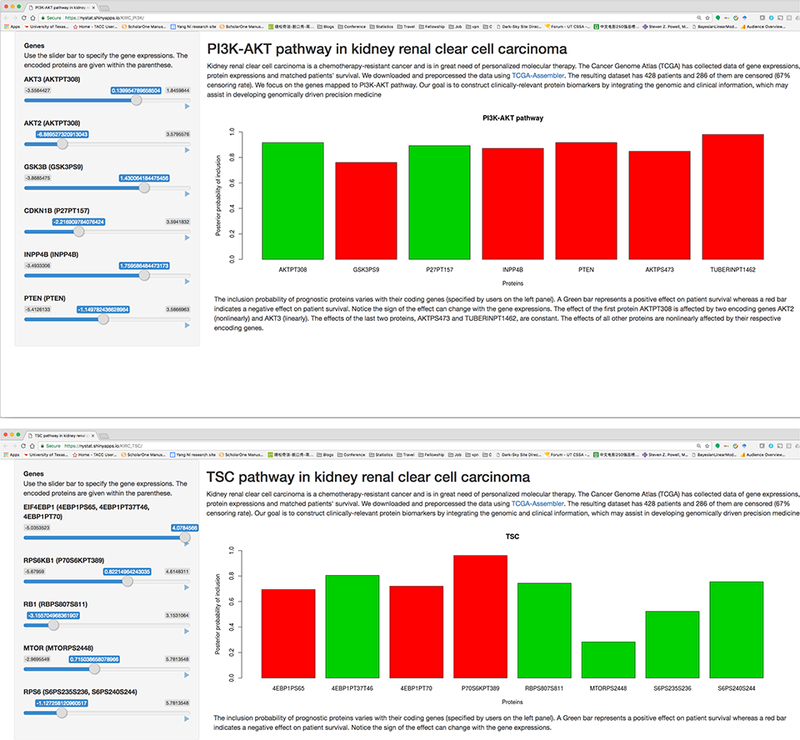
Screenshots of varying protein effects in respective encoding genes the web application. The application interactively displays the response to the user’s choice of the desired expressions of their through sliders in the left panel.
Supplementary materials and the Matlab program implementing our method are available with this paper at the journal’s website.
8. Discussion
In this article, we propose a general regression framework, Bayesian hierarchical varying- sparsity regression (BEHAVIOR), to model complex interactions between multiple-levels of hierarchical covariates on a given outcome. Our semi-parametric spline-based formulations allow for flexible relationships between the covariates as well as distinguish the functional form of the relationships. Furthermore, through a combination of spike-slab priors and thresholding functions, we impose a two-levels of sparsity, both in outcome-covariate and covariate-covariate relationships. We show that the traditional varying coefficient models are a special case of our model and show that BEHAVIOR outperforms VCM in terms of both variable selection and prediction.
Our methods are motivated by a novel dataset in proteogenomics, wherein we model patients’ survival times integrating their corresponding genomic and proteomic data across multiple cancers. Applying BEHAVIOR to this TCGA proteogenomic dataset, we found proteins and pathways that are prognostic for only some specific cancers as well as proteins and pathways that are shared by multiple cancers. We reconstruct the functional form of the relationship between genomically driven protein markers and their coding genes, which may potentially aid in developing personalized treatments that target these specific markers. Our analysis for KIRC demonstrates how the effect of a prognostic marker changes across patients according to their genomic profiles, and therefore the traditional “one-size-fits-all” treatment may have disparate outcomes for different patients. Our study also suggests that some markers may function in groups and their interactions are nonlinear and complex, which in turn implies that a treatment that blocks protein markers and their close interactants may be more effective than a treatment that targets one marker alone.
We do note that currently BEHAVIOR only considers one cancer at a time and therefore may be less efficient than a joint approach that models different cancers simultaneously. This inefficiency may be somewhat mitigated as we obtain more mature data for each cancer. From a modeling perspective, a joint approach that accounts for associations across cancers may be more efficient and possibly detect more signals from the existing data. This is one direction for our future work.
In our current framework, we only utilize transcript expressions of known isoforms that are available from TCGA. However, de novo isoforms also provide important information complementary to existing measurable isoform and protein abundances. Inference on novel isoforms is by itself an interesting research topic, which is, however, not the focus of this paper.
We also remark that BEHAVIOR does not take into account the uncertainty or error in the data quantification and bioinformatics pre-processing procedures for the raw-level transcriptomic and proteomic data. To fully account for the uncertainty, researchers need to work directly with the raw data, which is both statistically and computationally challenging.
While the focus of this paper is prognostic models, a varying-sparsity coefficient can be incorporated into many other models. For example, we may use logistic regression to classify cancer subpopulations with a varying-sparsity coefficient that is conditional on clinical covariates. This would allow each patient to have his/her unique set of covariates that are relevant for classification. Similarly, in quantile regression, the quantile regression coefficients can also be replaced by varying-sparsity coefficients. We plan to work on extensions of our model in the future.
Another contribution of our work is towards establishing the translational relevance of the functional proteome and pathways in research and clinical settings. To this end, we have created an online repository of all our results, scores and pathway signatures that are easily accessible to the scientific and research community.
Supplementary Material
References
- Akbani R, Ng PKS, Werner HM, Shahmoradgoli M, Zhang F, Ju Z, Liu W, Yang J-Y, Yoshihara K, Li J, et al. (2014). A pan-cancer proteomic perspective on the cancer genome atlas. Nature communications, 5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alfaro JA, Sinha A, Kislinger T, and Boutros PC (2014). Onco-proteogenomics: cancer proteomics joins forces with genomics. Nature methods, 11(11):1107–1113. [DOI] [PubMed] [Google Scholar]
- Anvekar RA, Asciolla JJ, Missert DJ, and Chipuk JE (2011). Born to be alive: a role for the bcl-2 family in melanoma tumor cell survival, apoptosis, and treatment. Frontiers in oncology, 1(34). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Banumathy G and Cairns P (2010). Signaling pathways in renal cell carcinoma. Cancer biology & therapy, 10(7):658–664. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barbieri MM, Berger JO, et al. (2004). Optimal predictive model selection. The annals of statistics, 32(3):870–897. [Google Scholar]
- Cantley LC and Neel BG (1999). New insights into tumor suppression: Pten suppresses tumor formation by restraining the phosphoinositide 3-kinase/akt pathway. Proceedings of the National Academy of Sciences, 96(8):4240–4245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang W, Cheng J, Allaire J, Xie Y, and McPherson J (2015). shiny: Web Application Framework for R. R package version 0.12.2.
- Chen M and Manley JL (2009). Mechanisms of alternative splicing regulation: insights from molecular and genomics approaches. Nature reviews Molecular cell biology, 10(11):741–754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chintakuntlawar AV, Okuno SH, and Price KA (2016). Systemic therapy for recurrent or metastatic salivary gland malignancies. Cancers of the Head & Neck, 1(1):11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Church GM (2004). Proteogenomic mapping as a complementary method to perform genome annotation. Proteomics, 4:59–77. [DOI] [PubMed] [Google Scholar]
- Dalin MG, Watson PA, Ho AL, and Morris LG (2017). Androgen receptor signaling in salivary gland cancer. Cancers, 9(2):17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davies M, Hennessy B, and Mills GB (2006). Point mutations of protein kinases and individualised cancer therapy. [DOI] [PubMed]
- De Bono J and Ashworth A (2010). Translating cancer research into targeted therapeutics. Nature, 467(7315):543–549. [DOI] [PubMed] [Google Scholar]
- Fan J, Ma Y, and Dai W (2014). Nonparametric independence screening in sparse ultra-high-dimensional varying coefficient models. Journal of the American Statistical Association, 109(507):1270–1284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gygi SP, Rochon Y, Franza BR, and Aebersold R (1999). Correlation between protein and mrna abundance in yeast. Molecular and cellular biology, 19(3):1720–1730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hartwell LH, Hopfield JJ, Leibler S, and Murray AW (1999). From molecular to modular cell biology. Nature, 402:C47–C52. [DOI] [PubMed] [Google Scholar]
- Hastie T and Tibshirani R (1993). Varying-coefficient models. Journal of the Royal Statistical Society. Series B (Methodological), pages 757–796. [Google Scholar]
- Heppner GH and Miller BE (1983). Tumor heterogeneity: biological implications and therapeutic consequences. Cancer and Metastasis Reviews, 2(1):5–23. [DOI] [PubMed] [Google Scholar]
- Jacob F, Goldstein DR, Fink D, and Heinzelmann-Schwarz V (2009). Proteogenomic studies in epithelial ovarian cancer: established knowledge and future needs. Biomarkers in medicine, 3(6):743–756. [DOI] [PubMed] [Google Scholar]
- Kitano H (2002). Computational systems biology. Nature, 420(6912):206–210. [DOI] [PubMed] [Google Scholar]
- Lee CT, Genega EM, Hutchinson B, Fearn PA, Kattan MW, Russo P, and Reuter VE (2003). Conventional (clear cell) renal carcinoma metastases have greater bcl-2 expression than high-risk primary tumors In Urologic Oncology: Seminars and Original Investigations, volume 21, pages 179–184. Elsevier. [DOI] [PubMed] [Google Scholar]
- Lessene G, Czabotar PE, and Colman PM (2008). Bcl-2 family antagonists for cancer therapy. Nature reviews Drug discovery, 7(12):989–1000. [DOI] [PubMed] [Google Scholar]
- Li B and Dewey CN (2011). Rsem: accurate transcript quantification from rna-seq data with or without a reference genome. BMC bioinformatics, 12(1):323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li J, Lu Y, Akbani R, Ju Z, Roebuck PL, Liu W, Yang J-Y, Broom BM, Verhaak RG, Kane DW, et al. (2013). Tcpa: a resource for cancer functional proteomics data. Nature methods, 10(11):1046–1047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lim YC, Kang HJ, Kim YS, and Choi EC (2012). All-trans-retinoic acid inhibits growth of head and neck cancer stem cells by suppression of wnt/β-catenin pathway. European Journal of Cancer, 48(17):3310–3318. [DOI] [PubMed] [Google Scholar]
- Lin F, Zhang PL, Yang XJ, Prichard JW, Lun M, and Brown RE (2006). Morphoproteomic and molecular concomitants of an overexpressed and activated mtor pathway in renal cell carcinomas. Annals of Clinical & Laboratory Science, 36(3):283–293. [PubMed] [Google Scholar]
- Locard-Paulet M, Pible O, de Peredo AG, Alpha-Bazin B, Almunia C, Burlet- Schiltz O, and Armengaud J (2016). Clinical implications of recent advances in pro- teogenomics. Expert review of proteomics, (just-accepted). [DOI] [PubMed] [Google Scholar]
- Longo DL (2012). Tumor heterogeneity and personalized medicine. N Engl J Med, 366(10):956–957. [DOI] [PubMed] [Google Scholar]
- Margulis V, Lin J, Yang H, Wang W, Wood CG, and Wu X (2008). Genetic susceptibility to renal cell carcinoma: the role of dna double-strand break repair pathway. Cancer Epidemiology Biomarkers & Prevention, 17(9):2366–2373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McLendon R, Friedman A, Bigner D, Van Meir EG, Brat DJ, Mastrogianakis GM, Olson JJ, Mikkelsen T, Lehman N, Aldape K, et al. (2008). Comprehensive genomic characterization defines human glioblastoma genes and core pathways. Nature, 455(7216):1061–1068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nagalakshmi U, Waern K, and Snyder M (2010). Rna-seq: a method for comprehensive transcriptome analysis. Current protocols in molecular biology, pages 4–11. [DOI] [PubMed] [Google Scholar]
- Nesvizhskii AI (2014). Proteogenomics: concepts, applications and computational strategies. Nature methods, 11(11):1114–1125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Omberg L, Ellrott K, Yuan Y, Kandoth C, Wong C, Kellen MR, Friend SH, Stuart J, Liang H, and Margolin AA (2013). Enabling transparent and collaborative computational analysis of 12 tumor types within the cancer genome atlas. Nature genetics, 45(10):1121–1126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paweletz CP, Charboneau L, Bichsel VE, Simone NL, Chen T, Gillespie JW, Emmert-Buck MR, Roth MJ, Petricoin E, and Liotta LA (2001). Reverse phase protein microarrays which capture disease progression show activation of pro-survival pathways at the cancer invasion front. Oncogene, 20(16):1981–1989. [DOI] [PubMed] [Google Scholar]
- Pinto N, Black M, Patel K, Yoo J, Mymryk JS, Barrett JW, and Nichols AC (2014). Genomically driven precision medicine to improve outcomes in anaplastic thyroid cancer. Journal of oncology, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rades D, Seibold N, Schild S, Gebhard M, and Noack F (2013). Androgen receptor expression. Strahlentherapie und Onkologie, 189(10):849–855. [DOI] [PubMed] [Google Scholar]
- Ruppert D, Wand MP, and Carroll RJ (2003). Semiparametric regression. Number 12 Cambridge university press. [Google Scholar]
- Scheipl F, Fahrmeir L, and Kneib T (2012). Spike-and-slab priors for function selection in structured additive regression models. Journal of the American Statistical Association, 107(500):1518–1532. [Google Scholar]
- Scott JG, Berger JO, et al. (2010). Bayes and empirical-bayes multiplicity adjustment in the variable-selection problem. The Annals of Statistics, 38(5):2587–2619. [Google Scholar]
- Soper MS, Iganej S, and Thompson LD (2014). Definitive treatment of androgen receptor-positive salivary duct carcinoma with androgen deprivation therapy and external beam radiotherapy. Head & neck, 36(1):E4–E7. [DOI] [PubMed] [Google Scholar]
- Squarize CH, Castilho RM, Abrahao AC, Molinolo A, Lingen MW, and Gutkind JS (2013). Pten deficiency contributes to the development and progression of head and neck cancer. Neoplasia, 15(5):461–471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- TCGA (2012). Comprehensive genomic characterization of squamous cell lung cancers. Nature, 489(7417):519–525. [DOI] [PMC free article] [PubMed] [Google Scholar]
- TCGA (2013). Comprehensive molecular characterization of clear cell renal cell carcinoma. Nature, 499(7456):43–49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thorstenson YR, Roxas A, Kroiss R, Jenkins MA, Kristine MY, Bachrich T, Muhr D, Wayne TL, Chu G, Davis RW, et al. (2003). Contributions of atm mutations to familial breast and ovarian cancer. Cancer Research, 63(12):3325–3333. [PubMed] [Google Scholar]
- Tibes R, Qiu Y, Lu Y, Hennessy B, Andreeff M, Mills GB, and Kornblau SM (2006). Reverse phase protein array: validation of a novel proteomic technology and utility for analysis of primary leukemia specimens and hematopoietic stem cells. Molecular cancer therapeutics, 5(10):2512–2521. [DOI] [PubMed] [Google Scholar]
- Wang H, Zhang P, Lin C, Yu Q, Wu J, Wang L, Cui Y, Wang K, Gao Z, and Li H (2015). Relevance and therapeutic possibility of pten-long in renal cell carcinoma. PloS one, 10(2):e114250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang K, Singh D, Zeng Z, Coleman SJ, Huang Y, Savich GL, He X, Mieczkowski P, Grimm SA, Perou CM, et al. (2010). Mapsplice: accurate mapping of rna-seq reads for splice junction discovery. Nucleic acids research, 38(18):e178–e178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang L, Li H, and Huang JZ (2008a). Variable selection in nonparametric varying-coefficient models for analysis of repeated measurements. Journal of the American Statistical Association, 103(484):1556–1569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang S, Nan B, Zhu J, and Beer DG (2008b). Doubly penalized buckley-james method for survival data with high-dimensional covariates. Biometrics, 64(1):132–140. [DOI] [PubMed] [Google Scholar]
- Wang Z, Gerstein M, and Snyder M (2009). Rna-seq: a revolutionary tool for tran-scriptomics. Nature Reviews Genetics, 10(1):57–63. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weinstein JN, Collisson EA, Mills GB, Shaw KRM, Ozenberger BA, Ellrott K, Shmulevich I, Sander C, Stuart JM, Network CGAR, et al. (2013). The cancer genome atlas pan-cancer analysis project. Nature genetics, 45(10):1113–1120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang F, Zeng Q, Yu G, Li S, and Wang C-Y (2006). Wnt/β-catenin signaling inhibits death receptor-mediated apoptosis and promotes invasive growth of hnscc. Cellular signalling, 18(5):679–687. [DOI] [PubMed] [Google Scholar]
- Zhu Y, Qiu P, and Ji Y (2014). Tcga-assembler: open-source software for retrieving and processing tcga data. Nature methods, 11(6):599–600. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


