One model to rule them all? Modelling approaches across OneHealth for human, animal and plant epidemics

Abstract

One hundred years after the 1918 influenza outbreak, are we ready for the next pandemic? This paper addresses the need to identify and develop collaborative, interdisciplinary and cross-sectoral approaches to modelling of infectious diseases including the fields of not only human and veterinary medicine, but also plant epidemiology. Firstly, the paper explains the concepts on which the most common epidemiological modelling approaches are based, namely the division of a host population into susceptible, infected and removed (SIR) classes and the proportionality of the infection rate to the size of the susceptible and infected populations. It then demonstrates how these simple concepts have been developed into a vast and successful modelling framework that has been used in predicting and controlling disease outbreaks for over 100 years. Secondly, it considers the compartmental models based on the SIR paradigm within the broader concept of a ‘disease tetrahedron’ (comprising host, pathogen, environment and man) and uses it to review the similarities and differences among the fields comprising the ‘OneHealth’ approach. Finally, the paper advocates interactions between all fields and explores the future challenges facing modellers.

This article is part of the theme issue ‘Modelling infectious disease outbreaks in humans, animals and plants: approaches and important themes’. This issue is linked with the subsequent theme issue ‘Modelling infectious disease outbreaks in humans, animals and plants: epidemic forecasting and control’.

1. Introduction

Infectious diseases of humans, animals and plants have adversely affected humanity throughout recorded history. This was recognized over 3000 years ago in the Bible, which identified threats to human, animal and plant health: ‘Cursed shall be the fruit of thy body [human], and the fruit of thy land [plant], the increase of thy kine [cows] [animals], and the flocks of thy sheep [animals]’ (Deuteronomy 28:18, King James Version).

In the wake of World War I, the 1918 influenza epidemic caused approximately 50 million deaths and was one of the biggest pandemics in the history of humankind [1]. Twenty-five years later, while another World War was raging, a ‘perfect storm’ [2] of environmental and political disasters led to a series of disease outbreaks in India. In October 1942, a fungal infection, Cochliobolus miyabeanus (brown spot), spread through rice fields in Bengal. The impact of the disease was intensified by tropical storms which caused the fungal spores to be widely distributed, leading to estimated yield losses of up to 91% of the key staple crop, rice [3]. The local population faced severe food shortages which were further magnified by the concurrent political situation, leading to massive starvation and a decrease in resistance to diseases. Meanwhile, the weather also created conditions conducive to mosquito breeding, leading to an outbreak of malaria, causing twice as many cases in 1943 as reported in the preceding years [4]. In combination with other human diseases like cholera and smallpox, which also thrived in an already affected population, an estimated 2–3 million people died as a result. More suffering and displacement followed in what became known as the Bengal Famine.

These events, as well as other similar epidemics, such as Asian flu [5], black death [6], foot-and-mouth [7] and the Irish potato famine [8], clearly demonstrate the interconnectedness between the health of humans, animals, plants and ecosystems: the underlying principle of the OneHealth concept [9].

If we are to avoid future outbreaks such as the 1918 influenza pandemic or the 1942–1943 Bengal Famine, we need to create an approach that is collaborative, interdisciplinary and cross-sectoral, which includes human and veterinary medicine, and plant epidemiology, as well as mathematical modelling. Mathematical models have extensively been used to understand, predict and control disease outbreaks with many successes [10,11]. However, a continuing need exists to facilitate the collaboration between the modellers working across these different fields, enabling knowledge exchange and the development of approaches that take into account more than one system.

This paper attempts to facilitate this dialogue by reviewing the ways in which different research communities apply the compartmental models based on the susceptible–infected–removed (SIR) paradigm. Our approach then embeds the SIR framework in the even broader concept of a ‘disease tetrahedron’, originating in plant epidemiology. By doing so, we show how the SIR model family can be adapted to address particular modelling needs which are both specific to the individual areas and generic across all fields of epidemiology. Finally, we look at some future directions of further model development.

This review is necessarily brief, and further detail is available from many books and papers that illustrate these developments, from a historical point of view and from mathematical and epidemiological angles. For medical epidemiology, the textbook of Anderson & May [10] is still one of the best options, with Keeling & Rohani [12] providing a more recent overview. Anderson & May [13,14] and Kao [15] contain additional references for animal diseases, and Madden et al. [11] and Gilligan [16] for compartmental models of plant pests. The three volumes of the 1993 programme at the Isaac Newton Institute, Cambridge, UK [17–19], and the follow-up in Epidemics a decade later [20], also provide a valuable overview of past, current and future challenges.

2. Key components of an epidemic

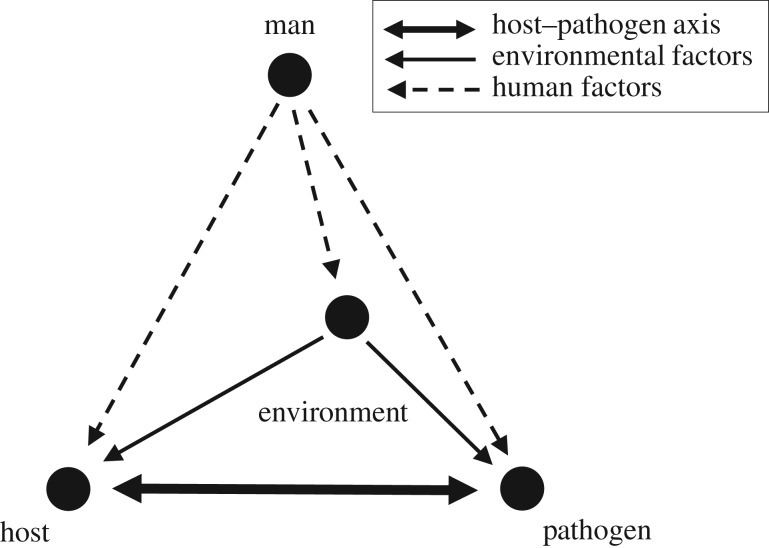
For both an outbreak to be initiated and the pathogen to spread, a number of conditions need to be fulfilled. Van der Plank [21] and Zadoks & Schein [22] summarized these conditions in the form of a disease tetrahedron, with corners comprising host, pathogen, environment and man (figure 1). Firstly, the host and the pathogen need to be in a state that is conducive to the disease and able to interact at the same time and in the same location (figure 1; thick arrows). The host and pathogen states are, in turn, affected by the environmental drivers (figure 1; thin arrows). All three elements are influenced by human actions, including prevention, interference and control (figure 1; broken arrows).

Figure 1.

Disease tetrahedron; modified after Zadoks & Schein [22]. Nodes correspond to the main determinants of a disease outbreak: host, pathogen, environment and man. The thick double arrow represents the host–pathogen axis. Thin solid arrows indicate the influence of environment on the host–pathogen combination. Broken arrows represent the human factor affecting all components.

3. The model

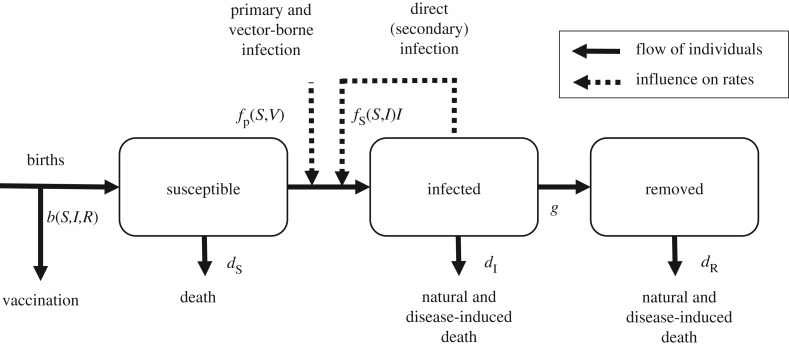
Compartmental models provide a widely used framework for describing the interaction between the host and the pathogen. The key feature of the generic SIR model is that the population of N individuals is split into three classes: susceptible (S), infected and infectious (I), and recovered or removed (R) (figure 2). This reflects the assumption that there are no internal dynamics in the status of an infected individual and in its capacity to pass on the infection (a microparasite infection as defined in [10]). The models based on this paradigm may have different mathematical structures and we review some here, starting with a continuous-time and deterministic model,

$$\begin{array}{rl}\frac{\mathrm{d}S}{\mathrm{d}t}=\hspace{0.17em}& b(S,I,R)-f_{\mathrm{p}}(S,V)-f_{\mathrm{s}}(S,I)I-d_{S}S,\\ \frac{\mathrm{d}I}{\mathrm{d}t}=\hspace{0.17em}& f_{\mathrm{p}}(S,V)+f_{\mathrm{s}}(S,I)I-gI-d_{I}I\\ \mathrm{and}\frac{\mathrm{d}R}{\mathrm{d}t}=\hspace{0.17em}& gI-d_{R}R.\end{array}\}$$ 3.1

Figure 2.

A basic SIR model with primary and secondary infections, births, deaths, culling and natural and disease-induced death, as represented in equation (3.1). Solid arrows represent the flows of individuals between classes within the population (S, susceptible; I, infected; R, removed/recovered). Dashed lines represent the dependence of the infection rate on external and internal factors. Vaccination at birth effectively removes a proportion of individuals before they enter the population.

Above, b(S,I,R) represents the influx into the susceptible class, either from births or from a transition back from the removed class, minus potential vaccination. The rates, d_x (with x = S, I, R), quantify removal from either natural or disease-induced causes; g represents the removal of infected individuals into the R class which can be interpreted as removed or recovered and immune. The term b(S,I,R) is often constant, linear or logistic in its dependence on the population variables; the death and removal terms are typically linear, corresponding to exponentially distributed lifespan and infectious periods [23]. However, gamma-distributed infectious periods have been found to characterize the epidemiology of a number of diseases more accurately [24,25]. The two functions describing the primary or vector-based infection, f_p(S,V), and the secondary or direct infection, f_s(S,I), are discussed below.

The basic SIR model has been modified to suit many different systems. Other compartments, such as a latent class (infectious but asymptomatic) or a detected class [10,26,27], have been proposed to provide more fine-grained division. Age-structured models have also been introduced, either by utilizing sub-classes for the susceptible and infected individuals [28] and using a Who-Acquired-Infection-From-Whom matrix [10], or by adapting equation (3.1) into integro-differential equations by separating time and age variables [29].

Other extensions include difference, rather than differential, equations which use discrete time steps, rather than continuous time, with time interval often equal to the infectious period [30]. Discrete time is often assumed for stochastic and network models, and for the purpose of parameter estimation [31].

Different stochastic approaches have existed since the early days of mathematical epidemiology [32,33], and their correspondence to the deterministic case was put on firm footing by Kurtz and co-workers [34,35]. Variation in the infection rate can also be used to account for environmental and demographic stochasticity [36,37].

4. Hosts and pathogens

Before the model can be used to describe a real-life system, its key elements must be populated. The three host groups (humans, animals and plants) have different requirements and hence require different approaches while preserving the basic structure of the SIR family of models.

(a). Hosts

In medical epidemiology, there is only one primary host: the human being. This assumption, however, hides a possibility of alternative hosts and living stages of a pathogen, as it is now recognized that many human diseases are of zoonotic origin [38]. Veterinary epidemiology deals with two types of hosts: domestic (livestock and companion animals) and wild animals, with only a few species classed as important from a societal standpoint. The situation is very different for plants, where there exist a large number of domesticated and wild plant genera (both often in proximity to each other). Despite this, most models consider only a single host species.

The basic modelling unit is typically a single individual (human, animal or plant), although in the continuous approach summarized in equation (3.1), S and I are often densities per unit area. For animal diseases [15], and even more often for plant diseases [11], S and I can represent groups of individuals such as flocks or fields [15].

(b). Pathogens

The SIR paradigm describes the dynamics of microparasites, as defined by Anderson & May [10]. An alternative framework describing macroparasitic infection, where an individual load of infection is important, has attracted significant attention in medical and veterinary epidemiology [10,39], but less so for plant diseases [40]; these are not covered in this review.

Many human diseases (e.g. Ebola [41]) and animal diseases (e.g. bovine tuberculosis [42]) involve alternative hosts whose dynamics could be incorporated into the models. Malaria and dengue are examples of vector-borne diseases of humans [10,43], whereas bluetongue is an example of a vector-borne disease of animals [44]. Others, such as a measles virus [45], are confined to one host and directly transmitted. Few human and animal fungal disease outbreaks have been described by the SIR paradigm [46,47]; by contrast, the UK Plant Health Risk Register [48] currently lists 180 fungal pathogens and related species, but only 57 bacteria and 116 viruses. It is the sheer number of plant pathogens, many of which have a broad range of hosts, e.g. Xylella spp. [49], which makes their impact difficult to model. Despite this, compartmental models have been successfully used to describe the spread and control of plant and forest pathogens [11,50,51].

5. Host–pathogen axis

The functions f_p(S,V) and f_s(S,I) capture different aspects of host–pathogen interactions. The term f_p(S,V) describes an external source of infection, with V representing the external force of infection coming from the wider environment (e.g. primary inoculum for soil- or water-borne plant diseases [40]), from alternative hosts (e.g. bats [38]) or an indirect transmission mediated by vectors (e.g. mosquitoes [30]). There will often be a separate equation describing the dynamics of V and its link to the infectious population, I [13,14].

The f_s(S,I) term describes the direct transmission component which depends on the number of currently infected individuals. Different forms have been proposed which attempt to capture various aspects of the interaction. The most common approach [52,53] assumes that the rate at which new infections are produced is proportional to (i) the number of existing susceptible individuals, S; (ii) the proportion of existing infectious individuals, I/N; (iii) a factor capturing the rate of contacts between individuals, C(N), which is often dependent on the total population size, N; and (iv) a per-contact probability of infection, β. This results in

$$f_{\mathrm{s}}(S,I)I=\beta \hspace{0.17em}C(N)\hspace{0.17em}\frac{I}{N}S,$$ 5.1

with C(N) = N for density-dependent transmission and C(N) independent of N for frequency-dependent transmission [28,50,54].

The simplest SIR model removes the birth, death and primary infection terms from equation (3.1) and assumes a fixed population size, N, and a linear secondary infection term, equation (5.1). The resultant model describes the characteristic rise-and-fall, bell-shaped curve for I(t) often seen in medical and veterinary science [45,55]. When there is no discernable recovery or removal, the basic SIR model with frequency-dependent transmission can be rewritten as an SI model equivalent to a logistic growth model; this is often used in plant epidemiology [56].

6. Effective and basic reproduction rates

Another way of applying an SIR model uses the idea of an effective (or apparent) reproduction rate, R_t [21]. It is defined as the number of newly infected individuals produced by a single infected individual during its infectious period, at a given time t during the epidemic [57]. The rate R_t typically decreases as the susceptible individuals are removed from the population; its maximum value is denoted by R₀ and forms one of the most important concepts in epidemiology [10,52]. Surprisingly, for the 1918 influenza pandemic, the R₀ value estimate was only in the range of 2–3 [58], but it can be much higher for other diseases, e.g. 10–18 for measles [10].

The main advantage of characterizing an epidemic by the basic reproduction rate lies in the simplicity and predictive power of R₀. The number of infected individuals will never increase if R₀ < 1, and so the outbreak can be prevented or stopped by lowering the value of R₀. This condition is the foundation of many successful vaccination and control programmes [59]. The threshold dependence of the disease dynamics is well known in demography and ecology, and has been applied to vector-borne diseases [30], to directly transmitted human diseases [55] and to plant–pathogen systems [21,60]. The pathogen's evolutionary history has also been linked to the value of the reproduction rate [61].

7. Parameter estimation

Although qualitative results, like the threshold behaviour, can be obtained from studying the mathematical structure of the SIR equations, any potential to predict the size of the new epidemic, or impact of control measures, requires estimation of parameters [62]. In practice, it is often necessary to attempt to construct a predictive model based on insufficient and noisy data, which limits the capacity of models to capture all details of the real-world processes [15]. Among the parameters, the infection functions, f_p(S,V) and f_s(S,I), are most difficult to identify as they attempt to capture many complex processes [63]. Two broad approaches can be distinguished, with estimation based directly on the outbreak data using different proxies [57], including observed cases [64]; or through secondary data, e.g. serological studies for estimating the proportion of individuals having a contact with the disease in the past [65,66], or sociological studies yielding the contact patterns between individuals [67]. The two methods often produce different results, as the observation of cases can be biased by under-reporting [31].

Different statistical and modelling techniques [63] can be employed to estimate parameters in the presence of considerable within- and between-sample variation and to augment data, and can reveal different aspects of the disease dynamics (see [56] for least-squares method, [33] for a maximum-likelihood method and [68] for a full Bayesian treatment of the same dataset).

8. Environment: temporal heterogeneity

The functions f_p(S,V) and f_s(S,I) can depend on temperature, humidity and hence on time [36], thus making R₀ temporally variable [66,69]. This variation can be short-term (e.g. weather-driven) or long-term (e.g. climate-driven). Models have successfully been used to study the effect of environment on cholera outbreaks in humans [70,71]. The periodicity of school holidays has been shown to lead to complex dynamics in, for example, measles epidemics [72]. Less attention has been given to short-term weather effects on animal diseases [66]. Plant pathogens often have complex life cycles driven by environmental conditions (e.g. temperature and rainfall); this can be captured in compartmental models by varying rates in space and time [73,74].

The effects of climate change can be captured by variations in compartmental model parameters on a time-scale longer than the epidemic itself [70,75]. Vector-borne diseases have received particular attention owing to their dependence on insect populations which are characterized by narrower ranges of environmental factors that are conducive to their survival and spread [76].

9. Environment: spatial heterogeneity

Basic compartmental models effectively assume that each susceptible individual can be equally affected by any infected individual in the population, a property often called ‘homogeneous mixing’ [52]. This is often not true as some individuals can be separated by great distance. While humans and animals can travel large distances, their movements are often geographically and socially stratified, concentrated around schools, work and transportation routes. This is even more important for plants, which generally do not move (if we ignore trade), although the pathogens and their spores can travel large distances, owing to either wind or vectors. Mathematical epidemiologists have approached this problem in different ways, with some approaches more common in different areas.

Some plant epidemiologists [11,21] concentrate on independent pathogen movement (e.g. spores transported by wind or water) and thus convert the SIR differential equations into integro-differential ones [11], allowing transmission rates to be dependent on spatial distance [77].

Alternatively, by assuming that susceptible and/or infected individuals move randomly, the SIR model turns into reaction–diffusion equations, such as those describing spread of rabies [78] or plant pathogens [79]. Again, stochastic versions of the model have been developed, dealing with some artefacts of the continuous model [80].

Another solution, a metapopulation model, splits a geographical space into sub-compartments, then assumes that individuals fully mix within each compartment. The additional force of infection comes from other compartments, either from the nearest neighbours or with some distance-dependence [74,81].

In the early 1980s, a new paradigm was proposed, first by physicists [82,83] and later by epidemiologists [84]. Individuals are represented by vertices of a graph (network), and transmission is only possible if two vertices are connected by an edge. These network SIR models are currently at the forefront of epidemiological modelling for human diseases [12], animal diseases [85] and plant pathogens [86–88].

In the late 1990s, an approximation to network models was developed that captured some of the contact structure by measuring not only the average values of epidemiological variables (first moments), but also correlations between them (higher moments) [89]. This leads to modified SIR equations which may be easier to analyse than the spatially structured models.

10. Adding a human factor

The simple model shown above, equations (3.1) and (5.1), effectively ignores various ways in which our actions affect the infection dynamics and, conversely, the impact of disease on our behaviour. However, these feedbacks are an essential factor determining our ability to predict and control outbreaks [7,90,91]. Accordingly, models are continually being adapted to include the impact of human influence on disease transmission. Firstly, different groups of individuals can behave in different ways and hence experience different forces of infection. Thus, the division into SIR compartments can be expanded to capture different behaviours, such as hospitalization or avoidance of contacts (possibly due to fear or spread of rumours) [92]. The SIR compartments can also be subdivided into components representing location, social status or different risk groups (e.g. for sexually transmitted diseases). The infection term, here f_s(S,I), can be modified accordingly through the inclusion of, for example, a simple spatial structure [93], a city–satellite model [31] or various household models [94].

Secondly, the assumption that the combined infection term, f_s(S,I)I, is linear in the number of susceptible and infected individuals can be relaxed [28]. The power function is often used in this context [95–97], for example, to account for the heterogeneity of contacts between hosts, and was found to capture the dynamics of measles [95] and Ebola [96].

11. Conclusion: from genes to the globe

So, are we prepared for the next pandemic [98]? Like the 1918 influenza, and many other outbreaks, any future epidemics would most probably be associated with a ‘perfect storm’ of events. A combination of genetic (host and pathogen), environmental, economic and socio-political factors must be studied to understand how a pathogen can emerge and spread globally [9].

The world is now faced with new challenges which can combine again into a ‘perfect storm’ associated with issues such as climate change, the rise of antimicrobial resistance (AMR) and globalization which allows hosts and pathogens to travel long distances quickly.

The call to epidemiology is to bridge all scales, from a genetic to a global level. The catalyst for this interdisciplinary approach is the application of mathematical modelling. Here, we have argued that compartmental models can be, and indeed have been, used successfully to capture the complexities of the host–pathogen–environment interactions. However, we still need to improve our ability to work across different disciplines and fields comprising the OneHealth approach.

Three major opportunities are identified here as immediate areas for development. Firstly, we are now equipped with an unprecedented capacity to gather and analyse ‘big data’. Advances in data collection and computing power allow modellers to carry out simulations in which agents are traced as they move and interact, as vectors fly, or spores move with the wind. These individual-based models have been used, for example, to predict the threat posed by influenza in Southeast Asia [99], and the spread of sudden oak death in the USA [74]. Much attention in recent years has been given to social networks that explicitly incorporate the granularity of individual interactions and the heterogeneity of their behaviour, including animal and plant movements by trade [81,85]. We can now include the detailed genetic information about hosts and pathogens to augment modelling techniques to improve traceability of the progress of epidemics [100]. Linking detailed weather and climate change models with epidemic models allows us to predict any future outbreaks in more detail [70].

Secondly, human, animal and plant pathogens are in a constant race with their hosts, with evolution driving the resistance to any treatments or immunological responses. AMR is a rapidly rising problem that has the potential to enable epidemics not experienced since the pre-antibiotic era [101]. The environment is known to act as a ‘mixing bowl’ for water (containing antimicrobials) from humans, agriculture, plants and aquaculture [102]. However, it is still not known to what extent AMR genes transfer between species (e.g. livestock and humans) via the environment [103]. An SIR framework has been used to model AMR either at a host/patient level [104] or even at a cellular/within-host level [102]. The novelty of the latter approach is that S represents the antibiotic-sensitive bacterial cells, and I represents the antibiotic-resistant bacterial cells (‘infected’ with a resistant gene). Resistance has also been a major problem in plant diseases, leading to significant advances in modelling [105]; this is one area where cross-fertilization between plant and human/animal epidemiology can be very beneficial.

Thirdly, epidemiological models increasingly need to be merged with an economic and behavioural framework [106]. Epi- or bio-economic models [107] capture the individual or the corporate decision to engage in particular actions, such as changing the contact structure [108,109], engaging with prevention (e.g. vaccination) [110] or control by culling [26]. Recently, it has been argued that compartmental models can be extended to explicitly include adaptive behavioural responses to disease risk [111]. Thus, instead of a priori specifying the infection term f_s(S,I) in terms of S and I, the new approach uses explicit behavioural models describing how individuals formulate predictions on the effects of their decision whether to engage in a contact that might lead to infection. This prediction then informs their decision-making process, which often involves maximization of their profit or utility [111]; the infection process emerges from such considerations. Such models [109] can be used to explain the multiple waves of the 1918 influenza pandemic [112].

So, are we equipped to deal with the next pandemic? According to Blackburn et al. [98], the answer currently is a qualified ‘no’. However, the tools and processes may already be available to allow a more emphatic ‘yes’ to be the answer. Our future success in preventing and combating pandemics requires close collaboration across disciplines and systems. As demonstrated by their long and successful history, the SIR paradigm and the disease tetrahedron concept are essential tools facilitating such an approach.

Data accessibility

This article has no additional data.

Authors' contributions

A.K. conceived the design and wrote the first draft of the document. A.H. and P.M. contributed to the text; all authors revised the manuscript.

Competing interests

We have no competing interests.

Funding

This work was partly funded by the Tree Health and Plant Biosecurity Initiative (phase 2) grant by BBSRC, Defra, ESRC, Forestry Commission, NERC and Scottish Government, BB/L012561/1, the BBSRC project BB/M008894/1 and the NSF grant no. 1414374 as part of the joint NSF-NIH-USDA Ecology and Evolution of Infectious Diseases Program.