Virus epidemics, plant-controlled population bottlenecks and the durability of plant resistance

Abstract

Plant qualitative resistances to viruses are natural exhaustible resources that can be impaired by the emergence of resistance-breaking (RB) virus variants. Mathematical modelling can help determine optimal strategies for resistance durability by a rational deployment of resistance in agroecosystems. Here, we propose an innovative approach, built up from our previous empirical studies, based on plant cultivars combining qualitative resistance with quantitative resistance narrowing population bottlenecks exerted on viruses during host-to-host transmission and/or within-host infection. Narrow bottlenecks are expected to slow down virus adaptation to plant qualitative resistance. To study the effect of bottleneck size on yield, we developed a stochastic epidemic model with mixtures of susceptible and resistant plants, relying on continuous-time Markov chain processes. Overall, narrow bottlenecks are beneficial when the fitness cost of RB virus variants in susceptible plants is intermediate. In such cases, they could provide up to 95 additional percentage points of yield compared with deploying a qualitative resistance alone. As we have shown in previous works that virus population bottlenecks are at least partly heritable plant traits, our results suggest that breeding and deploying plant varieties exposing virus populations to narrowed bottlenecks will increase yield and delay the emergence of RB variants.

This article is part of the theme issue ‘Modelling infectious disease outbreaks in humans, animals and plants: approaches and important themes’. This issue is linked with the subsequent theme issue ‘Modelling infectious disease outbreaks in humans, animals and plants: epidemic forecasting and control’.

1. Introduction

Plant disease qualitative resistance, i.e. resistance that almost totally prevents any plant infection, does not often provide durable resistance to fungal, bacterial and viral pathogens [1–3]. For viruses, only one or two mutations in their genome may be sufficient to break down the resistance [4]. Once the resistance-breaking (RB) mutant has appeared, it has a disproportionate selective advantage to settle in a hitherto resistant cultivar [3].

By contrast, plant quantitative resistance partially reduces or delays disease development [5]. Combining qualitative and quantitative resistances may help increase the durability of qualitative resistances, as exemplified with the pvr2³ qualitative resistance gene to potato virus Y (PVY) in pepper plants [6]. This effect can result from a reduction in the fixation probability of RB mutations beneficial to the virus [7]. Two main evolutionary forces can modulate fixation probabilities of mutations: selection and genetic drift [8,9]. Selection is a deterministic force favouring the fittest variants. Genetic drift generates random fluctuations in variant frequencies, potentially purging variants regardless of their selective value [10]. Genetic drift is stronger in populations with smaller effective population size N_e [11], which can be defined as the size of an ideal population displaying the same fluctuations in allele frequencies as the population under study [12]. For a fixed selective value, the fixation probability of a beneficial mutation decreases with N_e [8].

Small N_e can be observed for viruses during colonization of new plant cells and leaves because population bottlenecks are rather common for those pathogens [12,13]. Depending on the plant–virus pair, N_e estimates vary from 1.15 to 1515 [14–16]. Moreover, during host-to-host transmission, N_e may be as low as 0.5–3.2 virus infectious units on average at inoculation of a plant by one insect vector [17,18]. Importantly, N_e of viruses during plant infection (at inoculation or during systemic movement) has been recently shown to be genetically controlled by pepper genotype for PVY and cucumber mosaic virus [15,16]. Such quantitative resistances reducing pathogen N_e are likely to be widespread at least for plant viruses. Thus, as proposed in medicine to limit the emergence of antibiotic-resistant bacteria [19], plant breeders may take advantage of these quantitative resistance factors to slow down pathogen adaptation and decrease the risks of RB [17,18].

Most epidemiological models of pathogen adaptation to a control method assume infinite pathogen population size [20]. However, intra-host N_e of PVY is negatively correlated to the durability of pvr2³ [21]. More generally, demographic stochasticity endured by pathogens within their hosts impacts the effectiveness of control methods, as exemplified for the speed of kill of the gypsy moth by a baculovirus [22]. Also, Lo Iacono et al. [23] proposed a stochastic model approximating the pathogen population size by the densities of infected hosts. They showed that stochastic extinctions of infected hosts occurring typically at the start of an epidemic impact resistance durability. Refining how stochasticity affects pathogen populations can be a critical and promising aspect to consider.

Here, we tested whether combining a quantitative resistance narrowing virus population bottleneck (decreasing N_e) with a qualitative resistance can increase the durability of the latter. We introduce a stochastic plant epidemic model based on classical healthy–infected deterministic models, coupling epidemiology and population genetics, and featuring mixtures of susceptible and resistant plants. By comparing yield benefits provided by a resistant cultivar combining qualitative and quantitative resistances (named pyramided resistance) with those of a resistant cultivar carrying only the qualitative resistance (named monogenic resistance), we estimated the added value of combining quantitative and qualitative resistances. We investigated the effects of the interactions between agroecosystem features (epidemic intensity, proportion of resistant cultivar) and the characteristics of the qualitative (fitness cost imposed on RB variants in susceptible plants) and quantitative (pathogen N_e) resistances on yield benefits. We found that those characteristics are essential to identify the strategies maximizing yield benefits.

2. Model overview

The model is based on [24]. It merges virus epidemic processes at the field scale and virus population genetics processes. It describes, during a cropping season lasting n_d days, the epidemic dynamics in a field composed of susceptible (S) and resistant (R) plants. The field has a constant number of plants, N^p, among which a proportion φ are R plants (number of R plants N^R = φN^p, and of S plants N^S = (1 − φ)N^p). Two virus variants are considered: the wild-type (WT) and RB variants. Only the RB variant can infect R plants, whereas both variants can infect S plants. Bottlenecks undergone by virus populations are considered both for host-to-host transmission and for subsequent within-host infection, from colonization of inoculated leaves (cell-to-cell movement) until the onset of systemic infection (electronic supplementary material, figure S1) [12]. During these steps, selection and mutation forces are neglected as we assume that demographic stochasticity is the dominant process. The model summarizes the global effect of all bottlenecks in a unique effective population size, denoted $N_{\mathrm{e}}^{\mathrm{R}}$ in R plants and $N_{\mathrm{e}}^{\mathrm{S}}$ in S plants. For R plants with monogenic resistance, i.e. without quantitative resistance narrowing bottlenecks, we set $N_{\mathrm{e}}^{\mathrm{R}}=N_{\mathrm{e}}^{\mathrm{S}}={10}^4$ to represent negligible demographic stochasticity, whereas for R plants with pyramided resistance, i.e. with additional quantitative resistance, we have $N_{\mathrm{e}}^{\mathrm{R}}<N_{\mathrm{e}}^{\mathrm{S}}$. The number of virus particles surviving bottlenecks is drawn from Poisson distributions, and determines the success of infection of a target plant (see electronic supplementary material, text S1 for details). After the bottlenecks have been passed, i.e. during systemic infection if it occurs, we assume that virus populations grow quickly to large sizes and thus only selection and mutation are considered. We assume that virus populations reach instantaneously their mutation–selection equilibrium, with 100% of RB variant in R plants and a frequency f_RB of RB variant in S plants. The equilibrium frequency f_RB results from the balance between the production of RB variants through recurrent mutations and their counter-selection in S plants because of the fitness costs associated with these RB mutations [25]. The frequency f_RB characterizes the qualitative resistance gene. For a given mutation rate, it depends on the number of mutations required for resistance breakdown and their associated fitness costs in S plants [24]. Main parameters are detailed in table 1.

Table 1.

Description of model parameters and values used for numerical simulations.

parameter	designation	unit	range or reference value
Ωint	epidemic intensity before deployment of R plants	unitless	[0.1, 0.9]
nd	duration of the cropping season	day	120
Np	number of plants in the field	plant	103
φ	proportion of R plants	unitless	[0.05, 0.95]
fRB	frequency of RB variant in S plants	unitless	[10−8, 0.5]
$N_{\mathrm{e}}^{\mathrm{R}}$	virus effective population size in R plants	virus or infectious unit	small: [1, 100] large: 104
$N_{\mathrm{e}}^{\mathrm{S}}$	virus effective population size in S plants	virus or infectious unit	104
niter	number of simulation iterations for each set of parameter values	unitless	500

Descriptions of deterministic and stochastic forms of the model are available in electronic supplementary material, text S1. The deterministic form is used to attribute meaningful values to a parameter representative of epidemic intensity in a reference field before deployment of R plants, whereas the stochastic form is used to conduct all simulations of R plant deployment.

3. Results

The analyses are based on ratios of the areas under the disease progress curves (AUDPCs), allowing assessment of the benefit of deploying R plants with monogenic or pyramided resistances (see electronic supplementary material, text S2 for details).

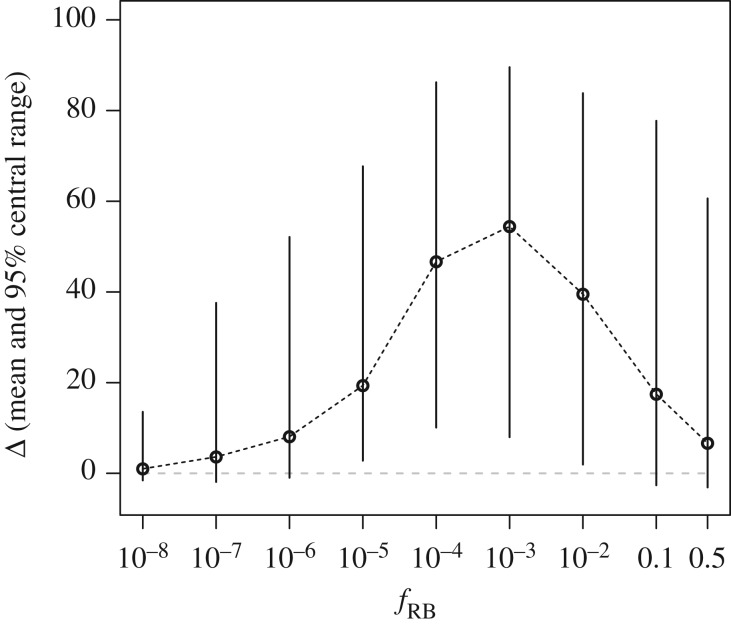
We first explored the percentage points of additional relative benefit, Δ, provided by the deployment of a pyramided resistance, δ_Rp, compared with a monogenic one, δ_Rm, as a function of RB variant frequency in S plants, f_RB, for all values of the other parameters (table 1). The frequency f_RB strongly impacts the value of Δ (figure 1), intermediate f_RB maximizing Δ. For f_RB in the range [10⁻⁵, 0.1], mean Δ remains above 17 percentage points. The highest Δ values are reached for f_RB = 10⁻³, with a mean of 54 percentage points and 95% of Δ values falling between 8 and 90 percentage points. Outside this range (f_RB < 10⁻⁵ or >0.1), the mean Δ remains less than 10 percentage points.

Figure 1.

Additional relative benefit Δ as a function of RB variant frequency in susceptible plants, f_RB. All values of the other parameters are combined and Δ corresponds to mean benefits over the 500 stochastic simulations for each combination of parameter values. Dots indicate means of Δ and segments indicate 95% central range for each f_RB value (over all combinations of the other parameters). The grey dashed line indicates the limit Δ = 0.

We then looked at the combined effects of the four factors Ω_int (epidemic intensity before deployment of R plants), f_RB, φ and $N_{\mathrm{e}}^{\mathrm{R}}$ on Δ to disentangle their specific impact (figure 2). Overall, optimal strategies correspond to large φ and small $N_{\mathrm{e}}^{\mathrm{R}}$ values. Let us first focus on the smallest f_RB value tested in figure 2 (10⁻⁴). When Ω_int is small or intermediate (0.2 or 0.5), $N_{\mathrm{e}}^{\mathrm{R}}$ has no visible effect on Δ. Highest Δ values are reached for largest φ, providing up to 50–60 percentage points of additional yield benefit when Ω_int = 0.2, and up to 80 percentage points when Ω_int = 0.5. When Ω_int is higher (0.8), a slight effect of $N_{\mathrm{e}}^{\mathrm{R}}$ appears, with Δ values up to 90–100 percentage points for small $N_{\mathrm{e}}^{\mathrm{R}}$ and large φ.

Figure 2.

Effect of four parameters representative of the host, the virus, epidemic intensity and the field on the additional relative benefit, Δ. Contour plots represent Δ as a function of the proportion of resistant plants φ (y-axis) and of virus effective population size in resistant plants $N_{\mathrm{e}}^{\mathrm{R}}$ (x-axis). Panel rows represent contrasted epidemic intensities, Ω_int, and panel columns contrasted RB variant frequencies in S plants, f_RB.

For the intermediate f_RB tested (0.01), $N_{\mathrm{e}}^{\mathrm{R}}$ has an influence for any epidemic intensity, generating J-shaped contour lines when Ω_int is small or intermediate.

For the largest f_RB (0.5), the effect of φ blurs and the area corresponding to significant Δ values (e.g. greater than or equal to 10 percentage points) is reduced to small $N_{\mathrm{e}}^{\mathrm{R}}$ values (less than 5). This area shrinks as Ω_int increases, moving towards very small $N_{\mathrm{e}}^{\mathrm{R}}$ (<2) and large φ (>0.6) values. Values of Δ can reach up to 70 percentage points when Ω_int = 0.2 and this maximum decreases to 20 percentage points when Ω_int = 0.8.

A description of epidemic dynamics simulated with the model under various scenarios can be found in electronic supplementary material, text S3 and figure S2.

4. Discussion

The model presented here is to our knowledge the first one to analyse the impact of within-host demographic stochasticity, tuned by pyramiding plant quantitative resistance reducing virus N_e with qualitative resistance, on the durability of the latter. Beyond simulating the impact of demographic stochasticity, the model proposes an original framework for breeders and farmers to decrease pathogen yield losses and increase qualitative resistance durability.

Globally, the additional relative benefit follows a skewed bell-shaped curve as a function of the frequency of the RB variant in S plants, with both ends corresponding to very low Δ values (figure 1). When f_RB is small (≤10⁻⁶), the qualitative resistance is hardly breakable, even without combining it with a quantitative resistance, as it typically requires the virus to accumulate numerous mutations associated with high fitness costs in S plants [24]. Such highly durable qualitative resistances have been reported in agroecosystems, such as the Pvr4 gene in pepper against PVY, requiring only one mutation for breakdown, but with a high fitness cost in S plants [26]. In our model, the probability that at least one RB particle survives the bottlenecks in monogenic R plants when the contact is from an infected S plant is at most 10⁻² (see calculation details in electronic supplementary material, text S1). As a result, epidemics are already well contained with monogenic R plants, especially at large proportions of R plants (figure 2; electronic supplementary material, figure S3 and text S4).

When f_RB is high (≥0.1; typically, one mutation for resistance breakdown associated with low fitness cost in S plants), the qualitative resistance is easily broken down, even when combining it with a quantitative resistance decreasing virus $N_{\mathrm{e}}^{\mathrm{R}}$. Such cases of poorly durable qualitative resistance have also been reported, as for the Tm1 gene in tomato against tomato mosaic virus [1]. The probability that at least one RB virus particle survives the bottlenecks in R plants with pyramided resistance when the contact is from an infected S plant is at least 10⁻¹, and increases very fast with $N_{\mathrm{e}}^{\mathrm{R}}$ (see calculation details in electronic supplementary material, text S1). Thus, even the deployment of R plants with pyramided resistance results in important damage, except when virus $N_{\mathrm{e}}^{\mathrm{R}}$ is very small (=1) and the proportion of R plants is large (figure 2; electronic supplementary material, figure S3 and text S4). Strong epidemic intensities and large f_RB drastically reduce optimal combinations of cropping ratios and bottleneck sizes, owing to an increasing number of inoculation events combined with higher probabilities of transmitting the RB variant from an infected S plant.

Resistance pyramiding provides the largest additional benefits for intermediate f_RB because the qualitative resistance is neither highly nor poorly durable. In those common intermediate cases [2,24], quantitative resistance controlling bottleneck sizes can protect a qualitative resistance by decreasing the success probability of inoculation events from infected S plants to healthy R plants. The best strategy combines a large proportion of R plants and a small virus N_e.

Several conceptual reviews discuss the effect of pathogen N_e on the evolutionary potential of pathogens confronted with a qualitative resistance in plants [2,10,27]. Our modelling results are in agreement with their advice of reducing N_e and go further by showing that the interaction between N_e and selection, via f_RB, is critical for the added value of reducing N_e in terms of additional yield benefit. Zhan et al. [10] highlight agricultural practices that can help reduce N_e, such as seasonal fallows, field hygiene, intercropping or crop rotation. Here, as we recently identified plant loci controlling N_e [15,16], we propose an alternative and original way of managing pathogen N_e through plant breeding. Our model and proposed breeding method should be directly applicable to plant pathogens that multiply within-host and constitute mixed populations, such as viruses and bacteria. Plant fungi form monoclonal lesions; thus the competition is not direct and the model would need to be adapted for these pathogens.

More generally, our model averages host-to-host and intra-host N_e in a global N_e, but model parameters could be easily refined depending on the pathosystem. In a paper summarizing current and future challenges in modelling pathogen dynamics, Gog et al. [28] emphasize the importance of transmission bottlenecks, characterized by infection probability and the number and diversity of pathogen particles transferred to a new host, in pathogen evolutionary dynamics. Interestingly, transmission bottleneck sizes are increasingly estimated for both animal and plant pathogens (see [29] and references therein). Decreasing transmission probability by reducing host-to-host N_e is of particular interest for human pathogens, such as preexposure prophylaxis for human immunodeficiency virus. Then, if a host gets infected, an efficient treatment, creating a narrower bottleneck in virus populations, would slow down the appearance of drug resistant strains by creating a hard selective sweep [30]. Overall, bottlenecks are being increasingly studied in animal, human and plant pathogens. Depending on the host, the method for narrowing pathogen bottlenecks can be adapted, but the general concept remains the same.

Coming back to plant resistance deployment, intermediate proportions of R plants were predicted to be optimal for yield benefit in several studies [24,31] (but [23] predicted that yield benefit increases with the proportion of R plants). Here, we predict a positive correlation between additional relative benefits and the proportion of R plants. This result may be due to our modelling framework, which imposes a link between the proportion of R plants and population bottlenecks encountered by viruses, as we only allowed pyramiding qualitative and quantitative resistances. For example, allowing the quantitative resistance to be introduced in the S cultivar would break this link and could slow down the infection spread through S plants and be beneficial for smaller φ values. To this end, the mutation–selection equilibrium assumed in S plants could be replaced by a mutation–selection–drift equilibrium [32]. More generally, N_e at the field scale can be estimated by the product of intra-plant N_e and the total number of newly infected plants [33]. With our pyramiding strategy, φ is also the proportion of plants carrying the quantitative resistance; hence increasing φ should decrease N_e at the field scale, because of the associated conversion of S plants into pyramided R plants, which have lower N_e.

Future developments should include long-term and large-scale (several seasons within an agricultural landscape) simulations to match the scales at which epidemics spread [34] and should consider diverse deployment strategies (rotation, mixture, mosaic, gene pyramiding). They could benefit from models developed to assess resistance durability for plant viruses [35] and fungi [36]. The model ignores the adaptation of the virus to the quantitative resistance controlling N_e. Pathogen adaptation to quantitative resistance has been observed, as for PVY in pepper [37], but, up to now, the mutational pathways leading to such erosion is largely unknown. These evolutionary aspects could be considered in future work, for example, based on Rimbaud et al.’s [36] framework that features random mutational processes for the adaptation to qualitative and quantitative resistances.

Deleterious effects of narrow bottlenecks for virus epidemic control have been reported in nature, e.g. for Trypanosoma cruzi, the agent of Chagas disease [38]. The authors argue that seasonal reduction in host population can result in an increased prevalence of T. cruzi in the vector population when they feed on a small number of infected hosts, creating a considerable force of infection. A similar effect is likely to occur for vector-borne viruses of annual crops that are solely hosted by limited wild plant species during the crop-free period. Additionally, narrow bottlenecks during cell-to-cell movement in plants might help isolate variants with adaptive mutations from non-adapted ones, allowing selection to operate more efficiently [39], especially when the fitness of a transitional mutant is lower than those of WT and adapted variants [13]. In our model, narrowing bottlenecks can not be harmful because the probability of infecting an R plant is a strictly increasing function of $N_{\mathrm{e}}^{\mathrm{R}}$. Future developments could consider more realistic within-host virus dynamics than the instantaneous mutation–selection(–drift) equilibrium hypothesis. In particular, any new viral mutant with selection coefficient s in a drift regime (N_e s ≪ 1) has a decreasing fixation probability with decreasing N_e, while fixation time increases with N_e [40]. This trade-off between probability of and time to fixation could counteract the positive relationship between $N_{\mathrm{e}}^{\mathrm{R}}$ and resistance durability [9,41].

Our study demonstrates that integrating population genetic principles to minimize the evolutionary potential of plant pathogens, by playing on their effective population size, can guide disease resistance management strategies towards increased resistance durability and epidemic control [10,27]. Our simple model provides insightful guidelines to optimal strategies for breeders and growers, and shows the benefit of using quantitative resistance reducing virus N_e, particularly when the combined qualitative resistance is neither highly nor poorly durable.

Data accessibility

R scripts for model simulations and analyses are available in the supplementary material.

Authors' contributions

E.R., M.B., F.F., L.M. and F.G. conceived the model. E.R. and M.B. carried out model simulations. E.R., M.B., F.F., B.M., L.M. and F.G. analysed the data. E.R. wrote the first draft of manuscript. All authors made critical revisions and approved the final version.

Competing interests

We declare we have no competing interests.

Funding

The authors acknowledge the support of the French Agence Nationale de la Recherche (ANR) under grant ANR-13-BSV7-0011 (project FunFit). B.M. was supported by the SMaCH (Sustainable Management of Crop Health) metaprogramme of INRA.