Mechanisms of Calcium Leak from Cardiac Sarcoplasmic Reticulum Revealed by Statistical Mechanics

Abstract

Heart muscle contraction is normally activated by a synchronized Ca release from sarcoplasmic reticulum (SR), a major intracellular Ca store. However, under abnormal conditions, Ca leaks from the SR, decreasing heart contraction amplitude and increasing risk of life-threatening arrhythmia. The mechanisms and regimes of SR operation generating the abnormal Ca leak remain unclear. Here, we employed both numerical and analytical modeling to get mechanistic insights into the emergent Ca leak phenomenon. Our numerical simulations using a detailed realistic model of the Ca release unit reveal sharp transitions resulting in Ca leak. The emergence of leak is closely mapped mathematically to the Ising model from statistical mechanics. The system steady-state behavior is determined by two aggregate parameters: the analogs of magnetic field (h) and the inverse temperature (β) in the Ising model, for which we have explicit formulas in terms of SR [Ca] and release channel opening and closing rates. The classification of leak regimes takes the shape of a phase β-h diagram, with the regime boundaries occurring at h = 0 and a critical value of β (β^∗) that we estimate using a classical Ising model and mean field theory. Our theory predicts that a synchronized Ca leak will occur when h > 0 and β > β^∗, and a disordered leak occurs when β < β^∗ and h is not too negative. The disorder leak is distinguished from synchronized leak (in long-lasting sparks) by larger Peierls contour lengths, an output parameter reflecting degree of disorder. Thus, in addition to our detailed numerical model approach, we also offer an instantaneous computational tool using analytical formulas of the Ising model for respective ryanodine receptor parameters and SR Ca load that describe and classify phase transitions and leak emergence.

Significance

This report provides quantitative insights into problem of Ca leak from sarcoplasmic reticulum. Our numerical model simulations discovered sharp transitions in operation of Ca release unit resulting in Ca leak. The leak emergence is closely mapped mathematically to the Ising model from statistical mechanics, namely to two types of phase transitions known for this model: magnetization (i.e., spontaneous synchronization of spins’ orientation) and the Onsager’s order-disorder transition. Thus, our model offers a new, to our knowledge, classification of leak that takes the form of a phase diagram representing normal function and two leak types: disorder leak and synchronized leak. The model also offers an instantaneous computational tool to describe phase transitions as a function of release channel and sarcoplasmic reticulum parameters.

Introduction

In heart muscle, electrical excitation is coupled to contraction via Ca signaling between L-type Ca channels of the plasma membrane and Ca release channels (ryanodine receptors, RyRs) residing in the sarcoplasmic reticulum (SR), a major Ca store within cardiac cells. Opening of L-type Ca channels leads to synchronous openings of neighboring RyRs as the open probability of RyR is increased by cytoplasmic [Ca]. The resultant Ca-induced-Ca-release (CICR) (1) triggers displacement of myofilaments and cell contraction.

The synchronized activation of RyRs during systole is followed by the robust release termination, causing muscle relaxation. However, under pathological conditions, Ca release does not terminate but continues during diastole (2), causing a Ca leak. Deteriorating effects of Ca leak on heart function include (2, 3) 1) reduced systolic SR Ca levels, leading to systolic dysfunction; 2) elevated diastolic Ca, leading to diastolic dysfunction; 3) energy drain to repump Ca; and 4) triggered arrhythmias.

The mechanisms and regimes of SR operation generating abnormal leak remain elusive. The RyR is a huge molecule, featuring extremely complex regulation via numerous post-translational modifications and multiple regulatory proteins (2, 4, 5). In pathological conditions, Ca leak can be caused by increased sensitivity of RyRs to Ca due to RyR phosphorylation by CaMKII (2, 3). Furthermore, diastolic Ca leak is a multiscale complex phenomenon. In ventricular myocytes, RyRs are organized in clusters of 10–300 channels (6) residing in the junctional SR (JSR), forming Ca release units (CRUs), which can generate a local elementary Ca release dubbed a Ca spark (7, 8). Ca leak can range from “invisible” or “nonspark” events originating from openings of just one or several RyRs (9), diastolic Ca sparks (8), macrosparks, and small abortive Ca waves up to Ca waves of a cell size (review (10)). The invisible releases and sparks that fail to terminate have been extensively studied using computational models (11, 12, 13, 14, 15, 16, 17). Although numerical simulations showed that the leak is facilitated by rapid inter- and intra-SR Ca diffusion (15, 16) or faster JSR refilling rate with Ca (13), the mechanisms of the leak as an emerging, macroscopic phenomenon remain unclear.

Thus, our understanding of Ca leak would greatly benefit if the numerical modeling were combined with an appropriate statistical model to describe the collective behavior of RyRs underlying leak emergence. Regulation of cardiac muscle contraction strength has been described via statistics of success and failure of L-type Ca channels to ignite a Ca spark (7). More recently, we also showed that the lattice of open and closed RyRs in CRUs (Fig. S1) and lattice of spins in ferromagnets behave mathematically identically, namely like the Ising model from statistical physics (18). Our mapping the CRU to a lattice of spins is based on a clear analogy of interactions between RyRs and spins. Indeed, spins could be in two positions, + or −, and RyRs also can be either in open or closed state. A spin “wants” to turn its neighbor to the same state, and RyRs do the same: an open RyR also “wants” to open its neighbor via CICR, whereas a closed RyR “wants” to close its neighbor via interrupting ongoing CICR (13) (i.e., induction decay (19) or “pernicious attrition” (20)). In our mapping, RyRs become and act as spins, and their Ca profiles become interaction profiles.

Using this approach, we have shown that sparks normally terminate via a classical transition known for the lattice of spins as magnetization or polarity reversal, when magnetic field (h) changes sign from positive to negative (18). Magnetization in the classical Ising model is defined as the number of plus-spins minus the number of minus-spins, divided by the total number of spins to normalize it. It depends on the external magnetic field h and temperature. When the temperature is low, spin-to-spin interactions are very strong, and the spins will align, yielding a magnetization of plus or minus 1. The sign of the external magnetic field will determine whether it is plus or minus 1 that minimizes the configuration energy. As temperature increases, the spin interactions wane, but the magnetization will stay near plus or minus 1. As the temperature approaches a critical value (known as Curie temperature), magnetization will decrease, hitting a first-order phase transition (Onsager’s order-disorder transition) at Curie temperature. In terms of system behavior, as the temperature increases to above Curie temperature, the spins become effectively independent, and the change from order to disorder is abrupt. Once this transition occurs, the value of magnetic field plays a key role in establishing what proportion of spins is up. As we have established in (18) that the CRU is isomorphic to an Ising model, all these phenomena are expected to occur also in the CRU, which is exactly the main purpose of this work.

The order-disorder transition for the classical nearest-neighbor Ising model was first shown by Peierls in (21). The model we use here has interactions that are more than nearest-neighbor interaction but have fast decay at infinity. The statement of the analogous order-disorder transition appears as Proposition 2.1 in (22) with proof and supporting references and history. In this work, we use the term “phase transition” with respect to the analytical Ising model but “phase-like transition,” when we consider our numerical Ca spark model (13).

In our previous study (18), from our exact mapping, we have derived formulas for the analogs of the magnetic field h and inverse temperature β in terms of natural biophysical parameters of CRU:

$$h=\frac{1}{2\beta }\ln \left(\frac{\lambda }{C}\right)+2\pi {\int }_{r>.5}\varphi \left(r,C{a}_{JSR}\right)dr,$$ (1)

$$\mathit{\beta =}\mathit{\gamma \psi }\left(\mathit{U, C}{\mathit{a}}_{\mathit{JSR}}\right)/\mathit{4},$$ (2)

where ϕ(r) = ψ(Ur)/ψ(U) is a normalized and scaled version of ψ(r) at each given Ca_JSR and grid size. The function ψ gives Ca_dyad as a function of distance r from one open RyR, and U is the distance to the channel nearest neighbor (Fig. S2 A). Here, the constants λ, C, and γ are parameters of RyR channel kinetics, namely C is the closing rate, whereas λ and γ correspond to parameters of an exponential in local Ca (Ca_dyad) that describes the RyR opening rate (Fig. S2 C). Further details on the relationship between the abstract Ising model and ion channels and CRU parameters are given in Table S1. Derivation of Eqs. 1 and 2 are given in the section “Ising model methods” in Supporting Materials and Methods.

Here, we employed a realistic detailed numerical model of a CRU (13) combined with our analytical Ising approach (18) to explore and classify leak regimes generated by the statistical ensemble of RyRs within a CRU for various values of h and β. Thus, our sensitivity analyses of the numerical model were guided by predictions of the analytical model in terms of specific model parameters and their ranges for the simulations. Our study rationale and results are summarized in a respective phase diagram (Fig. 1), in which model behaviors are classified based on their values of h and β and their relation to particular values of extreme importance, namely h = 0 and β = β^∗ (corresponding to Curie temperature). We identified two leak regimes: one is linked to a failure of h to change its sign and the other is linked to disorder, i.e., Onsager’s “order-disorder” transition. In magnetism, disorder occurs when the temperature becomes too high (above Curie temperature), overwhelming the interactions. In the CRU model, when RyR interactions are weakened, for example, by a low SR level, we observe a similar disordered state. We derive analytical formulas for exact relations between RyR parameters and SR Ca load for both leak regimes. Both leak regimes were found in our numerical model simulations.

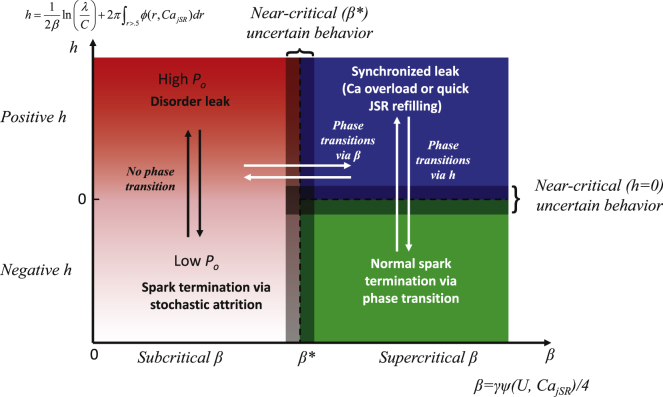
Figure 1.

The phase diagram of CRU operation predicted by analytical Ising model. Relations of spark termination regimes and types of Ca leaks with respect to phase transitions via h polarity reversal and order-disorder transition via β^∗ are shown. The different regimes of CRU operation with phase transition boundaries are shown by different shades. In the subcritical β regime, the the shade shows the degree of leak, which is gradual (i.e., not a phase transition). To see this figure in color, go online.

Methods

We used our previously reported numerical model of a Ca spark (Stern model) (13). The model is illustrated in Fig. S1. We also used a recent analytical model of Ca spark termination via an Ising-type phase transition (18) (Supporting Materials and Methods). We constructed an exact mapping between two systems in two dimensions: 1) the lattice of interacting RyRs and 2) the Ising model of interacting spins within a ferromagnet, so that both systems are described by the same mathematical formulations. We further formulated four general conditions for a system of RyRs to satisfy the mapping:

• 1)The RyRs are arranged in a lattice structure, with a nearest-neighbor distance U.
• 2)Each RyR can be in an open or closed state, corresponding to the plus and minus states of the Ising model.
• 3)At each given [Ca] in JSR (Ca_JSR), the interaction profile ψ(r,Ca_JSR), defined as local [Ca] distribution in dyadic space caused by unitary current (i_RyR) (Video S6. A Smaller Peierls Contour in Case of Supercritical, Synchronized Leak, Video S7. A Larger Peierls Contour in Case of Subcritical Disorder Leak, Document S2. Article plus Supporting Material A), is roughly stable in time (Fig. S2 B), corresponding to time invariance of RyR interactions, and roughly the same for any RyR in the lattice, corresponding to translation invariance. In this study, we demonstrated a minor effect of driving force reduction due to open neighboring RyRs on the interaction profile (Fig. S3; Table S2).
• 4)The RyR opening rate k_o depends exponentially on Ca_dyad, i.e., k_o = λ^∗exp(γ^∗Ca_dyad) (Video S2. Pathological Spark with Synchronized Leak via JSR Quick Refiling with Ca in Supercritical Regime, Video S3. Pathological Spark with Synchronized Leak under Ca Overload in Supercritical Regime, Video S4. Disorder Leak that Oscillates Near Criticality, β∗, Video S6. A Smaller Peierls Contour in Case of Supercritical, Synchronized Leak, Video S7. A Larger Peierls Contour in Case of Subcritical Disorder Leak C, red curve), and the closing rate C is a constant (C = 0.117 ms⁻¹ in Stern model).

All four above conditions are met in our CRU model (18).

Results

Estimates of β^∗ using analytical approaches

The exact value of β^∗ is known for the classical Ising model, in which spin interactions are limited to the nearest neighbors. However, in the Ising model that is isomorphic to the CRU, the RyRs (corresponding to spins) interact via a Gaussian-like interaction profile (Video S6. A Smaller Peierls Contour in Case of Supercritical, Synchronized Leak, Video S7. A Larger Peierls Contour in Case of Subcritical Disorder Leak, Document S2. Article plus Supporting Material A), i.e., the interactions spread to other, more distant neighbors within the RyR grid. Although this precludes a precise analytic computation of β^∗, the interaction strength notably weakens for the second (and higher)-order neighbors, so that the exact value of β^∗ (β^∗_Ising = 0.138; see Supporting Materials and Methods) of the classical model can serve as an upper-bound estimate for the “order-disorder” transition in the CRU. We also obtained a lower-bound estimate of β^∗ using the mean field approximation (β^∗_{mean_field} = 0.0784; Supporting Materials and Methods) that represents an extreme case when all RyRs in a CRU would interact equally. Thus, our β^∗ estimates from the two analytical approaches provide a fairly narrow range for the true β^∗ in our CRU system, i.e., 0.0784 < β^∗ < 0.138.

Order-disorder phase-like transition and the value of critical β in numerical simulations

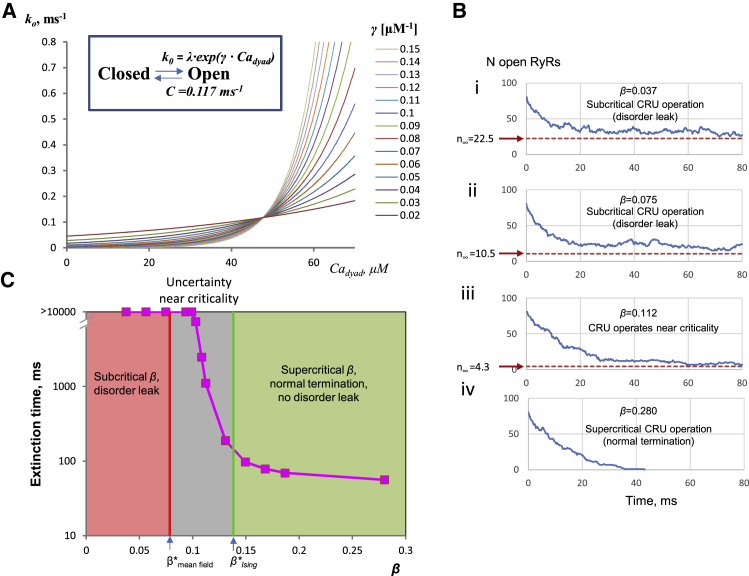
We tested whether “order-disorder” phase-like transition can occur via β at h = 0 in a CRU by varying λ and γ in numerical simulations. We achieved h = 0 by clamping Ca_JSR at 0.1 mM, so that the integral in Eq. 1 and interaction profile ψ in Eq. 2 became fixed. Solving Eq. 1 for h = 0 yields a one-to-one correspondence between β and λ (with C = 0.117 ms⁻¹ = const). As Ca_JSR is fixed, so is ψ(U), and hence Eq. 2 yields a one-to-one correspondence between β and γ. Using this correspondence, we computed β and λ pairs for γ varying from 0.02 to 0.15 μM⁻¹ (Table S3). The plots of opening rate (k_o) versus local [Ca] in dyadic space (Ca_dyad) for respective pairs of λ and γ are shown in Fig. 2 A. For each β and its respective λ-γ pair, we performed a simulation of 100 sparks using the Stern model (examples in Fig. 2 B), and for each spark, we determined its median extinction time, i.e., when all RyRs become closed. As β decreased, we observed a sharp increase in extinction times. In simulations with β > 0.13, sparks robustly terminated, with median extinction times being roughly between 50 and 200 ms, but with β < 0.1, the median extinction times suddenly became basically infinite on the heartbeat cycle scale, i.e., >10,000 ms (Fig. 2 C). Thus, the phase-like transition in our CRU model occurred at β^∗ ∼ 0.1, i.e., indeed between the analytically computed upper and lower bounds of β^∗ (Fig. 2 C, gray band).

Figure 2.

Onsager’s “order-disorder” phase-like transition via β in a CRU in numerical simulations under Ca_JSR clamp. (A) Plots of opening rate (k_o) of RyR as a function of Ca_dyad are shown, with our choices of γ, λ, C (Table S3) that keep h = 0 but allow β to vary in a wide range, including near criticality. The inset shows our RyR gating scheme. (B) Examples of spark simulations with phase-like transition via β and emergence of disorder leak in the subcritical regime are shown. Dash lines show the low-bound estimates for open number of RyRs at a steady state (n_∞) in the supercritical and near-critical regimes. (C) “Order-disorder” phase-like transition in terms of median extinction times (100 sparks for each data point) versus β is shown. Arrows show lower and upper bounds estimates for β^∗ obtained analytically (β^∗_{mean_ field} and β^∗_Ising). The phase-like transition happens in the model within these bounds that define the near-critical area. To see this figure in color, go online.

Using electron microscopy, Franzini-Armstrong et al. reported average numbers of RyRs per couplon in dyads: 90, 128, and 267, for dog, mouse, and rat, respectively (Table 2 in (6)). Thus, Fig. 2 C shows the phase-like transition for a relatively small CRU of 81 RyRs. Our additional numerical simulations revealed a similar phase-like transition for a much larger cluster of 169 RyRs (Fig. S4). Thus, our results indicate that the phase-like transitions in the numerical model of Ca spark occur independently of the number of channels in the CRU, and their β^∗ can be well-approximated analytically within the physiological range of CRU sizes known for mammalian species.

Subcritical regime (β < β^∗): Stochastic attrition and disordered leak

Our model simulations show a substantial leak in the subcritical and near-critical regimes (Fig. 2 B) when h is near 0. We further explored the nature of this leak and estimated its level based on RyR parameters. In the subcritical regime, RyRs do not effectively interact, and their gating becomes disordered (happening effectively independently of each other). The leak then depends almost entirely on the open probability (P_o) of RyR at a steady state. If P_o is very small (compared with the inverse of the number of RyRs in a CRU), the spark will terminate via pure stochastic attrition; if P_o is relatively high, then the spark will decay to a steady-state level with disordered RyR activity generating the disorder-type leak. In general, a lower bound on P_o can be obtained by neglecting interactions and assuming that channels operate independently. In this case, P_o is given as a balance between opening and closing rates (Video S6. A Smaller Peierls Contour in Case of Supercritical, Synchronized Leak, Video S7. A Larger Peierls Contour in Case of Subcritical Disorder Leak, Document S2. Article plus Supporting Material A): P_o = (λ/C)/(1 + λ/C). Please note that P_o ≈ λ/C at low λ/C. The probability that all channels (N_RyR) close, i.e., sparks terminate via stochastic attrition, is given as P_{all_closed} = (1 − P_o)ˆN_RyR (Fig. S5 B), and the lower-bound estimate of average number of open RyRs creating the leak will be n_∞ = P_o × N_RyR. The respective levels of n_∞ closely describe a lower bound for the number of open RyRs after spark decay in our spark simulations in both the subcritical and near-critical regimes (Fig. 2 B i, ii, and iii).

For RyRs with λ_fit = 0.0002482 ms⁻¹ that was fitted to experimental data (Video S2. Pathological Spark with Synchronized Leak via JSR Quick Refiling with Ca in Supercritical Regime, Video S3. Pathological Spark with Synchronized Leak under Ca Overload in Supercritical Regime, Video S4. Disorder Leak that Oscillates Near Criticality, β∗, Video S6. A Smaller Peierls Contour in Case of Supercritical, Synchronized Leak, Video S7. A Larger Peierls Contour in Case of Subcritical Disorder Leak C) and with C = 0.117 ms⁻¹, we obtain P_o = 0.002117. This yields a relatively low n_∞ = 0.17 and high P_{all_closed} = 0.842 (for a 9 × 9 RyR grid). It means that such sparks, even in the subcritical regime, will likely terminate (via stochastic attrition). We tested this prediction by numerical simulations, in which we achieved a low β range by clamping Ca_JSR at relatively low levels, decreasing i_RyR, i.e., the current via one RyR. Indeed, the median extinction time was normal (i.e., short, near 40 ms) throughout both the subcritical and supercritical regimes of β (Fig. 3, A–C). On the other hand, RyRs generate substantial leak in our simulations in the subcritical regime as λ increases, yielding higher P_o and n_∞ (Fig. 3 D).

Figure 3.

Spark termination via stochastic attrition in the subcritical β regime for a CRU with experimentally measured RyR parameters. (A) Plot shows our choice of Ca_JSR levels for SR Ca clamp that define respective values of β. The respective values of h are given in Table S4. (B) Median extinction times versus β (n = 100 sparks for each data point) are shown. (C) Examples of spark termination in subcritical, near-critical, and supercritical ranges are shown. (D) Simulations illustrating disorder leak as λ increases by 10- and 100-fold from its normal (experimentally measured) value are shown. λ_fit, P_o, and P_all_closed were calculated as shown in Fig. S5. Dash lines show the low-bound estimates for open number of RyRs at a steady state (n_∞). To see this figure in color, go online.

Supercritical regime (β > β^∗)

In the range of β > β^∗, the CRU behavior is determined by the sign of h. When h is positive, RyRs strongly interact via CICR and remain mainly open (i.e., generating Ca leak), but when h is negative, RyRs tend to close, shown by the blue and green areas, respectively, in the phase diagram in Fig. 1. We have previously demonstrated that the transition from an all-open to an all closed state is sharp and is analogous to the phase transition in ferromagnets on h reversal (18). This transition can be illustrated by generating sparks when Ca_JSR is clamped at various levels, which yields the respective range of h calculated via Eq. 1. Fig. S6 shows an example of such h calculation for a 9 × 9 RyR grid and simulations of the phase-like transitions when h reverses its sign.

Complex realistic CRU behaviors featuring “free-running” SR

So far, we have demonstrated the basic steady-state properties of CRU operation using a reductionist approach, i.e., at a steady state when the Ca SR content was clamped. Under physiological conditions, the content of JSR (Ca_JSR) is obviously not fixed: Ca is released via RyRs and refilled from FSR via a diffusional resistance (parameter τ_fill in the model). The realistic CRU behaviors with “free-running” SR can now be understood and interpreted in terms of the phase diagram in Fig. 1, which summarizes basic CRU properties gleaned from our above reductionist studies. To illustrate the utility of our approach, we simulated emergence of different types of Ca leaks with “free-running” SR. In these simulations, β was calculated as a (linear) function of Ca_JSR according to Eq. 2, with γ fixed at its physiological value γ_fit.

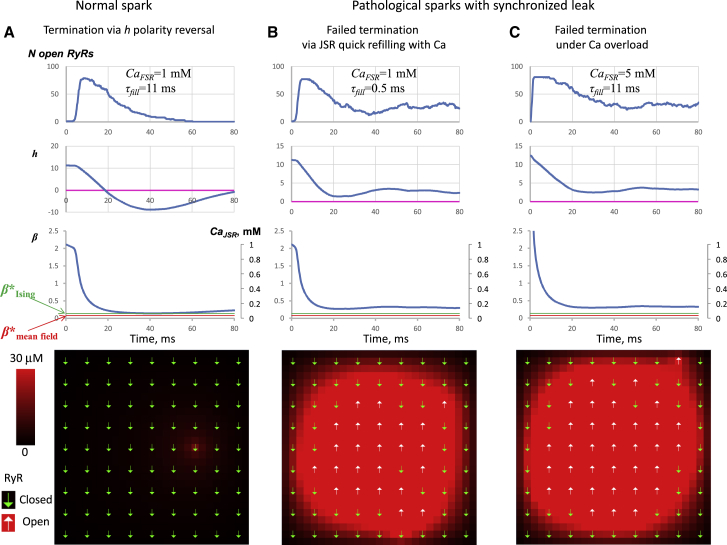
One simple example is normal spark termination in the supercritical regime when JSR Ca content becomes depleted to the level that h reverses its sign (18) (green area in phase diagram Fig. 1; see also an example in Fig. 4 A; Video S1). Thus, the leak can occur when h simply fails to change its sign. In this case, the system does not undergo a phase transition, and spark termination fails. In our phase diagram in Fig. 1, this leaky CRU behavior is shown by blue color. This happens when i_RyR remains large enough to maintain CICR among neighboring RyRs. The interacting RyRs remain partially synchronized in time and space, which keeps the spark alive. Thus, any factor favoring a larger or more sustained i_RyR will facilitate the synchronized leak, resulting in long-lasting sparks. For example, one such factor is how quickly JSR is refilled with Ca from free SR (FSR) (parameter τ_fill). Another factor is a higher FSR Ca concentration (Ca_FSR), mimicking Ca overload. Both factors generate leak via synchronized RyRs because they both impede the SR from depletion and therefore sustain substantial i_RyR. These leaky CRU behaviors are shown in respective examples of our simulations (in Fig. 4, B and C; see also Videos S2 and S3) in which we used the RyR opening rate parameters of λ and γ (λ_fit and γ_fit) fitted to experimental data obtained by Laver et al. (19) under physiological conditions (Video S2. Pathological Spark with Synchronized Leak via JSR Quick Refiling with Ca in Supercritical Regime, Video S3. Pathological Spark with Synchronized Leak under Ca Overload in Supercritical Regime, Video S4. Disorder Leak that Oscillates Near Criticality, β∗, Video S6. A Smaller Peierls Contour in Case of Supercritical, Synchronized Leak, Video S7. A Larger Peierls Contour in Case of Subcritical Disorder Leak C) but different (i.e., abnormal) refilling rate τ_fill or FSR Ca (resulting in Ca overload). Our analytical estimates on β^∗ indicate that both normally terminating sparks and this type of synchronized leak occur in our model simulations in the supercritical regime because β always remains above the upper-bound β^∗ estimate (shown by green lines in Fig. 4).

Figure 4.

Examples of numerical simulations for normal and failed spark termination in the supercritical β regime in a free-running JSR. (A) A normal spark terminated by phase-like transition via h polarity reversal (Video S1) is shown. (B and C) Spark termination fails with JSR quick-refilling rate or under Ca overload is shown. Each panel shows dynamics of open RyR number, h, β, and Ca_JSR. Horizontal lines show upper-bound and lower-bound estimates of β^∗ (β^∗_Ising = 0.138 and β^∗_{mean_field} = 0.0784, respectively). Key parameters (Ca_FSR and τ_fill) are shown at the traces. Bottom panels show respective distributions of RyR states at t = 80 ms, i.e., when sparks usually terminate. Up and down arrows show open and closed RyRs. Ca_dyad is coded by shades: from 0 to 30 μM (saturated). See also Videos S2 and S3. To see this figure in color, go online.

Video S1. Normal Spark Termination in Supercritical Regime

Related to Fig. 4 A. Total simulation time is 80 ms. Ca_FSR=1 mM, τ_fill=11ms. Ca_dyad is coded by red shades: from 0 to 30 μM (saturated).

Video S2. Pathological Spark with Synchronized Leak via JSR Quick Refiling with Ca in Supercritical Regime

Related to Fig. 4 B. Total simulation time is 80 ms. Ca_FSR=1 mM, τ_fill=0.5ms. Ca_dyad is coded by red shades: from 0 to 30 μM (saturated).

Video S3. Pathological Spark with Synchronized Leak under Ca Overload in Supercritical Regime

Related to Fig. 4 C. Total simulation time is 80 ms. Ca_FSR=5 mM, τ_fill=11 ms. Ca_dyad is coded by red shades: from 0 to 30 μM (saturated).

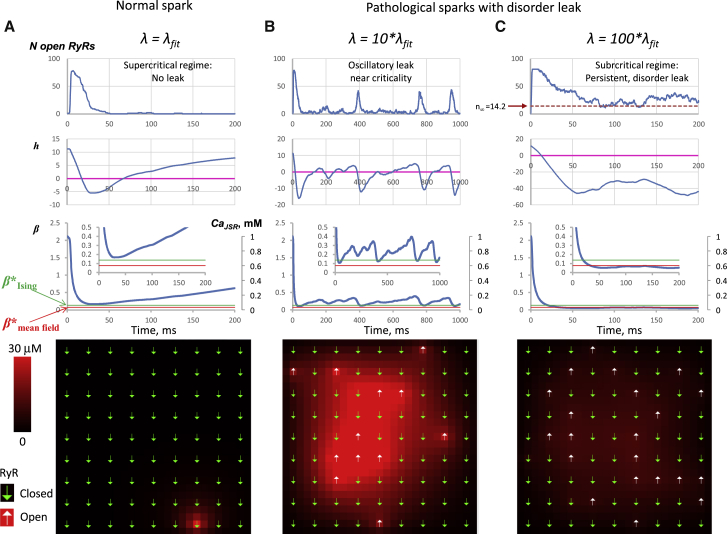
We also generated different spark behaviors with free-running SR as λ increases (Fig. 5). We found a different degree of RyR synchronization and respective different behaviors of the system with respect to the criticality at β^∗ that can be interpreted using our phase diagram in Fig. 1. Synchronized activity resulted in normal spark termination at supercritical β as h changed its sign; partially synchronized (self-synchronized) activity resulted in oscillations near criticality (Video S4); and unsynchronized, completely disordered RyR activity caused leak in the subcritical regime (Video S5).

Figure 5.

Examples of pathological sparks with disorder leak emerging at higher λ (i.e., higher P_o) in a free-running JSR. (A) Normal supercritical spark with no leak is shown. (B) Oscillatory leak near β criticality is shown. (C) Persistent disorder leak in the subcritical regime is shown. Respective λ values are shown as multiple of λ_fit (× 1, × 10, × 100). Horizontal lines show upper-bound and lower-bound estimates of β^∗ (β^∗_Ising = 0.138 and β^∗_{mean_field} = 0.0784, respectively). Dash line in (C) shows the low-bound estimate for open number of RyRs at a steady state (n_∞). Insets show β dynamics with respect to criticality in a more detailed y scale. Bottom panels show respective distributions of RyR states and Ca_dyad at t = 200 ms. Ca_dyad is coded by shades: from 0 to 30 μM (saturated). See also Videos S4 and S5. To see this figure in color, go online.

Video S4. Disorder Leak that Oscillates Near Criticality, β∗

Related to Fig. 5 B. Total simulation time in the video is 500 ms. λ = 10^∗λ_fit. Ca_dyad is coded by red shades: from 0 to 30 μM (saturated).

Video S5. Persistent Disorder Leak in Subcritical Regime

Related to Fig. 5 C. Total simulation time in the video is 200 ms. λ = 100^∗λ_fit. Ca_dyad is coded by red shades: from 0 to 30 μM (saturated).

Peierls contour distinguishes disorder leak and synchronized leak

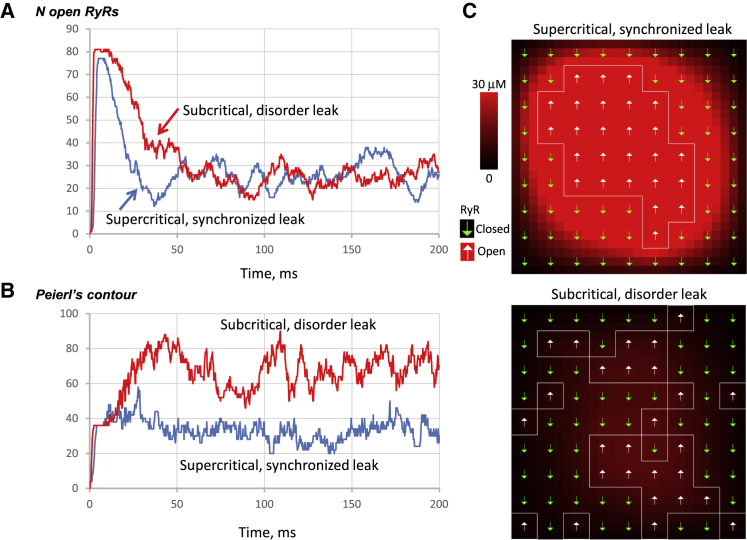
Here, we have described two means of spark termination failure. In one, the magnetic field remains too high, and synchronization of open RyRs remains substantial (Fig. 4, B and C). In the other, termination fails because low β results in effectively independent RyR openings (Fig. 5 C). These two mechanisms can be distinguished by comparing the lengths of Peierls contours (21) of the open RyRs in the grid. Peierls contours are used in statistical physics as a measure of disorder. We constructed the contours in our CRU model as a set of borders between open and closed RyRs (the borders between neighboring open RyRs were excluded). The contour length reflects the degree of disorder in openings among neighboring RyRs, in extreme cases representing a checkerboard. In contrast, the smaller contour length indicates a higher local synchronization of opening among neighboring RyRs.

We computed the lengths of Peierls contours in two series of simulations performed for spark failure of different types for the same grid size (see examples in Fig. 6). We obtained different patterns: open RyRs in supercritical, synchronized leak tend to form big clusters, whereas in disorder leak, RyR openings appear disorganized. These different patterns are clearly reflected by Peierls contour length, being about twice as long for a disordered leak (Fig. 6 B; Videos S6 and S7).

Figure 6.

Peierls contour distinguishes disorder leak and synchronized leak. (A and B) Time course of number of open RyRs and respective length of Peierls contour in spark termination failure via two different mechanisms are shown: the blue curve shows Ca leak in the supercritical regime (synchronized leak, τ_fill = 0.5); red curve shows Ca leak in the subcritical regime (disorder leak, λ = 100 × λ_fit). (C) Distribution of CRU states at time 200 ms. Ca_dyad is coded by shades: from 0 to 30 μM (saturated). Peierls contours are shown by white lines over open RyR clusters. See also Videos S6 and S7. To see this figure in color, go online.

Video S6. A Smaller Peierls Contour in Case of Supercritical, Synchronized Leak

Related to Fig. 6. Total simulation time is 200 ms. Ca_FSR=1 mM, τ_fill=0.5ms (similar to Video S2). Ca_dyad is coded by red shades: from 0 to 30 μM (saturated).

Video S7. A Larger Peierls Contour in Case of Subcritical Disorder Leak

Related to Fig. 6. Total simulation time is 200 ms. λ = 100^∗λ_fit. Ca_dyad is coded by red shades: from 0 to 30 μM (saturated).

Discussion

We approached the problem of abnormal SR Ca leak by application of numerical modeling and statistical mechanics to the CRU viewed as an ensemble of RyRs interacting via CICR. Based on our previous finding that the spark termination can be described by a phase transition in an Ising model (Fig. 4 A; Video S1) (18), here, we explored and classified the CRU behaviors when spark termination fails and generates the abnormal leak. We summarized our results of numerical and analytical modeling with respect to the β-h interplay in Fig. 1. CRU can undergo two types of phase transitions: via h polarity reversal and via β, that is, Onsager’s “order-disorder” transition (23).

The magnitude of β, particularly the binary fact of whether β < β^∗ or β > β^∗, determines whether the RyR interactions are important. When β > β^∗, RyR states synchronize. In this case, the magnitude of h, and again the binary fact of whether h is positive or negative, becomes the determining factor for all the RyR states at steady state. Thus, when h changes from positive to negative, spin orientations flip from plus to minus, and correspondingly, RyRs also flip their states collectively from open to closed (in the case of spark termination). In fact, the dividing line between these regimes is identical to the segment of discontinuity of magnetization in the Ising model (see, e.g., Fig. 1.2 of Baxter (24)).

On the other hand, in physics, β < β^∗ corresponds to a high-temperature regime. The high temperature brings disorder by decreasing the interactions of spins to the point that they cease to be important. We have demonstrated that a similar phenomenon occurs in the CRU as the analog of β quantity changes, with a phase-like transition as it passes its critical value β^∗. The RyRs become effectively independent. Once this happens, the magnetic field h again plays a key role in RyR behavior. However, when β is subcritical, there is no phase transition in h. On the contrary, as h decreases, the steady-state number of open channels slowly decreases (β < β^∗, red shaded area). In the CRU model, this disordered regime happens at low SR Ca loads, with i_RyR and hence RyR interactions via CICR being reduced. The magnitude of the disorder leak is determined by P_o, i.e., the leak increases at high opening rates and/or low closing rates (as the ratio of λ/C increases; Fig. S5). At very low P_o, sparks still terminate in the subcritical regime via pure stochastic attrition (lower almost white area in Fig. 1). This type of spark termination does not seem to be physiological because it happens at extremely low SR loads (Fig. 3 C, bottom panel).

In the supercritical regime (β > β^∗), the leak can occur when h fails to change its sign (remaining within blue area in Fig. 1). In this case, partially synchronized RyR openings persist resulting in long-lasting sparks. This synchronized leak happens when the SR does not sufficiently deplete and RyRs keep interacting via CICR. More efficient connectivity of JSR with FSR or larger SR Ca loads facilitates the leak (Fig. 4, B and C; Videos S2 and S3). Conditions for both synchronized leak and disorder leak are now defined deterministically by simple analytical formulas (dashed lines in Fig. 1 for h = 0 and β^∗).

Different leak types: Distinctive patterns and different functional consequences

Although both leak regimes may look similar in terms of average number of open RyRs, they have a different nature, causing different system behavior. In simulations, they appear differently to the eye as locally synchronized openings versus noisy and disordered RyR firing. The two regimes can be also distinguished objectively and quantitatively by calculating Peierls contour lengths (21) (Fig. 6; Videos S6 and S7). The Peierls contour length is solely an output parameter and can provide deep insight into the mechanism of leak even in cases when the input parameters are unavailable.

We found different levels of synchronization of RyR openings: synchronized for long-lasting sparks (Fig. 4), unsynchronized for disorder leak, and partially synchronized (self-synchronized) oscillatory activity near criticality (Fig. 5). Long-lasting sparks with highly synchronized RyR activity extend toward diastole and can therefore contribute to initiation of arrhythmia via early afterdepolarizations (EADs) or delayed afterdepolarizations (DADs). Ca overload and high connectivity of JSR with FSR support persistent high-amplitude i_RyR and thus facilitate synchronized leak (via long-lasting sparks) that may provoke Ca waves and DADs (3) and sometimes also EADs (25). A long-lasting spark is more likely to trigger a Ca wave than a normal short-lived spark simply because of the longer exposure of the neighboring CRU to the Ca released by the longer spark. Similarly, once the wave is initiated, long-lasting sparks on its way will better support the wave propagation. This supporting role of long-lasting sparks in wave generation and propagation has been discussed earlier by Brochet et al. (9).

The partially synchronized oscillatory activity of RyRs near criticality (Fig. 5 B; Video S4) is reminiscent of Ca embers (26). Such embers and spontaneous oscillatory sparks can also provoke DAD (even EADs if oscillation period is short). On the other hand, this type of spontaneous oscillatory releases during diastole may be involved in normal pacemaker function via the so-called “calcium clock” (27, 28, 29, 30).

Disorder leak is expected to deteriorate contraction amplitude of heart muscle because of low SR Ca levels associated with this leak type (Fig. 5 C). However, the cause-effect relation between SR Ca level and disorder leak could be tricky. A low SR Ca level is required (but not sufficient) for the disorder leak. For the leak to become notable, P_o should be high. On the other hand, if the disorder leak becomes substantial, it can further deplete SR Ca levels. For example, in our simulations in Fig. 5, λ facilitates RyR open state, resulting in substantial Ca depletion of JSR that, in turn, shifts the CRU operation toward criticality and further to the disorder leak regime. On the other hand, once CRU operates within the disorder regime, the increasing leak via λ/C is not a phase transition per se. We estimated a lower bound on the expected number of open channels given by the binomial approximation, i.e., larger λ/C → larger P_o → more leak (Fig. 3 D; Fig. S5).

Insights into normal CRU operation: RyR interactions must be balanced

Under physiological conditions Ca_JSR becomes depleted during spark termination. As Ca_JSR declines, β and h change simultaneously with time. With values of λ_fit and γ_fit fitted to experimental data from Laver et al. (19) obtained under physiological conditions (Video S2. Pathological Spark with Synchronized Leak via JSR Quick Refiling with Ca in Supercritical Regime, Video S3. Pathological Spark with Synchronized Leak under Ca Overload in Supercritical Regime, Video S4. Disorder Leak that Oscillates Near Criticality, β∗, Video S6. A Smaller Peierls Contour in Case of Supercritical, Synchronized Leak, Video S7. A Larger Peierls Contour in Case of Subcritical Disorder Leak C), our simulations show that β remains supercritical throughout the duration of the spark, i.e., it remains above our upper estimate of 0.138 (Fig. 4 A). This means that CICR interactions between RyRs remain the key aspect of the system operation, and abrupt and robust termination indeed occurs via “polarity reversal” phase transition. When h does not reverse, termination fails, and the CRU generates synchronized leak (Fig. 4, B and C). Our results also demonstrate that the normal spark termination requires balanced RyR interactions. Because in our model, h and β are inversely related, high RyR interactions yield both a high supercritical β and a positive h through the duration of the spark. This combination does not allow termination, as both interactions of open RyRs remain strong, and the RyR preferred state (indicated by the sign of h) is to be open. However, RyR interactions that are too low (e.g., via low SR Ca load) would yield a low β, which makes termination less robust (white area in Fig. 1), i.e., prone to substantial disorder leak at higher P_o or near-critical oscillations with uncertain outcome (Fig. 5 B).

Different leak types require different treatments

The two leak types will require different treatments to shift leaky CRU operation toward normal spark termination. One possibility for effective treatment of synchronized leak would decrease the unitary current i_RyR, e.g., by decreasing Ca overload. On the other hand, treatments of the disorder leak would target the number of open RyRs or RyR gating to decrease P_o. This approach would at least help to convert disorder leak into spark termination via stochastic attrition (faint red to white in Fig. 1). But, to fully normalize spark termination via phase transition (green area in Fig. 1), we have to increase β (i.e., RyR interactions). This is the opposite to synchronized leak treatment. Moreover, treatments must be delicate and balanced to get exactly into the normal spark termination, avoiding overtreatment shifts from one pathological leak to the other (red and blue areas).

Another important insight offered by our study is that the transitions from one regime to another (and respective treatments) are abrupt, via the respective criticalities shown by dash lines in Fig. 1. It means that 1) a treatment may remain ineffective if its effect remains within the same functional paradigm (same color in Fig. 1), 2) it can be uncertain if we reach the near-critical regimes including spontaneous oscillations (Fig. 5 B), and 3) the effect can be abrupt when we cross the criticality and shift into another functional paradigm (another color). Thus, our leak classification and exact mathematical formulas for the boundaries of different functional paradigms can be helpful in developing and optimizing treatments of different types of leak to restore normal CRU operation and normal heart function.

Our results are in line with prior studies

Prior numerical simulation studies characterized the invisible releases (subsparks and quarks) and sparks that fail to terminate (11, 12, 13, 14, 15, 16, 17). The invisible releases are similar to disorder leak in subcritical β regime reported here in our model. The prior reports that long-lasting sparks are facilitated by rapid inter- and intra-SR Ca diffusion (15, 16) or faster JSR refilling rate with Ca (13) is in line with our results (Fig. 4 B). In general, we show here that any factors increasing and supporting unitary current i_RyR would prevent phase transition via h polarity reversal and facilitate a synchronized leak (the system remains locked in blue area in Fig. 1).

Because Ca sparks are rare events during diastole, smaller “nonspark” events (often called invisible releases) are thought to be responsible for a major part of SR Ca leak (31). The occurrence of spark-mediated leak and nonspark (invisible) leak was experimentally studied by Zima et al. (32). They showed that spark-mediated leak sharply increases as the SR Ca load surpasses 500 μM, whereas nonspark leak dominates at lower loads. We interpret the experimentally measured nonspark leak as a manifestation of disorder leak (in our terms) that occurs in our model at low SR Ca loads, when CICR is negligible and RyRs cannot effectively interact. At higher loads, CICR generates sparks, whereas the nonspark leak becomes saturated (32) (see their Fig. 3 A). This saturation can be explained by that the net Ca flux is determined by the product of i_RyR (i.e., single RyR current) and the total number of nonspark RyR openings (Nopen). While Nopen decreases, i_RyR increases at higher SR loads, so that the product i_RyR × Nopen does not change or change a little. An additional factor that supports nonspark leak at higher loads could be also oscillating tails of “quarky” releases (see next section).

Ca quarks and quarky Ca releases

The term “Ca quark” was introduced by Lipp and Niggli (33) when they claimed to resolve experimentally openings of individual RyR within a CRU triggered by flash photolysis of caged Ca. The term “quarky calcium release” as a new type of Ca leak contributing to “invisible” leak was introduced in 2011 by Brochet et al. (9). Their measurements resolved a finer structure of sparks and showed that some sparks consist of an initial stereotypical high-flux release followed by a highly variable “quarky” release that is attributable to CICR. By this description, this type of CICR-driven leak is similar to oscillatory leak in a CRU near criticality (in our terms); see Fig. 5 B and Video S4. Brochet et al. speculated that quarky release occurs because of CRU imperfections, including rogue RyRs or subclusters of RyRs (Fig. 7 in their work (9)). On the other hand, our study shows that a quarky release can also occur within a perfect RyR grid.

Limitations and future directions

Our model features a perfect lattice of RyRs (Fig. S1). In reality, the CRU geometry features various sizes and morphologies (34), and some (e.g., phosphorylated) RyRs may have different gating properties. Furthermore, we cover here leaks emerging within a CRU. Other leak types, e.g., spontaneous sparks and waves, may have different mechanisms.

Our numerical model of spark (13) is reduced to a minimal gating scheme of one open and one closed state (Fig. 2 A, inset), i.e., RyRs interact exclusively via CICR. Other possible interactions, such as allosteric coupling, are not considered in our reductionist approach here. Furthermore, the real Ca near couplon during cell contraction will vary depending on numerous factors, such as Ca fluxes via RyRs in neighboring CRUs, L-type Ca channels, Na/Ca exchanger, Ca pumps, cytosol Ca buffers, Ca diffusion in cytosol, etc. Thus, although cell Ca signaling/dynamics is clearly a multiscale problem, our reductionist study focuses on a single spark model at a background cytosolic Ca level near 100 nM.

Future directions

• 1)To the best of our knowledge, our approach offers a new view and terminology on the problem of Ca leak in the heart. In addition to the mathematical clarity of the model in simplified reductionist settings, our formulas provide an effective computational tool to aid in detailed numerical modeling of Ca dynamics and multi-dimensional, computationally intensive parametric search. Knowledge of just two aggregate parameters, h and β, in conjunction with our phase diagram yields hitherto unknown instantaneous information about the system’s steady state (i.e., where the system “wants” to be).
• 2)The Ising model and other systems at and near criticality exhibit very special behaviors, quite different from their behaviors away from criticality. First off, the time of convergence to equilibrium is long. This means, in terms of RyRs, that if we start with all RyRs open, the termination time might be long even if h is negative, making criticality particularly dangerous. Secondly, the spin correlations exhibit long range order, i.e., event sizes are large and exhibit heavy tails. Lastly, event sizes (closely related to spin-to-spin correlation length) near criticality in every known magnetic material obey a universal formula (with “universal exponents”), and we would expect it to also hold in the CRU. All these near-critical phenomena merit further exploration.
• 3)Our mapping to the Ising model gives a formula for the steady-state probability of every configuration of open and closed RyRs. Although this formula is not computationally tractable, the ratio of probabilities of any two possible configurations is easy to obtain. This yields powerful information that has not truly been utilized and remains to be understood.
• 4)The CRU oscillatory behaviors (e.g., in Fig. 5 B) are similar to spontaneous Ca oscillations found in pacemaker cells, i.e., the “calcium clock” (27, 28, 29, 30). In terms of statistical physics, this may be analogous to superheating, which can be explored using hysteresis in the Ising model.
• 5)Recent results (34) indicate that RyR positioning is not a perfect grid. There are three main differences that may impact system behavior: the small deviations of most RyRs away from the perfect grid positions, missing RyRs, and the nontrivial nonsquare shape of the whole cluster. Each of these differences merits further study, with different methodology. The small deviations could be modeled as disorder in the interaction function. The missing RyRs would correspond to a dilute Ising model (35), which is currently actively studied in mathematical physics. The interesting shapes of clusters require a careful analysis of how system behavior depends on the shape of its boundary.

Lastly, the Ising model is a powerful and universal tool recently introduced into this field. We hope it will spur a new way of thinking about the clinical problem of Ca leak in mathematical terms. Thus, a key envisaged future direction would be to classify possible interventions in terms of their effects on Ising parameters h and β and to use this knowledge in designing new effective therapies. Our finding that leak emerges abruptly as underlying parameters change only a little (as shown in Fig. 1) will have important implications for drug design and dosage.

Conclusions

This study considered the mechanisms of the pathological SR Ca leak as an emerging, macroscopic phenomenon, i.e., generated by a statistical ensemble of interacting individual RyRs within a CRU. Using the Ising model from statistical mechanics, we discovered two types of phase transitions and two types of emergent leak. One leak type is a synchronous release by RyRs, which strongly interact via CICR (e.g., in Ca overload). Another type is a disorder leak with no effective RyR interactions (e.g., at low SR Ca levels). The disorder leak is distinguished from synchronized leak by larger Peierls contour lengths. Normal spark termination and leak regimes are summarized in a β-h phase diagram (Fig. 1), which can guide future treatments to inhibit leak and normalize Ca release by a CRU.

Our numerical simulations and Ising model separately and together demonstrate the two major points: 1) any factor that increases i_RyR (unitary current via one RyR) will increase RyR interactions via CICR and prevent spark termination, facilitating Ca leak. These factors include JSR quick refilling with Ca and Ca overload (Fig. 4, B and C, respectively); 2) when i_RyR is small and channels do not interact, the leak is determined simply by opening rate of a single channel (i.e., P_o in terms of ion channel gating) (Figs. 3 D and 5 C).

Author Contributions

A.V.M. designed research, performed research, wrote the manuscript, contributed analytic tools, and analyzed data. M.D.S. designed research and contributed numerical model tools. V.A.M. designed research, performed research, wrote the manuscript, analyzed data, and developed visualization software.

Editor: Arthur Sherman.

Supporting Citations

References (36, 37, 38) appear in the Supporting Material.