Abstract
A computationally inexpensive mathematical solution approach using orthogonal collocations for space discretization with temporal Fourier series is proposed to compute subject-specific blood flow in distensible vessels of large cerebral arterial networks. Several models of wall biomechanics were considered to assess their impact on hemodynamic predictions. Simulations were validated against in vivo blood flow measurements in six human subjects. The average root-mean-square relative differences were found to be less than 4.3% for all subjects with a linear elastic wall model. This discrepancy decreased further in a viscoelastic Kelvin-Voigt biomechanical wall. The results provide support for the use of collocation-Fourier series approach to predict clinically relevant blood flow distribution and collateral blood supply in large portions of the cerebral circulation at reasonable computational costs. It thus opens the possibility of performing computationally inexpensive subject-specific simulations that are robust and fast enough to predict clinical results in real time on the same day.
Keywords: One-dimensional blood flow, Fluid-structure interaction, Cerebral arterial tree, Quantitative magnetic resonance angiography, Pulsatile flow
1. Introduction
Quantitative magnetic resonance angiography has allowed non-invasive quantification of blood flow in the cerebral arteries. This in vivo imaging method, however, is limited to a few large cerebral arteries. More complete simulations of cerebral circulation would better inform about normal vascular status or blood flow distributions that occur in pathologies or after endovascular interventions. Many studies have been devoted on performing hemodynamic analysis of the cerebral vasculature based on one-dimensional (Alastruey, et al., 2007; Huang & Muller, 2015; Liang, et al., 2011; Zagzoule & Marc-Vergnes, 1986) and three-dimensional formulations (Xiao, et al., 2014; Ghaffari, et al., 2017). Three-dimensional formulations have been especially significant in determining hemodynamic risks in cerebrovascular diseases (Cebral, et al., 2005; Evju, et al., 2013; Ghaffari, et al., 2018).
One-dimensional models with distensible vessel walls are the method of choice to quantify fluid-structure interactions between blood flow and wall biomechanics. Some examples of the work contributed in this field are (Hughes & Lubliner, 1973; Zagzoule & Marc-Vergnes, 1986; Stergiopulos, et al., 1992; Olufsen, et al., 2000; Formaggia, et al., 2003; Sherwin, et al., 2003a; Müller & Toro, 2014). These studies differed in the respective formulations of the governing equations and numerical methods for time integration.
In a recent study, substantial gains in CPU time and mesh size reduction was achieved for large arterial tree simulations with a parametric structured meshing technique (Ghaffari, et al., 2018). However, the 3D study only considered rigid walls. For clinical translation, a robust computationally efficient with modest complexity would enable surgeons to perform same day blood flow predictions needed in interventional planning (Ghaffari, et al., 2017; Ghaffari, et al., 2018). The ability to perform simulations in real-time could inform clinicians even during the surgical procedure.
A computationally highly efficient method for time integration entails Fourier series. This choice has been previously considered to solve for blood flow (Womersley, 1955; Miekisz, 1963) or wave propagation in distensible blood vessels (Park & Payne, 2011). Advantages of this approach include the speed of the computations and concise prediction of phase shifts between multiple wave propagation phenomena without the need for time step control. In this study, blood flow dynamics on large portions of cerebral arterial trees of six specific human subjects were simulated based on an area-averaged one-dimensional theory with several biomechanics wall models (tube laws). A method of weighted residuals with Fourier series in time is introduced and validated against an existing discontinuous spectral Galerkin approach with second-order time integration (Sherwin, et al., 2003a; Sherwin, et al., 2003b). Their scheme was previously compared with several other one-dimensional numerical schemes and three-dimensional simulations (Boileau, et al., 2015). In this paper, simulation results obtained from the two numerical schemes were compared and analyzed. Moreover, predictions were also compared with quantitative in vivo flow measurements. Different wall models with respective parameters were varied to quantify the flow, area and pressure dynamics for subject-specific arterial trees. The methodology shown here provides total discretization in space and time suitable to predict wave propagation phenomena stemming from pulsatile flow with dynamic blood vessel wall mechanics.
2. Method
2.1. Data acquisition and cerebral vasculature reconstruction
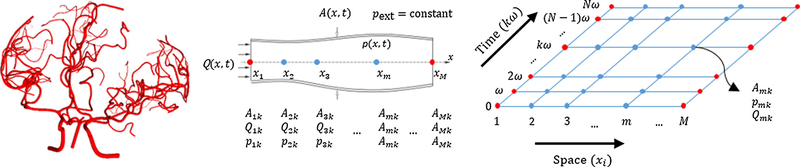
MR imaging was used to acquire in vivo data of the cerebral arterial tree morphology as well as blood flow in the arteries around the circle of Willis and its main branching arteries. Details of the imaging protocol, flow measurements, and vascular skeletonization can be found in the appendix (section A). Figure 1 shows a sample image of the cerebral arterial network for subject I.
Figure 1.
A sample representation of the cerebral arterial network for subject I (left). One-dimensional discretization of vascular segments (splines) using M collocation nodes for the Lagrange polynomials (middle). The full space-time discretization grid for the FSTD method with N Fourier coefficients (right).
2.2. Full space-time discretization (FSTD) with method of weighted residuals and Fourier series (Method-1)
An area-averaged linearized one-dimensional form of blood flow in a deformable arterial network was solved using a method of weighted residuals to discretize the spatial domain along the vessel centerlines with Fourier series for time. Figure 1 shows the full discretization scheme with collocation of Lagrange polynomials along the vessel axis and Fourier series. The dynamic cross-sectional area of the lumen, A(x, t), volumetric flow rate, Q(x, t), and pressure, p(x, t), along the axial co-ordinate of the vessel, x, for each point in time, t, are shown in the form of equations (1)-(3).
| (1) |
| (2) |
| (3) |
where amk are the area coefficients, lm(x) are suitable Lagrange polynomials, i is the imaginary number, ω is the angular frequency, qmk is the coefficient of the volumetric flow rate and pmk is the coefficient of the pressure. M determines the number of collocation nodes considered along the vessel centerline and N stands for the order of the Fourier series frequency. Our approach (1D model) has the advantage over lumped models (0D model) of requiring only a single spline for the entire vessel segment. Note that our assumptions imply periodic flow and pressure distributions. Figure 1 shows a sample cerebral arterial network with cylindrical blood vessels with deformable walls. A fully discretized space-time grid is shown with the unknown coefficients and the location of the spatial nodes on a cylindrical blood vessel with deformable walls.
The area-averaged one-dimensional form of the continuity and momentum equation can be derived from the two-dimensional cylindrical form (Payne, 2004; Smith, et al., 2002). For an incompressible fluid, the continuity equation can be expressed in terms of the area and volumetric flow rate.
| (4) |
The momentum equation can be written in linearized form as in equation (5).
| (5) |
where α is the momentum correction factor, and are the mean flow and area, respectively, ρ is the density of blood and f = 2π(ζ + 2)μ/ρ is the frictional term dependent on the velocity profile parameter, ζ, the dynamic viscosity, μ and ρ. The pressure-area relationship required for problem closure with viscoelastic wall properties (Alastruey, et al., 2011; Alastruey, 2011) can be written in linearized form as in equation (6).
| (6) |
where is the mean pressure, is related to wall elasticity, E, and is the wall damping term. E is the Young’s modulus, h is the wall thickness and φ is the wall viscosity. More details on the linearization procedure can be found in the appendix (section B).
Harmonic analysis with Fourier series has the advantage of time step size independence of the solution and the possibility of computing phase differences consistently. It has the additional benefit that there are no interactions between the different harmonics such that the individual harmonic coefficients can be computed separately, thus substantially reducing the computational burden. This is a critical benefit for large-scale arterial network simulations.
The first step of the numerical implementation was to solve for time-averaged flow, , and area, , which were computed using steady-state flow conditions. These values were needed to compute the higher harmonic coefficients by substituting equations (1)–(3) into equations (4)–(6) and equating matching harmonic coefficients at each node m. The continuity and linearized momentum equations for each vessel element can be expressed as equations (7) and (8), respectively.
| (7) |
| (8) |
where lmj = lm(xj), , is the spatial derivative of the Lagrange polynomials at xj. The linearized pressure-area relationship can be expressed as equation (9).
| (9) |
2.3. Discontinuous spectral Galerkin method (Method 2)
Next, we assessed whether the relatively simpler FSTD could achieve results comparable to rigorous algorithms. Although there were several excellent numerical methods available (Boileau, et al., 2015; Müller & Toro, 2014; Steele, et al., 2011), a discontinuous Galerkin scheme with a spectral spatial discretization with second-order Adams-Bashforth time integration scheme was chosen. The reader is directed to (Sherwin, et al., 2003a; Sherwin, et al., 2003b; Alastruey, et al., 2011) for its derivation.
2.4. Initial and boundary conditions
Pulsatile flows were imposed at the network inlets using a mass flow corrected MR flow measurements. A discrete Fourier series with a truncation order of N was considered to exactly encode the measured volumetric flow rates. The Fourier series for blood flow at the carotid and basilar arteries of subject I is provided in the appendix (section C). At the junctions where arterial branches bifurcate or merge, conservation of mass and total pressure were considered (in linearized form). Total pressure consists of the sum of static pressure and dynamic pressure. Conservation of total pressure originates from Bernoulli’s principle, which is an expression of the conservation of the total energy.
| (10) |
| (11) |
where the subscript i denote the nodes of the vessels at the junctions. Note that some studies conserved static pressure (Steele, et al., 2011) rather than total pressure; this alternative can be implemented by suitable modification of equation (11). At the network outlets, pressure distributions were specified with values inferred from flow measurements as outlined in the subsection 2.6.
2.5. Properties of blood and wall biomechanics
Table 1 shows the baseline parameters considered for the simulations throughout this paper. Vessel wall elasticity was set according to an empirical relation (Olufsen, 1999) shown in equation (12),
| (12) |
where k1, k2 and k3 are empirical coefficients, listed in Table 1, and R0 is the vessel radius. Values for viscous wall property were based on an in vivo study on the carotid artery of the human (Valdez-Jasso, et al., 2011).
Table 1.
Model parameters considered for the simulations.
| Property | Value | Units | Reference |
|---|---|---|---|
| Blood | |||
| Density, ρ | 1055 | kg m−3 | Ghaffari et al., 2018 |
| Dynamic viscosity, μ | 4.0 | mPa s | Pedley 1980 |
| Velocity profile order, ζ | 2 | - | |
| Momentum correction factor, α | 4/3 | - | |
| Wall biomechanics | |||
| Empirical coefficient, k1 | 2.0 | MPa | Olufsen 1999 |
| Empirical coefficient, k2 | −2253 | m−1 | Olufsen 1999 |
| Empirical coefficient, k3 | 86.5 | kPa | Olufsen 1999 |
| Ratio of damping term, , to elasticity term, | 10 | % | Valdez-Jasso et al., 2011 |
2.6. Parameter estimation and inference of boundary conditions
In this study, clinically measured volumetric flow rate waveform were set at the inlet vessels; an inversion problem was solved to optimally determine boundary conditions that best align the measured volumetric flow rates with simulated flows. Details of the inversion problem can be found in the Appendix (section D).
2.7. Space/time mesh choices
The number of nodes prescribed for each vessel segment were chosen as function of arc length. Eight harmonic terms were adequate for fitting the quantitative MR flow measurements. Specific choices are listed in the Appendix (section E).
3. Results
Global large-scale simulations were conducted on six subject-specific cerebral arterial networks, using the collocation/Fourier series approach, and compared with the quantitative magnetic resonance flow measurements. In all cases, the inlet flows were set at the basilar artery (BA) and left and right internal carotid arteries (LICA and RICA), and the outlet pressures were set at the outlet vessels of the territories supplied by the anterior (LACA and RACA), middle (LMCA and RMCA) and posterior cerebral arteries (LPCA and RPCA). For each territory, equal outlet vessel pressures were considered following a previously considered method (Ghaffari, et al., 2018). The difference between the results was estimated using the root-mean-square and maximum relative difference, εRMS and εMAX respectively. These were obtained using the following metrics (Boileau, et al., 2015)
| (13) |
| (14) |
| (15) |
where the hat over the variables represent either the measured values or the predicted values using method-2. Note that the metric εRMS accounts for mean integral errors in both the space-time domain.
3.1. Comparison between method-1 and method-2
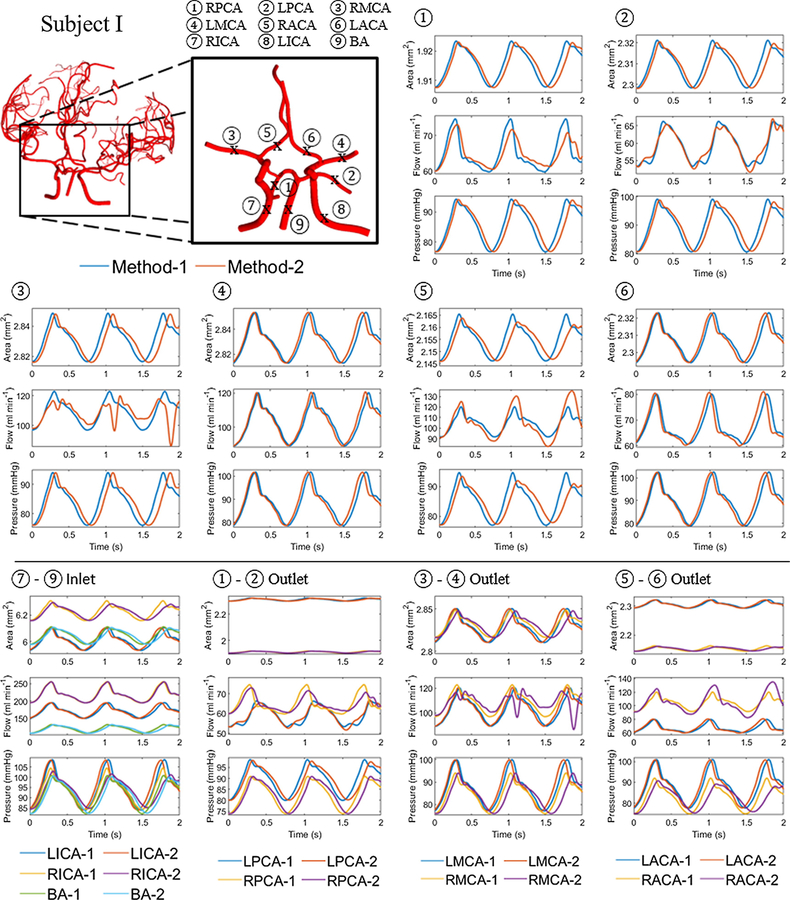
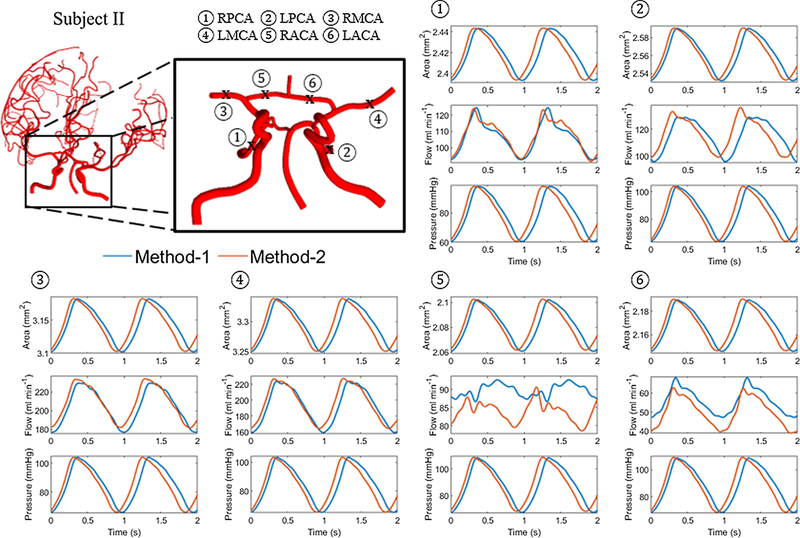
Comparison between methods-1 and 2 were performed on reduced networks comprising of the circle of Willis and its immediate branching spline. In method-2, the momentum correction factor, α, was set to unity to simplify the treatment of the boundary conditions. Thus, α of unity was also prescribed for method-1 for comparison with method-2. This setting was relaxed when method-1 was compared with the clinical measurements. Figure 2 and Figure 3 show area, flow and pressure trajectories at the middle of the vessel length for sample vessels located in the circle of Willis for subjects I and IV, respectively. The blue lines correspond to the trajectories for method-1 and the red lines to method-2. Visual inspection of several segments showed good quantitative and qualitative agreement between the simulations obtained by the two different algorithms. Both solutions showed a decrease in the time-averaged area and pressure along the blood flow direction throughout the cerebral arterial network. An increase in area corresponded to a pressure rise. A phase difference in area, flow and pressure were observed between the two methods that increased in time. Modulation of the periodic waveform was observed in some of the segments in method 2. This effect was due to wave reflections at the outlet of outflow terminal branches, which could have possibly been remedied by more dissipative boundary choices. In this study, the boundary conditions were inferred from in vivo flow measurements, so that resulting boundary conditions could not be fine-tuned to avoid wave reflections. The reader is referred to the original studies for more insight into wave reflections (Sherwin, et al., 2003a; Sherwin, et al., 2003b).
Figure 2.
Hemodynamic prediction for interior and boundary segments with method-1 and method-2. Area, flow and pressure trajectories at the middle section of the vessel length (x = L/2) for the main vessels located in or branching from the circle of Willis for subject I. The blue and red lines represent methods-1 and 2, respectively. Note that some segments show modulation of the periodic waveform with method-2. The bottom row, show trajectories at inflow and outflow boundary nodes that were used for methods-1 and 2. Flow inlet and pressure outlet assignments were identical, but the implementation of method-2 requires conversion of pressures to area information, and it also enforces boundary conditions at phantom nodes (not shown). These implementation differences explain the observed deviations at the physical inlet and outlet nodes.
Figure 3.
Comparison of blood blow simulation results with method-1 and method-2. Area, A, flow, Q, and pressure, p, trajectories at the middle section of the vessel length (x = L/2) for the main vessels located in or branching from the circle of Willis for subject II. The blue and red lines represent methods-1 and 2 respectively. Modulation of the periodic waveform occur in method-2 simulations, probably due to reflections at the boundaries.
Figure 2 also shows area, flow and pressure trajectories at the inlet of inflow vessels (BA and ICA) and at the outlet of outflow vessels (ACA, MCA and PCA) for subject I. Flow inlet and pressure outlet assignments were identical, but the implementation of method-2 requires conversion of pressures to area information. Moreover, method-2 enforces boundary conditions merely at phantom nodes and computes trajectories for the physical boundary using a Riemann problem. These implementation differences explain the deviations observed in Figure 2-(bottom rows) at the physical inlet and outlet nodes for results with method-1 versus method-2.
Table 2 provides data of the number of splines, the number of nodes (which is equal to the number of equations for each frequency) and the simulation time for methods-1 and 2 in the circle of Willis. Method-2 was simulated with time step size, Δt = 10−5, and the simulation time represents the CPU time to obtain results for a single cardiac cycle. All simulations were performed with MATLAB using an Intel Core i7, 3.00 GHz CPU. Table 2 shows the average root-mean-square relative difference across all vessels in the solution obtained by method-1 from method-2, respectively. Mesh information for the circle of Willis considered for the simulations and the CPU times are also provided. The value range of the root-mean square relative difference for the vessel lumen area, volumetric flow rate and pressure for the six subjects were 0.10–0.69%, 1.4–5.5% and 1.1–5.4%, respectively. The largest average root-mean square relative difference in all subjects considered was observed in the volumetric flow rate, followed by the pressure and the vessel lumen area.
Table 2.
Average root-mean-square relative deviation (in per cent) of method-1 with respect to method-2 and the mesh information for the circle of Willis considered for the simulations. Simulation results were compared at the midpoint of each vessel.
| Subject | # of splines | # of nodes | Simulation time (s) |
||||
|---|---|---|---|---|---|---|---|
| Method 1 | Method 2 | ||||||
| I | 0.13 | 3.4 | 2.2 | 14 | 94 | 9.8 | 842 |
| II | 0.31 | 4.2 | 5.6 | 16 | 104 | 10.4 | 1314 |
| III | 0.10 | 3.9 | 1.1 | 14 | 94 | 8.4 | 820 |
| IV | 0.18 | 4.6 | 3.1 | 12 | 92 | 8.5 | 899 |
| V | 0.14 | 2.3 | 1.1 | 13 | 93 | 8.2 | 1000 |
| VI | 0.20 | 3.6 | 1.7 | 10 | 72 | 6.8 | 639 |
3.2. Comparison of quantitative magnetic resonance flow measurements with predicted flow of full network simulations using method-1
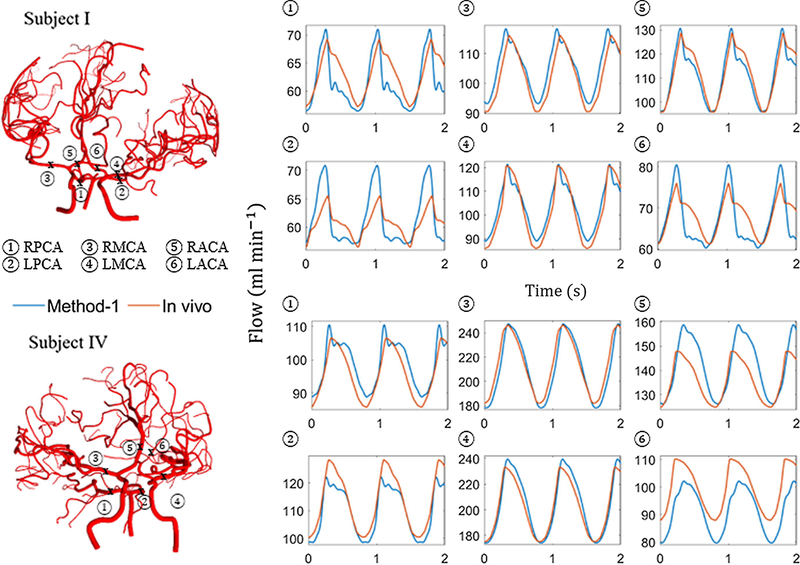
Figure 4 shows area, flow and pressure trajectories (blue) with time at the middle of the vessel length for sample vessels for subject I. The results were compared with in vivo blood flow measurements (red). Visual inspection showed that there was reasonable quantitative and qualitative agreement between simulated and measured flows. Table 3 summarizes the differences between flow measurements and flow simulations with elastic vessels for three subjects. The value range of the root-mean square relative difference for the volumetric flow rate for subjects I, II and IV were 2.7–5.5%, 1.5–5.7% and 2.8–7.6%, respectively. The average root-mean-square relative difference for all vessels in each subject was found to be less than 3.6%, which falls within experimental error bounds of the MR flow measurements.
Figure 4.
In vivo blood flow measurements in comparison to FSTD (method-1) simulation results. Two sample images of subject-specific cerebral arterial trees considered in this study and comparison of simulated versus measured volumetric blood flow rates. The simulation (blue) and the in vivo blood flow measurement (red) at the different locations.
Table 3.
Relative differences (in per cent) with respect to clinical measurements for elastic wall mechanics. Simulation values were taken at the midpoint of each vessel.
| Vessel | Subject I |
Subject II |
Subject IV |
|||
|---|---|---|---|---|---|---|
| LACA | 5.5 | 10.5 | 2.9 | 6.7 | 7.6 | 13.9 |
| RACA | 2.7 | 4.1 | 5.7 | 9.2 | 6.2 | 10.0 |
| LMCA | 3.1 | 5.2 | 1.5 | 2.5 | 2.7 | 4.3 |
| RMCA | 3.4 | 6.5 | 2.8 | 6.9 | 2.8 | 6.0 |
| LPCA | 5.0 | 9.9 | 4.5 | 7.7 | 3.2 | 7.2 |
| RPCA | 4.7 | 9.3 | 2.3 | 4.2 | 3.7 | 6.6 |
3.3. Wall mechanics and full network visualization
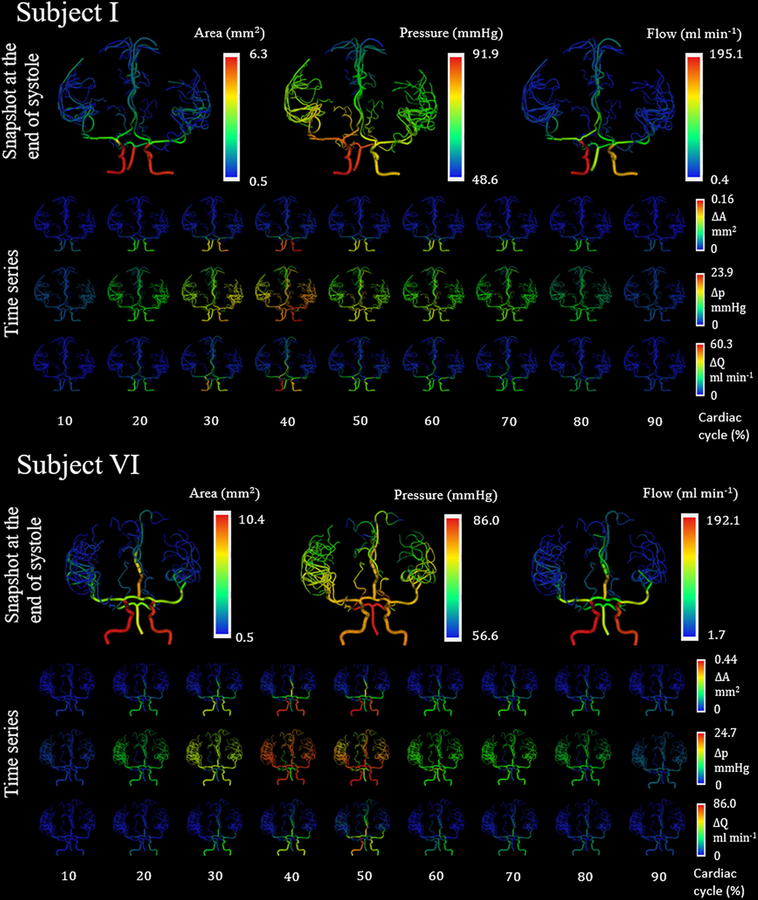
Parametric variations in fluid and wall properties were considered next. Uncertainty in diameter information was explored. For a set pressure drop, a 1% increase in diameter caused the flow to increase by 4% (data not shown). An increase in the fluid viscosity resulted in a larger decrease in the time-averaged area and pressure drop along the axial length of each vessel as expected. Making the vessel walls more rigid by increasing Ḡ, reduced the amplitude of the area deformations, but maintained its principal waveform. The specific waveform of the area, flow and pressure followed the waveform set at the terminal nodes underscoring the significance of boundary choices. Figure 5 shows the diameter, flow and pressure distribution at the end of diastole and how it varies across various time points in a cardiac cycle for subjects I and IV using an elastic wall model. Peak diameters, flows and pressures are observed at around 40% of a cardiac cycle. Figure 6 summarizes the area, flow and pressure distribution for elastic and viscoelastic wall models. The linear elastic wall model exhibits no phase difference between the area and the pressure distribution leading to a straight line in the pressure-area plot. The introduction of the wall damping term introduces a phase shift between the area and the pressure trajectories, leading to the hysteresis loop observed in the pressure-area plots, which is proportional to dissipated work by the vascular wall. The phase difference increases and the peak pressure amplitudes decreases with more dissipative wall damping. Table 4 summarizes the differences between flow measurements and flow simulations with viscoelastic vessel wall properties for three subjects. The average root-mean-square relative difference for all vessels in each subject was found to be less than 3.1%, which is slightly better than the linear elastic case.
Figure 5.
Simulated hemodynamics in distensible blood vessels for human subjects I and IV for one cardiac cycle. The first row, for each subject, shows the diameter, flow and pressure distribution at the end of diastole with an elastic wall model. The second and third row shows the change in flow and pressure distribution, respectively, in each vessel from its respective baseline value at the different time points within a cardiac cycle represents the cardiac period.
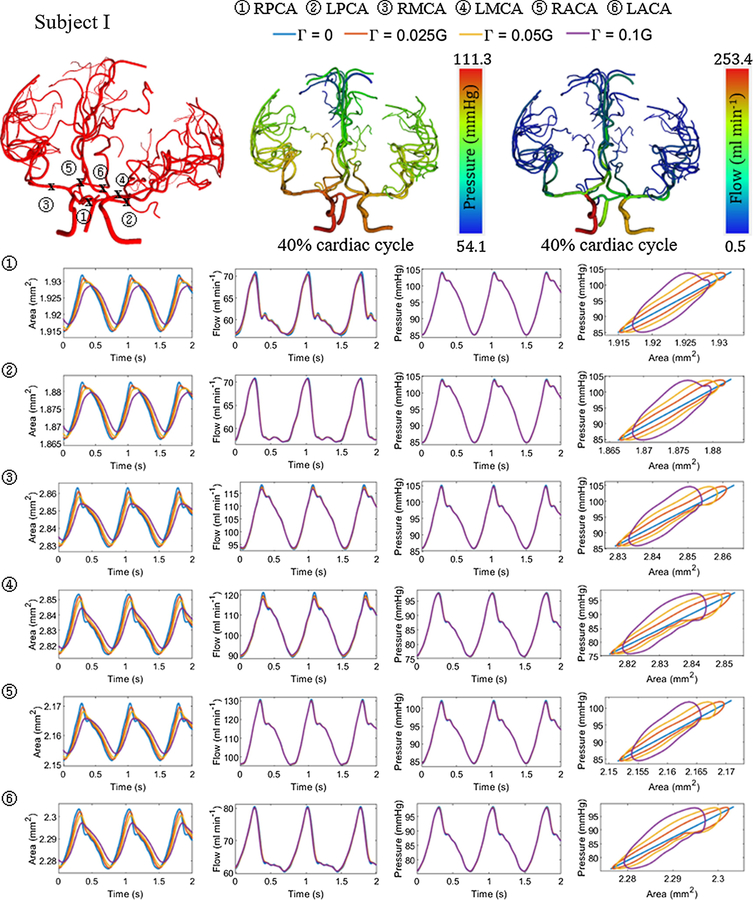
Figure 6.
Area, flow and pressure trajectories with time at the left and right ACA, MCA and PCA with varying wall viscoelastic properties for subject I. The viscoelastic wall parameter value was set at 2.5%, 5% and 10% of the wall elastic stiffness. Three cerebral arterial networks are also shown with the location of the vessels and snapshot of the flow and pressure distribution at 40% cardiac cycle for with viscoelastic wall properties .
Table 4.
Relative differences (in per cent) with respect to clinical measurements for viscoelastic wall mechanics . Simulation values were taken at the midpoint of each vessel.
| Vessel | Subject I |
Subject II |
Subject IV |
|||
|---|---|---|---|---|---|---|
| LACA | 5.6 | 9.9 | 2.7 | 6.2 | 7.5 | 13.6 |
| RACA | 2.8 | 3.9 | 5.7 | 9.2 | 5.5 | 9.1 |
| LMCA | 3.4 | 5.4 | 1.2 | 2.3 | 2.0 | 3.6 |
| RMCA | 3.5 | 6.6 | 3.2 | 6.8 | 2.0 | 4.6 |
| LPCA | 5.0 | 10.1 | 4.2 | 6.8 | 3.2 | 7.7 |
| RPCA | 5.1 | 9.0 | 2.4 | 4.6 | 3.7 | 7.0 |
Table 5 shows the total baseline volume of the cerebral arterial trees and maximum volume expansion and contraction. Absolute values and percentages of baseline are listed for different elastic and viscoelastic wall models. In general, peak volume expansion was found to be greater than the peak contraction. The subject-averaged stroke volume displacement was found to be 1.6% and 1.1% of the baseline volume for the elastic and viscoelastic wall model, respectively. Simulations for the entire visible portion of the cerebral arterial network showed stroke volumes of up to 0.047–0.154 ml for the elastic wall model (and 0.030–0.101 ml for the viscoelastic wall model). The total volumetric strain was equal to approximately 0.9–2.3% for the elastic wall model (and 0.6–1.8% for the viscoelastic wall model). Quantification of the total vasculature volume and its periodic expansion is relevant for explaining CSF motion in the spinal and cranial subarachnoid spaces.
Table 5.
Total baseline volume and the maximum volume expansion and contraction in the cerebral arterial tree with elastic and viscoelastic wall models.
| Subject | Baseline volume (ml) | Elastic wall |
Viscoelastic wall |
||||
|---|---|---|---|---|---|---|---|
| ΔV+ | ΔV− | ΔV | ΔV+ | ΔV− | ΔV | ||
| I | 5.0 | 0.038 | −0.010 | 0.047 | 0.026 | −0.004 | 0.030 |
| II | 4.5 | 0.050 | −0.054 | 0.104 | 0.037 | −0.044 | 0.081 |
| III | 6.4 | 0.036 | −0.028 | 0.064 | 0.022 | −0.019 | 0.041 |
| IV | 6.9 | 0.073 | −0.064 | 0.137 | 0.052 | −0.050 | 0.101 |
| V | 10.6 | 0.077 | −0.039 | 0.115 | 0.050 | −0.027 | 0.077 |
| VI | 6.9 | 0.103 | −0.050 | 0.154 | 0.054 | −0.033 | 0.087 |
4. Discussion
This study introduced an efficient full space-time discretization (FSTD) method for predicting subject-specific blood flow for large portions of the arterial circulation (method-1). The new FSTD algorithm was also validated against a previously developed spectral method with explicit time integration (method-2). Predicted flow, area and pressure obtained from methods-1 and 2 showed some quantitative differences. The largest average root-mean-square relative difference occurred in volumetric flow rate, followed by the pressure and the vessel lumen area. This finding, which agrees with observations of a previous comparative study (Boileau, et al., 2015), we believe to be due to the flow resistance sensitivity, which is inversely proportional to the square of the vessel lumen area, thus magnifying its effects. A further cause for the deviations is attributable to the use of linearized equations in method-1, as well as the effect caused by the penalty term necessary for boundary assignments in method-2.
Comparison between the simulated flow using FSTD and the quantitative magnetic resonance flow measurements showed reasonable quantitative and qualitative agreement. For simulations with elastic wall properties, the average root-mean-square relative difference was found to be less than 3.6% for all subjects. The introduction of the viscoelastic term slightly improved the average root-mean-square relative difference (by around 0.5%) in all six cases. These differences were within previously reported differences between the spectral Galerkin with explicit time integration (method-2) and experiments, which were 4% for pressure and 19% for the volumetric flow rate (Matthys, et al., 2007). These observed deviations also need to be assessed with respect to experimental uncertainties. For example, quantitative flow measurements performed on phantom models have reported inaccuracies of 5–10% (Zhao, et al., 2000). Reported in vivo quantitative MR flow measurements errors were up to 27% (Hofman, et al., 1995). Moreover, considerable uncertainties pertain to the elastic and viscoelastic wall properties. Few data are available for arteries of different wall thickness and diameters that have been determined in vivo for human (Valdez-Jasso, et al., 2011). Therefore, observed differences between simulations with FSTD method-1 and method-2 or method-1 and in vivo experiments seem reasonable given the significant uncertainties in flow quantification, anatomical centerline and diameter information and biomechanical properties (for example wall thickness, Young’s modulus and viscous coefficients).
A change in the viscoelastic term led to a phase shift between area and pressure peaks. Previous studies have shown that the inclusion of the viscoelastic in the biomechanics of vessel walls improved the ability to predict realistic blood pressure and area dynamics (Steele, et al., 2011; Alastruey, et al., 2012; Alastruey, et al., 2011). We demonstrated that the wall viscosity term can be introduced into method-1 at little extra effort and marginally higher computational cost.
Subject-specific cerebral arterial network simulations allowed the computation of the total volume displacement, which is of great interest for explaining oscillatory CSF motion in the cranial and spinal subarachnoid space. One hypothesis attributes pulsatile CSF motion to periodic expansion and contractions of the cerebral vasculature during the cardiac cycle (Enzmann & Pelc, 1993). The CSF stroke volume in the cervical region was previously found to be around 0.5–2 ml (Tangen, et al., 2017; Tangen, et al., 2015). Here, the total peak-to-peak volumetric expansion of the cerebral arterial network amounted to merely 0.154 ml (with the linear elastic model). These predictions seem to suggest that arterial expansion only accounts for a minor portion of the observed CSF displacement in the cervical region (with a stroke volume 1–2 ml per heart beat). More analysis is required to correlate vascular expansion to induced CSF motion.
The computational cost to perform the FSTD simulations for the circle of Willis and its immediate branches was around 10 seconds, and took only 70 seconds for full arterial networks with about 100 segments. On average, the computational time for the FSTD with method-1 was less than 1% of the cost for a single cardiac cycle in method-2. Considering that it may take up to one period for method-2 to reach a stable cycle, the computational time savings would be even higher. The computational cost depends on the number of collocation nodes and harmonic terms considered. The area, flow and pressure distributions with changing number of collocation nodes (results not shown) showed that the number of nodes chosen was sufficient to accurately predict the blood flow distributions.
The main computational advantage stems from the use of Fourier series which enable dynamic flow computations by solving linear algebraic sub-problems for each harmonic separately. The required number of harmonics in the simulations should be set equal to the highest coefficient count needed to perform discrete Fourier transforms of blood flow measurements. Fortunately, each harmonic can be separated, such that the additional frequencies only affect the number of linear algebraic sub-problems. Moreover, FSTD time integration requires no time step control.
The proposed FSTD is also suited for use inside an inversion method than can infer unknown boundary conditions from incomplete and noisy in vivo blood flow measurements at the main arteries of the circle of Willis and branching vessels (interior boundary conditions). The computational efficiency opens the possibility of using FSTD to solve fluid-structure interaction problems for the entire arterial circulation. Its efficiency may be critical in applications where simulation results are needed in real time.
Several assumptions were made in this study; linearization of the equations for simulating dynamic blood flow in distensible vessels allowed global time discretization in the frequency domain. Blood was assumed to be an incompressible Newtonian fluid, which is generally valid for the size of the vessels considered. All MR flow measurement data were synchronized to ensure that inlet flow data (at the basilar and internal carotid arteries) had no phase differences. Moreover, total inlet and outlet flow of in vivo MR measurements did not balance. This discrepancy is expected because the imaging modality does not detect smaller branching arteries. To compensate for flows through undetected blood vessels, simulations were performed based on mass-balance corrected fluxes such that the volumetric flow rate values at the three inlet vessels matched the total outflows.
More than fifty dynamic blood flow wave forms acquired over large portions of the cerebral arterial networks in six human subjects were used to validate subject-specific blood flow simulations. Since the emphasis was on validating predictions for a specific subject, increasing the experimental cohort would not strengthen the predictive power for an individual simulation run. We acknowledge that more subjects would consolidate confidence in the routine use of the method, but not improve subject specificity. Thus, the data for six volunteers was deemed reasonable.
5. Conclusions
The computational cost to perform the FSTD simulations was about one hundred times faster than the rigorous spectral method with multistep time integration. Low computation time might be useful for solving multi-scale networks comprising of arterial and microvascular networks. Large-scale computations performed over massive brain-wide networks including the microcirculation (Park & Payne, 2013; Gould & Linninger, 2015; Gould, et al., 2017) would provide insight to organ-wide blood flow dynamics and regulation. Efficient computational methods are necessary for simulation of the whole cerebral circulation (Hartung, et al., 2018), which couple arterial networks with microcirculation and venous drainage.
Supplementary Material
Acknowledgments
The authors would like to gratefully acknowledge partial support of this project by NIH NINDS 1R21NS099896 and NSF grant of CBET-1301198.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Conflict of interest statement
None of the authors have a conflict of interest regarding this work.
References
- Alastruey J, 2011. Numerical assessment of time-domain methods for the estimation of local arterial pulse wave speed. Journal of Biomechanics, Volume 44, 885–891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alastruey J et al. , 2011. Pulse wave propagation in a model human arterial network: Assessmentof 1-D visco-elastic simulations against in vitro measurements. Journal of Biomechanics, Volume 44, 2250–2258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alastruey J et al. , 2007. Modelling the circle of Willis to assess the effects of anatomical variations and occlusions on cerebral flows. Journal of Biomechanics, Volume 40, 1794–1805. [DOI] [PubMed] [Google Scholar]
- Alastruey J, Passerini T, Formaggia L & Peiró J, 2012. Physical determining factors of the arterial pulse waveform: theoretical analysis and calculation using the 1-D formulation. Journal of Engineering Mathematics, Volume 77, 19–37. [Google Scholar]
- Blanco PJ, Watanabe SN & Feijóo RA, 2012. Identification of vascular territory resistances in one-dimensional hemodynamics simulations. Journal of Biomechanics, Volume 45, 2066–2073. [DOI] [PubMed] [Google Scholar]
- Boileau E et al. , 2015. A benchmark study of numerical schemes for one-dimensional arterial blood flow modelling. International Journal for Numerical Methods in Biomedical Engineering, Volume 31, e02732. [DOI] [PubMed] [Google Scholar]
- Cebral JR et al. , 2005. Characterization of cerebral aneurysms for assessing risk of rupture by using patient-specific computational hemodynamics models. American Journal of Neuroradiology, Volume 26, 2550–2559. [PMC free article] [PubMed] [Google Scholar]
- Chnafa C, Brina O, Pereira VM & Steinman DA, 2018. Better than nothing: a rational approach for minimizing the impact of outflow strategy on cerebrovascular simulations. American Journal of Neuroradiology, Volume 39, 337–343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Enzmann DR & Pelc NJ, 1993. Cerebrospinal fluid flow measured by phase-contrast cine MR. American Journal of Neuroradiology, Volume 14, 1301–1307. [PMC free article] [PubMed] [Google Scholar]
- Evju Ø, Valen-Sendstad K & Mardal KA, 2013. A study of wall shear stress in 12 aneurysms with respct to different viscosity models and flow condtiions. Journal of Biomechanics, Volume 46, 2802–2808. [DOI] [PubMed] [Google Scholar]
- Formaggia L, Lamponi D & Quarteroni A, 2003. One-dimensional models for blood flow in arteries. Journal of Engineering Mathematics, Volume 47, 251–276. [Google Scholar]
- Ghaffari M et al. , 2018. Quantification of near-wall hemodynamic risk factors in large-scale cerebral arterial tree. International Journal for Numerical Methods in Biomedical Engineering, Volume 34, e2987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghaffari M et al. , 2018. Validation of parametric mesh generation for subject-specific cerebroarterial trees using modified Hausdorff distance metrics. Computers in Biology and Medicine, Volume 100, 209–220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghaffari M et al. , 2017. Large-scale subject-specific cerebral arterial tree modeling using automated parametric mesh generation for blood flow simulation. Computers in Biology and Medicine, Volume 91, 353–365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gould IG, Tsai P, Kleinfeld D & Linninger A, 2017. The capillary bed offers the largest hemodynamic resistance to the cortical blood supply. Journal of Cerebral Blood Flow and Metabolism, Volume 37, 52–68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gould I & Linninger A, 2015. Hematocrit distribution and tissue oxygenation in large microcirculatory networks. Microcirculation, Volume 22, 1–18. [DOI] [PubMed] [Google Scholar]
- Guan D, Liang F & Gremaud PA, 2016. Comparison of the Windkessel model and structured-tree model applied to prescribe outflow boundary conditions for a one-dimensional arterial tree model. Journal of Biomechanics, Volume 49, 1583–1592. [DOI] [PubMed] [Google Scholar]
- Hartung G et al. , 2018. Simulations of blood as a suspension predicts a depth dependent hematocrit in the circulation throughout the cerebral cortex. PLOS Computational Biology, Volume 14, e1006549. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hofman MBM et al. , 1995. In vivo validation of magnetic resonance blood volume flow measurements with limited spatial resolution in small vessels. Magnetic Resonance in Medicine, Volume 33, 778–784. [DOI] [PubMed] [Google Scholar]
- Hsu C et al. , 2017b. Gap-free segmentation of vascular networks with automatic image processing pipeline. Computers in Biology and Medicine, Volume 82, 29–39. [DOI] [PubMed] [Google Scholar]
- Hsu CY et al. , 2017a. Automatic recognition of subject-specific cerebrovascular trees. Magnetic Resonance in Medicine, Volume 77, 398–410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang PG & Muller LO, 2015. Simulation of one-dimensional blood flow in networks of human vessels using a novel TVD scheme. International Journal for Numerical Methods in Biomedical Engineering, Volume 31, e02701. [DOI] [PubMed] [Google Scholar]
- Hughes T & Lubliner J, 1973. On the one-dimensional theory of blood flow in the larger vessels. Mathematical Biosciences, Volume 18, 161–170. [Google Scholar]
- Lee TC, Kashyap RL & Chu CN, 1994. Building skeleton models via 3-D medial surface/asxis thinning algorithms. CVGIP: Graph Models and Image Processing, Volume 56, 462–478. [Google Scholar]
- Liang F, Fukasaku K, Liu H & Takagi S, 2011. A computational model study of the influence of the anatomy of the circle of Willis on cerebral hyperperfusion following carotid artery surgery. Biomedical Engineering Online, Volume 10, 84. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matthys KS et al. , 2007. Pulse wave propagation in a model human arterial network: Assessment of 1-D numerical simulations against in vitro measurements. Journal of Biomechanics, Volume 40, 3476–3486. [DOI] [PubMed] [Google Scholar]
- Miekisz S, 1963. The flow and pressure in elastic tube. Physics in Medicine and Biology, Volume 8, 319–324. [DOI] [PubMed] [Google Scholar]
- Müller L & Toro E, 2014. A global multiscale mathematical model for the human circulation with emphasis on the venous system. International Journal for Numerical Methods in Biomedical Engineering, Volume 30, 681–725. [DOI] [PubMed] [Google Scholar]
- Olufsen M et al. , 2000. Numerical simulation and experimental validation of blood flow in arteries with structured-tree outflow conditions. Annals of Biomedical Engineering, Volume 28, 1281–1299. [DOI] [PubMed] [Google Scholar]
- Olufsen MS, 1999. Structured tree outflow condition for blood flow in larger systemic arteries. American Journal of Physiology, Volume 276, H257–H268. [DOI] [PubMed] [Google Scholar]
- Park CS & Payne SJ, 2011. Nonlinear and viscous effects on wave propagation in an elastic axisymmetric vessel. Journal of Fluids and Structures, Volume 27, 134–144. [Google Scholar]
- Park CS & Payne SJ, 2013. A generalized mathematical framework for estimating the residue function for arbitrary vascular networks. Interface Focus, Volume 3, 20120078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Payne SJ, 2004. Analysis of the effects of gravity and wall thickness in a model of blood flow through axisymmetric vessels. Medical and Biological Engineering and Computing, Volume 42, 799–806. [DOI] [PubMed] [Google Scholar]
- Pedley TJ, 1980. The fluid mechanics of large blood vessels Cambridge: Cambridge University Press. [Google Scholar]
- Sherwin SJ, Formaggia L, Peiró J & Franke V, 2003a. Computational modelling of 1D blood flow with variable mechanical properties and its application to the simulation of wave propagation in the human arterial system. International Journal for Numerical Methods in Fluids, Volume 43, 673–700. [Google Scholar]
- Sherwin SJ, Franke V, Peiró J & Parker K, 2003b. One-dimensional modelling of a vascular network in space-time variables. Journal of Engineering Mathematics, Volume 47, 217–250. [Google Scholar]
- Smith NP, Pullan AJ & Hunter PJ, 2002. An anatomically based model of transient coronary blood flow in the heart. SIAM Journal of Applied Mathematics, Volume 62, 990–1018. [Google Scholar]
- Steele BN, Valdez-Jasso D, Haider MA & Olufsen MS, 2011. Predicting arterial flow and pressure dynamics using a 1D fluid dynamics model with a viscoelastic wall. SIAM Journal of Applied Mathematics, Volume 71, 1123–1143. [Google Scholar]
- Stergiopulos N, Young DF & Rogge TR, 1992. Computer simulation of arterial flow with applications to arterial and aortic stenoses. Journal of Biomechanics, Volume 25, 1477–1488. [DOI] [PubMed] [Google Scholar]
- Tangen KM, Hsu Y, Zhu DC & Linninger AA, 2015. CNS wide simulation of flow resistance and drug transport due to spinal microanatomy. Journal of Biomechanics, Volume 48, 2144–2154. [DOI] [PubMed] [Google Scholar]
- Tangen KM, Leval R, Mehta AI & Linninger AA, 2017. Computational and in-vitro experimental investigation of intrathecal drug distribution – parametric study of the effect of injection volume, cerebrospinal fluid pulsatility, and drug uptake. Anesthesia and Analgesia, Volume 124, 1686–1696. [DOI] [PubMed] [Google Scholar]
- Valdez-Jasso D et al. , 2011. Linear and nonlinear viscoelastic modeling of aorta and carotid pressure-area dynamics under in vivo and ex vivo conditions. Annals of Biomedical Engineering, Volume 39, 1438–1456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Womersley JR, 1955. Method for the calculation of velocity, rate of flow and viscous drag ini arteries when the pressure gradient is known. Journal of Physiology, Volume 127, 553–563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xiao N, Alastruey J & Figueroa CA, 2014. A systematic comparison between 1-D and 3-D hemodynamics in compliant arterial models. International Journal for Numerical Methods in Biomedical Engineering, Volume 30, 204–231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zagzoule M & Marc-Vergnes JP, 1986. A global mathematical model of the cerebral circulation in man. Journal of Biomechanics, Volume 19, 1015–1022. [DOI] [PubMed] [Google Scholar]
- Zhao M et al. , 2000. Improved phase-contrast flow quantification by three-dimensional vessel localization. Magnetic Resonance Imaging, Volume 18, 697–706. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.