SUMMARY
L1 retrotransposon-derived sequences comprise approximately 17% of the human genome. Darwinian selective pressures alter L1 genomic distributions during evolution, confounding the ability to determine initial L1 integration preferences. Here, we generated high-confidence datasets of greater than 88,000 engineered L1 insertions in human cell lines that act as proxies for cells that accommodate retrotransposition in vivo. Comparing these insertions to a null model, in which L1 endonuclease activity is the sole determinant dictating L1 integration preferences, demonstrated that L1 insertions are not significantly enriched in genes, transcribed regions, or open chromatin. By comparison, we provide compelling evidence that the L1 endonuclease disproportionately cleaves predominant lagging strand DNA replication templates, while lagging strand 3’-hydroxyl groups may prime endonuclease-independent L1 retrotransposition in a Fanconi anemia cell line. Thus, acquisition of an endonuclease domain, in conjunction with the ability to integrate into replicating DNA, allowed L1 to become an autonomous, interspersed retrotransposon.
Keywords: LINE-1, transposable element, retrotransposon, human genome, integration, DNA replication, evolution, transcription, chromatin, Fanconi anemia
Graphical Abstract
IN BRIEF
The examination of de novo engineered L1 retrotransposition events in cultured human cells reveals that L1 endonuclease activity and DNA replication dictate L1 insertion preferences and promote its widespread integration throughout the human genome.
INTRODUCTION
Long Interspersed Element-1 (L1) sequences comprise ~17% of human DNA and amplify by a process termed retrotransposition (Lander et al., 2001). The human genome contains a small number of retrotransposition-competent L1s (RC-L1s) that are responsible for the bulk of de novo L1 insertions (Beck et al., 2010; Brouha et al., 2003). Human RC-L1s are ~6kb in length and contain a 5’ untranslated region (UTR) with an RNA polymerase (Pol) II promoter, two open reading frames (ORF1 and ORF2), and a 3’UTR that ends in a poly(A) tract (Figure 1A) (Richardson et al., 2015). The L1-encoded proteins (ORF1p and ORF2p) and full-length polyadenylated L1 RNA are required for retrotransposition (Doucet et al., 2015; Feng et al., 1996; Moran et al., 1996).
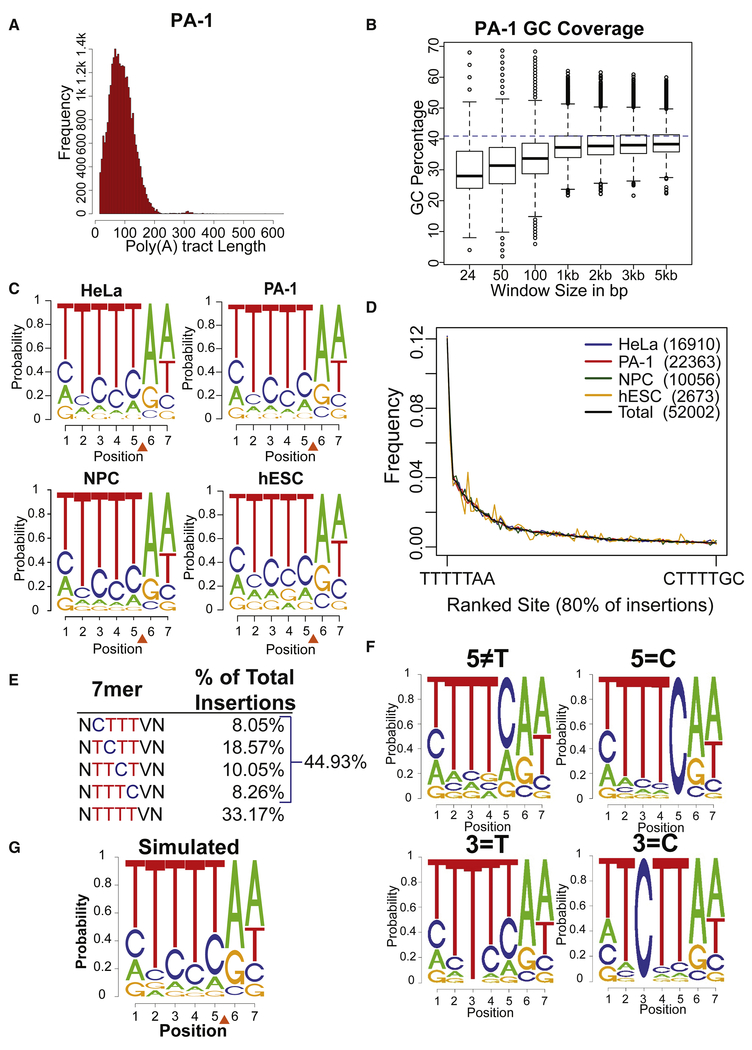
Figure 1: Recovering thousands of de novo engineered L1 retrotransposition events.
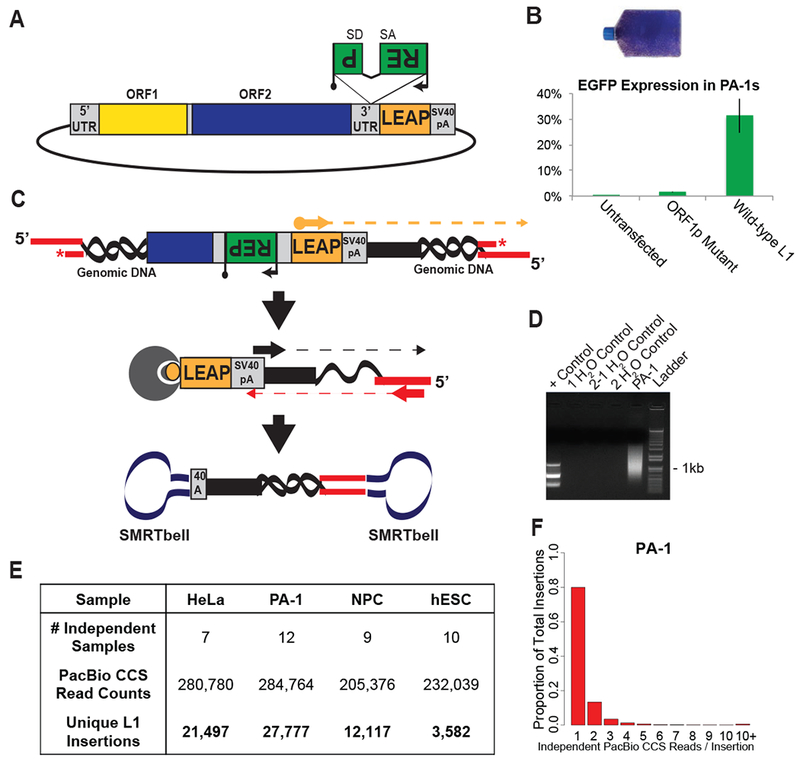
(A) Engineered human L1 expression plasmids contain a retrotransposition indicator cassette (mneoI or mEGFPI) within their 3’UTR (green rectangle with the backward ‘REP’ for ‘Reporter’). The reporter (black arrow, promoter; black lollipop, polyadenylation signal) is in the opposite transcriptional orientation of the L1 and is interrupted by an intron (SD, splice donor; SA, splice acceptor) in the same transcriptional orientation as the L1.
(B) Representative flask of G418-resistant HeLa-JVM cells (top), and the proportion of FACS-sorted EGFP-positive PA-1 cells. Untransfected cells and an L1 ORF1p mutant served as negative controls.
(C) Genomic DNA isolated from cells harboring L1 integration events was sheared and ligated to adapters containing a blocking 3’ amine group (red asterisk). Linear amplification utilized a biotinylated primer specific to the engineered L1 (orange arrow). Products were captured on streptavidin beads (gray circle) and subjected to nested PCR utilizing primers specific to the SV40pA signal (black arrow) and ligated adapter (red arrow). Ligation of SMRTbell adapters (navy dumbbells) facilitated PacBio CCS sequencing.
(D) Gel image of a library created from PA-1 cells shows a smear indicative of many recovered L1 insertions (Lane 5). Lane 1, expected products for a parallel PC39 positive control preparation. Lanes 2 to 4 are water blanks.
(E) Numbers of independent samples, PacBio CCS reads, and unique L1 insertions obtained from the four analyzed cell lines.
(F) Frequency distribution of the number of independent CCS reads (i.e., those with different shear points) supporting L1 insertion events from PA-1 cells.
L1 integrates into genomic DNA by target-site primed reverse transcription (TPRT) (Feng et al., 1996; Luan et al., 1993). An apurinic/apyrimidinic endonuclease (APE)-like domain at the ORF2p amino terminus (L1 EN) cleaves the degenerate consensus sequence 5’-TTTT/AA-3’ to expose a 3’-OH group (Feng et al., 1996; Jurka, 1997). Annealing between a short stretch of genomic thymidine bases and the 3’ L1 poly(A) tract establishes a primer/template structure that is used by the L1 reverse transcriptase (RT) to generate (−) strand L1 cDNA (Kulpa and Moran, 2006; Monot et al., 2013). Subsequent steps likely require L1 and host protein activities (Liu et al., 2018; Richardson et al., 2015).
ORF1p and/or ORF2p can also act in trans to mediate retrotransposition of Short Interspersed Element RNAs, small uracil-rich nucleolar and nuclear RNAs, and cellular mRNAs (Richardson et al., 2015). Thus, L1-mediated events have generated ~30%, or 1 Gbp, of human DNA (Lander et al., 2001). Germline L1-mediated integration events generate inter-individual genetic diversity (Richardson and Faulkner, 2018), whereas somatic events lead to intra-individual genetic diversity (Faulkner and Garcia-Perez, 2017). L1-mediated integration events are responsible for ~130 known human disease cases (Hancks and Kazazian, 2016), may act as driver mutations in cancers (Scott and Devine, 2017), and contribute to neuronal somatic mosaicism (Faulkner and Garcia-Perez, 2017).
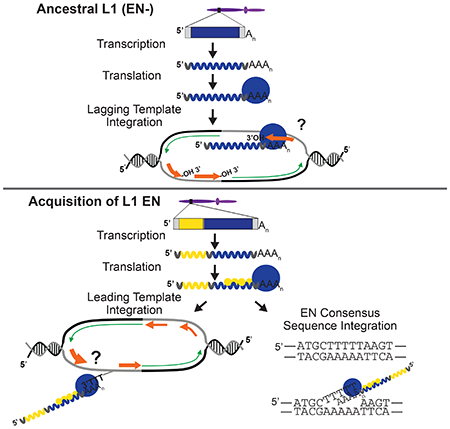
Interactions between transposable element (TE)-encoded proteins and host factors have allowed many TEs to target genomic “safe havens,” which presumably minimizes their impact on host genomes, facilitating TE propagation (Levin and Moran, 2011; Sandmeyer et al., 2015; Sultana et al., 2017). For example, Drosophila P elements preferentially integrate into origin recognition complex binding sites (Spradling et al., 2011) and a subset of group II introns (an ancient predecessor of L1) retrotranspose by an EN-independent mechanism that is proposed to use 3’-OH groups on Okazaki fragments to prime cDNA synthesis (Zhong and Lambowitz, 2003). Saccharomyces cerevisiae Ty1 and Ty3 and Schizosaccharomyces pombe Tf1 retrotransposons integrate into RNA Pol III or RNA Pol II promoters of transcribed genes, respectively (Levin and Moran, 2011; Sandmeyer et al., 2015; Sultana et al., 2017). Similarly, the Moloney murine leukemia virus (MLV) retrovirus preferentially integrates into active promoters and strong enhancers (LaFave et al., 2014).
Darwinian selective pressures skew L1 distributions over evolutionary time (Lander et al., 2001); thus, analyzing older extant human L1s may not reveal initial L1 insertion preferences. An alternative approach uses recombinant DNA vectors to drive the retrotransposition of engineered L1s in cultured cells or animal models (Richardson et al., 2015). Engineered L1s contain an indicator cassette in their 3’UTR, which consists of a “backward” copy of a reporter gene interrupted by an intron in a configuration that ensures the reporter gene only becomes activated after splicing and retrotransposition of the L1 transcript (Figure 1A) (Heidmann et al., 1988; Moran et al., 1996). Engineered L1s have uncovered molecular details about TPRT (Richardson et al., 2015), enumerated how L1 integration can lead to structural genomic changes (Beck et al., 2010), and revealed that L1s can utilize 3’-OH groups generated at sites of DNA damage to integrate by an EN-independent (ENi) mechanism (Morrish et al., 2007; Morrish et al., 2002). However, fewer than two hundred de novo engineered L1 integration events have been characterized in detail (Gilbert et al., 2005; Gilbert et al., 2002; Symer et al., 2002).
We report a large high-confidence dataset of engineered L1 insertions in cultured human cell lines. Gene content, transcription, and the local epigenetic environment of target site DNA prior to retrotransposition had minimal or negative effects on L1 insertion profiles beyond the sequence preference of the L1 EN and RT enzymes. By comparison, positive (+) strand L1 cDNA insertion positions derived from engineered RC-L1s were consistently skewed toward integration into leading strand DNA templates, while an L1 lacking EN activity preferentially integrated into lagging strand templates in a Fanconi anemia mutant cell line. These data suggest that ancestral L1 elements targeted replicating DNA and that subsequent acquisition of the EN domain enhanced an innate capacity of L1 to disperse throughout the human genome.
RESULTS
Libraries of Engineered L1 Retrotransposition Events in Four Human Cell Lines
We generated engineered L1 integration events in four female human cell lines that are proxies for cell types that accommodate endogenous L1 retrotransposition: HeLa-JVM and PA-1 cancer cell lines, H9 human embryonic stem cells (hESCs), and H9 hESC-derived neural progenitor cells (NPCs) (STAR Methods). De novo L1 integration events were enriched using G418 selection (HeLa-JVM and hESCs), enhanced green fluorescent protein (EGFP) cell sorting (PA-1) (Figure 1B), or captured without enrichment (NPCs) (Supplemental Datasets 1 and 2) after a small number of cell divisions. Ligation-mediated PCR captured the 3’ ends of newly inserted L1s and their flanking genomic DNA (Figure 1C), yielding a distribution of amplicon sizes (Figure 1D). To minimize bias, amplicons were characterized using Pacific Biosciences (PacBio) long circular consensus sequence (CCS) reads (Figure S1A; ~600bp).
More than 200,000 CCS reads were obtained for each cell type over 38 independent experiments (Figure 1E). We kept CCS reads only if they had identifiable primers and poly(A) tracts and could be confidently assigned to a single best genomic location (Figure S1B, S1C, S1D; see STAR Methods). Inspection of CCS alignment positions revealed a qualitative ability of engineered L1s to insert into alpha satellite centromeric repeats, repeat sequences near telomeres, or tandem repeats (1,026 unique reads across the four cell lines). The repetitive nature of these sequences, and unknown copy number, prohibited us from calculating a meaningful size-normalized L1 insertion frequency; thus, these reads and genomic regions were also excluded (Supplemental Dataset 3). Our final pipeline had a mapping sensitivity of 98% and a precision of >99% at base-pair resolution (STAR Methods).
The 64,973 called L1 insertions had characteristics of bona fide L1 integration events. Two or more unique CCS reads corroborated many integration events and the extent of repeated detection correlated inversely with the number of independent L1 integration events from each cell population (Figures 1F and S1E). The L1s ended in 3’ poly(A) tracts (range 15-635, median 70 bases; Figures 2A and S2A). Finally, the predicted L1 insertion positions were located in genomic regions with a high local AT content (Figures 2B and S2B) at a L1 EN consensus cleavage site (Feng et al., 1996; Jurka, 1997; Morrish et al., 2002) (Figures 2C, and S2C).
Figure 2: Local L1 integration site preferences.
(A) Frequency distribution of the poly(A) tract lengths of L1 insertions in PA-1 cells.
(B) GC content of different sized windows of genomic sequence surrounding L1 insertion positions. A blue dashed line represents the genome average of 41%. Similar results were observed for all cell lines.
(C) Logo plots of the 7bp degenerate L1 EN consensus sequence for insertions from four cell types. The orange triangle indicates the L1 EN cleavage position.
(D) Frequency distribution of L1 7mer integration site sequences. Plotted sites correspond to 80% of all observed insertions arranged in rank order frequency over all cell lines.
(E) Percentage of L1 insertions that utilized 7mers with T bases, or 3 T bases plus 1 C base, at site positions 2 through 5. N, any nucleotide; V, any nucleotide except T, which cannot be present at position 6 (see text).
(F) Logo plots of subsets of observed L1 integration sites where different nucleotide positions were constrained as indicated above each plot to illustrate the co-dependence of positions 2 through 5.
(G) Logo plot of 7bp L1 EN cleavage ses from one iteration of our weighted random simulation.
L1 Integration Target Sequences
Logo plots of the mapped insertion positions prior to retrotransposition revealed a 7mer consensus sequence, 5’-TTTTT/AA-3’, on the DNA strand cleaved by L1 EN (Figures 2C and S2C). The first 5’ T base is designated position 1; position 6 can never be a T due to the method used to disambiguate genomic insertion positions (Figure S1B). This consensus sequence was identical for the four cell lines with a highly reproducible rank order of individual integration site frequencies, suggesting L1 ORF2p enzymatic properties mainly dictate local L1 integration preferences (Figures 2C, 2D, and S2D). 5’-TTTTT/AA-3’ was the most frequently used single site, but it only accounted for 9.6% of insertions (Figures 2D and S2D) and dropped to the 21st most preferred site after normalizing for genomic site frequencies (Supplemental Dataset 4). Many L1 integration sites (45%) contained a single C base in positions 2 to 5 (Figure 2E), suggesting a co-dependence between these bases that was confirmed by mutual information analysis (Figure S2E) and logo plots with bases fixed at specific positions (Figure 2F). The A bases at positions 6 and 7 are likely contacted by L1 EN (Repanas et al., 2007; Weichenrieder et al., 2004) and were independent of bases at positions 1 to 5, which are likely involved in RT priming (Figures 2F and S2E) (Kulpa and Moran, 2006; Monot et al., 2013).
There are 12,288 sequences (5’-NNNNN/VN-3’) that can serve as possible L1 integration sites. Only 743 (6%) of these 7mers were used by three or more L1 integration events, accounted for 97% of the L1 insertions, and represent 23% (~750 Mb) of the human genome. We constructed a composite model for use in enrichment analyses that appropriately weighted the uncommon 7mer sites while not distorting data at the preferred sites (Figure S2F; STAR Methods). Simulated L1 insertions picked according to this model yielded logo plots and AT base densities very similar to the empirical L1 dataset (Figures 2G vs. 2C and Figures S2G vs. 2B). Thus, the model accurately represented our null hypothesis that only ORF2p enzymatic activities dictate L1 insertion positions.
Engineered L1s Integrate Throughout the Genome and in Transposon-Free Regions
Engineered L1 integration events did not display distinct integration “hot spots” relative to our weighted simulated dataset (Figures 3A, 3B, and S3A). The number of L1 insertions on a chromosome directly correlated with chromosome size (Figures 3A and S3A). Intriguingly, PA-1, hESC, and NPC displayed a statistically significant increase in L1 integration events on the X-chromosome when compared to chromosome size or our null weighted model (Figures 3A, 3B, and S3A). HeLa-JVM cells displayed more L1 integration events than expected on chromosome 5.
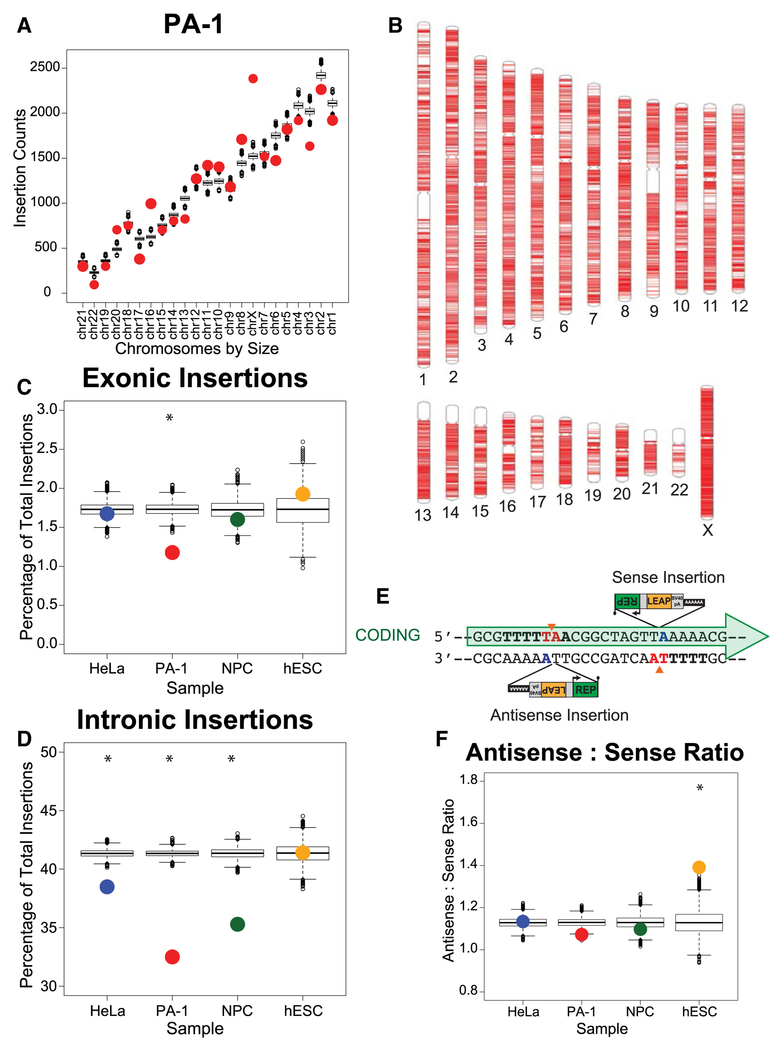
Figure 3: L1 integrates throughout the human genome.
(A) L1 insertion counts by chromosome, sorted by increasing chromosome size. PA-1 insertion counts are plotted as red circles (Spearman’s rho: 0.933; p= 3.15×10−6). Boxplots show the distribution of counts from 10,000 iterations of the weighted random simulation.
(B) Chromosome ideograms depicting the genomic positions of all PA-1 insertions (red lines).
(C) Frequency of exonic L1 insertions stratified by cell line. Colored circles represent the observed insertion counts. Boxplots show distributions from 10,000 simulation iterations. PA-1 χ2 test p= 4.82 × 10−8.
(D) Frequency of intronic L1 insertions stratified by cell line, plotted similarly to (C). HeLa-JVM, PA-1 and NPC cells χ2 test p-values: 1.48 × 10−9, <2.2 × 10−16, and <2.2 × 10−16, respectively.
(E) Cartoon showing L1 insertions in sense and antisense orientations with respect to a gene (green arrow). L1 EN cleavage (orange triangles) on the coding and non-coding strands leads to antisense and sense L1 insertions, respectively.
(F) Antisense to sense ratio of L1 insertions stratified by cell line, plotted similarly to (C). hESC χ2 test p= 5.76×10−4.
Approximately 21-26% of insertions occurred into genomic L1s, whereas approximately 6-7% occurred into genomic Alus (Supplemental Dataset 5). We observed rare instances where L1 integrated at the same nucleotide positions among biological replicates (HeLa-JVM: 10 events; PA-1: 18 events; NPC: 1 event; hESC: 55 events) or between cell lines (0.09% of total insertions) (Supplemental Datasets 6). We identified insertions into genes known to harbor disease-causing L1-mediated integration events (Hancks and Kazazian, 2016), but none occurred at the same nucleotide positions. Engineered L1s did not preferentially integrate into common fragile site loci (Supplemental Dataset 5). Finally, we readily identified insertions into genomic transposon-free regions (TFRs) (1,282 insertions across cell types) (Simons et al., 2007; Simons et al., 2006), and ultra-conserved elements (UCEs) (1-4 insertions per cell type) (Bejerano et al., 2004; McCole et al., 2014) (Supplemental Dataset 5).
Expressed Genes Are Not Preferred L1 Integration Targets
Studies using smaller datasets reported somatic L1 insertion enrichments in expressed genes (Baillie et al., 2011; Jacob-Hirsch et al., 2018; Upton et al., 2015). Engineered L1s readily integrated into the introns (HeLa-JVM: 38.5%; PA-1: 32.5%; NPC: 35.3%; hESC: 41.4%) and exons (HeLa-JVM: 1.7%; PA-1: 1.2%; NPC: 1.6%; hESC: 1.9%) of genes. However, genes were not preferential L1 integration targets (Figures 3C and 3D). In PA-1 cells, we observed significantly fewer genic L1 insertions than expected when compared to the distribution of simulated random insertions (Figure 3C and 3D). In all cell types, except hESCs, we observed fewer insertions into introns than expected (Figure 3D).
Endogenous L1s accumulate in the antisense transcriptional orientation of genes (i.e., at a 1.8 antisense to sense ratio) (Smit, 1999). The median antisense to sense ratio of genic insertions from our 10,000 simulation iterations was 1.13, demonstrating that preferred T-rich L1 integration sites are enriched on coding DNA strands (Figures 3E and 3F). This non-random strand distribution is consistent with the nucleotide composition skew in the genome (Langley et al., 2016; Touchon et al., 2005) and accounted for the entire excess of antisense insertions observed in HeLa-JVM, PA-1, and NPCs. An antisense enrichment beyond the weighted simulations was observed in hESCs (Figure 3F).
To address gene expression directly, we generated RNA-seq data for each cell line. L1 integration was generally depleted in expressed genes (Figure S3B). Insertions from HeLa-JVM, PA-1, and NPCs, but not hESCs, were significantly overrepresented in unexpressed genes (Figure S3B), and the level of expression was not directly correlated with integration. PA-1 and NPCs had significantly more insertions than expected in genes with low-level expression (Figure S3C).
Transcription and Open Chromatin Do Not Promote Local L1 Integration
Open chromatin associated with transcription could make DNA more accessible to L1 integration, whereas transcription bubbles or associated R-loops could expose the non-template DNA strand to L1 EN cleavage (Figure 4A). We performed strand-specific Bru-seq nascent RNA sequencing (STAR Methods) on two biological replicates of PA-1 and HeLa-S3 cells to interrogate such transcriptional effects independently of RNA turnover or gene annotations (Paulsen et al., 2014). HeLa-JVM insertions (32.6%) and PA-1 insertions (19.4%) occurred within actively transcribed genomic regions (Figures 4B and S4A; Supplemental Dataset 7). However, transcribed regions incurred significantly fewer L1 insertions than predicted by weighted simulated insertion distributions (Figure 4B). Thus, transcribed DNA was not a preferential L1 integration target (Figure 4C).
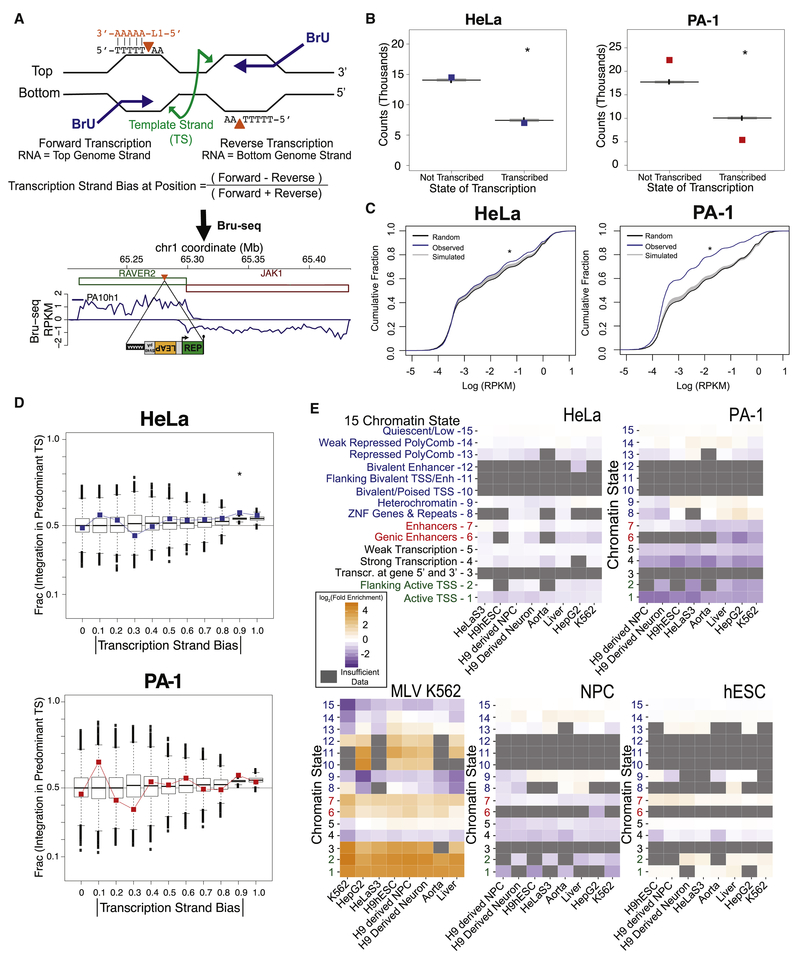
Figure 4: L1 does not preferentially target transcribed regions or open chromatin.
(A) Possible cleavage by L1 EN (orange triangles) on non-template (i.e. coding) DNA strands during transcription initiates TPRT as the L1 RNA (orange) anneals to the poly(T) stretch. Example PA-1 Bru-seq data below surround an actual L1 insertion in the antisense orientation of the RAVER2 gene. Green and red rectangles, genes with forward and reverse orientations, respectively. Bru-seq signal, blue line, plotted as positive and negative RPKM for transcription in the forward and reverse directions, respectively.
(B) L1 events stratified by transcription of their insertion positions. Observed insertion counts are plotted as colored symbols; boxplots show distributions from 10,000 simulation iterations. HeLa-JVM and PA-1 χ2 test: p= 6.2× 10−6 and p< 2.2 × 10−16, respectively.
(C) Cumulative distribution functions (CDFs) of Bru-seq transcription for random genomic L1 insertions (black), 10,000 simulated insertion iterations (gray), and actual L1 insertions (blue). Both HeLa-JVM and PA-1 contained more insertions than expected at lower transcription levels (KSbt p< 1 × 10−6).
(D) Absolute values of transcription strand bias [see panel (A)] were separated into intervals from 0 to 1 (x-axis). The plotted fraction of insertions in genomic regions matching each interval that arose by integration of the L1 (+) strand cDNA into the template strand (TS) (y-axis). Cell line data plotted as colored squares; boxplots depict 10,000 simulation iterations. Asterisk indicates χ2 test p< 0.05. See text for interpretation.
(E) Insertion sample sets were compared to Roadmap Epigenomics Consortium chromatin state data (y-axes) derived from a series of cell lines (x-axes). The most relevant cell type is leftmost on the x-axis. States are grouped as: enhancers (red), promoters (green), transcribed regions (black), and heterochromatin (blue). Box colors represent the log2 fold enrichment of the insertions relative to the set of genomic regions defined by each chromatin state/cell type combination. Gray boxes mask states with <30 expected insertions. MLV integration events from the K562 cell line (LaFave et al., 2014), down-sampled to the same number of events as observed in our PA-1 insertions, illustrate the appearance of a transposable element with a strong state enrichment.
We next defined Bru-seq transcription strand bias such that extreme values of 1 or −1 identify genomic regions where transcription was only occurring in the forward or reverse directions, respectively (Figures 4A and S4B; STAR Methods). We plotted the fraction of L1 sense strand integration events into the predominant template DNA strand in a transcribed region (i.e., where L1 EN cleaved the non-template strand allowing the insertion of L1 (+) strand cDNA into the template strand) as a function of the absolute value of the local transcription strand bias (Figure 4D). If L1 exclusively integrated into template strands, the plotted fraction would increase from 0.5 to 1 as the absolute bias value increases from 0 to 1 (Figure 4D; displayed as |bias|). Simulated insertions were again slightly skewed because L1 7mer integration sites are more prevalent on template strands (Figures 3F and 4D). Observed L1 insertions exhibited a slight, sometimes statistically significant, additional preference to integrate into the template DNA strand (Figures 4D, S4C, and S4D). However, the magnitude of this effect was far less than expected if non-template strand cleavage were a driver of L1 integration, especially because transcription did not promote retrotransposition (Figures 4B and 4C).
We further compared our L1 insertions to 15 chromatin states defined by hidden Markov models (HMM) in comparable cell types (Roadmap Epigenomics et al., 2015). L1 insertions were not strongly enriched in any of the chromatin states assigned to genomic segments by the HMM (Figures 4E and S4E). HeLa-JVM and hESC insertions showed minimal (less than 2-fold) enrichment in some enhancer states when compared to the known strong enrichment of MLV insertions at chromatin marks associated with transcriptional start sites and strong enhancers (Figure 4E and S4E) (LaFave et al., 2014). As with Bru-seq analyses, L1 insertions were slightly depleted in genomic regions containing epigenetic marks indicative of active transcription (Figures 4B, 4E, and S4E).
DNA Replication Fork Direction Influences L1 Insertion Preferences
Data suggest L1 retrotransposition predominantly occurs during S-phase (Mita et al., 2018), creating an opportunity for L1 to integrate throughout the genome. Thus, we compared our L1 insertions to published HeLa and lymphoblastoid Okazaki fragment sequencing (OK-seq) profiles (Petryk et al., 2016), which provide precise information about replication fork initiation, directionality, and termination (Figure 5A). We show L1 insertion profiles in HeLa-JVM cells compared to HeLa-MRL2 OK-seq data and PA-1, hESC, and NPCs insertion profiles compared to GM06990 OK-seq data (Figures 5 and S5), but obtained similar results regardless of the OK-seq dataset.
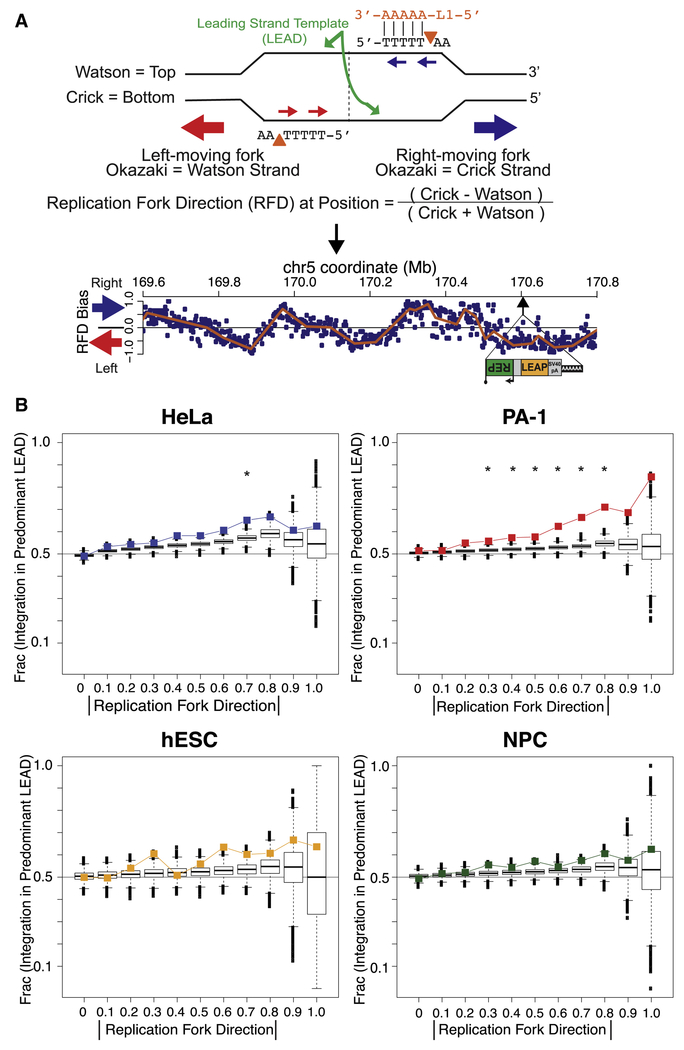
Figure 5: L1 integrates more often into leading strand templates.
(A) Possible cleavage by L1 EN (orange triangles) on lagging strand templates during replication as the L1 RNA (orange) anneals to the poly(T) stretch and initiates TPRT. HeLa OK-seq data from Petryk et al. (2016) (below) surround an actual L1 insertion at which L1 EN cleaved the bottom/Crick strand resulting in (+) strand L1 cDNA integration into the top/Watson strand. Replication fork direction (RFD) is plotted for 2kb genomic bins (blue dots) with a fitted composite linear model (orange lines). The negative RFD at the L1 insertion reveals that this position is replicated predominantly by left-moving forks and thus that the cleaved strand was more often the lagging strand template.
(B) Absolute RFD values were separated into eleven intervals from 0 to 1 (x-axis). The plotted fraction of insertions in genomic regions matching each interval that arose by (+) strand L1 cDNA integration into the predominant leading strand template (LEAD) are indicated (y-axis). Cell line data are plotted as colored squares; boxplots show distributions from 10,000 simulation iterations. Asterisks denote intervals with a significant difference between observed and simulated data (χ2 test p<0.05).
As defined (Petryk et al., 2016), replication fork direction (RFD) values of 1 and −1 indicate genomic regions where replication forks move exclusively in the forward (i.e. rightward) or reverse (i.e. leftward) directions, respectively (Figure 5A). We plotted the fraction of insertions where (+) strand L1 cDNA integrated into the predominant leading strand template (LEAD in plots) as a function of the magnitude (i.e. absolute value, displayed as |RFD|) of the local RFD (Figure 5B). Analogous to transcription strand bias, if L1 exclusively integrated into leading strand templates the plotted fraction would increase from 0.5 to 1 across |RFD| intervals from 0 to 1. Simulated insertions were skewed toward leading strand templates (Figure 5B). However, L1 insertions in several cell types displayed an additional preference to integrate into leading strand templates beyond that predicted by the genomic site distribution, especially in PA-1 cells (Figures 5B and S5A). L1 insertion enrichments were not observed in regions of replication fork initiation or termination, which are identified by the RFD slope (Figure S5B) (Petryk et al., 2016).
EN-independent Retrotransposition in FANCD2-Deficient Cells Targets Replication Forks
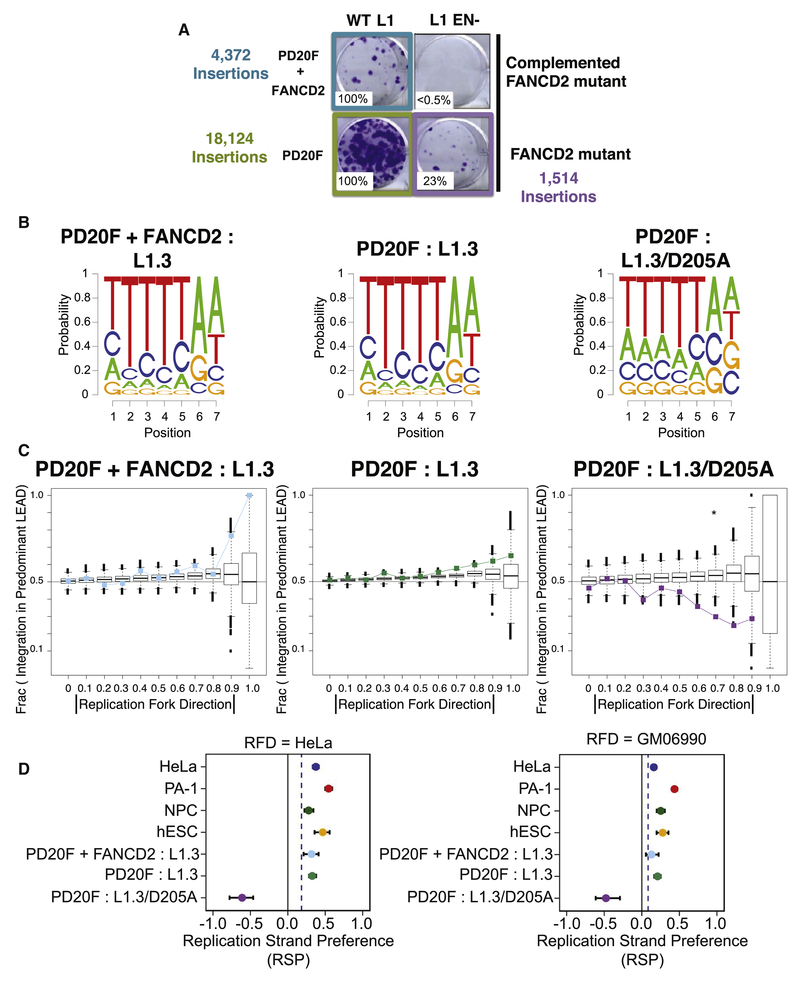
The Fanconi anemia (FA) pathway is involved in the repair of inter-strand DNA crosslinks and in replication fork maintenance (Ceccaldi et al., 2016), and mutations in FA genes (e.g., SLXFANCP, FANCD2, FANCB, FANCI, and FANCF) lead to increases in L1 retrotransposition in cultured cells (Bregnard et al., 2016; Liu et al., 2018). Because L1 can use endogenous DNA lesions to initiate retrotransposition by an ENi mechanism (Coufal et al., 2011; Morrish et al., 2007; Morrish et al., 2002), we used RC-L1 and EN-deficient (L1.3-D205A; STAR Methods) expression vectors to generate 24,010 insertions in a male FANCD2 mutant immortalized fibroblast cell line, PD20F, and complemented PD20F cells (Pulsipher et al., 1998).
RC-L1 insertions occurred at higher efficiencies in the FANCD2 mutant cell line when compared to FANCD2-complemented cells, and ENi insertions occurred at much higher efficiencies in FANCD2 mutant cells than FANCD2-complemented cells (Figure 6A). RC-L1 insertions derived from both FANCD2 mutant and complemented PD20F cells displayed a degenerate L1 EN consensus integration sequence and other properties similar to HeLa-JVM, PA-1, hESC, and NPCs (Figures 2C, S6A, 6B, and S6B). In contrast, predictable differences were apparent for insertions derived from the L1 EN mutant in PD20F cells (Figure 6B). The T base preferences at positions 1 to 5 of the 7mer were present, but reduced, in comparison to RC-L1 insertions, while the minor C base preference at positions 2 through 5 was absent and the proportion of A bases at positions 6 and 7 was reduced.
Figure 6. EN-deficient L1 integrates into lagging strand templates in FANCD2-deficient cells.
(A) Representative Wild Type (WT; left column) or ENi (right column) L1 retrotransposition assays in FANCD2-complemented (top row) or FANCD2 mutant (bottom row) cells, with the numbers of L1 insertions characterized from each cell line.
(B) Logo plots of 7bp L1 EN cleavage sites from FANCD2-complemented (left, PD20F + FANCD2) and FANCD2-deficient PD20F cell lines (middle and right). The rightmost plot shows data from an EN-mutant L1 expression construct, which reduced L1 integration site specificity.
(C) Replication fork direction (RFD) bias plots similar to Figure 5B for the insertion datasets represented by the logo plots in panel (B).
(D) Replication strand preference (RSP) with 95% confidence intervals for all L1 insertion sets as compared to both HeLa and GM06990 OK-seq RFD data sets. Blue dashed lines denote the medianvalue from 100 simulation iterations.
PD20F cells further revealed a striking reversal of the preferred replication target strand as a function of L1 EN status (Figures 6C and S6C). RC-L1 (+) strand L1 cDNA again preferentially integrated into the leading strand template, but was not enriched in replication origins or termination zones (Figure S6D). However, L1 EN mutant insertions exhibited the opposite strand bias, indicating that they preferentially integrated into the predominant lagging strand template (Figures 6C and S6C). Because this pattern switch was specific to the L1 EN mutation it cannot be attributed to a change in the DNA replication program resulting from FANCD2 deficiency.
To quantify the magnitude of the difference between RC-L1 and ENi L1 insertions, we established a “replication strand preference” metric (RSP; STAR Methods). RSP reflects the tendency of L1 to integrate into leading strand (RSP of 1) or lagging strand templates (RSP of −1). Unlike the significant bias toward positive RSP values across nearly all RC-L1 insertion sets, ENi insertions were strongly shifted to a negative RSP in PD20F cells (Figures S5A, 6D, and S6C; see Discussion).
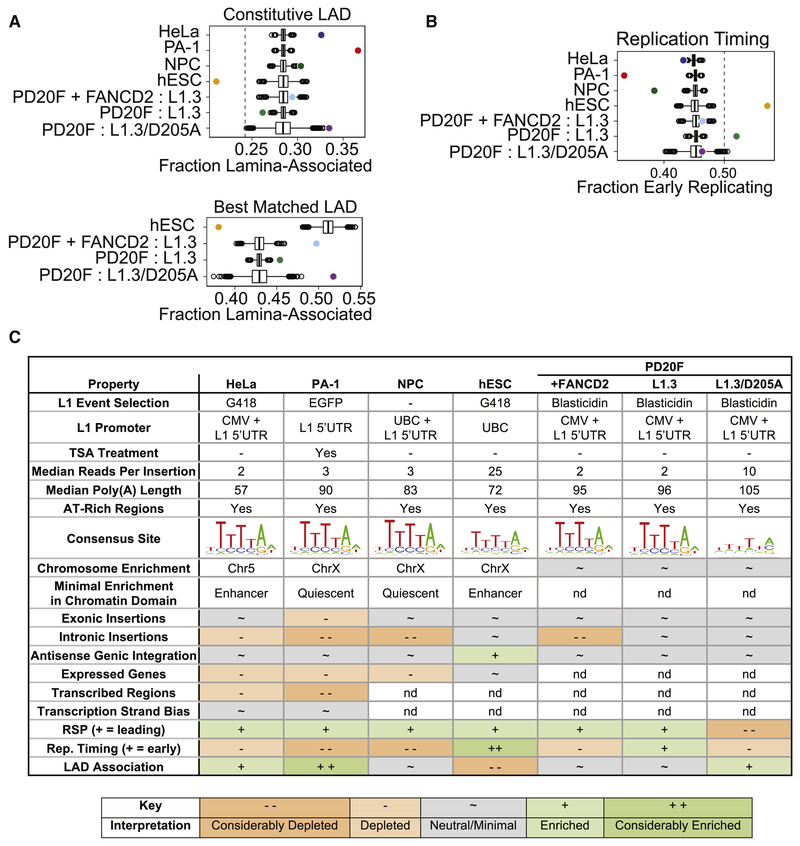
Replication Timing and Nuclear Architecture Influence L1 Integration in a Cell Line Dependent Manner
Nuclear lamina associated domains (LADs) comprise approximately one-third of the human and mouse genomes and correspond to heterochromatin at the nuclear periphery that display: high A/T content; high LINE content; low gene density; low transcription levels; and replication in late S-phase (van Steensel and Belmont, 2017). Simulated L1 insertions demonstrated that preferred L1 EN 7mer sites are enriched in constitutive LADs (Figures 7A and S7A; STAR Methods) (Guelen et al., 2008; Meuleman et al., 2013). However, we observed a markedly variable enrichment of L1 insertions into LADs across cell lines (Figures 7A and S7A). Constitutive LADs were strongly enriched for L1 insertions in HeLa-JVM and PA-1 cells, but were strongly depleted of L1 insertions in hESCs. hESCs were even more strongly depleted of LAD insertions when we compared our data to LADs that were well matched based on cell type (Figures 7A and S7A).
Figure 7: L1 dependence on nuclear architecture varies between cell lines.
(A) Fraction of insertions into LADs for the indicated L1 and LAD data sets. Colored circles represent observed insertions; boxplots show distributions from 10,000 simulation iterations. A dashed line denotes the fraction of constitutive LADs in the genome. In the best-matched panel, hESC L1 insertions were compared to hESC LADs while PD20F insertions were compared to Tig3 fibroblast LADs.
(B) Fraction of L1 insertions into early replicating portions of the genome, plotted similarly to (A). L1 vs. replication timing data pairings were: HeLa-JVM vs. HeLaS3, PA-1 vs. H9-derived-NPCs, NPC vs. H9-derived-NPCs, hESC vs. H9-hESC, and all PD20F vs. IMR90 fibroblasts.
(C) Summary of all reported results, stratified by sample. Note that chromatin state enrichments are less than 2-fold for all cell types listed. “nd”; not done.
We finally compared our L1 insertions to well matched replication timing datasets (Weddington et al., 2008). Simulated insertions revealed that L1 insertions are more often found in later replicating DNA (Figures 7B and S7B). Relative to this baseline, late replicating regions were enriched for observed L1 insertions in NPCs, more strongly enriched in PA-1s, but strongly depleted in hESCs, where there was a preference for early replication. Because LADs and replication timing are correlated (van Steensel and Belmont, 2017), we tested whether one of these features predominates with respect to L1 retrotransposition (see STAR Methods). Results with PA-1 and hESCs each implied that replication timing is the more dominant parameter (Figure S7C), but this conclusion does not provide an explanation for the opposite effects in the two cell lines.
DISCUSSION
Thorough validations give high confidence that our experimental processes could identify bona fide L1 insertions throughout the human genome (Figures 1 and 7C). The resulting >88,000 de novo engineered L1 integration events represent a >400-fold increase over previous studies (Gilbert et al., 2005; Gilbert et al., 2002; Symer et al., 2002).
L1 integrated into a typical degenerate 7mer consensus sequence (5’-TTTTT/AA-3’) (Feng et al., 1996; Jurka, 1997; Morrish et al., 2002). The T-rich stretch is often interrupted by a single C nucleotide, which we hypothesize enhances the ability of L1 EN to cleave DNA substrates at flexible 5’-TpA-3’ nucleotide junctions (Cost and Boeke, 1998; Repanas et al., 2007). The fact that this sequence preference was invariant over five cell types indicates that the biochemical properties of L1 ORF2p are the predominant driver of insertion site selection. Importantly, the T-rich character of preferred L1 insertion sites leads to their non-random distribution with respect to both genomic locus (due to the variability in GC content of functional DNA elements) and replication and transcription strands (due to the known periodic replication-dependent shifts in nucleotide skew throughout the genome) (Huvet et al., 2007; Langley et al., 2016; Touchon et al., 2005). Nevertheless, nearly 25% of the human genome (~750Mb) matches one of the 743 L1 7mer sites we observed three or more times.
L1 insertions occurred throughout the genome. In contrast to polymorphic human L1 insertions (Genomes Project et al., 2015), we readily identified L1 insertions into genic exons, although genes were not preferential L1 integration targets (Figure 3C and Figure 3D). The L1 insertions within genes exhibited an antisense insertion orientation preference, which was entirely accounted for in HeLa-JVM, PA-1, and NPCs, but not hESCs, by the enrichment of L1 EN cleavage sites on coding strands (Figure 3F). These data differ significantly from the antisense orientation bias of endogenous genic L1 insertions (Smit, 1999), suggesting that L1 insertions occurring in the same transcriptional orientation as genes exert a higher fitness cost than antisense insertions (Han et al., 2004). We also readily identified L1 insertions into TFRs and UCEs (Supplemental Dataset 5), suggesting that Darwinian selective pressures lead to the removal of deleterious Ll-containing alleles in these genomic regions from the human population.
Approximately 30% of L1 insertions occurred within endogenous L1 or Alu sequences (Supplemental Dataset 5). Because the 3’ ends of L1s and Alu end in poly(A) tracts, these data suggest that L1 insertions into existing TE-derived sequences could lead to the generation of L1 “graveyards” within the genome over evolutionary time (Churakov et al., 2010), and may lead to the generation of L1-mediated genomic deletions either during (Gilbert et al., 2005; Gilbert et al., 2002; Symer et al., 2002) or after L1 integration (Beck et al., 2011; Richardson et al., 2015). However, in contrast to a previous study, endogenous TEs did not serve as “lightning rods” for engineered L1 insertions (Jacob-Hirsch et al., 2018).
Engineered L1s did not preferentially insert into expressed genes, which counters earlier reports (Baillie et al., 2011; Jacob-Hirsch et al., 2018; Upton et al., 2015) (Figure S3B). Similarly, chromatin status had only minor influences on L1 integration (Figure 4E). By comparison, L1 integration was non-random with respect to replication, suggesting that it predominantly occurs at progressing replication forks during S-phase (Figure 5B) (Mita et al., 2018). OK-seq experiments revealed a significant excess of L1 (+) strand cDNAs inserted into leading strand templates (Petryk et al., 2016), whereas ENi L1 insertions in a FANCD2 mutant cell line exhibited the opposite strand preference (Figure 6C). Several possibilities could explain these findings. For example, RC-L1s might have easier access to cleave the lagging strand template during DNA replication, whereas EN-deficient L1s may initiate priming of (−) strand L1 cDNA from 3’ OH groups present on Okazaki fragments in FANCD2 mutant cells. Alternatively, EN-deficient L1s might use 3’ OH groups generated by host-factor mediated cleavage of the leading strand template in FANCD2 mutant cells. Either model provides a plausible explanation for the ability of L1 to insert without respect to chromatin state, as the entire genome is replicated and exposed once per cell cycle.
With regard to higher order nuclear properties, L1 insertions in PA-1 cells preferentially occurred in genomic regions with significantly later replication and a higher correspondence to LADs. L1 RNPs may first encounter LADs and the inactive X-chromosome first because they are associated with the nuclear periphery (Chen et al., 2016; van Steensel and Belmont, 2017). Alternatively, L1 might preferentially integrate into the genome in late S phase. We provide evidence that replication timing might be the more important of these two factors; however, the directionality of the correlations between L1 insertions and replication timing were strongly cell line dependent. In particular, L1 insertions in hESCs behaved in precisely the opposite fashion as PA-1 cells (Figure 7C). We suggest that distinct aspects of the cell cycle biology of hESCs may influence L1 retrotransposition, but cannot rule out influences of technical differences in obtaining L1 insertions from different cell lines.
Other caveats are that our method was blind to the 5’ ends of L1 insertions. Also, the use of engineered L1s and cultured cells may not reflect L1 activities in biologically relevant cell types. However, data obtained with engineered L1s have predicted or recapitulated numerous aspects of in vivo L1 biology (Beck et al., 2011; Richardson et al., 2015). Finally, our reliance on an expressed reporter gene may not allow the detection of integration events in heterochromatic DNA. However, engineered L1s did not preferentially integrate into transcribed chromatin and L1 insertion profiles were similar in NPCs, where insertions were subjected to neither selection nor screening.
Our findings have implications for both L1 and human genome evolution. We propose that ENi retrotransposition mimics an ancestral L1 integration mechanism whereby 3’-OH groups present at replication forks and endogenous DNA lesions acted to prime L1 (−) strand cDNA synthesis (Kopera et al., 2011; Malik et al., 1999). Acquisition of an APE-like EN domain, coupled with DNA replication association, subsequently allowed L1 EN to generate 3’-OH groups to allow its interspersion throughout the genome at a time in the cell cycle when the entire genome is accessible to integration. This strategy markedly differs from that of other retrotransposons where the acquisition of a site-specific EN (e.g., (Luan et al., 1993)) or interactions between TE- and host proteins (Levin and Moran, 2011; Sandmeyer et al., 2015; Sultana et al., 2017) allowed them to target specific genomic regions.
STAR METHODS
CONTACT FOR REAGENT AND RESOURCE SHARING
Further information and requests for resources and reagents should be directed to, and will be fulfilled by the Lead Contact, John V. Moran (moranj@umich.edu).
EXPERIMENTAL MODEL AND SUBJECT DETAILS
Cultured human cell lines
The following four female cell lines were used in this study: HeLa-JVM and PA-1 cancer cell lines (Garcia-Perez et al., 2010; Zeuthen et al., 1980); H9-human embryonic stem cells (hESCs), a diploid cell line that mimics early stages in human embryonic development (Garcia-Perez et al., 2007; Thomson et al., 1998); and H9-hESC-derived neural progenitor cells (NPCs) (Coufal et al., 2009). The following two male cell lines were used in this study: PD20F and PD20F+D2 cells (PD20F cells complemented with a retroviral vector containing the human FANCD2 cDNA) (Pulsipher et al., 1998).
Growth of cultured human cell lines
HeLa-JVM, PA-1, H9-hESC and H9-hESC-derived NPCs were grown at 37°C in the presence of 7% CO2 at 100% humidity. PD20F cells were grown at 37°C in the presence of 5% CO2 and atmospheric O2. The absence of Mycoplasma spp. was confirmed at least once a month using a Polymerase chain reaction (PCR)-based assay (Minerva or Sigma). Short tandem repeat (STR)-genotyping was used to validate the identity of the PD20F, PD20F+FANCD2 (PD20F+D2 cells [PD20F cells complemented with a retroviral vector containing the human FANCD2 cDNA]), PA-1, HeLa-JVM, H9-hESC, and H9-hESC-derived NPC cell lines at least once a year (LorGen, Granada, Spain). SKY-FISH was used to confirm the karyotypes of HeLa-JVM, PA-1, H9-hESC, and H9-hESC-derived NPCs used in this study (not shown).
HeLa-JVM cells were grown in Dulbecco’s Modified Eagle Medium (DMEM) high glucose (4500mg/L) (Invitrogen) supplemented with 10% Fetal Bovine Serum (FBS) (Sigma) and 1× penicillin/streptomycin/glutamine (Invitrogen) (Moran et al., 1996). PA-1 (Zeuthen et al., 1980) and PC39 cells (Garcia-Perez et al., 2010) were cultured in Minimum Essential Media (MEM) (Invitrogen) supplemented with 10% heat-inactivated FBS (Sigma), 1× penicillin/streptomycin/glutamine (Invitrogen), and 0.1mM non-essential amino acids (Invitrogen). PC39 is a clonal PA-1 cell line that contains two previously characterized engineered LRE3-mEGFPI insertions (pc-39-A and pc-39-B) (Garcia-Perez et al., 2010). A third LRE3-mEGFPI insertion (pc-39-C) was identified in this study. Genomic DNA from the PC39 cell line was used as a positive control in L1 retrotransposition capture PCR reactions (see below).
H9-human embryonic stem cells (WA09/H9-hESCs (Thomson et al., 1998)) were obtained from WiCell and maintained in human foreskin fibroblast (HFF)-conditioned media (HFF-CM) as described previously (Garcia-Perez et al., 2007; Macia et al., 2017). HFFs were grown in Iscove’s Modified Dulbecco’s Medium (IMDM) supplemented with 25 mM 4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid (HEPES, ThermoFisher Scientific), 2mM L-glutamine (ThermoFisher Scientific) and 10% heat-inactivated FBS (HyClone). To prepare HFF-CM, 4×107 HFFs were mitotically inactivated by γ-irradiation using 3000-3200 rads (at Hospital Universitario Clinico San Cecilio, Granada, Spain), counted on a hemocytometer (Sigma), seed on T225 cm2 tissue culture flasks (3×106 mitotically inactivated HFFs were seed per flask, Corning) and cultured on hESC media [KnockOut DMEM (ThermoFisher Scientific) supplemented with 4 ng/ml human basic fibroblast growth factor (FGF-2, Miltenyi Biotech), 20% Knockout serum replacement (ThermoFisher Scientific), 1mM L-glutamine (ThermoFisher Scientific), 0.1 mM β-mercaptoethanol (ThermoFisher Scientific) and 0.1mM non-essential amino acids (ThermoFisher Scientific)] for 24 h. After 24h, HFF-CM was collected and we repeated this process during 7 consecutive days. To avoid variability among results, we pooled all the collected HFF-CM after 7 days and we prepared ten liter batches. H9-hESCs were cultured on matrigel-coated plates (BD Biosciences) using HFF-CM supplemented with fresh FGF-2 (20 ng/ml, Miltenyi Biotech), and we passage cells using TrypLE select (ThermoFisher Scientific). To prevent cell death (Watanabe et al., 2007), H9-hESCs were treated with 10μM Y-27632 (Sigma) for 1 hour prior to passaging H9-hESCs.
Neuronal progenitor cells (NPCs) were differentiated from H9-hESCs using previously described protocols (Coufal et al., 2009) with some modifications. Briefly, H9-hESCs were grown on Matrigel coated plates for at least 5 passages, and then were cultured in N2 media (Dulbecco’s Modified Eagle’s Medium/Ham’s F12 (DMEM/F12 50/50; ThermoFisher) with 1× (25 mM) HEPES, 50 U/ml penicillin, 50 μg/ml streptomycin (ThermoFisher Scientific), and 1× N2 supplement (ThermoFisher) supplemented with 1μm of dorsomorphin (Merck) and 10μm of the TGF-β inhibitor SB43154 (Sigma)) for two days. Undifferentiated H9-hESCs then were detached using a cell-scraper and transferred to low-attachment plates (Corning) to allow for embryo body (EB) formation using the same culture media. Once EBs formed (4-6 days), they were replated in a 60mm matrigel-coated plate (Corning), and cultured for 5-7 days using NB medium (0.5× N2 supplement, 0.5× B-27, 20ng/ml of FGF-2 (Miltenyi Biotec) and 50 U/ml penicillin-and 50 μg/ml streptomycin), changing the media every other day. Neural rosettes were collected, dissociated, and replated on poly-L-ornithine/laminin coated plates (Sigma) using NPC plating medium (KnockOut DMEM/F-12 (ThermoFisher) containing 1× Stem Pro Neural Supplement (ThermoFisher), 1mM L-Glutamine, and 1× Penicillin-Streptomycin (10,000 U/mL)). NPCs were cultured in KnockOut DMEM/F-12 (ThermoFisher Scientific) media supplemented with 1× StemPro Neural Supplement (ThermoFisher Scientific), 10 ng/mL epidermal growth factor (EGF) (R&D Systems), 200 μM Glutamax (ThermoFisher), and 20 ng/mL FGF-2 (Miltenyi Biotech). When confluent, NPCs were expanded using StemPro Accutase Cell Dissociation Reagent (ThermoFisher Scientific); the NPCs were used for up to 15 passages. To induce neural differentiation from confluent NPCs, 1μM all-trans Retinoic acid (RA; Sigma) was added to the NPC culture media (Garcia-Perez et al., 2010).
PD20F cells were grown using DMEM high glucose medium supplemented with 200μM GlutaMAX (ThermoFisher), 10% FBS (HyClone) (ThermoFisher), 50 U/mL penicillin (ThermoFisher), and 50 mg/ml streptomycin (ThermoFisher).
METHOD DETAILS
Expression plasmids
The L1 expression vectors listed below give optimal L1 retrotransposition yields in the transfected cell lines used in this study. All plasmids were propagated in Escherichia coli strain DH5α (F-ϕ80lacZΔM15Δ[lacZYA-argF] U169 recA1 endA1 hsdR17 [rk−, mk+] phoA supE44 λ- thi-1 gyrA96 relA1) (Invitrogen). Competent E. coli were prepared and transformed using previously described methods (see (Moran et al., 1996)). Plasmids were prepared using the Qiagen Plasmid Midi Kit according to the manufacturer’s instructions. We only used highly supercoiled preparations of plasmid DNA for transfections. When transfecting H9-hESCs and H9-hESC-derived NPCs, plasmid DNAs were filtered through a 0.22 μm filter (Merck).
pCEP4/GFP: contains the coding sequence of the humanized Renilla reniformis green fluorescent protein (hrGFP) from phrGFP-C (Stratagene). GFP expression is driven by a cytomegalovirus (CMV) immediate early promoter and terminated at a simian virus 40 (SV40) late polyadenlyation signal present in the pCEP4 plasmid backbone (Life Technologies) (Alisch et al., 2006). This vector was used to calculate transfection efficiencies.
pJM101/L1.3: contains a full-length RC-L1 (L1.3, accession number #L19088) that contains the mneoI retrotransposition indicator cassette within its 3’UTR (Sassaman et al., 1997). A CMV promoter and SV40 polyadenlyation signal in the pCEP4 plasmid backbone facilitate L1.3 expression. This vector was used to assay for L1 retrotransposition in HeLa cells.
pJM105/L1.3: is identical to pJM101/L1.3 except for the presence of a missense mutation (D702A) in the L1.3 ORF2p reverse transcriptase (RT) domain, which renders L1.3 retrotransposition-defective (Wei et al., 2001). This vector was used as a negative control in HeLa cell L1 retrotransposition assays.
pCEP4/LRE3-mEGFPI: contains a full-length RC-L1 (LRE3) with an mEGFPI retrotransposition indicator cassette within its 3’UTR. LRE3 expression is driven from its native 5’UTR. The LRE3 expression construct was cloned into a version of pCEP4 that lacks the CMV promoter. A puromycin-resistance selectable marker replaced the hygromycin-resistance selectable marker in pCEP4 (Garcia-Perez et al., 2010). This vector was used to assay for L1 retrotransposition in PA-1 and HeLa cells.
pCEP4/JM111/LRE3-mEGFPI: is identical to pCEP4/LRE3-mEGFPI except that it contains two missense mutations in LRE3 ORF1p (RR261-262AA), which renders LRE3 retrotransposition-defective (Zhang et al., 2014). This vector was used as a negative control in PA-1 and HeLa cell L1 retrotransposition assays.
pKUB102/L1.3-sv+: is similar to pJM101/L1.3 except that it is cloned into a modified pBSKS-II plasmid backbone (Stratagene) that contains a human ubiquitin C promoter (nucleotides 125398319-125399530 of human chromosome 12 (hg19)) that drives the expression of an L1.3 derivative that lacks its native 5’UTR (Sassaman et al., 1997; Wissing et al., 2012). The modified vector also contains a SV40 polyadenylation signal downstream of the mneoI tagged L1.3 sequence to facilitate transcription termination and polyadenylation of the engineered L1 mRNA. This vector was used to assay for L1 retrotransposition in H9-hESCs.
pKUB105/L1.3-sv+: is identical to pKUB102/L1.3-sv+ but contains a missense mutation in the L1.3 ORF2p reverse transcriptase (RT) domain (D702A), which abolish retrotransposition (Moran et al., 1996; Wei et al., 2001). This vector was used as a negative control in H9-hESCs L1 retrotransposition assays.
pCEP99/UB-LRE3-mEGFPI: is a derivative of pCEP4/LRE3-mEGFPI in which LRE3 expression is driven by the human ubiquitin C promoter (nucleotides 125398319-125399530 of human chromosome 12 (hg19)) and native L1 5’ UTR (Coufal et al., 2009). This vector was used to assay for L1 retrotransposition in H9-hESC-derived NPCs.
pCEP99/JM111/UB-LRE3-mEGFPI: is a derivative of pCEP99/UB-LRE3-mEFFPI that contains two missense mutations in LRE3 ORF1p (RR261-262AA), which renders LRE3 retrotransposition-defective (Coufal et al., 2009). This vector was used as a negative control in H9-hESC-derived NPC L1 retrotransposition assays.
pJJ101/L1.3: is similar to pJM101/L1.3, but contains an mblastl retrotransposition indicator cassette within its 3’UTR (Kopera et al., 2011). A CMV promoter and SV40 polyadenlyation signal in the pCEP4 plasmid backbone facilitate L1.3 expression. This vector was used to assay for L1 retrotransposition in PD20F and PD20F+D2 cells.
pJJ101/L1.3-D205A: is identical to pJJ 101/L1.3 except for the presence of a missense mutation (D205A) in the L1.3 ORF2p endonuclease (EN) domain, which renders L1.3 retrotransposition-defective (Kopera et al., 2011). This vector was used to assay for L1 retrotransposition in PD20F and PD20F+D2 cells.
pJJ101/L1.3-D702A: is identical to pJJ 101/L1.3 except for the presence of a missense mutation (D702A) in the L1.3 ORF2p Reverse Transcriptase (RT) domain, which renders L1.3 retrotransposition-defective (Kopera et al., 2011). This vector was used as an internal negative control for L1 retrotransposition assays in PD20F and PD20F+D2 cells.
L1 retrotransposition assays
HeLa-JVM cells
Retrotransposition assays in HeLa-JVM cells were carried out as previously described (Moran et al., 1996; Wei et al., 2000) with the following modifications. Cells were plated at densities of 1.5×106 cells in T-175 flasks (Fisher Scientific) and 150mm × 25mm tissue culture dishes, or at 5×105 cells/well in 6-well tissue culture plates (Fisher Scientific). Eighteen hours after plating, transfections were carried out using the FuGENE 6 transfection reagent (Promega) and Opti-MEM (ThermoFisher/Invitrogen), according to the manufacturer’s instructions (3μl FuGENE 6 and 97μl Opti-MEM per μg of DNA transfected in 6-well and 19μg of DNA with 58μl FuGENE 6 in T-175 flask or 150mm × 25mm dishes). Transfection efficiency was determined from the percent of green fluorescent protein (GFP) expressing HeLa cells in a 6-well dish co-transfected with an equal amount of pCEP4/GFP and flow sorted using an Accuri C6 flow cytometer 72 hours post transfection. On average, transfection efficiency was ~75% for HeLa cells. To generate ~99% of retrotransposition events, HeLa cells were transfected with pJM101/L1.3 and the cells were subjected to selection with 400μg/ml G418 (Gibco) starting 72 hours post-transfection. Selection media was replaced every other day and selection was continued for 11 additional days. After selection, the HeLa cells were washed with 1× PBS (ThermoFisher), and prepped for genomic DNA isolation. An additional flask of cells was washed with 1× PBS, fixed, washed again, and stained with crystal violet to visualize foci representing successful retrotransposition events. As a negative control, HeLa cells were transfected with pJM105/L1.3 in parallel.
For the remaining ~1% of retrotransposition events generated using pCEP4/LRE3-mEGFPI, transfections were carried out in T-175 flasks at the same plating densities and using the same FuGENE 6 transfection reagent to recombinant DNA ratio as described above. Forty-eight hours post transfection cells were selected for the presence of the L1 expression vector using media containing 2μg/mL of puromycin (ThermoFisher) and selection continued an additional five days. Eight days post-transfection, cells were sorted by fluorescence activated cell sorting (FACS) to capture EGFP expressing cells. Cells positive for EGFP expression were then plated into a small T-25 flask. Once confluent, the cells were passaged to a T-175 flask. Once confluent again, cells were collected for genomic DNA isolation.
PA-1 cells
Retrotransposition assays in PA-1 cells were carried out as previously described (Garcia-Perez et al., 2010) with the following modifications. Cells were plated at densities of 3×106 cells in T-175 flasks (Fisher Scientific) and 150mm × 25mm dishes (Fisher Scientific), at 2.5×106 cells in T-75 flasks (Fisher Scientific), or at 1×106 cells/well in 6-well tissue culture plates (Fisher Scientific). To study L1 integration in PA-1s, cells were transfected with pCEP4/LRE3-mEGFPI 18 hours after plating. For transfections, we used FuGENE HD transfection reagent (Promega) at 8μl per 2.0 μg of plasmid DNA per well of a 6 well tissue culture plate. T-175 flasks (Fisher Scientific) or 150mm × 25mm dishes (Fisher Scientific) were transfected with 32μg of plasmid DNA and 128μl FuGENE HD transfection reagent (Promega). Forty-eight hours post transfection cells were selected for transfection with media containing 2μg/mL of puromycin and selection continued for four additional days. As a control, we always transfected an aliquot of PA-1s with pCEP4/GFP only; similarly an aliquot of PA-1s were co-transfected with equal amounts pCEP4/GFP and pCEP4/LRE3-mEGFPI to determine the transfection efficiency using FACS-sorting 72 hours post-transfection (note: LRE3-mEGFPI retrotransposition events are epigenetically silenced either during or immediately after retrotransposition (Garcia-Perez et al., 2010); thus, LRE3-mEGFPI retrotransposition does not significantly contribute to the percentage of GFP-positive cells). On average, the transfection efficiency was ~20% for PA-1 cells. Seven days post-transfection, cells were chemically treated for 14-16 hours with 0.5μM trichostatin A (TSA, Sigma) (Garcia-Perez et al., 2010), or 18-24 hours with 2μM anisomycin (Sigma) to reverse epigenetic silencing of the retrotransposed EGFP reporter gene. Following drug treatment (on day 8 post-transfection), the chemically treated cells were subjected to FACS-sorting to isolate EGFP positive cells (~1×106 cells). EGFP-positive cells then were plated into a small T-25 flask. Once confluent, the cells were treated with trypsin and moved to a T-175 flask. Once confluent, cells in the T-175 flask were collected for genomic DNA isolation. Additionally, some untreated PA-1 cells, not subjected to FACS-sorting, were collected for isolation of genomic DNA. As a negative control, PA-1 cells were transfected with pCEP4/JM111/LRE3-mEGFPI in parallel reactions.
H9-human embryonic stem cells (hESCs)
We used a previously described protocol, with minor modifications (Garcia-Perez et al., 2007), to transfect hESCs. Specifically, H9-hESCs were transfected with pKUB102/L1.3-sv+ using a Nucleofector II device (Lonza) and the Human Stem Cell Nucleofector Kit 2 (Lonza) solution, using program A-23. As described (Watanabe et al., 2007), and to prevent cell death during selection, cells were cultured with HFF-CM containing 10μM Y-27632 (Sigma) for 1 hour prior to harvesting hESCs. Y27632 is a selective Rho-associated kinase inhibitor (iROCK) that is used to increase the clonability of hESCs (Watanabe et al., 2007). Next, cultured H9-hESCs were detached from matrigel-coated plates using TrypLE-Select (ThermoFisher) following the manufacturer’s instructions. The collected H9-hESCs were washed twice with pre-warmed (37°C) HFF-CM containing 4ng/ml Human FGF-2 (Miltenyi biotech) and 10μM Y-27632. Finally, H9-hESCs were filtered through a strainer (70μm Nylon, Corning). An aliquot of harvested H9-hESCs was treated with 0.05% trypsin-EDTA and used to calculate the number of cells/ml. We routinely used 2-4×106 H9-hESCs and 4μg of each plasmid DNA per transfection, and 0.1ml of Human Stem Cell Nucleofector Kit 2 solution (Lonza) per transfection.. An aliquot of H9-hESCs was co-transfected with equal amounts pCEP4/GFP and pKUB102/L1.3-sv+ to determine the transfection efficiency by using a FACS Aria flow cytometer 48 hours after nucleofection. On average, the transfection efficiency was ~15% for H9-hESCs. After nucleofection, transfected hESCs were slowly recovered from the nucleofection cuvette and seeded on a 10cm matrigel-coated plate. Media was replaced 6-8 hours post-transfection using pre-warmed HFF-CM (370) containing 20ng/ml Human FGF-2 (Miltenyi biotech) and 10μM Y-27632. L1 retrotransposition events were selected with G418; transfected hESCs were first cultured during four days using HFF-CM supplemented with fresh FGF-2 (20ng/ml) and 10μM Y-27632 and culture media was changed daily. After four days, H9-hESCs were selected with 50μg/ml G418 (ThermoFisher) for 7 days, and then were selected with 100μg/ml G418 for an additional 7 days using HFF-CM supplemented with fresh FGF-2 (20ng/ml) and 10μM Y-27632. During antibiotic selection, the media was changed every day. As a control for G418 selection, H9-hESCs were transfected in parallel with the RT-mutant plasmid pKUB105/L1.3-sv+, as the retrotransposition of RT-mutant L1s occurs at background levels. Notably, we did not expand cells after selection and instead harvested genomic DNAs directly after the selection process to avoid possible artifactual enrichments of L1 insertion sites in hESCs.
H9-hESC-derived neural progenitor cells (NPCs)
We used a previously described protocol to transfect NPCs (Coufal et al., 2009; Macia et al., 2017). Briefly, H9-hESC derived NPCs were transfected using a Nucleofector II device and the Rat Neuronal Stem Cell Nucleofector Kit (Lonza) using program A-33. Confluent cultures of H9-hESC derived NPCs (with passage numbers that ranged between 3 and 15) were used in nucleofection experiments. Briefly, cells were detached using StemPro Accutase Cell Dissociation Reagent (ThermoFisher). Next, H9-hESC-derived NPCs were washed twice with pre-warmed (37°C) H9-NPC media (KnockOut™ DMEM/F-12 media supplemented with 1× StemPro Neural Supplement, 10 ng/mL EGF (R&D), 200 μM Glutamax, and 20 ng/mL FGF-2 (Miltenyi biotech) and filtered through a cell strainer (70μm Nylon, Corning)). An aliquot of NPCs was treated with 0.05% trypsin-EDTA and used to calculate the number of cells/ml. We routinely used 1×106 H9-hESC-derived NPCs and 8μg plasmid DNA (pCEP99/UB-LRE3-mEGFPI), and 0.1ml of Rat Neuronal Stem Cell Nucleofector Kit solution (Lonza) per transfection. An aliquot of NPCs was transfected with equal amounts pCEP4/GFP and pCEP99/UB-LRE3-mEGFPI to determine the transfection efficiency by using a FACS Aria flow cytometer 48 hours after nucleofection (note: as described above for PA-1 cells, most retrotransposition events in hESC-derived NPCs are epigenetically silenced either during or immediately after retrotransposition (Coufal et al., 2009); thus, retrotransposition does not significantly contribute to the percentage of GFP-positive cells). On average, the transfection efficiency was ~60% for H9-hESC-derived NPCs. After nucleofection, the transfected NPCs were slowly recovered from the nucleofection cuvette and seeded into 3 wells of a poly-L-ornithine/Laminin coated 6-well tissue culture dish (Sigma). The media was replaced 6-8 hours post-transfection. To select for cells containing the L1 expression vector, 1μg/ml puromycin was added to H9-NPC media 48 hours posttransfection and NPCs were cultured for 7 days, changing the media every day. Upon completion of selection, cells were harvested using 0.05% trypsin-EDTA and genomic DNA was isolated for L1 library preparation. The retrotransposition efficiency was determined using a FACS Aria flow cytometer. Briefly, 7 days post-transfection, cells were treated with 500nM trichostatin A (TSA) to reverse silencing of the engineered L1 insertions and then were cultured for an additional 18 hours prior to FACS analyses (Coufal et al., 2009; Garcia-Perez et al., 2010). TSA treatment was not used for cells harvested for L1 library preparation. As a negative control, NPCs were transfected with a retrotransposition-defective L1 plasmid (pCEP99/UB-JM111/LRE3-mEGFPI) to determine the background level of auto-fluorescence encountered during FACS-sorting. In experiments conducted with differentiating NPCs, we transfected NPCs using the same method as noted above, but added 1 μM RA to the NPC media (starting with the first change of media 6-8 hours post-transfection). In total, 4.8% of final NPC L1 insertions came from cultures treated with RA (Supplemental Dataset 2). As with H9-hESCs, we did not expand cells after the completion of the retrotransposition assays to avoid possible artifactual enrichments of L1 insertion sites in NPCs.
PD20F and PD20F+D2 cells
PD20F male immortalized fibroblasts and PD20F+D2 cells (PD20F cells complemented with a retroviral vector containing the human FANCD2 cDNA) (Pulsipher et al., 1998) were transfected using FuGENE 6 (Promega) according to the manufacturer’s instructions. Briefly, 8×104 cells were plated per 100 mm culture plates (Corning, previously coated with Gelatin (2% w/v, Sigma)) and transfected 16 hours later using 10ml of FuGENE 6 (Promega) and 4μg of plasmid DNA in OptiMEM medium (ThermoFisher) according to the manufacturer’s instructions. PD20F and PD20F complemented cells were both transfected with pJJ101/L1.3, pJJ101/L1.3-D205A or pJJ101/L1.3-D702A. Twenty-four hours later, fresh media was added and cells were cultured for 4 days, changing the media every other day. Five days post-transfection cells were selected with 2μg/ml blasticidin-S (Invitrogen) for 7 days, with one media change after three days. After selection, blasticidin-resistant foci were harvested by treatment with 0.05% trypsin-EDTA for genomic DNA extraction. To monitor transfection efficiency, cells were co-transfected with pCEP4/GFP and pJJ101/L1.3, pJJ101/L1.3-D205A or pJJ 101/L1.3-D702A and sorting using a FACS Aria flow cytometer determined the percentage of GFP-positive cells 48 hours post-transfection. On average, the transfection efficiency was ~15% for PD20F and PD20F complemented cells. PD20F and PD20F+D2 cells transfected with pJJ101/L1.3-D702A were used as an internal negative control for selection and retrotransposition.
Genomic DNA isolation
Once retrotransposition assays were completed, cells were treated with 0.05% trypsin-EDTA, harvested, and genomic DNA was extracted and purified using phenol-chloroform extraction or a DNeasy Blood & Tissue Mini Kit (Qiagen) (H9-hESC, H9-hESC-derived NPCs, PD20F, and PD20F+D2 cells) or the Blood and Cell Culture DNA Midi Kit (Qiagen) (HeLa and PA-1 cells). DNA concentrations were measured using a NanoDrop spectrophotometer (ThermoFisher) and an aliquot (1μg) was analyzed on a 0.75% agarose gel to assess the integrity of genomic DNA.
L1 retrotransposition capture libraries
Adapter ligation and L1 fragment amplification
All oligonucleotides used in this study were synthesized by Integrated DNA Technologies (IDT; Coralville, Iowa) and purified by high-performance liquid chromatography (HPLC). Adapter sequences modified from (Iskow et al., 2010) were annealed by incubating 10μM concentrations of top (5’-GGAAGCTTGACATTCTGGATCGATCGCTGCAGGGTATAGGCGAGGACAACT-3’) and bottom (5’-/5Phos/GTTGTCCT/3AmMO/−3’, where 3AmMO is 3’ amino modifier) strands at 95°C for 5 minutes in 1× T4 DNA ligase buffer (New England Biolabs, NEB) and allowing the tube to cool passively to room temperature.
Genomic DNA (15μg) was randomly sheared to ~3kb fragments using a Covaris S220/E220 with blue miniTUBEs according to the manufacturer’s instructions. Sheared genomic DNA was purified using the QIAquick PCR Purification Kit (Qiagen), subjected to end repair by the NEBNext End Repair Module (NEB), and purified again with QIAquick PCR Purification Kit. A 3’-A base was added using the NEBNext dA-Tailing Module (NEB) and the DNA was purified using the MinElute PCR Purification Kit (Qiagen). Adapters were ligated onto the DNA fragments by mixing 1μg DNA with annealed adapter at a final concentration of 4.5μM in a 20μl reaction with 1μl (200U) of T4 DNA ligase (New England Biolabs) in 1× T4 DNA ligase buffer (NEB). Ligation reactions were incubated overnight at 16°C and then at 65°C for 20 minutes. Excess adapters were removed using QIAquick PCR Purification Kit and adapter-ligated genomic DNA products were eluted in 50μl EB Buffer.
Linear amplification of de novo integrated L1 molecules derived from transfected plasmids was performed with Roche Expand Long Range dNTPack PCR Kit. Reactions contained 500ng of adapter-ligated genomic DNA, 1× Expand Long Range Buffer including 12.5mM MgCl2, 0.25μM biotinylated LEAP primer (5’ Dual Biotin; 18bp internal spacer; 5’-/52-Bio//iSp18/GTTCGAAATCGATAAGCTTGGATCC-3’), 500μM PCR nucleotide mix (dATP, dCTP, dGTP, dTTP at 10mM each), 3% DMSO, and 3.5U of Expand Long Range Enzyme in a 50ml total reaction volume. Reactions were incubated at 94°C for 5 minutes, followed by 30 cycles of 94°C, 15s; 65°C, 30s; 68°C, 3 minutes, with a final 7 minute extension at 68°C. Extended products were purified using the QIAquick PCR Purification Kit and then captured using the Dynabeads kilobaseBINDER Kit (Invitrogen) for 3 hours at room temperature with rotation. Beads were harvested on a magnet and washed twice with Wash Buffer and once with ddH2O. Final products were eluted into 30μl ddH2O.
For the final amplification, captured products (10μl) were used as substrates in three 50μl PCR reactions using the Roche Expand Long Range dNTPack PCR kit. Each reaction additionally contained Expand Long Range Buffer including 12.5mM MgCl2, 0.25μM adapter primer (5’-ATCGATCGCTGCAGGGTATAGG-3), 0.25μM SV40-polyA-start site primer (5’-GCAATAAACAAGTTAACAACAAAAAAAAA-3’), 500μM PCR nucleotide mix (dATP, dCTP, dGTP, dTTP at 10mM each), 3% DMSO and 3.5U of Expand Long Range Enzyme. Reactions were incubated at 94°C for 3 minutes, followed by 35 cycles of 94°C, 10s; 57°C, 30s; 68°C, 2 minutes, with a final 7 minute extension at 68°C. Final L1 amplification products were purified with QIAquick PCR Purification Kit and eluted into 50μl EB Buffer.
Library validation and sequencing
To validate L1 fragment libraries, PCR products were cloned into the TA Cloning Kit Dual Promoter (pCR II) cloning vector (Invitrogen) and transformed into E. coli. Plasmid DNA was recovered by mini-prep (Promega SV Mini-Prep kit). Individual clones were Sanger sequenced with M13 Forward and M13 Reverse primers and verified to match GRCh37/hg19 using BLAT (http://genome.ucsc.edu/) (Kent, 2002). We also made a parallel control library using PC39 DNA for each target cell preparation. We digested PC39 genomic DNA (Garcia-Perez et al., 2010) with the PacI and NdeI restriction enzymes instead of random shearing. These restriction enzyme sites are downstream of two known engineered insertions in PC39 cells, pc-39-A and pc-39-B, respectively, resulting in expected PCR products of 580bp (pc-39-A) and 330bp (pc-39-B). We observed an additional band at ~1.2kb that led to discovery of a third previously unidentified engineered L1 insertion in PC39, which we labeled pc-39-C. Sanger sequencing of pc-39-C identified a poly(A) tract of 33bp, and 1,111 bp of 3’ flanking genomic sequence, flanked by an NdeI restriction site. Walking with primer sequences along pc-39-C showed the insertion to be 5’ truncated, containing the last 100bp of ORF2 sequence. This pc-39-C insertion is flanked by an 18bp target site duplication (5’-AAGAAATGGTAAATGCTT-3’) and has a cleavage site of 5’-TTCTT/GG-3’ on chromosome 19 at GRCh37/hg19 position 13627881 on the top (+) strand. Thus, the appearance of three bands from PC39 libraries and an appropriately blank water control were required to validate successful library preparation (Figure 1D). Qualified libraries were finally quantified using a Qubit Fluorometer (Invitrogen) and subjected to PacBio Single Molecule Real Time (SMRT) circular consensus sequencing (CCS) at the University of Michigan DNA Sequencing Core (PacBio RS II Sequencer).
QUANTIFICATION AND STATISTICAL ANALYSIS
Read processing and alignment pipeline
The data processing pipeline used to characterize PacBio CCS sequencing reads and perform enrichment analyses employed a combination of publicly available software tools (specified below) and custom code written in Perl and R.
Read alignment and refinement
PacBio CCS reads were first aligned to the adapter primer and SV40pA primer sequences with Bowtie2 (v2.1.0, options -N1 -L3 --ma 3 -a -q --local) (http://bowtie-bio.sourceforge.net/bowtie2/index.shtml) (Langmead and Salzberg, 2012). Reads that failed to align to both primer sequences or aligned with two or more mismatches per each primer alignment were not analyzed further. Adapter and SV40pA primer sequences were trimmed from the ends of the reads that passed primer alignment and the remaining read sequences were oriented so that the 5’ end corresponded to the sequence adjacent to the SV40pA primer. Our homopolymer utility (v1.0.0, option -z 0.1) was then used to attempt to find a poly(A) tract within the 5’-end of each trimmed and oriented read. Briefly, the homopolymer utility solves a Hidden Markov model (HMM) with 5 states (no homopolymer and A, C, G and T homopolymers) to find base runs in a sequence with an allowance for sequencing errors or other run disruptions. Trimmed reads that were found to have a 5’ terminal poly(A) tract of at least 15 nucleotides were next aligned to GRCh37/hg19 (and separately to GRCh38/hg38) with Bowtie2 (v2.1.0, options --local –k 100) allowing up to 100 possible alignments per read. Reads that failed to align in this first attempt were tried again without the local mapping option (Bowtie2 v2.1.0, options -k 100). The candidate best mapping location was determined for each read as the alignment that started within the first 1% of the length of the read near the poly(A) tract and that aligned up to the last 2.5% of the read. If multiple alignments fit this criterion, the highest scoring alignment was used only if its Bowtie2 alignment score was better by at least 20 than the next best alignment (Figure S1B). All other reads were rejected as unmappable. Since the HeLa, PA-1, H9-hESC, and H9-hESC-derived NPC cell lines were derived from females, any CCS reads with a best-mapped alignment on the Y chromosome were discarded.
CCS reads containing long poly(A) tracts tended to show incorrectly gapped initial genomic alignments because Bowtie2 attempted to align the entire read instead of maintaining the longest contiguous stretch of genomic A nucleotides and clipping the RNA-derived poly(A) segment. To resolve this mapping disparity, we applied the Smith-Waterman algorithm (Smith and Waterman, 1981) to refine genomic alignments (smith_waterman v1.0.0, match score of 1, mismatch penalty of −1.5, gap open penalty of −2.5, gap extension penalty of −1). Reads were re-aligned to their best-mapped genomic location plus an additional 50bp (if the poly(A) tract was less than 50bp) or 100bp (if the poly(A) tract was greater than 50bp) upstream and downstream of the span of the mapped read. All poly(A) bases present in the read that were also present in the genome at the point of integration were assigned as genomic bases, as opposed to bases added during synthesis of the poly(A) tail on the L1 RNA (Figure S1B, this conservative assignment decision is referred to throughout as “A-sliding”). Thus, the base-pair immediately 5’ to the integration site could never be an A, and since the inferred cleavage site is the reverse complement of the integration site, a T could never be in the 6th position of the final inferred 7bp cleavage site.
Once final genomic insertion positions were assigned, reads were re-assessed to verify that at least a 15bp poly(A) tract was present that could not be attributed to the genome. Multiple insertions called at the same genomic position were counted as replicate detections of a single integration event if they came from the same sample, but were considered to be independent events if they were from different biological replicates (Supplemental Dataset 6). Insertion calls from the same biological replicate were further examined for insertion pairs within 10bp of each other for which one insertion position had only one corresponding CCS read. The insertion position with just one read was assigned to the nearby position if the latter had 2 or more corresponding CCS reads. Such situations most likely represented the same insertion for which amplification or sequencing errors led to incorrect mapping of one read.
Finally, certain highly repetitive sequences in the genome such as centromeric or telomeric regions were found to contain highly non-random clusters of insertions. For example, we detected L1 insertions into alpha satellite centromeric repeat sequences, repeat sequences near telomeres, or tandem repeat sequences located on different chromosomes (HeLa-JVM: 142 reads [38 are unique]; PA-1: 2,883 [433 are unique] reads; NPC: 1,841 reads [383 are unique]; hESC: 3,666 reads [172 are unique]. These regions create two uncertainties in mapping and counting. First, we could over-count independent insertions if multiple reads that correspond to the same integration event mapped to different reference positions. Second, unknown numbers of copies of the repeat sequence are present in the physical genome of a cell, often many more than in the reference genome sequence, which makes it impossible to accurately determine the insertion frequency per unit DNA length. Accordingly, we filtered out any insertions called within these regions of the genome (Supplemental Dataset 3) and similarly excluded these regions from consideration in all enrichment analyses below.
Alignment pipeline validation
To test our alignment algorithm, we randomly picked 100,000 strand-specific positions in the hg19 human reference genome and retrieved segments of DNA 3’ to these positions by randomly picking segment lengths from the frequency-weighted distribution of read lengths from our observed insertion dataset (Figure S1A). We then added simulated poly(A) tracts to these genomic sequences by similarly picking lengths from the frequency-weighted distribution of observed poly(A) lengths. The final simulated reads thus mimicked the distribution of structures of our actual reads (Figures 2A and S2A). When these simulated reads were analyzed with our pipeline, 2.13% could not be uniquely aligned. A separate 0.12% of simulated reads were aligned to positions in the reference genome different than the known source position. Thus, our mapping sensitivity was 98%, indicating that we were able to map insertions into the majority of the human genome, with an accuracy of >99%, indicating that our results were not substantially influenced by alignment errors.
Insertion site characterization and simulations
L1 cleavage site consensus sequence
The consensus cleavage site was determined from all 64,973 aligned and non-excluded insertions from HeLa, PA-1, H9-hESCs, and H9-hESC-derived NPCs (Supplemental Dataset 1). Regions of 25bp surrounding mapped insertion positions were aligned based on their inferred cleavage position and logo plots created with the Bioconductor R package ‘SeqLogo’ (https://bioconductor.org/packages/release/bioc/html/seqLogo.html) (Bembom, 2009). A 7mer consensus, 5’-TTTTT/AA-3’, was identified (Figure S2C). Corrected logo plots were calculated by dividing the proportion of nucleotides observed at each 7mer position by the proportion of A, C, G and T nucleotides at that same position over all 7mers found in the human genome (Figure 2C). To test for co-dependence of base positions within this motif, we calculated the mutual information of all seven bases using the R package ‘entropy’ (https://cran.r-project.org/web/packages/entropy/index.html) (Hausser and Strimmer, 2009) (Figure S2E). Specific mutuality hypotheses were further tested by re-creating logo plots based on subsets of the observed cleavage sites that were filtered for the presence or absence of specific bases at specific positions (Figure 2F).
Weighted random simulations of L1 integration
Explorations of L1 integration event enrichment in specific genomic regions demanded a baseline model that accounted for the locations of preferred L1 insertion sites (i.e., 7 bp sequences) in the human genome. Toward this goal, we first determined the observed frequencies of all possible variations of the inferred L1 7mer cleavage site sequence for each cell line from the bases surrounding the mapped insertion positions. Due to the A sliding method used during mapping (see above) there were only 12,288 possible sites (i.e., 5’-NNNNN/VN-3’, where N represents A, C, G, or T and V represents A, C, or G). Because all cell types displayed a similar distribution of 7mer usage frequencies (Figure 2D), we created a single simulation model based on all observed insertions over all cell types.
We next constructed a custom position weight matrix (PWM) based on the observed patterns of co-dependence between the bases at different positions of the 7mer site (Figure S2E). The PWM allowed any of the four bases (A, C, G and T) at motif position 1, with values set as the frequencies of the four bases among all observed insertions. Positions 2-5 were grouped as one unit and positions 67 as one unit, with values set as the frequencies of the 256 4-mers and 12 possible 2-mers observed over those position ranges, respectively. Calculated site frequencies were the products of the values of all possible combinations of the three PWM elements. Final modeled site frequencies were chosen from observed frequencies when a site had three or more observed insertions and from the PWM in all other cases (Figure S2F). The composite model thus mainly used observed L1 insertion frequencies, but allowed for broad sampling of less preferred sites throughout the genome via the PWM, even if we had never observed any insertions at a specific site due to the limited size of our data set. To facilitate random picking from the genome, we converted modeled frequencies to sampling weights for each site by normalizing to the observed frequency of the most common cleavage site, 5’-TTTTT/AA-3’.
To establish site frequencies in the human genome, we tabulated the cleavage site that would be called if L1 EN were to cleave each of the 5,669,914,180 GRCh37/hg19 strand-specific genomic positions that were not in gaps or among the excluded repeat regions of the genome (see above). The same A-sliding logic was applied as during mapping of CCS reads, which resulted in some genome positions and associated sites being counted zero times, while other positions were counted multiple times based on the number of bases in the A run that slid into them (Figure S1B). These counts were used to weight each genomic position during simulations. Thus, our genome model accounted for the unavoidable uncertainty created by integration of poly(A)-containing L1 elements into genomic A runs.
An algorithm was finally devised to efficiently and randomly pick simulated insertion events from the genome based on the combined insertion site and genomic position weights. Briefly, a large table was created whose rows corresponded to all callable genomic positions (after taking A-sliding into account) sorted by their associated 7mer sequences. An associated index listed all 12,288 possible 7mer sites and the range of matching parent table rows. The R sample function was utilized to first pick a site, with replacement, from among the 12,288 possible 7mers based on the site weights from the composite model. For each chosen 7mer, we then randomly picked from among the matching table rows retrieved from the index to obtain a final weighted random genomic position and strand. In this way we picked the same number of random integration positions as our actual insertion data set to establish one simulation iteration; we then repeated the process to generate 10,000 iterations.
Simulation validation
The validity of the obtained simulation sets with respect to L1 insertion site preferences was established by repeating the cleavage site analyses, including site frequency distribution and logo plots, on ten simulation iterations (Figure 2G). The randomness of the selected genomic positions was validated by comparing insertion positions over 10 simulation iterations, which showed that on average 0.11% (69, range 50 to 87) of the 64,973 selected positions were the same between any two iterations. This limited overlap between iterations was consistent with the relatively small size of our insertion data set as compared to the large number of preferred positions in the genome.
L1 integration enrichment analysis
Several strategies were used to test whether preferred L1 insertion sites and observed insertion positions were non-randomly distributed with respect to specific genomic features. Some strategies were specific to the nature of each comparison data set (see below), while others were general. Chromosome ideograms (Figure 3B) were created using PhenoGram from the Ritchie Lab at Pennsylvania State University (http://visualization.ritchielab.psu.edu/phenograms/plot) (Wolfe et al., 2013).
Kolmogorov-Smirnov bootstrap test
The Kolmogorov-Smirnov bootstrap test (KSbt) was used as a general strategy for querying L1 integration enrichment as a function of quantifiable properties of different genomic regions (Figures 4C, S4C, S4D, S5B, S6D). Each gene, fixed-width bin or similar span of the genome was assigned a score reflecting the property of interest (see specific cases below). We next used BEDTools intersect (v2.16.2, option –c) to count the number of observed and simulated L1 insertions whose assigned positions fell within each bin or span (https://bedtools.readthedocs.io/en/latest/) (Quinlan and Hall, 2010). Empirical cumulative distribution functions (CDFs) were then constructed using the R aggregate and stepfun functions for the observed L1 integration events, as well as each iteration of the weighted random simulation (blue and gray lines in CDF plots, respectively), based on the paired property scores and insertion counts over all bins or spans. For comparison, we similarly constructed an unweighted CDF for the entire human genome for each property of interest by counting the number of potential L1 cleavage positions in the genome that would be assigned to each bin or span after taking A-sliding into account (black line in plots). This latter model represented the expected score distribution if L1 integration events occurred randomly without respect to sequence or any other genomic feature. The composite CDF plots can thus reveal whether L1 preferred cleavage sites present in the genome are enriched for a property score (by comparing gray versus black lines), regardless of whether we actually observed insertions at those positions. CDF plots can additionally reveal whether the integration positions we observed in our dataset differed from the null hypothesis that only L1 site preferences determine its integration positions (by comparing blue versus gray lines).
Statistical differences between CDFs were assessed using the ks.boot function from the R package ‘Matching’ (v4.8-3.4) (https://cran.r-proiect.org/web/packages/Matching/index.html) (Sekhon, 2011) with 10,001 boot iterations. A KSbt was required because L1 integration data can have discontinuous tied values when two or more insertions occur in a genome span with a single score. We used ks.boot to calculate a p-value between the distribution of scores from the actual insertion data (blue line) and each individual simulation iteration (gray lines). If >95% of these 10,000 comparisons resulted in p-values <0.05 then the p-value was reported as <0.05. If >99% gave p-values <0.01 then the p-value was reported as < 0.01, etc.
Gene annotation analysis
L1 integration events were compared to the boundaries of gene exons (including 5’UTR, protein coding, and 3’UTR exons) and introns as defined by the UCSC Genome browser (UCSC genome browser table Genes track; table: knownGene hg19 ref) (Figures 3C, 3D, and 3F). To determine if insertions were biased towards antisense integration we calculated the ratio of antisense to sense genic (i.e., intronic plus exonic) insertions (Figure 3F). Significance was determined by a χ2 test applied to the sense and antisense counts from the observed genic L1 insertions and the median values from the weighted random simulations.
Mature and nascent RNA sequencing
RNA-seg
Total RNA was extracted from confluent H9-hESCs and H9-hESC-derived NPCs using Trizol (Invitrogen) and from confluent HeLa-JVM and PA-1 cells using the RNeasy Mini kit (Qiagen). Ribosomal RNA (rRNA) was removed using the Illumina Ribo-Zero rRNA Removal Kit and libraries were made with the Illumina TruSeq Stranded mRNA Library Prep Kit, using the low sample protocol and beginning at the elute-prime-fragment step. We used a 1 min fragmentation to generate a 190bp average target insert size and only 12 cycles of PCR. A first biological replicate of each cell type was subjected to 100bp paired-end Illumina HiSeq sequencing at the University of Michigan DNA Sequencing Core, with all four samples multiplexed into one lane. A second biological replicate for each cell type was similar but yielded 125bp paired-end Illumina HiSeq sequencing reads.
RNA-seq reads were aligned to GRCh37/hg19 with Tophat (v2.1.1, options --library-type fr-firststrand) using illumina iGenomes’ ENSEMBL GRCh37/hg19 transcripts (Trapnell et al., 2009; Zerbino et al., 2018). The Cufflinks Suite (v2.2.1) was utilized to run Cufflinks to obtain assembled transcripts and isoforms (options -b -u --library-type fr-firststrand --max-bundle-frags 10000) (https://github.com/cole-trapnell-lab/cufflinks) (Roberts et al., 2011; Trapnell et al., 2010). Cuffmerge with default options provided a final transcriptome assembly. Cuffquant quantified gene and transcript expression. Cuffnorm was finally used to merge biological replicates and normalize samples to a common scale for further comparisons (options --library-type fr-firststrand --library-norm-method geometric --output-format cuffdiff). All gene expression values are expressed as fragments per kilobase of transcript per million mapped reads (FPKM).
To correlate L1 integration to RNA-seq results, we first randomly sub-sampled each simulation iteration to contain the same number of insertions within ENSEMBL transcript regions of the genome (https://support.illumina.com/sequencing/sequencing_software/igenome.html) (Zerbino et al., 2018) as the actual data for a given cell line (HeLa: 6,614; PA-1: 6,125; NPC: 3,353; hESC: 1,660). We then divided the genome into expressed (FPKM >0.3) vs. non-expressed transcripts. Significance of the association between L1 integration and expression was assessed using the χ2 test applied to the number of observed insertions in expressed and non-expressed genes and the median counts from the weighted random simulations. We also divided the observed range of gene FPKM values into 30 intervals such that each interval corresponded to an approximately equal bp fraction of the reference genome. For each simulation iteration, we counted the number of actual and simulated insertions that fell within and outside of the transcription interval and performed the χ2 test on the resulting contingency table. We then determined the proportion of the 10,000 iterations for which the χ2 test p-value was below a given threshold (p-value <0.05, 0.01, 0.001, 0.0001, 0.00001, or 0.000001).
Bru-seq nascent RNA sequencing
Bru-seq nascent RNA sequencing and initial data analysis were performed as previously described (Paulsen et al., 2014). Briefly, this established workflow calculated reads per kilobase of transcript per million mapped reads (RPKM) values for 1kb bins throughout the genome and then used a HMM to identify contiguous segments of transcription at 1 kb resolution (segment v1.0.0). Data were visually compared to the ENSEMBL gene annotation in a custom genome browser (MiBrowser) (Figure 4A) to empirically determine an appropriate segment RPKM threshold that corresponded to bona fide transcription. For PA-1, the threshold of 0.024 RPKM corresponded to 5,391 observed L1 insertions within actively transcribed regions of the genome and 35.3% of the human genome. The HeLa threshold of 0.022 RPKM corresponded to 6,617 insertions within actively transcribed regions of the genome and 34.1% of the genome. We then tested for L1 enrichment relative to these transcribed vs. non-transcribed states, as well as to 30 intervals of increasing transcription levels, using the χ2 test exactly as described for RNA-seq (Figure S4A). Bru-seq replicates for each cell line were highly correlated (Spearman’s rho of 0.8536 and 0.935 for HeLa and PA-1, respectively); thus, we report data from one replicate.
Transcription strand bias was calculated as the absolute value of the difference in RPKM values between the top (+) and bottom (−) reference strands at a genome position divided by the summed RPKM value of both strands (Figures 4A and S4B). The range of possible bias values from 0.0 to 1.0 was divided into 11 equal 0.1 incremented intervals. We counted the number of actual or simulated insertions whose bias values matched each interval, as well as the fraction of those events in which L1 (+) cDNA integrated into the DNA template strand that corresponded to the transcription direction with the highest strand-specific RPKM value, referred to as the predominant template strand. For example, if the top and bottom strands at a genome position (corresponding to the forward and reverse transcription directions, respectively) had Bru-seq RPKM values of 1.0 and 0.1, respectively, the bias would be 0.818 (0.9 divided by 1.1) and the predominant template strand would be the bottom strand (Figure 4A). Importantly, L1 (+) strand cDNA integration into the bottom genome strand is synonymous with L1 EN cleavage of the top strand. For each cell line, we plotted the fraction of observed and simulated insertions in each transcription bias interval at which L1 had integrated into the predominant template strand (TS) (Figure 4D). To determine significance at each transcription bias interval for each simulation iteration, we counted the number of actual and simulated insertions that occurred on the predominant template and non-template strands and performed the χ2 test on the resulting contingency table. If 99% of the 10,000 iterations showed a χ2 test p-value less than 0.01 then the overall χ2 test p-value was determined to be <0.01. We performed this comparison to a p-value <0.00001.
Chromatin state enrichment analysis
Chromatin state bed files (15-state) published by the Roadmap Epigenomics Consortium were downloadedm from the following website: (http://egg2.wustl.edu/roadmap/data/bvFileType/chromhmmSegmentations/ChmmModels/coreMarks/iointModel/final) (Roadmap Epigenomics et al., 2015). Specifically, we downloaded the 15-state mnemonics bed files for: H9-hESC cells (identifier E008); H9-hESC-derived neuronal progenitor cultured cells (E009); H9-hESC-derived neuron cultured cells (E010); aorta (E065); liver (E066); HeLa-S3 cervical carcinoma cells (E117); HepG2 hepatocellular carcinoma cells (E118); and K562 leukemia cells (E123). As a positive control for strong transposable element enrichment and depletion we downloaded the MLV integration events in K562 (LaFave et al., 2014). The Genome Structure Correction tool was utilized to determine enrichment or depletion of insertions with respect to the different chromatin states (Consortium et al., 2007). The following settings were used after empirically determining the r and s values that resulted in the least over-dispersion: block_bootstrap.py -r 0.20 -s 0.15 -n 10000 -t rm -B -v. Enrichment was then calculated for insertions in each individual state and a heat map created using the R ggplot function (Figure 4E). States that covered a small proportion of the genome and therefore resulted in fewer than 30 expected insertions were masked as gray boxes in the heat map since these states had insufficient power to find a true enrichment or depletion.
Okazaki fragment sequencing data analysis
Previously published EdU-labeled HeLa-MRL2 and GM06990 Epstein-Barr immortalized lymphoblastoid cell OK-seq read data were downloaded from the NCBI Sequence Read Archive accession SRP065949 (Petryk et al., 2016) and mapped to GRCh37/hg19 using BWA MEM (http://bio-bwa.sourceforge.net/) (Li and Durbin, 2010) with default parameters. The genome was divided into 2kb bins and the replication fork direction (RFD) was calculated for each bin as defined by Petryk et al. by subtracting its Watson/top reference strand Okazaki fragment count from its Crick/bottom strand count and dividing by the total counts, considering only unique non-duplicated reads (Petryk et al., 2016). Positive RFD values thus indicate a higher frequency of rightward moving replication forks with respect to the reference genome orientation (Figure 5A).
Additional processing on bin RFD values was performed to create a stabilized RFD model in which bin values were adjusted based on values of nearby bins. Wavelet smoothing was first performed at two smoothing levels (smooth utility v1.0.0, options -j 3 and -j 4, LA8 wavelet) on the subset of genome bins with total Okazaki fragment counts between 25 and 500, which excluded unmappable and unreliable genomic regions. A heuristic algorithm was then applied to find contiguous genome bins with a common RFD slope. Adjacent bins for each smoothed input were first merged into runs where the bin-to-bin RFD change had the same sign. Runs were declared as 0 sloped (i.e., flat) if the RFD change across all bins was less than 0.35 and adjacent 0 sloped runs were fused. Adjacent series of three runs were further fused into a single run if the outer runs had the same slope sign and the middle run represented no more than 10 bins or 33% of all bins. Linear regression was applied to each final run of bins, weighted by the total read count in each bin. The two sets of runs obtained for each smoothing level were then split at all run endpoints and the best linear regression model was chosen for each split run as the model that minimized the weighted sum of squares of error over the run. Short split runs of less than 5 bins were finally fused back to adjacent runs of the same smooth level and minor adjustments made in order to join adjacent runs at vertices.
Final linear models are shown as orange lines in Figure 5A relative to blue dots corresponding to each bin’s unsmoothed RFD value. These linear models provided the RFD values and slopes that we used when examining association of L1 integration with local replication properties. The two available OK-seq datasets for HeLa, and two for GM06990, showed Spearman’s rho correlation coefficients of 0.962 and 0.954, respectively, as applied to these modeled RFD values. Because of these strong correlations within a cell line we show only one replicate in figures, although we performed all analyses for all replicates (Figure 5B). Modeled HeLa and GM06990 RFD values showed a Spearman’s rho of 0.61 relative to each other, demonstrating a substantial preservation of RFD even across cell lines.
Assessments of the replication strand bias of L1 integration were performed in a manner entirely analogous to the analysis of transcription strand bias described above, except that for OK-seq data we examined the fraction of retrotransposition events where L1 integrated into the predominant leading strand template as a function of RFD (e.g. the bottom genome strand is the predominant leading strand template for bins with positive RFD values, Figure 5A). CDF plots of RFD slope provided information on association of L1 integration with replication origin and termination zones, according to the logic described by (Petryk et al., 2016) that human origins occur in regional clusters (Figures S5B and S6D) (Petryk et al., 2016).
Determining L1 replication strand preference
It is important to establish the potential L1 replication strand bias data patterns that are possible. We used an estimation based on two extreme hypotheses and an intermediate mixed hypothesis, which together are represented by a parameter we termed “replication strand preference” (RSP). RSP describes the tendency of L1 to integrate into a specific strand at a replication fork, while RFD describes the frequency at which replication forks move to the left or right (as defined by the reference genome).
Null hypothesis
Under the null hypothesis, L1 has no RSP. When L1 encounters DNA is it equally likely to integrate into preferred target sites (i.e., sequence motifs) on the leading and lagging strand DNA templates. The null hypothesis is consistent with retrotransposition during or outside of S phase. In the simplest scenario, L1 would integrate independently of RFD. Even if L1 targeted genomic regions with a highly polarized RFD due to an unknown associated property, integration would be equally likely to occur into top or bottom reference genome strands. However, L1 strand integration depends on the availability of preferred 7mer target sites. Accordingly, a replication strand bias could be detected under the null hypothesis if preferred 7mer sites are distributed asymmetrically with respect to RFD, which is expected since differences in mutagenic processes between leading and lagging strands have led to a genome-wide nucleotide skew such that lagging strand DNA templates tend to be more T-rich (Petryk et al., 2016; Touchon et al., 2005).
Alternative hypothesis
Under the extreme alternative hypothesis, L1 only integrates into a specific replication strand (either the leading or lagging strand template, but not both). This model is most consistent with L1 integrating during S phase at an active replication fork. Critically, even under the pure alternative model of a complete RSP, L1 could integrate into either reference genome strand (i.e. top or bottom strand) at a given genome position across a population of cells if the magnitude of the RFD was not 1. At all other RFD values, L1 could sometimes integrate into either strand depending on the instantaneous direction of replication in the specific cell in which retrotransposition occurred. This relationship limits the maximum extent of strand bias that can be observed in data. If cells had a random replication program, there would never be an observed strand usage bias even if the alternative hypothesis were true.
Mixed hypothesis
Finally, L1 could show an incomplete RSP. L1 might have more than one mode of integration (one replication dependent, the other not), or L1 might always integrate during replication but with a differential avidity for the two strands based on some property such as relative accessibility, a bound protein factor, or another unknown feature.
Calculating RFD probability distributions based on RSP
We formalized RSP in a manner analogous to RFD by rescaling the probability (P) that L1 will integrate (int) into the leading strand DNA template (LEAD) upon encountering DNA, which typically means that L1 EN cleaved (clv) the lagging strand DNA template (LAG).
Thus, a RSP of 0 represents the null hypothesis while values of 1 and −1 represent the extreme alternative hypotheses that L1 demands leading and lagging strand integration, respectively. We sought to estimate RSP by measuring two RFD frequency distributions (F) from a set of genomic L1 insertion positions (ins) distinguished by the reference genome strand into which L1 integrated, either the top (TOP) or bottom (BOT) strand.
| (1) |
| (2) |
In observed data these strand distributions may be the same or different. They might also differ within a set of simulated L1 insertion positions selected according the weighted random model if L1 preferred site frequencies correlate with RFD. However, if L1 integrated completely randomly (rnd), including the absence of any sequence preference, the distributions would be the same as they represent independent sub-samplings of the same genome (gen).
Our goal was to find the value of RSP that matched a given set of insertions, such that:
| (3) |
| (4) |
To achieve this we used Bayes theorem to solve the probability that L1 would randomly integrate into each strand (STR) of each 2kb genome bin under a given RSP model.
| (5) |
The prior probability of L1 using each bin was obtained by counting the genomic positions whose assigned mapping position fell in the bin (M) and normalizing to all bins in the genome.
| (6) |
To calculate other components of equation (5), we rescaled the RFD calculation described by Petryk (Petryk et al., 2016) to match the probability that an encountered replication fork would be moving in the forward direction; i.e. that the bottom reference strand would act as the leading strand template, at a given genomic position across a cell population (similar to RSP conversion, above).
| (7) |
We used equation (7) to calculate the probability that L1 would integrate into a specific reference genome strand under a specific RSP model as a function of RFD.
| (8) |
| (9) |
Equations (7) and (8) yield the following values of P(intBOT|RFD)RSP, which exemplify the relationship between RFD and RSP.
| P(intBOT|RFD)RSP | P(intLEAD) | |||||||||||
| 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1 | ||
| RSP | ||||||||||||
| RFD | P(BOT = LEAD|RFD) | −1 | −0.8 | −0.6 | −0.4 | −0.2 | 0 | 0.2 | 0.4 | 0.6 | 0.8 | 1 |
| −1 | 0 | 1 | 0.9 | 0.8 | 0.7 | 0.6 | 0.5 | 0.4 | 0.3 | 0.2 | 0.1 | 0 |
| −0.8 | 0.1 | 0.9 | 0.82 | 0.74 | 0.66 | 0.58 | 0.5 | 0.42 | 0.34 | 0.26 | 0.18 | 0.1 |
| −0.6 | 0.2 | 0.8 | 0.74 | 0.68 | 0.62 | 0.56 | 0.5 | 0.44 | 0.38 | 0.32 | 0.26 | 0.2 |
| −0.4 | 0.3 | 0.7 | 0.66 | 0.62 | 0.58 | 0.54 | 0.5 | 0.46 | 0.42 | 0.38 | 0.34 | 0.3 |
| −0.2 | 0.4 | 0.6 | 0.58 | 0.56 | 0.54 | 0.52 | 0.5 | 0.48 | 0.46 | 0.44 | 0.42 | 0.4 |
| 0 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| 0.2 | 0.6 | 0.4 | 0.42 | 0.44 | 0.46 | 0.48 | 0.5 | 0.52 | 0.54 | 0.56 | 0.58 | 0.6 |
| 0.4 | 0.7 | 0.3 | 0.34 | 0.38 | 0.42 | 0.46 | 0.5 | 0.54 | 0.58 | 0.62 | 0.66 | 0.7 |
| 0.6 | 0.8 | 0.2 | 0.26 | 0.32 | 0.38 | 0.44 | 0.5 | 0.56 | 0.62 | 0.68 | 0.74 | 0.8 |
| 0.8 | 0.9 | 0.1 | 0.18 | 0.26 | 0.34 | 0.42 | 0.5 | 0.58 | 0.66 | 0.74 | 0.82 | 0.9 |
| 1 | 1 | 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1 |
We then calculated the denominator of equation (5) using likelihood normalization.
| (10) |
Substituting equations (6), (8), (9) and (10) as needed into equation (5) established the strand-specific posterior probability that L1 would use each genome bin at a given RSP under a random model with no site preference.
Estimating the RSP of insertion datasets
Each observed or simulated sample has two subsets of insertion positions, corresponding to each reference genome strand, that establish two RFD frequency distributions [expressions (1) and (2)]. These distributions are independent because no integration event influences any other event. We used the difference between the medians of the strand-specific RFD values as a metric for characterizing the degree of strand usage bias observed in a sample.
| (11) |
Each RFD median need not be zero under a random integration model if more of the genome is replicated in one direction than another. However, ΔRFDRSP=0 is exactly zero by definition. We calculated ΔRFDRSP=1 the expected value of ΔRFD if L1 always integrates into a leading strand DNA template, by first weighting all genomic bins by the posterior probabilities calculated for each reference strand using equation (5). We then calculated the weighted median of the bin RFD values for each strand and took the difference similar to equation (11). We finally estimated the value of RSPins that satisfied expressions (3) and (4) by interpolating ΔRFDins on the line defined by ΔRFDRSP=0 and ΔRFDRSP=1.
Bootstrapped confidence intervals of RSP
We used bootstrapping to establish confidence intervals for the value of RSPins obtained for an insertion set. We separately resampled the top and bottom strand RFD values with replacement from within their respective sets, recalculated RSPins for each of 1000 bootstrap iterations, and reported the 0.025 and 0.975 quantiles of the bootstrapped values. This estimate was insensitive to errors in our weighted random model because it used only observed RFDs.
Violin plots
Figures S5A and S6C show overlaid violin plots (R ggplot2 geom_violin, options trim=FALSE, adjust=0.5) of P(RFD|intTOP) and P(RFD|intBOT), i.e. RFD distributions for L1 integrations into the top and bottom strand of the reference genome, respectively, for observed and 100 pooled simulation insertion sets as well as for calculated models at RSP values of 1 (labeled “Maximum”, for pure leading strand integration) and RSPobs (labeled “Modeled”). The two violin plots are superimposed under the random model, but look progressively more like the Maximum limit plots as RSP increases. All violin plots on a graph were adjusted to have the same total area. Median lines permit visual estimation of ΔRFD.
Lamina Associated Domains (LADs)
The van Steensel laboratory previously generated lamina-associated domain (LAD) data sets by using DNA adenine methyltransferase (Dam) identification (DamID) and a Dam-lamin B1 fusion protein (Guelen et al., 2008; Meuleman et al., 2013). Tig3 fibroblast data were obtained as genomic LAD spans from supplemental file #1 of Guelen et al. 2008, while SHEF-2 hESC and HT1080 fibrosarcoma data were obtained as probe LAD state calls from GEO accession GSE22428. hESC and HT1080 LAD data were converted to genomic spans by identifying runs of probes with a LAD state of 1. All resulting hg18 data files were converted to BED6 file format and then to hg19 coordinates using the liftover tool of the UCSC genome browser with standard settings. Finally, we filled the regions between LAD segments and to the ends of chromosomes with features in the non-LAD state of 0 prior to enrichment analysis. We generated a set of constitutive LADs as the regions common to all of the overlaid Tig3, hESC and HT1080 hg18 LAD data sets, followed by conversion to hg19 and filling of non-LAD segments as above (Figure 7A). A total of 0.68 Gbp of the hg19 reference genome were found in LADs in all three input data sets, corresponding to 40% of the 1.7 Gbp found in LADs in any input.
Replication timing
All replication timing data used in this study were downloaded from the replication domain database maintained by the Gilbert laboratory, https://www2.replicationdomain.com/ (Weddington et al., 2008). Data sets used in plots were RT_HeLaS3_Cervical_Carcinoma_Int95117837_hg19, RT_H9_ESC_Ext29405702_hg19, RT_H9_Neural_Progenitor_Int89790558_hg19, and RT_IMR90_Fibroblast_Int94339003_hg19. We also corroborated findings with additional data sets. IMR90 data were obtained by genomic sequencing and provided as 1 kb genomic bins. For other samples, we converted the provided microarray probe-based BEDGRAPH-formatted data into genomic spans in BED file format by extending the coordinates of each probe to the positions halfway between the probe and the nearest probes on either side, or to the end of the chromosome. Thus, every genome position was assigned a replication timing based on the nearest probe. Otherwise, replication timing values were used as provided, where positive and negative numbers reflect early and late replication timing, respectively. We further classified genomic segments as early or late replicating by comparing them to the median segment score weighted by the number of genomic positions whose mapping position fell into each segment. Early and late replicating segments were those with replication timing values above and below this median, respectively (Figure 7B).
Multivariate analysis of replication timing and LADs
We used observed insertion counts for a specific cell line to establish weights for each binned replication timing or LAD value. We used these value weights in the R ‘sample’ function to pick otherwise random insertions from among 100 input unweighted simulation iterations per output iteration without replacement, thus allowing us to pick 100 independent weighted output simulation iterations from our sets of 10,000 input iterations. We validated that the process and the size of the inputs pools were sufficient by comparing violin plots of replication timing distributions, or fractions of insertions into LADs, for observed, unweighted, and weighted insertions. In all cases, the weighted simulations matched well to the observed insertions. We finally replotted our observed fractions for the non-matched values against both the weighted and unweighted simulation distributions to determine if a residual effect persisted for the non-matched value after controlling for the matched value in simulations.
DATA AND SOFTWARE AVAILABILITY
Our general utilities used in the pipeline (homopolymer, smith_waterman, segment and smooth) are available at https://git.umms.med.umich.edu/wilson_lab_public/utilities.
ALL RNA-seq data (except HeLa): SRA: PRJNA432733
HeLa RNA-seq data: dbGaP: phs001671
PacBio CCS-fastq files (except HeLa) and PA-1 Bru-Seq: SRA: SRP151191
HeLa PacBio CCS-fastq, and HeLa Bru-Seq: dbGaP: phs001669
Supplementary Material
Figure S1, related to Figure 1. Recovering thousands of de novo engineered L1 retrotransposition events.
(A) Frequency distribution of the CCS read lengths that support insertion calls from HeLa-JVM, PA-1, NPC, and hESC samples.
(B) Alignment pipeline steps. Only CCS reads bearing both the SV40pA (gray box) and adapter (red rectangle) oligonucleotide primer sequences, as well as a poly(A) tract of at least 15bp (black box), were aligned to the genome after trimming the primer sequences from reads. Best mapped locations were chosen as an alignment covering at least 96.5% of the read with an alignment score difference (ASDIF) of 20 compared to the next best alignment. Insertions in genomic A tracts lead to an uncertainty in calling that was handled by assigning ambiguous A bases to the genome, not to the L1 poly(A) tract (referred to as “A-sliding”). Thus, the 5’-most A base was assigned as the insertion position (blue A with asterisk). L1 EN cleaves the opposite strand (black triangle).
(C) Breakdown of the observed outcomes of the initial filtering of CCS reads for each cell line. The blue pie slices indicate the proportion of CCS reads that passed this filtering.
(D) Breakdown of the alignment outcomes of CCS reads that passed initial filtering. CCS reads were aligned to both GRCh37/hg19 and GRCh38/hg38. The large majority of usable CCS reads could be productively mapped to yield insertion calls (dark and light blue pie slices). Only small differences were noted between the two reference genomes.
(E) Frequency distribution of the number of independent CCS reads supporting engineered L1 insertion events in the HeLa-JVM, NPC, and hESC samples.
Figure S5, related to Figure 5. L1 integrates more often into leading strand templates.
(A) Overlaid violin plots of RFD frequency distributions. Each panel compares one L1 insertion set to HeLa OK-seq RFD values. The top row in each panel compares 100 simulation iterations (gray) and observed insertions (blue) aggregated on both strands. The second and third rows show the simulated and observed insertions stratified by integration strand. “Modeled” shows the expected distribution for the RSP value calculated for the observed insertions, while “Maximum” shows the distribution for a pure leading strand integration preference, i.e. a RSP of 1. For all but the top rows, colors identify L1 integration into the top (orange) and bottom (green) reference genome strands, which means that L1 cleaved the bottom and top strands, respectively. Vertical lines denote the distribution medians.
(B) CDF plots of the slope of RFD values surrounding L1 insertions. Positive RFD slopes occur in regions where replication origins are firing while negative slopes correlate with replication termination (Petryk et al. 2016). While all L1 insertion datasets differed significantly from the simulations (KSbt P-values: HeLa-JVM: < 0.001; PA-1: < 1×10−6; NPC: < 0.01; hESC: < 0.05), the deviation from the null hypothesis is small, inconsistent between samples, and not suggestive of a strong L1 preference for integration at origins or termination zones. For example, in PA-1 cells, the excess of insertions relative to the simulated data occurs at neutral slopes, which are regions of stable replication fork movement.
Figure S6, related to Figure 6. EN-deficient L1 integrates into lagging strand templates in FANCD2-deficient cells.
(A) Frequency distribution of the poly(A) tract lengths of engineered L1 insertions in PD20F cells.
(B) L1 insertion counts by chromosome in PD20F cells (colored circles), sorted by increasing chromosome size. Boxplots show the distribution of counts from 10,000 iterations of the weighted random simulation.
(C) Overlaid violin plots of RFD frequency distributions. Each panel compares one L1 insertion set to HeLa OK-seq RFD values. Labels and plotting are the same as in Figure S5A. Numbers to the left of FANCD2 deficient conditions are the corresponding modeled RSP values.
(D) CDF plots of the slope of RFD values surrounding L1 insertions from the PD20F cell libraries, plotted similarly to Figure S5B. The L1.3 insertion dataset in PD20F cells differed significantly from the weighted random model (KSbt p-value < 0.05), but similar to Figure S5B the magnitude of the effect was very small.
Figure S7, related to Figure 7. L1 dependence on nuclear architecture varies between cell lines.
(A) Fraction of insertions into LADs, similar to Figure 7A. Black boxplots identify L1 data sets considered to be well-matched to the LAD reference data.
(B) Fraction of insertions into early replicating portions of the genome, similar to Figure 7B. Black boxplots highlight comparisons considered to be well-matched with respect to cell type.
(C) Boxplots show 100 simulated insertions weighted either by the 7mer insertion site alone (‘random’) or additionally such that the distribution of the x-axis parameter for each iteration matched the observed insertions for the indicated cell lines (‘sim=obs’). Colored symbols show the observed value. Matching the simulation iterations to the observed distribution of the x-axis parameter decreased the magnitude of the effect for the y-axis parameter in all cases, but the degree of the decrease was larger when matching for replication timing, suggesting that the fraction of insertions in LADs might be secondary to replication timing. All plots used hESC replication timing data and constitutive LADs.
Supplemental Dataset 1, Related to Figure 1. Engineered L1 Insertion Coordinates, Characteristics, and Sequences. Table of all insertion coordinates providing chromosome, position of insertion both 0-based and 1-based (hg19 coordinates), insertion id which corresponds to the supporting PacBio CCS read, strand of the genome the L1 integrated into, the L1 EN cleavage sequence for that insertion, the called poly(A) tract for all supporting CCS reads of that insertion, the primer clipped CCS read/s that support the insertion site, and the biological sample the insertion was obtained from. Sheet labels refer to the corresponding cell type insertions were generated and identified from.
Supplemental Dataset 2, Related to Figure 1. Retrotransposition Assay Conditions. Independent biological sample details for each cell type are shown. For each independent cell culture condition experiment the provided biological sample name, selection condition, number of insertions obtained from experiment and the percentage of the total insertions for that cell type are given. The summary of identified insertions that came from selection experiments is also shown in bottom tables.
Supplemental Dataset 3, Related to Figure 1. Blacklisted Regions of Human Genome. Regions of the genome that included alpha satellite centromeric, telomeric, and tandem repeats in the human genome reference (hg19) that were excluded from downstream data analysis.
Supplemental Dataset 4, Related to Figure 2. Top Weighted 7mer Sequences in Models. A listing of the top weighted 7mer sequences in our uncorrected and corrected weighted models.
Supplemental Dataset 5. Related to Figure 3. L1 Insertions in Genomic Regions of Interest. For each cell type, the number of insertions found in genomic LINE and SINE sequences, fragile and non-fragile sites, ultra-conserved elements, ultra-conserved noncoding elements and transposon free regions in the genome are provided as well as the minimum, median, and max value observed from the 10,000 simulations found in each of these regions of interest.
Supplemental Dataset 6, Related to Figure 3. Duplicate L1 Insertions. Identified duplicate insertion sites from independent biological replicates of a given cell type and duplicate insertion sites from independent cell types. Sheet labeled “Summary” provides number of insertions. Sheet labeled “Sample Insertion Key” provides codes used to identify CCS reads from each biological sample. Sheet labeled “Insertions” provides all the insertion sites giving the chromosome, position (0-based), position (1-based), insertion ID corresponding to the supportive CCS read, biological sample insertion was identified in, strand, and then the same information for the other biological sample in which the same insertion site was identified. Sheetl describes each column.
Supplemental Dataset 7, Related to Figure 3. Genic L1 Insertion Characteristics. A listing of all genic (5’UTR, intronic, exonic, or 3’UTR) insertions based on the UCSC genome browser’s defined gene coordinates (hg19). Also included are expression values on both strands of the genome from RNA-seq (FPKM) or Bru-seq (RPKM) experiments if available for that gene or transcript respectively in the genome. Each sheet label represents the cell type where the insertions were identified. Sheet 1 provides the description of each column.
Figure S2, related to Figure 2. Local L1 integration site preferences.
(A) Frequency distribution of the poly(A) tract lengths of engineered L1 insertions from HeLa-JVM, NPC, and hESC samples.
(B) Base observation frequencies over positions from 100bp upstream to 100bp downstream of PA-1 insertions. The 7mer insertion site lies between the vertical lines at positions 0 and 7.
(C) Extended logo plot showing information content for sequences from 25bp upstream to 25bp downstream of PA-1 insertions 7mer site.
(D) Frequency distribution of the Hamming distances (i.e. number of mismatches) between all possible 7mer sites and the L1 integration site consensus sequence, 5’-TTTTT/AA-3’.
(E) Mutual information plot displaying the degree of co-dependence between paired nucleotide positions in the 7mer L1 integration site (blue boxes reflect co-dependent position pairs).
(F) Correlation plot of modeled and observed log10 weights for the 12,288 possible 7mer L1 integration sites. Point colors reflect the number of insertions that utilized each site (see legend). A gray unity line identifies sites where the two weights were equal. To help visualize individual points, we applied the R jitter function to y-axis values. Sites with an observed weight of 0 (infinite log10 weight) are plotted separately.
(G) Plot showing the GC content of different sized windows of genomic sequence surrounding simulated L1 insertion positions. A blue dashed line represents the genome average of 41%.
Figure S3, related to Figure 3. L1 integrates throughout the human genome.
(A) Insertion counts for the indicated cell lines are plotted as colored diamonds or squares (Spearman’s rho: HeLa-JVM: 0.948, p= 2.859 × 10−6; NPC: 0.927, p= 2.214 × 10−10; and hESC: 0.932, p= 3.165 × 10−6). Chromosomes are sorted by increasing size. Boxplots show the distribution of counts from the 10,000 simulation iterations. The X chromosome contained more insertions than expected in the NPC and hESC datasets, while chromosome 5 was a significant outlier in HeLa-JVM cells (Bonferroni corrected p-value from linear model outlier test: NPC: 0.0026; hESC: 0.0063; HeLa-JVM: 0.0049).
(B) L1 insertion counts stratified by gene expression as determined by RNA-seq. Expressed genes had an FPKM value greater than 0.3. Colored squares represent the observed insertion counts in the indicated cell lines. Boxplots show the distribution of counts from the 10,000 simulation iterations. A significant depletion of insertions in expressed genes was observed for HeLa-JVM, PA-1, and NPC (χ2 p-values: 1.651 × 10−12, < 2.2 × 10−16, < 2.2 × 10−16 respectively).
(C) Expressed genes were divided into 30 ranked intervals of RNA-seq FPKM, each representing approximately the same fraction of the genome. For each interval, the count of observed L1 insertions for the indicated cell line is plotted as colored symbols, while boxplots show the distribution of values from the 10,000 simulation iterations. Significant deviations (p<0.05) between observed and simulated values are indicated with an asterisk.
Figure S4, related to Figure 4. L1 does not preferentially target transcribed regions or open chromatin.
(A) Transcribed regions of the genome were divided into 30 intervals of increasing transcription rate (x-axis), with each interval corresponding to approximately equal fractions of the genome. Colored squares represent the counts of L1 insertions in the indicated cell lines for each interval, while boxplots show the distribution of values from the 10,000 simulation iterations. Asterisks denote statistically significant differences between the observed and simulated counts (χ2 test p<0.05).
(B) Example HeLa-JVM Bru-seq data and corresponding segmental transcription strand biases. Green and red rectangles indicate genes with forward and reverse orientations, respectively, while Bru-seq signal (RPKM) is plotted as positive and negative values for forward and reverse transcription, respectively. Note that different segments can be transcribed on one (bias of 1 or −1) or both strands (bias between −1 and 1).
(C) Hypothetical CDF plots of transcription strand bias illustrating the patterns expected when L1 cleaves either the top or bottom reference genome strand for either a strong template or non-template strand cleavage preference. Note that the top strand of the reference genome will act as the template and non-template strand in different regions to an extent described by the local transcription bias.
(D) CDF plots of transcription strand bias for insertions at which L1 cleaved either the top or bottom reference genome strands for random genomic L1 insertions (black), 10,000 simulated insertion iterations (gray), and actual L1 insertions (blue). Panels with significant differences (KSbt p-value < 0.05) between observed and simulated data are indicated with an asterisk.
(E) Simplified overall representation of Figure 4E showing log2 fold expression changes for each set of insertions as compared to the most relevant cell type (leftmost column in Figure 4E heat plots; see legend) data of the ENCODE 15 Chromatin States.
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Antibodies | ||
| Mouse anti-BrdU | BD Pharmingen | 555627 |
| Bacterial and Virus Strains | ||
| MAX Efficiency DH5α-T1 Competent Cells | ThermoFisher Scientific | 12034013 |
| Chemicals, Peptides, and Recombinant Proteins | ||
| all-trans Retinoic acid | Sigma | R2625 |
| Anisomycin from Streptomyces griseolus, ≥ 98% (HPLC), solid | Sigma-Aldrich | A9789 |
| B-27 | ThermoFisher Scientific / Gibco | 17504044 |
| beta-mercaptoethanol | ThermoFisher Scientific / Gibco | 21985023 |
| Blasticidin-S HCl | ThermoFisher Scientific / Gibco | A1113903 |
| (−)-5-Bromouridine | Sigma–Aldrich | 850187 |
| Dorsomorphin | Merck | 171261 |
| Epidermal Growth Factor (EGF) | R&D Systems | PHG0311 |
| FuGENE 6 | Promega | E2692 |
| FuGENE HD | Promega | E2312 |
| Gelatin | Sigma | G9391 |
| Geneticin™ Selective Antibiotic (G418 Sulfate) | ThermoFisher Scientific / Gibco | 10131035 |
| GlutaMAX | ThermoFisher Scientific / Invitrogen | 35050061 |
| Human basic fibroblast growth factor (FGF-2) | Miltenyi Biotec | 130–093-838 |
| Human Foreskin Fibroblasts (HFF-1) | ATCC | SRC-1041 |
| L-glutamine | ThermoFisher Scientific / Gibco | 25030081 |
| Laminin | Sigma | L4544 |
| Matrigel-coated plates | BD Biosciences | 354234 |
| poly-L-ornithine | Sigma | P4957 |
| Puromycin Dihydrochloride | ThermoFisher Scientific / Gibco | A1113802 |
| SB43154 | Sigma | S4317 |
| Stemolecule SB431542 | StemGent | 04-0010-05 |
| StemPro Accutase Cell Dissociation Reagent | ThermoFisher Scientific | A1110501 |
| StemPro Neural Supplement | ThermoFisher Scientific | A1050801 |
| Trichostatin A (TSA) | Sigma-Aldrich | T1952–200UL |
| TrypLE Select Enzyme (1×) | ThermoFisher Scientific | 12563011 |
| UltraPure Dnase/Rnase Free Distilled Water | Invitrogen's Gibco by Life Technologies | 10977023 |
| Y-27632 | Sigma | Y0503 |
| Critical Commercial Assays | ||
| Blood and Cell Culture DNA Midi Kit | Qiagen | 13343 |
| Covaris microTUBE-50 | Covaris | PN 520166 |
| Covaris miniTUBE, blue | Covaris | PN 520064 |
| Dneasy Blood & Tissue Kit | Qiagen | 69504 |
| Dynabeads kilobaseBINDER Kit | Invitrogen | 60101 |
| Expand Long Range dNTPack PCR Kit | Sigma-Aldrich (ELONGN-RO Roche) | 04829042001 |
| Human Stem Cell Nucleofector Kit 2 | Lonza | VPH-5022 |
| Illumina Ribo-Zero rRNA Removal Kit | Illumina | MRZH116 |
| Illumina TruSeq Stranded mRNA Library Prep Kit | Illumina | RS-122-2101 |
| MiSeq Reagent Kit v3 (600-cycle) | Illumina | MS102-3003 |
| NEBNext dA-tailing Module Protocol | NEB | E6053 |
| NEBNext End Repair Module | NEB | E6050 |
| NEBNext Ultra End Repair/dA-Tailing Module | NEB | E7442 |
| Platinum Taq DNA Polymerase | Invitrogen | 10966018 |
| Qiagen Plasmid Midi Kit | Qiagen | 12125 |
| Qiagen's MinElute PCR column purification | Qiagen | 28004 |
| QIAquick Gel Extraction Kit | Qiagen | 28704 |
| QIAquick PCR Purification Kit | Qiagen | 28104 |
| Rat Neural Stem Cell Nucleofector Kit | Lonza | VPG-1005 |
| Rneasy Mini Kit | Qiagen | 74106 |
| Topo TA Cloning Kit for Sequencing, without Competent Cells | ThermoFisher Scientific / Invitrogen | 450030 |
| Ventor GeM Classic Mycoplasma Detection Kit for Conventional PCR | Sigma | MP 0025-1KT |
| Wizard Plus SV Minipreps DNA Purification Systems | Promega | A1330 |
| Deposited Data | ||
| PacBio CCS-fastq files (except HeLa) and PA-1 Bru-Seq data | This paper | SRA: SRP151191 |
| HeLa PacBio CCS-fastq, and HeLa Bru-Seq | This paper | dbGAP: phs001669 |
| ENSEMBL GRCh37/hg19 transcripts | Zerbino et al., 2018 | https://support.illumina.com/sequencing/sequencing_software/igenome.html |
| RNA-seq data (except HeLa) | This paper | SRA: PRJNA432733 |
| HeLa RNA-seq data | This paper | dbGaP: phs001671 |
| Roadmap Epigenomics Consortium Mnemonics chromatin state bed files | Roadmap Epigenomics et al., 2015 | http://egg2.wustl.edu/roadmap/data/byFileType/chromhmmSegmentations/ChmmModels/coreMarks/jointModel/final |
| OK seq data | Petryk et al., 2016) | SRA: SRP065949 |
| Lamina Associated Domains | Guelen et al., 2008; Meuleman et al., 2013 | Supplemental file #1 of Guelen et al. 2008; GEO GSE22428 from Meuleman et al. 2013 |
| Replication Timing Data | Weddington et al., 2008 | RT_HeLaS3_Cervical_Carcinoma_Int95117837_hg19, RT_H9_ESC_Ext29405702_hg19, RT_H9_Neural_Progenitor_Int89790558_hg19, and RT_IMR90_Fibroblast_Int94339003_hg19; https://www2.replicationdomain.com/ |
| Experimental Models: Cell Lines | ||
| Human: HeLa-JVM cells | Moran et al., 1996 | N/A |
| Human: PA-1 cells | Zeuthen et al., 1980 | ATCC CRL-1572 |
| Human: PD20F and PD20F+D2 cells | Pulsipher et al., 1998 | N/A |
| Human: WA09/H9-hESC cells (NIH approval number NIHhESC-10-0062) | Thomson et al., 1998 | hESC Cell Line: H9 |
| Human: WA09/H9-hESC-derived neural progenitor cells (NPCs) | This paper | hESC Cell Line: H9 |
| Oligonucleotides | ||
| Adapter Primer: 5’-ATCGATCGCTGCAGGGTATAGG-3’ | This paper; IDT | N/A |
| Biotinylated LEAP: 5’-/52-Bio//iSp18/GTTCGAAATCGATAAGCTTGGATCC-3’ | This paper; IDT | N/A |
| Bottom strand adapter with 5’ phosphorylation and 3’ amino modifier: 5’-/5Phos/GTTGTCCT/3AmMO/-3’ | This paper; IDT | N/A |
| SV40-polyA-start Site: 5’-GCAATAAACAAGTTAACAACAAAAAAAAA-3’ | This paper; IDT | N/A |
| Top strand adapter with T overhang: 5’-GGAAGCTTGACATTCTGGATCGATCGCTGCAGGGTATAGGCGAGGACAACT-3’ | This paper; IDT | N/A |
| Recombinant DNA | ||
| pCEP4 | Life Technologies | V04450 |
| pCEP4/GFP | Alisch et al., 2006 | N/A |
| pCEP4/JM111/LRE3-mEGFPI | Zhang et al., 2014 | N/A |
| pCEP4/LRE3-mEGFPI | Garcia-Perez et al., 2010 | N/A |
| pCEP99/JM111/UB-LRE3-mEGFPI | Coufal et al., 2009 | N/A |
| pCEP99/UB-LRE3-mEGFPI | Coufal et al., 2009 | N/A |
| phrGFP-C | Stratagene | 240035 |
| pJJ101/L1.3 | Kopera et al., 2011 | N/A |
| pJJ101/L1.3-D205A | Kopera et al., 2011 | N/A |
| pJJ101/L1.3-D702A | Kopera et al., 2011 | N/A |
| pJM101/L1.3 | Sassaman et al., 1997 | N/A |
| pJM105/L1.3 | Wei et al., 2001 | N/A |
| pKUB102/L1.3-sv+ | Wissing et al., 2012 | N/A |
| pKUB105/L1.3-sv+ | Wissing et al., 2012 | N/A |
| Software and Algorithms | ||
| Bowtie2 v2.1.0 | Langmead and Salzberg, 2012 | http://bowtie-bio.sourceforge.net/bowtie2/ |
| Homopolymer v1.0.0 | This paper; Wilson public software | https://git.umms.med.umich.edu/wilson_lab_public/utilities |
| smith_waterman v1.0.0 | This paper; Wilson public software | https://git.umms.med.umich.edu/wilson_lab_public/utilities |
| Bioconductor SeqLogo R package v1.36.0 | Bembom O, 2009 | https://bioconductor.org/packages/release/bioc/html/seqLogo.html |
| Entropy R package | Hausser and Strimmer, 2009 | https://cran.r-project.org/web/packages/entropy/index.html |
| Matching R Package | Sekhon, J., 2011 | https://cran.r-project.org/web/packages/Matching/index.html |
| PhenoGram | Wolfe et al., 2013 | http://visualization.ritchielab.psu.edu/phenograms/plot |
| Tophat v2.1.1 | Trapnell et al., 2009 | https://ccb.jhu.edu/software/tophat/index.shtml |
| Cufflinks Suite v2.2.1 | Roberts et al., 2011; Trapnell et al., 2010 | http://cole-trapnell-lab.github.io/cufflinks/ |
| Genome Structure Correction tool | Consortium et al., 2007 | https://github.com/ParkerLab/encodegsc |
| BWA | Li and Durbin, 2010 | http://bio-bwa.sourceforge.net/ |
| Segment v1.0.0 | Paulsen et al. 2014; Wilson public software | https://git.umms.med.umich.edu/wilson_lab_public/utilities |
| Smooth v1.0.0 | Paulsen et al. 2014; Wilson public software | https://git.umms.med.umich.edu/wilson_lab_public/utilities |
| BedTools v2.16.2 | Quinlan and Hall, 2010 | https://bedtools.readthedocs.io/en/latest/ |
HIGHLIGHTS.
Characterization of >88,000 engineered L1 insertions in five human cell lines
L1 integration events do not target genes, transcribed regions, or open chromatin
The endonuclease (EN) domain allowed L1 to become an interspersed retrotransposon
Wild-type and EN-deficient L1 integration prefer different replication strands
ACKNOWLEDGEMENTS
We thank members of the Moran laboratory and Brain Somatic Mosaicism Network, Shanda Birkeland, Arushi Varshney, Jeff Kidd, Patrick O’Brien, Saurabh Agarwal, and Stephen Parker for suggestions and comments; John Moldovan and Owen Funk for RNA isolations; Suyapa Amador-Cubero and Cesar Lopez-Ruiz (Genyo) for preparing PD20F samples; Purificacion Catalina (Biobanco SAS) for SKY-FISH and karyotype analyses; Santiago Morell and Martin Munoz-Lopez for sharing unpublished L1 retrotransposition data in FA mutant cells; Manhong Dai for administering the University of Michigan (UM) Molecular and Behavioral Neurosciences Institute computing cluster; Michelle Paulsen, Karan Bedi, and Brian Magnuson for performing Bru-seq experiments; and Robert Lyons and the UM DNA Sequencing Core for generating sequencing data. We are grateful to Henrietta Lacks, now deceased, and to her surviving family members for their contributions to biomedical research. The HeLa cell line that was established from her tumor cells without her knowledge or consent in 1951, have made significant contributions to scientific progress and advances in human health. Funding support: D.A.F, NIH training grant T32 HG000040; M.L., NIH grant UM1 HG009382; J.L.G.P., grants MINECO-FEDER (SAF2017-89745-R), the European Research Council (ERC-Consolidator ERC-STG-2012-233764), and the Howard Hughes Medical Institute (HHMI; IECS-55007420), T.E.W., NIH grants CA200731 and GM120767; and J.V.M., NIH grants GM060518 and U01MH106892 and HHMI.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
SUPPLEMENTAL INFORMATION
Supplemental information includes seven supplemental figures and seven supplemental datasets.
DECLARATION OF INTERESTS
JVM is an inventor on patent US6150160, is a paid consultant for Gilead Sciences and a privately held company founded by Flagship Pioneering, and is on the American Society of Human Genetics Board of Directors. The other authors do not have competing interests.
REFERENCES
- Alisch RS, Garcia-Perez JL, Muotri AR, Gage FH, and Moran JV (2006). Unconventional translation of mammalian LINE-1 retrotransposons. Genes Dev 20, 210–224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baillie JK, Barnett MW, Upton KR, Gerhardt DJ, Richmond TA, De Sapio F, Brennan PM, Rizzu P, Smith S, Fell M, et al. (2011). Somatic retrotransposition alters the genetic landscape of the human brain. Nature 479, 534–537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beck CR, Collier P, Macfarlane C, Malig M, Kidd JM, Eichler EE, Badge RM, and Moran JV (2010). LINE-1 retrotransposition activity in human genomes. Cell 141, 1159–1170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beck CR, Garcia-Perez JL, Badge RM, and Moran JV (2011). LINE-1 elements in structural variation and disease. Annu Rev Genomics Hum Genet 12, 187–215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bejerano G, Pheasant M, Makunin I, Stephen S, Kent WJ, Mattick JS, and Haussler D (2004). Ultraconserved elements in the human genome. Science 304, 1321–1325. [DOI] [PubMed] [Google Scholar]
- Bembom O (2009). seqLogo: Sequence logos for DNA sequence alignments. R package version 1360. [Google Scholar]
- Bregnard C, Guerra J, Dejardin S, Passalacqua F, Benkirane M, and Laguette N (2016). Upregulated LINE-1 Activity in the Fanconi Anemia Cancer Susceptibility Syndrome Leads to Spontaneous Pro-inflammatory Cytokine Production. EBioMedicine 8, 184–194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brouha B, Schustak J, Badge RM, Lutz-Prigge S, Farley AH, Moran JV, and Kazazian HH Jr. (2003). Hot L1s account for the bulk of retrotransposition in the human population. Proc Natl Acad Sci U S A 100, 5280–5285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ceccaldi R, Sarangi P, and D’Andrea AD (2016). The Fanconi anaemia pathway: new players and new functions. Nat Rev Mol Cell Biol 17, 337–349. [DOI] [PubMed] [Google Scholar]
- Chen CK, Blanco M, Jackson C, Aznauryan E, Ollikainen N, Surka C, Chow A, Cerase A, McDonel P, and Guttman M (2016). Xist recruits the X chromosome to the nuclear lamina to enable chromosome-wide silencing. Science 354, 468–472. [DOI] [PubMed] [Google Scholar]
- Churakov G, Grundmann N, Kuritzin A, Brosius J, Makalowski W, and Schmitz J (2010). A novel web-based TinT application and the chronology of the Primate Alu retroposon activity. BMC Evol Biol 10, 376. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Consortium EP, Birney E, Stamatoyannopoulos JA, Dutta A, Guigo R, Gingeras TR, Margulies EH, Weng Z, Snyder M, Dermitzakis ET, et al. (2007). Identification and analysis of functional elements in 1% of the human genome by the ENCODE pilot project. Nature 447, 799–816. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cost GJ, and Boeke JD (1998). Targeting of human retrotransposon integration is directed by the specificity of the L1 endonuclease for regions of unusual DNA structure. Biochemistry 37, 18081–18093. [DOI] [PubMed] [Google Scholar]
- Coufal NG, Garcia-Perez JL, Peng GE, Marchetto MC, Muotri AR, Mu Y, Carson CT, Macia A, Moran JV, and Gage FH (2011). Ataxia telangiectasia mutated (ATM) modulates long interspersed element-1 (L1) retrotransposition in human neural stem cells. Proc Natl Acad Sci U S A 108, 20382–20387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coufal NG, Garcia-Perez JL, Peng GE, Yeo GW, Mu Y, Lovci MT, Morell M, O’Shea KS, Moran JV, and Gage FH (2009). L1 retrotransposition in human neural progenitor cells. Nature 460, 1127–1131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doucet AJ, Wilusz JE, Miyoshi T, Liu Y, and Moran JV (2015). A 3’ Poly(A) Tract Is Required for LINE-1 Retrotransposition. Mol Cell 60, 728–741. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Faulkner GJ, and Garcia-Perez JL (2017). L1 Mosaicism in Mammals: Extent, Effects, and Evolution. Trends Genet 33, 802–816. [DOI] [PubMed] [Google Scholar]
- Feng Q, Moran JV, Kazazian HH Jr., and Boeke JD (1996). Human L1 retrotransposon encodes a conserved endonuclease required for retrotransposition. Cell 87, 905–916. [DOI] [PubMed] [Google Scholar]
- Garcia-Perez JL, Marchetto MC, Muotri AR, Coufal NG, Gage FH, O’Shea KS, and Moran JV (2007). LINE-1 retrotransposition in human embryonic stem cells. Hum Mol Genet 16, 1569–1577. [DOI] [PubMed] [Google Scholar]
- Garcia-Perez JL, Morell M, Scheys JO, Kulpa DA, Morell S, Carter CC, Hammer GD, Collins KL, O’Shea KS, Menendez P, et al. (2010). Epigenetic silencing of engineered L1 retrotransposition events in human embryonic carcinoma cells. Nature 466, 769–773. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Genomes Project C, Auton A, Brooks LD, Durbin RM, Garrison EP, Kang HM, Korbel JO, Marchini JL, McCarthy S, McVean GA, et al. (2015). A global reference for human genetic variation. Nature 526, 68–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilbert N, Lutz S, Morrish TA, and Moran JV (2005). Multiple fates of L1 retrotransposition intermediates in cultured human cells. Mol Cell Biol 25, 7780–7795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilbert N, Lutz-Prigge S, and Moran JV (2002). Genomic deletions created upon LINE-1 retrotransposition. Cell 110, 315–325. [DOI] [PubMed] [Google Scholar]
- Guelen L, Pagie L, Brasset E, Meuleman W, Faza MB, Talhout W, Eussen BH, de Klein A, Wessels L, de Laat W, et al. (2008). Domain organization of human chromosomes revealed by mapping of nuclear lamina interactions. Nature 453, 948–951. [DOI] [PubMed] [Google Scholar]
- Han JS, Szak ST, and Boeke JD (2004). Transcriptional disruption by the L1 retrotransposon and implications for mammalian transcriptomes. Nature 429, 268–274. [DOI] [PubMed] [Google Scholar]
- Hancks DC, and Kazazian HH Jr. (2016). Roles for retrotransposon insertions in human disease. Mob DNA 7, 9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hausser J, and Strimmer K (2009). Entropy inference and the James-Stein estimator, with application to non-linear gene association networks. J Mach Learn 10, 1469–1484. [Google Scholar]
- Heidmann T, Heidmann O, and Nicolas JF (1988). An indicator gene to demonstrate intracellular transposition of defective retroviruses. Proc Natl Acad Sci U S A 85, 2219–2223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huvet M, Nicolay S, Touchon M, Audit B, d’Aubenton-Carafa Y, Arneodo A, and Thermes C (2007). Human gene organization driven by the coordination of replication and transcription. Genome Res 17, 1278–1285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iskow RC, McCabe MT, Mills RE, Torene S, Pittard WS, Neuwald AF, Van Meir EG, Vertino PM, and Devine SE (2010). Natural mutagenesis of human genomes by endogenous retrotransposons. Cell 141, 1253–1261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jacob-Hirsch J, Eyal E, Knisbacher BA, Roth J, Cesarkas K, Dor C, Farage-Barhom S, Kunik V, Simon AJ, Gal M, et al. (2018). Whole-genome sequencing reveals principles of brain retrotransposition in neurodevelopmental disorders. Cell Res 28, 187–203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jurka J (1997). Sequence patterns indicate an enzymatic involvement in integration of mammalian retroposons. Proc Natl Acad Sci U S A 94, 1872–1877. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kent WJ (2002). BLAT--the BLAST-like alignment tool. Genome Res 12, 656–664. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kopera HC, Moldovan JB, Morrish TA, Garcia-Perez JL, and Moran JV (2011). Similarities between long interspersed element-1 (LINE-1) reverse transcriptase and telomerase. Proc Natl Acad Sci U S A 108, 20345–20350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kulpa DA, and Moran JV (2006). Cis-preferential LINE-1 reverse transcriptase activity in ribonucleoprotein particles. Nat Struct Mol Biol 13, 655–660. [DOI] [PubMed] [Google Scholar]
- LaFave MC, Varshney GK, Gildea DE, Wolfsberg TG, Baxevanis AD, and Burgess SM (2014). MLV integration site selection is driven by strong enhancers and active promoters. Nucleic Acids Res 42, 4257–4269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lander ES, Linton LM, Birren B, Nusbaum C, Zody MC, Baldwin J, Devon K, Dewar K, Doyle M, FitzHugh W, et al. (2001). Initial sequencing and analysis of the human genome. Nature 409, 860–921. [DOI] [PubMed] [Google Scholar]
- Langley AR, Graf S, Smith JC, and Krude T (2016). Genome-wide identification and characterisation of human DNA replication origins by initiation site sequencing (ini-seq). Nucleic Acids Res 44, 10230–10247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Langmead B, and Salzberg SL (2012). Fast gapped-read alignment with Bowtie 2. Nat Methods 9, 357–359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levin HL, and Moran JV (2011). Dynamic interactions between transposable elements and their hosts. Nat Rev Genet 12, 615–627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H, and Durbin R (2010). Fast and accurate long-read alignment with Burrows-Wheeler transform. Bioinformatics 26, 589–595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu N, Lee CH, Swigut T, Grow E, Gu B, Bassik MC, and Wysocka J (2018). Selective silencing of euchromatic L1s revealed by genome-wide screens for L1 regulators. Nature 553, 228–232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luan DD, Korman MH, Jakubczak JL, and Eickbush TH (1993). Reverse transcription of R2Bm RNA is primed by a nick at the chromosomal target site: a mechanism for non-LTR retrotransposition. Cell 72, 595–605. [DOI] [PubMed] [Google Scholar]
- Macia A, Widmann TJ, Heras SR, Ayllon V, Sanchez L, Benkaddour-Boumzaouad M, Munoz-Lopez M, Rubio A, Amador-Cubero S, Blanco-Jimenez E, et al. (2017). Engineered LINE-1 retrotransposition in nondividing human neurons. Genome Res 27, 335–348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malik HS, Burke WD, and Eickbush TH (1999). The age and evolution of non-LTR retrotransposable elements. Mol Biol Evol 16, 793–805. [DOI] [PubMed] [Google Scholar]
- McCole RB, Fonseka CY, Koren A, and Wu CT (2014). Abnormal dosage of ultraconserved elements is highly disfavored in healthy cells but not cancer cells. PLoS Genet 10, e1004646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meuleman W, Peric-Hupkes D, Kind J, Beaudry JB, Pagie L, Kellis M, Reinders M, Wessels L, and van Steensel B (2013). Constitutive nuclear lamina-genome interactions are highly conserved and associated with A/T-rich sequence. Genome Res 23, 270–280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mita P, Wudzinska A, Sun X, Andrade J, Nayak S, Kahler DJ, Badri S, LaCava J, Ueberheide B, Yun CY, et al. (2018). LINE-1 protein localization and functional dynamics during the cell cycle. Elife 7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Monot C, Kuciak M, Viollet S, Mir AA, Gabus C, Darlix JL, and Cristofari G (2013). The specificity and flexibility of l1 reverse transcription priming at imperfect T-tracts. PLoS Genet 9, e1003499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moran JV, Holmes SE, Naas TP, DeBerardinis RJ, Boeke JD, and Kazazian HH Jr. (1996). High frequency retrotransposition in cultured mammalian cells. Cell 87, 917–927. [DOI] [PubMed] [Google Scholar]
- Morrish TA, Garcia-Perez JL, Stamato TD, Taccioli GE, Sekiguchi J, and Moran JV (2007). Endonuclease-independent LINE-1 retrotransposition at mammalian telomeres. Nature 446, 208–212. [DOI] [PubMed] [Google Scholar]
- Morrish TA, Gilbert N, Myers JS, Vincent BJ, Stamato TD, Taccioli GE, Batzer MA, and Moran JV (2002). DNA repair mediated by endonuclease-independent LINE-1 retrotransposition. Nat Genet 31, 159–165. [DOI] [PubMed] [Google Scholar]
- Paulsen MT, Veloso A, Prasad J, Bedi K, Ljungman EA, Magnuson B, Wilson TE, and Ljungman M (2014). Use of Bru-Seq and BruChase-Seq for genome-wide assessment of the synthesis and stability of RNA. Methods 67, 45–54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petryk N, Kahli M, d’Aubenton-Carafa Y, Jaszczyszyn Y, Shen Y, Silvain M, Thermes C, Chen CL, and Hyrien O (2016). Replication landscape of the human genome. Nat Commun 7, 10208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pulsipher M, Kupfer GM, Naf D, Suliman A, Lee JS, Jakobs P, Grompe M, Joenje H, Sieff C, Guinan E, et al. (1998). Subtyping analysis of Fanconi anemia by immunoblotting and retroviral gene transfer. Mol Med 4, 468–479. [PMC free article] [PubMed] [Google Scholar]
- Quinlan AR, and Hall IM (2010). BEDTools: a flexible suite of utilities for comparing genomic features. Bioinformatics 26, 841–842. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Repanas K, Zingler N, Layer LE, Schumann GG, Perrakis A, and Weichenrieder O (2007). Determinants for DNA target structure selectivity of the human LINE-1 retrotransposon endonuclease. Nucleic Acids Res 35, 4914–4926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Richardson SR, Doucet AJ, Kopera HC, Moldovan JB, Garcia-Perez JL, and Moran JV (2015). The Influence of LINE-1 and SINE Retrotransposons on Mammalian Genomes. Microbiol Spectr 3, MDNA3–0061-2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Richardson SR, and Faulkner GJ (2018). Heritable L1 Retrotransposition Events During Development: Understanding Their Origins: Examination of heritable, endogenous L1 retrotransposition in mice opens up exciting new questions and research directions. Bioessays 40, e1700189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roadmap Epigenomics C, Kundaje A, Meuleman W, Ernst J, Bilenky M, Yen A, Heravi-Moussavi A, Kheradpour P, Zhang Z, Wang J, et al. (2015). Integrative analysis of 111 reference human epigenomes. Nature 518, 317–330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roberts A, Trapnell C, Donaghey J, Rinn JL, and Pachter L (2011). Improving RNA-Seq expression estimates by correcting for fragment bias. Genome Biol 12, R22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sandmeyer S, Patterson K, and Bilanchone V (2015). Ty3, a Position-specific Retrotransposon in Budding Yeast. Microbiol Spectr 3, MDNA3–0057-2014. [DOI] [PubMed] [Google Scholar]
- Sassaman DM, Dombroski BA, Moran JV, Kimberland ML, Naas TP, DeBerardinis RJ, Gabriel A, Swergold GD, and Kazazian HH Jr. (1997). Many human L1 elements are capable of retrotransposition. Nat Genet 16, 37–43. [DOI] [PubMed] [Google Scholar]
- Scott EC, and Devine SE (2017). The Role of Somatic L1 Retrotransposition in Human Cancers. Viruses 9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sekhon JS (2011). Multivariate and Propensity Score Matching Software with Automated Balance Optimization: The Matching package for R. Jounal of Statistical Software 42, 1–52. [Google Scholar]
- Simons C, Makunin IV, Pheasant M, and Mattick JS (2007). Maintenance of transposon-free regions throughout vertebrate evolution. BMC Genomics 8, 470. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simons C, Pheasant M, Makunin IV, and Mattick JS (2006). Transposon-free regions in mammalian genomes. Genome Res 16, 164–172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smit AF (1999). Interspersed repeats and other mementos of transposable elements in mammalian genomes. Curr Opin Genet Dev 9, 657–663. [DOI] [PubMed] [Google Scholar]
- Smith TF, and Waterman MS (1981). Identification of common molecular subsequences. J Mol Biol 147, 195–197. [DOI] [PubMed] [Google Scholar]
- Spradling AC, Bellen HJ, and Hoskins RA (2011). Drosophila P elements preferentially transpose to replication origins. Proc Natl Acad Sci U S A 108, 15948–15953. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sultana T, Zamborlini A, Cristofari G, and Lesage P (2017). Integration site selection by retroviruses and transposable elements in eukaryotes. Nat Rev Genet 18, 292–308. [DOI] [PubMed] [Google Scholar]
- Symer DE, Connelly C, Szak ST, Caputo EM, Cost GJ, Parmigiani G, and Boeke JD (2002). Human l1 retrotransposition is associated with genetic instability in vivo. Cell 110, 327–338. [DOI] [PubMed] [Google Scholar]
- Thomson JA, Itskovitz-Eldor J, Shapiro SS, Waknitz MA, Swiergiel JJ, Marshall VS, and Jones JM (1998). Embryonic stem cell lines derived from human blastocysts. Science 282, 1145–1147. [DOI] [PubMed] [Google Scholar]
- Touchon M, Nicolay S, Audit B, Brodie of Brodie EB, d’Aubenton-Carafa Y, Arneodo A, and Thermes C (2005). Replication-associated strand asymmetries in mammalian genomes: toward detection of replication origins. Proc Natl Acad Sci U S A 102, 9836–9841. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trapnell C, Pachter L, and Salzberg SL (2009). TopHat: discovering splice junctions with RNA-Seq. Bioinformatics 25, 1105–1111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trapnell C, Williams BA, Pertea G, Mortazavi A, Kwan G, van Baren MJ, Salzberg SL, Wold BJ, and Pachter L (2010). Transcript assembly and quantification by RNA-Seq reveals unannotated transcripts and isoform switching during cell differentiation. Nat Biotechnol 28, 511–515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Upton KR, Gerhardt DJ, Jesuadian JS, Richardson SR, Sanchez-Luque FJ, Bodea GO, Ewing AD, Salvador-Palomeque C, van der Knaap MS, Brennan PM, et al. (2015). Ubiquitous L1 mosaicism in hippocampal neurons. Cell 161, 228–239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Steensel B, and Belmont AS (2017). Lamina-Associated Domains: Links with Chromosome Architecture, Heterochromatin, and Gene Repression. Cell 169, 780–791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watanabe K, Ueno M, Kamiya D, Nishiyama A, Matsumura M, Wataya T, Takahashi JB, Nishikawa S, Nishikawa S, Muguruma K, et al. (2007). A ROCK inhibitor permits survival of dissociated human embryonic stem cells. Nat Biotechnol 25, 681–686. [DOI] [PubMed] [Google Scholar]
- Weddington N, Stuy A, Hiratani I, Ryba T, Yokochi T, and Gilbert DM (2008). ReplicationDomain: a visualization tool and comparative database for genome-wide replication timing data. BMC Bioinformatics 9, 530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wei W, Gilbert N, Ooi SL, Lawler JF, Ostertag EM, Kazazian HH, Boeke JD, and Moran JV (2001). Human L1 retrotransposition: cis preference versus trans complementation. Mol Cell Biol 21, 1429–1439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wei W, Morrish TA, Alisch RS, and Moran JV (2000). A transient assay reveals that cultured human cells can accommodate multiple LINE-1 retrotransposition events. Anal Biochem 284, 435–438. [DOI] [PubMed] [Google Scholar]
- Weichenrieder O, Repanas K, and Perrakis A (2004). Crystal structure of the targeting endonuclease of the human LINE-1 retrotransposon. Structure 12, 975–986. [DOI] [PubMed] [Google Scholar]
- Wissing S, Munoz-Lopez M, Macia A, Yang Z, Montano M, Collins W, Garcia-Perez JL, Moran JV, and Greene WC (2012). Reprogramming somatic cells into iPS cells activates LINE-1 retroelement mobility. Hum Mol Genet 21, 208–218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolfe D, Dudek S, Ritchie MD, and Pendergrass SA (2013). Visualizing genomic information across chromosomes with PhenoGram. BioData Min 6, 18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zerbino DR, Achuthan P, Akanni W, Amode MR, Barrell D, Bhai J, Billis K, Cummins C, Gall A, Giron CG, et al. (2018). Ensembl 2018. Nucleic Acids Res 46, D754–D761. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeuthen J, Norgaard JO, Avner P, Fellous M, Wartiovaara J, Vaheri A, Rosen A, and Giovanella BC (1980). Characterization of a human ovarian teratocarcinoma-derived cell line. Int J Cancer 25, 19–32. [DOI] [PubMed] [Google Scholar]
- Zhang A, Dong B, Doucet AJ, Moldovan JB, Moran JV, and Silverman RH (2014). RNase L restricts the mobility of engineered retrotransposons in cultured human cells. Nucleic Acids Res 42, 3803–3820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhong J, and Lambowitz AM (2003). Group II intron mobility using nascent strands at DNA replication forks to prime reverse transcription. eMbO J 22, 4555–4565. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Figure S1, related to Figure 1. Recovering thousands of de novo engineered L1 retrotransposition events.
(A) Frequency distribution of the CCS read lengths that support insertion calls from HeLa-JVM, PA-1, NPC, and hESC samples.
(B) Alignment pipeline steps. Only CCS reads bearing both the SV40pA (gray box) and adapter (red rectangle) oligonucleotide primer sequences, as well as a poly(A) tract of at least 15bp (black box), were aligned to the genome after trimming the primer sequences from reads. Best mapped locations were chosen as an alignment covering at least 96.5% of the read with an alignment score difference (ASDIF) of 20 compared to the next best alignment. Insertions in genomic A tracts lead to an uncertainty in calling that was handled by assigning ambiguous A bases to the genome, not to the L1 poly(A) tract (referred to as “A-sliding”). Thus, the 5’-most A base was assigned as the insertion position (blue A with asterisk). L1 EN cleaves the opposite strand (black triangle).
(C) Breakdown of the observed outcomes of the initial filtering of CCS reads for each cell line. The blue pie slices indicate the proportion of CCS reads that passed this filtering.
(D) Breakdown of the alignment outcomes of CCS reads that passed initial filtering. CCS reads were aligned to both GRCh37/hg19 and GRCh38/hg38. The large majority of usable CCS reads could be productively mapped to yield insertion calls (dark and light blue pie slices). Only small differences were noted between the two reference genomes.
(E) Frequency distribution of the number of independent CCS reads supporting engineered L1 insertion events in the HeLa-JVM, NPC, and hESC samples.
Figure S5, related to Figure 5. L1 integrates more often into leading strand templates.
(A) Overlaid violin plots of RFD frequency distributions. Each panel compares one L1 insertion set to HeLa OK-seq RFD values. The top row in each panel compares 100 simulation iterations (gray) and observed insertions (blue) aggregated on both strands. The second and third rows show the simulated and observed insertions stratified by integration strand. “Modeled” shows the expected distribution for the RSP value calculated for the observed insertions, while “Maximum” shows the distribution for a pure leading strand integration preference, i.e. a RSP of 1. For all but the top rows, colors identify L1 integration into the top (orange) and bottom (green) reference genome strands, which means that L1 cleaved the bottom and top strands, respectively. Vertical lines denote the distribution medians.
(B) CDF plots of the slope of RFD values surrounding L1 insertions. Positive RFD slopes occur in regions where replication origins are firing while negative slopes correlate with replication termination (Petryk et al. 2016). While all L1 insertion datasets differed significantly from the simulations (KSbt P-values: HeLa-JVM: < 0.001; PA-1: < 1×10−6; NPC: < 0.01; hESC: < 0.05), the deviation from the null hypothesis is small, inconsistent between samples, and not suggestive of a strong L1 preference for integration at origins or termination zones. For example, in PA-1 cells, the excess of insertions relative to the simulated data occurs at neutral slopes, which are regions of stable replication fork movement.
Figure S6, related to Figure 6. EN-deficient L1 integrates into lagging strand templates in FANCD2-deficient cells.
(A) Frequency distribution of the poly(A) tract lengths of engineered L1 insertions in PD20F cells.
(B) L1 insertion counts by chromosome in PD20F cells (colored circles), sorted by increasing chromosome size. Boxplots show the distribution of counts from 10,000 iterations of the weighted random simulation.
(C) Overlaid violin plots of RFD frequency distributions. Each panel compares one L1 insertion set to HeLa OK-seq RFD values. Labels and plotting are the same as in Figure S5A. Numbers to the left of FANCD2 deficient conditions are the corresponding modeled RSP values.
(D) CDF plots of the slope of RFD values surrounding L1 insertions from the PD20F cell libraries, plotted similarly to Figure S5B. The L1.3 insertion dataset in PD20F cells differed significantly from the weighted random model (KSbt p-value < 0.05), but similar to Figure S5B the magnitude of the effect was very small.
Figure S7, related to Figure 7. L1 dependence on nuclear architecture varies between cell lines.
(A) Fraction of insertions into LADs, similar to Figure 7A. Black boxplots identify L1 data sets considered to be well-matched to the LAD reference data.
(B) Fraction of insertions into early replicating portions of the genome, similar to Figure 7B. Black boxplots highlight comparisons considered to be well-matched with respect to cell type.
(C) Boxplots show 100 simulated insertions weighted either by the 7mer insertion site alone (‘random’) or additionally such that the distribution of the x-axis parameter for each iteration matched the observed insertions for the indicated cell lines (‘sim=obs’). Colored symbols show the observed value. Matching the simulation iterations to the observed distribution of the x-axis parameter decreased the magnitude of the effect for the y-axis parameter in all cases, but the degree of the decrease was larger when matching for replication timing, suggesting that the fraction of insertions in LADs might be secondary to replication timing. All plots used hESC replication timing data and constitutive LADs.
Supplemental Dataset 1, Related to Figure 1. Engineered L1 Insertion Coordinates, Characteristics, and Sequences. Table of all insertion coordinates providing chromosome, position of insertion both 0-based and 1-based (hg19 coordinates), insertion id which corresponds to the supporting PacBio CCS read, strand of the genome the L1 integrated into, the L1 EN cleavage sequence for that insertion, the called poly(A) tract for all supporting CCS reads of that insertion, the primer clipped CCS read/s that support the insertion site, and the biological sample the insertion was obtained from. Sheet labels refer to the corresponding cell type insertions were generated and identified from.
Supplemental Dataset 2, Related to Figure 1. Retrotransposition Assay Conditions. Independent biological sample details for each cell type are shown. For each independent cell culture condition experiment the provided biological sample name, selection condition, number of insertions obtained from experiment and the percentage of the total insertions for that cell type are given. The summary of identified insertions that came from selection experiments is also shown in bottom tables.
Supplemental Dataset 3, Related to Figure 1. Blacklisted Regions of Human Genome. Regions of the genome that included alpha satellite centromeric, telomeric, and tandem repeats in the human genome reference (hg19) that were excluded from downstream data analysis.
Supplemental Dataset 4, Related to Figure 2. Top Weighted 7mer Sequences in Models. A listing of the top weighted 7mer sequences in our uncorrected and corrected weighted models.
Supplemental Dataset 5. Related to Figure 3. L1 Insertions in Genomic Regions of Interest. For each cell type, the number of insertions found in genomic LINE and SINE sequences, fragile and non-fragile sites, ultra-conserved elements, ultra-conserved noncoding elements and transposon free regions in the genome are provided as well as the minimum, median, and max value observed from the 10,000 simulations found in each of these regions of interest.
Supplemental Dataset 6, Related to Figure 3. Duplicate L1 Insertions. Identified duplicate insertion sites from independent biological replicates of a given cell type and duplicate insertion sites from independent cell types. Sheet labeled “Summary” provides number of insertions. Sheet labeled “Sample Insertion Key” provides codes used to identify CCS reads from each biological sample. Sheet labeled “Insertions” provides all the insertion sites giving the chromosome, position (0-based), position (1-based), insertion ID corresponding to the supportive CCS read, biological sample insertion was identified in, strand, and then the same information for the other biological sample in which the same insertion site was identified. Sheetl describes each column.
Supplemental Dataset 7, Related to Figure 3. Genic L1 Insertion Characteristics. A listing of all genic (5’UTR, intronic, exonic, or 3’UTR) insertions based on the UCSC genome browser’s defined gene coordinates (hg19). Also included are expression values on both strands of the genome from RNA-seq (FPKM) or Bru-seq (RPKM) experiments if available for that gene or transcript respectively in the genome. Each sheet label represents the cell type where the insertions were identified. Sheet 1 provides the description of each column.
Figure S2, related to Figure 2. Local L1 integration site preferences.
(A) Frequency distribution of the poly(A) tract lengths of engineered L1 insertions from HeLa-JVM, NPC, and hESC samples.
(B) Base observation frequencies over positions from 100bp upstream to 100bp downstream of PA-1 insertions. The 7mer insertion site lies between the vertical lines at positions 0 and 7.
(C) Extended logo plot showing information content for sequences from 25bp upstream to 25bp downstream of PA-1 insertions 7mer site.
(D) Frequency distribution of the Hamming distances (i.e. number of mismatches) between all possible 7mer sites and the L1 integration site consensus sequence, 5’-TTTTT/AA-3’.
(E) Mutual information plot displaying the degree of co-dependence between paired nucleotide positions in the 7mer L1 integration site (blue boxes reflect co-dependent position pairs).
(F) Correlation plot of modeled and observed log10 weights for the 12,288 possible 7mer L1 integration sites. Point colors reflect the number of insertions that utilized each site (see legend). A gray unity line identifies sites where the two weights were equal. To help visualize individual points, we applied the R jitter function to y-axis values. Sites with an observed weight of 0 (infinite log10 weight) are plotted separately.
(G) Plot showing the GC content of different sized windows of genomic sequence surrounding simulated L1 insertion positions. A blue dashed line represents the genome average of 41%.
Figure S3, related to Figure 3. L1 integrates throughout the human genome.
(A) Insertion counts for the indicated cell lines are plotted as colored diamonds or squares (Spearman’s rho: HeLa-JVM: 0.948, p= 2.859 × 10−6; NPC: 0.927, p= 2.214 × 10−10; and hESC: 0.932, p= 3.165 × 10−6). Chromosomes are sorted by increasing size. Boxplots show the distribution of counts from the 10,000 simulation iterations. The X chromosome contained more insertions than expected in the NPC and hESC datasets, while chromosome 5 was a significant outlier in HeLa-JVM cells (Bonferroni corrected p-value from linear model outlier test: NPC: 0.0026; hESC: 0.0063; HeLa-JVM: 0.0049).
(B) L1 insertion counts stratified by gene expression as determined by RNA-seq. Expressed genes had an FPKM value greater than 0.3. Colored squares represent the observed insertion counts in the indicated cell lines. Boxplots show the distribution of counts from the 10,000 simulation iterations. A significant depletion of insertions in expressed genes was observed for HeLa-JVM, PA-1, and NPC (χ2 p-values: 1.651 × 10−12, < 2.2 × 10−16, < 2.2 × 10−16 respectively).
(C) Expressed genes were divided into 30 ranked intervals of RNA-seq FPKM, each representing approximately the same fraction of the genome. For each interval, the count of observed L1 insertions for the indicated cell line is plotted as colored symbols, while boxplots show the distribution of values from the 10,000 simulation iterations. Significant deviations (p<0.05) between observed and simulated values are indicated with an asterisk.
Figure S4, related to Figure 4. L1 does not preferentially target transcribed regions or open chromatin.
(A) Transcribed regions of the genome were divided into 30 intervals of increasing transcription rate (x-axis), with each interval corresponding to approximately equal fractions of the genome. Colored squares represent the counts of L1 insertions in the indicated cell lines for each interval, while boxplots show the distribution of values from the 10,000 simulation iterations. Asterisks denote statistically significant differences between the observed and simulated counts (χ2 test p<0.05).
(B) Example HeLa-JVM Bru-seq data and corresponding segmental transcription strand biases. Green and red rectangles indicate genes with forward and reverse orientations, respectively, while Bru-seq signal (RPKM) is plotted as positive and negative values for forward and reverse transcription, respectively. Note that different segments can be transcribed on one (bias of 1 or −1) or both strands (bias between −1 and 1).
(C) Hypothetical CDF plots of transcription strand bias illustrating the patterns expected when L1 cleaves either the top or bottom reference genome strand for either a strong template or non-template strand cleavage preference. Note that the top strand of the reference genome will act as the template and non-template strand in different regions to an extent described by the local transcription bias.
(D) CDF plots of transcription strand bias for insertions at which L1 cleaved either the top or bottom reference genome strands for random genomic L1 insertions (black), 10,000 simulated insertion iterations (gray), and actual L1 insertions (blue). Panels with significant differences (KSbt p-value < 0.05) between observed and simulated data are indicated with an asterisk.
(E) Simplified overall representation of Figure 4E showing log2 fold expression changes for each set of insertions as compared to the most relevant cell type (leftmost column in Figure 4E heat plots; see legend) data of the ENCODE 15 Chromatin States.
Data Availability Statement
Our general utilities used in the pipeline (homopolymer, smith_waterman, segment and smooth) are available at https://git.umms.med.umich.edu/wilson_lab_public/utilities.
ALL RNA-seq data (except HeLa): SRA: PRJNA432733
HeLa RNA-seq data: dbGaP: phs001671
PacBio CCS-fastq files (except HeLa) and PA-1 Bru-Seq: SRA: SRP151191
HeLa PacBio CCS-fastq, and HeLa Bru-Seq: dbGaP: phs001669