Mapping hydroxyl variability throughout the global remote troposphere via synthesis of airborne and satellite formaldehyde observations

Significance

The hydroxyl radical (OH) is the central oxidant of the lower atmosphere. OH is highly variable in space and time, but current observation-based methods cannot resolve local and regional OH gradients. We combine the robust chemical relationship between OH and formaldehyde (HCHO) (a ubiquitous hydrocarbon oxidation product) with satellite-based HCHO observations to infer total-column OH throughout the remote troposphere. This dataset concurs with previous global average OH estimates while revealing unique features that highlight a dichotomy of regional/seasonal variability and global/annual balance. Such fine-scale constraints can help to identify and quantify natural and anthropogenic perturbations and guide efforts to improve simulations of atmospheric composition.

Abstract

The hydroxyl radical (OH) fuels tropospheric ozone production and governs the lifetime of methane and many other gases. Existing methods to quantify global OH are limited to annual and global-to-hemispheric averages. Finer resolution is essential for isolating model deficiencies and building process-level understanding. In situ observations from the Atmospheric Tomography (ATom) mission demonstrate that remote tropospheric OH is tightly coupled to the production and loss of formaldehyde (HCHO), a major hydrocarbon oxidation product. Synthesis of this relationship with satellite-based HCHO retrievals and model-derived HCHO loss frequencies yields a map of total-column OH abundance throughout the remote troposphere (up to 70% of tropospheric mass) over the first two ATom missions (August 2016 and February 2017). This dataset offers unique insights on near-global oxidizing capacity. OH exhibits significant seasonality within individual hemispheres, but the domain mean concentration is nearly identical for both seasons (1.03 ± 0.25 × 10⁶ cm⁻³), and the biseasonal average North/South Hemisphere ratio is 0.89 ± 0.06, consistent with a balance of OH sources and sinks across the remote troposphere. Regional phenomena are also highlighted, such as a 10-fold OH depression in the Tropical West Pacific and enhancements in the East Pacific and South Atlantic. This method is complementary to budget-based global OH constraints and can help elucidate the spatial and temporal variability of OH production and methane loss.

The hydroxyl radical, OH, defines the oxidizing capacity of the troposphere and controls the lifetime of methane (CH₄), carbon monoxide (CO), some ozone-depleting substances, nitrogen oxides (NO_x), and numerous other gases relevant to climate and air quality. OH is short-lived (typical lifetime, ∼1 s) and sensitive to perturbations in both its sources (mainly O₃ photolysis and secondary radical propagation) and sinks (CO, CH₄, other hydrocarbons, etc.). It is thus challenging—but vital—to accurately predict the spatial and temporal variability of tropospheric OH.

State-of-the-art global models demonstrate differences of as much as 25% in calculated global mean OH concentrations, with multimodel means ∼10% higher than observation-based estimates (1). Models also struggle to capture interannual variability (2, 3) and hemispheric gradients (4) in OH. Discrepancies likely stem from a combination of factors, including meteorology, emissions, and chemical mechanisms. Such errors propagate into inversion-based emissions estimates; for example, several recent studies have highlighted the ambiguous role of OH as a driver of CH₄ variability over the past three decades (5–7). Accurate representation of OH is also important for quantifying emissions of CO (8), NO_x (9), and isoprene (10).

Globally integrated OH is typically inferred through budget closure or formal inversion of measurements of a long-lived gas for which emissions are well known and for which the primary sink is reaction with OH. In particular, methyl chloroform (MCF) has informed efforts to constrain OH for over four decades (11, 12). Early MCF investigations implied significant trends and interannual variability in global annual OH (13–17), although uncertainties in anthropogenic emissions, ocean exchange, and long-range transport have undermined these results (18–20). Dramatic reductions in MCF emissions since the 1987 Montreal Protocol and its amendments have narrowed uncertainties in the MCF budget, and recent work suggests that global OH interannual variability is 2.3 ± 1.5% (3).

Although powerful, MCF-derived OH constraints are also inherently limited in several respects. Declining MCF concentrations presage reduced precision for inferred OH in the coming decade, leading the community to seek alternatives (21–24). All budget/inversion methods convolute source and sink anomalies, and uncertainties in emissions are not always well known (22). Furthermore, such top-down approaches provide global or hemispheric annual means, and it is not possible to probe drivers of variability or diagnose model errors at smaller scales. Direct measurements of OH enable process-level insights (25); however, such measurements are challenging, sporadic, and often focused on near-surface continental regions where nonmethane hydrocarbons are the main sinks of OH.

There is a clear need for new OH constraints, especially those that can bridge globally integrated and process-level perspectives. Key considerations for any chemical proxy include accuracy, resolution, and coverage. High accuracy requires a quantifiable relationship with OH. Spatiotemporal resolution is related to chemical lifetime, with shorter-lived gases being more representative of local oxidation. Broad coverage is possible if the proxy is ubiquitous and observable via satellite-based remote sensing.

In this light, formaldehyde (HCHO) is a promising candidate for constraining OH. Nearly all hydrocarbons generate HCHO during their photochemical lifecycle, and multiple satellite-based instruments support total-column HCHO retrievals with daily near-global coverage (26). The chemical link between HCHO and OH can be complex; however, CH₄ is the dominant precursor in remote regions and represents ∼80% of the global HCHO source (8). CH₄ is generally well-mixed (lifetime ∼9 y), while HCHO is concentrated near its sources (lifetime ∼hours). Together, these facts imply a strong and localized relationship between HCHO and OH. Previous efforts have exploited this connection to probe the evolution of remote OH on millennial timescales (27) and to investigate HCHO variability over terrestrial regions (10).

Here, we combine in situ observations from NASA’s Atmospheric Tomography (ATom) mission with HCHO column retrievals from the Ozone Monitoring Instrument (OMI) to quantify OH throughout the remote troposphere. ATom provides unprecedented constraints on global remote atmospheric composition, and we use this dataset both to quantify the relationship between OH and HCHO production/loss and to validate OMI retrievals. Amalgamation of ATom-derived scaling factors with OMI HCHO columns and model-derived HCHO loss frequencies yields a global distribution of remote tropospheric OH. Using this dataset, we explore the seasonality, interhemispheric gradients, and regional variability of remote oxidizing capacity.

Theoretical Link Between OH and HCHO

We first establish a theoretical foundation for the relationship between HCHO and OH. HCHO production is rate-limited by initial oxidation of any gas X and can be represented as a first-order reaction:

$$OH+X\to {\alpha }_{x}HCHO.$$ [R1]

α_X represents an effective yield (α_CO = 0, α_CH4 ≤ 1, etc.). Following Valin et al. (10), this formulation intrinsically includes all OH loss reactions even though some pathways do not generate HCHO. Summing over all such reactions gives the instantaneous HCHO production rate (P_HCHO, molecules per cubic centimeter per second):

$$P_{HCHO}={\displaystyle \sum {\alpha }_X{k}_{X+OH}\left[OH\right]\left[X\right]}+P_0=\alpha k_{OH}^{\prime }\left[OH\right]+P_0.$$ [1]

Here, α is the effective yield weighted over all OH reactions, k_X+OH is a reaction rate coefficient, and $k_{OH}^{\prime }={\displaystyle \sum k_{X+OH}\left[X\right]}$ is the pseudo–first-order OH reactivity. P₀ represents HCHO production from minor non-OH sources, such as hydrocarbon oxidation by other oxidants (O₃, halogens) or heterogeneous chemistry. Photolysis (j_HCHO) and OH (with rate coefficient k_HCHO+OH) destroy HCHO with a typical diurnal lifetime of hours. For ATom 1, average fractional HCHO losses via photolysis and OH reaction are 77% and 23%, respectively (SI Appendix, Fig. S1B). Assuming steady-state conditions for HCHO yields:

$$\left[HCHO\right]=\frac{\alpha k_{OH}^{\prime }\left[OH\right]+P_0}{j_{HCHO}+k_{HCHO+OH}\left[OH\right]}.$$ [2]

The steady-state assumption for HCHO is generally justified during the daytime in remote regions, as HCHO sources and sinks are both sunlight-driven, the HCHO lifetime is relatively short (hours), and nonphotochemical sources usually exert little influence on the local budget (28, 29). Strong convection can be an exception to the latter (30).

Eq. 2 encapsulates the key drivers of HCHO abundance. HCHO production depends on the abundance and reactivity of hydrocarbons (part of k′_OH), the structure and fate of reactive intermediates (α), and the abundance of OH. Within the remote ATom study region, the hydrocarbon speciation is relatively uniform, consisting mostly of long-lived gases like CH₄ and CO with occasional influence from biomass burning or long-range pollution transport. Thus, we assert (and will later show) that, in remote regions, variability in HCHO production/loss chiefly reflects variability in OH. Caveats to this simplified theory, including the nonlinear OH dependence and the influence of OH sink speciation, are discussed further below.

Eqs. 1 and 2 can also be written in terms of the OH production rate by substituting the steady state relationship for OH $\left(P_{OH}=k_{OH}^{\prime }\left[OH\right]\right)$. The ATom payload includes both direct OH measurements and all observations needed to constrain P_OH (Methods). Thus, we can assess this theory via two independent metrics and segregate the influence of α and k′_OH.

ATom Constraints

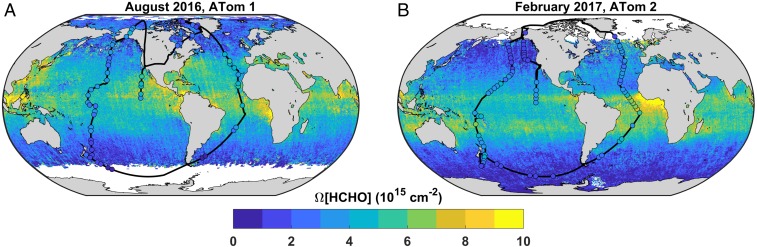
Our goal is to apply this theory to infer OH concentrations and production rates throughout the remote troposphere. To this end, we use ATom observations to (i) quantify the relationships between HCHO, OH, and P_OH and (ii) validate satellite HCHO retrievals. Employing the NASA DC-8 aircraft instrumented with an extensive suite of in situ measurements, ATom has executed four around-the-world circuits with frequent vertical profiling from near-surface (<200 m) to upper troposphere (10 to 12 km). We utilize observations from the first two missions (August 2016 and February 2017). Fig. 1 shows the flight tracks for these missions, and SI Appendix, Table S1 summarizes pertinent measurement details. In situ data are column-integrated from 0 to 10 km for this analysis, as denoted by the prefix Ω (Methods). SI Appendix, Fig. S2 shows vertical profile statistics for [HCHO], [OH], P_OH, and k′_OH.

Fig. 1.

ATom maps the variability of the remote troposphere. Black lines show flight tracks for ATom 1 (A) and 2 (B), with colored circles indicating HCHO column densities integrated over ATom profiles. Only profiles used in the present analysis are displayed (n = 139). Data are overlain on OMI HCHO column densities averaged over each mission. The color bar saturates at both ends; 1σ uncertainties are 1 × 10¹⁵ cm⁻² for OMI and ∼5% for ATom.

Pseudolinear Scaling Factors.

Application of this theory to a satellite product requires expressing Eq. 2 in a column-integrated form. Accordingly, we define the following pseudolinear function (see SI Appendix, Text S1 for derivation):

$$\text{Ω}\left[HCHO\right]=s_{OH}\frac{\text{Ω}\left[OH\right]}{k_{HCHO}^{\prime }}+\text{Ω}{\left[HCHO\right]}_0.$$ [3]

The slope s_OH represents the HCHO production frequency (s⁻¹), analogous to the product αk′_OH in Eq. 2. A similar equation holds for P_OH but with a slope s_POH analogous to α (unitless). The intercept, Ω[HCHO]₀, represents HCHO from minor non-OH sources. The HCHO loss frequency, k′_HCHO, is an HCHO-weighted column average. Note that the functional relationship here is between Ω[OH] and the column-integrated HCHO production/loss rate, not Ω[HCHO] alone.

The inherent dependence of k′_HCHO on [OH] (SI Appendix, Eq. S2) gives rise to nonlinearity in Eq. 3, which can be characterized by two limiting cases. When j_HCHO >> k_HCHO+OH[OH], we expect a linear relationship between Ω[HCHO] and Ω[OH]/k′_HCHO. At the opposite extreme, we expect Ω[HCHO] to be independent of Ω[OH]/k′_HCHO. For column-integrated ATom observations, photolysis comprises 81 ± 9% (mean ± 1σ) of total HCHO loss. Thus, we anticipate the pseudolinear model to be representative for most remote regions.

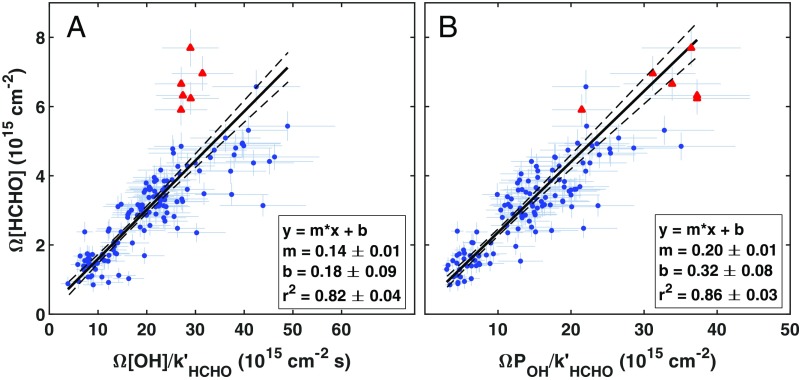
ATom observations reveal a striking correlation between Ω[HCHO], Ω[OH]/k′_HCHO, and ΩP_OH/k′_HCHO (Fig. 2). When normalized by k′_HCHO, Ω[OH] and ΩP_OH explain 82% and 86% of the variance in Ω[HCHO], respectively. The P_OH slope (s_POH = 0.20 ± 0.01) concurs with the “effective yield” range of 0.21 to 0.24 predicted by Valin et al. (10) for low NO_x, low hydrocarbon regions in the Southeast United States. The OH slope (s_OH = 0.14 ± 0.01 s⁻¹) is equivalent to the product of s_POH and the column-weighted k′_OH of 0.69 ± 0.03 s⁻¹, with the latter derived from a fit of ΩP_OH vs. Ω[OH] (SI Appendix, Fig. S2). Insolation is the primary driver for overall variability in Ω[HCHO], ΩP_OH, Ω[OH], and k′_HCHO, as evidenced by the latitudinal gradient in Ω[HCHO] (Fig. 1). Biomass burning can also exert a strong regional influence. Five of the six highest recorded Ω[HCHO] values correspond to African fires sampled in the equatorial Atlantic during ATom 2 (red points in Fig. 2). Reactive hydrocarbons in these air masses amplify k′_OH (up to 5 s⁻¹ for individual measurements), drawing down OH concentrations while stimulating HCHO and OH production. These outliers are excluded from the fit in Fig. 2A (including these points would increase the slope by 13%). The observed relationships may exhibit some curvature at the highest values due to HCHO loss via OH, but the sparsity and uncertainty of observations makes this difficult to confirm.

Fig. 2.

Total-column HCHO loss tracks oxidizing capacity in the remote troposphere. ATom observations (n = 139) of Ω[HCHO] against HCHO loss frequency-normalized Ω[OH] (A) and ΩP_OH (B) obey the theoretical relationship described by Eq. 3. Error bars reflect the combined 1σ uncertainty of observations and rate coefficients. Red triangles denote fire-impacted columns sampled near Equatorial Africa during ATom 2. Solid black lines represent uncertainty-weighted “least-squares cubic” regressions that minimize error-weighted residuals along both axes (56). Dashed lines are 1σ fit CIs. Fit coefficients are given with their 1σ uncertainty. Fire-impacted points are excluded from the fit in A.

The relationships displayed in Fig. 2 are fairly robust across ATom meteorological and chemical regimes. SI Appendix, Table S2 shows fit slopes for various observation subsets. Slopes are statistically indistinguishable at the 1σ level when data are segregated by season or ocean basin. A systematic difference in s_POH between the South (0.24 ± 0.01) and North (0.20 ± 0.01) Hemispheres stems from competition between CO and hydrocarbons (mainly CH₄) as sinks of OH. CO, which does not produce HCHO, is ∼40% higher in the North Hemisphere according to ATom observations, as expected due to the predominance of combustion emissions. A similar trend emerges when segregating data by lower/upper 50th percentiles of fractional loss of OH to CO or total column oxidized nitrogen (NO_y), the latter reflecting colocated combustion sources of CO and NO_x. Slopes do not vary with NO_x, however, as ATom typically sampled aged air where NO_x variability is relatively low. The slope of Ω[HCHO] vs. Ω[OH]/k′_HCHO is less variable across these categories, which in some cases reflects compensation between α and k′_OH (e.g., increasing CO lowers the effective HCHO yield while increasing total OH reactivity). None of the slopes presented in SI Appendix, Table S2 differ from those derived for the whole dataset at the 2σ level, supporting the use of a single set of scaling factors across all regions for which ATom is representative. Note, we expect more variability in these relationships for finer-resolution (i.e., not column-integrated) observations.

The fit intercepts in Fig. 2 imply a residual HCHO column of 0.26 ± 0.06 × 10¹⁵ cm⁻² that is not directly tied to OH. Potential explanations include HCHO production from halogen-mediated hydrocarbon oxidation (31) or heterogeneous conversion of methanol (32). The intercept is small enough that we cannot rule out the potential influence of a minor bias in one or more observations.

Inversion of Eq. 3 yields a transform for estimation of Ω[OH] from Ω[HCHO], k′_HCHO, and the fit coefficients:

$$\text{Ω}\left[OH\right]=\frac{k_{HCHO}^{\prime }}{s_{OH}}\left(\text{Ω}\left[HCHO\right]-\text{Ω}{\left[HCHO\right]}_0\right).$$ [4]

A similar equation holds for ΩP_OH. As an internal check, we apply this transform to back-calculate ΩP_OH and Ω[OH] from ATom data (SI Appendix, Fig. S4). For both Ω[OH] and ΩP_OH, normalized mean bias is −3 to −4% and normalized mean absolute error is 18 to 20%. These metrics indicate that observed values differ from the pseudolinear model by ∼20% on average, but over- and underestimations mostly compensate one another.

Two notable deviations from the pseudolinear model illustrate the sensitivity of these relationships to air mass composition. First, overpredictions of up to 50% for Ω[OH] are associated with biomass burning (red triangles in Fig. 2 and SI Appendix, Fig. S4A), where elevated reactive hydrocarbons lead to more HCHO produced per OH consumed (higher column-specific s_OH). Similar biases are absent in predicted ΩP_OH (SI Appendix, Fig. S4B) because P_OH is locally enhanced alongside HCHO via increased O₃ and NO_x. Second, underpredictions of 25 to 35% can occur at the high end of observed Ω[OH] (above 6 × 10¹² cm⁻²). These profiles, mostly located over the Tropical East Pacific, include regions of significant cloud-related OH enhancements in the middle/upper troposphere (up to 2.5 × 10⁷ cm⁻³ for 30-s averages). The slope parameter s_OH inherently depends on the vertical distribution of the product of [OH] and k′_OH (SI Appendix, Eq. S3), and k′_OH decreases by a factor of 8, on average, between the surface and 10 km (SI Appendix, Fig. S2D). Thus, in cases where clouds significantly shift the balance of the OH column toward higher altitudes, the full ATom s_OH will be higher than the column-specific value and Ω[OH] will be underpredicted. Predictions of ΩP_OH are immune to such effects, both because s_POH does not depend explicitly on [OH] or k′_OH and because ΩP_OH is typically weighted toward lower altitudes than Ω[OH] (SI Appendix, Fig. S2).

OMI Evaluation.

Global application of Eq. 4 requires knowledge of the global distribution of Ω[HCHO], for which we use the OMI Smithsonian Astrophysical Observatory retrieval (OMI-SAO v003) (33). OMI resides on the sun-synchronous Aura satellite, with an equatorial crossing time of ∼1330 local solar time (LST). Further details on the retrieval are provided in Methods and SI Appendix, Text S2. Here, we evaluate HCHO retrievals against ATom observations.

Space-based Ω[HCHO] observations are especially challenging in remote regions. Typical magnitudes are below the single-scene detection limit (5 to 12 × 10¹⁵ cm⁻²) for current-generation sensors (26). On the other hand, the real atmosphere is fairly uniform in such regions and averaging over space and time can improve precision by a factor of 10 or more (34). For the resolution utilized here (0.5° × 0.5°, 26-d averages), we estimate a 1σ precision of 1 × 10¹⁵ cm⁻² based on median variability over the remote Pacific (Methods).

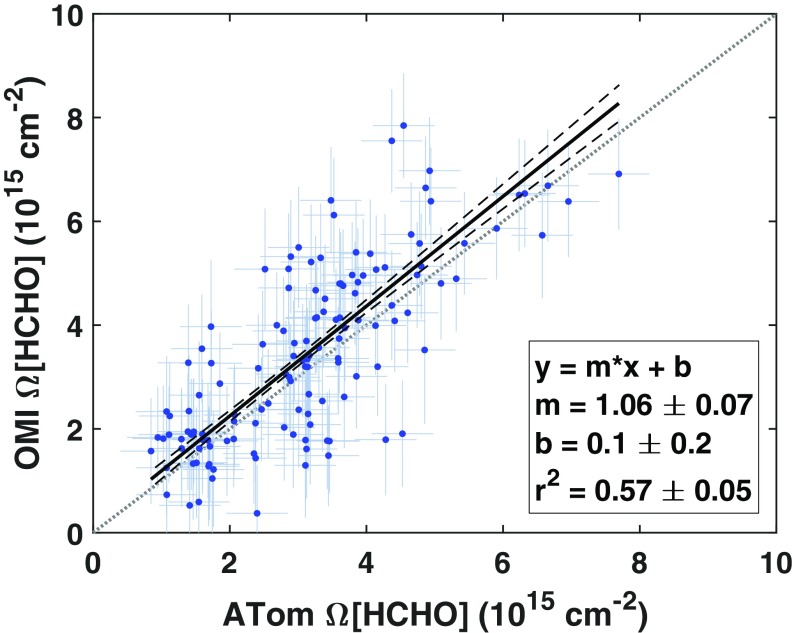
Sampling differences between ATom and OMI preclude direct validation, but comparison is possible with consideration of atmospheric variability. ATom profiles are single samples from a month-long distribution. Using output from a global model simulation (Methods and SI Appendix, Text S3), we estimate an average Ω[HCHO] SD of 0.45 × 10¹⁵ cm⁻² due to population subsampling. Individual ATom profiles typically traverse 200 to 450 km in the horizontal and thus amalgamate partial columns from the equivalent of 9 ± 5 campaign-average OMI grid boxes. To compare with ATom, we average all grid boxes intersected by each profile without weighting and use the nominal OMI precision of 1 × 10¹⁵ cm⁻² as the uncertainty estimate. Fig. 3 shows a linear relationship between ATom and OMI observations, with a slope of 1.06 ± 0.07 and a correlation coefficient of 0.57 ± 0.05. Seventy-two percent of the ATom-OMI pairs in Fig. 3 agree within combined 1σ uncertainties and 94% at 2σ. The OMI-SAO retrieval is thus not systematically biased in remote regions, and precision is the major source of uncertainty.

Fig. 3.

OMI accurately captures large-scale variability in remote HCHO. This plot compares OMI-SAO Ω[HCHO] against ATom profiles mapped in Fig. 1 (n = 134). OMI retrievals are gridded and averaged over each mission before sampling along ATom flight tracks. For each ATom profile, the corresponding OMI value represents an unweighted average over all grid cells intersected by the flight path. OMI columns are scaled using ATom-derived AMFs (SI Appendix, Text S2) and corrected for the fraction of Ω[HCHO] residing below 10 km, as determined by a priori profiles. Error bars represent estimated 1σ sampling precision. The solid line is a “least-squares cubic” regression that minimizes error-weighted residuals along both axes (56). Dashed lines are 1σ fit CIs. The gray dotted line is a 1:1 relationship.

In SI Appendix, Text S2, we consider the potential impact of a priori profiles and background corrections. The “a priori,” a model-generated vertical concentration profile, is one component of the air mass factor (AMF) used to convert slant column density to vertical column density. Evaluation against ATom vertical HCHO profiles reveals a high bias of 4 ± 7% in OMI-SAO AMFs and a corresponding low bias in vertical columns (SI Appendix, Fig. S5). Correcting for this error slightly degrades agreement with ATom, suggesting that it may partially offset other biases. We do not apply this correction when utilizing global Ω[HCHO]. The “reference sector” correction adjusts for detector background/drift and spectral artifacts; because of this correction, some fraction of the final column is effectively a global model value. The magnitude of this correction varies significantly over the retrieval domain (SI Appendix, Fig. S6), with an average value of −1.3 ± 1.2 × 10¹⁵ cm⁻². This correction can be a significant fraction of reported column densities in some regions, but it is typically within ±30% of Ω[HCHO] in regions with the highest HCHO and OH (the Tropics). Furthermore, OMI retrievals possess significant information on HCHO variability even without this correction (SI Appendix, Fig. S7). Overall, this evaluation supports the application of ATom-derived relationships to OMI-SAO Ω[HCHO] observations.

The OMI-SAO product is one of several HCHO retrievals currently available, and interproduct differences can be substantial (26). For example, a cursory evaluation of the Royal Belgian Institute for Space Aeronomy OMI retrieval (35) shows relatively poor correlation with ATom 1 observations (SI Appendix, Fig. S8). Validation is a vital prerequisite to scientific application of satellite retrievals. We caution against applying the method developed here to other retrieval products unless they are vetted against ATom or other observations of the remote atmosphere.

Near-Global Oxidizing Capacity

To extend the relationships inferred from ATom results, we must define the conditions under which the scaling factors derived above are applicable. ATom sampled a wide range of chemical environments, including “background” regions far-removed from anthropogenic emissions, continental outflow (aged urban and biomass burning plumes), and convectively influenced air masses. The ATom dataset is biased toward less cloudy conditions; however, the same is true of many satellite products. Furthermore, the spatiotemporal variability of ATom Ω[HCHO] is generally consistent with campaign-average satellite observations (Figs. 1 and 3). Although ATom observations are by no means comprehensive, they are the most representative subsample of the remote troposphere to date.

The definition of “remote” is somewhat ambiguous and should not be confused with “pristine.” For simplicity, we restrict our analysis here to all nonland areas. This assumption is coarse but consistent with the first-order linear behavior of the full ATom dataset (Fig. 2). Output from a Global Modeling Initiative (GMI) chemistry-climate simulation suggests that more than 99% of nonland tropospheric columns fall within the range of Ω[HCHO] and Ω[OH]/k′_HCHO values sampled during ATom (SI Appendix, Text S3 and Fig. S9). GMI Ω[HCHO] values outside this range accompany nonmethane hydrocarbon influence, and this again highlights the potential for bias in inferred OH near regions of continental outflow (e.g., fire points in Fig. 2A).

Global application of Eq. 4 requires a model-assisted estimate of k′_HCHO. For this purpose, we rescale GMI column-average HCHO photolysis frequencies (j′_HCHO) using the ATom relationship between j′_HCHO and k′_HCHO (SI Appendix, Fig. S11). This procedure circumvents potential bias from model OH. Further details and GMI j′_HCHO validation are provided in SI Appendix, Text S3.

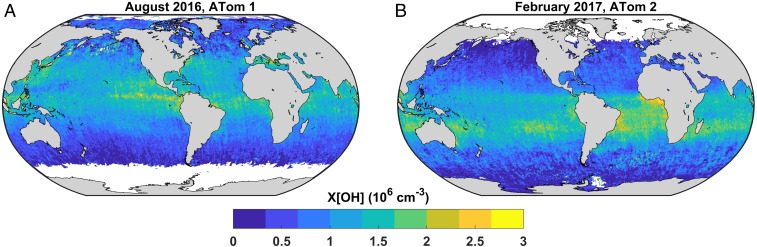
Fig. 4 shows the global OH distribution derived from Eq. 4 using ATom scaling factors, OMI Ω[HCHO], and GMI-derived k′_HCHO. Subsequent analysis here will center on OH concentrations rather than production rates due to substantial previous work on global OH. OH column densities are scaled to 24-h tropospheric column mean concentrations (X[OH]) by dividing by the GMI-calculated tropopause height and multiplying by the ratio of diel-average to 1300 LST GMI Ω[OH] for each grid cell. The median 1σ uncertainty in X[OH] for individual grid points (0.5° × 0.625° 26-d averages) is 0.35 × 10⁶ cm⁻³. Roughly 67% of the error budget is due to random error in OMI Ω[HCHO], while the remainder is systematic (30% from k′_HCHO, 3% from fit coefficients). Averaged over the full domain for both missions, mass-weighted mean X[OH] is 0.97 ± 0.25 × 10⁶ cm⁻³ (Table 1). This value is statistically indistinguishable from MCF-based global annual estimates of ∼1.1 × 10⁶ cm⁻³ (13, 14), although the mean is 12% lower. A lower mean [OH] might be expected, both because we exclude terrestrial regions with relatively higher O₃ and NO_x and because of potential differences in spatial weighting (see below). The equivalent remote tropospheric CH₄ lifetime against OH is 11.4 ± 3.7 y (SI Appendix, Text S5 and Table S4).

Fig. 4.

Remote tropospheric OH varies significantly in time and space. Diel-average tropospheric column mean OH concentrations (X[OH]) are mapped for the periods of ATom 1 (A) and 2 (B). X[OH] is scaled from OMI and ATom-derived Ω[OH] as described in Near-Global Oxidizing Capacity. Median 1σ uncertainty in individual grid cells is ±0.35 × 10⁶ cm⁻³.

Table 1.

Statistics for diel-average tropospheric column mean OH (X[OH], 10⁶ cm⁻³)

Period	All X[OH]	NH X[OH]	SH X[OH]	NH/SH (global sOH)	NH/SH (best estimate)*
August	1.02 ± 0.24	1.26 ± 0.29	0.81 ± 0.19	1.20 ± 0.06	1.26 ± 0.05
February	1.04 ± 0.25	0.88 ± 0.21	1.14 ± 0.28	0.57 ± 0.05	0.60 ± 0.04
Average†	0.97 ± 0.25	1.03 ± 0.26	0.92 ± 0.25	0.85 ± 0.08	0.89 ± 0.06

All averages are weighted by tropospheric column mass. Uncertainties are 1σ.

^*Weighted mean of NH/SH ratios calculated from X[OH] using a single value for s_OH (this table) and hemisphere-dependent values (SI Appendix, Tables S2 and S3).

^†Gridded X[OH] is averaged over both missions before calculating statistics (Methods). Grid cells with missing X[OH] for one mission only are filled with 0 before averaging.

The X[OH] product derived here is fundamentally different from the information afforded by budget analyses of MCF and other tracers. The latter integrate OH over hemispheric-to-global and annual-to-multiannual scales (3, 4, 13–19). The ∼5-y lifetime of MCF is central to this method; however, this same property also limits achievable spatial and temporal resolution. In contrast, the lifetime of HCHO is ∼hours; thus, X[OH] derived by this method reflects local chemical variability. Our X[OH] product is restricted to remote regions with satellite coverage, complicating direct comparison with prior studies of global OH. Nonetheless, there is significant value in focusing on this domain. Indeed, a comparison with the box model climatology of Spivakovsky et al. (36) shows little difference between global and over-water average X[OH] (SI Appendix, Fig. S18).

Another key distinction is spatial weighting. Global OH proxies preferentially weight regions of fastest loss. A CH₄-based global OH proxy will be weighted toward lower altitudes than an MCF proxy owing to the steeper temperature dependence of the CH₄ + OH rate coefficient, and both are weighted toward tropical regions. This weighting is not synonymous with a bias, rather it implies a proxy’s sensitivity to changes in the spatial distribution of OH. Global-scale X[OH] averages will be weighted similar to CH₄-based proxies in this respect, given that CH₄ is the primary HCHO precursor. Variability in X[OH] is also weighted by OMI’s vertical sensitivity. For remote regions, the OMI AMF density peaks at an altitude of 1.5 to 3.5 km and falls off by half below 200 m and above 6 km (SI Appendix, Fig. S5B). Thus, X[OH] is most sensitive to chemistry in the lower free troposphere but integrates information throughout the tropospheric column, except the lowermost portion of the boundary layer.

The dataset shown in Fig. 4 covers ∼68% of total tropospheric mass and ∼75% of the tropical troposphere. This coverage estimate is purely spatial; temporal coverage is limited by OMI, which (for 2016 and 2017) requires 2 d for global sampling and is filtered to exclude pixels with cloud cover >30%. SI Appendix, Text S4 explores the potential influence of cloud cover on X[OH]. We find little evidence for significant cloud-related biases except possibly in the Southern Ocean, where systematic clear-sky biases in OMI Ω[HCHO] may be relatively large (up to −50%) but are well below the OMI precision of 1 × 10¹⁵ cm⁻². Use of cloud-filtered OMI retrievals mitigates the potential for low biases due to cloud effects on the slope parameter. The resolution of X[OH] lends itself to investigations of seasonality, interhemispheric gradients, and fine-scale phenomena with greater detail and precision than heretofore possible. In the following sections, we explore several areas where X[OH] illustrates OH variability across scales.

The Balance of Global Remote OH.

Average X[OH] is statistically indistinguishable between August (ATom 1) and February (ATom 2) (Table 1). Systematic errors dominate the uncertainty of ∼25%, and a two-sample t test indicates that mean values for the two missions are identical at a significance level of 99.97%. These missions occurred near the peaks of North and South Hemisphere (NH and SH) summer, suggesting that global remote OH is aseasonal (at least for this time period). This is surprising given the marked differences in X[OH] spatial patterns (Figs. 4 and 5), although it reinforces the notion that tropospheric OH is not highly variable when averaged on large scales (3). Mean X[OH] is not biased by the seasonal shift in the satellite’s viewing window; for example, the difference remains small if we restrict the averaging domain to latitudes of ±60°, where OMI data are available for both seasons (SI Appendix, Table S3). Accounting for the small difference in scaling factors between the two ATom deployments or between hemispheres alters global averages by <7%, within 1σ error bounds.

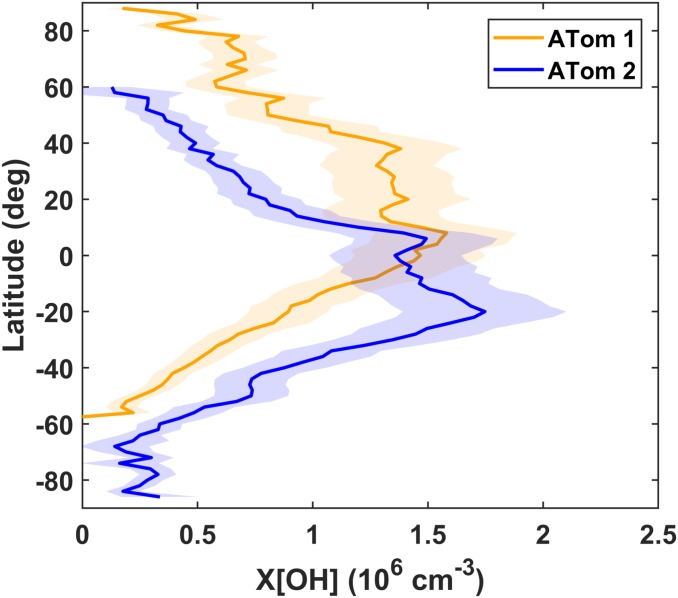
Fig. 5.

Remote zonal mean X[OH] exhibits complex seasonal asymmetry. Averages for ATom 1 (orange) and 2 (blue) are taken over 2° latitude bins and weighted by the mass of air in each column. Shaded regions represent the 1σ uncertainty range.

In contrast, the NH and SH independently exhibit pronounced seasonality. The broad peak in zonally averaged X[OH] generally follows the sun with a similar maximum magnitude in both seasons (Fig. 5). The shape of this profile is seasonally asymmetric, with a broadening to northern midlatitudes in the NH summer that is not mirrored in the SH. This difference may reflect the influence of continental outflow from Asia and North America on remote OH production. A more extensive analysis of other airborne and satellite observations could elucidate the underlying causes of this feature, such as transport of O₃ and/or NO_x reservoirs. The box model climatology of Spivakovsky et al. (36) shows a similar pattern but with more OH at southern latitudes during the Austral summer (SI Appendix, Fig. S18). This discrepancy would be consistent with a cloud-related low bias for X[OH] in the Southern Ocean (SI Appendix, Text S4).

The seasonal cycle of global OH has been minimally constrained by observations and thus largely unexplored. It is possible to extract this information from formal MCF inversions (18), but to our knowledge, such features have not been studied in detail. Chemical transport models predict a ∼20% increase in the global CH₄ lifetime between August and February (37). In conjunction with the aseasonality of mean remote OH, this suggests that the continental troposphere drives global seasonality. In SI Appendix, Text S5, we explore the possibility of discerning continental OH variability through reconciliation of remote X[OH] with top-down MCF-based global estimates. Cumulative uncertainties preclude robust conclusions regarding any such “ocean-land” contrast.

The NH/SH ratio is a useful summary metric of interhemispheric OH gradients. Considering only the statistical uncertainties in X[OH], the uncertainties in the NH/SH ratio are relatively small due to partial cancellation of systematic errors. For this calculation, however, we might also account for the hemispheric difference in the ATom-derived slope (SI Appendix, Table S2), causing a 12% upward adjustment of the NH/SH ratio. It is not immediately clear which set of scaling factors is appropriate, since the geographic equator is an arbitrary boundary and not equivalent to a chemical or dynamic boundary such as the intertropical convergence zone (SI Appendix, Text S7). Thus, we take the ratios derived from a global scaling factor as a lower limit, those from distinct NH and SH scaling factors as an upper limit, and the mean of the two as our best estimate (Table 1). From this assumption, we derive best-estimate NH/SH ratios of 1.26 ± 0.05 for August, 0.60 ± 0.04 for February, and 0.89 ± 0.06 averaged over both missions. Ratios do not change significantly if data are restricted to ±60° latitude (SI Appendix, Table S3).

The biseasonal remote troposphere NH/SH ratio derived here (0.89 ± 0.06) falls within the range of global values reported by previous studies (0.85 to 0.98) (4, 13, 16, 18, 19). Although our “remote” averages are not fully equivalent to global estimates, we take this agreement as a strong validation of our method. These results also provide further independent evidence that global models likely overestimate the NH/SH ratio of tropospheric OH (1). The spatial and temporal resolution inherent to X[OH] may facilitate more detailed assessments of the issues underlying such model biases.

Taken together, these results indicate a large-scale balance of global remote OH, where decreases in one region are compensated by increases in another. Individual hemispheres exhibit significant seasonal variability, but mean remote tropospheric X[OH] observed 6 mo apart differs by less than 2%. This notion is consistent with the model analysis of Lelieveld et al. (38), who link buffering capacity to the efficiency of radical propagation and long-range O₃ transport. X[OH] may reveal other unique modes of variability, such as the influence of El Niño (15, 16, 39), lightning (40), or exceptional wildfires (15, 41). Such applications, however, must thoroughly consider factors modulating the relationship between HCHO and OH, particularly the competition between CO, CH₄, and reactive hydrocarbons as sinks of OH.

Regional Phenomena.

Fig. 4 suggests significant regional variability in tropospheric oxidizing capacity. Given the simplicity of the pseudolinear transform, it is not surprising that spatial variability in X[OH] closely tracks Ω[HCHO]. Casting these observations in terms of OH abundance, however, conveys a different perspective on the underlying processes. Small-scale features must be interpreted with caution, as HCHO sensitivity to local hydrocarbon emissions is not represented in our simple relationship. We focus briefly on four regions of interest: the OH minimum in the Tropical West Pacific, enhancements in the equatorial East and Southeast Pacific, and the broad South Atlantic maximum.

Fig. 4A shows a relative minimum in X[OH] in the Tropical West Pacific, centered at 17°N and 158°E and extending west toward the Philippines. Minimum X[OH] in this region is ∼0.14 × 10⁶ cm⁻³, roughly 10 times lower than in the surrounding area. The existence of this “OH hole” has been postulated based on observations of low tropospheric O₃ in this region (42) but never directly observed. Potential explanations include suppression of primary OH production due to low O₃ (<15 parts per billion by volume) (42) or a lack of secondary production due to low NO (<10⁸ cm⁻³) (43). Nicely et al. (44) find no evidence for an OH minimum based on box model calculations constrained by in situ observations acquired in February 2015. Comparison of Fig. 4 suggests that this feature is absent in February 2017. Our results are thus consistent with previous work on this subject. This region may serve as a gateway for transport of ozone-depleting substances to the lower stratosphere, but further measurements in the region are needed to test this hypothesis. In situ observations of O₃, HO_x, NO_x, and related species, at the optimal time and location, are crucial for both understanding this anomaly and validating the contrast in X[OH] reported here.

The Tropical East Pacific exhibits a marked enhancement in X[OH] in August (Fig. 4A). This is a region of intense biological and convective activity. The belt of maximum X[OH] is centered around 5 to 10°N and is ∼17% greater than X[OH] averaged over the entire latitudinal band. The band is offset north of the equatorial region of high ocean productivity (45) by several hundred kilometers; thus, enhanced hydrocarbon emissions (46) are an unlikely explanation. Early satellite-based retrievals of glyoxal (CHOCHO, a small hydrocarbon similar to HCHO) suggested significant column densities in this area (47), while more recent retrievals have not shown the same feature (48). Convectively lofted water vapor in this region may have contributed to an artifact in earlier satellite glyoxal products, and this would also provide a mechanism for enhanced primary OH production throughout the column.

A similar-scale enhancement in X[OH] occurs in the Southeast Pacific in February (Fig. 4B). This feature is coincident with the minimum in ocean chlorophyll associated with the South Pacific gyre (45), but this does not immediately suggest a viable explanation. This region is seemingly unremarkable from an atmospheric chemistry standpoint, with no known mechanisms that could amplify production of OH or HCHO. Glyoxal retrievals are especially sensitive to ocean liquid water absorption here (48), but such issues are not expected for the HCHO retrieval. Again, further measurements in this data-sparse region are needed to validate this observation.

A final feature of note is the broad region of elevated X[OH] stretching across the South Atlantic in February (Fig. 4B). Biomass burning influences coastal equatorial Africa, and X[OH] may be biased high by as much as 50% (note red triangles in SI Appendix, Fig. S4A). On the other hand, decomposition of NO_x reservoirs like peroxyacetyl nitrate in transported biomass burning plumes may sustain secondary OH production in this region (49). Similarly, X[OH] enhancements observed down to 30°S and off the South American coast may be related to transport of labile isoprene nitrates (50).

The degree to which features such as those described above reflect legitimate atmospheric processes versus artifacts (due to retrievals or scaling factors) remains open to further investigation. Nonetheless, such constraints have the potential to broaden our understanding of global OH variability beyond the limits of MCF and similar budget-based analyses.

Conclusions and Next Steps

We have quantified a robust link between total-column HCHO production/loss and OH concentrations in the remote troposphere based on analysis of the global-scale ATom dataset. We combined this relationship with satellite-based tropospheric HCHO column observations and model-estimated HCHO loss frequencies, tropopause heights, and OH diurnal scaling factors to construct a spatially and temporally explicit estimate of column-integrated OH extending to roughly 70% of total tropospheric mass. Preliminary analyses show agreement between this product and MCF-inferred global OH magnitude and hemispheric gradients. This dataset can help to elucidate the details of OH variability. Despite significant seasonality in hemispheric OH gradients, average global remote OH differs by less than 2% between August 2016 and February 2017, and the NH/SH ratio is slightly less than unity when averaged over both months. This finding supports model-based assertions that global atmospheric oxidizing capacity is buffered against anthropogenic or natural source/sink perturbations. Several unique features are also identified in the spatially resolved dataset, including seasonal OH depletion in the Tropical West Pacific and enhancements in the East Pacific and South Atlantic. Some of these features are consistent with known or proposed atmospheric processes, while others are unexpected and motivate further study. These regional phenomena require additional confirmation due to the potential for biases arising from satellite HCHO retrievals, cloud cover, and assumptions inherent to the HCHO–OH transform.

This work establishes the viability of a method that will improve with future refinements. The ATom relationship captures >80% of the variance in ATom-observed OH, which is sufficient when averaging X[OH] over global or monthly scales. Constraining regional variability or long-term trends, however, requires more rigorous consideration of second-order impacts from variations in atmospheric composition. We might reduce such biases by exploiting additional satellite observation (e.g., CO) to more accurately constrain the parameters modulating the HCHO–OH relationship. It is even conceivable that this method could be extended to some terrestrial regions. OH reactivity is highly variable over land due to reactive hydrocarbons (38), but the ratio of HCHO to OH production (essentially the effective yield, α) is only expected to vary by a factor of 2 (10). Thus, it may be more feasible to constrain XP_OH than X[OH] in regions with abundant nonmethane hydrocarbons. Potential biases arising from the influence of cloud cover on chemistry and retrieval representativeness also warrant closer examination. We find that clouds may impart a low bias of 25 to 50% to X[OH] in certain locations, but such effects are not easily quantified and will depend on cloud top height, cloud persistence, insolation, vertical profiles of trace gases, and other parameters. Indeed, clouds are likely the largest source of unquantified uncertainty in the X[OH] product.

It is also crucial to build confidence in satellite HCHO observations in remote environments. Even in regions with copious HCHO like the Southeast United States, retrieval products can differ dramatically in both absolute magnitude and variability (26). Evaluation of multiple HCHO retrievals against observations from ATom and other missions will help reduce uncertainties and artifacts. Next-generation satellite sensors, such as the TROPOspheric Monitoring Instrument, will be more sensitive and less prone to potential biases (34).

With additional refinements, X[OH] inferred from space-based HCHO observations may be a valuable tool for process analysis and model evaluation. Extension across the satellite record would permit a fresh exploration of OH variability, both interannually/globally and at finer resolution. Additional constraints on the CH₄ loss rate may also permit a more robust estimate of emissions patterns (5) and assist efforts to assess model O₃ and CH₄ budgets (51). This work is complementary to continuing research into budget-based global OH constraints (23, 24). Such methods are inherently subject to uncertainties in emissions and transport; in contrast, our method hinges on our understanding of atmospheric composition and chemistry. Enhanced spatial and temporal information is a key advantage of the X[OH] product, and we expect this to improve in concert with remote sensing capabilities.

Methods

Data Availability.

ATom observations are publicly available at https://daac.ornl.gov/cgi-bin/dsviewer.pl?ds_id=1581 (52). The specific datasets utilized here, including the ATom OH merge, ATom integrated columns, gridded OMI HCHO columns, Ω[OH] and X[OH], are available at https://daac.ornl.gov/cgi-bin/dsviewer.pl?ds_id=1669 (53).

ATom Data Selection and Column Integration.

SI Appendix, Table S1 lists the measurement techniques, temporal resolution, and uncertainties for the subset of ATom data used in this analysis. All fast observations are averaged to the native OH time base (30 s for ATom 1, 20 s for ATom 2) and converted from mixing ratios to number density. Rate coefficients are taken from the latest Jet Propulsion Laboratory Handbook recommendations (54). All measurement and rate coefficient uncertainties are given as 1σ (68% confidence level) and are propagated through to column values. Measurement uncertainties are treated as random unless specifically stated otherwise in data files.

ATom profiles were executed “in route” along the flight track (as opposed to spirals) and typically spanned 200 to 450 km of horizontal distance. For each profile, concentrations and reaction rates are averaged to an altitude grid of 0 to 10 km with 200-m spacing using altitude above mean sea level as the vertical coordinate. Missing points in each gridded profile are filled with linear interpolation (for points within the minimum and maximum sampling altitude) and constant-value extrapolation (using the mean of the last two adjacent valid points) to the surface and/or 10 km. Following trapezoidal integration, columns are filtered for solar zenith angle (SZA) <80°, profile-sampling altitude range at least 0.6 to 8 km, fraction of missing HCHO or OH observations <30%, fraction of interpolated gridded OH <40%, and fraction of extrapolated HCHO <25%. These limits are determined by visual identification of outliers in Fig. 2 and inspection of vertical profiles. Three additional profiles are removed due to intermittent cloud cover, which can decouple OH and HCHO. Two profiles over the central United States are also removed. Fit coefficients shown in Fig. 2 are insensitive to the choice of altitude grid, interpolation/extrapolation method, profile altitude range, or reasonable adjustments to filter thresholds. All linear fits use a MATLAB toolbox available at https://www.mbari.org/products/research-software/matlab-scripts-linear-regressions/ (55).

Total column OH production is calculated by summing column-integrated rates for O₃ photolysis, HO₂ + NO, HO₂ + O₃, and H₂O₂ photolysis. All rates are calculated directly from observations, and O(¹D) is assumed to be in steady state for deriving OH production from O₃ photolysis. Separate measurement-constrained 0-D box model simulations (SI Appendix, Text S6) indicate that these reactions respectively comprise 38%, 35%, 15%, and 6% of mean OH production over the ATom 1 dataset (SI Appendix, Fig. S1A). The remaining 6% is chiefly photolysis of oxygenated hydrocarbons. A small linear correction $\left(\text{Ω}{P}_{OH}^{corr}=1.06\text{Ω}{P}_{OH}+8.6\times {10}^{10}\hspace{0.17em}{\text{cm}}^{-2}\right)$ is also applied to account for OH production beyond the four main sources. The slope for this correction is based on simulated rates from the 0-D box model, while the offset is chosen to force the intercept of a plot of ΩP_OH vs. Ω[OH] to pass through zero (SI Appendix, Fig. S3). We add an additional systematic error of 6% to ΩP_OH as a result of this correction.

The column-weighted first-order HCHO loss frequency, k′_HCHO, is calculated following SI Appendix, Eq. S2. We further define j′_HCHO (used below) in analogy to this equation but without the OH reaction.

OMI Observations.

Global HCHO columns are taken from NASA’s operational OMI product provided by the Smithsonian Astrophysical Observatory (OMI-SAO v003) (33), available at https://mirador.gsfc.nasa.gov/ (SI Appendix, Text S2). Level 2 daily vertical column densities are screened for a cloud fraction <0.3, a SZA <70°, and a main data quality flag of 0 before performing an error-weighted average to a spatial resolution of 0.5° × 0.5°. The SE for each grid cell (σ_f) is calculated using the individual uncertainties for each pixel (σ_f,i) as the weighted SD of the mean:

$${\sigma }_f={\left(N{\displaystyle \sum _i\frac{1}{{\sigma }_{f,i}^2}}\right)}^{-0.5}.$$ [5]

Here, N is the total number of valid pixels contributing to that average. Daily gridded columns are averaged over each campaign (for ATom 1: July 29 to August 23, 2016; for ATom 2: January 26 to February 21, 2017) using a σ_f-weighted mean. A priori profiles and scattering weights are filtered in a similar fashion and averaged without weighting for comparison with ATom. Ω[HCHO] precision is estimated as follows: (i) for each grid cell, calculate the σ_f-weighted SD of the mean when averaging over each campaign; and (ii) find the median of all such values over the remote Pacific reference sector region (140 to 160°W, all latitudes). This estimate (1 × 10¹⁵ cm⁻²) is a reasonable upper limit as it may include some influence from true atmospheric variability.

Calculation of Global Ω[OH]/ΩP_OH and Related Metrics.

Scaling coefficients from ATom (Fig. 2), Ω[HCHO] from campaign-average OMI retrievals, and k′_HCHO derived from GMI output and ATom observations (SI Appendix, Text S3) are used with Eq. 4 to calculate global Ω[OH]. OMI HCHO is interpolated from 0.5° × 0.5° to the model grid of 0.5° × 0.625°. Ω[OH] is converted to 24-h tropospheric mean concentration (X[OH]) by dividing the vertical column density by GMI tropopause height and multiplying by a GMI-derived diel scaling factor (the ratio of 24-h mean to 1300 LST Ω[OH]). The latter is typically a factor of ∼0.3. This scaling does not significantly alter the spatial patterns shown in Fig. 4.

Uncertainties in each term are propagated to X[OH] using formal methods where possible. For this calculation, we assume 1σ uncertainties of 15% for model j′_HCHO (identical to that for j_HCHO observations) and 1 × 10¹⁵ cm⁻² for OMI Ω[HCHO]. When spatially averaging, we assume that OMI uncertainties are random (and thus reduce with the square root of the number of points in the average), while uncertainties in fitting coefficients and k′_HCHO are systematic.

When averaging X[OH] over both missions, we fill grid cells with a concentration of 0 when X[OH] is missing for one mission but not the other. This is a conservative lower limit for the average, as OH is likely not 0 here but these cells are always near the poles where SZA is high. This procedure has a minor impact on large-scale X[OH] averages as tropospheric mass in these regions is smaller than in high-OH regions (the Tropics).