Developmental Trends of Performance Monitoring Measures in 7-to 25-year-olds: Unravelling the Complex Nature of Brain Measures

Abstract

This study explores how trial-to-trial latency variability contributes to the developmental trends observed in ERN amplitude found in the incorrect trials of a performance monitoring task, the visual flanker task. An Adaptive Woody Filter was used to measure and correct for the trial-to-trial latency variability of the ERN in 240 participants aged 7–25 years. Using three measures of latency variability, the degree of trial-to-trial latency variability was shown to decrease as the age of the participants increased from 7 to 25 years. The success of the Adaptive Woody Filter technique to remove the trial-to-trial latency variability was demonstrated in a straightforward manner by the significant changes in the measures of fit and intra-individual variability obtained before and after applying the filter. After the latency variability effects were removed and adjusted averaged ERPs were obtained, a more subtle but significant nonlinear developmental trend was still found in the amplitude of the ERN component.

1. Introduction

In past decades, the research on error-related negativity (ERN), a specific event-related potential (ERP), has increased considerably across multiple domains. The ERN represents response monitoring, error detection, or conflict detection processes when participants perform a forced choice task (Coles, Scheffers & Holroyd, 2001; Gehring & Fencsik, 2001; Falkenstein, Hohnsbein, Hoormann, & Blanke, 1991). The ERN is a negative deflection over fronto-central regions of the scalp with its amplitude peaking around 50–100 milliseconds (ms) after commission of an error (Coles, et al., 2001; Falkenstein et al., 1991). Both electroencephalogram (EEG) dipole modeling and functional magnetic resonance imaging (fMRI) studies have confirmed that the anterior cingulate cortex (ACC) is the neural generator of the ERN (Holroyd, Dien, & Coles, 1998; Mathalon, Whitfield, & Ford, 2003; van Veen & Carter, 2002; Carter et al., 1998; Coles et al., 2001). Lesion studies also provided evidence that the ACC is a key brain region in the generation of the ERN, as people with ACC lesions have demonstrated reduced or absent ERNs compared to control groups (Stemmer, Segalowitz, Witzke, & Schonle, 2004).

The ERN and performance monitoring have been specifically associated with disorders or conditions such as anxiety (for a review see Moser, 2017) and depression (e.g., Ladouceur, Slifka, Dahl, Birmaher, Axelson, & Ryan, 2012). Additionally, studies have documented developmental changes in ERN amplitude (Hajcak, Franklin, Foa, & Simons, 2008; Hanna, et al., 2012; Ladouceur et al., 2012; Davies, Segalowitz, & Gavin, 2004; Segalowitz and Davies, 2004; Segalowitz & Dywan, 2009). For a review of these developmental studies and an extensive description of the neural basis of the ERN, see Tamnes, Walhovd, Torstveit, Sells, & Fjell (2013). In short, Tamnes and colleagues argue that functional maturation of brain structures and neural circuits associated with the generation of the ERN may be important for the developmental changes in the ERN. A brief summary of a literature review on the ERN age-related changes in neurotypical children, adolescents, and adults can be found in the Supplementary Table.

However, the nature of these developmental changes in the ERN amplitude across development are only recently being explored. One possible explanation of the progressive changes in ERN amplitude as a function of increasing age is trial-to-trial latency variability (a.k.a., latency jitter). While averaged ERPs are accepted in mainstream neurophysiology as a way to capture the brain activity representative of an individual’s typical response to a stimulus event, this approach has a major flaw that is often ignored. The primary assumption of the averaging method is that the brain response to an event is unique, invariant, and phase-locked to the onset of the event in the same manner for each presentation of the event. Thus, by averaging a sufficient number of segments, researchers are able to obtain an averaged waveform that reflects brain activity to specific stimuli or responses (e.g. error responses) with background noise cancelled out (Luck, 2014). However, the assumption may not always be true especially for data collected from children (DuPuis, Ram, Willner, Karalunas, Segalowitz, & Gatzke-Kopp, 2015; Segalowitz & Dywan, 2009) or individuals with neurological or psychological disorders (Ford, et al., 1994). For instance, when there is considerable trial-to-trial latency variability in the ERP component of interest, not only is the latency measure of the averaged ERP distorted, but the amplitude of the component will be attenuated as a direct function of the variability in the latency across segments (Luck, 2014; Lukie, et al., 2014; Unsal & Segalowitz, 1995; van Boxtel, 1998). In their review, Tamnes and colleagues (2013) recommended that further developmental studies be conducted to enhance the understanding of the interaction of latency variability with the development trajectory of the ERN amplitude. Since that review, two developmental studies have provided some evidence that latency variability in the ERP component of interest decreases with increasing age (DuPuis et al., 2015; Lukie, et al., 2014).

Lukie, et al. (2014) explored the reward positivity, an ERP component elicited by feedback stimuli and measured this as a difference wave between electrophysiological responses to two feedback conditions (i.e., positive reward and no reward), in children (8–13 years), adolescents (14–17 years), and young adults (18–23 years). Though there were differences in sites for maximum amplitude across groups, comparisons of mean amplitudes across groups were not significant nor were group differences at the FCz site significant. While the differences in mean latency between groups were not significant, Lukie and colleagues noted that visual inspection of group grand averages suggested the possibility of latency variability of the reward positivity in children. To illustrate possible latency variability effects, they time-locked segments to the reward positivity maximum amplitude with a window extending 250 ms before to 250 ms after the maximum for each individual and then re-averaged across participants within each group to create the latency corrected grand average. Thus, their latency variability correction addressed inter-individual differences within groups. Consequently, Lukie and colleagues were only able to demonstrate that their latency variability correction alters the visual appearance of the grand averaged waveforms, but the latency variability could not be statistically tested (Lukie, et al., 2014). The approach used by Lukie and colleagues only qualitatively addressed inter-individual (i.e., between subject) latency variability. In addition, they did not report any direct measurement of intra-individual (i.e., within subject) differences in the latency variability at the trial level. Only correction of latency variability at the trial level for each individual would alter the amplitude of components in each individual’s averaged ERP and thus would have the possibility of leading to changes in statistical outcomes.

In a study of children ranging from 5 to 8 years of age assessed annually in kindergarten, first, and second grades, DuPuis et al. (2015) did make direct measurement of the latency variability at the trial level. The investigators obtained a signal temporal consistency measure (i.e., latency variability) for each participant by performing a time-frequency decomposition analyses on each ERP of the errors committed during a Go/No-go task, and then averaging across the trials the phase coherence values within the theta waveband during the period of 0 to 100 ms post response. DuPuis and colleagues found that temporal consistency significantly mediated the relationship between age and ERN amplitude (DuPuis et al., 2015). Moreover, the researchers suggested that the greater level of intra-individual variability in the temporal consistency might attenuate the average ERN amplitude in younger children (DuPuis et al., 2015). However, the approach used by DuPuis and colleagues only obtained measures of phase variability for the underlying theta oscillations across trials. Their study did not include procedures for correcting the ERPs to remove the latency variability from the averaged ERPs and, then obtain a direct measure of the ERN amplitude after correction. Interestingly though, signal strength measured as the average spectral power of the theta band from 0 to 100 ms did not correlate with temporal consistency (i.e., phase coherence values) suggesting that power and phase coherence each may contribute independently to ERN amplitude. Thus, DuPuis, et al. only measured the phase coherence aspect of the ERN signal and did not accordingly adjust the signal strength or amplitude of the ERN typically measured from averaged ERPs. These findings suggest that further examination is still needed to determine how intra-individual variability in latency affects the developmental trend of the ERN amplitude from young children to adulthood.

To resolve the issue of possible confounding of the amplitude measurement of an ERP component by latency variability, a method referred to as the Adaptive Woody Filter (Harris & Woody, 1969; Woody, 1967) was developed early in ERP research. In this approach, a template is created for each individual using the traditional averaging procedures. The term “adaptive” suggests that this template is not predefined; rather, it is empirically produced based on each participant’s originally-averaged ERP waveform. Then, for each participant, the Adaptive Woody Filter procedure shifts the ERP waveform of each segment forward or backward in time until a “best” fit is found to the averaged ERP template (Luck, 2014; Harris & Woody, 1969; Woody, 1967). Finally, the adjusted averaged ERP is created for the participant by averaging these re-aligned segments (Harris & Woody, 1969; Woody, 1967). The practical performance of the adaptive filter in adjusting for latency variability has been demonstrated in a variety of stimulus locked ERP measures in adults, including the N1-P2 (e.g., Wastell, 1977), P300 (e.g., Ford, Sullivan, Marsh, & White, 1994; Ruchkin & Sutton, 1978), and the early P50 component (Patterson et al., 2000). However, studies have yet to use the Adaptive Woody Filter on ERPs based on time-locking to responses obtained during error monitoring tasks or explore the implications of trial-to-trial latency variability in the context of brain maturation.

Thus, the overall objective of our study was not only to determine the developmental trend of trial-to-trial latency variability of the ERN from age 7- to 25 years of age but also to determine the nature of the developmental trend of the ERN amplitude after correcting for latency variability. In this study, we used an expanded data set than was originally reported in Davies et al., 2004. Specifically, the present study had two aims. The first aim was to use the Adaptive Woody Filter technique to determine the extent to which objective measures of trial-to-trial variability of the ERN latency obtained for each participant differ across the developmental period of 7 to 25 years. Since visual inspection of ERP grand averages suggested greater latency variability in children than in adults (Lukie, et al., 2014) and measures of phase coherence values were found to increase from age 5 to 8 years of age (DuPuis, et al., 2015), we hypothesized that measures of trial-to-trial variability of the ERN latency will be greatest in young children and decrease with increasing age. The second aim was to compare the developmental trend of ERN amplitude before and after correcting for trial-to-trial latency variability. We hypothesized that a developmental trend in the ERN amplitude would still exist following the adjustment of latency variability due to brain maturation (see Tamnes, et al., 2013 for review). However, the developmental trajectory of the ERN would be modified following the correction for latency variability, which removes latency variability effects across the developmental span of our study.

2. Method

2.1. Participants

Overall, two hundred and fifty-five children and adolescents, 7-to 18-years of age, and 33 adults, 19- to 25-years of age (total N = 288 participants) were recruited from the local community to serve as the basis of this study. The majority of the children were recruited through presentations given at youth organizations and schools within the community. In the recruitment protocol for participants, neurological and major psychopathological disorders were listed as exclusionary, thus most participants that enlisted in the study were free of these conditions. To ensure that participants that came to the study were free of exclusionary disorders, a parent of each child participant filled out a demographic form including information about the presence or absence of neurological and major psychopathological disorders for the child. The adult participants filled out a similar form. Among these 288 participants, four participants did not perform the EEG session, and 16 participants were excluded due a report on the demographic form of having attention deficit hyperactivity disorder (ADHD) or attention deficit disorder (ADD; n=5), depression (n=2), learning disorder (n=3), or ADHD/ADD comorbid with other disorders including reading disability (n=1), brain injury (n=1), depression (n=1), autism spectrum disorder (n=1), bipolar (n=1), and head injury (n=1). Thus, only data from 268 participants were collected or analyzed.

In preparation for data analysis, an additional 25 participants were excluded due to issues related to task performance. Specifically, among these participants, seven participants failed to complete the ERN task (five 7-year-olds; two 10-year-olds), 11 participants completed the task with too many incorrect trials (> 30% of 480 trials) (one 7-year-old; one 8-year-old; three 9-year-olds; one 10-year-old; two 13-year-olds; one 14-year-old; one 15-year-old; one adult), and seven participants completed the task with too few incorrect trials (< 2.5% of 480 trials) for adequate ERN analyses (one 13-year-old; two 16-year-olds; one 17-year-old; three adults). While least six trials are recommended for producing stable measures of ERN activity (Olvet & Hajcak, 2009; Pontifex et al., 2010), requiring at least twelve error trials (i.e., the 2.5% criterion) for this study assures that each ERN measure from ERPs used for determining the split-half reliability (i.e., internal consistency) reported below would have the recommended six trials or more. Other than the issues related to task performance, two participants were excluded because of a lack of visible ERN component within the time window based upon visual inspection before or after Adaptive Woody Filter correction (one 13-year-old; one 16-year-old); one 7-year-old participant was excluded because the ERN amplitude was an outlier within the age group (exceeded three standard deviations in the age group). Thus, only data from 240 participants were reported in this study.

The participants of this study included all but 5 of the participants (2 7-year olds and 3 adults) reported in Davies et al. (2004) along with additional participants whose data were collected after this initial publication using the same protocol. Specifically, 89 participants targeted to age 9, age 11, and teenagers aged 14, 16, and 17 years were added to 151 participants reported in Davies et al. (2004). As in Davies, et al. (2004), young adults were included in this study as an anchor point for studying the developmental trends because, they represent as a group, the participants in many of the past ERN studies. See Table 1 for details on the distribution of participants based on age and sex.

Table 1.

Distribution of Participants Organized by Age Group and Sex. The number of participants added to the present study that were not in Davies, et al. (2004) are indicated as positive values in parentheses in the Analyzed columns. Negative values in parentheses indicates number of participants were in Davies, et al. (2004) but now are excluded from the present study.

Age Group	Collected			Excluded			Analyzed
	Male	Female	Total	Male	Female	Total	Male	Female	Total
7	10	10	20	4	3	7	6 (−2)	7 (3)	13 (1)
8	10	10	20	1	0	1	9 (7)	10 (2)	19 (9)
9	9	15	24	2	1	3	7 (1)	14 (2)	21 (3)
10	9	9	18	1	2	3	8 (2)	7 (3)	15 (5)
11	9	11	20	0	0	0	9 (5)	11 (4)	20 (9)
12	11	10	21	0	0	0	11 (1)	10 (2)	21 (3)
13	9	10	19	3	1	4	6 (3)	9 (4)	15 (7)
14	9	13	22	0	1	1	9 (6)	12 (6)	21 (12)
15	9	8	17	1	0	1	8 (5)	8 (3)	16 (8)
16	9	11	20	1	2	3	8 (6)	9 (5)	17 (11)
17	9	11	20	0	1	1	9 (6)	10 (7)	19 (13)
18	7	8	15	0	0	0	7 (4)	8 (3)	15 (7)
Adults	15	17	32	2	5	4	13 (4)	15 (−3)	28 (1)
Adult Age Subgroups
19–20	2	3	5	0	0	0	2	3	5
21–22	10	4	14	1	2	3	9	2	11
23–24	2	6	8	1	0	1	1	6	7
25	1	4	5	0	0	0	1	4	5
Total	125	143	268	15	13	28	110	130	240

Note. Adults Group refers to participants from 19–25 years old; M = male, F = female, T = Total; Adult Age Subgroups breaks the adult participants into subgroups based on age with each group containing 2 years.

2.2. Procedures

All participants completed two sessions; a session of EEG data collection that included 4 separate ERP paradigms lasting about 1½ hours, and a session of behavioral testing, including neuropsychological measures, requiring about 1 hour (to be reported elsewhere). Only the data on the third ERP paradigm, the visual flanker task (Eriksen & Eriksen, 1974), are reported in this paper. Procedures for this study were approved by the human research committee at Colorado State University. Written informed consents were obtained from adult participants and from parents of child participants. All child participants signed assent forms prior to participating in the study.

2.3. Electrophysiological Paradigm

The variation of the visual flanker task used for EEG data collection (Eriksen & Eriksen, 1974) in this study consisted of randomly presenting one of four different character arrays on each trial. Each character array consisted of combinations of the letters “H” or “S”: two congruent arrays, “HHHHH” and “SSSSS” (80 trials each); and two incongruent arrays, “SSHSS” and “HHSHH” (160 trials each). The character arrays were displayed for 250ms each, and the screen was blank until the next array appeared. Participants were instructed to press the right or left button corresponding to the central letter, either an S or an H. Mapping between the button press and the central letter was counterbalanced across participants. Participants were instructed to respond as quickly and accurately as possible. For participants aged 10–25, the stimulus onset asynchrony (SOA) was set to 1100ms; for participants 7–9 years old and older children who failed to perform 2 practice runs with at least 50% accuracy with faster speed, the SOA was set to 1500ms (Davies et al. 2004). The percent of children by age that were administered the 1500ms SOA were: 100% of 7 year-olds (n = 13), 89.5% of 8 year olds (n = 17), 71.4% of 9 year olds, 6.7% of 10 year olds (n=1), and 5% of 11 year olds (n = 1). All other participants in the study were administered the 1100ms SOA. Trials were presented in two blocks of 240 trials (480 total) with a break between blocks during which another ERP paradigm was conducted. See Davies, et al., 2004 for more details regarding the paradigm.

2.4. Electrophysiological Recording

The electroencephalogram (EEG) was recorded from 29 tin electrodes embedded in a Quick-cap using a portable QuickTrace system (NeuroScan Company, Charlotte, NC, USA) according to the American Electroencephalographic Society nomenclature guidelines (American Electroencephalographic Society, 1994) with AFz as ground. Only data from Cz were analyzed for the purposes of this study. EEG was recorded with the left earlobe as reference and the right earlobe as an active site. Two bipolar electrooculograms (EOG) were recorded from tin electrodes placed on the left and right outer canthi for horizontal eye movements (HEOG), and on the left supraorbital and infraorbital regions for vertical eye movements (VEOG). Continuous EEG data were recorded with a sampling rate of 500 Hz. Signals were amplified with a hardware gain of 1000. Impedances for the EEG and EOG channels were maintained below 5 kΩ.

Raw EEG data were analyzed offline using the software Brain Vision Analyzer 2.0 (Brain (www.brainproducts.com). Data were referenced to averaged bilateral earlobe electrodes and filtered with a bandpass of 0.23–30 Hz and were segmented into 1400ms duration epochs, spanning from 600ms before to 800ms after incorrect responses. The data were then baseline corrected based on the mean voltage 600 to 400ms preceding response onset. Eye movement artifacts were removed using a regression approach based on VEOG (Segalowitz, 1996) and then baseline-corrected again using the period of 600 to 400ms prior to the response. All segments were then examined for amplitude deviations greater than ± 100 μV and if found, rejected. All segmented data were written to individual files for further processing in MATLAB.

2.5. Adaptive Woody Filter

The individual files of segmented data are then passed to a custom-built MATLAB program that implements the Adaptive Woody Filter procedure to measure and adjust for the trial-to-trial variability in the latency of the ERN component. This template-matching procedure has the following steps. First, a template is obtained by averaging all the incorrect trials as in the traditional manner for generating an averaged ERP for an individual. Then, each segment is analyzed for maximal alignment to the template by calculating a correlation coefficient for a data points in a window representing the 0 to 300 ms of the template, followed by shifting the data 150 times in increments of 1 data point in the segment to the left and then to the right recalculating the correlation coefficient after each shift to find the maximum correlation coefficient as the indicator of best alignment. Once maximal alignment is determined, then the shifted segments are then averaged to obtain a “latency-adjusted” averaged ERP waveform for measuring the ERN component.

Three measures of latency variability were derived for each segment: 1) The correlation coefficient, representing the degree of fit for the shape of the ERP waveform of the segment to the template prior to time shifting the segment; 2) The maximal correlation found after time shifting, which represents the degree of the best fit for the shape of the ERP waveform of the segment to the template; and, 3) The shift value, representing the degree of time shifting, backward or forward, required to obtain the maximal correlation coefficient for the segment. To summarize the degree of success achieve by the latency correction procedure, two types dependent measures were derived for each participant. One type, an indicator for the degree of fit across all segments for each participant, was computed first as the mean of the correlation coefficients computed before any time shifting occurred and then again as the mean of the correlation coefficients computed after the maximal shift was found. The second type, an indicator for the degree of intra-individual variability found in each participant, was computed as the standard deviation of the shift values across all segments.

For both the unadjusted and adjusted averaged ERPs of each participant, peak amplitudes were measured within the time window of −100ms to 50ms for the positive deflection preceding ERN (P300/P3r) and 0–180ms for ERN using a custom-built MATLAB routine (Gavin, 2013) which allows for automatic scoring and visual inspection of ERP components, and, when necessary, allows for manual marking of components. The P3r served as a baseline to calculate the peak-to-peak ERN amplitude. The peak-to-peak ERN amplitude was calculated by subtracting the ERN amplitude from the P3r amplitude. Thus, the ERN measures are reported as nonnegative values reflecting the maximal amount of change in the downward deflection found in ERN window from the maximum peak of the preceding P3r.

To determine which one of the three commonly used methods for measuring the ERN to use in the statistical analyses for this study, the internal consistency (i.e., split-half reliability on odd vs even numbered segments) was calculated for the following amplitude measures; baseline-to-peak, peak-to-peak, and area (i.e., average voltage for a 0 to 100 ms window). Across all participants, internal consistency was the highest for the peak-to-peak ERN measure with r(240) c= .71, p < 0.0001 followed by the baseline-to-peak measure with r(240) = .66, p < 0.0001. The internal consistency was the lowest for the area measure with r(240) = .56, p < 0.0001. In addition to having the highest internal consistency, the peak-to-peak measure was chosen because as illustrated in the individual plots in Figure 1 and the grand averages in Figure 5, the ERN peak can be above the baseline, especially for the youngest children and using peak-to-peak measures preserves the negative deflection of the ERN component. Peak-to-peak measures were also used in Davies, et al. (2004).

Figure 1.

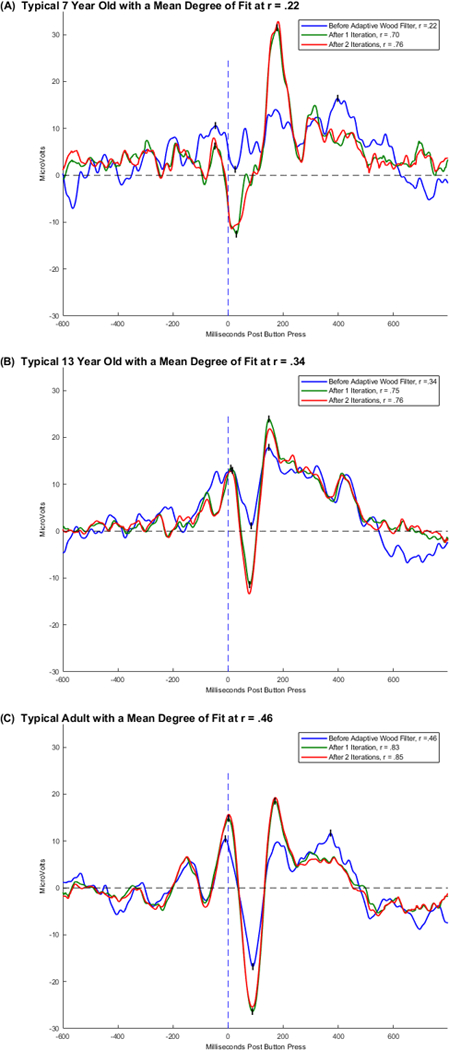
Overlaid plots of averaged ERPs for three individuals who each represent the mean correlation coefficients of fit for their age group prior to use of the Adaptive Woody Filter. For each individual the blue plot represents the individual’s averaged ERP before latency variability correction of incorrect response segments time-locked to the button press (i.e., 0 ms). The green plot represents the same segments averaged after the 1st iteration of the Adaptive Woody Filter used to remove latency variability effects. The red plot represents the same segments averaged after the 2nd iteration of the Adaptive Woody Filter.

Figure 5.

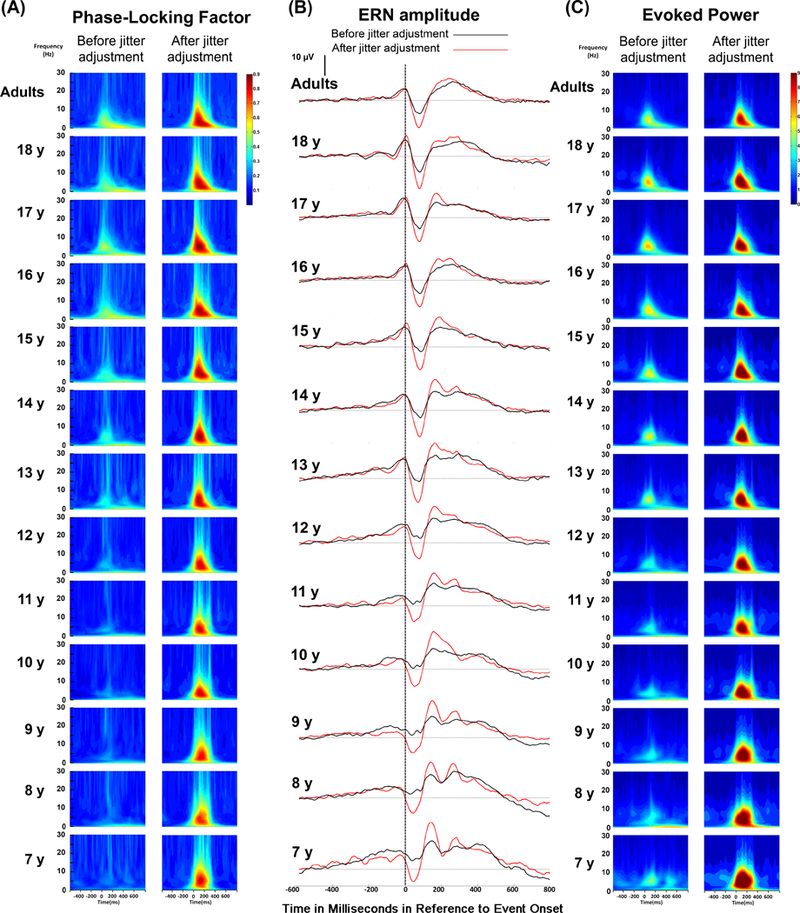
(A) Phase locking factor from time-frequency analysis before and after Adaptive Woody Filter technique. (B) Grand average response-locked ERP for each age group at Cz for error trials before and after applying Adaptive Woody Filter technique. Black line represents the waveform before the adaptive Woody filter; red line represents the waveform after the adaptive Woody filter. C) Evoked power from time-frequency analysis before and after Adaptive Woody Filter technique.

2.6. Time Frequency Analysis

Before and after applying the Adaptive Woody Filter to the individual files of segmented data, a time-frequency analysis was performed on each segment in order to validate the effect of the Adaptive Woody Filter on correcting the latency variability. Using a MATLAB program, a 3 cycle, Morlet wavelet transform was conducted for a frequency range of 1 to 30 Hz in accordance to Roach and Mathalon (2008). To better observe any small changes between groups as a result of maturation or applying the Adaptive Woody Filter, baseline correction was not performed. Two measures, evoked power and phase locking factor (PLF), were computed. Evoked power refers to the signal intensity averaged across trials and PLF refers to signal synchronization across trials. Specifically, evoked power was measured as region of interest (ROIs) and was calculated as the average evoked power from 0–180ms after responses of theta band (4–7 Hz); the PLF was calculated as the average PLF from 0–180ms after responses of theta band.

2.7. Data Analysis

The descriptive data such as means, standard deviations, and standard error of measurements are provided in the tables or figures organized by age groups. These data are reported by age groups (i.e., truncated to year) for individuals < 18 years old and one “adult” age group. All adult participants (i.e., age > 18 years old) were considered as a single group. However, all regression analyses used the exact age (i.e., to the hundredths of years) for all participants, including the adults.

Indices of behavioral performance were measured as the error rate, response time on correct trials, and response time on incorrect trials. Because all plots of the chronological age on the error rate, response time in correct trials, and response time in incorrect trials demonstrated nonlinear trends with two inflections points in each line plot indicative of a possible cubic component and verified with curve fitting, these the data were evaluated using polynomial regressions. Specifically, we included linear, squared, and cubed terms of the chronological age along with sex and an age-by-sex interaction all entered together in a five-variable regression model to predict each of the three behavioral measures, respectively. Additionally, to evaluate the post-error slowing effect, a two factor ANCOVA (2 sexes × 2 trial types) with age as a covariate variable was used. Specifically, the two levels for the trial type were correct trials immediately following correct trials and correct trials immediately following errors.

To evaluate the changes in latency variability before and after the use of the Adaptive Woody Filter technique, the two averaged correlation coefficients for the segment fit before and after latency correction and the standard deviation of the shift were analyzed using the regression analysis. Only age, sex and the age-by-sex interaction variables were used as inputs given that the line plots had no significant inflection points as verified by curve fitting analyses; i.e., the quadratic and cubic components were not statistically significant.

For the EEG analysis, separate analysis of co-variance analyses (ANCOVAs) were performed to test the effect of the Adaptive Woody Filter technique on the baseline-to-peak P3r and the peak-to-peak ERN amplitudes with the condition (before and after latency correction) as the single within factor and a covariate variable, chronological age, as the controlled variable. Because the relationship between age and the ERN amplitude before and after the Adaptive Woody Filter technique also showed nonlinear trends with two inflections points in each line plot indicative of a possible cubic component, a polynomial regression analysis was used to analyze the effect of age on the ERN amplitude before, and after the Adaptive Woody Filter technique. Sex and age-by-sex interaction were also included as predictors to examine the effect of these variables in a manner similar to Davies, et al. (2004). The time-frequency measures of PLF and evoked power obtained before and after latency variability correction were also analyzed using a similar polynomial regression design.

Given that a total of 17 omnibus F tests were conducted with ANCOVA or polynomial regression procedures, a Bonferroni correction procedure was applied to preserve the experiment-wise alpha level of .05. This resulted in the test-wise alpha level being .003 (.05 / 17). Evaluation of beta weight values from the regression analyses were judged at the traditional .05 level as they serve primarily as within-test comparison descriptors. All statistical analyses were performed using SPSS 23.0 for Windows (IBM SPSS Statistics, IBM Corporation).

3. Results

3.1. Behavioral Performance

3.1.1. Error Rate.

The error rate ranged from 2.5% to 29.32% (M = 10.97%, SD = 5.95) across all participants. A paired-sample t test showed that participants made more errors in incongruent trials (M = 12.41%, SD = 6.69) than in congruent trials (M = 8.10%, SD = 5.35), t(239) = −15.664, p < 0.001. Additionally, the Pearson correlation test showed that error rates were not significantly correlated with response times on correct trials (r = −0.071, p = 0.271) or with response times on error trials (r = −0.111, p = 0.086), indicating that participants tried to maintain both accuracy and speed on the task; this result was in line with Davies et al. (2004).

To validate the effect of age, sex, age-by-sex, and age², age³ on the error rate, a step-wise polynomial regression analysis was performed. In the first step age by itself accounted for 6.8% of the variance, Δ F = 17.32, p < 0.0001. In the second step, sex accounted for significant amount of variance, Δ R² = .003, Δ F(1,237) = 8.769, p = 0.002. Thus, after controlling for the effect of age on the error rate, sex contributed significantly to predicting the error rate, β = −0.19, t(239) = −2.961, p = 0.003. Specifically, the error rate in all males (M = 12.14%, SD = 6.02) was significantly higher than all females (M = 9.98%, SD = 5.72). After all five were entered, the predictors significantly accounted for 11.70% variance in the error rate with an adjusted R² = .098, F(5,234) = 6.196, p < 0.0001. However, none of the beta weights of any predictors were significant; i.e., p > 0.05.

3.1.2. Response Time.

To determine the effect of stimuli congruency and response accuracy on the response time, a 2 (congruent vs incongruent stimuli) × 2 (correct vs incorrect response) repeated measured ANCOVA with age as covariate was used. The interaction between congruency and accuracy was significant, F(1,238) = 13.783, p < 0.001, η_p² = .055. Post hoc analyses demonstrated that, for correct trials, the response time on incongruent stimuli (M = 480.95ms, SD = 126.68) was significantly longer than congruent stimuli (M = 451.96ms, SD = 122.85), q = −13.98, p < 0.01; for incorrect trials, no difference was found between the response time on congruent stimuli (M = 379.35ms, SD = 117.94) and incongruent stimuli (M = 376.08ms, SD = 112.80), q = 1.58, p > 0.05. For congruent stimuli, the response time on incorrect trials (M = 379.35ms, SD = 117.94) was significantly faster than correct trials (M = 451.96ms, SD = 122.85), q = 35.01, p < 0.01; for incongruent stimuli, the response time on incorrect trials (M = 376.08ms, SD = 102.80) was significantly faster than correct trials (M = 480.95ms, SD = 126.68), q = 50.57, p < 0.01. The findings are also consistent Davies et al. (2004).

The polynomial regression analyses were used to validate the effect of age, sex, age-by-sex, and age², age³ on the response time separately for correct and incorrect trials. The results are shown in Table 3 and Figure 2. For correct trials, the five predictors together significantly accounted for 73.7% variance in the response time in correct trials with an adjusted R² = .732, F(5,234) = 163.82, p < 0.001. While all three age variables were significant predictors (i.e., beta values with p-values < .001), sex and age-by-sex were not significant. For incorrect trials, the first step regression analyses revealed that age by itself accounted for 40.5% of the variance, Δ F(1,238) = 161.718, p < 0.0001. In the second step, sex accounted for significant amount of variance, Δ R² = .012, Δ F(1,237) = 4.841, p = 0.029. Thus, after controlling for the effect of age, sex contributed significantly to predicting the error rate of incorrect trials, β = .109, t(237) = 2.200, p = 0.029. Specifically, the response time in incorrect trials for males (M = 365.14ms, SD = 96.52) was significantly faster than females (M = 388.40ms, SD = 106.94). When all five predictors were entered together, they significantly accounted for 62.8% variance in the response time in incorrect trials with an adjusted R² = .620, F(5,234) = 79.091, p < 0.0001. However, while all three age variables were again significant predictors, sex and age-by-sex were not significant.

Table 3.

Summary of Regression Models of the Effect of Age, Sex and Age-by-Sex on the Response Times of correct and incorrect trials, Correlation Coefficients, PLF, and theta power before and after latency correction using the Adaptive Woody Filter.

DV	Model Statistics				Standardized Coefficient
	R2	Adj R2	F	p	IVs	β	p
RT in correct trials	.737	.732	131.40	<0.0001	Age	−6.452	<0.0001
					Sex	.177	0.120
					Age x Sex	−.132	0.277
					Age2	9.332	<0.0001
					Age3	−3.620	0.002
RT in error trials	.628	.620	79.091	<0.0001	Age	−8.053	<0.0001
					Sex	.209	0.123
					Age x Sex	−.125	0.385
					Age2	12.891	<0.0001
					Age3	−5.531	<0.0001
Correlation coefficients of the segment fits before correction	.324	.315	37.690	<0.0001	Age	.592	<0.0001
					Sex	.131	0.465
					Age x Sex	−.079	0.676
Correlation coefficients of the segment fits after correction	.055	.043	4.538	0.004	Age	.206	0.035
					Sex	−.104	0.625
					Age x Sex	−.015	0.948
Standard deviation of the shift	0.293	0.285	32.680	<0.0001	Age	−.538	<0.0001
					Sex	.031	0.866
					Age x Sex	−.011	0.955
PLF before correction	0.387	0.374	29.601	<0.0001	Age	−1.770	0.265
					Sex	.307	0.079
					Age x Sex	−.223	0.228
					Age2	6.062	0.064
					Age3	−3.744	0.032
PLF after correction	0.118	0.099	6.245	<0.0001	Age	−2.780	0.145
					Sex	.128	0.539
					Age x Sex	−.130	0.559
					Age2	7.727	0.049
					Age3	−4.827	0.022
Theta power before correction	0.128	0.109	6.844	<0.0001	Age	−3.766	0.048
					Sex	.070	0.736
					Age x Sex	.020	0.930
					Age2	9.339	0.017
					Age3	−5.445	0.009
Theta power after correction	0.103	0.084	5.372	<0.0001	Age	−5.311	0.006
					Sex	−.162	0.442
					Age x Sex	.193	0.390
					Age2	10.297	0.010
					Age3	−5.456	0.010

Note. PLF = phase locking factor; DVs = dependent variables; IVs = independent variables; Adj R² = Adjusted R²; Sig = significant; F = F value; p = p value; β = standardized coefficient

Figure 2.

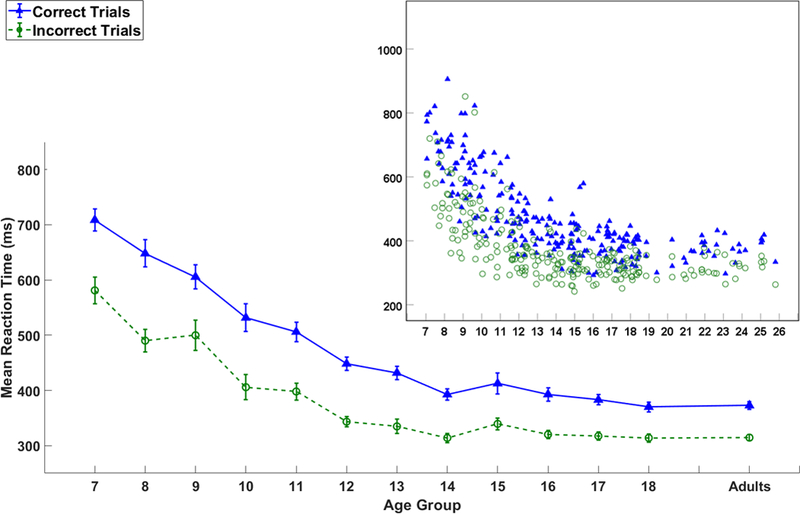
The line graph shows mean response time (ms) of correct and incorrect trials for each age group. Error bars represent +/− 1 standard error. The scatter plot insert shows the dispersion of response times by age as a continuous variable.

3.1.3. Post-Error Slowing.

To evaluate the post-error slowing effect shown in Figure 3, we used a two factor ANCOVA with sex (male vs female) as a between subject factor, trial type as a within subject factor, and age as a covariate. Specifically, the two levels in the trial type were response time in correct trials immediately following correct trials and response time in correct trials immediately following an error trial. The results showed that only the main effect of trial type was significant, F(1,237) = 9.109, p = 0.003, η²_p = .037. Specifically, the response time in correct trials following an error (M = 502.16ms, SD = 140.79) was significantly longer than the response time in correct trials following correct trials (M = 469.57ms, SD = 127.19) for all participants regardless of the age and sex, indicating that for all participants, even those as young as seven-years-old, there was a significant slowing of response speed after errors.

Figure 3.

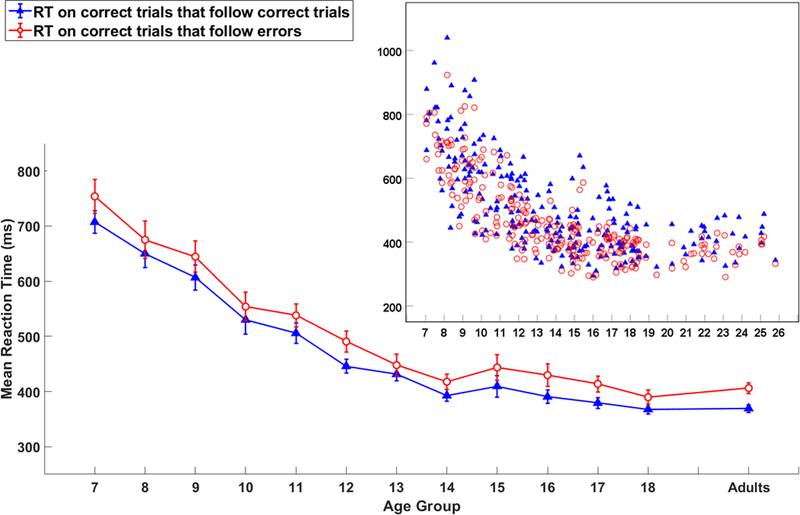
The line graph shows mean post-error slowing (ms) of correct and incorrect trials for each age group. Error bars represent +/− 1 standard error. The scatter plot insert shows the dispersion of post-error slowing by age as a continuous variable.

3.2. Changes in Latency Variability across the Developmental Period

The first aim of this study was to determine if the degree of trial-to-trial variability of the ERN latency systematically changed across the developmental period of 7 to 25 years. To address this aim three summary measures of trial-to-trial variability of the ERN latency were derived for each individual participant. Two measures were derived from the Adaptive Woody Filter procedure, the mean correlation coefficients and the standard deviation of shift. The third measure, the phase locking factor, was obtained from the time-frequency analysis. Analysis of each of these three variables are reported in the following three sections.

3.2.1. Correlation coefficients of the segment fits.

Table 2 lists the mean correlation coefficients for eash age group before and after the Adaptive Woody Filter correction. Figure 4A plots these means and the standard error of the mean of each age group to show visually how the measures of segment fit to the template changes across the developmental period. A two factor ANOVA with age as the between factor (13 age groups) and filter condition as a within factor (pre vs post Adaptive Woody Filter) was used to compare the correlation coefficients of the segment fits before and after adjustement. The results showed there was a significantly better segment fit across all ages after the Adaptive Woody Filter correction, mean r = .75, compared to the mean correlation coefficient before the Adaptive Woody Filter, mean r = .33; F(1,227) = 5168.954, η²_p = .958, p < 0.001 (Table 2). Moreover, the interaction of age and the Adaptive Woody Filter correction was also significant, F(12,227) = 10.622, η²_p = .36, p < 0.001, thus two separate polynomial regression analyses were used to determine the specific effects of the age, sex and age-by-sex on the correlation coefficients before and after the correction, respectively (Table 3).

Table 2.

Mean correlation coefficients (and standard deviation), shift, standard deviation of the shift and phase-locking factor before and after applying Adaptive Woody Filter correction.

		Mean correlation coefficients before adjustment		Mean correlation coefficients after adjustment		Standard deviation of Shift		Phase-locking factor before adjustment		Phase-locking factor after adjustment
Age	n	M	SD	M	SD	M	SD	M	SD	M	SD
7	13	0.22	0.09	0.72	0.04	83.98	13.53	0.21	0.10	0.75	0.15
8	19	0.28	0.10	0.75	0.04	78.23	8.18	0.20	0.09	0.70	0.13
9	21	0.24	0.10	0.73	0.05	83.07	8.18	0.22	0.11	0.71	0.18
10	15	0.25	0.10	0.75	0.05	81.46	9.56	0.22	0.09	0.74	0.12
11	20	0.28	0.08	0.74	0.06	81.16	5.86	0.24	0.10	0.75	0.15
12	21	0.28	0.10	0.75	0.04	78.83	9.60	0.27	0.10	0.76	0.12
13	15	0.33	0.10	0.75	0.04	66.24	14.43	0.32	0.10	0.79	0.12
14	21	0.34	0.12	0.75	0.06	70.29	16.72	0.37	0.12	0.82	0.08
15	16	0.35	0.10	0.75	0.06	67.95	13.36	0.36	0.13	0.81	0.13
16	17	0.42	0.14	0.76	0.06	61.63	15.28	0.42	0.14	0.82	0.10
17	19	0.42	0.12	0.76	0.05	64.76	13.22	0.45	0.12	0.84	0.06
18	15	0.40	0.10	0.75	0.06	64.67	13.14	0.40	0.11	0.81	0.11
Adults	28	0.46	0.14	0.77	0.06	59.35	13.22	0.43	0.14	0.79	0.13
Average		0.33	0.13	0.75	0.05	72.04	14.72	0.32	0.14	0.77	0.13

Note. n = number of participants; M = Mean; SD = standard deviation; the unit for the shift and the SD of shift is data points where 1 data point = 2 ms; Adults group refers to participants 19 to 25 years old.

Figure 4.

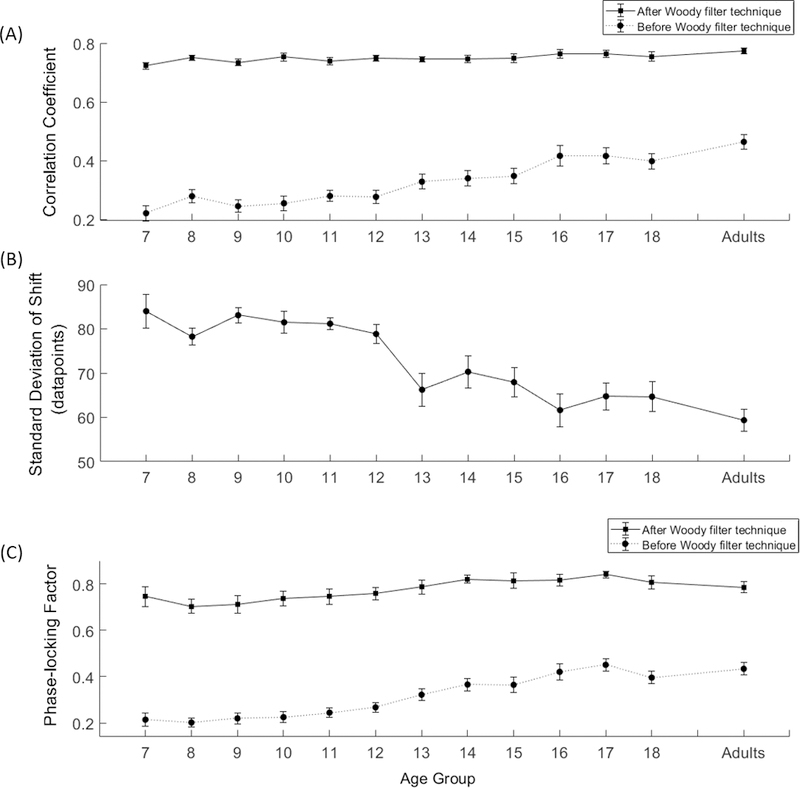
Plots of the three measures of latency variability before and after Adaptive Woody Filter correction showing converging evidence of the presence of trial-to-trial latency for each age group: (A) mean correlation coefficients, (B) mean standard deviation of shifts, and (C) mean phase-locking factors. Error bars depict +/−1 standard error about the means.

The results of the first regression analysis showed that prior to latency correction, the three variable model accounted for a significant portion of the overall variance of segment fit coefficients, R² = 0.32, adj R² = 0.32, F(3,236) = 37.69, p < 0.001. However, only one of the three predictors, age, was found to significantly contribute to prediction of the segment fit coefficients alone when controling for the other predictors. The second regression analysis showed that after latency correction, the three variable model accounted for a small portion of the overall variance of segment fit coefficients as this effect was drasticallly reduced, R² = .06, adj R² = 0.04, F(3,236) = 4.54, p = 0.004 (Table 3). However as a followup, a regression analysis with linear trend of age as the only predictor of segment fit coefficients showed that the linear relationship is significant both before and after latency variability adjustment but again, the relationship was considerably weaker after Adaptive Woody Filter correction: Before adjustment the model statistics were R² = 0.32, adj R² = 0.317, F(1,238) = 111.939, p < 0.001 with a significant linear trend β = 0.566, t(238) = 10.58, p < 0.001; After adjustment the model statistics were R² = 0.041, adj R² = 0.037, F(1,238) = 10.146, p = 0.002, with a significant linear trend, β = 0.202, t(238) = 3.185, p = 0.002. Moreover, the finding also indicated that with increasing age, individual segments more closely match the averaged template. This finding provides evidence for a developmental trend in latency variability such that children exhibit more trial-to-trial variability in ERN peak-to-peak amplitude than adults.

3.2.2. Standard deviation of the shift.

Measures of the average amount of segment shifting and the standard deviation of the segment shifts are presented in Table 2 as group means and standard deviations for each age group. A plot of mean standard deviation of shifts for each age group is shown in Figure 4B. The polynomial regression analysis was used to determine the effect of age, sex and age-by-sex on the standard deviation of the shifts. The results showed that the three variable model accounted for a significant portion of the overall variance of segment fit coefficients, R² = 0.29, adj R² = 0.28, F(3,236) = 32.68, p < 0.0001. However, of the three predictors, only age was found to significantly contribute to prediction of the segment fit coefficients alone when controling for the other predictors (Table 3). However as a followup, a regression analysis with linear trend of age as the only predictor the standard deviation of the shift, the overall model was significant; R² = 0.293, adj R² = 0.29, F(1,238) = 98.657, p < 0.001 with β = −0.541, t(238) = −9.933, p < 0.001. These results demonstrate only a significant linear effect of age on the latency variability; therefore, it is a critical factor that needs to consider in the data analysis.

3.2.3. Phase locking Factor.

Measures of phase locking derived from time-frequency analyses were also used to validate the effect of the Adaptive Woody Filter technique. The group means and corresponding standard deviations for each age are presented in Table 2 and are plotted in Figures 4C and 5A. An ANCOVA with filter condition as a within factor (pre vs post Adaptive Woody Filter) and age as covariate showed that the phase locking factor of theta band (4–7 Hz) from 0–180ms after incorrect responses significantly increased regardless of age after implementing the Adaptive Woody Filter, F(1,238) = 700.64, p < 0.0001, η²_p =.75. This finding supports the conclusion that the Adaptive Woody Filter technique effectively corrected for the latency variability by increasing the signal synchronization across trials for all age groups.

In general, the PLF coefficients showed increasing values with increasing age. Polynomial regression analyses of the phase locking coefficients prior to latency correction showed that the five variable model accounted for a significant portion of the overall variance of PLF coefficients, R² = 0.39, adj R² = 0.37, F(4,235) = 29.6, p < 0.0001. Only the cubic relationship between age and PLF was a significant predictor variable (Table 3). After implementing the Adaptive Woody Filter, there was considerably less change in the PLF coefficients with increasing age. Though the five variable regression model still accounted for a significant portion of the overall variance of segment fit coefficients, the amount of variance accounted for was reduced, R² = 0.12, adj R² = 0.10, F(5,234) = 6.24, p < 0.0001. Furthermore, both the quadratic and the cubic relationship between age and PLF were significant predictor variables (Table 3).

3.3. Changes in ERN Amplitude across the Developmental Period

The second aim of this study was to determine if the nature of developmental trend of ERN amplitude changed after correcting for trial-to-trial latency variability. To address this aim we compared the mean peak-to-peak ERN amplitudes measured before and after latency correction. Because the ERN amplitude reflects theta band activity, we also compared mean theta power before and after latency correction. Regression analyses were then used to determine the relative contribution age, sex, latency variability (PLF) and theta power measures to the variability of the ERN amplitude found in the study sample. These analyses are reported in the following sections beginning with the analysis of changes in theta power.

3.3.1. Evoked Theta Power.

To evaluate the effect of the Adaptive Woody Filter on the evoked power, an ANCOVA with filter condition as a within factor (pre vs post Adaptive Woody Filter) and age as covariate showed that the evoked power of theta band (4–7 Hz) from 0–180ms after incorrect responses significantly increased regardless of age after implementing the Adaptive Woody Filter, F(1,238) = 576.87, p < 0.001, η²_p = .71. The group means and corresponding standard deviations for each age are presented in Table 4 and are plotted in Figure 5C. This finding suggested that the Adaptive Woody Filter technique produced greater signal power at the theta band for all age groups.

Table 4.

Mean peak-to-peak amplitude of ERN (and standard deviation) and theta power before and after application of the Woody filter technique. The ERN measures reflect the maximal amount of change in the downward deflection of the ERN from the maximum of the preceding positivity, the P3r.

		ERN before adjustment (μV)		ERN after adjustment(μV)		Theta power before adjustment		Theta power after adjustment
Age	n	M	SD	M	SD	M	SD	M	SD
7	13	11.75	4.82	23.72	15.00	4.01	2.47	12.60	3.94
8	19	8.98	4.60	21.25	7.40	3.36	1.37	10.25	3.07
9	21	9.29	4.44	19.57	9.38	3.27	1.73	9.99	3.40
10	15	8.87	5.13	22.00	7.77	3.27	1.56	10.02	3.13
11	20	8.11	3.05	19.48	6.84	3.39	1.38	8.96	2.73
12	21	10.05	5.57	21.18	7.46	3.54	1.52	9.18	2.24
13	15	13.27	5.59	23.98	8.07	4.37	1.54	9.27	2.20
14	21	13.85	6.87	24.63	8.76	4.73	2.15	9.78	2.79
15	16	15.00	7.66	27.17	10.10	4.92	2.55	9.98	3.33
16	17	15.79	8.55	23.57	9.09	5.15	2.53	8.77	2.73
17	19	17.27	6.62	24.62	7.69	5.39	1.88	8.94	2.14
18	15	17.73	8.68	27.99	11.70	5.41	3.06	9.31	3.91
Adults	28	15.72	7.58	22.52	8.93	4.67	1.96	7.81	2.83
Average		12.74	6.99	22.99	9.18	4.26	2.11	9.47	3.06

Note. n = number of participants; M = Mean; SD = standard deviation; Adults group refers to participants 19 to 25 years old.

Prior to latency correction, evoked theta power was found to only slightly decrease with increasing age and the five variable regression model did account for a significant portion of the overall variance of evoked theta power, R² = 0.13, adj R² = 0.11, F(5,234) = 8.59, p < 0.001. However, after correction, evoked theta power showed a much stronger tendency to decrease as age increased (as illustrated in changes of mean theta power shown in Table 4). After applying the Adaptive Woody Filter, the five variable regression model showed that the amount of evoked theta power variance accounted for was reduced but still significant, R² = 0.10, adj R² = 0.085, F(4,235) = 6.54, p < 0.001 (Table 3). The results showed that the linear, quadratic, and cubic relationships between age and evoked power were strong predictors both before and after implementing the Adaptive Woody Filter (Table 3). After controlling for age, sex and the age-by-sex interaction variables did not significantly predict the evoked power both before and after Adaptive Woody Filter correction.

3.3.2. Validity of Peak-to-Peak Measures of ERN.

To assure that the peak-to-peak measurement of the ERN was still valid after latency correction, two evaluations were conducted. First, a repeated measure ANCOVA was performed to assess the effect of the Adaptive Woody Filter technique on baseline-to-peak P3r amplitudes. The results showed that the main effect of the Adaptive Woody Filter technique was not statistically significant, F(1,238) = .49, p = 0.48, η²_p = .002, suggesting that after controlling for chronological age, the amplitude of the Adaptive Woody Filter adjusted P3r (M = 9.35 μV, SD = 7.01) was not significantly larger than the amplitude P3r before the adjustment (M = 9.09 μV, SD = 6.0). The covariate of age was also not significant, F(1,238) = .17, p = 0.68, η²_p = .001.

Next, the internal consistency was again evaluated for the peak-to-peak ERN measure and, for completeness, contrasted to the other two frequently reported measures of ERN, baseline-to-peak and area measures. For the peak-to-peak ERN, the measure that had the highest internal consistency across all participants before latency adjustment with an r(240) = .712, p < 0.0001, significantly increased to r(240) = .784, p < 0.0001 after latency adjustment, one-tail Fisher Z(240) = 1.77, p = 0.038. The internal consistency for the baseline-to-peak measure also increased from r(240) = .663, p < 0.0001 before latency adjustment to r(240) = .707, p < 0.0001 after adjustment but the increase was not statistically significant, one-tail Fisher Z(240) = .90, p = 0.184. Interestingly, the area measure which had the lowest internal consistency before latency adjustment with an r(240) = .556, p < 0.0001, showed the greatest change to an r(240) = .732, p < 0.0001 which was also statistically significant, one-tail Fisher Z(240) = 3.33, p = 0.0009.

3.3.3. Changes in ERN Peak-to-Peak Amplitude.

A repeated measure ANCOVA was used to test the effect of the Adaptive Woody Filter technique on peak-to-peak ERN amplitudes. The results showed that the main effect of the Adaptive Woody Filter technique was statistically significant, F(1,238) = 157.000, p < 0.001, η²_p = .397, suggesting that after controlling for chronological age, the amplitude of the Adaptive Woody Filter-adjusted ERN (M = 22.99 μV, SD = 9.18) was significantly larger than the amplitude ERN before the correction (M = 12.74 μV, SD = 6.99; see group means and standard deviations in Table 4 and Figures 5B and 6). The covariate of age was significant, F(1,238) = 15.69, p < 0.001, η²_p = .062. The results show that after applying the Adaptive Woody Filter the ERN increased in amplitude across all age groups. No systematic changes were found for ERN peak latency before and after Adaptive Woody Filter corrections across the age groups (Table 5).

Figure 6.

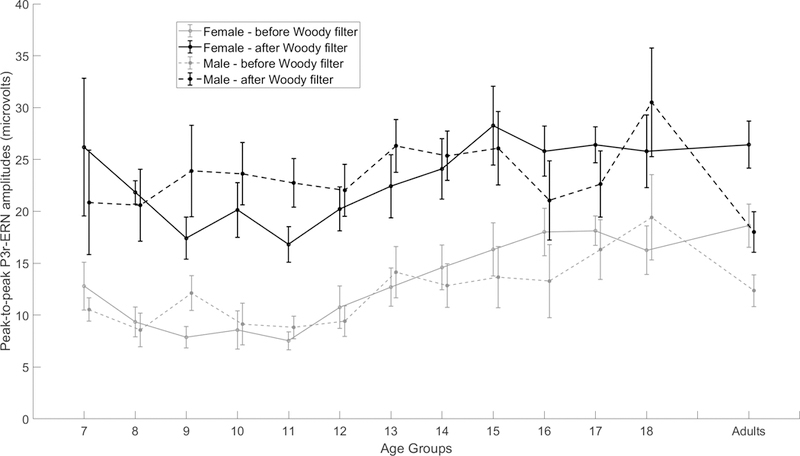
Mean peak-to-peak ERN amplitude at Cz for each age group by sex before and after applying the Adaptive Woody Filter technique. Error bars denote +/−1 standard error of means.

Table 5.

Mean latencies of ERN peak (and standard deviation) before and after application of the Woody filter technique.

		Latency before adjustment		Latency after adjustment
Age	n	M	SD	M	SD
7	13	38.77	31.25	41.54	36.88
8	19	44.95	34.56	42.63	25.57
9	21	45.81	31.79	56.95	29.22
10	15	62.00	44.69	65.07	37.56
11	20	58.40	34.36	58.90	30.33
12	21	66.38	19.91	68.57	20.37
13	15	72.27	15.29	69.73	11.08
14	21	79.43	16.00	79.62	17.91
15	16	87.63	16.48	85.38	14.94
16	17	75.53	19.73	79.41	17.83
17	19	74.53	19.82	75.37	16.64
18	15	81.73	21.92	82.67	13.52
Adults	28	76.29	17.37	77.36	16.78
Average		66.44	24.86	67.94	22.20

Note. n = number of participants; M = Mean; SD = standard deviation;

Adults group refers to participants 19 to 25 years old.

Two two-step polynomial regression models were used to validate the predictors of the individual differences in ERN amplitude, one before and one after the Adaptive Woody Filter technique. Variables entered in the first step included: age, sex, age-by-sex, age², age³ (Model 1) and the variables of the PLF and power of theta were added to these in the second step (Model 2). The results of the bivariate correlations of each of the seven predictor variables to ERN amplitude are shown in Table 6 and the results of the regression analyses are shown in Table 7. Before applying the Adaptive Woody Filter, the five variable model in the first step (Model 1) accounted for a significant portion of the overall variance of ERN amplitude, R² = 0.21, adj R² = 0.19, F(5,234) = 12.45, p < 0.0001. The principal variables accounting for a significant amount of variance for the ERN amplitude in Model 1 were the linear, quadratic, and cubic relationships of age along with the age-by-sex interaction. In the second step, the addition of PFL and power derived for theta oscillations together accounted an additional 5.2% of the variance in ERN amplitude (Δ F(2,232) = 8.25, p = 0.0003) with this seven variable model also being significant, R² = 0.26, adj R² = 0.24, F(7,232) = 11.80, p < 0.0001. All variables except sex accounted for a significant portion of the overall variance.

Table 6.

Descriptive correlations performed to provide foundation for the subsequent regression analyses conducted to evaluate predictors of ERN peak-to-peak amplitude.

		Bivariate Correlations
		Age	Sex	Age-by-Sex	Age2	Age3	Evoked theta power	Phase Locking Factor
Before correction	ERN amplitude	.389	.073	.221	.372	.342	.194	.279
	Age		−.006	.324	.986	.949	−.054	.416
	Sex			.901	.004	.016	.115	.076
	Age-by-Sex				.333	.338	.084	.191
	Age2					.988	−.069	.379
	Age3						−.081	.333
	Evoked theta power							.711
After correction	ERN amplitude	.115	.001	.076	.100	.079	.156	.031
	Age		−.006	.324	.986	.949	−.520	−.079
	Sex			.901	.004	.016	.054	.065
	Age-by-Sex				.333	.338	−.110	.036
	Age2					.988	−.480	−.064
	Age3						−.434	−.048
	Evoked theta power							.706

Table 7.

Summary of Regression Models evaluating the variables of Age, Sex, Age-by-Sex, along with the phase locking factor (PLF) and power of theta to predict ERN amplitude measured before and after latency correction using the Adaptive Woody Filter.

DV	Model Statistics				Standardized Coefficient
	R2	Adj R2	F	p	IVs	β	p
ERN amplitude before correction (Model 1)	.210	.193	12.453	<0.0001	Age	−4.987	0.006
					Sex	−.359	0.070
					Age x Sex	.503	0.017
					Age2	11.494	0.002
					Age3	−6.448	0.001
ERN amplitude before correction (Model 2)	.263	.240	11.803	<0.0001	Age	−5.277	0.003
					Sex	−.365	0.058
					Age x Sex	.486	0.018
					Age2	12.392	0.001
					Age3	−6.950	0.0004
					Theta power	.363	0.0003
					PLF	−.225	0.041
ERN amplitude after correction (Model 1)	.065	.045	3.261	0.007	Age	−4.208	0.033
					Sex	−.533	0.014
					Age x Sex	.612	0.008
					Age2	9.284	0.022
					Age3	−5.300	0.014
ERN amplitude after correction (Model 2)	.209	.185	8.769	<0.0001	Age	−2.888	0.114
					Sex	−.487	0.015
					Age x Sex	.557	0.009
					Age2	7.904	0.035
					Age3	−4.877	0.015
					Theta power	.729	<0.0001
					PLF	−.433	<0.0001

After applying the Adaptive Woody Filter, in the first step all five variables accounted for significant amount of variance but overall, the variance of ERN amplitude accounted for was greatly reduced and no longer significant based on the test-wise alpha level, R² = 0.06, adj R² = 0.04, F(5,234) = 3.261, p = 0.007 (Table 7). However, in the second step, the addition of PFL and power derived for theta oscillations together accounted an additional 14.4% of the variance in ERN amplitude (Δ F(2,232) = 21.14, p < 0.0001) with this seven variable model being significant, R² = 0.21, adj R² = 0.18, F(7,232) = 8.77, p < 0.0001. All variables except age accounted for a significant portion of the overall variance.

4. Discussion

The purpose of this study was to evaluate the degree to which trial-to-trial latency variability in ERPs could account for part of the maturation effects observed in the ERN amplitude measured during a performance monitoring task. Although latency variability has been known to attenuate the averaged ERP amplitude, which can in turn lead to inaccurate interpretation of the results, few researchers address this issue in their study designs. In this study, we applied the Adaptive Woody Filter technique to adjust for latency variability in ERN data collected from 240 participants aged 7–25 years. The simplicity of the Adaptive Woody Filter technique allowed for a straightforward demonstration and measurement of the trial-to-trial variability found in the ERPs of all participants across age groups. The wide age range of participants allowed us to study the effect of age on ERN amplitude as well as on latency variability. Furthermore, our implementation of the Adaptive Woody Filter not only allowed for the measurement of variability but also removed the latency variability effect from each individual’s averaged ERP allowing for the assessment of developmental trends of the ERN without the confound of trial-to-trial variability. Including this technique in the study design allows researchers to disassociate the maturational effects of trial-to-trial latency variability from the maturational effects on ERN amplitude. By implementing this approach, researchers will have a measure of the developmental trajectory of performance monitoring, not confounded by the maturation of trial-to-trial latency variability.

Several findings emerged from this study related to our first hypothesis which predicted measures of trial-to trial variability of the ERN latency to be greatest in young children and decrease with increasing age. First, as expected, the presence of trial-to-trial latency variability of the ERN component was found in individuals at all ages using several measures of fit and intra-individual variability. Second, for each latency variability measure, the degree of trial-to-trial variability was shown to decrease as the age of the participants increased. Third, the success of the Adaptive Woody Filter technique to remove the trial-to-trial variability was demonstrated in a straightforward manner in the changes in the measures of fit and intra-individual variability before and after applying the filter. However, even after the latency variability effects were removed and adjusted averaged ERPs were obtained, a more subtle but significant nonlinear developmental trend was still found in the amplitude of the ERN component. This third finding addresses our second hypothesis that a modified developmental trend in ERN amplitude would exist following the correction of latency variability compared to the developmental trend prior to adjustments.

Interpretation of the results reported in this paper should take into account that the younger children included in this study were administered the paradigm with a longer SOA of 1500 ms when they were not able to perform two practices with at least 50% accuracy with the stimuli presented faster (i.e., SOA 1100 ms). This study design was based on two assumptions. First, the longer SOA was necessary to preserve enough children at the younger ages in the study because if their accuracy rate was no better than chance their data would need to be excluded. Second, in several studies that have manipulated speed and accuracy, it was found that the ERN was smallest in the speeded condition compared to the accuracy condition (Gehring, et al 1993) and Falkenstein, Hoormann, Christ, & Hohnsbein (2000) argued that speed pressure impairs the response determination process for both correct and error trials. Therefore, to better equalize the speed accuracy trade-off affect across ages, two SOAs were utilized in this study. It is possible however that the SOA selected for the young children may still have provided too much speed pressure relative to the speed pressure required for the adults causing the ERN amplitude to be smaller in children.

4.1. Development Trends of Latency Variability

The three measures of latency variability (i.e., mean correlation coefficients, SD of Shifts, and phase locking factors) showed converging evidence of the presence of trial-to-trial latency variability across all ages (Figure 4). Regression analyses revealed that significant linear age effects were found for predicting for the latency variability measures of correlation coefficients and SD of shift and not for PLF when controlling for the effects both sex and age-by-sex interaction variables. In contract, the sex and the age-by-sex interaction variables were not significant predictors of the three measures of latency variability when controlling for the effects of age. Furthermore, all three measures showed a similar pattern of developmental changes where latency variability was the greatest at in the 7 year olds and decreased as age increased to 25 years of age.

Before latency correction, the average correlation coefficients revealed that the relationship of segments to the template for the voltage measures in the period the 0 to 300 ms (i.e., the P3r-ERN-Pe window) is quite variable at the youngest ages with a mean r value of .22 for 7 year olds but does improve with increasing age up to a mean r value of .46 for the adults. The amount of latency deviation from the maximal peak of ERN in the template for a given individual is reflected in the standard deviation (SD) of the temporal shifts measure (SD of Shifts). SD of Shifts was found to be the greatest at the youngest age group (M = 83.98) and progressively decreased across the age range with the adults having the lowest mean value (M = 59.35). The phase locking factor (PLF), a measure of the degree of synchrony of the theta band oscillations across the segments of an individual, revealed significant cubic trends with the lowest value found at the youngest age group (M = .21) and progressively increasing across age with the adults having the highest mean value (M = .43) before latency correction. These results indicate that the ERN component may not always be well synchronized to the actual button press as the traditional averaging procedure for the ERPs has assumed. Furthermore, this traditional assumption is even less valid for performance monitoring studies when the participants are drawn from younger age groups.

The differences in trial-to-trial latency variability in the ERN found across the age groups is not surprising, as it is quite reasonable to expect the performances of children during an error processing task to be more variable than those of adults. In this study, the measure of the latency variability is still referenced to the button press and; therefore, the temporal variation in the motor systems may also contribute to the latency variability in the ERN. Specifically, the variations in the timing of the activation and the coordination of various neural circuits related to the attentional control, stimulus recognition, response planning, motor activation, and response evaluation could be potential reasons for the latency variability. Identifying the specific sources of neural activity that contribute to the trial-to-trial variability will require more elaborate procedural control strategies and measures in future studies beyond those implemented in this study. Therefore, caution should be observed in directly associating the variability in the ERN timing to any one of the neural systems related to response monitoring.

4.2. Removing the Latency Variability Effects

The success of the Adaptive Woody Filter technique to remove the trial-to-trial variability was demonstrated in a straightforward manner in the statistically significant changes in the measures of fit and intra-individual variability found after applying the filter compared to the measures obtain before the filter was applied. Our data suggested that only a single iteration of the Adaptive Woody Filter is needed to produce a substantial sharpening of the shape of the ERN component and an increased negativity in ERN amplitude in each individual’s averaged ERP. The effects of the Adaptive Woody Filter are visually apparent in the examples of individual averaged ERPs (Figure 1) and grand averaged ERPs (Figure 5B). Furthermore, after applying the Adaptive Woody Filter the finding that the mean correlation coefficients values were nearly equal across all age groups varying only between .72 and .77 with nearly equal standard deviations suggest it does well in standardizing the ERPs in the time domain (Table 2). Additionally, the mean phase locking values were more similar across all age groups after applying the filter with values ranging from .70 to .84 than before applying the filter which ranged from .20 to .45 (Table 2). Combined, these data suggest that the Adaptive Woody Filter successfully removes the latency variability effect from each individual’s averaged ERP. Moreover, while a number of ERNs of larger amplitude were obtained in adult participants after applying the filter, the sharpening effects were even more pronounced in child participants (Figure 1). Thus, the use of the Adaptive Woody Filter reveals the definitive presence of the ERN in the adjusted waveforms, especially for younger children age 7–11 years where its presence was distorted and attenuated in the unadjusted grand averaged ERPs.

The performance of the Adaptive Woody Filter to adjust for latency variability of the ERN is similar to that seen for other ERP measures previously investigated, such as the N1-P2 (Wastell, 1977), P300 (Ford et al., 1994; Ruchkin & Sutton, 1978), P50 measures (Patterson et al., 2000). It should be noted that other methods, such as the maximum-likelihood method (e.g., Tuan, Mocks, Kohler, & Gasser, 1987), have been found to be slightly superior to the Woody Filter when signal amplitude varies from trial to trial and background amplitudes are “realistic” (Jaskowski & Verleger, 2000)—that is, when background noise reflects levels found in most adult recordings. However, these studies of the maximum-likelihood method utilized simulated EEG data rather than actual EEG recordings. Direct comparison of these two approaches in the future may provide additional insights regarding the degree of trial-to-trial variability of the ERN component in children and adults. Both the Adaptive Woody Filter and the maximum-likelihood methods can be used to measure the degree of latency variability within a set of segments (i.e., ERPs) but more importantly, both can also be used to re-align the segments thereby removing the latency variability when one produces adjusted averaged ERPs. The ability to re-align segments goes beyond the approach used by DuPuis et al., 2015. Their measures of signal temporal consistency from time-frequency decomposition could only measure the phase-locking factor but cannot be used to find the best fit and, thus, re-align the single segments for the averaging process. Interestingly, once the segments are re-aligned in time, time-frequency decomposition processing can be used to evaluate the effects of removing latency variability on oscillatory and phase-locking measures as well.

DuPuis and colleagues, 2015, reported that average spectral power of the theta band from 0 to 100 ms did not correlate with temporal consistency (i.e., phase coherence values). DuPuis and colleagues purported that this finding suggests that power and phase coherence each may contribute independently to ERN amplitude. However, in our study evoked theta power and phase locking factor (i.e., temporal consistency; PLF) demonstrated a strong relationship before (r = .71) and after latency correction (r = .71; Table 6). One difference in these two studies that could account for this difference is that we used a 0–180 window to measure evoked power and PLF and the DuPuis et al., 2015 study used a 0 – 100 window. Although our results suggest that evoked theta power and phase locking factor are strongly related, both evoked theta power and PLF uniquely contributed to the ERN amplitude, especially after latency correction shown by the regression models (Table 7), providing evidence that power and temporal consistency contribute independently to ERN amplitude.

While this study demonstrates the validity of the application of the Adaptive Woody Filter technique to the ERN component of an error monitoring task, the utility of this technique for ERP components from other paradigms should not be assumed. The success of the Adaptive Woody Filter in this study can be directly attributed to the unique aspects of the ERN component itself. Although the original averaged ERP for young children at times yielded a small and possibly distorted ERN component, it could easily be measured in the individuals included in the data analysis. Furthermore, the ERN can often be identified visually in single trials. Finally, the stability across all age groups of the mean correlation coefficients measuring the fit of the individual trial segments to the averaged ERP after the latency jitter adjustments support the robustness of technique to identify the ERN component at all ages. If other ERP components lack similar robustness as in the ERN and are difficult to visually identify in single trials, the Adaptive Woody Filter may not be a valid technique to “sharpen” the components, and thus may not yield new information about brain processing abilities, as this study shows for the development of the ERN amplitude.

4.3. Development Trends of the ERN Measures

The developmental trend of the ERN measures found in this study prior to our application of the Adaptive Woody Filter are consistent with the results of previous studies. First, we found a significant linear and nonlinear developmental trend in ERN amplitude from age 7 to age 25. This finding supports that ERN amplitude is a developmental phenomenon that reflects the age-related changes of underlying neural processes and is consistent with other studies that demonstrate the effect of age on the ERN amplitude (Davies, et al., 2004; DuPuis et al., 2015; Hajcak, et al., 2008; Hanna, et al., 2012; Ladouceur et al., 2012). Since ERN amplitude reflects the maturation of anterior cingulate cortex (ACC), our results support the protracted maturation of the ACC from childhood throughout adulthood (Kelly et al., 2009; Luu, Tucker, Derryberry, Reed, & Poulsen, 2003). However, in addition to the significant linear and quadratic relationship of age and the ERN amplitude reported in Davies, et al. (2004), a significant cubic relationship between age and the ERN amplitude was found in the present study. Specifically, based on the visual inspection, such a cubic relationship has a descending trend from 7 year-old to 11 year-old, and the trend arises from 11 year-old to 18 year-old and again slightly descends through early adulthood (Figure 6). Considering that the sample size in the present study is larger than the sample size reported in Davies et al. (2004), and given that the Adaptive Woody Filter technique removes the latency variability in the ERN component, we believe that the cubic relationship found in this study might be a better description of the developmental trend of ERN amplitude from age 7–25 year-old. Also, consistent with Davies et al. (2004), we found that the age-by-sex interaction variable but not sex to be a significant predictor of ERN amplitude both before latency correction after controlling for the effects of age (linear and curvilinear), theta power, and PLF. Interestingly, the sex and age-by-sex interaction variables were not significant predictors of either PLF or theta power before or after latency correction. A novel finding from this study is the evidence that theta power and PLF are also significant predictors of ERN peak-to-peak amplitude before, and more so after, latency correction after controlling for the effects of age (linear, curvilinear and cubic), sex, and age-by-sex interaction.

One possible explanation for the fluctuations in ERN amplitude among age groups might be related to the maturation of the dopamine system since the mesencephalic dopamine system plays a major role in production of ERN amplitude (Holroyd & Coles, 2002). A multitude of changes of the dopamine system occur during development with dopaminergic innervation in the PFC peaking during adolescence evidenced by increased dopamine fiber density and dopamine concentration (Kalsbeek et al, 1988; Leslie et al., 1991; Wahlstrom, et al., 2007; Wahlstrom, et al, 2010). However, development of the dopaminergic system is very complex (see Lambe, et al., 2000) and interactions with other neural systems likely account for development of cognitive functions such as performance monitoring and these interactions possibly contribute to nonlinear trajectories.

The developmental trend of phase locking factor found in this study prior to our application of the Adaptive Woody Filter indicates that synchrony of theta oscillations increases from childhood to adulthood in our cross-sectional sample (Figure 5A). Concomitant with phase locking factor, the evoked theta power before correction of latency variability decreases from childhood to adulthood. These findings suggest that the synchrony of the signals increases with age, implying that latency trial-to-trial variability decreases with age. These results are consistent with the recent longitudinal study conducted with young children, ages 5 – 8 years, that temporal consistency increased in the children as they aged, but the magnitude of the signal decreased in children as they aged (DuPuis et al., 2015). However, once the Adaptive Woody Filter successfully adjusted the trial-to-trial variability, the mean phase locking values were more similar across all age groups after applying the filter and the observed developmental trend of the evoked power of the theta band reverses. That is, the evoked theta power after adjustment for latency variability was found to decrease with both linear and nonlinear trends from childhood to adulthood (Figure 5C).

4.4. Conclusion

The overall objective of this study was to determine the developmental trend of trial-to-trial latency variability of the ERN from 7 to 25 years of age and also to determine the nature of the developmental trend of the ERN amplitude after correcting for latency variability. The primary results of this study were as follows. Using three measures of latency variability, the degree of trial-to-trial latency variability was shown to decrease as the age of the participants increased from 7 to 25 years. The Adaptive Woody Filter technique was successful in removing the trial-to-trial latency variability and results were validated by the demonstration of changes in the measures of fit and intra-individual variability before and after applying the filter. Finally, a more subtle but significant nonlinear developmental trend was still found in the amplitude of the ERN component after removing the latency variability compared to the developmental trend before the adjustment.