Cognition as a Window into Neuronal Population Space

Abstract

Understanding how cognitive processes affect the responses of sensory neurons may clarify the relationship between neuronal population activity and behavior. However, tools for analyzing neuronal activity have not kept up with technological advances in recording from large neuronal populations. Here, we describe prevalent hypotheses of how cognitive processes affect sensory neurons, driven largely by a model based on the activity of single neurons or pools of neurons as the units of computation. We then use simple simulations to expand this model to a new conceptual framework that focuses on subspaces of population activity as the relevant units of computation, uses comparisons between brain areas or to behavior to guide analyses of these subspaces, and suggests that population activity is optimized to decode the large variety of stimuli and tasks that animals encounter in natural behavior. This framework provides new ways of understanding the ever-growing quantity of recorded population activity data.

INTRODUCTION

Cognitive processes that improve perception, such as attention, learning, and motivation or arousal, are unique tools in the study of the relationship between neurons and behavior. Understanding what changes in the responses of sensory neurons when behavioral performance improves is key to understanding what aspects of the neural code are most important for encoding sensory stimuli and guiding behavior in the first place.

The effects of cognition on small numbers of sensory neurons are well studied. Numerous studies have shown that cognitive processes multiplicatively scale, or change the gain of, the trial-averaged responses of individual sensory neurons (Gilbert & Sigman 2007, Maunsell 2015). Recently, a growing number of studies have demonstrated that cognition also affects the response variability shared between pairs of neurons [termed spike count or noise correlations, or r_SC] (for a review, see Cohen & Kohn 2011).

However, linking these changes in small numbers of neurons to performance has been difficult. The relationship between single sensory neurons and behavior is weak and requires large amounts of data to quantify (Nienborg et al. 2012). Models have focused on whether response changes associated with cognition improve the amount of sensory information encoded by neuronal populations, but the relationship between single neurons, noise correlations, and information is complex (Kohn et al. 2016).

Most models designed to relate neuronal activity to perception are built on the idea that the individual neuron is the critical unit of neural computation. These models have been invaluable for generating hypotheses and integrating experimental data. However, while improvements in recording technology have made it possible to monitor the responses of larger populations of neurons, our understanding of neural coding has not kept pace with the technology. It has become clear that understanding the relationship between large populations and performance is not simply a matter of scaling up old analyses and models.

Instead, we propose that the relationship between sensory neurons and behavior requires a new conceptual framework and experimental and analytical strategy. We propose the following:

1. The relevant units of computation are arbitrary combinations of the responses of many neurons rather than average firing rates of groups of neurons with certain properties.

2. To gain insight into how these subspaces guide behavior, it is critical to compare population activity to either the activity of neuronal populations in other brain areas or the animal’s behavior on a trial-to-trial basis.

3. Rather than optimally discriminating responses to a specific pair of stimuli in a laboratory task, animals naturally read out stimulus features using decoding strategies that would work for the large set of stimuli and behavioral tasks they encounter in natural vision.

   Here, we describe the framework that has guided much of the research in this field, review insights from new experiments, and use novel simulations to investigate the implications of these new ideas.

THE POOLING MODEL

The conceptual foundation for nearly all efforts to understand the relationship between sensory neurons and behavior is a simple model that is often referred to as the pooling model (Shadlen et al. 1996). This model has provided a rigorous basis for making and testing predictions about the relationship between neuronal activity and behavior, and it is arguably the primary reason that our understanding of the neural computations underlying perceptual decision making outpaces our understanding of the mechanisms underlying other systems and behaviors. Accordingly, the pooling model has had a broad influence across many fields of neuroscience (Brody & Hanks 2016, Carandini & Churchland 2013, Gold & Shadlen 2007, Heekeren et al. 2008).

The pooling model was developed to explain the responses of motion direction-selective neurons in the middle temporal area (MT) while rhesus monkeys performed a challenging perceptual discrimination task (Parker & Newsome 1998). In the basic conception of the model, the responses of groups of MT neurons encode sensory evidence in favor of each of the two possible behavioral choices. For example, in a left-right discrimination task, a pool of leftward-preferring MT neurons would provide evidence in favor of leftward choices and an analogous pool would provide evidence in favor of rightward choices. The model makes decisions by comparing the average responses of the neurons in the two pools.

For the study of cognition and behavior, the pooling model’s greatest strength is that its simple conceptual framework generated many testable hypotheses about how neuronal activity might depend on cognition and how those changes might improve perception. In fact, although it is rarely cited for this inspiration, all the predominant hypotheses about how cognition improves perception can be thought of as coming from the framework of the pooling model.

PREDOMINANT HYPOTHESES ABOUT HOW COGNITIVE PROCESSES IMPROVE PERCEPTION

Hypothesis 1: Cognitive Processes Improve Sensory Information Encoding

Support

The first and, by far, most studied hypothesis is that cognitive processes improve performance by improving the amount of stimulus information that is encoded in the activity of a population of neurons. In the context of the pooling model, improving the signal-to-noise ratio of the mean rate of the neurons in each pool would create a larger difference between the responses of the two pools.

Essentially all studies that have focused on how cognitive processes affect the responses of neurons in one area of visual cortex have addressed this first hypothesis. Numerous studies spanning many visual cortical areas and tasks have revealed that directing attention to a particular location or feature increases the gain of the mean firing rates of neurons that are tuned for that location or feature (for reviews, see Anton-Erxleben & Carrasco 2013, Desimone & Duncan 1995, Maunsell 2015, Maunsell & Cook 2002, Maunsell & Treue 2006, Reynolds & Chelazzi 2004, Yantis & Serences 2003), and global cognitive processes such as arousal have similar effects (Boudreau et al. 2006). Attention (Cohen & Maunsell 2009, Mitchell et al. 2007) and learning (Raiguel et al. 2006) are also associated with modest decreases in the trial-to-trial variability of individual neurons. Both of these observations are consistent with the idea that cognition improves perception by increasing the signal-to-noise ratio of single neurons.

Additionally, the pooling model suggests that noise correlations can affect stimulus information because positively correlated noise cannot be averaged out by the pooled signal (Abbott & Dayan 1999, Averbeck et al. 2006, Shadlen et al. 1996). A seminal study by Zohary and colleagues (1994) made the now oft-replicated (Kohn et al. 2016) finding that noise correlations between pairs of MT neurons in the direction discrimination task tend to be small but positive.

Although recent studies suggest that the relationship between noise correlations and information coding is more complex than the simple idea that lower correlation is good (Kohn et al. 2016), many studies have shown that performance improves in situations in which noise correlations decrease. Predominantly, attention decreases noise correlations between neurons that have similar tuning properties (Cohen & Maunsell 2009, 2011; Gregoriou et al. 2014; Herrero et al. 2013; Luo & Maunsell 2015; Mayo & Maunsell 2016; Mitchell et al. 2009; Nandy et al. 2016; Ruff & Cohen 2014a; Verhoef & Maunsell 2017; Zénon & Krauzlis 2012). Other cognitive processes, such as arousal (Ruff & Cohen 2014b) and learning (Gu et al. 2011, Jeanne et al. 2013, Yan et al. 2014), are also associated with decreases in noise correlations.

The pooling model makes a second prediction about the role of noise correlations in decision making. In contrast to correlations between pairs of neurons in the same pool, positive noise correlations between neurons in different pools should help information coding, because shared variability can be subtracted out when the activity of the two pools is compared. We recently tested this hypothesis by recording from groups of neurons in area V4 that represented evidence in favor of both possible choices during a contrast discrimination task (Ruff & Cohen 2014a). Consistent with model predictions, we found that attention increased noise correlations between pairs of those same neurons when they were in different pools (while decreasing correlations within each pool). Together, these results suggest that attention and other cognitive processes change correlations in ways that are broadly consistent with the predictions of the pooling model.

Limitations

It is curious that so much evidence supports the prediction that cognitive processes improve information coding despite recent modeling efforts suggesting that only a very small subset of these changes to correlations should affect information at all (Kanitscheider et al. 2015b, Kohn et al. 2016, Moreno-Bote et al. 2014). This work shows that information coding is affected only by the small subset of correlated variability that aligns with the dimensions in population space in which the signal (e.g., motion direction) is encoded (called information-limiting correlations) when the neuronal population is large enough. This argument is based on the sensory information that could be gleaned by an optimal, high-dimensional decoder that has unlimited access to information about the stimuli being discriminated, as opposed to access to the average activity of pools of neurons. The intuition is that with large enough neuronal populations (and therefore very high-dimensional representations), correlated activity is likely to be orthogonal to (and easily separated from) the dimensions in which a particular stimulus feature is encoded. Whether animals can decode stimuli in this way is an open question that we address below.

Another probable limitation of the hypothesis that attention improves performance by improving information coding is that it relies on the idea that the amount of sensory information encoded in sensory cortex is what limits behavioral performance. However, numerous examples show that even small populations of neurons can encode far more information than a monkey appears to use (Parker & Newsome 1998). Therefore, cognition-related improvements in perception may instead, or may also, result from changes in other aspects of neural processing.

Hypothesis 2: Cognitive Processes Improve Communication Between Cortical Areas

Support

An alternative explanation for the improvements in performance associated with cognitive processes is that cognition reduces the information that is lost (Sprague et al. 2015) when it is communicated to downstream areas (i.e., the areas that perform the pooling; Figure 1). Quantifying the amount of stimulus- or task-related information that is communicated between areas is difficult, but evidence suggests that attention increases the interdependence of neural activity in different areas across a range of timescales from both recordings (Bichot et al. 2005, Bosman et al. 2012, Buschman & Miller 2007, Fries 2015, Fries et al. 2001, Gregoriou et al. 2009, Lakatos et al. 2008, Miller & Buschman 2013, Saalmann et al. 2007, Saproo & Serences 2014, Womelsdorf & Fries 2007, Womelsdorf et al. 2006) and causal manipulations such as electrical microstimulation (Briggs et al. 2013; Dagnino et al. 2015; Klink et al. 2017; Moore & Armstrong 2003; Ruff & Cohen 2016a, 2017). Furthermore, spatial attention increases noise correlations between neurons in different cortical areas (Oemisch et al. 2015; Pooresmaeili et al. 2014; Ruff & Cohen 2016a,b).

Figure 1.

Schematic of the pooling model (adapted from Shadlen et al. 1996), highlighting cognition-related changes to neuronal responses that would provide evidence in favor of each of the three hypothesized underlying mechanisms (color coded for each mechanism). Abbreviation: r_SC, spike count or noise correlation.

Limitations

In general, task-related changes in communication between areas, across all timescales, are small. This potentially limits their role in the framework in a simple pooling model, in which synchrony affects communication between different pools of neurons. Furthermore, there is something fundamentally strange about the observed increase in noise correlations between pairs of neurons in different areas while there is simultaneously a decrease in noise correlations between pairs of neurons within an area. It is tempting to think that the decreases in correlation within an area serve to improve the information represented in that area, which, in turn, is then more faithfully communicated to a downstream area via increased correlations. However, mathematical and biological constraints may limit the strength and importance of correlation changes whose sign is different within and across areas.

Hypothesis 3: Cognitive Processes Improve the Way Sensory Information Is Decoded from Neuronal Populations

Support

At its most basic, the pooling model suggests that the readout of sensory information by a downstream neuron or a decision-related brain area simply involves comparing the average response of neurons in the two competing pools (i.e., that the responses of all neurons that belong to a pool are given the same weight). One possibility is that cognitive processes improve performance by changing the weighting function to make readout closer to optimal.

One of the most common tools used to make inferences about readout is choice probability, which measures the relationship between choices and the trial-to-trial fluctuations in an individual neuron’s responses (Britten et al. 1996, Nienborg et al. 2012). This measure is, by definition, correlative, and there has been ample debate surrounding the origins of choice-predictive activity in sensory neurons (Cohen & Newsome 2009, Cumming & Nienborg 2016, Nienborg & Cumming 2009, Wimmer et al. 2015).

However, there is evidence consistent with the idea that the weighting of different neurons for decision making depends on their tuning. It has commonly been observed that neurons or voxels that are best tuned for the task at hand are also those with highest choice probability (Nienborg et al. 2012). Furthermore, choice probabilities of the most informative neurons increase throughout learning (Law & Gold 2008). More generally, researchers have suggested that a neuron’s contribution to behavior can be changed by training (Chowdhury & DeAngelis 2008, Liu & Pack 2017).

Limitations

In many ways, the idea that readout weights are flexible has to be true. For the direction discrimination task, it may seem straightforward for the brain to divide neurons into appropriate pools based on their direction tuning, a feature which is neatly organized in columns in MT (Albright & Desimone 1987, Born & Bradley 2005). However, several factors suggest that readouts must involve flexible, nonuniform weights. Neurons are tuned for multiple stimulus features, there are many tasks and features where a clean division into pools would be complicated, and the mapping from stimuli to behavior is extremely flexible, making it unlikely that the brain solves tasks by cleanly dividing neurons into groups. A more realistic possibility is that decisions are based on flexibly weighted combinations (or subspaces) of the activity of the entire population (Cunningham & Yu 2014). In this scenario, cognitive processes such as attention could improve performance by making weightings more optimal.

The biggest limitation of this idea is the lack of experimental evidence. Although several studies have discussed the idea that subspaces of population activity, rather than groupings of neurons, are the important units of computation for readout (Churchland et al. 2012, Cunningham & Yu 2014, Elsayed et al. 2016, Elsayed & Cunningham 2017, Kaufman et al. 2014, Miri et al. 2017, Semedo et al. 2016, Yuste 2015), few studies have analyzed the relationship between population subspace activity and either the activity of downstream neurons or behavior. Some insights about how population subspace activity guides behavior have come from brain-machine interfaces (BMIs) in the motor system (Golub et al. 2016). BMI studies have shown that the representation of different actions and motor plans is relatively low dimensional and that animals cannot learn to access neuronal activity outside of key subspaces (Ganguly et al. 2011, Golub et al. 2016, Law et al. 2014, Sadtler et al. 2014). In sensory systems, the idea that decisions are based on population subspaces, not pools, has been slower to take hold (but see DiCarlo & Cox 2007, DiCarlo et al. 2012, Kriegeskorte 2009, Jazayeri & Afraz 2017, Pitkow & Angelaki 2017, Quian Quiroga & Panzeri 2009), but we believe that it will be of critical importance. A successful example of this approach has been in the study of visual object processing where population recordings and deep-learning neural networks have begun to elucidate the nature of high-level object representations (Cadieu et al. 2014, Khaligh-Razavi & Kriegeskorte 2014, Pagan et al. 2013, Yamins et al. 2014, Yamins & DiCarlo 2016).

MOVING BEYOND PAIRS OF NEURONS: SUBSPACES OF POPULATION ACTIVITY AS THE UNITS OF NEURAL COMPUTATION

While technological advancements have led to rapid growth in the number of studies using multineuron recordings in behaving monkeys, our understanding has lagged behind these new data. We propose that progress has been slow because our data analysis techniques take the pooling model too literally and focus on single neurons or average firing rates in a pool as the units of neural computation. As explained below, there is reason to believe that focusing on population subspaces (Figure 2) will allow us to understand the relative importance of the three hypothesized neuronal mechanisms underlying cognitive processes and can resolve several paradoxes in the current literature.

Figure 2.

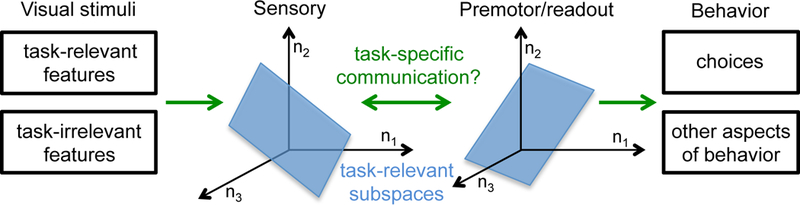
Schematic of a population subspace framework. Visual stimuli contain many features, a subset of which are relevant for a given perceptual task. For example, populations of MT neurons encode both motion direction and spatial frequency, even when the task concerns only motion direction. The activity of k MT neurons (neurons n₁, n₂, n₃,…, n_k) can be plotted in a k-dimensional space, but the subspace corresponding to motion direction (blue) is likely lower dimensional. Similarly, neuronal populations in downstream areas encode a variety of stimulus, cognitive, and premotor factors, a subset of which are relevant for perceptual choices. We hypothesize that communication between the areas (double-ended arrow) will also be low dimensional and task specific. The subspaces of neural activity that are relevant for each task can be thought of as linear (or nonlinear) combinations of the responses of all of the neurons in the population.

In the face of correlated variability, it is difficult to use population recordings to infer the role, or weighting, of each neuron in the decision-making process and therefore to infer the amount of sensory information that is communicated to downstream readout areas. Simulations have shown that an animal’s choices can be predicted from the responses of neurons that play no role in the decision but whose responses are correlated with those of neurons that do (Cohen & Newsome 2009, Nienborg et al. 2012). Inferring the contribution of different neurons in a population or the extent to which correlated variability affects the amount of stimulus information encoded in a population of neurons would require simultaneous recordings from many thousands of neurons over an even larger number of behavioral trials (Kanitscheider et al. 2015b, Kohn et al. 2016, Moreno-Bote et al. 2014). Although technology for recording from more and more neurons is ever improving, the work ethic of experimental subjects is not, and the number of behavioral trials required to infer the role of all of those neurons is prohibitive [which theoretical work suggests is an order of magnitude larger than the number of neurons (Bishop et al. 2017)].

We performed a simple simulation to gain intuition about what can and cannot be learned from recordings from small subsets of large populations of neurons over hundreds or thousands of trials. We made many simplifying assumptions, and the result is almost certainly not an accurate account of perceptual decision making in the brain. Our goal was illustrative and to suggest directions for future work.

Our simulation takes as its basis the published pooling model (Shadlen et al. 1996), but instead makes decisions based on arbitrary combinations of many neurons instead of the average firing rate of groups of neurons with different properties. We imagined that perceptual decisions about a single sensory feature (e.g., motion direction discrimination) are based on a linear combination of the responses of 5,000 neurons. The neurons in our simulation had cosine tuning for two sensory features (e.g., motion direction and binocular disparity). We imposed trial-to-trial noise correlations so that the variance of the spike count equaled the mean rate. Using previously published methods (Cohen & Maunsell 2009, Shadlen et al. 1996) and consistent with published observations (Cohen & Kohn 2011, Kohn & Smith 2005), we imposed noise correlations that were proportional to signal correlations (where signal correlations reflected mean responses to all combinations of the two sensory features).

As in the original pooling model, our simulation made decisions based on the combined responses of many neurons. However, our simulation incorporated decisions based on the activity of subspaces of the population. Population subspaces can be thought of as linear combinations of large numbers of neurons. We therefore imposed flexible weighting: We assigned each neuron a weight (which could be positive, negative, or 0) using one of several candidate weighting functions and based decisions on whether the weighted average response of the population was positive or negative. We then selected random subsets of 100 neurons to determine what we could and could not learn from the responses of this subset of simulated neurons and the simulation’s behavior on each trial.

Our simulations give good reason for optimism, and this optimism can be tested in future experiments. The responses of small populations can be used effectively to understand important qualities of the entire simulated neural population, can be used to evaluate the relative importance of the three hypothesized ways that cognitive processes improve perception, and can offer a resolution to a longstanding paradox about whether animals can optimally decode sensory information from neuronal populations. Put another way, the detailed weightings of each neuron in a large population are not important: Many weightings achieve similar performance in simple tasks. In this situation, small populations can be used to distinguish between different decoding strategies without identifying the precise neuron weights. Whether this will hold in systems with complex dynamics or nonlinear decoding strategies remains to be seen. But these simulations suggest that the hypothesis that subspaces of the responses of populations of neurons are the units of neural computation will be testable in experimentally feasible data sets.

Insights Related to Hypothesis 1: Small Populations Can Reveal the Stimulus or Behavioral Information that Is Encoded by or Communicated Between Neural Populations

The first hypothesis posits that cognitive processes improve perception by improving the amount of sensory information encoded by a neural population. Calculating information in neural populations is tricky because it relies on assumptions about the readout functions that can be used in the brain (da Silveira & Berry 2014, Kanitscheider et al. 2015a, Kohn et al. 2016). We discuss this issue separately below.

A related hypothesis that is more straightforward to address is that cognitive processes improve the sensory information that is used to make decisions or that is communicated to downstream areas. We tested this idea in our simulation by using linear regression to infer the weights of the 100 selected neurons that would allow us to best predict the simulation’s choices (which are based on the entire population) on one set of 500 trials and then calculating the simulation’s performance at a different simulated stimulus coherence using those weights on a separate set of 500 trials.

This simulation showed that although the discrimination performance of small populations is worse than that of the entire simulated population, the performance of decoders based on small populations covaries with the performance of the population. Figure 3a plots the proportion of correct discriminations using the weighted sum of the responses of the 100 selected neurons and of the entire population. Although the full population outperformed the selected subset of neurons, the similar relationship between the full and subpopulations and coherence suggests that recordings from small populations can be used to determine whether cognitive processes have improved the sensory information used to guide an animal’s choices.

Figure 3.

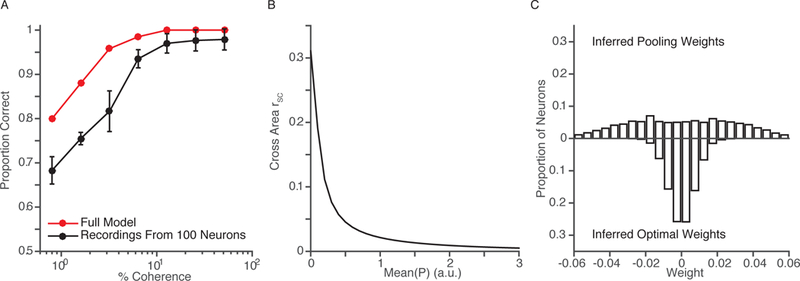
Insights from a set of simple simulations. (a) Proportion of correct discriminations of the full population (red) and of subsets of 100 selected neurons (black) using weights inferred from the simulation’s choices (which are based on the full population). Error bars represent 95% confidence intervals based on 1,000 random draws (without replacement) of 100 neurons. The full population outperforms the subsets, but performance using small populations covaries with that of the full population. If this property is true in real neuronal populations, modest improvements in the sensory information that the animals use should be observable from recordings of realistic numbers of recorded neurons. (b) When neuronal responses are based on linear combinations of inputs that are either shared or private to each neuron, correlations between simulated populations are inversely related to the strength of private inputs. In this scenario, changes in the proportion of private and shared inputs could be observed by measuring r_SC between areas. (c) Differences in weighting functions can be detected using recordings from small populations. The distribution of inferred weights of a conventional pooling model (top) is bimodal and broad. The distribution of inferred weights from a model that uses an optimal readout scheme (bottom) is narrow and unimodal.

Insights Related to Hypothesis 2: Small Populations Can Reveal the Strength of Communication Between Subspaces of Different Neuronal Populations

The second hypothesis posits that cognitive processes change the efficiency or strength of functional communication between brain areas.

Detecting such changes requires simultaneous recordings from multiple areas, and a measure of functional communication. Previous studies have used r_Sc between neurons in different areas as such a measure (Ruff & Cohen 2016a, Klink et al. 2017, Poort et al. 2016).

To illustrate how changes in the number or activity of shared or independent inputs might change cross-area r_SC, we extended our simulation to include a second population of neurons. We simulated the activity of each neuron in the second population as a linear combination of the responses of neurons in the first population (shared inputs) and independent inputs (that could come from any other area).

In this scenario, when the number or activity of independent inputs is small (so most inputs come from the first population), cross-area r_SC is high (Figure 3b, small numbers on the x-axis). When the number or activity of independent inputs is large, cross-area r_SC is low (large numbers on the x-axis).

In real recordings, correlations between projections onto subspaces of population activity in each area may be even better measures of functional connectivity. Standard statistical methods like canonical correlation analysis may be especially useful for identifying subspaces of activity that are shared between populations (Semedo et al. 2016) and determining how the strength of functional communication depends on cognitive processes like attention.

Insights Related to Hypothesis 3: Small Populations Can Reveal the Weighting Function Used to Make Decisions but Not the Weights of Particular Neurons

The third hypothesis posits that cognitive processes improve performance by changing the way that sensory information is read out to guide behavior (e.g., by changing the weighting, or contribution, of each neuron). Our simulation suggests that while recordings from small populations cannot be used to infer the weightings of any particular neurons, they can be used reliably to detect the distribution of weights and therefore whether that distribution changes. We used two weighting schemes to make our simulation make choices based on the responses of the full population. The first scheme is the one used in the pooling model: Each neuron had a weight of −1, 0, or 1 depending on whether its responses contributed to the first pool, no pool, or the second pool. In the second scheme, we used the weights that would comprise an optimal linear decoder for this stimulus feature (obtained using linear regression). We then tested subsets of 100 randomly selected neurons on 1,000 randomly selected trials and used linear regression to infer a set of weights that would allow us to best predict the simulation’s choices from the responses of the 100 selected neurons as above.

The results suggest that recordings from small populations on reasonable numbers of trials can easily distinguish between the two weighting schemes. Figure 3c shows the distributions of inferred weights in the pooling and optimal schemes. A Hartigan’s dip test found significant bimodality in the inferred weights in 88% of the 1,000 resampled small populations using the pooling scheme and only 4.8% of resampled populations using the optimal scheme. Furthermore, the inferred weights correlated with each individual neuron’s ability to distinguish two adjacent stimuli (quantified as the d’ between responses to the two stimuli over 1,000 trials) in the optimal but not the pooling scheme (R = 0.33, P < 10⁻⁵ in the optimal scheme; R = 0.01, P = 0.38 in the pooling scheme).

However, our simulations indicate that recordings from small populations cannot be used to infer the actual weightings of individual neurons. The correlation between the inferred and actual weights was 0.04 (P = 0.12) in the pooling scheme and 0.03 (P = 0.18) in the optimal scheme.

USING POPULATIONS TO FIGURE OUT THE ROLE OF NOISE CORRELATIONS

Together, our simulations suggest that recordings from small subsets of a large population can provide important insights about the mechanisms underlying cognitive improvements in perception. However, these simulations are gross oversimplifications of the complexity of real neuronal population data. We therefore provide an example from our own work of the insights that can be gleaned by considering population subspaces.

The role of correlated variability in limiting performance on perceptual tasks has been under heavy debate. Theoretical studies show that the bulk of correlated variability should not affect the amount of information encoded by a neuronal population because it is not part of the subspaces of activity (oriented along the same dimensions) that are read out by optimal stimulus decoders. However, this finding seems at odds with the large number of studies showing that cognitive processes such as attention, learning, and arousal change correlations (Cohen & Maunsell 2009, 2011; Gregoriou et al. 2014; Gu et al. 2011; Herrero et al. 2013; Jeanne et al. 2013; Luo & Maunsell 2015; Mayo & Maunsell 2016; Mitchell et al. 2009; Nandy et al. 2016; Ruff & Cohen 2014a,b, 2016a, Verhoef & Maunsell 2017, Yan et al. 2014, Zenon & Krauzlis 2012). We recently analyzed subspaces of simultaneously recorded V4 neuronal population activity to show that noise correlations are much more closely aligned with the population subspaces that matter for behavior than theoretical studies suggest they should be (Ni et al. 2017).

Noise correlations are by definition calculated over many trials. Determining the relationship between correlated variability and individual choices required us to derive a single trial measure of correlated variability from the activity of the populations of V4 neurons we recorded while monkeys performed an orientation change-detection task. We used principal component (PC) analysis on population responses to repeated presentations of the same stimulus to identify the axis in population space that accounted for the most correlated variability. The variance explained by the first PC during each recording session was highly correlated with the mean noise correlation of all neuron pairs recorded during that session, consistent with recent observations that noise correlations are typically low dimension (Ecker et al. 2016; Goris et al. 2014, Kanashiro et al. 2017, Rabinowitz et al. 2015) (Figure 4a).

Figure 4.

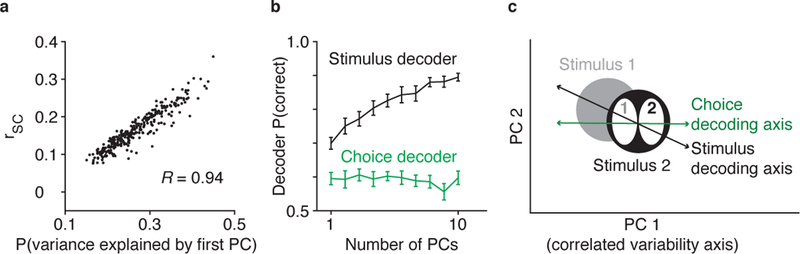
Correlated variability is related to performance (Ni et al. 2017). (a) The variance explained by the first PC, based on PCA of the recorded population’s responses to repeated presentations of the same stimulus, was highly correlated with the mean r_SC of all neuron pairs in the recorded population across experiments. Thus, the first PC provided a single trial measure of rSC. (b) The first PC (and thus correlated variability) explained essentially all the choice-related population activity, as the choice decoder performed just as well based on the first PC as it did with additional PCs. In contrast, the stimulus decoder’s performance improved with additional PCs. (c) Population responses illustrated for the first and second PCs only. The first PC (x-axis) is by definition the axis that explains the most correlated variability. The stimulus decoding axis (black line) detects differences between neuronal responses to stimulus 51 and stimulus 2, while the choice decoding axis (green line) detects differences between when the subject made the correct versus the incorrect choice [e.g., target 2 would be the correct choice, and target 1 the incorrect choice, when stimulus 2 was presented (ovals 2 and 1)]. Abbreviations: PC, principal component; PCA, principal component analysis; r_SC, spike count or noise correlation.

To determine the relationship between this correlated variability axis and the monkey’s choices, we projected the population responses to the stimulus the monkey was charged with detecting onto the PCs calculated as described above. We then compared those projections between trials in which the monkey correctly versus incorrectly detected the stimulus.

We found that we could predict the monkey’s choices using just the first PC as well as we could from the entire recorded population response (Figure 4b, green line). Put another way, projections onto the first PC, our single trial measure of correlated variability, explained essentially all the available choice-predictive activity in the recorded neuronal population.

This relationship between correlated variability and the performance of the choice decoder is particularly striking when compared to the relationship between correlated variability and the performance of an optimal stimulus decoder. The stimulus decoder (Figure 4b, black line) distinguished between the population responses to the two stimuli. Unlike the choice decoder (Figure 4b, green line), the stimulus decoder’s performance improved significantly when based on more PCs, meaning that it was not as influenced by correlated variability. This is in line with a prior study that found that while correlated variability decreased with training on a perceptual task, those changes in correlated variability had little effect on the population coding efficiency of an optimal stimulus decoder (Gu et al. 2011).

The schematic in Figure 4c illustrates a potential scenario that could explain why correlated variability has a different relationship with choice and stimulus decoders. The choice decoding axis may be aligned with the correlated variability axis (the first PC), while the stimulus decoding axis may be based on multiple PCs. This finding suggests that monkeys are suboptimal in a very specific and perplexing way: Their decisions are aligned with the axis of correlated variability. Below, we discuss a potential explanation: The animals may be optimal, but for something other than the very specific task they performed in each trial in the lab.

A NEW HYPOTHESIS: OPTIMALITY FOR GENERALITY

We propose an explanation for the relationship between the effects of cognitive processes on sensory neurons (which by all theoretical accounts should have a very limited effect on information coding) and behavior: that animals perform optimally, but for the much more general set of tasks they encounter in the natural world rather than the limited task they perform in the lab. We hypothesize that the relationship between signal and noise correlations that has been observed in many cortical areas means that this general sensory readout is truly affected by correlated variability and by the mean rates of sensory neurons.

The logic behind most conventional analyses [e.g., computing neurometric thresholds in single neurons (Britten et al. 1992, Parker & Newsome 1998) or decoding stimulus information from neuronal populations] is that there could be a new decoder (i.e., new weights) for each pair of stimuli. In the context of the motion direction discrimination task, one decoder is set up to discriminate 3% coherence leftward motion from 3% coherence rightward motion, and a separate decoder is set up to discriminate 6% coherence leftward motion from 6% coherence rightward motion. (This is the way we set up the decoding in Figure 3a.) In a fine discrimination task, the decoders might be very different for each stimulus pair: The neurons that would be most useful for discriminating a difference between 30°- and 32°-oriented gratings are different from the neurons that would be most useful for discriminating between 120°- and 122°-oriented gratings.

This scenario is not suitable for natural vision. If you are about to cross a busy street, you need to determine whether a car is headed your way, no matter its starting position or its features. Features such as color, size, or shape are irrelevant for motion discrimination but still modulate the responses of the same MT neurons that guide motion discrimination. Likewise, the many-decoders scenario is not likely to be true even for simple laboratory tasks. For monkeys to use a decoder that depends on the stimulus implies that they use a two-step decision process: identifying the stimulus followed by doing the actual discrimination. This is extremely unlikely; if animals could successfully identify the stimulus, there would be nothing left to discriminate.

A much more realistic scenario is that animals use a more general decoder that is at least capable of discriminating arbitrary pairs of the stimuli used in any task. For example, animals performing the motion direction discrimination task might use a general motion decoder that can discriminate any moving object.

As a decoder gets more general (i.e., it has to contend with stimuli that vary in more feature dimensions), its weights depend on more and more tuning properties. Consider, for example, two rightward-selective MT neurons in the context of a left-right motion direction discrimination task. If they have the same binocular disparity tuning, then a large response from them might indicate rightward motion, near disparity, or a combination of those two features. This is irrelevant if the decoder considers only stimuli with identical disparity, but a more general decoder would need to resolve this discrepancy by choosing weights of these and other neurons that take their disparity tuning into account.

Therefore, the weights in a more general decoder would depend on the tuning of all neurons to all stimulus features to which they respond, which means that decoding weights would depend on exactly the same factors as noise correlations. It is well established that noise correlations depend on tuning similarity for all features. For example, spike count correlations between pairs of MT neurons depend on tuning similarity for motion direction (Bair et al. 2001, Cohen & Newsome 2008, Solomon et al. 2015, Zohary et al. 1994), speed (Huang & Lisberger 2009), sensory normalization (Ruff et al. 2016), and, as has been shown in other areas, cortical distance (Smith & Kohn 2008, Smith & Sommer 2013).

This dependence of signal and noise on the same feature set means that the optimal decoder might be aligned with the population subspaces containing the most correlated variability (as in Figure 4). Put another way, correlated variability is in a position to have a large effect on the performance of the generalized optimal decoder.

The idea that the weights of a general decoder depend on the same features as noise correlations explains some confusing results in the literature. Noise correlations can either help or hurt the performance of a specific optimal decoder (Abbott & Dayan 1999, Averbeck et al. 2006), but the vast majority of studies report that attention and other cognitive processes decrease correlations overall (Cohen & Maunsell 2009, Gregoriou et al. 2014; Gu et al. 2011; Herrero et al. 2013; Jeanne et al. 2013; Luo & Maunsell 2015; Mayo & Maunsell 2016; Mitchell et al. 2009; Nandy et al. 2016; Ruff & Cohen 2014a, Verhoef & Maunsell 2017; Yan et al. 2014; Zenon & Krauzlis 2012). Similarly, attention and other cognitive processes typically increase the trial-averaged response gains of all neurons, regardless of their tuning for the specific stimuli to be discriminated (Maunsell 2015, McAdams & Maunsell 1999). Both results make sense if a generalized, rather than a specific, decoder is being optimized.

DESIGNING EXPERIMENTS TO TEST THE IDEA OF OPTIMALITY FOR GENERALITY

What would experimental evidence for the idea of a general decoder look like? Our simulations suggest that experiments should incorporate a richer stimulus set or behavioral task, but that a small amount of richness can go a long way.

To illustrate this idea, we adapted our simulation to make the neurons tuned for two features [i.e., direction and disparity, two features whose tuning preferences in MT are independent and largely separable (DeAngelis & Uka 2003, Smolyanskaya et al. 2013)1, and we had the simulation discriminate the direction of stimuli whose disparity varied. For example, the simulation needed to discriminate rightward from leftward motion in the face of stimuli with highly variable disparities. The neuron weights of the optimal decoder that has to contend with variable disparity are only weakly correlated with those of a decoder that works only on stimuli with constant disparity (R = 0.18; Figure 5a). Furthermore, changing the mean noise correlation across the population from 0.1 to 0.05 (which is in the range of attention- and learning-related changes in mean r_SC) had a much greater effect on the decoder that contended with multiple disparities than on the decoder that dealt only with constant disparity (compare the left and right sets of bars in Figure 5b). This large effect of changing noise correlations on the general decoder’s performance is much more in line with our prior experimental findings than the effect of noise correlations on the decoder that only dealt with constant disparity. We found a robust, consistent relationship between changes in noise correlations and changes in behavioral performance, whether those changes occurred quickly with attention or slowly with learning (Ni et al. 2017). Our simulation suggests that this relationship between changes in noise correlations and behavioral performance is better explained by a general decoder.

Figure 5.

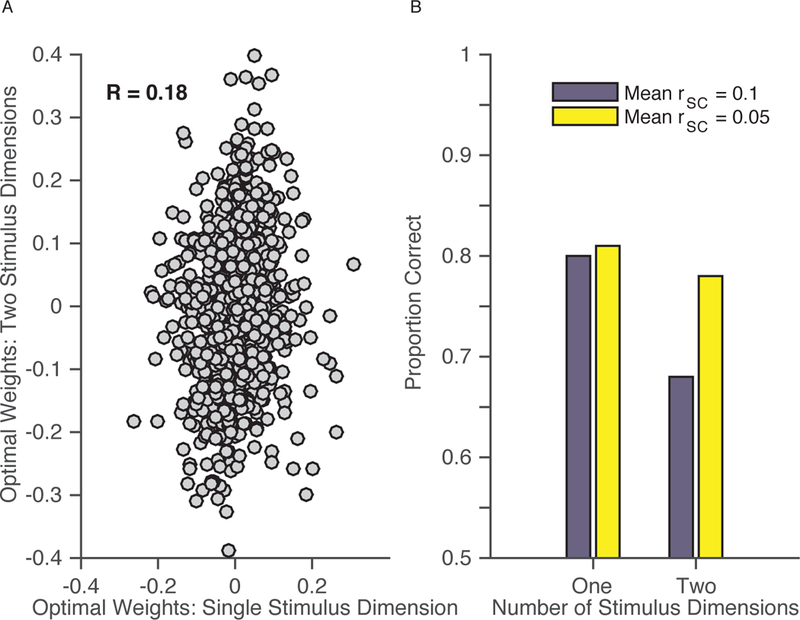
An optimal general decoder uses very different weights than an optimal decoder tailored for each stimulus and accounts for known experimental results. (a) In simulation, the weights of a decoder that contends with two stimulus features (one task-relevant and one task-irrelevant feature; y-axis) are only weakly correlated with the weights of a decoder that contends with stimuli that vary only in a single, task-relevant feature. (b) Changing the mean r_SC has a much larger effect on the general decoder that contends with variability in two stimulus features (right) than the decoder for stimuli that vary only in a single stimulus dimension (left).

These simulations suggest that adding a small amount of complexity to laboratory tasks might provide qualitatively new insights. It is not necessary to move to natural stimuli and uncontrolled behaviors. Instead, our simulations suggest that using stimuli that vary in a single, task-irrelevant stimulus feature or adding a small amount of complexity to the behavior is sufficient to distinguish between specific and general decoders. For example, simple statistical techniques to infer the neuron weights that best explain activity in another brain area or the animal’s choices would give very different answers if the true decoder were specific or general.

Our simulations suggest that general decoders may provide a superior account of the effects of cognitive processes like attention and learning on behavior. For this reason, determining whether animals in fact use general decoders and the extent to which their decoders depend on the particular stimuli and task conditions will be an important avenue for future work.

EXPERIMENTAL EVIDENCE FOR AND AGAINST OPTIMALITY

Even though there are practical benefits of decoding a feature in a general enough way to work for all stimuli, it is reasonable to hypothesize that a trained animal might optimize its decoder for the set of stimuli or task conditions it encounters in the lab. Indeed, a few studies have shown that the effects of attention or learning on spike count correlations depend on the relationship between the tuning of the neurons and the stimulus dimension being discriminated (Jeanne et al. 2013, Ruff & Cohen 2014a, Verhoef & Maunsell 2017). These results suggest that the effects of cognitive processes on sensory neurons can be optimized for a specific task. However, attention was associated with overall decreases in average correlation in addition to the tuning-specific effects in two of those studies (Ruff & Cohen 2014a, Verhoef & Maunsell 2017), suggesting that the extent to which decoders can be optimized is limited.

A study by Clery and colleagues (2017) found that while neurons in area V2 exhibited decision-related activity in a fine disparity discrimination task, the relationship between the neuronal responses and the monkeys’ psychophysical performance levels was not compatible with an optimal linear readout of available sensory information. Even when they restricted their analysis to sessions in which the psychophysical performance of the monkeys exceeded neuronal sensitivity, they monkeys did not appear to read out the sensory information in V2 optimally.

On the other hand, numerous studies have shown that in certain situations, subjects do appear to behave optimally based on the available sensory information (Drugowitsch et al. 2014, Ernst & Banks 2002, Fetsch et al. 2011, Jacobs 1999, Knill 2007, Pitkow et al. 2015). Provocatively, many of these studies suggesting optimal decoding strategies have used multisensory stimuli or otherwise involved the integration of multiple modalities of sensory information (Chandrasekaran 2017, Kording & Wolpert 2006). In a study by Fetsch and colleagues (2011), monkeys demonstrated the ability combine visual and vestibular inputs in a near-optimal manner, with the activity of multimodal neurons in the dorsal medial superior temporal area giving a fair account of this behavioral optimization.

One possibility is that animals always read out stimulus information as if the stimuli vary across multiple task-relevant and -irrelevant feature dimensions, regardless of whether the task requires them to do so. Consistent with this idea, in our simulation, merely accounting for a second additional feature dimension makes readout appear nearly optimal. In this case, behavior would approach optimality for studies using multisensory stimuli.

There might be a biological explanation for why even well-trained animals might settle on a strategy that uses a generalized decoder. We and our collaborators recently showed that the simplest way to modulate spike count correlations and rates in cortical circuit models in ways that are consistent with physiological data is to change the balance of excitation and inhibition (Huang et al. 2017, Kanashiro et al. 2017). For example, modulating inhibition more than excitation increases response gain and decreases correlated variability in ways that are consistent with data from attention tasks. Perhaps this sort of simple mechanism by which cognitive processes affect visual cortex is easier to implement in biological circuits than the complex weight changes required for stimulus- or task-specific cognitive effects.

CONCLUSION

Much of our understanding of the neuronal basis of behavior is based on a framework that focuses on the activity of single neurons or pools of neurons as the units of neural computation. However, true population activity is far richer, and we propose that considering subspaces of population activity as the relevant units of computation and considering the wide variety of stimuli and tasks that animals contend with in natural behavior will allow us to gain a better understanding of neuronal computations. We suggest methods for finding the population subspaces relevant to behavioral performance: comparisons of population activity to trial-by-trial behavioral choices, or comparisons to the activity of neuronal populations in other brain areas. This conceptual framework for understanding how neuronal activity relates to behavior will allow our analytical techniques to keep pace with our ever-growing technical abilities.

This is an especially exciting time to be a neuroscientist interested in understanding the relationship between the activity of neurons and behavior. Standing on the shoulders of decades of important experimental and quantitative work, the field is ideally positioned to ask critical questions about this relationship. We believe, with the guidance provided by this new theoretical framework bolstered by the use of bleeding edge technology, that we have never been better positioned to find these answers.