Abstract
We have analyzed the geometry, geography, and functional organization of human cerebral cortex using surface reconstructions and cortical flat maps of the left and right hemispheres generated from a digital atlas (the Visible Man). The total surface area of the reconstructed Visible Man neocortex is 1570 cm2(both hemispheres), ∼70% of which is buried in sulci. By linking the Visible Man cerebrum to the Talairach stereotaxic coordinate space, the locations of activation foci reported in neuroimaging studies can be readily visualized in relation to the cortical surface. The associated spatial uncertainty was empirically shown to have a radius in three dimensions of ∼10 mm. Application of this approach to studies of visual cortex reveals the overall patterns of activation associated with different aspects of visual function and the relationship of these patterns to topographically organized visual areas. Our analysis supports a distinction between an anterior region in ventral occipito-temporal cortex that is selectively involved in form processing and a more posterior region (in or near areas VP and V4v) involved in both form and color processing. Foci associated with motion processing are mainly concentrated in a region along the occipito-temporal junction, the ventral portion of which overlaps with foci also implicated in form processing. Comparisons between flat maps of human and macaque monkey cerebral cortex indicate significant differences as well as many similarities in the relative sizes and positions of cortical regions known or suspected to be homologous in the two species.
Keywords: atlas, human, macaque monkey, cerebral cortex, Visible Man, visual areas, computerized neuroanatomy
Human cerebral cortex is a thin sheet of tissue that is extensively convoluted in order for a large surface area to fit within a restricted cranial volume. Convolutions occur to varying degrees in the cortices of many species and have long been a source of both fascination and frustration for neuroscientists. The fascination arises because of curiosity about how the convolutions develop and what they signify functionally (Welker, 1990; Van Essen, 1997). The frustrations arise because cortical sulci are irregular in shape and vary in configuration and location from one individual to the next, making it difficult to analyze experimental data accurately and systematically across cases.
These difficulties can be alleviated to a considerable extent by analyzing cortical organization and function in relation to explicit representations of the cortical surface. A particularly useful display format involves cortical flat maps, which allow the entire surface of the hemisphere to be visualized in a single view (Van Essen and Maunsell, 1980). Recent advances in computerized neuroanatomy allow large expanses of highly convoluted cortex to be digitally reconstructed and flattened (Dale and Sereno, 1993; Carman et al., 1995; Sereno et al., 1995; DeYoe et al., 1996; Drury et al., 1996a). Here, we generate surface reconstructions and cortical flat maps for both hemispheres of the Visible Man, a digital atlas of a human body (Spitzer et al., 1996). This surface-based atlas allows complex patterns of experimental data to be visualized in relation to identified gyral and sulcal landmarks and in relation to a coordinate system that respects the topology of the cortical surface.
A surface-based atlas is particularly useful for comparing results across the burgeoning number of neuroimaging studies that use positron emission tomography (PET) or functional magnetic resonance imaging (fMRI). Typically, the centers of activation foci are localized by reporting their stereotaxic coordinates in Talairach space (Fox et al., 1985; Talairach and Tournoux, 1988; Fox, 1995). To analyze the distribution of foci in relation to the cortical surface, we introduce a method that includes objective estimates of the associated uncertainty in spatial localization. We also demonstrate how the accuracy of localization can be improved using measurements based on distances along the cortical surface.
Human visual cortex is a suitable domain for exploring the utility of this approach. Recent neuroimaging studies of human visual cortex have revealed six topographically organized visual areas (Sereno et al., 1995; DeYoe et al., 1996) plus many activation foci related to specific aspects of visual function, such as motion, form, and color processing (e.g., Corbetta et al., 1991; Tootell et al., 1996). Many issues remain unresolved, however, concerning the degree of functional specialization in different areas and regions. We show that existing neuroimaging data are consistent with substantial overlap or close interdigitation of different functions in many regions; involvement in just a single aspect of visual function has been convincingly demonstrated in only a few regions.
Our understanding of cortical organization in humans can be aided by comparisons with nonhuman primates, particularly the macaque monkey and owl monkey (Sereno et al., 1995). Detailed interspecies comparisons are impeded not so much by the differences in absolute brain size but by the pronounced differences in the degree and pattern of folding. We illustrate the utility of cortical flat maps as a substrate for obtaining more accurate interspecies comparisons.
MATERIALS AND METHODS
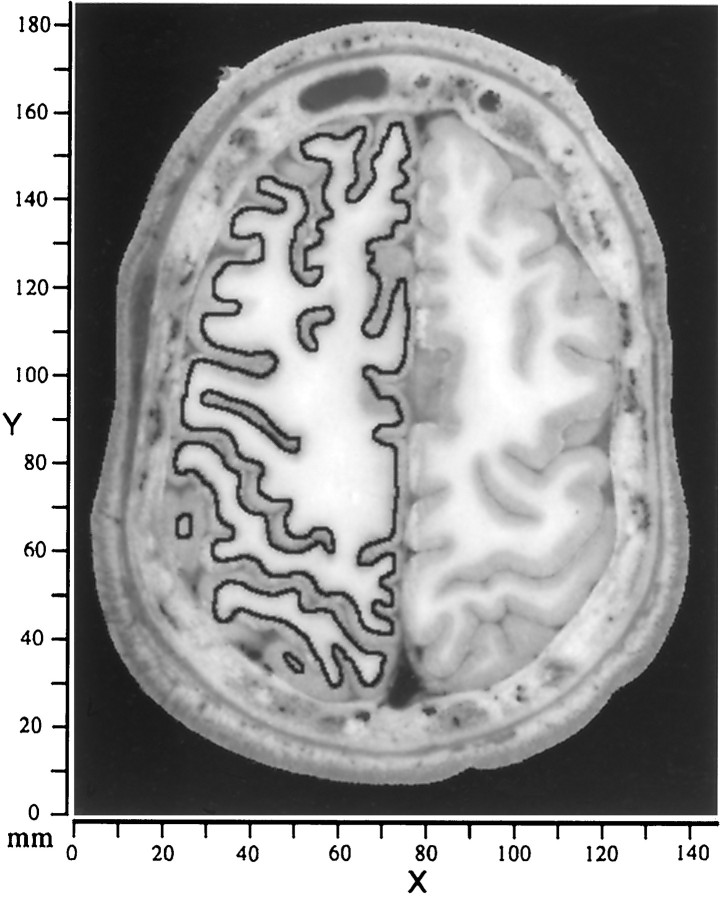
Images, contours, and raw coordinates.Reconstructions of cerebral cortex from the Visible Man (Visible Human Project, National Library of Medicine) were derived from digital images of the cut brain surface. These images were acquired at 1 mm intervals in a plane oriented approximately transverse to the long axis of the body (Spitzer et al., 1996). Figure 1shows a representative image through the dorsal part of the cerebrum, illustrating the clear distinction in most regions between gray and white matter in unstained tissue. Contours running midway through the estimated thickness of the cortical gray matter were manually traced on an Apple Macintosh computer using a mouse-driven tracing option in NIH Image software (National Institutes of Health, Bethesda, MD). This choice of contour depth associates each unit area of the reconstructed surface with approximately the same volume of cortex, whereas reconstructions based on the pial surface or on the boundary between gray and white matter give biased estimates of the extent of gyral or sulcal regions (Van Essen and Maunsell, 1980). Gaps associated with natural termination points of the neocortex (e.g., at its juncture with the corpus callosum) were temporarily closed by adding artificial line segments, because the algorithm used to generate a wire frame reconstruction operates only on closed contours.
Fig. 1.
Image of the cut brain surface from the Visible Man cerebrum, taken 46 mm from the top of the head (26 mm from the beginning of cortex). A contour representing the estimated trajectory of cortical layer 4 is drawn for the left hemisphere. In regions where the cortex was cut obliquely, close scrutiny of several nearby sections was often needed to infer the most likely contour for layer 4. Cerebral cortex was contained in 108 images (1 mm intervals), with an in-plane resolution of 2048 × 1216 pixels (0.33 mm/pixel). The raw data coordinate system associated with this stack of images is represented by an x–y-axis with origin at thebottom left of each image. The section number relative to the topmost image indicates the value for thez-axis.
Surface reconstructions and area estimates. Each image was thresholded to show only the traced contours, which were then converted to a discrete sequence of points using the wand tool of NIH Image. After transfer to a Silicon Graphics (Mountain View, CA) UNIX workstation, contours were subsampled to a spacing of ∼1.5 mm between nodes and loaded into custom software [Computerized Anatomical Reconstruction and Editing Tools (CARET)], which is designed for the interactive viewing and editing of surface reconstructions and associated experimental data. A wire frame reconstruction was generated using the Nuages software (Geiger, 1993). Topologically inappropriate links (typically occurring where contours change shape markedly between sections) were corrected by manual editing of the surface. After deleting the artificial links between terminations of neocortex, the resulting surface contained 51,408 nodes (99,920 triangular tiles) in the left hemisphere and 53,833 nodes (104,559 tiles) in the right hemisphere.
A smoothing algorithm was used to remove nonbiological surface irregularities in the initial three-dimensional (3-D) reconstruction. The optimal amount of smoothing, judged by visual inspection, involved 100 iterations with a smoothing parameter of 0.05 (cf. Drury et al., 1996a). A visibly under-smoothed reconstruction (smoothed for only 50 iterations and containing numerous artifactual irregularities) was 10% larger in surface area. When viewed in relation to the cortical volume using VoxelView software (Vital Images, Fairfield, IA), the smoothed surface deviates systematically from its starting position in regions where the cortex is sharply creased, lying closer to the white matter along gyral regions and closer to the pial surface along the fundus of sulcal folds. The degree to which this smoothed surface underestimates the surface area of a perfect midthickness representation is difficult to determine precisely but is unlikely to exceed 10%.
Surface geometry. A curvature estimation algorithm (Malliot et al., 1993; Drury et al., 1996a) was used to compute the principal curvatures along the major and minor axes (kmaxand kmin) for each node in the reconstruction. These values were used to calculate the mean curvature (the average of the two principal curvatures), which is a measure of local folding, and the intrinsic (Gaussian) curvature (the product of the two principal curvatures), which indicates whether the surface is locally curved like a sphere or a saddle. A gray scale or color scale representation of these surface characteristics can be readily transferred to a smoothed or flattened surface, thereby preserving a visually intuitive portrayal of the original 3-D geometry.
Two dimensionless indices were used to calculate measures of overall surface geometry, independent of the absolute scale of the hemisphere. The intrinsic curvature index (ICI) was computed by integrating across all regions of positive intrinsic curvature and dividing by 4π (the integrated intrinsic curvature for a perfect sphere of any size). The ICI is calculated as:
| Equation 1 |
where k′ = ‖kmaxkmin‖ if kmaxkmin > 0, or else k′ = 0. Excluding regions of negative intrinsic curvature ensures that the spherical component of each dimple or bulge is not canceled by the saddle-shaped zone around its perimeter. Any local dimple or bulge having the shape of a half-sphere increments the intrinsic curvature index by a value of 0.5, independent of its size.
The folding index (FI) was computed by integrating the product of the maximum principal curvature and the difference between maximum and minimum curvature and dividing by 4π (the integral for a cylinder the length of which equals its diameter). The folding index is:
| Equation 2 |
Any ridge or furrow having the shape of a half-cylinder increments the folding index in proportion to its length, starting at 0.5 if its length equals its diameter. Thus, the folding index increments quickly per unit length of sharply folded regions, slowly for loosely curled or folded regions, and not at all for spherical or saddle-shaped regions.
Cortical flattening. Cuts in the reconstruction were introduced to reduce distortions in surface area when flattening the cortex. The surface was taken through multiple cycles of our multiresolution flattening algorithm (Drury et al., 1996a), using empirically established parameter values for obtaining a near-optimal flat map. To generate a square grid for displaying surface-based coordinates, the flattened surface was resam-pled to create a regular array of nodes that are 1 mm apart on the cortical flat map.
Coordinate spaces and transformations. We used the Spatial Normalization software (Lancaster et al., 1995) to transform the coordinate system for the Visible Man from the initial raw data coordinate system [x, y, z]vm-raw in which the images were acquired to a cardinal coordinate space[x, y, z]VM-3D that is aligned relative to the midline of the brain and to standard anatomical landmarks. The origin was placed at the anterior commissure (AC); the midsagittal plane was aligned to the y = 0 plane; and the posterior commissure (PC) was placed on the x-axis, making the AC–PC line coincident with the x-axis. The six parameters defining this transformation were encoded in a 4 × 4 matrix that was applied to both volume and surface data.
The origin and alignment of the Visible Man cardinal axes are identical to those used in the Talairach stereotaxic atlas (Talairach and Tournoux, 1988), but the Visible Man brain is slightly smaller than the Talairach brain. In a second normalization stage we used a “bounding box” method to match the overall dimensions of the Visible Man to those of the Talairach atlas. Transforming the Visible Man volume and surface representations into Talairach space, [x, y, z]T’88 entailed expanding them by 3% along thex-dimension (left–right), 1% in the z-dimension (superior–inferior), and none in the y-dimension (anterior–posterior).
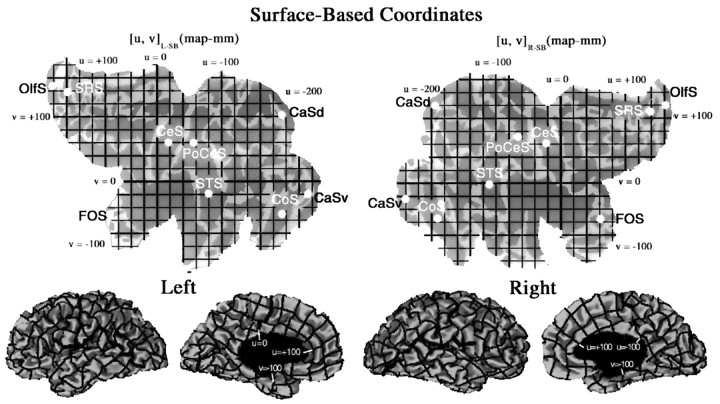
Slices through the Visible Man surface can be visualized in different cardinal planes (parasagittal, coronal, or horizontal) using a resectioning algorithm that displays portions of the surface lying within selected ranges along the appropriate x-,y-, or z-axis. This was particularly useful for delineating isocontour lines (constant x, y, orz values) in Talairach space. We also defined a surface-based coordinate system that respects the topology of the cortical surface (Anderson et al., 1994; Drury et al., 1996a). Surface-based coordinates are designated as [u, v]R-SB for points on the right hemisphere map and [u, v]L-SB for points on the left hemisphere map, with the subscripts reflecting the fact that each hemisphere was reconstructed as a separate surface.
Projection of stereotaxic data. Any experimental data point with its location reported in Talairach stereotaxic space can be linked to the nearest point on the Visible Man surface after transformation to Talairach space. For each point of interest (generally the center of an activation focus from a neuroimaging study), the projection algorithm identifies the nearest tile on the Visible Man surface and determines the closest point within that tile (or along the perimeter of the tile if the projection to the plane lies outside the tile). Activation foci reported in the 1967 Talairach space (Talairach and Tournoux, 1967) were converted to the Talairach and Tournoux (1988) space using the relationship [x, y, z]T’88 = [0.9x, 1.06(y − 14), 1.07z]T’67 (T. Videen, personal communication).
Activation foci were visualized on the cortical flat map by displaying the center of the focus in relation to the closest tile on the 3-D surface. To visualize nearby portions of the cortical surface that are potentially associated with each activation focus, we identified all tiles within a core region up to a defined radius from the center in 3-D space (generally set to 10 mm). An additional option allows visualization of all tiles within a surrounding shell region (generally 10–15 mm from the center; see Fig. 8).
Fig. 8.
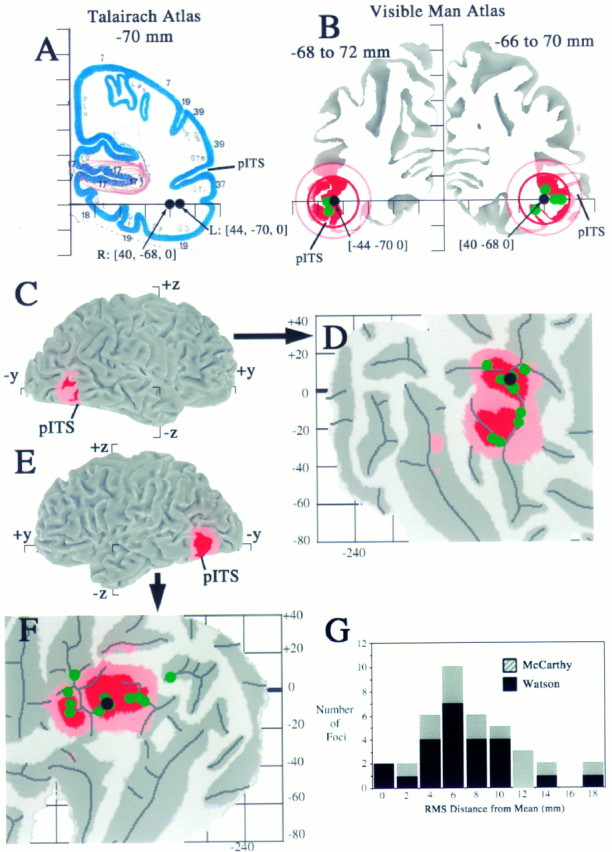
Stereotaxic projection of neuroimaging data to the cortical surface with estimation of spatial uncertainties.A, Activation foci from a study of motion analysis (Watson et al., 1993, their Table 3) are plotted on the nearest coronal section from the Talairach atlas (y = −70 mm). Black dots show the group means for the left and right hemisphere activation foci, which are located in white matter under the inferior temporal sulcus. B, The same foci are plotted in relation to coronal slices (5 mm thick) through the Visible Man atlas. Black dots show the group mean for each hemisphere; green dots show activation foci from individual subjects that intersect this slab of cortex. The redand pink circles are drawn at radii of 10 and 15 mm from the group means, respectively, and portions of the surface within each ring are shaded accordingly. C, E, Lateral views of the left and right hemispheres, respectively, showing where the foci and associated uncertainty zones are located in 3-D in and near the posterior inferior temporal sulcus (pITS). The pITS has also been identified as the ascending limb of the ITS byWatson et al. (1993). D, F, Flat maps of occipito-temporal cortex from the left and right hemispheres, respectively, showing where the group means (black dots) and individual values (green dots) project to the nearest point on the cortical surface and where the 10 and 15 mm uncertainty zones map in the vicinity of each group mean. Occlusion by overlying dots prevents some of the individual points from being visible. The activation foci for the group means have similar surface-based coordinates on the two cortical maps ([−158, +3]R-SB vs [−162, +2]L-SB). The maximum linear extent of each domain on the map is about twice the diameter of the corresponding 3-D sphere (∼45 map-mm for the 10 mm radius spheres, ∼60 map-mm for the 15 mm radius spheres).G, Histogram of the 3-D (RMS) distance between each individual focus and the group mean for that hemisphere from the data of Watson et al. (1993) (black bars) and for a corresponding data set from the fMRI study of motion processing by McCarthy et al. (1995), based on seven subjects (14 hemispheres).
Reconstruction of macaque cerebral cortex. As a substrate for interspecies comparisons of cortical organization, we used a previously published reconstruction of the right cerebral hemisphere of the macaque monkey. This reconstruction (case 79-0) was based on a series of Nissl-stained sections that were aligned, reconstructed, and flattened as described previously (Carman et al., 1995; Drury et al., 1996a), except that one of the cuts was placed in the middle of V1 rather than along its perimeter (Van Essen, 1997).
RESULTS
Geography and geometry of the Visible Man cerebral cortex
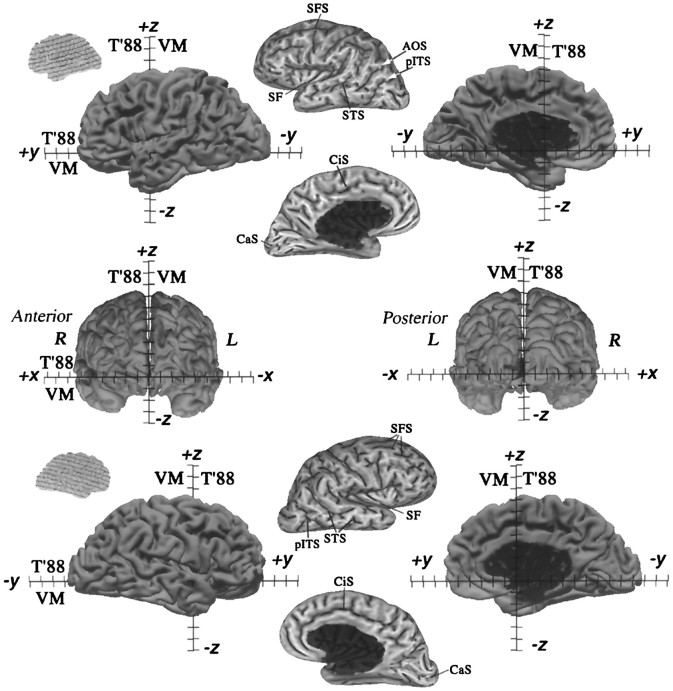
We begin with an analysis of cortical geography and geometry that provides useful information about human cerebral cortex in general, about similarities and differences between the left and right hemispheres of the Visible Man, and about the suitability of the Visible Man as an atlas on which to represent functional neuroimaging data. Cortical geography can best be appreciated by viewing the convolutions in several formats, including 3-D views of the original surface (Fig. 2, left,right columns), extensively smoothed surface representations (Fig. 2, center column), and cortical flat maps (Fig. 3). Figure 2 shows four views of each hemisphere after alignment of the Visible Man cerebrum to its cardinal axes (see Materials and Methods). The tick marks labeled VM along each axis, spaced at 1 cm intervals, represent the dimensions of the Visible Man surface in its cardinal coordinate space [x, y, z]VM-3D. Those labeled T’88 indicate the slight scale changes needed to transform the Visible Man cerebrum into the Talairach stereotaxic space.
Fig. 2.
Surface reconstructions of the Visible Man. Lateral, medial, anterior, and posterior views are shown for both hemispheres. The origin was placed at the anterior commissure, the midsagittal plane was aligned to the y = 0 plane, and the anterior and posterior commissures were aligned to thex-axis. Native Visible Man (VM) and Talairach (T’88) coordinate systems are shown for each axis with tick marks at 1 cm intervals.Insets at the far left show the orientation of the original quasi-horizontal slices relative to the cardinal axes, with solid lines indicating 1 cm intervals. The maximum extent of the Visible Man surface is 68, 166, and 110 mm, respectively in the x, y, andz dimensions for the left hemisphere and 68, 171, and 106 mm, respectively, for the right hemisphere. After transforming the Visible Man brain to Talairach space, these values are 3% larger in the x dimension, 1% larger in the zdimension, and identical in the y dimension. After this transformation, the posterior pole of the Visible Man has ay value of −107, compared with −106 of the Talairach brain, and the anterior pole has a y value of +59, identical to the +59 of the Talairach brain. Panels in themiddle show extensively smoothed surfaces for both hemispheres (500 iterations with a smoothing parameter of 0.5). These are shaded to reflect mean curvature of the original 3-D surface, with inward folds (fundi of sulci) shown in dark and outward folds (crests of gyri) in lighter shades. See Results and for abbreviations. We compared the locations in stereotaxic space of nine major sulci with those illustrated for a population of 20 normal brains by Steinmetz et al. (1990). In the left hemisphere, the trajectories are within the normal range for the central, precentral, postcentral, superior temporal, and calcarine sulci and for the Sylvian fissure and its posterior and anterior ascending rami. In the right hemisphere, the trajectories for these sulci are all within the normal range, except that the central, precentral, and postcentral sulci and the posterior ascending ramus of the Sylvian fissure were more posterior (by 3–10 mm) than in any of the cases illustrated by Steinmetz et al. (1990). Interestingly, the same sulci show a similar posterior displacement in the hemisphere illustrated in the atlas of Talairach and Tournoux (1988). Finally, the callosal sulcus in both the left and right hemispheres of the Visible Man appears to have a slightly abnormal shape, with the rostral extrema (genu of corpus callosum) slightly more posterior than normal and the superior margin slightly higher than normal.
Fig. 3.
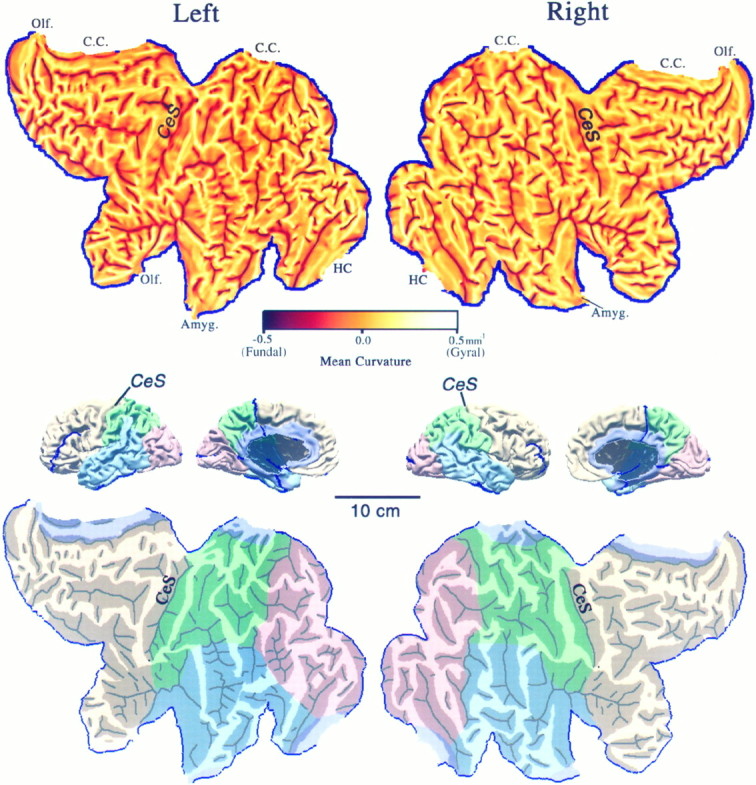
Flat maps of the left and right cerebral hemispheres. Top panels show flat maps with mean curvature displayed to represent cortical geography. Each map was aligned by making the mean orientation of the fundus of the central sulcus on the flat map match the visually estimated average orientation of the lips of the central sulcus in the 3-D reconstruction. For a region that is folded but not intrinsically curved, a mean curvature of ±0.5 mm−1 (maximum on the scale) is equivalent to a cylinder of 1 mm radius. Middle panels show medial and lateral views of the intact hemispheres, with lobes identified according to landmarks delineated by Ono et al. (1990) and suitably colored (occipital lobe in pink, parietal lobe ingreen, temporal lobe in blue, frontal lobe in beige, and limbic lobe inlavender). C.C., Corpus callosum;HC, hippocampus; Amyg., amygdala; andOlf., olfactory cortex. Bottom panelsshow the same flat maps with lobes colored and with darker shading applied to all regions of buried cortex, i.e., cortex not externally visible in the intact hemisphere, as determined from the original image slices (compare Fig. 1) and from the 3-D surface and volume reconstructions. Black lines indicate sharply creased regions (fundi) within each sulcus that were traced manually on the curvature maps. The scale applies to all panels. Artificial cuts (blue lines) were introduced to reduce distortion in the flat maps.
Extensive smoothing of the surface reconstruction leads to surfaces having the shape of a lissencephalic brain similar to that of an owl monkey (Fig. 2, center column). The original pattern of folds is represented by a gray scale display of mean curvature (seeMaterials and Methods). Dark streaks in Figure 2represent “inward folds,” where the crease runs along the fundus of a sulcus, and light streaks represent “outward folds,” where the crease runs along the crown of a gyrus. Sulci that are similar in location and overall extent in left and right hemispheres include the central sulcus (Ces) and Sylvian fissure (SF) on the lateral side and the cingulate sulcus (CiS) and calcarine sulcus (CaS) on the medial side. In many other regions the folding pattern differs markedly between hemispheres. One example relevant to functional neuroimaging results discussed below is the posterior inferior temporal sulcus (pITS), which is a single deep furrow in the left hemisphere but has a y-shaped branching pattern in the right hemisphere. Also, an additional sulcus [the anterior occipital sulcus (AOS)] is interposed between the pITS and the superior temporal sulcus (STS) in the left hemisphere but not the right. Another example is the superior frontal sulcus (SFS), which is a single long crease in the left hemisphere but is broken into several shorter creases in the right hemisphere.
We used two approaches to assess whether the cortical convolutions of the Visible Man have any gross abnormalities that would make this brain unsuitable as an atlas. First, we compared the pattern of convolutions with those described and illustrated for 25 normal brains by Ono et al. (1990). Throughout both hemispheres of the Visible Man, the folding pattern is similar to one or another of the patterns they described. Second, we analyzed the location of sulci in stereotaxic space by measuring the coordinates at selected points along each of nine major sulci and comparing these trajectories to those described by Steinmetz et al. (1990) for 20 normal brains. Except for a few modest deviations described in the legend to Figure 2, the positions and trajectories of the Visible Man sulci were all within the normal range. Altogether, we consider the Visible Man to be a reasonable choice for an atlas of the cerebral cortex (see Discussion).
Cortical flat maps
Figure 3 shows cortical flat maps of the entire left and right hemispheres of the Visible Man generated using our automated flattening procedure (see Materials and Methods). The top panelsdisplay cortical geography on the flat maps using the same map of mean curvature that was shown on the extensively smoothed surfaces in the preceding figure. To establish a standard orientation, the central sulcus on the map is aligned approximately parallel to its average orientation in the lateral view of the intact hemisphere. This convention makes the orientation of human flat maps similar to that commonly used for macaques and other nonhuman primates (see Fig. 13below). To reduce distortions in surface area on the flat map, five artificial cuts were made in geographically corresponding locations in each hemisphere, as indicated by blue lines on Figure 3 and in the 3-D reconstructions. The segments representing the true margins of neocortex include its juncture with the corpus callosum (C.C.), hippocampus (HC), amygdala (Amyg.), and olfactory cortex (Olf.), as indicated along the margins of each map.
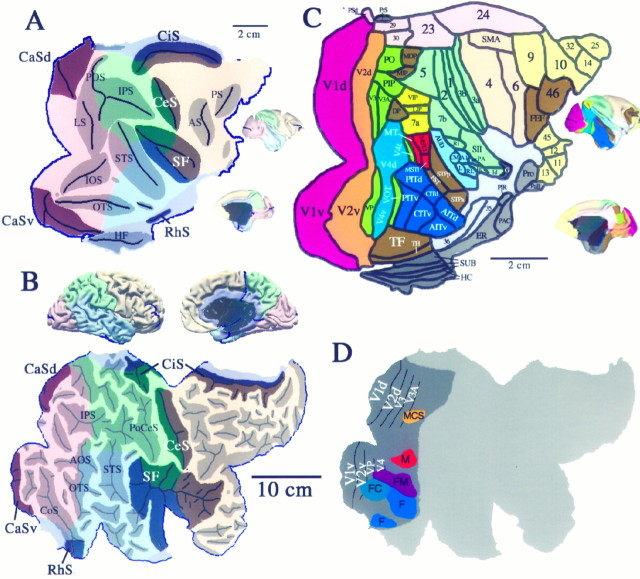
Fig. 13.
Interespecies comparisons between macaque and human cerebral cortex. A, 3-D surface reconstructions and a flat map of the macaque monkey (case 79-0; Drury et al., 1996a). The surface is colored to delineate the different cortical lobes, and shaded regions on the flat map indicate cortex buried within various sulci (abbreviations are a subset of those listed for Figure 5 (see ), except thatAS stands for arcuate sulcus; PS, the principal sulcus; and HF, the hippocampal fissure). The extent of different lobes in the macaque is based on designations byBonin and Bailey (1947) and Felleman and Van Essen (1991). Instead of making a cut along the V1/V2 boundary, as has been done for most previous cortical flat maps of the macaque (e.g., Van Essen and Maunsell, 1980; Drury et al., 1996a), a cut was made along the horizontal meridian representation in V1 (cf. Van Essen, 1997) to correspond better to the human flat map. Scale bars in A(and C) apply to the flat maps but not the 3-D views.B, 3-D reconstruction and cortical flat map of the Visible Man, modified from Figure 3. The more darkly shaded sulci in A and B are likely to correspond to one another, because they contain cortical areas that are known or likely to be homologous (see Results).C, Cortical areas in the macaque, according to the partitioning scheme of Felleman and Van Essen (1991). Note that the macaque map includes 3 cm2 of hippocampus and other archicortical and paleocortical structures, all limbic regions that were not included in the Visible Man reconstruction. As a basis for comparing surface geometry, we used the same indices as in Figure 4 and determined that the macaque cortex has about one-fourth of the intrinsic curvature of human cortex (ICI = 14 vs 55 for Visible Man) and one-third of the folding (FI = 160 vs 510 for Visible Man). D, Visual areas and functionally specialized visual regions displayed on the right hemisphere map of the Visible Man (adapted from Fig. 12D).
The bottom panels in Figure 3 display sulci and gyri in an alternative format, in which buried cortex (not visible from the exterior of the hemisphere) is shown in darker shades. Black lines indicate sharply creased folds (fundi) within each sulcus. In addition, the five lobes of the hemisphere are colored on the map and on the accompanying lateral and medial views of the hemisphere. This helps in visualizing the locations of the various cuts, which include deep cuts into the occipital and frontal lobes, plus smaller cuts at the parieto-frontal junction, the fronto-temporal junction, and near the occipito-temporal junction.
To determine surface areas for each lobe and for the entire hemisphere, we summed the area of all individual tiles over the relevant portion of each 3-D reconstruction (Table 1). The total cortical surface area of 1570 cm2 for both hemispheres is similar to the estimate of Jouandet et al. (1989). It is ∼20% lower than the mean reported by Tramo et al. (1995), but the real difference is probably smaller, because our value is likely to be a slight underestimate (see Materials and Methods). The frontal lobe occupies more than one-third of each hemisphere (36%), whereas the temporal, parietal, and occipital lobes each occupy ∼20% and the limbic lobe only 6% of total cortex. Cortex buried in sulci (Fig. 3,shaded regions) occupies 70% of the total surface area of the reconstruction. This is equivalent to a gyrification index (ratio of total surface area to exposed area) of 3.3. This is substantially higher than the mean gyrification index of 2.55 reported by Zilles et al. (1988), which corresponds to 61% buried cortex. The correct value probably lies between these two estimates, because the extent of gyral regions tends to be overestimated by the analysis of Zilles et al. (1988) (which is based the pial surface rather than layer 4) and tends to be underestimated by our analysis (because the smoothed surface lies deep to layer 4 in gyral regions).
Table 1.
Surface area measurements of cortical lobes
| Region | Left hemisphere [cm2(%)] | Right hemisphere [cm2 (%)] |
|---|---|---|
| Total neocortex | 766 (100) | 803 (100) |
| Frontal | 278 (36) | 297 (37) |
| Temporal | 161 (21) | 161 (20) |
| Parietal | 139 (18) | 161 (20) |
| Occipital | 144 (19) | 145 (18) |
| Limbic | 46 (6) | 40 (5) |
| Total sulcal | 536 (70) | 554 (69) |
| Total gyral | 230 (30) | 249 (31) |
Areal measurements are based on summing the areas of tiles in the 3-D reconstructions, not on the flat maps.
Surface geometry
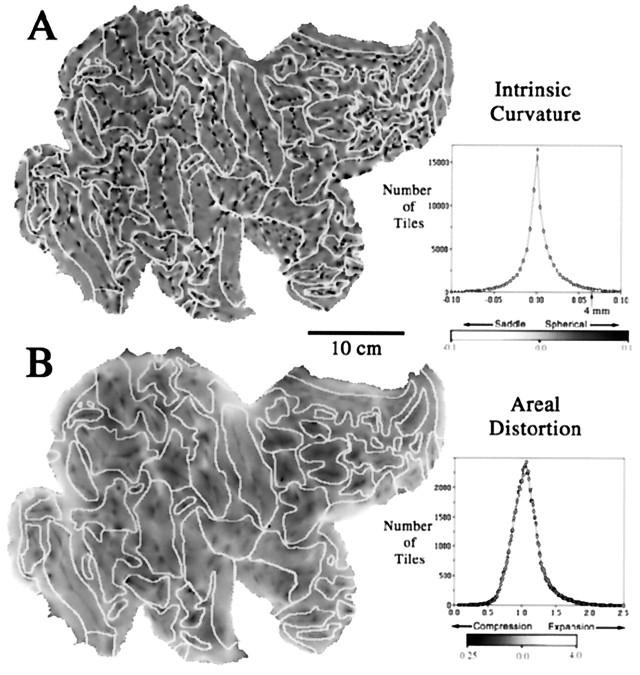
The overall extent of the dark and bright streaks in Figure 3indicates that crease-like folds occupy a significant fraction of total cortical surface area. However, in many places the surface is not just folded along a single axis but instead has significant intrinsic (Gaussian) curvature. The intrinsic curvature of the surface in 3-D is displayed on a flat map of the right hemisphere in Figure4A, with dark regions denoting positive intrinsic curvature (rounded bulges or indentations) and light regions denoting negative intrinsic curvature (saddle-shaped regions). The map is peppered with hundreds of foci of elevated intrinsic curvature. Individual foci are typically 1–2 mm across and are mainly concentrated along crests of gyri and fundi of sulci, as can be seen in relation to the pattern of sulcal margins (Fig. 4A, fine white lines). High intrinsic curvature tends to occur where creases terminate or bifurcate, as can be determined by comparison with the map of mean curvature in Figure3.
Fig. 4.
A, Intrinsic curvature of the cortical surface, displayed on a map of the right hemisphere. There are numerous regions of positive (spherical) curvature (dark) and of negative (saddle-shaped) curvature (light). A histogram of intrinsic curvature values is shown to the right. The mean value (0.004 mm−2) is slightly positive, reflecting the overall convex shape of the hemisphere. Only a small fraction of the cortical sheet (2% of total surface area) has an intrinsic curvature exceeding that of a sphere 4 mm in radius (i.e., intrinsic curvature >0.0625 mm−2). B, Areal distortion of the right hemisphere flat map. Dark and light regions represent tiles that are compressed or expanded, respectively, relative to their area in the 3-D reconstruction. A histogram of distortion ratios is shown to the right. The mean distortion ratio is 1.09, corresponding to an average of 9% greater surface area on the flat map compared with the corresponding area on the 3-D surface. For the left hemisphere map, the mean distortion ratio is 1.12; 6% of the tiles are expanded by more than 50% on the cortical map, and 2% of the tiles are compressed to an equivalent degree.
An interesting question relating to surface geometry is whether human cerebral cortex is dominated by intrinsic curvature (like the pock-marked surface of a golf ball), as suggested by Griffin (1994). Alternatively, the cortex may be dominated by folding (like a crumpled sheet), as suggested by the greater expanse of folded versus intrinsically curved regions evident in comparing Figures 3Aand 4A. To address this issue quantitatively, we calculated an intrinsic curvature index and a folding index, each a dimensionless number that reflects shape characteristics integrated across the entire surface (see Materials and Methods). The intrinsic curvature index exceeds 50 for both hemispheres (56 for the left and 54 for the right hemispheres). In this respect, each hemisphere is equivalent to a surface covered with more than 100 hemispheric indentations. However, the folding index is an order of magnitude greater (500 for the left hemisphere and 520 for the right). Thus, each hemisphere contains ∼about 500 times greater folding than a simple cylinder the length of which equals its diameter, signifying a marked predominance of folding over intrinsic curvature.
Significant distortions of surface area are unavoidable when a surface containing an irregular pattern of intrinsic curvature is transformed to a flat map (or even to a smooth 3-D surface such as an ellipsoid). To reduce global distortions associated with the overall rounded shape of the hemisphere, we found it necessary to make five cuts along the margins of the hemisphere. The residual areal distortions on the flat map were quantified by taking the ratio between the area of each tile in the 3-D reconstruction and its area on the cortical map. These distortion ratios are displayed as a gray scale representation for the right hemisphere (Fig. 4B). The map shows numerous regions of local compression (darker regions) or expansion (lighter regions) relative to surface area in the intact hemisphere but only modest variations in the average distortion for the different lobes. Comparison of the maps in Figure 4, A andB, reveals significant correlations between the patterns for distortion and for intrinsic curvature. Most notably, local compression occurs at many hot spots of positive (spherical) intrinsic curvature, as should be expected when flattening a bumpy surface. The histogram to the right of the map shows the number of tiles having different distortion ratios. Only 4.5% of the surface tiles (triangles) are expanded by more than 50% (distortion ratio, >1.5), and only 2.4% are compressed to an equivalent degree (distortion ratio, <0.67). The total area of the flat map divided by the total 3-D surface area is 1.10, signifying that the flat map is 10% expanded overall in areal extent, equivalent to ∼5% in linear dimensions.
A geographic atlas
Gyri and sulci that can be recognized by their characteristic shape and location represent useful geographical landmarks that facilitate comparisons of results across hemispheres. We identified 47 sulci and 34 gyri in one or both hemispheres of the Visible Man using the atlas of Ono et al. (1990) as a primary guide. All identified gyri and sulci are denoted by abbreviations on the Visible Man flat maps illustrated in Figure 5, with full names (plus a few alternate names) given in the .
Fig. 5.
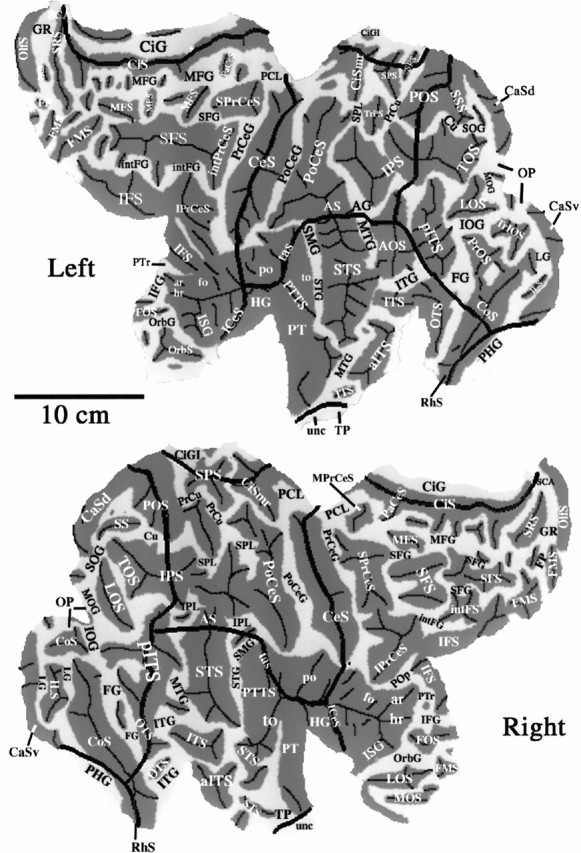
A geographical atlas showing sulci and gyri in the Visible Man. Sulcal and gyral abbreviations are listed in the, alphabetically for each lobe. Designations are based mainly on the atlases of Ono et al. (1990) and Jouandet et al. (1989). In cases of ambiguity or multiple terminology (usually in regions of high variability), we based our choice on the sulcal pattern that best matched the geography of the Visible Man. The pattern of convolutions in the Visible Man lies within the range of variability illustrated and analyzed by Ono et al. (1990) for a population of 25 brains.
Only a few of the larger sulci, such as the CeS and CiS, contain a single uninterrupted fold and also are completely isolated from their neighbors. Some sulci are broken into multiple creases separated by intervening gyral protrusions, as occurs for the SFS in the right hemisphere. Other sulci merge with one or more neighboring sulci to form a larger expanse of completely buried cortex, often with ambiguity as to the exact border between one sulcus and the next. One prominent example includes the region of the STS, angular sulcus, and postcentral sulcus, near the center of each map. These sulci are confluent with one another in both hemispheres and in addition merge with different sets of neighboring sulci in the left and right hemispheres.
Coordinate systems on the cortical surface
The irregular shapes and uncertain boundaries of most gyri and sulci limits their utility in describing precise spatial locations across the cortical surface. One option for assigning spatial coordinates to the cortical surface is to display isocontour lines, where the surface is intersected by planes of constant x,y, or z value in stereotaxic space (cf. DeYoe et al., 1996). Figure 6 shows isocontours taken at 1 cm intervals for the right hemisphere of the Visible Man (after transformation to Talairach space) for lines of constantx value (Fig. 6A), constant yvalue (Fig. 6B), and constant z value (Fig. 6C). The Talairach coordinates for any given geographical location can be readily determined by reading thex, y, and z coordinates successively from the three maps. For example, the ventral tip of the central sulcus, shown by black dots in Figure6A–C, has Talairach coordinates of [56, −11, 17]T’88. Although every point on the map has unique stereotaxic coordinates, the converse is not true, because randomly chosen points in 3-D space will not lie precisely on the reconstructed surface. However, a linkage can be made by determining the nearest point on the surface and the distance and direction to the point in 3-D space.
Fig. 6.
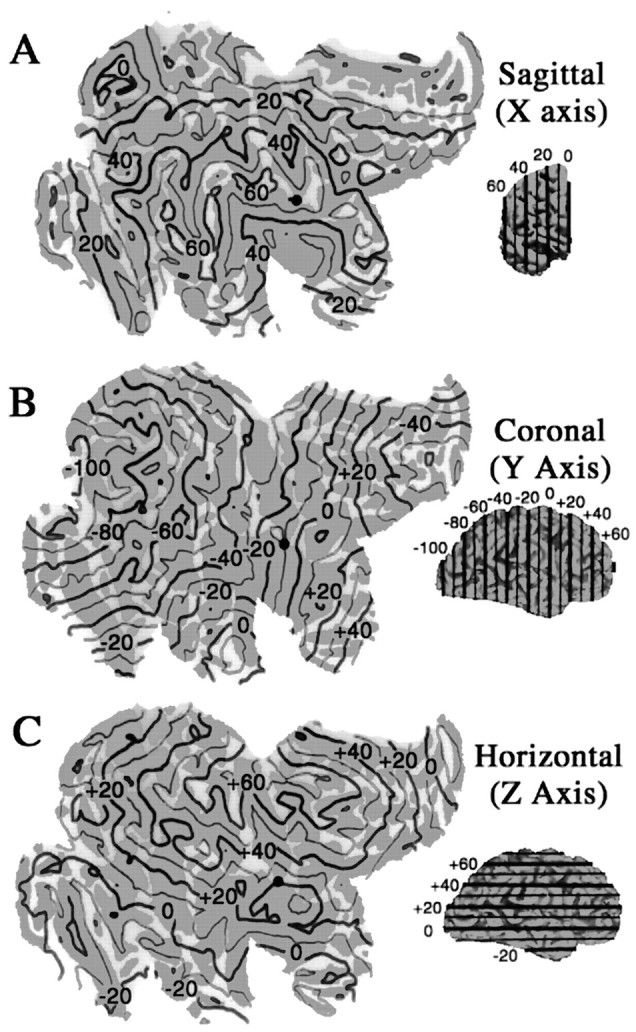
Stereotaxic (Talairach) isocontours displayed on the Visible Man surface. Contours at 10 mm intervals in 3-D are displayed on flat maps for constant x(A), constant y(B), and constant z(C) values. For any point on the map, its Talairach coordinates can be determined by interpolation between contours on each panel. In the reverse direction, given a set of Talairach coordinates, the nearest point on the cortical map can be estimated by looking for intersection points on the appropriate isocontours.
A complementary strategy is to establish a coordinate system that respects neighborhood relationships on the cortical surface (Anderson et al., 1994; Drury et al., 1996a). Just as latitude and longitude are invaluable for designating different locations on the surface of the earth, surface-based coordinates provide an objective, precise, and convenient metric for cortical cartography. Flat maps provide a natural substrate on which to establish a Cartesian surface-based coordinate system, as shown in Figure 7 for both hemispheres of the Visible Man. We chose the ventral tip of the central sulcus to be the origin, because it is centrally located and consistently identifiable. Surface-based coordinates are denoted by [u, v]R-SB for points on the right hemisphere map and by [u, v]L-SB for points on the left hemisphere map. The positive direction for the horizontal (u) axis is leftward for the left hemisphere and rightward for the right hemisphere, reflecting the mirror symmetry of the two maps. Units on the cortical map are designated asmap-millimeters (map-mm). They differ from millimeters in the 3-D brain anywhere that the flat map is expanded, compressed, or sheared. In regions where distortions are not large, a straight line between any two points on the cortical map should be a reasonable approximation to a geodesic, i.e., the shortest possible trajectory along the surface in 3-D. The grid lines, placed at intervals of 20 map-mm on each map, are shown in the bottom panels after transformation back to the original 3-D configuration of each hemisphere.
Fig. 7.
A surface-based coordinate system for the left hemisphere [u, v]L-SB and right hemisphere [u, v]R-SB of the Visible Man, displayed on a map of cortical geography. The origin corresponds to the ventral tip of the central sulcus, and grid lines are spaced at 20 map-mm on each map. The horizontal (u) axis extends from −253 to +170 map-mm for the left hemisphere and from −254 to +171 map-mm for the right hemisphere. The vertical (v) axis extends from −145 to +188 map-mm for the left hemisphere and from −134 to +174 for the right hemisphere. The bottom panels show lateral and medial views of the hemisphere, with the surface-based coordinate system wrapped up into 3-D space. The mean separation between adjacent resampled nodes in 3-D was 0.95 mm for the left hemisphere and 0.96 mm for the right hemisphere. This signifies an average linear expansion of 5% on the flat maps. Any point in the volume that lies above or below the surface can be represented in 3-D surface-based coordinates, using its distance from the surface in 3-D as one coordinate (w) and the nearest point on the surface for the other two coordinates ([u, v, w]R-SB or [u, v, w]L-SB, depending on the hemisphere). To determine the correspondence of the surface-based coordinates of major geographical landmarks, the centers of gravity (white dots) were determined for nine sulci: the central, postcentral, superior temporal, collateral, olfactory, fronto-orbital, and superior rostral sulci, plus dorsal and ventral halves of the calcarine sulcus (see Results and Table 2).
The overall dimensions of the left and right hemisphere maps are similar, as reflected by their total horizontal extent (424 vs 426 map-mm, respectively) and total vertical extent (333 vs 306 map-mm, respectively). This consistency makes surface-based coordinates useful for quantitative comparisons between hemispheres. From visual inspection, it is evident that corresponding sulci in the two hemispheres generally have similar surface-based coordinates, just as they have similar 3-D stereotaxic coordinates except for the mirror reflection about the horizontal axis. We confirmed this quantitatively by determining the geometric center of gravity on the flat map for each of nine sulci that are well delineated in both hemispheres (Fig. 7,white dots). In Table 2, the two-dimensional (2-D) map coordinates are listed on the left, along with the misalignment between corresponding points on each map (R-L2D). Overall, the difference between the left and right centers of gravity on the cortical flat maps was small (9 map-mm median value, 15 map-mm mean value) and in no case was >7% of the total length of the flat map.
Table 2.
Surface-based and 3-D coordinates of geographic landmarks (sulcal centers of gravity)
| Left map (map-mm) | Right map (map-mm) | R-L2-D | 3-D (left) (mm) | 3-D (right) (mm) | R-L3-D | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| u | v | u | v | x | y | z | x | y | z- | |||
| CeS | 21 | 62 | 20 | 60 | 2 | −30 | −26 | 48 | 37 | −30 | 49 | 8 |
| PoCeS | 60 | 62 | 64 | 70 | 9 | −39 | −39 | 52 | 34 | −47 | 56 | 10 |
| STS | 83 | −17 | 107 | −4 | 27 | −46 | −39 | 18 | 48 | −52 | 14 | 14 |
| CaSd | 196 | 104 | 192 | 118 | 15 | −10 | −80 | 11 | 1 | −85 | 0 | 15 |
| CaSv | 237 | −17 | 241 | −24 | 8 | −4 | −74 | 7 | 3 | −80 | 1 | 9 |
| CoS | 194 | −56 | 188 | −55 | 6 | −28 | −49 | 1 | 24 | −53 | −2 | 6 |
| OlfS | −158 | 150 | −162 | 120 | 30 | −7 | 34 | −14 | 7 | 35 | −14 | 1 |
| SRS | −135 | 140 | −139 | 108 | 32 | 0 | 42 | 0 | 10 | 42 | 3 | 10 |
| FOS | −68 | −51 | −63 | −57 | 8 | −45 | 37 | 1 | 41 | 32 | 11 | 12 |
| Median | 9 | 10 | ||||||||||
| Mean | 15 | 9 | ||||||||||
For full names of sulci in column 1, see . Column 6, R-L2-D indicates the misalignment between left and right hemisphere surface-based (map) coordinates. Column 13, R-L3-D indicates the misalignment between left and right hemisphere 3-D (stereotaxic) coordinates.
The corresponding 3-D coordinates are listed in Table 2 on the right, along with the misalignment between points in 3-D (R-L3D). The misalignment between the corresponding centers of gravity in 3-D was comparable in the absolute extent (10 mm median, 9 mm mean value), making it a higher percentage of the total length of the hemisphere. This degree of misalignment is about what should be expected, given that the scatter in position of major sulci is typically ∼2 cm after transformation to stereotaxic space (Steinmetz et al., 1990; Thompson et al., 1996).
By these measures, surface-based coordinates are at least as consistent as 3-D stereotaxic coordinates in describing positional relationships in the two hemispheres of the Visible Man. The lack of perfect symmetry reflects a combination of individual variability in the pattern of convolutions and various technical factors such as alignment of the hemispheres and, for the flat maps, the exact placement of the cuts. It is likely that there will be somewhat greater variability between flat maps made from hemispheres of different individuals, but this does not pose a problem for how we have used surface-based coordinates in the examples illustrated below.
Mapping functional organization
Projection via stereotaxic coordinates
A common analysis strategy in neuroimaging studies involves transforming data from individual brains into Talairach space and reporting the stereotaxic (Talairach) coordinates for the center (or peak) of each statistically significant activation focus (Fox et al., 1985; Talairach and Tournoux, 1988; Fox, 1995). Given its stereotaxic coordinates, the center of any activation focus can be projected to the nearest location on the Visible Man surface and can be represented in relation to this surface when it is smoothed or flattened (see Materials and Methods). However, it can be misleading to visualize only the nearest point on the surface without indicating the spatial uncertainties associated with that localization. One major source of uncertainty arises from the aforementioned residual variability of ∼2 cm in the location of identified sulcal landmarks. Additional sources include variability in the position of identified cortical areas in relation to nearby geographical landmarks (Rademacher et al., 1993;Roland and Zilles, 1994) and the limited spatial resolution of neuroimaging techniques, particularly PET.
To estimate the aggregate uncertainty from all factors combined, we analyzed neuroimaging data in which the coordinates of activation foci were reported for individual subjects as well as for the group means within that study. Figure 8 illustrates the distribution of foci in a study that compared responses to moving versus stationary stimuli using the PET technique (Watson et al., 1993). The group means for responses averaged across all 12 subjects had similar Talairach coordinates for the left hemisphere ([+40, −68, 0]T’88) and right hemisphere ([−44, −70, 0]T’88). When plotted on the nearest coronal slice through the Talairach atlas (y = 70; Fig.8A), both foci were centered in the white matter, ∼5 mm below the pITS. When displayed on coronal slices through the Visible Man after transformation to Talairach space (Fig. 7B, black dots), both foci were located closer to the gray matter of the pITS. The green dots show the location of foci from individual subjects that were contained within these coronal slices. Regions of the surface within 10 mm of the group mean arered; regions within a surrounding shell, 10–15 mm from the group mean, are pink.
The full extent of this pattern is shown for the right hemisphere on 3-D lateral views and on flat maps of the occipito-temporal cortex for the left (Fig. 8C,D) and right (Fig.8E,F) hemispheres. On both flat maps, cortex within 10 mm 3-D distance from the mean (red) occurs as two separate blobs of comparable size, whereas cortex within 15 mm is almost entirely contained in a single larger region. The irregular shapes of these shaded regions (e.g., elongated vertically for the right hemisphere and horizontally for the left) reflect the particular way that the local convolutions of Visible Man surface intersect the spheres of 10 and 15 mm radius in each hemisphere.
All but two of the individual activation foci lie within 15 mm of the group mean, and most of them lie within 10 mm. The 3-D distance between each individual activation focus and the associated group mean is shown quantitatively in the histogram of Figure 8G(black bars). The gray bars show analogous results for seven subjects (14 hemispheres) in a study that used a similar visual stimulation paradigm but was based on fMRI instead of PET (McCarthy et al., 1995). Despite the higher spatial resolution of fMRI, the average distance from the group mean is slightly larger for the fMRI study (10 mm) than the PET study (7 mm). This suggests that factors other than instrument resolution are the dominant sources of uncertainty in the stereotaxic localization of activation foci. Taken together, these findings suggest that a 10 mm radius around the mean captures most of the spatial uncertainty associated with any given focus and that a 15 mm radius captures nearly all of this uncertainty. Similar values were reported by Hunton et al. (1996) for a wider variety of activation paradigms, suggesting that this degree of spatial uncertainty is generally applicable to neuroimaging data converted to Talairach space by conventional transformation algorithms.
The uncertainty zones visualized using this method reflect the geographical range over which the center of an activation focus might have occurred if the neuroimaging paradigm had been performed in the Visible Man. It implies nothing about the extent of cortex actually involved, which requires information about the number of voxels activated in each individual hemisphere by a given paradigm. Despite the obvious importance of this issue, we have not incorporated it into the analyses presented below, because the requisite quantitative data are not available.
Estimating the extent of area V1
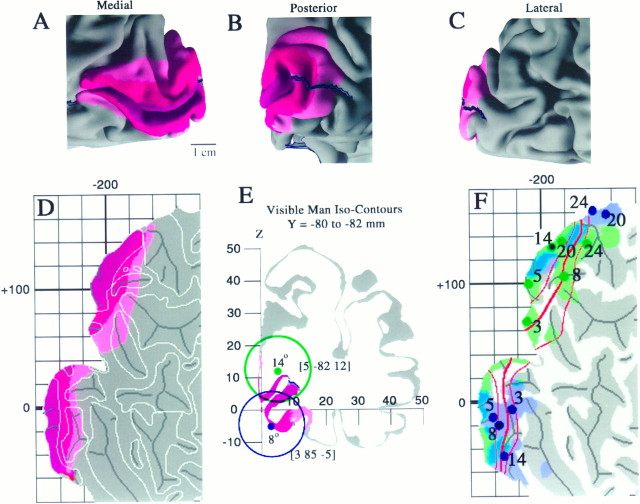
We used data from conventional architectonic analyses as well as modern neuroimaging studies to estimate the extent of primary visual cortex (area V1) on the Visible Man reconstruction. Our starting point was the postmortem histological analysis of architectonically identified V1 in 20 hemispheres by Rademacher et al. (1993). We used their data to estimate the minimal, maximal, and average extent of V1 in relation to the calcarine sulcus and nearby geographical landmarks of the Visible Man. The results are shown on medial, posterior, and lateral views of occipital cortex in Figure9A–C. The same data are displayed on a cortical flat map in Figure 9D, where V1 is split into dorsal and ventral halves by the cut along the fundus of the calcarine sulcus. Maroon regions represent cortex that is part of area V1 in nearly all hemispheres. This includes the calcarine sulcus plus a narrow strip along its dorsal and ventral lips.Red indicates a surrounding belt of cortex that is part of V1 in most hemispheres, and pink represents an additional belt into which V1 extends in a minority of cases. The “average” border of V1 indicated by this analysis lies at the juncture of thered and pink regions. The surface area for an average-sized V1 (i.e., the maroon and redregions combined) is 22 cm2, which constitutes 2.7% of total neocortex in the right hemisphere. The corresponding value for V1 in the left hemisphere is 26 cm2 (3.4% of total neocortex). These values are within the range of 15–37 cm2 reported by Stensaas et al. (1974) and 22–29 cm2 reported by Filiminoff (1932) for human V1 in one hemisphere.
Fig. 9.
Estimated location and variability in extent of visual area V1 in the Visible Man. A–C, Medial, posterior, and lateral views of V1 determined from the postmortem architectonic study of Rademacher et al. (1993). Maroonregions represent cortex that belongs to V1 in all or nearly all of the 20 hemispheres illustrated by Rademacher et al. (1993) in a series of medial and lateral drawings of each hemisphere.Red regions incorporate an additional belt of cortex that is part of V1 in about half of the hemispheres.Pink includes cortex that is part of V1 in a minority of cases, based on estimated distances from the margins of the calcarine sulcus and other geographical landmarks. D, The same inner, most likely, and outer border estimates for V1 are shown on a cortical flat map of the occipital lobe in relation to gyral and sulcal outlines. E, Two foci along the V1/V2 boundary taken from the fMRI mapping study of DeYoe et al. (1996) are shown in relation to a coronal slice through the Visible Man. The blue dot represents 8° eccentricity along the superior vertical meridian, and the blue ring indicates the 10 mm uncertainty zone surrounding this stereotaxic location. Similarly, thegreen dot and ring represent 14° along the inferior vertical meridian. F, Projection of activation foci and associated 10 mm uncertainty zones for five eccentricities along the superior vertical meridian (blue dots and shading) and five eccentricities along the inferior vertical meridian (green dots andshading). Blue-green represents portions of the surface within 10 mm of both types of focus.
As an independent basis for localizing area V1, we used results from an fMRI study of visual topography by DeYoe et al. (1996). The Talairach coordinates of selected points along the V1 boundary were determined from their summary map of topographic organization overlaid on maps of isocontours in Talairach space (compare Fig. 6 above). Figure9E shows two such points on a coronal slice through the right hemisphere of the Visible Man. The blue dot, representing 8° along the superior vertical meridian, lies along the ventral lip of the calcarine sulcus, close to the expected location of the V1 border (Fig. 9A–D). The green dot, representing 14° along the inferior vertical meridian, lies in white matter dorsal to the calcarine sulcus. The nearest point on the surface lies deep in the calcarine sulcus, far from where the V1 border ever occurs. Nevertheless, the region along the medial wall of the hemisphere where the V1 boundary is likely to occur (red andpink regions) lies within the green ring (10 mm uncertainty zone). Thus, there is no conflict between the two methods for estimating the V1 border, even though the stereotaxically identified uncertainty zone encompasses a much larger cortical extent.
Results for 10 topographically identified points along the V1 boundary are plotted on a flat map of occipital cortex in Figure 9F. The map is violet where the surface is within 10 mm (in 3-D) of a superior vertical meridian site, green where it is within 10 mm of an inferior vertical meridian site, andblue-green where it is within 10 mm of both meridia. For half of these sites, the closest point on the cortical surface (blue or green dots) lies within the estimated boundary zone for V1 (thin orange lines). The remaining sites are all within 10 mm 3-D distance from this zone. As expected, central visual fields (3° and 5° eccentricity) are represented posteriorly in the cortex, toward the occipital pole, whereas peripheral fields are represented more anteriorly (toward the top and bottom of the map). The steps in this progression are somewhat irregular because of errors inherent in the stereotaxic projection method. Also, there are two systematic asymmetries evident on the map. First, for the 20° and 24° superior vertical meridian loci, the closest point on the Visible Man surface lies dorsal rather than ventral to the calcarine sulcus. Second, any given eccentricity is represented closer to the occipital pole for the inferior vertical meridian than for the superior vertical meridian. These asymmetries are attributable to individual differences in the orientation of the calcarine sulcus and in the shape of the occipital lobe, which are not compensated by the methods used to transform different brains into Talairach space. Altogether, these neuroimaging-based stereotaxic estimates for the V1 border are consistent with those based on architectonic data, but they show greater variability and provide looser constraints for border localization.
Extrastriate visual areas
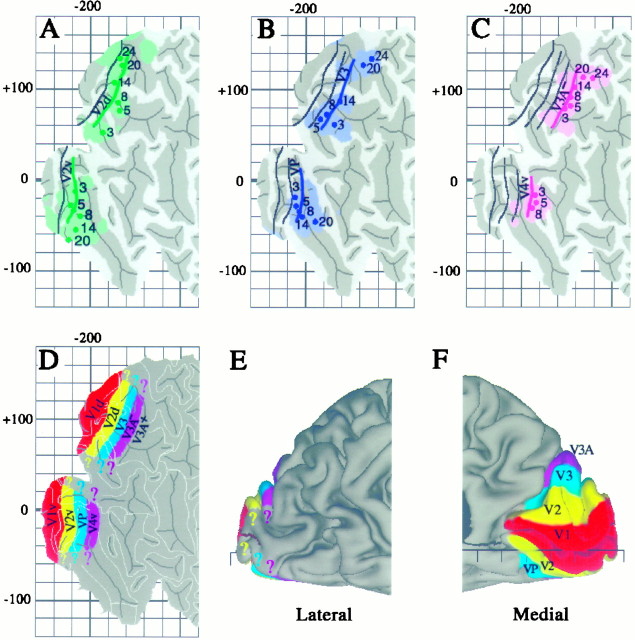
To estimate the boundaries of topographically organized visual areas V2, V3, VP, V3A, and V4v on the Visible Man atlas, we used both surface-based measurements and the stereotaxic projection method. The surface-based measurements involved determining the average width of each area on the summary flat maps published in the fMRI studies ofSereno et al. (1995) and DeYoe et al. (1996). The stereotaxic projection method was applied to Talairach coordinates determined for selected points along the summary map of DeYoe et al. (1996) (compare Fig. 9 above). Figure10A illustrates these estimates for the horizontal meridian representation along the border between dorsal V2 and V3 and between ventral V2 and VP. Based on an average width of about 12 mm for dorsal V2, the estimated V2d/V3 border (green line) is drawn 12 map-mm away from the average V1 border (black line, transposed from Fig. 9). Ventral V2 is slightly wider (15 map-mm), and the V2v/VP border was drawn correspondingly more distant from the ventral V1 border. Green dots and shading illustrate the stereotaxic-based estimates for selected eccentricities along the V2d/V3 and V2v/VP borders. Almost all of the individual eccentricity points lie within 10 mm 3-D distance of the surface-based border estimate.
Fig. 10.
Boundaries of topographically organized visual areas on the Visible Man cortex estimated using surface-based and stereotaxic projection methods. A, Boundaries between V2/V3 (top of map) and V2/VP (bottom of map) shown in green, relative to the most likely V1/V2 boundary transferred from Figure 9 and shown in black.Green contours represent boundaries estimated on the basis of distances along the cortical surface, taken from the summary cortical maps of DeYoe et al. (1996) and Sereno et al. (1995).Green dots and shading represent specific eccentricities along these borders, the Talairach coordinates of which were determined using the isocontour maps of DeYoe et al. (1996) and then projected to the cortical surface along with associated 10 mm uncertainty zones. B, Boundaries between V3/V3A (top) and VP/V4v (bottom), estimated using the same strategies as in A. C, The horizontal meridian representation of V3A (top) and of V4v (bottom), again using the same methods. The estimated extent of areas V1 (red), V2 (yellow), V3 and VP (blue-green), and lower-field V3A and upper-field V4 (purple) are displayed on a flat map (D), a lateral view (E), and a medial view (F).
Figure 10, B and C, extends this analysis to additional borders progressing away from V1. In particular, Figure10B shows the estimated vertical meridian representation along the V3/V3A border dorsally and VP/V4v ventrally (blue lines, dots, and shading), based on average widths of 12 map-mm measured for V3 and VP. Figure 10C shows the estimated horizontal meridian representation in V3A and V4v (purple), based on average widths of 15 map-mm measured for V4v and 13 map-mm for the lower-field representation in V3A.
As with the stereotaxic projection method, the limitations of which have already been discussed, several sources of error can affect surface-based estimates of areal boundaries. For example, errors would occur wherever the representation of linear distances is compressed or expanded to a different degree on the Visible Man map and on the maps used for measuring the widths of areas. Unfortunately, insufficient data on distortion values are available to quantify these errors for the maps in Figure 10. Nonetheless, the fact that the stereotaxically based points and halos are distributed fairly evenly around each surface-based border estimate signifies reasonable agreement between the two methods and suggests that systematic errors are modest, at least for this particular data set.
The overall arrangement of topographically organized areas is summarized on a cortical map in Figure 10D and on medial and lateral views of the right hemisphere in Figure 10,E and F. Area V2 is yellow, V3 and VP are blue, and lower-field V3A (designated V3A−) and V4v are purple. Also indicated is the approximate location of an upper-field representation (V3A+) that has been reported anterior to V3A− (Tootell et al., 1996). The uncertainties associated with the borders of all of these extrastriate areas are presumably comparable to those estimated for area V1, i.e., approximately ±1 cm in most regions (compare Fig. 9). Because these uncertainty limits exceed the width of the individual areas, it is impractical to illustrate them on the summary map. The colored question marks reflect uncertainty concerning how far each area extends toward the representations of the fovea and far periphery.
Analyses of functional specialization
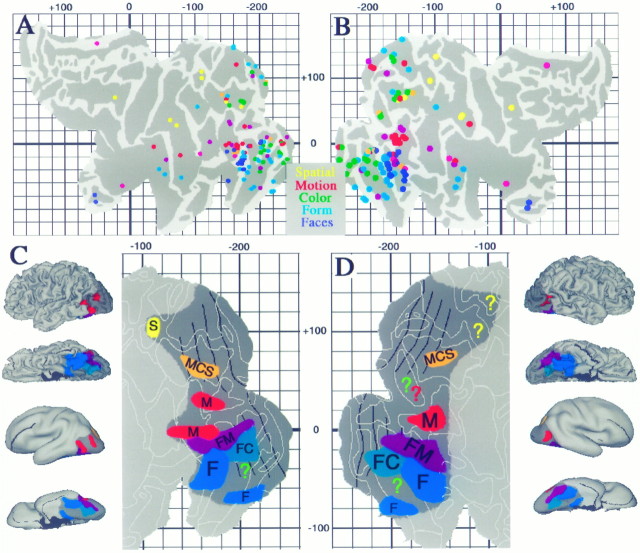
We used the stereotaxic projection method to analyze functional specializations for visual processing that have been reported for 118 foci in a dozen PET and fMRI studies (Figs.11, 12, Table 3). In Figure 11, the data are grouped according to the type of activation involved (processing of color, motion, objects, faces, or spatial relationships) and are displayed on 3-D views as well as cortical flat maps. The shaded regions represent cortex within 10 mm (3-D distance) of at least one focus of that class. The boundaries of topographically organized areas, transferred from Figure 10, are shown in black.
Fig. 11.
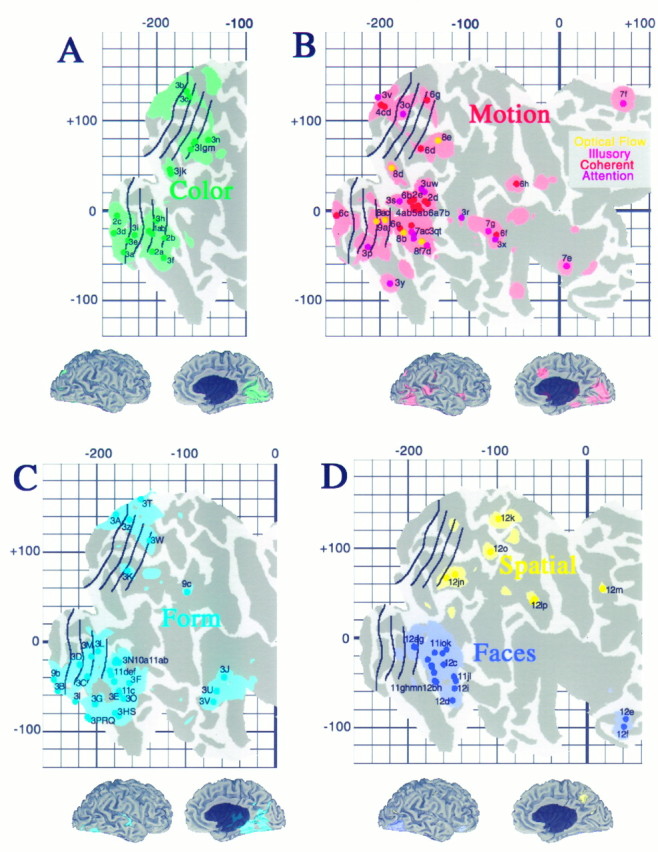
Distribution of activation sites associated with specific aspects of visual function. Each panel shows individual activation foci, identified according to the labels in Table 2, and cortex within the surrounding 10 mm uncertainty zone, for activations associated with processing of color (A, green), motion (B, red), form (inanimate objects or textures; C, light blue), faces (D, dark blue), and spatial relationships (D, yellow).
Fig. 12.
Combined analysis of activation foci for all foci listed in Table 3. Top panels, All 118 foci projected to flat maps of the left and right hemispheres. Note that activation foci originally reported for both the left hemisphere (x< 0 in Table 3, column 5) and the right hemisphere (x > 0) are plotted on each map. When patterns were examined separately for data obtained from the left and right hemispheres, no pronounced hemispheric asymmetries were evident. Although not labeled on either map, individual foci can be identified by determining their surface-based coordinates and finding the corresponding focus in Table 3. The distribution of foci is generally similar on the two maps, but with a number of notable exceptions (see text). Note that on the left hemisphere map a few foci lie outside the perimeter of the map (blue dots near the parahippocampal gyrus on the bottom right). This is because of their distance and orientation relative to the nearest tile on the surface.Bottom panels, Estimated extent of cortex likely to be specialized for particular visual functions, including motion (M) in red, form (F) in blue, spatial analysis (S) in yellow, and of cortex involving overlapping or closely interdigitation of multiple functions, including form and color (FC) combined (blue-green); form and motion (FM) combined (purple); and motion, color, and spatial, (MCS) combined (orange). Results are displayed in three formats for each hemisphere, including lateral and ventral 3-D views, lateral and ventral smoothed views, and flat maps of the posterior half of each hemisphere. The total extent of visually responsive cortex estimated from the pattern of activation foci is shown in dark gray.
Table 3.
Vision-related activation foci
| Focus | Task | Baseline | Zstat | Talairach ′88 (mm) | Left map (map-mm) | Right map (map-mm) | R-L2-D | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| x | y | z | u | v | u | v | |||||
| Color | |||||||||||
| Lueck et al., 1989 | View color | Gray | |||||||||
| 1a (T1) | – | 22 | −73 | −8 | −206 | −10 | −208 | −23 | 13 | ||
| 1b (T1) | – | −24 | −70 | −5 | −201 | −14 | −205 | −26 | 13 | ||
| Zeki et al., 1991 | |||||||||||
| 2a (T1) | 2.9 | 20 | −66 | −4 | −204 | −28 | −205 | −46 | 18 | ||
| 2b (T1) | 3.9 | −26 | −68 | −8 | −193 | −25 | −191 | −30 | 5 | ||
| 2c (T1) | 13 | −4 | −90 | 0 | −236 | −1 | −244 | −6 | 9 | ||
| Corbetta et al., 1991 | Attend color | Passive | |||||||||
| 3a (5) | 2.0 | −5 | −61 | 9 | −236 | −31 | −236 | −46 | 15 | ||
| 3b (5a) | 2.0 | −5 | −65 | 14 | −242 | −24 | −166 | 133 | 174* | ||
| 3c (5b) | 2.0 | −6 | −71 | 15 | −188 | 109 | −164 | 127 | 30 | ||
| 3d (6) | 2.0 | −8 | −76 | 4 | −230 | −14 | −247 | −25 | 20 | ||
| 3e (6a) | 2.0 | −6 | −71 | 4 | −232 | −17 | −232 | −33 | 16 | ||
| 3f (23) | 2.2 | −24 | −52 | 0 | −200 | −43 | −192 | −52 | 12 | ||
| 3g (24) | 2.0 | −21 | −80 | 19 | −174 | 67 | −158 | 75 | 18 | ||
| 3h (25) | Attend color | Div att’n | 2.2 | −24 | −80 | −4 | −204 | −3 | −200 | −11 | 9 |
| 3i (26) | 2.0 | 19 | −76 | 2 | −216 | −3 | −224 | −27 | 25 | ||
| 3j (27) | 2.2 | −26 | −80 | 6 | −209 | 91 | −184 | 42 | 55 | ||
| 3k (27a) | 2.2 | −24 | −82 | 11 | −175 | 62 | −185 | 46 | 19 | ||
| 3l (27b) | 2.0 | −23 | −82 | 15 | −175 | 64 | −162 | 68 | 18 | ||
| 3m (27c) | 2.0 | −21 | −81 | 21 | −170 | 65 | −157 | 77 | 18 | ||
| 3n (28) | 2.0 | 23 | −77 | 32 | −154 | 59 | −142 | 79 | 24 | ||
| Motion | |||||||||||
| Zeki et al., 1991 | Coherent motion | Static | |||||||||
| 2d (T2) | 5.6 | 38 | −62 | 8 | −152 | 0 | −150 | 10 | 10 | ||
| 2e (T2) | 4.5 | −38 | −74 | 8 | −175 | 29 | −162 | 12 | 21 | ||
| Watson, 1993 | |||||||||||
| 4a (T1) | 7.8 | −44 | −70 | 0 | −168 | −7 | −159 | 1 | 12 | ||
| 4b (T1) | 9.0 | 40 | −68 | 0 | −165 | −10 | −157 | 5 | 17 | ||
| 4c (T1) | 11 | 2 | −88 | 0 | −238 | −3 | −195 | 116 | 127* | ||
| 4d (T1) | 11 | 4 | −88 | 4 | −238 | −1 | −199 | 118 | 125* | ||
| McCarthy et al., 1995 | Incoherent motion | Blinking | |||||||||
| 5a (T1) | 43 | −64 | 7 | −147 | −2 | −146 | 8 | 10 | |||
| 5b (T1) | −45 | −67 | 1 | −164 | −2 | −155 | 1 | 9 | |||
| Dupont et al., 1994 | Coherent motion | Static | |||||||||
| 6a (T1) | 4.9 | 46 | −72 | 0 | −175 | 2 | −162 | 1 | 13 | ||
| 6b (T1) | 5.7 | −32 | −74 | 8 | −176 | 26 | −166 | 10 | 19 | ||
| 6c (T1) | 4.2 | 8 | −90 | 0 | −232 | 2 | −248 | −5 | 17 | ||
| 6d (T1) | 4.6 | 24 | −74 | 16 | −164 | 121 | −154 | 69 | 53 | ||
| 6e (T1) | 4.6 | 40 | −72 | −12 | −177 | −15 | −178 | −20 | 5 | ||
| 6f (T1) | 3.9 | 52 | −38 | 16 | −77 | −19 | −70 | −27 | 11 | ||
| 6g (T1) | 3.9 | 20 | −74 | 28 | −149 | 70 | −147 | 123 | 53 | ||
| 6h (T1) | 4.4 | 48 | −28 | 36 | −36 | −5 | −48 | 30 | 37 | ||
| Zeki et al., 1993 | Coherent motion | Static | |||||||||
| 7a (T2) | 5.9 | −42 | −68 | −4 | −166 | −10 | −165 | −17 | 7 | ||
| 7b (T2) | 4.3 | 40 | −72 | 0 | −185 | −4 | −162 | 5 | 25 | ||
| 7c (T1) | Illusory | Static | 4.1 | −38 | −66 | 0 | −163 | −10 | −165 | −24 | 14 |
| 7d (T2) | 3.9 | 42 | −58 | −12 | −161 | −19 | −147 | −39 | 24 | ||
| 7e (T3) | 3.9 | 40 | 10 | 0 | 12 | −64 | 8 | −62 | 4 | ||
| 7f (T3) | 3.9 | 6 | 14 | 40 | 53 | 154 | 71 | 119 | 39 | ||
| 7g (T3) | 3.6 | −60 | −44 | 12 | −108 | −16 | −79 | −23 | 30 | ||
| DeJong et al., 1994 | Optical flow | Coherent | |||||||||
| 8a (T1) | 3.9 | −28 | −80 | −8 | −201 | 0 | −194 | −10 | 12 | ||
| 8b (T1) | 4.6 | 40 | −66 | −8 | −165 | −13 | −173 | −24 | 14 | ||
| 8c (T1) | 4.1 | 22 | −86 | 4 | −216 | 7 | −203 | −12 | 23 | ||
| 8d (T1) | 4.0 | 22 | −86 | 8 | −210 | 94 | −186 | 47 | 53 | ||
| 8e (T1) | 3.8 | 22 | −76 | 36 | −144 | 76 | −135 | 78 | 9 | ||
| 8f (T1) | 3.8 | −38 | −60 | −8 | −161 | −14 | −153 | −35 | 22 | ||
| Corbetta et al., 1991 | Attend motion | Passive | |||||||||
| 3o (2) | 2.7 | 5 | −78 | 15 | −191 | 102 | −174 | 108 | 18 | ||
| 3p (3) | 2.2 | 14 | −65 | −4 | −211 | −19 | −213 | −41 | 22 | ||
| 3q (15) | 2.0 | −37 | −61 | 2 | −158 | −4 | −162 | −26 | 22 | ||
| 3r (16) | 2.0 | −39 | −50 | 9 | −123 | 2 | −109 | −8 | 17 | ||
| 3s (17) | 2.0 | 33 | −78 | 2 | −184 | 25 | −178 | 11 | 15 | ||
| 3t (18) | 2.0 | 30 | −59 | 0 | −200 | −38 | −162 | −31 | 39 | ||
| 3u (19) | 2.0 | −30 | −65 | 17 | −152 | 33 | −150 | 21 | 12 | ||
| 3v (4) | Attend motion | Div att’n | 2.2 | 14 | −84 | 6 | −242 | 10 | −202 | 126 | 123* |
| 3w (20) | 2.2 | −39 | −70 | 17 | −155 | 30 | −154 | 24 | 6 | ||
| 3x (21) | 2.2 | 53 | −29 | 17 | −55 | −25 | −71 | −32 | 17 | ||
| 3y (22) | 2.2 | −21 | −35 | −13 | −199 | −69 | −189 | −81 | 16 | ||
| Orban et al., 1995 | Attend motion | Passive | |||||||||
| 9a (F3) | −25 | −88 | −1 | −210 | 10 | −201 | −12 | 24 | |||
| Focus | Task | Baseline | Zstat | Talairach ′88 (mm) | Left map (map-mm) | Right map (map-mm) | R-L2-D | ||||
| x | y | z | u | v | u | v | |||||
| Form | |||||||||||
| Malach et al., 1995 | |||||||||||
| 10a (p 8136) | Objects | Textures | 43 | −73 | −18 | −174 | −14 | −178 | −20 | 7 | |
| Puce et al., 1995 | |||||||||||
| 11a (T2) | Letters | Faces | −40 | −66 | −17 | −173 | −22 | −175 | −23 | 2 | |
| 11b (T2) | Textures | −37 | −71 | −22 | −176 | −20 | −179 | −23 | 4 | ||
| 11c (T2) | Textures | Faces | 22 | −49 | −16 | −180 | −44 | −175 | −55 | 12 | |
| 11d (T2) | −24 | −67 | −12 | −196 | −24 | −185 | −32 | 14 | |||
| 11e (T2) | Letters | 21 | −59 | −16 | −183 | −36 | −180 | −44 | 9 | ||
| 11f (T2) | −21 | −64 | −16 | −198 | −27 | −183 | −37 | 18 | |||
| Corbetta et al., 1991 | Attend shape | Passive | |||||||||
| 3z (7) | 2.6 | −8 | −63 | 15 | −183 | 121 | −163 | 137 | 26 | ||
| 3A (8) | 2.6 | 12 | −69 | 13 | −195 | 119 | −179 | 142 | 28 | ||
| 3B (9) | 2.6 | 14 | −65 | 2 | −217 | −29 | −243 | −55 | 37 | ||
| 3C (29) | 2.6 | −17 | −69 | 0 | −214 | −25 | −210 | −39 | 15 | ||
| 3D (29a) | 2.6 | −17 | −71 | −4 | −212 | −11 | −219 | −25 | 16 | ||
| 3E (30) | 2.6 | −17 | −42 | −15 | −181 | −45 | −174 | −58 | 15 | ||
| 3F (31) | 2.6 | 35 | −48 | −11 | −169 | −39 | −163 | −46 | 9 | ||
| 3G (32) | 2.6 | −14 | −42 | −4 | −219 | −57 | −202 | −70 | 21 | ||
| 3H (33) | 2.6 | 28 | −31 | −6 | −190 | −67 | −179 | −80 | 17 | ||
| 3I (34) | 2.2 | 15 | −46 | 6 | −160 | 149 | −224 | −67 | 225* | ||
| 3J (35) | 2.2 | 39 | −23 | 9 | −44 | −39 | −57 | −39 | 13 | ||
| 3K (10) | Attend shape | Div att’n | 2.6 | 14 | −78 | 15 | −203 | 102 | −165 | 79 | 44 |
| 3L (36) | 2.2 | −26 | −82 | −4 | −206 | 3 | −198 | −10 | 15 | ||
| 3M (36a) | 2.2 | −23 | −78 | −4 | −202 | −6 | −205 | −16 | 10 | ||
| 3N (37) | 2.6 | −41 | −65 | −13 | −175 | −18 | −176 | −23 | 5 | ||
| 3O (38) | 2.0 | 24 | −38 | −15 | −175 | −55 | −169 | −64 | 11 | ||
| 3P (39) | 2.6 | −15 | −35 | 4 | −221 | −72 | −212 | −82 | 13 | ||
| 3Q (40) | 2.6 | 19 | −33 | −4 | −217 | −74 | −207 | −87 | 16 | ||
| 3R (41) | 2.2 | 15 | −31 | 4 | −218 | −73 | −210 | −84 | 14 | ||
| 3S (42) | 2.0 | 30 | −27 | −6 | −186 | −70 | −175 | −83 | 17 | ||
| 3T (43) | 2.6 | 15 | −46 | 9 | −159 | 146 | −151 | 160 | 16 | ||
| 3U (44) | 2.2 | −48 | −14 | 4 | −53 | −48 | −66 | −55 | 15 | ||
| 3V (45) | 2.6 | 50 | −12 | −2 | −79 | −52 | −69 | −67 | 18 | ||
| 3W (46) | 2.6 | −17 | −74 | 32 | −150 | 73 | −141 | 113 | 41 | ||
| Orban et al., 1995 | Attend shape | Passive | |||||||||
| 9b (F3) | 3.6 | 9 | −73 | 7 | −230 | −19 | −248 | −42 | 29 | ||
| 9c (T1) | 3.2 | 23 | −56 | 34 | −103 | 57 | −99 | 56 | 4 | ||
| Face | |||||||||||
| Puce et al., 1995 | Faces | Letters | |||||||||
| 11g (T2) | 30 | −54 | −20 | −175 | −41 | −170 | −48 | 9 | |||
| 11h (T2) | 36 | −66 | −17 | −177 | −24 | −178 | −24 | 1 | |||
| 11i (T2) | 47 | −64 | −1 | −149 | −13 | −157 | −13 | 8 | |||
| 11j (T2) | −38 | −59 | −21 | −169 | −29 | −149 | −43 | 24 | |||
| 11k (T2) | −40 | −74 | −3 | −182 | −4 | −170 | −17 | 18 | |||
| 11l (T2) | Faces | Textures | −39 | −54 | −23 | −166 | −31 | −146 | −48 | 26 | |
| 11m (T2) | 31 | −54 | −21 | −174 | −42 | −168 | −49 | 9 | |||
| 11n (T2) | 38 | −62 | −18 | −172 | −27 | −174 | −31 | 4 | |||
| 11o (T2) | 43 | −65 | −4 | −163 | −7 | −161 | −17 | 10 | |||
| Haxby et al., 1994 | Faces | Location + control | |||||||||
| 12a (T2) | 6.2 | 30 | −84 | −8 | −202 | 3 | −193 | −10 | 16 | ||
| 12b (T2) | 4.6 | 36 | −62 | −16 | −174 | −27 | −173 | −33 | 6 | ||
| 12c (T2) | 3.6 | 34 | −58 | 0 | −160 | −10 | −160 | −30 | 20 | ||
| 12d (T2) | 5.5 | 38 | −40 | −16 | −151 | −58 | −150 | −70 | 12 | ||
| 12e (T2) | 4.8 | 24 | 30 | 4 | 54 | −78 | 43 | −91 | 17 | ||
| 12f (T2) | 3.5 | 24 | 34 | −12 | 53 | −89 | 41 | −99 | 16 | ||
| 12g (T2) | 4.3 | −28 | −82 | −12 | −201 | 1 | −191 | −11 | 16 | ||
| 12h (T2) | 4.7 | −36 | −58 | −16 | −172 | −31 | −171 | −39 | 8 | ||
| 12i (T2) | 4.4 | −38 | −42 | −20 | −150 | −57 | −148 | −56 | 2 | ||
| Spatial | |||||||||||
| Haxby et al., 1994 | Location | Faces + control | |||||||||
| 12j (T3) | 4.2 | 24 | −76 | 24 | −148 | 63 | −147 | 71 | 8 | ||
| 12k (T3) | 6.0 | 10 | −58 | 44 | −110 | 110 | −99 | 133 | 25 | ||
| 12l (T3) | 4.5 | 32 | −38 | 36 | −62 | 36 | −59 | 43 | 8 | ||
| 12m (T3) | 4.1 | −24 | −6 | 44 | 23 | 71 | 17 | 55 | 17 | ||
| 12n (T3) | 4.3 | −30 | −80 | 16 | −171 | 57 | −157 | 67 | 17 | ||
| 12o (T3) | 4.6 | −16 | −64 | 48 | −109 | 100 | −108 | 96 | 4 | ||
| 12p (T3) | 4.4 | −36 | −44 | 36 | −72 | 28 | −61 | 40 | 16 | ||
Focus number assigns an identity to each focus (see Results, Fig.11). Reference to each focus in the original study is given as a table number (e.g., T1), figure number (e.g., F1), or (for Corbetta et al., 1991) their designated focus number. Task and Baseline refer to stimulus characteristics and behavioral requirements of the primary task and baseline control task. Statistical significance of each focus is reported as a Z statistic (Z stat). Talairach ′88 coordinates are as reported in the study or after converstion from Talairach ′67 coordinates (see Materials and Methods). Surface-based coordinates are determined from the nearest point on the left and right hemisphere flat maps. In the last column, R-L2-D indicates the misalignment between left and right hemisphere map coordinates.
Key information pertaining to each activation focus is listed in Table3. Data are grouped by the type of function (color, motion, etc.) and by the particular study. Successive columns indicate an identification code for the focus (1a, 1b, etc.); the focus identity or location (table or figure) from the source study, the primary activation task and the baseline task used for comparison, the statistical significance of the activation focus (Z statistic, with higher values being more significant), the reported Talairach stereotaxic coordinates, the surface-based coordinates for each focus as plotted on the left and right hemisphere maps, and the degree of misalignment between foci projected to the left versus right hemisphere flat maps. Given the surface-based coordinates listed in the table, the location of any focus can be quickly pinpointed on the appropriate cortical map using the surrounding grid work.
Because of the spatial uncertainties inherent in the stereotaxic projection method, the shaded regions on each panel of Figure 11 represent regions that are only potentiallyassociated with the indicated visual function. The likelihood of a genuine association for any particular location increases with the number of foci that project to its immediate vicinity. Hence, we will mainly discuss regions where pronounced clusters are evident. Also, because it is hardly surprising that early visual areas are concurrently involved in motion, form, and color processing, we will not discuss the detailed pattern of foci in areas V1 and V2.
Activation foci related to color processing are shown ingreen in Figure 11A. Foci outside areas V1 and V2 include one cluster located ventrally (foci 1a,b, 2a,b, 3f,h, centered around [−200, −40]R-SB on the map), another located dorsally (foci 3g,l,m,n, centered around [−160, +70]R-SB), and a pair of foci that are located laterally (foci 3j,k, centered at [−180, +40]R-SB). The ventral cluster maps mainly to the collateral sulcus, in the vicinity of areas VP and V4v, but it includes one focus (3f) that maps outside the estimated limits of V4v. The dorsal cluster maps to the vicinity of area V3A in the intraparietal sulcus. The lateral foci map to the presumed foveal representation of what might be either V3A or possibly a dorsal subdivision of V4 (V4d) in the lateral occipital sulcus.
Regions associated with motion processing include an extended swath of cortex in occipito-temporal cortex plus assorted clusters and individual foci in other parts of the hemisphere (Fig.11B). Regions within 10 mm of any motion-related focus are pink, whereas the different colored dots identify the specific aspect of motion processing, including activation related to coherent motion (red), optical flow (yellow), illusory motion (pink), and attention to the speed of motion (purple). The dense cluster associated with coherent motion analysis (centered around [−160, +10]R-SB in the pITS) is widely presumed to include the human homolog of macaque area MT (see below). Below this cluster (ventral and medial in 3-D) is a strip of motion-activated foci that map mainly to the occipito-temporal sulcus. This strip is strongly associated with optical flow analysis (Fig. 11B, foci 8b,c,f,g) but includes foci associated with other aspects of motion processing as well. In addition, there are motion-associated foci in the intraparietal sulcus (Fig. 11B, foci 6d, 8c) that overlap significantly with the intraparietal color-associated foci shown in Figure 11A, plus a cluster that maps to cortex in the Sylvian fissure and posterior to it (foci 3r,x, 6f, 7g, centered around [−80, −30]R-SB).
Foci associated with the analysis of inanimate objects and textures arelight blue in Figure 11C. One cluster (foci3C,D,L,M, centered around [−200, −30]R-SB) maps to the collateral sulcus, in area VP and/or V4v, where there is extensive overlap with the color-associated foci shown in Figure 10A. Nearby is an elongated strip of form-associated foci mapping to much of the fusiform gyrus. This includes the region identified as the lateral occipital area by Malach et al. (1995) (Fig. 11C, focus10a at [−178, −20]R-SB). Below this strip is another form-associated cluster that maps to the parahippocampal gyrus and adjoining part of the collateral sulcus (around [−200, −180]R-SB). The triplet of form-associated foci in the STS and Sylvian fissure (foci3J,U,V, centered around [−60, −60]R-SB) maps to a region ventral and anterior to the motion-related foci illustrated in Figure11B.
Foci related to the analysis of faces (Fig. 11D, dark blue) map mainly to a strip along the fusiform gyrus and the occipito-temporal sulcus. This strip overlaps partially with the region implicated in object-related form processing but lies mainly above it on the cortical map (lateral in 3-D). There is also significant overlap between this region and the strip related to motion analysis in the occipito-temporal cortex (Fig. 11B). Finally, regions activated by tasks involving the analysis of spatial relationships (Fig. 11D, yellow) are scattered across several locations in the parietal lobe, including foci in the intraparietal sulcus (foci 12j,n, around [−150, +65]R-SB) that overlap with foci implicated in motion and color analysis.
The exact pattern of activation foci on the cortical flat map depends not only on the coordinates of the data points themselves but also on the particular convolutions of the hemisphere to which the data are projected. The magnitude of this dependency is illustrated in Figure12, A and B, where all 118 foci are projected, respectively, to the left and right hemispheres of the Visible Man. For clarity, the 10 mm uncertainty zones surrounding each focus are omitted. In general, most foci project to similar geographic locations in the two hemispheres, but there are numerous exceptions. We quantified this by calculating the misalignment of surface-based coordinates for foci projected to the left versus right hemisphere map (Table 3, last column). The median value of 16 map-mm is larger than the misalignment of 9 map-mm previously determined for the geographic centers of gravity of sulci (Table 2). This is not surprising, because many activation foci project to noncorresponding geographical locations in the two hemispheres (e.g., to opposite banks of a sulcus or even to different sulci altogether). The largest values (Table 3, asterisks) represent foci that project to opposite sides of one of the cuts made to reduce distortions in the flat map. These occasional artificial discontinuities can be avoided altogether by mapping the cortex to a continuous 3-D surface such as an ellipsoid (Sereno et al., 1996).
What do the patterns of activation foci in Figures 11 and 12,A and B, signify regarding the degree of functional specialization versus overlap (multiplexing) or close interdigitation of function in human visual cortex? One strategy for addressing this issue is to delineate regions that are dominated by a single type of activation focus and to separately delineate regions that include considerable intermixing of different types. Using this approach, we identified several functional domains associated largely or exclusively with a single function and several associated with multiple functions (Fig. 12C,D). Blue indicates regions specialized for form processing by these criteria (labeledF, including face analysis as well as object analysis);red indicates regions specialized for motion processing (M), and yellow indicates regions specialized for spatial analysis (S). Regions where multiple functions are likely to overlap or to be interdigitated (at a resolution of 1–2 cm) are indicated by blue-green for form and color combined (FC), purple for form and motion (FM), and orange for motion, color, and spatial (MCS). Possible candidates for regions involved exclusively in color processing are indicated by green question marks.
The patterns of functional specialization suggested by this analysis are broadly similar for data projected to the two hemispheres. The most prominent difference is that the motion-related foci map to a single cluster in the right hemisphere but to two separate regions in the left hemisphere. This difference may reflect the highly variable folding in this portion of occipito-temporal cortex (Ono et al., 1990; Watson et al., 1993). Whether these patterns substantially overestimate or underestimate the actual degree of functional segregation in any individual hemisphere is difficult to ascertain in view of the uncertainties associated with the stereotaxic projection method.
Dark gray shading in Figure 12, C andD, indicates our estimate for the total extent of cortex implicated in visual processing, based on this extensive (but not exhaustive) set of vision-related neuroimaging studies. It includes a few regions with the occipital lobe that lie between known visually responsive regions but were not activated in the studies analyzed here, and it excludes several more anterior regions that contain scattered vision-related foci but are likely to be dominated by other functions (e.g., audition and somatic sensation). The estimated border of visual cortex runs anterior to the boundary of the occipital lobe and includes a total surface area of 197 cm2 (25% of neocortex) in the right hemisphere reconstruction and 164 cm2(21% of neocortex) in the left hemisphere reconstruction.
Comparisons between human and macaque cortex
To facilitate cross-species comparisons of structure and function, Figure 13 illustrates cortical geography and functional organization in the right hemisphere of the Visible Man and in the right hemisphere of a macaque monkey (case 79-0; Drury et al., 1996a). In Figure 13, A andB, cortical geography is illustrated in lateral and medial views and on cortical flat maps, with the lobes shown in different colors and buried cortex shaded more darkly. The surface area of the macaque neocortex is 72 cm2, only 9% of that for the Visible Man. Buried cortex occupies 59% of neocortex in the macaque, significantly less than the average of 70% for the Visible Man. The proportion of cortex associated with the frontal lobe is considerably smaller in the macaque than in the Visible Man (26 vs 36%), whereas the occipital lobe is significantly larger (32 vs 19%).
Given the differences in complexity of folding patterns, it is obvious that there cannot be an overall one-to-one mapping of gyral and sulcal landmarks between species. Nonetheless, a number of sulci are likely to contain homologous areas and can therefore be considered corresponding in the two species. One obvious correspondence involves the central sulcus, which in both species contains primary somatosensory cortex on its posterior bank and primary motor cortex on its anterior bank (Brodmann, 1905, 1909). Another correspondence involves the calcarine sulcus, which contains area V1 in both species, although the foveal representation is displaced more laterally in the macaque than in humans. The rhinal sulcus, although one of the shallower folds, fits the criterion for correspondence because it occurs along the margins of entorhinal cortex in both species (Brodmann, 1905, 1909; Amaral et al., 1987). The Sylvian fissure is by far the largest single sulcus in both species, and it contains many homologous areas or regions, including auditory areas (Merzenich and Brugge, 1973; Petersen et al., 1989; Wise et al., 1991) and higher somatosensory areas (Robinson and Burton, 1990a,b; Burton et al., 1993; Ledberg et al., 1995). Finally, much of the cingulate sulcus appears to correspond in macaque and human cortex, based on architectonic similarities (Petrides and Pandya, 1994) and functional similarities of cingulate motor areas (Picard and Strick, 1996). All five presumed sulcal correspondences are indicated by thedark shading in Figure 13, A andB.
In other regions, plausible correspondences can be inferred by considering the overall extent of cortex contained in different geographic regions. An instructive example is the wedge-shaped region bounded by the cingulate and central sulci on one side and the Sylvian fissure and the superior temporal sulcus on the other side. This wedge includes only a single sulcus (the intraparietal) in the macaque, whereas it includes the entire postcentral sulcus and part of the intraparietal sulcus in humans. Thus, some of the cortical areas that lie within the intraparietal sulcus in the macaque may correspond to cortex situated more anteriorly in humans (e.g., within the postcentral sulcus).
As a framework for functional comparisons, Figure 13C shows a partitioning scheme for 78 different cortical areas identified in the macaque (adapted from Felleman and Van Essen, 1991). The 32 areas largely or entirely visual in function collectively occupy 54% of the surface area of neocortex, i.e., more than twice the fraction estimated above for human visual cortex. The three largest visual areas are colored individually (V1 in purple, V2 in orange, and V4 in blue-green). Each of them contains a dorsal half representing lower visual fields (V1d, V2d, and V4d) and a ventral half representing upper visual fields (V1v, V2v, and V4v). Other areas are colored according to major functional groupings, with the remaining topographically organized areas shown in yellow-green, areas of the inferotemporal complex (IT) in blue, the MT/MST (motion) complex in red, the posterior parietal complex inyellow, and all other extrastriate visual areas inbrown. Somatosensory, auditory, motor, olfactory, hippocampal, cingulate, and other regions are indicated in variouspastel or gray shades.
Figure 13D shows the arrangement of topographically organized visual areas and functionally specialized regions in humans, adapted from Figure 12D. Areas V1 and V2 are the two largest visual areas in humans, but each occupies no more than a few percent of total cortical area, compared with ∼13% and ∼9% for V1 and V2, respectively, in the macaque. In humans, areas V3 and VP are significantly smaller than V1 and V2, but the size disparity is not as pronounced as in the macaque. Area V4 in humans has a topographically well defined ventral subdivision (V4v) that is presumably homologous to V4v in the macaque. Surprisingly, fMRI studies have failed to reveal a clear candidate for a corresponding dorsal subdivision of human V4.
The motion-related region in and near the pITS is likely to include the human homolog of area MT (also known as V5) (Zeki et al., 1991; Watson et al., 1993). This implies that the posterior bank of the macaque STS corresponds to a region considerably farther posterior in humans. Recent fMRI data suggest a human homolog of the MST complex in the region anterior to MT (Tootell et al., 1996), similar to the arrangement in the macaque. Because many MSTd neurons are well driven by optical flow stimuli (Tanaka and Saito, 1989; Duffy and Wurtz, 1991), it is puzzling that the optical flow activations reported in human occipito-temporal cortex (DeJong et al., 1994) lie mainly ventral rather than anterior to MT.
An attractive candidate for the inferotemporal complex in humans is the form-associated region in the fusiform gyrus and occipito-temporal sulcus, lateral and anterior to area V4v. The partial separation between foci associated with face analysis and object analysis in this region is consistent with physiological results in macaque inferotemporal cortex (Baylis et al., 1987; Desimone, 1991). The region of interdigitation or overlap of motion and face processing in the occipito-temporal sulcus may be homologous to macaque area STP or TPO, which has also been implicated in both form and motion analysis (Baylis et al., 1987). Finally, the fact that foci associated with spatial analysis are localized to the parietal lobe fits with previous evidence in humans as well as the macaque (Ungerleider and Mishkin, 1982). However, it is not obvious which of the many parietal areas in the macaque are most likely to be homologous to the spatial-related activation foci reported in humans.
DISCUSSION
This study has used surface-based representations of human cerebral cortex for three broad purposes. The first establishes the Visible Man as a computerized surface-based atlas and characterizes its cortical geography and geometry. The second introduces a method for objectively representing the large degree of spatial uncertainty that is present for all data reported in stereotaxic coordinates but with a magnitude that may not be appreciated by many readers of the neuroimaging literature. The third uses the Visible Man atlas, the stereotaxic projection method, and surface-based measurements collectively to analyze the functional organization of human visual cortex and its relationship to visual areas in the macaque.
Atlases, transformations, and individual variability
The widely used Talairach stereotaxic atlas (Talairach and Tournoux, 1988) is based on drawings of sections taken at widely spaced intervals (typically 4 mm) through a single hemisphere. This and other limitations have spurred the development of alternative stereotaxic atlases of human cerebral cortex (e.g., Greitz et al., 1991; Evans et al., 1994; Roland et al., 1994; Toga et al., 1994). The Visible Man surface-based atlas introduced here has several advantageous characteristics. Most notably, it includes an explicit surface representation that can be visualized in multiple formats, linked to multiple coordinate systems, and related to standard geographical landmarks. The surface reconstructions are freely available and can be visualized using software that runs on standard Silicon Graphics workstations. Efforts are under way to make the atlas interactively accessible via the internet, which will facilitate routine examination of a far greater range of experimental data and analysis conditions than the selected examples illustrated here and elsewhere (Drury and Van Essen, 1997).
It is important that an atlas be based on a brain with convolutions that are reasonably normal (Roland and Zilles, 1994; Roland et al., 1994). The convolutions of the Visible Man cortex lie within the normal range in terms of their overall pattern and in the positions of major sulci in stereotaxic space, with only a few exceptions (compare Fig. 2legend). In this respect, the Visible Man is at least as representative as the hemisphere on which the Talairach and Tournoux atlas is based. Once accurate surface reconstructions become available for a brain with convolutions that are demonstrably more representative of a population of normal brains, it will be desirable to switch to this as a standard atlas.
An alternative approach to digital atlases involves creation of a volume-based population average, in which MRI scans from many individuals are merged after transformation to stereotaxic space (Andreasen et al., 1994; Evans et al., 1994). Although this approach provides valuable information about statistical variations in the distribution of gray matter and of various segmented subregions, it yields an inherently blurred representation of cortical structure, particularly in regions of high variability. Also, the absence of an associated surface reconstruction impedes analysis using the various surface-based formats illustrated here. On the other hand, because both types of atlas lie in Talairach space, analyses performed on one atlas can be converted and viewed on the other, making them highly complementary to one another.
Whatever brain is used for an atlas, a critical issue concerns the spatial uncertainties that arise when mapping experimental data onto the atlas. Standard methods for warping experimental brains to match the shape of a target atlas lead to registration errors often exceeding 1 cm in 3-D distance (Steinmetz et al., 1990; Hunton et al., 1996;Thompson et al., 1996), which translates to even greater distances along the cortical surface (see Figs. 8, 12 above). A promising alternative involves high-dimensional warping algorithms that use local shape information to drive the deformation from source to target brain (Christensen et al., 1994; Evans et al., 1994; Joshi et al., 1997). This approach will make it feasible to preserve information about the shape and total extent of activated cortex associated with each focus—information that is typically not reported or is degraded using current transformation methods. An important variant on shape-based deformation algorithms involves warping one cortical flat map to match the shape of another (Drury et al., 1995, 1996a,b, 1997). The reduction in dimensionality makes the warping computationally much more tractable and can ensure a topologically continuous mapping between an individual brain and the target atlas even in regions where the pattern of convolutions differs markedly. The approach is also amenable to warpings that are driven by functional as well as geographical landmarks. This is important because functional borders do not have a fixed relationship to folding patterns (Rademacher et al., 1993; Roland and Zilles, 1994; Van Essen, 1997).
Several coordinate systems can be used to describe the location of points in the Visible Man cortex. The Cartesian surface-based coordinates introduced here are particularly useful for rapidly pinpointing locations on cortical flat maps. They also allow ready calculation of the approximate distance separating any two points along the cortical surface. For greater accuracy, it is possible to calculate geodesics, i.e., minimum distances between points along the surface in 3-D (Wolfson and Schwartz, 1989; N. Khaneja, M. I. Miller, and U. Grenander, unpublished observations). Surface-based coordinates also provide a natural interface to databases, which are an increasingly important resource for rapid and flexible accessing of functioning neuroimaging data. Because each coordinate system has its own advantages and limitations, it makes sense to include surface-based coordinates (ellipsoidal as well as Cartesian) along with Talairach coordinates in future generations of neuroimaging databases such as BrainMap (Fox et al., 1994).
Functional organization and interspecies comparisons
Our estimate that 20–25% of human neocortex is implicated in vision provides a useful starting perspective on an intriguing but largely unexplored issue. Naturally, this estimate will be subject to revision as additional studies are incorporated and as better methods are introduced for representing the total amount of cortex activated in a given test paradigm. These estimates will also depend on the criteria used to decide whether a region should be categorized as visual cortex if it is also implicated in higher cognitive functions such as reading or visual memory.
The debate over segregation versus multiplexing of function remains a major theme in contemporary visual neuroscience (DeYoe and Van Essen, 1988; Livingstone and Hubel, 1988; Merigan and Maunsell, 1993; Van Essen and Gallant, 1994). Our analysis of functional specialization confirms that there are major differences in the overall pattern of cortical activation associated with the analysis of color, form, motion, and spatial relationships. It also illustrates the difficulty of drawing unambiguous conclusions about the degree of functional segregation versus overlap in human visual cortex, given the uncertainties associated with stereotaxically projected neuroimaging data. Our analysis nonetheless supports previous arguments that there are separate cortical regions specialized for motion and form processing. It also supports the suggestion that cortex in the vicinity of VP and ventral V4 is implicated in form as well as color processing (Corbetta et al., 1991), which is in accord with physiological and lesion data in the macaque (cf. Heywood et al., 1992; Schiller, 1993;Van Essen and Gallant, 1994). The alternative suggestion, that area V4 is primarily linked to color processing (Lueck et al., 1989; Zeki et al., 1991, 1993), appears less likely but cannot be ruled out.
It is now feasible to attack issues of functional specialization more incisively using fMRI, which provides high spatial resolution and allows multiple tests to be performed in each subject, including mapping of topography as well as function. Nonetheless, it is not practical to perform all tests of interest in every individual. The need to make detailed comparisons of results across individuals will continue unabated and will drive the refinement of methods for accurately visualizing experimental data on surface-based atlases.
Comparisons with nonhuman primates will be increasingly helpful for elucidating the functional organization of human cortex. Of the dozens of areas identified in the macaque, only a small handful have clear homologs in humans at the level of individual areas, although considerably more cortex can be matched at the level of functionally distinct clusters of areas (e.g., the IT complex). Cortical flat maps allow one cortical sheet to be mapped to the other with preservation of neighborhood relationships despite major species differences in the pattern of convolutions (Van Essen et al., 1997). This allows analyses to be focused on the relative sizes of various areas, their topological arrangement across the cortical sheet, and the possibility that numerous cortical areas are present in humans but absent in the macaque. The nature and magnitude of interspecies differences, and whether they are more pronounced in regions specialized for higher cognitive functions, are now tantalizingly accessible to exploration.
Sulcal (s.) and gyral (g.) abbreviations used in figures and Table2. Frontal lobe: CeS, central s.; CiG, cingulate g.; Cis, cingulate s.; FMS, fronto-medial s;FOS, fronto-orbital s.; FP, frontal pole;GR, gyrus rectus; IFG, inferior frontal g.;IFS, inferior frontal s.; intFS, intermediate frontal s.; intFG, intermediate frontal g.;intPrCeS, intermediate precentral s.; IPrCeS, inferior precentral s.; IRS, inferior rostral s.;LOS, lateral orbital s.; MFG, medial frontal g.;MFS, medial frontal s.; MOS, medial orbital s.;MPrCeS, medial precentral s.; OlfS, olfactory s.;OrbG, orbital g.; OrbS, orbital s.;PaCeS, paracentral s.; PCL, paracentral lobule;POp, pars opercularis; PrCeG, precentral g.;PTr, pars triangularis; SCA, subcallosal area;SFG, superior frontal g.; SFS, superior frontal s.; SPrCeS, superior precentral s.; SRS, superior rostral s.
Occipital lobe: AOS, anterior occipital s.; CaSd, calcarine s. (dorsal); CaSv, calcarine s. (ventral);CoS, collateral s.; Cu, cuneus; FG, fusiform g.; ILS, intra-lingual s.; IOG, inferior occipital g.; LG, lingual g.; LOS, lateral occipital s.; MOG middle occipital g.; OP, occipital pole; OTS, occipito-temporal s.; PHG, parahippocampal g.; pITS, posterior inferior temporal s.;PrOS, preoccipital s.; SOG, superior occipital g.; SS, sagittal s.; SSS, superior sagittal s.;TOS, transverse occipital s.; TrIOS, transverse inferior occipital s.
Temporal lobe: AG, angular g.; AITS, anterior inferior temporal s.; intTG, intermediate temporal g.;ITG, inferior temporal g; ITS, inferior temporal s.; MTG, middle temporal g.; RhS, rhinal s.;SMG, supramarginal g.; STG, superior temporal g.;STS, superior temporal s.; TP, temporal pole;unc, uncus.
Sylvian fissure: ar, ascending ramus; fo, frontal operculum; PTTS, posterior transverse temporal s.;HG, Heschl’s g.; hr, horizontal ramus;ICeS, insular central s.; ISG, insular short g.;po, parietal operculum; PT, planum temporale;tas, terminal ascending segment; to, temporal operculum.
Parietal lobe: AS, angular s.; CiGI, cingulate gyrus isthmus; CiSmr, cingulate s. marginal ramus;IPL, inferior parietal lobule; IPS, intraparietal s.; PoCeG, postcentral g.; PoCeS, postcentral s.; POS, parieto-occipital s.; PrCu, precuneus; SPL, superior parietal lobule; SPS, subparietal s.; TrPS, transverse parietal s.
Footnotes
This project was supported by National Institutes of Health Grant EY02091 and joint funding from the National Institute of Mental Health, NASA, and the National Institute on Drug Abuse under Human Brain Project MH/DA52158. Information about the Visible Man image data set is available athttp://www.nlm.nih.gov/research/visible/visible_human.html. Information on acquiring the CARET software (in executable form) and surface reconstructions (3-D and 2-D) of the Visible Man is available athttp://v1.wustl.edu/caret.html. We thank Drs. M. Raichle, S. Petersen, J. L. Price, M. Corbetta, and E. A. DeYoe for valuable discussions, S. Kumar for cortical contouring and technical assistance, and S. Danker for manuscript preparation.
Correspondence should be addressed to David C. Van Essen, Department of Anatomy and Neurobiology, Washington University School of Medicine, 660 South Euclid Avenue, St. Louis, MO 63110.
REFERENCES
- 1.Amaral DG, Insausti R, Cowan WM. The entorhinal cortex of the monkey. I. Cytoarchitectonic organization. J Comp Neurol. 1987;264:326–355. doi: 10.1002/cne.902640305. [DOI] [PubMed] [Google Scholar]
- 2.Anderson CH, Drury HA, Lee CW, Carman GJ, Van Essen DC. Computerized reconstruction and flattening of macaque cerebral cortex. Soc Neurosci Abstr. 1994;20:428. [Google Scholar]
- 3.Andreasen NC, Arndt S, Swayze V, II, Cizadlo T, Flaum M, O’Leary D, Ehrhardt C, Yuh WTC. Thalamic abnormalities in schizophrenia visualized through magnetic resonance image averaging. Science. 1994;266:294–298. doi: 10.1126/science.7939669. [DOI] [PubMed] [Google Scholar]
- 4.Baylis GC, Rolls ET, Leonard CM. Functional subdivisions of the temporal lobe neocortex. J Neurosci. 1987;7:330–342. doi: 10.1523/JNEUROSCI.07-02-00330.1987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Bonin GV, Bailey P. The neocortex of Macaca mulatta. University of Illinois; Urbana, IL: 1947. [Google Scholar]
- 6.Brodmann K. Beitrage zur histologischen Localisation der Grosshirnrinde. Dritte Mitteilung. Die Rindenfelder der niederen Affen. J Psychol Neurol. 1905;4:177–226. [Google Scholar]
- 7.Brodmann K. Vergleichende Lokalisationslehre der Grosshirnrinde. Barth; Leipzig, Germany: 1909. [Google Scholar]
- 8.Burton H, Videen TO, Raichle ME. Tactile vibration activated foci in insular and parietal opercular cortex studied with positron emission tomography: mapping the second somatosensory area in human. Somatosens Mot Res. 1993;10:297–308. doi: 10.3109/08990229309028839. [DOI] [PubMed] [Google Scholar]
- 9.Carman GJ, Drury HA, Van Essen DC. Computational methods for reconstructing and unfolding the cerebral cortex. Cereb Cortex. 1995;5:506–517. doi: 10.1093/cercor/5.6.506. [DOI] [PubMed] [Google Scholar]
- 10.Christensen GE, Rabbitt RD, Miller MI. 3D brain mapping using a deformable neuroanatomy. Phys Med Biol. 1994;39:609–618. doi: 10.1088/0031-9155/39/3/022. [DOI] [PubMed] [Google Scholar]
- 11.Corbetta M, Miezin F, Dobmeyer S, Shulman G, Petersen S. Selective and divided attention during visual discrimination of shape, color, and speed: functional anatomy by positron emission tomography. J Neurosci. 1991;11:2383–2402. doi: 10.1523/JNEUROSCI.11-08-02383.1991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Dale A, Sereno M. Improved localization of cortical activity by combining EEG and MEG with MRI cortical surface reconstruction: a linear approach. J Cognit Neurosci. 1993;5:162–176. doi: 10.1162/jocn.1993.5.2.162. [DOI] [PubMed] [Google Scholar]
- 13.DeJong BM, Shipp S, Skidmore B, Frackowiak RSJ, Zeki S. The cerebral activity related to the visual perception of forward motion in depth. Brain. 1994;117:1039–1054. doi: 10.1093/brain/117.5.1039. [DOI] [PubMed] [Google Scholar]
- 14.Desimone R. Face-selective cells in the temporal cortex of monkeys. J Cognit Neurosci. 1991;3:1–8. doi: 10.1162/jocn.1991.3.1.1. [DOI] [PubMed] [Google Scholar]
- 15.DeYoe EA, Van Essen DC. Concurrent processing streams in monkey visual cortex. Trends Neurosci. 1988;11:219–226. doi: 10.1016/0166-2236(88)90130-0. [DOI] [PubMed] [Google Scholar]
- 16.DeYoe EA, Carman G, Bandetinni P, Glickman S, Wieser J, Cox R, Miller D, Neitz J. Mapping striate and extrastriate visual areas in human cerebral cortex. Proc Natl Acad Sci USA. 1996;93:2382–2386. doi: 10.1073/pnas.93.6.2382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Drury HA, Van Essen DC (1997) Analysis of functional specialization in human cerebral cortex using the visible man surface based atlas. Hum Brain Mapp, in press. [PubMed]
- 18.Drury HA, Van Essen DC, Joshi S, Miller MI, Anderson CH, Coogan T. Analysis of cortical organization and individual variability using computerized flat maps. Soc Neurosci Abstr. 1995;21:923. [Google Scholar]
- 19.Drury HA, Van Essen DC, Anderson CH, Lee CW, Coogan TA, Lewis JW. Computerized mappings of the cerebral cortex: a multiresolution flattening method and a surface-based coordinate system. J Cognit Neurosci. 1996a;8:1–28. doi: 10.1162/jocn.1996.8.1.1. [DOI] [PubMed] [Google Scholar]
- 20.Drury HA, Van Essen DC, Joshi SC, Miller MI. Analysis and comparison of areal partitioning schemes using two-dimensional fluid deformations. NeuroImage. 1996b;3:S130. [Google Scholar]
- 21.Drury HA, Van Essen DC, Snyder AZ, Shulman GL, Akbudak E, Ollinger JM, Conturo TE, Raichle M, Corbetta M. Warping fMRI activation patterns onto the visible man atlas using fluid deformations of cortical flat maps. NeuroImage. 1997;5:S421. [Google Scholar]
- 22.Duffy CJ, Wurtz RH. Sensitivity of MST neurons to optic flow stimuli. I. A continuum of response selectivity to large-field stimuli. J Neurophysiol. 1991;65:1329–1345. doi: 10.1152/jn.1991.65.6.1329. [DOI] [PubMed] [Google Scholar]
- 23.DuPont P, Orban GA, De Bruyn B, Verbruggen A, Mortelmans L. Many areas in the human brain respond to visual motion. J Neurophysiol. 1994;72:1420–1424. doi: 10.1152/jn.1994.72.3.1420. [DOI] [PubMed] [Google Scholar]
- 24.Evans AC, Kamber M, Collins DL, MacDonald D. An MRI-based probabilistic atlas of neuroanatomy. In: Shorvon SD, editor. Magnetic resonance scanning and epilepsy. Plenum; New York: 1994. pp. 263–274. [Google Scholar]
- 25.Felleman DJ, Van Essen DC. Distributed hierarchical processing in primate visual cortex. Cereb Cortex. 1991;1:1–47. doi: 10.1093/cercor/1.1.1-a. [DOI] [PubMed] [Google Scholar]
- 26.Filiminoff IN. Uber die variabilitat der grosshirnrindenstruktur. Mitteilung II. Regio occipitalis beim erwachsenen Menshchen. J Psychol Neurol. 1932;44:1–96. [Google Scholar]
- 27.Fox PT. Spatial normalization origins: objectives, applications, and alternatives. Hum Brain Mapp. 1995;3:161–164. [Google Scholar]
- 28.Fox PT, Perlmutter JS, Raichle ME. A stereotactic method of anatomical localization for positron emission tomography. J Comput Assist Tomogr. 1985;9:141–153. doi: 10.1097/00004728-198501000-00025. [DOI] [PubMed] [Google Scholar]
- 29.Fox PT, Mikiten S, Davis G, Lancaster JL. A database of human functional brainmapping. In: Thatcher, Zeffiro, Huerta M, editors. Advances in functional neuroimaging: Technical foundations. Academic; Orlando, FL: 1994. pp. 95–105. [Google Scholar]
- 30.Geiger B (1993) Three-dimensional modeling of human organs and its application to diagnosis and surgical planning. Technical Report 2105. Institut National de Recherche Informatique et Automatique.
- 31.Greitz T, Bohm C, Holte S, Eriksson L. A computerized brain atlas: construction, anatomical content, and some applications. J Comput Assist Tomogr. 1991;15:26–38. [PubMed] [Google Scholar]
- 32.Griffin LD. The intrinsic geometry of the cerebral cortex. J Theor Biol. 1994;166:261–273. doi: 10.1006/jtbi.1994.1024. [DOI] [PubMed] [Google Scholar]
- 33.Haxby JV, Horwitz B, Ungerleider LG, Maisog JM, Pietrini P, Grady CL. The functional organization of human extrastriate cortex: a PET-rCBF study of selective attention to faces and locations. J Neurosci. 1994;14:6336–6353. doi: 10.1523/JNEUROSCI.14-11-06336.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Heywood CA, Gadotti A, Cowey A. Cortical area V4 and its role in the perception of color. J Neurosci. 1992;12:4056–4065. doi: 10.1523/JNEUROSCI.12-10-04056.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Hunton DL, Miezen FJ, Buckner RL, van Mier HI, Raichle ME, Petersen SE. An assessment of functional-anatomical variability in neuroimaging studies. Hum Brain Mapp. 1996;4:122–139. doi: 10.1002/(SICI)1097-0193(1996)4:2<122::AID-HBM4>3.0.CO;2-5. [DOI] [PubMed] [Google Scholar]
- 36.Joshi SC, Miller MI, Grenander U (1997) On the geometry and shape of brain sub-manifolds. In: Processing of MR images of the human brain. Int J Pattern Recognition Artif Intell, Special issue, in press.
- 37.Jouandet M, Tramo M, Herron D, Hermann A, Loftus W, Bazell J, Gazzaniga M. Brainprints: computer-generated two-dimensional maps of the human cerebral cortex in vivo. J Cognit Neurosci. 1989;1:88–117. doi: 10.1162/jocn.1989.1.1.88. [DOI] [PubMed] [Google Scholar]
- 38.Lancaster JL, Glass TG, Lankipalli BR, Downs H, Mayberg H, Fox PT. A modality-independent approach to spatial normalization of tomographic images of the human brain. Hum Brain Mapp. 1995;3:209–223. [Google Scholar]
- 39.Ledberg A, O’Sullivan BT, Kinomura S, Roland PE. Somatosensory activations of the parietal operculum of man. A PET study. Eur J Neurosci. 1995;7:1934–1941. doi: 10.1111/j.1460-9568.1995.tb00716.x. [DOI] [PubMed] [Google Scholar]
- 40.Livingstone M, Hubel D. Segregation of form, color, movement, and depth: anatomy, physiology, and perception. Science. 1988;240:740–749. doi: 10.1126/science.3283936. [DOI] [PubMed] [Google Scholar]
- 41.Lueck CJ, Zeki S, Friston KJ, Deiber MP, Cope P, Cunningham VJ, Lammertsma AA, Kennard C, Frackowiak RSJ. The colour centre in the cerebral cortex of man. Nature. 1989;340:386–389. doi: 10.1038/340386a0. [DOI] [PubMed] [Google Scholar]
- 42.Malach R, Reppas JB, Benson RR, Kwong KK, Jiang H, Kennedy WA, Ledden PJ, Brady TJ, Rosen BR, Tootell RBH. Object-related activity revealed by functional magnetic resonance imaging in human occipital cortex. Proc Natl Acad Sci USA. 1995;92:8135–8139. doi: 10.1073/pnas.92.18.8135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Malliot J, Yahia H, Verroust A (1993) Interactive texture mapping. In: Computer Graphics Proceedings, Annual conference series, pp 27–34.
- 44.McCarthy G, Spencer M, Adrignolo A, Luby M, Gore J, Allison T. Brain activation associated with visual motion studied by functional magnetic resonance imaging in humans. Hum Brain Mapp. 1995;2:234–243. [Google Scholar]
- 45.Merigan WH, Maunsell JHR. How parallel are the primate visual pathways? Annu Rev Neurosci. 1993;16:369–402. doi: 10.1146/annurev.ne.16.030193.002101. [DOI] [PubMed] [Google Scholar]
- 46.Merzenich MM, Brugge JF. Representation of the cochlear partition on the superior temporal plane of the macaque monkey. Brain Res. 1973;50:275–296. doi: 10.1016/0006-8993(73)90731-2. [DOI] [PubMed] [Google Scholar]
- 47.Miller M, Christensen G, Amit Y, Grenander U. A mathematical textbook of deformable neuroanatomies. Proc Natl Acad Sci USA. 1993;90:11944–11948. doi: 10.1073/pnas.90.24.11944. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Ono M, Kubick S, Abernathey CD. Atlas of the cerebral sulci. Thieme; New York: 1990. [Google Scholar]
- 49.Orban GA, DuPont P, De Bruyn R, Vogels R, Vandenberghe R, Mortelmans L. A motion area in human visual cortex. Proc Natl Acad Sci USA. 1995;92:993–997. doi: 10.1073/pnas.92.4.993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Petersen SE, Robinson DL, Currie JN. Influences of lesions of parietal cortex on visual spatial attention in humans. Exp Brain Res. 1989;76:267–280. doi: 10.1007/BF00247887. [DOI] [PubMed] [Google Scholar]
- 51.Petrides M, Pandya DN. Comparative architectonic analysis of the human and the macaque frontal cortex. In: Boller F, Grafman J, editors. Handbook of neuropsychology, Vol 9. Elsevier; Amsterdam: 1994. pp. 17–58. [Google Scholar]
- 52.Picard N, Strick PL. Motor areas of the medial wall: a review of their location and functional activation. Cereb Cortex. 1996;6:342–353. doi: 10.1093/cercor/6.3.342. [DOI] [PubMed] [Google Scholar]
- 53.Puce A, Allison A, Gore JC, McCarthy G. Face-sensitive regions in human extrastriate cortex studied by functional MRI. J Neurophysiol. 1995;74:1192–1199. doi: 10.1152/jn.1995.74.3.1192. [DOI] [PubMed] [Google Scholar]
- 54.Rademacher J, Caviness VS, Jr, Steinmetz H, Galaburda AM. Topographical variation of the human primary cortices: implications for neuroimaging, brain mapping, and neurobiology. Cereb Cortex. 1993;3:313–329. doi: 10.1093/cercor/3.4.313. [DOI] [PubMed] [Google Scholar]
- 55.Robinson CJ, Burton H. Somatotopographic organization of the second somatosensory area of M. fascicularis. J Comp Neurol. 1980a;192:43–67. doi: 10.1002/cne.901920104. [DOI] [PubMed] [Google Scholar]
- 56.Robinson CJ, Burton H. Organization of somatosensory receptive fields in cortical areas 7b, retroinsula, postauditory and granular insula of M. fascicularis. J Comp Neurol. 1980b;192:69–92. doi: 10.1002/cne.901920105. [DOI] [PubMed] [Google Scholar]
- 57.Roland PE, Zilles K. Brain atlases—a new research tool. Trends Neurosci. 1994;17:458. doi: 10.1016/0166-2236(94)90131-7. [DOI] [PubMed] [Google Scholar]
- 58.Roland PE, Gaufelds CJ, Wahlin J, Ingelman L, Andersson M, Ledberg A, Pedersen J, Akerman S, Dabringhaus A, Zilles K. Human brain atlas for high-resolution functional and anatomical mapping. Hum Brain Mapp. 1994;1:173–184. doi: 10.1002/hbm.460010303. [DOI] [PubMed] [Google Scholar]
- 59.Schiller PH. The effects of V4 and middle temporal (MT) area lesions on visual performance in the rhesus monkey. Vis Neurosci. 1993;10:717–746. doi: 10.1017/s0952523800005423. [DOI] [PubMed] [Google Scholar]
- 60.Sereno MI, Dale AM, Reppas JB, Kwong KK, Belliveau JW, Brady TJ, Rosen BR, Tootell RBH. Borders of multiple visual areas in humans revealed by functional magnetic resonance imaging. Science. 1995;268:889–893. doi: 10.1126/science.7754376. [DOI] [PubMed] [Google Scholar]
- 61.Sereno MI, Dale AM, Liu A, Tootell RBH. A surface-based coordinate system for a canonical cortex. NeuroImage. 1996;3:S252. [Google Scholar]
- 62.Spitzer V, Ackerman MJ, Scherzinger AL, Whitlock DJ. The Visible Male: a technical report. J Am Med Informat Assoc. 1996;3:118–130. doi: 10.1136/jamia.1996.96236280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Steinmetz H, Furst G, Freund HJ. Variation of perisylvian and calcarine anatomic landmarks within stereotaxic proportional coordinates. Am J Neuroradiol. 1990;11:1123–1130. [PMC free article] [PubMed] [Google Scholar]
- 64.Stensaas SS, Eddington DK, Dobelle WH. The topography and variability of the primary visual cortex in man. J Neurosurg. 1974;40:747–755. doi: 10.3171/jns.1974.40.6.0747. [DOI] [PubMed] [Google Scholar]
- 65.Talairach J, Tournoux P. Atlas d’anatomie stereotaxique due telencephale. Masson Cie; Paris: 1967. [Google Scholar]
- 66.Talairach J, Tournoux P. Coplanar stereotaxic atlas of the human brain. Thieme; New York: 1988. [Google Scholar]
- 67.Tanaka K, Saito H-A. Analysis of motion of the visual field by direction, expansion/contraction, and rotation cells clustered in the dorsal part of the medial superior temporal area of the macaque monkey. J Neurophysiol. 1989;62:626–641. doi: 10.1152/jn.1989.62.3.626. [DOI] [PubMed] [Google Scholar]
- 68.Thompson P, Schwartz C, Lin RT, Khan AA, Toga AW. Three-dimensional statistical analysis of sulcal variability in the human brain. J Neurosci. 1996;16:4261–4274. doi: 10.1523/JNEUROSCI.16-13-04261.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Toga AW, Ambach KL, Quinn B, Hutchin M, Burton JS. Post-mortem anatomy from cryosectioned human brain. J Neurosci Methods. 1994;54:239–252. doi: 10.1016/0165-0270(94)90196-1. [DOI] [PubMed] [Google Scholar]
- 70.Tootell RBH, Dale AM, Sereno MI, Malach R. New images from human visual cortex. Trends Neurosci. 1996;19:481–489. doi: 10.1016/S0166-2236(96)10053-9. [DOI] [PubMed] [Google Scholar]
- 71.Tramo MJ, Loftus WC, Thomas CE, Green RL, Mott LA, Gazzaniga MS. Surface area of human cerebral cortex and its gross morphological subdivisions: in vivo measurements in monozygotic twins suggest differential hemisphere effects of genetic factors. J Cognit Neurosci. 1995;7:292–302. doi: 10.1162/jocn.1995.7.2.292. [DOI] [PubMed] [Google Scholar]
- 72.Ungerleider LG, Mishkin M. Two cortical visual systems. In: Ingle DG, Goodale, Mansfield RJQ, editors. Analysis of visual behavior. MIT; Cambridge, MA: 1982. pp. 549–586. [Google Scholar]
- 73.Van Essen DC. A tension-based theory of morphogenesis and compact wiring in the central nervous system. Nature. 1997;385:313–318. doi: 10.1038/385313a0. [DOI] [PubMed] [Google Scholar]
- 74.Van Essen DC, Gallant JL. Neural mechanisms of form and motion processing in the primate visual system. Neuron. 1994;13:1–10. doi: 10.1016/0896-6273(94)90455-3. [DOI] [PubMed] [Google Scholar]
- 75.Van Essen DC, Maunsell JHR. Two-dimensional maps of the cerebral cortex. J Comp Neurol. 1980;191:255–281. doi: 10.1002/cne.901910208. [DOI] [PubMed] [Google Scholar]
- 76.Van Essen DC, Drury HA, Joshi SC, Miller MI. Comparisons between human and macaque using shape-based deformation algorithms applied to cortical flat maps. NeuroImage. 1997;5:S41. [Google Scholar]
- 77.Watson JDG, Myers R, Frackowiak RSJ, Hajnal JV, Woods RP, Mazziotta JC, Shipp S, Zeki S. Area V5 of the human brain: evidence from a combined study using positron emission tomography and magnetic resonance imaging. Cereb Cortex. 1993;3:37–94. doi: 10.1093/cercor/3.2.79. [DOI] [PubMed] [Google Scholar]
- 78.Welker W. Why does cerebral cortex fissure and fold? A review of determinants of gyri and sulci. In: Jones EG, Peters A, editors. Cerebral cortex, Vol 8B. Plenum; New York: 1990. pp. 3–136. [Google Scholar]
- 79.Wise R, Chollet F, Hadar U, Friston K, Hoffner E, Frackowiak R. Distribution of cortical neural networks involved in word comprehension and word retrieval. Brain. 1991;114:1803–1817. doi: 10.1093/brain/114.4.1803. [DOI] [PubMed] [Google Scholar]
- 80.Wolfson E, Schwartz EL. Computing minimal distances on arbitrary two-dimensional polyhedral surfaces. IEEE Pattern Anal Machine Intell. 1989;11:1001–1005. [Google Scholar]
- 81.Zeki S, Watson JDG, Lueck CJ, Friston KJ, Kennard C, Frackowiak RSJ. A direct demonstration of functional specialization in human visual cortex. J Neurosci. 1991;11:641–649. doi: 10.1523/JNEUROSCI.11-03-00641.1991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Zeki S, Watson JDG, Frackowiak RSJ. Going beyond the information given: the relation of illusory visual motion to brain activity. Proc R Soc Lond [Biol] 1993;252:215–222. doi: 10.1098/rspb.1993.0068. [DOI] [PubMed] [Google Scholar]
- 83.Zilles K, Armstrong E, Schleicher A, Kretschmann H-J. The human pattern of gyrification in the cerebral cortex. Anat Embryol. 1988;179:173–179. doi: 10.1007/BF00304699. [DOI] [PubMed] [Google Scholar]