A neural network protocol for electronic excitations of N-methylacetamide

Significance

UV absorption spectroscopy is an effective technique for characterizing protein structure. However its theoretical interpretation requires expensive first-principles simulations. We employ a neural network strategy to predict UV electronic spectra of peptide bonds. The protocol establishes structure–property relations and predicts ground-state dipole moments, as well as transition dipole moments. We establish machine learning as a useful spectroscopy simulation tool.

Abstract

UV absorption is widely used for characterizing proteins structures. The mapping of UV spectra to atomic structure of proteins relies on expensive theoretical simulations, circumventing the heavy computational cost which involves repeated quantum-mechanical simulations of excited-state properties of many fluctuating protein geometries, which has been a long-time challenge. Here we show that a neural network machine-learning technique can predict electronic absorption spectra of N-methylacetamide (NMA), which is a widely used model system for the peptide bond. Using ground-state geometric parameters and charge information as descriptors, we employed a neural network to predict transition energies, ground-state, and transition dipole moments of many molecular-dynamics conformations at different temperatures, in agreement with time-dependent density-functional theory calculations. The neural network simulations are nearly 3,000× faster than comparable quantum calculations. Machine learning should provide a cost-effective tool for simulating optical properties of proteins.

Structure determination is crucial for understanding protein activity and function (1). Their secondary and tertiary structure can be characterized by the UV absorption spectra of its backbone peptide bonds (2, 3). Interpreting these signals requires extensive electronic structure simulations, since the time-averaged optical response is affected by conformational and environmental fluctuations. The repeated application of high-level quantum-mechanical tools to represent ensembles of structures of systems of thousands of atoms is computationally prohibitive. It makes the understanding of complex systems like proteins at atomic precision a formidable task. More cost-effective approaches are called for.

The map method has long been used to estimate key excited-state parameters, avoiding expensive quantum-mechanical calculations (4–9). Empirical formulas are employed to obtain transition energies from given ground-state structures of the target molecule. Empirical fitting of peptides and proteins containing hundreds of atoms by the map method is not an easy task. N-methylacetamide (NMA), which is the simplest molecule that can capture the essence of UV response of the protein backbone, has been extensively used to construct spectroscopic maps and model the spectra of the amide group of the peptide backbone (6). However, this method has a limited predictive power and transferability since it is based on a few-parameter fit of observables to key structural parameters. The inability to predict transition dipoles is another limitation. Developing a cost-effective solution for predicting both excitation energies and transition dipoles of peptides is an open challenge.

Machine learning is a family of statistics-based methods that enable a computer code to make predictions without being explicitly programmed. In computational chemistry, it has the ability to predict properties of molecules, avoiding computationally demanding high-level electronic structure calculations (10). These include the band gap for inorganic compounds (11), molecular atomization energies (12), atomization and total energies of molecules (13), and intrinsic bond energies (14).

We shall employ a subclass of machine-learning algorithms, known as neural network (NN). A standard NN consists of input, hidden, and output layers connected by artificial neurons. Input signals are passed through a weighted connection and processed by an activation function to produce the neuron output (15). Unlike the map method which relies on an empirical polynomial fit with a limited set of parameters, NN can create the structure–property relationship by iterative learning based on a complex high-dimensional function in a much larger, essentially unlimited parameter space. These make it a much more adaptable, flexible, and accurate tool compared with simple maps.

In this work, we employ NN to establish a quantitative relationship between the electronic excited-state properties of NMA and its ground-state geometry and charge distribution. Based on iterative learning of quantum-chemistry calculations for 70,000 molecular-dynamics conformations, we show that NN can satisfactorily predict the nπ* and ππ* transition energies and transition dipole moments. The UV spectra of NMA at different temperatures predicted by NN are in good agreement with results from time-dependent density-functional theory (TDDFT). We demonstrate that machine learning can provide an efficient tool for simulating spectra.

Results and Discussion

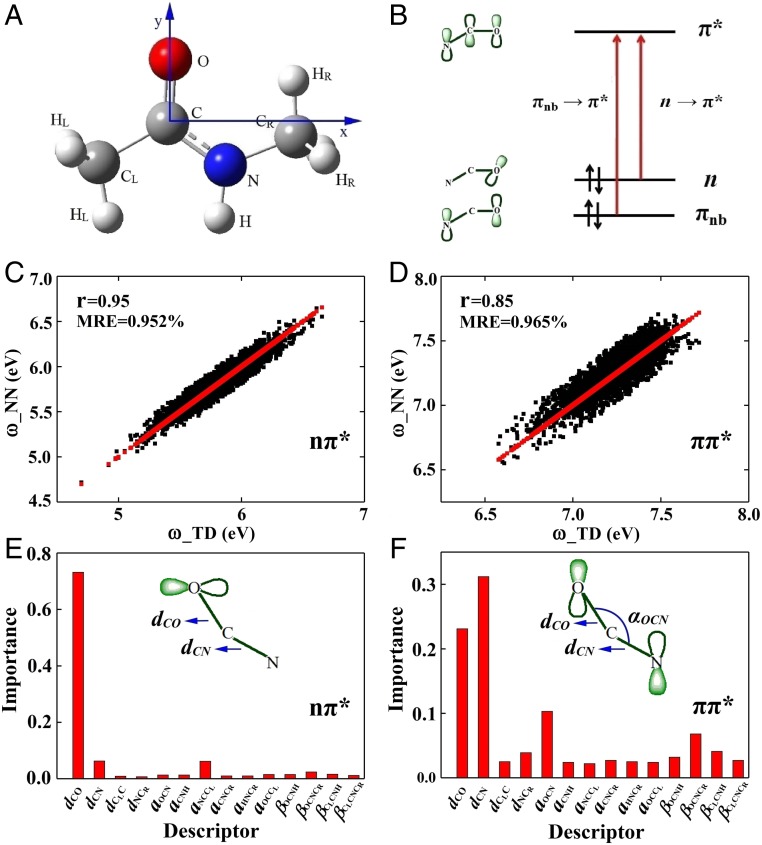
The nπ* and ππ* excitations of NMA (Fig. 1 A and B), regarded as a simplified model for the UV absorption of protein backbone, have been well studied by various electronic structure methods, including TDDFT and wavefunction-based electron correlation methods (16, 17). Compared with expensive electron correlation methods such as coupled-cluster single and double excitation equation of motion approach (EOM-CCSD) and complete active space with second-order perturbation theory (CASPT2), TDDFT is able to obtain satisfactory electronic excitation energies of various types of molecules at a modest computation cost. For NMA, Perdew–Burke–Ernzerhof hybrid functional (PBE0) functional has been employed in previous study by Gordon and coworkers (17). PBE0 has an error of about 0.3 eV in calculating transition energies of various molecules (18). Therefore, using PBE0 results as the reference data for NN training is a reasonable choice.

Fig. 1.

The structure and electronic transitions of NMA and prediction of the NMA transition energy by NN and descriptor importance analysis by random forest. (A) NMA gas-phase geometry optimized at the B3LYP/6–311++G** level of DFT. (B) Valence molecular orbitals and electronic transitions of amides. (C) Comparison of TDDFT nπ* transition energies (ω_TD) and NN (ω_NN) on test data. (D) Same as C but for the ππ* transition. The red lines/dots represent the transition energies (ω_TD) of NMA calculated by TDDFT at the PBE0/cc-pvdz level. Descriptor importance analysis of transition energies for nπ* (E) and ππ* (F) transitions.

The distribution of NMA nπ* and ππ* transition energies shows that the snapshot structures of NMA extracted from molecular-dynamics simulation trajectories are highly diverse (SI Appendix, Fig. S2 A and B). This allows us to employ both map and NN method to establish structure–property relationship for the UV absorption of NMA. Specifically, the map method uses formulas obtained by least-square fitting of data to establish the relationship between the transition energies and ground-state geometric parameters. This formula was then used to predict vibrational or electronic excitations. The electronic transitions of a molecule are complex functions of its parameters. However, maps only employ simple empirical formulas (details in SI Appendix) that do not fully capture the complexity of electronic transitions. In contrast, the NN technique employed here does not require explicit knowledge or guess of the relationship between input and output. Instead, the structure–property relationship is established by using a high-dimensional complex mapping between input and output. The training process of the model requires identification and screening descriptors for the problem of interest, and optimizing parameters for the NN model is nontrivial. In addition, overfitting of model is a known shortcoming of NN methods that needs to be carefully taken care of in practice. In this work, we have mitigated the overfitting issue in the NN training process using well-established procedures (details in SI Appendix).

We first examined the conventional map method (4) for the transition energies (ω) (SI Appendix, Fig. S2 C and D). Different datasets yield different maps, suggesting lack of transferability (SI Appendix, Fig. S3 A–D). Predictions by the map method have large errors and poor correlation with TDDFT. The selected descriptors for NN only require readily available ground-state information. Fourteen internal coordinates (SI Appendix, Fig. S1) were then used as input for NN to predict transition energies, and the produced data are then compared with TDDFT calculations (Fig. 1 C and D). The Pearson correlation coefficient (r) between pairs of descriptors show that most descriptors have low linear correlations (SI Appendix, Fig. S4), which significantly improve the performance of NN prediction. The mean relative error (MRE) of NN on the test set are 0.95% for nπ* and 0.96% for ππ*, and the Pearson correlation coefficient (r) are 0.95 for nπ* and 0.85 for ππ*, demonstrating highly accurate NN predictions with nearly 3,000× faster than traditional quantum calculations once the NN model was established (SI Appendix, Table S1). We note that the optimized NN model can always reproduce the result from a specific method that has been used for generating training data (Fig. 2 C and D and SI Appendix, Fig. S3 E and F). Therefore, we only need to take into account the accuracy of the chosen density functional on the transition energy of NMA. And, the NN results predict transition energies better than the maps.

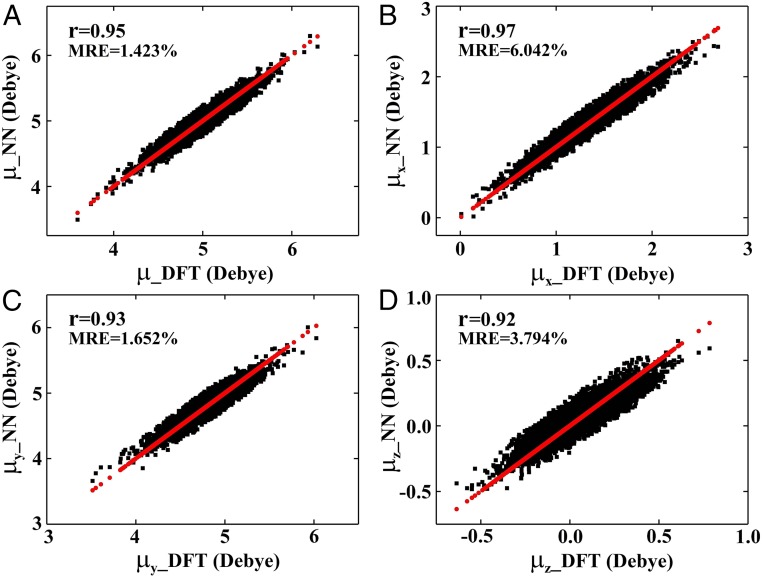
Fig. 2.

Prediction of the NMA ground-state dipole moment by NN. (A) Correlation plots of the DFT dipole moment (μ_DFT) and NN (μ_NN) on test data. (B–D) Comparison of the DFT dipole moment in the x, y, z direction (μ_x_DFT, μ_y_DFT, μ_z_DFT) and NN (μ_x_NN, μ_y_NN, μ_z_NN) on test data. The red lines/dots represent μ_DFT, μ_x_DFT, μ_y_DFT, and μ_z_DFT of NMA calculated by DFT at the PBE0/cc-pvdz level, respectively.

With the random forest algorithm for the descriptor importance analysis, we found that the C–O bond length is the dominant descriptor (Fig. 1E) for the nπ* excitation. This reflects the localized nature of nπ* transition. For the ππ* transition, the important descriptors are the C–N and C–O bond lengths and ∠OCN angle (Fig. 1F). The diverse nature of important descriptors for the ππ* transition arises from its nonlocal nature with strong dependences on the entire amid group structure. This conclusion is further verified by orbital localization analysis based on Mulliken populations (19). The localized molecular orbitals involved in the nπ* transition (SI Appendix, Fig. S5) clearly shows the dominant effect of the C-O bond, while the ππ* transition is determined by the entire amide group (SI Appendix, Fig. S5).

We have further applied the NN to predict the ground-state dipole moments. To eliminate orientational differences during NN training, we applied a rotation matrix operation by setting the carbonyl C atom of each NMA as the origin of coordinate, the C–O bond as the positive y axis, and the ∠OCN being fixed in the xy plane (Fig. 1A). The coordinates of five atoms (C_L, O, N, H, and C_R) were used as NN training descriptors. These adequately predict both the magnitude and direction of ground-state dipole moments (Fig. 2 and SI Appendix, Fig. S6). The most important descriptors for the total dipole moment are the y coordinate of the O atom and the x coordinate of the N atom (SI Appendix, Fig. S7). For the x component of dipole, the most important descriptors are the x coordinates of the N and C_R atom. Similarly, the y coordinate of the O atom has the largest influence on the y component of dipole. The most important descriptors of dipole moment along z are the z coordinates of the C_R and H atom. We have thus constructed the relationship between the molecular dipole moment and its structure, which allows us to rapidly predict the dipole moment (SI Appendix, Table S1) compared with quantum-chemistry calculations.

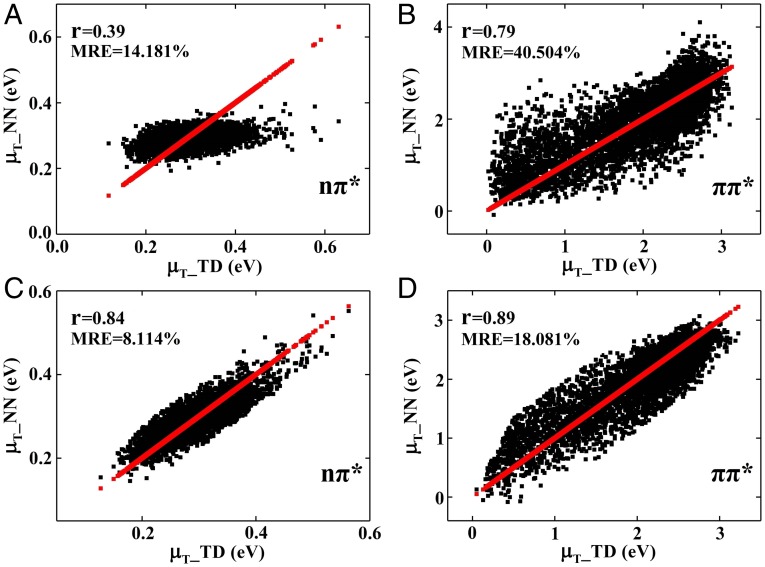
Then we aimed at the prediction of the transition dipole moment which governs the strength of electronic transition. However, it poses great challenge to the NN training because of the involvement of two different electronic states. We failed to get satisfactory results by using the regular coulomb matrix (CM) (10) as descriptors. We thus replaced the fixed point charge in the force field by the natural population analysis (NPA) charges which is regarded as a reliable parameter for describing charge distribution of atoms in molecules. For the nπ* transition, the peptide bond was used to construct the CM based on NPA charge. The α₁-angle, dihedral angles β₂ and β₃ of NMA (SI Appendix, Fig. S1), the components of the y and z coordinates of the C atom [C(y), C(z)], and the y coordinate of the O atom [O(y)] were chosen as descriptors for the nπ* transition dipole moment. For the ππ* transition, the descriptors were the NPA charge-derived CM_Q of the peptide bonds. The CM_Q gave a better fit in NN training and smaller MRE compared with the traditional CM (Fig. 3).

Fig. 3.

NN prediction of the NMA transition dipole moment. (A) Correlation plots of nπ* transition dipole moment by TDDFT (μ_T_TD) and NN (μ_T_NN) using descriptors of CM on test data. (B) Same as A but for the ππ* transition. (C) Comparison of nπ* transition dipole moment by TDDFT (μ_T_TD) and NN (μ_T _NN) using descriptors of CM based on NPA charge (CM_Q) on test data. (D) Same as C but for the ππ* transition. The red lines/dots represent the μ_T_TD of NMA calculated by TDDFT at the PBE0/cc-pvdz level.

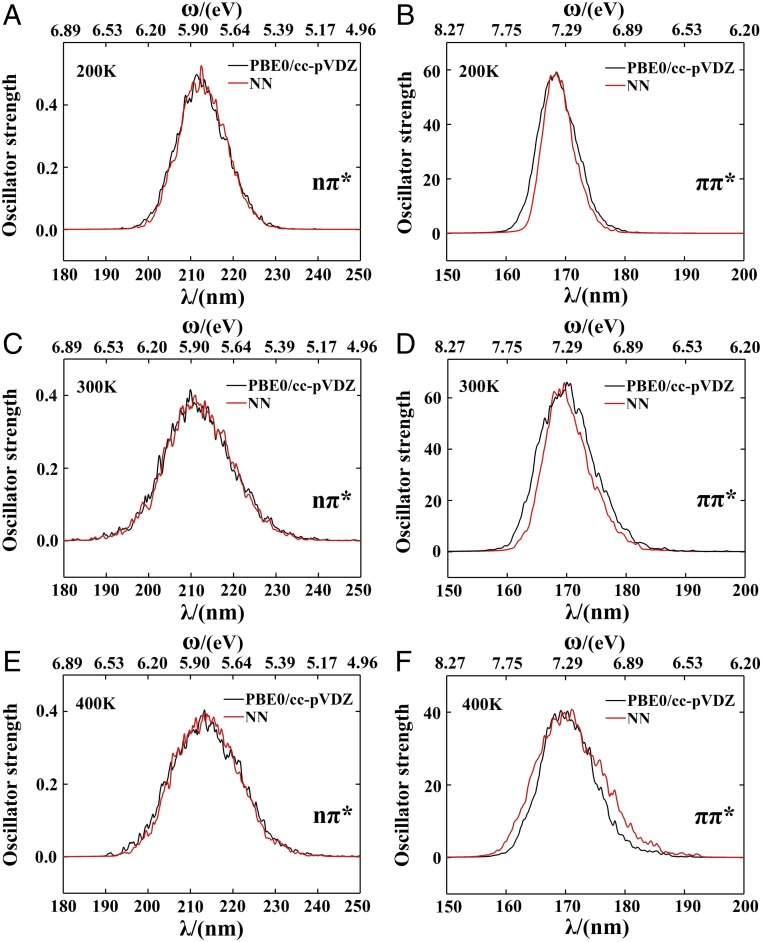
Using NN-generated excitation energies and transition dipole moments, we have calculated the oscillator strength $f=\frac{2}{3}\omega {\left|\mu \right|}^2$, where ω and μ represent the transition energy and transition dipole moment, respectively. For each temperature considered (200, 300, 400 K), UV spectra generated using a Lorentzian lineshape with 30-meV width (details in SI Appendix) from 5,000 randomly selected structures show good agreements to the TDDFT results (Fig. 4). For both the average maximum of the frequency and full width at half maximum of the UV absorption spectra at different temperatures, NN results are in good agreement with TDDFT results (Tables 1 and 2).

Fig. 4.

(A) The nπ* UV spectra at 200 K of 5,000 NMA structures calculated by TDDFT and NN. (B) Same as A but for the ππ* transition. (C and D) Same as A and B but at 300 K (E and F) Same as A and B but at 400 K. TDDFT calculations are at the PBE0/cc-pvdz level.

Table 1.

Comparison of the average maximum (in nanometers) of the frequency of nπ* and ππ* absorption bands of NMA in aqueous solution at different temperatures between simulation (TDDFT, NN) and experiment

Temperature	200 K	300 K	400 K
nπ*
TDDFT	212.74	211.94	213.83
NN	212.94	211.95	213.95
Expt	—	212.00†	—
ππ*
TDDFT	168.96	170.87	170.93
NN	169.19	171.28	170.90
Expt	—	186.00†	—

^†The maxima of nπ* and ππ* absorption bands of NMA in aqueous solution measured by Nielsen and Schellman (20).

Table 2.

The full width at half maximum (in nanometers) of the UV absorption spectra at different temperatures of NMA by TDDFT and NN

Temperature	200 K	300 K	400 K
nπ*
TDDFT	13.56	17.85	18.36
NN	12.15	17.19	18.87
ππ*
TDDFT	7.47	9.32	11.34
NN	6.32	8.24	12.64

As shown in Table 1, the transition energies of nπ* and ππ* of NMA calculated at PBE0/Dunning’s correlation-consistent polarized valence double-zeta basis set (cc-pVDZ) are 5.85 eV (211.94 nm) and 7.26 eV (170.87 nm), in line with the available experiment data––5.85 eV (212.00 nm) for nπ* and 6.67 eV (186.00 nm) for ππ*, respectively (20). The nπ* transition primarily involves the highest occupied to lowest unoccupied molecular orbital transition, for which the agreement between TDDFT and experiment is excellent. The ππ* transition is known to have multireference character which can be mixed with higher excited states; therefore, the prediction of the corresponding transition energy is very challenging even for highly accurate wavefunction-based electron correlation method, like EOM-CCSD (17). Given an ∼0.3 eV error of TDDFT methods for transition energies (18), PBE0/cc-PVDZ provides a reasonably good prediction of the ππ* transition energy of NMA compared with experiment.

The NN model was trained using data at 300 K, and then applied to predict UV spectra of NMA at other temperatures (200 and 400 K). The agreement between NN-predicted and TDDFT-computed UV spectra at different temperatures suggests good transferability. These excellent agreements thus demonstrate the ability of NN to reproduce spectra, based solely on the molecular geometry and charge distribution.

Conclusions

An NN protocol was developed to represent the transition energy, the dipole moment, and the electronic spectra of NMA based solely on ground-state information (structure and charge distribution). NN predictions are more robust and accurate than the conventional map method for describing excited-state properties. It is also cheaper than repeated quantum-chemistry calculations. We have chosen the model structure of NMA as a first step to test the methodology of applying machine-learning technique to the optical response of biomolecules. Our study shows that NN is a versatile practical tool for simulating UV spectra of the NMA molecule. We are currently using NN to map the electronic properties of all 20 amino acids with their respective atomic structures, and use the acquired NN model to study the UV spectra of NMA in other solvents. It is a key step toward the machine-learning prediction of UV spectra of proteins in various solvents. The NN protocol for predicting transition energies and dipole moments in this work is being used to construct model Hamiltonian for specific proteins toward simulation of their UV spectra. The NN model for dipoles developed here may be extended to investigate optical spectroscopy of large biological complexes, and also be applied to many other important properties involving key parameters of electric and magnetic dipole moments such as chemical reactions, optoelectronic conversion, and information processing.

Methods

Molecular-dynamics simulations were performed using the GROMACS code (21) for isothermal-isobaric ensemble with all-atom optimized potentials for liquid simulations (22) force fields for one NMA in the solution of 875 Jorgensen’s transferable intermolecular potential four point water model water molecules (4) generating 70,000 configurations at three temperatures (T = 200 K, T = 300 K, T = 400 K) (details in SI Appendix). The excited-state properties of these structures were calculated by first-principles TDDFT with PBE0/cc-pVDZ implemented in the Gaussian 09 package (23). Solvation effects were modeled implicitly by the integral equation formalism polarizable continuum model (24). Calculations by Becke’s three-parameter hybrid functionals with the Becke exchange and the Lee-Yang-Parr correlation functional, in conjunction with Pople’s split-valence double-zeta basis set with additional polarization functions [B3LYP/6-31G(d,p)] and B3LYP/6–311G ++(d,p) were performed for another set of 10,000 data points at 300 K, so as to verify if NN results are predictable well under different functional and basis sets. The nπ* transition involves the highest occupied to lowest unoccupied molecular orbital transition, while the ππ* transition has multireference character so that it can involve more than one electronic transition depending on the geometry. To unify the training dataset, we had discarded data points involving much higher excitations in the ππ* transition.

Transition energies, ground-state, and transition dipole moments were targets for the trainings and tests of the NN protocol. Fourteen internal coordinates (SI Appendix, Fig. S1) were used as input variables (descriptors) to predict transition energies. The xyz representation was used as input for the dipole moment. For the modulus of the transition dipole moment, the CM (10) based on atomic NPA charge (CM_Q) was defined as descriptors of $U_{ij}=\{\begin{array}{cc}0.5Q_i^{2.4}& \forall i=j\\ Q_i{Q}_j/\left|R_i-R_j\right|& \forall i\ne j\end{array}$, where $i$ and $j$ are atomic indices, $\left|R_i-R_j\right|$ is the interatomic distance, and $Q_i$ represents NPA charge.

Multilayer perceptrons (25) were used in the NN training to establish the relationship between excited-state properties and ground-state geometry and charge distributions (details in SI Appendix). Our protocol includes 50,000 data points at 300 K, and 10,000 at 200 and 400 K. The training set includes 40,000 data points randomly selected from a 300-K simulation. We have further used the random forest algorithm (26) to analyze the importance of each descriptor in NN. The Pearson correlation coefficient (r) is used to evaluate the NN performance, which measures the linear correlation between predicted and actual values. The MRE and cross-validation technique (12) were employed to verify the accuracy and robustness of the NN.