Expanding the TNM for cancers of the colon and rectum using machine learning: a demonstration

Abstract

Objective

The American Joint Committee on Cancer (AJCC) system for staging cancers of the colon and rectum includes depth of tumour penetration, number of positive lymph nodes and presence or absence of metastasis. Using machine learning, we demonstrate that these factors can be integrated with age, carcinoembryonic antigen (CEA) interpretation and tumour location, to form prognostic systems that expand the tumour, lymph node, metastasis (TNM) staging system.

Methods

Two datasets on colon and rectal cancers were extracted from the Surveillance, Epidemiology and End Results Programme of the National Cancer Institute. Dataset 1 included three factors (tumour, lymph nodes and metastasis). Dataset 2 contained six factors (tumour, lymph nodes, metastasis, age, CEA interpretation and tumour location). The Ensemble Algorithm for Clustering Cancer Data (EACCD) and the C-index were applied to generate prognostic groups.

Results

The EACCD prognostic system based on dataset 1 stratified patients into 10 risk groups, analogous to the 10 stages of the AJCC staging system. There was a strong inter-system association between EACCD grouping and AJCC staging (Spearman’s rank correlation=0.9046, p value=1.6×10⁻¹⁷). However, the EACCD system had a significantly higher survival prediction accuracy than the AJCC system (C-index=0.7802 and 0.7695, respectively for the EACCD system and AJCC system, p value=4.9×10⁻⁹¹). Adding age, or CEA interpretation, or location improved the prediction accuracy of the prognostic system-involving tumour, lymph nodes and metastasis. The EACCD prognostic system based on dataset 2 and all six factors stratified patients into 10 groups with the highest survival prediction accuracy (C-index=0.7914).

Conclusions

The EACCD can integrate multiple factors to stratify patients with colon or rectal cancer into risk groups that predict survival with a high accuracy.

Key questions.

What is already known about this subject?

• The tumour, lymph node, metastasis (TNM) staging system has served as the standard classification for cancers of the colon and rectum.

• Integrating additional factors into the TNM staging system is needed for more accurate patient classification and survival prediction.

• The existing Cox regression model-based approach improves the survival prediction but is not adept at-risk stratification.

What does this study add?

• We introduced a novel machine learning approach to create prognostic systems for colon and rectal cancer that handles both stratification and prediction.

• We used primary tumour, lymph node status, metastasis, age, interpretation of carcinoembryonic antigen (CEA) test results, and tumour location to create a prognostic system that extends the TNM staging system.

• We studied the effects of age, CEA, location, as well as their levels on survival prediction.

How might this impact on clinical practice?

• This work has the potential to advance in predicting outcomes and optimising treatment strategies for patients of cancers of the colon and rectum.

Introduction

Estimating patient outcome for cancer of the colon or rectum (CRC) depends on the synthesis of multiple factors that include clinical presentation, functional status, histopathological diagnosis, extent of disease and biological factors that are prognostic for survival and possibly predictive of therapeutic response. Traditionally, the tumour, lymph node, metastasis (TNM) staging system,1 based on the anatomic factors of tumour extent, nodal status and metastatic spread, has provided basic information for tumour evaluation, treatment and prognosis. However, CRC is no longer characterised by the anatomic extent of disease, but by a combination of host and biological factors. Given the ongoing discovery of prognostic factors such as those from molecular findings, new and important factors need to be integrated in order to augment prognostic evaluation and management decisions for CRC.

Several systems have been developed toward this goal. The Mayo Clinic developed the ACCENT-based web calculator for stage III colon cancer.2 Valentini et al and Roselló et al developed the prediction model for locally advanced rectal cancer.3 4 Weiser et al built a model for predicting survival after colectomy using data from the Surveillance, Epidemiology and End Results (SEER) Programme.5 6 In addition, there are systems targeting different types of CRCs.1 All of these systems rely on analytic methods such as Cox regression modelling for fitting to the data and thus focus mainly on prediction. As a result, there is no clear rule that stratifies patients into risk groups analogous to the American Joint Committee on Cancer (AJCC) stages.

In this study, we introduced a novel approach using the Ensemble Algorithm for Clustering Cancer Data (EACCD)7–12 to create prognostic systems for colon and rectal cancer. This approach combines stratification and prediction. We used the SEER database. Apart from tumour size (T), lymph node status (N) and metastasis (M), we included age (A), interpretation of carcinoembryonic antigen (CEA) test results (C)13 and tumour location (L). Study has shown that older age (>80 years) independently predicts less favourable operative outcomes after CRC procedures.14 CEA is used to aid in CRC diagnosis and evaluate prognosis.15 Strong evidence for the prognostic effect of primary tumour location is available in the literature.16 As claimed by AJCC, new prognostic systems have been called to incorporate additional factors including the above to advance in predicting outcomes and optimising treatment strategies in the 21st century medicine.1

We built two prognostic systems using EACCD. One system, based on T, N, M, was primarily employed to compare our approach with AJCC. The second system, based on T, N, M, A, C and L expanded the traditional staging system based on T, N, M only. These prognostic systems serve the same role as the TNM staging system but have a higher accuracy in survival prediction than the TNM.

Materials and methods

Data

Dataset 1 contains certain cases with complete information on T, N, M, survival time (in months) and SEER cause-specific death classification variable.17 The year of diagnosis was restricted from 2010 to 2012. T (six levels: Tis, T1, T2, T3, T4a, T4b), N (four levels: N0, N1, N2a, N2b) and M (three levels: M0, M1a, M1b) are defined in online supplementary table S1. The cause-specific death classification was used to identify the censoring status. We define a combination as a subset of the data corresponding to one level of each factor and we use levels of factors to denote combinations (eg, T1N0M0 represents a subset of patients with T=T1, N=N0, M=M0). Dataset 1, including 70 815 cases, consists of 45 combinations (in terms of T, N, M) each containing at least 100 patients.

Dataset 2 contains certain cases with complete information on T, N, M, A, C, L, survival time and SEER cause-specific death classification variable. T (five levels: Tis, T1, T2, T3, T4), N (three levels: N0, N1, N2), M (two levels: M0, M1), A (two levels: A1, A2), C (two levels: C1, C2) and L (three levels: Lr, Ll, Lb) are defined in online supplementary table S1. The year of diagnosis was restricted from 2004 to 2010. Dataset 2, including 88 970 cases, consists of 137 combinations (in terms of T, N, M, A, C, L) each containing at least 100 patients. Additional details on datasets are provided as online supplementary data.

Ensemble Algorithm for Clustering Cancer Data

The EACCD is a machine-learning algorithm designed to stratify survival data, which involves three steps: (1) defining initial dissimilarities between survival functions of any two combinations of patients; (2) obtaining learnt dissimilarities by using initial dissimilarities and an ensemble learning process; and (3) applying hierarchical clustering analysis to cluster combinations by the learnt dissimilarities and a linkage method. The output of the EACCD is a tree-structured dendrogram, which represents the relationship of survival among different combinations. More details on EACCD and how to realise each step in this paper are provided as online supplementary methods.

Prognostic systems

Cutting the dendrogram at a dissimilarity value generates prognostic groups that correspond to a C-index,18 an estimate of the probability that a subject who experienced an event (eg, death) in an earlier time had a shorter predicted time than a subject who experienced the event in a later time. The curve of the C-index versus the number of groups increases for relatively small numbers of groups and then plateaus as more groups are generated. The C-index curve can be used to find the optimal number of groups (denoted by n*) for the model, which balances the simplicity and accuracy of the system. The number n* is usually chosen near the horizontal coordinate of the knee point of the C-index curve.

Survival curves using Kaplan-Meier estimates19 were plotted for prognostic groups to visually evaluate the survival differences among groups. The final system is a collection of the dendrogram, the group assignment, the C-index and the survival curves for the prognostic groups.

The approach of using machine learning to create prognostic system can be applied to any dataset. When additional data become available, we can combine them with older data and then apply the approach to the combined data. This is expected to produce more robust results because the combined data contain more patients than the original data. If the size of the new data is large, the machine learning approach can be applied directly to the new data. This may generate prognostic systems that possess certain properties inherent in the new data.

Results

Prognostic system on T, N and M

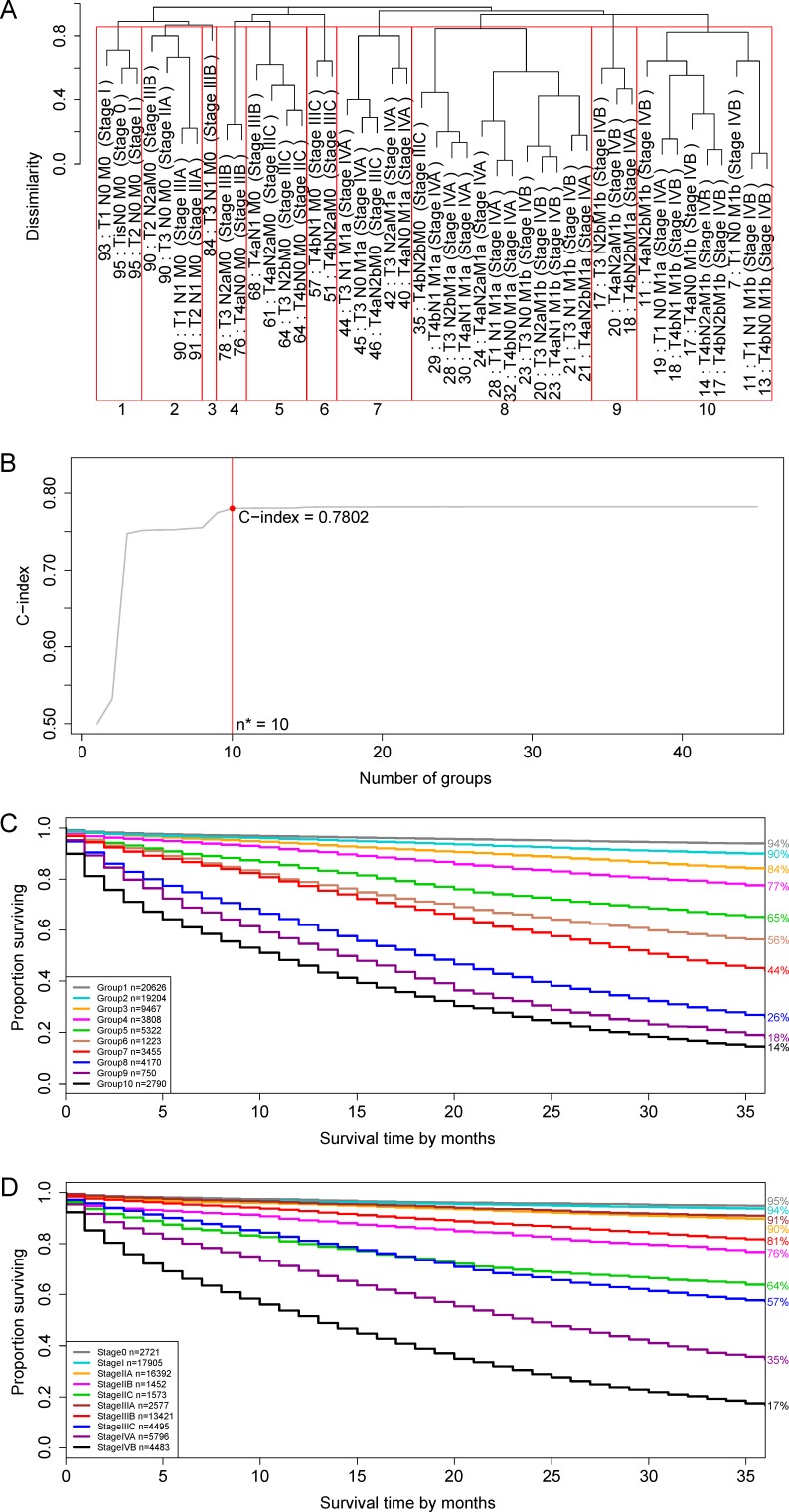
Applying EACCD to dataset 1 yielded the dendrogram (in black colour) in figure 1A. The C-index curve, shown in figure 1B, was used to find the optimal number of prognostic groups n*. The knee point of the curve corresponds to n*=10 groups and a C-index of 0.7802. Figure 1A shows cutting the dendrogram into 10 groups (in red square boxes), whose survival rates are plotted in figure 1C. The survival curves are well separated and do not overlap, which confirms that n*=10 is an appropriate number of prognostic groups, based on T, N and M. In contrast, the 7th edition of AJCC divides dataset 1 into 10 stages whose survival curves are shown in figure 1D. A comparison between the EACCD prognostic system and the AJCC TNM staging system is given in the Discussion section.

Figure 1.

Ensemble Algorithm for Clustering Cancer Data prognostic groups and American Joint Committee on Cancer (AJCC) stages on the basis of dataset 1 involving T, N and M. (A) The tree-structured dendrogram (in the black colour). A 3-year cancer-specific survival rate is given beneath each combination. Cutting the dendrogram according to n*=10 in (B) creates 10 prognostic groups, shown in red square boxes. Listed on the bottom are the group numbers. (B) C-index curve based on the dendrogram in (A). The number 0.7802 is the C-index corresponding to n*=10 prognostic groups. (C) Cancer-specific survival of 10 prognostic groups in (A). The 3-year cancer-specific survival rates for 10 groups are listed on the right side. (D) Cancer-specific survival of 10 AJCC stages. The 3-year cancer-specific survival rates for 10 stages are listed on the right side.

The dendrogram with cutting in figure 1A, the corresponding C-index value in figure 1B and the survival curves in figure 1C define a prognostic system for colon and rectal cancer that incorporates T, N and M. The risk of the prognostic group within the prognostic system increases as the group number (ie, 1, 2, 3, …, 10) of the group increases.

Prognostic system on T, N, M, A, C and L

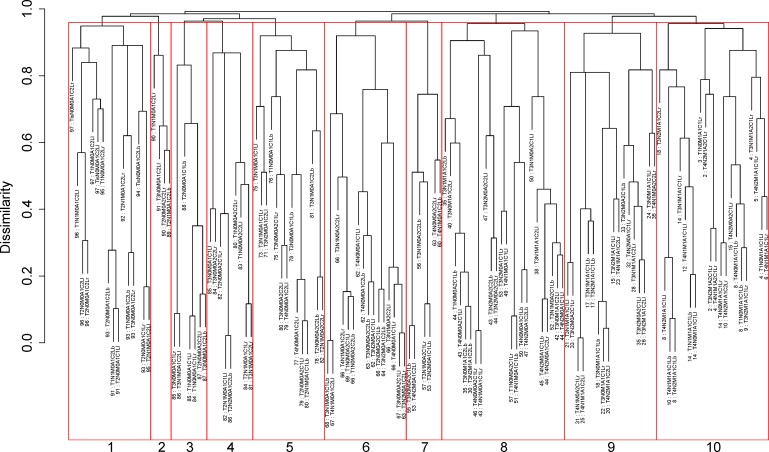
Figure 2 presents the dendrogram with cutting, based on all six factors (T, N, M, A, C, L). The number of prognostic groups n*=10 is suggested by the ‘knee’ point of the red C-index curve in figure 3A. A detailed definition for all 10 groups is listed in online supplementary table S2. Figure 3B shows the survival curves for the 10 prognostic groups. Again, the risk of the prognostic group increases as the group number increases.

Figure 2.

Dendrogram for T, N, M, A, C and L on dataset 2 and cutting the dendrogram to produce 10 groups. Running Ensemble Algorithm for Clustering Cancer Data results in the tree-structured dendrogram (in black colour). A 5-year cancer-specific survival rate in percentage is given beneath each combination. Red square boxes show cutting the dendrogram into 10 prognostic groups according to n*=10 for the red curve {T, N, M, A, C, L} in figure 3 (A). Listed on the bottom are the group numbers.

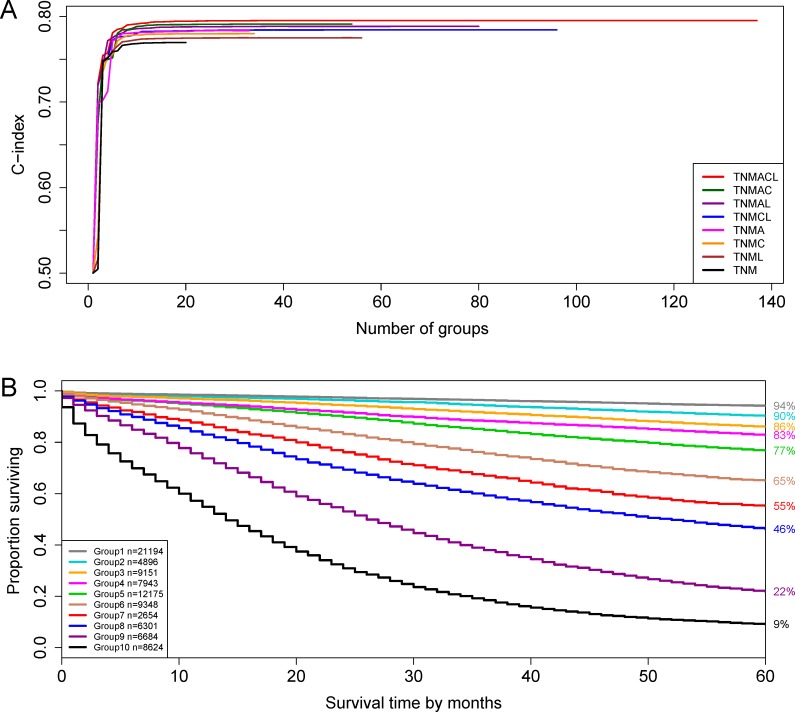
Figure 3.

C-index curves and survival curves on the basis of dataset 2. (A) C-index curves of {T, N, M}, {T, N, M, L}, {T, N, M, C}, {T, N, M, A}, {T, N, M, C, L}, {T, N, M, A, L}, {T, N, M, A, C} and {T, N, M, A, C, L}. The optimal number of groups n*, determined using the red curve of {T, N, M, A, C, L}, equals 10 with a corresponding C-index of 0.7914. (B) Cancer-specific survival of 10 prognostic groups in figure 2. The 5-year cancer-specific survival rates for 10 groups are listed on the right side.

Discussion

Comparing the EACCD with the TNM

The 8th edition of the AJCC staging system requires the M level ‘m1c’ that is not available in SEER. Therefore, we compare the EACCD prognostic system (figure 1A−C) with the 7th edition of AJCC TNM (figure 1D). The following differences were observed. First, a prognostic group in the EACCD with a higher group number has a less favourable survival, while a higher stage group in AJCC TNM does not always indicate a less favourable survival. For example, the survival of stage IIIA in the AJCC TNM is more favourable than the survival of stage IIA (figure 1D), which is counter-intuitive. Second, survival curves of different prognostic groups in the EACCD do not overlap, but overlapping can occur for different stage groups of AJCC. For example, the survival curves of stage IIC and Stage IIIC cross each other, which could cause confusion in decision-making. Third, the EACCD system has a higher prediction accuracy than the AJCC TNM in terms of the C-index. In fact, the AJCC TNM has a C-index of 0.7695, which is significantly smaller than the C-index=0.7802 of the EACCD system (p value=4.9×10⁻⁹¹ by the test in Kang et al20).

Despite the difference, the EACCD prognostic system and AJCC staging system are highly correlated in terms of assignments of patients. In fact, the two assignments have a large Spearman’s rank correlation coefficient of 0.9046 with a p value of 1.6×10⁻¹⁷. This indicates that in general, the higher the stage the patient is assigned to by the AJCC system, the higher-risk group the patient is assigned to by the EACCD, and vice versa. Additional insight regarding the correlation can be gained by examining the distribution of patients in each of 10 AJCC stages over the 10 prognostic groups of the EACCD system (online supplementary table S3). The main disagreement between the assignments of the two systems is that AJCC assigns many patients with quite optimistic survival to stage IIIA or IIIB. For example, combination T2N2aM0 with a 3-year cancer-specific survival rate 90% (figure 1A) is assigned to stage IIIB by AJCC.

Comparing EACCD with Cox regression models

Efforts have been made to expand the AJCC staging system by integrating additional factors. The main approach available in the literature is based on Cox regression modelling.2 3 6 Cox regression models, focusing on optimal fitting to the data, can achieve a high accuracy in survival prediction. The main downside is that no clear rule can be extracted from the output (eg, the nomogram) to stratify patients into risk groups analogous to AJCC stages.

In contrast, the EACCD approach introduced in this paper computes the survival difference between any two cohorts of patients and utilises these differences to stratify patients, where the number of groups from stratification is determined by the C-index curve. Therefore, this approach takes into account both stratification and prediction.

Effect of factors on prediction

Figure 3A plots C-index curves on the basis of dataset 2 for eight scenarios corresponding to the integration of {A, C, L} into {T, N, M}. The height of the C-index curve after levelling off represents the prediction accuracy of the prognostic system involving corresponding factors. Since the C-index curve of {T, N, M, A, C, L} is the highest, adding all of factors A, C and L to {T, N, M} leads to the biggest improvement on the prediction accuracy of the system based on {T, N, M}. (An interesting finding to note is that the curve of {T, N, M, A} has almost the same height as {T, N, M, C, L}, showing that the effect of adding A to {T, N, M} is virtually the same as the effect of adding C and L simultaneously.)

Effect of factor levels on survival

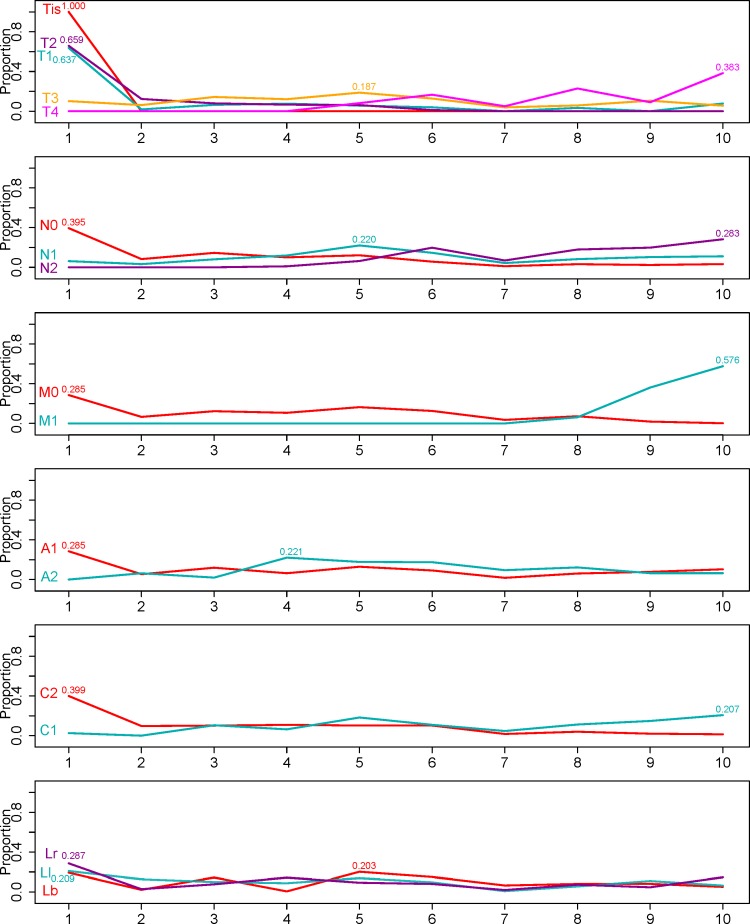
The EACCD prognostic system on factors T, N, M, A, C and L can help to explain the effects of factor levels on survival. Figure 4 shows the profiles of the factors, which depict the distribution of patients associated with a factor level across the prognostic groups. The number at the peak shows the maximum proportion of patients falling into the corresponding group. Because the prognostic groups from EACCD are ordered in terms of risk, the profile for a factor level provides an overall picture on how this factor level affects survival throughout the entire course of the disease. For example, T1 curve peaks at group 1 with the maximum proportion 0.637, indicating that patients with T1 are most likely to be distributed into group 1. If we divide all 10 prognostic groups into two categories, low-risk comprising groups 1–5 and high-risk comprising groups 6–10, then patients with T1 tend to fall into the low-risk category. Similarly, patients with any of the following levels tend to be considered as low-risk: Tis, T2, N0, M0, A1 and C2, and those with any of the following levels as high-risk: T4, N2, M1, A2 and C1. Patients with T3 or N1 fall into the boundary between the two categories. However, a fixed level of location does not seem to show favour of any risk category.

Figure 4.

Profiles of factor levels across prognostic groups shown in figure 2. In each panel, one factor is concerned, and for each level of the factor, the distribution of associated patients (10 proportions at 10 groups) is presented. The number shown for each distribution is the maximum proportion achieved at the corresponding group.

Tumour location

In Effect of factor levels on survival section, we showed that location by itself may not provide much useful information on prognosis since no clear relationship between the assignment of prognostic group and the level of tumour location was observed in the profile plot that studies factors marginally. However, figure 3A and Effect of factors on prediction section show that incorporating tumour location can increase the C-indices of prognostic systems, which implies that tumour location has a notable prognostic effect when adjusting other factors. This finding further confirms the prognostic effect of tumour location reported in the literature.

Clinical application of EACCD prognostic systems

Essentially the EACCD prognostic systems can serve the same role as the AJCC staging system. However, since EACCD systems involving more factors become more individualised and consequently more accurate stratification and prediction are achieved, they provide particular insights into managing patient care. As an example, we propose below a three-step approach of utilising the EACCD stratification to identify high-risk patients who could participate in adjuvant treatment trials.

One main issue in current clinical practice is to identify the subgroup of stage II patients (T3/4+N0+M0) who will benefit from adjuvant chemotherapy.21 This is not a trivial task because stage II represents a rather heterogeneous cohort. For instance, our EACCD system created in this report using T, N, M, A, C and L shows that T4N0M0A2C1Ll (5-year cancer-specific survival: 43%) is in group 8 while T4N0M0A1C2Ll (5-year cancer-specific survival: 79%) is in group 5. In contrast to the TNM stages, each prognostic group from the EACCD system is more homogeneous, and as a result, an EACCD system has the potential to guide the design of related clinical trials and analysis of resulting results. At step 1, we enrol into the trials patients of interested prognostic groups from the EACCD prognostic system based on T, N, M, A, C and L, or an EACCD system based on multiple prognostic factors such as immunoscore, Oncotype DX and ColoPrint gene profiling assays. At step 2, we apply EACCD to the results from the trials, which will present stratification based on the outcomes from the trials. At step 3, we identify the patients who benefit from the adjuvant chemotherapy by comparing the prognostic groups selected at step 1 with groups obtained in step 2.

Limitation

We used SEER cause-specific classification variable to study colon and rectal cancer-specific survival. The variable was collected by taking into account elements (eg, tumour sequence, site of the original cancer diagnosis and comorbidities) other than cause of death. Though it can better identify cause-specific deaths than the traditional cause-of-death variable, its record is still affected by inaccurate identification of death certificates. Another limitation is that some rare but important combinations could be excluded from the study due to the restriction of a minimum sample size of 100 cases. In general, EACCD requires a relatively large size for each combination in order to produce robust estimates of survival. However, the impact of this limitation will be minimised as more data become available. Finally, the information on treatment (eg, adjuvant chemotherapy) was not explicitly used in our study. Incorporating treatment, which is viewed as a factor, is expected to improve both stratification and prediction of the prognostic systems created by EACCD.

Conclusion

Using SEER data, we have demonstrated how to create prognostic systems for colon and rectal cancer using a machine learning algorithm, the EACCD. We showed that the EACCD can not only stratify CRC patients into risk groups but also predict survival with a high accuracy. Our approach to creating prognostic systems can accept any number of prognostic factors. Therefore, as data for new important variables/factors (eg, KRAS and NRAS22) become available, they can be integrated into the existing systems to provide timely refinements in risk stratification and outcome prediction.