Abstract
Multiple cognitive risk products (dysfunctional attitudes [DA], negative inferential style [NIS], self-criticism, dependency, rumination) predict internalizing disorders; however, an optimal structure to assess these risks is unknown. We evaluated the fit, construct validity, and utility of a bifactor, single, and correlated factor model in a community sample of 382 adolescents (age 11–15 years; 59% female). The bifactor, hierarchical single, and correlated factor models all fit well. The bifactor model included a common factor (c), capturing covariance across all cognitive risk measures, and specific latent factors for DA, NIS, dependency and rumination. Construct validity of these factor structures was evaluated with external validators, including depression and anxious arousal (AA) symptoms, positive affect (PA) and negative affect (NA), and onset of depression diagnostic onset over 2 years. C was associated with higher depression, NA, and AA; lower PA; and predicted depressive episodes. Hierarchical single and correlated factor models also related to external validators.
Keywords: cognitive risk, adolescent, factor analysis, depression, anxiety, negative affect, positive affect
Cognitive vulnerability models of psychopathology posit that individuals with maladaptive ways of thinking are at increased risk to develop psychopathology (Riskind & Alloy, 2006). Cognitive risks can be understood as products or processes. Cognitive risk products include negative attitudes, beliefs, or interpretation styles that are posited to result from cognitive risk processes, such as maladaptive attention and memory biases (Ingram, Miranda, & Segal, 1998). The present study focuses on several of the most well supported cognitive risk products from distinct theoretical paradigms including dysfunctional attitudes from Beck’s cognitive model (Beck, 1976); negative inferential style from hopelessness theory (Abramson, Metalsky, & Alloy, 1989); self-criticism and dependency—two maladaptive cognitive-personality styles (Blatt, 1974); and rumination from response styles theory (Nolen-Hoeksema & Morrow, 1991). These cognitive vulnerabilities have been well established as correlating with and prospectively predicting depression in youth and adults (e.g., Abela & Hankin, 2008; Alloy et al., 2012; Hankin, Snyder, & Gulley, 2016). More recently, these cognitive risks have been examined as transdiagnostic risk factors and processes for other forms of psychopathology, particularly within the internalizing spectrum (e.g., Hankin, Snyder, & Gulley, 2016a; Nolen-Hoeksema & Watkins, 2011).
An important principle in scientific inquiry is to have nonredundancy of constructs and to make sure that constructs are conceptualized and measured in an accurate way (Cronbach & Meehl, 1955). Accuracy and consistency of measurement across studies is important in order to make findings across studies comparable, and to remove nuisance variance that can impede replicability. The traditional and currently widely implemented approach of conceptualizing and measuring these cognitive risk products is to consider them as distinct constructs, and to measure them independently on a manifest level in relationship to different psychopathological outcomes. However, these cognitive risks may share common variance reflecting a broad underlying dimension. Thus, measuring and examining each cognitive risk independently in relationship to outcomes and interpreting the results as the effects of discrete risk factors may not be entirely accurate. Elucidating a reliable, optimal latent structure of cognitive risk products could contribute to more accurate assessment and conceptualization of these constructs.
It is possible that relationships that have emerged in prior work between each of these cognitive risks and various internalizing outcomes may be more parsimoniously explained by a “common core” essence that is present across these purportedly distinct cognitive risks (Hong & Cheung, 2015). Indeed, some factor analytic work suggests that multiple cognitive risks are manifestations of a single underlying construct and are best understood as a single latent factor (Hong & Cheung, 2015). Conversely, findings indicating differences in specificity to outcomes could suggest that there are unique aspects of cognitive risks, and that there is value in measuring and examining them independently. For instance, negative inferential style has predicted future depression, but not anxiety, in youth and adults (Alloy et al., 2000; Hankin, 2008a; Hankin, Abramson, Miller, & Haeffel, 2004) and some factor analytic work suggests that several cognitive risk products are better understood as independent, yet correlated constructs (Adams, Abela, & Hankin, 2007; Hankin, Lakdawalla, Carter, Abela, & Adams, 2007). Taken together, there appears to be both overlapping and distinct aspects of these prominent cognitive risks; however, researchers have not yet examined whether they could be organized in a dimensional latent model that would organize their shared and unique components.
Surprisingly few studies have empirically examined the structure and organization of these cognitive risk products. Evidence supporting both single and correlated factor structures could suggest that cognitive risks may be more optimally organized with a model that allows for both overlapping and distinct aspects to be disentangled and organized. A latent bifactor model allows for manifest measures of cognitive risks to be organized into a single latent factor that accounts for the common variance across measures (i.e., common factor) as well as organizes any unique variance not accounted for by the common factor into specific latent factors (Holzinger & Swineford, 1937). Bifactor models have been utilized successfully and validated for a variety of complex psychological phenomena, including intelligence (e.g., Carroll, 1993; Holzinger & Swineford, 1937), psychopathology (e.g., Caspi et al., 2014; Lahey et al., 2012), temperament (Snyder et al., 2015), and executive functioning (Miyake & Friedman, 2012). However, no study has yet investigated whether a bifactor model might more accurately organize prominent cognitive risk products for psychopathology.
The present study addresses how several prominent cognitive risk products are organized. We investigate this question in a sample of early adolescents because it is a high-risk period when rates of many common internalizing psychopathologies surge (e.g., Costello, Copeland, & Angold, 2011; Hankin et al., 1998; Merikangas et al., 2010), and many prominent cognitive risk products have emerged and stabilized into relatively trait-like risks for psychopathology (Hankin, 2008b). We examine a bifactor model and other plausible models that have been found in prior literature (i.e., single, hierarchical single, and correlated factor models). In addition, we examine the construct validity of these structural models by examining the pattern of associations with important external validators. Given that cognitive risks have been associated with depression, and that several cognitive risk products have also been associated with other internalizing outcomes (e.g., anxiety) (Hankin, Snyder, & Gulley, 2016), external validators include depression symptoms and the future onset of clinical depression as well as negative affectivity (NA), positive affectivity (PA), and anxious arousal (AA) symptoms—three important factors organizing overlapping and relatively specific symptoms of depression and anxiety (Mineka, Watson, & Clark, 1998). Examining the pattern of relationships between dimensions of the structural models and these external validators enables the evaluation of the utility of structural models. Thus, we consider both model fit as well as construct validity supported by associations with external validators as means to evaluate structural models of cognitive product risks to psychopathology.
Key Cognitive Risk Products and Associations With Internalizing Problems
Dysfunctional attitudes (DA) reflect negative maladaptive self-schemas, or cognitive structures, which bias information processing (e.g., attention) toward schema-congruent information (Beck, 1976; Beck & Haigh, 2014). Themes of DA include excessive standards of perfectionism, performance, contingencies of self-worth, and needing approval from others (Beck, 1976). A negative inferential style (NIS) is a way of explaining the causes of negative events as being internal (i.e., due to one’s self and not external circumstances), stable (i.e., likely to recur) and global (i.e., likely to affect other domains of life). Additionally, the individual makes negative inferences about the self (e.g., that one is inept) and consequences of negative events (i.e., other aversive outcomes will follow; Abramson et al., 1989). Self-criticism (SC) and dependency are maladaptive cognitive-personality styles (e.g., Blatt, 1974; Blatt & Luyten, 2009; Blatt & Zuroff, 1992). Individuals high in self-criticism are excessively focused on achievement and status in order to gain approval from others, whereas those high in dependency experience instability in relationships and have a sense of self-worth that depends on meeting the needs of others (e.g., Blatt, 1974). Last, rumination is a passive, repetitive thinking style where one dwells on the potential meaning, causes, and consequences of one’s symptoms of distress (e.g., sad mood; Nolen-Hoeksema & Morrow, 1991).
A large body of evidence supports the concurrent and prospective relationship between these cognitive risk products and depression. More recently, evidence shows that these cognitive vulnerabilities contribute to other psychopathologies, particularly other forms of internalizing disorders (e.g., see Abela & Hankin, 2008; Gibb & Coles, 2005; Riskind & Alloy, 2006; and Hankin, Snyder, & Gulley, 2016; for reviews). Rumination relates to anxiety in youth and adults concurrently and prospectively (e.g., McLaughlin & Nolen-Hoeksema, 2011; Selby, Anestis, & Joiner, 2008); self-criticism relates to social phobia and posttraumatic stress disorder (PTSD) in adults (e.g., Cox, Fleet, & Stein, 2004; Sharhabani-Arzy, Amir, & Swisa, 2005); and NIS has been linked to PTSD (e.g., Elwood, Hahn, Olatunji, & Williams, 2009). These findings are consistent with the perspective that cognitive risks may be transdiagnostic risks for internalizing psychopathology (Nolen-Hoeksema & Watkins, 2011).
The Structure of Cognitive Risk Products
Studies that have examined the latent factor structure of sub-sets of these cognitive risk products find evidence for both single factor and correlated factor structures. These past studies have varied in terms of the type and breadth of cognitive risk products that were included in analyses; the inclusion of different measured variables can affect conclusions regarding factor structure. For instance, some work has focused on traditionally depression-related risks (e.g., DA, NIS, rumination, self-criticism, dependency) (Adams et al., 2007; Hankin et al., 2007; Joiner & Rudd, 1996; Reno & Halaris, 1989; Pössel & Knopf, 2011), whereas other work has also included traditionally anxiety-related risks (e.g., intolerance of uncertainty, fear of negative evaluation) (Hong & Cheung, 2015). Some studies of DA and NIS find a single factor structure in adults (Reno & Halaris, 1989) and adolescents (Garber, Weiss, & Shanley, 1993), whereas other work finds a correlated factor structure in adults (Gotlib, Lewinsohn, Seeley, & Rhode, 1991; Joiner & Rudd, 1996) and adolescents (Gotlib, Lewinsohn, Seeley, Rohde, & Redner, 1993). Studies including DA, NIS, and rumination have also found evidence for a single (Hong & Cheung, 2015) and correlated factor organization in adults (Hankin et al., 2007; Pössel & Knopf, 2011). Finally, work including NIS, rumination, self-criticism, and dependency found correlated factors in early adolescents (Adams et al., 2007).
There are two key limitations of prior work. First, studies have varied in terms of whether manifest indicators are based on global or subscale level scores, which can also affect factor structure. For instance, Hong and Cheung (2015) used scale level data and found evidence for a single factor structure, whereas others (e.g., Adams et al., 2007; Hankin et al., 2007) used subscale level data and found evidence for correlated factor structures. In order to properly compare alternative cognitive risk product structures, it is important for researchers to specify models that align as closely as possible with those investigated in prior work. Second, few studies (Adams et al., 2007; Garber et al., 1993; Gotlib et al., 1993) have focused on the structure of cognitive risk products in adolescents—a key developmental period when several cognitive risk products have stabilized and many common psychopathologies first onset (e.g., depression) (Hankin et al., 1998).
In short, we still do not know what an optimal structure of cognitive risk products may be. A bifactor model may be a plausible, more parsimonious structure that integrates prior patterns of findings suggesting that there are both common and unique components of cognitive risks. In addition, the bifactor model may offer increased utility relative to correlated and single factor models because it can allow researchers to investigate how common and specific dimensions of cognitive risk may relate to different psychopathological outcomes.
Present Study
The main goal of the present study was to appraise if several prominent cognitive risk products may be more optimally organized with a bifactor model as compared with other structures that have been found in prior work, specifically, single- and correlated-factor models. We also evaluated the construct validity and utility of the bifactor model, as well as single- and correlated-factor models, by investigating relationships with important external validators. We investigated these questions in a community sample of adolescents aged 11 to 15 years. We expected that a bifactor model would demonstrate good fit and provide enhanced utility in associating with external validators. We investigated the construct validity of a bifactor model of cognitive risk by examining concurrent associations with depression symptoms, NA, PA, AA, and then prospective onset of depressive episodes over a 2-year follow-up. We hypothesized that c would be positively associated with depression symptoms, NA, and AA, negatively associated with PA, and prospectively predict depressive episode onsets.
Method
Participants
Participants were recruited from Montreal, Quebec, Canada, and Chicago, Illinois, USA, through ads placed in local newspapers and the greater community about a study of adolescent development. Participants were English speaking. The final sample consisted of 382 adolescents (225 girls and 157 boys) drawn from 327 families, along with one parent from each family. Participants for the current study were those that completed the cognitive risk, affect, and psychopathology measures at the initial in-person lab visit as well as follow-up diagnostic interviews. Comprehensive details of the demographic characteristics of both samples are reported in Abela and Hankin (2011). Adolescents’ ages ranged from 11 to 15 years with a median of 13 years. There were no significant differences between the samples for adolescent gender, χ2(1) = 0.42, ns; age, t(380) = 0.62, ns; grade, t(380) = 0.47, ns; highest level of education completed by mother and father, F(1, 380) = 2.10, ns and F(1, 330) = 0.62, ns, respectively; and family income, F(1, 380) = 0.24, ns. The Chicago sample had a greater proportion of ethnic minority youth, χ2 (1) = 17.36, p < .001, and youth from single-parent households, χ2(1) = 8.84, p < .01 compared with the Montreal sample.
Materials and Procedure
Participants initially completed assessments in-person at a lab visit when adolescents were between the ages of 11 and 15 years. Two research assistants met with each adolescent–parent pair. Parents completed a demographics and consent form for themselves and their child; the adolescent completed an assent form. A research assistant verbally administered all questionnaires described in the following sections, while the adolescent followed along and responded to questions using her/his/their own copy. A trained diagnostician interviewed the child and parent individually about the child’s current and past depressive symptoms and episode occurrence using the Schedule for Affective Disorders and Schizophrenia in School-Age Children (K-SADS; Kaufman, Birmaher, Brent, Rao, & Ryan, 1996). Telephone follow-up assessments were conducted during the 2 years following the initial assessment. At the 6-, 12-, 18-, and 24-month follow-up assessments, a diagnostician obtained information on the adolescent’s depressive symptoms during the past 6 months from both the parent and the adolescent using the K-SADS. If a parent–adolescent pair missed one of these follow-up assessments, information pertaining to that time interval was obtained in the subsequent K-SADS administration. Participants were compensated monetarily.
Child Dysfunctional Attitudes.
Nine items from the Dysfunctional Attitudes Scale (Weissman & Beck, 1978) were used to assess DA. Items are rated on a 5-point scale with higher scores indicating greater DA. These items load onto the same factor (Andrews, Lewinsohn, Hops, & Roberts, 1993) and correlate with a longer version of the scale (r = .93; Lewinsohn, Joiner, & Rohde, 2001). This scale has prospectively predicted depressive symptoms and diagnoses in adolescents (Hankin, Wetter, Cheely, & Oppenheimer, 2008; Lewinsohn et al., 2001). We obtained an alpha of .69, which is similar to prior work (e.g., α = .74; Lewinsohn et al., 2001).
Negative Inferential Style.
The Adolescent Cognitive Style Questionnaires (ACSQ; Hankin & Abramson, 2002) assesses NIS with five subscales (internal, stable, global, consequence, self). Items are scored from 1 to 7 with higher scores indicating greater NIS. This measure had nine hypothetical negative event scenarios relevant to adolescents. Participants write down one cause for each of the events and rate the degree to which the cause is internal, stable, and global; that negative consequences will follow; and that the cause indicates that the individual is deficient. The ACSQ is reliable and valid in adolescents (e.g., Calvete, 2011; Hankin & Abramson, 2002; Kindt, Kleinjan, Janssens, & Scholte, 2015; Lakdawalla, Hankin, & Mermelstein, 2007). The hopelessness theory of depression (Abramson et al., 1989) de-emphasized internal attributions in the conceptualization and measurement of NIS. Because the ACSQ was intended to assess NIS based on hopelessness theory, we used the stable, global, consequence, and self-subscales. The following alphas were obtained: .78 (stable), .83 (global), .85 (consequence), .88 (self) and .94 (total).
Rumination-Brooding.
Brooding was measured with a subset of six items from the Child Response Styles Questionnaire-Rumination Subscale (CRSQ-RS; Abela, Brozina, & Haigh, 2002) that were most reflective of brooding—the more maladaptive subcomponent of rumination (Treynor, Gonzalez, & Nolen-Hoeksema, 2003). Participants indicate how much they respond in a certain way when they are feeling sad using a 4-point scale. Higher scores indicate greater brooding. Two items from the CRSQ-RS were used that overlap with an extended version of the CRSQ (CRSQ-Ext), which has reliably measured brooding and related to depressive symptoms in children (e.g., alphas ranged from .78 to .86 over a year; Verstraeten, Bijttebier, Vasey, & Raes, 2011; Verstraeten, Vasey, Raes, & Bijttebier, 2010). Four items from the CRSQ-RS were identified as representing brooding given self-blaming and negative self-evaluative content. We obtained an alpha of .78.
Self-Criticism and Dependency.
Self-criticism and dependency were assessed using 8 items each from the self-criticism and dependency subscales of an abbreviated version of the Depressive Experiences Questionnaire for Adolescents (DEQ-A; Fichman, Koestner, & Zuroff, 1994). Participants rate the extent to which statements describe them on a 7-point scale. Higher scores indicate greater levels of self-criticism/dependency. The scale relates to depression (Fichman et al., 1994) and shows acceptable consistency (alphas ranging from .65 to .75 for self-criticism and from .70 to .82 for dependency) (Fichman et al., 1994; Kopala-Sibley, Zuroff, Hankin, & Abela, 2015). The present study obtained alphas of .61 for self-criticism and .73 for dependency.
Negative and Positive Affect.
Negative and positive affect were assessed with the Positive and Negative Affect Scale for Children (PANAS-C; Laurent et al., 1999). Participants rate how much they have experienced different feelings and emotions (e.g., sad, excited) during the past few weeks on a 5-point scale. Greater scores indicate higher levels of PA/NA. The scales relate to anxiety and depression in children (Hughes & Kendall, 2009; Laurent et al., 1999). The present study obtained alphas of .88 for both NA (15 items) and PA (12 items).
Anxious Arousal.
Anxious arousal symptoms were assessed using 10 items from the anxious arousal subscale of the Mood and Anxiety Symptom Questionnaire (MASQ; Watson & Clark, 1991) to assess somatic tension and hyperarousal symptoms (e.g., heart racing). Participants rate the extent to which they have experienced each of the symptoms over the past week on a 5-point scale. This abbreviated measure demonstrates reliability and validity in adolescents (e.g., Hankin, 2008a, 2008b; Hankin et al., 2008; Lee & Hankin, 2009). The present study obtained an alpha of .74.
Depressive Symptoms.
Depressive symptoms over the past week were assessed via the 27-item Children’s Depression Inventory (CDI; Kovacs, 1985). The CDI is the most frequently used measure of depression among adolescents and has demonstrated reliability and validity (Klein, Dougherty, & Olino, 2005). The present study obtained an alpha of .87.
Depression Diagnoses.
Depression diagnoses were measured using the Schedule for Affective Disorders and Schizophrenia for School-Age Children (K-SADS; Kaufman et al., 1996), a semistructured clinical interview that assesses Diagnostic and Statistical Manual of Mental Disorders, Fourth Edition (DSM-IV) diagnoses in children and adolescents. No other diagnoses were assessed in this study. The K-SADS was administered to a parent and adolescent individually and summary diagnoses were based on both reports. The K-SADS is the most frequently used psychiatric diagnostic interview with youth and is reliable and valid (Klein et al., 2005). In the current study, we assessed current and past histories of major depressive episodes. Diagnostic interviewers completed an intensive training program for administering the K-SADS, for assigning DSM-IV and research diagnostic criteria diagnoses, and received weekly supervision (see Technow, Hazel, Abela, & Hankin, 2015 for more details). Interrater reliability for the K-SADS, based on 20% of the sample interviews, was good (κ = .87).
Data Analytic Plan
Overview of Cognitive Risk Factor Structure Analyses.
Confirmatory factor analyses were conducted with Mplus (L. K. Muthén & Muthén, 2012) using the robust maximum likelihood estimator (MLR) given the nonnormal distributions of indicators. Factor variance was set to 1 for all models in order for item loadings to be estimated and standardized with respect to the latent factor variance (i.e., STD Standardized). For all models, “good fit” was defined as root mean square error of approximation (RMSEA) equal to or less than .06; confirmatory fit index (CFI) greater than or equal to .95; and standardized root mean square residual (SRMR) equal to or less than .08. “Acceptable fit” was defined as RMSEA equal to or less than .08, and CFI equal to or greater than .90 (Hu & Bentler, 1998, 1999). We prioritized convergence across fit indices as indicating a good model because researchers have regarded these thresholds as suggested cut-offs and have cautioned against considering them as universal rules (e.g., Chen, Curran, Bollen, Kirby, & Paxton, 2008; Hu & Bentler, 1999; Marsh, Hau, & Wen, 2004). The fit of the bifactor, single, and correlated factor models were compared using Akaike information criteria (AIC) and Bayesian information criteria (BIC) because the models were nonnested (lower values indicate better fit; Δ > 10 is considered a rough rule of thumb of nonequivalency of models; Burnham & Anderson, 2003).
Manifest indicators for cognitive risks were created by parceling items using a correlational parceling approach (Landis, Beal, & Tesluk, 2000; Rogers & Schmitt, 2004). For constructs that had multiple subscales (i.e., NIS), a facet-representative approach was utilized such that a parcel was constructed for each subscale of the construct (Kishton & Widaman, 1994; Little, Cunningham, Shahar, & Widaman, 2002; Little, Rhemtulla, Gibson, & Schoemann, 2013). Both of these approaches aim to group items together that share the highest overlapping variance and have been recommended for multidimensional constructs because what is shared among items or facets of constructs is preserved (e.g., Little et al., 2002; Little et al., 2013; Williams & O’Boyle, 2008). Parceling reduces the indicator-to-sample size ratio; thus, making the parameter estimates in the model more accurate (e.g., Little et al., 2013; Williams & O’Boyle, 2008). Item level indicators were not used because there would not be enough degrees of freedom to estimate latent factor models of external validators or associations with external validators after estimating the parameters for the full cognitive risk model.
For each of the individual cognitive risk measures, the bivariate correlations for all items within each measure were examined. The correlational parceling procedure was as follows: the two items with the highest correlation were selected for the first parcel, and the next two items with the highest correlation were grouped into the second parcel and so on. For scales that had an odd number of items, this remaining item was assigned to the parcel that it had the strongest correlation with. As just-identified models have been recommended (Little et al., 2013), we aimed to have approximately three indicators per construct. Parcel indicators were composed of two to three items. For the multifaceted measure of NIS, each manifest indicator was composed of all items within each subscale. Parcels for all models were the average of all items within the parcel. Table S1 in Supplemental Materials, available in the online version of the article, shows the items that were within each parcel for latent factors of cognitive risk.
Model development and testing consisted of two main steps. The first step examined the latent factor structure of each cognitive risk construct considered individually according to their respective theoretical conceptualizations. Each individual cognitive risk model was checked for adequate indicator loadings because weak loadings can be significant with large sample sizes. A cutoff of .30 was chosen, and indicators falling below this threshold were removed (Kline, 2010). The second step examined the fit of the bifactor model relative to single- and correlated- factor models in order to investigate if the bifactor model more optimally organizes cognitive risks relative to these alternative models. Comprehensive models of cognitive risk products were constructed that included all cognitive risk product measures across theoretical paradigms. The next sections detail the specific analytical steps and results for the individual cognitive risk factor structure analyses and the comprehensive cognitive bifactor, single factor, and correlated factor models (see Supplemental Materials, available in the online version of the article, for additional details).
Bifactor Cognitive Risk Structure Analyses.
We followed recommended, standard procedures for developing, evaluating, and refining a latent bifactor model (Caspi et al., 2014; Chen, Hayes, Carver, Laurenceau, & Zang, 2012; Chen, West, Sousa, 2006; Friedman et al., 2008; Lahey et al., 2015; Snyder et al., 2015). The bifactor model of cognitive risk included all measures of cognitive risk and included a common factor as well as the specific latent factors from part one of model testing. All indicators were initially loaded directly onto a common factor, which captures the shared variance across all manifest indicators. In addition, all indicators were also initially loaded onto their respective cognitive risk measure factors, which capture the unique variance of each measure of cognitive risk that is not accounted for by the common factor (e.g., Chen et al., 2006; Chen et al., 2012; Friedman et al., 2008; Snyder et al., 2015). Because the common factor captures the shared variance across these cognitive risk measures, the unique cognitive risk measure latent factor correlations were set to zero (Chen et al., 2006; L. K. Muthén & Muthén, 2012).
The bifactor model was initially tested and respecified based on the pattern of indicator loadings and the significance of factor variances.1 Specific factors were eliminated when indicator loadings were nonsignificant or negative for the specific factor and strong for the common factor, or if the specific factor variance was not significantly different from zero. In each of these cases, results suggest that the variance among the indicators was fully accounted for by the common factor, so the specific factor should not be considered as a distinct dimension from the common factor. This same criterion for loadings was applied to the respecification of indicator loadings on the common factor. If factor loadings for indicators were strong on a specific factor and nonsignificant or negative on the common factor, the item loadings onto the common factor were removed because this suggested that the specific factor accounted for variance among indicators that was distinct from the common factor.
The bifactor model was further evaluated with the following indices (Dueber, 2017; Rodriguez, Reise, & Haviland, 2016a, 2016b): OmegaH (ωH), which reflects the proportion of variance accounted for by the common factor after accounting for the specific factors (Reise, Bonifay, & Haviland, 2013); OmegaHS (ωHS), which reflects the proportion of variance accounted for by the specific factors after accounting for the common factor (Reise et al., 2013); percentage of uncontaminated variance (PUC), which represents the percentage of covariance terms that only reflect variance from the common factor (Dueber, 2017); construct reliability (H), which reflects the degree to which a factor is well represented by its indicators (Rodriguez, Reise, & Haviland, 2016a); factor determinancy (FD), which is the correlation between factor scores and the factors indicating if factors scores can be used; and the average relative parameter bias (ARPB), which is the difference between indicator loadings when they load onto a single latent factor relative to when they load onto a common factor (in the bifactor model), divided by the common factor loadings in the bifactor model (Rodriguez, Reise, & Haviland, 2016b).
External Validator Analyses.
To examine the construct validity of the various structural models, we examined regressions with the latent factors and concurrent associations with depressive symptoms (CDI), negative affect (NA; PANAS-C), positive affect (PA; PANAS-C), and anxious arousal symptoms (MASQ) as well as prospective relationships with clinical depression onset over 2 years controlling for history of clinical depression at baseline (K-SADS). External validator measures of depression symptoms, NA, PA, and AA were examined as latent factors with parceled indicators using the same procedure explained earlier for the cognitive risk models. The external validator measure of onset of depressive episodes occurring over the 24-month follow-up and the control variable of history of depression at baseline were categorical, binary (i.e., 0 = no, 1 = yes), and manifest. Separate regressions were conducted for each external validator. Regressions were conducted in an SEM framework with Mplus (L. K. Muthén & Muthén, 2012) using MLR given the nonnormal distributions of indicators. Each external validator (latent or manifest) was regressed on each latent dimensional model of cognitive risk products. For cognitive risk models that had multiple dimensions (bifactor, correlated factors), all dimensions were simultaneously included as predictors of each external validator. Given that rates of internalizing psychopathology increase throughout adolescence and that gender differences in some cognitive risks and depression emerge in adolescence (Hankin & Abramson, 2001), gender and age were controlled for in all regression analyses. The two-stage false discovery rate (Benjamini, Krieger, & Yekutieli, 2006) was used to hold the family-wise error rate at p = .05 across all regression analyses.
Results
Descriptive statistics for manifest measures of cognitive risk, internalizing outcomes and demographics are provided in Table 1. Correlations between individual manifest measures of cognitive risks were all significant and ranged from r = .14 to r = .44. Correlations between individual manifest measures of cognitive risks and internalizing outcomes were predominantly significant and ranged from r = .11 to r = .50 (Table 2).
Table 1.
Descriptive Statistics for Manifest Measures of Cognitive Risk, External Validators, and Control Variables.
| Variable | N | Range | M | SD |
|---|---|---|---|---|
| CDAS | 372 | 9–40 | 21.78 | 5.91 |
| ACSQ | 367 | 36–211 | 86.20 | 29.27 |
| DEQ-A, SC | 325 | 8–50 | 26.78 | 7.47 |
| DEQ-A, D | 322 | 8–56 | 32.05 | 8.75 |
| CRSQ, Brood | 367 | 0–18 | 5.20 | 3.70 |
| CDI | 370 | 0–35 | 8.85 | 6.58 |
| MASQ, AA | 320 | 0–25 | 10.11 | 5.14 |
| PANAS-C, NA | 378 | 15–63 | 28.54 | 9.43 |
| PANAS-C, PA | 378 | 17–60 | 44.49 | 8.30 |
| KSADS, Dep. Dx Onset | 369 | 0–1 | 0.27 | 0.45 |
| KSADS, Dep. Dx History | 382 | 0–1 | 0.12 | 0.32 |
| Age | 380 | 10–15 | 12.57 | 1.11 |
| Gender | 379 | 0–1 | 0.59 | 0.49 |
Note. CDAS = Child Dysfunctional Attitudes Scale; ACSQ = Adolescent Cognitive Style Questionnaire; DEQ-A, SC = Depressive Experiences Questionnaire, Self-Criticism subscale; DEQ-A, D = Depressive Experiences Questionnaire, Dependency subscale; CRSQ, Brood = Child Response Styles Questionnaire, brooding items; CDI = Children’s Depression Inventory; MASQ, AA = Mood and Anxiety Symptom Questionnaire, anxious arousal items; PANAS-C, NA = Positive and Negative Affect Scale for Children, Negative Affectivity subscale; PANAS-C, PA = Positive and Negative Affect Scale for Children, Positive Affectivity subscale; KSADS, Dep. Dx Onset = Schedule for Affective Disorders and Schizophrenia for School-Age Children, major depression diagnosis onset anytime over 2 year follow-up; KSADS, Dep. Dx History = Schedule for Affective Disorders and Schizophrenia for School-Age Children, lifetime history of major depression diagnosis at baseline.
Table 2.
Correlations Among Manifest Measures of Cognitive Risk, External Validators, and Control Variables.
| Variable | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1. CDAS | — | ||||||||||||
| 2. ACSQ | 0.33 | — | |||||||||||
| 3. DEQ-A, SC | 0.26 | 0.44 | — | ||||||||||
| 4. DEQ-A, D | 0.14 | 0.25 | 0.44 | — | |||||||||
| 5. CRSQ, Brood | 0.22 | 0.38 | 0.39 | 0.41 | — | ||||||||
| 6. CDI | 0.17 | 0.41 | 0.50 | 0.24 | 0.43 | — | |||||||
| 7. MASQ-AA | 0.01 | 0.24 | 0.38 | 0.19 | 0.22 | 0.31 | — | ||||||
| 8. PANAS-C, NA | 0.22 | 0.35 | 0.40 | 0.37 | 0.45 | 0.68 | 0.24 | — | |||||
| 9. PANAS-C, PA | −0.10 | −0.22 | −0.31 | −0.04 | −0.19 | −0.60 | −0.27 | −0.42 | — | ||||
| 10. KSADS, Dep. Dx. Onset | −0.06 | 0.18 | 0.24 | 0.22 | 0.20 | 0.33 | 0.20 | 0.28 | −0.19 | — | |||
| 11. KSADS, Dep. Dx. History | −0.02 | 0.11 | 0.08 | 0.06 | 0.19 | 0.21 | 0.07 | 0.18 | −0.16 | 0.24 | — | ||
| 12. Age | −0.03 | 0.08 | 0.00 | 0.13 | 0.12 | 0.08 | 0.13 | 0.06 | −0.08 | 0.13 | 0.03 | — | |
| 13. Gender | −0.12 | −0.07 | −0.04 | 0.19 | 0.03 | 0.08 | 0.23 | 0.18 | 0.00 | 0.19 | 0.08 | 0.06 | — |
Note. CDAS = Child Dysfunctional Attitudes Scale; ACSQ = Adolescent Cognitive Style Questionnaire; DEQ-A, SC = Depressive Experiences Questionnaire, Self-Criticism subscale; DEQ-A, D = Depressive Experiences Questionnaire, Dependency subscale; CRSQ, Brood = Child Response Styles Questionnaire, brooding items; CDI = Children’s Depression Inventory; MASQ, AA = Mood and Anxiety Symptom Questionnaire, Anxious Arousal items; PANAS-C, NA = Positive and Negative Affect Scale for Children, Negative Affectivity subscale; PANAS-C, PA = Positive and Negative Affect Scale for Children, Positive Affectivity subscale; KSADS, Dep. Dx Onset = Schedule for Affective Disorders and Schizophrenia for School-Age Children, major depression diagnosis onset anytime over 2 year follow-up; KSADS, Dep. Dx History = Schedule for Affective Disorders and Schizophrenia for School-Age Children, lifetime history of major depression diagnosis at baseline. rs > .10 are significant at p < .05. rs > .14 are significant at p < .01.
Individual Measurement Models for Cognitive Risks
Single factor models were created for DA, NIS, self-criticism, dependency, and brooding. The DA model had four indicators and good fit by CFI, RMSEA, and SRMR (CFI = .99, RMSEA = .03, SRMR = .02). The NIS model had four indicators and good fit by CFI, SRMR and nearly acceptable fit by RMSEA (CFI = .99, SRMR = .02, RMSEA = .096). The dependency model had four indicators and good fit by CFI, SRMR and nearly acceptable fit by RMSEA (CFI = .97, SRMR = .03, RMSEA = .09). The self-criticism and brooding models were just-identified (three indicators), so model fit statistics cannot be computed. All factor loadings for models were adequate (see Table S1 in Supplemental Materials, available in the online version of the article, for more details).
Comprehensive Cognitive Risk Structure Models
Bifactor Model.
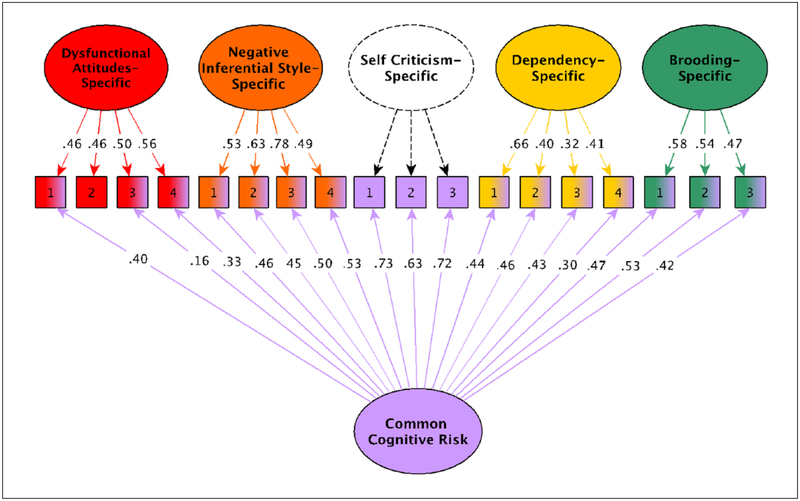
The initial bifactor model of cognitive risk products included a common cognitive risk factor and five specific factors for DA, NIS, self-criticism, dependency and brooding. There were 18 indicators in total. The initial bifactor model had good fit by RMSEA, SRMR, and acceptable fit by CFI (RMSEA = .05, SRMR = .05, CFI = .93). There was no significant variance associated with the specific self-criticism factor and loadings onto this factor were nonsignificant. In contrast, indicators of self-criticism loaded significantly and strongly onto the common cognitive risk. This suggested that the variance across indicators of self-criticism was accounted for by the common cognitive risk factor and not the specific self-criticism dimension. Thus, the specific self-criticism factor was eliminated. Examination of factor loadings revealed that one indicator of DA did not have a significant loading for the common cognitive risk factor but did have a significant loading for the specific DA factor suggesting that the variance for this indicator was not accounted for by the common factor. This nonsignificant item loading for the common factor was removed. All other factors had significant variance and all other indicators had significant factor loadings (Figure 1; see Table S2 in supplemental materials, available in the online version of the article, for more details).
Figure 1. Bifactor model for cognitive risks.
Note. The common cognitive risk factor captures what is shared across all cognitive risk indicators, whereas each specific factor captures what is unique to the indicators in that measure. Numbers in the boxes are indicator numbers for parcels composed of two or more items from each cognitive risk measure. Numbers on straight arrows are standardized factor loadings. The specific self-criticism latent factor has a dashed outline and loadings because it was subsumed by the common cognitive risk factor.
With these respecifications, model fit was good by RMSEA and SRMR, and acceptable by CFI (RMSEA = .05, SRMR = .05, CFI = .94) (see Table 3). Additional bifactor model measurement indices provided added support for the measurement model. The percentage of reliable variance in total scores attributed to individual differences in the common factor (ωH) was 81%, and the percentage of reliable variance due to specific factors (ωHS) was 79% for specific DA; 53% for specific brooding; 52% for specific dependency, and 60% for specific NIS. This suggests that the variance in scores across cognitive risk measures predominantly and most reliably reflects the common factor. Similarly, the PUC showed that 86% of indicator covariances reflect common factor variance. The ARPB was 22%, which exceeds the 15% threshold (B. Muthén, Kaplan, & Hollis, 1987), suggesting that it would not be appropriate to treat these cognitive risk measures as purely unidimensional (Rodriguez et al., 2016b). In terms of construct reliability, H was .86, .57, .54, .56, and .75 for the common factor, specific DA, specific brooding, specific dependency, and specific NIS, respectively. According to the .70 criterion (Hancock & Mueller, 2001), the common and specific NIS factors are well represented by the indicators and are most likely to replicate across samples, whereas the specific DA, brooding, and dependency factors may need more or better indicators (Rodriguez et al., 2016a, 2016b). FD scores were .98, .97, .95, .95, and .98 for the common factor, specific DA, specific brooding, specific dependency, and specific NIS, respectively. According to the FD > .90 criterion (Gorsuch, 1983), all factor scores of the cognitive risk dimensions may be utilized.
Table 3.
Full Cognitive Risk Model Fit Statistics.
| Model | χ2 (df) | S-B scaling factor | CFI | RMSEA (90% CI) | SRMR | AIC | BIC |
|---|---|---|---|---|---|---|---|
| 1 Factor | 828.82 (135)* | 1.06 | .61 | .12 (.II-.I2) | .10 | 17751.85 | 17964.62 |
| 1 Factor hierarchical | 266.08 (130)* | 1.07 | .92 | .05 (.04-.06) | .06 | 17165.76 | 17398.23 |
| 5 Factor correlated | 242.39 (125)* | 1.06 | .94 | .05 (.04-.06) | .05 | 17149.24 | 17401.41 |
| Common cognitive risk + Subscale-specific | 237.46 (121)* | 1.06 | .94 | .05 (.04-.06) | .05 | 17151.85 | 17419.78 |
Note. S-B = Satorra-Bentler; CFI = confirmatory fit index; RMSEA = root mean square error of approximation; SRMR = standardized root mean square residual; AIC = Akaike information criterion; BIC = Bayesian information criterion.
p < .001.
Single-Factor Model.
Two single factor models were tested that each represented the specifications of single factor models that were examined in prior work. Both models included all 18 manifest indicators across all cognitive measures (DA, NIS, self-criticism, dependency, brooding) and had adequate item loadings. The first single factor model was created by allowing all manifest indicators to load directly onto a single latent factor (e.g., see Hankin et al., 2007). Model fit was not acceptable by SRMR, RMSEA, or CFI (SRMR = .10, RMSEA = .12, CFI = .61). The second single factor model was a hierarchical model that included all five of the latent factors from each of the individual cognitive risk factor models (DA, NIS, self-criticism, dependency, brooding). Each of these individual cognitive risk latent factors then loaded onto a single higher order latent factor (e.g., see Hong & Cheung, 2015). Model fit was good by RMSEA, SRMR and acceptable by CFI (RMSEA = .05, SRMR = .06, CFI = .92).
Correlated-Factor Model.
A correlated factor model was created that included all 18 manifest indicators across all cognitive risk product measures and all five of the latent factors from each of the individual cognitive risk factor models (DA, NIS, self-criticism, dependency, brooding). Model fit was good fit by RMSEA, SRMR and acceptable by CFI (RMSEA = .05, SRMR = .05, CFI = .94). All item loadings were adequate. Correlations between latent factors were weak (r = .23, dependency and DA) to strong (r = .70, self-criticism and dependency), with all but one relationship falling in the moderate to strong range (i.e., rs > .30).
Comparing the Different Factor Models for Cognitive Risk and Measurement Invariance
Model fit of the bifactor model (AIC = 17151.85, BIC = 17419.78) was better than the single factor model (AIC = 17751.85, BIC = 17964.62; ΔAIC = 600, ΔBIC = 544.84; see Table 3). Model fit of the bifactor model was better than the hierarchical single factor model (AIC = 17165.76, BIC = 17398.23) by AIC, but was worse by BIC (ΔAIC = 13.91, ΔBIC = −21.55). Model fit of the bifactor model was similar to the correlated factor model (AIC = 17149.24, BIC = 17401.41) by AIC, but was worse by BIC (ΔAIC = −2.61, ΔBIC = −18.37). Model fit of the correlated factor model was better than the single factor hierarchical model by AIC and was similar by BIC (ΔAIC = 16.52, ΔBIC = −3.18).2 In short, the bifactor, hierarchical single, and correlated factor models all fit the data well.
Last, two sets of multiple sample confirmatory factor analyses’ were conducted to examine measurement invariance (configural [model form], metric [factor loadings], and scalar [indicator intercepts]) by gender (females vs. males) and site (Montreal vs. Chicago; Chen, Sousa, & West, 2005; Kline, 2011). Measurement invariance examines the degree to which a measurement model is psychometrically equivalent across groups and reflects the degree to which a construct has the same structure and meaning across groups. Configural invariance means that the same model structure holds across groups (i.e., the two groups have the same pattern of loadings and factor organization) and that the same factors are being measured with the same indicators. To examine configural invariance, the same factor model was estimated in each group. Metric invariance means that groups have equal factor loadings and that each manifest indicator contributes to the factor to the same degree across groups (i.e., the factors have similar meaning). At this level of invariance, the two groups have the same unit of measurement and relationships between each of the factors and external factors can be compared across the groups because one unit of change in one group would be the same as one unit change in the other. To test metric invariance, factor loadings were constrained to be equal across groups. Scalar invariance means that the origin of the scale (intercept) is the same across groups. To test scalar invariance, item intercepts were constrained to be equal across groups. Scalar invariance is necessary for comparing group means because it means that the groups have the same unit of measurement (factor loadings; metric) as well as the same origin (indicator intercept) (Chen et al., 2005).
Because chi-square difference tests can be significant with large samples even when the absolute differences between model estimates are marginal in size (Cheung & Rensvold, 2002; Meade, Johnson, & Braddy, 2008), we compared differences in model fit between unconstrained and constrained models by examining convergence across CFI and RSMEA indices such that change in CFI less than or equal to .01, and change in RMSEA less than or equal to .015 suggests measurement invariance (Chen, 2007; Cheung & Rensvold, 2002; Meade et al., 2008). Detailed measurement invariance results by gender and site for the bifactor, hierarchical single, and correlated factors models are located in the Supplemental Materials, available in the online version of the article. In brief, results suggested that the bifactor and correlated factors models were invariant across gender at the scalar level, and the hierarchical single factor model was invariant across gender at the metric level. Regarding site invariance, results suggested that the bifactor, hierarchical single, and correlated factor models were invariant at the metric level.
If researchers are interested in examining gender or geographical site differences in the relationships between cognitive risk product factors and outcomes, results suggest that any of the models (bifactor, hierarchical single, correlated factors) can be used. If researchers are interested in examining mean gender differences in these cognitive risk products, results suggest that the bifactor and correlated factor models can be utilized. If researchers are interested in examining mean gender differences for the hierarchical single factor model, or are interested in examining mean differences according to different geographical locations for any of the models (bifactor, hierarchical single, correlated factors), it is recommended that the source of potential noninvariance be examined further (e.g., by releasing factor loading constraints systematically and conducting additional model comparisons) until partial scalar model invariance is achieved (Putnick & Bornstein, 2016). As these invariance results did not show consistent and demonstrable problems across gender or sites, we used the data from all youth (both genders; both sites) to have maximal statistical power to provide well estimated effect sizes for relations with various external validators (i.e., internalizing outcomes) in order to evaluate the external validity and utility of these structural models by examining associations with internalizing outcomes.
External Validator Regressions
Bifactor Model.
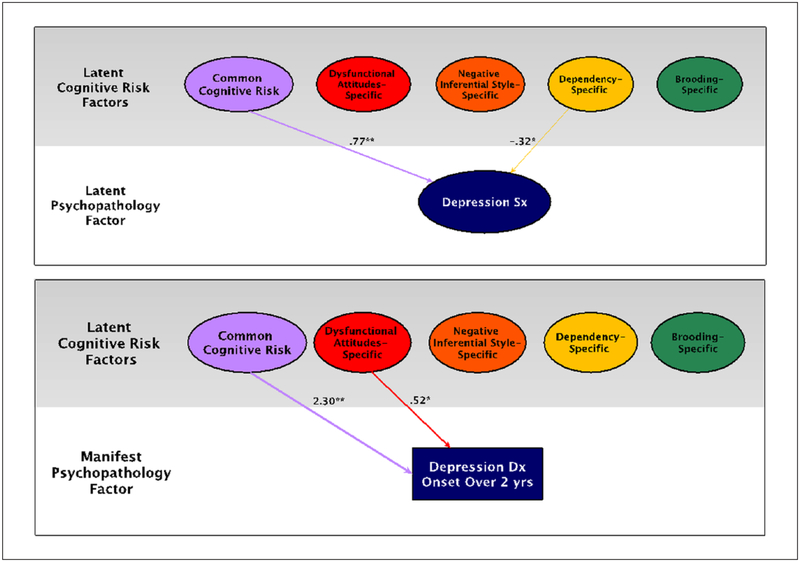
Regression results are reported in Table 4 and Table 7. Links between each dimension of cognitive risk and external validators are depicted in Figure 2 and in Supplemental Materials (Figure S1, available in the online version of the article). All analyses controlled for age and gender. Higher common cognitive risk was associated with higher depressive symptoms (β = 0.77), higher NA (β = 0.63), lower PA (β = −0.45), and higher AA (β = 0.62) (all ps < .01). Importantly, higher common cognitive risk predicted an increased likelihood of experiencing future onset of depressive episode over a 2-year follow-up even after controlling for history of depression at baseline (odds ratio = 2.30, p < .01). Significant associations between specific latent cognitive risk factors and external validators also emerged. Specific-brooding was associated with higher NA (β = 0.19, p = .01). Specific-dependency was associated with lower depression symptoms (β = −0.32) and higher PA (β = 0.29) (ps = .02). Specific-DA predicted a decreased likelihood of experiencing future onset of depression (odds ratio = 0.52, p = .01).
Table 4.
External Validator Regressions for Bifactor Model of Cognitive Risk and Internalizing Symptoms.
| DV | IV | β | b | SE (b) | Z | Uncorrected p | FDR-corrected p | R2 |
|---|---|---|---|---|---|---|---|---|
| CDI | .75 | |||||||
| C.CR | 0.77 | 1.54 | 0.35 | 4.42 | .00 | .00* | ||
| DA-Spec. | −0.15 | −0.31 | 0.18 | −1.67 | .10 | .13 | ||
| Brood.-Spec. | 0.05 | 0.10 | 0.15 | 0.67 | .51 | .48 | ||
| Depend.-Spec. | −0.32 | −0.64 | 0.25 | −2.58 | .01 | .02* | ||
| NIS-Spec. | 0.01 | 0.01 | 0.15 | 0.07 | .95 | .61 | ||
| Age | 0.02 | 0.04 | 0.08 | 0.51 | .61 | .53 | ||
| Gender | 0.13 | 0.52 | 0.21 | 2.49 | .01 | .03* | ||
| PANAS-C, NA | .46 | |||||||
| C.CR | 0.63 | 0.85 | 0.13 | 6.66 | .00 | .00* | ||
| DA-Spec. | −0.05 | −0.07 | 0.11 | −0.62 | .54 | .48 | ||
| Brood.-Spec. | 0.19 | 0.26 | 0.11 | 2.39 | .02 | .03* | ||
| Depend.-Spec. | −0.03 | −0.04 | 0.12 | −0.30 | .77 | .58 | ||
| NIS-Spec. | 0.01 | 0.01 | 0.10 | 0.13 | .89 | .60 | ||
| Age | 0.01 | 0.02 | 0.06 | 0.29 | .77 | .58 | ||
| Gender | 0.15 | 0.43 | 0.12 | 3.62 | .00 | .00* | ||
| PANAS-C, PA | .32 | |||||||
| C.CR | −0.45 | −0.55 | 0.11 | −4.84 | .00 | .00* | ||
| DA-Spec. | 0.11 | 0.14 | 0.14 | 0.98 | .33 | .34 | ||
| Brood.-Spec. | 0.10 | 0.12 | 0.11 | 1.02 | .31 | .34 | ||
| Depend.-Spec. | 0.29 | 0.36 | 0.14 | 2.55 | 0.01 | .02* | ||
| NIS-Spec. | 0.05 | 0.06 | 0.09 | 0.65 | 0.52 | .48 | ||
| Age | −0.06 | −0.07 | 0.06 | −1.15 | 0.25 | .30 | ||
| Gender | −0.02 | −0.05 | 0.13 | −0.37 | 0.71 | .56 | ||
| MASQ, AA | .44 | |||||||
| C.CR | 0.62 | 0.83 | 0.18 | 4.56 | 0.00 | .00* | ||
| DA-Spec. | 0.07 | 0.10 | 0.13 | 0.76 | 0.45 | .45 | ||
| Brood.-Spec. | −0.02 | −0.03 | 0.16 | −0.15 | 0.88 | .60 | ||
| Depend.-Spec. | 0.05 | 0.06 | 0.15 | 0.41 | 0.68 | .56 | ||
| NIS-Spec. | −0.11 | −0.15 | 0.14 | −1.08 | 0.28 | .32 | ||
| Age | 0.10 | 0.12 | 0.10 | 1.20 | 0.23 | .30 | ||
| Gender | 0.18 | 0.48 | 0.20 | 2.41 | 0.02 | .03* | ||
Note. N = 380. DV = dependent variable; IV = independent variable; C.CR = common cognitive risk dimension; Spec. = specific dimension; DA = dysfunctional attitudes; Brood. = Brooding; Depend. = Dependency; FDR = false discovery rate; NIS = Negative inferential style; CDI = Children’s Depression Inventory; MASQ, AA = Mood and Anxiety Symptom Questionnaire, Anxious arousal items; PANAS-C = Positive and Negative Affect Scale for Children; NA = Negative affectivity; PA = Positive affectivity.
p < .05 (based on the two-stage FDR-adjusted p value, or q value).
Table 7.
External Validator Logistic Regressions for the Single-Factor Hierarchical, Five-Factor Correlated, and Bifactor Model of Cognitive Risk and Onset of Depression Diagnosis.
| Model | Variable | b | SE | Z | Odds | Uncorrected p | FDR-corrected p | R2 |
|---|---|---|---|---|---|---|---|---|
| Single-factor hierarchical | .23 | |||||||
| CR | 0.68 | 0.17 | 3.98 | 1.98 | .00 | .00* | ||
| Dep. Dx | 1.36 | 0.39 | 3.46 | 3.88 | .00 | .00* | ||
| History | ||||||||
| Age | 0.23 | 0.12 | 1.92 | 1.26 | .06 | .04* | ||
| Gender | 0.91 | 0.28 | 3.28 | 2.49 | .00 | .00* | ||
| Five-factor correlated | .29 | |||||||
| DA | −0.65 | 0.26 | −2.48 | 0.52 | .01 | .03* | ||
| Brood. | 0.07 | 0.23 | 0.29 | 1.07 | .77 | .59 | ||
| Depend. | 0.22 | 0.24 | 0.91 | 1.24 | .36 | .40 | ||
| Self Crit. | 0.90 | 0.30 | 2.98 | 2.45 | .00 | .01* | ||
| NIS | 0.13 | 0.21 | 0.63 | 1.14 | .53 | .49 | ||
| Dep. Dx | 1.38 | 0.42 | 3.32 | 3.97 | .00 | .01* | ||
| History | ||||||||
| Age | 0.25 | 0.13 | 1.92 | 1.28 | .06 | .08 | ||
| Gender | 0.85 | 0.30 | 2.84 | 2.35 | .01 | .02* | ||
| Common cognitive risk + Subscale-specific | .32 | |||||||
| C.CR | 0.83 | 0.21 | 3.96 | 2.30 | .00 | .00* | ||
| DA-Spec. | −0.65 | 0.23 | −2.86 | 0.52 | .00 | .01* | ||
| Brood.-Spec. | −0.02 | 0.20 | −0.11 | 0.98 | .91 | .60 | ||
| Depend.-Spec. | 0.13 | 0.24 | 0.54 | 1.14 | .59 | .50 | ||
| NIS-Spec. | 0.05 | 0.18 | 0.25 | 1.05 | .80 | .58 | ||
| Dep. Dx | 1.29 | 0.42 | 3.10 | 3.63 | .00 | .01* | ||
| History | ||||||||
| Age | 0.22 | 0.13 | 1.71 | 1.24 | .09 | .13 | ||
| Gender | 0.83 | 0.31 | 2.69 | 2.29 | .01 | .02* | ||
Note. N = 380. The dependent variable was the onset of a major depressive diagnosis anytime over the 2-year follow-up. CR = Cognitive risk; C.CR = Common cognitive risk dimension; Spec. = Specific dimension; DA = Dysfunctional attitudes; Brood. = Brooding; Depend. = Dependency; Self Crit. = Self-criticism. NIS = Negative inferential style; Dep. Dx. History = lifetime history of major depression diagnosis at baseline; FDR = false discovery rate.
p < .05 (based on the two-stage FDR adjusted p value, or q value).
Figure 2. Regression effects for bifactor model for cognitive risks and depression external validators.
Note. Numbers on straight arrows are standardized regression coefficients for depression symptoms (top panel) and odds ratios for depression onset (bottom panel). Different thickness of straight arrows is presented to aid visual comparison of the relative magnitude of associations between dimensions of cognitive risk and external validators.
*p < .05. **p < .01 (based on the two-stage false discovery rate [FDR]–adjusted p value, or q value).
Hierarchical Single-Factor Model.
Regression results are reported in Tables 5 and 7. All analyses controlled for age and gender. Higher cognitive risk was associated with higher depressive symptoms (β = 0.73), higher NA (β = 0.66), lower PA (β = −0.36), and higher AA (β = 0.61) (all ps < .01). Higher cognitive risk predicted an increased likelihood of experiencing future onset of depression after controlling for history of depression (odds ratio = 1.98, p < .01).
Table 5.
External Validator Regressions for the Single-Factor Hierarchical Model of Cognitive Risk and Internalizing Symptoms.
| DV | IV | β | b | SE (b) | Z | Uncorrected p | FDR-corrected p | R2 |
|---|---|---|---|---|---|---|---|---|
| CDI | .55 | |||||||
| CR | 0.73 | 1.09 | 0.16 | 6.64 | .00 | .00* | ||
| Age | 0.04 | 0.05 | 0.06 | 0.77 | .44 | .23 | ||
| Gender | 0.10 | 0.31 | 0.15 | 2.13 | .03 | .02* | ||
| PANAS-C, NA | .46 | |||||||
| CR | 0.66 | 0.90 | 0.12 | 7.42 | .00 | .00* | ||
| Age | 0.03 | 0.04 | 0.06 | 0.60 | .55 | .27 | ||
| Gender | 0.16 | 0.43 | 0.12 | 3.50 | .00 | .00* | ||
| PANAS-C, PA | .14 | |||||||
| CR | −0.36 | −0.39 | 0.09 | −4.50 | .00 | .00* | ||
| Age | −0.07 | −0.07 | 0.06 | −1.16 | .25 | .14 | ||
| Gender | 0.01 | 0.03 | 0.11 | 0.25 | .80 | .37 | ||
| MASQ, AA | .41 | |||||||
| CR | 0.61 | 0.79 | 0.15 | 5.37 | .00 | .00* | ||
| Age | 0.11 | 0.13 | 0.09 | 1.48 | .14 | .09 | ||
| Gender | 0.17 | 0.45 | 0.19 | 2.43 | .02 | .01* | ||
Note. N = 380. DV = dependent variable; IV = independent variable; CR = Cognitive risk; CDI = Children’s Depression Inventory; MASQ, AA = Mood and Anxiety Symptom Questionnaire, Anxious arousal items; PANAS-C = Positive and Negative Affect Scale for Children; NA = Negative affectivity; PA = Positive affectivity; FDR = false discovery rate.
p < .05 (based on the two-stage FDR-adjusted p value, or q value)
Correlated Five-Factor Model.
Regression results are reported in Tables 6 and 7. All analyses controlled for age and gender. Higher brooding was associated with higher depressive symptoms (β = 0.26, p =.04) and higher NA (β = 0.34, p = .01). Higher dependency was associated with lower depressive symptoms (β = −0.54, p =.02) and higher PA (β = 0.46, p =.01). Higher self-criticism was associated with higher depressive symptoms (β = 0.99, p < .01), higher NA (β = 0.48, p = .02), and lower PA (β = −0.75, p =.01). Higher self-criticism predicted a higher likelihood of experiencing future depression onset (odds ratio = 2.45, p = .01), whereas higher DA predicted a lower likelihood of experiencing future depression onset (odds ratio = 0.52, p = .03) after controlling for history of depression at baseline.
Table 6.
External Validator Regressions for the Five-Factor Correlated Model of Cognitive Risk and Internalizing Symptoms.
| DV | IV | β | b | SE (b) | Z | Uncorrected p | FDR-corrected p | R2 |
|---|---|---|---|---|---|---|---|---|
| CDI | .70 | |||||||
| DA | −0.11 | −0.20 | 0.19 | −1.04 | .30 | .36 | ||
| Brood. | 0.26 | 0.48 | 0.22 | 2.21 | .03 | .04* | ||
| Depend. | −0.54 | −1.00 | 0.37 | −2.69 | .01 | .02* | ||
| Self Crit. | 0.99 | 1.83 | 0.51 | 3.61 | .00 | .00* | ||
| NIS | 0.01 | 0.01 | 0.18 | 0.07 | .95 | .63 | ||
| Age | 0.05 | 0.08 | 0.07 | 1.06 | .29 | .36 | ||
| Gender | 0.14 | 0.51 | 0.19 | 2.72 | .01 | .02* | ||
| PANAS-C, NA | .45 | |||||||
| DA | −0.03 | −0.04 | 0.13 | −0.28 | .78 | .59 | ||
| Brood. | 0.34 | 0.45 | 0.15 | 3.04 | .00 | .01* | ||
| Depend. | −0.13 | −0.17 | 0.19 | −0.91 | .37 | .40 | ||
| Self Crit. | 0.48 | 0.65 | 0.25 | 2.60 | .01 | .02* | ||
| NIS | 0.01 | 0.02 | 0.12 | 0.14 | .89 | .63 | ||
| Age | 0.03 | 0.03 | 0.06 | 0.52 | .60 | .52 | ||
| Gender | 0.16 | 0.44 | 0.12 | 3.69 | .00 | .00* | ||
| PANAS-C, PA | .27 | |||||||
| DA | 0.02 | 0.02 | 0.12 | 0.18 | .86 | .63 | ||
| Brood. | −0.04 | −0.05 | 0.14 | −0.33 | .74 | .59 | ||
| Depend. | 0.46 | 0.54 | 0.21 | 2.53 | .01 | .02* | ||
| Self Crit. | −0.75 | −0.88 | 0.26 | −3.43 | .00 | .01* | ||
| NIS | 0.07 | 0.08 | 0.12 | 0.65 | .52 | .49 | ||
| Age | −0.09 | −0.09 | 0.06 | −1.50 | .14 | .19 | ||
| Gender | −0.03 | −0.07 | 0.12 | −0.57 | .57 | .51 | ||
| MASQ, AA | .41 | |||||||
| DA | 0.10 | 0.13 | 0.16 | 0.80 | .43 | .43 | ||
| Brood. | 0.05 | 0.07 | 0.20 | 0.32 | .75 | .59 | ||
| Depend. | 0.02 | 0.03 | 0.25 | 0.11 | .91 | .63 | ||
| Self Crit. | 0.56 | 0.73 | 0.34 | 2.13 | .03 | .05 | ||
| NIS | −0.10 | −0.14 | 0.16 | −0.84 | .40 | .42 | ||
| Age | 0.11 | 0.13 | 0.10 | 1.34 | .18 | .24 | ||
| Gender | 0.18 | 0.47 | 0.20 | 2.39 | .02 | .03* | ||
Note. N = 380. DV = dependent variable; IV = independent variable; DA = Dysfunctional attitudes; Brood. = Brooding; Depend. = Dependency; Self Crit. = Self-criticism; NIS = Negative inferential style; CDI = Children’s Depression Inventory; MASQ, AA = Mood and Anxiety Symptom Questionnaire, Anxious arousal items; PANAS-C = Positive and Negative Affect Scale for Children; NA = Negative affectivity; PA = Positive affectivity; FDR = false discovery rate.
p < .05 (based on the two-stage FDR-adjusted p value, or q value).
Discussion
The present study examined the validity and utility of a bifactor model of cognitive risk products using key constructs from several prominent theoretical paradigms, including Beck’s theory (dysfunctional attitudes), hopelessness theory (negative inferential style), Blatt’s personality theory (self-criticism, dependency), and response styles theory (rumination-brooding). Results indicated that the latent bifactor model, as well as the hierarchical single factor and correlated factor models, exhibited good fit. The bifactor model consisted of a common cognitive risk factor (c) as well as multiple specific cognitive risk dimensions. The construct validity of c was demonstrated with links to internalizing outcomes that were in line with prior literature and predictions. The usefulness of the bifactor model was demonstrated by examining patterns of relationships to internalizing outcomes across the three structural models. Our results suggest that the links to internalizing outcomes that were found for both the hierarchical single factor and correlated factor models were predominantly captured by the bifactor model. Importantly, the latent bifactor model represented a more parsimonious pattern of relations between dimensions of cognitive risk and internalizing outcomes as compared with the traditional, widely used analytical approach of examining these cognitive risk products independently using manifest measures. Below we discuss the main insights from the study regarding the structure and organization of cognitive risk products, the relationship of the latent bifactor model of cognitive risk to internalizing outcomes, and suggested directions for future research.
Structure of Cognitive Risks
Analyses comparing the fit of the bifactor model to two single latent factor (single factor and hierarchical single factor), and correlated latent factor models showed that the latent bifactor, hierarchical single, and correlated factor models all fit the data well. However, model fit alone is not sufficient to justify the use of a particular model (Bonifay, Lane & Reise, 2017; Snyder & Hankin, 2017). It is important for researchers to consider which structural model is most well suited for their research question and purpose. A key advantage of the bifactor model is that it allows for common and unique variance of cognitive risks to be organized and then these dimensions can be examined in relationship to outcomes. Thus, if researchers are interested in examining whether common and unique aspects of cognitive risk products are relatively broadly or specifically related to different forms of psychopathology, the bifactor model would be most appropriate. In contrast, if researchers are interested in examining how common or unique aspects of cognitive risk products relate to outcomes, then a hierarchical single factor or correlated factor model could be used, respectively.
The bifactor model consisted of a common cognitive risk factor (c) as well as specific cognitive risk dimensions for measures of dysfunctional attitudes, negative inferential style, dependency, and brooding. C can be thought of as accounting for what is shared across cognitive risk measures or the endorsement of a wide span of items across scales. On the other hand, specific cognitive risk factors reflect unique variance of cognitive risk measures or patterns of endorsement for specific subscales that are not accounted for by c. These results align with and reconcile prior ostensibly mixed findings supporting both a single factor (e.g., Hong & Cheung, 2015) and correlated factor structure (e.g., Adams et al., 2007; Hankin et al., 2007) and indicate that, despite their origins in distinct theoretical paradigms, cognitive risks share substantial overlap and have some unique components. All measures of cognitive risk products loaded onto the c factor, suggesting that it reflects underlying themes across cognitive risks. This finding also overlaps with prior work that found a “common core” of prominent cognitive risk products (Hong & Cheung, 2015).
Examination of factor loadings onto the c factor provides insight into the possible nature of c. Variance across selfcriticism indicators was fully accounted for by c. The strongest factor loadings onto c were for self-criticism, brooding on negative-self evaluative content (e.g., “There must be something wrong with me or I wouldn’t feel this way”) and negative inferential style. This suggests that some core features of c could be a tendency to hold negative self-evaluations and a pessimistic view of the future, to experience hopelessness, and to dwell on negative self-focused content (Abramson et al., 1989; Blatt, 1974; Nolen-Hoeksema & Morrow, 1991). The next strongest loadings onto c were for dependency and dysfunctional attitudes indicators, which reflected relational concerns, and needing approval from others (Beck, 1976; Blatt, 1974).3
Links Between Cognitive Risks and Internalizing Outcomes
The bifactor model of cognitive risk revealed a clear and theoretically useful pattern of associations between common and specific dimensions of cognitive risk and internalizing outcomes. The value of using a latent bifactor model to structure cognitive vulnerabilities can be seen by comparing the effect sizes for relations between manifest cognitive risks and internalizing outcomes with the effect sizes for relations between the latent c and unique cognitive risk dimensions and internalizing outcomes. Using traditional manifest measures, correlations between individual manifest measures of cognitive risk products and depression diagnosis onset, NA, PA, and AA reveal a multitude of weak to moderate associations that do not have as large as an effect size as relations with the latent c factor. The c factor emerged as a particularly potent and consistent predictor of all internalizing problems. A direct comparison of effect sizes of correlations with c relative to average correlations with manifest cognitive risk measures illustrates that c is more strongly associated with internalizing outcomes for depression symptoms (r = .75 for c vs. average r = .35 for manifest risks), AA (r = .62 for c vs. average r = .25 for manifest risks), NA (r = .65 for c vs. average r = .36 for manifest risks), and PA (r = −.40 for c vs. average r = −.19 for manifest risks). These findings for manifest cognitive risks, including their effect size, are consistent with prior literature (e.g., see Hankin, Snyder, & Gulley, 2016 for a review). At the same time, relationships between internalizing problems and most unique cognitive factors, when identified via the bifactor model, either decreased in size or did not significantly differ from zero (Table 2). Thus, in contrast to the traditional approach of examining cognitive risk products independently in relationship to outcomes using manifest measures, the latent bifactor model of cognitive risk greatly simplifies and refines the pattern of associations with internalizing outcomes. Finally, these results suggest that the c factor accounts for the transdiagnostic nature of several cognitive risks in relating to internalizing problems (cf., Hankin, Snyder, Gulley, Schweizer, et al., 2016) given that links with depression symptoms and diagnosis, as well as associations with broad dimensions associated with internalizing disorders (negative affectivity, positive affectivity, anxious arousal) were largely driven by c.
In addition to c, specific cognitive risk dimensions were also significantly related to external validators, though associations were sparse and varied depending on the specific cognitive risk factor and the outcome. Examination of links between specific dimensions and outcomes yielded two important insights. First, specific aspects of cognitive risk appear to have varying degrees of strength and specificity in relation to different psychopathological outcomes, which helps to clarify the extent to which cognitive risk products are transdiagnostic or specific to different forms of internalizing psychopathology. For instance, the brooding-specific factor was associated with higher NA, which is consistent with previous evidence linking brooding to depression and internalizing problems more broadly (e.g., Holm-Denoma & Hankin, 2010; McLaughlin & Nolen-Hoeksema, 2011; Selby et al., 2008). Second, two theoretically intriguing links were revealed, both of which were also observed with the correlated factor model. The dependency-specific factor was associated concurrently with lower depression symptoms and higher positive affect, and the dysfunctional attitudes-specific factor was associated with a lower likelihood of experiencing a depressive episode over the 2-year follow-up.
Like many psychosocial risks, dependency and DA are a heterogeneous admixture that appear to include both maladaptive and adaptive elements (e.g., Haeffel et al., 2003; Zuroff, Mongrain, & Santor, 2004). Dependency encompasses negative themes of loneliness and fears of abandonment, but also heightened concern for being close to others, which may have positive effects in some cases. Although dependency is related to depression (Fichman et al., 1994), negative life events (Shahar & Priel, 2003) and interpersonal problems (Fichman et al., 1994), it is also associated with agreeableness and support seeking (Zuroff & Fitzpatrick, 1995), higher perceived social support (Mongrain, 1998; Priel & Shahar, 2000), intimacy in close relationships (Fichman et al., 1994), and positive life events (Shahar & Priel, 2003). Similarly, DA are thought to reflect rigid rules of living involving perfectionism, performance, and contingencies of self-worth (Beck, Rush, Shaw, & Emery, 1979). However, some DA, such as perfectionism, may be adaptive when occurring in the context of high self-esteem, ability, or efficacy (Abramson et al., 2002; Bardone, Vohs, Abramson, Heatherton, & Joiner, 2000). Thus, our results suggest the possibility that c may capture those maladaptive aspects of dependency and DA that are shared across cognitive risks; this allows the unique remaining variance in the specific dependency and DA factors to reflect the components of these constructs tapping potentially adaptive functions—the motivation to invest in and seek social support in the case of dependency (Hokanson & Butler, 1992), or striving to meet high standards in the case of DA (Bardone et al., 2000). In other words, when the negative aspects of dependency and DA are included in the variance in c, the remaining unique variance can be revealed in a purer manner.
Comparison of Links to Internalizing Outcomes Across Models.
Examination of the patterns of findings across the bifactor, hierarchical single, and the correlated factor models suggests that the bifactor model represented the main findings that emerged for both the hierarchical single factor and correlated factor models. As such, the bifactor model appears to demonstrate incremental utility by its combining, in one model, the majority of the external validator results of the two alternative models. The relationships found for c and the hierarchical single factor closely paralleled one another in magnitude and direction.4 The bifactor model similarly replicated the main patterns of findings identified with the correlated factor model. Across both the bifactor and correlated factors models, similar relations with validators emerged for dimensions tapping self-criticism (c and self-criticism factors); dysfunctional attitudes (specific-DA and DA factors); dependency (specific-dependency and dependency factors); and brooding (specific-brooding and brooding factors).5 In other words, results suggest that c corresponds to the hierarchical single factor, whereas the specific dimensions of the bifactor model generally resemble the dimensions in the correlated factor model. The bifactor model combined features of both alternative models and allowed for key links with outcomes to be identified.
Future Directions and Limitations
Not all specific dimensions in the bifactor model were related to internalizing outcomes (i.e., specific negative inferential style). We caution that this does not necessarily suggest that specific cognitive risk factors should be eliminated as they contained significant variance and could still be related to other outcomes or psychopathologies that were not assessed in the present study. In the case of NIS, it appears that associations reported in prior work linking manifest measures of NIS to internalizing problems including depression (Alloy et al., 2006; Jacobs, Reinecke, Gollan, & Kane, 2008) and PTSD (Elwood et al., 2009) may be explained by common variance in c. Future work may find important links between other external validators and specific cognitive factors.
Another key future direction for research using this latent bifactor structure of cognitive risk products is to examine connections with emerging latent factor dimensional models of psychopathology (e.g., Caspi et al., 2014; Lahey et al., 2015; Snyder, Young, & Hankin, 2016). Such research has the potential to advance our knowledge of how latent cognitive risk products might contribute to comorbidity and specificity of mental illness (see Hankin, Snyder, Gulley, Schweizer, et al., 2016). Certain aspects of cognitive risk could be generally or uniquely associated with different dimensions of psychopathology (e.g., specific internalizing, specific externalizing, p factor) or particular manifestations of psychiatric syndromes (e.g., depression). Aspects of cognitive risk that are associated with multiple psychiatric syndromes or at least one dimension of psychopathology would help to explain patterns of comorbidity. Dimensions of cognitive risk uniquely associated with particular psychiatric syndromes could help explain specificity.
Certain limitations provide avenues for future research. First, our measures of cognitive risk focused on a subset of prominent cognitive risk product constructs that have primarily been studied in relation to depression. Future work should examine if a bifactor model of cognitive risk organizes a wider breadth of cognitive risk products including, for example, fear of negative evaluation and intolerance of uncertainty, which have traditionally been studied in relation to anxiety (Hong & Cheung, 2015). Second, our measure of self-criticism had lower reliability than is typically recommended. However, loadings for self-criticism indicators were adequate when represented as a latent factor suggesting that error variance captured at a manifest level was likely reduced when modeled on a latent level.6 Third, the specific brooding, DA, and dependency dimensions in the bifactor model had lower reliability. Thus, it will be important for future work to utilize more indicators for these constructs. Fourth, we used self-reports to assess cognitive risks. Self-report methods have consistently demonstrated validity and utility for predicting mental health outcomes and understanding risk processes (Haeffel & Howard, 2009; Samuel, Suzuki, & Griffin, 2016), including for cognitive risks. Still, it will be important for future work to utilize multiple methods across units of analysis (e.g., behavioral tasks) as part of Campbell and Fiske’s (1959) multitrait–multimethod matrix to improve the assessment of construct validity of the bifactor model of cognitive risk. For instance, including measures of attention biases for emotional information (e.g., Shechner et al., 2013) or negative self-referential memory biases (e.g., Taylor & Ingram, 1999) could provide additional information about cognitive risk processes that is not captured by the self-report measures of cognitive risk products that were used in present study (e.g., Kelvin, Goodyer, Teasdale, & Brechin, 1999).
Last, to further examine the validity and generalizability of the current bifactor model, future work should examine replicability in other samples including different age groups and investigate model stability and change over the life span. A recent prospective study found that a single latent factor model of cognitive risk (akin to the hierarchical single latent factor model in the present study) exhibited a stable trajectory across middle childhood in a community sample (Hong, Lee, Tsai, & Tan, 2017). This suggests that c exhibits stability starting in middle childhood; this has yet to be investigated.
Conclusion
Over the past several decades, multiple influential cognitive risk paradigms for psychopathology have been proposed, and key cognitive risk products from these models have been examined independently in relation to psychopathological problems, particularly internalizing disorders. The bifactor modeling approach for examining the organization of constructs has grown in prominence within clinical psychology (e.g., Caspi et al., 2014). Given concerns regarding such bifactor models (e.g., Bonifay et al., 2017), we did not solely rely on model fit indices to evaluate the bifactor model. We also incorporated additional suggested statistics for examining its psychometric properties (Rodriguez et al., 2016a, 2016b) and examined construct validity via patterns with external validators (Cronbach & Meehl, 1955). The present study showed that, rather than considering these cognitive risk products as either entirely distinct or overlapping, they can be structured with a bifactor model, which includes a common cognitive risk factor (shared variance), or c, as well as several specific cognitive risk dimensions (unique variance). C appears to account for the transdiagnostic nature of multiple cognitive risks and reflects their shared essence. The hierarchical single factor model and the correlated factor model also fit the data well and demonstrated links to external validators. This study’s evaluation of structural models to organize cognitive risk products can inform which model may be optimally matched to specific investigators’ questions regarding assessment of cognitive risks in psychopathology.
Supplementary Material
Acknowledgments
We thank John R. Z. Abela for making significant contributions to this research before his untimely death.
Funding
The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: The research reported in this article was supported by research grants from the Social Sciences and Research Council of Canada and the National Alliance for Research on Schizophrenia and Depression awarded to John R. Z. Abela, by research grants from the National Institute of Mental Health (R03-MH 066845) and the American Foundation for Suicide Prevention awarded to Benjamin L. Hankin, and National Institute of Mental Health Grant 5 R01 MH077195 awarded to Benjamin L. Hankin.
Footnotes
Declaration of Conflicting Interests
The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
The significance of item loadings was tested by setting the factor variance to 1. The significance of factor variances was tested by setting the first item loading to 1. Model fit remains constant across both of these parameterizations.
The AIC and BIC model comparisons were incongruent because the BIC penalizes model complexity more heavily than the AIC. Thus, because the bifactor model has more parameters than both the hierarchical single and correlated factor model, the BIC index for the bifactor model was penalized more heavily than for the alternative models.
Standardized factor loadings onto c ranged from .42 to .73 for self-criticism, brooding on negative-self evaluative content and NIS indicators; and ranged from .33 to .44 for dependency and DA indicators reflecting interpersonal concerns and contingent self-worth on others’ approval (see Supplemental Materials for more details, Table S1, available in the online version of the article).
β = 0.77 and β = 0.73 for depressive symptoms; β = 0.63 and β = 0.66 for NA; β = −0.45 and β = −0.36 for PA; β = 0.62 and β = 0.61 for AA; and odds ratios were 2.30 and 1.98 for predicting onset of depressive episodes over 2 years, for c and hierarchical single factor, respectively.
The self-criticism factor (correlated factor model) paralleled the majority of findings that emerged for c and internalizing outcomes (i.e., both factors related to higher depression symptoms and likelihood of depression onset, higher NA, and lower PA). Dimensions tapping DA predicted lower likelihood for depression onset in the correlated factor model (DA factor) and the bifactor model (specific-DA factor). Dimensions tapping dependency related to lower depression symptoms and higher PA in the correlated factor model (dependency factor) and the bifactor model (specific-dependency factor). Dimensions tapping brooding related to higher NA in the correlated factor model (brooding factor) and the bifactor model (specific-brooding).
In the single factor model for self-criticism, all standardized factor loadings were significant and were .72 for Indicator 1, .66 for Indicator 2, and .71 for Indicator 3 (see Supplemental Materials, Table S1, available in the online version of the article, for more details).
Supplemental Material
Supplemental material for this article is available online.
References
- Abela JRZ, Brozina K, & Haigh EP (2002). An examination of the response styles theory of depression in third- and seventh-grade children: A short-term longitudinal study. Journal of Abnormal Child Psychology, 30, 515–527. doi: 10.1023/A:1019873015594 [DOI] [PubMed] [Google Scholar]
- Abela JRZ, & Hankin BL (2008). Handbook of depression in children and adolescents. New York, NY: Guilford Press. [Google Scholar]
- Abela JRZ, & Hankin BL (2011). Rumination as a vulnerability factor to depression during the transition from early to middle adolescence: A multiwave longitudinal study. Journal of Abnormal Psychology, 120, 259–271. doi: 10.1037/a0022796 [DOI] [PubMed] [Google Scholar]
- Abramson LY, Alloy LB, Hankin BL, Haeffel GJ, MacCoon DG, & Gibb BE (2002). Cognitive vulnerability-stress models of depression in a self-regulatory and psychobiological context In Gotlib IH & Hammen CL (Eds.), Handbook of depression (pp. 268–294). New York, NY: Guilford Press. [Google Scholar]
- Abramson LY, Metalsky GI, & Alloy LB (1989). Hopelessness depression: A theory-based subtype of depression. Psychological Review, 96, 358–372. [Google Scholar]
- Adams P, Abela JR, & Hankin BL (2007). Factorial categorization of depression-related constructs in early adolescents. Journal of Cognitive Psychotherapy, 21, 123–139. doi: 10.1891/088983907780851540 [DOI] [Google Scholar]
- Alloy LB, Abramson LY, Hogan ME, Whitehouse WG, Rose DT, Robinson MS, … Lapkin JB (2000). The Temple-Wisconsin Cognitive Vulnerability to Depression Project: Lifetime history of axis I psychopathology in individuals at high and low cognitive risk for depression. Journal of Abnormal Psychology, 109, 403. doi: 10.1037/0021-843X.109.3.403 [DOI] [PubMed] [Google Scholar]
- Alloy LB, Abramson LY, Whitehouse WG, Hogan ME, Panzarella C, & Rose DT (2006). Prospective incidence of first onsets and recurrences of depression in individuals at high and low cognitive risk for depression. Journal of Abnormal Psychology, 115, 145–156. doi: 10.1037/0021-843X.115.1.145 [DOI] [PubMed] [Google Scholar]
- Alloy LB, Black SK, Young ME, Goldstein KE, Shapero BG, Stange JP, … Abramson LY (2012). Cognitive vulnerabilities and depression versus other psychopathology symptoms and diagnoses in early adolescence. Journal of Clinical Child & Adolescent Psychology, 41, 539–560. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andrews JA, Lewinsohn PM, Hops H, & Roberts RE (1993). Psychometric properties of scales for the measurement of psychosocial variables associated with depression in adolescence. Psychological Reports, 73, 1019–1046. doi: 10.2466/pr0.1993.73.3.1019 [DOI] [PubMed] [Google Scholar]
- Bardone AM, Vohs KD, Abramson LY, Heatherton TF, & Joiner TE (2000). The confluence of perfectionism, body dissatisfaction, and low self-esteem predicts bulimic symptoms: Clinical implications. Behavior Therapy, 31, 265–280. [Google Scholar]
- Beck AT (1976). Cognitive therapy and the emotional disorders. New York, NY: International Universities Press. [Google Scholar]
- Beck AT, & Haigh EA (2014). Advances in cognitive theory and therapy: The generic cognitive model. Annual Review of Clinical Psychology, 10, 1–24. doi: 10.1146/annurev-clinpsy-032813-153734 [DOI] [PubMed] [Google Scholar]
- Beck AT, Rush AJ, Shaw BF, & Emery G (1979). Cognitive therapy of depression. New York, NY: Guilford Press. [Google Scholar]
- Benjamini Y, Krieger A, & Yekutieli D (2006). Adaptive linear step-up procedures that control the false discovery rate. Biometrika, 93, 491–507. doi: 10.1093/biomet/93.3.491 [DOI] [Google Scholar]
- Blatt SJ (1974). Levels of object representation in anaclitic and introjective depression. Psychoanalytic Study of the Child, 29, 109–157. [PubMed] [Google Scholar]
- Blatt SJ, & Luyten P (2009). A structural–developmental psychodynamic approach to psychopathology: Two polarities of experience across the life span. Development and Psychopathology, 21, 793–814. doi: 10.1017/S0954579409000431 [DOI] [PubMed] [Google Scholar]
- Blatt SJ, & Zuroff DC (1992). Interpersonal relatedness and self-definition: Two prototypes for depression. Clinical Psychology Review, 12, 527–562. doi: 10.1016/0272-7358(92)90070-O [DOI] [Google Scholar]
- Bonifay W, Lane SP, & Reise SP (2017). Three concerns with applying a bifactor model as a structure of psychopathology. Clinical Psychological Science, 5, 184–186. [Google Scholar]
- Burnham KP, & Anderson DR (2003). Model selection and multimodel inference: A practical information-theoretic approach. New York, NY: Springer. [Google Scholar]
- Calvete E (2011). Temporal relationships between inferential style and depressive symptoms in adolescents. International Journal of Cognitive Therapy, 4, 438–457. doi: 10.1521/ijct.2011.4.4.438 [DOI] [Google Scholar]
- Campbell DT, & Fiske DW (1959). Convergent and discriminant validation by the multitrait-multimethod matrix. Psychological Bulletin, 56, 81–105. [PubMed] [Google Scholar]
- Carroll JB (1993). Human cognitive abilities: A survey of fac- tor-analytic studies. New York, NY: Cambridge University Press. [Google Scholar]
- Caspi A, Houts RM, Belsky DW, Goldman-Mellor SJ, Harrington H, Israel S, … Moffitt TE(2014). The p factor: One general psychopathology factor in the structure of psychiatric disorders? Clinical Psychological Science, 2, 119–137. doi: 10.1177/2167702613497473 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen FF (2007). Sensitivity of goodness of fit indexes to lack of measurement invariance. Structural Equation Modeling, 14, 464–504. [Google Scholar]
- Chen FF, Curran PJ, Bollen KA, Kirby J, & Paxton P (2008). An empirical evaluation of the use of fixed cutoff points in RMSEA test statistic in structural equation models. Sociological Methods & Research, 36, 462–494. doi: 10.1177/0049124108314720 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen FF, Hayes A, Carver CS, Laurenceau J-P, & Zhang Z (2012). Modeling general and specific variance in multifaceted constructs: A comparison of the bifactor model to other approaches. Journal of Personality, 80, 219–251. doi: 10.1111/j.1467-6494.2011.00739.x [DOI] [PubMed] [Google Scholar]
- Chen FF, Sousa KH, & West SG (2005). Teacher’s corner: Testing measurement invariance of second-order factor models. Structural Equation Modeling, 12, 471–492. [Google Scholar]
- Chen FF, West SG, & Sousa KH (2006). A comparison of bifactor and second-order models of quality of life. Multivariate Behavioral Research, 41, 189–225. doi: 10.1207/s15327906mbr4102_5 [DOI] [PubMed] [Google Scholar]
- Cheung GW, & Rensvold RB (2002). Evaluating goodness-of-fit indexes for testing measurement invariance. Structural Equation Modeling, 9, 233–255. [Google Scholar]
- Costello EJ, Copeland W, & Angold A (2011). Trends in psychopathology across the adolescent years: What changes when children become adolescents, and when adolescents become adults? Journal of Child Psychology and Psychiatry, 52, 1015–1025. doi: 10.1111/j.1469-7610.2011.02446.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cox BJ, Fleet C, & Stein MB (2004). Self-criticism and social phobia in the US national comorbidity survey. Journal of Affective Disorders, 82, 227–234. [DOI] [PubMed] [Google Scholar]
- Cronbach LJ, & Meehl PE (1955). Construct validity in psychological tests. Psychological Bulletin, 52, 281–302. [DOI] [PubMed] [Google Scholar]
- Dueber DM (2017). Bifactor indices calculator: A Microsoft Excel–based tool to calculate various indices relevant to bifactor CFA models. doi: 10.13023/edp.tool.01 [DOI] [Google Scholar]
- Elwood LS, Hahn KS, Olatunji BO, & Williams NL (2009). Cognitive vulnerabilities to the development of PTSD: A review of four vulnerabilities and the proposal of an integrative vulnerability model. Clinical Psychology Review, 29, 87–100. [DOI] [PubMed] [Google Scholar]
- Fichman L, Koestner R, & Zuroff DC (1994). Depressive styles in adolescence: Assessment, relation to social functioning, and developmental trends. Journal of Youth and Adolescence, 23, 315–330. doi: 10.1007/BF01536722 [DOI] [Google Scholar]
- Friedman NP, Miyake A, Young SE, DeFries JC, Corley RP, & Hewitt JK (2008). Individual differences in executive functions are almost entirely genetic in origin. Journal of Experimental Psychology: General, 137, 201–225. doi: 10.1037/0096-3445.137.2.201 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garber J, Weiss B, & Shanley N (1993). Cognitions, depressive symptoms, and development in adolescents. Journal of Abnormal Psychology, 102, 47–57. doi: 10.1037/0021-843X.102.1.47 [DOI] [PubMed] [Google Scholar]
- Gibb BE, & Coles ME (2005). Cognitive vulnerability-stress models of psychopathology In Hankin BL & Abela JRZ (Eds), Development of psychopathology: A vulnerability- stress perspective (pp. 104–135). Thousand Oaks, CA: Sage. [Google Scholar]
- Gotlib IH, Lewinsohn PM, Seeley JR, & Rohde P (1991, November). Cognition in depression: A separation of pessimism and attributional style. Paper presented at the Sixth Annual Meeting of the Society for Research in Psychopathology, Boston, MA. [Google Scholar]
- Gotlib IH, Lewinsohn PM, Seeley JR, Rohde P, & Redner JE (1993). Negative cognitions and attributional style in depressed adolescents: An examination of stability and specificity. Journal of Abnormal Psychology, 102, 607–615. doi: 10.1037/0021-843X.102.4.607 [DOI] [PubMed] [Google Scholar]
- Gorsuch RL (1983). Factor analysis (2nd ed.). Hillsdale, NJ: Erlbaum. [Google Scholar]
- Haeffel GJ, Abramson LY, Voelz ZR, Metalsky GI, Halberstadt L, Dykman BM, … Alloy LB (2003). Cognitive vulnerability to depression and lifetime history of Axis I psychopathology: A comparison of negative cognitive styles (CSQ) and dysfunctional attitudes (DAS). Journal of Cognitive Psychotherapy, 17(1), 3–22. [Google Scholar]
- Haeffel GJ, & Howard GS (2009). Self-report: psychology’s four-letter word. American Journal of Psychology, 123, 181–188. [DOI] [PubMed] [Google Scholar]
- Hancock GR, & Mueller RO (2001). Rethinking construct reliability within latent variable systems In Cudeck R, du Toit S & Sörbom D (Eds.), Structural equation modeling: Present and future—A Festschrift in honor of Karl Jöreskog (pp. 195–216). Lincolnwood, IL: Scientific Software International. [Google Scholar]
- Hankin BL (2008a). Cognitive vulnerability–stress model of depression during adolescence: Investigating depressive symptom specificity in a multi-wave prospective study. Journal of Abnormal Child Psychology, 36, 999–1014. doi: 10.1007/s10802-008-9228-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hankin BL (2008b). Stability of cognitive vulnerabilities to depression: A short-term prospective multiwave study. Journal of Abnormal Psychology, 117, 324. doi: 10.1037/0021-843X.117.2.324 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hankin BL, & Abramson LY (2001). Development of gender differences in depression: An elaborated cognitive vulnerability–transactional stress theory. Psychological Bulletin, 127, 773–796. doi: 10.1037/0033-2909.127.6.773 [DOI] [PubMed] [Google Scholar]
- Hankin BL, & Abramson LY (2002). Measuring cognitive vulnerability to depression in adolescence: Reliability, validity, and gender differences. Journal of Clinical Child and Adolescent Psychology, 31, 491–504. doi: 10.1207/S15374424JCCP3104_8 [DOI] [PubMed] [Google Scholar]
- Hankin BL, Abramson LY, Miller N, & Haeffel GJ (2004). Cognitive vulnerability- stress theories of depression: Examining affective specificity in the prediction of depression versus anxiety in three prospective studies. Cognitive Therapy and Research, 28, 309–345. doi: 10.1023/B:COTR.0000031805.60529.0d [DOI] [Google Scholar]
- Hankin BL, Abramson LY, Moffitt TE, Silva PA, McGee R, & Angell KE (1998). Development of depression from preadolescence to young adulthood: Emerging gender differences in a 10-year longitudinal study. Journal of Abnormal Psychology, 107, 128–140. doi: 10.1037/0021-843X.107.1.128 [DOI] [PubMed] [Google Scholar]
- Hankin BL, Lakdawalla Z, Carter IL, Abela JR, & Adams P (2007). Are neuroticism, cognitive vulnerabilities and self-esteem overlapping or distinct risks for depression? Evidence from exploratory and confirmatory factor analyses. Journal of Social and Clinical Psychology, 26(1), 29–63. doi: 10.1521/jscp.2007.26.1.29 [DOI] [Google Scholar]
- Hankin BH, Snyder HR, & Gulley LD (2016). Cognitive risks in developmental psychopathology In Cichetti D (Ed.), Developmental psychopathology: Maladaptation and psychopathology (Vol. 3, pp. 312–385). Hoboken, NJ: Wiley. [Google Scholar]
- Hankin BL, Snyder HR, Gulley LD, Schweizer TH, Bijttebier P, Nelis S, … Vasey MW (2016). Understanding comorbidity among internalizing problems: Integrating latent structural models of psychopathology and risk mechanisms. Development and Psychopathology, 28, 987–1012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hankin BL, Wetter E, Cheely C, & Oppenheimer CW (2008). Beck’s cognitive theory of depression in adolescence: Specific prediction of depressive symptoms and reciprocal influences in a multi-wave prospective study. International Journal of Cognitive Therapy, 1, 313–332. doi: 10.1521/ijct.2008.1.4.313 [DOI] [Google Scholar]
- Hokanson JE, & Butler AC (1992). Cluster analysis of depressed college students’ social behaviors. Journal of Personality and Social Psychology, 62, 273–280. doi: 10.1037/0022-3514.62.2.273. [DOI] [PubMed] [Google Scholar]
- Holm-Denoma JM, & Hankin BL (2010). Perceived physical appearance mediates the rumination and bulimic symptom link in adolescent girls. Journal of Clinical Child & Adolescent Psychology, 39, 537–544. doi: 10.1080/15374416.2010.486324 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holzinger KJ, & Swineford F (1937). The bifactor method. Psychometrika, 2, 41–54. doi: 10.1007/BF02287965 [DOI] [Google Scholar]
- Hong RY, & Cheung MWL (2015). The structure of cognitive vulnerabilities to depression and anxiety evidence for a common core etiologic process based on a meta-analytic review. Clinical Psychological Science, 3, 892–912. doi: 10.1177/2167702614553789 [DOI] [Google Scholar]
- Hong RY, Lee SSM, Tsai FF, & Tan SH (2017). Developmental trajectories and origins of a core cognitive vulnerability to internalizing symptoms in middle childhood. Clinical Psychological Science, 5, 299–315. [Google Scholar]
- Hu LT, & Bentler PM (1998). Fit indices in covariance structure modeling: Sensitivity to underparameterized model misspecification. Psychological Methods, 3, 424–453. doi: 10.1037/1082-989X.3.4.424 [DOI] [Google Scholar]
- Hu LT, & Bentler PM (1999). Cutoff criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives. Structural Equation Modeling, 6, 1–55. doi: 10.1080/10705519909540118 [DOI] [Google Scholar]
- Hughes AA, & Kendall PC (2009). Psychometric properties of the Positive and Negative Affect Scale for Children (PANAS-C) in children with anxiety disorders. Child Psychiatry and Human Development, 40, 343–352. doi: 10.1007/s10578-009-0130-4 [DOI] [PubMed] [Google Scholar]
- Ingram RE, Miranda J, & Segal ZV (1998). Cognitive vulnerability to depression. New York, NY: Guilford Press. [Google Scholar]
- Jacobs RH, Reinecke MA, Gollan JK, & Kane P (2008). Empirical evidence of cognitive vulnerability for depression among children and adolescents: A cognitive science and developmental perspective. Clinical Psychology Review, 28, 759–782. doi: 10.1016/j.cpr.2007.10.006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joiner TE Jr., & Rudd MD (1996). Toward a categorization of depression-related psychological constructs. Cognitive Therapy and Research, 20, 51–68. doi: 10.1007/BF02229243 [DOI] [Google Scholar]
- Kaufman J, Birmaher B, Brent B, Rao U, & Ryan N (1996). The schedule for Affective disorders for school-age children. Pittsburgh, PA: University of Pittsburgh Medical Center. [Google Scholar]
- Kelvin RG, Goodyer IM, Teasdale JD, & Brechin D (1999). Latent negative self-schema and high emotionality in well adolescents at risk for psychopathology. Journal of Child Psychology and Psychiatry and Allied Disciplines, 40, 959–968. [PubMed] [Google Scholar]
- Kindt KC, Kleinjan M, Janssens JM, & Scholte RH (2015). Cross-lagged associations between adolescents’ depressive symptoms and negative cognitive style: The role of negative life events. Journal of Youth and Adolescence, 44, 2141–2153. doi: 10.1007/s10964-015-0308-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kishton JM, & Widaman KF (1994). Unidimensional versus domain representative parceling of questionnaire items: An empirical example. Educational and Psychological Measurement, 54, 757–765. doi: 10.1177/0013164494054003022 [DOI] [Google Scholar]
- Klein DN, Dougherty LR, & Olino TM (2005). Toward guidelines for evidence-based assessment of depression in children and adolescents. Journal of Clinical Child and Adolescent Psychology, 34, 412–432. doi: 10.1207/s15374424jccp3403_3 [DOI] [PubMed] [Google Scholar]
- Kline R (2010). Principles and practice of structural equation modeling (3rd ed.). New York, NY: Guilford Press. [Google Scholar]
- Kopala-Sibley DC, Zuroff DC, Hankin BL, & Abela JR (2015). The development of self-criticism and dependency in early adolescence and their role in the development of depressive and anxiety symptoms. Personality and Social Psychology Bulletin, 41, 1094–1109. doi: 10.1177/0146167215590985 [DOI] [PubMed] [Google Scholar]
- Kovacs M (1985). The children’s depression inventory. Psychopharmacology Bulletin, 21, 995–998. [PubMed] [Google Scholar]
- Lahey BB, Applegate B, Hakes JK, Zald DH, Hariri AR, & Rathouz PJ (2012). Is there a general factor of prevalent psychopathology during adulthood? Journal of Abnormal Psychology, 121, 971–977. doi: 10.1037/a0028355 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lahey BB, Rathouz PJ, Keenan K, Stepp SD, Loeber R, & Hipwell AE (2015). Criterion validity of the general factor of psychopathology in a prospective study of girls. Journal of Child Psychology and Psychiatry, and Allied Disciplines, 56, 415–422. doi: 10.1111/jcpp.12300 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lakdawalla Z, Hankin BL, & Mermelstein R (2007). Cognitive theories of depression in children and adolescents: A conceptual and quantitative review. Clinical Child and Family Psychology Review, 10, 1–24. doi: 10.1007/s10567-006-0013-1 [DOI] [PubMed] [Google Scholar]
- Landis RS, Beal DJ, & Tesluk PE (2000). A comparison of approaches to forming composite measures in structural equation models. Organizational Research Methods, 3, 186–207. doi: 10.1177/109442810032003 [DOI] [Google Scholar]
- Laurent J, Catanzaro SJ, Joiner TE Jr., Rudolph KD, Potter KI, Lambert S, … Gathright T (1999). A measure of positive and negative affect for children: Scale development and preliminary validation. Psychological Assessment, 11, 326–338. doi: 10.1037/1040-3590.11.3.326 [DOI] [Google Scholar]
- Lee A, & Hankin BL (2009). Insecure attachment, dysfunctional attitudes, and low self-esteem predicting prospective symptoms of depression and anxiety during adolescence. Journal of Clinical Child & Adolescent Psychology, 38, 219–231. doi: 10.1080/15374410802698396 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lewinsohn PM, Joiner TE Jr., & Rohde P (2001). Evaluation of cognitive diathesis-stress models in predicting major depressive disorder in adolescents. Journal of Abnormal Psychology, 110, 203–215. doi: 10.1037/0021-843X.110.2.203 [DOI] [PubMed] [Google Scholar]
- Little TD, Cunningham WA, Shahar G, & Widaman KF (2002). To parcel or not to parcel: Exploring the question, weighing the merits. Structural Equation Modeling, 9, 151–173. doi: 10.1207/S15328007SEM0902_1 [DOI] [Google Scholar]
- Little TD, Rhemtulla M, Gibson K, & Schoemann AM (2013). Why the items versus parcels controversy needn’t be one. Psychological Methods, 18, 285–300. doi: 10.1037/a0033266 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marsh HW, Hau KT, & Wen Z (2004). In search of golden rules: Comment on hypothesis-testing approaches to setting cutoff values for fit indexes and dangers in overgeneralizing Hu and Bentler’s (1999) findings. Structural Equation Modeling, 11, 320–341. doi: 10.1207/s15328007sem1103_2 [DOI] [Google Scholar]
- McLaughlin KA, & Nolen-Hoeksema S (2011). Rumination as a transdiagnostic factor in depression and anxiety. Behaviour Research and Therapy, 49, 186–193. doi: 10.1016/j.brat.2010.12.006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meade AW, Johnson EC, & Braddy PW (2008). Power and sensitivity of alternative fit indices in tests of measurement invariance. Journal of Applied Psychology, 93, 568–592. [DOI] [PubMed] [Google Scholar]
- Merikangas KR, He JP, Burstein M, Swanson SA, Avenevoli S, Cui L, … Swendsen J (2010). Lifetime prevalence of mental disorders in US adolescents: Results from the National Comorbidity Survey Replication–Adolescent Supplement (NCS-A). Journal of the American Academy of Child & Adolescent Psychiatry, 49, 980–989. doi: 10.1016/j.jaac.2010.05.017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mineka S, Watson D, & Clark LA (1998). Comorbidity of anxiety and unipolar mood disorders. Annual Review of Psychology, 49, 377–412. doi: 10.1146/annurev.psych.49.1.377 [DOI] [PubMed] [Google Scholar]
- Miyake A, & Friedman NP (2012). The nature and organization of individual differences in executive functions four general conclusions. Current Directions in Psychological Science, 21(1), 8–14. doi: 10.1177/0963721411429458 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mongrain M (1998). Parental representations and support-seeking behaviors related to dependency and self-criticism. Journal of Personality, 66, 151–173. doi: 10.1111/1467-6494.00007 [DOI] [PubMed] [Google Scholar]
- Muthén B, Kaplan D, & Hollis M (1987). On structural equation modeling with data that are not missing completely at random. Psychometrika, 52, 431–462. [Google Scholar]
- Muthén LK, & Muthén BO (2012). Mplus user’s guide (7th ed.). Los Angeles, CA: Muthén & Muthén. [Google Scholar]
- Nolen-Hoeksema S, & Morrow J (1991). A prospective study of depression and posttraumatic stress symptoms after a natural disaster: The 1989 Loma Prieta earthquake. Journal of Personality and Social Psychology, 61, 115–121. doi: 10.1037/0022-3514.61.1.115 [DOI] [PubMed] [Google Scholar]
- Nolen-Hoeksema S, & Watkins ER (2011). A heuristic for developing transdiagnostic models of psychopathology explaining multifinality and divergent trajectories. Perspectives on Psychological Science, 6, 589–609. doi: 10.1177/1745691611419672 [DOI] [PubMed] [Google Scholar]
- Pössel P, & Knopf K (2011). Bridging the gaps: An attempt to integrate three major cognitive depression models. Cognitive Therapy and Research, 35, 342–358. doi: 10.1007/s10608-010-9325-z [DOI] [Google Scholar]
- Priel B, & Shahar G (2000). Dependency, self-criticism, social context and distress: Comparing moderating and mediating models. Personality and Individual Differences, 28, 515–525. doi: 10.1016/S0191-8869(99)00116-6 [DOI] [Google Scholar]
- Putnick DL, & Bornstein MH (2016). Measurement invariance conventions and reporting: The state of the art and future directions for psychological research. Developmental Review, 41, 71–90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reise SP, Bonifay WE, & Haviland MG (2013). Scoring and modeling psychological measures in the presence of multidimensionality. Journal of Personality Assessment, 95, 129–140. [DOI] [PubMed] [Google Scholar]
- Reno RM, & Halaris AE (1989). Dimensions of depression: A comparative longitudinal study. Cognitive Therapy and Research, 13, 549–563. doi: 10.1007/BF01176067 [DOI] [Google Scholar]
- Riskind JH, & Alloy LB (2006). Cognitive vulnerability to psychological disorders: Overview of theory, design, and methods. Journal of Social and Clinical Psychology, 25, 705–725. [Google Scholar]
- Rodriguez A, Reise SP, & Haviland MG (2016a). Applying bifactor statistical indices in the evaluation of psychological measures. Journal of Personality Assessment, 98, 223–237. [DOI] [PubMed] [Google Scholar]
- Rodriguez A, Reise SP, & Haviland MG (2016b). Evaluating bifactor models: Calculating and interpreting statistical indices. Psychological Methods, 21, 137–150. doi: 10.1037/met0000045 [DOI] [PubMed] [Google Scholar]
- Rogers WM, & Schmitt N (2004). Parameter recovery and model fit using multidimensional composites: A comparison of four empirical parceling algorithms. Multivariate Behavioral Research, 39, 379–412. doi: 10.1207/S15327906MBR3903_1 [DOI] [Google Scholar]
- Samuel DB, Suzuki T, & Griffin SA (2016). Clinicians and clients disagree: Five implications for clinical science. Journal of Abnormal Psychology, 125, 1001–1010. doi: 10.1037/abn0000201 [DOI] [PubMed] [Google Scholar]
- Selby EA, Anestis MD, & Joiner TE (2008). Understanding the relationship between emotional and behavioral dysregulation: Emotional cascades. Behaviour Research and Therapy, 46, 593–611. doi: 10.1037/a0015711 [DOI] [PubMed] [Google Scholar]
- Shahar G, & Priel B (2003). Active vulnerability, adolescent distress, and the mediating/suppressing role of life events. Personality and Individual Differences, 35, 199–218. doi: 10.1016/S0191-8869(02)00185-X [DOI] [Google Scholar]
- Sharhabani-Arzy R, Amir M, & Swisa A (2005). Self-criticism, dependency and posttraumatic stress disorder among a female group of help-seeking victims of domestic violence in Israel. Personality and Individual Differences, 38, 1231–1240. [Google Scholar]
- Shechner T, Jarcho JM, Britton JC, Leibenluft E, Pine DS, & Nelson EE (2013). Attention bias of anxious youth during extended exposure of emotional face pairs: An eye- tracking study. Depression and Anxiety, 30(1), 14–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Snyder HR, & Hankin BL (2017). All models are wrong, but the p factor model is useful: Reply to Widiger and Oltmanns (2017) and Bonifay, Lane, and Reise (2017). Clinical Psychological Science, 5, 187–189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Snyder HR, Gulley LD, Bjittebier P, Hartman CA, Oldehinkel AJ, Mezulis A, Young J, & Hankin BL (2015). Adolescent emotionality and effortful control: Pinning down the core latent constructs of the early adolescent temperament questionnaire revised. Journal of Personality and Social Psychology: Personality Processes and Individual Differences, 109, 1132–1149. doi: 10.1037/pspp0000047 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Snyder HR, Young JF, & Hankin BL (2016). Strong homotypic continuity in common psychopathology, internalizing and externalizing factors across 18 months in adolescents. Clinical Psychological Science, 5, 98–110. doi: 10.1177/2167702616651076 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor L, & Ingram RE (1999). Cognitive reactivity and depressotypic information processing in children of depressed mothers. Journal of Abnormal Psychology, 108, 202–210. [DOI] [PubMed] [Google Scholar]
- Technow JR, Hazel NA, Abela JR, & Hankin BL (2015). Stress sensitivity interacts with depression history to predict depressive symptoms among youth: Prospective changes following first depression onset. Journal of Abnormal Child Psychology, 43, 489–501. doi: 10.1007/s10802-014-9922-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Treynor W, Gonzalez R, & Nolen-Hoeksema S (2003). Rumination reconsidered: A psychometric analysis. Cognitive Therapy and Research, 27, 247–259. doi: 10.1023/A:1023910315561 [DOI] [Google Scholar]
- Verstraeten K, Bijttebier P, Vasey MW, & Raes F (2011). Specificity of worry and rumination in the development of anxiety and depressive symptoms in children. British Journal of Clinical Psychology, 50, 364–378. doi: 10.1348/014466510X532715 [DOI] [PubMed] [Google Scholar]
- Verstraeten K, Vasey MW, Raes F, & Bijttebier P (2010). Brooding and reflection as components of rumination in late childhood. Personality and Individual Differences, 48, 367–372. doi: 10.1016/j.paid.2009.11.001 [DOI] [Google Scholar]
- Watson D, & Clark LA (1991). The mood and anxiety symptom questionnaire. Unpublished manuscript, Department of Psychology, University of Iowa, Iowa City.
- Weissman AN, & Beck AT (1978, March 27–31). Development and validation of the Dysfunctional Attitude Scale: A preliminary investigation. Paper presented at the Annual Meeting of the American Educational Research Association, Toronto, Ontario, Canada. [Google Scholar]
- Williams LJ, & O’Boyle EH (2008). Measurement models for linking latent variables and indicators: A review of human resource management research using parcels. Human Resource Management Review, 18, 233–242. doi: 10.1016/j.hrmr.2008.07.002 [DOI] [Google Scholar]
- Zuroff DC, & Fitzpatrick DK (1995). Depressive personality styles: Implications for adult attachment. Personality and Individual Differences, 18, 253–265. doi: 10.1016/0191-8869(94)00136-G [DOI] [Google Scholar]
- Zuroff DC, Mongrain M, & Santor DA (2004). Conceptualizing and measuring personality vulnerability to depression: Comment on Coyne and Whiffen (1995). Psychological Bulletin, 130, 489–511. doi: 10.1037/0033-2909.130.3.489 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.