High-Throughput Screening of Solid-State Li-Ion Conductors Using Lattice-Dynamics Descriptors

Summary

Low lithium-ion migration barriers have recently been associated with low average vibrational frequencies or phonon band centers, further helping identify descriptors for superionic conduction. To further explore this correlation, here we present the computational screening of ∼14,000 Li-containing compounds in the Materials Project database using a descriptor based on lattice dynamics reported recently to identify new promising Li-ion conductors. An efficient computational approach was optimized to compute the average vibrational frequency or phonon band center of ∼1,200 compounds obtained after pre-screening based on structural stability, band gap, and their composition. Combining a low computed Li phonon band center with large computed electrochemical stability window and structural stability, 18 compounds were predicted to be promising Li-ion conductors, one of which, Li₃ErCl₆, has been synthesized and exhibits a reasonably high room-temperature conductivity of 0.05–0.3 mS/cm, which shows the promise of Li-ion conductor discovery based on lattice dynamics.

Graphical Abstract

Highlights

• •High-throughput screening of ∼14,000 Li-containing compounds for new Li-ion conductors
• •A new method to compute phonon band center with only 2 DFT calculations per compound
• •One of the 18 predicted materials, Li₃ErCl₆ has ionic conductivity of 0.05–0.3 mS/cm

Computational Method in Materials Science; Energy Materials; Solid State Physics

Introduction

The use of organic liquid electrolytes (Xu, 2014) in the commercial Li-ion batteries (LIB) poses a major safety issue due to the high flammability of the solvent, which can lead to catastrophic fires (von Sacken et al., 1995). Replacing liquid electrolytes with inorganic solid-state lithium conductors will not only lower such safety concerns but also could potentially increase the energy density by reducing the volume of battery packing required to avoid leakage of liquid electrolytes and especially by hopefully enabling the use of lithium metal as the negative electrode (Janek and Zeier, 2016, Manthiram et al., 2017). Several structural and chemical families of solid Li-ion conductors such as LISICON (Kanno and Murayama, 2001, Khorassani and West, 1982, Rodger et al., 1985, Tachez et al., 1984) and Argyrodites (Deiseroth et al., 2011, Deiseroth et al., 2008, Kong et al., 2010) have been shown to exhibit ionic conductivity spanning over 10 orders of magnitude at room temperature (RT) (Bachman et al., 2016). Since the discovery of lithium superionic conductor Li₁₀GeP₂S₁₂ (LGPS) by Kanno et al. (Kamaya et al., 2011) with RT ionic conductivity of 12 mS/cm, several compounds having RT Li-ion conductivity exceeding that of ethylene carbonate and dimethyl sulfite mixture (EC:DMS) with LiPF₆ (∼10 mS/cm) have been discovered such as Li₇P₃S₁₁ (17 mS/cm) (Seino et al., 2014), argyrodite Li_6.6Ge_0.6P_0.4S₅I (18 mS/cm) (Kraft et al., 2018), and LGPS-like Li_9.54Si_1.74P_1.44S_11.7Cl_0.3 (25 mS/cm) (Kato et al., 2016), which has the highest RT Li-ion conductivity to date. Unfortunately, these most conducting electrolytes have been shown to exhibit narrow electrochemical stability windows (∼0.4 V for LGPS, 0.24 V for argyrodite Li₆PS₅Cl) (Richards et al., 2016, Zhu et al., 2015) and high chemical instability against electrode materials (Auvergniot et al., 2017, Han et al., 2016, Kato et al., 2016, Koerver et al., 2017b, Koerver et al., 2017a, Xu et al., 2018). In addition, electrolytes have to be soft to accommodate volume expansion of the electrodes for several thousand cycles (Koerver et al., 2018) without cracking and prevent dendrite formation (Manthiram et al., 2017). These requirements impose very stringent conditions on the ideal candidate materials, which explains why to this date all-solid LIB using ceramic electrolytes are not yet on the market and the search for new materials and optimization of solid-state LIB is still an active area of research (Kerman et al., 2017, Takada, 2016, Zhang et al., 2018).

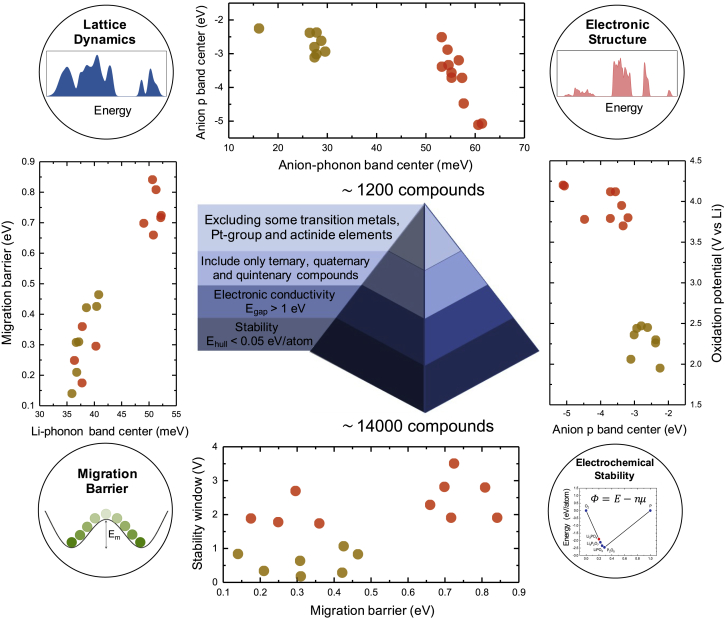
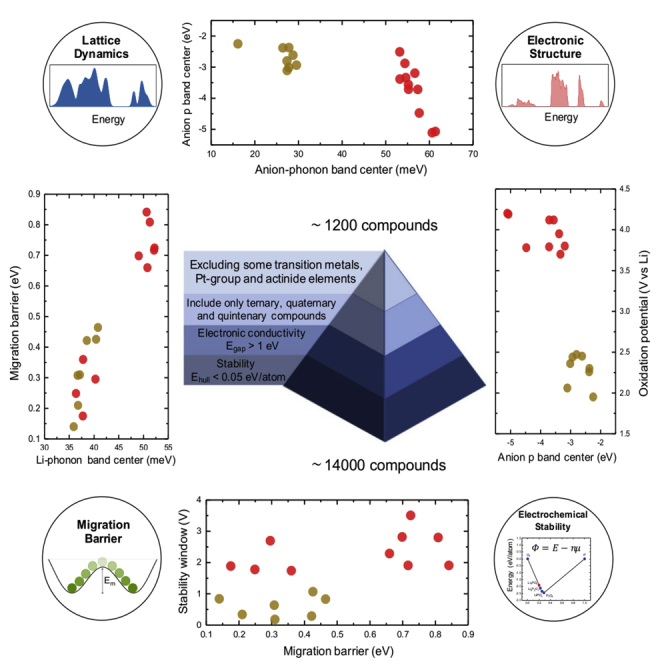
In recent years, the influence of the softness of a lattice, i.e., the average vibrational frequencies or phonon band center, has been shown to influence the ionic transport in solid electrolytes (Muy et al., 2018b, Muy et al., 2018a, Krauskopf et al., 2017, Krauskopf et al., 2018b, Kraft et al., 2017). To further employ this understanding of the influence of lattice dynamics on ion mobility, in this article, we present the result of a high-throughput (HT) study of more than 1,000 Li-containing compounds using a lattice dynamic descriptor called the lithium-phonon band center, which is a measure of the average vibrational frequency of the lithium sublattice and has been proposed as a descriptor for the migration barrier or enthalpy of migration of lithium conductors in LISICON and olivine families (Muy et al., 2018b), in addition to several correlations between electronic structures, lattice dynamics, migration barrier, and electrochemical stability (Figure 1). Previous HT studies employed descriptors that were designed essentially based on static structural features (Avdeev et al., 2012, Wang et al., 2015) or using machine learning techniques to capture underlying correlations between the input features and the target properties from a database (Jalem et al., 2013, Sendek et al., 2018, Sendek et al., 2017). For instance, Wang et al. (Wang et al., 2015) have proposed that a body-center cubic (BCC) structure provides the ideal framework for Li-ion conduction, where the deviation from the ideal BCC structure can be used as a descriptor for faster Li-ion conductors. Sendek et al. (Sendek et al., 2017) have used a logistic regression technique to train a model to classify a given material as superionic or normal Li-ion conductors. After training the model on a database of experimentally measured ionic conductivity, they used their model to classify several thousands of Li-containing compounds and suggested a few candidates that might exhibit superionic conductivity.

Figure 1.

Schematic of the HT Screening as well as Various Correlations Studied in This Work

Electronic and phonon-related descriptors were shown to correlate with the migration barrier E_m and electrochemical stability of lithium-ion conductors. Data points in red correspond to oxides, whereas those in brown correspond to sulfides and were taken from previous work (Muy et al., 2018b).

HT calculation of phonon-related properties has been hindered by the high computational cost associated with full density functional theory (DFT) calculations. Although HT infrastructure to compute vibrational properties of materials including phonon density of states (DOS) has been demonstrated enabling automatic workflow of phonon calculations to be executed with minimal human intervention (Petretto et al., 2018a), the computational time required for each phonon calculation is still high. To overcome the high computational cost associated with the calculation of phonon DOS using DFT (Petretto et al., 2018b), we employed and optimized an approximate method called Quickhess, which allowed us to compute phonon band center (at Γ-point) with only two single-point DFT calculations independent of the symmetry and size of the unit cell (Voss and Vegge, 2008). The computed phonon band centers with Quickhess exhibit accuracy comparable to the full DFT calculations. Moreover, we found a strong positive correlation between the computed total-phonon band centers and anion-phonon band centers, which are both related to the oxidation potential of Li-ion conductors. Lithium-phonon band centers exhibit only weak correlation with the total- and anion-phonon band centers. Based on the computed lithium-phonon band centers and the computed electrochemical windows, we proposed 18 compounds as promising Li-ion conductors, 17 of which (LiCa₉Mg(PO₄)₇, Li₂Pr(NO₃)₅, LiPF₆, LiAsF₆, LiSbF₆, LiK₂AlF₆, Li₁₀Mg₇Cl₂₄, Li₃ErCl₆, LiCs₂LuCl₆, LiCs₂YCl₆, Li₃CsCl₄, LiYb₂Cl₅, Li₂CsCl₃, LiCsCl₂, LiRbBr₂, Li₃ErBr₆, and LiSr₄(BN₂)₃) have not been reported to date. In addition to phonon band centers, we also examined the electronic band centers across different chemistries and found a negative correlation with the phonon band centers: the lower the phonon band centers, the closer the electronic anion p-band centers to the Fermi level. Finally, we also examined the correlation between the electrochemical stability and found a correlation between the oxidation potentials and the anion-phonon band centers, largely in agreement with previous study (Muy et al., 2018b). This work further strengthens the correlation of the phononic properties of the lattice to the stability and migration barriers by extending it to much larger chemical or structural families of Li-ion conductors, thus providing a new predictor of high ionic conductivity in HT screening approaches to find novel ionic conductors.

Results and Discussions

Benchmark of Computed Phonon Band Centers Computed with Quickhess

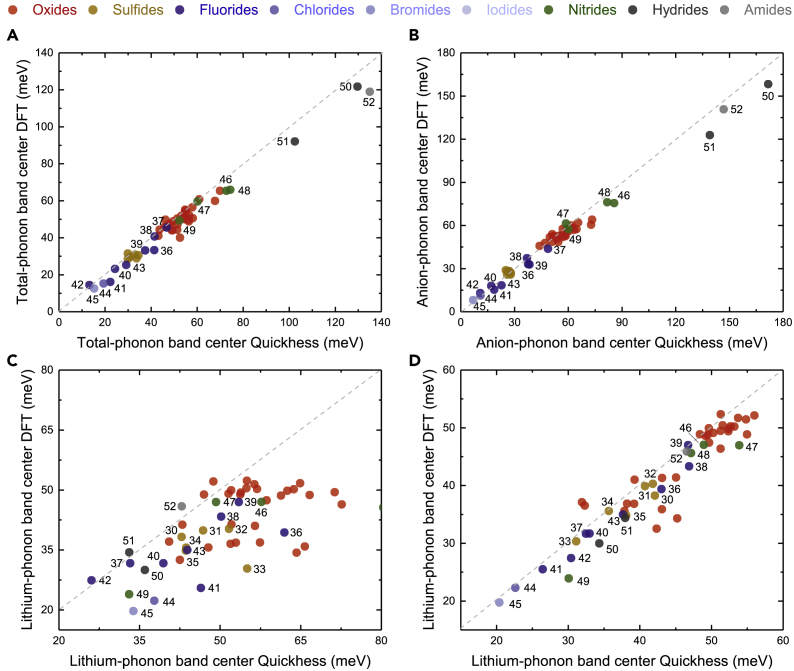
To benchmark the accuracy of the Quickhess method, we have selected 53 compounds to cover several chemistries and structures of known Li-ion conductors and computed their phonon band centers within the full DFT calculations with finite-displacement method using the same parameters as in our previous work (Muy et al., 2018b). The computed phonon band centers of these 53 compounds using the Quickhess method was found to be comparable to those obtained from full DFT calculations once the parameter ɛ in Equation S2 was optimized. We tested two methods for choosing $\varepsilon$, one by referring it to the number of atoms in the unit cell and the other one by referring to the volume of the unit cell. We found that better accuracy was achieved by referring ɛ to the volume per ions in the unit cell, which is given by:

$$\varepsilon =\frac{\sqrt[3]{V_{cell}}}{N_1.N_{atom}}$$ (Equation 1)

where V_cell and N_atom are the volume of the unit cell and the number of atoms in the unit cell, respectively. The parameter N₁ was introduced to allow for variation of ɛ and for assessing its influence on the accuracy of the computed phonon band centers. The comparison of total-, anion-, and lithium-phonon band centers computed with full DFT (the computational details and different DFT parameters [number of K-points, plane-wave energy cutoff …] are the same as in our previous works; Muy et al., 2018b) and the Quickhess method using N₁=5 are shown in Figures 2A–2C, respectively. The agreement in the computed total and anion band centers from Quickhess with those obtained from full DFT is quite remarkable, with a mean absolute error (MAE) of only ∼3.85 meV. However, the agreement in the computed lithium-phonon band center obtained from Quickhess is much worse, with MAE ∼10.93 meV, which is too large for HT screening. Better accuracy of the lithium-phonon band center with Quickhess was obtained by employing one additional DFT calculation, where only the Li ions were displaced. This displacement was generated by adding all the Li-projected eigenvectors obtained in the previous step, and phonon energies were then again approximated using Equation S1 for h_i. A new DFT Hessian was constructed, and the new eigenvalues were extracted in exactly the same way as in the previous step. The length-scaling parameter

$${\varepsilon }^{\prime }=\frac{\sqrt[3]{V_{cell}}}{N_2.N_{atom}}$$ (Equation 2)

for this second displacement was again calibrated by extensive testing. The parameter N₂ allowed us to vary ɛ^′ and assess its influence on the accuracy of the computed phonon band centers. With this additional step, the agreement between computed lithium-phonon band centers by Quickhess and full DFT was much improved, as shown in Figure 2D with N₂=10.

Figure 2.

Comparison between Computed Band Centers Using Full DFT Calculations and Quickhess Method

(A–D) Comparison for (A) total-phonon band centers, (B) anion-phonon band centers, and (C) the Li-ion band centers. The agreement in the computed Li-ion phonon band centers between full DFT and Quickhess was improved significantly with one additional displacement constructed from the sum of Li-projected eigenvectors shown in (D). The oxides include Li₃XO₄ (X = P, As, Sb, V), Li₂XYO₄ (X = Na, Mg, Cd; Y=Si, As, Ge), LiXYO₄ (X = Mg, In, Sc, Al, Mn, Ni, Cd; Y = Si, Ge, As, P, V), Li_3.25Ge_0.25X_0.75O₄ (X = P, V), Li_3.25Ge_0.25V_0.75O₄, Li₃V_0.25P_0.75O₄, LiAlO₂, Li₆HfO₇, LiNbO₃, Li₂SnO₃, Li₈SnO₆, Li₄GeO₄, and sulfides Li₃SbS₄(31), Li₄XS₄ (X = Ge(35), Sn(36)), Li₂CdXS₄ (X = Si(32), Ge(33)); fluorides: Li₂ZrF₆(37), LiPF₆(38), Li₃AlF₆(39), LiYF₄(40); chlorides: Li₂MgCl₄(41), LiSnCl₃(42), LiCsCl₂(43), LiAlCl₄(44); bromides: Li₂ZnBr₄(45); Iodides: Li₂ZnI₄(46); nitrides: LiPN₂(47), Li₃BN₂(48), LiSi₂N₃(49), LiSr₄(BN₂)₃(50); hydrides: LiBH₄(51), LiAlH₄(52); and amides: LiNH₂(53). These computed phonon band centers from full DFT were taken from or computed with the same parameters as in previous work (Muy et al., 2018b).

Computed lithium-phonon band centers with Quickhess were examined systematically by varying N₁ and N₂, where the MAE of lithium-phonon band centers smaller than 2.5 meV could be achieved with suitable values of N₁ and N₂, as shown in Figure S1. Based on these tests, N₁ = 2 and N₂ = 10 were chosen for all the computed phonon band centers shown in the remainder of this work. Moreover, in addition to the 53 compounds in Figure 2, we have also computed the lithium-phonon band centers of additional 72 compounds using the Quickhess method and compared them with the full DFT calculations available on Materials Project database (Figure S2). As these 72 compounds were not used during the optimization of the parameters N₁ and N₂, they can be viewed as our “validation set.” The very good agreement between the Quickhess method and these 72 DFT calculations (Figure S2) further confirms the accuracy of our method. Finally, to test the robustness of our method, we computed the phonon band centers of all ∼1,200 compounds using two sets of parameters N₁=2; N₂=10 and N₁=5; N₂=10. The difference in the computed phonon band centers by Quickhess with these two sets of N₁ and N₂ was found to fluctuate around zero as expected, with the exception of a few compounds, whose values of phonon band center change drastically upon variation of ɛ and ɛ^′ signaling potential issues (Figure S3). Based on this test, we excluded all compounds having difference in the computed phonon band centers with different sets of N₁ and N₂ larger than 5 meV resulting in ∼1,000 compounds retained for the remaining part of the paper.

Computed Phonon Band Centers of ∼1,000 Li-Containing Inorganic Compounds by Quickhess

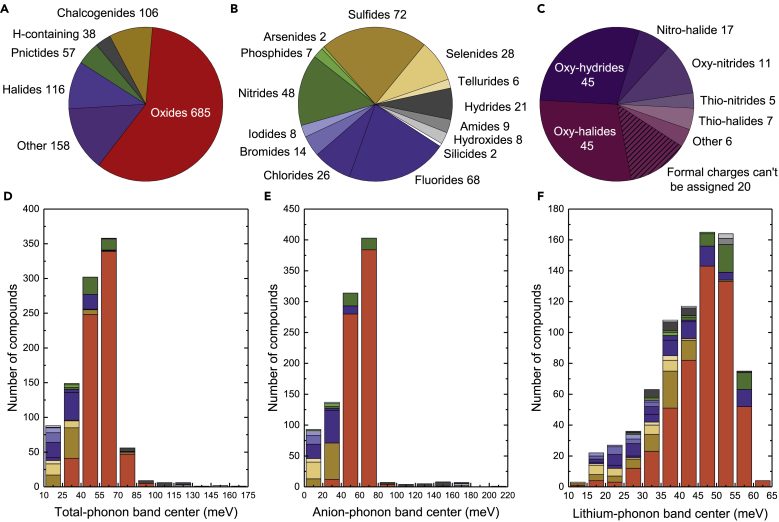
Total-, anion-, and lithium-phonon band centers of ∼1,000 Li-containing inorganic compounds were computed by Quickhess (Figure 3). The most dominant chemistry in our study is the oxide family, which is followed by chalcogenides and halides and a smaller fraction of pnictides as well as hydrogen-containing compounds (essentially hydrides, hydroxides, and amides) (Figure 3A). A more detailed distribution of different chemistries is shown in Figure 3B, and the “other” compounds are shown in Figure 3C, which include mixed-anion compounds such as oxy-halides and oxy-nitrides. There are also a small number of compounds whose formal charge could not be assigned using the bond valence method, which are henceforth excluded from the analysis. The total-phonon band centers of oxides are centered at ∼60 meV, whereas the total-phonon band centers of chalcogenides (sulfides, selenides and tellurides) were lower (Figure 3D), in agreement with previous work using 24 compounds (Muy et al., 2018b). In Figures S4A–S4C, the same histograms as Figure 3D excluding the oxide family are shown so that the distribution across other chemistries can be seen more clearly. Interestingly, the total-phonon band centers of fluorides are lower than for the oxides, on the order of 30 meV, whereas the total-phonon band centers of nitrides closely mirror those of the oxides. Hydrogen-containing compounds such as hydrides, hydroxides, and amides tend to have their total-phonon band centers skewed toward higher values owing to the small mass of the hydrogen atom (Figure 3D).

Figure 3.

Number of Compounds and Phonon Band Center Distribution across Different Chemistries

(A–F) (A) The number of Li-containing compounds in each chemistry included in this study. (B) More detailed distribution of different families of compounds in each chemistry, excluding the oxides. (C) The distribution among the mixed-anion compounds and the number of compounds whose formal charge cannot be assigned using bond valence method. Histograms of (D) computed total-phonon band centers, (E) computed anion band centers, and (F) lithium-phonon band centers. Figures 3D–3F are replotted in Figure S4 excluding all oxides from the count to show the distribution of other chemistries more clearly.

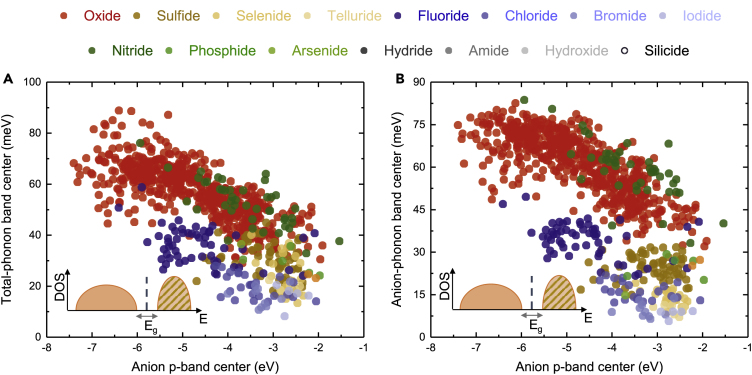
The histogram of anion-phonon band centers (Figure 3E) is similar to that of the total-phonon band centers, suggesting a strong correlation, which will be discussed in detail in the next section. In contrast, the histogram of lithium-phonon band centers (Figure 3F) is markedly different from those of total- and anion-phonon band centers, especially for the oxides. In agreement with our previous study (Muy et al., 2018b), most of the Li-phonon band centers of oxides tend to center at ∼40–50 meV, whereas those of chalcogenides tend be lower, around 30–40 meV. It is of great interest to note that there are a significant number of oxides having particularly low Li-phonon band centers <30 meV, which are promising materials with potentially high mobility of Li-ions (Muy et al., 2018b) and will be discussed in more detail in a later section. Another noteworthy observation is that the Li-phonon band centers of some hydrides tend to be on the lower side of the distribution despite having very high total and anion band centers. This observation agrees with the experimental findings that several hydride lithium superionic conductors are known especially in their high-temperature phase (Matsuo et al., 2007, Mohtadi and Orimo, 2017).

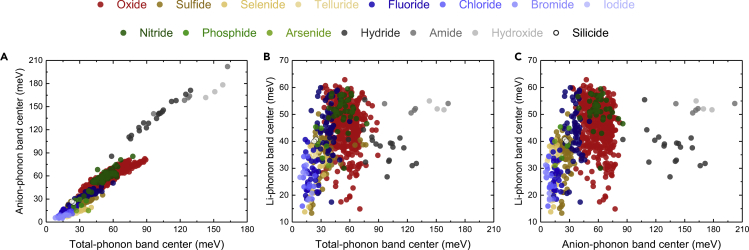
It is significant to note that the computed anion-phonon band centers increase linearly with greater total-phonon band centers across a much larger structural and compositional space of ∼1,000 Li-containing compounds, as shown in Figure 4A. In contrast, there is no correlation between Li- and total- (Figure 4B) or anion- (Figure 4C) phonon band centers within each chemical series (e.g., oxides, halides), although a broad linear correlation appears to exist across different chemistries. These results are in agreement with those of our previous study (Muy et al., 2018b) of 24 lithium-ion conductors in LISICON and olivine families, which show similar correlations between the total- and anion-phonon band centers, whereas the lithium-phonon band centers are essentially uncorrelated with other phonon band centers. Interestingly, there are a few oxides that have high total- and anion-phonon band centers (greater than ∼40 meV) but relatively low Li-ion-phonon band centers (smaller than ∼30 meV), indicating potentially low migration barriers. A common feature for compounds with low Li-ion-phonon band centers is the long Li-O bonds (1.9–2.5 Å) (Figure S5), where the average Li-anion bond distance appears to be the best descriptor for the Li-phonon band centers we found in this study. Some of these compounds are well-known Li-ion conductors (Enciso-Maldonado et al., 2015, Morgan et al., 2004, Muy et al., 2018b), including olivine LiTmSiO₄ (Jalem et al., 2012) or LiInGeO₄ (Jalem et al., 2012, Rajkumar et al., 2010) and NASICON-like compounds such as LiM₂(PO₄)₃ (M = Ge, Sn, and Zr) (Arbi et al., 2011, Martínez-Juárez et al., 1998, Winand et al., 1991). Less-well-known compounds include LiLnO₂ (Ln = Gd, Er and Lu), whose structures have been well characterized but have not been studied as Li-ion conductors (Cantwell et al., 2011, Hashimoto et al., 2002).

Figure 4.

Correlations among Phonon Band Centers

(A–C) Correlation between (A) computed anion- and total-phonon band centers, (B) lithium-phonon band centers and total-phonon band centers, and (C) Li-phonon band centers and anion-phonon band centers of ∼1,000 compounds shown in Figure 3 by Quickhess, excluding 158 with the mixed anions and those whose formal charge cannot be assigned.

Correlation between Computed Phonon and Electronic Band Centers

Lowering the total- (Figure 5A) or anion- (Figure 5B) phonon band centers was found to scale with computed electronic anion p-band centers closer to the top of valence band. It is of great interest to relate anion-phonon band centers to electronic ligand band centers as anion p-band centers have been proposed as descriptors for catalytic activity (Lee et al., 2011), stability (Grimaud et al., 2013), and oxygen migration (Mayeshiba and Morgan, 2016) in perovskites. A strong correlation between the total- as well as anion-phonon band centers with the anion p-band centers (with respect to mid-gap) was found across different chemical series, whereas the correlation was much weaker within each chemical family, with the exception of oxides. Hydrogen-containing compounds (hydrides, hydroxides, and amides) were excluded owing to the low mass of hydrogen and the difference in the nature of bonding involving the s-orbital instead of p-orbitals. These trends remain valid if we used the top of the valence band instead of the mid gap as the reference for the anion p-band centers (Figure S6). As the electronic anion p-band center relative to the top of the valence band is a measure of covalency or ionicity (Hong et al., 2017), this correlation suggests that more covalent compounds tend to have lower vibrational frequencies of bonds involving nonmobile species. In contrast, no correlation was found between Li-phonon band centers and electronic band centers (Figure S7), which is in agreement with previous studies of 24 Li-ion conductors (Muy et al., 2018b).

Figure 5.

Correlations between Phonon Band Centers and Electronic p-band Centers

(A and B) Correlation between (A) computed total- and (B) anion-phonon band centers from Quickhess with computed anion electronic p-band centers of ∼1,000 compounds. The inset shows the schematic of anion-projected electronic DOS. The anion p-band centers were computed by integrating over the occupied states with respect to the mid-gap indicated by the dashed line. Hydrogen-containing compounds (hydrides, hydroxides, and amides) were excluded due to the particular low mass of hydrogen and the difference in the nature of bonding, which involves the s-orbital instead of p-orbitals.

Correlation between Electrochemical Stability and Phonon or Electron Band Centers

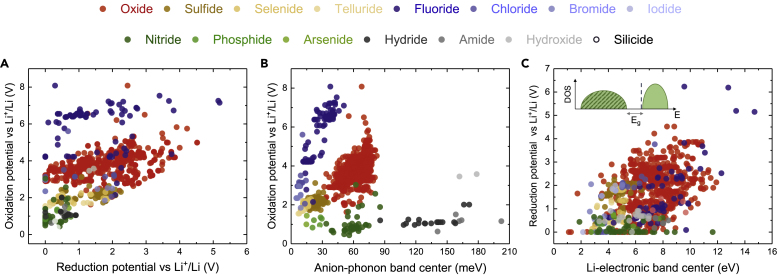
As the electrochemical stability of an electrolyte is governed by tendency of the material to give or accept electrons from the electrodes, which is in turn related to the positions of the conduction and valence band with respect to the Fermi level, the correlation between the anion p-band centers and anion-phonon band centers hints at the existence of another correlation between the electrochemical stability and phonon band centers. To quantify the electrochemical stability of these ∼1,000 Li-containing compounds, we employed a computational method based on the construction of the grand-potential phase diagram (Richards et al., 2016, Zhu et al., 2016, Zhu et al., 2015), which allowed us to compute the oxidation and reduction potential (versus Li⁺/Li). In agreement with previous studies (Richards et al., 2016, Zhu et al., 2016, Zhu et al., 2015), the oxidation potentials were largely determined by the nature of the anion in the structures, decreasing in the order from fluorides > chlorides ∼ oxides > bromides > iodides ∼ sulfides ∼ selenides ∼ tellurides > pnictides ∼ hydrides, as shown in Figure 6A. In contrast, the reduction potentials show no apparent trend across any of the chemistries other than the fact that nitrides tend to be stable against reduction by lithium, in agreement with previous studies (Zhu et al., 2016, Zhu et al., 2015). There are a few compounds that are both stable against reduction by lithium (having reduction potential ∼0 V versus Li⁺/Li) and against oxidation above 4 V versus Li⁺/Li, highlighting the challenges to search for stable electrolytes in LIB. Moreover, the computed oxidation potentials were found to broadly increase with greater anion-phonon band (Figure 6B) and total-phonon band centers (Figure S8A), but not with lithium-phonon band centers (Figure S8B), in agreement with previous work of LISICON and olivine Li-ion conductors (Muy et al., 2018b). Specifically, the correlation falls into three separate groups, namely, group 15 (nitrides, phosphides, and arsenides), group 16 (oxides, sulfides, selenides, and tellurides), and group 17 (fluorides, chlorides, bromides, and iodides). This trend is consistent with the fact that compounds that have stiffer lattices and hence higher phonon energy (e.g., higher total- and anion-phonon band centers) are less covalent; having electronic anion p-band center further away from the top of valence band (Figure 5) correlates with greater oxidation potentials (more difficult to extract electrons from anion p-bands). This correlation is also consistent with the observation that the computed electrochemical stability windows, which are the difference between the computed oxidation and reduction potentials, increase with increasing band gap as expected (Figure S8F). Moreover, we found no correlation between the reduction potentials and the phonon band centers (Figures S8C–S8E) in agreement with previous study (Muy et al., 2018b). Interestingly, increasing reduction potentials were found to correlate with greater band centers of Li-projected electronic DOS integrated over the conduction band (Figure 4C). This trend could be rationalized by the following: the propensity of a material to be reduced is determined by the (thermodynamic) driving force to accept an electron to the conduction band, which can be approximately captured by the electronic band center computed over the conduction bands. Finally, we would like to emphasize that the correlations between phonon band centers, electronic band centers, and electrochemical stability are simply different manifestations of the covalency or ionicity across these materials, which are governed by the orbital overlap, electronegativity difference, and polarity between elements that make up the chemical bonds within these structures.

Figure 6.

Computed Oxidation and Reduction Potentials and Their Correlations with Phonon and Electronic Band Centers

(A) Computed oxidation and reduction potential (versus Li⁺/Li) for ∼1,000 Li-containing compounds in the study.

(B) Correlation between computed oxidation potential and anion-phonon band center.

(C) Correlation between reduction potential and the electronic band center computed over the Li-projected conduction bands. The inset shows the schematic of the Li-projected electronic DOS. The Li-electronic band centers were computed by integrating over the unoccupied states with respect to the bottom of the conduction band indicated by the dashed line. All hydrogen-containing compounds (hydrides, hydroxides, and amides) fall into a separate region due to the very different nature of bonding in these compounds, which involves the s-orbital of hydrogen instead of p-orbitals of other anions and the particularly low mass of hydrogen.

Prediction of Promising Li-Ion Conductors and Experimental Validation

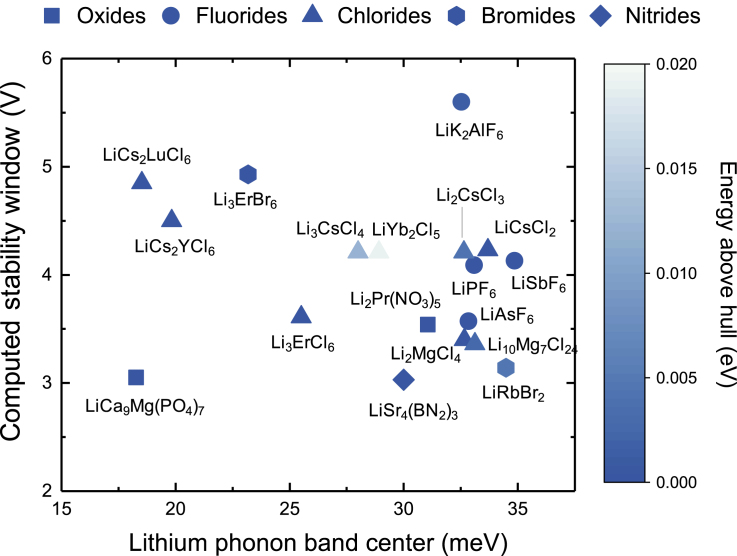
By screening the phonon band centers and electrochemical stability of ∼1,000 Li-containing compounds, 18 compounds were found to have small lithium-phonon band centers (less than 35 meV), key to have low lithium migration barrier, computed electrochemical stability window against oxidation and reduction larger than 3 V, and the energy above hull smaller than 20 meV/atom, which served as a proxy for structural stability, as shown in Figure 7. Only two oxides (LiCa₉Mg(PO₄)₇ and Li₂Pr(NO₃)₅) and no chalcogenide were found, which can be attributed to the fact that most of oxides having low Li phonon band center (Figure 4C) and chalcogenides tend to exhibit narrow electrochemical window (Figure 6A). Four fluorides (LiK₂AlF₆, LiPF₆, LiAsF₆, and LiSbF₆) possess large electrochemical window but relatively high lithium-band center, whereas the chloride family was noted prominently in Figure 7, having 10 chlorides that have high stability and low lithium-phonon band centers.

Figure 7.

The 18 Most Promising Compounds Identified in This Study

These compounds were selected based on their stability window, which is larger than 3 V; Li-phonon band center smaller than 35 meV; along with their energy above hull, which serves as a proxy for their stability. Compounds having non-zero energy above hull are thermodynamically unstable at 0 K, although they can be stabilized at higher temperature by entropic contributions. Only two oxides and no chalcogenide are present due to their small stability windows, whereas only four fluorides are present despite having large electrochemical windows due to their high Li-phonon band centers. The most promising Li-ion conductors were found in the chloride family, which features prominently in the figure. A similar figure including compounds having stability window smaller than 3 V is shown in Figure S9, and numerical values of all compounds along with their unique MP identifiers are shown in Table S1.

Although the poor electrochemical stability of known fast ionic conductors such as the thiophosphates is clearly problematic, one can still make use of their high ionic conductivity by exploiting their kinetic stability (Han et al., 2016, Park et al., 2018) and by using protective layers on electrode materials to extend their stability window. Therefore, we further relaxed the electrochemical stability criteria, and our screening study then includes several known Li-ion conductors such as the Li superionic conductor LGPS (Kamaya et al., 2011) and its derivative Li₁₀SiP₂S₁₂ (Kato et al., 2014) and Li₁₀SnP₂S₁₂ (Bron et al., 2013, Kato et al., 2014) as can be seen in Figure S9. In addition, we recovered lithium borohydride LiBH₄, which was one of the first Li superionic conductor discovered in the hydride family (Matsuo et al., 2007). Similarly, our results indicated that the lower stability electrolytes such as Li₃InCl₆ and Li₆MgBr₈ are good Li-ion conductors in agreement with the experimental finding that the ionic conductivity of the solid solution Li₃InBr_6-xCl_x is on the order of 0.05–2 mS/cm (Tomita et al., 2008, Yamada et al., 2006). Our results also include previously predicted fast Li-ion conductors using a machine learning technique (logistic regression) such as Li₅B₇S₁₃, Li₃ErCl₆, LiKTe, … (Sendek et al., 2018, Sendek et al., 2017) (Figure S9). Numerical values of stability window, lithium-phonon band center, and energy above hull of all compounds shown in Figures 7 and S9 along with their unique Materials Project ID are given in Table S1.

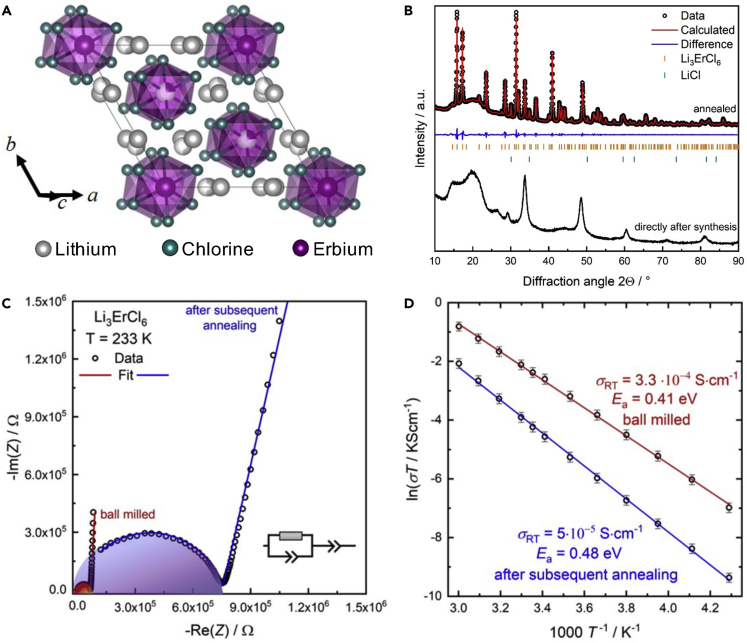
More recently, two Li-ion conductors Li₃YCl₆ and Li₃YBr₆, which are structurally and chemically very similar to Li₃ErCl₆ and Li₃ErBr₆ in Figure 7, have been shown to have high ionic conductivity ∼1 mS/cm and good cycling performance in all-solid-state batteries (Asano et al., 2018). Based on this study and to further validate the results of our HT screening, we have synthesized one of the predicted materials, Li₃ErCl_6. The structure of Li₃ErCl₆ was initially solved by Bohnsack et al. using single crystals obtained by a slow-cooling synthesis method of a stoichiometric mixture of ErCl₃ and LiCl, and the structure is shown in Figure 8A (Bohnsack et al., 1997). The chloride atoms build up a hexagonally closed packed lattice with octahedral voids that are partially occupied. Every ErCl₆³⁻ octahedron is surrounded by six LiCl₆⁶⁻ octahedra. X-ray diffraction was used to characterize the samples and further investigate the structure. Figure 8B shows the diffraction patterns for the ball-milled sample directly after the synthesis and after subsequent annealing. The diffraction pattern collected directly after the ball-milling process exhibits broad reflections with low intensity, owing to the strong amorphization during the ball milling. The diffraction pattern for the crystalline sample that was collected after subsequent annealing of the ball-milled sample can be indexed to the trigonal space group P$\overline{3}$m1. A Pawley fit leads to the lattice parameters a = b = 11.1693(2) and c = 6.0363(1). A minor amount of around 5 ± 1 wt. % LiCl impurity was found to exist using a tentative Rietveld refinement. However, due to the low scattering form factor of Li no full structural characterization by a Rietveld refinement was performed.

Figure 8.

Synthesis, Structural Characterization, and EIS Measurements of Li₃ErCl₆

(A) Structural features within the unit cell, showing face-sharing ErCl₆³⁻ octahedra with Li⁺ in chains along the c-axis.

(B) Comparison of the diffraction patterns for the synthesized Li₃ErCl₆ compounds directly after milling (bottom) and subsequent crystallization (top).

(C and D) (C) Comparison of exemplary impedance data at −30°C and (D) Arrhenius plot showing the room-temperature conductivities and activation barriers for ionic motion.

AC impedance spectroscopy was performed to assess the ionic conductivity and activation barriers for ion migration within the synthesized materials. The Nyquist plots of the impedance data collected at 233 K can be found in Figure 8C, and the corresponding Arrhenius plots can be found in Figure 8D. The impedance data for every measured temperature were fit using one parallel constant phase element (CPE)—resistor unit, which is fit in series to another CPE that represents the gold electrodes. The capacitances C of the combination R/CPE where estimated using the Brug formula (Brug et al., 1984). Although no contribution of bulk and grain boundaries can be seen, the obtained capacitances (48 pF/cm²) and ideality factor α of >0.85 correspond well with bulk transport. The obtained conductivities and activation barriers for Li₃ErCl₆ are 0.3 mS/cm (E_A = 0.41 eV) and 0.05 mS/cm (E_A = 0.48 eV) for the ball-milled and the crystalline samples, respectively. The ball-milled sample without subsequent annealing has a noticeably increased conductivity. It has been previously shown that ball-milled samples exhibit a higher conductivity, likely related to introducing defects while using the harsh conditions of ball milling, or resulting from subtle structural changes in the glassy state (Krauskopf et al., 2018a).

Further structural studies will be needed to elucidate the underlying reasons for the difference in the ionic conductivity between the samples in depth; however, these results clearly show that the HT screening of materials proposed for novel ionic conductors is successful. We expect that the ionic conductivity can be further enhanced with the compositional optimization, for example, via aliovalent substitution to optimize the concentration of mobile species (Culver et al., 2018). Besides Li₃ErCl₆, as synthesized in this work, and Li₂MgCl₄ (Lutz et al., 1981, Nagel et al., 2002), to the best of the authors' knowledge no other compound in Figure 7 has been studied as Li-ion conductor with the exception of LiPF₆, LiAsF₆, and LiSbF₆, which are used as lithium salts in liquid electrolytes (Xu, 2014), therefore representing an exciting opportunity to discover new families of Li-ion conductors having potentially both high ionic conductivity and electrochemical stability.

Limitations of the Study

We would like to emphasize that the lithium-phonon band center has been proposed as a descriptor for the migration barrier which, in stoichiometric compounds, is not the same as the measured activation energy, which also contains contribution from defect formation energy. To exhibit high ionic conductivity, optimal concentration of mobile species is also needed in addition to low migration barrier. Therefore, aliovalent substitution might be necessary, and thus a complementary computational study of dopability might also be necessary. Finally, the migration barriers we considered here are only indicative of the local jumps between two adjacent sites. These sites have to be connected to form a percolating network for the long-range diffusion to occur. Therefore, additional study for the presence of percolating pathways in the structures is necessary to fully assess the potential of these materials as new lithium superionic conductors.

Methods

All methods can be found in the accompanying Transparent Methods supplemental file.

Published: June 28, 2019