Cell lineage and communication network inference via optimization for single-cell transcriptomics

Abstract

The use of single-cell transcriptomics has become a major approach to delineate cell subpopulations and the transitions between them. While various computational tools using different mathematical methods have been developed to infer clusters, marker genes, and cell lineage, none yet integrate these within a mathematical framework to perform multiple tasks coherently. Such coherence is critical for the inference of cell–cell communication, a major remaining challenge. Here, we present similarity matrix-based optimization for single-cell data analysis (SoptSC), in which unsupervised clustering, pseudotemporal ordering, lineage inference, and marker gene identification are inferred via a structured cell-to-cell similarity matrix. SoptSC then predicts cell–cell communication networks, enabling reconstruction of complex cell lineages that include feedback or feedforward interactions. Application of SoptSC to early embryonic development, epidermal regeneration, and hematopoiesis demonstrates robust identification of subpopulations, lineage relationships, and pseudotime, and prediction of pathway-specific cell communication patterns regulating processes of development and differentiation.

INTRODUCTION

Our ability to measure the transcriptional state of a cell—and thus interrogate cell states and fates (1,2)—has advanced dramatically in recent years (3) due in part to high-throughput single-cell RNA sequencing (scRNA-seq) (4). This shift, permitting delineation of different sources of heterogeneity (5,6), requires appropriate dimension reduction techniques, cell clustering, pseudotemporal ordering of cells and lineage inference.

Many clustering methods have been used to identify cell subpopulations via some combination of dimensionality reduction and learning of cell-to-cell similarity measures that best capture relationships between cells from their high dimensional gene expression profiles. Seurat and CIDR, for example, first embed single-cell gene expression data into low dimensional space by principal components analysis (PCA), and then cluster cells using a smart local moving algorithm, or hierarchical clustering, respectively (7,8). SIMLR learns a cell–cell similarity matrix by fitting the data with multiple kernels, before using spectral clustering to identify cell subpopulations (9). An alternative recent method, SC3, constructs a cell–cell consensus matrix by combining multiple clustering solutions, and then performs hierarchical clustering with complete agglomeration on this consensus matrix (10). Cell subpopulations can also be identified using machine learning approaches (11,12) or by analyzing cell-specific gene regulatory networks (13). The number of subpopulations is usually required as input, but can also be determined by statistical approaches (10) or via the eigengap of the cell–cell similarity matrix (9). Unsupervised prediction of the number of cell subpopulations from data remains challenging.

Marker genes—the genes that best discriminate between cell subpopulations—can be estimated by differential gene expression analysis between pairs of subpopulations (14). For example, SIMLR uses the Laplacian score to infer marker genes for each cell subpopulation (9). SC3 infers marker genes using a paired-difference test on ranked mean expression values (10). Currently, most methods for marker gene identification (e.g. (7,10)) are carried out after clustering and identification of the cell subpopulations, i.e. without any direct link to the choice of clustering method. Below, we present a factorization method that performs clustering and marker gene identification in the same step.

Pseudotime, or pseudotemporal ordering of cells, describes a 1D projection of single-cell data that is based on a measure of similarity between cells (e.g. a distance in gene expression space). In conjunction with pseudotime inference, cell trajectories or lineages can be inferred that describe cell state transitions over (pseudo) time (15,16). Two major classes of methods for the estimation of pseudotime and cell trajectories are: (i) performing dimensionality reduction on the full data and then fitting principle curves to the cells in low-dimensional space; (ii) constructing a graph for which cells are nodes and edges connect similar cells (in high or low dimensional space), and then calculating the minimum spanning tree (MST) on this graph (17). Of the class (i) methods: Monocle 2 (18) infers pseudotime using a principle curve generated by iteratively computing mappings between a high-dimensional gene expression space and a low-dimensional counterpart. Pseudotime is then predicted by measuring the geodesic distance from each cell to a root cell. SLICER uses locally linear embedding for dimensionality reduction before constructing a minimum spanning tree (MST) on the low-dimensional space to infer trajectories (19). DPT uses a distance-based pseudotime after calculating transition probabilities between cells using a diffusion-like random walk (20,21). TSCAN (22) and Waterfall (23) employ similar strategies by embedding data into low-dimensional space and constructing a MST. Current methods in class (ii) include Wanderlust (24) and Wishbone (25): these construct a cell–cell graph and infer pseudotime by computing the distances from each cell to a root cell. A recent method, scEpath, takes an alternative approach by inferring a single-cell energy landscape and using this to estimate transition probabilities between cell states, and thus cellular trajectories (26). In a similar vein, CellRouter uses flow/transportation networks to identify cell state transitions (27). For the whole family of methods for pseudotime inference (the mathematical foundations of which vary considerably, see (28) for review), experimental validation of the temporal ordering of cells is difficult (15).

Despite efforts to predict lineages between cells from RNA (or DNA (29)) sequencing, significant challenges remain. Most current pseudotime inference methods can predict lineage relationships, however inferring multiple lineage branch points often remains beyond reach (30) (BioRxiv: https://www.biorxiv.org/content/early/2018/11/16/261768). Slingshot (31) can infer multiple branch points, but may require branch-specific (end point) information to do so. Monocle (18) can infer multiple branch points, however (similar to most trajectory inference methods) it identifies cell subpopulations separately from lineage relationships.

Predicting cell-to-cell communication between single cells or cell subpopulations is a major unaddressed challenge. This is in part due to the difficulty of integration: multiple inferred properties, including cell subpopulations, lineages, and marker genes, are all involved in cell–cell communication, thus inferring cell communication is a high-level task that will only be successful following coherent characterization of each of these constituent properties.

Here, we present SoptSC to address these challenges and infer cell lineage and communication networks. SoptSC, similarity matrix-based optimization for single-cell data analysis, performs multiple inference tasks based on a cell–cell similarity matrix that we introduce. The cell–cell relationships learned via the similarity matrix define which cells are clustered together, and complex lineages with multiple branches can be reconstructed. In the same step (i.e. decomposition of the similarity matrix), SoptSC also predicts marker genes for each cell subpopulation and along pseudotime. Communication networks between single cells are inferred using a probability model based on cell-specific expression of relevant sets of ligands, receptors, and target genes. By combination of these networks with the inferred cell lineage, SoptSC is able to predict complex regulatory interactions governing cell state transitions.

To study the clustering performance of SoptSC, we apply it to nine published scRNA-seq datasets with verified cluster labels, compare the results with other current clustering methods, and assess the ability of SoptSC to infer the number of clusters from the data. To quantitatively measure the accuracy and robustness of pseudotemporal ordering, we apply SoptSC to embryonic developmental systems where biological stages (and thus experimental time) are well-characterized. We compare SoptSC to DPT (21) and Monocle 2 (18). We go on to apply SoptSC to skin regeneration (32) to investigate lineage relationships, cell communication networks and crosstalk between cells. We also apply SoptSC to two datasets on hematopoiesis (33,34) and find a coherent set of consensus predictions between the two datasets that are supported by evidence from the literature.

MATERIALS AND METHODS

Overview

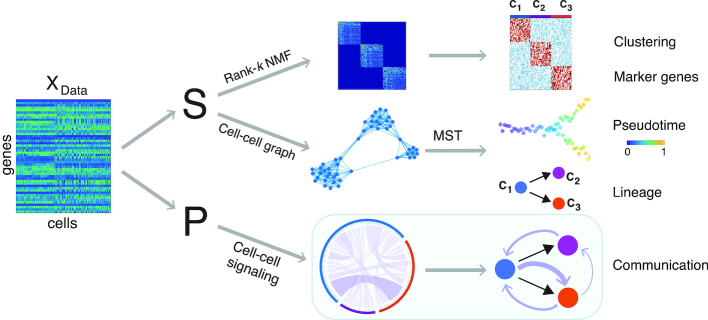
The methods of SoptSC are based on a cell–cell similarity matrix learned from the original gene-cell data matrix using a low-rank representation model (35). Clustering is obtained through the non-negative matrix factorization (NMF) of the similarity matrix (Figure 1). By computing the eigenvalue spectra of the associated graph Laplacian of a truncated consensus matrix, we estimate the number of clusters. Within the same NMF step as clustering, we also obtain an ordered list of marker genes for each cluster by comparing the relative weights of genes in each cluster. Pseudotime is inferred from a cell-to-cell graph, and cell lineage relationships between clusters are predicted using the minimal spanning tree of a cluster-to-cluster graph.

Figure 1.

Overview of the SoptSC framework and outputs generated. SoptSC takes a gene expression matrix X as an input and learns a proper cell-to-cell similarity matrix S. Cell clustering is carried out by performing non-negative matrix factorization on S. Marker genes for each cluster are found via the product of the factorized latent matrix and X. A cell–cell graph (constructed from S) is used to infer pseudotime by calculating the shortest path distance between cells on this graph. The lineage relationships are constructed via a minimum spanning tree over the cluster–cluster graph derived from the cell–cell graph. Cell-cell communication is predicted by SoptSC via cell–cell signaling probabilities that are based on single-cell gene expression of specific genes within a pathway in sender-receiver cell pairs.

To infer cell–cell communication networks (Figure 1), we identify signaling relationships based on the single-cell gene expression matrix for a pathway of interest. Signaling probabilities are defined based on weighted co-expression of signaling pathway activity in sender-receiver cell pairs. As input, the user provides a ligand (or a set of ligands) and cognate receptor (or a set of receptors), for example, ligands from the Wnt family, and Frizzled receptors. For each pathway, a set of target genes is also specified: a candidate list of genes that are known to be differentially regulated downstream of a ligand–receptor interaction, along with their sign (upregulated or downregulated). SoptSC computes signaling probabilities between sender cells (expressing ligand) and receiver cells (expressing receptor and exhibiting differential target gene activity). These single-cell signaling probabilities are combined to produce summaries and determine higher-level (e.g. cluster-to-cluster consensus) communication networks. Combining the consensus signaling networks with the lineage path allows SoptSC to infer feedback or feedforward interactions mediated by signaling factors. Below follows description of the key methods comprising SoptSC; full details of the methods can be found in the Supplemental Information: Extended Methods.

Cell-to-cell similarity matrix and cell clustering

The input to SoptSC is a single-cell gene expression matrix X of size m × n, with m genes and n cells. SoptSC learns a coefficient matrix Z of size n × n by minimizing the difference between X and XZ with low-rank and sparse constraints (35). The matrix Z captures the representation of gene expression in a single cell as a linear combination of gene expression in other cells. A similarity matrix is defined through symmetric weights S = max {|Z|, |Z^⊤|}, where Z^⊤ is the transpose of Z, |Z| (or |Z^⊤|) is a matrix with each element being the absolute value of the corresponding element in Z (or Z^⊤), and S_{i, j} (=S_{j, i}) for all i, j represents each component of the matrix S. S thus quantifies the similarity between cells.

To cluster cells based on their similarity, we use symmetric non-negative matrix factorization to decompose the (non-negative) similarity matrix S into the product of a non-negative low rank matrix H (of size n × k for k clusters) and its transpose, i.e. S = HH^⊤ (36,37). With this representation, the columns of H represent the cluster centroids, and the rows of H provide the relative weights of cells in each cluster. We assign cell i to the jth cluster when the largest element of the ith row of H is located at the jth position.

To estimate the number of clusters k, we construct a truncated consensus matrix and its graph Laplacian by performing NMF multiple times for different values of k (38,39). Upper and lower bounds are estimated for k: the lower bound is given by the number of near-zero eigenvalues of 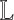(below a threshold ε), and the upper bound is given by the largest eigenvalue gap in 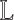. In practice, the upper bound is usually used to estimate k.

Marker gene identification

The non-negative low rank matrix H is also used to identify marker genes for each cluster. The element H_{i, j} represents a relative weight by which cell i belongs to the jth cluster. The jth column of H then defines a distribution of weights over all cells in the jth cluster. The weight for gene v in the jth (1 ≤ j ≤ k) cluster is given by

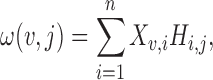(1)

where X_{v, i} denotes expression of the vth gene in cell i. Analysis of these weights then determines relative significance, giving a method to determine how well gene v delineates cluster j from the others. Marker genes are then defined: gene v is a marker for cluster j, if ω(v, j) reaches its largest value in cluster j, i.e. ω(v, j) = max _{1 ≤ u ≤ k}{ω(v, u)}.

Inference of pseudotime and cell lineage

To infer the cell lineage and pseudotemporal ordering of cells, we construct a cell-to-cell graph G based on the adjacency matrix A, which is derived from the similarity matrix S such that A_{i, j} = 1 if S_{i, j} > 0 and A_{i, j} = 0 otherwise. The distance between cells on G is defined as the shortest path length. We also construct a weighted cluster-to-cluster graph 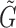, with edge weights given as the average distances between the cells comprising each of the two clusters. The cell lineage, which describes the cell state transitions between clusters, is inferred by computing the minimal spanning tree (MST) of the graph 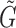. If the initial cluster can be set in advance, we construct the MST by setting this as the root. Otherwise, the initial cluster is estimated as the state that maximizes the path length over the MST.

Pseudotemporal ordering of cells is calculated by finding and sorting the shortest path lengths between each cell and the initial cell on G. An initial cell (if not provided in advance) is estimated such that the temporal ordering of cells and the cell lineage have highest concordance: for each cell w in the initial cluster, compute the shortest path distances between w and all other cells, and take the average of the distances between cell w and all other cells in each cluster. We let the concordance be defined by the Kendall rank correlation between the pseudotime values (averaged within clusters) and the relative positions of the clusters according to the lineage tree, and take the initial cell as that which maximizes the concordance (correlation).

Pathway-mediated cell–cell signaling network inference

In order to study how paracrine signals are sent from and received by single cells, we implement a method to predict cell–cell signaling networks mediated by specific ligand–receptor interactions. Directed edges are inferred between two cells where a high probability of signaling is predicted by the expression of ligand in a ‘sender’ cell, and the expression of its cognate receptor in a ‘receiver’ cell, along with appropriate expression of target genes of the pathway in the receiver cell. While such probabilities are not fully sufficient to define an interaction between a pair of cells, they represent necessary conditions for signaling, and can be indicative of spatial proximity of cells within a sample. Whereas previous works (40,41) (BioRxiv: https://www.biorxiv.org/content/early/2017/09/27/191056) have considered signaling activity by summing over cells within a given cluster, we seek to account for the heterogeneity between cells within the same cluster.

For a given pathway (e.g. Wnt signaling), we define a set of ligands as the protein products of the gene family, and a set of receptors as the proteins that bind these ligands. Also necessary as input is a set of target genes affected by the pathway along with their sign, i.e. upregulated or downregulated in response to pathway activation. Given such a ligand–receptor pair, with L and R denoting the distributions of gene expression over all cells for ligand and receptor, respectively, then let Y = [Y_{i, j}] (of size m₁ × n) denote the gene expression matrix of the m₁ genes that are upregulated by the pathway, and 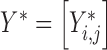(of size m₂ × n) denote the gene expression matrix of the m₂ genes that are downregulated by the pathway. The probability that a signal is sent from cell i to cell j via this pathway is then given by:

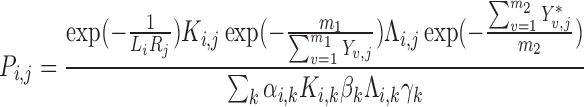(2)

where

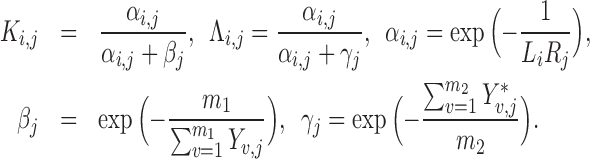The first exponential term, 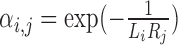, in Equation (2) estimates the likelihood of an interaction between cell i and cell j given the expression level of ligand in cell i and the associated receptor in cell j. If both are high, then the interaction probability is high; if either L_i or R_i is zero, the interaction rate is zero. The second exponential term (β_j) quantifies the expression of ‘activating’ target genes, i.e. those that are upregulated in cell j following a signaling cascade initiated by the ligand–receptor interaction. This term is weighted by coefficient K_{i, j}, which specifies that target genes only increase the signaling probability if the ligand–receptor interaction term α_i.j is sufficiently large. Similarly, the third exponential term (γ_j) quantifies the expression of ‘inhibiting’ target genes, i.e. those that are downregulated by the signaling pathway. This term is weighted by coefficient Λ_{i, j}, which acts similarly to K_{i, j}, considering the effects of inhibiting target genes only subsequent to a ligand–receptor interaction. The signaling probabilities are normalized by the sum of all signaling probabilities within the pathway.

The intuition underlying this formula is that if a ligand is highly expressed in cell i, the cognate receptor is highly expressed in cell j, and the target gene activity in cell j suggests that the signaling pathway may have been activated in this cell, then there is a chance that communication occurred between these two cells, quantified by the signaling probability P_{i, j}.

Consensus signaling networks and cluster-to-cluster communication

Given a ligand–receptor pair for a specific signaling pathway, the signaling network inferred is given by the weighted graph, in which the weights between cells are defined by P = [P_{i, j}], the probability of a signal being passed from cell i to cell j. For visualization of these networks between single cells we use the circlize package in R (42).

We also derive a number of summary statistics from the probability matrix P for use in various contexts. Let P^r be the probability matrix for {Lig_r, Rec_r}, and let {Lig_r, Rec_r; r = 1, 2, ..., N} denote a set of ligand–receptor pairs (for example a set could comprise ligand or receptor gene paralogs within a pathway, or co-signaling factors or co-receptors, or indeed ligands and receptors from distinct pathways). Then it is useful to consider the consensus signaling probability matrix, P^tot, which is constructed by taking the cell-wise average over all signaling probability matrices, P^r, i.e.

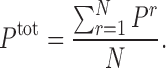(3)

It is also informative to consider the cluster-to-cluster signaling networks in order to predict where feedforward/feedback interactions may occur, and to compare with previous methods for cell–cell signaling study that have focussed on cluster-level signaling (40). Let c = {c₁, c₂, ..., c_k} give a clustering of cells by assigning each cell to one of k clusters. Then the probability of a signal passed between cluster u and v, mediated by a given ligand–receptor pair, is given by

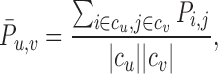(4)

where |c_u| represents the number of cells in cluster u.

RESULTS

SoptSC clusters cells in agreement with known identities

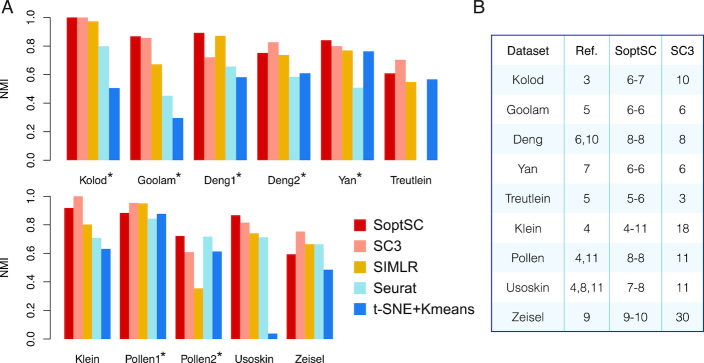
To assess the performance of SoptSC for clustering we compare it to four existing clustering methods: SC3 (10), SIMLR (9), Seurat (7) and tSNE (43) followed by k-means clustering (44) (tSNE + k-means) (Figure 2A). We use nine previsouly analyzed scRNA-seq datasets from a variety of biological systems (Supplementary Table S1) (45–53). For each of these datasets, cluster labels have been identified; five of these are considered “gold-standard” as they have been annotated and verified by experiments whereas the other four were identified computationally. Two of the gold-standard datasets (Deng (47) and Pollen (46)) have two different possible clusterings: we test the methods against both. In order to measure the agreement between verified and predicted cluster labels, we use the Normalized Mutual Information (NMI) (54) as a test statistic. The value of NMI ranges from zero to one, where one indicates perfect agreement between cluster labels.

Figure 2.

Benchmarking SoptSC against current methods for clustering. (A) Five clustering methods (SoptSC, SC3, SIMLR, Seurat, and t-SNE + k-means) are applied to a range of single-cell datasets where cell cluster labels are known or were previously validated. Normalized mutual information (NMI) is used as a measure of accuracy. Datasets marked by an asterisk are annotated ‘gold-standard’ for comparison purposes. (B) Prediction of the number of clusters by SoptSC or SC3, compared to a reference number of clusters (Ref.) from the original study; SoptSC predicts both lower and upper bounds.

For the three gold standard datasets with only one possible clustering, SoptSC has the highest NMI across all methods compared. SoptSC also performs well for two of the datasets where two possible clusterings exist (Deng and Pollen). For the remaining four datasets, the performance of SoptSC is comparable with SC3, and better than the other methods tested except for Zeisel (Figure 2A). When comparing the number of clusters predicted by SoptSC and SC3 against the ‘true’ number of clusters, i.e. that identified in the original study, denoted as ‘Ref.’ (Figure 2B and Supplementary Figure S1), SoptSC cluster prediction was in agreement with the true number in six out of nine cases with a difference of no more than one. For SC3, this level of agreement was observed in only 4/9 cases.

Thus, SoptSC and SC3 exhibit superior performance overall to the other methods tested. SoptSC and SC3 show comparable clustering performance with only slight differences: SoptSC outperforms SC3 for certain datasets and vice versa; SoptSC outperforms SC3 in terms of ability to predict the number of clusters a priori.

SoptSC infers pseudotime and cell lineage relationships consistent with biological trajectories

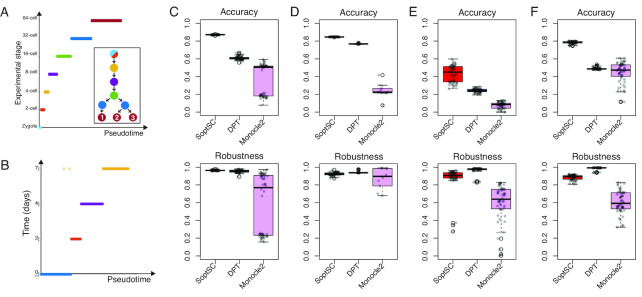
Assessment of pseudotemporal ordering of cells is challenging as there are few examples of data for which the true ordering of cells is known or can be reliably estimated. One way to assess pseudotime is through its correlation with experimental time, e.g. using the Kendall rank correlation coefficient measured between pseudotime and the experimental time labels obtained during data collection (21). Such a correlation can measure the ‘accuracy’ of pseudotime, with the caveats that this test can only be made at the experimental time points, and that cells are often not synchronized by developmental stage. (Indeed, this is one of the reasons we infer pseudotime in the first place.) Assessment of the robustness of pseudotemporal ordering can be made by subsampling the data, and calculating the robustness as the correlation between the pseudotime of the subsample and that of the full data.

Using these statistics to quantify pseudotime accuracy and robustness, we compared SoptSC to diffusion pseudotime (DPT) (21), which uses a diffusion map to determine low-dimensional coordinates, and Monocle 2 (18), which uses reversed graph embedding to infer pseudotime. We test these methods against datasets chosen for their clear temporal structure: early embryonic development (55), embryonic stem cell differentiation (52), and bone-marrow-derived dendritic cell differentiation (56). We also include a dataset from interfollicular epidermis where cell stage (temporal ordering) was inferred from the original study (32).

For each of these datasets, the pseudotemporal ordering inferred by SoptSC was found to be consistent with known developmental stages (Figure 3 A-B and Supplementary Figures S2–S4). We also found that the accuracy of the pseudotime inference was higher for SoptSC than for DPT or Monocle 2 in each case (Figure 3C–F). Under subsampling, SoptSC was more robust than Monocle 2, and within 10% of DPT in terms of robustness (Figure 3C–F), indicating that SoptSC is more accurate - and comparable in robustness—as the current state-of-the-art for studying pseudotime by these criteria.

Figure 3.

Assessment of SoptSC for pseudotime inference. (A) Pseudotemporal ordering of data from mouse early embryo development (55) is compared with the known biological stage. Inset shows the lineage inferred by SoptSC, colored by experimental stage of origin for each cluster. (B) Pseudotemporal ordering of embryonic stem cell data from (52) compared with experimental time. (C) Comparison of three methods for pseudotime inference with data from (55) using the Kendall rank correlation between pseudotime and experimental stage as a measure of accuracy, and by subsampling 90% of cells from the data 50 times (and comparison of subsets) to measure robustness. (D) Comparison as for (C) with embryonic stem cell data from (52). (E) Comparison as for (C) with bone-marrow-derived dendritic cells (56). (F) Comparison as for (C) with cells from the murine epidermis (32). Here the accuracy is measured by comparison with the pseudotime inferred in the original study.

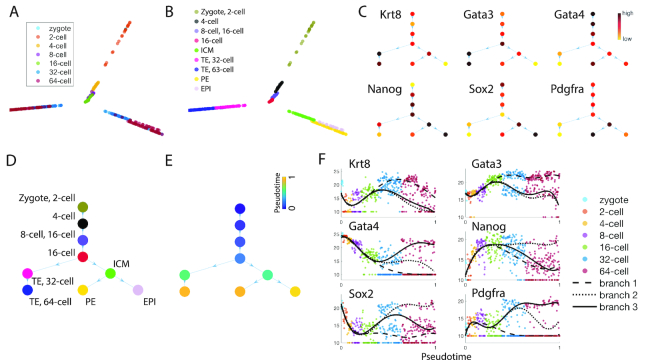
To assess lineage inference and marker gene identification in SoptSC, we analyzed two well-characterized embryonic datasets, for which the early lineage relationships are well-characterized (45,55). For Guo et al. (55) SoptSC identifies nine cell subpopulations that can be ascribed biological labels using predicted marker genes (Figure 4A–C). SoptSC inferred these stages from zygote to epiblast with high fidelity, giving rise to two branch points and three final cell types: trophectoderm (TE), primitive endoderm (PE), and the epiblast (EPI) (Figure 4D). Pseudotime along this trajectory was consistent with developmental stages (Figure 4E). In addition, we compared cluster identity with alternative methods (SC3, Seurat, and SIMLR), and pseudotime (Monocle2 and DPT). We found that SoptSC best recovers known biological information for clustering and pseudotime (Supplementary Figures S2 and S12A). For full details of the methods used for this comparison (and similar comparisons below) see the Supplemental Information: Extended Data Analysis.

Figure 4.

Inference of cell lineage and pseudotime during early embryonic development. (A) Visualization of data from mouse early embryonic development (55) by SoptSC, colored by the experimental labels from the original study. (B) Nine clusters were identified by SoptSC; labels were ascribed following marker gene expression profiling. (C) Lineage tree inferred by SoptSC, with average inter-cluster expression of selected markers shown. (D) Lineage relationships inferred by SoptSC, colored by clusters from (B), and labeled by the identified experimental stages from (A). (E) Pseudotime projected onto the lineage tree. (F) Marker genes plotted along pseudotime; lines correspond to polynomial regression for each branch. TE: Trophectoderm; PE: Primitive Endoderm; EPI: Epiblast.

SoptSC can also resolve branch-specific marker gene dynamics along pseudotime. Six marker genes identified by SoptSC are plotted along pseudotime (Figure 4F), showing distinguishable signatures for each lineage branch. By Gata4 alone, it is possible to identify all three lineages at a point in pseudotime around the 32- to 64-cell stage.

For the second embryonic dataset (45), SoptSC identifies subpopulations corresponding to known human developmental stages (Supplementary Figure S5), and a linear lineage from oocyte to blastocyst that is consistent with pseudotime (Supplementary Figure S5C–F). It is worth noting that SoptSC was able to extract distinct developmental stages for even this very small dataset (88 cells). Gene dynamics along pseudotime for embryonic markers (Supplementary Figure S5H) show good agreement between the predicted dynamics and previous studies (57).

Sequential cell signaling dynamics regulate epidermal regeneration during telogen

The mammalian epidermis, stratified into basal, suprabasal, and terminally differentiated layers, is a well-characterized adult stem cell system (58). However, significant questions remain regarding the cell subpopulations, heterogeneity, and cell–cell interactions (59,60). We applied SoptSC to an epidermal dataset of quiescent skin, where we analyzed the interfollicular epidermis (IFE), comprising 720 single cells (32). In the original study, five subpopulations were found in the IFE, one of which was the basal stem cell population (Figure 5A). SoptSC identified seven subpopulations, three of which comprise the basal stem cell population (clusters C₁, C₄, and C₅, Figure 5B). Thus we identified multiple basal subpopulations in the IFE in contrast to the original computational analysis.

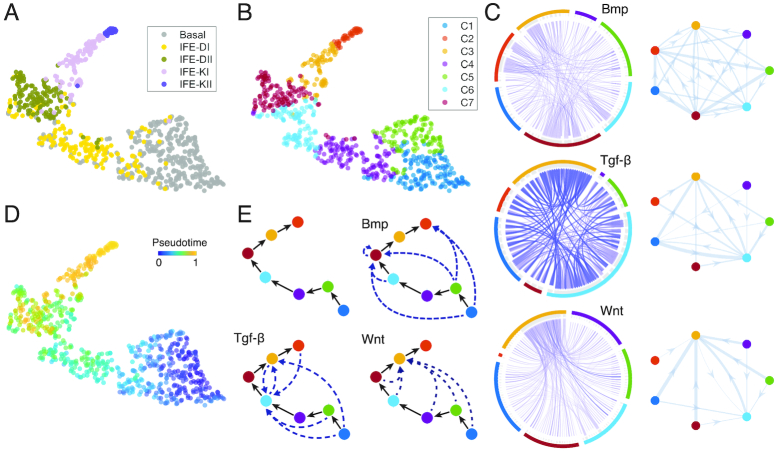
Figure 5.

Inference of epidermal lineage and signaling networks. (A) Cells from (32) projected into low dimension by SoptSC and colored by the cluster labels from the original study. (B) Cells colored by cluster labels identified by SoptSC. (C) Single-cell communication networks predicted for three pathways. Left: samples from full networks where edge weights represent the probability of signaling between cells. Right: cluster-to-cluster signaling interactions where edge weights represent sums over inter-cluster interactions. Colors correspond to cluster labels from part b. (D) Pseudotemporal ordering of cells. (E) SoptSC infers a linear lineage from basal to differentiated epidermal cells (top left). Summaries of the cluster-to-cluster signaling interactions with highest probability are given for the Bmp, Tgf-β and Wnt pathways.

We also compared the clusters identified by SoptSC with alternative methods (SC3, Seurat, and SIMLR) and the inferred pseudotime with Monocle2 and DPT. We found that SoptSC best recovers known biological information, for both clustering and pseudotime inference (Figure 3F and Supplementary Figures S6, S12B).

The pseudotime and cell lineage inferred by SoptSC show a linear trajectory, suggesting an initial basal stem cell state that gives rise to two further basal states before differentiating (clusters C₂, C₃, C₆, and C₇) (Figure 5D–E and Supplementary Figure S7). We found that markers genes identified by SoptSC overlapped considerably with known markers (Supplementary Figure S7B) and that the predicted lineage recapitulates known epidermal differentiation.

To study how cell–cell signaling regulates cell state transitions during epidermal differentiation, we constructed single-cell communication networks for Bmp, Tgf-β, and Wnt pathways (Figure 5C and Supplementary Figures S8 and S9), and observe distinct signaling patterns for each. For the Bmp pathway, the highest probabilities of pathway activation occur in the mid-differentiated epidermal population C₇, marked by Krt77 and Ptgs1. For the Tgf-β pathway the highest activation probabilities occur in C₆ and C₃ that mark early differentiated cells and late differentiated keratinocytes, respectively. Experimental work has demonstrated that Tgf-β is crucial for the terminal differentiation of keratinocytes (61). For the Wnt pathway, the highest activation probabilities occur in C₃, the subpopulation comprising terminally differentiated keratinocytes. Studies have shown that Wnt-Bmp signaling crosstalk regulates the development of mature keratinocytes (62), supporting the cell–cell communication predictions. In combination, these predictions constrain the signaling pathway dynamics: Tgf-β is activated earliest during epidermal differentiation, followed by Bmp, and then Wnt.

Hematopoietic lineage and cell–cell communication predictions suggest subpopulation-specific signaling interactions regulating differentiation

Hematopoiesis is the hierarchical formation of different blood cell types from a common multipotent stem cell and involves complex cell state transitions and cell fate decisions that are still incompletely understood (63,64). The prevailing model of a multistep differentiation process is under challenge from single-cell studies (65–68). The system thus provides an ideal test bed for lineage inference methods.

Olsson et al. (33) investigated myelopoiesis (hematopoiesis restricted to myeloid cells), and found an intriguing cell state preceding the granulocyte/monocyte cell fate decision, containing cells of mixed lineage identity, denoted ‘MultiLin’. Analysis by SoptSC found eight subpopulations (Figure 6A and B), which include the MultiLin state, and corresponds well to known hematopoietic stages. We compared the clusters identified by SoptSC with alternative methods (SC3, Seurat, and SIMLR) and inferred pseudotime with Monocle2 and DPT. We found that in each case SoptSC best recovers the biological information that is known about the system (Supplementary Figures S10, S11 and S12C–D).

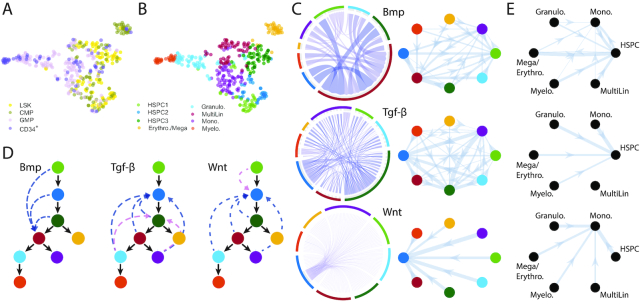
Figure 6.

Inference of subpopulations, pseudotime, lineage paths and signaling networks during myelopoiesis. (A) Cells from (33) projected into low dimension by SoptSC and colored by the cluster labels from the original study. LSK: Lin⁻Sca1⁺c-Kit⁺; CMP: common myeloid progenitor; GMP: granulocyte monocyte progenitor; CD34⁺: LSK CD34⁺ cells. (B) Cells colored by cluster labels identified by SoptSC. (C) Single-cell communication networks predicted for three pathways. Left: samples from full networks where edge weights represent the probability of signaling between cells. Right: cluster-to-cluster signaling interactions where edge weights represent sums over inter-cluster interactions. Colors correspond to cluster labels from part B. (D) Lineage inferred by SoptSC. Summaries of the cluster-to-cluster signaling interactions with highest probability are given for the Bmp, Tgf-β, and Wnt pathways. Blue: signaling prediction is supported by literature; pink: new signaling prediction. (E) Comparison of cluster-to-cluster signaling networks for Bmp, Tgf-β and Wnt (top down). Signaling probabilities from part (C) plotted on clusters identified in Seurat. Cluster identities ascribed via marker gene expression.

The inferred lineage contained two branch points, giving rise to an erythrocyte/megakaryocyte progenitor subpopulation (yellow), and to granulocyte/monocyte lineages from the ’MultiLin’ state (33) (Figure 6D). Notably, this lineage contains multiple successive branch points inferred in a single step with SoptSC, in comparison with previous analyses of these data that restricted inference of branch points to subsets of the data containing only one branch point at a time (18). Although distinct gene expression signatures for each branch were resolved along pseudotime (Supplementary Figure S10E), the heterogeneity present within the system is evident in the marker gene expression heatmap displaying considerable noise (Supplementary Figure S10D). Nonetheless, we found sufficient discriminative power to identify the cell subtypes present. For example, Gata2 marks the erythrocytic progenitors, and Fos marks the hematopoietic progenitor cells.

We next studied cell–cell communication during hematopoiesis mediated by Bmp, Tgf-β and Wnt (Figure 6C and D). SoptSC predicts that the strongest effects due to both Wnt and Tgf-β occur as feedback signals onto multipotent cell subpopulations. Experimental studies support the result that Wnt is most active during early hematopoiesis (69); however Wnt signaling during hematopoiesis is controversial (70,71), highlighting the need for single-cell studies to test competing hypotheses. Tgf-β is known to play a key role in the self-renewal of hematopoietic stem cells (72), in agreement with the predictions of SoptSC. We compared our predictions with a human-specific ligand–receptor interaction database (41) and found evidence for interactions between CD34⁺ and CD133⁺ stem/progenitor cells mediated by TGF-β. Bmp signaling is predicted to be most active in the MultiLin subpopulation (Figure 6D and Supplementary Figures S13–S15). This mixed lineage state is interesting as it defines a state immediately preceding the granulocytic/monocytic cell fate choice (33). Crisan et al. (73) showed that Bmp is crucial for maintaining the correct balance of myeloid cells, lending support to our prediction of its activation in myeloid progenitors.

In order to compare the cell communication predictions of SoptSC with alternative methods, we studied the clustering produced by Seurat combined with the cluster-to-cluster signaling probabilities inferred by SoptSC (Figure 6E and Supplementary Figure S11E, G–H). For Seurat clustering, we found that the reduced granularity (6 rather than 8 clusters) missed effects found by SoptSC, e.g. activation of Bmp in myeloid progenitor cells; the Seurat clustering showed activation only in an HSPC population. For Tgf-β signaling, both methods predicted activation in HSPCs. For Wnt signaling, the Seurat clustering predicted activation in the monocyte progenitor population, downstream of HSPCs. This highlighted possible discrepancies due to clustering and the need for methods that are consistent across tasks.

We also analyzed a hematopoietic dataset from Nesterowa et al. (34), offering an opportunity to compare single-cell hematopoietic studies and assess similarities and differences between them. SoptSC identifies six subpopulations (Figure 7A and Supplementary Figure S16), which can be readily mapped to known hematopoietic states via marker gene expression (Supplementary Figure S16D). In this analysis, granulocyte and monocyte progenitors are clustered together (GM) and distinct branches are found for lymphoid progenitors (L) and for erythrocyte/megakaryocyte progenitors (EM) (Figure 7C). The three branches inferred by SoptSC correspond well with the original analysis (see Figure 4A in (34) and Supplementary Figure S16). It was not possible to perform similar comparisons to other methods in this case, since no previously identified cluster labels were available with which to compare. However, we can compare the predictions here with those for the Olsson et al. data above. Doing so immediately suggests consistency between the lineages, except that the Olsson data do not contain lymphoid cells. Thus we are able to derive a ‘consensus lineage’ that combines both datasets (Figure 7D).

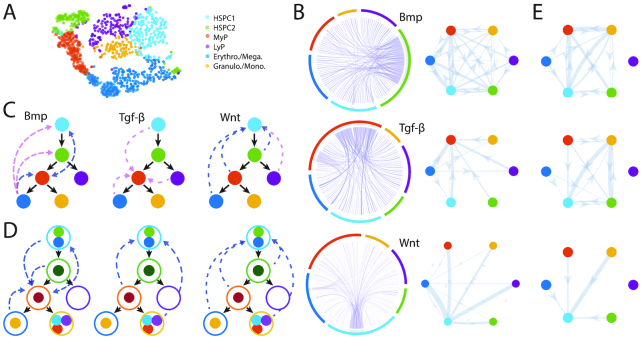
Figure 7.

Inference of subpopulations, pseudotime, lineage paths and signaling networks for mouse hematopoietic stem cell differentiation. (A) Visualization and clustering of cells from HSPCs (34) by SoptSC. MyP: Myeloid Progenitor; LyP: Lymphoid Progenitor. (B) Single-cell signaling networks predicted for three pathways. Left: samples from full networks where edge weights represent the probability of signaling between cells. Right: cluster-to-cluster signaling interactions where edge weights represent sums over inter-cluster interactions. Colors correspond to cluster labels from part A. (C) Lineage inferred by SoptSC. Summaries of the cluster-to-cluster signaling interactions with highest probability are given for the Bmp, Tgf-β, and Wnt pathways. Blue: signaling prediction supported by literature; pink: new signaling prediction. (D) Comparison of lineage and signaling predictions from Olsson and Nesterowa datasets. Consensus lineage shown: solid circles for Olsson clusters (correspond to Figure 6); open circles for Nesterowa clusters. Edges denote signaling predictions made either for Olsson or Nesterowa data analysis that are supported by evidence from literature. (E) Signaling probabilities from Olsson data are plotted on the consensus lineage from panel (D), enabling direct comparison of predicted cluster–cluster communication between Olsson and Nesterowa (panel B).

To infer signaling interactions and cell–cell communication, we again use Bmp, Tgf-β and Wnt signaling (Figure 7B–C and Supplementary Figures S17–S19). Overall, we see higher levels of ligand expression than in the previous two datasets analyzed, and fewer ‘activated’ cells (cells that express receptor and regulate downstream target genes accordingly). We found that Bmp signaling was predicted to provide feedback onto the multipotent progenitor populations from myeloid (GM) progenitors. The pathway was also predicted to be active within the myeloid progenitor population, in close agreement with previous predictions (33) and the literature (73). Wnt signaling provided feedback onto the most naive stem cell population, which is in concordance with predictions with SoptSC for Olsson et al. and with experimental work (69). Notably, for (34), lymphoid progenitor cells signal to multipotent cells via Wnt: such communication could improve the robustness of the myeloid-lymphoid branching cell fate decision (74). For Tgf-β, the highest probability of signaling occurs to myeloid progenitors, suggesting different feedback signals, in part mediated by the lymphoid progenitors that are not present within the Olsson et al. dataset. We also find interactions mediated by Tgf-β signaling to stem cells (Figure 7 B) as predicted for Olsson et al.; these are not plotted on the cell lineage as they are below the threshold used to identify top interactions, but they still may play an important regulatory role. Overall, the consensus cell communication networks and the comparison of communication predictions between Olsson and Nesterowa datasets demonstrate high levels of consistency for Bmp and Wnt, with some overlap for Tgf-β (Figure 7D and E).

DISCUSSION

Here, we present optimization-based methods to infer cell lineage and communication networks from scRNA-seq data. At the heart of SoptSC is a structured cell-to-cell similarity matrix, which preserves intrinsic global and local structure with appropriate low-rank constraints (35). Local information is learned from a low-dimensional data representation by t-distributed stochastic neighbor embedding: this is a key step for the construction of a structured cell–cell similarity matrix. SoptSC then clusters cells, and infers pseudotime, marker genes, and lineage relationships from the similarity matrix. By numerous tests on recently published datasets, and with comparison to current methods, we have found SoptSC to produce results substantially consistent with the known biology, and identify new predictions to be tested in the lab.

Importantly, the methods employed for inference of clusters, pseudotime, lineage, and marker genes derive from a single theoretical framework, making them directly and intuitively comparable. This is in contrast with most current scRNA-seq analysis pipelines (e.g. Seurat (7), SCANPY (75), and Monocle (18)), which combine multiple methods to analyze data. Seurat, for example, uses distinct methods to cluster cells and to find marker genes by differential expression. SoptSC finds marker genes by identifying genes most likely to be expressed in each subpopulation, and consequently these are unique for each cluster. To study large, complex, or heterogeneous data, it is often worthwhile to perform multiple analyses by complementary means and seek the consensus between them, e.g. for trajectory inference (bioRxiv: https://www.biorxiv.org/content/early/2018/03/05/276907).

The combination of cell lineage and cell communication predictions facilitates biological discovery by identifying how cell state transitions can be regulated by specific pathways at the level of cell-to-cell communication. These shed light on regulatory interactions that occur during development or differentiation. For example, during hematopoiesis, analysis via SoptSC of two independent datasets predicted that myeloid progenitor cell populations were targeted specifically by Bmp signaling. Target populations for Wnt or Tgf-β signaling were found to be more varied. During epidermal regeneration, temporally constricted signaling was predicted to regulate keratinocyte differentiation, with Tgf-β signaling earliest to basal cells within the epidermis, before subsequent cell–cell communication by Bmp and then Wnt.

Recent studies have made significant progress in predicting gene regulatory networks from single-cell data (13,76,77). SoptSC could also be combined with optimization approaches for gene regulatory network construction (78). Remaining significant challenges for scRNA-seq data analysis include confounding biological effects (e.g. due to cell cycle stages) and effects due to dropout (79,80). Complementary methods developed to address these can be directly applied to input data as a preprocessing step before using SoptSC. For example, a recent method for imputation to handle gene dropout effects can enhance scRNA-seq data quality by predicting which transcripts are likely to be affected by dropout noise (80). This could be helpful for SoptSC signaling predictions by identifying ligands or receptors that are likely affected by dropout, in order to perform imputation on these genes specifically, rather than on the full dataset, thus helping to remove effects due to technical variation while preserving biological variation across cells. Several methods to regress out the effects of the cell cycle (81,82) could also ameliorate data preprocessing.

Assessment of new cell subpopulations predicted by scRNA-seq analyses often begins by demonstrating that cells of the new subpopulation can be marked in vivo, e.g. by in situ hybridization using predicted marker genes. To ascribe function, experiments such as clonogenic or differentiation assays, or genetic perturbations to target genes within the new subpopulation are required. Predictions by SoptSC of cell-to-cell communication also require rigorous testing in vivo. To do so, cells isolated from putative subpopulations could be plated and their responses to extraneous ligands tested. Subsequently, genetic perturbations to members of a given pathway can offer further validation.

To probe new cell states in higher resolution we should make greater use of single-cell signaling predictions, by analyzing individual transcriptional states of different ‘signaling’ cells within a subpopulation. We must be cautious here of confounding effects due to technical noise (see discussion of dropout above). At the same time, simultaneous signaling pathway analyses provide additional means with which to handle dropout: i.e. by combining candidate ‘dropout’ genes with details on signaling pathway co-expression from curated signaling pathways as a means to improve the predictions of effects due to dropout.

As datasets of cells become widespread (67,83,84), computational efficiency becomes a challenge for many current single-cell data analysis methods, and new approaches are needed (85). For SoptSC, the computational cost associated with NMF contributes the most to the overall computational cost. As such, improvements and better algorithms for NMF will significantly improve the efficiency overall (86).

Lineage inference for complex heterogeneous data remains challenging. Compounding this is the lack of data for which the ground truth is known: in many cases even the cell states are not known, making validation of lineage relationships infeasible. SoptSC has nonetheless managed to infer complex lineage hierarchies that are consistent with current knowledge. If we compare the lineage predicted by SoptSC for the Olsson et al. dataset (33) with previous analysis of these data (18), we find that SoptSC is able to resolve multiple branch points simultaneously. Despite this, improvements to lineage inference are still needed. These include automatically detecting multiple disconnected lineages and inferring bidirectional arrows for certain cell state transitions. Both of these require alternative approaches, since the minimal spanning tree-based methods used here and elsewhere (18,31,87,88) do not permit such features.

Single-cell transcriptomic data analysis comes with a particular set of promises and pitfalls. The key strength of these data lies in the ability to measure many thousands of signals simultaneously and provide a global quantification of the transcriptional state of a cell. This comes at the expense of accuracy in the measurement of individual transcripts, due to noise and technical effects. With these challenges in mind, we have developed methods to perform multiple single-cell data analysis tasks coherently and unsupervised. While much remains to be done, these methods enable new predictions of important cellular relationships, such as lineage hierarchies and the single-cell communication networks that direct them.

SOFTWARE AVAILABILITY

SoptSC is available as a MATLAB (Naticks, MA) package at: https://github.com/WangShuxiong/SoptSC, and as an R package at: https://mkarikom.github.io/RSoptSC.

DATA AVAILABILITY

All the datasets used in this paper are publicly available; below we give the relevant accession numbers. The datasets used for evaluating the performance of clustering (Figure 2) are downloaded from https://hemberg-lab.github.io/scRNA.seq.datasets/. Other datasets are available from: www.sciencedirect.com/science/article/pii/S1534580710001103 for mouse embryonic development (55) (Supplementary Table S4); GSE36552 for human embryonic development (45); GSE67602 for epidermal regeneration (32); GSE70245 for myelopoiesis (33); GSE81682 for hematopoiesis (34); GSE48968 for bone-marrow-derived dedritic cell stimulation (56).

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

National Institutes of Health [R01GM107264 to Q.N., R01NS095355 to Q.N., R01GM123731 to Q.N., U01AR073159 to Q.N.]; National Science Foundation [DMS1562176 to Q.N., DMS1763272 to Q.N.]; Simons Foundation [594598 to Q.N.]. Funding for open access charge: National Institutes of Health.

Conflict of interest statement. None declared.