Group SLOPE - adaptive selection of groups of predictors

Abstract

Sorted L-One Penalized Estimation (SLOPE, Bogdan et al., 2013, 2015) is a relatively new convex optimization procedure which allows for adaptive selection of regressors under sparse high dimensional designs. Here we extend the idea of SLOPE to deal with the situation when one aims at selecting whole groups of explanatory variables instead of single regressors. Such groups can be formed by clustering strongly correlated predictors or groups of dummy variables corresponding to different levels of the same qualitative predictor. We formulate the respective convex optimization problem, gSLOPE (group SLOPE), and propose an efficient algorithm for its solution. We also define a notion of the group false discovery rate (gFDR) and provide a choice of the sequence of tuning parameters for gSLOPE so that gFDR is provably controlled at a prespecified level if the groups of variables are orthogonal to each other. Moreover, we prove that the resulting procedure adapts to unknown sparsity and is asymptotically minimax with respect to the estimation of the proportions of variance of the response variable explained by regressors from different groups. We also provide a method for the choice of the regularizing sequence when variables in different groups are not orthogonal but statistically independent and illustrate its good properties with computer simulations. Finally, we illustrate the advantages of gSLOPE in the context of Genome Wide Association Studies. R package grpSLOPE with an implementation of our method is available on CRAN.

1 Introduction

Consider the classical multiple regression model of the form

$$y=X\beta +z,$$ (1.1)

where y is the n dimensional vector of values of the response variable, X is the n by p experiment (design) matrix and z ~ 𝒩(0, σ²I_n). We assume that y and X are known, while β is unknown. In many applications the purpose of the statistical analysis is to recover the support of β, which identifies the set of important regressors. Here, the true support corresponds to truly relevant variables (i.e. variables which have impact on observations). Common procedures to solve this model selection problem rely on minimization of some objective function consisting of the weighted sum of two components: first term responsible for the goodness of fit and second term penalizing the model complexity. Among such procedures one can mention classical model selection criteria like the Akaike Information Criterion (AIC) (Akaike, 1974) and the Bayesian Information Criterion (BIC) (Schwarz, 1978), where the penalty depends on the number of variables included in the model, or LASSO (Tibshirani, 1996), where the penalty depends on the ℓ₁ norm of regression coefficients. The main advantage of LASSO over classical model selection criteria is that it is a convex optimization problem and, as such, it can be easily solved even for very large design matrices.

LASSO solution is obtained by solving the optimization problem

$$\underset{b}{\text{argmin}}\left\{\frac{1}{2}{\Vert y-Xb\Vert }^2+{\lambda }_L{\Vert b\Vert }_1\right\},$$ (1.2)

where λ_L is a tuning parameter defining the trade-off between the model fit and the sparsity of solution. In practical applications the selection of good λ_L might be very challenging. For example it has been reported that in high dimensional settings the popular cross-validation typically leads to detection of a large number of false regressors (see e.g. Bogdan et al., 2015). The general rule is that when one reduces λ_L, then LASSO can identify more elements from the true support (true discoveries) but at the same time it generates more false discoveries. In general the numbers of true and false discoveries for a given λ_L depend on unknown properties on the data generating mechanism, like the number of true regressors and the magnitude of their effects. A very similar problem occurs when selecting thresholds for individual tests in the context of multiple testing. Here it was found that the popular Benjamini-Hochberg rule (BH Benjamini and Hochberg, 1995), aimed at control of the False Discovery Rate (FDR), adapts to the unknown data generating mechanism and has some desirable optimality properties under a variety of statistical settings (see e.g. Abramovich et al., 2006; Bogdan et al., 2011; Neuvial and Roquain, 2012; Frommlet and Bogdan, 2013). The main property of this rule is that it relaxes the thresholds along the sequence of test statistics, sorted in the decreased order of magnitude. Recently the same idea was used in a new generalization of LASSO, named SLOPE (Sorted L-One Penalized Estimation, Bogdan et al., 2013, 2015). Instead of the ℓ₁ norm (as in LASSO case), the method uses FDR control properties of J_λ norm, defined as follows; for sequence ${\{\lambda \}}_{i=1}^p$ satisfying λ₁ ≥ … ≥ λ_p ≥ 0 and b ∈ ℝ^p, $J_{\lambda }(b):={\sum }_{i=1}^p{\lambda }_i{\mid b\mid }_{(i)}$, where |b|₍₁₎ ≥ … ≥ |b|_(p) is the vector of sorted absolute values of coordinates of b. SLOPE is the solution to a convex optimization problem

$$\underset{b}{\text{argmin}}\left\{\frac{1}{2}\Vert y-Xb{\Vert }^2+J_{\lambda }(b)\right\},$$ (1.3)

which clearly reduces to LASSO for λ₁ = … = λ_p =: λ_L. Similarly as in classical model selection, the support of the solution defines the subset of variables estimated as relevant. In (Bogdan et al., 2013, 2015) it is shown that when the sequence λ corresponds to the decreasing sequence of thresholds for BH then SLOPE controls FDR under orthogonal designs, i.e. when X^TX = I_n. Moreover, in (Su and Candès, 2016) it is proved that SLOPE with this sequence of tuning parameters adapts to unknown sparsity and is asymptotically minimax under orthogonal and random Gaussian designs.

In the sequence of examples presented in (Bogdan et al., 2013, 2015; Brzyski et al., 2017) it was shown that SLOPE has very desirable properties in terms of FDR control in the case when regressor variables are weakly correlated. While there exist other interesting approaches which allow to control FDR under correlated designs (e.g. Barber and Candès, 2015), the efforts to prevent detection of false regressors which are strongly correlated with true ones inevitably lead to a loss of power. An alternative approach to deal with strongly correlated predictors is to simply give up the idea of distinguishing between them and include all of them into the selected model as a group. This leads to the problem of group selection in linear regression, extensively investigated and applied in many fields of science. In many of these applications the groups are selected not only due to the strong correlations but also by taking into account the problem-specific scientific knowledge. It is also common to cluster dummy variables corresponding to different levels of qualitative predictors.

Probably the most well known convex optimization method for selection of groups of explanatory variables is the group (gLASSO Bakin, 1999). For a fixed tuning parameter, λ_gL > 0, the gLASSO estimate is most frequently (e.g. Yuan and Lin, 2006; Simon et al., 2013) defined as a solution to optimization problem

$$\underset{b}{\text{argmin}}\left\{\frac{1}{2}{\Vert y-\sum _{i=1}^m{X}_{I_i}{b}_{I_i}\Vert }^2+\sigma {\lambda }_{gL}\sum _{i=1}^m\sqrt{\mid I_i\mid }{\Vert b_{I_i}\Vert }_2\right\},$$ (1.4)

where the sets I₁, …, I_m form a partition of the set {1, …, p}, |I_i| denotes the number of elements in set I_i, X_Ii is the submatrix of X composed of columns indexed by I_i and b_Ii is the restriction of b to indices from I_i. The method introduced in this article is, however, closer to the alternative version of gLASSO, in which penalties are imposed on ||X_Ii b_Ii||₂ rather than ||b_Ii||₂. This method was formulated in (Simon and Tibshirani, 2013), where the authors defined an estimate of β by

$${\beta }^{\text{gL}}:=\underset{b}{\text{argmin}}\left\{\frac{1}{2}{\Vert y-\sum _{i=1}^m{X}_{I_i}{b}_{I_i}\Vert }_2^2+\sigma {\lambda }_{gL}\sum _{i=1}^m\sqrt{\mid I_i\mid }{\Vert X_{I_i}{b}_{I_i}\Vert }_2\right\},$$ (1.5)

with the condition ${\Vert X_{I_i}{\beta }_{I_i}^{\text{gL}}\Vert }_2>0$ serving as a group relevance indicator.

Similarly as in the context of regular model selection, the properties of gLASSO strongly depend on the shrinkage parameter λ_gL, whose optimal value is the function of unknown parameters of true data generating mechanism. Thus, a natural question arises of whether the idea of SLOPE can be used for construction of a similar adaptive procedure for the group selection. To answer this query in this paper we define and investigate the properties of the group SLOPE (gSLOPE). We formulate the respective optimization problem and provide the algorithm for its solution. We also define the notion of the group FDR (gFDR), and provide the theoretical choice of the sequence of regularization parameters, which guarantees that gSLOPE controls gFDR in the situation when variables in different groups are orthogonal to each other. Moreover, we prove that the resulting procedure adapts to unknown sparsity and is asymptotically minimax with respect to the estimation of the proportions of variance of the response variable explained by regressors from different groups. Additionally, we provide a way of constructing the sequence of regularization parameters under the assumption that the regressors from distinct groups are independent and use computer simulations to show that it allows to control gFDR. Good properties of group SLOPE are illustrated using the practical example of Genome Wide Association Study. R package grpSLOPE with an implementation of our method is available on CRAN. All scripts used in simulations as well as in real data analysis are available at https://github.com/dbrzyski/gSLOPE. This repository contains also R scripts which were used to generate article figures.

2 Group SLOPE

2.1 Formulation of the optimization problem

Let the design matrix X belong to the space M(n, p) of matrices with n rows and p columns. Furthermore, suppose that I = {I₁, …, I_m} is some partition of the set {1, …, p}, i.e. I_i’s are nonempty sets, I_i ∩ I_j = ∅ for i ≠ j and ⋃I_i = {1, …, p}. We will consider the linear regression model with m groups of the form

$$y=\sum _{i=1}^m{X}_{I_i}{\beta }_{I_i}+z,$$ (2.1)

where X_Ii is the submatrix of X composed of columns indexed by I_i and β_Ii is the restriction of β to indices from the set I_i. We will use notation l₁, …, l_m to refer to the ranks of submatrices X_I1, …, X_Im. To simplify notation later, we will assume that l_i > 0 (i.e. there is at least one nonzero entry of X_Ii for all i). Besides this, X may be an arbitrary matrix, in particular linear dependence inside each of the submatrices X_Ii is allowed.

In this article we will treat the value ||X_Ii β_Ii||₂ as a measure of an impact of i^th group on the response and we will say that the group i is truly relevant if and only if ||X_Ii β_Ii||₂ > 0. Thus our task of the identification of the relevant groups is equivalent with finding the support of the vector ⟦β⟧_I,X := (||X_I1β_I1||₂, …, ||X_Im β_Im||₂)^⊤.

To estimate the nonzero coefficients of ⟦β⟧_I,X, we will use a new penalized method, namely group SLOPE (gSLOPE). For a given nonincreasing sequence of nonnegative tuning parameters, λ₁, …, λ_m, a given sequence of positive weights, w₁, …, w_m, and a design matrix, X, the gSLOPE estimator of regression coefficients, β^gS, is defined as any solution to the optimization problem

$${\beta }^{\text{gS}}:=\underset{b}{\text{argmin}}\left\{\frac{1}{2}{\Vert y-Xb\Vert }_2^2+\sigma J_{\lambda }(W{⟦b⟧}_{I,X})\right\},$$ (2.2)

where W is a diagonal matrix with W_i,i := w_i, for i = 1, …, m. The estimate of ⟦β⟧_I,X support is simply defined by the indices corresponding to nonzeros of ⟦β ^gS ⟧_I,X.

It is easy to see that when one considers p groups containing only one variable (i.e. singleton groups situation), then taking all weights equal to one reduces (2.2) to SLOPE (1.3). On the other hand, taking $w_i=\sqrt{\mid I_i\mid }$ and putting λ₁ = … = λ_m =: λ_gL, immediately gives gLASSO problem (1.5) with the smoothing parameter λ_gL. The gSLOPE could be therefore treated both: as the extension to SLOPE, and the extension to group LASSO.

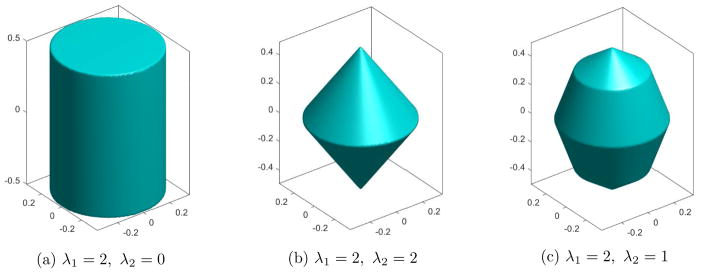
As shown in Appendix B the function J_λ,I,W,X(b) := J_λ(W⟦b⟧_I,X) is a seminorm and becomes a norm when the design matrix X is of the full rank. Figure 1 illustrates how the shape of the unit ball in the norm J_λ,I,W(b) := J_λ(W⟦b⟧_I) depends on the selection of the λ sequence. In this example p = 3, m = 2, I₁ := {1, 2} and I₂ := {3}. In case when only the first coefficient in the λ sequence is larger than zero J_λ,I,W(b) = λ₁ max_i∈{1,2} w_i||β_Ii||₂, and the corresponding ball takes form of the cylinder. The privileged solutions occur on the “edges” of this cylinder and have the same weighted group effects for both groups (i.e. $w_1\sqrt{{\beta }_1^2+{\beta }_2^2}=w_2\mid {\beta }_3\mid$). When λ₁ = λ₂ > 0 then the the ball takes the form of the “spinning top”, with “edges” occuring when at least one group effect is equal to zero. Then the group SLOPE reduces to the group LASSO and has a tendency to select a sparse solution. When λ₁ > λ₂ > 0 the corresponding ball has both types of edges and encourages the dimensionality reduction in both ways: by inducing the sparsity and making some of the weighted group effects to be equal to each other.

Figure 1.

Unit balls of J_λ,I,W norm for different λ. Weights w₁ and w₂ are equal to $\sqrt{2}$ and 1. The edges in (a) correspond to the same weighted group effects, i.e. $w_1\sqrt{{\beta }_1^2+{\beta }_2^2}=w_2\mid {\beta }_2\mid =0.5$; all edges in (b) contain at least one zero group effect (gLASSO); in (c) both types of edges appear.

Now, let us again consider an arbitrary m > 0, define p̃ = l₁+…+l_m and examine the following partition, 𝕀 = {𝕀₁, …, 𝕀_m}, of the set {1, …, p̃}

$${\mathbb{I}}_1:=\{1,\dots ,l_1\},{\mathbb{I}}_2:=\{l_1+1,\dots ,l_1+l_2\},\dots ,{\mathbb{I}}_m:=\left\{\sum _{j=1}^{m-1}{l}_i+1,\dots ,\sum _{j=1}^m{l}_i\right\}.$$

Observe that each X_Ii can be represented as X_Ii = U_iR_i, where U_i is a matrix with l_i orthogonal columns of a unit l₂ norm, whose span coincides with the space spanned by the columns of X_Ii, and R_i is the corresponding matrix of a full row rank. Define n by l matrix X̃ by putting X̃_𝕀i := U_i for i = 1, …, m. Now observe that after defining vector ω by conditions ω_𝕀i := R_ib_Ii for i ∈ {1, …, m}, we immediately obtain

$$\begin{gathered} Xb={\sum }_{i=1}^m{X}_{I_i}{b}_{I_i}={\sum }_{i=1}^m{U}_i{R}_I{b}_{I_i}={\sum }_{i=1}^m{\stackrel{\sim }{X}}_{{\mathbb{I}}_i{\omega }_{{\mathbb{I}}_i}}=\stackrel{\sim }{X}\omega , \\ {\left({⟦b⟧}_{I,X}\right)}_i={\Vert X_{I_i}{b}_{I_i}\Vert }_2={\Vert R_i{b}_{I_i}\Vert }_2={\Vert {\omega }_{{\mathbb{I}}_i}\Vert }_2 \end{gathered}$$ (2.3)

and for ⟦ω⟧_𝕀 := (||ω_𝕀1||₂, …, ||ω_𝕀m||₂)^⊤ the problem (2.2) can be equivalently presented in the form

$${\omega }^{\text{gS}}:=\underset{\omega }{\text{argmin}}\left\{\frac{1}{2}{\Vert y-\stackrel{\sim }{X}\omega \Vert }_2^2+\sigma J_{\lambda }(W{⟦\omega ⟧}_{\mathbb{I}})\right\},$$ (2.4)

where ω^gS and β^gS are linked via conditions ${\omega }_{{\mathbb{I}}_i}^{\text{gS}}:=R_i{\beta }_{I_i}^{\text{gS}}$, i = 1, …, m. Therefore to identify the relevant groups and estimate their group effects it is enough to solve the optimization problem (2.4). We will say that (2.4) is the standardized version of the problem (2.2).

Remark 2.1

The formulation of the group SLOPE was proposed independently in (Brzyski et al., 2015) (earlier version of this article) and in (Gossmann et al., 2015). In (Gossmann et al., 2015) only the case when the weights w_i are equal to the square root of the group size is considered and penalties are imposed directly on ||β_Ii||₂ rather than on group effects ||X_Ii β_Ii||₂. This makes the method of (Gossmann et al., 2015) dependent on scaling or rotations of variables in a given group. In comparison to (Gossmann et al., 2015), where a Monte Carlo approach for estimating the regularizing sequence was proposed, our article lays theoretical foundations and provides the guidelines for the choice of the sequence of smoothing parameters, so gSLOPE can control FDR and has desired estimation properties.

2.2 Numerical algorithm

We will at first show that the problem of solving (2.4) can be easily reduced to the situation when W is the identity matrix. For this aim we define a diagonal matrix M such that for $j\in {\mathbb{I}}_i{M}_{j,j}:=w_i^{-1}$. Then observe that

$$J_{\lambda ,\mathbb{I},W}(\omega )=J_{\lambda }(W{⟦\omega ⟧}_{\mathbb{I}})=J_{\lambda }({⟦M^{-1}\omega ⟧}_{\mathbb{I}})=J_{\lambda ,\mathbb{I},{\mathbf{I}}_{\stackrel{\sim }{p}}}(M^{-1}\omega )=:J_{\lambda ,\mathbb{I}}(M^{-1}\omega ).$$ (2.5)

Since M is nonsingular, we can substitute η := M⁻¹ω and consider equivalent formulation of (2.4), ${\eta }^{\ast }:={\text{argmin}}_{\eta }\left\{\frac{1}{2}{\Vert y-\stackrel{\sim }{X}M\eta \Vert }_2^2+J_{\sigma \lambda ,\mathbb{I}}(\eta )\right\}$, and recover ω^gS as ω^gS = Mη^*. This allows to recast gSLOPE as a problem with unit weights.

Now, the above problem is of the form $\underset{b}{\text{minimize}}\{\underset{g(b)}{\underbrace{{\Vert y-\mathcal{X}b\Vert }_2^2/2}}+\underset{h(b)}{\underbrace{J_{\lambda ,\mathbb{I}}(b)}}\}$, where g and h are convex functions and g is differentiable. There exist efficient methods, namely proximal gradient algorithms, which could be applied to find numerical solution in such situation. To design efficient algorithms, however, h must be prox-capable, meaning that there is known fast algorithm for computing the proximal operator for h,

$${\text{prox}}_{th}(u):=\underset{b}{\text{argmin}}\left\{\frac{1}{2t}{\Vert u-b\Vert }_2^2+h(b)\right\},$$ (2.6)

for each u ∈ ℝ^p̃ and t > 0.

To derive the proximal operator for the group SLOPE, we at first assume without the loss of generality that σ = 1. Now, we need to find the algorithm to minimize $\frac{1}{2t}{\Vert u-b\Vert }_2^2+J_{\lambda ,\mathbb{I}}(b)$, for any u ∈ ℝ^p̃ and t > 0, which is equivalent to finding the numerical solution to the problem

$${\text{prox}}_J(u):=\underset{b}{\text{argmin}}\left\{\frac{1}{2}{\Vert u-b\Vert }_2^2+J_{\overline{\lambda },\mathbb{I}}(b)\right\},\text{for}\stackrel{\sim }{\lambda }:=t\lambda .$$ (2.7)

As discussed in Appendix D, this problem can be solved in two steps

$$\{\begin{array}{l}{c}^{\ast }:={\text{argmin}}_{c\in R^m}\left\{\frac{1}{2}{\Vert {⟦u⟧}_{\mathbb{I}}-c\Vert }_2^2+J_{\stackrel{\sim }{\lambda }}(c)\right\}\hfill \\ {({\text{prox}}_J(u))}_{{\mathbb{I}}_i}=c_i^{\ast }{({\Vert u_{{\mathbb{I}}_i}\Vert }_2)}^{-1}{u}_{{\mathbb{I}}_i},i=1,\dots ,m\hfill \end{array}$$ (2.8)

Consequently, calculating prox_J (u) in fact reduces to identifying c^*, which can be efficiently done using the fast prox algorithm for regular SLOPE, provided e.g. in (Bogdan et al., 2013, 2015).

After defining the proximal operator, the solution to the gSLOPE can be obtained by the Procedure 1. There exist many ways in which t_i’s can be selected to ensure that f(b^(k)) converges to the optimal value (see e.g. Beck and Teboulle, 2009; Tseng, 2008). In our R package grpSLOPE available on CRAN (The Comprehensive R Archive Network) the accelerated proximal gradient method known as FISTA (Beck and Teboulle, 2009) is applied, which uses the specific procedure for choosing steps sizes, to achieve a fast convergence rate. To derive the proper stopping criterion, we have considered the dual problem to gSLOPE and employed the strong duality property. The detailed description of the dual norm, conjugate of grouped sorted l₁ norm and the stopping criterion are provided in the Appendix C.

Procedure 1.

Proximal gradient algorithm

input: b[0] ∈ ℝp̃, k=0

while ( Stopping criteria are not satisfied) do b[k+1] = proxtkh (b[k] − tk𝒳⊤(𝒳b[k] − y)); k ← k + 1.

end while

2.3 Group FDR

Group SLOPE is designed to select groups of variables, which might be very strongly correlated within a group or even linearly dependent. In this context we do not intend to identify single important predictors but rather want to point at the groups which contain at least one true regressor. To theoretically investigate the properties of gSLOPE in this context we now introduce the respective notion of group FDR (gFDR).

Definition 2.2

Consider model (2.1) and let β^gS be an estimate given by (2.2). We define two random variables: the number of all groups selected by gSLOPE (Rg) and the number of groups falsely discovered by gSLOPE (Vg), as

$$Rg:=\mid \{i:{\Vert X_{I_i}{\beta }_{I_i}^{\text{gS}}\Vert }_2\ne 0\}\mid ,Vg:=\mid \{i:{\Vert X_{I_i}{\beta }_{I_i}\Vert }_2=0,{\Vert X_{I_i}{\beta }_{I_i}^{\text{gS}}\Vert }_2\ne 0\}\mid .$$

Definition 2.3

We define the false discovery rate for groups (gFDR) as

$$\mathit{gFDR}=\mathit{gFDR}(X,\beta ,{\sigma }^2):=\mathbb{E}\left[\frac{Vg}{max\{Rg,1\}}\right].$$ (2.9)

2.4 Control of gFDR when variables from different groups are orthogonal

Our goal is the identification of the regularizing sequence for gSLOPE such that gFDR can be controlled at any given level q ∈ (0, 1). In this section we will provide such a sequence, which provably controls gFDR in case when variables in different groups are orthogonal to each other. In subsequent sections we will replace this condition with the weaker assumption of the stochastic independence of regressors in different groups. Before the statement of the main theorem on gFDR control, we will recall the definition of χ distribution and define a scaled χ distribution.

Definition 2.4

We will say that a random variable X₁ has a χ distribution with l degrees of freedom, and write X₁ ~ χ_l, when X₁ could be expressed as $X_1=\sqrt{X_2}$, for X₂ having a χ² distribution with l degrees of freedom. We will say that a random variable X₁ has a scaled χ distribution with l degrees of freedom and scale 𝒮, when X₁ could be expressed as X₁ = 𝒮 · X₂, for X₂ having a χ distribution with l degrees of freedom. We will use the notation X₁ ~ 𝒮χ_l.

Theorem 2.5 (gFDR control under orthogonal case)

Consider model (2.1) with the design matrix X satisfying $X_{I_i}^{\top }{X}_{I_j}=0$, for any i ≠ j. Denote the number of zero coefficients in ⟦β⟧_I,X by m₀ and let w₁, …, w_m be positive numbers. Moreover, define the sequence of regularizing parameters ${\lambda }^{max}={({\lambda }_1^{max},\dots ,{\lambda }_m^{max})}^{\top }$, with

$${\lambda }_i^{max}:=\underset{j=1,\dots ,m}{max}\left\{\frac{1}{w_j}{F}_{{\chi }_{l_j}}^{-1}\left(1-\frac{q·i}{m}\right)\right\},$$ (2.10)

where F_χlj is a cumulative distribution function of χ distribution with l_j degrees of freedom. Then any solution, β^gS, to problem gSLOPE (2.2) generates the same vector ⟦β^gS⟧_I,X and it holds

$$\mathit{gFDR}=\mathbb{E}\left[\frac{Vg}{max\{Rg,1\}}\right]\le q·\frac{m_0}{m}.$$

Proof

Consider the standardized version of the gSLOPE problem, given by (2.4). Since X is orthogonal at groups level, X̃ in problem (2.4) is an orthogonal matrix, i.e. X̃^⊤ X̃ = I_p̃. It is easy to show that this implies ${\Vert y-\stackrel{\sim }{X}b\Vert }_2^2={\Vert {\stackrel{\sim }{X}}^{\top }y-b\Vert }_2^2+C$, where C does not depend on b (see Appendix D). Hence under orthogonal situation the optimization problem in (2.4) can be recast as

$$b^{\ast }:=\underset{b}{\text{argmin}}\left\{\frac{1}{2}{\Vert \stackrel{\sim }{y}-b\Vert }_2^2+\sigma J_{\lambda }(W{⟦b⟧}_{\mathbb{I}})\right\},$$ (2.11)

where ỹ:= X̃^⊤y is a whitened version of y, which has the multivariate normal distribution 𝒩(β, σ²I_p̃), with β̃_𝕀i := R_iβ_Ii, i = 1, …, m. As discussed in the previous section the problem (2.11) can be equivalently formulated as

$$\{\begin{array}{l}{c}^{\ast }:={\text{argmin}}_c\left\{\frac{1}{2}{\sum }_{i=1}^m{({\Vert {\stackrel{\sim }{y}}_{{\mathbb{I}}_i}\Vert }_2-w_i^{-1}{c}_i)}^2+J_{\sigma \lambda }(c)\right\}\hfill \\ b_{{\mathbb{I}}_i}^{\ast }=c_i^{\ast }{(w_i{\Vert {\stackrel{\sim }{y}}_{{\mathbb{I}}_i}\Vert }_2)}^{-1}{\stackrel{\sim }{y}}_{{\mathbb{I}}_i},i=1,\dots ,m\hfill \end{array}.$$ (2.12)

The above formulation yields the conclusion, that indices of groups estimated by gSLOPE as relevant coincide with the support of the solution to the SLOPE problem with the diagonal design matrix D such that $D_{ii}=w_i^{-1}$. After defining β̃ ∈ ℝ ^p̃ by conditions β̃_𝕀i := R_iβ_Ii, i = 1, …, m, we also have ỹ ~ 𝒩(β̃, σ²I_p̃).

Now, we define random variables $R:=\mid \{i:c_i^{\ast }\ne 0\}\mid$ and $V:=\mid \{i:{\Vert {\stackrel{\sim }{\beta }}_{I_i}\Vert }_2=0,c_i^{\ast }\ne 0\}\mid$ Clearly, then Rg = R and V g = V. Consequently, it is enough to show that

$$\mathbb{E}\left[\frac{V}{max\{R,1\}}\right]\le q·\frac{m_0}{m}.$$

Without loss of generality we can assume that groups I₁, …, I_m0 are truly irrelevant, which gives ||β̃_𝕀1||₂ = …= ||β̃_𝕀m0||₂ = 0 and ||β̃_𝕀j||₂ > 0 for j > m₀. Suppose now that r, i are some fixed indices from {1, …, m}. From definition of ${\lambda }_r^{max}$

$${\lambda }_r^{max}\ge \frac{1}{w_i}{F}_{{\chi }_{l_i}}^{-1}\left(1-\frac{qr}{m}\right)\Rightarrow 1-F_{{\chi }_{l_i}}({\lambda }_r^{max}{w}_i)\le \frac{qr}{m}.$$ (2.13)

Now, let us assume that i ≤ m₀. Since σ⁻¹||ỹ_𝕀i||₂ ~ χ_li we have

$$\mathbb{P}\left(w_i^{-1}{\Vert {\stackrel{\sim }{y}}_{{\mathbb{I}}_i}\Vert }_2\ge \sigma {\lambda }_r^{max}\right)=\mathbb{P}\left({\sigma }^{-1}{\Vert {\stackrel{\sim }{y}}_{{\mathbb{I}}_i}\Vert }_2\ge {\lambda }_r^{max}{w}_i\right)=1-F_{{\chi }_{l_i}}({\lambda }_r^{max}{w}_i)\le \frac{qr}{m}.$$ (2.14)

Denote by R̃ⁱ the number of nonzero coefficients in SLOPE estimate (2.12) after eliminating i^th group of explanatory variables. Thanks to lemmas E.6 and E.7 in the Appendix, we immediately get

$$\{{⟦\stackrel{\sim }{y}⟧}_{\mathbb{I}}:c_i^{\ast }\ne 0\text{and}R=r\}\subset \{{⟦\stackrel{\sim }{y}⟧}_{\mathbb{I}}:w_i^{-1}{\Vert {\stackrel{\sim }{y}}_{{\mathbb{I}}_i}\Vert }_2>\sigma {\lambda }_r^{max}\text{and}{\stackrel{\sim }{R}}^i=r-1\},$$ (2.15)

which together with (2.14) raises

$$\begin{gathered} \mathbb{P}(c_i^{\ast }\ne 0\text{and}R=r)\le \mathbb{P}\left(w_i^{-1}{\Vert {\stackrel{\sim }{y}}_{{\mathbb{I}}_i}\Vert }_2>\sigma {\lambda }_r^{max}\text{and}{\stackrel{\sim }{R}}^i=r-1\right) \\ =\mathbb{P}(w_i^{-1}{\Vert {\stackrel{\sim }{y}}_{{\mathbb{I}}_i}\Vert }_2>\sigma {\lambda }_r^{max})\mathbb{P}\left({\stackrel{\sim }{R}}^i=r-1\right) \\ \le \frac{qr}{m}\mathbb{P}\left({\stackrel{\sim }{R}}^i=r-1\right), \end{gathered}$$ (2.16)

where the equality follows from the independence between ||ỹ_𝕀i||₂ and R̃ⁱ. Therefore

$$\begin{gathered} \mathbb{E}\left[\frac{V}{max\{R,1\}}\right]=\sum _{r=1}^m\mathbb{E}\left[\frac{V}{r}{𝟙}_{(R=r)}\right]=\sum _{r=1}^m\frac{1}{r}\mathbb{E}\left[\sum _{i=1}^{m_0}{𝟙}_{\{c_i^{\ast }\ne 0\}}{𝟙}_{\{R=r\}}\right]= \\ \sum _{r=1}^m\frac{1}{r}\sum _{i=1}^{m_0}\mathbb{P}(c_i^{\ast }\ne 0\text{and}R=r)\le \sum _{i=1}^{m_0}\frac{q}{m}\sum _{r=1}^m\mathbb{P}({\stackrel{\sim }{R}}^i=r-1)=\frac{q{m}_0}{m}, \end{gathered}$$ (2.17)

which finishes the proof.

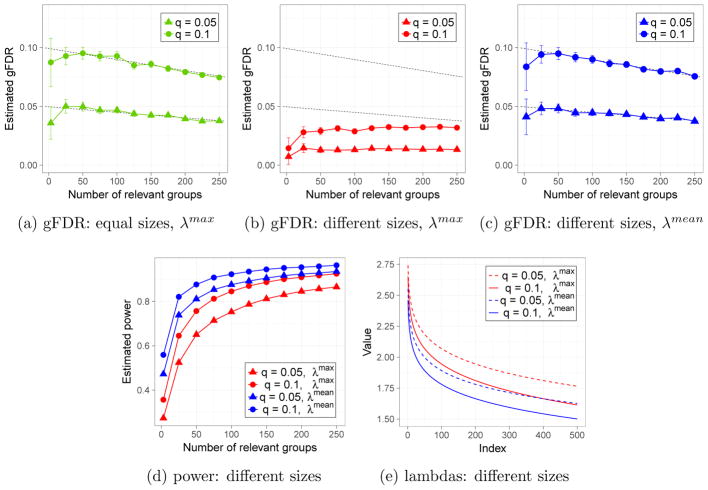
Figure 2 illustrates the performance of gSLOPE under the design matrix X = I_p (hence l_i, the rank of group i, coincides with its size), with p = 5000. In Figure 2(a) all groups are of the same size l = 5, while in Figures 2(b)–(d) the explanatory variables are clustered into m = 1000 groups of sizes from the set {3, 4, 5, 6, 7}; 200 groups of each size. Each coefficient of β_Ii, in a truly relevant group i, was generated independently from a U[0.1, 1.1] distribution and then β_Ii was scaled such that ${({⟦\beta ⟧}_{I,X})}_i=a\sqrt{l_i}$. Parameter a was selected to satisfy the condition

Figure 2.

Orthogonal situation with n = p = 5000 and m = 1000. In (a) all groups are of the same size l = 5, while in (b)–(d) there are 200 groups of each of sizes l_i ∈ {3, 4, 5, 6, 7}. In (a) and (b) gSLOPE works with the regularizing sequence λ^max, while in (c) and (d) λ^mean is used. First 500 elements of different λ sequences are shown in (e). For each target gFDR level and true support size, 300 iterations were performed. Bars correspond to ±2SE. Black straight lines represent the “nominal” gFDR level q · ((m − k)/m), for k being true support size. Weights are defined as $w_i:=\sqrt{l_i}$.

$$a\sum _{i=1}^m\sqrt{l_i}=\sum _{i=1}^m\sqrt{4ln(m)/(1-m^{-2/l_i})-l_i},$$

which, according to the calculations presented in the Appendix H, yields signals comparable to the maximal noise. Such signals can be detected with moderate power, which allows for a meaningful comparison between different methods.

Figure 2(a) illustrates that the sequence λ^max keeps gFDR very close to the “nominal” level when groups are of the same size. However, Figure 2(b) shows that for groups of different size λ^max is rather conservative, i.e. the achieved gFDR is significantly lower than assumed. This suggests that the shrinkage (dictated by λ) could be decreased, such that the method gets more power and still achieves the gFDR below the assumed level. Returning to the proof of Theorem 2.5, we can see that for each i ∈ {1, …, m} we have

$$1-F_{{\chi }_{l_i}}({\lambda }_r^{max}{w}_i)\le \frac{qr}{m},$$ (2.18)

with equality holding only for i being the index of the maximum in (2.10). In the result the inequality in (2.17) is usually strict and the true gFDR might be substantially smaller than the nominal level. The natural relaxation of (2.18) is to require only that

$$\sum _{i=1}^m(1-F_{w_i^{-1}{\chi }_{l_i}}({\lambda }_r))\le qr.$$ (2.19)

Replacing the inequality in (2.19) by equality yields the strategy of choosing the relaxed λ sequence

$${\lambda }_r^{\text{mean}}:={\overline{F}}^{-1}\left(1-\frac{qr}{m}\right)\text{for}\overline{F}(x):=\frac{1}{m}\sum _{i=1}^m{F}_{w_i^{-1}{\chi }_{l_i}}(x),r\in \{1,\dots ,m\},$$ (2.20)

where $F_{w_i^{-1}{\chi }_{l_i}}$ is the cumulative distribution function of scaled chi distribution with l_i degrees of freedom and scale $\mathcal{S}=w_i^{-1}$. In Figure 2(c) we present estimated gFDR, for tuning parameters given by (2.20). The results suggest that with a relaxed version of tuning parameters, we can still achieve the “average” gFDR control, where the “average” is with respect to the uniform distribution over all possible signal placements. As shown in Figure 2(d), application of λ^mean allows to achieve a substantially larger power than the one provided by λ^max. Such a strategy could be especially important in situations where differences between the smallest and the largest quantiles (among distributions $w_i^{-1}{\chi }_{l_i}$) are relatively large and all groups have the same prior probability of being relevant.

2.5 The accuracy of estimation

Up until this point, we have only considered the testing properties of gSLOPE. Though originally proposed to control the FDR, surprisingly, SLOPE enjoys appealing estimation properties as well, (see e.g Su and Candès, 2016; Bellec et al., 2016b,a). It thus would be desirable to extend this link between testing and estimation for gSLOPE. In measuring the deviation of an estimator from the ground truth β, as earlier, we focus on the group instead of an individual level. Accordingly, here we aim to estimate parts of variance of Y explained by every group, which are contained in the vector ⟦β⟧_X,I := (||X_I1β_I1||₂, …, ||X_Imβ_Im||₂)^⊤ or ⟦β̃⟧_𝕀 := (||β̃_𝕀1||₂, …, ||β̃_𝕀m||₂)^⊤, equivalently. For illustration purpose, we employ the setting described as follows. Imagine that we have a sequence of problems with the number of groups m growing to infinity: the design X is orthonormal at groups level; ranks of submatrices X_Ii, l_i, are bounded, that is, max l_i ≤ l for some constant integer l; denoting by k ≥ 1 the sparsity level (that is, the number of relevant groups), we assume the asymptotics k/m → 0. Now we state our minimax theorem, where we write a ~ b if a/b → 1 in the asymptotic limit, and ||⟦β⟧_I,X||₀ denotes the number of nonzero entries of ⟦β⟧_I,X. The proof makes use of the same techniques for proving Theorem 1.1 in (Su and Candès, 2016) and is deferred to the Appendix.

Theorem 2.6

Fix any constant q ∈ (0, 1), let w_i = 1 and ${\lambda }_i=F_{{\chi }_l}^{-1}(1-qi/m)$ for i = 1, …, m. Under the preceding conditions m → ∞ and k/m → 0, gSLOPE is asymptotically minimax over the nearly black object {β : ||⟦β⟧||_I,X||₀ ≤ k}, i.e.,

$$\underset{{\Vert {⟦\beta ⟧}_{I,X}\Vert }_0\le k}{sup}\mathbb{E}\left({\Vert {⟦{\beta }^{\text{gS}}⟧}_{I,X}-{⟦\beta ⟧}_{I,X}\Vert }_2^2\right)~\underset{\widehat{\beta }}{inf}\underset{{\Vert {⟦\beta ⟧}_{I,X}\Vert }_0\le k}{sup}\mathbb{E}\left({\Vert {⟦\widehat{\beta }⟧}_{I,X}-{⟦\beta ⟧}_{I,X}\Vert }_2^2\right),$$

where the infimum is taken over all measurable estimators β̂(y, X).

Notably, in this theorem the choice of λ_i does not assume the knowledge of sparsity level. Or putting it differently, in stark contrast to gLASSO, gSLOPE is adaptive to a range of sparsity in achieving the exact minimaxity. Combining Theorems 2.5 and 2.6, we see the remarkable link between FDR control and minimax estimation also applies to gSLOPE (Abramovich et al., 2006; Su and Candès, 2016). While it is out of the scope of this paper, it is of great interest to extend this minimax result to general design matrices.

2.6 The impact of chosen weights

In this subsection we will discuss the influence of chosen weights, ${\{w_i\}}_{i=1}^m$, on results. Let I = {I₁, …, I_m} be a given partition into groups and l₁, …, l_m be ranks of submatrices X_Ii. Assume the orthogonality at group level, i.e., that it holds $X_{I_i}^{\top }{X}_{I_j}=0$, for i ≠ j, and suppose that σ = 1. The support of ⟦β⟧_I,X coincides with the support of vector c^* defined in (2.12), namely

$$c^{\ast }=\underset{c}{\text{argmin}}\left\{\frac{1}{2}{\Vert {⟦\stackrel{\sim }{y}⟧}_{\mathbb{I}}-W^{-1}c\Vert }_2^2+J_{\lambda }(c)\right\},$$ (2.21)

where W⁻¹ is a diagonal matrix with positive numbers $w_1^{-1},\dots ,w_m^{-1}$ on the diagonal. Suppose now, that c^* has exactly r nonzero coefficients. From Corollary E.4 in the Appendix E, these indices are given by {π(1), …, π(r)}, where π is permutation which orders W⁻¹⟦ỹ⟧_𝕀. Hence, the order of realizations ${\{w_i^{-1}{\Vert {\stackrel{\sim }{y}}_{{\mathbb{I}}_i}\Vert }_2\}}_{i=1}^m$ decides about the subset of groups labeled by gSLOPE as relevant. Suppose that groups I_i and I_j are truly relevant, i.e., ||β̃_𝕀i||₂ > 0 and ||β̃_𝕀j||₂ > 0. The distributions of ||ỹ_𝕀i||₂ and ||ỹ_𝕀j||₂ are noncentral χ distributions, with l_i and l_j degrees of freedom, and the noncentrality parameters equal to ||β̃_𝕀i||₂ and ||β̃_𝕀j||₂, respectively. Now, the expected value of the noncentral χ distribution could be well approximated by the square root of the expected value of the noncentral χ² distribution, which gives

$$\mathbb{E}(w_i^{-1}{\Vert {\stackrel{\sim }{y}}_{{\mathbb{I}}_i}\Vert }_2)\approx w_i^{-1}\sqrt{\mathbb{E}({\Vert {\stackrel{\sim }{y}}_{{\mathbb{I}}_i}\Vert }_2^2)}=w_i^{-1}\sqrt{l_i+{\Vert {\stackrel{\sim }{\beta }}_{{\mathbb{I}}_i}\Vert }_2^2}.$$

Therefore, roughly speaking, truly relevant groups I_i and I_j are treated as comparable, when it occurs $l_i/w_i^2+{\Vert {\stackrel{\sim }{\beta }}_{{\mathbb{I}}_i}\Vert }_2^2/w_i^2\approx l_j/w_j^2+{\Vert {\stackrel{\sim }{\beta }}_{{\mathbb{I}}_j}\Vert }_2^2/w_j^2$. This gives us the intuition about the behavior of gSLOPE with the choice $w_i=\sqrt{l_i}$ for each i. Firstly, gSLOPE treats all irrelevant groups as comparable, i.e. the size of the group has a relatively small influence on it being selected as a false discovery. Secondly, gSLOPE treats two truly relevant groups as comparable, if groups effect sizes satisfy the condition ${({⟦\beta ⟧}_{I,X})}_i/{({⟦\beta ⟧}_{I,X})}_j\approx \sqrt{l_i}/\sqrt{l_j}$. The derived condition could be recast as ${\Vert X_{I_i}{\beta }_{I_i}\Vert }_2^2/l_i\approx {\Vert X_{I_j}{\beta }_{I_j}\Vert }_2^2/l_j$. This gives a nice interpretation: with the choice $w_i:=\sqrt{l_i}$, gSLOPE treats two groups as comparable, when these groups have similar squared effect group sizes per coefficient. One possible idealistic situation, when such a property occurs, is when all β_i’s in truly relevant groups are comparable.

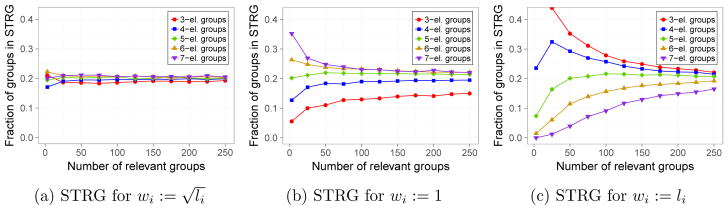
In Figure 3 we see that when the condition ${({⟦\beta ⟧}_{I,X})}_i/{({⟦\beta ⟧}_{I,X})}_j\approx \sqrt{l_i}/\sqrt{l_j}$ is met, the fractions of groups with different sizes in the selected truly relevant groups (STRG) are approximately equal. To investigate the impact of selected weights on the set of discovered groups, we performed simulations with different settings, namely we used w_i = 1 and w_i = l_i (without changing other parameters). With the first choice, larger groups are penalized less than before, while the second choice yields the opposite situation. This is reflected in the proportion of each groups in STRG (Figure 3). The values of gFDR are very similar under all choices of weights.

Figure 3.

Fraction of each group sizes in selected truly relevant groups (STRG). Beyond the weights, this simulation was conducted with the same setting as in experiments summarized in Figure 1 for λ^mean. In particular, for truly relevant groups i and j, it occurs ${({⟦\beta ⟧}_{I,X})}_i/{({⟦\beta ⟧}_{I,X})}_j=\sqrt{l_i}/\sqrt{l_j}$. Target gFDR level was fixed as 0.05.

2.7 Independent groups and unknown σ

The assumption that variables in different groups are orthogonal to each other can be satisfied only in rare situations of specifically designed experiments. However, in a variety of applications one can assume that variables in different groups are independent. Such a situation occurs for example in the context of identifying influential genes using distant genetic markers, whose genotypes can be considered as stochastically independent. In this case a group can be formed by clustering dummy variables corresponding to different genotypes of a given marker. Though the difference between stochastic independence and algebraic orthogonality seems rather small, it turns out that small sample correlations between independent regressors together with the shrinkage of regression coefficients lead to magnifying the effective noise and require the adjustment of the tuning sequence λ (see Su et al., 2015, for discussion of this phenomenon in the context of LASSO). Concerning regular SLOPE, this problem was addressed by heuristic modification of λ, proposed in (Bogdan et al., 2013, 2015). This modified sequence was calculated based upon the assumption that explanatory variables are randomly sampled from the Gaussian distribution. However, simulation results from (Bogdan et al., 2015) illustrate that it controls FDR also in case when the columns of the design matrix correspond to additive effects of independent SNPs and the number of causal genes is moderately small.

To derive the similar heuristic adjustment for the group SLOPE we will at first confine ourselves to the case σ = 1, l₁ = … = l_m := l, w₁ = … = w_m := w.

The first step in our derivation relies on specifying the optimality conditions for the standardized version of group SLOPE provided in (2.4), under which $X_{I_i}^{\top }{X}_{I_i}={\mathbf{I}}_l$, for all i ∈ {1, …, m}.

Theorem 2.7 (Optimality conditions)

Let X be the standardized design matrix satisfying $X_{I_i}^{\top }{X}_{I_i}={\mathbf{I}}_l$ for each i and let β̂ be the solution to the gSLOPE problem. Let us order the groups such that ||β̂_I1||₂ > … > ||β̂_Is||₂ > 0 and ||β̂_Ii||₂ = 0 for i > s and consider the partition of I into I^S := {I₁, …, I_s} and I^C := {I_s+1, …, I_m}. Moreover, let us define $v_{I_i}:=X_{I_i}^{\top }\left(y-X_{\backslash I_i}{\widehat{\beta }}_{\backslash I_i}\right)$, where X_\Ii is a matrix X without columns from I_i. Then the following two sets of conditions are met

$$\{\begin{array}{l}{X}_{I_i}^{\top }(y-X\widehat{\beta })=w{\lambda }_i\frac{{\widehat{\beta }}_{I_i}}{{\Vert {\widehat{\beta }}_{I_i}\Vert }_2},i<s\hfill \\ {⟦X^{\top }(y-X\widehat{\beta })⟧}_{I^c}\in C_{w{\lambda }^c}\hfill \end{array}\mathit{and}\{\begin{array}{l}\left|{\Vert v_{I_i}\Vert }_2-w{\lambda }_i\right|={\Vert {\widehat{\beta }}_{I_i}\Vert }_2,i\le s\hfill \\ {⟦v⟧}_{I^c}\in C_{w{\lambda }^c}\hfill \end{array},$$ (2.22)

where $v:={(v_{I_1}^{\top },\dots ,v_{I_m}^{\top })}^{\top }$, λ^c = (λ_s+1, …, λ_m) and $C_{w{\lambda }^c}:=\left\{x\in {ℝ}^{m-s}:{\sum }_{i=1}^k{\mid x\mid }_{(i)}\le {\sum }_{i=1}^{k}w{\lambda }_i^c,k=1,\dots m-s\right\}$ is the unit ball of the dual norm to J_wλ^c.

Proof

The proof of Theorem 2.7 is provided in Appendix G.

The task now is to select λ_i’s such that the condition ⟦v⟧_I^C ∈ C_wλ^c regulates the rate of false discoveries. Let us at first observe that

$$v_{I_i}=X_{I_i}^{\top }\left(X\beta -X_{\backslash I_i}{\widehat{\beta }}_{\backslash I_i}+z\right)={\beta }_{I_i}+X_{I_i}^{\top }{X}_{\backslash I_i}({\beta }_{\backslash I_i}-{\widehat{\beta }}_{\backslash I_i})+X_{I_i}^{\top }z.$$ (2.23)

Note that under the orthogonal design the last expression reduces to $X_{I_i}^{\top }z$ for i > s and has χ distribution with l degrees of freedom. This fact was used in subsection 2.4 to define the sequence λ. In the considered near-orthogonal situation, the term $X_{I_i}^{\top }{X}_{\backslash I_i}({\beta }_{\backslash I_i}-{\widehat{\beta }}_{\backslash I_i})$ does not vanish and creates an additional “noise”, which needs to be taken into account when designing the λ sequence. To approximate the distribution of v_Ii under the assumption of independence between different groups we will use the following simplifying assumptions. To estimate the distribution of v_Ii we will first simplify the situation by assuming that true and estimated signals define the same set of relevant groups, with indices from the set {1, …, s}, and that the signal strength is sufficiently large to assume that $\frac{{\widehat{\beta }}_{I_i}}{{\Vert {\widehat{\beta }}_{I_i}\Vert }_2}$ can be well approximated by $\frac{{\beta }_{I_i}}{{\Vert {\beta }_{I_i}\Vert }_2}$ for i ≤ s. After defining I_S := ∪_i≤s I_i, from the left set of conditions in (2.22) we get that

$$X_{I_S}^{\top }(X_{I_S}{\beta }_{I_S}-X_{I_S}{\widehat{\beta }}_{I_S})+X_{I_S}^{\top }z\approx w\underset{H_{\lambda ,\beta }}{\underbrace{{({\lambda }_1{\beta }_{I_1}^{\top }/{\Vert {\beta }_{I_1}\Vert }_2,\dots ,{\lambda }_s{\beta }_{I_s}^{\top }/{\Vert {\beta }_{I_s}\Vert }_2)}^{\top }}},$$ (2.24)

which gives $X_{I_i}^{\top }{X}_{I_S}({\beta }_{I_S}-{\widehat{\beta }}_{I_S})\approx X_{I_i}^{\top }{X}_{I_S}{(X_{I_S}^{\top }{X}_{I_S})}^{-1}(w{H}_{\lambda ,\beta }-X_{I_S}^{\top }z)$. Finally, combining the last expression with (2.23) let us to assume v_Ii ≈ v̂_Ii, where

$${\widehat{v}}_{I_i}:=X_{I_i}^{\top }{X}_{I_S}{(X_{I_S}^{\top }{X}_{I_S})}^{-1}\left(w{H}_{\lambda ,\beta }-X_{I_S}^{\top }z\right)+X_{I_i}^{\top }z.$$ (2.25)

Now, we will assume that the distribution of v̂_Ii can be well approximated by assuming that the individual entries of X come from the normal distribution $\mathcal{N}(0,\frac{1}{n})$. This assumption can be justified if the distribution of the individual entries of X is sufficiently regular and n is substantially larger than lm₀. The following Theorem 2.8 provides the expected value and the covariance matrix of the random vector v̂_Ii for i > s under the assumption of normality.

Theorem 2.8

Assume that the entries of the design matrix X are independently drawn from 𝒩(0, 1/n) distribution. Then for each i > s the expected value of v̂_Ii is equal to 0 and the covariance matrix of this random vector is given by

$$\mathit{Cov}({\widehat{v}}_{I_i})=\left(\frac{n-ls}{n}+w^2\frac{{\Vert {\lambda }^S\Vert }_2^2}{n-ls-1}\right){\mathbf{I}}_l,\mathit{where}{\lambda }^S:={({\lambda }_1,\dots ,{\lambda }_s)}^{\top }.$$ (2.26)

Proof

The proof of Theorem 2.8 is provided in Appendix G.

Now, if n is large enough with respect to sl, then by the Central Limit Theorem the distribution of v_Ii can be approximated by the multivariate normal distribution and the distribution of ||v_Ii||₂ by the scaled χ distribution with l degrees of freedom and a scale parameter $\mathcal{S}=\sqrt{\frac{n-ls}{n}+\frac{w^2{\Vert {\lambda }_S\Vert }_2^2}{n-sl-1}}$. Now, analogously to the orthogonal situation, lambdas could be defined as ${\lambda }_i:=\frac{1}{w_i}{F}_{\mathcal{S}{\chi }_l}^{-1}(1-\frac{q·i}{m})=\frac{\mathcal{S}}{w_i}{F}_{{\chi }_l}^{-1}(1-\frac{q·i}{m})$. Since s is unknown, we will apply the strategy used in (Bogdan et al., 2013): define λ₁ as in orthogonal case and for i ≥ 2 define λ_i by incorporating the scale parameter corresponding to the sparsity s = i − 1. This yields the following procedure.

Procedure 2.

Selecting lambdas under the assumption of independence: equal groups sizes

input: q ∈ (0, 1), w > 0, p, n, m, l ∈ ℕ

${\lambda }_1:=\frac{1}{w}{F}_{{\chi }_l}^{-1}(1-\frac{q}{m})$;

For i ∈ {2, . . . , m}:

λS := (λ1, . . . , λi−1)⊤;

$\mathcal{S}:=\sqrt{\frac{n-l(i-1)}{n}+\frac{w^2{\Vert {\lambda }^S\Vert }_2^2}{n-l(i-1)-1}}$;

${\lambda }_i^{\ast }:=\frac{\mathcal{S}}{w}{F}_{{\chi }_l}^{-1}(1-\frac{q·i}{m})$;

if ${\lambda }_i^{\ast }\le {\lambda }_{i-1}$, then put ${\lambda }_i:={\lambda }_i^{\ast }$. Otherwise, stop the procedure and put λj := λi−1 for j ≥ i;

end for

Consider now the Gaussian design with arbitrary group sizes and a sequence of positive weights w₁, . . . , w_m. One possible approach is to construct consecutive λ_i by taking the largest scaled quantiles among all distributions, i.e. as $\underset{j=1,\dots ,m}{max}\{\frac{{\mathcal{S}}_j}{w_j}{F}_{{\chi }_{l_j}}^{-1}(1-\frac{q·i}{m})\}$, with the scale parameter 𝒮_j adjusted to l_j (the conservative strategy). In this article, however, we will stick to the more liberal strategy based on λ^mean, which leads to the modified sequence of tuning parameters presented in Procedure 3.

Procedure 3.

Sequence of tuning parameters for independent groups

input: q ∈ (0, 1), w1, . . . , wm > 0, p, n, m, l1, . . . , lm ∈ ℕ

${\lambda }_i:={\overline{F}}^{-1}(1-\frac{q·i}{m})$, for $\overline{F}(x):=\frac{1}{m}{\sum }_{i=1}^m{F}_{w_i^{-1}{\chi }_{l_i}}(x)$;

for i ∈ {2, . . . , m}:

λS := (λ1, . . . , λi−1)⊤;

${\mathcal{S}}_j:=\sqrt{\frac{n-l_j(i-1)}{n}+\frac{w_j^2{\Vert {\lambda }^S\Vert }_2^2}{n-l_j(i-1)-1}}$, for j ∈ {1, . . . , m};

${\lambda }_i^{\ast }:={\overline{F}}_{\mathcal{S}}^{-1}(1-\frac{qi}{m})$, for ${\overline{F}}_{\mathcal{S}}(x):=\frac{1}{m}{\sum }_{j=1}^m{F}_{{\mathcal{S}}_j{w}_j^{-1}{\chi }_{l_j}}(x)$;

if ${\lambda }_i^{\ast }\le {\lambda }_{i-1}$, then put ${\lambda }_i:={\lambda }_i^{\ast }$. Otherwise, stop the procedure and put λj := λi−1 for j ≥ i;

end for

Up until this moment, we have used σ in gSLOPE optimization problem, assuming that this parameter is known. However, in many applications σ is unknown and its estimation is an important issue. When n > p, the standard procedure is to use the unbiased estimator of σ², ${\widehat{\sigma }}_{\text{OLS}}^2$, given by

$${\widehat{\sigma }}_{\text{OLS}}^2:={(y-X{\beta }^{\text{OLS}})}^{\top }(y-X{\beta }^{\text{OLS}})/(n-p),\text{for}{\beta }^{\text{OLS}}:={(X^{\top }X)}^{-1}{X}^{\top }y.$$ (2.27)

For the target situation, with p much larger than n, such an estimator can not be used. To estimate σ we will therefore apply the procedure which was dedicated for this purpose in (Bogdan et al., 2015) in the context of SLOPE. Below we present algorithm adjusted to gSLOPE (Procedure 4). The idea standing behind the procedure is simple. The gSLOPE property of producing sparse estimators is used, and in each iteration columns in design matrix are first restricted to support of β^gS, so that the number of rows exceeds the number of columns and (2.27) can be used. Algorithm terminates when gSLOPE finds the same subset of relevant variables as in the preceding iteration.

Procedure 4.

gSLOPE with estimation of σ

input: y, X and λ (defined for some fixed q)

initialize: S+ = ∅;

repeat

S = S+;

compute RSS obtained by regressing y onto variables in S;

set σ̂2 = RSS/(n − |S| − 1);

compute the solution βgS to gSLOPE with parameters σ̂ and sequence λ;

set S+ = supp(βgS);

until S+ = S

To investigate the performance of gSLOPE under the Gaussian design and various group sizes, we performed simulations with 1000 groups. Their sizes were drawn from the binomial distribution, Bin(1000; 0.008), so as the expected value of the group size was equal to 8 (Figure 4(c)). As a result, we obtained 7917 variables, divided into 1000 groups (the same division was used in all iterations and scenarios). For each sparsity level and the gFDR level 0.1, and each iteration we generated entries of the design matrix using $\mathcal{N}(0,\frac{1}{n})$ distribution, then X was standardized and the values of response variable were generated according to model (2.1) with σ = 1 and signals generated as in simulations for Figure 2. To identify relevant groups based on the simulated data we have used the iterative version of gSLOPE, with σ estimation (Procedure 4) and lambdas given by Procedure 3. We performed 200 repetitions for each scenario, n was fixed as 5000. Results are represented in Figure 4 and show that our procedure allows to control gFDR at the assumed level.

Figure 4.

Results for the example with independent regressors and various group sizes: m = 1000, p = 7917 and n = 5000. Bars correspond to ±2SE. Entries of design matrix were drawn from 𝒩(0, 1/n) distribution and truly relevant signal, i, was generated such as ${\Vert X_{I_i}{\beta }_{I_i}\Vert }_2=\frac{1}{m}{\sum }_{i=1}^{m}B(m,l_i)$, where B(m, l) is defined in (H.4).

Additionally, Figure 4 compares gSLOPE to gLASSO with two choices of the smoothing parameter λ. Firstly, we used $\lambda ={\lambda }_1^{\text{mean}}$, which allows control of the gFDR under the total null hypothesis. Secondly, for each of the iterations we chose λ based on leave-one-out cross-validation. It turns out that the first of these choices becomes rather conservative when the number of truly relevant groups increases. Then gLASSO has a smaller FDR but also a much smaller power than SLOPE (by a factor of three for k = 60). Cross-validation works in the opposite way - it yields a large power but also results in a huge proportion of false discoveries, which in our simulations systematically exceeds 60%.

2.8 Simulations under Genome-Wide Association Studies

To test the performance of gSLOPE in the context of Genome-Wide Association Studies (GWAS) we have used the North Finland Birth Cohort (NFBC1966) dataset, available in dbGaP with accession number phs000276.v2.p1 (http://www.ncbi.nlm.nih.gov/projects/gap/cgi-bin/study.cgi?study_id=phs000276.v2.p1) and described in detail in (Sabatti et al., 2009). The raw data contains 364, 590 markers for 5, 402 subjects. To obtain roughly independent SNPs this data set was initially screened using the clump procedure in the PLINK software (Purcell et al., 2007; Purcell, 2009) and additional screening in R such that in the final data set the maximal correlation between any pair of SNPs does not exceed $\sqrt{0.1}=0.316$. The reduced data set contains p = 26, 315 SNPs. The details of the screening procedure are provided in Appendix I.

The explanatory variables for our genetic model were defined in Table 1, where a denotes the less frequent (variant) allele. In case when population frequencies of both alleles are the same, variables X̃ and Z̃ are uncorrelated. In other cases correlations between these variables is different from zero and can be very strong for rare genetic variants. Since each SNP is described by two dummy variables, the full design matrix [X̃ Z̃] contains 52, 630 potential regressors. This matrix was then centered and standardized, so the columns of the final matrix [X Z] have zero mean and unit norm.

Table 1.

Coding for explanatory variables

	Genotype aa	Genotype aA	Genotype AA
additive dummy variable X̃	2	1	0
dominance dummy variable Z̃	0	1	0

The trait values are simulated according to two scenarios. In Scenario 1 we simulate from an additive model, where each of the causal SNPs influences the trait only through the additive dummy variable in matrix X,

$$y=X{\beta }_X+\epsilon .$$ (2.28)

Here ε ~ 𝒩(0, I), the number of ‘causal’ SNPs k varies between 1 and 80 and each causal SNP has an additive effect (non-zero components of β_X) equal to 5 or −5, with P(β_Xi = 5) = P(β_Xi = −5) = 0.5. In each of 100 iterations of our experiment causal SNPs were randomly selected from the full set of 26, 315 SNPs.

Since SNPs were selected in such a way that they are only weakly correlated, the identification of ”causal” mutations based on the additive model (2.28) can be done with regular SLOPE, as it was demonstrated in (Bogdan et al., 2015). However, the additive model (2.28) implicitly assumes that for each of the SNPs the expected value of the trait for the heterozygote aA is the average of expected trait values for both homozygotes aa and AA. This idealistic assumption is usually not satisfied and many of the SNPs exhibit some dominance effects. To investigate the performance of model selection criteria in the presence of the dominance effects, we simulated data according to Scenario 2;

$$y=[\begin{array}{ll}X\hfill & Z\hfill \end{array}]\left[\begin{array}{l}{\beta }_X\hfill \\ {\beta }_Z\hfill \end{array}\right]+\epsilon$$ (2.29)

which differs from Scenario 1 by adding dominance effects (non-zero components of β_Z), which for each of k selected SNPs are sampled from the uniform distribution on [−5, −3] ∪ [3, 5]. Now, the influence of i-th SNP on the trait is described by the vector β_i = (β_Xi, β_Zi), containing its additive and dominance effects, which sets the stage for the application of the gSLOPE.

The data simulated according to Scenario 1 and Scenario 2 were analyzed using three different approaches:

• A.1gSLOPE with p = 26, 315 groups, where each of the groups contains two explanatory variables, for the additive and the dominance effect of the same SNP,
• A.2SLOPE_X, where the regular SLOPE is used to search through the reduced design matrix X (as in Bogdan et al., 2015; Brzyski et al., 2017),
• A.3SLOPE_XZ, where the regular SLOPE is used to search through the full design matrix [X Z].

In all versions of SLOPE we used the iterative procedure for estimation of σ and the sequence λ heuristically adjusted to the case of the Gaussian design matrix, as implemented in the CRAN packages SLOPE and grpSLOPE. All scripts used in simulations as well as in real data analysis are available at https://github.com/dbrzyski/gSLOPE.

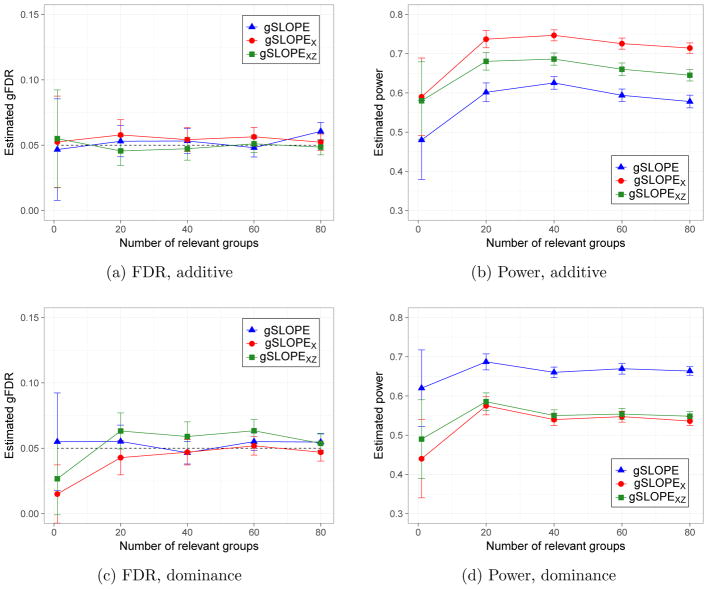
Figure 5 summarizes this simulation study. Here FDR and power are calculated at the SNP level. Specifically, in case of SLOPE_XZ the SNP is counted as a one discovery if the corresponding additive or the dominance dummy variable is selected.

Figure 5.

Simulations using real SNP genotypes: n = 5, 402, p = 26, 315. Power and gFDR are estimated based on 100 iterations of each simulation scenario. Upper panel illustrates the situation where all causal SNPs have only additive effects, while in lower panel each causal SNP has also some dominance effect.

As shown in Figure 5, for both of the simulated scenarios all versions of SLOPE control gFDR for all considered values of k. When the data are simulated according to the additive model the highest power is offered by SLOPE_X, with the power of gSLOPE being smaller by approximately 13% over the whole range of k. However, in the presence of large dominance effects the situation is reversed and gSLOPE offers the highest power, which systematically exceeds the power of SLOPE_X by the symmetric amount of 13%. In our simulations SLOPE_XZ has intermediate performance and does not substantially improve the power of SLOPE_X in the presence of dominance effects.

Thus our simulations suggest that gSLOPE provides an information complementary to SLOPE_X and our recommendation is to use both these methods when performing GWAS. SNPs detected by gSLOPE and not detected by SLOPE_X almost certainly exhibit strong dominance effects and might represent rare recessive variants, as suggested by the real data analysis reported in the following section.

2.9 gSLOPE under GWAS application: real phenotype data

Finally, we have applied group SLOPE to identify SNPs associated with four lipid phenotypes available in NFBC1966 dataset. This data set contains many characteristics of individuals from the Northern Finland Birth Cohort 1966 (NFBC1966) ((Rantakallio, 1969; Jarvelin et al., 2004)), a sample that enrolled almost all individuals born in 1966 in the two northernmost Finnish provinces. The most advantageous feature of this study is that ”participants derive from a genetic isolate that is relatively homogeneous in genetic background and environmental exposures and that has more extensive linkage disequilibrium (i.e. neighboring markers are more strongly correlated) than in most other populations”(see Sabatti et al., 2009). The second of these features allows to capture the associations resulting from mutations which are not genotyped (i.e. they are represented in the design matrix only through their neighbors). In (Sabatti et al., 2009) this data set was used to look for associations for ”nine quantitative traits that are heritable risk factors for cardiovascular disease (CVD) or type 2 diabetes (T2D): body mass index (BMI), fasting serum concentrations of lipids (triglycerides (TG), high-density lipoproteins (HDL) and low-density lipoproteins (LDL)), indicators of glucose homeostasis (glucose (GLU), and insulin (INS)) and inflammation (CRP), and systolic (SBP) and diastolic (DBP) blood pressure. Extreme values of these traits, in combination, identify a metabolic syndrome, hypothesized to increase risks for both CVD and T2D”. In (Brzyski et al., 2017) four lipid phenotypes: HDL, LDL, TG, and total cholesterol (CHOL), were reanalyzed using the geneSLOPE method based on SLOPE_X. The results were compared to those obtained with the up-to-date EMMAX procedure (Kang et al., 2010), which controls for the polygenic background by using the mixed model approach. The study reported in (Brzyski et al., 2017) shows that in this example geneSLOPE usually points at the same genomic regions as EMMAX, but allows to obtain a better resolution of gene location. Here we analyze the same four traits (HDL, LDL, TG, and CHOL) with the geneSLOPE based on SLOPE_XZ and group SLOPE and compare the results with those obtained with SLOPE_X and reported in (Brzyski et al., 2017).

We started with 5, 402 individuals and 334, 103 SNPs, obtained after first step of screening procedure described in details in Appendix I. Since this pre-processing selects most promising SNPs by performing multiple testing on the full set of p = 334, 103 SNPs, the sequence of the tuning parameters for SLOPE needs to be adjusted to this value of p rather than to the number of selected representatives (see Brzyski et al., 2017). The algorithm for GWAS analysis with SLOPE (the entire procedure is called geneSLOPE) is implemented in R package geneSLOPE and its details are explained in (Brzyski et al., 2017). According to an extensive simulation study and real data analysis reported in (Brzyski et al., 2017), geneSLOPE allows to control FDR for the analysis with full size GWAS data.

In our data analysis we used three methods: geneSLOPE for additive effects (as in Brzyski et al., 2017), geneSLOPE_XZ, with the design matrix extended by inclusion of dominance dummy variables, and gene group SLOPE (geneGSLOPE). In geneSLOPE_XZ and geneGSLOPE representative SNPs were selected based on one-way ANOVA tests. For all these procedures the pre-processing was based on p-value threshold p < 0.05 and the correlation cutoff ρ < 0.3, which allowed to reduce the data set to roughly 8500 of interesting representative SNPs (this number depends on the phenotype). For the convenience of the reader, the Procedure 5 for the full geneGSLOPE analysis is provided below.

Procedure 5.

geneGSLOPE procedure

Input: r ∈ (0, 1), π ∈ (0, 1]

Screen SNPs:

(1) For each SNP calculate independently the p-value for the ANOVA test with the null hypothesis, H0: μaa = μaA = μAA.

(2) Define the set ℬ of indices corresponding to SNPs whose p-values are smaller than π.

Cluster SNPs:

(3) Select the SNP j in ℬ with the smallest p-value and find all SNPs whose Pearson correlation with this selected SNP is larger than or equal to r.

(4) Define this group as a cluster and SNP j as the representative of the cluster. Include SNP j in 𝒮, and remove the entire cluster from ℬ.

(5) Repeat steps (3)–(4) until ℬ is empty. Denote by m number of all clumps (this is also the number of elements in 𝒮).

Selection:

(6) Apply the iterative gSLOPE method (i.e. gSLOPE with σ estimation and correction for independent regressors) on X𝒮, being matrix X restricted to columns corresponding to the set 𝒮 of selected SNPs. Here, the tuning parameters, vector λ, is defined as in Procedure 3, with p being the number of all initial SNPs, and then this vector is restricted only to first m coefficients.

(7) Representatives which were selected indicate the selection of entire clumps.

Results in the context of number of discoveries given by geneSLOPE, geneSLOPE_XZ and geneGSLOPE are summarized in Table 2, where we can observe that both geneSLOPE and geneSLOPE_XZ, gave identical results for LDL, CHOL and TG. Compared to these methods geneGSLOPE did not reveal any new response-related SNPs for LDL and CHOL. Actually, for these two traits geneGSLOPE missed some SNPs detected by the other two methods. A different situation takes place for TG, where geneGSLOPE identifies 6 additional SNPs as compared to the other two methods. All these detections have a similar structure, showing a significant recessive effect of the minor allele. In all these cases the minor allele frequency was smaller than 0.1. The detection of such “rare” recessive effects by the simple linear regression model is rather difficult, since the regression line adjusts mainly to the two prevalent genotype groups and is almost flat (Lettre et al., 2007).

Table 2.

Number of discoveries in real data analysis

	HDL	LDL	TG	CHOL
geneSLOPE	7	6	2	5
geneSLOPEXZ	8	6	2	5
geneGSLOPE	8	4	8	4
New discoveries: geneSLOPEXZ	1	0	0	0
New discoveries: geneGSLOPE	2	0	6	0

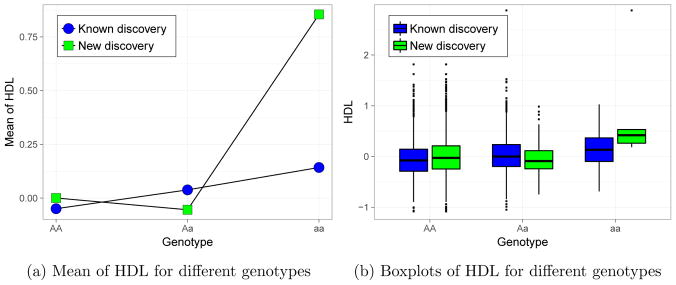
In case of HDL all three versions of SLOPE gave different results. geneSLOPE_XZ identifies one new SNP as compared to geneSLOPE, while geneGSLOPE identifies one more SNP and misses one of the discoveries obtained by other two methods. In Figure 6 we compare two exemplary discoveries: one detected at the same time by geneSLOPE and geneGSLOPE (known discovery) and one detected only by geneGSLOPE (new discovery). This example clearly shows the additive effect of the previously detected SNP and the recessive character of the second SNP. In case of new discovery there are only 5 individuals in the last genotype group, which makes the change in the mean not detectable by simple linear regression.

Figure 6.

Comparison of a discovery detected by both geneSLOPE and geneGSLOPE (known discovery), and a discovery detected only by geneGSLOPE (new discovery). The mean values of HDL for different genotypes are shown in (a) and the corresponding boxplots are presented presented in (b).

The results of real data analysis agree with results of simulations. They show that geneGSLOPE has a lower power than geneSLOPE for detection of additive effects but can be very helpful in detecting rare recessive variants. Thus these two methods are complementary to each other and should be used together to enhance the power of detection of influential genes.

3 Discussion

Group SLOPE is a new convex optimization procedure for selection of important groups of explanatory variables, which can be considered as a generalization of group LASSO and of SLOPE. In this article we provide an algorithm for solving group SLOPE and discuss the choice of the sequence of regularizing parameters. Our major focus is the control of group FDR, which can be obtained when variables in different groups are orthogonal to each other or they are stochastically independent and the signal is sufficiently sparse. After some pre-processing of the data such situations occur frequently in the context of genetic studies, which in this paper serve as a major example of applications.

The major purpose of controlling FDR rather than absolutely eliminating false discoveries is the wish to increase the power of detection of signals which are comparable to the noise level. As shown by a variety of theoretical and empirical results, this allows SLOPE to obtain an optimal balance between the number of false and true discoveries and leads to very good estimation and predictive properties (see e.g. Bogdan et al., 2013, 2015; Su and Candés, 2016). Our Theorem 2.6 illustrates that these good estimation properties are inherited by group SLOPE.

We provide the regularizing sequence λ^max, which provably controls gFDR in case when variables in different groups are orthogonal. Additionally, we propose its relaxation λ^mean, which according to our extensive simulations controls “average” gFDR, where the average is with respect to all possible signal placements. This sequence can be easily modified taking into account the prior distribution on the signal placement. Such “Bayesian” version of gSLOPE and the proof of control of the respective average gFDR remains an interesting topic for a further research.

Another important topic for a further research is the formal proof of gFDR control when variables in different groups are independent and setting precise limits on the sparsity levels under which it can be done. Asymptotic formulas, which allow for accurate prediction of FDR for LASSO under Gaussian design are provided in (Su et al., 2015). We expect that similar results can be obtained for SLOPE and gSLOPE and generalized to the case of random matrices, where variables are independent and come from sub-Gaussian distributions. We consider this as an interesting topic for a further research.

While we concentrated on control of FDR in case when groups of variables are roughly orthogonal to each other, it is worth mentioning that original SLOPE has very interesting properties also in case when regressors are strongly correlated. As shown e.g. in (Figueiredo and Nowak, 2016), the Sorted L-One norm has a tendency to average estimated regression coefficients over groups of strongly correlated predictors, which enhances the predictive properties. This also allows not to lose important predictors due to their correlation with other features. Moreover, minimax estimation and prediction properties of SLOPE under correlated designs have been recently proved in (Bellec et al., 2016b) and (Bellec et al., 2016a). We expect similar properties to hold for gSLOPE, which would pave the way for the applications in a variety of applications, where the groups of predictors are not necessarily independent.

Our proposed construction of the group SLOPE allows for the estimation of the group effects but does not allow to estimate the regressor coefficients by individual explanatory variables. We believe that the estimation of the individual effects would require a modification of the penalty term, so that a penalty would be imposed not only on entire groups, but also on individual coefficients. Such an idea was used in (Simon et al., 2013) in the context of sparse-group LASSO, where an additional l₁ penalty on individual coefficients was used. The modification of gSLOPE in this direction would be an interesting contribution, since it could be applied for a bi-level selection the selection of groups and particular variables within the selected groups at the same time. However, achieving gFDR control with such a modified penalty currently seems to be a challenging task.

We proposed a specific application of gSLOPE for Genome Wide Association Studies, where groups contain different effects of the same SNP. It is also worth mentioning that gSLOPE can be used to group SNPs based on biological function, physical location etc. We also expect this method to be advantageous in the context of identification of groups of rare genetic variants, where considering their joint effect on phenotype should substantially increase the power of detection. Going beyond genetic analysis group SLOPE could be used also for example in neuroimaging studies, where one can group voxel-wise brain activity measures, such as the ones derived from functional magnetic resonance imaging (fMRI), using the region of interest (ROI) definitions given by available anatomical atlases. Apart from these bioinformatics and medicine applications, one could also consider application of a group SLOPE for a variety of compressed sensing tasks. Here the most basic application of block/group sparsity is the extension to complex numbers in which the real and imaginary parts are split (and all represented by their coefficient), with each pair forming a group (see e.g. van den Berg and Friedlander, 2008; Maleki et al., 2013). As discussed e.g. in (Elhamifar and Vidal, 2012) block sparsity arises also in a variety of other applications such as reconstructing multiband signals, face/digit/speech recognition or clustering of data on multiple subspaces etc (see Elhamifar and Vidal, 2012, for the respective references). Another interesting application discussed in (van den Berg and Friedlander, 2011) is the identification of the temporal signals arriving from different, unknown, but stationary directions. Here the sparsity is the direction of arrival, whereas the L₂-norm is over the time series corresponding to this direction. These few possible applications represent only a small part of the real life group sparsity scenarios and exciting potential applications for the group SLOPE and we look forward investigating practical properties of group SLOPE in these real life problems.