Effect of Asymmetric Tension on Biomechanics and Metabolism of Vertebral Epiphyseal Plate in a Rodent Model of Scoliosis

Abstract

Objective

To investigate the effect of asymmetric tension on idiopathic scoliosis (IS) and to understand its pathogenic mechanism.

Methods

The rodent model of scoliosis was established using Sprague–Dawley rats with left rib‐tethering from T ₆ to T ₁₂, tail and shoulder amputation, and high‐cage feeding. Vertebrae epiphyseal cartilage plates were harvested from the convex and concave sides. To analyze differences on the convex and concave sides, finite element analysis was carried out to determine the mechanical stress. Protein expression on epiphyseal cartilage was evaluated by western blot. Micro‐CT was taken to evaluate the bone quality of vertebral on both sides.

Results

Scoliosis curves presented in X‐ray radiographs of the rats. Finite element analysis was carried out on the axial and transverse tension of the spine. Stresses of the convex side were −170.14, −373.18, and −3832.32 MPa (X, Y, and Z axis, respectively), while the concave side showed stresses of 361.99, 605.55, and 3661.95 MPa. Collagen type II, collagen type X, Sox 9, RunX2, VEGF, and aggrecan were expressed significantly more on the convex side (P < 0.05). There was asymmetric expression of protein on the epiphyseal cartilage plate at molecular level. Compared with the convex side, the concave side had significantly lower value in the BV/TV and Tb.N, but higher value in the Tb.Sp (P < 0.05). There was asymmetry of bone quality in micro‐architecture.

Conclusions

In this study, asymmetric tension contributed to asymmetry in protein expression and bone quality on vertebral epiphyseal plates, ultimately resulting in asymmetry of anatomy. In addition, asymmetry of anatomy aggravated asymmetric tension. It is the first study to show that there is an asymmetrical vicious circle in IS.

Introduction

The prevalence of idiopathic scoliosis (IS) in young people is 2%–4%1. It is a multi‐factorial disease with unclear etiology, which is possibly attributed to genetic factors, growth abnormalities, hormonal and neuromuscular dysfunction. Surgical treatment of IS is associated with high risk, cost and postoperative recurrence; thus, it can result in a heavy economic and psychological burden to families and society.

Scoliosis has never been found in vertebrates other than humans2. A key reason that human vertebrates are different from others is that humans walk upright. The position of center‐of‐gravity is located above the pelvis in the human body. A number of relevant animal models have been created, including pinealectomy in a chicken model, an immature goat model, and a porcine early‐onset model3, 4, 5. Among all such models, a bipedal rat model simulated human upright walking well.

The vertebral epiphyseal plate is a hyaline cartilage plate in the metaphysis. The growth of the human spine mainly relies on the upper and lower sides of the epiphyseal plate by continuous development and proliferation. The orientation of collagen fibers in the growth plate and contiguous structures of a growing long bone were demonstrated by polarized light microscopy. Five major groups of collagen fibers were established: transphyseal (longitudinal), perichondrial−periosteal (longitudinal), epiphyseal (radial), perichondrial ring (circumferential), and metaphyseal bone (circumferential)6. These fiber groups are staggered to form a collagen fiber web. This structural basis determines the mechanical properties of the epiphyseal plate

The human body is asymmetrical. Kouwenhoven and other scholars analyzed CT images of normal spine segments and identified a rotation to the left in the high thoracic vertebrae, whereas there was a rotation to the right in lower segments7. Asymmetric tension in scoliosis is reflected in muscle hypertrophy of the concave side and muscle atrophy of the convex side8. In recent years, through anatomical studies of scoliosis patients, asymmetry has been found to arise from discs, which results in distortion of the epiphyseal cartilage9. Wolff’s theories state that vertebral body shape change is the result of force, and force is the direct effect of the micro‐structure of the vertebral epiphyseal plate, which changes before scoliosis10. Axial load (perpendicular to the main plane of the epiphyseal plate) can accelerate or reduce the osteogenesis of the epiphyseal plate. Furthermore, shear load can make the vertebrae tilt, intermittent torsion contributes to its rotation, and sustained load can change the viscoelastic properties of epiphyseal plate. The range of the load value and the time of its action are two important determinants of vertebral development. This view reflects our understanding of the complex biological and biomechanical multifactorial processes11.

Scoliosis is a 3‐D deformity, and mechanical imbalance is the key factor in the occurrence and development of scoliosis. At present, the research method applied to scoliosis is mainly retrospective analysis of clinical cases due to the lack of an effective scoliosis model. Research on the effect of asymmetric tension on the growth of scoliosis generally as well as from the perspective of biomechanics and molecular biology is still lacking.

In this study, we assume that there is a biomechanical or metabolic pathway through which asymmetric tension leaded to scoliosis. This study is the first to investigate the effect of asymmetric tension on IS, and follows three steps: (i) to investigate the feasibility of a rodent model of scoliosis; (ii) to demonstrate the differences in mechanical stress, protein expression, and bone quality on the convex and concave sides; and (iii) to explore the relationships among stress, protein expression, bone quality, and asymmetry of anatomy.

Methods

Animal Models

Eight 4‐week‐old virgin female Sprague–Dawley rats (weight: 65–75 g) were housed in a laboratory at 22.2°C under a 12‐h light and 12‐h dark cycle and maintained on a Purina laboratory rodent chow diet (The second Military Medical University, Shanghai, China). An operation was performed at 4 weeks after birth, with: (i) left rib tethering procedure from T₆ to T₁₂ with a nonadsorbable No. 0 suture (Ethicon, Somerville, NJ, USA); (ii) tail amputation; (iii) shoulders amputation; and (iv) rats fed in high cages. Rats remained upright most of the time (Fig. 1). At the end of the 4‐week treatment, an X‐ray of the total spine was taken (Fig. 2). Rats with Cobb angle >10° were euthanized, and the apical vertebra of rats is T₁₁. This study was approved by the ethics committee of the hospital.

Figure 1.

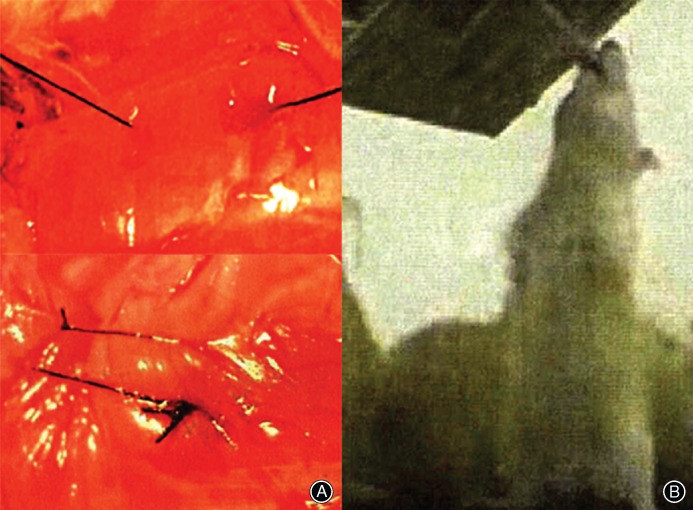
An operation was performed at 4 weeks after birth (A). Rats were fed in high cages (B).

Figure 2.

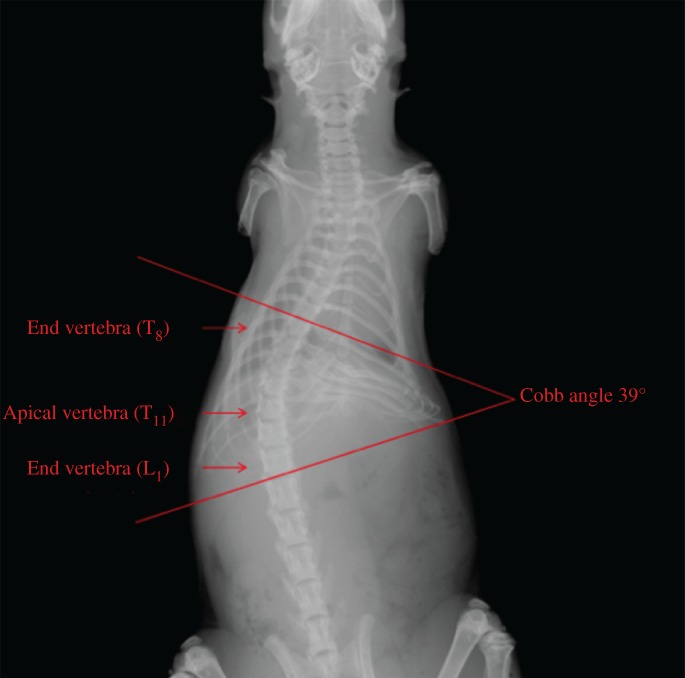
X‐ray shows the dead rat scoliosis model (AP), and Cobb angle was 39.00°, and the apical vertebra of rats was T ₁₁.

Finite Element Analysis

Development of Finite Element Model

In a 17‐mm sample holder in the cranial–caudal direction, the spine (T₈–L₁) was scanned using a high‐resolution μCT system (μCT35, Scanco, MicroCT systems and Software, Brüttisellen, Zurich, Switzerland). After scanning, the 2‐D image data was converted to 3‐D images using Mimics 17 (Materialise’s interactive medical image control system, Materialise, Belgium). The reconstructed images of one apical vertebra (T₁₁) were converted to finite element (FE) models by converting the voxels (Fig. 3B).

Figure 3.

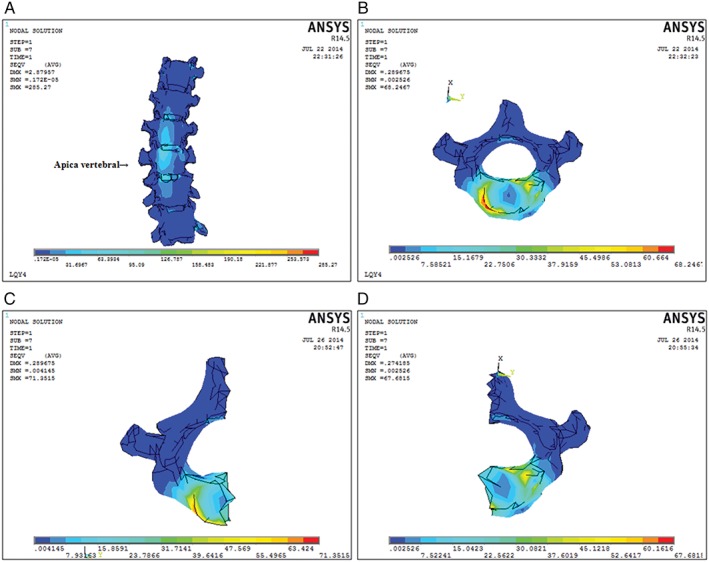
The reconstruction images of the spine (T ₈–L ₁). (A) Each scoliosis vertebra was divided into convex and concave sides by midcourt line. 3‐D finite element (FE) model of the apical vertebra (B) shows typical difference in forces on the convex and concave sides. In resultant stress there was a difference between convex (C) and concave (D) sides (6593.02 vs 5022.48), and the convex side was observed to increase (31.27%) in the vertical direction of the vertebral body.

Material Properties

Osseous tissues of the vertebrae and cartilaginous endplates in this study were modeled as isotropic homogeneous linearly‐elastic materials12. The texture parameter of each ligament was defined as nonlinear, as shown in Table 1. Intervertebral disc and intercostal ligaments were the only differing material properties.

Table 1.

The module of model components in the finite element

Model component	Modulus (MPa)	Poisson’s ratio
Vertebral body	1000	0.3
Rib	1000	0.3
Intervertebral disc	3.5–14.9	0.3
Intercostal ligaments	1.5–6.5	0.3

Boundary and Loading Conditions

In the whole model, each disc was tied between its adjacent end plates, and each two contiguous superior and inferior facets were set to sliding contact without friction. We assumed that gravity was the cause of axial loading. Axial loading of 2.4 N (calculated by measuring the dead rats) was applied to simulate the spine under gravitational force. The 3‐D model was validated according to geometric validation. In this study, the FE model was first tested with pure unconstrained linear moments from 0 to 4 N under loading conditions of flexion, extension, and lateral bending (Fig. 4). We changed the size of force to ensure that the FE model of the spine was contrasted to the rat’s X‐ray plate to validate the model’s geometric similarity according to their coincidence. The indexes of testing included coronal Cobb angle. Finally, resultant force (2.6 N) was given on T₈ on the left side to simulate asymmetric tension in the vertical direction.

Figure 4.

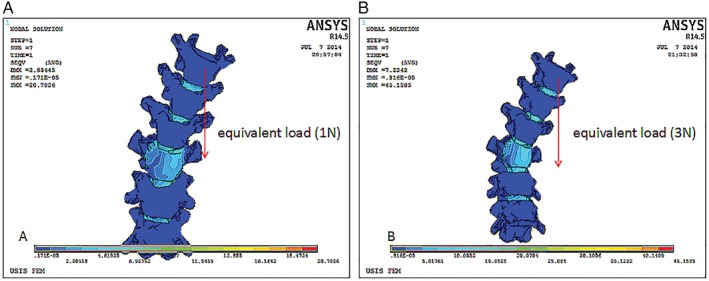
The finite element (FE) model was tested to simulate loading conditions. It shows reconstruction images of the spine under equivalent load 1 N (A) and 3 N (B). The force was given on T ₈ in the vertical direction to simulate asymmetric tension.

Convex and concave sides of the apical vertebra were constructed using the ANSYS 14.5 FE package (ANSYS, Canonsburg, PA, USA). The FE model was used to compute the compressive stress distribution on the convex and concave sides. In this coordinate system, the X axis was pointing upward, the Y axis was oriented from right to left, and the Z axis was oriented anteriorly. In applying this method, the original geometries of the spine provided the biomechanical basis for asymmetric tension.

Western Blot

Vepiphyseal cartilage plates of four rats were harvested from the convex and concave sides. The protein samples were divided into two groups (convex group and concave group). Samples were carefully separated under a microscope. After washing with sterile phosphate‐buffered saline (PBS), the attached connective tissue and muscle were removed. Then samples were stored in a saline‐soaked gauze at −20°C until analysis13. Protein samples (−50 μg) were fractionated by SDS‐PAGE (7.5%–10% polyacrylamide gels). Separated proteins were blot transferred onto a nitrocellulose membrane. After blocking with 0.1% Tween 20 and 5% nonfat dry milk in Tris‐buffered saline at room temperature for 1 h, the membrane was incubated overnight at 4°C in the following primary antibodies: VEGF (R&D, USA) (1:200), Collagen Type X (Boster, CN) (1:400), collagen type Π (NeoMarkers, CA, USA) (1:400), Sox‐9 (Santa Cruz, CA, USA) (1:500), aggrecan (Santa Cruz, CA, USA) (1:500), RUNX2 (Santa Cruz, CA, USA) (1:500) and β‐actin (Santa Cruz, CA, USA) (1:1000) as an internal control. The membrane was incubated with horseradish peroxidase‐conjugated secondary antibody (1:2000) for 1 h and detected using the Enhanced Chemiluminescence (ECL) Western blot System (Amersham Biosciences, Buckinghamshire, http://www.nsti.org/directory/countries/UK).

Micro‐CT

Four rats were assessed for bone quality based upon micro‐CT images (μCT35, Scanco, MicroCT systems and Software, Brüttisellen, Zurich, Switzerland). Each scoliosis vertebra was divided into convex and concave sides by the midcourt line. The trabecular bone of cancellous bone was extracted from the vertebral body as a volume of interest (VOI) by mapping along the margin between the cortical shell and trabeculae.

The convex and concave sides were calculated using the built‐in software of the μCT scanner, generating the following data: the bone volume fraction (BV/TV, fraction of trabecular bone per total volume); trabecular number (Tb.N, number of trabeculation per mm); trabecular thickness (Tb.Th, trabecular thickness); trabecular separation (Tb.Sp, distance of each trabeculation); and structure model index (SMI, index referring to the plate‐like or rod‐like structure of trabeculation).

Statistical Analysis

Statistical analysis was performed using the computer program SPSS (version 20, SPSS, Chicago, IL, USA), and values were expressed as mean ± standard deviation (SD). All data had been tested and verified to be of a normal distribution, and the paired samples t‐test was used for statistical analysis. A significance level of 0.05 was adopted.

Results

Cobb Angles of Scoliosis Models

The Cobb angle was measured by Image‐Pro Plus 6.0 (version 6, http://mail.qq.com/cgi-bin/mail_spam?action=check_link&spam=0&spam_src=1&mailid=ZL2924-FQfF1MIACe2McXInU~Whe55&url=http%3A%2F%2Fwww%2Eupdatestar%2Ecom%2Fpublisher%2FMedia+Cybernetics%2C+Inc%2E USA) (Fig. 1). X‐rays showed that in the rat scoliosis models the Cobb angles ranged from 22° to 48° and always had http://mail.qq.com/cgi-bin/viewdocument?sid=zN4VlYN_sVXUaWo-&filename=Blinded+Manuscript.docx&mailid=ZL2924-FQfF1MIACe2McXInU~Whe55&retry=true&t=attachments_content&ef=qfunc&s=yozo (1.88° ± 0.41°). The average and standard deviation of the Cobb angle in subjects with a main left thoracic deformity was 35.11° ± 7.62°.

Mechanical Stress

Finite element analysis was carried out on the axial and transverse tension of the spine. The forces in all directions were computed using digital records and the direction and magnitude of the resultant stress are given in Table 2. Stresses of the convex side were −170.14, −373.18 and −3832.32 MPa (X, Y, Z, respectively). Relatively, the concave side showed stress of 361.99, 605.55 and, 3661.95 MPa, respectively. In the resultant stress there was a difference between convex and concave sides (6593.02 vs 5022.48, Fig. 3), and the convex side was observed to increase (31.27%) in the vertical direction of the vertebral body. Therefore, stress on the vertebral and epiphyseal plate is asymmetric.

Table 2.

Stress results of the apical vertebral in all directions (MPa)

Seqv value	Convex	Concave	Total
X axis	−170.14	361.99	191.88
Y axis	−373.18	605.55	232.58
Z axis	−3832.32	3661.95	−171.65
Stress results	6593.02	5022.48	11615.20

Protein Expression of Vertebral Epiphyseal Plate

Western blot results are shown in Fig. 3. The integrated option density (IOD) was computed by Image Pro Plus (version 6.0, Media Cybernetics, Beijing, China). The mean values of aggrecan, collagen type II, Sox 9, RunX2, VEGF, and collagen type X were 9510.42 ± 4363.33, 21 353.78 ± 1678.87, 17 462.43 ± 3281.85, 23 374.15 ± 2871.86, 23374.15 ± 4917.86, and 24.93 ± 3.52 on the convex group. The mean values of the other group were 1701.54 ± 844.40, 9548.80 ± 2062.11, 5617.48 ± 2467.14, 10245.89 ± 3677.83, 10245.89 ± 1471.85, and 7.17 ± 5.95 (Table 3). VEGF and aggrecan were typical markers of chondrogenic differentiation. Compared with the concave group, the convex group showed increases in aggrecan (458.93%), collagen type II (123.62%), Sox 9 (210.86%), RunX2 (128.13%), VEGF (129.15%), and collagen type X (247.70%). There were obvious differences between convex and concave sides in the levels of the chondrogenic markers (P < 0.05). Significant differences were noted in the contribution of collagen type II, collagen type X, and RunX2 between the convex and concave sides (P < 0.01, Fig. 5). These protein expression differences between the convex and concave sides tend to show asymmetry of endochondral ossification and, thus, might account for eventual IS development.

Table 3.

Integrated option density (IOD) of labeled proteins on the convex and concave sides (mean ± standard deviation)

Variables	Convex	Concave	P‐value	t‐value
Aggrecan	9510.42 ± 4363.33	1701.54 ± 844.40	0.049	3.214
Collagen type II	21 353.78 ± 1678.87	9548.80 ± 2062.11	0.006	7.131
Sox 9	17 462.43 ± 3281.85	5617.48 ± 2467.14	0.024	4.255
RunX2	23 374.15 ± 2871.86	10 245.89 ± 3677.83	0.009	6.032
VEGF	23 374.15 ± 4917.86	10 245.89 ± 1471.85	0.048	3.241
Collagen type X	24.93 ± 3.52	7.17 ± 5.95	0.001	12.528

Figure 5.

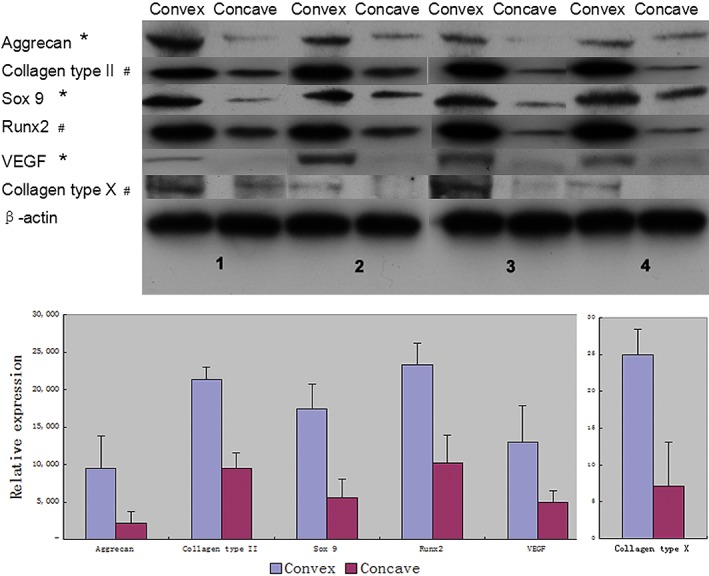
Expression of collagen type II, collagen type X, Sox 9, RunX2, VEGF, and aggrecan were assessed by western blotting. The different values from convex and concave sides were shown on the electrophorogram and column charts. All values are shown as mean ± SD. *P < 0.05 and ^# P < 0.01.

Micro‐Architecture of Trabecular Bone

Micro‐CT scans of the apical vertebral revealed the micro‐architecture of trabecular bone and returned numerical values so as to the bone quality of the apical vertebral (Fig. 6). The mean values of BV/TV, Tb.N, Tb.Sp, Tb.Th, and SMI for the convex and concave sides were 0.33 ± 0.02 versus 0.26 ± 0.02, 4.88 ± 0.19 versus 4.40 ± 0.17, 0.08 ± 0.01 versus 0.07 ± 0.00, 0.19 ± 0.01 versus 0.21 ± 0.01 and 0.36 ± 0.25 versus 0.83 ± 0.20 (Table 4). The asymmetry of micro‐architecture of trabecular bone was observed in the convex and concave sides. Compared with the concave group, the convex group showed increases in the BV/TV (26.92%) and Tb.N (10.90%), as well as increases in the Tb.Sp (9.52%, P < 0.05). Asymmetry in IS is not only found in anatomy, but also found in micro‐architecture and bone quality. Asymmetry of bone quality should be the result of asymmetric expression of protein on the epiphyseal cartilage plate.

Figure 6.

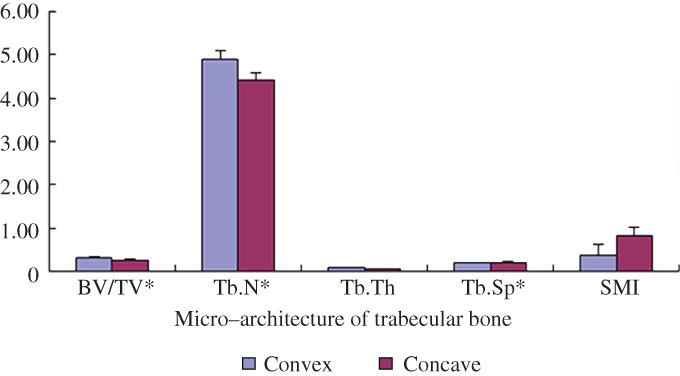
The column chart shows the micro‐architecture of the apical vertebra trabecular bones. Numerical value was shown to describe the bone quality of the apical vertebra on convex and concave sides. All values are shown as mean ± SD. *P < 0.05.

Table 4.

Histomorphometry indices of the apical vertebral trabecular bones (mean ± standard deviation)

Variables	Convex	Concave	P‐value	t‐value
BV/TV (%)	0.33 ± 0.02	0.26 ± 0.02	0.024	3.375
Tb.N (1/mm)	4.88 ± 0.19	4.40 ± 0.17	0.013	6.023
Tb.Th (mm)	0.08 ± 0.01	0.07 ± 0.00	0.130	1.960
Tb.Sp (mm)	0.19 ± 0.01	0.21 ± 0.01	0.027	3.286
SMI	0.36 ± 0.25	0.83 ± 0.20	0.062	0.1440

BV/TV, bone volume fraction (fraction of trabecular bone per total volume); Tb.N, trabecular number (number of trabeculation per mm); Tb.Th, trabecular thickness (trabecular thickness); Tb.Sp, trabecular separation (distance of each trabeculation); SMI, structure model index (index referring to the plate‐like or rod‐like structure of trabeculation).

Discussion

Scoliosis is a complex 3‐D structural deformity, involving lordotic and kyphosis lateral bending and rotation14. To study the asymmetrical growth of scoliosis, Roth first reported that scoliosis is caused by the spinal cord being relatively short or excessive growth of the spinal column15, 16. Moreover, Porter considered that asymmetry of the spinal cord and vertebral growth may be the root cause of scoliosis17, 18. Here we focus on asymmetric tension in scoliosis and its effects on the biomechanics and metabolism of the vertebral epiphyseal plate, principally exploring whether asymmetric tension could contribute to scoliosis development. In this paper, we first propose a concept of a vicious circle in scoliosis and provide an introduction on its pathogenic mechanism.

Animal models have played an important role in the study of scoliosis over the past 20 years19, 20, 21, 22. In this study of complex scoliosis, bipedal rats fed in high cages were used as a model for the human spine. Asymmetric tension on the rat’s thoracic vertebra contributed to spinal deformity. In the coronal plane, all samples’ Cobb angles were greater than 10°. Asymmetric tension on bipedal rats creates a successful model of scoliosis. Knowledge of the microstructure changes contributing to scoliosis would be valuable.

The FE model can provide insight into the structure–functional relationships of bone and the forces involved23. Patient‐specific FE models have been used to explore the effects of biomechanical factors on scoliosis24. Gravity and a pre‐existent asymmetry curves in the spine were identified as scoliosis‐promoting factors25. In our study, http://mail.qq.com/cgi-bin/viewdocument?sid=zN4VlYN_sVXUaWo-&filename=Blinded+Manuscript.docx&mailid=ZL2924-FQfF1MIACe2McXInU~Whe55&retry=true&t=attachments_content&ef=qfunc&s=yozo http://mail.qq.com/cgi-bin/viewdocument?sid=zN4VlYN_sVXUaWo-&filename=Blinded+Manuscript.docx&mailid=ZL2924-FQfF1MIACe2McXInU~Whe55&retry=true&t=attachments_content&ef=qfunc&s=yozo was evaluated using FE and showed that epiphyseal cartilage had asymmetric tension in the vertical direction and this tended to contribute to a vicious cycle of asymmetry asymmetric tension26. However, this alone cannot explain the root cause of scoliosis, for which the molecular players should be identified.

Longitudinal spine growth occurs through the epiphyseal cartilage plate27. Endochondral ossification depends upon a variety of cytokines that regulate stromal cell differentiation into cartilage cells, thereby regulating synthesis of type II collagen in cartilage cells28. Similarly, as one of the related Runt gene family members, RunX2 is involved in multiple cytokine interactions and adjustments to bone metabolism and bone formation. Zheng reports that in the cartilage generation process, Runx2 directly affects collagen type X genes and regulates the expression of collagen29. Type II collagen is the major structural protein of the epiphyseal plate cartilage, and as with type X collagen, cartilage proteoglycan glycans (Aggrcan) is evaluated together with the widely used chondrocyte proliferation. Reports have demonstrated that multiple VEGF are involved in the process of neovascularization30. The above proteins are key proteins related to growth of the epiphyseal cartilage plate, which have been reported in many studies. Synthesis and metabolism of protein are controlled by the upstream or downstream regulatory proteins. Despite the presence of interactions and adjustments, proteins on the epiphyseal cartilage present positive feedback in the growth stage. The biomechanics and metabolism of the vertebral–epiphyseal plate is easy to study.

Bone quality describes bone micro‐architecture and contributes to the level of bone turnover and bone micro‐damage. BV/TV is an index that reflects the amount of bone mass, whereas the Tb.Sp, Tb.Th, and SMI parameters better explain changes in bone microarchitecture31. Bone growth has been reported to be accompanied by increases in Tb.Th, BV/TV, and Tb.N, but decreases in Tb.Sp. In our study, there is a significant difference in the bone mass (BV/TV) between the convex group and the concave group, with the convex group having significantly higher BV/TV than the concave group, which is consistent with the expression of protein on epiphyseal cartilage plate. We propose that expression of protein on the epiphyseal cartilage plate contributed to the growth of bone density.

Before the onset of IS, there will have already been changes in the bone microstructure, conforming to Wolff’s law. Through long‐term and in‐depth study of Wolff’s law, it has been shown that the microstructure of bone dynamically adjusts and realigns itself in precise relation to changes in the loading direction32, 33. This raises the possibility that a pathway exists, in which asymmetric tension affects molecular mechanisms to induce changes in vertebral epiphyseal plate microstructure, which subsequently act on the mechanical properties of the rat vertebral body. As children and adolescents grow and develop into adults, loading stresses bring about dynamic changes, which might exacerbate scoliosis.

Scoliosis is a multifactorial disease. Previous studies might have focused on only one or two aspects. The lack of systematic assumptions could be problematic. We investigated the relationships among stress, protein expression, bone quality, and asymmetry of anatomy and suggested that there was an asymmetrical vicious circle in scoliosis, ultimately resulting in coronal decompensation (Fig. 7). This assumption can be explained as follows. First, we found that asymmetry of anatomy contributed to asymmetry of stress by building a scoliosis rat model and finite element analysis. Second, protein expression and bone quality on the convex and concave sides suggested that there was an asymmetry on micro‐architecture of scoliosis, which also proved Wolff’s theories. Third, eventually, asymmetry of protein expression and bone quality aggravated the deterioration of scoliosis. In addition, in the current research, most causes could be explained by this assumption. Genetic factors are always thought of as a possible contributor, as they may cause the asymmetry of protein expression leading to scoliosis. Because external fixation is used as a treatment for scoliosis, it is easy to explain that reducing the asymmetry of stress is the effective way to block the loop and, finally, to slow the progression of the disease.

Figure 7.

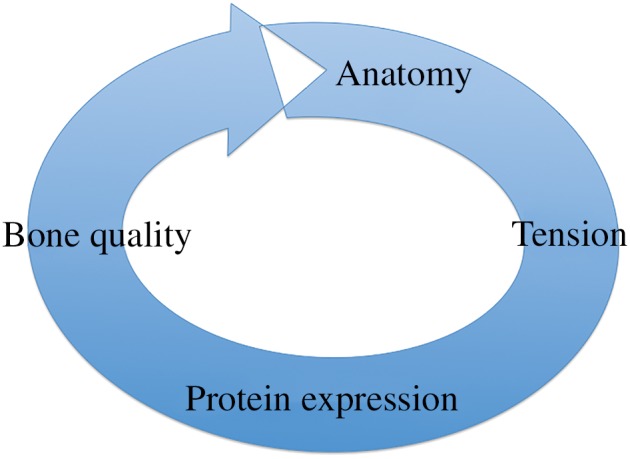
The cycle of asymmetry. Asymmetry of anatomy contributes to asymmetry of stress, then protein expression, then bone quality and eventually asymmetry of anatomy.

This study has several limitations. First, the sample size is small: only 8 rats underwent this modeling and the overall result was good. Second, we did not present a control group without any rib tethering, which has indicated the effect of the regiment on the spine. The use of such a group will similarly enhance the bone histomorphometry and gene‐based analysis. Third, modeling is confined to thoracic scoliosis, and the analysis of lumbar scoliosis might differ considerably from the results reported here. Tethering between ilium and ribs should greatly solve the problem. Our method is easier to operate and can be a supplement in cases for prospective studies of scoliosis. Fourth, while scoliosis is involved in whole spine changes at the mechanics and molecular level, in the present study only apical vertebra underwent experimental analysis and comparison between the convex and concave sides. Stress analysis of the whole spine would be expected to show compensatory bending in the lumbar spine. Microstructure and stress at each vertebral scoliosis do not mean the same thing. However, this method requires a large amount of work and strict control of models’ individual differences. At this stage, analysis of apical vertebra in our study was effective and feasible and could be an option for these spine surgeons.

In conclusion, asymmetrical loading might be a cause of scoliosis, because genetic and neurohormonal factors have been identified as related etiological factors. Above all, the discovery of the vicious circle in scoliosis may lead to a more accurate description of the biomechanical behavior of the spine, which is crucial for the planning of surgical scoliotic correction.