Impact of optical aberrations on axial position determination by photometry

Reporting Summary

Further information on research design is available in the Nature Research Reporting Summary linked to this article.

To the Editor —

"Recently, Franke et al.¹ introduced a way to estimate the axial position of single molecules (temporal radial-aperture-based intensity estimation (TRABI)). To this end, they compared the detected photon count from a TRABI estimation to the estimated count from Gaussian point-spread function (PSF) fitting to the data. Empirically they found that the photometric ratio is ~0.7–0.8 at points close to focus and decreases as the distance from the focal plane increases. Here we explain this reported but unexplained discrepancy and, furthermore, show that the photometric ratio as an indicator for axial position is susceptible even to typical optical aberrations.

In Fig. 1a we show the photon count from a 45-nm bead imaged with an aberration- corrected microscope² (details are provided in the Supplementary Methods), estimated by three different methods (Gaussian PSF fit, TRABI and vectorial PSF fit³) as a function of aperture radius or fit box size (for reproducibility see Supplementary Fig. 1). It is evident that the estimated count increased with increasing area for all three methods—that is, no method found the true count for a realistic area, as the true microscope PSF has a very long tail. Simulations of full-vectorial PSFs supported this conclusion (Supplementary Fig. 2), showing that the tail deviates substantially from the Airy PSF model³. It is also evident that with any aperture-based method the true count could be approximated only up to 90% with aperture radii less than 1 Δm (Supplementary Fig. 3) and that Gaussian PSF fitting performed worse than the other methods, as a Gaussian cannot fit the long tail at all. This, however, does not bias the localization estimate of Gaussian fitting for round spots³. We investigated the suitability of subdiffraction-sized beads for these experiments in a simulation and found that they increased the full width at half-maximum (FWHM) by only a few nanometers compared with the single-molecule PSF (Supplementary Fig. 4) while giving access to more light over a longer period during the experiment.

Fig. 1|. Photon-count estimation and the effects of aberrations on the photometric ratio.

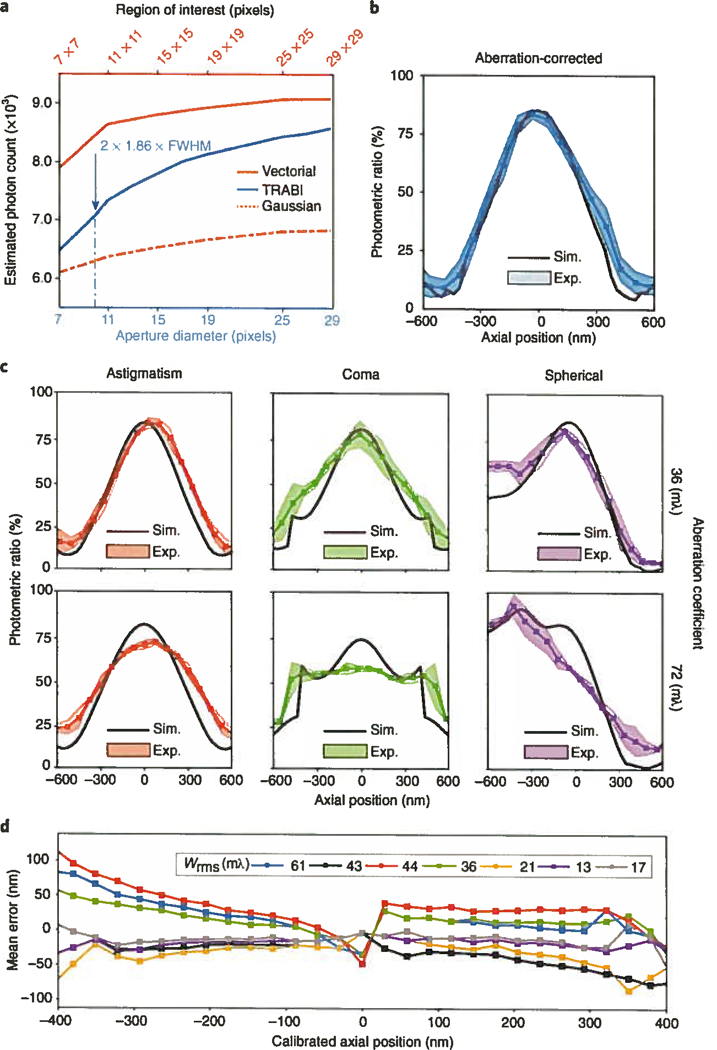
a, Estimated photon count for a 45-nm-diameter bead imaged with an aberration-corrected microscope as a function of analysis area on the camera. The three curves show the counts for fitting with a fully fledged vectorial PSF model, a simplified Gaussian PSF model, and TRABI. FWHM, 214 5 nm; pixel size, 80 nm. Aperture diameter of 2 × 1.86 × FWHM used as suggested by Franke et al.¹. b, The photometric ratio (Gaussian fit over TRABI value) across six bead measurements as a function of the axial position. The shaded error band indicates one s.d. Area of fit, 7×7 pixels; aperture radius, 1.86 × FWHM. c, Effect on the photometric ratio for beads single-mode aberrated with r.m.s. aberration coefficients set at half (36 mλ; top row) and full diffraction limit (72 mλ; bottom row). d, Axial estimation error for seven typical aberration uncorrected microscopes. W_rms is the mean measured wavefront error. Sim., simulation; Exp., experiment.

Next, we varied the axial position of the sample while imaging aberration-corrected beads and evaluated the photometric ratio between photon count estimates from Gaussian fitting and from TRABI as a function of defocus, as shown in Fig. 1b (see Supplementary Fig. 2 for sensitivity to fit area). The residual wavefront aberration was 24 mλ root-mean-square (r.m.s.; see Supplementary Fig. 5 for experimentally retrieved aberration coefficients). Simulations using the fitted residual aberrations resulted in photometric ratios that agreed well with experimental values. We found a photometric ratio of 85%, in contrast to the values of ~75% in focus reported by Franke et al.¹, which we attribute to aberrations present in their experiment. To assess the influence of aberrations, we experimentally engineered PSFs with small amounts of astigmatism, coma or spherical aberration. Photometric ratios obtained from these experiments matched those obtained from simulations with added aberrations (Fig. 1c). The maximum value of the photometric ratio in focus, overall shape and values strongly depended on the aberrations, which resulted in curves that were broadened, flattened or made asymmetrical. The amounts of added aberrations used here still represent a lens that is referred to as diffraction limited (the Maréchal diffraction limit is 72 mλ), indicating that these aberration levels and combinations thereof are seen in typical setups. We estimated the effects of these small aberrations on the expected axial-position error by carrying out a comparison to an aberration-corrected calibration and found errors between ±100 and ± 200 nm over an 800-nm dynamic range (Supplementary Fig. 6). Sample-induced refractive index mismatch, caused by, for example, the use of an oil-immersion objective in a watery enviroment, leads to spherical aberration but also nonspherical components⁴ on the same order as what we simulated here. In Fig. 1d we show the axial estimation error for seven noncorrected systems from different vendors and labs (details in the Supplementary Methods), which we found to be on the order of ±50 to ±100 nm. We measured the aberrations in these systems via through-focus bead acquisition (see Supplementary Fig. 7 for details on the individual wavefront errors). We then calculated the axial estimation error as the difference between the calibrated aberration-free photometric-ratio-based position estimate and the simulated estimate with aberrations equaling the experimentally determined microscope aberrations. We conclude that in order for the photometric ratio to be converted to a viable, accurate depth map, the optical aberrations must be known to a very high degree (wavefront uncertainty < 10 mλ results in axial uncertainty < 20 nm).