Computational algorithms for in silico profiling of activating mutations in cancer

Abstract

Methods to catalog and computationally assess the mutational landscape of proteins in human cancers are desirable. One approach is to adapt evolutionary or data-driven methods developed for predicting whether a single-nucleotide polymorphism (SNP) is deleterious to protein structure and function. In cases where understanding the mechanism of protein activation and regulation is desired, an alternative approach is to employ structure-based computational approaches to predict the effects of point mutations. Through a case study of mutations in kinase domains of three proteins, namely, the anaplastic lymphoma kinase (ALK) in pediatric neuroblastoma patients, serine/threonine-protein kinase B-Raf (BRAF) in melanoma patients, and erythroblastic oncogene B 2 (ErbB2 or HER2) in breast cancer patients, we compare the two approaches above. We find that the structure-based method is most appropriate for developing a binary classification of several different mutations, especially infrequently occurring ones, concerning the activation status of the given target protein. This approach is especially useful if the effects of mutations on the interactions of inhibitors with the target proteins are being sought. However, many patients will present with mutations spread across different target proteins, making structure-based models computationally demanding to implement and execute. In this situation, data-driven methods—including those based on machine learning techniques and evolutionary methods—are most appropriate for recognizing and illuminate mutational patterns. We show, however, that, in the present status of the field, the two methods have very different accuracies and confidence values, and hence, the optimal choice of their deployment is context-dependent.

Electronic supplementary material

The online version of this article (10.1007/s00018-019-03097-2) contains supplementary material, which is available to authorized users.

Introduction

Tumorigenesis was first posited to be an evolutionary process by Nowell in 1976 [1]. Since then, the idea that cancer cells undergo selection on the path from normal to the cancerous cell has continued to gain traction [2]. This idea is predicated upon the knowledge that tumors are composed of a heterogeneous population of cells, in terms of mutations, gene expression levels, somatic copy number, and epigenetic factors [3, 4]. These factors are then selected upon for robustness and their ability to promote proliferation, alter the tumor microenvironment, and invade neighboring tissues [2]. Of all the functional alterations that a cancer cell undergoes, among the easiest ones to understand conceptually, and to measure unambiguously, are mutations that directly alter protein function. Mutations that ablate a protein’s regular function are often observed in cancer cell lines, especially among tumor suppressors such as TP53 and RB1 [3, 4]. The transformation from normal to the cancerous cell is often marked by a gradual accumulation of mutations over time that eventually increases the ability of the cancer cell to sustain itself and reproduce [2]. Cancer cells may acquire mutations at a faster rate than normal somatic cells or may acquire more mutations due to increased proliferation. Not all mutations drive cancer progression. Mutations that confer a selective advantage on the cancer cell line are known as ‘driver’ mutations, whereas ‘passenger’ mutations are neutral in terms of selective advantage [5]. All cells acquire mutations over their life cycle from differentiation to senescence, but cancer cells do so at a faster rate than normal cells, and this rate increases over time [6]. Most mutations fall in intergenic regions or within introns of the coding sequences of proteins [7], and their consequences are unclear. Some affect protein splicing or regulation, but how these contribute to cancer progression is not well understood. The clearest oncogenic mutations are those that cause changes in the amino acid sequence of a protein with direct effects on protein function.

One of the grand challenges in understanding cancer progression is to find mechanistic links between molecular alterations and the hallmarks of cancers such as increased proliferation and survival, aggressive invasion and metastasis, evasion of cell death, and increased metabolism [3, 4]. This challenge is also of clinical importance, because the patient outcome of therapy (both in terms of initial response and subsequent development of resistance) is now known to depend on the genetic alterations (primary or acquired) in the individual patients [8–11]. Many targets for therapeutic intervention/inhibition have been evaluated in the past few years based on strong promise suggested by preclinical investigations. Experience has shown, however, that clinical trials are often unsuccessful when the drugs are administered to un-cohorted patient populations—accentuating the need to employ targeted therapies on select populations of patients classified based on molecular/genetic alterations [11]. Rapid genotyping platforms and advances in sequencing cancer genomes allow detection of genetic aberrations in clinical samples. These approaches allow the identification of relevant molecular targets in each patient, and also the tracking of acquired molecular changes [12] (expression [13, 14], mutation [15–18], epigenetic changes [19], post-translational modifications [20], etc.) during disease progression or during treatment. Relating the molecular profile of a given patient to disease prognosis and the efficacy of a particular therapy is a grand challenge in clinical oncology. The goal is to map high-dimensional data from an array of techniques to a set of viable cellular mechanisms and, thus, to infer treatment options. Integrating quantitative data on protein expression (from immunohistochemistry), gene copy number and mutations (from sequencing and other DNA analyses), and gene expression (from fluorescence in situ hybridization, polymerase chain reaction or microarray technology, single-cell imaging) is a daunting task [21]. A further problem is the heterogeneity of tumors [22], leading to differential expression patterns within a tumor, in different tumor areas within an individual, or in different individuals. The question then is: how precisely can a tumor be characterized by these techniques? Tackling the heterogeneity represents a promising opportunity for in silico modeling approaches.

Mining molecular/mutation data from cancer atlases

Recent large-scale sequencing projects have generated extensive data on somatic mutations in cancer. Tumor resequencing efforts have led to a substantial accumulation of data on cancer somatic mutations [23]. The ongoing decrease in the price of genome and exome sequencing has led to the creation of online databases for cancer genome sequence information such as the Catalog Of Somatic Mutations In Cancer, COSMIC [23] and The Cancer Genome Atlas, TCGA (http://cancergenome.nih.gov/). This cataloging, in turn, has allowed researchers to catalog which proteins are frequently mutated in various cancer types, and has spurred efforts to determine the driver status of mutations [24].

Kinase domain mutations: Kinases are involved in cellular signaling processes that control differentiation, proliferation, and other cellular behavior [25]. Some of the first oncogenic mutations to be discovered were those that activate kinases, leading to constitutive activation and upregulation of cell proliferation [4, 25, 26]. Gain-of-function mutations of this type tend to occur at ‘hotspots’ in the protein, whereas loss-of-function mutations (as seen in tumor suppressors in cancer) are more distributed throughout the molecule. Moreover, the fact that kinase domains experience large and well-characterized conformational differences between their active and inactive forms [27] makes experimental detection and computational prediction of activating mutations possible [24, 28–30]. Kinases are frequently mutated proteins in cancer, accounting for 2% of all mutations in the COSMIC database (taking into account clinical data subject to whole genome sequencing only). Mutations that activate kinase domains and upregulate cell proliferation are well represented among known driver mutations. Many have been clinically observed [23] and experimentally verified, but determining a priori which mutations in a given kinase are activating is still quite challenging.

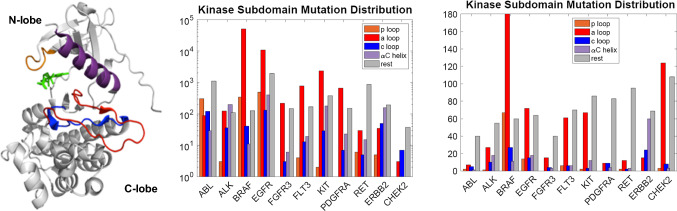
Although many previous studies have shown that specific kinase domain mutations can lead to constitutive activation, no systematic study of mutational clustering in the various structural subdomains of the canonical kinase fold has previously been undertaken. We reasoned that the subdomain location of kinase domain mutations would be linked to their ability to promote constitutive activation, and might serve to help predict which novel mutations promote signaling deregulation and lead to oncogenesis. The COSMIC database (version 68) [23] was used as the source for mutational data to obtain information on subdomain clustering of kinase domain mutations. A multiple sequence alignment of kinase domains was performed using ClustalW2 [31], and the residues comprising functionally important structurally defined subdomains (see Fig. 1) were extracted. These subdomains include the nucleotide-binding loop (P-loop), the catalytic-loop (C-loop), the αC-helix, and the activation loop (A-loop). By binning clinically observed cancer mutations in kinase domains in this manner, we can observe whether or not mutations preferentially segregate to any of these subdomains or whether there is a more uniform distribution of mutations across the kinase domain. The number of observed mutations in select kinases classified according to cancer type and according to the subdomain of the protein kinase where the mutation occurs is provided in Fig. 1.

Fig. 1.

(Left) structure of a tyrosine kinase domain with different subdomains colored; see labels on legends in middle and right panels. The structure derived from the epidermal growth factor receptor tyrosine kinase (PDB ID: 2GS2). The nucleotide binding loop (p-loop), αC helix, activation loop (A loop), and the catalytic loop (C loop) are highlighted. (Middle) histograms of number of clinically observed cancer mutations in kinase domains constructed from COSMIC (version v87, 2018); here each count is an observation in one patient. (Right) histograms of number of amino acids mutated in the kinase domain pooled from clinically observed cancer mutations in kinase domains constructed from COSMIC (year 2018); here each count is a mutation at an amino acid location. We note that the middle panel include patient data from targeted sequencing as well as whole genome sequencing while the right panel includes data from whole genome sequencing only. These figures are provided to motivate the prevalence of mutations in cancer patients only. As a cautionary note, any statistical analysis on such data should consider the bias factors involved in targeted sequencing

One of the most frequently observed single mutations in COSMIC is the BRAF V600E mutation, which is located in the activation loop of the BRAF kinase domain and has been shown to lead to its constitutive activation [32]. This mutation is frequently observed in several cancer types, including thyroid, colon, skin, leukemia, and lung cancers. A notable contrast to the highly predominant single mutation that characterizes BRAF is the case of the epidermal growth factor receptor (EGFR), where more than half of the residues in the kinase domain have been observed to be mutated in lung cancer samples. While exon 19 insertion–deletion class of mutations (e.g., Del747–753 Ins S) is the most prevalent EGFR mutations in human cancers [33], the most common EGFR single point mutation in cancer is L858R (using pro-EGFR numbering, where the mature protein begins at residue 25). L858 is in the EGFR activation loop and is known to cause constitutive activation of the kinase [24]. The next most frequently observed EGFR mutation is the so-called gatekeeper mutation, known as T790M, which is not located in any of the kinase subdomains under consideration but does lead to constitutive activation. This mutation is frequently observed to arise after treatment with EGFR-specific inhibitors, as it reduces the ability of first-generation EGFR inhibitors to compete with ATP for the active site, leading to treatment resistance [24]. Much less common than either of these mutations, but still causing constitutive EGFR activation are the P-loop mutation G719S and the activation loop mutation L861Q. Curiously, although some studies have shown that L861Q increases kinase activity, transforms cell lines, and promotes drug resistance, no research to date has made a direct measurement of L861Q kinase activity. Other such mutations in EGFR include E709G and S768I similarly known to be activating. The majority of the remaining mutations seen in the EGFR kinase domain in lung cancer samples are only mutated relatively infrequently. Many of these mutations are of unknown consequence, but several have been shown to lead to constitutive activation. The ErbB family member ErbB2, also known as HER2, is frequently mutated in breast cancer and also often mutated in colorectal cancer as well. The most frequent mutations are in the catalytic loop (V842I) and the αC-helix (I767M, D769Y, and V777L). All of these mutations have been studied in vitro and in vivo, and appear to be activating [34, 35]. The L755S mutation, which is not with any of the listed subdomains, but lies N-terminal to the αC-helix, has been shown to have minimal cell transforming abilities but to confer drug resistance, and has yet resisted attempts to characterize its catalytic activity [34–36]. Another kinase that is frequently mutated in cancers, especially leukemia, skin cancer, and gastrointestinal stromal tumors (GIST), is the stem cell growth factor receptor known as c-kit. Again, the majority of the mutations in this protein are observed in the activation loop, with the most frequent being the D816V mutation observed in leukemia [37]—known to lead to constitutive activation. Much less frequently, mutations are also observed in the αC-helix of c-kit, with K642E being the most common. This mutation has also been shown to lead to constitutive activation [38]. There is also one relatively frequent mutation in kit that is not in a subdomain, namely the V654A mutation that falls between the αC-helix and the catalytic loop and leads to increased kinase activity [39]. FLT3, PDGFRα, and FGFR3 all have been observed to have activation loop mutations in cancer samples. In FLT3, the D835Y/V/E/H/N activation loop mutations have all been shown to lead to constitutive activation [40]. Likewise, the PDGFRα D842V activation loop mutation is constitutively activating [41], as are the FGFR3 activation loop mutations K650M/E in skin cancers [42].

There are a few interesting cases of kinase domains that are frequently mutated in COSMIC for which the most recurrent mutations are not in the activation loop—perhaps indicating a different mechanism of activation of these kinases. The RET M918T mutation, located a few residues N-terminal to the activation loop, is frequently observed in thyroid cancer [43]. Another interesting case is that of ABL, which was the first tyrosine kinase to have a clinically approved inhibitor [44]. After treatment with inhibitors such as imatinib, the oncogenic BCR-ABL fusion protein acquires the so-called gatekeeper mutation T315I, between the αC-helix and the activation loop, which confers resistance to many BCR-ABL specific inhibitors by sterically hindering their binding [45]. Several other mutations that prevent inhibitor binding via steric hindrance are also observed in the P-loop of BCR-ABL [45].

Perhaps, the most remarkable case of constitutive activation of a kinase by a mutation is that of JAK2. JAK2 has two kinase domains called JH1 and JH2. The second kinase domain, JH2, has only weak (if any) kinase activity and is thought to function to regulate the JH1 kinase domain [46]. A V617F mutation—in the N-lobe of the JH2 pseudokinase domain—is the most frequently observed single mutation in COSMIC at this time and is known to lead to constitutive JAK2 activation [47]. The mechanism that causes this activation is still a subject of debate. We also investigated the juxtamembrane region (JMR) of receptor kinases for mutational clustering. By far, the most frequently mutated JMR was that of c-kit, which is frequently mutated at residues V559 and V560—typically to Asp (less frequently to Gly or Ala). Kit L576P and W557R mutations are also sometimes observed. The V560G mutation has also been shown to lead to constitutive kit dimerization [48], as well as activation and is susceptible to inhibition by imatinib [49]. The V559D mutation has also been shown to cause constitutive activation [50]. Other receptors appear to be much less prone to activation by JMR mutations (data not shown).

Interesting phenomena emerge when we analyze the most prevalent mutations as a group rather than individually on a per kinase basis. One interesting observation is that several prevalent mutations occur at the same residue in different proteins, as determined by sequence alignment. In receptor tyrosine kinases, the D835Y/V/E/H/N in FLT3, D816V/H/Y/F mutations in KIT, D842V mutation in PDGFRα, and L861Q mutation in EGFR all occur in the same place in the kinase domain. Most of these have been shown to lead to ligand-independent constitutive activation. Another general feature of activation loop mutations shows up when we examine this list. Many frequently observed oncogenic mutations involve substituting a charged amino acid to a non-charged amino acid, or vice versa. The residues at which such mutations occur are all involved in or close to a salt bridge predicted to stabilize the inactive state of the kinase.

In effect, many of these mutations are changing the electrostatic environment of a wild-type stabilizing interaction, or creating a new stabilizing interaction for the active state. Several activation loop mutations also result in the loss or formation of a salt bridge, which biases the system towards the active state. The EGFR L858R mutation results in a new salt bridge that favors the active state [51]. The BRAF V600E mutation does not result in the formation of a new salt bridge, but, instead, destabilizes an existing salt bridge by changing the electrostatic environment of the neighboring residue K601, which normally is involved in a salt bridge with the αC-helix in the inactive conformation [52]. However, it is important to emphasize that the mechanistic basis for how mutations impact protein function is not understood in most cases.

Given that there is mutational clustering in kinase proteins, it is natural to ask whether there might be similar trends in other protein classes. A summary is provided in Supplementary Information (SI) section S1 where we discuss mutation statistics for GTPase/G-proteins and other proteins. For the remainder of the review, we, however, focus our discussions on evaluating the functional effects of kinase mutations using computational methods.

In silico methods for structure–function mapping

Although the frequently observed mutations (hotspot mutations) are studied in detail to determine their effects on protein function, cell line proliferation, or both, many more mutations remain unstudied. It may not be practical to carry out detailed mechanistic or transformation assays for every mutation that is observed—making predictive approaches desirable. To treat patients effectively, or even classify patients into different cohorts for treatment, it would be of great value to have a general description of how the mutational landscape of a particular patient will alter best treatment practices. The issue is particularly significant in molecularly targeted therapies, where drugs target specific proteins, and, perhaps, even specifically mutated proteins. Here, we discuss several computational approaches that can help bridge the gap that exists between assessing mutational landscapes in individual proteins, their effect on signaling pathways, cellular response, and the implications on cancer hallmarks and ultimately the clinical outcome.

Extensive cataloging of mutational data such as those summarized in “Mining molecular/mutation data from cancer atlases” has led to efforts to computationally assess/classify which of these mutations are drivers and which are passengers—using the definitions outlined earlier. Most of these efforts have been adaptations of methods developed for predicting whether a single-nucleotide polymorphism (SNP), not necessarily cancer-related, is deleterious to protein structure and function. Among these methods, the most popular are sequence alignment or structure-based [53–59], machine learning [60–63], and statistical [7, 64] approaches. The sequence-/structure-based methods are accurate and sensitive over the whole genome, but are less accurate than protein family-specific methods [61]. The statistical methods generally try to assess deleteriousness by calculating the difference between expected and observed mutation rates and locations [7], but give no mechanistic insight into why a specific mutation is (or is not) deleterious. Of the protein family-specific methods, the machine learning-based support vector machines (SVM) is the most widely used. Alternatively, ab initio (physics-based) methods such as molecular dynamics (MD) simulations have been employed to interrogate the effects of mutations on structure, dynamics, and drug interactions at the molecular level—addressing mechanism directly.

Molecular dynamics simulations

Simulations and analysis reported here were carried out using the BioPhysCode software suite: (https://biophyscode.github.io/) developed in the Radhakrishnan laboratory. BRAF (active conformation) was modeled off PDB 4MNE, while BRAF (inactive conformation) was based on 3TV4. HER2 (active conformation) was modeled after 3PPO chain B, while HER2 (inactive conformation) was constructed from a homology model based on EGFR inactive structures 2GS7 chain A, and 4HJO chain A, 3W32 chain A and ErbB4 inactive structures 3BBW chain A, and 2R4B chain A. All homology models were constructed using MODELLER [65] and all mutations were introduced using the BioPhysCode Automacs routine based on MODELLER. Simulations were run with Automacs using GROMACS 4.6 [66] with the CHARMM27 forcefield [67] with TIP3P explicit solvent in a periodic water box with at least 12 Å between the protein and box edge. A salt concentration of 0.15 M NaCl was used, and the final charge of the full system was zero. Minimization was carried out using steepest descent, and the system was equilibrated first at constant volume and then at constant pressure simulations. The simulations included particle-mesh Ewald methods for long-range electrostatics, the center of mass translational motion removal during dynamics, and the LINCS method to constrain all hydrogens. Simulations were run for a total of 101 ns per replicate for each system, and two replicates were obtained for each system. Trajectories were analyzed over 100 ns, and the two replicates were averaged together. Structures were sampled from each trajectory at 20 ps intervals resulting in a total of 5001 structures for analysis. Plots were created with Omnicalc using matplotlib.

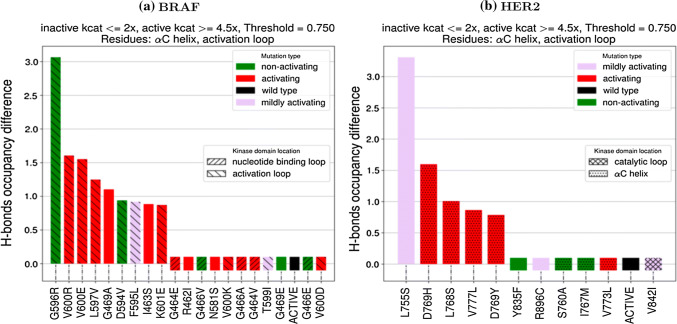
Hydrogen-bonding analysis: For each structure in a trajectory, the hydrogen-bond (H-bond) occupancy (O) was calculated by dividing the number of frames in which an H-bond is observed by the total number of frames. After computing the H-bond occupancy for each residue i in the inactive WT (O_WT,i) and in the inactive mutant (O_MUT,i), the occupancy difference in mutation MUT for residue i was calculated as Δ_MUT,i= O_MUT,i − O_WT,i. The occupancy difference is plotted in Fig. 2. For each residue i occupancy difference, if |Δ_MUT,i| > threshold, then Δ_MUT,i is added to an accumulator Δ_MUT,Total.The absolute value is checked against the threshold to allow for loss and gain of hydrogen bonds, but the signed values are added to the accumulator to see whether an individual system is gaining and/or losing H-bonds. Here, threshold is set to 0.75 and a mutation is considered to have a different occupancy than WT if Δ_MUT,Total is non-zero. The threshold value of 0.75 was chosen by varying the threshold from 0 to 2 and plotting either the receiver-operating characteristic area under the curve, a measure of how well a classifier can distinguish between positive and negative examples, or true positives minus false positives. In both cases, each system had a peak value between 0.7 and 0.8, though, in some cases, this peak spanned a larger region.

Fig. 2.

Scoring functions computed from MD trajectories for mutants of BRAF and ErbB2. A mutation with a scoring function value different from zero by a threshold is predicted as activating. The colors of the histogram represent the activation status from experiments (see SI Table S1)

Structure-based computational methods for profiling mutations

Statistically, the majority of patients will harbor the most frequently observed mutations. That is not to say that there is no need to determine treatments for patients with less frequently observed and\or less well-understood mutations, however, who represent large numbers across the population. In the case of kinases, for which many drugs have been developed, structure-based methods have been used to try to determine the effects of specific mutants and how different drugs might work on these mutants. These methods include the use of molecular dynamics (MD) simulations, drug docking, and various statistical methods.

Numerous groups have used MD simulations to assess the effects of mutations [24]. One method to determine the effect of a mutation is to simply run an MD simulation and see if there is evidence for a transition (or the beginning of a transition) from the inactive to the active conformation. The principal limitation of this method is that it is computationally expensive and requires a long simulation time for the results to be useful. Even the use of a custom-built supercomputer was not able to observe a transition from inactive to active in the EGFR L858R mutation [68]. To overcome this limitation, enhanced sampling methods that allow for more rapid exploration of conformational space and determination of energy landscapes can be used. A recent report exploring EGFR mutants [69] used a method called metadynamics to determine the difference in activation barrier between wild-type and the most frequent mutants. This study showed that whereas wild-type EGFR has lower free energy in the inactive state, the L858R mutant has its lowest free-energy state in a conformation in between active and inactive. This study also showed that both the T790M mutant and the L858R–T790M double mutant have their respective lowest free-energy states in the active conformation [69], showing why these mutants lead to constitutive activation and oncogenesis. EGFR is not the only kinase studied by such methods. Simulations of ABL [70], ALK [71], B-RAF [52], CDK5 [72], c-KIT [37], HCK [73], RET and MET [70], and SRC [74] have all been carried out to investigate the effects of mutations on protein structure and function, and/or the impact of allostery on conformational changes. The limitation of these studies is that they have either only looked at conformational changes in the wild-type protein or in a few mutating proteins, generally, the most frequently observed in a particular protein. While detailed insight into allosteric mechanisms of regulation as provided by such studies can be insightful, in the case of the mechanism of imatinib binding Abl [75], these studies have often shown that individual mutations can have specific and even unique mechanisms of allosteric regulation. The subtleties of the molecular context of each individual mutation make it difficult to generalize mechanistic insights across mutations in a single protein, let alone classes of structurally related proteins. To overcome the limitations imposed by performing such detailed mechanistic studies of normal activation mechanisms in kinases, a recent study of several mutants of ALK used scoring functions calculated from short MD trajectories to systematically investigate a series of clinically observed mutations and determine what their likely activation status would be [30]. When compared to experimental kinase activity assays, the MD method proved quite accurate [30]. As extensions of these ALK studies, we report in Fig. 2, the scoring functions computed based on MD simulations for different mutants of BRAF and ErbB2 found in cancer patients. In these figures, the scoring function records the net difference in hydrogen bonds in the mutant kinase involving the A-loop and αC-helix regions between the inactive mutant and inactive wild-type conformations. A scoring function of > 0.75 or < − 0.75 is predicted to be activating. The experimental status of activation is color-coded (green = not activating, red = activating, and purple = mildly activating). The performance of the MD on the BRAF and HER2 systems is further discussed in “Machine learning—support vector machine (SVM)” when MD is compared to other data-driven methods and with experiments. Given the evidence that even single mutations can lead to tumor colony growth, at least in vitro [76, 77], studies such as these are likely to be increasingly relevant going forward.

Machine learning—support vector machine (SVM)

Construction of data set: The kinase mutation data set was constructed via text mining of the UniProt database using a Perl script. Regular expressions were used to parse the MUTAGEN and VARIANT fields in Uniprot. Mutated residue entries in UniProt were classified as non-activating if they contained any of the following strings: ‘impairs’, ‘strongly impairs’, ‘reduce’, ‘strongly reduce’, ‘abolishes’, ‘diminished’, ‘loss .+ normal .+ order’ (where .+ denotes at least one other character of any type), and ‘abolishes down-regulation’. Mutated residue entries in UniProt were classified as activating: ‘increase’, ‘strongly increase’, ‘constitutive’, and ‘does not + constitutive’. The resulting training set was validated by searching the literature for a subset of the entire data set to ensure that class assignments were correct. This procedure not only showed the utility of the underlying method, but led to many papers that had mutations not in the original set in addition to those in the original set. Final set contained 784 total point mutations, with 204 activating, and 580 non-activating mutations.

Construction of feature vectors: For each mutation, a feature vector with a set of values for the descriptors in Table 1 was constructed, leading to a feature vector with 59 elements for each mutation. Each element of the resulting vectors is normalized, so that all values are in [− 1, 1]. A large number of the elements will be zero for each mutation.

Table 1.

List of features included in the SVM

Wild-type residue (one feature element for each of the 20 amino acids)

Mutant residue (one feature element for each of the 20 amino acids)

Wild-type residue type (from aliphatic, acidic, basic, aromatic, and polar)

Mutant residue type (from aliphatic, acidic, basic, aromatic, and polar)

Difference between wild-type and mutant residues for following: (1) Kyte–Doolittle hydropathy; (2) free energy of solvation; (3) normalized van der Waals radius; (4) polarity difference; (5) charge difference

Whether the mutation falls in one of the following kinase subdomains: (1) nucleotide-binding loop; (2) αC-helix; (3) catalytic loop; (4) activation loop

Construction of data matrix: Feature vectors were generated for each of the 784 mutations via a python script that extracted features from the data. The data file has the following information for each kinase: (1) the name of the kinase (BRAF, ALK, etc.); (2) the wild-type residue; (3) the mutant residue; (4) the location of the point mutation; (5) label (+ 1: activating; − 1: non-activating). The data matrix was generated with the features (normalized numerical values) and labels for each mutation.

Construction of training and test set: Data set was divided into a training set and a test set. The training set consists of all 784 mutations (including the ALK, BRAF, HER2, and ERBB2 mutations). The test set consists of all of the ALK, BRAF, HER2, and ERBB2 mutations (114 mutations). Since the data were imbalanced, the SMOTE algorithm [78, 79], for upsampling of the minority class, was performed on the training set, so that it consisted of an equal number of activating and non-activating mutations. SMOTE was only applied on the training set to prevent overfitting.

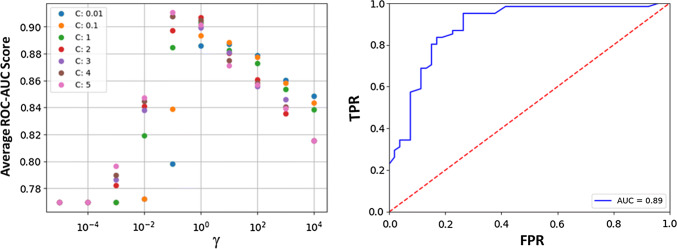
Model parameters, training, and hyperparameter search: The support vector machine (SVM), with the radial basis function (RBF) kernel, was chosen, since the data were numerical and the number of samples was much larger than the dimensions of the feature space. The training data were utilized to determine optimal hyperparameters. SVM, like any ML algorithm, has a number of parameters which can be optimized. For the SVM, the error penalty, C, and the Gaussian width γ can be optimized. The error penalty C controls how smooth the decision surface is, with larger values of C leading to an increasingly jagged boundary that attempts to classify every example correctly. The Gaussian width γ controls how large of a region in feature space (or any mapping of feature space) that the training examples take up, with larger values, meaning that training examples are ‘felt’ in a smaller region. Both C and γ are tuned in cross-validation (Fig. 3). To this end, a grid search was implemented over all combinations of values of γ ∈ [1 × 10 ^− 5, 1 × 10⁴] increasing by a factor of 10 in each iteration, C ∈ [0.01, 0.1, 1, 2, 3, 4, 5] for loss functions which maximize one of [F1, ROC–AUC]. The F1 score is a weighted average of the precision and recall, both of which are defined later when discussing the measures used in evaluating the performance of the model. The F1 score reaches its best value at 1 and the worst score at 0. The receiver-operator characteristic (ROC) is a plot of the false-positive rate (x-axis) versus the true-positive rate (y-axis) for a number of different candidate threshold values between 0.0 and 1.0. ROC-AUC calculates the area under the curve (AUC); the best possible AUC is 1, while the worst is 0.5 (the 45° line). F1 and ROC–AUC are more representative loss functions than accuracy, since the data are imbalanced. The grid search was conducted by performing fivefold cross-validation. The training data set was shuffled randomly and then split into five groups. For each unique group, that group is taken as the test data set and the remaining groups as a training data set. A model is fit on the training set and evaluated on the test set. The model is discarded after retaining the F1 and ROC–AUC scores, and the process is repeated for each unique group. The skill of the model with that particular combination of hyperparameter values is then summarized using the sample of model evaluation scores. For the training set used here, the F1 value was maximized for the parameters [‘C’: 1, ‘gamma’: 1, ‘kernel’: ‘RBF’], and ROC–AUC was maximized for the parameters [‘C’: 5, ‘gamma’: 0.1, ‘kernel’: ‘RBF’]. Further attempts at refining these parameters yielded only small increases in either AUC or F1, but allowed the selection of [‘C’: 5, ‘gamma’: 0.1, ‘kernel’: ‘RBF’] as the hyperparameters that were utilized for the evaluation of our data.

Fig. 3.

Optimal parameters for SVM from the hyperparameter search: (left) plot of ROC–AUC scores for combinations of γ and C values tested during cross-validation. Optimal combination of parameters found to be: [‘C’: 5, ‘γ‘: 0.1, ‘kernel’: ‘RBF’]. (right) ROC curve for the trained model on the test data in blue. Red; the dotted line is the 45-degree line. AUC = 0.89 found by calculating area under blue ROC curve

Using the trained model, we made predictions on the labels (1: activating; 0: non-activating) of the test set. The results are summarized in Tables 3, 4, 5 and 6. The following measures were used in evaluating the performance of the model: BACC = (TPR + TNR)/2, where, BACC = balanced accuracy, TPR = true-positive rate, TNR = true-negative rate. TPR = TP/(TP + FN), where TP = # of true positives, FN = # of false negatives; FPR = FP/(FP + TN), where FP = # of false positives, TN = # of true negatives. Other definitions include: Accuracy = (TP + TN)/(TP + FP + TN + FN), Precision = TP/(TP + FP), and Recall = TP/(TP + FN). The performance of the test set is summarized in Table 2, and the metrics are further summarized in Fig. 3.

Table 3.

BRAF mutations: comparison of MD, SVM, SIFT, and PolyPhen2, against experiments

Mutation, BRAF	MD prediction	SVM prediction	SIFT	PolyPhen2	Experimental
G596R	1	0	1	1	0
V600R	1	1	1	1	1
V600E	1	1	1	1	1
L597V	1	1	1	1	1
D594V	0	0	1	1	0
F595L	1	0	1	1	1
I463S	1	1	1	1	1
K601E	1	1	0	1	1
G464E	0	0	1	1	1
R462I	0	1	0	0	1
G466V	0	1	1	1	0
N581S	0	1	1	1	1
V600K	0	1	1	1	1
G466A	0	1	1	1	1
G464V	0	1	1	1	1
T599I	0	0	1	1	1
G469E	0	0	1	1	0
G466E	0	0	1	1	0
V600D	0	1	1	1	1
G469V	1	1	1	1	1
TPR	0.4666	0.8	0.8666	0.9333
FPR	0.2	0.2	1	1
BACC	0.6333	0.8	0.4333	0.4666

Table 4.

ALK mutations: comparison of MD, SVM, SIFT, and PolyPhen2, against experiments

Mutation, ALK	MD prediction	SVM prediction	SIFT	PolyPhen2	Experimental
F1174L	1	1	1	1	1
F1245V	1	1	1	1	1
F1245C	1	1	0	1	1
I1170N	0	1	1	1	1
I1170S	1	1	1	1	1
I1171N	1	1	1	1	1
Y1278S	0	1	1	1	1
R1192P	0	1	1	1	1
M1166R	1	1	0	1	1
R1275Q	0	1	1	1	1
T1151M	1	1	0	1	1
L1196M	1	1	0	1	1
G1128A	1	1	1	1	1
I1183T	0	1	1	1	0
L1204F	1	0	1	1	1
G1286R	0	0	0	1	0
A1200V	0	0	1	1	0
D1349H	0	1	1	1	0
T1343I	0	0	1	1	0
R1231Q	0	1	0	0	0
I1250T	0	0	1	1	0
G1286A	0	0	1	1	0
L1204F	1	0	1	1	0
D1270G	0	0	1	1	0
TPR	0.7143	0.9286	0.7143	1
FPR	0.1	0.3	0.8	0.9
BACC	0.8071	0.8143	0.4571	0.55

Table 5.

ErbB2 mutations: comparison of MD, SVM, SIFT, and PolyPhen2, against experiments

Mutation, ErbB2	MD prediction	SVM prediction	SIFT	PolyPhen2	Experimental
L755S	1	1	1	1	1
D769H	1	1	1	1	1
L768S	1	1	1	1	1
V777L	1	1	0	0	1
D769Y	1	0	1	1	1
Y835F	0	0	1	1	0
R896C	0	0	0	0	1
S760A	0	0	0	1	0
I767M	0	0	1	1	0
V773L	0	1	0	1	1
V842I	0	1	1	1	1
TPR	0.625	0.75	0.625	0.75
FPR	0	0	0.6666	1
BACC	0.8125	0.875	0.4792	0.375

Table 6.

BRAF, ALK ErbB2 mutations combined: comparison of MD, SVM, SIFT, and PolyPhen2, against experiments

Mutation (all)	MD prediction	SVM prediction	SIFT	PolyPhen2
TPR	0.5946	0.8378	0.7568	0.9189
FPR	0.1111	0.2222	0.8333	0.9444
BACC	0.7417	0.8078	0.4617	0.4872

Table 2.

Performance metrics of the test set

Measure	Value (%)
Accuracy	82.46
Balanced accuracy	81.50
Precision	77.33
Recall	95.08
ROC–AUC	88.74

Data-driven computational profiling methods for profiling mutations

Although MD simulations are useful for understanding, and even possibly predicting, the effects of a few mutations, they are generally too computationally intensive to be used on every observed mutation when real-time predictions (within minutes of wall clock time) are desirable. Therefore, several groups have investigated statistical and machine learning methods to understand the oncogenic potential of large numbers of mutations. The earliest attempts to understand how well sequence changes would be tolerated were not in the context of cancer, but, instead, were used for understanding evolutionary distances between sequences. These methods give probabilities of mutation frequencies based on phylogenetic trees [80] or sequence alignments [81]. These methods, while innovative when developed, were not designed to predict the effect of mutations on protein function. One of the first methods to predict whether a mutation would be deleterious, and still a benchmark in the field of mutation classification, is called Sorts Intolerant From Tolerant (SIFT) and uses sequence conservation to determine ‘deleteriousness’ [57, 82]. Since this pioneering method, several other algorithms have been developed that use sequence conservation or homology to predict the effects of SNPs [54, 58–60, 83]. In particular, PolyPhen-2 is a method that utilizes several sequence-based and structure-based features for classification of driver versus passenger mutations resulting from SNPs.

Although these methods should in principle work on any observed mutations, they have largely been developed and validated for use on SNP data and not on cancer mutations specifically. As cancer genome sequences have become more available, the desire to separate driver from passenger mutations has only increased. An early attempt to solve this problem was that of [7], which used the mutation rate of noncoding genomic regions as a baseline and then tried to determine genes in which there was a statistically significant deviation from this baseline. More recently, several groups have developed machine learning techniques to separate driver from passenger mutations. Methods used include random forest [62], entropic methods [84], and support vector machines (SVM) [61, 63].

Support vector is a machine learning technique that falls under the broad category of supervised machine learning, wherein the SVM classifier optimizes a loss function to find the maximum margin hyperplane to linearly segregate different classes (say activating mutations and non-activating mutations). Extensions of SVM that utilize a nonlinear kernel for segregation of data that cannot be classified using linear classification are also commonly employed. Once the SVM classifier has been built on the labeled training data (the fact that the data are labeled is why this is a supervised method), it can then be used to determine class membership of new cases. The accuracy and sensitivity of the classifier can be assessed via cross-validation, which consists of leaving some of the data used to build the classifier out of the training phase and then using the resulting classifier on the part of the data set that was left out [85, 86]. SVM classifiers are relatively easy to interpret when compared to other methods such as artificial neural networks, with excellent qualities including that the solution of an SVM problem is invariant to translation and rotation, and is only dependent on the distance between training examples—allowing preprocessing of the data without affecting the final result. An SVM can, in principle, correctly classify an arbitrary number of points based on a limited number of features, which could be biochemical factors. The SVM method has enjoyed some success in attempting to classify kinase somatic cancer mutations, but, generally, uses the whole protein as opposed to only the kinase domain, causing one of the leading predictors of driver status to be the location within the kinase domain [61–63]. Although this is useful for determining which proteins are likely to be involved in cancer, it is not necessarily accurate at the residue level, for example, to accurately predict the effects of different mutations in the same domain of the protein.

The SVM methods listed here (“Machine learning—support vector machine (SVM)”) have focused on kinase proteins, since they play such an outsized role in cancer progression. Machine learning methods can be quite powerful and have been somewhat successful when applied to cancer mutations. These methods are generally only as good as their training sets; however, with a balanced training set giving better results [87]. Furthermore, the procedure used to construct training sets can bias the results. For instance, one study [61] took all mutations that were found in a cancer sample to be driver mutations—which we know not to be the case. In a recent comparison of various methods for cancer mutant classification, another study [88] took every mutation observed to be mutated at least twice in COSMIC to be a driver mutation, which again is a demonstrably false assumption. Another method [53] reported the ability to differentiate driver mutations from passengers 98% of the time, but uses a data set where driver mutations are taken to be any mutations that are observed in COSMIC and passenger mutations are taken from a synthetic data set of computationally generated mutations of unknown function. The reliability of a method should be called into question if it makes a priori decisions about what is a driver or passenger mutation in a bid (in turn) to predict driver or passenger mutations.

To address the bias factor, we implemented a SVM classifier on a kinase mutation data set which consisted of construction of a training set from the UniProt database (http://www.uniprot.org), creation of feature vectors based on chemical identity and properties of the original and mutated amino acids, and structural features such as location of the mutation in the kinase. Using a training set consisting of 763 kinase domain mutations (see SI Table S1 for a partial list) and by employing 59 features, the trained and cross-validated SVM algorithm was shown to have a balanced accuracy (mean of the true-positive and true-negative rates) of 77%, with a receiver-operating characteristic area under the curve (ROC–AUC) of 82% [89]. The SVM method was implemented here on a data set consisting of 763 mutations. We then generated 59 feature vectors for each sample, focused heavily on the biochemistry of the mutations. We divided the data into test and training sets. In our SVM implementation, the test set consisted of all ALK, ErbB2, and BRAF mutations, and the training set consisted of all the other mutations. In our SVM implementation, the test set consisted of all ALK, ErbB2, and BRAF mutations, and the training set consisted of all the mutations (including the ALK, ErbB2, and BRAF mutations). Since our data are imbalanced (there being 190 activating mutations and 573 non-activating mutations in our overall data), the SMOTE algorithm (for upsampling of the minority class) was performed on the training set, such that the training set now consisted of an equal number of activating and non-activating mutations [78]. Fivefold cross-validation was then performed on the training set to determine the optimal hyperparameters that maximized both the F1 score and the ROC–AUC score. The SVM implementations were executed in Python. The SVM classifier was then generated using the optimal hyperparameters for each implementation and the model was then trained on the training set. The SVM Classifier was then used to make predictions on the test set (see Tables 3, 4, 5, 6).

Comparison of MD, SVM, and other data-driven methods for BRAF, HER2, and ALK mutations

To demonstrate the utility and performance of the various methods discussed in “Molecular dynamics simulations” and “Structure-based computational methods for profiling mutations”, we applied these methods to three clinical data sets consisting of BRAF (Table 3), ALK (Table 4), and ErbB2 (Table 5) mutations, and compared them against experimental results (Tables 3, 4, 5, 6; also see SI, Table S1). We compare the predictions of MD, SVM, SIFT, and PolyPhen-2 for the kinase mutation data sets, and report the performance (balanced accuracy) at the end of each table. In these tables, ‘0’ represents not activating and ‘1’ represents activating. The overall accuracy and precision of the algorithms across all the data sets presented in Tables 3, 4 and 5 are reported in Table 6.

We can discuss several trends from the predictions and comparisons with experiments. First, the predictions from SIFT and PolyPhen2 have a poor balanced accuracy, because they have an FPR of close to 1. The predictions of MD, in contrast, have the lowest FPR making it a conservative prediction algorithm. The performance of machine learning is slightly better than that of the MD when BACC is considered, but slightly worse on the basis of just FPR. However, we need to stress that the version of ML, we have implemented is a supervised learning method, and hence, some of the predictions in Tables 3, 4, 5 and 6 are part of the training set, which gives the ML an unfair advantage over MD. The predictions of MD are blind to the experimental data.

Another point that is worthy of note is that the MD scoring is purely based on hydrogen bonds perturbed in the αC-helix and A-loop regions during the simulations which, by itself, leads to an impressively high BACC. This suggests that several of the activating mutations perturb the hydrogen-bond network in the αC-helix and A-loop regions to differentially stabilize the active conformation establishing a universal mechanism for activating mutations. While the BACC of the ML methods is higher than that of the MD, a similar insight into the mechanism of activation is unavailable from the ML predictions.

We note that machine learning techniques have a powerful ability to recognize and illuminate patterns in a data set. Using machine learning to classify cancer mutations as drivers, we can arrive not only at a map of where in the kinase domain mutations segregate but also at the factors that drive these mutations to cause constitutive activation. Alternatively, molecular dynamics simulations and free-energy calculations can give us a mechanistic picture of how changes in the kinase structure (or at least its free-energy landscape, lead to activation. Although both methods have enjoyed success on their own, as noted above, they have never been combined into a coherent framework, for example in constructing balanced and effective classifiers. According to our results in Tables 3, 4, 5 and 6, since both these methods converge on similar accuracy, but employ very different ingredients to make predictions, we conclude that there lies a compelling opportunity to gainfully combine them to construct more accurate models and to shed insight on what mutations lead to constitutive kinase activation and why.

In closing, we would like to note that the accuracy of the methods was assessed based on comparison with experimental results of kinase activation based on the definition that an activating mutation is one which increases the catalytic rate (k_cat) by a factor of 4 over that of the wild type. What significance does this have to cancer? While one cannot generalize the effect of increase in k_cat of a single activator of a signaling to cancer initiation, for some receptor tyrosine kinase-driven tumors, a linear correlation between an increase in k_cat and colony transformation has been established [77], which makes our prediction algorithms valuable tools in oncology and personalized medicine.

Future of in silico methods and clinical implications

As reviewed by Valencia and Hidalgo [90], progress in sequencing and genomics has promised to deliver personalized cancer care and treatment. New technologies are available for identifying potential disease markers and accessible drug targets [91–93] that, coupled with medical data, will impact clinical decisions. Quoting the authors “The accessibility of new experimental techniques makes it all the more necessary to improve and adapt computational strategies to the new challenges. We emphasize the need for the collaboration between the bioinformaticians who implement the software and use the data resources, the computational biologists who develop the analytical methods, and the clinicians, the systems’ end users and those ultimately responsible for taking medical decisions.” While “Introduction”, “Mining molecular/mutation data from cancer atlases” and “In silico methods for structure–function mapping” focused on computational technologies for one aspect of this grand challenge, namely correctly classifying driver versus passenger mutations, in silico methods can be more broadly applied with far-reaching contributions to personalized cancer therapy, as discussed below.

Computational methods for inhibitor/drug interactions

Much effort has been put into the development of drugs that target proteins that are mutated in cancer cells. As mentioned previously, imatinib was the first of these drugs and was developed via screening, followed by lead optimization [44]. In this case, in invitro screens against a panel of protein kinases, imatinib was found to inhibit the autophosphorylation of essentially three kinases: BCR–ABL, c-KIT, and the platelet-derived growth factor (PDGF) receptor. Once leads, or even clinically approved drugs, have been developed, it is quite common for computation to be used to understand the mode of binding. Several methods can be used to this end, such as molecular docking, molecular dynamics, free-energy perturbation, and molecular-mechanics Poisson Boltzmann techniques, and even network models (discussed further below). One study using docking, MD and X-ray crystallography showed that the EGFR inhibitor erlotinib binds to both the active and inactive structure of the EGFR kinase domain, while lapatinib, another EGFR inhibitor, only binds the inactive conformation [94]. Another study using free-energy perturbation and MD showed that imatinib binds to ABL kinase and not the closely related Src kinase because of inherent differences in the stabilities of the inactive states in these proteins [75]. These studies, and many more like them, help us to understand how a particular drug works. Going forward, they can hopefully also be used to show what goes wrong when new mutations confer resistance, as in the case of the EGFR T790M mutation which is resistant to inhibition due to increased ATP affinity [95]. However, in general, the onset of drug sensitivity and resistance occur via mechanisms that are complex and involve not just ‘on target’ molecular alterations, but other changes in the cancer cell, as well [96–103].

In addition to the structural methods listed above, other computational methods can be used to help understand why current drugs are effective and how to develop new drugs. For instance, network pharmacology seeks to understand how different nodes in a protein interaction network might be susceptible to treatment by removing specific links (by inhibiting a given protein) or to take advantage of synthetic lethality which occurs when multiple proteins are targeted simultaneously [104]. This network view can also be used in the context of drug repositioning, which seeks find new uses for drugs that have been assessed at some stage of the development pipeline. This approach can significantly reduce the costs of drug development and can also utilize detailed knowledge of drug-binding sites in individual proteins as well as knowledge of network properties [105, 106].

Network models: towards bridging molecular activation and cell fate

One approach that we can deploy to interrogate cancer cells is systems biology in the context of cell signaling networks [107, 108]. Instead of giving insight into the effect of mutations on protein structure and function, this method allows us to look at the overall effect that cancer has on a signaling network. The basic premise of this approach is to measure rate constants for as many reactions as possible in a biochemical network and put this information on top of existing knowledge of protein interaction networks. The time evolution of the system can then be found by solving a set of ordinary differential equations or—if spatial information is needed—a system of partial differential equations [109]. There will, in general, be many reactions for which the rates are not known, so the system is underdetermined. Genetic algorithms can be used to narrow the solution set, or the unknown parameters can be varied over several orders of magnitude [102]. If kinetic parameters for mutant proteins abnormally high expression levels of specific proteins or kinetic changes induced by inhibitors are known, this information can also be incorporated into simulations. For example, a model of the EGFR signaling pathway showed that the EGFR L858R mutation changes the relative flux through downstream pathway components, but that inhibition by the EGFR inhibitor erlotinib restores the flux to its normal behavior [102]. While not specifically structure-based, this type of methodology can also be useful for understanding which members in a signaling pathway could be susceptible to inhibition, leading to an interface with the methods described in “Machine learning—support vector machine (SVM)”. Computational models validated by experiments have also shown that the sensitivity of tumor cell lines to the EGFR inhibitor gefitinib is determined by EGFR internalization efficiency [110], showing that simple models neglecting cellular trafficking are likely to miss important insights.

Multiscale modeling of intra- and inter-cellular networks can be used to factor in the effect of tumor microenvironment [111]. Network analyses can help to postulate functional relationships such as between gene expression, transcription factor activation, and signaling pathways [112]. A suite of network analysis and inference tools exists for the construction of network topologies (or interaction maps) surrounding transcriptional and proteomic measurements [112–115]. Implementation of efficient approaches for parameter optimization and network sensitivity analysis is then utilized to analyze and contrast the transcriptional, proteomic, and metabolic portraits of various cellular alterations/perturbations [101, 116]. Clinical implications of oncogenic mutations in the ErbB family kinases in the context of drug sensitivity as well as drug resistance have been explored through multiscale models [24, 102, 103, 117, 118]. Recently, cell intrinsic and extrinsic factors mediating drug resistance have been investigated through the use of network models [119]. Beyond intracellular signaling pathways, spatially regulated membrane-mediated phenomena such as cell adhesion and motility and intracellular trafficking are implicated in cancer progression [120]. Multiscale models based on physical systems biology [116, 121] offer a viable avenue to integrate such models within the systems biology framework, although they have not been pursued as yet in the context of cancer signaling pathways.

Multiscale modeling

One ongoing challenge to understand the effects of mutations is the problem of how to develop and study models that integrate multiple time and length scales, known as multiscale modeling. To illustrate the scope of the challenge, consider the different time scales involved in a signaling pathway such as that mediated by EGFR. Endocytic recycling of EGFR may take on the order of minutes, while phosphorylation reactions can take place on the order of seconds and molecular vibrations can take place on the order of femtoseconds [122]. This system has timescales that vary over more than 15 orders magnitude, yet is still only considering processes below the subcellular level! Many groups have made efforts to try to bridge the time and length scales encountered in modeling biological processes. There are two ways to model phenomena occurring at different scales that are prominent in the literature. The first is to use information gained from a simulation at one scale as an input to or for parameterization of a model at a different length scale. The other method, less common and more challenging, is to have iterative feedback between models of different scales [123].

Much effort has gone into translating the parts lists that result from genome sequencing projects into models of how cells function. There is rapid progress in determining crystal structures of many single proteins and some protein complexes, as well as rapid advances in understanding which proteins interact via methods such as yeast two-hybrid assays, affinity purification techniques, and mass spectrometry. In addition, many computational methods to predict the structures of proteins and protein complexes—as well as which proteins will interact—have been developed [124]. This information can be combined with experimentally determined rate constants for protein-mediated reactions to develop detailed multiscale models of cell signaling [115]. Zooming out to length scales beyond the individual cell can be productive in trying to understand the phenomena of cancer growth. Here again, multiscale modeling is a valuable tool. The main approaches here can be divided into three basic classes. In discrete models, individual cells or groups of cells are represented individually, and rules governing the growth, quiescence, or death of these cells are used to evolve the system. The advantage of such discrete models is that the internal processes of cells can be simulated to incorporate effects of mutations and tumor microenvironment, while the downside is that these systems rapidly increase in computational cost with increasing cell numbers. In continuum models, individual cells are neglected, and variables such as the distribution of nutrients or cell density are modeled as a continuous field. These models are more computationally tractable than in the discrete case but suffer from the lack of insight into the effects of small (molecular) perturbations to cellular context. Hybrid models seek to combine aspects of discrete and continuous models, and can bridge many orders of magnitude in scale at a moderate computational cost [114].

Clinical implications

The ability to predict how small perturbations in molecular structure can lead to profoundly altered intracellular signaling pathways and subsequent cell-fate decisions is also crucial for predicting the clinical outcome of cancer progression or efficacy of inhibition. In particular, the approaches summarized above permit the rationalization and prediction of the role and nature of molecular variability in networks by bridging the gap between the scales, as well as treatment and diagnosis modalities in the individual patient [8–11]. One viable mechanism for implementing these multiscale techniques to relate to the clinical setting directly is to create hyper-models, which are optimal and robust and can be used for predicting a physiological or a pathological function. Such a hyper-model-based decision support and treatment-planning system has been proposed within a framework called the “oncosimulator” [125, 126], which is a platform for simulating (using ab initio or physics-based methods), investigating, better understanding, and exploring (e.g., optimizing using control theory framework) the spatiotemporal phenomenon of cancer. Imaging, histological, molecular, pharmacogenomic, and clinical and treatment data at various time points constitute the main input of the oncosimulator. This integrative approach can facilitate the optimal development of new treatment strategies, support the design and interpretation of clinico-genomic trials, and finally inform doctors, researchers, and interested patients alike. The model predictions can be validated against multiscale clinical data in different cancer types. This vision brings to bear an in silico platform, one that will allow clinicians and researchers alike to readily navigate within the heavily multidimensional space of multiscale data of each patient, to easily comprehend it, to run model simulations in silico, and, finally, to design treatment in the most scientifically grounded, quantitative and patient individualized fashion. This vision for multidisciplinary and integrated research is being fostered by several large-scale program projects such as the United States National Institutes of Health-funded Physical Sciences in Oncology Centers (PSOC, http://physics.cancer.gov), Cancer Systems Biology Consortium (CSBC, https://csbconsortium.org/), and previously the Integrative Cancer Biology Program, (ICBP, http://icbp.nci.nih.gov), and the Tumor Microenvironment Network (TMEN, http://tmen.nci.nih.gov) Multidisciplinary Project Awards, the Cancer Research UK (CRUK, http://www.cancerresearchuk.org/), and the European Commission Funded Projects such as ContraCancrum (http://www.contracancrum.eu), TUMOR (http://www.tumor-project.eu), p-medicine (http://www.p-medicine.eu), and Computational Horizons in Cancer (CHIC, http://www.chic-vph.eu).

Electronic supplementary material

Below is the link to the electronic supplementary material.