Position-, Disorder-, and Salt-Dependent Diffusion in Binding-Coupled-Folding of Intrinsically Disordered Protein

Abstract

Successful extensions of protein-folding energy landscape theory to intrinsically disordered proteins’ (IDPs’) binding-coupled-folding transition can enormously simplify this biomolecular process into diffusion along a limited number of reaction coordinates, and the dynamics subsequently is described by Kramers’ rate theory. As the critical pre-factor, the diffusion coefficient D has direct implications on binding kinetics. Here, we employ a structure-based model (SBM) to calculate D in the binding–folding of an IDP prototype. We identify a strong position-dependent D during binding by applying a reaction coordinate that directly measures the fluctuations in a Cartesian configuration space. Using the malleability of the SBM, we modulate the degree of conformational disorder in an isolated IDP and determine complex effects of intrinsic disorder on D varying for different binding stages. Here, D tends to increase with disorder during initial binding but shows a non-monotonic relationship with disorder in terms of a decrease-followed-by-increase in D during the late binding stage. Salt concentration, which correlates with electrostatic interactions via Debye–Hückel theory in our SBM, also modulates D in a stepwise way. The speeding up of diffusion by electrostatic interactions is observed during the formation of the encounter complex at the beginning of binding, while the last diffusive binding dynamics is hindered by non-native salt bridges. Because D describes the diffusive speed locally, which implicitly reflects the roughness of the energy landscape, we are eventually able to portray the binding energy landscape, including that from IDPs’ binding, then to binding with partial folding, and finally to rigid docking, as well as that under different environmental salt concentrations. Our theoretical results provide key mechanistic insights into IDPs’ binding–folding that is internally conformation- and externally salt-controlled with respect to diffusion.

Graphical Abstract

The topography of binding energy landscape of intrinsically disordered protein is hierarchically heterogeneous and modulated by conformational disorder and salt concentration.

1. Introduction

The energy landscape theory has become a standard framework for our mechanistic understanding of protein folding over the last three decades^1,2. One remarkable postulate derived from the energy landscape theory is that despite the extreme complexity of the high-dimensional protein-folding process, which involves the intricate self-organization of hundreds or thousands of atoms, folding can be effectively described by a few (usually one or two) important collective reaction coordinates³. By means of such enormous simplifications, protein folding can be significantly simplified as a diffusive process along a limited number of coordinates. The low-dimensional free energy projection approach has been widely demonstrated to be effective in theory⁴, simulations^5–7, and experiments^8,9. The kinetics from this lowdimensional diffusive protein-folding model can be described by the Kramers’ rate theory^10,11, where the stochastic kinetics is determined exponentially by the thermodynamic free energy profile and a diffusion coefficient D as the pre-exponential factor in a diffusive dynamics formalism².

Quantifying the thermodynamic protein-folding free energy landscape experimentally has always been a challenging problem. Nevertheless, it can be plausibly achieved by carefully fitting the thermodynamic differential scanning calorimetry (DSC) thermogram to one-dimensional representations of folding free energy landscapes¹² or by analyzing the single-molecule (SM) spectroscopy trajectories along particular relevant reaction coordinates^13,14. However, measuring D is more elusive in experiments. The recently developed SM Förster resonance energy transfer (FRET) experiment technique seems to be a promising approach, by which D at the free energy barrier top can be inferred by directly comparing the folding and transition path times, as these two critical kinetic quantities depend differently on the thermodynamic barrier height¹⁵. In addition, D at the unfolded states can be estimated by probing the reconfiguration time based on the autocorrelation function of the end-to-end distance measurements¹⁶. Increasing experimental evidence implies that D is position-dependent during protein folding¹⁷, but it is still technically challenging in experiments to acquire reliable measurements of D along the folding process. Recent SM force spectroscopy experiments have underlined the difficulties in measuring D, because the inherent artifacts led by the handle linkers and probes in force spectroscopy experimental apparatus can signficiantly affect the results of D^18,19. As an informative complement, molecular dynamics simulations clearly show that D is highly configuration-, coordinate- and temperature-dependent and may have remarkable impacts on the protein-folding process^15,20–22.

D has been established to be critically influential to the folding kinetics in terms of rate or flux²³. One pronounced demonstration is to possibly shift the position of the kinetic transition state and barrier height^22,24–29. Such implications in kinetics may have significant impacts for fast-folding proteins that often inherently possess marginal thermodynamic barriers. In this case, the folding rate is close to the “speed-limit”³⁰, which is primarily controlled by the diffusion. In addition, the pre-factor of the diffusive chain dynamics from Kramers’ theory can be interpreted as an incorporation of the solvent external viscosity and protein internal friction^31,32. The latter is directly related to the protein intrinsic diffusion coefficient, which is embedded in the roughness of the folding energy landscape^4,33. It therefore provides a practical strategy to infer the topography of the energy landscape by measuring the protein internal diffusion coefficient¹⁶.

Intrinsically disordered proteins (IDPs), which lack a stable three-dimensional structure isolated in solution, often (not always) undergo a “binding-coupled-folding” transition during their functioning process^34–39. Recent experimental developments on measuring the internal friction of unfolded chains^16,40–42 have significantly improved our understanding of IDPs’ intra-chain conformational dynamics. However, it is still a challenge to extend it to the binding process because of the anticipative difficulties that seemingly come along with the complex coupled binding– folding transition. From kinetic aspects, the most prominent functional advantage of IDP may be adequately seizing the “flycasting” mechanism, which can accelerate the binding process by increasing the capture radius through flexibility⁴³. However, it is unclear how the conformational disorder impacts the diffusion at the late binding stage, where the coupled-folding often occurs concomitantly.

By quantifying the binding energy landscapes through molecular simulations^44,45, we found that introducing conformational disorders into the dissociative proteins increases the degree of funnelness of the binding energy landscape, intriguingly through decreasing the roughness of the binding energy landscape. The results uncovered an unprecedented effect of conformational disorder on IDPs’ binding, wherein flexibility can accelerate the diffusive binding dynamics by smoothing the binding energy landscape surface. It is worth noting that previous approaches calculated the average of the roughness based on the overall topography of the energy landscape, taking no account of the heterogeneity at different hierarchical layers of the energy landscapes^44–46; thus, they lack a description of the local diffusive dynamics at specific stages during binding. Because D encodes information about the energy landscape roughness, stepwise measuring D along IDPs’ binding–folding process can complement the quantification of the energy landscape and finally solidify our understanding of IDPs’ binding–folding from an energy landscape point of view.

Here, we implemented coarse-grained structure-based models (SBMs) to investigate the diffusive binding dynamics of an IDP prototype^47,48. Given their validity and computational efficiency for investigating protein folding, SBMs have been successfully extended to study IDPs’ binding-coupled-folding^49–52, relying on the hypothesis that binding occurs on a funneled binding energy landscape⁴⁸. We found that the binding D is strongly position-dependent along the binding process by applying a reaction coordinate that directly measures the fluctuations in Cartesian configuration space. D in general decreases when approaching bound states, similar to the protein-folding case^{16,27,28,40,53}. The binding D is correlated to the folding or collapsed degree in IDP, while the conformational disorder smooths the initial diffusive binding but impedes the diffusive formation of the binary complex in the last stage to a moderate degree. Electrostatic interactions are found to play a dual role with positive and negative effects on diffusion at the transition and post-transition stage. Finally, with quantitative knowledge of D as the binding process progresses, we are able to gain profound insights into the topography of the energy landscape for IDP binding.

2. Materials and methods

2.1. Structure-based models

We use SBMs to explore the binding-coupled-folding of a well-studied IDP system that includes the phosphorylated kinase inducible domain (pKID) of the cAMP response element-binding (CREB) protein, which is an IDP when isolated in solution⁵⁴, and the KIX domain of the coactivator CREB-binding protein (CBP), which is a natively structured three-helix bundle protein^55,56 (Figure S1, ESI†). Here, we utilize the SBM at the one-bead C_α level, initially taking only into account interactions in the native structure; thus, the folding–binding process is significantly accelerated in the SBM simulation at the cost of completely removing the non-native interactions. A typical potential of the plain SBM can be expressed as follows⁴⁷:

$$V_{SBM}^{(KIX,pKID,pKID-KIX)}=V_{Bond}+V_{Angle}+V_{Dihedral}+V_{Native}+V_{Non-native}$$

, where the first three terms describe local interactions, including bond stretching, angle bending, and dihedral rotations; the last two terms are non-local interactions, including native variant Lennard-Jones (LJ) interactions and non-native purely volume-repulsive interactions⁴⁷. The native contact map is built using the Contacts of Structural Units (CSU) software⁵⁷, which generates the numbers of intra-chain contacts for KIX and pKID (159 and 25), as well as the number of inter-chain contacts between KIX and pKID (50). The default parameters widely applied in previous research^44,48,50, are used here, unless explicitly specified.

To describe the binding process, we use the fraction of native contacts (Q) as a reaction coordinate. Q has been found to be an ideal reaction coordinate in SBM simulations to capture the transition states and distinguish native and non-native states⁵⁸. To make Q continuous, we instead used a switching function that is included in the PLUMED software⁵⁹: for r_ij ≤1.2r_ij0, Q=1, while for r_ij >1.2r_ij0, Q decays smoothly with the following expression:

$$Q=1-tanh(\frac{r_{ij}-1.2r_{i{j}_0}}{r_s})$$

, where r_s controls the steepness of the decaying function and is usually set to 0.01 nm. We have further normalized Q by dividing the number of contacts in the native structure to make Q be in the range from 0 (completely non-native) to 1 (fully native). To describe different dynamics, different parts of Q are used; for example, Q_F is used for pKID’s folding and Q_B is used for pKID-KIX binding.

As an alternative coordinate, we also introduce d_RMS ⁶⁰, which is defined as the difference in the distance r_ij between N_pairs native pairs

$$d_{RMS}=\sqrt{\frac{1}{N_{pairs}}\sum _{i<j-3}{\left(r_{ij}-r_{i{j}_0}\right)}^2}$$

, to measure the native similarity of folding. d_RMS is equal to 0 for the native structure and increases with unfolding. d_RMS preserves the magnitude of Cartesian space and is in units of length (nm here).

Upon binding, pKID undergoes a large-scale folding transition to form two perpendicularly placed helical structures (αA and αB), connected by a post-translational phosphorylated Serine133⁵⁵. To achieve different folding degrees for pKID in isolated states, a pre-factor (α) is applied to the dihedral and native LJ potentials in the SBM potential of pKID $(V_{SBM}^{pKID})$ (Figure S9, ESI†), as was previously used to control the conformational flexibility of IDP in SBM simulations^51,61,62.

To investigate the effects of salt concentration, an additional electrostatic potential, modeled by Debye-Hückel theory, is added to the aforementioned plain SBM with the following expression:

$$V_{Ele}=K_{Coulomb}B(\kappa )\sum \frac{q_i{q}_{j}exp\left(-\kappa r_{ij}\right)}{{\epsilon }_r{r}_{ij}}$$

, where K_Coulomb is a constant, B(κ)≈1 in dilute solutions, q_i is the point charge of the residue i, ε_r is the dielectric constant, and κ is the reciprocal of the Debye radius, which is directly related to the environmental salt concentration. To simplify, only Lysine and Arginine are modeled to take one positive charge, and Glutamic and Aspartic acids, as well as the phosphorylated serine, are modeled to take one negative charge. The typical parameters used in the Debye-Hückel model in SBM simulations can be found elsewhere^63–66. We have re-scaled the strength of LJ and electrostatic interactions for the oppositely charged residues that already form the native contacts to have a reasonable energetic balance⁶³ (Figure S11, ESI†).

All simulations are performed using Gromacs (Version 4.5.7)⁶⁷ following the standard protocol proposed by SMOG web tools⁶⁸. Reduced units are used, so the time, mass, and energy scales are set to 1, except that the length scale is in units of nm⁶⁸. The temperature is converted to energy units by multiplying by the Boltzmann constant. A Langevin dynamics with time step 0.0005 is applied. The friction coefficient is set to 1.0. All non-local interactions are cut-off at 3.0 nm. A periodic cubic box with dimensions of 10 nm × 10 nm × 10 nm is used to generate an effective concentration of molecules of 1.66 mM (only one pKID and KIX are placed in each box). For each replica-exchange molecular dynamics (REMD) simulation⁶⁹, 24 replicas are used, with a temperature range basically covering the binding–folding transition temperature, and the neighbor replica attempts to exchange every 2000 steps. The Weighted Histogram Analysis Method (WHAM) is then used to collect the data for all temperatures and generate the free energy landscapes⁷⁰.

The transition state ensembles are characterized by calculating the conditional probability p(TP|x) for the system on a transition path along the reaction coordinate x with Bayesian expression^71,72:

$$p\left(TP\right|x)=p(x\left|TP\right)p\left(TP\right)/p_{eq}\left(x\right)$$

, where p(x|TP) and p_eq(x) are the probabilities of the system with x being at the transition path and equilibrium ensemble, respectively; p(TP) is the probability of the system being on a transition path. In principle, the highest probability for the transition state lay along the transition path. If p(x|TP) is able to reach the theoretical maximum (0.5), x can be regarded as a good reaction coordinate to describe the system diffusion process. To calculate p(TP|x), six independent long constant-temperature simulations (1×10⁹ steps) starting from different dissociative conformations are performed. All trajectories are then collected and a total of ~ 1100 transitions are observed by monitoring the (un)binding along either d_RMS−B or Q reaction coordinates. This good sampling, especially on the transition path, provides reliable estimation of p(TP|x).

2.2. Diffusion coefficient calculations

We use restraining molecular simulations to calculate the diffusion coefficient along the binding reaction^{22,24–26,73,74}. The biasing potential is implemented with a harmonic potential centered at a set interested binding point x with strength K_x, where x is the reaction coordinate. Here, we use binding d_RMS−B instead of Q as the reaction coordinate because Q preserves 0 constantly at unbound states, leading to difficulty calculating the D there. By fulfilling a quasi-harmonic diffusive dynamics approximation, the coordinate-dependent diffusion coefficient (D(d_RMS−B)) can be calculated as:

$$D\left(d_{RMS-B}\right)=\frac{\mathrm{\Delta }{d}_{RMS-B}^2}{{\tau }_{corr}\left(d_{RMS-B}\right)}$$

, where $\mathrm{\Delta }{d}_{RMS-B}^2$ is the mean-squared fluctuation in d_RMS−B, and τ_corr(d_RMS−B) is the relaxation time for the autocorrelation function of d_RMS−B, $C_{d_{RMS-B}}(t)$. In practice, τ_corr(d_RMS−B) can be estimated by fitting $C_{d_{RMS-B}}(t)$ to an exponential decay (single or multiple) to obtain the relaxation time or by integrating $C_{d_{RMS-B}}(t)$ based on the knowledge that ${\tau }_{corr}\left(d_{RMS-B}\right)={\int }_0^{\infty }{C}_{d_{RMS-B}}(t)dt$. We use the latter to obtain the relaxation time and integrate $C_{d_{RMS-B}}(t)$ only up to the first zero-crossing^73,75. Note that the strength of the biasing potential $K_{d_{RMS-B}}$ should be high enough to make the landscape locally harmonic, fulfilling the need for quasi-harmonic approximation, but should not be too high when the underlying topology of the local energy landscape is completely distorted (Figure S6, ESI†)^{22,24–26,74}. Practically, the value of $K_{d_{RMS-B}}$ is determined by performing a series of simulations with different values of $K_{d_{RMS-B}}$ and choosing the one from a range when D(d_RMS−B) is independent of $K_{d_{RMS-B}}$, so that D(d_RMS−B) can probe the underlying landscape, rather than the artificially biasing potential (Figure S6, ESI†). There is another alternative way to calculate D using a Bayesian approach^20,21,27,28. It has been demonstrated that for small dipeptide dynamics and SBM folding, the values of D estimated from these two approaches are similar^20,21.

Constant long simulations with biasing potential (2 × 10⁸ MD steps for each simulation) are performed for each d_RMS−B with different strengths of $K_{d_{RMS-B}}$. To have sufficient statistics for D calculations, each long trajectory is then divided into 100 same-length pieces of segment to ensure the starting points to calculate the $C_{d_{RMS-B}}(t)$ are random and thus the resulting $C_{d_{RMS-B}}(t)$ from different pieces of trajectory segments are irrelevant. We note that such post-segmented trajectory (2 × 10⁶ MD steps for each) is long enough to ensure a good estimation of τ_corr, and then D (Figure S8, ESI†).

The effective free energy is calculated by taking into account the diffusion coefficient correction of kinetics with the following expression^22,24:

$$F_{eff}\left(d_{RMS-B}\right)=F\left(d_{RMS-B}\right)-kTln\left(D\left(d_{RMS-B}\right)/D_u\right)$$

, where D_u is the diffusion coefficient at unbound state, where d_RMS−B is sufficiently large with no interactions between two protein chains. Here, we choose d_RMS−B having a thermodynamic free energy minimum equal to 4.00 nm.

The diffusion coefficient D(x) of the system at x is related to the energy landscape roughness with the following relationship^33,76:

$$D(x)=D_{0}exp[-{(\mathrm{\Delta }E(x)/kT)}^2]$$

where D₀ is the diffusion coefficient in the absence of roughness and ΔE(x) is the energy roughness at x. The above expression is valid by assuming the energy roughness is random with a Gaussian distribution⁷⁶, and it gives a direct connection between the diffusion coefficient and energy roughness.

The mean D of a certain binding stage can be estimated from integration of D(x):

$$<D>=\int D(x)dx/\int dx$$

, where D(x) is the position-dependent diffusion coefficient at reaction coordinate x.

3. Results and discussion

3.1. Diffusion coefficient modulates the binding

Using the SBM, we quantified the free energy landscape along folding and binding reaction coordinates at the binding temperature (Fig. 1A and 1B). The binding temperature, analogous to the folding temperature, is defined as the temperature when the bound and unbound states are equally populated, so it can be practically extracted from the peak of the heat capacity curve. Simulations at the binding temperature can provide sufficient sampling of (un)binding transition events and are thus conducted in our work. Our results are valid based on the assumption that changing the temperature does not qualitatively change the binding mechanism, as a universal phase boundary between monomers and oligomers appears to exist in different ranges of conditions⁷⁷. We have also performed the simulations at different effective temperatures and salt concentrations and found that the binding mechanisms remain similar (See section “Effects of salt concentration on diffusive binding”). The free energy landscapes clearly show a coupled folding of pKID with binding to its target KIX (Fig. 1A and 1B). In detail, pKID remains unfolded over a broad range of conformational fluctuations when it is far away from KIX. Then, in the free energy barrier region, pKID initiates binding with anchoring KIX through unfolded conformations. Finally, pKID folds with strongly coupled binding after overcoming the barrier. This “binding prior to folding” mechanism, deduced from our 2D free energy landscape, is in line with previous simulations^49,51 and experiments⁷⁸, serving as the basis for the following investigations of the diffusion coefficient.

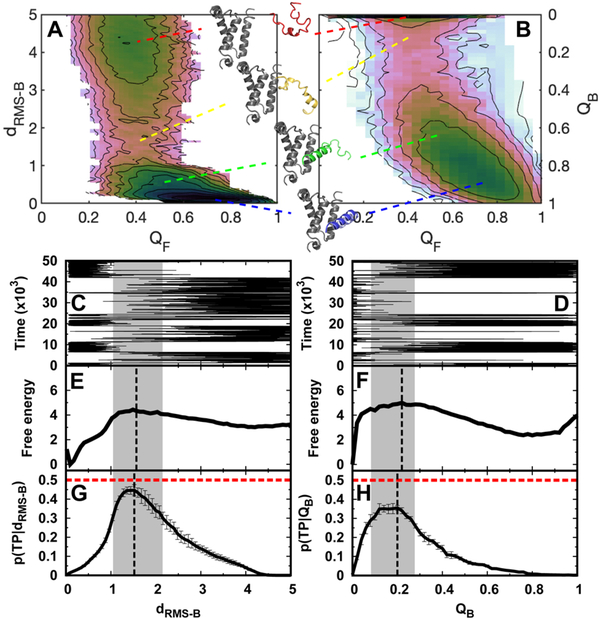
Fig. 1. Trajectories, transition path analyses, and free energy landscapes of binding-coupled-folding of pKID to KIX.

2D binding–folding free energy landscapes are calculated from REMD simulations and projected along (A) d_RMS−B, Q_F and (B) Q_B, Q_F. d_RMS−B is the root-meansquare deviation of the distances of binding native contact pairs to those in the native structure, while Q_B and Q_F are the fractions of binding and folding native contacts for pKID, respectively. The typical structures of pKID-KIX are shown corresponding to the indicated binding stages. A sample binding trajectory (C, D), 1D free energy landscape (E, F), and transition path analyses (G, H) are shown along d_RMS−B and Q_B, respectively. p(TP|x) is the conditional probability of being on a transition path, where x is the reaction coordinate. The dashed vertical lines in free energy landscapes and p(TP|x) are plotted according to the maximum values as an identification of the transition state. The values at the peak of p(TP|x) for d_RMS−B and Q_B are 0.45±0.03 and 0.35±0.01, respectively. The transition state locations are very similar, according to different identifications of the barrier of free energy landscapes and the peak of p(TP|x). In detail, for d_RMS−B, the transition states’ d_RMS−B are 1.49 and 1.52 from the free energy landscape and p(TP|x), respectively, while for Q_B, the transition states’ Q_B are 0.22 and 0.20 from the free energy landscape and p(TP|x), respectively. We denote the transition state ensembles that have p(TP|x) higher than 0.30 by gray shadow regions. The errors of p(TP|x) are calculated by analyzing different trajectories. A total of 1108 and 1099 (un)binding transition paths are observed along d_RMS−B and Q, respectively. Time is in reduced units, d_RMS−B is in units of nm, and free energy is in units of kT_B, where T_B is the binding temperature.

We then plotted the one-dimensional free energy landscape along binding d_RMS−B (Fig. 1E). It apparently shows a two-state binding transition, with a barrier located at d_RMS−B=1.49 nm, which appropriately separates the bound (0.01 nm) and unbound states (≥ 4.0 nm) (Fig. 1C). The barrier heights for binding and unbinding from The thermodynamic free energy landscapes are respectively 1.42 kT_B and 4.43 kT_B. Projection to another well-known SBM-optimized reaction coordinate Q_B ⁵⁸, which is the fraction of native binding contacts, also leads to a typical two-state binding process, but the free energy barriers for both binding and unbinding change drastically (5.00 kT_B and 2.65 kT_B) (Fig. 1D and 1F). Despite such differences in the free energy barrier, the positions of transition states that are obtained from the thermodynamic free energy landscape and kinetic transition path analyses^71,72 (Fig. 1G and 1H), which are performed by analyzing hundreds of (un)binding pathways within additional constant-temperature simulations, are very similar, based on both of the reaction coordinates. This indicates the validity of these two reaction coordinates to identify the characteristics of the transition states. In addition, it is interesting to note that d_RMS−B provides a better description of the binding kinetics because the conditional probability of the transition state being on the transition path identified by d_RMS−B is greater than that found along Q_B (0.45±0.03 versus 0.35±0.01), and is very close to the theoretical maximum 0.5. This implies that for IDP binding, d_RMS−B, which preserves the fluctuations in Cartesian space, seems to be a better binding reaction coordinate than Q_B, in contrast to protein-folding cases²⁷.

Because d_RMS−B offers a better description of the kinetics than Q_B does based on the transition path conditional probability calculation, D is calculated along d_RMS−B within restraining simulations. We extracted the values of D(d_RMS−B) at $K_{d_{RMS-B}}=500$, when D(d_RMS−B) roughly remains constant in a range of biasing potential strengths for each d_RMS−B, and the distributions of d_RMS−B are quasi-harmonic (Figure S6, ESI†). With quantified D(d_RMS−B) (Fig. 2), several interesting insights can be gained: (1) D(d_RMS−B) almost monotonically decreases as binding proceeds, in line with intuition and experiments on protein collapse¹⁶. The difference between unbound and bound states is 30-fold, showing a strong position-dependent D. (2) The initial slightly increasing D(d_RMS−B) from unbound states proceeding to transition states (d_RMS−B ~ 2 nm) implies that interfacial interactions may drive the binding using the “fly-casting” mechanism⁴³. (3) The sharply decrease of D(d_RMS−B) that occurs immediately after passing the transition states is similar to that observed in protein folding, where the formation of a native compact structure may increase the local barrier, hindering the diffusive dynamics^16,24. (4) The decrease in D(d_RMS−B) starts synchronously with binding after the transition states, giving a hint that the binding transition states are quite loose and the binding collapse may occur after the transition states, consistent with the structural analyses of the transition state ensemble (Figure S5, ESI†), previous simulations⁴⁹, and recent experiments⁷⁹. Furthermore, our findings imply that the considerable amount of interfacial disorders, which are retained after binding in terms of “fuzziness”⁸⁰, are capable of facilitating the diffusive dynamics existing in the binding complex, as theoretically proposed⁴³ and also observed in protein-protein/DNA recognition processes experimentally and computationally^81–83.

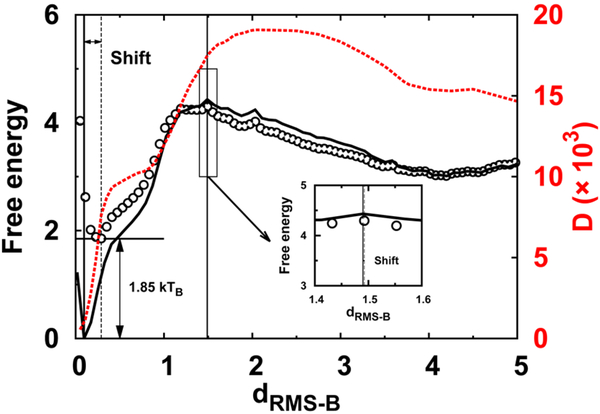
Fig. 2. Position-dependent diffusion coefficient and free energy landscapes.

1D binding thermodynamic (solid line), effective (circles) free energy landscapes, and the diffusion coefficient D are plotted along d_RMS−B. The insert plot indicates the slight height and position shift of the transition state between the thermodynamic and effective free energy landscapes. The free energy landscape is obtained from thermodynamic REMD simulations, and D is calculated from restraining simulations, at constant binding temperature. d_RMS−B is in units of nm, and free energy is in units of kT_B, where T_B is the binding temperature. D is in units of nm²/time

We are then able to have an effective kinetic free energy landscape by incorporating the position-dependent D into the thermodynamic free energy landscape (Fig. 2). The positions of transition states obtained from the thermodynamic and kinetic free energy landscapes are quite similar, consistent with the results from the transition path analysis (Fig. 1). Furthermore, as expected, the effective kinetic free energy remains quite similar to the thermodynamic one before the transition state, but changes dramatically after the transition state, finally resulting in a rising height shift of 1.85 kT_B and right barrier position shift at bound states. Therefore, the effective free energy barrier height for binding is almost the same as that obtained in the thermodynamic case, but differs by ~2 kT_B in the post-transition-state regions. This implies that for IDPs with such a binding mechanism, i.e., collapsed complex forms after crossing the barrier, the position-dependent D plays a major role at the last stage, which falls into the fast inactivated “downhill” regime, where the binding kinetics is fully determined by the diffusive dynamics. It would be very interesting to see how D influences the binding kinetics and effective free energy landscape when a compact transition state ensemble is formed during IDPs’ binding–folding.

3.2. Effects of conformational disorder on diffusive binding

The different degrees of conformational disorder in pKID are realized by changing the pre-factor α of intra-chain interaction strength in SBMs (Figure S9, ESI†). With α=5.0, pKID is almost fully folded, with negligible conformational disorder, while with α=0.1, pKID is quite flexible and extended with very few folded conformations. The monotonic relationship between the SBM parameter α and structured degree serves as the basis for the following investigations of the effects of conformational disorder on D. The two helical segments (αA and αB) of pKID were experimentally found to have different propensities for forming helical structures at unbound states⁵⁴. Further calibrating the strengths of intra-chain interactions at the corresponding segments in the SBM potential for experimental measurements could improve the precision of the current SBM^49,51; nevertheless, it was not performed in the current work. The uniform and gradual introduction of conformational disorder into pKID could help focus on characterizing the general effects of disorder on IDPs’ binding⁶².

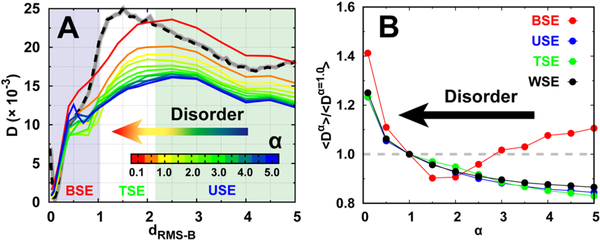
We observed a similar tendency for D along d_RMS−B compared with that of the default SBM parameter (α=1.0) for different degrees of conformational disorder (Fig. 3A). Then, we divided the binding process into three stages: the binding state ensemble (BSE), transition state ensemble (TSE), and unbinding state ensemble (USE), based on the transition path analysis at α=1.0 (Fig. 1). From Fig. 3A, we can see that while approaching the bound state (decreasing d_RMS−B), D slightly increases at USE, then starts to decrease at TSE, and finally decreases sharply at BSE for all degrees of conformational disorder. We applied SBMs with a wide range of flexibility-control parameter α, which basically covers binding from completely unfolded to partially folded, and finally fully folded, monomers. Therefore, our results here imply that such d_RMS−B−dependent D behavior, which is also similar to that observed in protein folding^27,28, may be applicable to general protein-protein binding cases. In addition, D(d_RMS−B) appears to increase with additional conformational disorder, in line with intuition and experimental findings that loosely unstructured conformation favors fast diffusion¹⁶.

Fig. 3. Diffusion coefficient at different degrees of conformational disorder.

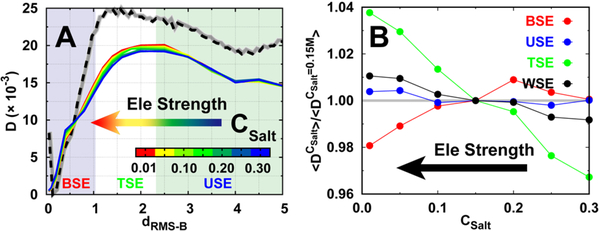
(A) The position-dependent D along d_RMS−B. Free energy landscape with default disorder parameter α =1.0 at binding temperature is shown with dashed line as a guidance of the binding process, which can be further divided into three stages: the binding state ensemble (BSE), transition state ensemble (TSE), and unbinding state ensemble (USE), based on the transition path analysis shown in Fig. 1E. (B) The ratio between the mean D(d_RMS−B) of different degrees and default (α =1.0) parameter of conformational disorder for different binding stages. “WSE” is an acronym for the “whole state ensemble”.

Interestingly, careful examination of the last binding stage within the BSE at low α (high degree of folding) shows an increase in D turnover as d_RMS−B decreases. This leads to an opposite result with respect to the relationship between conformational disorder and D(d_RMS−B), where a rigid protein chain can diffuse quickly. To quantitatively identify such an effect, we calculated the mean D(d_RMS−B) for the three typical aforementioned stages and also the entire process (WSE) (Fig. 3B). The mean Ds of USE, TSE, and WSE increase monotonically with decreasing α. This indicates that as the conformational disorder increases, the diffusion at the unbinding stage, transition stage, and for the whole binding process that the protein chain can achieve is faster. However, at the last binding stage (BSE), increasing conformational disorder initially decreases the diffusion rate, probably because of the boost in local barriers for the energy landscape, led by non-native conformational topology. Finally, the conformational disorder increases the diffusion rate because of the loose binding, the same result that occurred in other binding stages. Such dual effects of conformational disorder on D at different stages point to a complex binding diffusive process that the IDP inherently possesses.

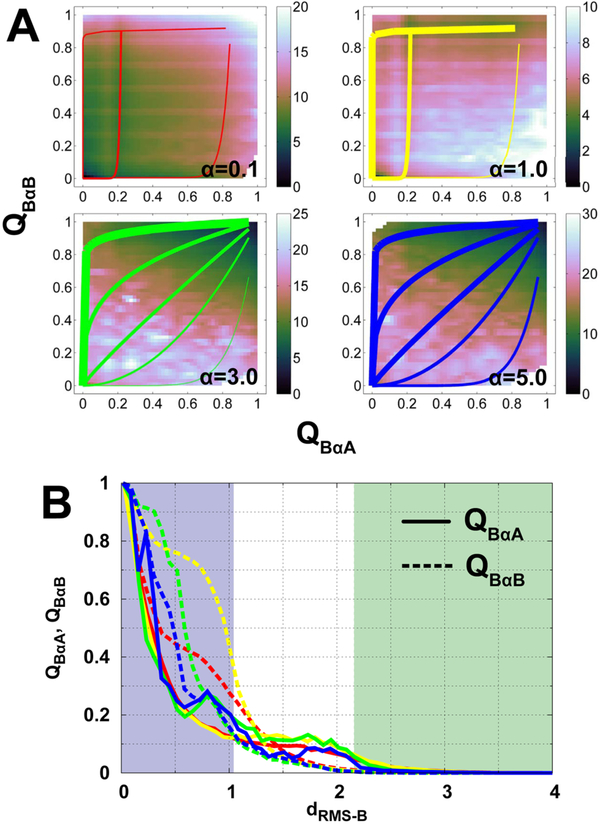
To explain the non-monotonic relation between conformational disorder and D, in particular at high values of α, we calculated the free energy landscapes and evolution of the two helices αA and αB along the binding (Fig. 4). It is interesting to see that the binding transition pathways are different at different degrees of conformational disorder. At low α (0.1 and 1.0), the two helices intend to bind primarily through two rectangular edges, along with an additional intermediate pathway from Q_BαA ~ 0.2,Q_BαB ~ 0.0 to Q_BαA ~ 0.2,Q_BαB ~ 0.8. These distinct pathways are separated from each other without apparent connections. These two parallel binding pathways were also observed in previous work, when a similar SBM approach was applied⁴⁹. At high α (3.0 and 5.0), many binding pathways emerge that can potentially connect the states reciprocally on the free energy landscapes. Such binding scenarios, along with different conformational disorders, can also be observed from the binding evolution of the two helices to KIX (Fig. 4B). Binding of the two helices starts to be distinct after passing the TSE, and at α = 1.0, the differences are the most prominent, with binding of αB accomplished prior to that of αA. This is probably due to the fact that αB has more binding contacts formed in the native structure than αA does. Decreasing or increasing α can modulate the two helices to bind synchronically; however, they have different mechanistic factors. At low α, entropy dominates the binding, so the energetic stabilization term has less effect on managing the pathway than that in α = 1.0. At high α, the stabilization of the binding complex largely comes from the intra-chain energetic term of pKID, so the inter-chain interactions become less dominant with respect to control of the binding pathway. The binding coupling between the two helices at high α with low conformational disorder can lead to multiple binding pathways, which increases the possible connections of states on the free energy landscape, facilitating the escape from local energetic or topological traps, which directly corresponds to the diffusion coefficient. The other factor that increases the diffusion coefficient at a high degree of conformational disorder may be contributed by the loose binding complex formed, according to previous experiments^40–42.

Fig. 4. Binding mechanisms at different degrees of conformational disorder.

(A) 2D binding free energy landscapes projecting onto Q_BαA and Q_BαB. Q_BαA and Q_BαB are the fractions of native binding contacts of helices αA and αB of pKID to KIX, respectively. The free energy landscapes of α=0.1, 1.0, 3.0, and 5.0 are plotted. The lines in each panel illustrate pathways, with thick ones indicating large flux and vice versa. (B) Evolutions of binding contacts of helices αA and αB of pKID along d_RMS−B. Solid and dashed lines are Q_BαA and Q_BαB, Respectively, and different colored lines correspond to different degrees of conformational disorder. The color of shadows and lines follow the same scheme used in Fig. 3A.

3.3. Effects of salt concentration on diffusive binding

Adding electrostatic interactions into the plain SBM will inevitably introduce non-native interactions beyond the repulsive volume term existing in the SBM. Intuitively, the non-native competing interactions decrease the stability, as also is observed in our simulations (Figure S13, ESI†), but realistically may have more complicated impacts on kinetics⁸⁴. To determine how the electrostatic interactions modulate D, we change the environmental salt concentration, which controls the length of the Debye radius, thus leading to different strengths of electrostatic interactions.

Binding with electrostatic interactions also leads to a similar tendency of D along d_RMS−B (Fig. 5A). With different salt concentrations, which lead to different strengths of electrostatic interactions, the change in D(d_RMS−B) is not significant and the effects seem to vary at different binding stages. We then calculated the mean D at different binding stages (Fig. 5B). The results show that electrostatic interactions have very little influence on the diffusion rate at USE, which corresponds to the completely unbinding stage, but facilitates diffusion at TSE, implying that the “flycasting” mechanism may be effective at TSE for diffusive binding with long-range steering electrostatic interactions, although they may be non-native⁵⁰. At the BSE, where pKID has overcome the barrier accompanying the coupled-folding occurring in a downhill manner, the electrostatic interactions slow down the binding diffusion, mostly because they are formed along with the increasing compactness of the binary complex, where the short-ranged nonnative electrostatic interactions will increase the roughness of the energy landscape. Finally, the mean rate of diffusive dynamics shows a slight increase with increasing electrostatic interactions, as a net gain from compensation between TSE and BSE. These findings are similar to those obtained from different conformational disorders of pKID and temperatures (Figure S17 and S18, ESI†), implying that a salt-dependent diffusion coefficient may persist for general protein-protein binding cases.

Fig. 5. Diffusion coefficient at different strengths of electrostatic interactions.

(A) The position-dependent D along d_RMS−B. Free energy landscape with moderate salt concentration C_Salt=0.15 M at binding temperature is shown with dashed line as a guidance of the binding process (B) The ratio between the mean D(d_RMS−B) of different salt concentrations and moderate salt concentration (C_Salt =0.15M) for different binding stages.

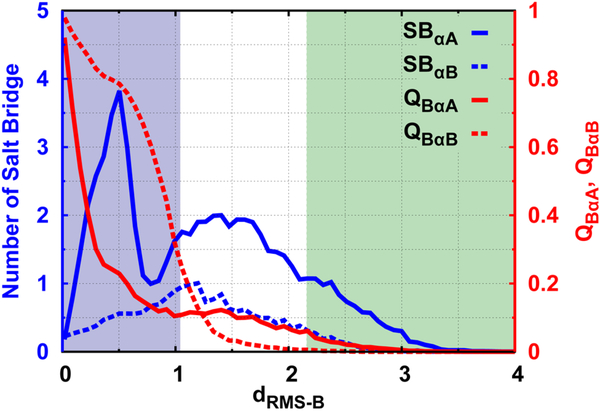
To explain such salt-dependent diffusive binding dynamics, we further calculated the number of non-native salt bridges progressively formed during the binding process (Fig. 6). From both the structural characteristic and free energy landscape (Figure S14, ESI†), the two helices αA and αB show unsynchronized steps with binding to KIX. The αA helix contains more charged residues than the αB helix does. This gives a hint that the electrostatic interactions may play more important roles in binding of the αA than the αB helix. In Fig. 6, there are more non-native salt bridges formed between KIX and αA helix than αB throughout the binding process. In particular, the number of salt bridges formed by αA with KIX initially increases in both the USE and TSE stages, then decreases slightly at the beginning of the BSE Stage, followed by a sharp increase at d_RMS−B ~ 0.5nm, and finally decreases to 0 at the completely bound state. The number of salt bridges formed by αB simply increases at the USE and TSE stage, and finally decreases in the BSE stage to 0 at the bound state. At different salt concentrations, stronger electrostatic interactions lead to a higher number of non-native salt bridges (Figure S16, ESI†). The distinct dependence of salt bridge formation in the two helices can shed light on the explanation of the relationship between D(d_RMS−B) and the salt concentration. Binding of pKID is steered by the long-range non-native sparsely formed interactions, which primarily rely on the highly charged αA helix in accordance with the “fly-casting” mechanism⁴³ at the USE and TSE stages (Figure S15, ESI†), whereby the diffusive binding dynamics is thought to be facilitated. When pKID and KIX are close in space to the BSE from d_RMS−B ~ 1.0 nm, the αB helix is triggered to specifically anchor with KIX through short-range native binding contacts prior to the αA helix. This is based on the fact that αB has a larger number of native binding contacts with KIX than αA. Therefore, the nonnative salt bridges between the αB helix with KIX are weakened. For the αA helix, the native binding shows only a slight change, but the number of non-native salt bridges decreases first because the native binding of the αB helix aids in eliminating the nonnative interactions. Then, the non-native salt bridge increases, mostly because the non-native interactions between _αA and KIX can guide the search for binding sites after αB accomplishes the binding (Figure S15, ESI†). Further proceeding, the binding of pKID to KIX in the BSE (d_RMS−B from ~ 0.5nm to ~ 0nm) mostly relates to a slight adaption of the αB helix by native contacts on the surface of KIX to native binding sites with further elimination of the non-native salt bridges, as well as native binding of the αA helix by breaking the strongly pre-formed non-native salt bridges. This will certainly lead to slow diffusive binding dynamics (Figure S15, ESI†). In summary, although the salt concentration exhibits little impact on the overall binding diffusion coefficient, it manipulates the diffusive dynamics step-by-step during binding by forming periodical intermittent non-native salt bridges and heterogeneous binding pathways.

Fig. 6. Non-native salt bridges and native contact formations of the two helices during binding at moderate salt concentration.

C_salt = 0.15M. SB is an acronym for “salt bridge”.

4. Conclusions

One functional advantage of IDPs is that (un)binding is efficiently fast thanks to the inherent disorder. To explain this effect, theory has successfully introduced a “fly-casting” mechanism⁴³, by which a flexible chain possesses a larger capture radius than a rigid one, to facilitate binding at the very beginning stage. The simulations and experiments also have unambiguously observed the phenomena of binding acceleration by conformational disorder^85–88. Previously, the “fly-casting” mechanism was interpreted in terms of free energy, where conformational disorder tends to lower the binding energy barrier⁴³, which contributes to the exponential term in Kramers’ theory. The pre-factor as diffusion coefficient was often ignored. Incorporating the effects of the diffusion coefficient by careful assessments of the “fly-casting” mechanism on binding rates has given contradictory results, where the influence of the “fly-casting” mechanism on the binding kinetics led by the conformational disorder is overestimated⁶¹. This occurs because the diffusion of a flexible chain is likely slowed down by its extended conformation because of the larger hydrodynamic radius³⁸. Based on our quantified D, one may draw another conclusion: as from Fig 3, when the two chains are completely dissociative at d_RMS−B > 4.0 with Q_B=0, D(d_RMS−B) increases monotonically with added conformational disorder. The seeming contradiction primarily occurs because d_RMS−B reflects the Cartesian coordinates of the residues evolved in the binding native contacts. This not only describes the binding process, but also captures the intra-chain dynamics. The conformational disorder has more flexible dynamics on each residue of the isolated IDP. This may result in a higher diffusion along d_RMS−B, compared with a rigid chain, where the diffusion of d_RMS−B only derives from binding.

Nevertheless, the effect of the “fly-casting” mechanism on diffusive binding dynamics is faithfully observed within our salt concentration-dependent simulations. The isolated IDP has an inherent diffusive characteristic, which is insensitive to ionic strength. However, the environment with low salt concentration has a weaker Debye screening effect on electrostatic interaction. Thus, the capture radius of the charged protein chain is relatively larger than that with high salt concentration. The initially formed electrostatic interactions, which are mostly non-specific and nonnative, can drive the two chains close to each other in space. This indirectly accelerates the diffusive binding until the transition state stage. Therefore, we state that the “fly-casting” mechanism can not only reduce the thermodynamic free energy barrier, but can also accelerate local diffusion at the beginning of binding. In general, IDPs hold higher percentages of charged residues than globular proteins^38,89, and the vicinity of IDP binding interfaces are rich in complementary charges⁹⁰. These facts likely enhance the effects of the “fly-casting” mechanism on IDPs’ binding kinetics in practice.

It is still controversial whether the pre-formed structures in IDPs aid or hinder binding^91–95. From a diffusion perspective, we have addressed the complex non-monotonic role of conformational disorder on IDP binding at the last stage, from initial to final complex. A large degree of conformational disorder can prevent the orientational restraints and steric hindrance as topological frustrations³⁹. This leads to loosely formed or fuzzy complexes⁸⁰ that consequently accelerate the local diffusion. Decreasing conformational disorder may partition the energy landscape into a handful of disconnected binding pathways, where the diffusion is likely hindered by limited directional constraint movements. Further decreasing conformational disorder into completely folded proteins, in some cases, boosts the possibility that a rigid protein can smoothly slide in the vicinity of the binding sites to accomplish docking, particularly when the binding interfaces are extended⁹⁶. This potentially increases the chance of escaping the traps on the energy landscape with the emergence of additional pathways. Our results regarding the impacts of conformational disorder on diffusive binding reveal an unprecedented complex binding mechanism for IDPs.

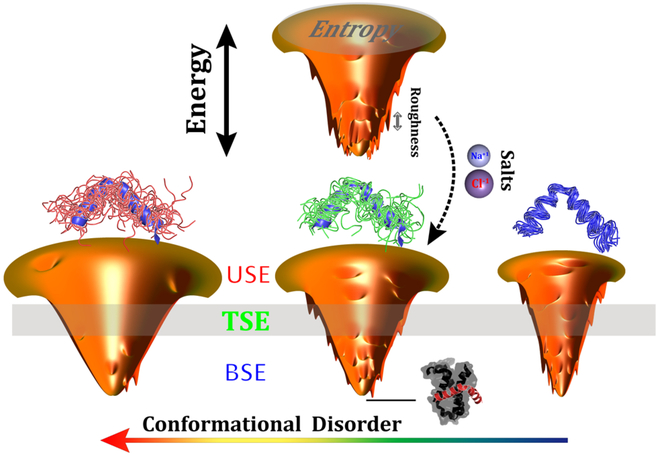
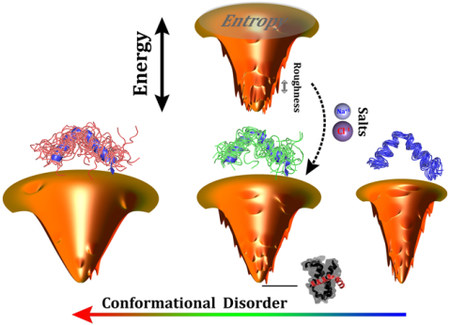
The quantified position-, disorder-, and salt-dependent diffusion coefficient, which inherently encodes the roughness of the energy landscape, provides a practical way to infer the topography of the binding energy landscape hierarchically. This moves beyond previous investigations^44–46, where the roughness was mostly estimated by implicit averaging from the overall energy landscape, lacking detail at each layer of the funnel. The topography of the energy landscape is quantified by the quantity $\Lambda =\delta E/(\mathrm{\Delta }E\sqrt{2S})$, where δE, ΔE, and S are the average energy gap, roughness, and entropy, respectively. Combined with our previous work on quantification of the energy landscape^44–46, we are now able to provide a more precise portrait of the binding energy landscape (Fig. 7): the roughness at the top of the binding funnel is moderate, then with binding proceeding to the middle of the funnel, the roughness tends to slightly decrease because of transiently formed attracting intermolecular interactions; finally, the roughness increases significantly at the bottom of the funnel when the compact binary complex forms. This funnel picture is in accord with the disconnectivity graph energy landscape representation of a protein-folding SBM^97,98, implying that even a native-centric model without any energetic frustration still has remarkable topology-led energy roughness, which varies stepwise differently during the binding/folding process.

Fig. 7. Scheme illustrating the effects of conformational disorder and salt concentrations on the topography of binding energy landscapes.

The deepness, the size, and the roughness of the funnels represent the energy gap, entropy, and energy roughness of the energy landscapes, respectively. The single funnel at the top shows binding with moderate conformational disorder and low salt concentration (strong electrostatic interactions). The three funnels at the bottom show the change according to the conformational disorder. Conformational ensembles of pKID are shown on the top of each funnel, with the native structure colored blue. The bound complex of pKID-KIX is shown at the basin of the funnel, indicating the destination of binding.

The increase in intrinsic disorder in binding protein has a distinct influence on increasing entropy, but decreasing energy roughness, in modulation of the binding energy landscape. This results in a higher _Λ, representing a more funneled binding energy landscape⁴⁵. Incorporating current studies based on quantifications of the diffusion coefficient, we therefore offer a profound understanding of the roles of intrinsic disorder on modulating the binding energy roughness (Fig. 7): a fully unfolded protein with a high degree of conformational disorder eliminates the roughness triggered by topological frustrations throughout the binding process, portraying a smooth binding energy landscape; decreasing the intrinsic disorder in a protein chain increases the binding roughness at every layer of the funnel, where the bottom layer of the binding funnel appears to be more affected as a result of the higher topological frustration that the compact complex potentially has; further decreasing the conformational disorder continuously increases the roughness at the funnel top, but smoothens the bottom of the funnel by means of multiple emerging binding pathways that assist to smooth the local topological barriers on the energy landscape. Overall, the global roughness of the binding energy landscape monotonically decreases with increasing conformational disorder, consistent with our previous work, where a completely different approach based on calculation of density of states was applied⁴⁵.

Electrostatic interactions, which are more common in IDPs than globular proteins^38,89,90, also have heterogeneous roles in modulation of the topography of the binding energy landscape (Fig. 7): removing the ions in the solution increases the strengths of electrostatic interactions by eliminating the ionic screening effect. This facilitates diffusive binding by smoothing the energy roughness at the middle of the funnel via non-native long-range transiently formed electrostatic interactions. Conversely, the nonnative salt bridges formed during the approach to the binding complex lead to energetic roughness at the bottom of the funnel. Such dual effects of electrostatic interactions on the roughness are compensated during the binding process and lead to a slightly decreasing global roughness of the binding energy landscape in the end. In addition, electrostatic interactions in IDPs have been found to contribute to the stabilization of the binding complex^99–101, which can deepen the bottom of the funnel and increase the energy gap. Conversely, the intra-chain electrostatic interactions of some IDPs, which in particular have high net or bipolar charge, are capable of collapsing the conformation of isolated IDPs, depending on the environment^65,102–106. These collapsed structures in IDPs, either native or non-native, are expected to have distinct effects on the energy gap and entropy. This adds baffling complexity into the effects of electrostatic interactions on the binding energy landscape, whereby the interpretation seems to proceed on a case-by-case basis.

The other advantage of intrinsic disorder in protein recognition is the capability of binding with high specificity but low affinity^{35,36,39,107–109}. However, it is always practically challenging to measure the specificity, which is conventionally defined as the relative affinities between all possible binding targets. We have verified the validity of transferring the conventional specificity to intrinsic specificity, which describes the distributions of different binding modes and is determined by the energy landscape^110–112. Therefore, measuring specificity is feasible by quantifying the topography of the binding energy landscape. Based on our previous work⁴⁵, the intrinsic binding specificity is found to increase with conformational disorder, along with decreasing energy roughness and increasing entropy, while the first factor dominates to eventually increase the degree of funnelness of the binding energy landscape. In the current work, we delineate this effect by means of the diffusion coefficient, whereby the conformational disorder increases the flexibility of the protein chain and therefore leads to dynamic interaction patterns in the complex concomitant with multiple binding pathways. This smooths the binding roughness and finally results in high binding specificity. By the same token, we can conclude a lower specificity for rigid docking than highly flexible binding. However, gradually increasing the partially stabilizing or pre-formed structures in IDPs’ isolated states has distinct effects on energy roughness during different binding process, so the specificity of binding is anticipated to be complicated to determine and be understood. The difficulty encountered here calls for future upgrades or completely new developments of theory, with deduction basically relying on each layer of the funnel hierarchically, rather than integrally.

Summarizing, we have addressed the position-, disorder-, and salt-dependent diffusion coefficient behavior of IDPs’ binding coupled with folding to targets. Our study has filled the gap in current research regarding IDPs, where major efforts are focused/based on using a free energy approach. With the quantified diffusion coefficient, the shape of the binding energy landscape can be inferred. Our theoretical investigations provide a profound understanding of the topography of the binding energy landscape in IDPs’ binding–folding and may provide guidance for biophysical experiments regarding the affinity/specificity engineering of IDPs by means of the energy landscape.