Abstract
Background and Aims
Branching is a main morphogenetic process involved in the adaptation of plants to the environment. In grasses, tillering is divided into three phases: tiller emergence, cessation of tillering and tiller regression. Understanding and prediction of the tillering process is a major challenge to better control cereal yields. In this paper, we present and evaluate WALTer, an individual-based model of wheat built on simple self-adaptive rules for predicting the tillering dynamics at contrasting sowing densities.
Methods
WALTer simulates the three-dimensional (3-D) development of the aerial architecture of winter wheat. Tillering was modelled using two main hypotheses: (H1) a plant ceases to initiate new tillers when a critical Green Area Index (GAIc) is reached, and (H2) the regression of a tiller occurs if its interception of light is below a threshold (PARt). The development of vegetative organs follows descriptive rules adapted from the literature. A sensitivity analysis was performed to evaluate the impact of each parameter on tillering and GAI dynamics. WALTer was parameterized and evaluated using an initial dataset providing an extensive description of GAI dynamics, and another dataset describing tillering dynamics under a wide range of sowing densities.
Key Results
Sensitivity analysis indicated the predominant importance of GAIc and PARt. Tillering and GAI dynamics of expt 1 were well fit by WALTer. Once calibrated based on the agronomic density of expt 2, tillering parameters allowed an adequate prediction of tillering dynamics at contrasting sowing densities.
Conclusions
Using simple rules and a small number of parameters, WALTer efficiently simulated the wheat tillering dynamics observed at contrasting densities in experimental data. These results show that the definition of a critical GAI and a threshold of PAR is a relevant way to represent, respectively, cessation of tillering and tiller regression under competition for light.
Keywords: Cessation of tillering, competition for light, critical GAI, Functional Structural Plant Model, L-systems, tiller regression, Triticum aestivum, wheat
INTRODUCTION
As sessile organisms, plants are shaped by phenotypic plasticity: their response to environmental conditions (Cahill and McNickle, 2011; Abley et al., 2016). Light is a major environmental factor affecting plant development through the quantity of absorbed photons, which determines the rate of photosynthesis and water transpiration; however, plants have also developed specific photoreceptors able to sense the spectral quality of light, mainly the red: far red (R: FR) ratio and the amount of blue light (Smith, 1982). Branching (i.e. the ability to produce a new ramification from an axillary bud) is one of the main morphogenetic processes involved in the adaptation of plant architecture to the environment. In Poaceae, tillers are ramifications that initiate from the bottom of the plant and their development is strongly affected by the density of neighbouring plants, leading to wide variability in the number of tillers produced per plant. For cereals, the number of tillers that complete their development and bear a spike is a key yield component (Gate, 1995), and tillering ability is therefore a central trait in breeding strategies. Tillering in cereals can be divided into three distinct phases: tiller emergence, the cessation of tillering and tiller regression (Porter, 1985; Xie et al., 2016).
The phase of tiller emergence is characterized by two aspects: (1) the rate of bud production and (2) the probability of bud outgrowth. The emergence of tillers in wheat and barley has been shown to be synchronized with that of leaves in the main stem: a tiller initiated from the axillary bud of leaf n on the main stem has the opportunity to emerge at the emergence of leaf n + 2 of the main stem (Masle-Meynard, 1982; Kirby et al., 1985). Once a tiller has emerged, it produces buds that may initiate a new tiller of a higher rank, and so forth until tiller cessation. Despite this synchronization between the emergence of tillers and leaves on the main stem, not all buds lead to emerged tillers. The probability of bud outgrowth is a result of multiple interactions between plants and the environment that can be mediated by changes in internal variables such as phytohormones or the trophic status of the plant (for reviews see Tomlinson and O’Connor, 2004; Assuero and Tognetti, 2010). The synchronism and probability of bud outgrowth have been described in plant models following various approaches. Some authors have modelled bud outgrowth according to the trophic status of the plant [Evers et al. (2010) for spring wheat; Luquet et al. (2006) for rice; Mathieu et al. (2009) for trees] while other studies are based on an empirical approach using fixed probabilities estimated from experimental observations (Barillot et al., 2014; Abichou et al, 2018).
The end of the phase of tiller emergence, i.e. tiller cessation, may occur when apices turn from vegetative to flowering status, although it generally takes place earlier. Variations in light quality, which result from the development of the canopy and its optical properties, act as photomorphogenetic signals regulating many processes, including tillering (Ballaré et al., 1987, 1990; Casal et al., 1990; Smith et al., 1990; Gautier and Varlet- Grancher, 1996; Barillot et al., 2010; Gommers et al., 2013). In the absence of other stresses, cessation of tillering seems to be related to the early detection of neighbouring plants, which is mainly sensed by plants through the R: FR ratio (Franklin, 2005; Casal, 2013). Thus, the quality of light perceived by plants is a signal characterizing the surrounding environment (neighbouring plants) and capable of inducing morphogenetic responses that allow plants to anticipate the trophic aspects of light competition, such as limitation in photosynthesis (for reviews see Franklin, 2005; Casal, 2013). When comparing contrasting sowing densities, some authors have observed almost identical R: FR values at the base of the canopy when tillering stopped (Evers et al., 2006; Sparkes et al., 2006; Dreccer et al., 2013). Evers et al. (2007a) modelled the cessation of tillering based on such an R: FR threshold value. However, their formalism based on a unique R: FR threshold value did not accurately reproduce the tillering patterns observed at three experimental sowing densities. Moreover, simulating the cessation of tillering from an R: FR ratio raises some complex questions (Demotes-Mainard, 2016): (1) Which parts of the plant are involved in the perception of the R: FR signal? (2) Over what period of time should the R: FR signal be integrated? In addition, using the strong correlation between the R: FR ratio and the Green Area Index (GAI) (Sattin et al., 1994), several authors proposed using a critical Leaf Area Index to predict the cessation of tillering in various species such as Italian ryegrass (Simon and Lemaire, 1987), wheat (Sparkes et al., 2006) and rice (Zhong et al., 2002; Wei et al., 2013).
Not all emerged tillers produce an ear, as a variable proportion of tillers dies between the onset of stem elongation and anthesis (Xie et al., 2016). The signals and mechanisms involved in tiller death are not fully understood, but one main hypothesis is based on resource limitation resulting in a competition between plant shoots (Sachs et al., 1993). A stable chronological order of tiller death has been well described in wheat: tillers die in reverse order of their emergence (Porter, 1985). Therefore, it can be assumed that tiller success in this competition depends on their relative size. Tiller death has been rarely modelled, probably because the underlying mechanisms are still poorly understood. Lafarge et al. (2005) proposed to model tiller death in grasslands according to probabilities depending on light extinction in the canopy, although to our knowledge a model that predicts the number of ears produced by cereals is missing.
Finally, despite its importance in cereal ecophysiology and its impact on crop yield, the whole tillering process remains difficult to analyse and to predict. Due to their explicit three-dimensional (3-D) description of plant structure, functional structural plant models (FSPMs) (Fourcaud et al., 2008; Vos et al., 2010; DeJong et al., 2011) are suitable tools to represent plant functioning and its complex interactions with environmental factors, and are particularly relevant to model tillering plasticity (Evers and Vos, 2013). In the present paper, we propose an individual-based 3-D model of wheat inspired from the ADEL-Wheat FSPM formalism (Fournier et al., 2003), which simulates tillering dynamics on the basis of the three previously described phases, i.e. emergence, cessation and regression. Contrary to ADEL-Wheat, which describes the three tillering phases using experimental data, WALTer is built on three main assumptions: (1) tiller emergence is modelled using fixed empirical probabilities, coupled with coordination rules between tiller emergence and leaf emergence on the main stem; (2) cessation of tillering is assumed to occur when a critical GAI is reached; and (3) tiller regression is assumed to occur for a threshold of light intercepted by the tiller. The model was evaluated through its ability to predict tillering dynamics within a wide range of sowing densities described by Darwinkel (1978).
MATERIALS AND METHODS
Model description
The present model, hereafter named WALTer, simulates the 3-D development of the aerial architecture of winter wheat from sowing to flowering. Here we describe the hypotheses and rules integrated within WALTer to represent plant development and particularly all steps of tillering. The model is defined at the plant scale, the crop being represented as a population of individual plants. The WALTer model is based on the L-systems formalism (Lindenmayer, 1968; Prusinkiewicz and Lindenmayer, 1990) using the L-Py simulation platform (Boudon et al., 2012). The L-systems formalism allows description of plant architecture through a dynamic set of modules representing the plant’s components, their topology and geometry. A plant is composed of several axes (main stem + tillers from primary order to higher orders). Each axis is built by an apex that initiates subunits called phytomers. Each phytomer consists of an axillary bud, an internode and a leaf composed of a sheath and a blade. WALTer includes both deterministic and adaptive processes. The development and extension of vegetative organs (blades, sheaths and internodes) follows descriptive rules. By contrast, tillering is described as a self-regulated process and is modelled through two simple rules considering (1) a critical GAI at which the emergence of tillers stops and (2) a critical amount of light intercepted by each tiller under which tiller death is triggered.
To simulate tiller regression, the interception of light by each tiller was computed by a radiative model (CARIBU: Chelle and Andrieu, 1998) applied to the 3-D representations of plants, and thus accounting for the competition for light among neighbouring plants. Competition for other resources, such as water, nitrogen or other nutrients, is not considered. The model is run with a daily time step and time is expressed as thermal time with a base temperature of 0 °C (Gate, 1995; Jamieson et al., 1998). The model is initiated at the emergence of the tip of the first leaf, considering a mean delay after sowing (Δse, °Cd).
For the sake of realism, some stochasticity was included in the model. We considered that the final number of main stem leaves, probability of tiller emergence, duration before plant emergence, and plant and organ positions depend partly or totally on probabilities, thus allowing the effect of micro-environmental heterogeneity or the variability usually observed in plant development to be taken into account.
The parameters used in the processes described below are indicated in Table 1, while other parameters can be found in corresponding supplementary appendices.
Table 1.
List of model parameters, definition, values and units. Parameters were estimated from (1) the literature, (2) directly from experimental data, (3) calibrated from experimental data or (4) pragmatically calibrated
| Parameter | Description | Estimation | Value | Unit |
|---|---|---|---|---|
| Development of vegetative organs | ||||
| Organ initiation, emergence, elongation | ||||
| Pls | Thermal time interval between the initiation of two successive vegetative phytomers | Expt 1 | 44.5 | °Cd |
| Phl | Thermal time interval between the emergence of two successive leaves | Expt 1 | 99 | °Cd |
| ED B | Duration from leaf emergence to end of extension | ADEL-Wheat* | 1.6 | °Cd per phylochron |
| ED S | Duration of sheath extension | ADEL-Wheat* | 0.4 | °Cd per phylochron |
| ED L | Duration of internode extension | ADEL-Wheat* | 2 | °Cd per phylochron |
| ED FB | Duration of the extension of the flag leaf blade | ADEL-Wheat* | 1 | °Cd per phylochron |
| Tiller emergence | ||||
| Duration between the initiation of a bud and the start of its activity | Calibrated | 1 | Plastochron | |
| Probability of emergence of a tiller (except coleoptile tiller) | Expt 1 | Table2 | Dimensionless | |
| p CT | Probability of emergence a coleoptile tiller | Expt 1 | Table2 | Dimensionless |
| Floral transition and final leaf number | ||||
| Final number of leaves on the main stem | Expt 1 | 11.3 | ||
| Duration between the floral transition of axes belonging to two consecutive cohorts | Abichou et al (2018) | 1/3 | Plastochron | |
| Mean (s.d.) delay between sowing and emergence | Expt 1 | 81 (30) | °Cd | |
| Number of primordia already preformed inside the seed | Jamieson (1998) | 4 | Primordia | |
| Organ death | ||||
| Date of the end of the first phase of leaf senescence | Abichou et al (2018) | 691 | °Cd | |
| Date of the end of the second phase of leaf senescence (only for tillers) | 1131 | °Cd | ||
| Date of the end of leaf senescence | 2000 | °Cd | ||
| Haun stage of the beginning of the first phase of leaf senescence | 4.75 | |||
| Number of green blades at the end of the first phase of leaf senescence | 3.31 | |||
| Number of green blades at the end of the second phase of leaf senescence (only for tillers) | 4.5 | |||
| Number of green blades at the end of leaf senescence | 0 | |||
| Thermal time between senescence of the flag leaf and the beginning of peduncle senescence | 100 | °Cd | ||
| Plant geometry | ||||
| Angle between blade inclination and y-axis | Calibrated | 40 | Degrees | |
| Angle between the azimuth of two consecutive blades | Calibrated | 185 | Degrees | |
| Angle between the zenith of two consecutive blades | Calibrated | 0 | Degrees | |
| Angle between the azimuth of two consecutive tillers | Calibrated | 40 | Degrees | |
| Mechanistic tillering rules | ||||
| Cessation of tillering and Green Area Index | ||||
| GAIc | Green Area Index threshold above which tillering stops | Fit on expt 1 and calibrated on expt 2 | Table2 | Dimensionless |
| d GAIp | Maximal range for plant detection | Calibrated | 1 | m |
| Buried length of the first sheath | Calibrated | 2 | cm | |
| Tiller death | ||||
| Date of the beginning of the regression | Expt 1 | Table2 | Haun stage | |
| Duration of the radiation integration to determine the survival of a tiller | Calibrated | 100 | °Cd | |
| PARt | PAR threshold below which a tiller does not survive | Fit on expt 1 and calibrated on expt 2 | Table2 | µmol cm−2 °Cd–1 |
| Thermal time interval during which two tillers of the same plant cannot die | Fit on expt 1 and calibrated on expt 2 | Table2 | °Cd | |
| Thermal time between the moment a tiller stops growing and its entire removal | Calibrated | 600 | °Cd |
* ADEL-Wheat is a 3-D model of wheat developed by Fournier et al. (2003).
Development of vegetative organs: the descriptive part of the model
Phytomer production, leaf emergence, the date of floral transition and tiller emergence are simulated by WALTer using descriptive functions derived from the ADEL-Wheat formalisms (Fournier et al., 2003), whereas organ elongation, organ final dimensions and organ death are derived from its more recent update Plantgen-ADEL (Abichou, 2016).
Phytomer production and leaf emergence
The apical meristem of each axis produces successive vegetative phytomers at fixed thermal-time intervals (Pls: plastochron) until the final leaf number is reached. The apex then turns into a reproductive state leading to floral transition and thus the production of an ear. Initiated leaves emerge acropetally at fixed intervals (Phl: phyllochron). Plastochron and phyllochron are model parameters, are identical for all axes and are constant during the whole simulation, as is commonly approximated in plant models (Jamieson et al., 1998).
Final leaf number and floral transition
Final leaf number on the main stem is a model parameter, and the floral transition of the main stem occurs when the apical meristem has produced all vegetative phytomers. As some authors have noted that the floral transition is not always synchronous between tillers and the main stem (Ljutovac, 2002; Abichou, 2016), we assumed a constant duration (ΨFT) between the floral transition of tillers belonging to two successive cohorts (first cohort: primary tillers initiated on the main stem, second cohort: tillers initiated on primary tillers, etc.). Therefore, the dates of floral transition of all tillers are calculated once the floral transition occurs on the main stem (Supplementary Data SI-A1).
Tiller emergence
The axillary buds, located at the basis of each phytomer of the main stem, remain inactive during a defined duration (Δb) and then start to produce the vegetative phytomers of a new tiller. The vegetative phytomers of a tiller also bear axillary buds following the same developmental rules, potentially leading to the production of secondary, tertiary or even higher order tillers. Each axillary bud may emerge according to empirically fixed probabilities (pT or pCT) but these developmental rules are modulated by self-adaptive rules described below, triggering the fate of axillary buds (death or production of vegetative phytomers). For those buds that develop in a tiller, coordination rules follow the work of Kirby et al. (1985), considering a strict coordination between the emergence of bud n on the main stem (tiller (1,n)) and the emergence of leaf n + 2 of the bearing stem.
Organ extension
Organs of a phytomer grow in a sequential order: (1) the blade extends, (2) the sheath starts to extend once the blade has reached its final length and (3) the internode starts to extend once the sheath has reached its final length. The length of an organ is assumed to increase linearly with thermal time during the period of extension. The durations of these periods are fixed, depending on organ type (i.e. blade, sheath, internode), but are identical for all phytomers and tiller orders (Supplementary Data SI-B1, SI-B2). Rates of extension are calculated so that the organ reaches its final dimension at the end of the extension period.
Final dimensions
For a given axis, blade final lengths are expressed as a function of both phytomer rank and final leaf number on the main stem. Final sheath lengths and blade maximal widths are computed from the final length of blades (Dornbusch et al., 2011a). Internode final lengths are expressed as a function of the phytomer rank and the rank of the last short internode. The number of elongated internodes is identical for all axes (Ljutovac, 2002). Analogous rules are used to compute internode, blade and sheath final lengths for the main stem and tillers, except that blade and sheath of lower leaves are slightly longer on tillers than on the main stem (Supplementary Data SI-C1–C5).
Organ death
All types of organs enter senescence according to an empirical function, considering a non-progressive senescence: an organ is either alive or dead. At the axis scale, the number of dead blades at time t (°Cd) is calculated as the difference between the Haun stage, i.e. the decimal number of ligulated leaves simulated by the model and the number of green blades, defined by an empirical function of thermal time (Supplementary Data, Eq SI-D1, SI-D2). The function for the number of green blades was obtained by a linear adjustment made on experimental observations on four different dates (Abichou, 2016). For sheaths, internodes, peduncles and ears, the timing of death was based on that of the blade. For the sheath and internode of phytomer n, death occurs synchronously with that of the blade of phytomer n + 1. For the peduncle and ear, a fixed duration after senescence of the blade of the last phytomer of an axis was assumed before triggering senescence. The lower dead blades are removed from the plant, while the five uppermost blades and all sheaths, internodes, peduncles and ears stay on the plant and therefore intercept light.
Plant geometry
The 3-D reconstruction of plants is based on simplified representations of organ geometry. Blades are represented as flat elements, the main part being a rectangle and the tip a triangle. Internodes and sheaths are represented by cylinders with a constant diameter during internode extension and identical for all phytomers. Blade orientation is defined by (1) a phyllotaxic angle (ΨBzen, degrees) parameterized to represent the alternate phyllotaxy of wheat and (2) an inclination angle (ΨBazi, degrees). The azimuth (ΨTzen, degrees) and zenith (ΨTazi, degrees) of successive tillers are parameterized pragmatically to avoid artificial overlap among tillers. Heterogeneity in plant representations was achieved by randomizing the azimuths and part of the inclinations of leaves and tillers.
Self-adaptive rules: the tillering process
In WALTer, the tillering process is modelled at the plant scale according to two self-adaptive rules that account for regulation of tillering by the plant environment. These original rules allow description of (1) the cessation of tiller emergence, according to a critical GAI reached around the plant and (2) tiller regression according to the amount of light intercepted by the tiller in question. Values for the tillering parameters are listed in Table 4.
Table 4.
Tillering parameters and their values used in the model. Parameters were fitted on expt 1 and expt 2 respectively
| Parameter | Value | Units | |
|---|---|---|---|
| Calibration on expt 1 | Calibration on expt 2 | ||
| GAIc | 0.6 | 0.52 | GAI |
| PARt | 30°000 | 35°000 | µmol cm−2 °Cd–1 |
| Δprot | 50 | 35 | °Cd |
Cessation of tillering and GAI
The cessation of tillering is calculated for each plant and is assumed to occur simultaneously for all axillary buds of a plant. For a given plant, the cessation of tillering occurs when the GAI around the plant reaches a critical threshold (GAIc). The surrounding plants taken into account for the calculation of GAI are those located within a given distance (dGAIp, cm) from the considered plant. When the GAIc is reached, all buds of the plant which have not yet emerged become inactive. After the plant has reached the GAIc, axillary buds do not follow the developmental rules described (i.e. tiller emergence based on probabilities).
GAI calculation integrates all visible and alive organs of an axis (i.e. blade, sheath, internode, peduncle and ear). The length of the first sheath (, cm) is not included in the calculation of GAI because it is usually partly buried in the soil.
Tiller death
The hypotheses implemented in WALTer are that (1) tiller death may occur only during a defined window of time, starting around the beginning of stem extension and (2) during that window, a tiller dies if the amount of intercepted light per unit area integrated over a given duration (Δl, °Cd) falls below a threshold (PARt, µmol cm−2 °Cd−1). When a tiller dies, its development is immediately stopped, and organ death follows sequentially, following the same rules as described above. Moreover, after a fixed protection period (Δsgc, °Cd), the organs remaining on the dead tiller (i.e. sheaths and internodes) are completely removed. Sequential death of tillers occurs according to their age, i.e. the tillers belonging to the youngest cohort die first. If several tillers belong to the youngest cohort, the tiller with the lowest amount of intercepted light dies first. Moreover, to more accurately represent the dynamics of tiller death, we assumed a duration (Δprot, °Cd) between the death of two successive tillers. That duration could originate from a reallocation of carbon from the dead tiller to the rest of the plant, as such fluxes between shoots have been identified (Quinlan and Sagar, 1962). The period during which tiller regression may occur starts at time (), which corresponds to the extension of the lower elongated internode and lasts until the heading of the main stem; is estimated following eqn (1):
| (1) |
where is the final number of leaves on the main stem and is a model parameter estimated from the experimental data of Abichou et al. (2018) for a plant with 11 leaves on the main stem.
To model the interception of light by plants we used the nested radiosity model Caribu (Chelle and Andrieu, 1998). The computations considered only diffuse radiation according to the standard overcast sky radiation distribution (Moon and Spencer, 1942). Diffuse radiation was approximated using a set of 20 light sources (five azimuths and four zeniths). Using the meteorological data of photosynthetically active radiation (PAR), the amount of intercepted light was calculated at the organ level and aggregated at the axis scale when needed.
Design of virtual crops
The virtual crop was sown on a rectangular surface, where seed positions followed a lattice defined by the distance between rows and by sowing density. As the edges of the virtual field were subject to border effects (lower shading), border strips were defined and trimmed after simulations, in order to analyse only the central plants, submitted to homogeneous radiation. All seeds were sown synchronously but a variable delay was generated between sowing and the emergence of the first leaf of each plant, as a result of random sampling according to a normal distribution. Four phytomers were assumed to be already present in the seeds (He et al., 2012).
Numerical methodology
WALTer uses a large number of parameters aimed at tuning organ size and rate of development. These were not the focus of this study, so Triticum aestivum ‘Maxwell’ was used as a reference cultivar for setting realistic values of the parameters that define the deterministic aspects of the model. Parameter values for plastochron, phyllochron, tiller emergence probabilities, number of leaves and organ dimensions were inferred from data from expt 1, an intensive phenotyping of ‘Maxwell’ sown at a density 217 plants m−2 (‘E08’ in Abichou et al., 2018).
The model was then evaluated through:
a sensitivity analysis focusing on parameters controlling GAI and tillering dynamics, to identify the inputs with the greatest impact on WALTer outputs;
the ability of WALTer to fit very detailed kinetics of GAI and tillering dynamics recorded in expt 1;
the ability of WALTer to predict tillering dynamics at sowing densities not used to fit the model, on the basis of expt 2 data that described tillering dynamics at seven contrasting sowing densities (Darwinkel, 1978).
Calibration of organ dimensions in the expt 1 dataset
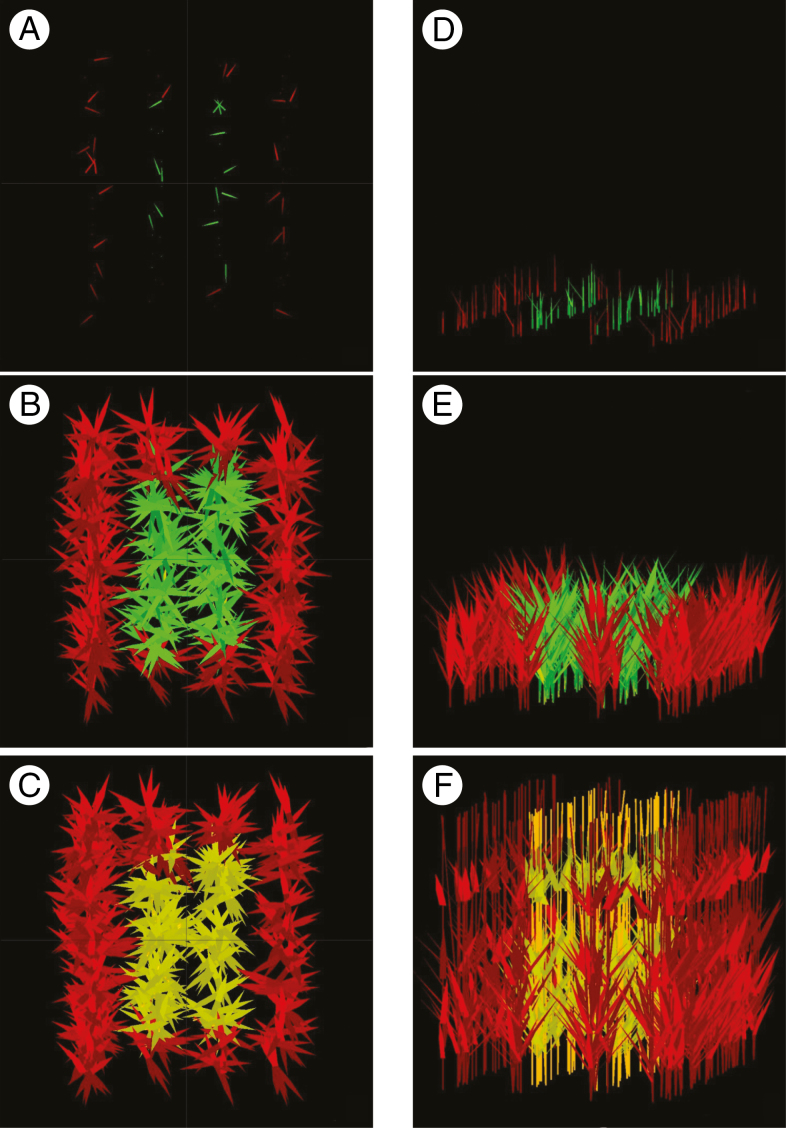
Plastochron, phyllochron, tiller emergence probabilities, as well as the parameters governing internode, blade and sheath final dimensions were parameterized using the expt 1 dataset and were kept constant in all simulations. The experiment was conducted at the INRA campus of Thiverval-Grignon, France. Winter wheat cultivar ‘Maxwell’ was sown on 26 October, 2010 at 217 plants m−2 with inter-row fixed at 17.5 cm (see Abichou et al., 2018 for more details). This sowing design was reproduced in the simulation scheme, using rectangular plots of 200 plants sown in eight rows, surrounded by a border of 20 cm (Fig. 1). Simulations were based on daily temperatures and PAR data collected at the meteorological station of Thiverval-Grignon for the year 2010/11.
Fig. 1.
Vertical (A, B, C) and oblique views (D, E, F) of a simulated plot at three stages of growth: at emergence (A, D), during mounting (B, E), and at the end of the cycle (C, F). The plot consists of 99 plants at 217 plants m–2 according to expt 1; red denotes border plants, green represents emerged and non-senescent organs, and yellow represents dead organs.
The nine parameters governing blade and internode final lengths were calibrated by fitting blade and internode final lengths to observed values with a grid approach. Optimal parameters were selected by minimizing the root mean square error (RMSE) criterion. RMSE between experimental data and outputs of WALTer were calculated for each axis and were weighted by the observed frequency of tiller emergence: the more frequent an axis, the more impact it had on the average RMSE. Linear regressions on blade final length were then performed to fit sheath final length and maximal blade width.
Sensitivity analysis
This was carried out by considering three steps: (1) selection of WALTer’s output of interest, (2) selection of major inputs that have an impact on tillering dynamics and (3) setting and analysis of an optimal simulation design.
Selection of output of interest
The two main outputs of interest of WALTer were (1) the tillering dynamics and (2) the GAI dynamics, which provided information at the crop scale. We defined a set of descriptors to summarize those dynamics in the most relevant way. GAI dynamics were characterized by two scalar measures: the maximum value of the simulated GAI during the crop cycle (GAImax) and the date at which GAImax was reached (DGAImax). Tillering dynamics were characterized by four scalar measures: the maximum number of axes produced per plant (), the duration of the tillering plateau (Δplateau), the number of ears produced per plant (Near) and the rate of tiller regression (Sreg) (Table 2).
Table 2.
List of the six output descriptors for the sensitivity analysis
| Output descriptor | Description | Units |
|---|---|---|
| GAImax | Maximum value of GAI (Green Area Index: ratio of green surfaces over soil surface) reached by the crop | GAI |
| D GAImax | Date at which the maximum value of GAI is reached (°Cd) | °Cd |
| N ear | Final number of ears per plant | Tiller |
| Maximum number of axes per plant | Tiller | |
| Δplateau | Duration of the tillering plateau | °Cd |
| S reg | Rate of regression | Tiller °Cd–1 |
Selection of input factors
WALTer was based on more than 50 input parameters, so a subset of input factors was selected for the sensitivity analysis. After discarding parameters with values known with good confidence from the literature, the effects of parameters with no/sparse experimental data and/or parameters directly impacting the tillering and GAI dynamics in WALTer formalism were investigated. Among the eight input parameters selected for the sensitivity analysis (Table 3), six were ecophysiological (detailed in Table 1): the critical GAI inducing cessation of tillering (GAIc), the threshold of PAR needed for the survival of a tiller (PARt), the protection duration between the death of two successive tillers of a plant (Δprot), the maximal length of the longest blade (), the final number of leaves on the main stem () and the range of the proximity GAI (dGAIp). Two ‘environmental’ parameters were also selected: sowing density, known to affect tillering dramatically, and incident light, which defines the amount of PAR incoming each day and on which tiller regression is based. The range of variation of each input parameter was set to represent the largest range using only three values. These values were chosen according to published and experimental data as well as exploratory simulations. For PAR, the range of variation over time was limited to minimum and maximum daily PAR values averaged over 10 years in five locations around France.
Table 3.
List of input parameters explored through the sensitivity analysis and their chosen ranges
| Parameter | Values | Units | ||
|---|---|---|---|---|
| Density | 50 | 200 | 600 | Plants m−2 |
| GAIc | 0.25 | 0.6 | 1 | GAI |
| PARt | 5000 | 50000 | 100 000 | µmol cm−2.°Cd |
| Δprot | 10 | 50 | 100 | °Cd |
| 15.0 | 22.5 | 30.0 | cm | |
| 10.3 | 11.3 | 12.3 | Blades | |
| d GAIp | 0.2 | 0.5 | 1 | m |
| Light | Low | Medium | High | – |
A fractional factorial design
Given the high number of potential inputs and the computational time needed for one simulation, a screening method (Iooss, 2011) based on a fractional factorial design (Monod et al., 2006) was chosen. Three levels were considered for each input in order to detect non-monotonic effects. A fractional factorial design of resolution V (Bailey, 2008) was chosen to ensure estimation with no confusion of main effects and pairwise interaction of input factors. It was assumed that third-order and higher-order interactions were negligible. This resulted in a design with only 243 simulations instead of the 6561 simulations needed for a complete factorial design.
The fractional factorial design was generated via the planor package (Kobilinsky et al., 2012) in R software.
The impact of each input factor on each output was estimated by computing the main effect indices (eqn 2) and the sensitivity indices for second-order interactions (eqn 3). For each output, the total interaction sensitivity indices (eqn 4) were computed to estimate the impact of all the second-order interactions on the variance. For each output, these indices were based on the sum of squares associated with main effects and second-order interactions in an analysis of variance model (Monod et al., 2006). For a given output, a and b are input factors, n is the total number of input factors in the analysis, SSa is the sum of squares associated with the main effect of a, SSa,b is the sum of squares associated with the effect of the interaction between a and b, and SST is the total sum of squares of the output. These sum of squares are used to compute Main Sensitivity index, MSi, Interaction Sensitivity index, ISi, and Total Interaction index, TISi, as follows:
| (2) |
| (3) |
| (4) |
Calibration of tillering parameters on the expt 1 dataset
fit of GAI and tillering dynamics. After using the expt 1 dataset to fit various architectural parameters (from plastochron to leaf dimensions), we also assessed the ability of WALTer to properly fit GAI and tillering dynamics.
Sensitivity analysis highlighted that GAIc and PARt and, to a lesser degree, Δprot and were the most important tillering parameters. Thus, was set at its experimental value according to data from the expt 1 dataset and GAIc, PARt and Δprot were calibrated based on expt 1 as we had no clear hints of their range. As the cessation of tillering takes place before tiller regression, calibration was performed sequentially, starting with GAIc, and then calibrating Δprot and PARt. The explored GAIc values ranged from 0.2 to 0.8 (dimensionless) with a 0.02 step. The best GAIc was selected based on the RMSE calculated from two outputs: the maximal number of active axes per plant () and the maximal number of active axes per m2 (); between experimental data and outputs of WALTer. Both outputs were weighted equally after centring and reduction. PARt values started at 1000 and then ranged from 5000 to 80 000 (µmol cm−2 °Cd–1) with a 5000 step. Six values were selected for Δprot: 5, 15, 25, 35, 50 and 75 (°Cd). The best set of PARt/Δprot was also selected based on the RMSE criterion calculated from four outputs: the final number of axes per plant Near, the final number of axes per area Nm2ear, the duration of tillering plateau (Δplateau) and the rate of tiller regression (Sreg). For each combination of four parameters, the RMSE between experimental data and outputs of WALTer were weighted equally after centring and reduction.
Cross validation by prediction of tillering dynamics on expt 2
A cross-validation of the tillering parameters was performed using expt 2 in which the winter wheat cultivar ‘Lely’ was sown on 19 October, 1975 at seven densities (5, 25, 50, 100, 200, 400 and 800 plants m−m) in plots of 1 m2 (Darwinkel, 1978). In this experiment, the author measured the dynamics of the mean number of axes per plant at each sowing density. Tillering parameters were estimated for one sowing density and predictions of WALTer using these parameters were compared to experimental data at other sowing densities.
The three most influential tillering parameters GAIc, PARt and Δprot were calibrated at a density of 200 plants m−2 of expt 2. The calibration process took place as explained above: GAIc was calibrated before PARt and Δprot. In these simulations, we kept ‘Maxwell’ parameters (expt 1) for organ dimensions, leaf emergence and senescence, and used the original sequence of PAR available in Darwinkel (1978) and a sequence of daily temperatures obtained by averaging Lelystad data from 2004 to 2014. Square plots of 200 plants were simulated, with plants equidistant from each other and sown on 19 October, 1975. The analysis was performed on the 50 central plants to discard border effects. The best set of GAIc/PARt/Δprot was selected based on the RMSE calculated on the same two and then four outputs as described previously. The optimal set of parameters was used to simulate the other six densities and simulations were compared with measurements to evaluate the prediction of tillering dynamics at a wide range of densities.
RESULTS
Representation of organ dimensions and growth for ‘Maxwell’ genotype from expt 1 dataset
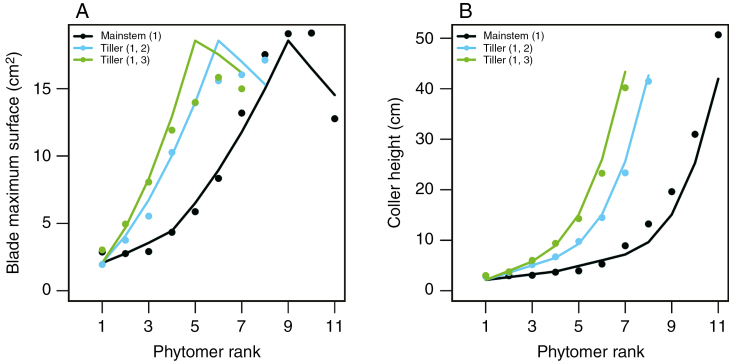
The representation of organ dimensions were summarized by two traits: (1) the surface of each blade and collar height (i.e. the insertion height of blades and thus internode final length and the length of the longest sheath). After fitting the associated parameters, blade surfaces and collar heights of both main stems and tillers were reasonably simulated by the model with an RMSE of 1.37 cm2 and 2.1 cm, respectively (Fig. 2). Thus, the simple formalisms used to describe organ growth and final dimensions in WALTer provided realistic dynamics of organ growth. The simple rules implemented for leaf senescence also allowed us to simulate the number of green leaves, similar to the measured dynamics (RMSE = 0.34, Supplementary Data, Fig SI-E1).
Fig. 2.
Blade maximum surface (A) and collar height (B), vs. phytomer rank for main stem (black), the first primary tiller (blue) and the second primary tiller (green). Dots represent experimental data: of expt 1 (‘Maxwell’) and lines represent simulations of the model after calibration.
Sensitivity analysis: the predominant influence of tillering parameters and density
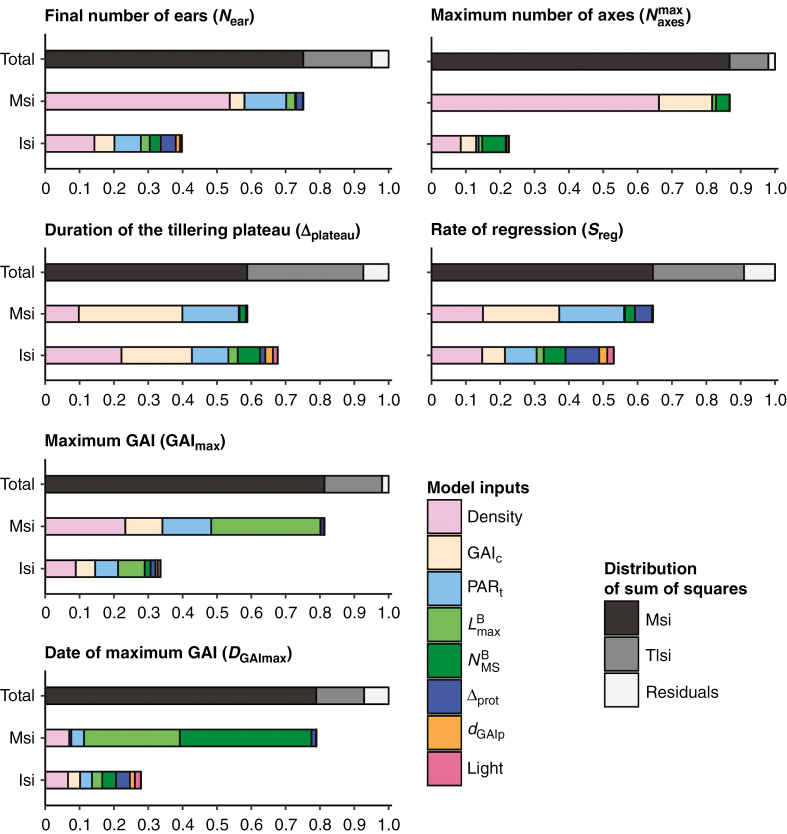
Sensitivity analysis allowed the variance of each output to be decomposed into main effects, second-order interactions (see Fig. 3) and residuals that represent the combined effects of higher-order interactions and of the stochasticity of WALTer. For all six outputs, the impact of the residuals never exceeded 9.02 %. For the number of ears per plant (Near), the maximum number of axes per plant (), the maximum GAI (GAImax) and the date at which the maximum GAI was reached (DGAImax), main effects explained at least 75 % of the variance, while second-order interactions explained between 11 % and 20 % of the variance. For the rate of tiller regression (Sreg) and for the duration of the tillering plateau (Δplateau), main effects explained a lower fraction of the variance (64.5 % and 58.8 %, respectively) and there was a greater importance of second-order interactions (26.5 % and 33.8 %, respectively).
Fig. 3.
Sensitivity indices for final number of ears, maximum number of axes, duration of the tillering plateau, rate of regression, maximum GAI and the date of maximum GAI. The upper bar shows the distribution of Msi and Isi while the two lower bars show impacts of model inputs.
When considering the total sensitivity indices, density explained the major part of the variance of all the studied outputs. As expected, the input parameters GAIc and PARt also had a considerable impact on the variance of the outputs, especially of those describing tillering dynamics. The leaf-size parameter () appeared important for both GAI-related outputs, while the final number of leaves () was only critical for DGAImax. Predictably, the duration of protection (∆prot) influenced the variance of the rate of tiller regression (Sreg), although this input did not have a large impact on the variance of the other outputs. Finally, for all studied outputs, the range of the proximity GAI (dGAIp) and the incident light were unimportant. GAIc and PARt, which lead the two rules aiming at representing tillering, were the parameters that impacted tillering dynamics the most.
WALTer reasonably reproduced the GAI and tillering dynamics of the expt 1 dataset
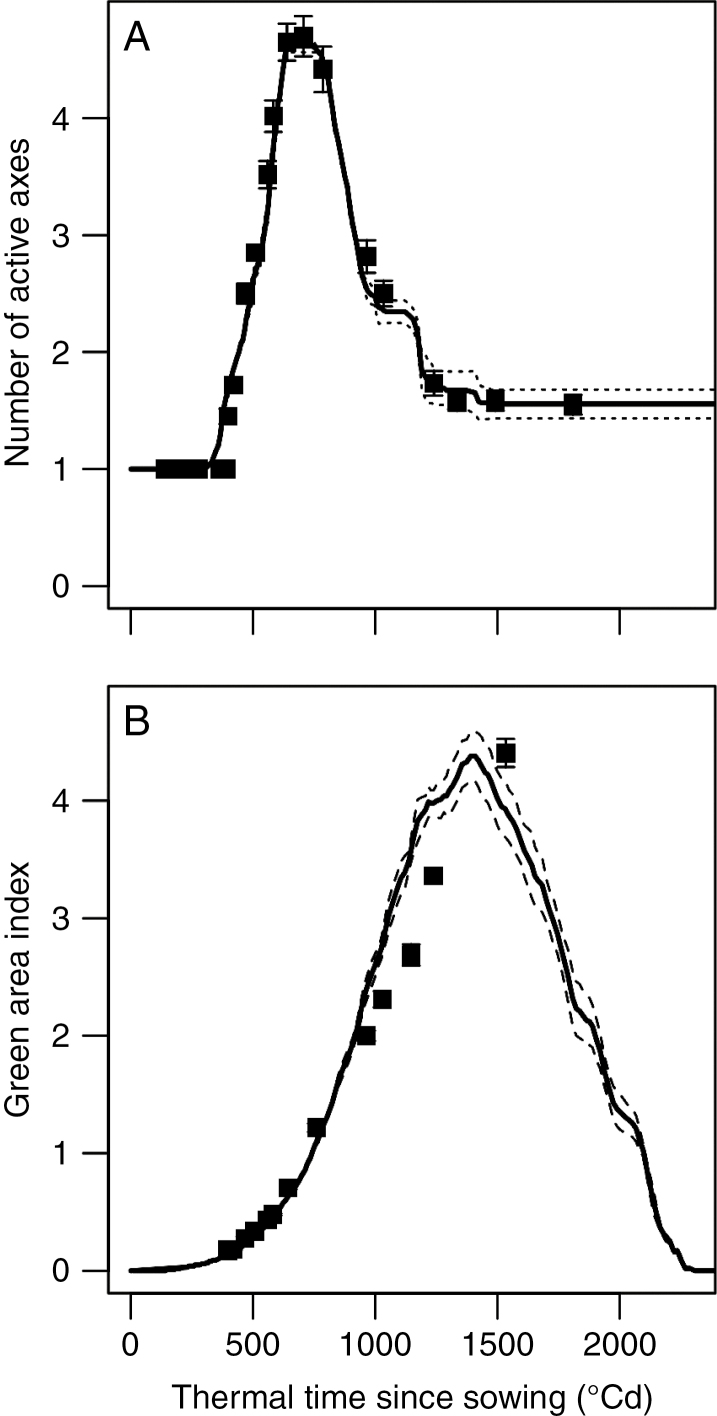
The calibration process led to a set of optimized parameters (Table 4) allowing the simulated tillering dynamics to closely match the number of active axes observed in expt 1 during the whole cycle of the crop (Fig. 4A). The model accounted for the three steps of tillering: emergence, cessation and regression. The simulated GAI (Fig. 4B) closely matched experimental data from emergence until 800 °Cd (GAI = 1.3). Then, the predicted GAI was slightly above the measured values, from 800 to 1500 °Cd (i.e. at flowering). Finally, experimental data and simulations provided consistent estimates of the GAI at tillering cessation: GAIc (~0.6) was reached at ~500 °Cd.
Fig. 4.
Tillering (A) and Green Area Index (B) dynamics vs. thermal time since sowing. Lines represent simulations made by the model calibrated on expt 1 (lines are mean, and dotted lines are standard errors, n = 5); dots are experimental data of expt 1. RMSE values of model verification were 0.2 for number of axes per plant and 0.31 for GAI.
Cross validation on expt 2: predictions of tillering dynamics at a wide range of sowing densities
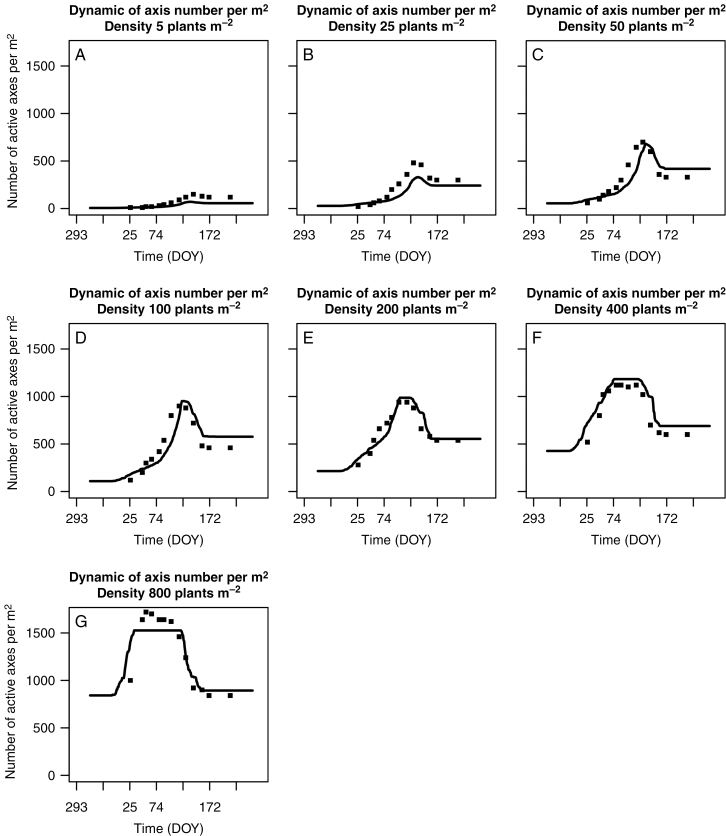
The predicted and observed dynamics of the number of axes per m2 for six sowing densities (Fig. 5A–D and F, G), as well as the fitted and observed dynamics at 200 plants m−2 (Fig. 5E), the density used to calibrate GAIc, PARt and Δprot of WALTer, were similar. Predicted dynamics were close to experimental data, especially for densities from 50 to 800 plants m−2. The duration of the plateau of tillering increased with increasing density both in the experiment (from 0 d at density 5 to ~66 d at density 800) and in the simulations (from 0 d at density 5 to ~87 d at density 800). Models and experiments also showed an increase in the fraction of regressing tillers from low to intermediate densities.
Fig. 5.
Number of tillers per m2 vs. thermal time since sowing at seven densities (5, 25, 50, 100, 200, 400 and 800 plants m–2). Dots are measurements from expt 2 and lines represent number of axes per m2 predicted by WALTer after calibration of the tillering parameters (Δprot, GAIc and PARt) to a density of 200 plants m–2 of expt 2.
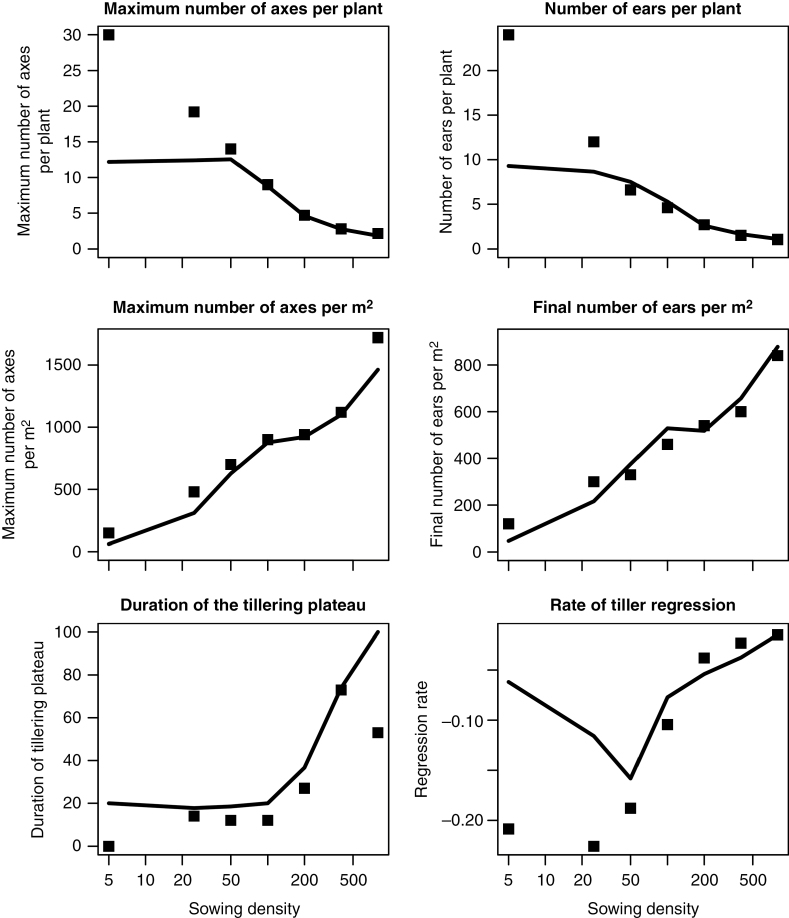
Simulated responses of the six key variables to plant density were nearly identical to the measurements at 50–400 plants m−2 (Fig. 6). However, at extreme densities, some discrepancies existed between predicted and observed data. At low densities (5 and 25 plants m−2) WALTer (1) strongly under-estimated the maximum number of axes and the number of ears per plant and (2) over-estimated the regression rate. The duration of the tillering plateau seemed to be over-estimated by WALTer, although this short plateau (20 °Cd) was not experimentally perceptible because of the precision of the expt 2 dataset. At the very high density (800 plants m−2) the maximum number of axes per m2 was under-estimated and the duration of the tillering plateau was overestimated. Differences of estimation quality were apparent between number of axes per plant and numbers of axes per m2: strong over-estimations of number of axes per plant at low densities have a moderate impact on RMSE of number of axes per m2 and, conversely, over-estimations of number of axes per m2 at high densities were barely noticeable when considering number of axes per plant.
Fig. 6.
Maximum number of axes per plant (A), number of ears per plant (B), duration of the tillering plateau (C), maximum number of axes per m2 (D), final number of ears per m2 (E) and rate of tiller regression (F) vs. sowing density. Lines are predictions of WALTer after calibration to a density of 200 plants m–2 of expt 2 and dots are measurements of expt 2.
DISCUSSION
Tillering regulation and tiller dynamics are an essential aspect of plants’ adaptation to their environment and mechanistic models able to simulate this behaviour are lacking. The main reasons for this are (1) limited knowledge of the mechanisms governing tillering cessation and tiller regression, and (2) the difficulty of representing these complex mechanisms in crop models. Individual-based models provide a natural frame for studying the tillering process, as they allow integration of morphogenetic rules governing the architecture of individual plants, and simulation of the developmental feedback loops stemming from plant–plant interactions. However, with a few exceptions (Evers et al., 2007b; Cici et al., 2008), these aspects of individual-based models have not been exploited until now.
In this work, we designed WALTer, an individual-based FSPM wheat model that simulates tiller dynamics based on simple hypotheses, and evaluated this approach against experimental datasets. As highlighted by Evers and Vos (2013), modelling branching in cereals can be based on three approaches: probabilistic, dose–response curves and mechanistic; only the last two allow simulation of tillering plasticity. Mechanistic approaches require modelling either carbohydrate, water, nitrogen, other nutrient metabolism or hormonal controls; or ideally these metabolic and regulatory processes would be integrated, leading to complex models. We adopted the dose–response strategy in order to develop a ‘light’ model of tillering plasticity that is able to integrate environmental cues (light shading) with a limited number of parameters and reasonable simulation time.
In WALTer, simulating how competition between plants impacts the dynamics of tillering was based on the following set of encoded assumptions. Tillering was the single degree of freedom considered, while the plasticity of the other components of plant architecture, such as leaf dimension, plant height or the rates of development and senescence, were neglected. The only environmental cues considered were temperature and light; interactions with water or nitrogen were not accounted for. The dynamics of tillering followed three successive phases, a phase of tiller emergence, a plateau and a phase of tiller regression. During tiller emergence, each axillary bud carried by a short internode was a potential site of tillering, and this phase stopped when either all potential tillers emerged or when the canopy around the plant reached a threshold value. During tiller regression, the youngest tiller of a plant may die at each time step depending on the amount of light it intercepted in the last 100 °Cd, except if another tiller of the plant died in the last 100 °Cd. The beginning of the phase of tiller regression was determined ontogenetically and the duration of this phase was undetermined.
Critical Green Area Index (GAIc) and cessation of tillering
To our knowledge, this work represents the first attempt to use GAIc to model the cessation of tillering. As shown in Figs 5 and 6, this hypothesis was highly efficient in simulating the maximum number of tillers across sowing densities in expt 2, with an excellent fit in the range 50–400 plants m−2. However, our simulations underestimated the number of tillers observed in Darwinkel’s results at densities of 5 and 25 plants m−2. In these cases, cessation of tillering in our simulations did not occur because the GAIc was reached but because the potential number of tillering sites was reached. From known responses to density, it seems very likely that plants at these low densities produced a higher numbers of leaves and thus of tillering sites (Ljutovac, 2002), a plasticity response not integrated in WALTer. Even if such very low densities are below those usually found in agronomic conditions, improving model behaviour should be helpful to better simulate compensation within heterogeneous crops, in local areas of low densities. The present model underestimated the maximum number of tillers by ~15 % and overestimated the duration of the tillering plateau at 800 plants m−2 by ~50 %. We observed a lack of 800 °Cd in the sum of temperature of the experimental sequence compared to characteristic sequences of the location. Therefore, the sequence of temperatures used to perform simulations with WALTer (daily mean from 2004 to 2014 in Lelystad) differed from the experimental sequence (decade mean for 1976 in Lelystad). This change, necessary for simulating reasonable plants, could explain the slight temporal shift observed in the prediction of tillering dynamics and the poor prediction of the duration of tillering plateau. Moreover, the rapid changes in slope in tiller emergence observed in the experiment and the limited number of measures performed during this period resulted in a low accuracy for the estimated duration of the tillering plateau at very high plant densities. Furthermore, we have no explanation for the differences between observed and predicted maximum number of axes but they do not represent a major shortcoming, as differences between experimentation and simulations remained moderate at common plant densities and 800 plants m−2 are not common under agronomic conditions. As expected, sensitivity analysis underlined the importance of the GAIc in estimation of the maximum axis number, while other ecophysiological parameters had minor effects. Moreover, GAIc had a major impact on the estimation of the duration of the tillering plateau (Δplateau), the rate of tiller regression (Sreg) and GAImax. Sensitivity analysis also indicated that the range of detection of neighbours (dGAIp) did not impact tillering dynamics under our conditions, a result that needs to be reconsidered when simulating plots with genetic heterogeneity, such as cultivar mixtures.
Our estimates of GAIc of ~0.6 for expt 1 and ~0.52 for expt 2 are very different from the value of ~ 3 reported for the cessation of tillering of ryegrass by Simon and Lemaire (1987). Similarly, Zhong et al. (2002) reported a critical GAI of ~3.5 for rice when N was not limiting, but with a strong decrease of GAIc with decreasing N nutrition. The high values of GAIc in these studies suggest that PAR availability, rather than R: FR, may have triggered the end of tillering in ryegrass and rice. In wheat, Evers et al. (2006) observed the cessation of tillering when the fraction of intercepted PAR by the canopy was 0.4 and the R: FR ratio was ~0.35, independent of plant density and for a large range of light intensities. Using an extinction coefficient of 0.82 for wheat (O’Connell et al., 2004), a GAIc of ~0.65 can be estimated for the study of Evers et al. (2006), which is much lower than in ryegrass and rice, but is in line with our estimates of 0.65. These values support the hypothesis that, in wheat, cessation of tillering is not triggered by a trophic effect of the competition. The differences between experimental and simulated values for expt 2 were remarkably small considering the various unknowns: organ dimensions and phenology of the ‘Lely’ cultivar (set to ‘Maxwell’ reference parameters for the simulations). These results are very promising for using GAIc as a proxy for R: FR when modelling. The use of a more mechanistic approach, based directly on tillering responses to R: FR, raises a number of issues, due to the limits of our knowledge of plant responses to light quality, and the difficulty with and high computation time to simulate the spatial distribution of R: FR and its dynamics. By contrast, GAI changes slowly with time and is easy to calculate from the model and to assess experimentally.
These results highlight several questions that remain to be investigated. A first question is the possible dependence of GAIc on N and light availability. Even if the low value of GAIc for wheat suggests a predominant role of R: FR in the cessation of tillering, an interaction with light availability cannot be excluded. For instance, empirical observations suggest that emergence of the first tiller probably depends on the carbon status of the plant (Friend, 1966). Similarly, the strong relationship between GAIc and the nitrogen status reported by Zhong et al. (2002) in rice invites an investigation of such interactions in wheat. A second question is the genotypic variability of GAIc. There is a variability of tillering abilities in wheat, part of which may be related to a differential sensitivity to the R: FR ratio, thus leading to different values of GAIc. This parameter is reasonably easy to estimate from field experiments in which the dynamics of GAI are monitored and the maximum number of tillers is measured. Such experiments therefore give the opportunity to use GAIc to quantify one of the components of the genotypic ability in tillering.
Intercepted light and the fate of tillers
The core hypothesis to represent tiller regression in the present model was that the fate of a tiller depends on the amount of light it intercepts per unit green area, but additional rules were required to accurately represent tillering behaviour. First, the existence of an ontogenetic stage for the beginning of tiller regression was proposed by Abichou et al. (2018) based on analysis of the dynamics of senescence under several experimental conditions. Without this limitation, our model would anticipate tiller regression in high-density treatments. The age-hierarchy among tillers, which restricts the ‘die or live’ decision to the youngest tiller of the plant, is consistent with experiments where this behaviour has been repeatedly reported (Porter, 1985). The age hierarchy, rather than local environmental conditions, actually seems to be a robust emerging property of the processes regulating apical dominance (Rameau et al., 2015). Finally, the model also assumes that there is a minimal duration between the death of two tillers in one plant in order to prevent tiller death from occurring too rapidly. Indeed, tiller death starts before stems reach a significant extent, i.e. when all tillers are subjected to a similar microclimate. Thus, the environmental conditions that would trigger the death of a tiller would generally result in predicting the death of another tiller at the next iteration of the model. Remobilization of carbohydrates from a senescing tiller probably contributes to the survival of the others (Irving, 2015). The rules needed to improve our simulation of tillering dynamics highlighted parameters whose influences were assessed based on a sensitivity analysis. Sensitivity analysis showed that the variance of four major descriptors of tillering dynamics (, Near, Sreg and Δplateau) were governed mainly by the variance of sowing density, GAIc and PARt. This was consistent with our starting assumptions. The duration of protection (Δprot) was required to represent reasonable tillering dynamics, although sensitivity analysis highlighted the low impact of this parameter compared to PARt and GAIc in the estimation of the output of interest. Moreover, the light parameter had no impact on the different outputs of WALTer. Therefore, the realistic range of variation explored for PAR was not large enough to influence tiller regression in WALTer.
The detailed measurements available in expt 1 allowed illustration that this simple model could accurately simulate the dynamics of tiller senescence. Parameter fitting allowed reproduction of the dynamics of tiller regression. The model was also able to accurately predict the final number of ears (per plant and per m−2) produced at the broad range of sowing densities applied in expt 2, with a single parameter set from one calibration at an agronomically realistic density (200 plants m−2). The dynamics of GAI were accurately simulated from sowing until 800 °Cd and were then slightly overestimated until flowering. We have no explanation for this overestimation, as the simulation of tillering and leaf senescence were good. However, there may have been some unknown factors affecting the simulation of organ size, and field measurement of GAI could have been also subject to some error. Experimental data for GAI were not available for the post-flowering period but because the dynamics of the number of green leaves were realistic, it is likely that the model allowed for a reasonable prediction of the GAI for this part of the cycle.
Genotypic variations have already been observed and characterized on the phyllochron (He et al., 2012) and organ dimensions (Dornbusch et al., 2011b), but we have not characterized genotypic variations of tillering traits due to the plasticity of tillering. Thus, WALTer could be used as a phenotyping tool to estimate GAIc and PARt of genotypes each sown at multiple densities (if experimental tillering dynamics are available). Furthermore, the fitted parameters in expt 1 and expt 2 could not be considered as purely genotypic characteristics. These datasets integrated genotype × environment (G×E) interactions, the tillering characteristics resulting both from wheat genotypes and from important environmental factors such as the availability of water, light or nitrogen. For example, expt 1 was characterized by a water stress that has been shown to impact crops, especially final ear number (less important than usual at this sowing density). However, the good predictive ability of WALTer, after the optimization of a few key parameters, showed that the model provided a way to characterize and compare tillering dynamics of a set of genotypes evaluated in the same cropping conditions. The parameterisation was therefore able to capture the G×E interactions, allowing WALTer to reproduce the dynamics of plant architecture in various conditions. WALTer does not integrate a dependency of tillering to nitrogen availability although this has a strong importance on tillering dynamics (Alzueta et al., 2012). As a first attempt to account for the effect of nitrogen availability on tillering, further versions of the model could be implemented with a dependency of GAIc and PARt on plant nitrogen status. In addition, WALTer could be coupled with other FSPMs accounting for nitrogen acquisition and allocation either by using the concept of critical N concentration and empirical relationships with light interception (Louarn and Faverjon, 2018, for legumes), or by using more mechanistic approaches describing the biological processes driving nitrogen and carbon metabolisms (Barillot et al., 2016a, b, for wheat at post-anthesis stages). However, not considering nitrogen in the tillering process in WALTer did not prevent accurate prediction of tillering dynamics at a large range of sowing densities.
CONCLUSIONS
Using simple rules, the WALTer model simulated the dynamics of tillering in response to plant density, providing a good fit with experimental data after fitting a relatively small number of parameters, and despite many unknowns in the experimental conditions. Indeed, remarkable features were reproduced by the model, in particular the tendency, with decreasing sowing density, to (1) shorten the duration of the plateau when the number of active tillers is maximal, (2) decrease the number of tillers regressing per °Cd and (3) decrease the fraction of tillers that regress. These results suggest that the small number of parameters in our model may be sufficient to represent the behaviour of a genotype. Despite its simplicity, the model improved understanding of the factors involved in tillering behaviour and identified parameters that can be used to quantify the genotypic differences in tillering in wheat. The modelling approach was applied to homogeneous canopies, but the construction of the model – an individual-based approach governed by intercepted light and local GAI – allows more general uses. One would be investigation of the consequences of early stresses affecting plant density, such as winter mortality. Indeed, WALTer could help to understand how the rate of mortality and the stage of plant development interact with tillering potential to determine the efficiency of tiller density recovery. A second use could be estimation of parameters for various genotypes and thus in performing genetic analyses. A third use could be in studying the behaviour of genetically heterogeneous canopies such as cultivar mixtures or intercropping systems involving several species. In these mixtures, competition for light may strongly modulate the composition of the crop (Barillot et al., 2014), with consequences for production or for synergistic interactions, such as disease control due to diverse resistance genes in the canopy (Vidal et al., 2017; see Borg et al., 2018, for a review). In addition, the benefit expected from mixed crops/varieties also come from the ability of one component to compensate for accidents affecting another component. Despite its simple rules, consideration of an explicit 3-D representation of a crop involves a non-negligible computational time. However, we have shown that by using an appropriate simulation design we can deal with this constraint and efficiently explore numerous combinations with a manageable number of simulations. Therefore, the performance of the model should make it an appropriate tool for investigating (1) the efficiency of combinations of architecture or even (2) the evolution of traits in populations sown over several generations.
Supplementary Material
ACKNOWLEDGEMENTS
We thank Franck Gauthier (INRA Jouy en Josas, France) and Didier Combes (INRA Lusignan, France) for valuable help in the development of the proximity GAI algorithm. We also thank the two anonymous referees and the editor Theodore DeJong for their useful comments that increased the quality of the manuscript. This work was supported by Region Ile-de-France (grant number 03-2010/GV-DIM ASTREA) and the National Research Agency (Wheatamix project; ANR-13-AGRO-0008).
LITTERATURE CITED
- Abley K, Locke JCW, Leyser HMO. 2016. Developmental mechanisms underlying variable, invariant and plastic phenotypes. Annals of Botany 117: 733–748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Abichou M. 2016. Modélisation de l’architecture 4D du blé: identification des patterns dans la morphologie, la sénescence et le positionnement spatial des organes dans une large gamme de situations de croissance. PhD thesis, AgroParisTech, France. [Google Scholar]
- Abichou M, Fournier C, Dornbusch T, et al. 2018. Parameterising wheat leaf and tiller dynamics for faithful reconstruction of wheat plants by structural plant models. Field Crops Research 218: 213–220. [Google Scholar]
- Alzueta I, Abeledo LG, Mignone CM, Miralles DJ. 2012. Differences between wheat and barley in leaf and tillering coordination under contrasting nitrogen and sulfur conditions. European Journal of Agronomy 41: 92–102. [Google Scholar]
- Assuero SG, Tognetti JA. 2010. Tillering regulation by endogenous and environmental factors and its agricultural management. The Americas Journal of Plant Science and Biotechnology 4: 35–48. [Google Scholar]
- Bailey RA. 2008. Design of comparative experiments. Cambridge Series in Statistical and Probabilistic Mathematics. Cambridge: Cambridge University Press. [Google Scholar]
- Ballaré CL, Sánchez RA, Scopel AL, Casal JJ, Ghersa CM. 1987. Early detection of neighbour plants by phytochrome perception of spectral changes in reflected sunlight. Plant, Cell & Environment 10: 551–557. [Google Scholar]
- Ballaré CL, Scopel AL, Sanchez RA. 1990. Far-red radiation reflected from adjacent leaves: an early signal of competition in plant canopies. Science 247: 329–332. [DOI] [PubMed] [Google Scholar]
- Barillot R, Frak E, Combes D, Durand JL, Escobar-Gutiérrez AJ. 2010. What determines the complex kinetics of stomatal conductance under blueless PAR in Festuca arundinacea? Subsequent effects on leaf transpiration. Journal of Experimental Botany 61: 2795–2806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barillot R, Escobar-Gutierrez AJ, Fournier C, Huynh P, Combes D. 2014. Assessing the effects of architectural variations on light partitioning within virtual wheat-pea mixtures. Annals of Botany 114: 725–737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barillot R, Chambon C, Andrieu B. 2016a. CN-Wheat, a functional–structural model of carbon and nitrogen metabolism in wheat culms after anthesis. I. Model description. Annals of Botany 118: 997–1013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barillot R, Chambon C, Andrieu B. 2016b. CN-Wheat, a functional–structural model of carbon and nitrogen metabolism in wheat culms after anthesis. II. Model evaluation. Annals of Botany 118: 1015–1031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Borg J, Kiær LP, Lecarpentier C, et al. 2018. Unfolding the potential of wheat cultivar mixtures: a meta-analysis perspective and identification of knowledge gaps. Field Crops Research 221: 298–313. [Google Scholar]
- Boudon F, Pradal C, Cokelaer T, Prusinkiewicz P, Godin C. 2012. L-Py: an L-system simulation framework for modeling plant architecture development based on a dynamic language. Frontiers in Plant Science 3: 1− 20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cahill JF, McNickle GG. 2011. The behavioral ecology of nutrient foraging by plants. Annual Review of Ecology, Evolution, and Systematics 42: 289–311. [Google Scholar]
- Casal JJ. 2013. Photoreceptor signaling networks in plant responses to shade. Annual Review of Plant Biology 64: 403–427. [DOI] [PubMed] [Google Scholar]
- Casal JJ, Sanchez RA, Gibson D. 1990. The significance of changes in the red/far-red ratio, associated with either neighbour plants or twilight, for tillering in Lolium multiflorum Lam. New Phytologist 116: 565–572. [Google Scholar]
- Chelle M, Andrieu B. 1998. The nested radiosity model for the distribution of light within plant canopies. Ecological Modelling 111: 75–91. [Google Scholar]
- Cici S-Z-H, Adkins S, Hanan J. 2008. A canopy architectural model to study the competitive ability of chickpea with sowthistle. Annals of Botany 101: 1311–1318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Darwinkel A. 1978. Patterns of tillering and grains production of winter wheat at a wide range of plant densities. Netherland Journal of Agricultural Science 26: 383–398. [Google Scholar]
- DeJong TM, Da Silva D, Vos J, Escobar-Gutierrez AJ. 2011. Using functional-structural plant models to study, understand and integrate plant development and ecophysiology. Annals of Botany 108: 987–989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Demotes-Mainard S, Péron T, Corot A, et al. 2016. Plant responses to red and far-red lights, applications in horticulture. Environmental and Experimental Botany 121: 4–21. [Google Scholar]
- Dornbusch T, Baccar R, Watt J, et al. 2011a. Plasticity of winter wheat modulated by sowing date, plant population density and nitrogen fertilisation: dimensions and size of leaf blades, sheaths and internodes in relation to their position on a stem. Field Crops Research 121: 116–124. [Google Scholar]
- Dornbusch T, Watt J, Baccar R, Fournier C, Andrieu B. 2011b. A comparative analysis of leaf shape of wheat, barley and maize using an empirical shape model. Annals of Botany 107: 865–873. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dreccer MF, Chapman SC, Rattey AR, et al. 2013. Developmental and growth controls of tillering and water-soluble carbohydrate accumulation in contrasting wheat (Triticum aestivum L.) genotypes: can we dissect them? Journal of Experimental Botany 64: 143–160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evers JB, Vos J. 2013. Modeling branching in cereals. Frontiers in Plant Science 4: 399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evers JB, Vos J, Andrieu B, Struik PC. 2006. Cessation of tillering in spring wheat in relation to light interception and red: far-red ratio. Annals of Botany 97: 649–658. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evers JB, Vos J, Chelle M, Andrieu B, Fournier C, Struik PC. 2007a. Simulating the effects of localized red:far-red ratio on tillering in spring wheat (Triticum aestivum) using a three-dimensional virtual plant model. New Phytologist 176: 325–336. [DOI] [PubMed] [Google Scholar]
- Evers JB, Vos J, Fournier C, Andrieu B, Chelle M, Struik PC. 2007b. An architectural model of spring wheat: evaluation of the effects of population density and shading on model parameterization and performance. Ecological Modelling 200: 308–320. [Google Scholar]
- Evers JB, Vos J, Yin X, Romero P, van der Putten PEL, Struik PC. 2010. Simulation of wheat growth and development based on organ-level photosynthesis and assimilate allocation. Journal of Experimental Botany 61: 2203–2216. [DOI] [PubMed] [Google Scholar]
- Fourcaud T, Zhang X, Stokes A, Lambers H, Korner C. 2008. Plant growth modelling and applications: the increasing importance of plant architecture in growth models. Annals of Botany 101: 1053–1063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fournier C, Andrieu B, Ljutovac S, Saint-Jean S. 2003. ADEL-wheat: a 3D architectural model of wheat development. In Hu B-G, Jaeger M, eds. Plant growth modeling and applications. 2003International Symposium on plant growth modeling, simulation, visualization and their applications. Beijing, P.R.China: Tsinghua University Press-Springer Verlag, 54–63. [Google Scholar]
- Franklin KA. 2005. Phytochromes and shade-avoidance responses in plants. Annals of Botany 96: 169–175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friend DJC. 1966. The effects of light and temperature on the growth of cereals. Presented at The Growth of Cereals and Grasses Twelfth Easter School in Agricultural Science, Nottingham, UK, 181–199. [Google Scholar]
- Gate P. 1995. Ecophysiologie du blé. Tec & Doc Lavoisier. [Google Scholar]
- Gautier H, Varlet‐Grancher C. 1996. Regulation of leaf growth of grass by blue light. Physiologia Plantarum 98: 424–430. [Google Scholar]
- Gommers CMM, Visser EJW, Onge KRS, Voesenek LACJ, Pierik R. 2013. Shade tolerance: when growing tall is not an option. Trends in Plant Science 18: 65–71. [DOI] [PubMed] [Google Scholar]
- He J, Le Gouis J, Stratonovitch P, et al. 2012. Simulation of environmental and genotypic variations of final leaf number and anthesis date for wheat. European Journal of Agronomy 42: 22–33. [Google Scholar]
- Iooss B. 2011. Review of global sensitivity analysis of numerical models. Journal de la Société Française de Statistique 152: 1–23. [Google Scholar]
- Irving LJ. 2015. Carbon assimilation, biomass partitioning and productivity in grasses. Agriculture 5: 1116–1134. [Google Scholar]
- Jamieson PD, Semenov MA, Brooking IR, Francis GS. 1998. Sirius: a mechanistic model of wheat response to environmental variation. European Journal of Agronomy 8: 161–179. [Google Scholar]
- Kirby EJM, Appleyard M, Fellowes G. 1985. Effect of sowing date and variety on main shoot leaf emergence and number of leaves of barley and wheat. Agronomie 5: 117–126. [Google Scholar]
- Kobilinsky A, Bouvier A, Monod H. 2012. PLANOR: an R package for the automatic generation of regular fractional factorial designs. Version 1.0. Technical report, MIA Unit, INRA Jouy-en-Josas. [Google Scholar]
- Lafarge M, Mazel C, Hill DRC. 2005. A modelling of the tillering capable of reproducing the fine-scale horizontal heterogeneity of a pure grass sward and its dynamics. Ecological Modelling 183: 125–141. [Google Scholar]
- Lindenmayer A. 1968. Mathematical models for cellular interactions in development I. Filaments with one-sided inputs. Journal of Theoretical Biology 18: 280–299. [DOI] [PubMed] [Google Scholar]
- Ljutovac S. 2002. Coordination dans l’extension des organes aériens et conséquence pour les relations entre les dimensions finales des organes chez le blé. PhD thesis, Institut National Agronomique Paris-Grignon, France. [Google Scholar]
- Louarn G, Faverjon L. 2018. A generic individual-based model to simulate morphogenesis, C–N acquisition and population dynamics in contrasting forage legumes. Annals of Botany 121: 875–896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luquet D, Dingkuhn M, Kim H, Tambour L, Clément-Vidal A. 2006. EcoMeristem, a model of morphogenesis and competition among sinks in rice. 1. Concept, validation and sensitivity analysis. Functional Plant Biology 33: 309–323. [DOI] [PubMed] [Google Scholar]
- Masle-Meynard J. 1982. Elaboration du nombre d’épis d’un peuplement de blé d’hiver en situation de compétition pour l’azote II. Modélisation du nombre d’épis. Agronomie 2: 17–24. [Google Scholar]
- Mathieu A, Cournede PH, Letort V, Barthelemy D, de Reffye P. 2009. A dynamic model of plant growth with interactions between development and functional mechanisms to study plant structural plasticity related to trophic competition. Annals of Botany 103: 1173–1186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Monod H, Naud C, Makowski D. 2006. Uncertainty and sensitivity analysis for crop models. In Wallach D, Makowski D, eds. Working with dynamic crop models: Evaluation, analysis, parameterization, and applications, 4 Elsevier; 55–100. [Google Scholar]
- Moon P, Spencer DE. 1942. Illumination from a non-uniform sky. Illuminating Engineering 37: 707–726. [Google Scholar]
- O’Connell MG, O’Leary GJ, Whitfield DM, Connor DJ. 2004. Interception of photosynthetically active radiation and radiation-use efficiency of wheat, field pea and mustard in a semi-arid environment. Field Crops Research 85: 111–124. [Google Scholar]
- Porter JR. 1985. Approaches to modelling canopy development in wheat. In Day W, Atkin RK, eds. Wheat growth and modelling. New York: Plenum Press, 69–81. [Google Scholar]
- Prusinkiewicz P, Lindenmayer A. 1990. The algorithmic beauty of plants. New York: Springer Science & Business Media. [Google Scholar]
- Quinlan JD, Sagar GR. 1962. An autoradiographic study of the movement of 14C-labelled assimilates in the developing wheat plants. Weed Research 2: 264–273. [Google Scholar]
- Rameau C, Bertheloot J, Leduc N, Andrieu B, Foucher F, Sakr S. 2015. Multiple pathways regulate shoot branching. Frontiers in Plant Science 5: 1–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sachs T, Novoplansky A, Cohen D. 1993. Plants as competing populations of redundant organs. Plant, Cell & Environment 16: 765–770. [Google Scholar]
- Sattin M, Zuin MC, Sartorato I. 1994. Light quality beneath field-grown maize, soybean and wheat canopies – red:far red variations. Physiologia Plantarum 91: 322–328. [Google Scholar]
- Simon JC, Lemaire G. 1987. Tillering and leaf area index in grasses in the vegetative phase. Grass and Forage Science 42: 373–380. [Google Scholar]
- Smith H. 1982. Light quality, photoperception, and plant strategy. Annual Review of Plant Physiology 33: 481–518. [Google Scholar]
- Smith H, Casal JJ, Jackson GM. 1990. Reflection signals and the perception by phytochrome of the proximity of neighbouring vegetation. Plant, Cell & Environment 13: 73–78. [Google Scholar]
- Sparkes DL, Holme SJ, Gaju O. 2006. Does light quality initiate tiller death in wheat? European Journal of Agronomy 24: 212–217. [Google Scholar]
- Tomlinson KW, O’Connor TG. 2004. Control of tiller recruitment in bunchgrasses: uniting physiology and ecology. Functional Ecology 18: 489–496. [Google Scholar]
- Vidal T, Boixel A-L, Durand B, de Vallaviaille-Pope C, Huber L, Saint-Jean S. 2017. Reduction of fungal disease spread in cultivar mixtures: impact of canopy architecture on rain-splash dispersal and on crop microclimate. Agricultural and Forest Meteorology 246: 154–161. [Google Scholar]
- Vos J, Evers JB, Buck-Sorlin GH, Andrieu B, Chelle M, de Visser PHB. 2010. Functional-structural plant modelling: a new versatile tool in crop science. Journal of Experimental Botany 61: 2101–2115. [DOI] [PubMed] [Google Scholar]
- Wei G, Rehmani MIA, Xiong J, Ding Y, Wang S. 2013. A simple tillering model for irrigated japonica rice based on measured relative SPAD for lower reaches of Yangtze River Delta, China. International Journal of Agriculture and Biology 15: 48–54. [Google Scholar]
- Xie Q, Mayes S, Sparkes DL. 2016. Optimizing tiller production and survival for grain yield improvement in a bread wheat × spelt mapping population. Annals of Botany 117: 51–66. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhong X, Peng S, Sheehy JE, Visperas RM, Liu H. 2002. Relationship between tillering and leaf area index: quantifying critical leaf area index for tillering in rice. The Journal of Agricultural Science 138: 269–279. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.