Abstract
Evolution is often deemed irreversible. The evolution of complex traits that require many mutations makes their reversal unlikely. Even in simpler traits, reversals might become less likely as neutral or beneficial mutations, with deleterious effects in the ancestral context, become fixed in the novel background. This is especially true in changes that involve large reorganizations of the organism and its interactions with the environment. The evolution of multicellularity involves the reorganization of previously autonomous cells into a more complex organism; despite the complexity of this change, single cells have repeatedly evolved from multicellular ancestors. These repeated reversals to unicellularity undermine the generality of Dollo's law. In this article, we evaluated the dynamics of reversals to unicellularity from recently evolved multicellular phenotypes of the brewers yeast Saccharomyces cerevisae. Even though multicellularity in this system evolved recently, it involves the evolution of new levels of selection. Strong selective pressures against multicellularity lead to rapid reversibility to single cells in all of our replicate lines, whereas counterselection favoring multicellularity led to minimal reductions to the rates of reversal. History and chance played an important role in the tempo and mode of reversibility, highlighting the interplay of deterministic and stochastic events in evolutionary reversals.
Keywords: Experimental evolution, historical contingency, multicellularity, natural selection, reversibility
The evolution of complex traits is often thought to be irreversible (Gould 1970), an observation known as Dollo's Law. The argument is that complex traits involving many genetic changes are unlikely to revert to their ancestral states because of the numerous genetic dependencies (Muller 1939; Gould 1970; Zufall and Rausher 2004). Even for simpler traits, adaptation to novel conditions might reduce the probability of reversal through the accumulation of neutral or beneficial mutations that have deleterious effects on the ancestral state (Bull and Charnov 1986). However, trait reversibility has been documented for complex traits (e.g., Wiens 2011), leading to questions about major directional trends and their underlying basis (Collin and Miglietta 2008; Goldberg and Igić 2008). In particular it has been proposed that the selective history of a complex trait might impede subsequent reversals (Zufall and Rausher 2004). For example, complex changes involving interactions between multiple genes or even cells (e.g., development) can result in complex changing adaptive landscapes, reducing the potential of reversibility (Bajić et al. 2018).
The origin of multicellularity is foundational in the evolution of biological complexity. It involves the evolutionary transition of single cells into larger and more complex organisms. Even in the evolution of relatively simple multicellularity, it opened up previously inaccessible avenues for adaptation, resulting in the exploitation and creation of new niches (Simpson 1944; Erwin 2008; Erwin et al. 2011; Rebolleda‐Gómez et al. 2016). Nevertheless, unicellular lineages have evolved from multicellular ancestors multiple times (Medina et al. 2003; Rossetti et al. 2010; Schirrmeister et al. 2011). And the potential for unicellular reversion is readily seen in the development of cancer, which requires changes from multicellular to unicellular organization (Aktipis et al. 2015; Chen et al. 2015; Tabassum and Polyak 2015). Questions of adaptation immediately come to mind: what are the ecological and evolutionary conditions favoring the disintegration of multicellular entities? What are the selective pressures maintaining multicellularity? Previous studies have suggested that intracellular conflict and other costs associated with increased size and local competition can lead to multicellular disintegration (Michod 1997; Rebolleda‐Gómez and Travisano 2018). These conflicts can be amplified by the accumulation of neutral mutations, facilitating reversibility to single cells in environments where multicellularity is not strongly favored. For example, the evolution of infectious cancers (where the fitness of the unicellular entity is independent of the multicellular organism) is favored by reduced genetic control due to strong bottlenecks in the Tasmanian devil (Miller et al. 2011) and increased probability of dispersal across bodies in both Tasmanian devils and dogs (Hamede et al. 2012; Strakova and Murchinson 2015). These factors reduce the ecological constraints for unicellular evolution regardless of their genetic architecture.
Does this mean that unicellular reversions are genetically unconstrained? The diversity of multicellular lineages itself suggests otherwise, that historical contingency critically affects multicellular evolution. The vast majority of multicellularity complexity has arisen from only three or four of the 25 independent multicellular transitions, and this signal of historical contingency may also be relevant to evolutionary dissolution of multicellularity. This is because the number and nature of the genetic changes required to evolve multicellularity in the first place might affect the probability of reversal to unicellularity (Muller 1939; Bull and Charnov 1986). In addition, the evolution of multicellularity involves a decoupling of fitness at the cell and multicellular levels (Buss 1987; Michod and Nedelcu 2003; Okasha 2005; Hammerschmidt et al. 2014) and the impact of multicellularity on its internal and external environment can readily change the effects of previous traits or novel mutations (Erwin 2008; Erwin et al. 2011; Newman and Baht 2009; Rebolleda‐Gómez et al. 2016). Therefore, adaptations at the multicellular level often come with a cost for single cells, and genetic changes in the multicellular environment are likely to be neutral or have deleterious effects for single cell living. These processes can entrench a multicellular state and reduce the probability of reversals over time (Libby and Ratcliff 2014).
We tend to think of these transitions as discrete processes (e.g., from unicellularity to multicellularity and back again), instead, it is likely that relative importance of selection at different levels changes over time, as the organization and interaction between cells changes. Selection, chance, and history are all likely to contribute to the reversibility of multicellularity, but their relative importance is still debated and might change during the transition itself. Strong selective pressures and high population sizes, for example, could overwrite the role of history and chance (Vermeij 2006). Even in these cases, history and chance might be important for the dynamics of these transitions, shaping the tempo (rates), and mode (patterns and processes) of reversibility. However, these evolutionary dynamics are often hard to study because cases of reversal are relatively rare and often highly derived. In this article, we evaluate the relative roles of selection, chance, and history on experimental evolution of reversals to unicellularity from incipient multicellular phenotypes of the brewer's yeast Sacharomyces cerevisiae.
These multicellular phenotypes evolved as a consequence of a selection experiment favoring an increase in size (Ratcliff et al. 2012). Ten out of the ten replicate populations evolved multicellular phenotypes through incomplete separation of mother and daughter cells after cell division. In previous work, we have shown that, in spatially structured environments where resources are localized, these multicellular phenotypes pay a large cost in fitness when compared to their unicellular ancestor and that evolution in this environment leads to rapid reversals to unicellularity (Rebolleda‐Gómez and Travisano 2018). Thus, in this system strong selection against multicellularity can overcome the effects of chance and history, leading to convergent reversals to unicellularity.
We hypothesized that adaptation would play an important role in the first steps of reversibility, but as the population adapts, and the strength of selection is reduced, we would expect to see the effects of chance. In addition, if genetic architecture is an important determinant of reversibility then, history would affect the dynamics of reversibility. Finally, we expected that opposing selection could lead to decreased rates of reversal and, at the same time, increase the contribution of genetic background due to differences in trade‐offs across selective pressures (Rodríguez‐Verdugo et al. 2014). In particular, we expected that exposure to ultraviolet radiation would select against single‐cells because, on average, cells in a multicellular group would be more protected. This kind of selection favoring protection within a group can reduce the effectiveness of selection in purging mutations with small deleterious effects at the cellular level (due to reduced effective population sizes, and differences in fitness effects of mutations at the cellular and multicellular level). In addition, ultraviolet radiation is a powerful mutagen, increasing the number of mutations that can accumulate at the cellular level and thus, the role of chance. These same processes of mutation accumulation might override the effects of previous changes, reducing the contribution of history. To evaluate these hypotheses, in this article, we examine the tempo and mode of evolution of reversals to unicellularity, and the interactions between history, chance, and adaptation in shaping these dynamics.
Methods
STRAINS AND MEDIA
The strains used in this study were (1) ten multicellular phenotypes of Sacharomyces cerevisiae evolved in the laboratory as a result of a selection experiment favoring larger sizes (Ratcliff et al. 2012) and (2) their shared unicellular ancestor, the diploid strain Y55. In that experiment, a single clone of the brewer's yeast Sacharomyces cerevisiae Y55 was used to initiate 10 replicate populations. Each day, for 60 days, each of these populations was exposed to settling selection, transferring only the first fraction to settle (favoring larger sizes). After 60 days, all populations had evolved multicellular phenotypes through incomplete separation of mother and daughter cells (Ratcliff et al. 2012). One single clone isolate of each of the populations was randomly selected for this experiment, representing a wide range of multicellular sizes (for isolation procedures see Rebolleda‐Gómez et al. 2012). Yeast isolates were grown in YPD (1% yeast extract; 2% peptone and 2% dextrose) or YPD with 15% agar for the plates. Cultures were incubated at 30°C.
SELECTION EXPERIMENT
To evaluate the roles of history (i.e., genetic background), chance, and adaptation in the dynamics of reversibility to unicellularity we performed a selection experiment on a structured environment (agar plates) in which we expect multicellularity to be maladaptive. In this environment, the larger a multicellular cluster, the larger the costs associated with local competition and access to resources, and thus, we readily observe reversals to unicellularity (Rebolleda‐Gómez and Travisano 2018). We propagated in batch‐culture each of ten multicellular strains of S. cerevisiae in three replicate plates with YPD agar (for a total of 30 plates). Every 24 hours, we resuspended each culture in 1 mL of saline solution (0.85% NaCl). These cultures were then diluted fourfold. We then plated 20 of these dilutions on a new YPD plate (for a total effective dilution of 1:200). As described in Travisano et al. (1995), changes in the cluster‐size grand mean (across all populations), would indicate adaptation (or changes due to selection on this spatially structured environment). Whereas variation in the derived cluster size among lines of different ancestral background would indicate the importance of history (or genetic background). Finally, differences within each ancestral line (among replicates) would indicate the importance of stochastic processes on the evolution of reversals to unicellularity (Fig. 1).
Figure 1.
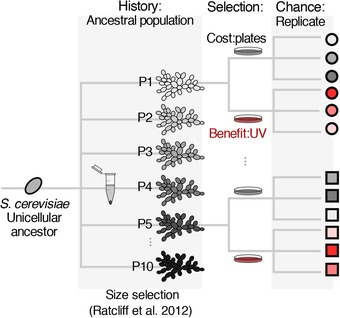
Diagram of the experimental design. To evaluate the role of history (or ancestral genetic background) we started lineages from ten different multicellular ancestors and transferred them every day on plates for a total of 30 transfers. From each of these ancestral lineages, we started three replicate lines to address the role of chance, and we evaluate the role of adaptation as the directional change in phenotypes. The effect of counterbalance selection forces was determined by exposing lines derived from the first five ancestral strains to 16 seconds of UV between transfers (In shades of gray are strains not exposed to UV and in red strains exposed to UV; see Methods for details).
COUNTERBALANCING SELECTION
We were interested in how trade‐offs between benefits at different levels (i.e., selection to maintain multicellularity vs. selection favoring growth of single cells) would change the dynamics of adaptation. We hypothesized that as a result of a larger multicellular size—more specifically a smaller surface area to volume ratio—cells of multicellular individuals will be more likely to survive exposure to UV light than the same number of unicellular individuals and that this might provide a counterbalance to the costs of multicellularity. To evaluate this hypothesis, we determined the percent of survival of several yeast strains along a gradient of UV light exposure. We grew ten multicellular isolates of different sizes and five unicellular isolates overnight in 10 mL of YPD in triplicate. Then, we plated them to varying dilutions depending on the average density of colony forming units (CFUs) for each strain and their survival. We exposed all the plates facing down and without lid to 0, 7, 14, 21, or 28 seconds of UV in a transilluminator (8 watt, 302 nm) and let the plates grow for 24 h at 30°C. Finally, we calculated survival as the proportion of CFUs per mL relative to the control plates. We fitted an exponential decay function of survival over time () starting from S 0 = 100% survival. Then, we evaluated the importance of differences between multicellular versus unicellular isolates in survival through a likelihood ratio test of a simpler model (excluding phenotype as a factor) and the complete model (including phenotype) (Ritz and Streibig 2008).
To evaluate the importance of selection and the change in dynamics with counterbalancing selective pressures, we started 15 additional lines (five multicellular isolates as ancestors with three replicate lines each—for the ancestors we chose those from populations 1–5 given that the numbering of populations was assigned randomly). We followed the same selection procedure with these 15 lines, except that, after plating our diluted culture we placed these plates facing down and without lid in a UVP LM‐20 transilluminator for 16 seconds at high intensity (302 nm, 6000 μW/cm). Samples from each replicate were frozen at 80°C in 20% glycerol every week (Fig. 1). Directional responses to either selective environment (either just plates or plates and UV) allowed us to evaluate the role of adaptation in each of those environments. Differences between environments allowed us to evaluate the effect of UV alone (after accounting for selection on spatially structured environments).
POPULATION SIZE OVER TIME
To determine the size distributions of each culture over time, we measured the size of samples from all the time points and all of the replicates. To compare UV and Non‐UV lines we only measured changes in size of half of the lines (those from the five multicellar ancestors used to start the UV lines). To measure size of all the individuals within each of our samples, we used a liquid flow through a microscope with a camera and a laser particle detection system (FlowCam‐Fluid Imaging Technologies). Before measurements, we grew the strains for 24 h of conditioning in YPD. Then, we transferred 10 μL of each culture into 10 mL of fresh YPD and let them grow again for 24 h. For the measurements, we diluted each of the samples 10‐fold in saline solution. One milliliter of each sample was run through the FlowCam using a 10X objective and a C70 syringe. The areas of all the clusters measured were recorded and air‐bubbles or other particles in the media were removed with circularity and size filters calibrated manually. To maintain consistency, the same settings and filters were used for all the samples.
DATA ANALYSIS
Differences in size distributions between treatments, isolates, and replicates were evaluated with a general linear model with time (as a continuous variable), treatment (UV or not), and ancestral population as the main factors. For our random effects we allowed our intercepts and slopes to vary with replicate nested within population, allowing for correlations through time (as repeated measures model). Because we captured images with a volume (not a number) limit, our sample size for populations with high frequency of single cells were orders of magnitude larger than our initial samples. To minimize the effects of this unbalanced design and constrain the size of our data frame (n = 20,405,616 observations) we resampled a number equal to the length of our smallest sample (n min = 735) for each of our samples to finish with (n small = 29,400) observations. With log transformation of the cluster area our residuals were approximately normally distributed. However, as time increases the variance rapidly decreases (Fig. S1). To correct for this heteroscedasticity we modeled the variance as an exponential function of time (Pinhero and Bates 2000) using the lme function from the nlme package (version 3.3.1–131, Pinheiro et al. 2017) in R (R version 3.4.3, R Core Team 2017). We chose this model because it minimized heteroscedasticity (Fig. S2), had the lowest AIC values and was a significantly better model for our data according to a log likelihood ratio test (Table S1).
To calculate the relative contributions of adaptation (UV and non‐UV), history (ancestral population), and chance (replicate populations) as proposed in Travisano et al. (1995), we used a simpler model (ancestral population and replicate nested within population as random factors) separately for each of the time points and for the different treatments (UV and no UV). Given that we analyzed separately each time point and environment, we were able to use the complete dataset for these analyses. The roles of history and chance were calculated as the square root of the variance among populations, or among replicates within populations, respectively. We calculated the confidence intervals for these parameters through bootstrapping with 1000 samples per estimate. The contribution of adaptation in each environment at each time point (tn) was calculated as the difference in grand means of tn and tn‐1 instead of always calculating against the ancestral values at t0. The magnitude of the response to UV selection alone was calculated as the difference between the grand means of “UV” and “no UV” treatments at each time point. In this way, we could calculate the relative contributions of ancestral background (“history”), stochastic variation across replicates (“chance”), and overall directional changes in particle size (“adaptation”) within each environment (avoiding potential changes in the adaptive landscape across environments). Then, comparing both treatments we were able to compare the magnitudes of the adaptation component across environments.
Results
To evaluate the role of adaptation, history, and chance in reversals to unicellularity from a recently evolved multicellular ancestor, we evolved 45 lines derived from different multicellular ancestors on a spatially structured environment (in which we expected multicellularity to be costly). To evaluate the role of history (or ancestral genetic background) we started lineages from ten different multicellular ancestors (in the case of the no‐UV treatment) and five (in the case of the UV treatment). From each of these ancestral lineages, we started three replicate lines to address the role of chance, and we evaluate the role of adaptation as the directional change in phenotypes. The effect of counterbalancing selection forces was evaluated by comparing the UV and non‐UV treatments.
CONVERGENCE IN REVERSIBILITY
After ∼200 generations, all of our 45 lines were dominated by unicellular phenotypes. On plates, all of the populations had exclusively small smooth “unicellular‐looking colonies” (Fig. 2A–B). However, plates overestimate the frequency of unicellular phenotypes because (1) very small multicellular isolates form smooth colonies indistinguishable from their unicellular counterparts and (2) multicellular isolates at very low frequencies are often not‐sampled on plates. Thus, to get a better estimation of the frequency of single cells and the temporal evolutionary dynamics, we took pictures and measured the size of every individual in 1 mL of sample for half of our lines at every time‐point (from the first five ancestors to compare with the UV treatment; see Methods).
Figure 2.

Rapid reversibility to unicellularity on plates (spatially structured environment). (A) Picture of multicellular (big and rugged) and unicellular (smooth) colonies. (B) Percentage of unicellular (smooth) colony forming units (CFUs). Each point is the mean value the three replicate lines of each ancestral background. In solid gray are those populations that we used for future analyses. (C) Distribution of sizes over time of each of the replicate lines (different shades of gray) of the ancestral populations 1 and 4.
All of our lines showed a decrease in median size over time, converging to a median size of (M = 54.03 μm2, SD among lines = 4.16 μm2; Fig. 2C; Fig. S3). This reduction of size is due to a decrease in multicellular size and a rapid increase in frequency of single cells (from 23 ± 3% SE at time 0 to 89 ± 1.3% SE after 30 transfers; Rebolleda‐Gómez and Travisano 2018; Fig. S4). Changes in size occur at a fast rate in all of the populations (a reduction in size of ∼25% in a week). These changes in size were largely due to an increase in frequency of single cells with unicellular phenotypes being dominant (frequency >50%) in all populations by 11 days (∼73 generations). This rapid change and high degree of phenotypic convergence is consistent with previous results showing a high cost of multicellularity due to increased local competition in structured environments (i.e., solid agar plates; Rebolleda‐Gómez and Travisano 2018).
EFFECT OF COUNTERBALANCING SELECTION FORCES
To evaluate the importance of selection for evolutionary reversals to unicellularity, we exposed different multicellular isolates to varying periods of UV radiation. Of the possible stresses often encountered by microorganisms (e.g., nutrient limitation, extreme temperatures, desiccation, toxins, salinity, and UV radiation), we selected UV radiation because it is easy to manipulate, imposes strong selection, and our isolates vary in their response to this environmental factor (Fig. 4).
Figure 4.
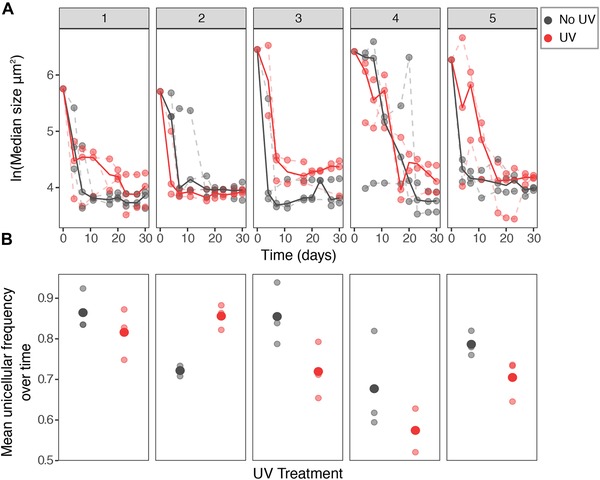
Dynamics of reversal to unicellularity. Different panels show different ancestral populations. (A) Graphs of median size over time. Solid circles indicate different replicate lines (n = 3) and solid lines the mean trajectory. Although all populations converge to unicellular phenotypes the mode and tempo of evolution differs between populations and even within replicate lines of the same population. (B) Except in population two, populations in the UV treatment have in average a lower frequency of unicellular individuals over the course of the experiment. There is substantial variation between and within ancestral backgrounds (populations).
We hypothesized that group formation would be beneficial and increase survival against UV radiation because internal cells would be protected against UV exposure (stresses like temperature or alcohol concentration might not create a strong gradient). In this way, the dynamics of UV protection should be dependent on the relation between surface area and volume in these clusters. In agreement with our expectations, multicellular isolates are more resistant to the effects of UV radiation than unicellular ones (the effect of phenotype is significant as compared by likelihood ratio test, F 1,209 = 4749.5, P < 0.00001). Unicellular isolates have a decay rate more than 1.5 greater than their multicellular counter‐parts (λmulticellular = 0.137 ± 0.006 s−1 SE and λunicellular = 0.227 ± 0.018 s−1 SE; Fig. 3). By 16 seconds of exposure to radiation, almost no single cell survives while large multicellular isolates still have a survival of ≈20% (Fig. 3).
Figure 3.
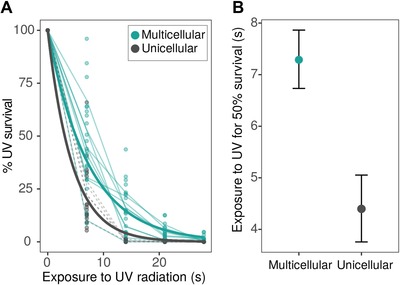
Survival curves in response to different exposure times to UV radiation. In general multicellular clusters are more resistant to UV radiation (solid turquoise) than their unicellular counterparts (dashed black) with the exception the smallest multicellular isolate (at the bottom, overlapping with the unicellular curves). (A) Each line represents the dynamics of a different isolate and was calculated as the mean value between three replicates. The thick lines are fitted exponential decay curves. (B) Estimates of half‐life (1/λ) or UV exposure time by which survival is 50% and their 95% confidence intervals.
This result could be due, as we had expected, to cells being protected by surrounding layers of cells, or because in a multicellular cluster only one cell has to survive for the whole cluster to survive. However, after 16 seconds of UV exposure, we observed, for most unicellular replicates, no colonies growing in the plate—even at 10‐times the cell density of multicellular plates. Moreover, small multicellular isolates (where we would expect all cells to be exposed to the radiation) had lower survival than their unicellular counterparts (Fig. 3).
Based on these observations we transferred three replicate populations from each of the five ancestral isolates together with our control lines, exposing the plates to 16 seconds of UV radiation after each transfer (Fig. 1). We observed rapid evolution of unicellular reversals, despite the strong benefits of multicellularity under UV exposure. As a result, the effect of UV on the intercept is not significant (“UV treatment” in Table 1), nor is the difference in rates due to treatment (“UV by time” in Table 1). However, populations differ in the effect of UV and in the rate of this change (Table 1). In all backgrounds, except ancestral population 2, the average frequency of single cells over the course of the experiment is lower (but not significant overall) in the UV treatments (Fig. 4). Similarly, in all backgrounds, except ancestral population 4, the estimated rate of reversal is lower in UV populations (Fig. 5A).
Table 1.
Generalized linear least squares model with variance weights as an exponential function of time (see Methods)
| Value | Std. error | DF | t‐value | P‐value | |
|---|---|---|---|---|---|
| (Intercept) | 4.946679 | 0.10617942 | 29370 | 46.58793 | 0 |
| Treatment.1UV | 0.088749 | 0.06434876 | 29370 | 1.37919 | 0.1678 |
| Time | –0.042782 | 0.00200905 | 29370 | –21.29444 | 0 |
| Population2 | 0.145513 | 0.09660227 | 8 | 1.50631 | 0.1704 |
| Population3 | 0.552997 | 0.09254791 | 8 | 5.97526 | 0.0003 |
| Population4 | –0.336568 | 0.11816417 | 8 | –2.84831 | 0.0215 |
| Population5 | 0.246886 | 0.09581923 | 8 | 2.57658 | 0.0328 |
| Treatment:Time | 0.00526 | 0.00271833 | 29370 | 1.93485 | 0.053 |
| Treatment:Population2 | –0.385574 | 0.08971347 | 29370 | –4.29784 | 0 |
| Treatment:Population3 | 0.185787 | 0.08134729 | 29370 | 2.28388 | 0.0224 |
| Treatment:Population4 | 0.477074 | 0.13458938 | 29370 | 3.54466 | 0.0004 |
| Treatment:Population5 | –0.052092 | 0.09165858 | 29370 | –0.56832 | 0.5698 |
| Time:Population2 | 0.003035 | 0.0027904 | 29370 | 1.0878 | 0.2767 |
| Time:Population3 | –0.017496 | 0.00260594 | 29370 | –6.71372 | 0 |
| Time:Population4 | 0.016281 | 0.00374319 | 29370 | 4.34962 | 0 |
| Time:Population5 | 0.001507 | 0.0027632 | 29370 | 0.54543 | 0.5855 |
| Treatment:Time:Population2 | 0.002514 | 0.00383924 | 29370 | 0.6549 | 0.5125 |
| Treatment:Time:Population3 | –0.001499 | 0.0034984 | 29370 | –0.42857 | 0.6682 |
| Treatment:Time:Population4 | –0.012051 | 0.00525268 | 29370 | –2.29433 | 0.0218 |
| Treatment:Time:Population5 | –0.003729 | 0.00385889 | 29370 | –0.96634 | 0.3339 |
Log transformed area is the response variable, treatment (UV or no UV), ancestral population (history), and replicate (chance, modeled as a nested random factor allowing for time autocorrelation). Time was modeled as a continuous covariate.
Figure 5.
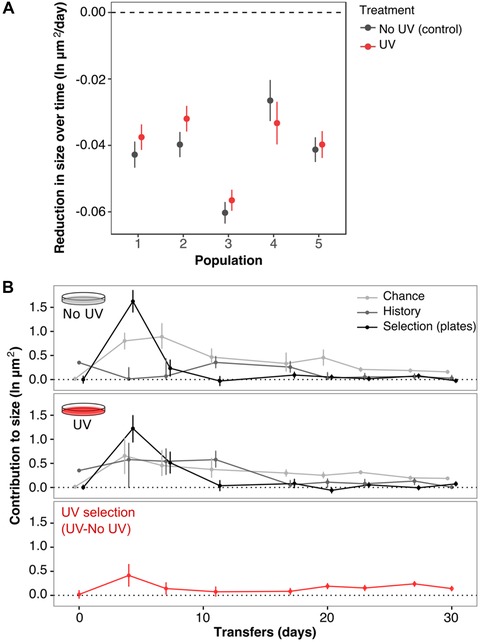
Relative roles of chance, history and selection. (A) Estimated marginal means of the reduction in size over time for lineages with different ancestral backgrounds (Population) exposed to different treatments (UV of control). (B) Contributions of chance (square root of variance among replicates, within populations), history (square root of variance among populations), and selection (difference in grand means, plates: Tn‐Tn‐1, UV: No UV‐UV) to changes in size throughout the experiment. Initially, selection acts strongly on size and small individuals are favored. As individuals become smaller, the contribution of selection decreases and the effects of chance and history are more evident. Error bars are 95% confidence intervals obtained through bootstrap (1000 samples for each point).
EVOLUTIONARY DYNAMICS AND THE IMPORTANCE OF CHANCE AND HISTORY
Despite a high degree of convergence between populations (and across treatments), and a clear effect of selection on size reduction, we still observed a high degree of variation in the tempo and mode of evolution. Different populations displayed different patterns of reversal (i.e., going directly from multicellular isolates to single cells vs. a more gradual reduction in size) and differences in the prevalence of multicellular individuals over time (Rebolleda‐Gómez et al. 2016; Figs. 4 and 5, Fig. S3). This variation is explained by the effect of history (ancestral source) as well as chance (variation among replicate lineages of the same ancestor) on the overall effect, as well as the tempo of reversals (interactions with time in Table 1) (Figs. 4 and 5). Although there is strong selection for a reduction of size, this reduction varies substantially among replicates within each population and among populations (Fig. 4 and 5B). Consistently, we observed significant differences across populations and their rates of change (“Population by Time interactions”, Table 1, Fig. 5A).
The contributions of adaptation, history, and chance to changes in size varied over the course of the experiment. After eleven days there was no significant overall change in size (Selection component is no different than 0; Fig. 5B). History contributed to differences in size from day eleven to the seventeenth transfer (contribution of history in No UV populations, Fig. 5B). The rate of reversal to unicellularity is slower in the population with a more continuous reduction in size (i.e., ancestral population 4, Fig. 5), with consistent larger sizes up to the twentieth transfer (Fig. 2C, Fig. 4A, Fig. S4). After twenty days all replicates and all populations have functionally reverted to single cells and variation between replicates is due to stochastic variation in the frequency and size of very small multicellular individuals (2–4 cells) (contribution of chance Fig. 5B).
Contrary to our expectations, the role of history was slightly more important in those populations exposed to UV, where the selective effects of the first changes (in terms of reduction of size) are partially counteracted by UV selection (Fig. 5B). This counteracting effect is dependent on genetic background (different populations). As a result, only population background (F4,19 =7.724, P = 0.0007) and the UV by population interaction (F4,19 = 3.92, P = 0.017) are significant when comparing the average frequency of single cells over the whole course of the experiment (Fig. 4B). Despite a probably increase in mutation rate, we did not observe differences in the contribution of chance across treatments, if at all, chance seems to contribute less to differences in size in UV exposed lines (Fig. 5B). In both treatments (UV and no UV) these results highlight the importance of different evolutionary processes (mode) in evolutionary rates (tempo).
Discussion and Conclusions
We have shown that costs of multicellular growth on spatially structured environments (Rebolleda‐Gómez and Travisano 2018) lead to high convergence in reversibility to unicellularity. However, history and chance play an important role in the rates of reversal. Whereas, counteracting selection favoring multicellularity had an insignificant effect on reversibility but increased the relative contribution of history.
Tracing the mode and tempo of evolution can provide insights into the evolutionary dynamics involved during this transition (Simpson 1944; Smith and Goldberg 2015) and provide clues into the topography of the adaptive landscape (e.g., Nahum et al. 2015). In this experiment, as populations adapt and multicellular clusters become rarer and smaller, selection becomes weaker and the role of chance more important. This result suggests a relatively flat peak, where many close phenotypes have a similar fitness value. Similarly, the early contributions of history suggest some ruggedness, with some populations being able to revert faster than others. In this case, history (genetic background) has a large effect on the first phenotypic changes, shaping the rate of reversibility from a more gradual versus a more discrete transition. For example, lines derived from population four led to a more gradual transition, with multicellular isolates persisting over a longer period of time. This effect was especially clear when there are opposing selection forces at work (UV vs. the cost of competition in spatially structured environments). In population five, UV and No‐UV lines follow a very distinct trajectory of reversibility. Non‐UV lines rapidly revert to multicellularity, whereas UV lines have a more gradual reversal trajectory (although this varies by replicate), similar to those of population four.
In this experiment, we used UV radiation as a counter‐acting selective pressure (one that would favor multicellularity over unicellularity). However, UV radiation also has severe mutagenic effects, potentially affecting not only the selective environment but the availability of variation. It is possible that increased variation at the cellular level could undermine the strength of selection at the multicellular level (Michod 1997; Okasha 2005), potentially explaining why we did not observe a strong effect of UV in slowing (or preventing) reversibility to unicellularity, or why we even observed the opposite effect in lines from population 2 (the smallest multicellular isolates in at the start). We expected that increased mutation rates would increase the role of chance and potentially overwrite the effects of the ancestral background. Instead, we observed no difference in the contributions of chance in the two different environments and the effect of history was stronger in the UV environment.
It is possible that our results are a combination of a change in the adaptive landscape in the new environment, changes in the relative strength of selection at different levels (multicellular and unicellular) with changes in size, and increased mutation rates. For example, different genetic backgrounds might affect the distribution of fitness effects of new mutations, potentially increasing the contribution of history with increased mutation loads. While increased mutations allow for a faster exploration of the adaptive landscape, if previous mutations changed the landscape (DeVos et al. 2018) then this exploration might take diverging routes. In the case of multicellular evolution, for example, the multicellular context could affect the mechanism of reversal and the effect of mutations for the cell. Increased knowledge of the genetic architecture of, not only the multicellular ancestors, but the unicellular descendants, as well as the fitness consequences of important mutations in different ancestral backgrounds can provide an answer to some of these questions. In a similar experiment, Kuzdzal‐Fick et al., found that in a haploid strain of yeast, reversibility to unicellularity was due (in most cases) to mutations in the same locus (AMN1), however, these lines were all descendent from the same small multicellular ancestor. It is still an open question if, as cells adapt to their multicellular context, their probability and mechanisms of reversal change, and in which ways.
Despite its relatively simple genetic basis in this case (Ratcliff et al. 2015), the evolution of multicellularity leads to increased ecological complexity; it changes the organization of cells affecting the internal (Newman and Bhat 2009; Gavrilets 2010) and external environment of the cells (Erwin 2008; Erwin et al. 2011; Rebolleda‐Gómez et al. 2016). These interactions between genetic changes and the environmental context can have an important effect on the evolution of complex innovations (Burmeister et al. 2016). The genetic architecture of a trait and the genetic basis for its reversal, as well as the interactions of these changes with the environment will shape the reversibility and the robustness of a trait. Slower and more gradual dynamics of reversal could maintain a complex and costly trait until compensatory mutations evolve. In the case of the evolution of costly antibiotic resistance, for example, reversals are often slow enough that compensatory mutations can arise, preventing the reversibility of resistance (Levin et al. 2000). Understanding not only the outcomes of reversals, but the tempo and mode of these changes provide insight into the architecture of a trait and could aid in the prediction of future changes.
Consistent with our results, experiments on the reversibility of different life‐history traits in Drosophila have shown that in the short term (50 generations) reversibility is highly contingent on previous history and that the importance of history and rate of reversal depend on the trait in question (Teotónio and Rose 2000). In contrast, other microbial experiments have shown that strong selection can overwrite the role of history (Travisano et al. 1995; Tenaillon et al. 2012), leading to a high convergence of reversals with relatively simple traits, high population sizes, and strong selective pressures. History and chance are more likely to play a role in traits with a weak impact on fitness (Travisano et al. 1995; Losos 2018). In this case, the initial steps involve a change of organization and a reversal of the ecological role of cells (from part of a larger whole to autonomous units capable of growth and reproduction of their own). These changes depend on the particular organization and interactions between cells in the multicellular organism, in the same way, that the origins of multicellularity are highly contingent on the cellular machinery already present (Rokas 2008; Niklas and Newman 2013; Sebé‐Pedrós et al. 2017). History matters in this first steps. However, the ecological costs of multicellularity are high and reversal to unicellularity occurred rapidly in all of our populations.
Major evolutionary changes are often deemed irreversible (Gould 1970; Bull and Charnov 1985) due to a low probability of the same series of changes occurring in reverse, or due to genetic constraints that arise through evolutionary change (Muller 1939; Bull and Charnov 1985). If the evolution of a trait was contingent on the order of mutations (e.g. Blount et al. 2008), then the probability of reversal might be low. History, chance, and time can all play a role in the evolution of reversibility (Muller 1939; Bull and Charnov 1985). Thus, understanding the dynamics of evolutionary reversals can highlight important aspects of the constraints involved in the evolution of complex traits.
Associate Editor: T. Cooper
Handling Editor: M. R. Servedio
Supporting information
Table S1. Summary of model comparisons.
Figure S1. Variance in size and the natural logarithm of this variance against time.
Figure S2. Plots testing normality (q‐q plot) and heteroscedasticity (fitted values vs. residuals) for the ANCOVA and the generalized linear least squares model (GLS) with variance weights modeled as an exponential function of time.
Figure S3. Distribution of sizes over time of each of the replicate lines (different shades of gray) of all of the populations in the control (upper panels) or UV (lower panels).
Figure S4. Changes in multicellular phenotypes over time.
Supporting Information
JOURNAL CLUB SLIDES
Journal club slides available at https://doi.org/10.6084/m9.figshare.7418441.v1.
AUTHOR CONTRIBUTIONS
M.R.G. and M.T. designed the experiments. M.R.G. conducted the experiments and analyzed the data with input from M.T. M.R.G. wrote the manuscript with substantial contributions from M.T.
ACKNOWLEDGMENTS
We would like to thank Emilie Snell‐Rood, Ruth Shaw, Alan Love, and Melanie Bowman for their feedback and thoughtful comments. This work was developed as part of MRG doctoral dissertation with support from ICGC as well as the IDF and DDF fellowships from the graduate school at the University of Minnesota. M.T. is funded by the John Templeton Foundation. This work was supported by NSF grant DEB‐1051115. The authors have no conflicting interests to declare.
DATA ARCHIVING
The doi for our data is https://doi.org/10.5061/dryad.b2s0dt4.
LITERATURE CITED
- Aktipis, C. A. , Boddy A. M., Jansen G., Hibner U., Hochberg M. E., Maley C. C., and Wilkinson G. S.. 2015. Cancer across the tree of life: cooperation and cheating in multicellularity. Philos. Trans. R. Soc. B. 370:201402219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bajic, D. , Vila J. C. C., Blount Z. D., and Sanchez A.. 2018. On the deformability of an empirical fitness landscape by microbial evolution. PNAS 115:11286–11291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blount, Z. D. , Borland C. Z., and Lenski R. E.. 2008. Historical contingency and the evolution of a key innovation in an experimental population of Escherichia coli . PNAS 105:7899–7906. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bull, J. J. , and Charnov E. L.. 1985. On irreversible evolution. Evolution 39:1149–1155. [DOI] [PubMed] [Google Scholar]
- Burmeister, A. R. , Lenski R. E., and Meyer J. R.. 2016. Host coevolution alters the adaptive landscape of a virus. Proc. R Soc. Lond. B 283:20161528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buss, L. W. 1987. The evolution of individuality. Princeton Univ. Press, Princeton, NJ. [Google Scholar]
- Chen, H. , Lin F., Xing K., and He X.. 2015. The reverse evolution from multicellularity to unicellularity during carcinogenesis. Nat. Comm. 6:6367. [DOI] [PubMed] [Google Scholar]
- Collin, R. , and Miglietta M. P.. 2008. Reversing opinions on Dollo's Law. Trends. Ecol. Evol. 23:602–609. [DOI] [PubMed] [Google Scholar]
- De Vos, M. G. J. , Schoustra S. E., and De Visser J. A. G. M.. 2018. Ecology dictates evolution? About the importance of genetic and ecological constraints in adaptation. Epl. 122 10.1209/0295-5075/122/58002. [DOI] [Google Scholar]
- Erwin, D. H. 2008. Macroevolution of ecosystem engineering, niche construction and diversity. Trends. Ecol. Evol. 23:304–310. [DOI] [PubMed] [Google Scholar]
- Erwin, D. H. , Laflamme M., Tweedt S. M., Sperling E. A., Pisani D., and Peterson K. J.. 2011. The Cambrian Conundrum: Early Divergence and Later Ecological Success in the Early History of Animals. Science 334:1091–1097. [DOI] [PubMed] [Google Scholar]
- Erwin, D. H. , and Tweedt S.. 2012. Ecological drivers of the Ediacaran‐Cambrian diversification of Metazoa. Evol. Ecol. 26:417–433. [Google Scholar]
- Gavrilets, S. 2010. Rapid transition towards the Division of Labor via evolution of developmental plasticity. PLoS Comput. Biol. 6:e1000805. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldberg, E. E. , and Igić B.. 2008. On phylogenetic tests of irreversible evolution. Evolution 62:2727–2741. [DOI] [PubMed] [Google Scholar]
- Gould, S. J. 1970. Dollo on Dollo's law: irreversibility and the status of evolutionary laws. J. Hist. Biol. 3:189–212. [DOI] [PubMed] [Google Scholar]
- Hamede, R. K. , McCallum H., and Jones M.. 2012. Biting injuries and transmission of Tasmanian devil facial tumour disease. J. Anim. Ecol. 82:182–190. [DOI] [PubMed] [Google Scholar]
- Hammerschmidt, K. , Rose C. J., Kerr B., and Rainey P. B.. 2014. Life cycles, fitness decoupling and the evolution of multicellularity. Nature 515:75–79. [DOI] [PubMed] [Google Scholar]
- Pinheiro, J. P. , Douglas B., Saikat D., Deepayan S., and R Core Team . 2017. nlme: linear and nonlinear mixed effects models. Retrieved from https://cran.r-project.org/package=nlme.
- Kuzdzal‐Fick, J. , Chen L., and Balazsi G.. 2016. Evolutionary trade‐offs between unicellularity and multicellularity in budding yeast. bioRxiv. 347609 10.1101/347609. [DOI] [Google Scholar]
- Levin, B. R. , Perrot V., and Walker N.. 2000. Compensatory mutations, antibiotic resistance and the population genetics of adaptive evolution in bacteria. Genetics 154:985–997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Libby, E. , and Ratcliff W. C.. 2014. Ratcheting the evolution of multicellularity. Science 346:426–427. [DOI] [PubMed] [Google Scholar]
- Lin, H. , Kazlauskas R. J., and Travisano M.. 2017. Developmental evolution facilitates rapid adaptation. Sci. Rep. 111:7:15891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Losos, J. B. 2008. Improbable destinies: fate, chance, and the future of evolution. Riverhead books, NYC, NY. [Google Scholar]
- Medina, M. , Collins A. G., Taylor J. W., Valentine J. W., Lipps J. H., Amaral‐Zettler L., and Sogin M. L.. 2003. Phylogeny of Opisthokonta and the evolution of multicellularity and complexity in Fungi and Metazoa. International Journal of Astrobiology 2:203–211. [Google Scholar]
- Michod, R. E. 1997. Cooperation and conflict in the evolution of individuality. I. Multilevel selection of the organism. Am. Nat. 149:607–645. [Google Scholar]
- Michod, R. E. , and Nedelcu A. M.. 2003. On the reorganization of fitness during evolutionary transitions in individuality. Integr. Comp. Biol. 43:64–73. [DOI] [PubMed] [Google Scholar]
- Miller, W. , Miller W., Hayes V. M., Ratan A., Petersen D. C., Wittekindt N. E., Miller J., Walenz B., Knight J., Qi J., et al. 2011. Genetic diversity and population structure of the endangered marsupial Sarcophilus harrisii (Tasmanian devil). PNAS 108:12348–12353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muller, H. J. 1939. Reversibility in evolution considered from the standpoint of genetics. Biol. Rev. 14:261–280. [Google Scholar]
- Nahum, J. R. , Godfrey‐Smith P., Harding B. N., Marcus J. H., Carlson‐Stevermer J., and Kerr B.. 2015. A tortoise–hare pattern seen in adapting structured and unstructured populations suggests a rugged fitness landscape in bacteria. PNAS 112:7530–7535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Niklas, K. J. , and Newman S. A.. 2013. The origins of multicellular organisms. Evol. Dev. 15:41–52. [DOI] [PubMed] [Google Scholar]
- Newman, S. A. , and Bhat R.. 2009. Dynamical patterning modules: a “pattern language” for development and evolution of multicellular form. Int. J. Dev. Biol. 53:693–705. [DOI] [PubMed] [Google Scholar]
- Okasha, S. 2005. Multilevel selection and the major transitions in evolution. Philos. Sci. 72:1013–1025. [Google Scholar]
- R Core Team . 2017. R: a language and environment for statistical computing. Vienna, Austria: Retrieved from https://www.r-project.org/. [Google Scholar]
- Ratcliff, W. C. , Denison R. F., Borrello M., and Travisano M.. 2012. Experimental evolution of multicellularity. PNAS 109:1595–1600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff, W. C. , Fankhauser J. D., Rogers D. W., Greig D., and Travisano M.. 2015. Origins of multicellular evolvability in snowflake yeast. Nat. Comm. 6 6102 10.1038/ncomms7102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rebolleda‐Gomez, M. , Ratcliff W., and Travisano M.. 2012. Adaptation and divergence during experimental evolution of multicellular Saccharomyces cerevisiae . in Adami C., Bryson D. M., and Pennock R. T., eds. Artificial life 13, proceedings of the thirteenth international conference on the simulation and synthesis of living systems. MIT press, Cambridge, MA. [Google Scholar]
- Rebolleda‐Gómez, M. , Ratcliff W. C., Fankhauser J., and Travisano M.. 2016. Evolution of simple multicellularity increases environmental complexity. bioRxiv. https://www.bioarxiv.org/content/early/2016/08/05/067991 [Google Scholar]
- Rebolleda‐Gomez, M. , and Travisano M. 2018. The cost of being big: local competition, importance of dispersal and experimental evolution of reversal to unicellularity. Am. Nat. 192:731–744. [DOI] [PubMed] [Google Scholar]
- Ritz, C. , and Streibig J. C.. 2008. Nonlinear regression with R. Springer, New York, NY. [Google Scholar]
- Rodríguez‐Verdugo, A. , Carrillo‐Cisneros D., González‐González A., Gaut B. S., and Bennett A. F.. 2014. Different tradeoffs result from alternate genetic adaptations to a common environment. PNAS 111:12121–12126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rokas, A. 2008. The origins of multicellularity and the early mistory of the genetic toolkit for animal development. Annu. Rev. Genet. 42:235–251. [DOI] [PubMed] [Google Scholar]
- Rossetti, V. , Schirrmeister B. E., Bernasconi M. V., and Bagheri H. C.. 2010. The evolutionary path to terminal differentiation and division of labor in cyanobacteria. Journal of Theoretical Biology 262:23–34. [DOI] [PubMed] [Google Scholar]
- Schirrmeister, B. E. , Antonelli A., and Bagheri H. C.. 2011. The origin in multicellularitty in cyanobacteria. BMC Evolutionary Biology 11:45 10.1186/1471-2148-11-45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sebé‐Pedrós, A. , Degnan B. M., and Ruiz‐Trillo I.. 2017. The origin of metazoan: a unicellular perspective. Nat. Rev. Gen. 18:498–512. [DOI] [PubMed] [Google Scholar]
- Simpson, G. G. 1944. Tempo and mode in evolution. Columbia Univ. Press, New York, NY. [Google Scholar]
- Smith, S. D. and Goldberg E. E.. 2015. Tempo and mode of flower color evolution. American Journal of Botany 102:1014‐1025. [DOI] [PubMed] [Google Scholar]
- Strakova, A. , and Murchison E. P.. 2015. The cancer which survived: insights from the genome of an 11000 year‐old cancer. Curr. Opin. Genet. Dev. 30:49–55. [DOI] [PubMed] [Google Scholar]
- Tabassum, D. P. , and Polyak K.. 2015. Tumorigenesis: it takes a village. Nat. Rev. Cancer. 15:473–483. [DOI] [PubMed] [Google Scholar]
- Teotónio, H. , and Rose M. R.. 2000. Variation in the reversibility of evolution. Nature 408:463–466. [DOI] [PubMed] [Google Scholar]
- Tenaillon, O. , Rodriguez‐Verdugo A., Gaut R. L., McDonald P., Bennett A. F., Long A. D., and Gaut B. S.. 2012. The Molecular Diversity of Adaptive Convergence. Science 335:457–461. [DOI] [PubMed] [Google Scholar]
- Travisano, M. , Mongold J. A., Bennett A. F., and Lenski R. E.. 1995. Experimental tests of the roles of adaptation, chance, and history in evolution. Sci. PNAS 267:87–90. [DOI] [PubMed] [Google Scholar]
- Vermeij, G. J. 2006. Historical contingency and the purported uniqueness of evolutionary innovations. PNAS 103:1804–1809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wiens, J. J. 2011. Re‐evolution of lost mandibular teeth in frogs after more than 200 million years, and re‐evaluating Dollo's law. Evolution 65:1283‐1296. [DOI] [PubMed] [Google Scholar]
- Zufall, R. A. , and Rausher M.. 2004. Genetic changes associated with floral adaptation restrict future evolutionary potential. Nature 428:847–850. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Table S1. Summary of model comparisons.
Figure S1. Variance in size and the natural logarithm of this variance against time.
Figure S2. Plots testing normality (q‐q plot) and heteroscedasticity (fitted values vs. residuals) for the ANCOVA and the generalized linear least squares model (GLS) with variance weights modeled as an exponential function of time.
Figure S3. Distribution of sizes over time of each of the replicate lines (different shades of gray) of all of the populations in the control (upper panels) or UV (lower panels).
Figure S4. Changes in multicellular phenotypes over time.
Supporting Information


