Abstract
The corpus of electron transfer (ET) theory provides considerable power to describe the kinetics and dynamics of electron flow at the nanoscale. How is it, then, that nucleic acid (NA) ET continues to surprise, while protein-mediated ET is relatively free of mechanistic bombshells? I suggest that this difference originates in the distinct electronic energy landscapes for the two classes of reactions. In proteins, the donor/acceptor-to-bridge energy gap is typically several-fold larger than in NAs. NA ET can access tunneling, hopping, and resonant transport among the bases, and fluctuations can enable switching among mechanisms; protein ET is restricted to tunneling among redox active cofactors and, under strongly oxidizing conditions, a few privileged amino acid side chains. This review aims to provide conceptual unity to DNA and protein ET reaction mechanisms. The establishment of a unified mechanistic framework enabled the successful design of NA experiments that switch electronic coherence effects on and off for ET processes on a length scale of multiple nanometers and promises to provide inroads to directing and detecting charge flow in soft-wet matter.
Keywords: electron transfer, flickering resonance, hopping, polaron, superexchange
1. INTRODUCTION
Biological energy transduction, oxidative stress, nucleic acid (NA) biosynthesis and repair, apoptosis, circadian clocks, nitrogen fixation, CO2 reduction, and water splitting all drive charge over nanometer and longer distances (1, 2). A milestone of twentieth-century physical chemistry was the establishment of successful theories to describe vibronically coupled electron transfer (ET) in a wide range of contexts (3–5). Electrons move through proteins by executing multistep, bridge (B)-mediated tunneling (superexchange) between charge-sequestering cofactors. The superexchange interactions are mediated by large band gap folded protein(s) that hold the cofactors in place (6–9). How does the considerable body of knowledge surrounding protein ET allow us to address the question posed in the title of this review? Intuitively, the answer ought to be linked to the extended π-stacking and the near periodicity of the DNA. However, the thickness of an amino acid is not so different from the thickness of a nucleobase; both structures contain saturated and unsaturated bonds, and the optical spectra of several amino acids (Tyr, Trp, and His) are qualitatively similar to those of the nucleobases. What are the specific structural, energetic, and dynamical features that make protein and DNA ET chemistry so different?
The large energy gap between the redox-active states of the cofactors and the surrounding amino acids of the protein prevents the cofactors from oxidizing or reducing the protein in most cases of simple electron transfer. Electron transfer between the protein and the redox cofactors can waste energy and produce chemical damage (9). Binding of the cofactors to the proteins protects the redox equivalents, programs the timescale of the redox reactions, and defines biomolecular redox partnerships. The protein superstructure accelerates transport by lowering electron tunneling barriers compared to water or to vacuum, and the protein-mediated tunneling is known as superexchange (10). Superexchange (a combination of through-bond and through-space tunneling) is one of the best understood manifestations of quantum mechanics in biology, underpinning the coherent propagation of electron amplitude through structured multipathway electron tunneling barriers (11).
This review explores how the electronic energy landscapes, and the electronic energy level fluctuations, make DNA and protein ET so different (12). We look beyond the minutiae of the underpinning synthesis, electrochemistry, break junctions, kinetics, quantum chemistry, and quantum dynamics to examine the sources of mechanistic differences between protein and DNA ET. Our exploration explains some of the surprising discoveries in the field of DNA charge transport (13), may help to explain some of the sociology of this research area (see the sidebar titled DNA Charge Transfer: A Field of Enthusiastic Debate and Promise), and points toward future applications. Indeed, NA ET makes strong contact with topics in biophysical chemistry, nanotechnology, and biomedicine, with exciting applications to functional self-assembling nanomachines, sensing at the nanoscale, intermolecular signaling, and DNA repair (23–30).
1.1. Quantum Mechanics in Biology?
The influence of quantum effects and of statistical fluctuations on biological function has been the focus of discussion for the last century. Schrödinger’s ruminations on the physical basis of Life turned largely to statistical fluctuations (31). Regarding quantum effects in biology, Longuet-Higgins cautioned that “we must be careful to avoid the aura of mystery which can so easily be produced by reference to ‘quantum-mechanical effects”‘ (32, p. 215). Hopfield stated succinctly, “The role of quantum mechanics in biology is central but trivial” (33, p. 9). Quantum effects take center stage in biological ET, as the motion of the very light electron through an insulating wrapper is enabled by quantum mechanical tunneling.
While the flow of electrons through proteins requires tunneling between charge-sequestering cofactors, we will find that the nature of electron flow through NAs is richer, with the capacity to access strongly localized or delocalized coherent (multibase) electronic states in different contexts. This Janus-like personality of NAs is in sharp contrast to proteins, which recruit spatially well localized, weakly coupled cofactors that essentially follow the rules of two-level quantum dynamics (34). The idea that delocalized (coherent) states may accelerate biophysical reactions is the subject of broad exploration in photobiology (35–37). Understanding how NA ET systems may access multiple regimes of localization and delocalization, and describing how structural fluctuations may direct the mechanism toward one outcome or another, could have broad implications in molecular biophysics, molecular signaling, and nanoscience. Deciding whether the underpinning quantum and statistical phenomena that decide the electron’s fate are trivial or not is left as an exercise to the reader.
1.2. Biology Cannot Wait: Proteins Use Multistep Hopping
Photosynthetic and mitochondrial ET chains in proteins use electron tunneling reactions to convert the electronic energy of redox species into transmembrane electrochemical gradients (38). The workhorse proteins of bioenergetics span thylakoid and mitochondrial membranes of 3–5 nm. The energy-transducing machinery strongly binds redox-active cofactors, and mobile electron carrier proteins also shuttle electrons between the transmembrane proteins (39). Why do the transmembrane energy-transducing proteins need to install multiple ET-active cofactors? An electron tunneling through a 2-eV barrier (typical of proteins) that is 3 nm wide would require more than a day for the journey (9, 40). As such, biology requires multiple redox cofactors to convey electrons across membranes on physiologically relevant timescales. For activationless ET, which typically burns 0.5–1.0 eV of free energy, a 1.6-nm distance can be traversed in approximately a millisecond. Activated ET events on the millisecond or shorter timescale (typical of biological processes) require even shorter tunneling distances. Evolution discovered the value of using multistep hopping to traverse transmembrane proteins at an affordable thermodynamic cost on productive timescales. Due to the large distances between redox cofactors in proteins, their interaction energies are tiny (e.g., ~10−6 eV at 1.6 nm). Since the probability that two chemically identical species in the condensed phase will have electronic energies that match within a tolerance of 10−6 eV is nearly zero, the electrons will be localized on just one cofactor at a time.
Evolution has discovered a stunning array of redox-active cofactors: chlorophylls, hemes, pheophytins, quinones, molybdopterins, iron–nickel complexes, flavins, manganese complexes, and iron–sulfur clusters; some are simple electron brokers, while others double as biocatalysts. We find that the energy barrier between typical charge-sequestering groups and the electron transfer bridge is as much as fivefold smaller in NAs compared to the gap in proteins. This difference is the source of the profound differences between protein and NA ET mechanisms. The average electronic energy landscape for proteins, and for through-bond and through-space tunneling interactions, is summarized in the sidebar titled Donor-Acceptor Interactions Mediated by Superexchange Through a Bridge and Figure 1. But simple energetics is not sufficient to explain many of the novel features of NA ET.
Figure 1.
In proteins, the DA energy-level broadening is <10% of the tunneling barrier height. The TB tunneling barrier (△ETB) height is about half the height of the TS tunneling barrier (△ETS), so the folded protein bonding orbitals (VB) dominate the electron tunneling mediation from D to A (6). Abbreviations: A, acceptor; CB, protein anti-bonding orbitals; D, donor; TB, through-bond; TS, through-space; VB, protein bonding orbitals.
1.3. Multistep Hopping Explains Protein Electron Transfer from Subnanometer to Centimeter Length Scales
While our focus will be on ET from tenths to tens of nanometers, biology has also evolved machinery to convey charge on distance scales of micrometers and larger (41, 42). Multistep charge tunneling also seems to underpin this very long-range charge transport. Extracellular appendages of bacteria move charge over cellular (micrometer) lengths (43, 44). Theory indicates that extracellular ET occurs via multistep hopping (tunneling), mediated by multiheme cytochromes (45–48) in some of these structures. Diffusing electron carriers (flavoproteins) and aromatic amino acid side chains may also provide transport channels (44, 49). Redox-active extracellular structures enable charge flow between living systems and abiotic electron sinks (rocks). These remarkable appendages play a central role in biogeochemistry, and create opportunities to create new technologies at the living/nonliving system interface (50). Figure 2 summarizes the mechanisms available to single- and multistep ET redox reactions. Most protein-mediated single-step reactions are nonadiabatic reactions; many engage multiple protein-mediated coupling routes (pathways) with fluctuations that are well described within the Condon approximation (42).
Figure 2.
Mechanistic decision points and physical factors that control (a) single-step and (b) multistep ET reactions. The theoretical machinery used to compute ET rates is determined by the mechanism at play, indicated by the branching points. Abbreviations: class., classical; DA, donor/acceptor; ET, electron transfer; FC, Franck-Condon; QM, quantum mechanical; τL, longitudinal reaction time; νn, nuclear frequency.
2. ELECTRON TRANSFER IN DNA
2.1. Early DNA Studies Used Appended/Intercalated Donors and Acceptors
DNA bases are susceptible to oxidation, and the holes left behind are mobile (13, 51, 52). Seminal experiments by Barton and colleagues, beginning in 1993 (53), indicated that charge flow across tens of nanometers through DNA could be extremely rapid (51, 52). How might this occur?
Our early assessments of the electronic energy landscape for photoinduced ET in DNA, namely, ET from a photoexcited intercalated Ru(II) complex to a distant intercalated Rh(III) complex, indicated a donor-B-acceptor (DBA) electronic energy landscape similar to that of many electron-transfer proteins (54). As such, if single-step tunneling were to rule the transport mechanism in NAs, one would expect transport over tens of nanometers to require time periods longer than the age of the universe. The close parallel between protein and DNA ET was found in our analysis because the Ru and Rh species were estimated to have redox potentials well removed from those of the DNA bases, similar to the 1- to 2-V gap found in protein ET systems (54, 55). But there is more than one way to move electrons over large distances. Indeed, theoretical studies found that thermal injection of carriers could explain weakly distance-dependent ET in DNA at long distances (56). In this mechanism, thermal barriers for charge injection and multistep hopping must be overcome, rather than a single insurmountable tunneling barrier.
2.2. Donor-Acceptor Chemistry with DNA Bases
Expansion of the DNA experimental arsenal was rapid, and next-generation experiments targeted DNA bases or chemically modified DNA bases for oxidation (13, 57–61). In many of the studies, ET redox-active species were embedded in the π-stack, with less uncertainty in structure, distance, and energetics. A growing body of data found a rapid drop-off of ET rates at short distances, followed by a soft distance dependence at longer distances, suggesting a change in mechanism with distance. It seemed that tunneling at short distances and incoherent hopping at longer distances would suffice to explain the data.
When charge carriers are injected into DNA (thermally or photochemically), they are expected to move rapidly through the structure because of the strong coupling (> kBT, where kB is Boltzmann’s constant and T is the temperature) among nearest-neighbor bases (13, 62–64). A random walk of charge carriers through DNA would produce diffusion over a length ΔX ≈ (Dt)½, where D = ka2/2 with k equal to the nearest-neighbor hopping rate and a equal to the hopping distance (2). For instance, G-to-G hole transfer in the GTTG sequence was estimated to occur via tunneling on a nanosecond timescale (65), so diffusion through a (GTT)n oligomer would cover just under a micrometer in 1 ms. However, diffusion-based nearest-neighbor hopping does not adequately describe the transport kinetics that is found in DNA (64, 66, 67).
What seems immediately to distinguish DNA from protein charge transport is (a) much lower tunneling barriers in DNA (tenths of electron volts rather than electron volts) when the D and A are DNA bases or energetically similar species, (b) small thermodynamic driving forces for base-to-base hopping, and (c) strong (> kBT) intrastrand nearest-neighbor coupling interactions among hopping sites. In contrast, ground state ET in proteins typically involves cofactors well beyond van der Waals contact distances (early steps in photosynthetic charge separation are the exception, as ultrafast ET is required for energy capture from the excited state). Close contact is expected to delocalize carriers somewhat among like bases on a single strand. Nuclear polarization in response to the electronic charge may also produce so-called polaron states (68, 69). Transfer of charge may therefore involve islands of charge spread over several bases with surrounding nuclear polarization (68, 69), and the extent of delocalization may fluctuate with time.
A crucial advance in DNA ET experiments was the development of hairpin constructs in which the DA distance could be varied systematically and the charge transfer could be triggered photo-chemically (70). ET rates in these systems show exponential distance dependence up to distances spanning approximately six bases and a weakly distance-dependent regime at longer distances (71). One of the redox partners is typically a guanine, oxidized by a terminal stilbene photoexcited state, and the B can be varied in structure and length (13, 51, 62, 63). Qualitatively similar ET behavior was found in NAs with modified backbones, such as peptide nucleic acids (PNAs) (72).
ET mechanisms, aside from nearest-neighbor hopping, variable-range hopping, coherent bandlike transport, and polaron transport, can produce weakly distance-dependent rates. For example, a photoexcited state with substantial D-to-B charge transfer character may produce soft distance dependences, as the initial state may be delocalized onto the B by the photoexcitation (73, 74).
Our understanding of NA transport mechanisms, especially in the short-distance regime, has evolved rapidly in the past 2–3 years. The finding of strongly distance-dependent ET rates in DNA at shorter distances is not surprising in the context of protein-mediated electron tunneling. However, tunneling barrier heights in NAs are typically less than half of the values in proteins when at least one NA redox partner is a modified base. We will discuss evidence from theory and experiment that points to an alternative mechanism of transport (at short distances) that engenders exponential distance decay of ET rates without engaging a tunneling mechanism. Exploration of this new mechanism sharpens our understanding of the energy and timescales that underpin B-mediated ET and points toward a special role for spatially extended coherence in some DNA ET reactions.
2.3. An Experimental Paradox: Exponential Distance Decay of Rates with Carrier Population on the Bridge
Stilbene photooxidation of a G base (separated by AT base pairs) produced exponential distance dependences, namely kET ∝ exp[−βRDA] with β ≈ 0.6 Å−1. This decay constant is one-half the β value found typically in proteins (70) and is consistent with a square tunneling barrier of ~0.3 eV (compared to ~2 eV in proteins; see the sidebar titled Small β Values Are Incompatible with Tunneling). Tenths of electron volt barrier heights are consistent with the gap in oxidation potential between purines (G and A). This energy landscape may seem to be consistent with tunneling transport, but we have neglected a key consideration: Thermal fluctuations of electronic energies are also on the scale of tenths of an electron volt and will transiently erase tunneling energy gaps as large as tenths of an electron volt. Indeed, the ultrafast studies of Lewis, Fiebig, and colleagues (75) discovered a hole population on the B for short-distance transfers, a finding that is incompatible with a pure tunneling mechanism in DNA.
How is it possible to reconcile the observation of exponential distance dependences with hole population on the B? This paradox motivates a more detailed examination of the electronic energy landscape for biomolecular ET and provides the focus for the remainder of this review.
3. REQUIREMENTS FOR COHERENT TRANSPORT VIA A MOLECULAR BRIDGE
For coherent delocalization, we require that the DB and BA electronic couplings (V) exceed the energy gap ΔE between D/A and B states. Clearly, this condition can be met in one of two ways. First, the average electronic state energies of D, B, and A may match each other within a tolerance given by their coupling interactions (34). Second, thermally induced energy level fluctuations of D, B, and A may bring the states fleetingly into degeneracy (76). Coherent transport also requires that nuclei not relax rapidly, thereby trapping the mobile charge during its transit, as this would terminate the coherence. Is resonant mixing of multiple states (D, B, and A) accessible in proteins and DNA?
3.1. The Energy Landscape for Proteins and Nucleic Acids (in More Detail)
In protein ET, the amino acid redox potentials are offset from the cofactor potentials by several volts (9, 38). What about the effective value of the electronic interaction |V | among amino acids? The characteristic size of an amino acid (3.5 Å) is approximately the same as the base-to-base van der Waals gap in DNA. Hopfield’s estimate of protein-mediated couplings as a function of distance predicts |V| ≈ 0.2 eV at 3.5 Å (9), so |V|/ΔE ≈ 0.1–0.2 for amino acids with ΔE = 1–2 eV. Similar tunneling pathway analysis of through-bond tunneling with a (standard) tunneling penalty per bond of 0.6 per bond (10), three bonds per amino acid, and a σ bond–to–σ bond electronic coupling of ~1 eV (77, 78) yields an effective coupling of |V| ≈ (0.6)3 × 1 eV ≈ 0.2 eV (11, 79). As such, |V| ≪ΔE in proteins. Thermal fluctuations of the electronic state energies (see Section 3.2), σE, are also much less than the energy gap; that is, σE ≪ ΔE. These estimates of the coupling |V| across an amino acid are further decreased if the dominant route for electron/hole amplitude to flow across the amino acid includes through-space propagation (8, 10, 80). In the high-temperature (Marcus) regime, σE is estimated to be tenths of an electron volt (see Section 3.2) (4, 9, 81). In proteins, electronic energy fluctuations on this scale will not bring D, B, and A energies into transient degeneracy, so coherent transport is not accessible. When the energy gap required to oxidize aromatic side chains is not prohibitively large—as in ribonucleotide reductase, cryptochromes, the oxygen-evolving complex, and cytochrome c peroxidase—aromatic side chains may play a more active role (81, 82). Extended aromatic stacking is uncommon in proteins; the most likely role for redox-active aromatics in proteins is as hopping stations.
3.2. Electron Transfer Theory in the Language of Energy Gaps and Their Fluctuations
The Marcus theory of ET focuses on the nonequilibrium polarization fluctuations that produce D and A electronic energy matching, a prerequisite for charge flow. The Hopfield theory of ET describes the probability of particle removal from a D at energy E [DD(E)] and of insertion on A [DA(E)] in terms of Gaussian spectral functions (9):
| 1a. |
| 1b. |
The standard deviation of the electronic energies in the high-temperature (Marcus) limit is:
| 2. |
Here, λ is the Marcus reorganization energy, assuming equal contributions from the D and A sites. For a typical reorganization energy of ~1 eV at room temperature, these fluctuations are on the scale of 160 meV. This energy-level broadening is critical, since energy fluctuations on this scale in NAs will bring D, B, and A transiently into degeneracy. Yet, fluctuations of this magnitude are an order of magnitude too small to wipe out the tunneling barriers in proteins.
Analysis of electronic energy fluctuations indicates that if a photooxidant (e.g., stilbene) can oxidize a guanine base, it can also transiently energy-match with adenine. Thus, one expects to find transient delocalization of G+· holes onto adenines of DNA. But how is it that experiments detect both bridge-localized carrier population and exponential distance in DNA photoinduced ET experiments? The observations of Lewis, Fiebig, and colleagues (75) present a compelling challenge to theory that brings the nature of NA ET at shorter distances into focus.
4. MULTISTATE ENERGY MATCHING IN DNA: FLICKERING RESONANCE
4.1. Transient Electronic Energy Matching Is Found in Simulation
Early theoretical studies of ET couplings in biomacromolecules were performed in a small number of geometries (10, 83, 84). A static approach is incomplete because of the sensitivity of coupling interactions to distance and geometry (6, 7). For example, in protein ET, multipathway interferences typically produce average coupling values very close to zero, 〈HDA〉 ≈ 0 (6, 85), although . In peptides (83), proteins (86, 87), and DNA (12, 88, 89), very rapid fluctuations of couplings were found in detailed simulations. The sidebar titled Bridge-Mediated Electron Transfer with Fluctuating Bridges and Figure 3 show how B-mediated coupling fluctuations may or may not impact the mean-squared couplings, which enter the ET rate in the nonadiabatic (weak coupling) regime.
Figure 3.
Donor-bridge-acceptor (DBA) systems with the same D-to-A distances may have different fluctuation characteristics. In panel a, the root mean square (rms) couplings are indicated as being very different, since the coupling widths are relatively small. In panel b, however, due to the large width of the geometry distribution for conformations indicated in blue, the rms couplings are not very different (1). Thus, the nature of thermal geometry fluctuations and of pathway interferences could wash out coupling pathway effects in proteins. Evidence from both theory (90) and experiment (40) supports the regime indicated by panel a as being most prevalent since secondary structure effects persist in biological electron-transfer kinetics. Tunneling pathway and distance-dependent tunneling effects in protein electron transfer are not believed to be washed out as a result of thermal fluctuations. Figure adapted with permission from Skourtis (91).
The influence of thermal fluctuations on ET is very different in the large and small barrier regimes. With large barriers, fluctuations influence the mean-squared coupling and thus the ET rate, without qualitatively changing the tunneling mechanism. For small barriers, D, B, and A (diabatic states) fluctuate in and out of resonance, causing large changes in the carrier localization across the molecule. Although the resonances are transient, their effects on transport can be profound. Below, I describe an approach to compute the influence of these transient resonances on ET.
4.2. Protein Electron Transfer Mechanisms Are Few; DNA Mechanisms Are Many
Figure 2 provides a roadmap to describe ET reactions. The accessible mechanisms in long-distance high-barrier ET are well understood: The nonadiabatic limit is typically valid, as is the Condon approximation (42). Tunneling interactions are mediated by few or many coupling pathways, depending on the protein’s fold (6, 87). Conformational gating is sometimes rate limiting (92, 93); thermal fluctuations are typically fast enough to guarantee that the mean-squared B-mediated DA coupling can be used in the Fermi’s golden rule rate expression (94, 95). Except for the fastest ET regimes, kinetics are not usually limited by medium relaxation (96–98).
DNA is built of four nucleotides and is quasi-one-dimensional (1D); proteins are built of 20 amino acids and are 3D. Nonetheless, protein ET is simpler because of the large separation between cofactor oxidation potentials and the amino acid oxidation potentials. DNA is more complex because thermal fluctuations bring D, B, and A states in and out of transient resonance. Polaron states may form in DNA as well, depending on the medium composition and its relaxation characteristics (68). Since the base-to-base couplings (|V|), σE, and ΔE are of similar size in DNA, it is likely that fluctuations, and the persistence of resonant structures, gate the transport.
4.3. The Blind Man and the Elephant
Probes of DNA electron transport based on excited-state lifetimes, transient spectroscopy, break-junction conductivity histograms, and electrochemical currents are of tremendous utility. These tools do not yet, however, reveal a comprehensive description of the electronic and nuclear dynamics that underpins charge flow through DNA.
4.4. Theoretical Tools Are Blunt
Theoretical approaches to DNA ET abound with approximations and errors: quasi-harmonic and linear-response approximations, approximations to describe wave function tail propagation, self-interaction and electron correlation errors, two-state approximations, van der Waals interaction errors, ionization potential/electron affinity gap errors, rare event sampling challenges, and Born-Oppenheimer/Condon approximations. Modeling nonadiabatic dynamics is challenging, and familiar methods [e.g., using Ehrenfest or surface-hopping methods (99, 100)] have pathologies. Nonetheless, theory, modeling, and simulation—executed in close collaboration with experiment—often capture enough of the essential features that govern charge flow at the nanoscale to pose useful hypotheses. After a brief digression, we will examine how the coincidence of exponential distance decay and B carrier population can be reconciled.
4.5. Coulomb Ramps, Hot Holes, and Mixed Transport Mechanisms
Single-ET events may involve charge shift (e.g., D−A → DA−) or charge separation (e.g., DA → D+A−) reactions. In the case of charge separation, the reaction free energy (ΔG) is distance dependent. The effect stabilizes a configuration like D−B+BB compared to D−BBB+. When a strongly oxidizing excited state (naphthalene diimide) was used rather than stilbene in DNA hairpins (101), carrier injection to the double helix was observed. Access to more distant base localized states requires (incoherent) thermally activated hole hopping.
4.6. Conveying Signals and Defusing Redox Bombs via Hole Hopping
When a protein’s redox catalysis goes awry, it may be advantageous to deactivate strongly oxidizing species by passing their holes to solution phase reductants by multistep hopping through the protein (102, 103). A mechanism of this kind, suggested by Gray & Winkler, could protect proteins from oxidative damage (102–104). Hole deactivation could be enabled by hole hopping through aromatic amino acids along a hopping pathway that may link redox cofactors to the protein surface. Such hopping could occur on a landscape similar to that of Figure 4. Experimental and theoretical efforts are underway to map hole exit channels (102–104).
Figure 4.
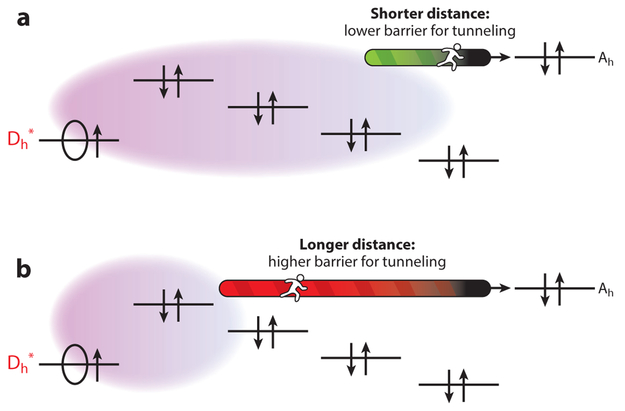
Photoinduced hole transfer in DNA hairpins with (a) a stronger and (b) a weaker photooxidant. With the stronger photooxidant (hole donor, D*), a hole can be promptly spread into the DNA, as indicated by the larger, light purple cloud. The Coulomb ramp for electron/hole separation is reflected in both panels by the distance-dependent bridge orbital energies and, therefore, the greater ease of oxidizing bases nearby because of the lower Coulomb penalty for short-distance charge separation. Figure adapted with permission from Beratan & Waldeck (105).
The window of biophysical redox potential is about 2 V wide, and the oxidation potentials for tryptophan and tyrosine oxidation are at the upper end of the range (38, 81). For an ET reaction to be spontaneous, its reaction free energy must be negative, although intermediate states in a redox chain may be thermodynamically uphill (106, 107).
4.7. Transitions Between Coherent and Incoherent Transport
Whatever the cause, NA ET rates show a weaker distance dependence at longer than at shorter distances (see Section 1.2). This trend is found in the ET kinetics of synthetic organic molecules (108), polypeptides, DNA, and bacterial nanowires (7) as well. The behavior is usually attributed to a transition from tunneling to multistep hopping (109), with a transition point around five or six base pairs in NAs. One can make an estimate of the carrier injection energy for hopping by equating the tunneling and the thermal injection probabilities at a particular distance:
| 3a. |
or
| 3b. |
With an experimental β value of 0.6Å−1 from the Lewis experiments (30, 70) and ΔEinj of ~400 meV (corresponding to the gap in the oxidation potentials of G and A bases), a tunneling/hopping crossover would be calculated at approximately eight base pairs, not far from the observed transition. The interplay of barrier heights and transport mechanisms is highlighted in the sidebar titled Small β Values Are Incompatible with Tunneling.
4.8. Flickering Resonance Transport
Lewis, Fiebig, and coworkers (75) found that (a) holes populate the AT B in advance of hole trapping on the GC in photoexcited stilbene DNA hairpins and (b) ET rates drop exponentially with distance. These observations motivated my group to explore mechanisms that could accommodate both findings. In either the superexchange or the hopping model, these observations would be mutually exclusive.
Sampling of classical (molecular dynamics) DNA geometries followed by electronic structure analysis identified a large number of structural snapshots where the highest occupied molecular orbital (HOMO) energy ordering of the purines (Gs and As) was reversed from their mean positions. This result is entirely consistent with the widths of the spectral functions of Equation 1a, b. The observation of transient degeneracy led us to ask whether extended delocalization could fleetingly span multiple bases in DNA, thus providing a coherent transport channel. We built an analytical model to predict the probability of multiple-level matching in this context by developing a many-level generalization of the Hopfield two-level ET theory. We found that extended de-localization could indeed span extended structures (76). It turns out that this energy-matching probability can meet or exceed the tunneling probabilities at shorter distances, drawing into question the dominance of tunneling at short distances.
The theoretical framework of transient or flickering resonance (FR) among multiple bases in DNA rationalizes the experimental findings of Fiebig, Lewis, and colleagues (75). FR can be applied to flat or Coulomb-ramp potentials by setting the mean positions of the Gaussians appropriately (76). If a carrier can move through the system during the persistence of the electronic resonance, the rate will be proportional to the product of the energy level–matching probability and the (inverse) time for the carrier to traverse the B. Energy levels may fluctuate in a correlated fashion (110, 111), so the probability of matching may be enhanced beyond our simple estimates. The FR mechanism thus provides an explanation of the finding of Fiebig, Lewis, and colleagues (75) of exponential distance dependence and bridge population in DNA ET. The mechanism may also be relevant to near-degenerate charge-transfer processes in proteins (112); the more strongly the B sites interact with one another (and also with D and A), the greater the likelihood of a FR transport mechanism.
The FR energy-matching probability drops exponentially with distance because the probability of level matching requires that multisite fluctuations occur simultaneously (76). The matching probability was estimated for a flat potential landscape as (76):
| 4a. |
| 4b. |
Here, σV is the standard deviation of the nearest-neighbor couplings, ΔR is the spacing between bases, and σE is the energy width ; the result of DNA simulations allowed us to determine σV and σE to estimate Φ = 0.6Å−1, consistent with the experimental rate decays found by Lewis and coworkers (30, 70, 75). The FR mechanism is accessible in these systems because base-to-base interactions (|V|), energy fluctuations (σE), and energy gaps among purines (ΔE) are all on the scale of hundreds of millielectron volts. Can the carrier traverse DNA during the finite lifetime of the transient resonance? The timescale to break energy matching at any site is approximately ħ/σE (~6 fs), but this time will grow if fluctuations in the DNA are correlated (as is indicated in simulations; 110, 111). The velocity for charge to move through a 1D band is (1/ħ)∂E/∂k. For a 1D tight-binding model, the velocity at midband is 2|V|a/ħ. When a ≈ 3.4Å and |V| ≈ 0.1 eV, the velocity is ~1 Å/fs (34). The timescales at play are about right to enable FR transport. In contrast to coherent transport rates, which are proportional to |V|, sequential hopping rates are proportional to |V|2. We used this important distinction to design a key test of the FR mechanism in DNA.
The decades-long linkage between exponential distance decay and a supposed superexchange ET mechanism in proteins and small molecules may well have biased thinking about DNA charge transport. FR, or other resonant carrier injection mechanisms, seems likely to be at play in systems whenever |V| ≃ σE ≃ ΔE. In this regime, the transitions among tunneling, FR, and hopping transport can depend in subtle ways on base sequence, counterions, and temperature, as well as on the D/A geometry and electronic structure. FR provides a manifestation of conformationally gated transport, an early concept in DNA ET (51). Importantly, FR produces an exponentially decreasing probability to align the many electronic states.
FR was examined recently as a possible transport mechanism in photolyase, where multiple aromatic side chains appear to be nearly degenerate with a photoexcited flavin (112), and it is possible that similar mechanisms assist hole escape in oxidative damage protection mechanisms of proteins (102). The likelihood of energy matching, essential for FR, grows as the intersite couplings grow, since larger couplings widen the window for multisite energy matching. The unique temperature-dependent characteristics of FR transport (7) are amenable to experimental testing (7, 76), and the nature of the transition between coherent and incoherent transport in NAs is a topic of intensive study (113–115). FR can involve multiple sites in strong electronic contact, or the charge flow among sites can require tunneling. In the latter case, the transport resembles resonant tunneling (although traditional resonant tunneling does not require the structure to first fluctuate into a multistate degenerate pose).
4.9. Indications of Resonant Transport in DNA Break Junctions
In addition to photochemical DNA ET, break-junction experiments on DNA and on PNA point toward resonant contributions to transport. Our analysis of PNA break-junction data found that resonant enhancements were needed to describe transport in (TA)3-(XY)-(TA)3 structures (116–118).
In molecular structures with extended (planar) π-mediated pathways, closely related questions regarding conductance and coherence also arise. We found that the structure and symmetry of the molecular linkage to the electrodes can select specific bridging orbitals that dominate the transport in molecules with extended conjugation. In structures with carbodithioate linkers, strong interactions with the electrodes produce mediation via orbitals other than the B frontier orbitals (119). This observation indicates that the barrier height need not map simply onto a structure’s frontier orbital energies.
4.10. A Critical Experimental Validation of the Flickering Resonance Transport Mechanism
Break-junction studies of Tao and coworkers (120) measured transport through double-stranded DNA built of G blocks followed by C blocks on one strand (i.e., GGGGCCCCGGGG…) and of alternating Gs and Cs (i.e., GCGCGCGC…) (Figure 5). In the G-block structures, indicated in Figure 5, the resistance oscillated with the number of G repeats in the blocks. In the GC alternating structures, no resistance oscillations were observed (120). The even-odd effect is a hallmark of coherence (120, 121). The observation that extended coherent delocalization can be created in the G-blocks suggests that we might be able to bring multiple blocks into FR to test predictions of the FR model. Our studies began with the simulation of molecular structures that are subjected to spatially and temporally correlated noise, (122) and translated these ideas to specific DNA constructs (121).
Figure 5.
Resistance data for break-junction measurements as a function of the number of Gs in an alternating (CG)n structure (orange) and a blocked (CnGn) structure (blue). The resistance oscillations in the blocked structure are a signature of coherent transport. Figure adapted with permission from Xiang et al. (120).
4.11. Engineering Coherent Transport Through Two Cross-Strand G-Blocks by Changing the Block-to-Block Coupling
FR based on multiple delocalized G-blocks should be realized if the coupling between the blocks is sufficiently strong. In contrast, transport through the blocks would occur by incoherent hopping if the link were too weak to sustain transient extended resonance. If incoherent, the hopping rate would be expected to scale in proportion to the squared block-to-block coupling, consistent with Fermi’s golden rule. However, if a pair of G-blocks enters transient extended resonance, the timescale for a carrier to flow from one block to the next will be proportional to |V|, as described above.
With the above ideas in mind, we designed G-block structures, indicated schematically in Figure 6, that would allow experimental probes of FR in break-junction experiments. Our design had two essential ingredients: (a) Odd-length G oligomers produce a nonbonding state at the middle of their band. In the case of G-blocks, this midband state is believed to be near resonant with the Fermi energy of gold. (b) Reversing the 3′−5′ orientation of the cross-strand G-blocks is computed to change the magnitude of the G-block–to–G-block coupling by approximately fourfold (76). With these characteristics in mind, we designed systems that we hypothesized would support coherent transport (in odd-length G-blocks, lengths (n) equal to 3 and 5, which would be resonant with the electrode Fermi levels) and systems that we hypothesized would support incoherent transport (in even-length G-blocks, lengths, n, equal to 4 and 6, as indicated in Figure 7) (121). The resistance was predicted to scale with |V| for the odd–chain length coherent structures but to scale with |V|2 in the even–chain length incoherent transport structures. In both cases, the coupling could be switched by a factor of 4, which would produce a factor of either 4 or 16 effect on the resistance, depending on whether the G-block length was even or odd (i.e., coherent or incoherent, respectively), and the effect would be readily measured in the break-junction experiments.
Figure 6.
Development of a band from a chain of 1–5 identical orbitals arrayed along a line from left to right and interacting with their nearest neighbors. The odd-length chains have an orbital at the midband position, while the even-length chains lack a midband state. As such, the odd-length chains always have a delocalized state at the energy of a monomer.
Figure 7.
Transport across double-stranded DNA consisting of G-blocks (as described in Section 4.10) on opposite strands. If the transport is coherent, the transit timescale is expected to be proportional to the strength of the cross-strand electronic coupling between the two G blocks. If the transport is incoherent, the transport rate is expected to be proportional to the square of the interblock coupling.
The even–chain length (incoherent) systems were found in experiments to have a resistance that grew approximately 15-fold on weakening the block-to-block coupling. The odd–chain length (coherent) systems were found to have a resistance that grew approximately fivefold on weakening the block-to-block coupling. These observations are consistent with FR transport for the odd-length G-block structures and with an incoherent transport mechanism for the even-length structures, as predicted (121) (Figure 8).
Figure 8.
How the cross-strand G-block–to–G-block coupling changes upon altering the 3′–5′ orientation of the sequences. In the G\G structure, the block-to-block coupling is about four times larger than in the G/G architecture. This design allowed us to probe the |V| versus |V|2dependence of the charge transmission in the coherent versus incoherent regime. Figure adapted with permission from Liu et al. (121).
4.12. Prospects
The strategies used to manipulate the coherence of DNA charge transport in G-block structures could be exploited more broadly to manipulate and control charge flow though self-assembling organic electronic circuitry. Progress toward this aim is accelerating, but access to forked or transistor-like devices seems essential. The sidebar titled DNA Charge Transfer: Moving Beyond One-Dimensional Constructs and Figure 9 highlight recent progress in developing charge combiner/splitter structures based on NAs. DNA may also provide an inroad to organic spintronics, through the chiral-induced spin-selectivity effect illustrated in Figure 10. It is remarkable that the coherence of transport at the multiple-nanometer scale can be switched on and off by manipulating a single 3.4Å scale electronic coupling interaction at the core of the construct. This kind of nonlocal influence on transport is well worth deeper exploration in the context of long-range signaling and sensing in biology.
Figure 9.
Two recent advances realized charge combiners and splitters, perhaps precursors to a DNA transistor: (a) DNA three-way junction, with π-stacked pathways that open and close stochastically to create a division point for charge flow (123, 126), and (b) G-quadruplex junction, with stable stacking, that could enable stable splitting of charge flow (124). These motifs are yet to approach the richness of DNA-based world maps, molecular-scale movies, chemical computers, baskets, or smiley faces (133). Panel a adapted with permission from Young et al. (123), and panel b adapted with permission from Sha et al. (124).
Figure 10.
DNA may act as a spin filter (127–130). The magnitude of the spin filtering found experimentally remains a challenge to compute. The orientation of spins transmitted through DNA was found recently to be interchanged as the double helix was switched between B and Z forms (131). Figure adapted with permission from Zwang et al. (131).
5. WHY ARE DNA AND PROTEIN ELECTRON TRANSFER SO DIFFERENT?
Three parameters control ET kinetics in molecular structures: (a) the site-to-site coupling energies (|V|s), (b) energy gaps between the D and A states and the mediating B states (ΔE), and (c) electronic energy fluctuations (σE). The recognition that fluctuations of DNA base energies are on the same scale as that of their redox potential gaps was poorly appreciated prior to the analysis of FR probabilities. The balance among the mechanisms—tunneling, incoherent hopping, and FR transport—will be determined by the values of these three parameters in particular molecular environments.
Tunneling transport is manifested when the time spent in the DA energy-matched configurations (the Landau-Zener region) is short compared to ħ/HDA and when the tunneling barrier height is much larger than thermal fluctuations of the D/A energies. Hopping transport arises when the probability of thermal carrier injection exceeds the tunneling probability (for a given distance). And FR transport can arise when V ≃ ΔE ≃ σE. For FR to be viable, energy matching must persist on the timescale of the electronic transit from D to A.
The D/A-to-B state gap in proteins is too large to enable thermally induced hopping or FR transport in most cases. (There may be exceptions for very strongly oxidizing redox cofactors or for aromatic hopping units in van der Waals contact.) In NAs, |V|, ΔE, and σE are of the same magnitude, so small changes in sequence, solvent conditions, or temperature may tilt the balance among tunneling, hopping, or FR. In this regime of near parameter matching, the observation of exponential distance dependence does not prove a transport mechanism.
5.1. The Richness of Near-Degenerate Charge Transport
FR is not the only way to produce a transition from exponential to power law distance decay in the presence of disorder. Recent studies by Michaeli et al. (132) examine transport at energies within the band of B states in systems that have B site-energy disorder on the same scale as the site-to-site coupling (|V|). These studies find that electric fields can induce a transition from exponential to power law distance dependence.
5.2. Looking Ahead
NA ET kinetics is likely to continue to provide surprises because transport operates in the regime of nearly equal parameters that controls the mechanism. Experiments that manipulate base chemistry, couplings, and flexibility will provide important diagnostics of the transport mechanisms (36). Use of nonbiological NAs may prove helpful in expanding the design space to access a wider range of the controlling parameters (e.g., PNAs may provide access to larger values of |V| and σE; NAs with locked backbones may decrease σE). In addition, functional self-assembling electronics that move beyond 1D to access the rich space provided by DNA origami and tiled structures promise to further expand the landscape for exploring the phenomena discussed here (133–135). In the biological context, transport coherence switching on the nanometer-length scale could be recruited by signaling networks, as suggested by Barton and coworkers (23, 24, 26).
6. CONCLUSIONS
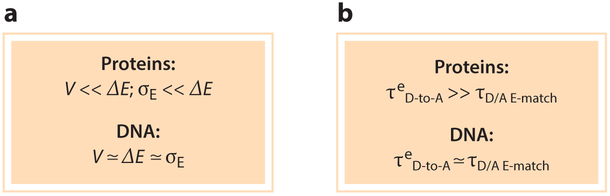
Proteins and DNA are very different in the way that they mediate the flow of electrical charge. Initial interpretations of DNA charge transport chemistry were viewed through the lens of protein ET, which lives largely in the world of single-step tunneling and few-step hopping (since |V|, σE ≪ ΔE). DNA ET is different because |V| ≃ σE ≃ ΔE. Understanding the uniqueness of the DNA electronic energy landscape empowered the design of novel structures with extended coherent transport on the scale of multiple nanometers. It seems likely that the principles for controlling transport at the multiple-nanometer and longer length scales will be tested further and advanced in both biological and human-made structures. The energy and timescale regimes that produce the differences between charge flow through proteins and DNA are summarized in Figure 11.
Figure 11.
(a) Protein electron transfer is defined by high tunneling barriers that cannot be surmounted by thermal fluctuations. In DNA, energy barriers, thermal fluctuations, and base-to-base couplings are on the same scale, enabling access to tunneling, conformationally gated resonant transport, and incoherent hopping. (b) In proteins, the Rabi time (time for an electron to propagate between energy-matched donor and acceptor species) is much shorter than the persistence time of the activated complex, so the transport is nonadiabatic. In DNA, the timescale for carrier transport is comparable to the persistence time of the activated complex, so the transport may be adiabatic, nonadiabatic, or medium relaxation–limited.
SUMMARY POINTS.
The energy landscapes for protein and DNA charge transport are very different, with DNA systems poised in a near-resonant regime (V ≃ σE ≃ ΔE) and protein electron transfer (ET) most often in the high-barrier tunneling regime (|V|, σE ≪ ΔE).
Typical tunneling barriers of proteins are much larger than thermal fluctuation widths, so electrons/holes are not injected into the protein through thermal fluctuations.
Energy gaps among the DNA bases are on the scale of hundreds of millielectron volts, so thermal fluctuations of electronic energies bring donor, acceptor, and bridge energies into transient resonance.
Both tunneling or flickering resonance (FR) transport mechanisms may account for exponential distance dependences at shorter distances, while hopping accounts for weak distance dependence at longer distances.
Tunneling and FR mechanisms can be distinguished by studies of temperature and sequence dependence on the transport currents and kinetics.
Three-way transport junction structures are emerging in DNA but have yet to be integrated into complex assemblies.
FUTURE ISSUES.
What conditions tip the balance among flickering resonance (FR), tunneling, hopping, and multirange hopping mechanisms in nucleic acid (NA) assemblies, and can transitions among the mechanisms be used to transmit biological signals?
Can a unified theoretical framework be developed that describes tunneling, FR, and multistep hopping that applies to biochemical, electrochemical, photochemical, and break-junction settings?
Can transport in self-assembled structures be expanded to much larger distances and more complex architectures by developing new schemes to energize the charge carrier flow and by incorporating DNA origami, bricks, and templated assemblies with high-conductivity elements?
Can the extent of prompt charge delocalization induced by photoexcitation be quantified experimentally?
Can multidimensional electronic spectroscopy be used to probe the coherence of charge transport in NAs?
How does the nature of the charge transport through NAs influence the spin degrees of freedom and spin filtering through the double helix?
Can nonbiological NA constructs be recruited to map the parameters that place NA electron transport into the tunneling, hopping, or FR transport regimes?
DNA CHARGE TRANSFER: A FIELD OF ENTHUSIASTIC DEBATE AND PROMISE.
The excitement in the DNA electron transfer (ET) community was well reflected by the headlines of the last few decades:
“Long-Range Photoinduced Electron-Transfer Through a DNA Helix” (14)
“DNA Double Helix Acts as ‘Molecular Wire”‘ (15)
“DNA Is Not a Molecular Wire” (16)
“Electron Transfer Between Metal Complexes Bound to DNA: Is DNA a Wire?” (17)
“Short-Circuiting the Molecular Wire” (18)
“Charge Transfer in DNA: A Controversy” (19)
“Double Helix Does Chemistry at a Distance—But How?” (20)
“DNA Conductance Convergence?” (21)
“DNA Charge Migration: No Longer an Issue” (22)
DONOR-ACCEPTOR INTERACTIONS MEDIATED BY SUPEREXCHANGE THROUGH A BRIDGE.
One often reads that donor-acceptor (DA) coupling is conveyed by bridge (B)-mediated superexchange interactions. This means that the electron, trapped on the D, couples to the A through virtual oxidized and reduced states of B that are localized in the space between D and A. Bridge-mediated tunneling thus engages a combination of through-bond and through-space interactions. In the absence of mediating B states (that would facilitate through-bond tunneling), the through-space tunneling barrier is defined by the ionization potential of D, typically 5–8 eV. With a chemical B present, this barrier is reduced to ~2 eV or less, depending on the chemistry of the species (9, 10). As such, through-bond interactions produce a tunneling rate decay exponent, known as β, that is much smaller (by approximately a factor of 2) than the β value for through-space tunneling. Hole-mediated superexchange refers to coupling mediated by virtual cation states of the B, while electron-mediated superexchange refers to coupling mediated by virtual anion states of the B. Protein electron transfer is most often dominated by hole-mediated superexchange.
SMALL β VALUES ARE INCOMPATIBLE WITH TUNNELING.
Many long-range DNA electron transfer (ET) studies report β values of 0.1Å−1 or less. In one-dimensional square-barrier tunneling models, , where △E is the tunneling barrier height. A value of β = 0.2Å−1 equates to a tunneling barrier △E of only 39 mV. Since thermal energies (kBT) are 25 mV at room temperature, a transport barrier of only 39 mV would allow thermal population of the electron or hole on the bridge, and the assumption of weak donor-acceptor interactions that underpin the nonadiabatic (Fermi’s golden rule) framework of ET theory will not be valid. Values of a tunneling barrier on the scale of kBT or less indicate that exponential rate laws and nonadiabatic approximations are not appropriate, and incoherent or resonant mechanisms may be at play.
BRIDGE-MEDIATED ELECTRON TRANSFER WITH FLUCTUATING BRIDGES.
While the mechanism of DNA electron transfer was being resolved, fine grained questions were being posed about electron tunneling mechanisms in protein. The tunneling pathway model predicted secondary structure effects on the tunneling barrier and the decay exponent β, and quantum-classical analysis indicated that the effects would not be washed out by thermal motion (90). Square barrier reductionist theories neglect differences in the tunneling barrier heights for helices compared to β-strands. The now classic experiments of Gray & Winkler (40) confirmed the theoretical prediction that secondary structure effects cause order of magnitude changes to protein ET rates at fixed distances (6).
DNA CHARGE TRANSFER: MOVING BEYOND ONE-DIMENSIONAL CONSTRUCTS.
Most discussion here focuses on linear nucleic acid (NA) structures. A dream of the molecular electron transfer field has been to build functional, self-assembling, electrically active structures. A key requirement for such structures seems to be the formation of branched or transistor-like elements. It has proved challenging to establish such structures that will sustain electrical contact. We have recently assisted in the design and analysis of two branched NA charge transfer motifs (123, 124).
Realizing the promise of using DNA to create nanoscale electrical circuitry requires the extension of NA motifs beyond canonical one-dimensional constructs (125). Rapid progress in DNA origami, tiles, and alternative backbone motifs is enabling the field to assemble electronically functional forked structures.
ACKNOWLEDGMENTS
This review is based a seminar presented at Caltech in December 2016. The complexity of the systems described here is considerable, and little progress would be made in the absence of enthusiastic interactions with talented experimentalists. I thank Catalina Achim, Fred Lewis, Ron Naaman, Ned Seeman, NJ Tao, Mike Therien, Dave Waldeck, and Mike Wasielewski for their intensive collaboration on nucleic acid systems. I am indebted to my senior theoretical collaborators, including Agostino Migliore, Spiros Skourtis, and Peng Zhang, for many insights and for hours of joyful exploration. The research described here is a product of the creative and diligent work of a talented cohort of graduate students and postdoctoral researchers. Their contributions over 20+ years led to the perspective described here. This work is supported by the National Institutes of Health (GM-48043) and the National Science Foundation (DMR-1608454).
DISCLOSURE STATEMENT
The author is not aware of any affiliations, memberships, funding, or financial holdings that might be perceived as affecting the objectivity of this review.
Glossary
- Tunneling
quantum mechanical penetration into regions that are classically excluded based on energetics
- Superexchange
tunneling facilitated by donor/acceptor mixing with virtual cation or anion states of a bridge, thus changing the tunneling barrier
- Through-bond and through-space tunneling
in biomolecules, electrons tunnel with higher probability through bonds than through empty space because of differences in the corresponding barrier heights
- Hopping
multiple electron transfer steps, each of which may be activated and may involve tunneling
- Nonadiabatic reactions
charge-transfer reactions where the time spent in DA near-degeneracy is short compared to the time for the electron to move between D and A localized states
- Polaron
an electronic state with a surrounding cloud of nuclear polarization
- Variable-range hopping
hopping transport in which the DA distances are disordered
- Coherent transport
transport based on wavelike motion that manifests interferences among coupling pathways
- Marcus theory
a high-temperature transition-state theory for electron transfer that describes the rate dependence on dielectric properties and reaction free energy
- Hopfield theory
a semiclassical electron transfer theory based on Fermi’s golden rule, framed in the context of electronic energy fluctuations, that includes nuclear tunneling effects and an explicit treatment of electronic tunneling barrier heights
- Flickering resonance (FR) transport
transport that results from the transient energetic alignment of multiple states, enabling coherent transport while the levels remain aligned
- Resonant tunneling
tunneling transport that arises from the alignment of multiple near-degenerate energy eigenstates separated by tunneling barriers
LITERATURE CITED
- 1.Bertini I, Gray HB, Stiefel EI, Valentine JS. 2007. Biological Inorganic Chemistry: Structure and Reactivity. Mill Valley, CA: Univ. Sci. Books [Google Scholar]
- 2.Phillips R, Kondev J, Theriot J, Garcia H. 2013. Physical Biology of the Cell. New York: Garland Sci; 2nd ed. [Google Scholar]
- 3.Marcus RA. 1993. Electron-transfer reactions in chemistry—theory and experiment. Rev. Mod. Phys 65:599–610 [Google Scholar]
- 4.Marcus RA, Sutin N. 1985. Electron transfers in chemistry and biology. Biochim. Biophys. Acta 811:265–322 [Google Scholar]
- 5.Balzani V 2001. Electron Transfer in Chemistry, Vol. 1–5 Weinheim, Ger.: Wiley-VCH [Google Scholar]
- 6.Beratan DN, Skourtis SS, Balabin IA, Balaeff A, Keinan S, et al. 2009. Steering electrons on moving pathways. Acc. Chem. Res 42:1669–78 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Beratan DN, Liu CR, Migliore A, Polizzi NF, Skourtis SS, et al. 2015. Charge transfer in dynamical biosystems, or the treachery of (static) images. Acc. Chem. Res 48:474–81 [DOI] [PMC free article] [PubMed] [Google Scholar]; This recent review describes the FR model and the role of fluctuations in biological ET.
- 8.Skourtis SS, Beratan DN. 1999. Theories of structure-function relationships for bridge-mediated electron transfer reactions. Adv. Chem. Phys 106:377–452 [Google Scholar]
- 9.Hopfield JJ. 1974. Electron transfer between biological molecules by thermally activated tunneling. PNAS 71:3640–44 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Beratan DN, Betts JN, Onuchic JN. 1991. Protein electron transfer rates set by the bridging secondary and tertiary structure. Science 252:1285–88 [DOI] [PubMed] [Google Scholar]
- 11.Beratan DN, Onuchic JN, Hopfield JJ. 1987. Electron-tunneling through covalent and noncovalent pathways in proteins. J. Chem. Phys 86:4488–98 [Google Scholar]
- 12.Venkatramani R, Keinan S, Balaeff A, Beratan DN. 2011. Nucleic acid charge transfer: black, white and gray. Coord. Chem. Rev 255:635–48 [DOI] [PMC free article] [PubMed] [Google Scholar]; This recent review of DNA ET theory, modeling, and simulation emphasizes the role of fluctuations and near-resonant processes.
- 13.Schuster GB. 2000. Long-range charge transfer in DNA: transient structural distortions control the distance dependence. Acc. Chem. Res 33:253–60 [DOI] [PubMed] [Google Scholar]
- 14.Murphy CJ, Arkin MR, Jenkins Y, Ghatlia ND, Bossmann SH, et al. 1993. Long-range photoinduced electron-transfer through a DNA helix. Science 262:1025–29 [DOI] [PubMed] [Google Scholar]
- 15.Baum R 1993. DNA double helix acts as ‘molecular wire.’ Chem. Eng. News 71:52–53 [Google Scholar]
- 16.Priyadarshy S, Risser SM, Beratan DN. 1996. DNA is not a molecular wire: protein-like electron-transfer predicted for an extended π-electron system. J. Phys. Chem 100:17678–82 [Google Scholar]
- 17.Stemp ED, Barton JK. 1996. Electron transfer between metal complexes bound to DNA: Is DNA a wire? Met. Ions Biol. Syst 33:325–65 [PubMed] [Google Scholar]
- 18.Lincoln P, Tuite E, Nordén B. 1997. Short-circuiting the molecular wire: cooperative binding of Δ-[Ru(phen)2dppz]2+ and Δ-[Rh(phi)2bipy]3+ to DNA. J. Am. Chem. Soc 119:1454–55 [Google Scholar]
- 19.Diederichsen U 1997. Charge transfer in DNA: a controversy. Angew. Chem. Int. Ed 36:2317–19 [Google Scholar]
- 20.Taubes G 1997. Double helix does chemistry at a distance—but how? Science 275:20–21 [DOI] [PubMed] [Google Scholar]
- 21.Wilson EK. 1999. DNA conductance convergence? New mechanisms claim to resolve much of the debate over how charge migrates through DNA—but questions remain. Chem. Eng. News 77:43–48 [Google Scholar]
- 22.Wilson EK. 2001. DNA charge migration: no longer an issue. Chem. Eng. News 79:29 [Google Scholar]
- 23.Zwang TJ, Tse ECM, Barton JK. 2018. Sensing DNA through DNA charge transport. ACS Chem. Biol 13:1799–809 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Teo RD, Rousseau BJG, Smithwick ER, Di Felice R, Beratan DN, Migliore A. 2019. Charge transfer between [4Fe4S] proteins and DNA is unidirectional. Implications for biomolecular signaling. Chem 5:122–37 [DOI] [PMC free article] [PubMed] [Google Scholar]; This theoretical study describes key thermodynamic constraints on ET signaling through DNA that may be associated with damage sensing.
- 25.Jones MR, Seeman NC, Mirkin CA. 2015. Programmable materials and the nature of the DNA bond. Science 347:1260901. [DOI] [PubMed] [Google Scholar]
- 26.O’Brien E, Holt ME, Thompson MK, Salay LE, Ehlinger AC, et al. 2017. The [4Fe4S] cluster of human DNA primase functions as a redox switch using DNA charge transport. Science 355:eaag1789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Sontz PA, Muren NB, Barton JK. 2012. DNA charge transport for sensing and signaling. Acc. Chem. Res 45:1792–800 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Teo RD, Smithwick ER, Migliore A, Beratan DN. 2019. A single AT-GC exchange can modulate charge transfer-induced p53-DNA dissociation. Chem. Commun 55:206–9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Migliore A, Naaman R, Beratan DN. 2015. Sensing of molecules using quantum dynamics. PNAS 112:E2419–28 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Lewis FD, Young RM, Wasielewski MR. 2018. Tracking photoinduced charge separation in DNA: from start to finish. Acc. Chem. Res 51:1746–54 [DOI] [PubMed] [Google Scholar]
- 31.Schrödinger E 1944. What Is Life? The Physical Aspect of the Living Cell and Mind. Cambridge, UK: Cambridge Univ. Press [Google Scholar]
- 32.Longuet-Higgins HC. 1962. Quantum mechanics and biology. Biophys. J 2:207–15 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Hopfield JJ. 2014. Whatever happened to solid state physics? Annu. Rev. Condens. Matter Phys 5:1–13 [Google Scholar]
- 34.Polizzi NF, Beratan DN. 2015. Open-access, interactive explorations for teaching and learning quantum dynamics. J. Chem. Educ 92:2161–64 [Google Scholar]
- 35.Fleming GR, Scholes GD, De Wit A, eds. 2011. 22nd Solvay conference on chemistry: quantum effects in chemistry and biology. Procedia Chem 3:1–366 [Google Scholar]
- 36.Scholes GD, Fleming GR, Chen LX, Aspuru-Guzik A, Buchleitner A, et al. 2017. Using coherence to enhance function in chemical and biophysical systems. Nature 543:647–56 [DOI] [PubMed] [Google Scholar]; This broad recent survey focuses on investigations of coherence effects in molecular and biophysics processes, including conceptual and experimental issues.
- 37.Mohseni M, Omar Y, Engel GS, Plenio MB, eds. 2014. Quantum Effects in Biology. Cambridge, UK: Cambridge Univ. Press [Google Scholar]
- 38.Cramer WA, Knaff DB. 1990. Energy Transduction in Biological Membranes: A Textbook of Bioenergetics. New York: Springer-Verlag [Google Scholar]
- 39.Aquino AJA, Beroza P, Beratan DN, Onuchic JN. 1995. Docking and electron-transfer between cytochrome c2 and the photosynthetic reaction-center. Chem. Phys 197:277–88 [Google Scholar]
- 40.Gray HB, Winkler JR. 2003. Electron tunneling through proteins. Q. Rev. Biophys 36:341–72 [DOI] [PubMed] [Google Scholar]
- 41.Pfeffer C, Larsen S, Song J, Dong MD, Besenbacher F, et al. 2012. Filamentous bacteria transport electrons over centimetre distances. Nature 491:218–21 [DOI] [PubMed] [Google Scholar]
- 42.Skourtis SS, Balabin IA, Kawatsu T, Beratan DN. 2005. Protein dynamics and electron transfer: electronic decoherence and non-condon effects. PNAS 102:3552–57 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.El-Naggar MY, Wanger G, Leung KM, Yuzvinsky TD, Southam G, et al. 2010. Electrical transport along bacterial nanowires from Shewanella oneidensis MR-1. PNAS 107:18127–31 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Reguera G, McCarthy KD, Mehta T, Nicoll JS, Tuominen MT, Lovley DR. 2005. Extracellular electron transfer via microbial nanowires. Nature 435:1098–101 [DOI] [PubMed] [Google Scholar]
- 45.Polizzi NF, Skourtis SS, Beratan DN. 2012. Physical constraints on charge transport through bacterial nanowires. Faraday Discuss. 155:43–62 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Blumberger J 2015. Recent advances in the theory and molecular simulation of biological electron transfer reactions. Chem. Rev 115:11191–238 [DOI] [PubMed] [Google Scholar]
- 47.Pirbadian S, El-Naggar MY. 2012. Multistep hopping and extracellular charge transfer in microbial redox chains. Phys. Chem. Chem. Phys 14:13802–8 [DOI] [PubMed] [Google Scholar]
- 48.Strycharz-Glaven SM, Snider RM, Guiseppi-Elie A, Tender LM. 2011. On the electrical conductivity of microbial nanowires and biofilms. Energ. Environ. Sci 4:4366–79 [Google Scholar]
- 49.Xu S, Jangir Y, El-Naggar MY. 2016. Disentangling the roles of free and cytochrome-bound flavins in extracellular electron transport from Shewanella oneidensis MR-1. Electrochim. Acta 198:49–55 [Google Scholar]
- 50.Conrado RJ, Haynes CA, Haendler BE, Toone EJ. 2013. Electrofuels: a new paradigm for renewable fuels In Advanced Biofuels and Bioproducts, ed. Lee JW, pp. 1037–64. New York: Springer [Google Scholar]
- 51.Genereux JC, Barton JK. 2010. Mechanisms for DNA charge transport. Chem. Rev 110:1642–62 [DOI] [PMC free article] [PubMed] [Google Scholar]; This comprehensive review discusses experimental and conceptual aspects of DNA ET.
- 52.Arnold AR, Grodick MA, Barton JK. 2016. DNA charge transport: from chemical principles to the cell. Cell Chem. Biol 23:183–97 [DOI] [PMC free article] [PubMed] [Google Scholar]; This review of DNA ET mechanisms includes links to cellular processes.
- 53.Murphy CJ, Arkin MR, Jenkins Y, Ghatlia ND, Bossmann SH, et al. 1993. Long-range photoinduced electron transfer through a DNA helix. Science 262:1025–29 [DOI] [PubMed] [Google Scholar]
- 54.Priyadarshy S, Risser SM, Beratan DN. 1996. DNA is not a molecular wire: protein-like electron-transfer predicted for an extended π-electron system. J. Phys. Chem 100:17678–82 [Google Scholar]
- 55.Beratan DN, Priyadarshy S, Risser SM. 1997. DNA: Insulator or wire? Chem. Biol 4:3–8 [DOI] [PubMed] [Google Scholar]
- 56.Felts AK, Pollard WT, Friesner RA. 1995. Multilevel redfield treatment of bridge-mediated long-range electron-transfer—a mechanism for anomalous distance dependence. J. Phys. Chem 99:2929–40 [Google Scholar]
- 57.Wan CZ, Fiebig T, Kelley SO, Treadway CR, Barton JK, Zewail AH. 1999. Femtosecond dynamics of DNA-mediated electron transfer. PNAS 96:6014–19 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Wan CZ, Fiebig T, Schiemann O, Barton JK, Zewail AH. 2000. Femtosecond direct observation of charge transfer between bases in DNA. PNAS 97:14052–55 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Lewis FD, Liu JQ, Weigel W, Rettig W, Kurnikov IV, Beratan DN. 2002. Donor-bridge-acceptor energetics determine the distance dependence of electron tunneling in DNA. PNAS 99:12536–41 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Giese B 2002. Long-distance electron transfer through DNA. Annu. Rev. Biochem 71:51–70 [DOI] [PubMed] [Google Scholar]
- 61.Beall E, Ulku S, Liu C, Wierzbinski E, Zhang Y, et al. 2017. Effects of the backbone and chemical linker on the molecular conductance of nucleic acid duplexes. J. Am. Chem. Soc 139:6726–35 [DOI] [PubMed] [Google Scholar]
- 62.Giese B 2000. Long-distance charge transport in DNA: the hopping mechanism. Acc. Chem. Res 33:631–36 [DOI] [PubMed] [Google Scholar]
- 63.Lewis FD, Letsinger RL, Wasielewski MR. 2001. Dynamics of photoinduced charge transfer and hole transport in synthetic DNA hairpins. Acc. Chem. Res 34:159–70 [DOI] [PubMed] [Google Scholar]
- 64.Bixon M, Jortner J. 2005. Incoherent charge hopping and conduction in DNA and long molecular chains. Chem. Phys 319:273–82 [Google Scholar]
- 65.Bixon M, Giese B, Wessely S, Langenbacher T, Michel-Beyerle ME, Jortner J. 1999. Long-range charge hopping in DNA. PNAS 96:11713–16 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Bixon M, Jortner J. 2002. Long-range and very long-range charge transport in DNA. Chem. Phys 281:393–408 [Google Scholar]
- 67.Renger T, Marcus RA. 2003. Variable-range hopping electron transfer through disordered bridge states: application to DNA. J. Phys. Chem. A 107:8404–19 [Google Scholar]
- 68.Conwell EM, Rakhmanova SV. 2000. Polarons in DNA. PNAS 97:4556–60 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Kurnikov IV, Tong GSM, Madrid M, Beratan DN. 2002. Hole size and energetics in double helical DNA: competition between quantum delocalization and solvation localization. J. Phys. Chem. B 106:7–10 [Google Scholar]
- 70.Lewis FD, Wu T, Zhang Y, Letsinger RL, Greenfield SR, Wasielewski MR. 1997. Distance-dependent electron transfer in DNA hairpins. Science 277:673–76 [DOI] [PubMed] [Google Scholar]; The first report of charge transfer in a DNA hairpin structure capped by a stilbene photooxidant shows exponential distance dependence of the rates.
- 71.Lewis FD, Wasielewski MR. 2013. Dynamics and efficiency of photoinduced charge transport in DNA: toward the elusive molecular wire. Pure Appl. Chem 85:1379–87 [Google Scholar]
- 72.Paul A, Watson RM, Wierzbinski E, Davis KL, Sha A, et al. 2010. Distance dependence of the charge transfer rate for peptide nucleic acid monolayers. J. Phys. Chem. B 114:14140–48 [DOI] [PubMed] [Google Scholar]
- 73.Skourtis S, Nitzan A. 2003. Effects of initial state preparation on the distance dependence of electron transfer through molecular bridges and wires. J. Chem. Phys 119:6271–76 [Google Scholar]
- 74.Levine AD, Iv M, Peskin U. 2016. Length-independent transport rates in biomolecules by quantum mechanical unfurling. Chem. Sci 7:1535–42 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Lewis FD, Zhu HH, Daublain P, Fiebig T, Raytchev M, et al. 2006. Crossover from superex-change to hopping as the mechanism for photoinduced charge transfer in DNA hairpin conjugates. J. Am. Chem. Soc 128:791–800 [DOI] [PubMed] [Google Scholar]; This report describes the carrier population on the ET bridge in the same systems that display exponential distance dependence.
- 76.Zhang YQ, Liu CR, Balaeff A, Skourtis SS, Beratan DN. 2014. Biological charge transfer via flickering resonance. PNAS 111:10049–54 [DOI] [PMC free article] [PubMed] [Google Scholar]; This article describes the FR model and its application to DNA charge transport.
- 77.Onuchic JN, Beratan DN. 1987. Molecular bridge effects on distant charge tunneling. J. Am. Chem. Soc 109:6771–78 [Google Scholar]
- 78.Beratan DN, Hopfield JJ. 1984. Calculation of electron-tunneling matrix-elements in rigid systems—mixed-valence dithiaspirocyclobutane molecules. J. Am. Chem. Soc 106:1584–94 [Google Scholar]
- 79.Onuchic JN, Beratan DN. 1990. A predictive theoretical model for electron tunneling pathways in proteins. J. Chem. Phys 92:722–33 [Google Scholar]
- 80.Onuchic JN, Beratan DN, Winkler JR, Gray HB. 1992. Pathway analysis of protein electron-transfer reactions. Annu. Rev. Biophys. Biomol. Struct 21:349–77 [DOI] [PubMed] [Google Scholar]
- 81.Migliore A, Polizzi NF, Therien MJ, Beratan DN. 2014. Biochemistry and theory of proton-coupled electron transfer. Chem. Rev 114:3381–465 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Jiang N, Kuznetsov A, Nocek JM, Hoffman BM, Crane BR, et al. 2013. Distance-independent charge recombination kinetics in cytochrome c–cytochrome c peroxidase complexes: compensating changes in the electronic coupling and reorganization energies. J. Phys. Chem. B 117:9129–41 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Wolfgang J, Risser SM, Priyadarshy S, Beratan DN. 1997. Secondary structure conformations and long range electronic interactions in oligopeptides. J. Phys. Chem. B 101:2986–91 [Google Scholar]
- 84.Curry WB, Grabe MD, Kurnikov IV, Skourtis SS, Beratan DN, et al. 1995. Pathways, pathway tubes, pathway docking, and propagators in electron-transfer proteins. J. Bioenerg. Biomembr 27:285–93 [DOI] [PubMed] [Google Scholar]
- 85.Balabin IA, Onuchic JN. 2000. Dynamically controlled protein tunneling paths in photosynthetic reaction centers. Science 290:114–17 [DOI] [PubMed] [Google Scholar]
- 86.Prytkova TR, Kurnikov IV, Beratan DN. 2005. Ab initio based calculations of electron-transfer rates in metalloproteins. J. Phys. Chem. B 109:1618–25 [DOI] [PubMed] [Google Scholar]
- 87.Prytkova TR, Kurnikov IV, Beratan DN. 2007. Coupling coherence distinguishes structure sensitivity in protein electron transfer. Science 315:622–25 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Hatcher E, Balaeff A, Keinan S, Venkatramani R, Beratan DN. 2008. PNA versus DNA: effects of structural fluctuations on electronic structure and hole-transport mechanisms. J. Am. Chem. Soc 130:11752–61 [DOI] [PubMed] [Google Scholar]; This paper describes the fluctuation-induced interchange of adenine and guanine HOMO positions based on quantum-classical simulations.
- 89.Tong GSM, Kurnikov IV, Beratan DN. 2002. Tunneling energy effects on GC oxidation in DNA. J. Phys. Chem. B 106:2381–92 [Google Scholar]
- 90.Balabin IA, Beratan DN, Skourtis SS. 2008. Persistence of structure over fluctuations in biological electron-transfer reactions. Phys. Rev. Lett 101:158102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Skourtis SS. 2013. Probing protein electron transfer mechanisms from the molecular to the cellular length scales. Biopolymers 100:82–92 [DOI] [PubMed] [Google Scholar]
- 92.Davidson VL. 2000. What controls the rates of interprotein electron-transfer reactions. Acc. Chem. Res 33:87–93 [DOI] [PubMed] [Google Scholar]
- 93.Davidson VL. 2008. Protein control of true, gated, and coupled electron transfer reactions. Acc. Chem. Res 41:730–38 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Skourtis SS, Waldeck DH, Beratan DN. 2010. Fluctuations in biological and bioinspired electron-transfer reactions. Annu. Rev. Phys. Chem 61:461–85 [DOI] [PMC free article] [PubMed] [Google Scholar]; This comprehensive review describes the fluctuation processes and timescales that enter ET reactions.
- 95.Skourtis SS, Lin J, Beratan DN. 2006. The effects of bridge motion on electron transfer reactions mediated by tunneling In Modern Methods for Theoretical Physical Chemistry of Biopolymers, ed. Starikov EB, Lewis JP, Tanaka S, pp. 357–82. Boston: Elsevier [Google Scholar]
- 96.Yue H, Khoshtariya D, Waldeck DH, Grochol J, Hildebrandt P, Murgida DH. 2006. On the electron transfer mechanism between cytochrome c and metal electrodes. Evidence for dynamic control at short distances. J. Phys. Chem. B 110:19906–13 [DOI] [PubMed] [Google Scholar]
- 97.Beratan DN, Onuchic JN. 1988. Adiabaticity and nonadiabaticity in bimolecular outer-sphere charge-transfer reactions. J. Chem. Phys 89:6195–203 [Google Scholar]
- 98.Skourtis SS, Dasilva AJR, Bialek W, Onuchic JN. 1992. A new look at the primary charge separation in bacterial photosynthesis. J. Phys. Chem 96:8034–41 [Google Scholar]
- 99.Subotnik JE, Jain A, Landry B, Petit A, Ouyang WJ, Bellonzi N. 2016. Understanding the surface hopping view of electronic transitions and decoherence. Annu. Rev. Phys. Chem 67:387–417 [DOI] [PubMed] [Google Scholar]
- 100.Woiczikowski PB, Steinbrecher T, Kubar T, Elstner M. 2011. Nonadiabatic QM/MM simulations of fast charge transfer in Escherichia coli DNA photolyase. J. Phys. Chem. B 115:9846–63 [DOI] [PubMed] [Google Scholar]
- 101.Renaud N, Harris MA, Singh APN, Berlin YA, Ratner MA, et al. 2016. Deep-hole transfer leads to ultrafast charge migration in DNA hairpins. Nat. Chem 8:1015–21 [DOI] [PubMed] [Google Scholar]
- 102.Gray HB, Winkler JR. 2015. Hole hopping through tyrosine/tryptophan chains protects proteins from oxidative damage. PNAS 112:10920–25 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103.Winkler JR, Gray HB. 2015. Electron flow through biological molecules: Does hole hopping protect proteins from oxidative damage? Q. Rev. Biophys 48:411–20 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104.Polizzi NF, Migliore A, Therien MJ, Beratan DN. 2015. Defusing redox bombs? PNAS 112:10821–22 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 105.Beratan DN, Waldeck DH. 2016. Hot holes break the speed limit. Nat. Chem 8:992–93 [DOI] [PubMed] [Google Scholar]
- 106.Peters JW, Beratan DN, Schut GJ, Adams MWW. 2018. On the nature of organic and inorganic centers that bifurcate electrons, coupling exergonic and endergonic oxidation-reduction reactions. Chem. Commun 54:4091–99 [DOI] [PubMed] [Google Scholar]
- 107.Zhang P, Yuly JL, Lubner CE, Mulder DW, King PW, et al. 2017. Electron bifurcation: thermodynamics and kinetics of two-electron brokering in biological redox chemistry. Acc. Chem. Res 50:2410–17 [DOI] [PubMed] [Google Scholar]; This paper describes electron bifurcation processes in the context of modern ET theory.
- 108.Weiss EA, Ahrens MJ, Sinks LE, Gusev AV, Ratner MA, Wasielewski MR. 2004. Making a molecular wire: charge and spin transport through para-phenylene oligomers. J. Am. Chem. Soc 126:5577–84 [DOI] [PubMed] [Google Scholar]
- 109.Berlin YA, Kurnikov IV, Beratan D, Ratner MA, Burin AL. 2004. DNA electron transfer processes: some theoretical notions In Long-Range Charge Transfer in DNA II, ed. Schuster GB, pp. 1–36. Top. Curr. Chem. 237 Berlin: Springer [Google Scholar]
- 110.Kubar T, Elstner M. 2008. What governs the charge transfer in DNA? The role of DNA conformation and environment. J. Phys. Chem. B 112:8788–98 [DOI] [PubMed] [Google Scholar]
- 111.Gutierrez R, Caetano R, Woiczikowski PB, Kubar T, Elstner M, Cuniberti G. 2010. Structural fluctuations and quantum transport through DNA molecular wires: a combined molecular dynamics and model Hamiltonian approach. New J. Phys 12:023022 [Google Scholar]
- 112.Cailliez F, Muller P, Firmino T, Pernot P, de la Lande A. 2016. Energetics of photoinduced charge migration within the tryptophan tetrad of an animal (6–4) photolyase. J. Am. Chem. Soc 138:1904–15 [DOI] [PubMed] [Google Scholar]
- 113.Renaud N, Berlin YA, Lewis FD, Ratner MA. 2013. Between superexchange and hopping: an intermediate charge-transfer mechanism in poly(A)-poly(T) DNA hairpins. J. Am. Chem. Soc 135:3953–63 [DOI] [PubMed] [Google Scholar]
- 114.Levine AD, Iv M, Peskin U. 2018. Formulation of long-range transport rates through molecular bridges: from unfurling to hopping. J. Phys. Chem. Lett 9:4139–45 [DOI] [PubMed] [Google Scholar]
- 115.Kim H, Segal D. 2017. Controlling charge transport mechanisms in molecular junctions: distilling thermally induced hopping from coherent-resonant conduction. J. Chem. Phys 146:164702. [DOI] [PubMed] [Google Scholar]
- 116.Venkatramani R, Davis KL, Wierzbinski E, Bezer S, Balaeff A, et al. 2011. Evidence for a near-resonant charge transfer mechanism for double-stranded peptide nucleic acid. J. Am. Chem. Soc 133:62–72 [DOI] [PubMed] [Google Scholar]
- 117.Venkatramani R, Wierzbinski E, Waldeck DH, Beratan DN. 2014. Breaking the simple proportionality between molecular conductances and charge transfer rates. Faraday Discuss. 174:57–78 [DOI] [PubMed] [Google Scholar]
- 118.Wierzbinski E, Venkatramani R, Davis KL, Bezer S, Kong J, et al. 2013. The single-molecule conductance and electrochemical electron-transfer rate are related by a power law. ACS Nano 7:5391–401 [DOI] [PubMed] [Google Scholar]
- 119.Xing YJ, Park TH, Venkatramani R, Keinan S, Beratan DN, et al. 2010. Optimizing single-molecule conductivity of conjugated organic oligomers with carbodithioate linkers. J. Am. Chem. Soc 132:7946–56 [DOI] [PubMed] [Google Scholar]
- 120.Xiang LM, Palma JL, Bruot C, Mujica V, Ratner MA, Tao NJ. 2015. Intermediate tunnelling-hopping regime in DNA charge transport. Nat. Chem 7:221–26 [DOI] [PubMed] [Google Scholar]; This paper describes experimental break-junction studies on DNA G-blocks that display resistance oscillations characteristic of electronic coherence.
- 121.Liu CR, Xiang LM, Zhang YQ, Zhang P, Beratan DN, et al. 2016. Engineering nanometre-scale coherence in soft matter. Nat. Chem 8:941–45 [DOI] [PubMed] [Google Scholar]; This article reports on theoretical designs and experimental validations of coherence engineering in nanometer-scale DNA constructs through exploiting FR mechanisms.
- 122.Liu CR, Beratan DN, Zhang P. 2016. Coarse-grained theory of biological charge transfer with spatially and temporally correlated noise. J. Phys. Chem. B 120:3624–33 [DOI] [PubMed] [Google Scholar]
- 123.Young RM, Singh APN, Thazhathveetil AK, Cho VY, Zhang YQ, et al. 2015. Charge transport across DNA-based three-way junctions. J. Am. Chem. Soc 137:5113–22 [DOI] [PubMed] [Google Scholar]
- 124.Sha RJ, Xiang LM, Liu CR, Balaeff A, Zhang YQ, et al. 2018. Charge splitters and charge transport junctions based on guanine quadruplexes. Nat. Nanotechnol 13:316–21 [DOI] [PubMed] [Google Scholar]; This paper describes the simulation and experimental characterization of a current splitter based on a DNA G4 box motif
- 125.Zhang YQ, Zhang WB, Liu CR, Zhang P, Balaeff A, Beratan DN. 2016. DNA charge transport: moving beyond 1D. Surf. Sci 652:33–38 [Google Scholar]
- 126.Zhang YQ, Young RM, Thazhathveetil AK, Singh APN, Liu CR, et al. 2015. Conformationally gated charge transfer in DNA three-way junctions. J. Phys. Chem. Lett 6:2434–38 [DOI] [PubMed] [Google Scholar]
- 127.Mondal PC, Fontanesi C, Waldeck DH, Naaman R. 2016. Spin-dependent transport through chiral molecules studied by spin-dependent electrochemistry. Acc. Chem. Res 49:2560–68 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 128.Naaman R, Waldeck DH. 2015. Spintronics and chirality: spin selectivity in electron transport through chiral molecules. Annu. Rev. Phys. Chem 66:263–81 [DOI] [PubMed] [Google Scholar]; This paper describes spin filtering in chiral structures, including DNA.
- 129.Michaeli K, Kantor-Uriel N, Naaman R, Waldeck DH. 2016. The electron’s spin and molecular chirality—How are they related and how do they affect life processes? Chem. Soc. Rev 45:6478–87 [DOI] [PubMed] [Google Scholar]
- 130.Naaman R, Waldeck DH. 2012. Chiral-induced spin selectivity effect. J. Phys. Chem. Lett 3:2178–87 [DOI] [PubMed] [Google Scholar]
- 131.Zwang TJ, Hurlimann S, Hill MG, Barton JK. 2016. Helix-dependent spin filtering through the DNA duplex. J. Am. Chem. Soc 138:15551–54 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 132.Michaeli K, Beratan DN, Waldeck DH, Naaman R. 2019. Voltage-induced long-range coherent electron transfer through organic molecules. PNAS 116:5931–36 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 133.Seeman NC. 2016. Structural DNA Nanotechnology. Cambridge, UK: Cambridge Univ. Press [Google Scholar]
- 134.Hong F, Zhang F, Liu Y, Yan H. 2017. DNA origami: scaffolds for creating higher order structures. Chem. Rev 117:12584–640 [DOI] [PubMed] [Google Scholar]
- 135.Wagenbauer KF, Sigl C, Dietz H. 2017. Gigadalton-scale shape-programmable DNA assemblies. Nature 552:78–83 [DOI] [PubMed] [Google Scholar]
RELATED RESOURCES
- DeVault D 1984. Quantum Mechanical Tunneling in Biological Systems. Cambridge, UK: Cambridge Univ. Press. 2nd ed. [Google Scholar]
- Hoffmann PM. 2012. Life’s Ratchet: How Molecular Machines Extract Order from Chaos. New York: Basic [Google Scholar]
- Jortner J, Bixon M, eds. 1999. Electron Transfer: From Isolated Molecules to Biomolecules, Parts 1–2 Adv. Chem. Phys Vols. 106–107. New York: Wiley [Google Scholar]
- May V, Kuhn O. 2011. Charge and Energy Transfer Dynamics in Molecular Systems. Weinheim, Ger.: Wiley-VCH. 3rd ed. [Google Scholar]
- Milo R, Phillips R. 2015. Cell Biology by the Numbers. New York: Garland [Google Scholar]
- Wagenknecht H-A, ed. 2006. Charge Transfer in DNA: From Mechanism to Applications. Weinheim, Ger.: Wiley-VCH [Google Scholar]