Abstract
Although helium pycnometry is generally the method of choice for skeletal density measurements of porous materials, few studies have provided a wide range of case studies that demonstrate how to best interpret raw data and perform measurements using it. The examination of several different classes of materials yielded signature traits from helium pycnometry data that are highlighted. Experimental parameters important in obtaining the most precise and accurate value of skeletal density from the helium pycnometer are as high as possible percent fill volume and good thermostability. The degree of sample activation is demonstrated to affect the measured skeletal density of porous zeolitic, carbon, and hybrid inorganic–organic materials. In the presence of a significant amount of physisorbed contaminants (water vapor, atmospheric gases, residual solvents, etc.), which was the case for ZSM-5, MIL-53, and F400, but not ZIF-8, the skeletal density tended to be overestimated in the low percent volume region. In addition, the kinetic data (i.e., skeletal density vs measurement cycle) reveals distinctive traits for a properly activated vs a nonactivated sample for all examined samples: activated samples with a significant amount of mass loss show a curved down plot that eventually reaches the equilibrium value, whereas nonactivated, nonporous, or extremely hydrophobic samples exhibit a flat line. This work illustrates how helium pycnometry can provide information about the structure of a material, and that, conversely, when the structure of the material and its percent mass loss after activation (amount of physisorbed contaminants) are known, the behavior of activated and nonactivated samples in terms of skeletal density, percent fill volume, and measurement cycle can be predicted.
Graphical abstract
INTRODUCTION
Many industries, such as adsorbent,1 agricultural,2 construction,3-4 and pharmaceutical5 industries rely on skeletal density measurements to determine engineering properties and the quality or performance of adsorbents, food particles, construction materials, and drug powders/tablets. The skeletal density of a sample is an intrinsic property equal to the ratio of its mass to its corresponding skeletal volume. There are several different types of density (bulk, true, skeletal), and they are distinguished by the types of volume used (Figure 1). Bulk volume, which is dependent on the particle packing, is the macroscopic volume of a sample that includes all pore spaces and interparticle spaces.6 In contrast, true volume only consists of the actual volume of the molecules or atoms that make up the material and excludes all pores (accessible and inaccessible) and interparticle spaces.6 The skeletal volume excludes all spaces that are accessible to the outside but includes the volume of all closed pores that are physically inaccessible.6-8
Figure 1.
Cross-sectional diagram of different types of volume. (left) Bulk volume includes all pores and interparticle spaces. (center) True volume excludes all pores and interparticle spaces. (right) Skeletal volume excludes accessible pores and interparticle spaces but includes closed pores. Black denotes region included in the volume. White denotes region excluded from the volume.
While there are different ways to determine the skeletal volume of a sample, probing pores and interparticle spaces with gas pycnometry is the most efficient and accurate method for microporous materials. The skeletal volume, in this case, is essentially the volume that very small gas atoms or molecules (e.g., helium) cannot penetrate. Consequently, measuring the skeletal volume is important to applications where the amount or volume of gas displaced must be known. For example, in adsorption-based applications, the skeletal volume of an adsorbent is relevant in gas adsorption measurements for void volume determination or buoyancy correction, which is needed to determine the surface excess gas uptake.1
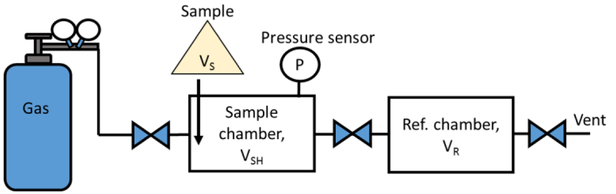
A gas pycnometer typically consists of a sample chamber and a reference chamber of known, calibrated volumes, VSH and VR, respectively. Very careful calibration of these volumes must be performed to ensure accurate measurements. In the configuration shown in Figure 2, the gas enters the sample chamber before the reference chamber; however, the order of these chambers could be reversed without affecting the measurement. Generally, the sample is activated, weighted (quantity will depend on size of sample holder), and placed into the sample holder, which is then quickly loaded (within a few seconds) into the sample chamber to avoid the uptake of moisture and other atmospheric contaminants. Ensuring the sample remains activated is important to obtain the true mass of the sample and avoid error in sample volume due to adsorbed water vapor, atmospheric gases, and/or volatile organic compounds. 9-10 With the sample inside, the sample chamber is then dosed with a gas (e.g., helium) to an initial pressure, Pi. The gas is then allowed to expand into the reference chamber, causing the pressure to drop to the final pressure, Pf. For the instrument configuration shown in Figure 2, the volume of the sample, VS, can be determined from the change in pressure and the known volumes of the reference and sample chambers using eq 1,
| (1) |
Figure 2.
Schematic of a typical helium pycnometer with sample chamber before reference chamber. A pressure sensor is located at the sample chamber and gives pressure reading of P. VSH is the volume of the sample chamber. VR is the volume of the reference chamber. VS is the skeletal volume of the sample.
The skeletal density of the sample, ρS, can then be calculated using eq 2,
| (2) |
where mS is the dry sample mass and VS is the skeletal volume of the sample. With the use of a gas probe with a small kinetic diameter, such as helium, at 0.26 nm,11 nearly all of the accessible pore spaces and surface roughness of the sample could be accessed to give the best approximation of the skeletal volume of the sample. The small size of helium also minimizes the error due to the annulus volume, which is the volume between the surface of the solid and the closest distance at which the gas molecule approaches it.7 This distance is 50 pm for He.7 Furthermore, given that helium is an inert and ideal gas, it can be assumed to be nonadsorbing, which is necessary to accurately determine the sample volume.12 A probe gas that is adsorbed/desorbed by the sample can alter the amount of free gas and, thereby, alter the pressure readings so that the change in pressure cannot be accurately related to the sample volume using eq 1.
Although helium pycnometry is generally the method of choice for skeletal density measurements for porous materials due to its simplicity, well-established accuracy, and existing measurement guidelines,9 few studies have provided real case studies that demonstrate how to best perform measurements and interpret raw data using it. The aims of this article are two-fold. The first aim is to illustrate how to collect reliable skeletal density from the helium pycnometer by examining the effect of several experimental parameters, such as sample holder percent fill volume, sample holder size, and analysis temperature. The second aim is to demonstrate the interpretation of the raw data (low percent volume region, high percent volume region, and kinetic data) in relation to the degree of sample activation to identify signature traits indicative of complete or incomplete sample activation by the use of different classes of materials.
EXPERIMENTAL SECTION
Certain commercially available items may be identified in this paper. This identification does not imply recommendation by the National Institute of Standards and Technology (NIST) nor does it imply that it is the best available for the purposes described.
Materials
NIST reference material, RM 8852 (ammonium ZSM-5 zeolite), was obtained from the NIST (Gaithersburg, MD). Silicon was purchased from American Elements (Los Angeles, CA). ZIF-8 (Basolite Z1200) was purchased from Sigma-Aldrich (St. Louis, MO). F400 activated carbon was obtained from Quantachrome Instruments (Boynton Beach, FL). All samples were used as-received without further modifications. N,N-dimethylformamide (DMF, >99.9%), aluminum nitrate nonahydrate (≥98%), and terephthalic acid (98%) for the synthesis of MIL-53 were acquired from Sigma Aldrich (St. Louis, MO). Helium (99.999%) was purchased from Roberts Oxygen Company, Inc. (Rockville, MD).
Synthesis of MIL-53(Al)
MIL-53(Al) was synthesized according to literature protocol with small modifications.13 Aluminum nitrate nonahydrate (12.48 g, 33.33 mmol), terephthalic acid (2.76 g, 16.67 mmol), and water (48 mL, 2.67 mol) were placed inside a 125 mL Teflon-lined acid digestion vessel (Parr Instrument Company, Moline, IL). The mixture was stirred for 2 min until the reagents were well dispersed (aluminum nitrate completely dissolved while terephthalic acid remained suspended in solution). The vessel was sealed and then placed into a basic 120 V gravity convection oven (VWR, Bridgeport, NJ) heated to 220 °C at a rate of ≈ 1 °C/min to 2 °C/min and held at 220 °C for 72 h. After cooling for ≈ 6 h to room temperature, the vessel was opened, and the resulting white solid that was suspended in a clear yellow solution was vacuum filtered over a fine-fritted funnel to give MIL-53(Al) as-syn as a white solid powder (≈4 g nonactivated sample). To remove the occluded terephthalic acid from the MOF framework, MIL-53(Al) (≈500 mg) was placed into an 8-dram vial and DMF (≈10 mL) was added to it. The suspension was heated at 120 °C overnight (16 h) in a sand bath on an IKA RET basic IKAMAG safety control hot plate (Sigma Aldrich, St. Louis, MO). The mixture was vacuum filtered over a fine-fritted funnel to recover the white solid, which was then activated under high vacuum (10−7 mbar) using a tube furnace (Lindberg Blue M, Thermo Fisher Scientific Inc., Waltham, MA) attached to an Edwards TIC pumping station (Edwards, West Sussex, UK) to remove the DMF solvent. The temperature was ramped up from room temperature to 200 °C at a rate of 1 °C/min, held at 200 °C for 18 h, and then cooled (over ≈6 h) to room temperature to give MIL-53(Al) ht (≈2 g, ≈58% yield) as a white solid. Upon exposure to air, the MOF adsorbs water and becomes MIL-53(Al) It, also a white solid. The powder X-ray diffraction patterns of the MIL-53(Al) It (Figure SI, Supporting Information) was collected on a Bruker D8 Discover X-ray diffractometer (Bruker, Billerica, MA) equipped with an area detector and a Cu Ka radiation X-ray source. The sample powder was packed into the sample holder, and 5 frames in steps of 7 2θ each with progressively larger 2θ range coverage were collected for 180 s each using the gadds (general area detector diffraction system) software (version 4.1.51) to cover the range of 5 to 50 2θ. The frames were overlaid, and peaks were integrated using DIFFRAC.EVA software (version 4.1.1).
Ex Situ Sample Activation
For measurements made in the helium pycnometer, activated samples were outgassed in a tube furnace (Lindberg Blue M, Thermo Fisher Scientific Inc., Waltham, MA) attached to an Edwards TIC pumping station (Edwards, West Sussex, UK) that was equipped with a nXDS6i scroll back pump (vacuum level of 10−2 mbar, Edwards, West Sussex, UK) and an EXT-75DX turbo pump (vacuum level of 10 −9 mbar, Edwards, West Sussex, UK). The following activation protocols were used with the porous samples.
For RM 8852, under high vacuum (10−3 mbar), the temperature was ramped up from room temperature to 350 °C at a rate of 1 °C/min, held at 350 °C for 12 h, and then cooled (over ≈7 h) to room temperature (final vacuum level of 10−7 mbar).
For MIL-53, under high vacuum (10−3 mbar), the temperature was ramped up from room temperature to 200 °C at a rate of 1 °C/min, held at 200 °C for 18 h, and then cooled (over ≈6 h) to room temperature (final vacuum level of 10−7 mbar).
For F400 carbon, under high vacuum (10−3 mbar), the temperature was ramped up from room temperature to 200 °C at a rate of 1 °C/min, held at 200 °C for 18 h, and then cooled (over ≈6 h) to room temperature (final vacuum level of 10 −7 mbar).
For ZIF-8, under high vacuum (10−3 mbar), the temperature was ramped up from room temperature to 150 °C at a rate of 1 °C/min, held at 150 °C for 8 h, and then cooled (over ≈6 h) to room temperature (final vacuum level of 10−7 mbar).
After activation, each sample was transferred under air-free conditions from the sealed activator tube to an argon glovebox (Inert Lab Glovebox, Innovative Technology, Port Washington, NY) for storage until helium pycnometry measurements were performed. The percent mass losses for the samples after activation are 7 % mass fraction for ZSM-5, 12 % mass fraction for F400, 6 % mass fraction for MIL-53, and 0.5 % mass fraction for ZIF-8.
Helium Pycnometer
Skeletal densities were measured in an AccuPyc II 1340 pycnometer (Micromeritics, Norcross, GA) with helium as the probe gas. The AccuPyc II 1340 pycnometer is equipped with three different size sample holders: 10 cm3, 3.5 cm3, and 1 cm3. Each sample holder also has a fritted cap that prevents fine materials from being displaced by helium gas during measurement. Before each measurement, each sample (except for Si and the nonactivated samples, which did not require outgassing) was activated ex situ (see procedure above) and loaded into one of the He pycnometer sample holders, capped with the fritted cap inside the glovebox, and then quickly transferred (≈ 5 s) to the He pycnometer sample chamber in order to avoid uptake of moisture and other atmospheric contaminants. The nonactivated samples were loaded into the sample holders in air. The amount of sample used was varied (milligrams to grams) from low to high percent fill volume. Each measurement was made by dosing the sample chamber with helium (to ≈ 134 kPa), which was then allowed to expand into the reference chamber. The pressure was determined by a 316L SS pressure sensor (Measurement Specialties, Fremont, CA) with ± 0.1% pressure nonlinearity in the pressure range of 0 kPa to 207 kPa. Each measurement collected data points from 50 cycles. Raw data were given for skeletal density vs measurement cycle number. For plots of skeletal density vs. volume %, each data point is the average value from measurements 11 through 50, to ensure only equilibrium values (i.e., the values from one cycle to the next should be nearly consistent) are mainly used and to keep the analysis consistent among the different samples. The skeletal density was determined from the best linear fit to the plot of sample mass (g) vs volume (cm3). The uncertainty U(k=2) in the skeletal density was determined from 2 standard error of the best fit. For measurements not made at room temperature (≈ 298 K), the temperature (± 0.1 K) was controlled by an add-on heater (Ascon Technologic, Cleveland, OH).
Computational Estimation of Skeletal Density
Computational methods were used to characterize the adsorbent pore structure and, therefrom, compute the average skeletal density of the crystalline materials examined in the present work (ZSM-5, MIL-53, and ZIF-8). The geometrical technique chosen is a variation of those previously used by some of the present authors and described in detail elsewhere.14-16 In short, the adsorbent free volume (i.e., the volume of the adsorbent unit cell not eclipsed by the radii of constituent atoms of the framework) is computed using the so-called accessible volume metric described by Frost et al. 17 For a given adsorbent structure (see below), each framework atom is assigned an atomic van der Waals (vdW) radius. The unit cell is then gridded into voxels18 with side length 10 pm or smaller. The technique then attempts to place a spherical probe atom (in this case, helium) at each voxel position; a voxel is counted as “free volume” if the probe atom does not overlap the vdW radius of any framework atoms. The skeletal density is then computed as the mass of the unit cell divided by the unit cell volume minus the free volume.
The crystal structure of each crystalline adsorbent was reconstructed from previously published XRD crystal structure data. Pristine ZIF-8 and MIL-53 (specifically, the MIL-53(Al) ht variant) crystals were reconstructed exactly as described in references 19 and 13, respectively.13, 19 ZSM-5 was reconstructed first as a silicate crystal according to the monoclinic structure given in reference 20;20 it was then converted to an aluminosilicate by randomly exchanging Si for Al according to the Löwenstein Rule until the Al/Si ratio of 3.3:92.7 was achieved. Ammonium cations were then randomly placed near the newly substituted Al atoms, with a bond distance of approximately 0.15 nm, while simultaneously avoiding overlap with other atoms in the framework. This randomization of the cationated aluminosilicate was repeated to obtain an ensemble of realized structures.
Atomic radii for the framework atoms and the He probe were assigned according to the vdW radii given in references. 21-23: 0.120 nm for H, 0.170 nm for C, 0.155 nm for N, 0.152 nm for O, 0.210 nm for Si, 0.184 nm for Al, 0.139 nm for Zn, and 0.114 nm for He.21-23 These radii were tested against the well-characterized skeletal density of ZIF-8 (1.4 g/cm3),24 at which point we found that this set of vdW radii systematically underestimated the skeletal density; in other words, the atomic radii were too large. We linearly adjusted the set of vdW radii to approximate the ZIF-8 density (since that experimental measurement closely corresponded with previous measurements by Zhou et al.24), settling on values at 80 % of the original vdW radii. (This is, admittedly, an empirical correction but is evidence that the conventional set of vdW radii was inadequate for the computational estimates desired here.) Computational estimates of the skeletal densities given in Table 1 are based on these adjusted radii. Uncertainty in the computed skeletal density was estimated by repeating the calculation for ten randomized realizations of the voxel grid and, if applicable, the cationated aluminosilicate framework, followed by application of a statistical jackknife to obtain 95 % confidence intervals.
Table 1.
Average Skeletal Density Values (g/cm3)
| Entries | silicon | ZSM-5 | F400 | MIL-53 | ZIF-8 | ||
|---|---|---|---|---|---|---|---|
| 1 | experimental | activated | 2.328 ± 0.007 | 2.349 ± 0.004 | 2.200 ± 0.007 | 1.613 ± 0.003 | 1.482 ± 0.002 |
| 2 | nonactivated | N/A | 2.178 ± 0.024 | 2.015 ± 0.033 | 1.609 ± 0.009 | 1.501 ± 0.004 | |
| 3 | computational (from this study) | activated | N/A | 2.31 ± 0.004 | N/A | 1.55 ± 0.00005 | 1.50 ± 0.00008 |
| 4 | nonactivated | N/A | N/A | N/A | 1.63±0.001 | N/A | |
| 5 | literature | activated | 2.32925 | N/A | 2.140 28 | N/A | ~1.424 |
RESULTS AND DISCUSSION
I. Influence of Experimental Parameters on Measurement using Si
Given that silicon (Si) has a known reference density from which a reliable measurement protocol could be applied, confirmed, and established, the skeletal density of Si using the helium pycnometer was determined first. Si has been certified with a skeletal density of 2.329 g/cm3, 25 which was determined by hydrostatic weighing and agreed well with a theoretical skeletal density of 2.330 g/cm3 from its face-centered diamond cubic crystal structure. As a nonporous material, the crystal density of Si is effectively identical to its true and skeletal density. The nonporous nature of Si also eliminates the need to activate the sample and consequently ensures moisture-free transfer to the pycnometer.
Several experimental parameters of the He pycnometer were explored to determine the best protocol to accurately determine the skeletal density of the sample. The skeletal density of Si was measured in the helium pycnometer using different sample percent fill volume, different size sample holders, and different analysis temperatures (298 K to 318 K). The percent fill volume here is defined as the percent of the sample chamber volume plus reference chamber volume that is filled with the skeletal volume of the sample.
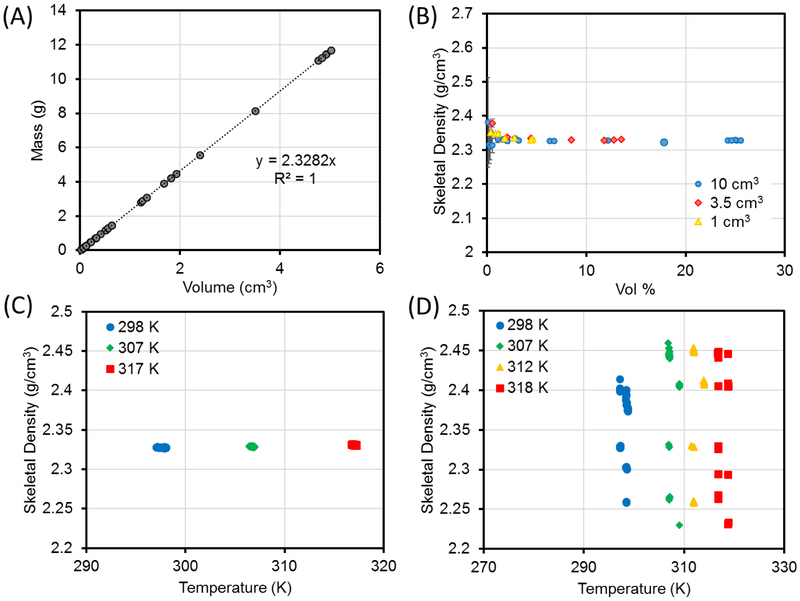
As can be seen in Figure 3A, an average fitted value of (2.328 ± 0.007) g/cm3 was determined from the slope of a plot of sample mass as a function of sample volume. This value is in agreement with the literature value of 2.329 g/cm3 and the theoretical value of 2.330 g/cm3. Figure 3B shows that the skeletal density of Si became more precise and accurate (approaches expected value of 2.330 g/cm3) as the percent fill volume increased whereas the noise and error grew drastically as the percent fill volume decreased. Thus, a fill volume as high as possible is recommended to achieve reliable measurements. This is in agreement with the recommendation made by ISO.9
Figure 3.
(A) The skeletal density of Si determined from the slope of the linear fit for the plot of mass vs volume. (B–D) The skeletal density of Si measured using a He pycnometer under varied experimental parameters. (B) Sample percent fill volume and sample holder used were varied. (C) Analysis temperature was varied. (D) Analysis under poor thermal stability (± 1 K). In panels A and B, each data point is the average value of (A) the skeletal volume or (B) skeletal density and percent fill volume (along with uncertainty) from measurement cycles made on a different aliquot of Si. In panels C and D, each data point is the skeletal density from an individual measurement cycle made on the same aliquot of Si.
The choice of sample holder size did not make a difference in the trends observed by different percent fill volume, although the size of the sample holder could limit the maximum sample percent fill volume that is possible for the analysis (Figure 3B). For example, the theoretical maximum sample percent fill volume possible for the small (1 cm3), medium (3.5 cm3), and large (10 cm3) sample holders are 25 %, 41 %, and 57 % for a nonporous material using the AccuPyc II 1340 pycnometer. For samples that are porous or cannot be packed well, those values may be even lower.
As the analysis temperature increased from 298 K to 307 K to 317 K, no significant difference in density could be observed for the same aliquot of Si. For example, the average density of a high-fill volume aliquot increased from 2.327 g/cm3to 2.328 g/cm3 to 2.331 g/cm3, but the difference is within the noise level of these measurements (± 0.003 g/cm3) (Figure 3C). If the sample was not thermally equilibrated, the measurement became noisier (Figure 3D). This is in agreement with interference due to thermal effect on pressure stability reported by the ISO.9
II. Helium Pycnometer Results for Activated and Nonactivated ZSM-5, F400, MIL-53, and ZIF-8
The effect of moisture on the measurement was also studied. The sample studied was NIST RM 8852 (also known as ZSM-5), a well-known zeolite that is being used as a zeolitic reference material to provide reference data for high-pressure isotherm measurements26 and has application in catalysis.27 On the basis of the results from the Si measurement, the skeletal density of ZSM-5 was measured using the He pycnometer at room temperature (≈ 298 K). However, unlike Si, ZSM-5 is a microporous material that requires activation before measurement to remove moisture and other physisorbed species. A sample is considered activated if it is outgassed to remove water vapor and other contaminants (and is transferred to the sample holder in the glovebox); a sample is considered nonactivated if it is not outgassed.
IIa. Kinetic Data
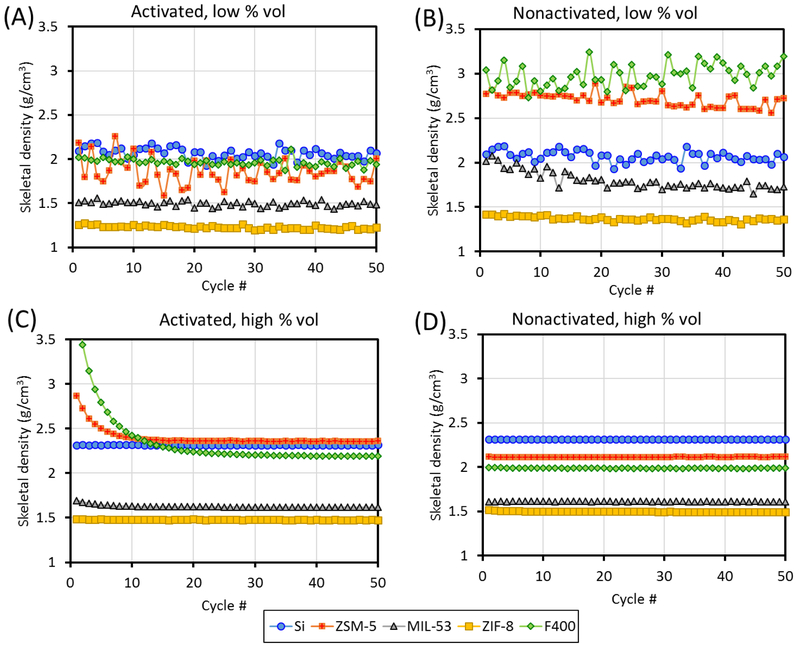
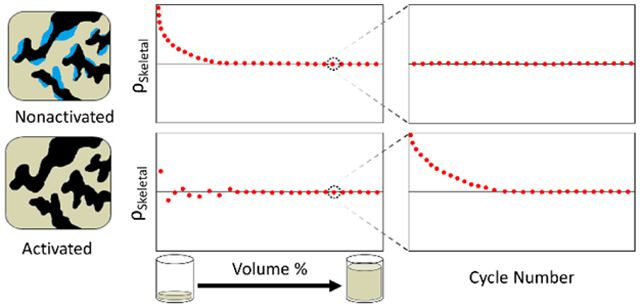
The kinetic data (skeletal density vs measurement cycle) for ZSM-5 was analyzed for four scenarios: (1) activated, high percent fill volume, (2) nonactivated, high percent fill volume, (3) activated, low percent fill volume, and (4) nonactivated, low percent fill volume. For the high vs low percent fill volume, the most obvious difference in the kinetic data is that the high percent fill volume data is significantly more steady than the low percent fill volume data (Figure 4). This is expected as the same uncertainty, x, in volume determination would have a smaller effect if Vs ≫ x than it would if Vs ≈ x. For the high percent fill volume kinetic data, two distinct behaviors are observed for the activated and nonactivated samples. The activated sample started off with a slightly higher skeletal density that quickly dropped and reached the equilibrium value after 10–20 cycles and remained stable, whereas the nonactivated sample appeared to have reached equilbrium since the first cycle. To explore whether such behavior is generalizable to other classes of porous materials and, thereby, potentially serves as an indicator of complete vs incomplete sample activation, the analysis was extended to three other porous samples: an activated carbon (F400) and two well-known metal-organic frameworks (MIL-53 and ZIF-8).
Figure 4.
Representative graphs of helium pycnometry kinetic data for the Si, ZSM-5, F400 carbon, MIL-53, and ZIF-8, in activated and nonactivated forms and at low and high percent fill volume. The data for Si, which was not activated but can be assumed to be free of physisorbed contaminants, is included in panels A and C, for the purpose of comparison only.
A possible explanation for the observed shape for the kinetic data of the activated samples has been suggested by the ISO to be attributable to a small amount of physisorbed atmospheric gases (nitrogen, oxygen, argon, etc.) during the transfer of the sample holder to the instrument. The amount of physisorbed species also appears to be correlated with the amount of contaminants (water vapor, solvents, volatile organic compounds, etc.) that was originally present in the sample (% mass loss after activation: 7 % mass fraction for ZSM-5, 12 % mass fraction for F400, 6 % mass fraction for MIL-53, and 0.5 % mass fraction for ZIF-8), with F400 taking the longest to reach equilibrium value, whereas the decreasing slope is barely noticeable in MIL53 and is not present for Si and ZIF-8. As the weakly physisorbed gas is being desorbed in the first few cycles, it causes the pressure to appear artificially higher during the volume expansion step and thus causes the sample volume to appear smaller, resulting in a greater calculated skeletal density. The amount of physisorbed gas left to be desorbed becomes smaller as the cycle number progresses, so the degree of overestimation in skeletal density decreases as a function of cycle number until all physisorbed species have been purged at which point the skeletal density reaches the equilibrium value.
For the nonactivated samples, the samples are already in equilibrium with moisture and other potentially viscous species (e.g., residual solvents or organic compounds during synthesis or sample preparation) so that it is possible that these species are being purged out very slowly (presumably for over more than a few hours) in low amounts for all measurement cycles, with each cycle taking ≈ (3 to 5) min, which explains the flat shape of the kinetic plot. The standard deviation in skeletal density is ≤ 0.005 g/cm3 over 50 cycles. Given that the shape of the kinetic plots for the activated and nonactivated samples can be generalized for all samples, it can serve as an indicator of whether the sample has been properly activated.
IIb. Skeletal Density Data
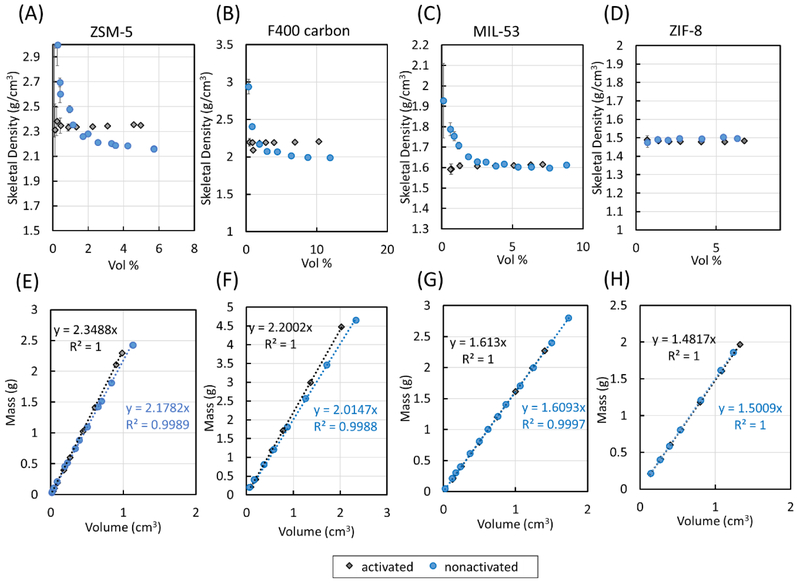
In the plots of skeletal density vs percent fill volume for the porous samples, each data point is the average value from measurement cycles 11 through #0 of the kinetic data to ensure only equilibrium values are mainly used (i.e., the values from one cycle to the next should be nearly consistent) (see Figure 4C). The same behavior as that for Si was observed in the data for activated ZSM-5, in which the measured skeletal density values began to converge at higher sample percent fill volume (see Figure 5A). As shown in Figure 5E, the slope of the linear fit to the data plotted as sample mass as a function of sample volume gave a calculated skeletal density of (2.349 ± 0.004) g/cm3.
Figure 5.
(A–D) Skeletal densities of ZSM-5, F400, MIL-53, and ZIF-8 measured using a He pycnometer with percent fill volume varied. (E–H) Skeletal densities of ZSM-5, F400, MIL-53, and ZIF-8 determined from a fitted linear regression.
The skeletal density of the nonactivated ZSM-5 also stabilized as the fill volume increased, but it has a lower skeletal density compared to the outgassed sample (Figure 5A,E). A skeletal density value of (2.178 ± 0.024) g/cm3 was calculated from the linear fit in the plot of sample mass vs sample volume for the non-activated sample (Figure 5E). That different degrees of sample activation can have an observable effect on the measured values for the skeletal density of a sample indicates that proper sample activation before skeletal density measurement is crucial to obtain the correct skeletal density value for the sample, in agreement with the recommendation made by ISO to ensure the sample is outgassed completely. 9
The behavior of the activated and nonactivated samples for measurements at low fill volume (<1 vol %) also differed. While the skeletal density of dry ZSM-5 was randomly over- or underestimated at low sample fill volume, it was systematically overestimated for the nonactivated sample.
The plots of skeletal density vs percent fill volume for both the activated and nonactivated forms of F400, MIL-53, and ZIF-8 are also shown in Figure 5B-D. Measurements of all activated samples provided skeletal density values that became more accurate with increasing percent fill volume (typically after 1–2 vol %). As was the case for non-activated ZSM-5, non-activated F400 and nonactivated MIL-53 also showed increasing skeletal density values as the percent fill volumes decreased. Nonactivated ZIF 8, however, exhibited the same behavior as the activated sample given that the sample had little physisorbed contaminants based on the 0.5% mass loss after activation.
The only difference between the non-activated samples and their activated counterparts is the presence of moisture or other physisorbed contaminants. The presence of moisture or other physisorbed species will affect (1) the behavior of the skeletal density as a function of percent fill volume at low percent fill volume and (2) the skeletal density at high percent fill volume in the plot of skeletal density vs percent fill volume.
The skeletal density of a nonactivated sample is greater at lower percent volume than that at higher percent volume because as water vapor or other viscous species are being purged out due to repeated helium probing, the measured equilibrium pressure will be higher than without them, causing the sample volume to appear smaller and thus the skeletal density to appear bigger. This effect is greater with a smaller sample size because the relative error in the sample volume is greater when the sample size is smaller. These explanations are consistent with the fact that nonactivated ZSM-5, F400, and MIL-53 all have downward curves at lower percent fill volume due to the significant amount of moisture or other contaminants in their nonactivated forms, whereas nonactivated ZIF-8, which has little moisture due to its highly hydrophobic nature, behaves similarly to its activated form.
The skeletal densities at high percent fill volume in the plots of skeletal density vs percent fill volume of the activated samples vs. their nonactivated counterparts also differed. Linear fits to the plots of sample mass as a function of sample volume as shown in Figure 5E-H provided calculated skeletal densities of (2.200 ± 0.007) g/cm3 for activated F400, (2.015 ± 0.033) g/cm3 for nonactivated F400, (1.613 ± 0.003) g/cm3 for activated MIL-53 (also known as MIL-53 ht), (1.609 ± 0.009) g/cm3 for nonactivated MIL-53 (also known as MIL-53 It), (1.482 ± 0.002) g/cm3 for activated ZIF-8, and (1.501 ± 0.004) g/cm3 for nonactivated ZIF-8 . The results are summarized in Table 1. As mentioned before, moisture and other contaminants can affect the sample mass and the sample volume, so it is expected that the skeletal densities of the nonactivated and activated samples may not be the same, which was what was observed for the majority of the samples. It also makes sense that the nonactivated samples have lower densities than the corresponding dry samples since the density of contaminants, such as water (≈1 g/cm3 at room temperature), atmospheric gases, and volatile organic compounds and solvents, which can be removed via outgassing, are typically lower than the densities of all the solids studied.2 Furthermore, the measured skeletal density values agree closely with computational estimates from this study.
CONCLUSION
In this article, instrumental parameters important to obtaining reliable skeletal density from the He pycnometer were established using a nonporous sample, Si. Measurements made under good thermostability using percent fill volumes that are as high as possible gave the most precise and accurate values of skeletal density. The effect of sample activation was also studied using several porous zeolitic, carbon, and hybrid inorganic–organic materials. By looking at the kinetic data, where skeletal density is plotted against measurement cycle, a properly activated porous sample can be distinguished from a nonactivated sample: activated samples show decreasing plots that eventually reach the equilibrium values as physisorbed gases (during transfer) are purged out through each cycle, whereas nonactivated samples typically show a flat line. This is true for all samples across the board. Results also demonstrated that the degree of sample activation could affect the measured skeletal density of the sample. In the low percent fill volume region, the behaviors of the plots of skeletal density vs. percent fill volume can be different for the activated and nonactivated sample if the percent mass losses after activation are significant, which was the case for ZSM-5, MIL-53, and F400, but not ZIF-8. In the presence of a significant amount of water vapor and other contaminants, the skeletal density is overestimated in the low percent volume region compared to values at high percent fill volume. These results indicated that helium pycnometry can provide information about the structures of materials; conversely, by knowing the structures of the materials and their percent mass losses, the behavior of nonactivated and activated samples in terms of density vs volume percent can be predicted.
Supplementary Material
ACKNOWLEDGEMENTS
H.G.T.N was supported by the NIST-NRC postdoctoral research associateship program. M.B. was supported by the NIST-SURF program. Instruments at the Facility for Adsorbent Characterization and Testing were funded by the Advanced Research Projects Agency-Energy (ARPA-E) through Interagency Agreement No. 1208-0000.
Footnotes
ASSOCIATED CONTENT
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.langmuir.8b03731.
Powder X-ray diffraction pattern for MIL-53 (PDF)
The authors declare no competing financial interest.
REFERENCES
- (1).Rouquerol F; Rouquerol J; Sing K Adsorption by Powers & Porous Solids: Principles, Methodology and Applications; Academic Press: London, UK, 1999. [Google Scholar]
- (2).Krokida MK; Maroulis ZB Quality change during drying of food materials In Drying Technology in Agriculture and Food Sciences; Mujumdar AS, Ed. Science Publishers Inc: Enfield, NH, 2000; pp 61–106. [Google Scholar]
- (3).Peyvandi A; Sbia LA; Soroushian P; Sobolev K Effect of the cementitious paste density on the performance efficiency of carbon nanofiber in concrete nanocomposite. Constr. Build. Mater 2013, 48, 265–269. [Google Scholar]
- (4).Amer N; Storey C Jr., Delatte NJ In Effect of Density on Mechanical Properties and Durability of Roller Compacted Concrete; Portland Cement Association R&D; Serial No. 2940, 2008. [Google Scholar]
- (5).Hancock BC; Colvin JT; Mullarney MP; Zinchuk AV The Relative Densities of Pharmaceutical Powders, Blends, Dry Granulations, and Immediate-Release Tablets. Pharm. Technol 2003, 27, 64–80. [Google Scholar]
- (6).ASTM International. D3766: Standard Terminology Relating to Catalysts and Catalysis. 2013. [Google Scholar]
- (7).Lowell S; Shields JE; Thomas MA; Thommes M Characterization of Porous Solids and Powders: Surface Area, Pore Size and Density; Springer (originally by Kluwer Academic Publishers): 2004. [Google Scholar]
- (8).Webb PA Volume and Density Determinations for Particle Technologists; 2001; pp 1–16. [Google Scholar]
- (9).International Organization of Standardization: ISO 12154. Determination of density by volumetric displacement — Skeleton density by gas pycnometry. Switzerland, 2014. [Google Scholar]
- (10).ASTM International. ASTM B923–16 Standard Test Method for Metal Powder Skeletal Density by Helium or Nitrogen Pycnometry. West Conshohocken, PA, 2016. [Google Scholar]
- (11).Matteucci S; Yampolskii Y; Freeman BD; Pinnau I, Transport of gases and vapors in glassy and rubbery polymers In Materials Science of Membranes for Gas and Vapor Separation, Yampolskii Y; Freeman BD; Pinnau I; John Wiley & Sons: 2006; pp. 1–47. [Google Scholar]
- (12).Keng EYH Air and Helium Pycnometer Powder Technol. 1969, 3, 179–180. [Google Scholar]
- (13).Loiseau T; Serre C; Huguenard C; Fink G; Taulelle F; Henry M; Bataille T; Férey G A Rationale for the Large Breathing of the Porous Aluminum Terephthalate (MIL-53) Upon Hydration. Chem. - Eur. J 2004, 10, 1373–1382. [DOI] [PubMed] [Google Scholar]
- (14).Espinal L; Wong-Ng W; Kaduk JA; Allen AJ; Snyder CR; Chiu C; Siderius DW; Li L; Cockayne E; Espinal AE; Suib SL Time-Dependent CO2 Sorption Hysteresis in a One-Dimensional Microporous Octahedral Molecular Sieve. J. Am. Chem. Soc 2012, 134, 7944–7951. [DOI] [PubMed] [Google Scholar]
- (15).Wong-Ng W; Culp JT; Chen YS; Zavalij P; Espinal L; Siderius DW; Allen AJ; Scheins S; Matranga C Improved synthesis and crystal structure of the flexible pillared layer porous coordination polymer: Ni(1,2-bis(4-pyridyl)ethylene)[Ni(CN)4]. CrystEngComm 2013, 15, 4684–4693. [Google Scholar]
- (16).Wong-Ng W; Kaduk JA; Siderius DL; Allen AL; Espinal L; Boyerinas BM; Levin I; Suchomel MR; Ilavsky J; Li L; Williamson I; Cockayne E; Wu H Reference diffraction patterns, microstructure, and pore-size distribution for the copper (II) benzene-1,3,5-tricarboxylate metal organic framework (Cu-BTC) compounds. Powder Diffr. 2015, 30, 2–13. [Google Scholar]
- (17).Frost H; Düren T; Snurr RQ Effects of Surface Area, Free Volume, and Heat of Adsorption on Hydrogen Uptake in Metal–Organic Frameworks. J. Phys. Chem. B 2006, 110, 9565–9570. [DOI] [PubMed] [Google Scholar]
- (18).Gelb LD; Gubbins KE Pore Size Distributions in Porous Glasses: A Computer Simulation Study. Langmuir 1999, 15, 305–308. [Google Scholar]
- (19).Wong-Ng W; Kaduk JA; Espinal L; Suchomel MR; Allen AJ; Wu H High-resolution synchrotron X-ray powder diffraction study of bis(2-methylimidazolyl)-zinc, C8H10N4Zn (ZIF-8). Powder Diffr. 2011, 26, 234–237. [Google Scholar]
- (20).Schmidt W; Wilczok U; Weidenthaler C; Medenbach O; Goddard R; Buth G; Cepak A Preparation and Morphology of Pyramidal MFI Single-Crystal Segments. J. Phys. Chem. B 2007, 111,13538–13543. [DOI] [PubMed] [Google Scholar]
- (21).Bondi A van der Waals Volumes and Radii. J. Phys. Chem 1964, 68, 441–451. [Google Scholar]
- (22).Mantina M; Chamberlin AC; Valero R; Cramer CJ; Truhlar DG Consistent van der Waals Radii for the Whole Main Group. J. Phys. Chem. A 2009, 773, 5806–5812. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (23).Rowland RS; Taylor R Intermolecular Nonbonded Contact Distances in Organic Crystal Structures: Comparison with Distances Expected from van der Waals Radii. J. Phys. Chem 1996, 100, 7384–7391. [Google Scholar]
- (24).Zhou W; Wu H; Hartman MR; Yildirim T Hydrogen and Methane Adsorption in Metal-Organic Frameworks: A High-Pressure Volumetric Study. J. Phys. Chem. C 2007, 111, 16131–16137. [Google Scholar]
- (25).National Institute of Standards and Technology Standard Reference Material 1841a: 200-g Silicon Density Standard. National Institute of Standards and Technology: Gaithersburg, MD, 1988. [Google Scholar]
- (26).Nguyen HGT; Espinal L; van Zee RD; Thommes M; Toman B; Hudson MSL; Mangano E; Brandani S; Broom DP; Benham MJ; Cychosz K; Bertier P; Yang F; Krooss BM; Siegelman RL; Hakuman M; Nakai K; Ebner AD; Erden L; Ritter JA; Moran A; Talu O; Huang Y; Walton KS; Billemont P; De Weireld G A reference high-pressure CO2 adsorption isotherm for ammonium ZSM-5 zeolite: results of an interlaboratory study. Adsorption 2018, 24, 531–539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (27).Turner S; Sieber JR; Vetter TW; Zeisler R; Marlow AF; Moreno-Ramirez MG; Davis ME; Kennedy GJ; Borghard WG; Yang S; Navrotsky A; Toby BH; Kelly JF; Fletcher RA; Windsor ES; Verkouteren JR; Leigh SD Characterization of chemical properties, unit cell parameters and particle size distribution of three zeolite reference materials: RM 8850 – zeolite Y, RM 8851 – zeolite A and RM 8852 – ammonium ZSM-5 zeolite. Microporous Mesoporous Mater. 2008, 107, 252–267. [Google Scholar]
- (28).Gensterblum Y; van Hemert P; Billemont P; Busch A; Charriere D; Li D; Krooss BM; De Weireld G; Prinz D; Wolf K European inter-laboratory comparison of high pressure CO2 sorption isotherms. I: Activated carbon. Carbon 2009, 47, 2958–2969. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.