Abstract
Single-entity electrochemistry aims to expand the toolkit for probing matter at the nanometer scale. Originally focused largely on electrochemically active systems, these methods are increasingly turning into versatile probes complementary to optical, electrical, or mechanical methods. Recent studies of the nucleation, structure, and stability of gas nanobubbles, which exploit electrochemistry at nanoelectrodes as generation and stabilization mechanisms, are prototypical examples. These measurements illustrate the interplay between advances in electrochemical methods and strategies for extracting microscopic information from the results.
In large part driven by the development of increasingly sophisticated nanoscale experimental tools, single-entity electrochemistry (SEE, reviewed recently)1 is redefining the boundaries of electroanalysis. Following in the footsteps of single-entity electrical, optical, and mechanical meso- and nanoscale experimental methods, SEE pursues two main aims. First, there is a need for direct observation and understanding of the properties of individual electroactive nanoparticles or macromolecules. Second, there is a desire to develop electrochemistry-based tools for studying systems that are not themselves necessarily electroactive in nature but can be interrogated via electrochemical means.
Single-entity assays offer several widely recognized benefits. Large numbers of measurements on single microscopic entities or time-resolved events contain more information than the mere ensemble average of these measurements, as is typically probed in macroscopic experiments. For fundamental research, single-entity assays enable researchers to probe variations within a population of analytes, detecting rare events and resolving microscopic dynamics.2 For applications, they form the basis for “digital” assays based on, for example, counting individual analytes instead of measuring an average response, which can help overcome drift in precision measurements.3 However, single-entity measurements are inherently stochastic. This randomness can have a static origin, for example, heterogeneities in a population, or can result from physically unavoidable intrinsic thermal and quantum fluctuations. Learning to identify, to measure, and to extract information from stochastic signals is thus at the heart of SEE.
In this issue of ACS Nano, Edwardset al. describe and analyze the electrochemically driven nucleation of individual nanobubbles.4 This work provides a fascinating snapshot of the state of the art for SEE methods and illustrates both the inherent experimental challenges as well as the more conceptual aspects of extracting meaningful microscopic information from stochastic data.
A Remarkable Experimental System
In electrochemical single-nanobubble generation, an approach introduced in 2013,5 a reduction or oxidation reaction generates gas molecules at the surface of a nanoelectrode. The dissolved gas near the surface of the electrode becomes highly supersaturated as a result, in turn driving the nucleation and rapid growth of a gas bubble. The bubble remains pinned to the electrode, partially blocking its surface and thus slowing down further gas generation. A dynamic equilibrium is eventually established in which gas generation at the partially blocked electrode is compensated for by diffusion away from the nanobubble, forming a stable nanometer-scale bubble that covers a large fraction of the electrode. The presence of the bubble is detectable as a decrease in the faradaic current at the electrode (ironically, interference from bubbles is an unwelcome phenomenon in most electrochemical experiments). This system is unique in the field of surface nanobubbles6−8 in that the mechanism for the formation of the bubble and its stability is fully understood and consistent with classical gas–liquid equilibrium and that bubbles can be created and annihilated at will and in real time via control of the electrode potential.
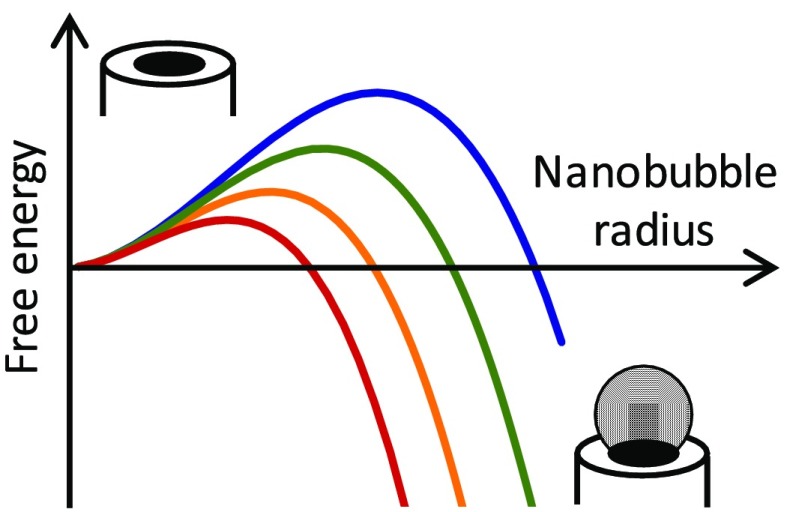
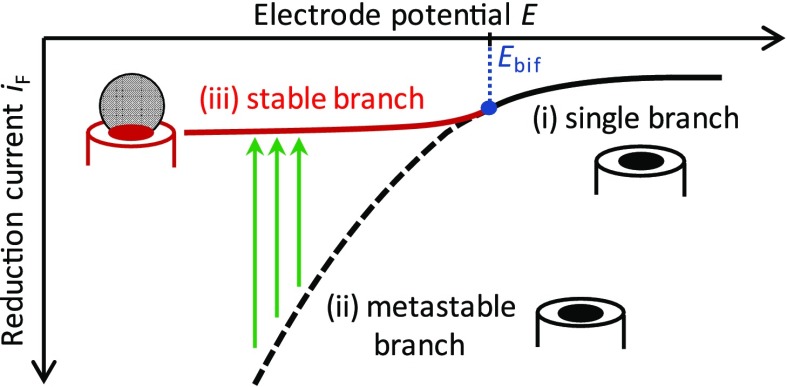
It is worth reflecting on the ingenuity of this approach and the careful balance of factors at play. Straightforwardly, the electrode must be sufficiently hydrophobic for the bubble to remain pinned to its surface (ensured by the choice of materials), and mass transport must be sufficiently rapid to establish a dynamical steady state with the bulk (ensured by the small electrode size). More subtly, stable bubbles can only exist if the rate at which gas molecules are electrochemically generated at the nanoelectrode is equal to the rate at which they diffuse into the bulk solution. Such a balance can be reproducibly achieved only because a negative feedback relation exists between the rate of mass transport of the electroactive substrate molecules to the electrode (which is proportional to the rate at which gas molecules are generated) and the size of the nanobubble (which determines the outward flux of gas molecules). This relationship is opposite to that in typical electrochemical measurements, where the mass transport rates of substrate and product either increase or decrease together upon changing the geometry of the electrode. Finally, the system exhibits a bifurcation between a metastable, nanobubble-free branch and a stable branch with a nanobubble at the electrode, as illustrated in Figure 1. To be experimentally observable, the transition from the metastable to the stable branch must occur at such a rate that an observable amount of time is spent in the metastable branch. Such fine-tuning is ensured because the bubble generation rate is a sensitive function of the electrode potential. The rate can thus be adjusted over several orders of magnitude until the experimentally practical time scale is attained.
Figure 1.
Bifurcation in the nanoelectrode–nanobubble system. Consider nanobubbles generated by a reduction reaction, for example, H+ reduction. The relation between the reduction current, iF, and the electrode potential, E, exhibits three distinct regimes: (i) For E higher than a critical bifurcation potential, Ebif (shown in blue), the formation of nanobubbles is thermodynamically unfavorable. In this potential range, no nanobubble is formed at the electrode, and the iF – E relation is single-valued (single branch, solid black line). (ii) At potentials E < Ebif, the stable dynamical state exhibits a nanobubble that blocks most of the electrode surface, thus limiting the magnitude of the reduction current (stable branch, solid red line). If nucleation of the nanobubble was instantaneous, the iF – E relation would transition smoothly between branches (i) and (ii). (iii) Nucleation of the nanobubble takes place at a finite rate. When the potential is switched or swept to E < Ebif, there is a time interval in which no nanobubble is present at the electrode. The reduction current is then larger than that in the stable branch at the same potential since the entire electrode surface participates in the reduction reaction (metastable branch, dashed black line). This results in a higher degree of gas supersaturation near the electrode, which in turns facilitates nucleation. Once nucleation occurs, the system switches from the metastable to the stable branch (green arrows), where it remains until the potential is increased to E > Ebif. In practice, the nanobubble nucleation rate is immeasurably slow near E = Ebif but increases rapidly with increasing current, thus permitting the experimental observation of nanobubbles.
A Stochastic Process
The feedback-generated stability of the electrode–bubble system permits characterizing individual, fully realized nanobubbles and yields detailed information about their geometry and stability.5,9−12 However, this concept in itself does not elucidate the process by which nanobubbles are created. The formation of a critical nucleus which can then grow to form the bubble is a process that occurs on time and length scales, yet smaller than the nanobubbles themselves; its direct observation, therefore, represents an additional formidable challenge. Interestingly, however, single-nanobubble measurements provide a unique window into the energetics of this process.
In a single-nanobubble assay, each observed nanobubble corresponds to a single random nucleation event which can, in principle, occur at any time. A nucleation rate J, therefore, cannot be deduced from a single measurement; for this, a statistically significant number of events must be averaged. The resulting experimental distribution of nucleation times contains additional information beyond the average rate, however.
In classical nucleation theory, the rate at which a critical nucleus is formed, J, takes the Arrhenius form:
| 1 |
where k is Boltzmann’s constant, T is the absolute temperature, J0 is the so-called attempt rate (an unknown constant), and ΔG⧧(c,θ) is the change in free energy to reach the transition state (a protobubble of critical size that then expands to form the nanobubble). For a given choice of materials, ΔG⧧ depends on the local concentration of gas molecules, c, and the geometry of the critical nucleus, here characterized by the (a priori unknown) contact angle θ as well as assorted materials parameters. In electrochemical generation at a nanoelectrode, the concentration of gas molecules at the surface of the electrode, c, is dictated by the rate at which these molecules are generated by the faradaic process. It is thus continuously tunable and experimentally measurable during an experiment, being simply proportional to the faradaic current, iF (that is, c ∝ iF). This means that the barrier height ΔG⧧ is a known function of a single unknown parameter, the contact angle θ. Rewriting this equation in a simple form in terms of the parameters of interest yields
| 2 |
where A is a (known) single constant that incorporates material parameters (surface tension, Henry’s constant, diffusion coefficient of gas molecules) and geometry (electrode radius), while Φ(θ) is a (known) function of the (unknown) contact angle θ.
Eq 2 shows why determining J in itself remains insufficient to shed light on the underlying microscopic processes: The expression for J contains two unknown parameters, the attempt rate J0 and the contact angle θ. Any assumed value of θ can be accommodated by a different choice of J0 and neither can be determined from a single measurement unless we make an assumption about the value of one of them. But θ, which encodes the geometry and size of the critical nucleus, represents the main information one can aim to extract from this experiment, while the attempt rate J0 is notoriously difficult to estimate a priori.
Extracting Quantitative Information
In order to determine the two independent parameters in eq 2, θ and J0, it is necessary to measure under two (or more) different experimental conditions so as obtain independent combinations of the parameters from which their separate values can be extracted. Eq 2 suggests at least two routes in which this can be achieved. First, the experiment could be repeated at two or more temperatures. A complication with this approach is that other properties, such as the diffusion coefficient of the gas molecules or the contact angle θ, can also depend on temperature, complicating the analysis. A far more practical option is to take advantage of the capability to tune the electrode potential in an electrochemical experiment and perform measurements at different values of the faradaic current, iF. This approach was successfully followed using controlled current (galvanostatic) experiments to measure the nucleation rate J at several fixed values of iF.13 A drawback, however, is that the measurement employs nonstandard experimental biasing schemes and protocols.
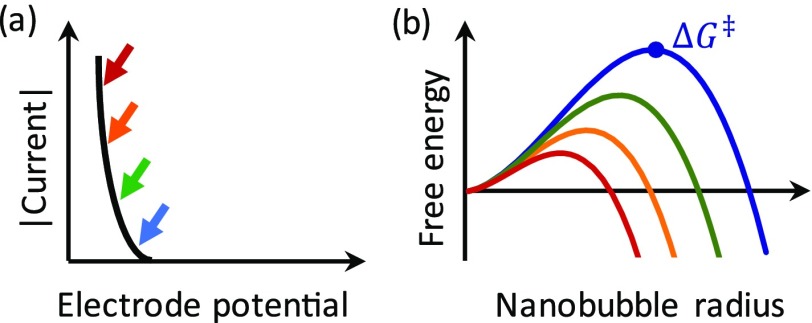
A variant on the fixed-current approach, explored by Edwards et al., is to vary the electrode potential continuously and to observe the resulting distribution of nucleation times.4 This approach reflects a philosophy akin to that of conventional cyclic voltammetry (CV), in which electron-transfer kinetics and mass transport are woven into a complex transient current response: Although often requiring substantial analysis to extract quantitative information, CV is among the most powerful and versatile tools in the arsenal of electrochemical methods. Here, the electrode potential is varied continuously at a rate ν (in V/s), and the distribution of nanobubble nucleation times is measured. Because the faradaic current changes continuously over the course of the measurement, a different barrier height is probed at each instant during the sweep (as sketched in Figure 2), and the resulting distribution of nucleation times reflects this distribution of barrier heights. How the events from multiple scans are distributed as a function of the electrode potential (or, equivalently, the faradaic current or the surface concentration), therefore, encodes information about how the shape and height of the barrier varies with the electrode potential. In fact, because in this particular case the transition-state energy is simply proportional to Φ(θ), the situation is particularly straightforward. The attempt rate can be directly extracted from the relative width of the distribution of nucleation times, following which the barrier and correspondingly value of θ can be deduced from the absolute nucleation rate.
Figure 2.
(a) The concentration of gas molecules at the electrode is proportional to the faradaic current, which is controlled by the electrode potential. (b) The height of the free energy barrier for nanobubble nucleation, θG⧧, depends on gas concentration and can, therefore, be tuned via the electrode potential (colors correspond to arrows in (a)).
A disadvantage of this approach is that theoretical analysis is required to translate the distribution of events into a free energy landscape (and hence into the parameters J0 and θ). This procedure is not necessarily transparent upon first approach (nor is the shape of a cyclic voltammogram!). It should, however, be appreciated that the factors that enter the calculation (nucleation model, assumptions about geometry, etc.) are identical to those that enter the (conceptually more straightforward) constant current approach13 and that, given the final equations,4 applying them to the reduction of experimental data is of comparable complexity in the two approaches. In return, one reaps the significant benefits of being able to carry out nanoscale nucleation experiments using the widely accessible workhorse of electrochemistry, CV. For similar usability reasons, the approach of continuously sweeping the driving force for extracting nucleation rates has already been adopted in a variety of experimental systems ranging from superconducting flux qubits14 to single-molecule biophysics, where it is known as dynamic force spectroscopy.15,16
Structural Disorder
The stochasticity discussed above has a fundamental origin, being driven by the thermodynamic energy fluctuations of a nanoscale system in thermal equilibrium with a heat reservoir (constant temperature). A related example is particle number fluctuations in systems in diffusive equilibrium (constant chemical potential), which can be observed in electrochemical nanodevices.17 In many SEE experiments, however, disorder often has a somewhat more prosaic cause: Matter tends to be rough on the atomic scale, and our ability to synthesize systems with atomic precision remains limited. Hence, investigations into the properties of, for example, textured electrodes or single catalytic nanoparticles inherently deal with distributions of properties across a population. This circumstance is nicely illustrated by recent results in so-called impact electrochemistry of nanoparticles18,19 and scanning electrochemical microscopy.20 It is also reflected in Edwards et al.:4 Although the overall nanobubble nucleation and stabilization behavior is robust, fluctuations in the microscopic parameters J0 and θ, both gradual and abrupt, occur over the course of the measurements. These changes reflect the evolution of quenched disorder in the structure of the electrode. This behavior is reminiscent of studies of noise caused by electrode corrosion,21 but here on the smallest relevant microscopic scale.
Outlook
Electrochemically driven nanobubble nucleation is a prototypical example of the possibilities offered by electrochemistry for studying single-entity, nanoscale experimental systems. The redox reaction acts as a driving force for nanobubble generation, provides a feedback mechanism by which the nanobubble is stabilized, and enables monitoring of the process with subms time resolution. Statistical analysis of the time evolution of individual events enables researchers to extract details of the underlying microscopic dynamics in a way analogous to, for example, single-molecule biophysical experiments based on optical or force-based techniques.
A potentially interesting future direction for this system concerns the dynamical equilibrium that exists after bubble formation. Once steady state is achieved, a nanobubble covers the bulk of the electrode, with only a ring with a width of order ca. 1 nm exposed to drive the residual electrochemical reaction that sustains the bubble. In this regime, any growth or shrinking of the bubble translates into a sizable change in the measured faradaic current. This susceptibility could represent a sensitive probe of the dynamics of the three-phase boundary between an electrode, an electrolyte, and a gas.
Acknowledgments
S.G.L. is grateful for past and ongoing discussions with the SEE community, in particular H. S. White, M. Zhang, P. S. Singh, and the SENTINEL consortium. S.G.L. also thanks the Tennant Corporation for general financial support.
The author declares no competing financial interest.
References
- Baker L. A. Perspective and Prospectus on Single-Entity Electrochemistry. J. Am. Chem. Soc. 2018, 140 (46), 15549–15559. 10.1021/jacs.8b09747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walter N. G.; Huang C.-Y.; Manzo A. J.; Sobhy M. A. Do-it-yourself guide: how to use the modern single-molecule toolkit. Nat. Methods 2008, 5 (6), 475–489. 10.1038/nmeth.1215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gooding J. J.; Gaus K. Single-Molecule Sensors: Challenges and Opportunities for Quantitative Analysis. Angew. Chem., Int. Ed. 2016, 55 (38), 11354–11366. 10.1002/anie.201600495. [DOI] [PubMed] [Google Scholar]
- Edwards M. A.; White H. S.; Ren H.. Voltammetric Determination of the Stochastic Formation Rate and Geometry of Individual H2, N2, and O2 Bubble Nuclei. ACS Nano 2019. 10.1021/acsnano.9b01015 [DOI] [PubMed] [Google Scholar]
- Luo L.; White H. S. Electrogeneration of Single Nanobubbles at Sub-50-nm-Radius Platinum Nanodisk Electrodes. Langmuir 2013, 29 (35), 11169–11175. 10.1021/la402496z. [DOI] [PubMed] [Google Scholar]
- Alheshibri M.; Qian J.; Jehannin M.; Craig V. S. J. A History of Nanobubbles. Langmuir 2016, 32 (43), 11086–11100. 10.1021/acs.langmuir.6b02489. [DOI] [PubMed] [Google Scholar]
- Lohse D.; Zhang X. H. Surface nanobubbles and nanodroplets. Rev. Mod. Phys. 2015, 87 (3), 981–1035. 10.1103/RevModPhys.87.981. [DOI] [Google Scholar]
- Sun Y.; Xie G.; Peng Y.; Xia W.; Sha J. Stability theories of nanobubbles at solid–liquid interface: A review. Colloids Surf., A 2016, 495, 176–186. 10.1016/j.colsurfa.2016.01.050. [DOI] [Google Scholar]
- Chen Q.; Luo L.; Faraji H.; Feldberg S. W.; White H. S. Electrochemical Measurements of Single H2 Nanobubble Nucleation and Stability at Pt Nanoelectrodes. J. Phys. Chem. Lett. 2014, 5 (20), 3539–3544. 10.1021/jz501898r. [DOI] [PubMed] [Google Scholar]
- Ren H.; German S. R.; Edwards M. A.; Chen Q.; White H. S. Electrochemical Generation of Individual O2 Nanobubbles via H2O2 Oxidation. J. Phys. Chem. Lett. 2017, 8 (11), 2450–2454. 10.1021/acs.jpclett.7b00882. [DOI] [PubMed] [Google Scholar]
- Chen Q.; Ranaweera R.; Luo L. Hydrogen Bubble Formation at Hydrogen-Insertion Electrodes. J. Phys. Chem. C 2018, 122 (27), 15421–15426. 10.1021/acs.jpcc.8b03770. [DOI] [Google Scholar]
- Chen Q.; Luo L. Correlation between Gas Bubble Formation and Hydrogen Evolution Reaction Kinetics at Nanoelectrodes. Langmuir 2018, 34 (15), 4554–4559. 10.1021/acs.langmuir.8b00435. [DOI] [PubMed] [Google Scholar]
- German S. R.; Edwards M. A.; Ren H.; White H. S. Critical Nuclei Size, Rate, and Activation Energy of H2 Gas Nucleation. J. Am. Chem. Soc. 2018, 140 (11), 4047–4053. 10.1021/jacs.7b13457. [DOI] [PubMed] [Google Scholar]
- van der Wal C. H.; ter Haar A. C. J.; Wilhelm F. K.; Schouten R. N.; Harmans C.; Orlando T. P.; Lloyd S.; Mooij J. E. Quantum superposition of macroscopic persistent-current states. Science 2000, 290 (5492), 773–777. 10.1126/science.290.5492.773. [DOI] [PubMed] [Google Scholar]
- Merkel R.; Nassoy P.; Leung A.; Ritchie K.; Evans E. Energy landscapes of receptor-ligand bonds explored with dynamic force spectroscopy. Nature 1999, 397 (6714), 50–53. 10.1038/16219. [DOI] [PubMed] [Google Scholar]
- Strunz T.; Oroszlan K.; Schafer R.; Guntherodt H. J. Dynamic force spectroscopy of single DNA molecules. Proc. Natl. Acad. Sci. U. S. A. 1999, 96 (20), 11277–11282. 10.1073/pnas.96.20.11277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zevenbergen M. A. G.; Krapf D.; Zuiddam M. R.; Lemay S. G. Mesoscopic concentration fluctuations in a fluidic nanocavity detected by redox cycling. Nano Lett. 2007, 7 (2), 384–388. 10.1021/nl062571g. [DOI] [PubMed] [Google Scholar]
- Kwon S. J.; Fan F.-R. F.; Bard A. J. Observing Iridium Oxide (IrOx) Single Nanoparticle Collisions at Ultramicroelectrodes. J. Am. Chem. Soc. 2010, 132 (38), 13165–13167. 10.1021/ja106054c. [DOI] [PubMed] [Google Scholar]
- Mirkin M. V.; Sun T.; Yu Y.; Zhou M. Electrochemistry at One Nanoparticle. Acc. Chem. Res. 2016, 49 (10), 2328–2335. 10.1021/acs.accounts.6b00294. [DOI] [PubMed] [Google Scholar]
- Bentley C. L.; Kang M.; Unwin P. R. Nanoscale Structure Dynamics within Electrocatalytic Materials. J. Am. Chem. Soc. 2017, 139 (46), 16813–16821. 10.1021/jacs.7b09355. [DOI] [PubMed] [Google Scholar]
- Williams D. E.; Westcott C.; Fleischmann M. Stocahstic models of pitting corrosion of stainless steels. 1. Modeling of the initiation and growth of pits at constant potential. J. Electrochem. Soc. 1985, 132 (8), 1796–1804. 10.1149/1.2114220. [DOI] [Google Scholar]